Baseline matching preprocessing of temperature perturbation infrared spectra

Abstract

An infrared spectrum baseline matching procedure that compensates for measurement drift and eliminates sloping baselines from sequentially acquired spectra is described. The theory underlying this procedure is provided and examples are given for three implementations based on infrared spectrum data sets containing at least 100 successively measured spectra. Consecutive spectra were acquired when the infrared beam contained: no sample, poly(styrene) powder, and a poly(styrene) film. The first two data sets consisted of 120 spectra and were used to characterize instrument reproducibility and identify short- and long-term measurement drifts. The 200 infrared spectra obtained while heating and then cooling a poly(styrene) film were subjected to baseline matching to reveal subtle temperature-dependent changes that are not evident when overlayed spectra are displayed. Baseline matching preprocessing is easily implemented on large numbers of similar spectra by using macro programming.

---

1. Introduction

Sample perturbation chemical analysis methods are used to elucidate and quantify the impacts of selected stimuli on sample properties.^1–6 Methods typically necessitate repeated measurements of the same sample while systematically varying the stimulus intensity. Because there is no sample-to-sample variability, measurement reproducibility is primarily determined by the analysis instrumentation and methodology.

Variable temperature infrared spectroscopy (VT-IR) is a perturbation analysis technique that employs temperature change as the stimulus and uses Fourier transform infrared (FTIR) spectroscopy for analysis.^2,7 Infrared spectra are measured at different sample temperatures and molecular vibration band variations that correlate with temperature changes are identified. The reproducibility of this methodology is compromised when infrared spectra exhibit random baseline offsets and slopes. These spectrum artifacts reduce the accuracy of infrared vibration band absorbance measurements. Preprocessing data manipulation techniques that improve baseline reproducibility can be implemented to minimize these errors and improve perturbation spectroscopy results.^8–15

The development of improved baseline correction methods continues to be an important research focus for spectroscopists. A wide variety of approaches have been proposed, ranging from simple polynomial function subtractions¹⁶ to sophisticated artificial intelligence techniques based on deep learning.¹⁷ Curve fitting methods require the selection of “baseline” anchor points and a polynomial function that can approximate the shape of the baseline to be removed.¹⁸ Multiscale analysis methods employ Fourier or Wavelet transformations to remove low frequency baseline variations while leaving higher frequency spectral information intact.¹⁰ Recently developed regression methods are often based on the popular penalty least squares (PLS) approach.¹⁹ Automatic baseline correction methods use the shape of the spectrum to remove offsets and slopes iteratively.^20–22 These correction methods attempt to remove broad spectrum baseline distortions while leaving the narrow peak and band shape information unchanged.

The baseline matching approach described here is an alternative to baseline correction. Instead of attempting to identify the baseline function and remove it from the spectrum, the baseline matching process attempts to make all the baselines in a series of spectra similar. When applied to VT-IR studies, errors in infrared band absorbance measurements may still exist but will be consistent from one spectrum to the next. Thus, although plots showing molecular vibration band intensity and/or wavenumber trends as a function of sample temperature may contain offsets, the shapes of these graphs are preserved.

2. Experimental

The poly(styrene) powder employed for studies described here was obtained from Sigma-Aldrich (St Louis, MO). The polymer had a molecular weight of 2500 and typical particle diameters of a few microns. To prepare the thin film used for the variable temperature infrared spectroscopy study, poly(styrene) particles were dissolved in chloroform to make a 10 mg mL⁻¹ solution. Two hundred micrograms of the polymer were deposited by solvent evaporation at the center of a 100 mesh stainless-steel button²³ sample holder. This was accomplished by using a 10 μL syringe to dispense small volumes while the button sample holder temperature was held at 100 °C. By using this approach, the polymer was distributed over a ca. 6 mm diameter region at the center of the stainless-steel base of the wire mesh. The film was annealed at 130 °C for an hour prior to the variable temperature infrared spectroscopy measurements.

A Mattson Instruments Inc. (Madison, WI) Nova Cygni 120 Fourier transform infrared (FTIR) spectrophotometer and a Harrick Scientific Inc. (Pleasantville, NY) praying mantis diffuse reflection accessory were used for infrared spectroscopy measurements. The FTIR employed a water-cooled infrared radiation source and liquid nitrogen cooled MCT detector with a signal cutoff below 650 cm⁻¹. Spectra were obtained over the 4000–700 cm⁻¹ range by signal averaging 64 scans at 8 cm⁻¹ resolution for both sample and background single beam measurements. Although all measurements were made at 8 cm⁻¹ resolution, interferogram zero filling prior to Fourier transformation yielded a 0.97 cm⁻¹ spectrum digitization interval. This spectral resolution was sufficient to accurately represent small changes in poly(styrene) absorbance bands and afforded greater spectral signal-to-noise ratio compared to higher resolution measurements.²⁴ The apparatus and methodologies employed for variable temperature infrared spectrum measurements are described in detail elsewhere.²⁵ Software employed for acquiring interferograms, recording sample temperatures, and performing baseline adjustments was written by using the Mattson Instruments macro programming language. The infrared spectrophotometer was purged with dry air to reduce artifacts caused by fluctuations in water vapor and carbon dioxide concentrations.

3. Theory

The FTIR is a single-beam infrared spectrophotometer. Therefore, it does not provide for real-time compensation of instrumental drift like double-beam instruments. Consequently, baseline fluctuations are commonly observed in measured spectra. Ideally, an FTIR transmittance spectrum (T(ν)_ideal) is calculated by dividing a sample single beam spectrum (S(ν)_sample) by a single beam spectrum obtained for a non-absorbing reference material (S(ν)_ref):

This ratio yields values below 1 at wavenumbers where radiation is absorbed by the sample and equal to 1 at wavenumbers where the sample does not absorb (i.e. baseline). In practice, baseline wavenumbers may have values greater or less than 1 due to single beam spectrum intensity fluctuations. These baseline offsets can be attributed to instrumental measurement variability. FTIR measurement signal-to-noise ratio and reproducibility depend on the instrument configuration and component quality. The stabilities of the infrared radiation source, moving mirror translation mechanism, and the detector largely determine the interferogram measurement repeatability. The stability of the electronics employed for amplification and digitization may also impact the measurement reproducibility. These instrument-based single beam measurement variations are included in a more realistic expression for transmittance:

where T(ν)_real denotes a typical transmittance spectrum and I(ν)_sample and I(ν)_ref arise from instrumental fluctuations during the sample and reference measurements, respectively. The corresponding absorbance spectrum (A(ν)_real) is obtained by:

A(ν)_real = −log₁₀T(ν)_real = −log₁₀T(ν)_ideal − log₁₀{I(ν)_sample/I(ν)_ref} (3)

If the −log₁₀{I(ν)_sample/I(ν)_ref} function is known, it can be removed from A(ν)_real to obtain a baseline corrected spectrum. The baseline correction methods included in commercial FTIR operating systems are provided to facilitate this process.

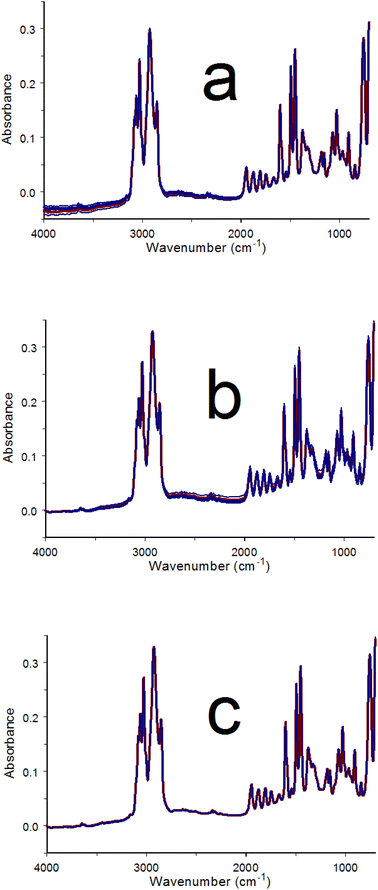
Successively acquired infrared spectrum measurements of the same sample that employ the same single beam reference spectrum (S(ν)_ref) should yield identical T(ν)_real results, except for baseline offsets and noise distributions. For example, Fig. 1a shows an overlay of two poly(styrene) infrared spectra computed by using the same reference single beam spectrum. These spectra overlap below 2000 cm⁻¹ but exhibit different baseline offsets at higher wavenumbers. The green curve in Fig. 1b was obtained by subtracting the black spectrum in Fig. 1a from the green spectrum. Because the measured sample was identical, the green line represents differences in the baselines and noise distributions of the subtracted spectra.

Fig. 1 (a) Poly(styrene) infrared spectra with different baselines. (b) The subtraction difference between the spectra in (a). (c) Overlay of the spectra in (a) after baseline matching the green spectrum.

Red lines in Fig. 1b represent three spectrum regions where baseline difference trends can be approximated by straight lines. The circles denote the wavenumbers representing the beginnings and ends of each red line segment. These lines span the: 4000 to 2400 cm⁻¹, 2400 to 1200 cm⁻¹, and 1200 to 700 cm⁻¹ spectral ranges. The black line in Fig. 1b shows the result of subtracting the three red lines from the green difference spectrum. The result is a horizontal line near zero exhibiting the same random noise fluctuations as the green plot. As shown in Fig. 1c, adding this black line to the black spectrum in Fig. 1a results in a new green spectrum that retains the random noise distribution of the original but now has nearly the same baseline offsets as the black spectrum. Although the Fig. 1c plot appears to be a single green spectrum, it is in fact an overlay of the green “baseline matched” spectrum on top of the Fig. 1a black spectrum. It should be noted that this technique does not correct baseline distortions. Rather, it provides a means for adjusting the baseline of one spectrum (the green line in Fig. 1a) to better match the baseline of another spectrum (the black line in Fig. 1a).

4. Results and discussion

The baseline matching process is ideally applied to successively acquired infrared spectra of the same sample. The first measured spectrum (A(ν)_real(1)) serves as a reference for all subsequently obtained spectra. Spectral subtractions are employed to calculate the differences between all successively acquired spectra. The first difference spectrum (A(ν)_real(2) − A(ν)_real(1)) represents intensity variations between the first and second acquired spectra at each wavenumber. The second difference spectrum contains differences between the second and third measured spectra (A(ν)_real(3) − A(ν)_real(2)). These calculations are repeated until differences between the last two spectra are obtained (A(ν)_real(n) − A(ν)_real(n − 1)). An overlay of all calculated difference spectra is displayed and wavenumber ranges are identified where intensity trends are approximately linear in all spectra. Next, a macro program is employed to subtract straight lines in these regions from the difference spectra. The lines employed for subtractions are calculated from each spectrum based on the selected starting and ending wavenumbers. An overlay of the adjusted difference spectra is used to verify that sloping baselines and offsets were adequately removed. If not, the straight-line trend identification and subtraction process can be repeated. Finally, a macro program is used to add the first adjusted difference spectrum to the initially acquired spectrum, which generates the “baseline matched” second spectrum. This process is repeated by adding subsequent adjusted difference spectra to the latest baseline matched spectrum until all spectra are regenerated. By using this approach, the initially measured spectrum is unchanged and all others are calculated from the previous baseline matched spectrum by adding back adjusted differences.

4.1 Instrument-derived baseline fluctuations

Spectrum-to-spectrum variations in the −log₁₀{I(ν)_sample/I(ν)_ref} function were characterized by successively measuring interferograms for a period of 60 min with an empty sample compartment. A total of 120 interferograms were acquired at 30 s intervals. These interferograms were Fourier transformed into single beam spectra and converted to transmittance (i.e. T(ν)_real) by dividing them by the same reference single beam spectrum, which was measured immediately before the first of the 120 interferogram data acquisitions. Because all single beam spectra were obtained without an absorbing sample in the infrared beam, absorbance spectra (i.e. A(ν)_real) consisted of sloping baselines near zero absorbance that were similar to the green plot in Fig. 1b. The greatest deviations from zero absorbance occurred near 4000 cm⁻¹. Fig. 2 shows the trend in 4000 cm⁻¹ absorbance for these spectra over the 60 min period. Overall, baseline absorbance at 4000 cm⁻¹ decreased by about 0.01 absorbance units during this period. In addition to this long-term drift, short-term negative and positive deviations were evident near spectrum numbers 65 and 100. Thus, both short- and long-term instrumental measurement fluctuations were detected for this FTIR.

Fig. 2 Absorbance at 4000 cm⁻¹ in baselines measured over a period of 60 min plotted as a function of acquired spectrum number.

Fig. 3a shows the first acquired absorbance baseline (red) along with overlays of baselines obtained at 10 min intervals. These spectra exhibit similarities. They contain varying offsets from zero that increase at higher wavenumbers. A small absorbance band near 2350 cm⁻¹ due to fluctuations in the purged sample compartment carbon dioxide concentration is present in these spectra. The fact that these peaks were consistently negative indicates that the carbon dioxide concentration was slowly decreasing over time.

Fig. 3 (a) Overlay of baselines recorded at 10 min intervals. (b) After subtracting absorbance offsets at 700 cm⁻¹ from the rest of the baseline. (c) After adjusting baseline differences by subtracting straight-line segments. (d) After baseline correcting the first spectrum followed by baseline matching the remaining spectra. Red plots denote the first measured baseline in the data set.

Fig. 3b shows the results of removing baseline offsets relative to a single baseline anchor point. This was accomplished by subtracting the absorbance at the lowest wavenumber in each spectrum (700 cm⁻¹) from all spectrum data points. This approach moved the baselines closer to zero and decreased the 4000 cm⁻¹ absorbance range only slightly. Fig. 3c shows the result of applying the baseline matching procedure. The initial baseline spectrum (red line in Fig. 3a) remained the same and the other baselines were adjusted to better match the first one. As a result, the absorbance range for the baselines was greatly diminished when compared to the plots shown in Fig. 3a and b. Fig. 3d shows the result of applying the baseline matching process after first using the FTIR data system software to manually “correct” the initial baseline so that it appeared flat and near zero absorbance. This resulted in a clustering like that shown in Fig. 3c, but with horizontal baselines close to zero absorbance over the entire wavenumber range. This illustrates the advantage of beginning the baseline matching procedure with an appropriately baseline-corrected spectrum.

4.2 Ambient temperature poly(styrene) spectrum baseline variations

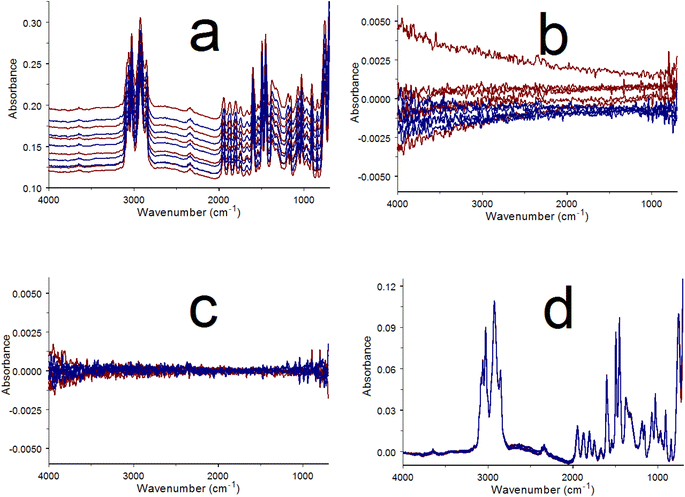
The baseline matching procedure was applied to a series of spectra acquired after loading an infrared absorbing material into the button sample holder. After acquiring a reference single beam spectrum by using the empty button, a small quantity of poly(styrene) powder was added to the button sample holder wire mesh. Infrared spectra (i.e. interferograms) were then acquired at 30 s intervals for 60 min. Fig. 4a shows an overlay of the first measured spectrum (red) along with six others obtained at 10 min intervals (blue). Consistent with the Fig. 3 results, the spectrum overlap was best below 2000 cm⁻¹ and baseline variations were greater at higher wavenumbers. Fig. 4b shows the results of single anchor point baseline offset removal by subtracting the absorbance at 4000 cm⁻¹ from the intensities at all wavenumbers. The convergence of spectrum baselines at high wavenumbers improved but overlap worsened below 2000 cm⁻¹. Fig. 4c shows the results of using the baseline matching procedure with the spectra shown in Fig. 4b. Note that spectrum overlap is consistently good at all wavenumbers and the baseline is zero at 4000 cm⁻¹.

Fig. 4 (a) Poly(styrene) powder infrared spectrum measured sequentially over a period of 60 min at ambient temperature. (b) After subtracting the 4000 cm⁻¹ absorbance at each wavenumber. (c) After applying the baseline matching process using the spectra in (b).

4.3 Variable temperature poly(styrene) spectrum variations

Fig. 5 shows results obtained by sample perturbation VT-IR. A poly(styrene) thin film was deposited on the metal base beneath the wire mesh of the button sample holder. This ensured good contact between the polymer and the heated surface and provided more accurate sample temperatures. The representative spectra shown in Fig. 5 exhibit bands with lower absorbance than those in Fig. 4 because the sample was present as a thin film instead of small particles. Temperature perturbation was applied by heating the film from 20 to 120 °C at a rate of 2 °C min⁻¹ and then immediately cooling it back to 20 °C at 2 °C min⁻¹. During this temperature program, two hundred infrared spectra were acquired at 30 s intervals. Each spectrum was measured over a 1 °C sample temperature increment. The selected spectra shown in Fig. 5a were acquired at 10 min (20 °C) intervals. Red spectra were obtained during sample heating whereas blue spectra were acquired while cooling. Generally, baseline offsets were larger when the sample temperature was higher. This trend is consistent with the characteristics of the Mercury–Cadmium–Telluride (MCT) infrared detector employed by the FTIR.²⁶ Because the poly(styrene) film was annealed prior to measuring the variable-temperature spectra, sample changes associated with the glass transition, which occurs near 100 °C, were minimized. Poly(styrene) melting occurs above 240 °C, therefore no other sample changes were anticipated between 20 and 120 °C. Fig. 5b shows difference spectra obtained by subtracting each of the spectra in Fig. 5a from the next acquired spectrum. The resulting difference spectrum baseline trends were similar to those observed for the successive ambient temperature measurements of the powder (Fig. 3). Fig. 5c shows the results of removing linear baseline segments from the Fig. 5b difference spectra. The baseline matched poly(styrene) spectra shown in Fig. 5d were obtained by adding back the adjusted differences shown in Fig. 5c. Spectral subtractions and absorbance band parameter temperature profiles that may be needed for identifying the effects of temperature on poly(styrene) molecular vibrations are more easily derived from the 200 baseline matched spectra than from those obtained while heating and cooling the sample (Fig. 5a).

Fig. 5 (a) Overlay of infrared spectra obtained while heating and then cooling a poly(styrene) film. (b) Differences between the spectra in (a) and the next acquired spectrum. (c) Baseline differences after subtracting straight-line segments. (d) Baseline matched infrared spectra.

The Fig. 5c baseline adjusted differences show no obvious temperature-dependent absorbance band features because they were masked by larger random noise fluctuations. However, absorbance band changes were larger when spectra measured at greater temperature intervals were subtracted. The results of subtracting the initial (i.e. 20 °C) poly(styrene) film spectrum from the baseline matched spectra obtained at 10 °C (5 min) increments between 30 and 120 °C are shown in Fig. 6a. Numerous sharp baseline deviations that grew with increasing temperature difference can be discerned. These features occurred at wavenumbers associated with specific poly(styrene) vibration bands. Relative to the baseline, absorbance increased at some wavenumbers and decreased at others. An absorbance decrease that occurred next to a comparable absorbance increase represented an intensity shift from the decreasing to the increasing absorbance wavenumber. Thus, the derivative-like features between 2000 and 1400 cm⁻¹ in Fig. 6a denote absorbance band shifts with temperature. The systematic absorbance variations revealed by the overlayed difference spectra were reversed when the sample was cooled, confirming that these spectrum changes were perturbation (i.e. temperature) dependent.²⁵

Fig. 6 (a) Overlay of difference spectra calculated by subtracting the first poly(styrene) film spectrum from spectra acquired at 10 °C (5 min) intervals. (b) Overlay of difference spectra calculated by subtracting the first poly(styrene) powder spectrum from spectra acquired at 5 min intervals at ambient temperature.

Fig. 6b shows an overlay of the ambient temperature poly(styrene) powder difference spectra computed by subtracting the initial spectrum from baseline matched spectra acquired at 5 min intervals. The baseline noise exhibited by the Fig. 6a and b overlay plots were comparable. Some poly(styrene) absorbance band changes are evident in Fig. 6b, but they are much smaller than those in Fig. 6a. In contrast to Fig. 6a, the Fig. 6b deviations are primarily found at wavenumbers associated with high absorbance vibration bands. These fluctuations are likely due to detector sensitivity non-linearities, which would be more severe when detector signals were lower.²⁷ This detector-dependent effect should also contribute to the Fig. 6a temperature-dependent variations. However, magnitudes of these sensitivity fluctuations would be less for the thin film measurements because maximum infrared band absorbances in measured spectra were about one-third of those in the powder sample spectra.

A comparison of poly(styrene) infrared spectrum properties characterizing functional group trends with temperature for C–H and C–C aromatic stretching vibrations in the powder spectra obtained over 60 min at ambient temperature and while heating and then cooling the thin layer sample are provided in Fig. 7. Blue plots represent changes in the integrated absorbance between 3150 and 2800 cm⁻¹, where the C–H stretching vibration bands occur. Red plots denote wavenumber shifts associated with the ca. 1600 cm⁻¹ band, which represents an aromatic ring C–C stretching vibration.

Fig. 7 Plots of the 3150–2800 cm⁻¹ integrated area (blue) and the ca. 1600 cm⁻¹ band shift (red) as a function of time derived from the baseline matched poly(styrene) powder (ambient) and poly(styrene) film infrared spectra. The black line denotes temperature measurements recorded while the poly(styrene) film spectra were acquired.

For the baseline matched ambient temperature poly(styrene) spectra, the integrated absorbance for the C–H stretching vibration bands decreased by about 1% between 5 and 20 min and then remained relatively constant. In contrast, the integrated absorbance rose by 7% in the baseline matched temperature perturbation spectra when the sample reached 120 °C. Cooling the sample back to 20 °C resulted in a gradual return to the initial band area, which confirmed that these changes were perturbation (i.e. temperature) dependent.

Fig. 6a contains several derivative-shaped features between 2000 and 1400 cm⁻¹. One of the largest baseline deviations occurs near 1600 cm⁻¹. The red plots in Fig. 7 represent peak maximum wavenumber shifts for this band in spectra obtained at ambient temperature and while heating and then cooling the sample. This band remained relatively constant over the entire 60 min ambient temperature period but exhibited red shifting (to lower wavenumber) when the polymer was heated. Like the C–H stretching vibration band region area, the C–C stretching band red shift was reversed when the sample cooled, confirming the perturbation dependence of this spectrum change.

This methodology differs from baseline correction and is only applicable to collections of spectra that contain few differences. Baseline matching will be difficult to implement when spectrum band shapes differ significantly. Like baseline correction methods based on polynomial subtractions, if the straight lines subtracted from spectra span a wavenumber range that is comparable to spectral feature widths, band shapes in that wavenumber range can be distorted. Short- and long-term measurement drifts in different FTIR instruments are likely to vary. Therefore, the straight line difference spectrum subtractions described here may not be applicable for all FTIR instruments.

5. Conclusions

Repeated FTIR measurements were made with and without an absorbing sample and while heating and then cooling a sample between 20 and 120 °C. In all cases, spectrum-to-spectrum baseline fluctuations were similar, indicating that they were associated with instrument measurement reproducibility rather than sample changes. The VT-IR raw spectra shown in Fig. 5a exhibit substantial temperature-dependent offsets superimposed on baselines with different shapes. After baseline matching, the overlayed spectra in Fig. 5d are almost identical. The subtle differences between these spectra shown in Fig. 6a would have been difficult to detect without the baseline matching process.

When short- and long-term instrument drift can be distinguished from sample spectrum changes, these effects can be removed by using the simple baseline matching process described here. The linear segment subtractions used here could be improved by using more complicated functions for sloping baseline removal. In fact, some automatic baseline correction approaches may work well for this purpose.

Results described here show that broad baseline variations can be distinguished from narrower sample absorbance band changes when slow VT-IR heating and cooling rates are employed. With faster temperature change rates, successive spectrum subtractions will reveal both instrument-derived broad baseline variations and narrower sample absorbance band changes, making baseline adjustments more difficult. Thus, care should be taken to ensure that sufficiently small stimuli increments are applied during perturbation spectroscopy measurements so that the baseline matching process described here can be employed more easily.

This technique may improve measurement sensitivity in other situations where small changes in sequentially measured infrared spectra must be detected. Other potential applications include: monitoring time-dependent changes in a flowing liquid or gas stream, assembly line quality control of manufactured product compositions, or the application of other sample perturbations, such as: pressure changes, exposure to high energy radiation (i.e. γ-rays, x-rays, etc.), time-controlled exposure of a sample to reactive substances, or characterizing the long-term stability of a sample under static environmental conditions.

Data availability

Data is not archived but can be provided by the author.

Conflicts of interest

The author declares that there is no conflict of interest.

References

1. Z. Y. Zhang, M. Sha and H. Y. Wang, J. Raman Spectrosc., 2017, 48, 1111–1115.
2. H. F. Noneman and R. L. White, Minerals, 2024, 14, 624.
3. I. Noda, J. Mol. Struct., 2014, 1069, 23–49.
4. H. Shinzawa, K. Hashimoto, H. Sato, W. Kanematsu and I. Noda, J. Mol. Struct., 2014, 1069, 176–182.
5. R. M. Clegg and B. W. Maxfield, Rev. Sci. Instrum., 1976, 47, 1383–1393.
6. M. A. Fourati, C. Pellerin, C. G. Bazuin and R. E. Prudhomme, Polymer, 2013, 54, 730–736.
7. H. F. Noneman, M. E. Hollingsworth, J. Singh and R. L. White, Spectrochim. Acta, Part A, 2021, 247, 119113.
8. A. Gaigneaux, J. M. Ruysschaert and E. Goormaghtigh, Appl. Spectrosc., 2006, 60, 1022–1028.
9. F. Zhang, X. Tang, A. Tong, B. Wang, J. Wang, Y. Lv, C. Tang and J. Wang, Spectrosc. Lett., 2020, 53, 222–233.
10. L. Shao and P. R. Griffiths, Environ. Sci. Technol., 2007, 41, 7054–7059.
11. R. B. Horton, E. Duranty, M. McConico and F. Vogt, Appl. Spectrosc., 2011, 65, 442–453.
12. X. Shen, S. Ye, L. Xu, R. Hu, L. Jin, H. Xu, J. Liu and W. Liu, Appl. Opt., 2018, 57, 5794–5799.
13. H. J. Butler, B. R. Smith, R. Fritzsch, P. Radhakrishnan, D. S. Palmer and M. J. Baker, Analyst, 2018, 143, 6121–6134.
14. J. Peng, S. Peng, A. Jiang, J. Wei, C. Li and J. Tan, Anal. Chim. Acta, 2010, 683, 63–68.
15. F. Vogt, H. Steiner, K. Booksh and B. Mizaikoff, Appl. Spectrosc., 2004, 58, 683–692.
16. A. F. Ruckstuhl, M. P. Jacobson, R. W. Field and J. A. Dodd, J. Quant. Spectrosc. Radiat. Transfer, 2001, 68, 179–193.
17. Q. Jiao, X. Guo, M. Liu, L. Kong, M. Hui, L. Dong and Y. Zhao, Chemom. Intell. Lab. Syst., 2023, 235, 104779.
18. A. Koch and J. V. Weber, Appl. Spectrosc., 1998, 52, 970–973.
19. P. H. Eilers, Anal. Chem., 2003, 75, 3631–3636.
20. P. Zucchiatti, E. Mitri, S. Kenig, F. Bille, G. Kourousias, D. E. Bedolla and L. Vaccari, Anal. Chem., 2016, 88, 12090–12098.
21. A. D. Surowka, G. Birarda, M. Szczerbowska-Boruchowska, M. Cestelli-Guidi, A. Ziomber-Lisiak and L. Vaccari, Anal. Chim. Acta, 2020, 1103, 143–155.
22. A. Kuzmiakova, A. M. Dillner and S. Takahama, Atmos. Meas. Tech., 2016, 9, 2615–2631.
23. R. L. White, Anal. Chim. Acta, 2020, 1098, 110–116.
24. D. Maraoulaite and R. L. White, Am. Lab., 2018, 50, 14–17.
25. R. L. White, Anal. Methods, 2023, 15, 6706–6715.
26. R. Lin and R. L. White, Anal. Chem., 1994, 66, 2976–2980.
27. R. L. White, Talanta, 2023, 258, 124474.

---