Waterborne protozoan parasite detection using two-frequency impedance flow cytometry

Abstract

Waterborne parasitic protozoa are common causes of gastrointestinal diseases in both humans and farm animals, even with standardized water treatment in place. This creates a need for continuous water monitoring to detect the presence of these micron-sized parasites in water sources to prevent potential outbreaks. This paper proposes a monitoring system consisting of a microfluidic channel embedded with micromachined microelectrodes to detect and evaluate protozoa at the individual (oo)cyst level in flowing water. To identify and discriminate between the (oo)cysts of Giardia and Cryptosporidium, two frequency-based impedance flow cytometry (IFC) is employed, where a high and a low frequency are applied to obtain the amplitude and phase variances of the samples. Using combination of amplitude and phase measurements at tested frequencies, the parasites and non-parasites (polystyrene) are identified, and a high degree of discrimination is also demonstrated for samples suspended in both DI water and filtered creek water. While impedance flow cytometry was utilized to detect waterborne protozoa, the system proposed in this paper is distinctive in the following ways. It employs differential coplanar electrodes instead of parallel electrodes to achieve a limit detection of <0.1% volume ratio between volume of a single (oo)cyst and the volume the electrodes occupy in the channel. It applies a low and high frequency simultaneously to obtain amplitude ratios to characterize sample populations instead of amplitude vs. phase at a single fixed frequency, potentially improving sample discrimination. This work also demonstrates detection and identification of protozoan (oo)cysts suspended in a natural water source, instead of in purified water, showing the proposed system's potential as a continuous waterborne parasitic protozoa monitoring system in a real environment.

---

1. Introduction

The transmission of waterborne parasitic protozoa remains a frequent global health risk in developing countries with inadequate water sanitation facilities and developed nations with well-established water treatment regulations and technologies. For instance, at least 381 outbreaks due to waterborne protozoan parasites were reported in the 4 year-period between 2011 and 2016, about 41% cases in North America, 9% cases in Europe.¹ These outbreaks not only led to terrible gastrointestinal sickness (e.g. diarrhea) but also resulted in substantial economic burdens, with costs amounting to tens of millions for managing the public crisis.^2,3 Amongst several groups of protozoa transmitting diarrheal diseases in humans (e.g., Amoeba), Giardia and Cryptosporidium are the most prevalent, responsible for approximately 1.2 million cases of giardiasis and 748 000 cases of cryptosporidiosis annually in the United States.^4,5 One probable reason for their widespread infection is their resistance to chlorination in their (oo)cyst forms, when chlorination is a very standard disinfection step in treating various water sources, including city drinking water.^6,7 Without upgrading city water treatment facilities with modern technologies (e.g., ozonation, microfiltration), regular water surveillance is the next essential step as a preventive measure to reduce the occurrences of major outbreaks.

The detection of Giardia cysts and Cryptosporidium oocysts in environmental water samples is primarily through visual examination under optical microscopes, and optical flow cytometry.⁸ Both methods often require some sort of sample pre-treatment, such as filtration and centrifugation to concentrate the samples for testing. While sample staining with fluorescent labels is prerequisite for optical flow cytometry since it utilizes fluorescent activated cell sorting (FACS),⁹ histochemical staining can be used to increase the measure of sample viability under a microscope. In addition, both detection methods require specialized personnel and equipment to perform effectively, adding up cost and labor.

Impedance flow cytometry (IFC) is an impedance-based flow cytometry method to detect and characterize single cells, by flowing them through microfluidic channels embedded with electrodes that are stimulated with ac voltages.^10,11 Impedance signal pulses are generated corresponding to cell passages across the electrodes. While cell enumeration is easily accomplished by counting the instances of signal pulses, the cells are characterized based on measured impedimetric responses (i.e. amplitude and phase) at frequencies ranging from kHz up to MHz. Microfabricated IFC-based devices have demonstrated the detection and differentiation of a plethora collection of cells from human erythrocytes and leukocytes,^12–15 to various cancer cell lines,^16–19 boar sperm cells,²⁰ plant cells,²¹ and even bacteria.²² In particular, McGrath et al., have utilized an IFC system with two pairs of parallel-facing electrode configuration to detect the cysts and oocysts of three parasitic protozoan species, G. lamblia, C. parvum, and C. muris suspended in PBS buffer.²³ The differentiation between the three species and the various states of C. parvum were analyzed using impedance amplitude versus frequency data, spanning from 250 kHz to 18.3 MHz. The analysis was based on the dielectric theory of cells in suspension,²⁴ where cells exhibit distinct dielectric dispersions corresponding to their properties and structures within specific frequency ranges. For instance, impedance measured at low frequencies can be used to characterize cell size distribution, while that at high frequencies can be used to characterize cell membrane capacitance and cytoplasm conductivity.²³

In this work, the cysts and oocysts of two major parasitic protozoa, the G. lamblia, and C. parvum, are measured with a microfabricated IFC device. In contrast to previous work, two frequencies, a low and high frequency, are applied at the same time to achieve (oo)cyst detection and characterization. By applying two different frequencies, more comprehensive cyst properties can be obtained therefore potentially enabling discrimination between cyst populations. The electrode design consists of three parallel electrodes in a coplanar configuration for differential measurement. In addition to DI water buffer, filtered natural creek water near a major city is used to suspend the samples to examine the robustness of the two-frequency IFC system. Polystyrene microspheres are also measured as a noncellular sample.

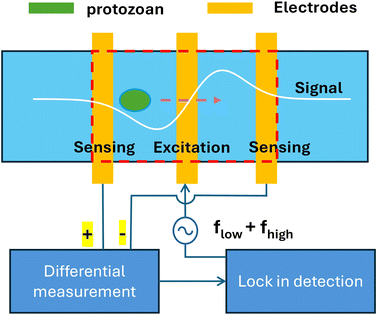
2. Working principle

The schematic view of the two-frequency IFC system for detecting waterborne protozoan parasitic (oo)cysts is shown in Fig. 1. To implement impedance flow cytometry, a conventional coplanar parallel electrode configuration is used.²⁵ An AC voltage excitation with a low and a high frequency is applied to the center electrodes while fluctuations in current are sensed at the two electrodes on the side. As an (oo)cyst traverses across the 1st pair of electrodes, a volume fraction of the buffer solution is displaced, leading to a change in the electrical property and, therefore, the impedance between the electrodes. Lock-in detection is then used to measure the impedance change vs. time in terms of amplitude and phase signals. Since there are two electrode pairs, differential measurement is made via subtracting the signals from the two pairs to create a time-of-flight measurement of the (oo)cyst as a double-peak signal. An example of a measured double-peak signal is shown in Fig. 3c. Magnitudes of the signal peaks (i.e., peak height) are analyzed in 2D domains, e.g., amplitude vs. phase, to associate with distinct species of parasites.

Fig. 1 Schematic view of a waterborne parasitic protozoa detection system implementing microfluidic impedance flow cytometry. Up to 2 frequencies are applied to the electrodes to examine the impedimetric response of the parasite samples at individual (oo)cyst level. The arrow indicates flow direction, while the red square indicates the sample detection zone, the curved line indicates measured time-of-flight signal for the protozoa.

The coplanar electrodes are relatively easy to fabricate compared to parallel-facing electrodes on either side of the walls defining the flow channel, at the expense of creating a vertical positional dependency such that the further away the sample is from the electrode surface, the weaker the signal strength.²⁶ However, it has the potential to improve the limit of detection by flowing the samples close to the electrodes to boost signal strength, compared to parallel facing electrodes inside the same channel cross-section. By taking the difference between the two electrode pairs, the signal-to-noise ratio (SNR) of the detector can be improved, allowing the detection of exceedingly small volume displacement. The lock-in amplifier is used to measure the transient impedimetric changes at desired frequencies while reducing various noises generated at other frequencies. While the amplitude data (in volts) is proportional to the (oo)cysts impedance, equivalent circuit models can be used to obtain cell electrical properties if desired for extensive characterization.

Two frequencies are applied at the same time to characterize the (oo)cysts. For instance, while a low frequency is traditionally associated with the volume of the cell,^14,15 a high frequency can be used to probe cell electrical properties such as membrane capacitance and cytoplasm conductivity.^18,27 Therefore, by applying a low and a high frequency at the same time, more than one (oo)cyst properties can be obtained at a single test. In addition, the ratio of the amplitude at low and high frequencies, known as opacity, is insensitive to the cell's vertical position and size variations while still reflecting cell properties.²⁸ Therefore, the differences in cell properties could be observed through the differences in amplitude ratio values. By applying two frequencies, the (oo)cysts could be compared with the variance (e.g., height) in measurement data being minimized for a sample population. More than two frequencies could be applied at the same time to increase the dimensions in data analysis when the capacity of the measurement instrument is increased.

3. Methods

3.1 Device fabrication

Waterborne parasitic protozoa detection devices utilizing two-frequency IFC consisted of (1) a PDMS slab with a straight microfluidic flow channel bonded to (2) a microscope glass slide patterned with parallel microelectrodes mentioned above. To fabricate the PDMS flow channel, conventional microfluidic soft lithography was employed by pouring and curing PDMS (10 : 1 silicone polymer : curing agent) on a channel mold – a 4-inch silicon wafer patterned with SU8 photoresist channel structures.²⁹ The cured PDMS channels were peeled off and cut to sizes, while the fluid connections were made using a biopsy punch to create vertical holes, which were pressure-fitted with Tygon tubing. Next, parallel microelectrodes were patterned onto glass slides using sputtering, photolithography, and lift-off processes. After an oxygen plasma surface treatment inside a plasma cleaner, the channel was manually aligned to the electrodes and bonded to the glass slide. The device fabrication process flow is shown in Fig. 2.

Fig. 2 (a) Illustration of a 7-step device fabrication process flow. The device is a PDMS microfluidic channel with integrated microelectrodes consisting of 3 parallel trace electrodes near the outlet. (b) Picture of fabricated device consisting of a straight PDMS flow channel (white line) embedded with 3 parallel microelectrodes for particle/cell detection.

3.2 Sample preparation

Protozoan (single-celled) parasite samples including G. lamblia cysts and C. parvum oocysts were purchased (Waterborne Inc, LA, USA). The samples (nonviable, 5–10% formalin and 0.01% tween in PBS) were directly diluted with DI water at 1 : 6 volume ratio for minimal preparation. The dilution increased the chance of measured events being a single (oo)cyst, while lowering the buffer conductivity. As a comparison to the parasite samples, 10 μm polystyrene microspheres (invitrogen) were also prepared by diluting with DI water at the same volume ratio. Samples were injected into the device using a syringe pump at 1 μL min⁻¹ flow rate.

To obtain a representative water sample, running creek water near a major city (Red Butte Creek, Salt Lake City, UT, USA) was collected. The creek water was filtered through a coarse paper filter with approximately 25 μm particle retention to remove large particulates and debris that could obstruct the channel. The filtered water was injected into the device to establish a signal baseline before spiking the parasite samples into the water for measurement. In addition, a mixture of G. lamblia cysts and C. parvum oocysts at equal concentrations were prepared by mixing 1 part of each sample together. The resulting mixture in PBS was diluted with filtered creek water at volume ratios ranging from 1 : 3 to 1 : 9. While the direct dilution prevented (oo)cysts from rupturing compared to conventional cell extraction methods (e.g. centrifugation), the dilution also altered the buffer solution conductivity, which was reflected in the measurement data values.

3.3 Data acquisition

For data acquisition, a custom circuit bord from our previous study³⁰ was used for differential measurement from the two electrode pairs. The circuit board consisted of two trans-impedance amplifiers (OPA656U) connected to two sensing electrodes. The two amplifiers were connected to an instrumentation amplifier (AD8429) to obtain a differential voltage signal from the electrodes. The amplifier gains were controlled by gain resistors. Lastly, an active low-pass filter with a cut-off frequency of 10 MHz was added to the board output. With the differential voltage signal as input, a lock-in amplifier (Zurich UHFLI) was utilized to obtain transient amplitude data in volts proportional to sample impedance magnitude and phase data in degrees. Both data were in the form of double peaks, as discussed earlier, indicating the time-of-flight impedance change between electrodes due to sample passages. The lock-in amplifier also provided sinusoidal voltage excitations at 300 mV at a low and a high frequency simultaneously to the center electrode.

3.4 Data analysis

Custom MATLAB algorithms were used for data analysis. First, baselines of the raw data (amplitude/phase vs. time) were corrected by subtracting the data from their moving averages. A sliding window was applied to the corrected data to find the characteristic double peaks sequentially. The size of the window was estimated from the data sampling rate and sample velocity, while the peak threshold was set according to the observed noise floor. Furthermore, the peaks at the same or different excitation frequencies were grouped together (e.g. [amplitude, phase]) if the time stamps of the maxima were within 5 data points or identical. All raw data were processed with the same parameters with the exception of peak threshold (different for amplitude and phase). Finally, the peak magnitudes of the amplitude data and phase data were extracted to present the sample amplitudes and phases and analyzed in 2D domains to differentiate between samples.

4. Results and discussion

A fabricated device for waterborne parasite detection is shown in Fig. 2b. The PDMS microfluidic channel was 41 μm in height and 60 μm in width, while the electrodes were Au electrodes, about 15 μm in measured width, 300 nm in thickness and 22 μm distance between electrodes.

Fig. 3a shows the microscope image of a Giardia lamblia cyst and a Cryptosporidium parvum oocyst near the parallel microelectrodes in the upper half of a PDMS flow channel. Fig. 3b shows a section of the measured amplitude data for the C. parvum sample with the x-axis indicating time and y-axis voltage, where the baseline was corrected to 0 V. Each double-peak voltage signal indicates a change in the impedance at that excitation frequency (500 kHz) as sample passes across the electrode pairs. From visual inspection with a microscope camera at a low sample flow rate, the detection of a single C. parvum and G. lamblia (oo)cyst was confirmed in real-time. Assuming the C. parvum oocyst was at most 4 μm in size, the device was capable of detecting ∼0.1% volume displacement of the volume inside the detection zone. A total of 36 double peaks are observed, corresponding to a 9 Hz parasite detection rate or 540 oocysts per minute. This detection rate can be increased with the flow rate at the expense of a lower signal-to-noise ratio since particles tend to move away from the electrodes at higher flow rates.

Fig. 3 (a) Microscope image of the coplanar parallel microelectrodes with a Giardia lamblia cyst and a Cryptosporidium parvum oocysts inside the PDMS flow channel. (b) 4 seconds of measured amplitude voltage data for C. parvum showing multiple double peaks at 0 V baseline. (c) Double peak voltage signals measured at 500 kHz and 4 MHz, representing a single event from (b), (d) the double peak voltage signal at 4 MHz from (c), and the fitted double peak signal using two normal distributions with opposite signs.

For high throughput operation at higher flow rates, the sampling frequency of the measurement instrument must be increased to match the reduced transit time of cells across the electrodes. Conversely, at high cell concentrations, the inter-electrode distance may need to be reduced to match the reduced space between consecutive cells, improving the likelihood that only one cell is present between the electrodes at any given time for maximum detection sensitivity. Although sheath flow modulation could optimize cell throughput and maintain detection sensitivity, our current microfluidic channel design does not include this functionality.

An example of double peak voltage signals at two frequencies is shown in Fig. 3c. Typically, for both the amplitude and phase measurements, the double peaks measured at 500 kHz exhibit a similar shape, but different maxima and minima (i.e. peak magnitude) compared to the peaks measured at 4 MHz, while the location of the peaks were on top of each other in the time axis. Alternatively, the peak magnitude can be obtained by fitting a normal distribution to the peak. With a sampling rate of about 1.7 kHz, there were enough data points such that the fitted peak produced a similar magnitude to the original peak, as shown in Fig. 3d. The difference between the fitted and the original peak height here was less than 400 μV close to the observed noise floor. The time duration between the fitted peaks was 7.6 ms, corresponding to a 5.3 mm s⁻¹ velocity.

Though the magnitudes of the left and right peaks are identical in theory, a difference due to impedance mismatch was observed across the data set, with the largest difference between the left and right peak magnitudes in the measured phase data. For subsequent analysis, the average of the two peak magnitudes was used when presenting sample amplitude and phase values.

Fig. 4 represents the amplitudes and phases (double peak average magnitudes) measured at a low (500 kHz) and a high (4 MHz) excitation frequency simultaneously for the samples diluted with DI water. Fig. 4a scatter plot shows the amplitude vs. phase at 500 kHz for the G. lamblia C. parvum (oo)cysts and polystyrene microspheres (10 μm Ø) with n = 462, 893, 637, respectively. The data points [amplitude, phase] aggregate in distinctive groups, showing clear separations with no visual overlap. The C. parvum has the largest phase value at 15.15 ± 6.13 degree and the smallest amplitude value at 2.78 ± 0.79 mV, while the polystyrene has the smallest phase value at 1.21 ± 0.39, and the largest amplitude value at 12.25 ± 4.09 mV. The G. lamblia is in between with a phase value of 5.32 ± 2.332 degree and an amplitude value of 9.76 ± 3.41 mV. The amplitude at this frequency seems to correlate well with sample size distribution consistent with literature,¹⁰ where low frequency (<10 MHz) provides information regarding cell size in impedance flow cytometry.

Fig. 4 Amplitude and phase measurements (double peak average magnitudes) for the G. lamblia, C. parvum (oo)cysts and polystyrene microspheres diluted in DI water at two excitation frequencies. (A) The amplitude vs. phase magnitudes at 500 kHz for the 3 samples. The dashed black lines are linear fits to the data points, showing separations. (B) Amplitude vs. phase magnitudes at 4 MHz for the 3 samples. (c and d) Bar plots of the amplitude over phase magnitudes from (a) and (b) respectively.

At 4 MHz (Fig. 4b), the separations between sample events are still visible, but with some overlap between the G. lamblia (n = 504) and C. parvum (n = 1084). The overlap could be a result of similar membrane capacitance, which is typically observed near this frequency for biological cells.²³ On the other hand, the polystyrene (n = 740) is still clearly separated from the rest, hinting that better discrimination between cells and nonbiological particles could be achieved in high-frequency ranges (MHz) using the amplitude and phase scatter plot. Going from low to high frequency, the phase of the C. parvum is 0.419 ± 0.13 degree, near 97% increase in mean, while the amplitude of C. parvum is 3.84 ± 1.44 mV, only a 38% increase in value. A change in both amplitude and phase also occurs in G. lamblia as well as the polystyrene, where the polystyrene has the largest decrease (61%) in the amplitude, while G. lamblia has the largest decrease (77%) in the phase. The increased sample events (n) suggest a better signal-to-noise ratio for detection at high excitation frequencies.

Linear regression lines are fitted as shown in the dashed line in Fig. 4a and b. Going from high (4 MHz) to low (500 kHz), an increased linearity is found across all samples, as evidenced by the R² values ranging from 0.68 to 0.99. The spread of amplitude or phase could be an indicator of size variations within the sample populations. However, considering the vertical positional effects on the signal strength, the amplitude alone may not be adequate to determine the size distribution within the same population. The correction of sample height variance in measured signal amplitudes with coplanar electrodes can be done by introducing a correlating parameter.²⁶

Due to the high linearity of the [amplitude, phase] data, a parameter that is the ratio of the amplitude over phase (inverse of the regression line slope) may be used to discriminate between the samples, indicating sample types. Fig. 4c and d are bar plots of this ratio. Two sample t-tests were performed across sample pairs, resulting in a p-value ≈of 0 for a greater than 99.9% confidence level, even for the G. lamblia and C. parvum in Fig. 4d. This result has shown that the tested samples can be discriminated against each other using conventional impedance flow cytometry with a single excitation frequency, potentially a result of decreased heterogeneity due to protein crosslinking in formalin. However, with the increasing complexity of the sample matrix (e.g., cell viability, buffer conductivity), the data overlap, such as that in Fig. 4b, could be significantly large for less accurate discrimination.

To examine the combined impedimetric responses of samples to the excitation frequencies, first, amplitudes from Fig. 4 were gathered in the scatter plot shown in Fig. 5a with the x-axis indicating the amplitudes at 500 kHz and the y-axis at 4 MHz. No data overlap was observed between the microspheres and (oo)cysts, while small overlap was observed between the (oo)cysts. The amplitudes at both frequencies correlate well with cell volume such that the C. parvum oocysts (n = 763) have the smallest amplitude distribution across the x and y-axis, while the G. lamblia cysts (n = 510) and polystyrene microspheres (n = 668) have comparable amplitude distributions. Linear regression lines were fitted to the data with R² = 0.97, 0.85, and 0.98 for the G. lamblia, C. parvum, and polystyrene, respectively. The slopes of the regression indicate the dominant amplitude, where the C. parvum produced larger amplitudes at 4 MHz, the polystyrene at 500 kHz, and no significant changes for the G. lamblia. To mitigate large amplitude variations, amplitude ratios (500 kHz/4 MHz) were calculated. Fig. 5b is the amplitude ratio histogram showing single and separated peak locations for the 3 samples. The small overlap in Fig. 5a is evident for the cell samples (G. lamblia and C. parvum) in the histogram, while the noncellular sample (polystyrene) has a histogram peak located furthest away from the rest. The distribution means are 1.21, 0.79 and 2.83 for the G. lamblia, C. parvum, and polystyrene, respectively.

Fig. 5 Combined frequency data plot for the G. lamblia, C. parvum (oo)cysts and polystyrene microspheres diluted in DI water. (a) Measured sample amplitude at 500 kHz vs. that at 4 MHz for the (b) histogram of amplitude ratios (low/high) from (a). (c) Measured phases at 500 kHz vs. that at 4 MHz for the 3 samples. (d) Histogram of phase ratios (low/high) from (c). Note that the count is limited to 120 to visualize the low counts for C. parvum. The dashed black lines are linear fitting lines.

Fig. 5c shows the scatter plot of measured sample phases at 500 kHz and 4 MHz. No visual data overlap was observed, suggesting that sample phases could be better at discriminating the samples than sample amplitudes. However, the phase data is less linear, as indicated by the slight skew to the right from the dashed regression lines and their R² values (<0.87) compared to the amplitude data in Fig. 5a). A similar trend was observed with the phase data for the parasite samples clustering more closely together compared to the phase data for the noncellular sample. The parasite samples G. lamblia cysts (n = 510) and C. parvum oocysts (n = 763) have shown the widest phase distribution at 500 kHz, compared to 4 MHz, while the noncellular sample polystyrene microspheres (n = 668) has shown the widest phase distribution at 4 MHz compared to 500 kHz. A Histogram of the phase ratios (500 kHz/4 MHz) was plotted in Fig. 5d. The phase ratios for C. parvum have 6.8 times wider ranges compared to G. lamblia and 46 times wider compared to polystyrene.

For the samples spiked into filtered city creek water, 4 MHz at 300 mV excitation was initially applied, and no amplitude data for the C. parvum oocysts were yielded. At 1 MHz, the amplitude data was recovered for the C. parvum oocysts, while the size of the phase data was reduced by more than half compared to the size of the amplitude data. This loss of measurements at high (>MHz) frequency can be attributed to the drastically different water contents of a natural water source as opposed to lab grade DI water. When the frequency was further reduced to 100 kHz, both amplitude and phase data were obtained at the same rate across samples. However, all the data points have shown no apparent separation – rather, lies in a straight line – in the two-frequency scatter plot. Furthermore, at both 500 kHz and 1 MHz, no double peaks were obtained for the filtered creek water without the samples (Fig. S1†), creating a blank signal baseline for analysis.

Fig. 6 shows the measured average amplitudes and phases for the parasite and non-parasite samples spiked in filtered city creek water. Fig. 6a is the amplitude vs. phase scatter plot for the G. lamblia cysts (n = 602), C. parvum oocysts (n = 597), and polystyrene spheres (n = 593) measured at 500 kHz. Compared to the amplitudes and phases measured at the same excitation frequency in DI water (Fig. 5a), a few differences are observed. First, the C. parvum data points are positioned between those of the G. lamblia and polystyrene, with noticeable visual overlap in the scatter plot. Whereas the C. parvum data points were isolated from the rest when measured in DI water. The measured amplitudes in creek water are significantly lower for G. lamblia and polystyrene, at 4.85 ± 2.88 mV and 9.10 ± 5.25 mV, respectively, while the amplitudes for C. parvum are 2.54 ± 2.19 mV showing a near two-fold increase in standard deviation. Both the parasite samples show decreased phase values when measured in creek water, whereas the polystyrene exhibits a slight increase. These changes can be reflected by the ratios of amplitude over phase: 1.62 ± 0.28, 2.30 ± 0.42, and 6.51 ± 1.98 mV degree⁻¹ for the G. lamblia, C. parvum and polystyrene respectively as shown in Fig. 6b.

Fig. 6 Amplitude and phase measurements for the G. lamblia, C. parvum (oo)cysts and polystyrene microspheres spiked in filtered natural creek water at a high and a low excitation frequencies. (a) Amplitude vs. phase scatter plot for the particles at 500 kHz excitation frequency. (b) Bar plot of amplitude over phase ratios from (a). (c) Scatter plot of amplitudes at 500 kHz and that at 1 MHz frequencies for the samples. (d) Histogram of amplitude ratios (high/low) from (c).

Fig. 6c is the sample amplitude scatter plot measured at 500 kHz and 1 MHz frequencies in filtered city creek water. Like Fig. 5a, where the high frequency is 4 MHz, a clear visual separation between the parasite and noncellular data points can be observed, while a section of the parasite sample data points overlap with each other. The linear regression lines (dashed lines) have an R² = 0.997, 0.999, and 0.845 for the G. lamblia, C. parvum, and polystyrene respectively, indicating a high sample homogeneity, especially for the parasite samples. Histograms of the amplitude ratios are plotted in Fig. 6d to represent the difference between samples in terms of their amplitudes at the two excitation frequencies. Note that the ratios here are calculated as the amplitude at 1 MHz over that at 500 kHz to prevent large histogram peaks shown in Fig. 5d. Normal distributions were fitted to the ratio histograms, where the means of the distributions were 0.43, 0.89, and 0.98 for the polystyrene, G. lamblia, and C. parvum respectively.

Fig. 7 shows an example measured amplitude-ratio (high/low) histogram for the sample mixture of G. lamblia and C. parvum oocysts (in PBS) at equal concentrations spiked in 6 parts of filtered creek water. By fitting normal distributions to the histogram, the characteristic amplitude ratio (1 MHz/500 kHz) was 0.93, corresponding to the mean of the distribution on the left (orange solid line), and 0.97, corresponding to the mean of the distribution on the right (blue solid line). Considering the result from Fig. 6d. 0.93 is most likely to be the characteristic amplitude ratio of the G. lamblia cyst population, while 0.97, the characteristic amplitude ratio of the C. parvum oocyst population. The characteristic amplitude ratios tended to be more similar in a mixed population, a possible result of interactions between the populations. The population counts in Fig. 7 are estimated to be 874 and 691 for the G. lamblia and C. parvum respectively.

Fig. 7 Example histogram of amplitude ratio (high/low) for a mixture of G. lamblia and C. parvum (oo)cysts spiked in filtered creek water. The red dashed line is fit to the histogram, while the remaining solid lines are fitted normal distributions.

When the sample mixture was diluted in 3 parts of the creek water (more concentrated (oo)cysts), the overall histogram saw a shift towards the left on the amplitude ratio axis (Fig. S2 1a†), likely due to increased solution conductivity. The discrimination between the G. lamblia and C. parvum populations was less prominent, since some (oo)cysts were flowing simultaneously at this concentration inside the device channel, generating mixed signals. At 9 parts dilution (Fig. S2 1c†), while the shift in histogram on the amplitude ratio axis was minimal from 6 parts dilution, the discrimination between the two (oo)cysts populations was not statistically observable, possibly due to reduced solution conductivity. These results suggest that there exists an optimal sample concentration and buffer solution conductivity to analyze mixtures of the (oo)cysts populations. The analysis can be further improved with sheath flows to ensure only one (oo)cysts passes through detection electrode at a time. In addition, the amplitude vs. phase scatter plots for the sample mixtures are indicated in Fig.S2 2.† However, no significant separation between data points were found, suggesting that the amplitude vs. phase data may be inadequate at discriminating G. lamblia cysts and C. parvum (oo)cysts in a mixture.

A key challenge of the current method is that applying two frequencies at a time may suffice to distinguish between G. lamblia and C. parvum (oo)cysts but may be insufficient to distinguish between the cysts and trophozoites of the G. lamblia or other microorganisms. The choice of frequency is critical in the analysis and may need to be optimized for various target organisms. In addition, changes in the conductivity of the water matrix can pose a challenge for obtaining consistent impedimetric responses. To distinguish (oo)cysts from other interferences in a more complex water sample, applying more than two excitation frequencies could enable more robust impedance spectroscopy. In the situation where only two frequencies can be applied simultaneously, the samples could instead be cycled through the device while adjusting the frequency range at each cycle to achieve a similar effect. Moreover, interferences can be further reduced by integrating a sorting channel (e.g., a spiral-shaped channel³¹) with size-based filtration before the detection channel.

5. Conclusion

The detection of waterborne parasitic protozoa including G. lamblia and C. parvum (oo)cysts, and polystyrene microspheres as a noncellular sample, was demonstrated utilizing two-frequency microfluidic impedance flow cytometry. The detection was implemented on PDMS channels embedded with a coplanar electrode system to generate double peak signals corresponding to single (oo)cyst crossing. The fabricated device has achieved detecting <∼0.1% volume displacement of the sample inside the detection zone. Combinations of impedimetric responses, such as amplitude vs. phase at 500 kHz and up to 4 MHz excitation frequencies, were used to characterize the measurement differences between the parasite and noncellular samples, and between parasite samples. Particularly, a metric that is the ratio of the amplitudes at a high (1–4 MHz) and a low (500 kHz) frequency was shown to be effective at discriminating between samples suspended in two different water sources, including filtered city creek water to demonstrate the robustness of the parasitic protozoa detection using the IFC system. To achieve optimal identification of parasites (i.e., minimized data overlap), different combinations of frequencies, such as extending the high frequency range up to 50 MHz, can be applied while modifying the conductivity of the buffer solution.

Data availability

Data will be made available on request.

Conflicts of interest

Authors Bruce K. Gale and Himanshu J. Sant have a financial/equity interest in Espira Inc., to which the SBIR Phase II grant was awarded.

Acknowledgements

This material is based upon work partially supported by the US Army Contracting Command-APG, Natick Contracting Division, Natick, MA under Contract No. W911QY-20-C-0061 and W911QY-17-C-0032. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the US Army Contracting Command-APG, Natick Contracting Division, Natick, MA. We also acknowledge the Department of Chemical Engineering, the University of Utah for support.

References

1. A. Efstratiou, J. E. Ongerth and P. Karanis, Waterborne transmission of protozoan parasites: Review of worldwide outbreaks - an update 2011–2016, Water Res., 2017, 114, 14–22.
2. M. Widerström, C. Schönning, M. Lilja, M. Lebbad, T. Ljung and G. Allestam, et al., Large outbreak of Cryptosporidium hominis infection transmitted through the public water supply, Sweden, Emerg. Infect. Dis., 2014, 20(4), 581–589.
3. A. J. Elliot, H. E. Hughes, J. Astbury, G. Nixon, K. Brierley and R. Vivancos, et al., The potential impact of media reporting in syndromic surveillance: an example using a possible cryptosporidium exposure in North west England, August to september 2015, Eurosurveillance, 2016, 21(41), 30368–30378.
4. K. M. Benedict, S. A. Collier, E. P. Marder, M. C. Hlavsa, K. E. Fullerton and J. S. Yoder, Case–case analyses of cryptosporidiosis and giardiasis using routine national surveillance data in the United States – 2005–2015, Epidemiol. Infect., 2019, 147, e178.
5. E. Scallan, R. M. Hoekstra, F. J. Angulo, R. V. Tauxe, M. A. Widdowson and S. L. Roy, et al., Foodborne illness acquired in the United States-Major pathogens, Emerg. Infect. Dis., 2011, 17(1), 7–15.
6. F. E. Adeyemo, G. Singh, P. Reddy, F. Bux and T. A. Stenström, Efficiency of chlorine and UV in the inactivation of Cryptosporidium and Giardia in wastewater, PLoS One, 2019, 14(5), e0216040.
7. D. Carmena, X. Aguinagalde, C. Zigorraga, J. C. Fernández-Crespo and J. A. Ocio, Presence of Giardia cysts and Cryptosporidium oocysts in drinking water supplies in northern Spain, J. Appl. Microbiol., 2007, 102(3), 619–629.
8. M. Bouzid, D. Steverding and K. M. Tyler, Detection and surveillance of waterborne protozoan parasites, Curr. Opin. Biotechnol., 2008, 19, 302–306.
9. H. Pereira, P. S. C. Schulze, L. M. Schüler, T. Santos, L. Barreira and J. Varela, Fluorescence activated cell-sorting principles and applications in microalgal biotechnology, Algal Res., 2018, 30, 113–120.
10. C. Honrado, P. Bisegna, N. S. Swami and F. Caselli, Single-cell microfluidic impedance cytometry: from raw signals to cell phenotypes using data analytics, Lab Chip, 2021, 21, 22–54.
11. F. Gökçe, P. S. Ravaynia, M. M. Modena and A. Hierlemann, What is the future of electrical impedance spectroscopy in flow cytometry?, Biomicrofluidics, 2021, 15(6), 061302–061307.
12. D. Holmes, D. Pettigrew, C. H. Reccius, J. D. Gwyer, C. Van Berkel and J. Holloway, et al., Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry, Lab Chip, 2009, 9(20), 2881–2889.
13. Y. Zheng, E. Shojaei-Baghini, A. Azad, C. Wang and Y. Sun, High-throughput biophysical measurement of human red blood cells, Lab Chip, 2012, 12(14), 2560–2567.
14. K. Cheung, S. Gawad and P. Renaud, Impedance spectroscopy flow cytometry: on-chip label-free cell differentiation, Cytometry A, 2005, 65(2), 124–132.
15. S. Gawad, L. Schild and P. Renaud, Micromachined impedance spectroscopy flow cytometer for cell analysis and particle sizing, Lab Chip, 2001, 1(1), 76–82.
16. Y. Zhou, D. Yang, Y. Zhou, B. L. Khoo, J. Han and Y. Ai, Characterizing Deformability and Electrical Impedance of Cancer Cells in a Microfluidic Device, Anal. Chem., 2018, 90(1), 912–919.
17. C. Honrado, A. Salahi, S. J. Adair, J. H. Moore, T. W. Bauer and N. S. Swami, Automated biophysical classification of apoptotic pancreatic cancer cell subpopulations by using machine learning approaches with impedance cytometry, Lab Chip, 2022, 22(19), 3708–3720.
18. H. L. Gou, X. B. Zhang, N. Bao, J. J. Xu, X. H. Xia and H. Y. Chen, Label-free electrical discrimination of cells at normal, apoptotic and necrotic status with a microfluidic device, J. Chromatogr. A, 2011, 1218(33), 5725–5729.
19. D. Spencer, F. Caselli, P. Bisegna and H. Morgan, High accuracy particle analysis using sheathless microfluidic impedance cytometry, Lab Chip, 2016, 16(13), 2467–2473.
20. B. De Wagenaar, S. Dekker, H. L. De Boer, J. G. Bomer, W. Olthuis and A. Van Den Berg, et al., Towards microfluidic sperm refinement: impedance-based analysis and sorting of sperm cells, Lab Chip, 2016, 16(8), 1514–1522.
21. Z. Han, L. Chen, S. Zhang, J. Wang and X. Duan, Label-Free and Simultaneous Mechanical and Electrical Characterization of Single Plant Cells Using Microfluidic Impedance Flow Cytometry, Anal. Chem., 2020, 92(21), 14568–14575.
22. X. Xie, M. Gong, Z. Zhang, X. Dou, W. Zhou and J. Li, et al., Optimization of an electrical impedance flow cytometry system and analysis of submicron particles and bacteria, Sens. Actuators, B, 2022, 360.
23. J. S. McGrath, C. Honrado, D. Spencer, B. Horton, H. L. Bridle and H. Morgan, Analysis of Parasitic Protozoa at the Single-cell Level using Microfluidic Impedance Cytometry, Sci. Rep., 2017, 7(1), 2601–2612.
24. H. P. Schwan, Electrical properties of tissue and cell suspensions, Advances in Biological and Medical Physics, ed. J. H. Lawrence, C. A. Tobias, Elsevier, 1957, vol. 5, pp. 147–209.
25. S. Zhu, X. Zhang, Z. Zhou, Y. Han, N. Xiang and Z. Ni, Microfluidic Impedance Cytometry for Single-Cell Sensing: Review on Electrode configurations, Talanta, 2021, 233, 122571–122591.
26. V. Errico, A. D. Ninno, F. R. Bertani, L. Businaro, P. Bisegna and F. Caselli, Mitigating positional dependence in coplanar electrode Coulter-type microfluidic devices, Sens. Actuators, B, 2017, 247, 580–586.
27. Y. Zheng, E. Shojaei-Baghini, C. Wang and Y. Sun, Microfluidic characterization of specific membrane capacitance and cytoplasm conductivity of single cells, Biosens. Bioelectron., 2013, 42(1), 496–502.
28. S. Gawad, K. Cheung, U. Seger, A. Bertsch and P. Renaud, Dielectric spectroscopy in a micromachined flow cytometer: theoretical and practical considerations, Lab Chip, 2004, 4(3), 241–251.
29. B. K. Gale, A. R. Jafek, C. J. Lambert, B. L. Goenner, H. Moghimifam and U. C. Nze, et al., A review of current methods in microfluidic device fabrication and future commercialization prospects, Inventions, 2018, 3, 60–85.
30. Y. Peng, B. K. Gale, M. D. Porter, L. Zang and H. J. Sant, Modified trident-shaped electrode design for particle lateral position detection in microfluidic impedance flow cytometry, Sens. Actuators, A, 2025, 381, 116062 . Available from: https://linkinghub.elsevier.com/retrieve/pii/S0924424724010562.
31. Y. Peng, B. K. Gale and H. J. Sant, A spiral channel with integrated microelectrodes for label-free particle lateral position and size characterization, Biomed. Microdevices, 2025, 27(13) DOI:10.1007/s10544-025-00742-5.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ay00184f

---