Open Access Article
Open Access ArticlePredicting the retention time of microparticles in electrokinetic migration†
Alaleh
Vaghef-Koodehi
 a,
Victor H.
Perez-Gonzalez
a,
Victor H.
Perez-Gonzalez
 *b and
Blanca H.
Lapizco-Encinas
*b and
Blanca H.
Lapizco-Encinas
 *a
*a
aMicroscale Bioseparations Laboratory and Biomedical Engineering Department, Rochester Institute of Technology, 160 Lomb Memorial Drive, Rochester, New York 14623, USA. E-mail: bhlbme@rit.edu
bTecnologico de Monterrey, School of Engineering and Sciences, Ave. Eugenio Garza Sada 2501 Sur, Col: Tecnológico, Monterrey, N.L. 64700, Mexico. E-mail: vhpg@tec.mx
First published on 10th July 2025
Abstract
Insulator based electrokinetic (iEK) devices have emerged as powerful tools for analyzing both nano- and microparticles due to their simplicity, robustness, and ability to integrate linear and nonlinear electrokinetic (EK) effects into a single platform. Recent studies emphasize the importance of nonlinear electrophoresis (EPNL) in particle analysis, for performing separations based on size, shape, and charge differences. Despite these advancements, the development of an empirical equation for predicting particle retention times in iEK-based systems that incorporates EPNL remains limited. This study presents a method for predicting particle retention time in iEK systems in scenarios where the linear EK regime allows for particles migration, while also incorporating EPNL and accounting for particle characteristics, applied electric fields, and microdevice features. Experiments were conducted using eight reference microparticles, grouped into four pairs with similar sizes (3.6 μm to 11.7 μm) but distinct zeta potentials (∼−20 mV and ∼−30 mV), across three distinct iEK microdevices: one with asymmetrical oval-diamond posts, one with symmetrical oval posts, and one postless design. Experimental retention times (tR,e) were measured at applied voltages ranging from 400 V to 1450 V. Using the collected tR,e data, three empirical equations were developed to describe particle velocity, incorporating both linear and nonlinear velocities. Validation with two control particles demonstrated prediction errors below 24% in all devices. These findings underscore the potential of the empirical equations in predicting particle behavior in iEK systems.
Introduction
Various conventional techniques such as capillary electrophoresis (CE) and chromatography are accessible for the analysis of nano-sized bioparticles, yet there is a scarcity of equally effective methods for analyzing micron-sized particles, such as microorganisms.1 Microfluidic systems have proven successful in investigating both nano- and micro-particles.1–3 Within the realm of microfluidics, electrokinetic (EK) techniques play a significant role in analyzing particles. Specifically, insulator based EK (iEK) systems have garnered attention recently due to their simplicity, robustness, and unique ability to merge linear and nonlinear EK effects within a single microfluidic device.4,5 In these systems, insulating structures integrated into microchannels modify the distribution of the externally generated electric field, leading to the creation of zones with higher electric field intensity that enable nonlinear EK effects therein, whereas only linear EK effects dictate particle dynamics in the remaining zones. The utilization of iEK devices has facilitated the separation of complex samples, encompassing bioparticles ranging from macromolecules to mammalian cells.6–10Numerous research groups have utilized iEK systems to analyze particles and cells based on differences in size and/or charge.11–13 Nevertheless, previous studies overlooked the inclusion of nonlinear electrophoresis (EPNL), also referred to as EP of the second kind, necessitating the use of empirically-determined correction factors to reconcile experimental and predicted outcomes.14
Recent reports revealed the importance of EPNL in iEK systems.15–17 Employing EPNL allows separations by exploiting shape and size differences, which are not possible with traditional methods, such as linear electrophoresis (EPL).18,19 Several recent studies by our group20–28 have integrated COMSOL Multiphysics simulations and experimental validation to predict and confirm particle and cells retention times (tR) in iEK systems. The charge-based separation of almost similar polystyrene analytes,20 the binary separation of cells,21,22 tertiary separation of particles24 under DC voltages, the utilization of different input voltages to transition between linear and nonlinear electrokinetic regimes,23 and EK separation experiments employing DC-biased AC voltages27 highlight the importance of EPNL in particle analysis. These efforts feature the criticality of accurately predicting the time it takes a given particle type to migrate through the microchannel, known as particle retention time, to optimize performance and expand the applicability of iEK systems.
Building on the understanding of the importance of EPNL, a practical approach to further enhance the efficiency of iEK systems is to develop empirical equations for predicting particle retention time. Such empirical equations enable rapid estimation of system behavior, conserving both time and resources. For instance, the Van Deemter equation in chromatography employs factors such as diffusion and mass transfer kinetics to relate the variance per unit length of a separation column to the linear mobile phase velocity.29
This study presents a novel approach to predicting particle retention time, based on key factors such as particle characteristics, applied voltages, and microdevice design features. Eight distinct types of microparticles, grouped into four pairs, were investigated to evaluate the proposed model's applicability. Each pair consisted of particles with nearly identical sizes ranging from 3.6 μm to 11.7 μm but differing zeta potentials, approximately −20 mV and −30 mV. The experiments were performed using three distinct microdevice configurations: two devices with insulating posts—one featuring asymmetrical posts and the other with symmetrical posts—and a postless device serving as a control. Particle velocities and retention times were systematically measured at eight applied DC voltages, ranging from 400 V to 1450 V. Within this range, a linear regime allows particles to move through the channel without being trapped by the non-negligible effects of EPNL present during the experiments as demonstrated by our previous studies.23
The experimental retention time data was used to derive three empirical correlation equations that describe particle velocity as a function of both linear and nonlinear EK velocity components for each device. These equations offer insights into the dynamics of particle migration under varying electric field conditions. To validate the proposed model, two control particles were tested across the three devices. The three empirical equations produced retention time predictions with errors remaining below 24%, underscoring the effectiveness of the proposed approach for rapidly predicting particle behavior in electrokinetic systems. Notably, while other studies30 have required correction factors larger than 100 to account for all phenomena present in similar systems (i.e., correcting prediction errors greater than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000%), our model achieved satisfactory predictions without such extensive corrections, making the 24% error particularly encouraging. These correlations can become valuable tools in the design of new separation processes, advancing microfluidic applications in biomedical and analytical research.
000%), our model achieved satisfactory predictions without such extensive corrections, making the 24% error particularly encouraging. These correlations can become valuable tools in the design of new separation processes, advancing microfluidic applications in biomedical and analytical research.
Theory
Electrokinetic phenomena are categorized based on their reliance on the electric field, as linear and nonlinear. The linear EK phenomena considered in this study are electroosmosis (EO) and linear electrophoresis (EPL). The velocities expressions of these phenomena are stated below:3,4,31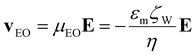 | (1) |
 | (2) |
| vEK = vEO + vEP,L = μEKE | (3) |
| v(3)EP,NL = μ(3)EP,NLE3âE | (4) |
| v(3/2)EP,NL = μ(3/2)EP,NLE3/2âE | (5) |
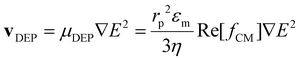 | (6) |
 | (7) |
The overall particle velocity in the iEK microchannel (Fig. 1) is determined by EK phenomena illustrated in Fig. 1a in the postless device and Fig. 1b in post devices for negatively charged particles. Given that the DEP force in our system is negligible16,17,31,35 and the 3/2 condition is either not met or occurs only in negligibly small regions based on the applied voltage (as detailed in Table S1†), the equation can be simplified as follows:
| vP = vEK + v(3)EP,NL = μEKE + μ(3)EP,NLE3âE | (8) |
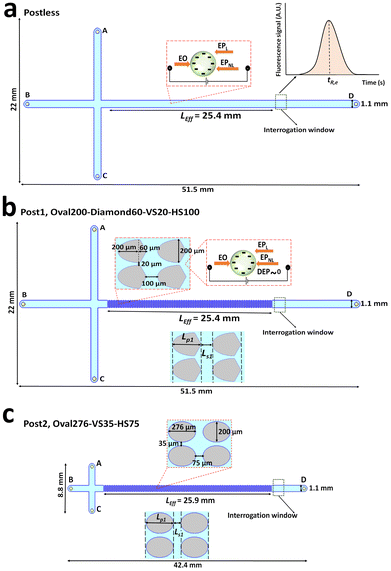 | ||
| Fig. 1 Illustration of the three device designs employed in this study. Schematic representation of (a) a postless microchannel, (b) a microchannel with asymmetrical posts (Post1 device), (c) a microchannel with symmetrical posts (Post2 device) with reservoirs, depicting the channel dimensions, and the interrogation window used for fluorescence measurements. The labels A–D refer to the four electrodes (see Table 2). The EK forces (EO, EPL, EPNL, and DEP) acting on the negatively charged particles in the microchannels are also shown in the figure inset in (a) and (b). Because the DEP force is negligible in magnitude when compared to the other EK forces, it is shown as DEP ∼ 0 in (b). The insets below the channels in (b) and (c) provide an illustration of the effective length (LEff) the length of one horizontal gap between posts (Ls1) and the length of one post (Lp1) for the post devices. The second inset in (a) illustrates where retention time data is obtained in an electropherogram. | ||
Experimental
Suspending medium and microparticles
This study utilized eight distinct types of polystyrene microparticles as reference particles (P1 to P8, as detailed in Table 1) sourced from Magsphere (Pasadena, CA, USA) and Spherotech (Lake Forest, IL, USA) with sizes ranging from 3.6 μm to 11.7 μm to develop the empirical equations. The particles were grouped into four pairs, each consisting of microparticles of nearly identical size but differing zeta potentials, approximately −20 mV and −30 mV. Additionally, two particles, referred to as control particles, were used to validate the empirical equations. One particle had a smaller size of 3.6 μm (particle P9), and the other had a larger size of 7.4 μm (particle P10). Both particles had characteristics within the range defined by the reference particles. The characteristics of particles P9 and P10 are detailed in Table 1. The concentration of particles ranged from ∼2 × 106 to ∼2 × 108 beads per ml. The sample concentration was kept consistent across both particle tracking velocimetry (PTV) and EK migration experiments; however, larger sample volumes were required for the EK migration experiments to aid in the visualization of eluting particles.| Particle ID | Diameter (μm) |
ζ
P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (mV) a (mV) |
μ EP,L × 10−8 (m2 V−1 s−1) | E for μ(3)EP,NL estimation (V cm−1) | β for μ(3)EP,NL estimation | Pe for μ(3)EP,NL estimation | μ (3)EP,NL × 10−18 (m4 V−3 s−1) |
|---|---|---|---|---|---|---|---|
| a The values for the ζP and μEP,L were estimated at β values between 0.2 and 0.9. | |||||||
| P1 | 3.6 ± 0.1 | −19.1 ± 3.2 | −1.5 ± 0.2 | 350 | 3.3 | 0.8 | −2.1 ± 0.3 |
| P2 | 4.1 ± 0.3 | −34.1 ± 2.5 | −2.6 ± 0.1 | 250 | 2.8 | 1.1 | −3.1 ± 0.3 |
| P3 | 5.8 ± 0.2 | −20.5 ± 2.2 | −1.6 ± 0.2 | 150 | 1.1 | 0.2 | −25.3 ± 2.5 |
| P4 | 5.7 ± 0.2 | −34.2 ± 3.3 | −2.7 ± 0.1 | 150 | 2.2 | 0.9 | −16.1 ± 1.1 |
| P5 | 7.4 ± 0.3 | −21.1 ± 1.6 | −1.6 ± 0.1 | 100 | 1.9 | 0.5 | −25.3 ± 2.3 |
| P6 | 7.6 ± 0.2 | −26.7 ± 1.8 | −2.1 ± 0.2 | 100 | 1.9 | 0.6 | −16.4 ± 1.7 |
| P7 | 11.7 ± 0.2 | −23.8 ± 1.1 | −1.9 ± 0.8 | 100 | 2.9 | 0.9 | −23.2 ± 1.6 |
| P8 | 10.5 ± 0.3 | −27.8 ± 4.6 | −2.2 ± 0.3 | 100 | 2.7 | 0.9 | −19.8 ± 1.1 |
| P9 | 3.6 ± 0.1 | −20.7 ± 2.7 | −1.6 ± 0.2 | 300 | 2.4 | 1.2 | −20.5 ± 3.0 |
| P10 | 7.4 ± 0.3 | −31.7 ± 1.8 | −2.5 ± 0.1 | 100 | 1.9 | 0.7 | −7.3 ± 0.6 |
The suspending media was a buffer solution of K2HPO4 (Solon, Ohio, USA) at a 0.2 mM concentration, with the addition of 0.05% (v/v) of Tween 20 (Solon, Ohio, USA) to prevent particle sticking. The media had a conductivity of 41 ± 3.0 μS cm−1 with a pH of 7.2 ± 0.5, which produced a wall zeta potential (ζW) of −60.1 ± 3.7 mV and μEO of 4.7 ± 0.3 × 10−8 m2 V−1 s−1 as measured with current monitoring.
Microdevices and equipment
Standard cast-molding techniques were employed to create the T-channel devices used in this study.36Fig. 1a–c represent the three microchannel designs, with a depth of 40 μm, used in this study; depicting insulating posts and channel dimensions, and the location of the fluorescence interrogation window. The labels A–D refer to the four electrodes (Table 2). The insulating posts were chosen to include one asymmetrical (Post1, Oval200-Diamond60-VS20-HS100) and one symmetrical (Post2, Oval276-VS35-HS75) design, as these are among the most commonly used shapes in iEK migration experiments and produce distinct electric field patterns.23,27 The design names are structured to comprise the shape of the asymmetric/symmetric posts along with their specific horizontal lengths, followed by the vertical spacing (VS) and horizontal spacing (HS) values. In addition to both device designs featuring different post geometries, the shorter arm of Post2 further modifies the electric field intensity in comparison to Post1, allowing for a meaningful comparison of retention times between the two. A postless device was selected as a reference to enable direct comparison with devices containing posts. To minimize the impact of PDMS aging on ζW all microdevices used in this study were 1–2 days old.37 The effective length (LEff) is fixed at approximately 2.5 cm, with post devices selected accordingly for retention time comparison, and the postless design includes a distance-marking feature above the channel to visually indicate the 2.5 cm endpoint during video recording. All experiments were recorded employing either of two inverted microscopes, a Zeiss Axiovert 40 CFL and a Leica DMi8. The Zeiss Axiovert 40 CFL microscope was used for the EK migration experiments, while both the Zeiss Axiovert 40 CFL and Leica DMi8 microscopes were used for the PTV experiments. A LabSmith high-voltage power supply (model HVS6000D) was used to apply the voltage sequences to the microchannels.Experimental procedure
Experimental work was carried out in two parts: (1) PTV experiments were conducted a 1 cm long postless channel to characterize the particles as reported in Table 1. (2) Electrokinetic migration experiments were performed to obtain the retention time of particles (tR,e) within the effective length of microchannels. For all experiments, the microchannels were pre-filled with the suspending medium and allowed to equilibrate for at least 12 hours to ensure stable electroosmotic flow. Low-voltage PTV experiments, using applied voltages ranging from 25 to 75 V, were performed to obtain values for μEP,L, which were then used to determine ζP. These low voltage magnitudes were selected to ensure that Pe and β remained much smaller than 1, maintaining a linear relationship with E. High-voltage PTV experiments were carried out at higher voltages to collect nonlinear electrophoretic data (μ(3)EP,NL) to satisfy moderate condition where Pe ≪ 1, arbitrary Du, and β ≤ 1. Table 1 presents the values of β and Pe used for estimating linear and nonlinear mobilities. Although these are not the exact values required, they represent the closest available approximations. A detailed description of the PTV experiments can be found in our previous reports.34,38,39 To obtain tR,e, electrokinetic migration experiments were performed employing a three-step EK sample injection process: loading, gating, and injection. The applied voltages in the injection step range from 400 V to 1450 V with an increment of 150 V (see Table 2). The voltage range was set between 400 V, the minimum required for EK injection, and 1450 V, the maximum at which particles can migrate within the channel while being affected (but not trapped) by EPNL effects. The run time refers to the duration of each voltage step; the duration of the injection step was determined by the time required for the particles to elute from the post array. Large liquid reservoirs (∼3–4 mL) were employed to decrease pressure-driven backflow. A 1–6 μL suspension of microparticles was introduced into reservoir A (shown in Fig. 1) using a pipette, followed by the placement of platinum wire electrodes into each of the four reservoirs. These experiments are thoroughly described in our earlier publications.20,21 The EK injection experiments were conducted at least three times for each particle at each voltage to ensure reproducibility. The fluorescence signal from each eluting particle peak was captured at the interrogation window shown in Fig. 1. EK migration videos were recorded and analyzed using ImageJ, which processed the videos based on fluorescence intensity. The fluorescence intensity for each EK migration video was quantified using the first frame of the interrogation window as a threshold. To ensure consistency, intensity values were normalized relative to the highest recorded intensity. The second inset in Fig. 1a represents an electropherogram generated from fluorescence analysis at the interrogation window, illustrating the tR,e in a single elution peak. tR,e, along with the standard deviations from these repetitions, are presented in Tables S2–S4† for different voltages and across three microfluidic devices.Data fitting
The “lsqnonlin” function in MATLAB R2024a was used to fit the experimental retention time data to the proposed model. This function optimizes the parameters by minimizing the sum of squared residuals between the predicted and observed values. Its flexibility in handling bounds and constraints made it particularly suitable for accurately modeling the nonlinear relationships in the system. Since the retention time of particles is determined by their overall velocity, which is the summation of the vEK and v(3)EP,NL, the equation for particle retention time can be expressed based on particles’ linear (μEK) and nonlinear (μ(3)EP,NL) mobilities as shown in eqn (8). Mobility is a key parameter in the proposed model because it effectively captures the system's physical behavior and is relatively straightforward to characterize, as demonstrated by a recent report.40 The average of electric fields (EAvg) along a cutline (Fig. S2†) was calculated using COMSOL Multiphysics and employed in the fitting process. This approach was chosen because of our observations of particles primarily migrating and aligning along the cutline rather than across the entire volume. In COMSOL, the Average tool computes the average electric field by integrating the field values over the length of the line and dividing by the total length. Table S7† presents the EAvg values across the cutlines for all devices. Detailed information about the computational modeling is provided in the ESI (Fig. S1–S2 and Tables S5–S6†). In this study, the experimental retention time data (tR,e), as reported in Tables S2–S4,† were individually fitted for the postless, Post1, and Post2 devices to derive three distinct equations for the predicted retention time of particles (tR,p). For the postless device, eqn (8) was reformulated as follows:| vP = A1μEKEAvg + A2μ(3)EP,NLE3AvgâE | (9) |
 | (10) |
Similarly, the equation can be adapted for post devices by accounting for the average electric field in the presence of the insulating posts:
 | (11) |
| LEff = Ls + Lp | (11a) |
| Ls = (Nc + 1)(Ls1) | (11b) |
| Lp = (Nc)(Lp1) | (11c) |
 | (12) |
Results and discussion
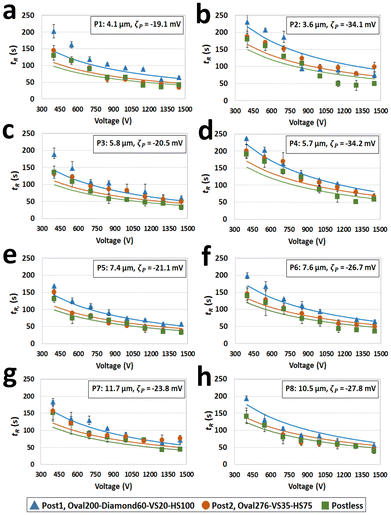
The experimental retention time of particles
This study developed empirical equations using eight types of polystyrene microparticles (P1 to P8, as shown in Table 1) to predict the retention time in microfluidic devices, with experiments conducted on three microdevice types (shown in Fig. 1a–c). The retention times of the particles, together with their standard deviations from repeated measurements, are provided in Tables S2–S4† for various voltages and three different microfluidic devices. Fig. 2a–h presents the experimental retention time of the microparticles in the three microfluidic devices, represented by markers with error bars. The model-predicted retention times are shown as solid lines, demonstrating a reasonable agreement with the experimental data. Across all devices, the relative error between tR,e and tR,p remains below 30% for all particles. A descending trend is observed for all particles across all devices as the applied voltage increases, except for a slight increase at higher voltages (reported in Tables S2–S4†).The retention time of particles is influenced by a combination of linear and nonlinear effects. As detailed in Tables S2–S4,† at lower voltages (400–700 V), where linear forces are more pronounced, the retention time decreases noticeably with increasing voltage, as expected. As the voltage increases to the mid-range (700–1000 V), the retention time decreases at a lower rate, and in some case retention time increases at the higher voltages (1000–1200 V), suggesting that EPNL effects counteract linear forces. Eventually, an increase in retention time is observed, likely due to the growing influence of nonlinear forces which are becoming comparable to linear effects. This trend, which is more obvious in Post1 device, underscores the complex interaction between linear and nonlinear phenomena at varying voltage levels. The performance of post devices in terms of producing longer retention times, considering EPNL, is expected to become more significant at higher voltages, as demonstrated in our previous work.23 However, due to concerns about particle trapping for larger particles, the voltage was not increased to that level.
The results revealed that, in general, the Post1 device (Oval200-Diamond60-VS20-HS100) produced longer retention times compared to the other two devices. Additionally, the Post2 device (Oval276-VS35-HS100) generally resulted in longer retention times than the postless device, although not to the extent of the Post1 device. On average, the Post1 device extended retention times by ∼40% (95% CI: 20% to 60%) compared to the postless device, while the Post2 device demonstrated a ∼20% increase (95% CI: 3% to 37%) in retention times relative to the postless configuration. These observations can be explained by electric field distributions and the magnitude of EPNL within the devices. In the postless device, the electric field distribution is uniform, which limits the emergence of EPNL compared to post devices. In postless device, particles can move more quickly toward the outlet, resulting in shorter tR,e. In contrast, insulating features intensify the magnitude of the electric fields at certain regions of the channel, enabling the simultaneous utilization of both linear and nonlinear electrokinetic phenomena within the post device, making the particle move slower toward the outlet and obtain longer tR,e. Furthermore, asymmetrical insulating posts (Post1 device) more effectively amplify the effects of EPNL on particles exposed to the electric field compared to symmetrical posts (Post2 device), as evident in the plots and consistent with the literature.14,36
Development of empirical equations for predicting particle retention time
The experimental retention times of particles (tR,e) across various devices and applied voltage ranges were utilized to develop an empirical equation for predicting particle retention time (tR,p) based on linear and nonlinear velocities. The equation for the postless device was fitted using the format specified in eqn (10), while the equations for the Post devices adhered to the format outlined in eqn (12). The solver determined the equation parameters using tR,e as the response variable in the postless device. This resulted in coefficients A1 = 1.31 and A2 = 1.32 for the postless device, corresponding to the contribution of vEP,L and vEP,NL, respectively. It is important to note that LEff must be provided in meters and EAvg in volts per meter (V m−1) for these equations to function correctly. For the postless device, given that LEff = 0.025 m, the resulting equation is as follows: | (13) |
For the Post1 device, the solver estimated the equation parameters by using tR,e obtained from Post1 device as the response variable. Knowing that LEff = 0.025, Ls/LEff = 0.3, and Lp/LEff = 0.7, this process yielded coefficients A1 = 0.63 and A2 = 0.32, which correct the estimation of linear electrokinetic effects and nonlinear phenomena, respectively. The equation derived for the Post1 device is expressed as follows:
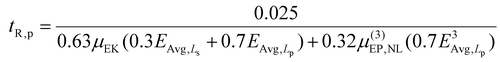 | (14) |
In the Post2 device given that LEff = 0.026, Ls/LEff = 0.2, and Lp/LEff = 0.8, the model estimated the equation parameters by employing tR,e obtained from Post2 device as the response variable. This process yielded coefficients A1 = 0.83 and A2 = 0.22. For the Post2 device, the resulting equation can be represented as:
 | (15) |
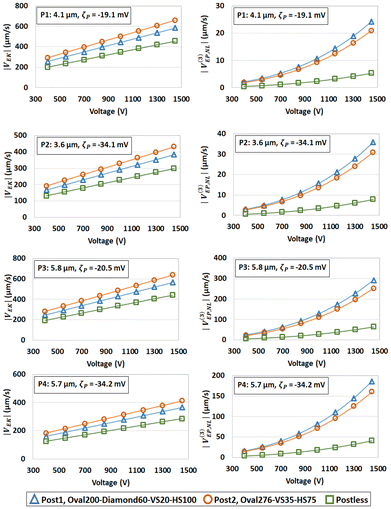
Fig. 3 illustrates predicted |vEK| and |v(3)EP,NL| for particles P1 to P4 derived from empirical equations for Post1, Post2, and postless devices. The absolute values of the predicted v(3)EP,NL were plotted for better visualization, as all μ(3)EP,NL values are negative for all particles in this study. For particles P1 to P4, it is evident that |vEK| is lowest in the postless device, with Post1 and Post2 showing almost equal values, although Post2 is slightly higher than Post1. This trend can be attributed to the combined influence of the electric fields EAvg,Ls and EAvg,Lp which contribute to a higher overall magnitude in the Post2 device compared to Post1, as detailed in Table S7.† This indicates that the linear terms in the equations are device-dependent, with the postless device featuring nonintensified electric fields generating lower |vEK| magnitudes. For all particles, it is apparent that the magnitude of |v(3)EP,NL| is the highest for Post1 device, and lowest for postless device. In the postless device, the uniform electric field distribution ensures a constant electric field throughout the entire migration channel at any applied voltage. In contrast, in Post devices, the presence of insulating features alters the electric field distribution, creating regions of higher field intensity. These localized high-intensity areas give rise to nonlinear electrokinetic phenomena, such as EPNL. As reported in Table S7,†EAvg,Lp in the Post1 device is higher in magnitude compared to the Post2 device, while the postless device exhibits the lowest EAvg among all the devices. The differences in the electric field distribution between the Post devices arise from variations in the insulating post dimensions, the vertical spacing (VS) between the insulating posts, the horizontal spacing (HS) between the posts, and length of the arms as reported in our previous studies.24,27 In this case, the Post1 device, with a vertical spacing (VS) of 20 μm, intensifies the local electric field in the constrictions, while the Post2 device, with a VS of 35 μm and shorter arms, exhibits a less concentrated electric field in Lp regions. The same trends for vEK and |v(3)EP,NL| are observed for particles P5 to P8 shown in Fig. S3.† These observations are consistent with previous reports from our group on improving iEK device design.24,27
The average value for the weighting coefficient A1, which corresponds to linear EK phenomena, in all three equations is 0.9 ± 0.3. This indicates that the corresponding variable or term contributes almost directly and proportionally to the outcome without requiring significant scaling or adjustment. This consistency demonstrates that the relationship between the variable and the response is neither excessively amplified nor diminished.
The main contributing factor to the observed A1 value is the use of experimental linear mobilities (μEP,L and μEO), which are derived under specific conditions where β ≪ 1 and have very small magnitudes. These conditions ensure reliable and consistent experimental measurements of linear electrokinetic mobilities. The A1 value close to 1 supports the validity of the experimental methodology and indicates that the electrokinetic term does not require further adjustment to reflect reality accurately.
The weighting coefficient A2, which corresponds to nonlinear electrokinetic phenomena, is 1.32 for the postless device. This suggests that the uniform electric field distribution minimizes the impact of nonlinear effects, as the term requires little adjustment to the governing equation. In contrast, for the Post1 and Post2 devices, A2 drops significantly to 0.32 and 0.22, respectively. These lower values indicate that the original equations substantially overestimate nonlinear contributions in the presence of posts. Assuming that EPNL primarily occurs in the regions between the posts (constrictions) where the electric field changes across the cutline, this observation can be attributed to the way that the electric field is calculated along the Lp region. In this region, the electric field distribution is non-uniform. Since it is not feasible to use the electric field for each individual point, averaging the electric field values along the cutline (EAvg,Lp) might affect the resolution of the calculations. In fact, there are points with maximum (or minimum) electric field values that are diminished (or increased) by averaging, thereby affecting their contribution to the overall nonlinear effect.
A further explanation for the observed A2 value is the condition of elevated electric field values required to satisfy the cubic dependence necessary for experimentally calculating μ(3)EP,NL. Compared to linear electrokinetic mobilities, μ(3)EP,NL is more challenging to determine and may be more prone to variability under these conditions. The results from the fitting process highlight that while the linear term remains dominant, the nonlinear term plays a role in determining the overall result.
Box and Whisker plots showing the relative error (RE) between tR,e and tR,p for the reference particles under all applied voltages are provided in Fig. 4. The plot illustrates the relative error RE of reference particles (P1 to P8) across three device configurations: postless (Fig. 4a), Post1 (Fig. 4b), and Post2 (Fig. 4c). The boxplots display the median (central line), interquartile range (IQR; box bounds: 25th to 75th percentiles), and whiskers (extending to 1.5× IQR or min/max values). Outliers are shown as individual points. Errors below 30% are considered acceptable, signifying good agreement between experimental and predicted values. The 30% error threshold was chosen based on previous studies demonstrating that successful separations were achieved even when the discrepancy between predicted and experimental data reached approximately 30%.20 Additionally, the literature14,30 shows that large correction factors are often applied to improve the agreement between experimental and predicted results, which inevitably increases the error beyond 30%, suggesting that this threshold is a reasonable benchmark for our study. Across all three configurations, most particles exhibit RE values within this acceptable range, demonstrating the reliable performance of the empirical equations for predicting particle retention times.
The R2 for the derived equations (eqn (13)–(15)) was approximately 0.8, which can be attributed to several factors. The main contributing factor to the observed R2 is the way electric fields are incorporated into the solver. To simplify the model, average electric field values are used. However, the non-uniform nature of the electric field in post devices, complicates precise calculations. By averaging the electric field along the cutline, the method neglects extreme values—both maximum and minimum—masking their contribution to the overall influence. This oversimplification makes it difficult to determine electric field values with high accuracy.
Another factor affecting the R2 value is the absence of an analytical model that accurately describes the experimental domain lying between the cubic model (where nonlinear velocity exhibits a cubic dependence on the electric field) and the 3/2 model (where nonlinear velocity follows a 3/2 dependence on the electric field). This gap in theoretical representation may contribute to the imperfect fit, as the existing models fail to fully capture the underlying physical or mathematical relationships governing the system. Despite these challenges, the derived equations remain consistent with the underlying physics of the system and provide an appropriate tool for predicting the retention time of particles in iEK systems.
Comparison of predicted and experimental results for control particles
To validate the empirical equations, two control particles (P9 and P10) were selected based on their characteristics, which align with the reference particles in terms of size, zeta potential, and mobilities as detailed in Table 1. These particles were introduced into the microchannels using the EK injection method described in the previous section and tested across three device configurations—postless, Post1, and Post2—under four applied voltages (400 V, 700 V, 1000 V, 1300 V, and 1450 V). The retention times for these particles were predicted using the derived empirical equations (eqn (13)–(15)) and compared to experimental results to assess the accuracy of the model. The experimental retention times (tR,e), including standard deviations over three repetitions, and predicted retention times (tR,p) for the control particles are presented in Tables S8 and S9.† Additionally, the percentage errors between the experimental and predicted values are provided in Tables S8–S10.†Fig. 5 illustrates the comparison between tR,p and tR,e for particles P9 and P10 across the three device configurations and the applied voltages. In all cases, the retention times decreased as the applied voltage increased, reflecting the expected behavior of the system. For the postless device, the deviations between experimental and predicted retention times were below 23% for both P9 and P10 across all applied voltages, indicating a consistent performance of the empirical equation in a uniform electric field. For the Post1 and Post2 devices, the deviations were below 24% demonstrating the empirical equation's ability to effectively capture localized nonlinear effects of the electric field in this device.
Overall, the results demonstrate the reliability and accuracy of the empirical equations in predicting retention times under varying conditions. The relatively low deviations (below 24% in all cases) indicate that the equations fairly capture key factors influencing retention time, including both linear and nonlinear electrokinetic phenomena. Additionally, the trends observed in Fig. 5 align with the theoretical expectations, further supporting the validity of the model. These findings confirm the empirical equations’ potential for fairly predicting particle retention times across different microchannel designs and operational conditions.
Conclusions
This study introduces a method for predicting particle retention time, accounting for both linear and nonlinear phenomena. The method combines particle characteristics, applied voltages, and microdevice design features. Using the collected experimental data, a set of empirical equations was developed to comprehensively describe the velocity of microparticles. These equations accounted for both electrokinetic and nonlinear velocity components, providing a reliable mathematical framework for predicting particle behavior under varying operational conditions. However, it is important to note that the model has limitations and is only applicable for predicting the retention time of particles within the provided range of particle characteristics. To validate the accuracy and reliability of the derived equations, two distinct control particles were tested across multiple device configurations. The validation results demonstrated good predictive capability, with prediction errors consistently remaining below 24% for all tested devices. This level of accuracy highlights the effectiveness of the empirical models in capturing the complex interplay of forces driving particle motion in electrokinetic systems. Potential strategies to further improve accuracy include refining the predictive model with advanced machine learning techniques and expanding the calibration dataset to capture broader experimental variability. Additionally, optimizing input parameters or reducing measurement noise in retention time data and mobilities could enhance precision beyond the current error threshold.These results underscore the potential of the proposed empirical equations in iEK systems for efficient prediction of particle behavior. To more thoroughly evaluate the nonlinear electrokinetic regime, future studies could focus on smaller particles that allow the use of higher electric fields without particle trapping, enabling a deeper exploration of the nonlinear velocity contribution. The method presented here offers significant advantages for advanced analytical applications, including enhanced accuracy, reduced processing time, and adaptability to diverse experimental conditions. By providing a reliable framework for modeling particle retention times, this study contributes to the advancement of microfluidic technologies, particularly in fields such as biomedical diagnostics, environmental monitoring, and chemical analysis, where precise control of particle behavior is critical.
Author contributions
Conceptualization, V. H. P. G. and B. H. L. E.; methodology, V. H. P. G. and B. H. L. E.; experimental data curation, A. V. K.; COMSOL simulations, A. V. K.; writing—review and editing, A. V. K., V. H. P. G. and B. H. L. E.; supervision, V. H. P. G. and B. H. L. E.; project administration, V. H. P. G. and B. H. L. E.; funding acquisition, B. H. L. E. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
This material is based upon work supported by the National Science Foundation under Award No. CBET-2127592. The authors acknowledge Research Computing at the Rochester Institute of Technology for providing computational resources and support that have contributed to the research results reported in this publication. V. H. P. G. acknowledges the Federico Baur Endowed Chair in Nanotechnology (0020240I03) and the Nanotechnology and Semiconductors Research Group from Tecnologico de Monterrey. V. H. P. G. also acknowledges the financial support provided by the Consejo Nacional de Humanidades, Ciencia y Tecnología (SNI Grant 62382). A. V. K. appreciates the helpful discussions provided by Carlos A. Mendiola-Escobedo, Viswateja Kasarabada, and Adrian Lomeli-Martin during the development of this work.References
- A. Vaghef-Koodehi and B. H. Lapizco-Encinas, Electrophoresis, 2022, 43, 263–287 CrossRef CAS PubMed.
- P. Rajapaksha, A. Elbourne, S. Gangadoo, R. Brown, D. Cozzolino and J. Chapman, Analyst, 2019, 144, 396–411 RSC.
- V. H. Perez-Gonzalez, Electrophoresis, 2021, 42, 2445–2464 CrossRef CAS PubMed.
- B. H. Lapizco-Encinas, Anal. Bioanal. Chem., 2022, 414, 885–905 CrossRef CAS PubMed.
- X. Xuan, Electrophoresis, 2022, 43, 167–189 CrossRef CAS PubMed.
- J. Ding, C. Woolley and M. A. Hayes, Anal. Bioanal. Chem., 2017, 409, 6405–6414 CrossRef CAS PubMed.
- P. V. Jones, G. L. Salmon and A. Ros, Anal. Chem., 2017, 89, 1531–1539 CrossRef CAS PubMed.
- M. Aghaamoo, A. Aghilinejad, X. Chen and J. Xu, Electrophoresis, 2019, 40, 1486–1493 CrossRef CAS PubMed.
- C. V. Crowther, S. H. Hilton, L. K. Kemp and M. A. Hayes, Anal. Chim. Acta, 2019, 1068, 41–51 CrossRef CAS PubMed.
- S. Soltanian-Zadeh, K. Kikkeri, A. N. Shajahan-Haq, J. Strobl, R. Clarke and M. Agah, Electrophoresis, 2017, 38, 1988–1995 CrossRef CAS PubMed.
- V. Calero, P. Garcia-Sanchez, A. Ramos and H. Morgan, Biomicrofluidics, 2019, 13, 054110 CrossRef PubMed.
- J. Zhu and X. Xuan, Biomicrofluidics, 2011, 5, 24111 CrossRef PubMed.
- S. Patel, S. Qian and X. Xuan, Electrophoresis, 2013, 34, 961–968 CrossRef CAS PubMed.
- N. Hill and B. H. Lapizco-Encinas, Anal. Bioanal. Chem., 2020, 412, 3891–3902 CrossRef CAS PubMed.
- A. S. Khair, Curr. Opin. Colloid Interface Sci., 2022, 59, 101587 CrossRef CAS.
- M. Rouhi Youssefi and F. J. Diez, Electrophoresis, 2016, 37, 692–698 CrossRef CAS PubMed.
- S. Tottori, K. Misiunas, U. F. Keyser and D. J. Bonthuis, Phys. Rev. Lett., 2019, 123, 14502 CrossRef CAS PubMed.
- F. A. Morrison, J. Colloid Interface Sci., 1970, 34, 210–214 CrossRef CAS.
- D. Li, in Interface Science and Technology, 2004, vol. 2, pp. 542–616 Search PubMed.
- A. Vaghef-Koodehi, C. Dillis and B. H. Lapizco-Encinas, Anal. Chem., 2022, 94, 6451–6456 CrossRef CAS PubMed.
- A. Vaghef-Koodehi, O. D. Ernst and B. H. Lapizco-Encinas, Anal. Chem., 2023, 95, 1409–1418 CAS.
- V. Kasarabada, N. N. Nasir Ahamed, A. Vaghef-Koodehi, G. Martinez-Martinez and B. H. Lapizco-Encinas, Anal. Chem., 2024, 96, 15711–15719 CrossRef CAS PubMed.
- A. Vaghef-Koodehi and B. H. Lapizco-Encinas, Biosensors, 2024, 14, 119 CrossRef PubMed.
- A. Vaghef-Koodehi, P. Cyr and B. H. Lapizco-Encinas, J. Chromatogr. A, 2024, 1722, 464853 CrossRef CAS PubMed.
- N. N. Nasir Ahamed, C. A. Mendiola-Escobedo, V. H. Perez-Gonzalez and B. H. Lapizco-Encinas, Micromachines, 2023, 14(12), 2239 CrossRef PubMed.
- N. N. Nasir Ahamed, C. A. Mendiola-Escobedo, O. D. Ernst, V. H. Perez-Gonzalez and B. H. Lapizco-Encinas, Anal. Chem., 2023, 95, 9914–9923 CrossRef PubMed.
- N. N. Nasir Ahamed, C. A. Mendiola-Escobedo, V. H. Perez-Gonzalez and B. H. Lapizco-Encinas, Analyst, 2024, 149, 2469–2479 RSC.
- N. N. Nasir Ahamed, C. A. Mendiola-Escobedo, V. H. Perez-Gonzalez and B. H. Lapizco-Encinas, Biosensors, 2024, 14, 237 CrossRef PubMed.
- D. A. Skoog, F. J. Holler and S. R. Crouch, Principles of instrumental analysis, CENGAGE Learning, 7th edn, 2017, vol. 56 Search PubMed.
- H. Moncada-Hernandez, J. L. Baylon-Cardiel, V. H. Pérez-González and B. H. Lapizco-Encinas, Electrophoresis, 2011, 32, 2502–2511 CrossRef CAS PubMed.
- B. Cardenas-Benitez, B. Jind, R. C. Gallo-Villanueva, S. O. Martinez-Chapa, B. H. Lapizco-Encinas and V. H. Perez-Gonzalez, Anal. Chem., 2020, 92, 12871–12879 CrossRef CAS PubMed.
- J. Bentor and X. Xuan, Electrophoresis, 2023, 45(7–8), 712–719 Search PubMed.
- J. Bentor, H. Dort, R. A. Chitrao, Y. Zhang and X. Xuan, Electrophoresis, 2023, 44, 938–946 CrossRef CAS PubMed.
- V. Kasarabada, O. D. Ernst, A. Vaghef-Koodehi and B. H. Lapizco-Encinas, J. Chromatogr. A, 2024, 1717, 464685 CrossRef CAS PubMed.
- A. Coll De Peña, A. Miller, C. J. Lentz, N. Hill, A. Parthasarathy, A. O. Hudson and B. H. Lapizco-Encinas, Anal. Bioanal. Chem., 2020, 412, 3935–3945 CrossRef PubMed.
- M. A. Saucedo-Espinosa, A. Lalonde, A. Gencoglu, M. F. Romero-Creel, J. R. Dolas and B. H. Lapizco-Encinas, Electrophoresis, 2016, 37, 282–290 CrossRef CAS PubMed.
- M. A. Saucedo-Espinosa and B. H. Lapizco-Encinas, Biomicrofluidics, 2016, 10, 033104 CrossRef PubMed.
- O. D. Ernst, A. Vaghef-Koodehi, C. Dillis, A. Lomeli-Martin and B. H. Lapizco-Encinas, Anal. Chem., 2023, 95, 6595–6602 CrossRef CAS PubMed.
- A. Lomeli-Martin, O. D. Ernst, B. Cardenas-Benitez, R. Cobos, A. S. Khair and B. H. Lapizco-Encinas, Anal. Chem., 2023, 95, 6740–6747 CrossRef CAS PubMed.
- J. M. de los Santos-Ramirez, C. A. Mendiola-Escobedo, J. M. Cotera-Sarabia, R. C. Gallo-Villanueva, R. Martinez-Duarte and V. H. Perez-Gonzalez, Analyst, 2024, 149, 3839–3849 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Predicting retention time of microparticles in electrokinetic separations. See DOI: https://doi.org/10.1039/d5an00515a |
| This journal is © The Royal Society of Chemistry 2025 |