Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Uranium particle age dating, aggregation, and model age best estimators†
Evan E.
Groopman
 *a,
Todd L.
Williamson
*a,
Todd L.
Williamson
 a,
Timothy R.
Pope
b,
Michael G.
Bronikowski
c,
Spencer M.
Scott
c and
Matthew S.
Wellons
c
a,
Timothy R.
Pope
b,
Michael G.
Bronikowski
c,
Spencer M.
Scott
c and
Matthew S.
Wellons
c
aMaterials Measurement Science Division, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA. E-mail: evan.groopman@nist.gov
bPacific Northwest National Laboratory, Richland, WA 99354, USA
cSavannah River National Laboratory, Aiken, SC 29808, USA
First published on 9th June 2025
Abstract
We present important aspects of uranium particle age dating by Large-Geometry Secondary Ion Mass Spectrometry (LG-SIMS) that can introduce bias and increase model age uncertainties, especially for small, young, and/or low-enriched particles. This metrology is important for applications related to International Nuclear Safeguards. We explore influential factors related to model age estimation, including the effects of evolving surface chemistry on inter-element measurements of particles (e.g., Th and U), detector background, and aggregation methods using simulated and actual particle samples. We introduce a new model age estimator, called “mid68”, that supplements 95% confidence intervals, providing a “best estimate” and uncertainty about the most likely age. The mid68 estimator can be calculated using the Feldman and Cousins method or Bayesian methods and provides a value with a symmetric uncertainty that can be used for calculations and approximate aggregation of processed model age values when the raw data and correction factors are not available. For particles yielding low 230Th counts amidst nonzero detector background, their underlying model age probability distributions are asymmetric, so the mid68 estimator provides additional robust information regarding the underlying model age likelihood. This study provides a comprehensive and timely examination of critical aspects of uranium particle age dating as more laboratories establish particle chronometry capabilities.
Introduction
Environmental sampling of nuclear facilities has been a routine Nuclear Safeguards practice for the International Atomic Energy Agency (IAEA) for the last several decades.1–3 Environmental uranium can be chemically and isotopically analyzed at the bulk (>nanogram) and particle (<nanogram) levels to infer the operational history of nuclear facilities. Similar types of analyses have been performed on interdicted nuclear materials for nuclear forensic purposes, e.g., Kristo4 and Moody et al.5 The IAEA Department of Safeguards has identified “age determination of U and Pu relevant to the origin of nuclear materials” to be a “top priority R&D need”.6 For decades, bulk analytical techniques have been used to determine dates for the purification or manufacture of nuclear material using the decay of radioisotopes, such as U and its decay products, e.g., 234U–230Th–226Ra and 235U–231Pa–227Ac. Model ages can be constructed by comparing the ratio of decay products to parent radioisotopes using their characteristic decay rates, under the assumption that the chronometers were initially “reset” from material processing, i.e., only parent isotopes were present at the time of material production. Incomplete purification of decay products would bias these analyses, resulting in artificially older model ages. Recently, the National Institute of Standards and Technology (NIST) extended the application of age dating using the 234U–230Th chronometer (t1/2 = 245.6 ka) to the regime of individual U microparticles using Large-Geometry Secondary Ion Mass Spectrometry (LG-SIMS).7 Challenges associated with the analyses of trace isotopes in atom-limited microparticles have long been acknowledged, highlighting the need for continued metrology and reference material development.7–15Several important factors impact the accuracy and precision of U particle age dating analyses by LG-SIMS.7,10 One set of factors regards intrinsic sample attributes, such as the enrichment level, particle mass, and material age. Generally, the higher the 234U enrichment (which is often correlated with 235U enrichment), the larger the sample mass, and the older the material, the more 234U and 230Th atoms will be available to analyze, which increases the relative precision of a measurement. Other factors are instrumentation and analysis protocol-related, including the ion yield and instrument transmission, detector background rate, measurement duty cycle per isotope, and fraction of the particle consumed. In addition, use of LG-SIMS instead of smaller-geometry instruments is important because of the high ion transmission and sensitivity achievable at the mass resolving power (MRP, defined as peak width at 10% peak height, or M/ΔM) necessary to discriminate certain molecular isobars from 230Th.7,9 In general, it is important to measure as many parent and decay product atoms as possible since particles are atom-limited. Finally, data processing and statistical considerations influence accuracy and precision, including aggregation of multiple particle measurements to determine a model age with lower uncertainty.
Particle age dating analyses typically involve the measurement of different parent/decay product elements. It has long been known that the SIMS relative sensitivity factor (RSF, or relative ionization rate) for each element is affected by the local surface chemical environment, which includes the influence of implanted primary beam atoms and redeposited or mixed neutral species from the sample and/or substrate.16,17 The implantation of reactive ion species (e.g., O or Cs) increases the secondary ion yields of elements of interest with dissimilar electronegativity.18 Reactive ion sputtering can result in orders of magnitude increases in secondary ion yields, which is why these beams are almost universally used on dynamic SIMS instruments today in lieu of non-reactive Ar or N species, for instance. During initial implantation of the (reactive) primary species, there exists a transient period where RSFs can change rapidly until an equilibrium between sputter removal and implanted atom concentration is reached. The magnitude and duration of this transient depends on the average implantation depth of the primary ions and whether the sample or substrate were reduced or oxidized initially. For analyses of macroscopic materials, it is often preferable to measure RSFs or unknown concentrations after this transient has passed and equilibrium is reached. For particles, waiting for equilibrium is often not feasible due to the amount of material removed or omitted from analysis, which reduces the sensitivity. Additionally, it can be difficult to robustly and reproducibly determine where the transition between transient and equilibrium occurs, as in the case of small particles whose secondary signals might continually evolve throughout a profile. Despite these challenges, it has been observed that consuming most of the particle (at least past 50% and including the initial transient) for both standards and unknowns results in highly reproducible inter-element analyses in particles, even with apparent changes in the RSF during profiling.7,10,19 When calculating an elemental or isotopic ratio from a profile, it is important to integrate each signal first, before dividing, to reduce potential bias (numeratortotal counts/denominatortotal counts).20–22 In addition, the choice of primary beam species and particle substrate can mitigate the duration and magnitude of the transient.10 For example, oxygen ion bombardment of particles on Si can lead to a phase change of the substrate to SiOx (x < 2), depending on the sputter rate and implantation depth of the primary ions.10,23,24 This phase change affects the sputter rate, RSFs, and useful yields of secondary ions, which also creates challenges for time interpolation of ion signals when using the monocollector. Primary O3− ions were found to reduce the phase change and transient effects while increasing useful yields, sensitivity, and precision.10 Substrate and surface chemistry effects appear to have a greater impact on inter-element measurements than on isotopic measurements of a single element.10,19
At NIST, we typically use a 50 μm Köhler primary beam spot for particle age dating measurements.7,10 In this setup, a micrometer-sized particle only covers approximately 0.04% of the sputtered area. Therefore, we would mostly sputter the substrate and redeposited sputtered neutrals from the particle onto the substrate and vice versa. One consequence of this setup is that the overall useful yield tends to be higher because sputtered neutrals have additional chances to be ionized when they are redeposited nearby. However, this setup also emphases the importance and relative scale of substrate sputtering vis-à-vis the particle of interest. While not reported here, we have observed similar RSF values and surface chemistry behavior when using a focused primary ion beam with square raster sizes ranging from 10 μm to 100 μm on a side. However, to our knowledge, there hasn't been a systematic study of the effect of beam spot or sputtered area size on RSF values and useful yields, in large part because there haven't been many monodisperse particles with certified mass to perform such an experiment reliably. Now that particle production technology has matured,25–30 this study could plausibly be performed in the near future.
Several laboratories have recently been qualified as producers of particle reference materials for the IAEA's Network of Analytical Laboratories (NWAL), including Pacific Northwest National Laboratory (PNNL) and Savannah River National Laboratory (SRNL) in the U.S. Department of Energy (DOE), and Forschungszentrum-Jülich (FZJ) in Germany. The objective is to produce isotopic and age dating particle reference materials for quality control, lab qualification and testing, and technique development. Several methods are currently used to produce uniformly sized and isotopically homogeneous particles, including: hydrothermal synthesis, vibrating orifice aerosol generation (VOAG), flow focusing monodisperse aerosol generation (FMAG), and inkjet printing. For age dating purposes, feedstock materials, such as NIST/New Brunswick Laboratory (NBL) certified reference materials (CRM), can be purified of their radiochronometer daughter products (e.g., 230Th and 231Pa) and remade as new monodisperse particles, optionally doped with daughter products to a specific model age.
As more particle age dating reference materials are produced, there will be a greater need for accurate and precise characterization of these materials at the bulk and particle level before they can be used for quality control or laboratory qualification purposes. As such, we believe it is timely to explore and discuss best practices for LG-SIMS age dating measurements and data interpretation, particularly in the context of young, low-enriched, and/or small particles. We will further demonstrate the efficacy of the particle consumption approach, compare the impact of different primary beam species, and address challenges including within-particle heterogeneity.
Low-count Poisson processes in the presence of detector background, such as the measurement of decay-product 230Th in a U microparticle, require subtle statistical interpretation. Eqn (1) shows the probability mass function for a Poisson distribution with parameter, μ, which gives the probability for observing n counts during a measurement:
 | (1) |
One generally does not have a priori knowledge of μ for an isotope and therefore must infer it from observations. The number of observed counts in a measurement, n, could be a reasonable estimator of μ, with a 1 standard deviation (SD) uncertainty of √n, if n were sufficiently large so that the relative uncertainty were small. Alternatively, a histogram of sufficiently many time-binned observations could be used to estimate the underlying distribution and its parameters. However, there are several regimes where this treatment is insufficient and requires more careful consideration. For example, in the case of zero observed counts, an uncertainty of zero would be both unphysical and unhelpful, since the observation did provide information about the likely value of μ (e.g., that the rate is small compared to the given measurement time). This is a well-known issue and many solutions have been proposed, though the general consensus has been that the appropriate treatment is application-dependent.31 Conventional propagation of errors (POE) techniques are based on the assumption of Gaussian-distributed uncertainties. However, by using POE to correct for the expected background on a small signal it is possible to produce an estimate that covers negative count values with its uncertainty, which would be unphysical. For example, if one measured three total counts but expected two background counts on average during the measurement, (3 ± √3) - (2 ± √2) = 1 ± 2.2, which spans negative values. Under some conditions, there may also be a nonzero statistical chance that the number of observed counts would be lower than the expected background, or even zero, which is a scenario not adequately addressed by POE. To address these statistical challenges, frequentist and Bayesian models, primary from the high-energy and astrophysics communities, have been suggested to produce confidence intervals (CI) for Poisson processes with and without background.8,31–37 The method of Feldman and Cousins (1998)35 was suggested by Szakal et al. (2019)7 as a means to produce a CI on the measurement of very small 230Th signals in the presence of non-negligible detector background. From this CI, a particle model age could be produced using the number of 234U counts and other scaling factors.
The model age of a single particle or aggregated set may be represented by a point estimate with propagated uncertainties, by a CI, or by a full probability distribution, depending on the chosen statistical analysis (POE, FC, and Bayesian methods, respectively). When there are sufficient counts of both the parent and progeny isotopes for their Poisson distributions to be approximately Gaussian (and the background counts are negligible), all three methods yield similar model age CIs. The Bayesian posterior distribution is symmetric in this scenario, having its mean and maximum likelihood values very similar, and these correspond both to the midpoint of the FC CI and the POE point estimate. This maximum likelihood location and its uncertainty to, e.g., 1 σ or 2 σ, is the traditional “best estimate” of the model age or any isotope ratio.
However, in cases where one or both isotopes are described by asymmetric Poisson distributions and/or the measurement background is not negligible, these methods do not yield obvious “best estimators”. The POE method is clearly unsatisfactory, as described above, with potential coverage of unphysical values. Szakal et al. recommended that the 95% FC CI be used to describe particle or aggregated model ages, however this only provides upper and lower confidence limits.35,37 Apart from the CI, there is no “best estimate” point, which can be useful for subsequent calculations or regressions. There is also no accepted systematic method for combining CIs that are not representative of Gaussian-distributed variables or parameters with asymmetric uncertainties.38 Therefore, individual particle model age CIs cannot be aggregated or averaged easily. Instead, the total counts from all particles must be summed first before a single model age CI can be calculated.
In this paper we discuss particle characterization and statistical interpretation factors and their impact on particle age dating measurements with an emphasis on atom-limited particles with low 230Th counts, e.g., young, low-enriched, and/or low-mass. We will also discuss particle data aggregation methods, potential sources of aggregation bias, and introduce a new “best estimate” parameter for a particle model age. From these we will make recommendations regarding particle age dating best practices by LG-SIMS.
Experimental
Szakal et al.7 established a method for U particle age dating by LG-SIMS, which we follow and extend here. This is a monocollection protocol, which involves consuming most of a particle for radiochronometry, cycling the magnet and measuring on an electron multiplier (EM) per cycle: 207Pb23Na+ (2 s), 230Th+ (20 s), and 234U+ (2 s). For particles of NIST/NBL CRM U900 (produced/purified January 24, 1958), which was used as an age dating reference, a typical chronometry measurement would last 20 cycles using a 50 μm Köhler primary ion beam of approximately 35 nA O- or 10 nA O3−.7,10,39 Following the chronometry measurement, a lower beam current was used to measure 232Th+, 234U+, 235U+, 236U+, 238U+, and 238U1H+ keeping the maximum count rate of any isotope at or below 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts per s to minimize deadtime corrections. Count times per isotope may vary depending on the enrichment of the material. For age dating measurements, a MRP of 3400 or greater was used to eliminate isobaric interferences. Szakal et al.7 also specified several important factors that must be well controlled and corrected for, including: interelement calibration and the measurement of an RSF, i.e., the difference in ionization rate between Th+ and U+; interference rejection, such as molecular isobars; abundance sensitivity (primarily low-energy tails from nearby abundant isotopes); and detector background.7 For particles with very low 230Th+ counts, Szakal et al.7 recommended using a statistical method proposed by Feldman and Cousins,35 which incorporates information about the average detector background rate to produce a CI for the 230Th+ counts (N230+), which can then be converted into a model age when combined with the 234U+ counts (N234+), the RSF, and the 234U decay constant, λ234 = (2.822 ± 0.003) × 10−6 a−1, using eqn (2).7,35,40
000 counts per s to minimize deadtime corrections. Count times per isotope may vary depending on the enrichment of the material. For age dating measurements, a MRP of 3400 or greater was used to eliminate isobaric interferences. Szakal et al.7 also specified several important factors that must be well controlled and corrected for, including: interelement calibration and the measurement of an RSF, i.e., the difference in ionization rate between Th+ and U+; interference rejection, such as molecular isobars; abundance sensitivity (primarily low-energy tails from nearby abundant isotopes); and detector background.7 For particles with very low 230Th+ counts, Szakal et al.7 recommended using a statistical method proposed by Feldman and Cousins,35 which incorporates information about the average detector background rate to produce a CI for the 230Th+ counts (N230+), which can then be converted into a model age when combined with the 234U+ counts (N234+), the RSF, and the 234U decay constant, λ234 = (2.822 ± 0.003) × 10−6 a−1, using eqn (2).7,35,40 | (2) |
Recently, several improvements to age dating protocols have also been published, such as the use of multicollection (MC),41,42 and surface chemistry modification through selection of primary ion beam species and sample substrate.10,43 Here we will discuss the impact of these different factors and the limits of various statistical models for interpreting model ages. For measurements reported here, we used an Ametek Cameca (Fitchburg, WI, USA) IMS 1270E7/1280 LG-SIMS at NIST fitted with an Oregon Physics (Beaverton, OR, USA) Hyperion-II radio-frequency plasma ion source.44 Most measurements were made using O3− primary ions projected into a 50 μm Köhler spot on the sample, unless otherwise specified. The mono- and multicollector EMs typically had dark noise count rates of 0.0012 counts·s−1 to 0.0015 counts·s−1. We maintain a running log of dark noise measurements collected overnight and blank measurements made on clean substrates for each EM. We then take the average count rate from the most recent 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s of these measurements as the detector background for a session with a typical uncertainty of 0.0005 counts·s−1. The abundance sensitivity on the monocollector was for 230Th+ was (1.0 ± 0.2) × 10−9 times the 235U+ intensity, inferred from the 234U+ intensity and scaled by the 235U/234U ratio.41
000 s of these measurements as the detector background for a session with a typical uncertainty of 0.0005 counts·s−1. The abundance sensitivity on the monocollector was for 230Th+ was (1.0 ± 0.2) × 10−9 times the 235U+ intensity, inferred from the 234U+ intensity and scaled by the 235U/234U ratio.41
For analyses here, we used both the FC method7,35 and a Bayesian Markov-Chain Monte Carlo (MCMC) approach developed for this work. While Bayesian approaches have been applied to similar problems before, (e.g., ref. 8, 32 and 36) this particular model incorporated the entire age dating framework. This allowed for a comparison of different aggregation methods and the development of a model age “best estimate” parameter that will be detailed later. Bayesian methods provide a full posterior probability distribution for the model age, which can be used to find the limits of the smallest-width interval that encompasses the desired probability level, e.g., 95%, which is sometimes called the highest density interval (HDI). This Bayesian credible interval is roughly equivalent to the frequentist CI, and for simplicity we will refer to all of these terms as CI here. The Bayesian model was built using the Python package PyMC.45 We chose truncated Gaussian prior distributions with lower bounds at zero for the Poisson parameters, background counts, and abundance sensitivity counts to ensure smoothness across all physical values. The background count and abundance sensitivity priors were set based on external observations; the isotope count priors were set with a very wide SD to be minimally informative. The sum was fit to a Poisson log-likelihood model. Decay constant and RSF priors were set based on literature values and standard measurements with associated uncertainties. The ESI† provides more details regarding the Bayesian model. Feldman–Cousins CIs were calculated using the Python package FCpy, written by the first author of this paper.46 To incorporate abundance sensitivity into the FC approach, the average expected abundance sensitivity count rate was added to the average expected background rate.
As a heretofore unique test case, NIST/NBL CRM U630 (purification date June 6, 1989) was dissolved and purified of its ingrown 230Th before being made into particles by hydrothermal synthesis at PNNL.25 These remade U630 particles were synthesized from a U630 solution that was purified on September 1, 2021 and were deposited on a vitreous carbon planchet. At NIST, we began to perform particle age dating measurements by LG-SIMS on December 10, 2021, and made measurements every three to six months until the particles were approximately 3.5 years old. CRM U900 on a carbon planchet was used as an RSF and isotopic reference for all analyses. Table 1 shows details of the analysis sessions over this time. These particles were measured using the monocollector EM age dating protocol from Szakal et al.7
| Analysis session | Number of particles analyzed | Primary beam species |
|---|---|---|
| December 10, 2021 | 20 | O− |
| March 28, 2022 | 6 | O3− |
| July 19, 2022 | 10 | O3− |
| October 14, 2022 | 10 | O3− |
| January 12, 2023 | 12 | O3− |
| July 5, 2023 | 10 | O3− |
| January 30, 2024 | 10 | O3− |
| August 6, 2024 | 13 | O3− |
| April 17, 2025 | 10 | O3− |
In addition to purified and remade CRM U630 particles, we analyzed mixed U–Th particles produced by SRNL's Thermally Evaporated Spray for Engineered Uniform particulateS (THESEUS) platform, comprised of a monodisperse aerosol generator with an inline heater and an aerodynamic particle sizer.26 Particles consisted of depleted uranium (DU) mixed with different concentrations of 232Th ranging from nominally pure DU, and nominally 1 μmol·mol−1 Th up to nominally 10% Th in powers of 10. The particles had a mean diameter of 1.06 μm ± 0.02 μm (1 σ). These particles were fully consumed on the LG-SIMS using the monocollector to cycle between 232Th+ and either 235U+ or 238U+, depending on the relative abundance of Th within the particles. Uranium isotopics (234U+, 235U+, 236U+, 238U+, and 238U1H+) were measured on separate batches of particles to calculate the total U/Th fraction in each particle. These particles were all deposited on Si substrates, so CRM U900 on Si was used as an RSF and isotopic reference.
To achieve a low detector background, we set our discriminator thresholds to −75 mV and adjusted the EM high-voltage (HV) to achieve a quantum efficiency of approximately 90% to 92% based on the pulse height distribution from a 235U+ signal of roughly 2 × 105 counts·s−1. We have observed that automated routines for setting the EM HV, such as comparing count rate measurements at two predetermined threshold values, often yield too high of an EM HV and quantum efficiency. The excessive HV broadens the tail of the detector noise, resulting in more counts registering above the discriminator threshold. We built a Faraday cage around the low-voltage electronics where power and analog EM threshold voltages are produced and fed into the discriminators. These are very sensitive to static electricity. We also placed all vacuum system hot ion gauges on extended elbows so that emitted electrons cannot have a line of sight with any detector without very many collisions with the vacuum chamber. In addition, we grounded all of our MC Faraday cups and repellers. The latter two modifications dramatically improved the MC EM noise performance. Vacuum conditions in our detection chamber were approximately 1.3 × 10−7 Pa (1 × 10−9 torr, 1.3 × 10−9 mbar).
Results and discussion
Purified and remade CRM U630
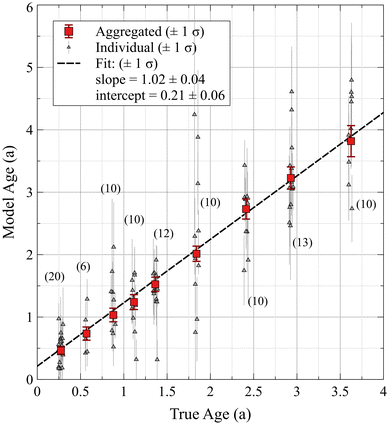
Ninety-one purified and remade U630 particles on a vitreous carbon planchet were measured by LG-SIMS over the course of approximately 3.5 years since their production. During that time, we observed the measurable ingrowth of 230Th in individual particles from radioactive decay of 234U. Fig. 1 shows the observed linear relationship between the true age of the particles (produced September 1, 2021) and the model ages measured during each session. The data were regressed using the York method.47,48 Each point (grey triangles) represents the particle model age best estimate ± 1 σ, while the red squares denote the aggregated model age for each session. Note, a small amount of random spacing was added to each session date for visual clarity. Details of the best estimate parameter and aggregation methods will be discussed later in this paper. The linear trend exhibits a slope equivalent to unity, within uncertainty, demonstrating the efficacy of age dating young particles and the lack of significant bias in the analyses over years of observation. The regression intercept of 0.21 a ± 0.06 a (1 σ) corresponds to the presence of initial 230Th that was not purified from the stock material. Therefore, the apparent production date was June 15, 2021 (± 21 days, 1 σ). Given the purification date for CRM U630 of June 6, 1989, this intercept corresponded to a removal of 99.3% ± 0.2% (1 σ) of the initially ingrown 230Th, which is quite efficient for a single-pass anion exchange column with UTEVA resin (Eichrom Technologies, LLC). These results emphasize a key assumption about chronometry measurements in general, which is that the model age determined from parent-daughter isotope measurements assumes 100% removal of all daughter isotope atoms during a production/purification process. When this assumption does not hold, including here (despite removal of >99% of decay product atoms), model ages will be biased older, often by more than the measurement uncertainty.Over the course of the 3.5-year measurement campaign, the average expected background and abundance sensitivity counts per measured particle were approximately 0.6 counts and 0.5 counts, respectively. The inferred abundance sensitivity signal scales with particle size and enrichment. The expected abundance sensitivity counts from the tailing of 234U were only approximately 0.02 counts per particle, on average, and were considered negligible. During the first measurement session three months after production, the relative fractions of the total m/z = 230 signal due to detector background and abundance sensitivity were 11.2% ± 3.1% and 9.3% ± 2.2%, respectively. During the final measurement session, these relative proportions were 1.9% ± 0.4% and 1.4% ± 0.3%, respectively, due to the larger number of ingrown 230Th atoms.
Mixed U–Th measurements in particles
CRM U900 is currently one of the best reference materials for measuring the Th/U RSF since it is both old (purification date January 3, 1958) and highly enriched. However, the 230Th abundance in U900 at the time of this writing was only on the order of 1 μmol·mol−1, or approximately 5 ag in a 5 pg particle. The size of U900 particles and particle clusters varies widely in a dispersion made on a planchet. For a radiochronometry measurement (230Th/234U) of U900, we typically collected on average 2700 ± 1500 (1 SD) 230Th counts from a particle or small cluster using and O3− primary ion beam, with a maximum 230Th count rate during the profile in the range of 5 counts·s−1 to 10 counts·s−1. The relative RSF uncertainty (1 SD) of many particle measurements on a C substrate was on the order of 3.5%, which places a limit on the precision of any particle age dating measurement.7,10 For unknown particles with low 230Th counts, the RSF uncertainty could be negligible compared to the Poisson statistical uncertainty when calculating a model age. For instance, one would need to measure approximately 785 230Th counts to yield a relative Poisson uncertainty of approximately 3.5% on the numerator, but a young, small, an/or low-enriched particle may yield only a few 230Th counts. However, for larger, older, and more enriched unknown particles, the RSF uncertainty would be a larger contributor to the overall uncertainty budget. It also remains unknown the extent to which U900 or any U-series CRM is homogeneous at the particle level or has been minorly altered by atmospheric humidity and other environmental effects. To date the variation observed in RSF measurements of U900 by LG-SIMS is slightly larger than would be expected by counting statistics alone,10 but these effects are difficult to deconvolve from instrumental spot-to-spot variability and ascribe wholly to sample heterogeneity. The production of homogeneous, monoisotopic, and monodisperse U particles with sufficiently high and known concentrations of Th would aid greatly in probing these effects and reducing the uncertainty on the Th/U RSF.Naes et al. reported on the production of mixed U–Th microparticles with a range of Th concentrations and their characterization by LG-SIMS and scanning electron microscopy (SEM).26 We also measured companion sets of these particles on Si planchets for this work. With Th concentrations ranging up to 10 atomic%, these particles help demonstrate the impact of the substrate, primary beam chemistry, and internal heterogeneity on the profiling and ionization behavior of different elements in actinide particles. Internal particle heterogeneity was found to increase with higher Th concentration, based on SIMS profiling, SEM observations, and aerodynamic density calculations. This is explainable given the kinetics and solubility limits of Th in a U oxide solution. We observed similar profiling behavior in the suites of particles measured at NIST. However, it can be difficult to deconvolve the combined effects of the initial profiling transient, intrinsic particle heterogeneity, and substrate phase changes, all while the particles were being sputtered away (i.e., their individual isotope count rate profiles were not constant due to the atom-limited nature of the sample). Both Naes et al.26 and we consumed most of each particle, them with an O− primary beam, and us with both O− and O3− on separate particles. The major difference in analysis protocols was that we used Th/U RSFs from U900 on Si (O− RSF on Si = 0.790 ± 0.025 (1 SD; ± 0.020 for 95% expanded standard error of the weighted mean); O3− RSF on Si = 0.624 ± 0.020 (1 SD; ± 0.016 for 95% standard error) to calculate the Th concentration in each particle, while Naes et al. used the nominal Th concentrations to calculate an RSF.26 This led to an interpretational difference in our results.
Fig. 2 shows the results of our single-particle measurements with blue circles denoting particles consumed using O− primary ions and red triangles denoting O3−. Particle-to-particle, the measurements were consistent and the results between primary ion species agreed. The O− measurements had lower statistical precision due to a 2× lower ion yields relative to O3−.10 The relative SDs of the of the particle sets were generally between approximately 1% and 4%. The nominally 1% Th/U and 1000 μmol·mol−1 Th/U particles showed the best relative variation 1.3% using an O3− primary ion beam, which would represent an improvement over CRM U900 for calculating an RSF if they were certified. The lower-right panel of Fig. 2 shows the nominal vs. measured concentration of Th in the particles, which exhibited a linear relationship: slope = 0.704 ± 0.006 (1 σ) and intercept = (53 ± 1) × 10−6. Therefore, it appears that on average the particles contained approximately 30% less Th than their nominal target values in addition to a constant background of approximately 53 μmol·mol−1 Th/U.
This discrepancy between the nominal and measured Th contents can be explained by the uptake of excess water in the highly hydroscopic thorium nitrate feedstock during weighting, resulting in a systematic overestimation of the nominal Th content. The feedstock solutions, which were prepared by the dissolution of solid precursors (uranyl oxalate, and thorium nitrate) in water to form mother solutions, and the subsequent volumetric mixing to create solutions with a range of U/Th elemental ratios, resulted in the observed linearity of U/Th across the range of samples. Furthermore, the observed Th background is the result of a residual Th in the uranyl oxalate feedstock. The oxalate precipitation reaction used during the synthesis from uranyl nitrate was expected to have resulted in the removal of much of the ingrown Th, however, the incomplete removal of Th manifested in consistent background observable in the nominally 0 μmol·mol−1 and 1 μmol·mol−1 Th/U particle specimens. Future efforts will seek to mitigate this overestimation by preparing feedstock solutions using a Th solution with a well-characterized Th concentration, eliminating the impacts of water uptake during handling of the solid feedstocks. Additionally, the Th background in the uranyl oxalate feedstock may be reduced using extraction chromatography prior to synthesis using the oxalate precipitation reaction.
These observations resolve a discrepancy noted by Naes et al.,26 in which their calculated Th/U RSF value on Si of 0.53 did not match values of approximately 0.79 (on Si with O−) and 0.67 (on C) published previously.7,10 Their RSF of 0.53 was approximately 33% lower than ours of 0.79 (O− on Si), which was remarkably close to our observed 30% depletion in the expected Th content. We applied our O− RSF value to their raw data and found good agreement between measurement results from the two labs. Naes et al.26 had originally suggested that the discrepancy in RSF values was due to differences in instrument tuning. However, from our experience and from other round-robin testing, this magnitude of variation was far too large to be plausibly the result of our relatively minor differences in instrument tuning.49–52 There will, of course, be small differences between instruments, operators, and laboratories; however, we assert that similar samples and acquisition conditions should yield results with close agreement. We believe these initially different interpretations are reconciled and that the Th/U RSF for U particles is similar to what has been published by Szakal et al.7 and Groopman et al.10
The Th/U RSF has been shown to evolve during a particle measurement, as it is influenced by several surface chemistry factors.7,10 However, consuming most or all of a particle yields reproducible results for both standards and unknown particles. The mixed U–Th particles illustrate this well. Fig. 3 shows the cycle-by-cycle integrated Th concentration for a characteristic particle profile from each set. At each cycle, the Th and U signals were each integrated up to that point and then divided and scaled by the RSF. Therefore, the profiles show the measured concentration had the analysis been stopped at that cycle. The shaded regions show the statistical uncertainty expanded by the mean square of the weighted deviates (MSWD, also known as the reduced chi-squared statistic) of the preceding ratio values. If the apparent concentration were changing more than expected from counting statistics, the MSWD would become large and inflate the confidence band. Also shown are the weighted mean (WM) values for each set and the expanded 95% CI of the standard error of WM from Fig. 2. The different numbers of cycles reflect different primary beam currents and sputter rates. Most of the profiles followed a similar pattern, where the apparent concentration based on the integrated signals varied during sputtering, but eventually plateaued to a value in agreement with the dataset mean. The point at which this plateau began indicates the minimum amount of the particle that would need to be consumed to yield reproducible results. This appeared to occur, on average, after at least 50% of the particle were consumed. There was generally larger variability in the O− profiles, due both to lower useful yield and the more significant impact of the aforementioned phase transition of Si. The nominally 10% Th particles exhibited especially interesting behavior. The profile expanded uncertainties were very large due to local concentration variability and elemental heterogeneity (statistical uncertainty shown for comparison in dark red). However, fully consuming the heterogeneous particles led to good overall agreement within the set (Fig. 2). The 10% Th particles showed more variation among their profiles than the other particle sets, supporting the interpretation of elemental heterogeneity, but also making it difficult to deconvolve exactly which surface chemistry effect was most pronounced at any cycle (e.g., RSF changes, substrate changes, internal compositional changes). We can therefore conclude that each aerosol droplet likely contained near-identical concentrations of Th and U, but these elements became segregated during drying and calcining. In summary, the suites of particle analyses demonstrate the magnitude of variability that can be introduced into standard and unknown particle measurements if not enough of the particle were consumed, regardless of the level of internal elemental homogeneity. These findings also emphasize the difficulty in creating correction models for particles of unknown composition based on the profiling behavior of standards. Reproducible inter-element particle analyses are possible by consuming most of the particle for standards and unknowns.
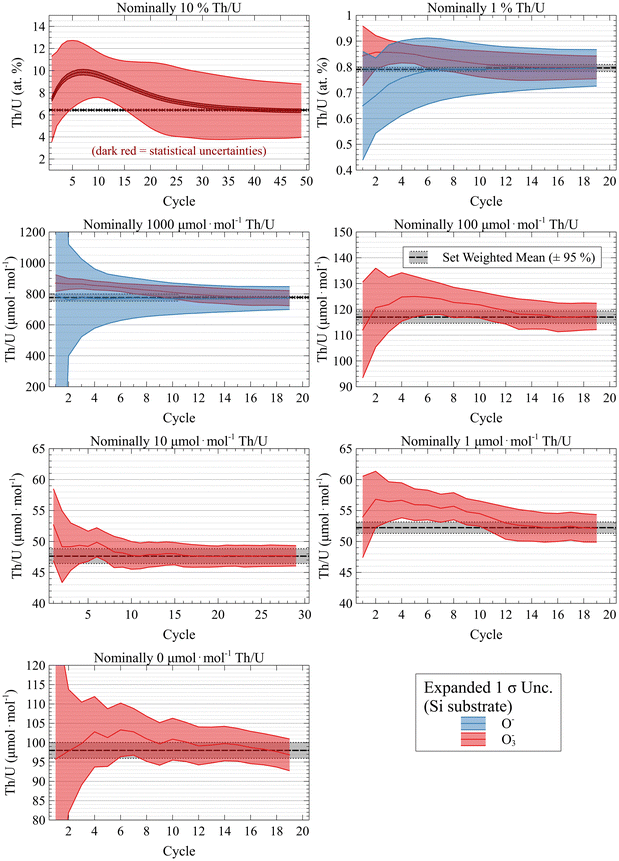 | ||
| Fig. 3 Integrated Th concentrations from SRNL U–Th particles. These demonstrate the necessity of consuming most of the particle to yield reproducible standard and unknown inter-element analyses. | ||
Poisson processes and model age confidence intervals
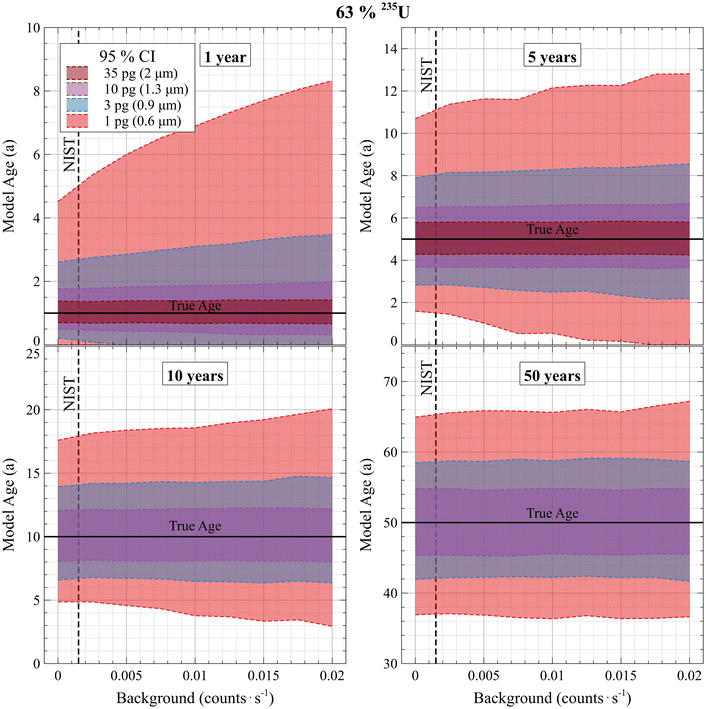
Fig. 4 demonstrates these effects for simulated particles with compositions matching CRM U200 (nominally 20% 235U), but of different masses and produced at different times. Uncertainty bands show Bayesian model age 95% CIs (described more later) for particles with initial ages of 0 a (red), 5 a (purple), and 10 a (blue). The top row shows analyses with O3− primary ions and the bottom with O− primary ions. As the time since the initial analysis increases, the CI bands grow larger, as described. This implies that at some time in the future, particles produced at unique times and that once had resolvable differences in model ages may no longer be distinguishable. The only potential remedy is to increase ionization efficiency or measure more material and/or aggregate particle measurements (discussed later), but these may not always be feasible. These examples highlight the importance of achieving as high of a useful yield as possible for all analyses, such as by using O3− primary ions. Another major implication is that there is effectively a “shelf-life” for any particle age dating reference materials produced whose purpose is to test the model age resolving power of a laboratory or analytical protocol. Particle size, composition, and instrument efficiency are all factors affecting how useful age dating reference materials may be to any given laboratory.
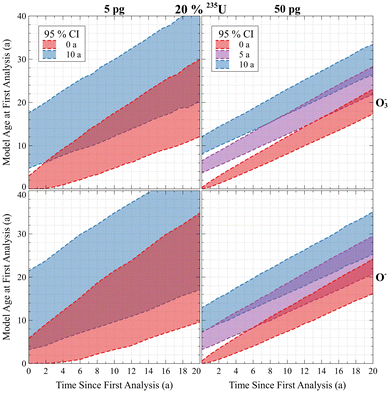 | ||
| Fig. 4 Simulations of ion yield and particle mass vs. model age time resolution. Absolute model age uncertainties always increase with particle age. | ||
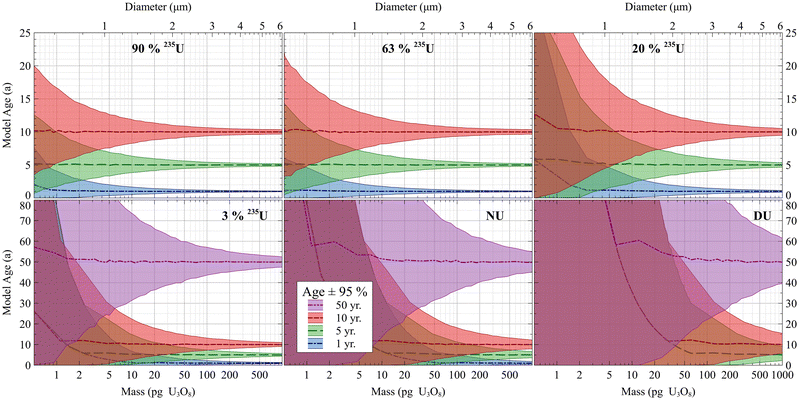
Fig. 5 shows a graphical version of Table 4 from Szakal et al.7 using our Bayesian model age CIs and simulating fully dense U3O8 particles with an O3− primary ion beam useful yield of 3.9%.10 The colored envelope labels represent the true particle ages and the dashed lines are the best estimate parameter, which is discussed in a later section. These plots further illustrate the relationships between mass (including aggregation and/or efficiency), enrichment, and age on the model age CIs. An interesting phenomenon is also apparent in the natural uranium (NU) and DU panels. Below a certain mass, there would be no expected 230Th counts, on average, for those ages. Therefore, the numerator of the model age ratio would plateau, but as mass decreases, the denominator, 234U, would also decrease. Even though the relative uncertainty of 230Th is almost always much larger than that of 234U, it remains critically important to count as many 234U atoms as possible to make a low- or zero-count observation of 230Th meaningful. The number of 234U counts acts as a lever arm, scaling the effective number of years of model age per each observed 230Th count. While a great deal of care must be used interpreting low-count 230Th measurements, at some point very large relative uncertainties on 230Th would be immaterial if enough 234U counts were collected. As an extreme example, it could plausibly matter very little if the relative uncertainty on a 230Th measurement were ± 100% in a scenario where there were enough 234U counts to scale the model age uncertainty to a highly precise value from a temporal perspective, such as a single day.
Detector background
Achieving a low and well characterized EM detector background is of utmost importance for particle age dating. The isotope of interest and background counts are produced by two independent Poisson processes. The sum of two or more independent Poisson random variables is also a Poisson random variable.53 This property applies to any number of independent variables, Xi, that follow Poisson processes, even with different parameters, μi:| Xi ∼ Poisson(μi) | (3) |
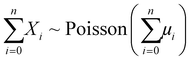 | (4) |
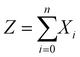 | (5) |
 | (6) |
| Z ∼ Poisson(μz) | (7) |
The processes are independent, in that the exact number of counts over a given time interval are drawn from their individual probability mass functions and are not influenced by which values were measured previously, only on the underlying Poisson parameters. These same equations apply to particle aggregation, detailed later. To deconvolve the observations into two independent Poisson processes, one must have information about one or more of the μ parameters, such as for the observed counts at m/z = 230: μobs = μ230Th + μbkgd. Since we generally do not have a priori knowledge of μ230Th, we can make long background and blank measurements before and after particle analysis to estimate the average μbkgd value and its uncertainty (the latter for Bayesian methods). One important aspect to note, however, is that even with precise knowledge of the average background rate, the accumulation of any background counts will increase the absolute uncertainty on the deconvolved μ230Th parameter. Traditional POE techniques can help illustrate this effect. If 10 counts were measured and two of them were expected to be background, (10 ± √10) − (2 ± √2) = 8.0 ± 3.5, which has a larger uncertainty than if eight counts were measured in the presence of zero background, since √8 ≈ 2.8. The same effect applies to Bayesian and frequentist CI methods and can be verified by numerical experimentation. Fig. 6 further illustrates this effect by showing Bayesian 95% model age CIs for simulated CRM U630 particles of different masses and ages plotted versus detector background rate assuming a useful yield of 3.9%. For reference, the LG-SIMS at NIST typically has an average monocollector EM background of 0.0015 ± 0.0005 counts·s−1. Depending on the particle mass, enrichment, and detection efficiency, higher detector background can add years onto a model age CI.
Model age confidence intervals
Szakal et al.7 chose the FC method35 for particle model age confidence intervals. In this paper we compare a Bayesian model developed for this work with the FC method and an updated version of FC by Roe and Woodroofe (RW).35,37 All of these methods incorporate information about the average detector background to produce CIs for the 230Th counts and/or the particle model age. Both the frequentist and Bayesian approaches tend to yield similar results when applied to identical problems, such as calculating a CI on counts of one isotope with a known average background rate. For a model age calculation, there are a few minor differences between the approaches. In the Bayesian method, all model parameters have an associated uncertainty, which is propagated numerically. In contrast, the FC and RW methods do not incorporate uncertainty on the average background count rate or abundance sensitivity. However, when the background count rate is relatively stable between analysis sessions, this uncertainty does not usually have a large impact on the model age results. In the Szakal et al.7 implementation, a FC CI for 230Th counts is produced and then scaled by the 234U counts, the RSF, and λ234 to produce a model age. When the number of 230Th counts can be well approximated by a Gaussian distribution, the FC method yields a CI that agrees with a traditional POE background subtraction, and POE can be used to include the uncertainties on 234U, the RSF, and λ234 on the model age; alternatively, the CI can be expanded symmetrically by the relative uncertainty on each parameter, which can be a decent approximation. However, for low 230Th counts or where the expected background counts are non-negligible by comparison, the underlying Poisson probability distribution represented by the FC CI is asymmetric. There is no accepted systematic method for combining CIs not representative of Gaussian-distributed variables or parameters with asymmetric uncertainties.38 However, in these cases it was assumed that the uncertainty on the 230Th measurement would be very much larger than all of the other uncertainty terms. To overcome the challenges of properly accounting for uncertainties in low 230Th count scenarios, aggregating particle data is useful because it can improve model age precision and also potentially make the 230Th counts more closely approximated by a Gaussian distribution where POE treatment becomes appropriate.Best estimate for a particle model age
In addition to a model age CI, it would be beneficial to have a robust point estimate that can be used for interpretation or subsequent calculations regardless of whether the probability distributions for the 230Th and 234U counts were symmetric or not. Bayesian methods provide a full posterior probability distribution for the model age and demonstrate that the probability is not symmetrically distributed within the 95% CI for low-count Poisson processes. Therefore, the midpoint of the 95% CI would be a biased estimator for Bayesian or FC methods. The Bayesian method allows for the calculation of descriptive parameters, such as the mode, mean, median, skew, and standard deviation of the posterior distribution. These descriptive statistics can be useful, especially since full probability distributions can be cumbersome to share or plot. However, the “best estimate” or most appropriate descriptive parameter of the distribution may depend on the application. Ideally, a best estimator should add value to the model age 95% CI and allow for easier manipulation and comparison of data from individual particles and aggregated model ages. For age dating of actinide particles, several quantitative criteria are desirable for a model age best estimate:• It should converge to the POE and maximum likelihood estimates in the limits that counts are large and background is negligible (i.e., distributions are approximately symmetric and Gaussian).
• Its uncertainty band should be able to include zero, but should not extend to non-physical negative values.
• It should cover the most probable values (i.e., represent the range of maximum likelihoods).
• It should be robust against Monte Carlo sampling variance and outlier values (for Bayesian methods).
• Symmetric uncertainties would be useful for plotting, subsequent POE, or use in regressions.
• Aggregation or averaging of individual particle “best estimates” should not be significantly biased relative to properly aggregated (summed) values.
• Ideally should be calculable using both Bayesian and FC methods, which are critical for analysis of low-count processes in the presence of background.
Several potential estimators were considered that could be calculated with the Bayesian method. Candidate estimators of central tendency of the model age posterior distribution were: mean ± SD; mode ± √mode; median ± median absolute deviation (MAD); Tukey biweight location ± biweight scale (robust mean and SD); trimmed mean (rejecting values outside of a Sigma threshold) ± trimmed SD; midpoint of the 95% CI ± CI half-width, “mid95”; and the midpoint of the 68.3% CI ± CI half-width, “mid68”. The mid68 estimator was found to be the only one considered that satisfied all of the above criteria, including being calculable using FC methods. Most estimators, such as the mean, median, and biweight, cannot be calculated using the FC method, since it only returns upper and lower confidence limits. When using the FC method, the CI calculation can be run twice: for the 68.3% CI to get the midpoint and half-width (1 σ) uncertainty, and for the 95% CI for expanded uncertainty about the mid68 location. Every other estimator we tried failed one or more criteria; see Table 2. A benefit of the mid68 estimator is that it is centered around the most probable 68.3% of the distribution, which excludes asymmetric tails that may have a large influence on the mean. A comparison of the 68.3% CI, with its midpoint as the “best estimate”, and 95% CI can be used to infer the level of asymmetry in the underlying probability distribution. This can help inform an analyst regarding interpretation of the CIs.
| Estimator | Uncertainty | Bayesian | FC | Can contain zero | Strictly non-negative | Robust | Converges to Gaussian | Covers majority of probability |
|---|---|---|---|---|---|---|---|---|
| Mean | SD | Yes | No | Yes | Yes | No | Yes | Yes |
| Mode | √Mode ? | Yes | No | Yes | No | No | Yes | Yes |
| Median | MAD | Yes | No | Yes | No | Yes | Yes | Yes |
| Biweight | Biweight scale | Yes | No | Yes | No | Yes | Yes | Yes |
| Trimmed Mean | Trimmed SD | Yes | No | Unknown | Unknown | Unknown | Yes | Yes |
| Midpoint of 95% CI | Quarter-width of 95% CI? | Yes | Yes | No | Yes | No | Yes | No |
| Midpoint of 68.3% CI (HDI) “mid68” | Half-width of 68.3% CI (HDI) | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
Fig. 7 demonstrates the utility of the Bayesian method for visualizing the underlying probability distributions of model ages beyond a 2-point CI. When the full posterior distribution is not available or is too cumbersome to share, the “mid68” best estimate adds significant information. Panels A through D in Fig. 7 show four simulated, hypothetical particles that have similar 95% CIs (approximately 0 to 10 years), despite different 230Th and 234U counts. The average expected background at m/z ∼230 for each particle was 0.6 counts (0.0015 counts·s−1 × 400 s). The number of 234U counts for each were (A) 15,650 counts (391 counts·s−1 over 40 s integration time for 234U), (B) 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 636 counts (566 counts·s−1), (C) 30,539 counts (763 counts·s−1), and (D) 39,060 counts (977 counts per s). The compare to the range of approximately 65
636 counts (566 counts·s−1), (C) 30,539 counts (763 counts·s−1), and (D) 39,060 counts (977 counts per s). The compare to the range of approximately 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 counts (1638 counts·s−1) to 929,400 counts (23
500 counts (1638 counts·s−1) to 929,400 counts (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235 counts·s−1) of 234U per particle for the SRNL purified U630 samples in Fig. 1. The particle represented in panel A is clearly more likely to be younger, e.g., less than 2 years old, than the panel C or D particles. As the number of 230Th counts increases, the mid68 increases and becomes resolved from zero. As the posterior distribution becomes more symmetric, the mean, mode, and mid68 estimators converge to the same value, with the mid68 remaining between the mean and mode. These simulated model age distributions have 95% CI midpoints that are approximately equal. If, by comparison to Gaussian statistics, we choose the quarter-width of the 95% CI to represent the “1 σ” uncertainty on the midpoint of the 95% CI (approximately 2.4 years to 2.5 years), we can see that significant fractions of the posterior probability would not be included in these examples. This estimator would result in bias when the posterior probability distributions are not symmetric, as in these examples. Furthermore, the quarter-width from the midpoint cannot, by definition, include zero or the lower bound of the CI. Unlike other proposed estimators, the midpoint of the 95% CI does not add any information about the underlying probability distribution beyond what is already captured in the CI limits itself, which, as demonstrated by this example, may not be sufficient to discriminate between different scenarios. Therefore, we conclude that the midpoint of the 95% CI is not an adequate best estimate for model ages.
235 counts·s−1) of 234U per particle for the SRNL purified U630 samples in Fig. 1. The particle represented in panel A is clearly more likely to be younger, e.g., less than 2 years old, than the panel C or D particles. As the number of 230Th counts increases, the mid68 increases and becomes resolved from zero. As the posterior distribution becomes more symmetric, the mean, mode, and mid68 estimators converge to the same value, with the mid68 remaining between the mean and mode. These simulated model age distributions have 95% CI midpoints that are approximately equal. If, by comparison to Gaussian statistics, we choose the quarter-width of the 95% CI to represent the “1 σ” uncertainty on the midpoint of the 95% CI (approximately 2.4 years to 2.5 years), we can see that significant fractions of the posterior probability would not be included in these examples. This estimator would result in bias when the posterior probability distributions are not symmetric, as in these examples. Furthermore, the quarter-width from the midpoint cannot, by definition, include zero or the lower bound of the CI. Unlike other proposed estimators, the midpoint of the 95% CI does not add any information about the underlying probability distribution beyond what is already captured in the CI limits itself, which, as demonstrated by this example, may not be sufficient to discriminate between different scenarios. Therefore, we conclude that the midpoint of the 95% CI is not an adequate best estimate for model ages.
Fig. 8 shows how several different estimators compare with respect to their point estimate (panels A and B), absolute uncertainty (panels C and D), and relative uncertainty (panels E and F) for a Poisson process with and without background. All calculations are from the Bayesian posterior distribution. The left-side panels show the estimators with no expected background. The right-side panels are shown with an expected background rate matching the NIST LG-SIMS of 0.0015 counts·s−1, or 0.6 counts on average over a 400 s measurement. The POE estimate is also shown for comparison, despite the expectation of only a fraction of a background count for the right-side panels. All of the estimators overlap within their uncertainties for a given n, but this does not make them equivalent or interchangeable. Since the point chosen for describing the central tendency of the model age is where a symmetric uncertainty is anchored, its location will have a distinct effect on interpretation at the 1 σ level. The mid68 estimator is robust against sampling variance and always yields physical, non-negative values. Of the robust estimators, the mid68 has the smallest absolute uncertainties. The coverage of a CI is defined as the probability that the CI will include the true value of the parameter of interest. If the CI is defined to be, e.g., 95%, then it is expected that nominally 95% of samples drawn from the underlying parameter distribution should have CIs that include the parameter's true value. All of the potential best central tendency estimators exhibit close-to-nominal coverage at the 68.3% level (Fig. 9), however, the mid68 achieves this with the smallest absolute uncertainties. These characteristics make it the preferable choice for a model age “best estimate” that adds resolution and interpretational value to a potentially asymmetric 2-point 95% CI.
 | ||
| Fig. 8 Model age estimator uncertainty and location comparison calculated from Bayesian posterior distributions. The mid68 estimator is robust and always yields physical values. | ||
The mid68 is the only estimator considered here that can be calculated using both the Bayesian and FC methods, whose 95% CIs otherwise find general agreement.46Fig. 10 shows a comparison of mid68 between the Bayesian, FC, and RW methods. The CIs at the 68.3% and 95% (panels A and B, respectively) levels show good agreement between the three methods. Note: the original FC method underestimates the CI width when the background counts are comparable or larger than the true, weak Poisson signal (e.g., n = 0 and 0.6 average expected background counts). The RW correction was developed to help resolve this issue and the Bayesian method implicitly mitigates it. Additional tables for the Bayesian mid68 values, 68.3% CIs, and 95% CIs are given in the ESI† for 230Th counts in the presence of background. In Fig. 10, the Bayesian method has the smallest absolute and relative uncertainties for most cases. The Bayesian method yielded the closest to the target coverage, with RW resulting in, on average, the most over-coverage (see ESI†). The larger relative and absolute uncertainties of the FC methods may explain the higher over-coverage in this scenario. However, all of these methods yield similar results and are generally in excellent agreement. The FC and RW methods were originally employed in particle age dating to address the challenges of interpreting weak Poisson signals amidst detector background. Bayesian methods complement these and have provided a path to identify estimators, such as mid68, that provide more information from particle age dating analyses and also work with the methods established by Szakal et al.7
 | ||
| Fig. 10 Comparison of mid68 estimators for Bayesian, FC, and RW methods. Both 68.3% CI and 95% CI are shown. | ||
Particle data aggregation
Aggregation of particle radiochronometry analyses has been considered as a method to increase the precision of a model age. Any such treatment must assume that the particles being aggregated represent the same source material, otherwise the aggregated result will simply represent the mixing and averaging of different sources, which may not be useful. Some information must be used to determine the validity of aggregation, such as a priori knowledge of the particles’ source, or sufficient similarity of elemental and isotopic compositions and/or individual model ages. Here, we will address the mathematical underpinnings of quantitative aggregation under the assumption that such aggregation is valid, which may need to be adjudicated on a case-by-case basis.As stated above, the sum of two or more independent Poisson random variables is also a Poisson random variable.53 This is, in fact, the property that allows an analyst to aggregate the number of counts of an isotope in a single particle measurement, which typically consists of repeated cycles of counting one or more isotopes. The number of counts in each cycle is independent, i.e., the number of counts in a measurement reflects statistical fluctuations at the collection time based upon the underlying μ parameter and not on the specific number of counts that were measured in the preceding or subsequent cycles. That is, the number of counts, n, in a cycle will follow the distribution shown in eqn (1) and will not be influenced by which n was observed previously. In addition, the mean Poisson parameter for a complete measurement would be the same whether the measurement were conducted over one long counting interval or were split into many cycles. There remain analytical and diagnostic reasons to split mass spectrometry measurements into shorter cycles, particularly on single-detector instruments, where the counts of different isotopes are not collected simultaneously and require time-interpolation. However, from a purely counting statistical standpoint, eqn (3)–(7) demonstrate the equivalency of the total- and split-measurement approaches. The μ parameter for an isotope can also evolve during a measurement, due to chemical sputtering effects, consumption of the particle, or changes in the primary beam intensity. However, the mean parameter of the total measurement can simply be recast as the aggregation of arbitrarily smaller, discretized measurement cycles, each with a different μi.
It follows that aggregating the counts from several particles will yield the mean count rate for each isotope over the cumulative measurement time. This is true regardless of the relative mass (size) of the particles or the total counting time per particle. Each parameter, μi, represents the average number of events to occur for measurement i. This is equivalent to the multiplication of the measurement time, ti, with a count rate, ri: μi = ri × ti. The rate can also be parameterized by, e.g., the particle size, si, the measurement efficiency of the isotope, μi (i.e., the useful yield, or the number of measured ions relative to the total number of atoms in the sample), the primary beam current, Ii, and many other factors, ci: μi = ci × Ii × μi × si × ti. However, since all of the factors affecting μi are multiplicative, such as particle size, it makes no difference to the resulting aggregation whether any of these factors varies between particles or vary during a measurement. From an aggregation perspective, the only thing that matters is the total number of counts collected for the isotopes of interest divided by their cumulative measurement times, which yield the average count rates and subsequently the aggregated model age. Spot-to-spot variation in signal intensity only matters if it differentially impacts or fractionates the isotope species being divided for the model age.
Szakal et al.7 performed aggregation by summing all of the 230Th and 234U counts from all particles, treating the sums as a single measurement. This is reasonable, since there isn't a general method for combining CIs without a deeper understanding of their underlying probability distributions. Here, we used our Bayesian framework to explore the validity of this treatment and verify eqn (3)–(7). We demonstrate that aggregating radiochronometry data cycle-by-cycle, particle-by-particle, or as a sum of all counts are equivalent. We also demonstrate that variations in μi due to, e.g., particle size or primary beam current, do not introduce bias into the aggregated results.
Aggregation simulations
To verify the equivalency of aggregation methods, we simulated 20 randomly sized particles with a target 230Th/234U ratio of 1 × 10−5, which would be comparable to a model age of approximately 3.5 years (assuming an RSF of unity for simplicity). Each particle consisted of 20 cycles with 20 s counting time on 230Th and 2 s counting 234U per cycle, consistent with a typical monocollector age dating measurement.7 Integer particle sizes were randomly selected between 1 and 5, where each integer value corresponded to 1 × 104 counts·s−1 of 234U on average per cycle, as shown in Table 3. Simulated counts of 230Th and 234U were drawn from Poisson distributions scaled by the particle sizes (see ESI†). A total of 111 230Th counts and 1,179,982 234U counts were simulated for all particles, yielding a maximum likelihood estimate (MLE) of the 230Th/234U ratio of (9.4 ± 0.9) × 10−6, which was consistent with the target ratio within statistical uncertainty. Three different background rates were chosen for the simulations: 0 counts per s, 0.0015 ± 0.0005 counts·s−1 (typical of the NIST LG-SIMS EMs), and 0.0150 ± 0.0016 counts·s−1 (10× NIST average). For the three background scenarios, 0 counts, 12 counts, and 120 counts were drawn, which corresponded exactly to the target background rates across the total simulated measurement time for the 20 particles. A simulation of identically sized particles with zero 230Th counts each was also performed to check for bias when measuring zero 230Th counts. All random numbers were drawn using the numpy.random module with a seed of “123456” in order: sizes, 230Th counts, 234U counts, background counts. Our Bayesian MCMC model was used to estimate the Poisson parameters under three scenarios. The Poisson log-likelihood models were fit to the same data but split into different numbers of observations: counts in each cycle, summed counts per particle, and total counts from all particles. Simulated, ground-truth data are presented here as a test of accuracy. However, the same methods also yield consistent results when using real particle data. Tables of the simulated counts are given in the ESI.†| Particle | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (×104 counts·s−1 234U) | 1 | 4 | 5 | 2 | 2 | 1 | 1 | 5 | 2 | 5 | 2 | 3 | 3 | 2 | 3 | 4 | 1 | 5 | 3 | 5 |
Aggregation with different background count rates
Table 4 and Fig. 11 show that the three aggregation scenarios agree with each other to within MCMC sampling variance, as they overlap almost precisely. As described above, there is no difference between summing all counts into a single observation, using summed counts per particle as observations, or using each individual cycle as an observation. This is true regardless of all of the other factors that influence count rates, such as particle size, primary beam current, particle consumption, etc. All of the aggregation scenarios also recovered the true underlying 230Th/234U ratio, within uncertainties. This naturally relied on good knowledge of the background count rate. The exact match in these cases between the central tendency estimators and true simulated ratio was a fortunate scenario since the number of simulated background counts over all particles exactly matched the average background rate. However, the number of drawn background counts could have easily been another value based on the Poisson variance. This would have caused the center of the posterior distribution to not fall exactly on the true ratio of the particles, just as the true number of 230Th and 234U counts in the simulated particles did not fall exactly on the target ratio of 1 × 10−5. However, this variance is clearly captured in the posterior distribution peak widths and the uncertainties on the mid68 and mean estimators. In the 10× typical background case, the number of simulated background counts was larger than the total number of 230Th counts (120 vs. 111), but the true ratio was still recovered. However, as demonstrated earlier, an increase in the background count rate increased the absolute uncertainty on the model age estimate. The mid68 uncertainty, SD, and 95% CI of the posteriors distributions all scaled with the background rate. The width of the 95% CI for the typical background case was approximately 12% larger than with no background; the CI width for the 10× typical background case was approximately 87% larger than with no background, and 67% larger than with typical background.| Background | Aggregation | Mid68 | 1 σ | Mean | 1 SD | 95% CI LL | 95% CI UL |
|---|---|---|---|---|---|---|---|
| Zero | Cycles | 9.45 | 0.90 | 9.50 | 0.90 | 7.78 | 11.30 |
| Zero | Particles | 9.43 | 0.90 | 9.49 | 0.90 | 7.74 | 11.25 |
| Zero | Total | 9.44 | 0.89 | 9.48 | 0.89 | 7.72 | 11.19 |
| Zero | Total FC | 9.43 | 0.93 | — | — | 7.74 | 11.30 |
| Typical | Cycles | 9.41 | 1.00 | 9.50 | 1.00 | 7.54 | 11.44 |
| Typical | Particles | 9.48 | 1.01 | 9.50 | 1.01 | 7.57 | 11.49 |
| Typical | Total | 9.40 | 1.01 | 9.49 | 1.01 | 7.50 | 11.44 |
| Typical | Total FC | 9.43 | 0.97 | — | — | 7.66 | 11.39 |
| 10× Typical | Cycles | 9.43 | 1.48 | 9.49 | 1.49 | 6.53 | 12.41 |
| 10× Typical | Particles | 9.43 | 1.49 | 9.50 | 1.49 | 6.57 | 12.40 |
| 10× Typical | Total | 9.49 | 1.49 | 9.49 | 1.50 | 6.64 | 12.47 |
| 10× Typical | Total FC | 9.43 | 1.31 | — | — | 6.98 | 12.06 |
| 10× Typical | Total RW | 9.43 | 1.31 | — | — | 6.98 | 12.06 |
Table 4 also shows the FC CIs for all background scenarios based on the total counts and RW for the 10× typical background scenario. For the zero-background case there was good agreement between the Bayesian and FC CIs. For the typical background case, the FC CI was approximately 5% narrower than the Bayesian CI, which may have been partly due to the additional uncertainty on the background rate incorporated into the Bayesian model. For the 10× typical background scenario, the FC and RW CIs were about 29% narrower than the Bayesian CI, and the mid68 uncertainty was roughly 21% smaller. The FC algorithms tend to underestimate the CI when the background counts are comparable to or larger than the true counts, which was the case here. However, the total aggregated counts were not near zero, so the RW correction did not yield any difference to the original FC algorithm.
Aggregation when all 230Th counts zero
We also performed aggregation simulations with the same randomly sized particles, but with all 230Th counts set to zero and with zero-background conditions, to check for any potential bias between the three aggregation methods. Fig. 12 panel A and Table 5 show the results of these simulations, where the three methods agreed very closely, to within MCMC sampling variance. Table 5 highlights the difference between the mid68 estimator and the posterior distribution mean, where the mid68 was much closer to the true value, whereas the mean was highly influenced by improbable but large-valued posterior samples.| Background | Aggregation | Mid68 | 1 σ | Mean | 1 SD | 95% CI LL | 95% CI UL |
|---|---|---|---|---|---|---|---|
| Zero | Cycles | 4.85 | 4.85 | 8.5 | 8.4 | 0 | 25.3 |
| Zero | Particles | 4.85 | 4.85 | 8.5 | 8.6 | 0 | 25.6 |
| Zero | Total | 4.85 | 4.85 | 8.5 | 8.5 | 0 | 25.3 |
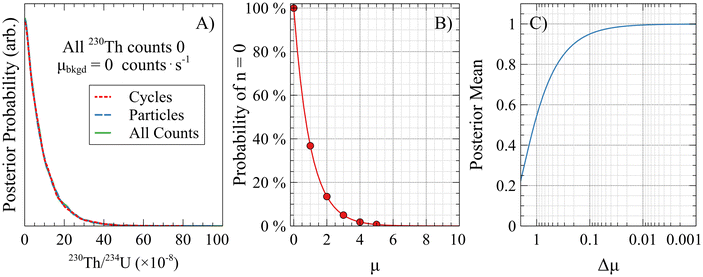
It may be unintuitive that upon measuring zero counts in an experiment, the mid68 or mean of the posterior probability distribution would be a non-zero positive number. However, consider a single Poisson process with a range of integer-valued μ parameters between 0 and 5. The probabilities of observing n = 0 counts for these different μ values using eqn (1) would be: 100%, 36.8%, 13.5%, 5.0%, 1.8%, and 0.7%, respectively (Fig. 12 panel B red circles). The mean of these six potential outcomes is 0.58 counts. However, all Poisson parameters that could reasonably yield n = 0 counts must be accounted for. Now let μ be a continuous variable greater than zero. If the range of considered μ values were increased to be between 0 and 10 counts, and the n = 0 probabilities for a larger number of closely-spaced μ values were calculated, it yields the (un-normalized) posterior probability distribution, essentially following Bayes’ theorem (Fig. 12 panel B red line). As the number of μ values increases towards the continuous limit (Δμ → 0), the mean of the posterior distribution approaches one (Fig. 12 panel C), which agrees exactly with a Bayesian MCMC fit to an observation of zero counts. The maximum likelihood of this distribution, located at zero, is equal to the Floor(mean) and Ceiling(mean) minus 1, consistent with the definition of a Poisson process. When using the mid68 estimator, it is important to be mindful that it may represent an underlying asymmetric probability distribution, so care must be taken when combining such values to avoid introducing bias into the final result.
Biased aggregation methods
The simulated data above were also used to demonstrate aggregation methods that result in bias and should be avoided. Fig. 13 panel A shows the equivalency of three aggregation scenarios for the zero-background case (for simplicity), as in Fig. 11 panel A. The 68.3% CI and 95% CI regions are shaded for clarity. In Fig. 13 panel B, the posterior distributions for each of the 20 particles are shown with light grey curves. Most of these posterior distributions are asymmetric due to the low number of 230Th counts. The dark black curve shows the mean of the posterior distributions themselves. This result is biased high of the true value, with a mean value of (1.1 ± 0.1) × 10−5 (1 σ), and a 95% CI of [8.9 × 10−6, 1.3 × 10−5]. This was resolvable from both the simulated target value of 1.0 × 10−5 and the observed value of (9.4 ± 0.9) × 10−6 at the 1 σ level and did not well represent the properly aggregated values. This type of bias can occur any time when the ratio of two variables is not described by a symmetric distribution, such as when measurements result in low 230Th counts. | ||
| Fig. 13 Example of biased (panel B) and less biased (panels A & C) aggregation methods of simulated particles. | ||
In mass spectrometry, this effect is well known, and it often occurs when taking the ratio of two isotopes that are orders of magnitude different in abundance so that the ratios are very small or very large. Over the course of a mass spectrometry measurement, particularly on a single-collector instrument, isotopes are collected serially by cycling the measurement of each isotope in turn and repeating. Breaking the measurement down into cycles provides time resolution to help troubleshoot acquisition artifacts and to determine when to conclude a measurement (e.g., if the sample is sputtering away). For particles, the count rates of each isotope change over time as the sample is consumed, so cycling improves time interpolation and proper characterization of the sample as it evolves. Often, instrument dynamic range considerations or sample size limitations mean that the underabundant isotope may not have an approximately Gaussian distribution of counts on a per-cycle basis (i.e., it will have very few counts). Therefore, the ratio of isotopes at each cycle will be defined by an asymmetric probability distribution. Taking the average of cycle-by-cycle ratios leads to bias and misinterpretation of results in these cases, e.g. ref. 20 and 21. It is more appropriate to sum the total counts of each isotope first before taking their ratio or apply some other ratio schema that accounts for correlations during the profile. This same effect is shown in the Fig. 13 panel B example, since the model age represents a scaled isotope ratio. As an alternative means to mitigate aggregation bias, we experimented with weighted and unweighted harmonic and geometric mean of model ages, posterior distributions, and cycle-by-cycle ratios, but these approaches did not appear to not be universally applicable in all circumstances.
Approximate aggregation using Mid68 estimators
Summing cycles, particles, and/or total counts is the most appropriate method to aggregate actinide particle data for constructing a model age, assuming that the particles of interest are truly from the same source and that the detector background for each measurement is well understood. This is particularly the case when the model age CIs include zero. However, there may be occasions where the raw count data and associated corrections or full posterior distributions are not available for each particle measurement, such as processed model ages for a suite of particles shared between laboratories. In these cases, it would be beneficial if the “best estimate” values and/or CIs could be used to produce a population (or subset) average that were not significantly biased from the properly aggregated value.Fig. 13 panel C shows the posterior distributions from panel B represented by mid68 ± half-width (1 σ) estimators (black circles with error bars). The arithmetic weighted mean (WM) and unweighted mean (AVG) of these estimators show good agreement with the properly aggregated values, within uncertainties. However, the WM is slightly lower than AVG for this selection of data and is less accurate. For the WM, weights are typically calculated as the inverse of the variance (square of the uncertainty), which minimizes the variance of the WM for normally distributed data. However, the model ages here are not normally distributed, so this weighting scheme may not be the most appropriate. For a Poisson process, the absolute uncertainty always increases with higher counts. Therefore, a particle with fewer 230Th counts simply due to statistical scatter would be weighted more heavily than a particle with more 230Th counts, even if they were drawn from the same distribution. Through empirical investigation, we found that rescaling the conventional inverse-variance weights by raising all weights to the power of 1/e, where e is Euler's number, results in exceptionally good agreement with the aggregated value. This value is labeled on the plot as WMexp.
There exists an edge case where using WMexp of the mid68 values may result in a biased aggregation estimate compared to summing counts, so some caution is required. As shown in Fig. 5, for each enrichment and age example, there exists a particle mass or size cutoff below which no 230Th counts would be expected, on average. A reduction in mass below this point yields inflated model age mid68 values due to the lower 234U counts. If most of the particle data to be aggregated were from this regime, the WMexp could be biased, especially with variations in particle size. In this case, summed aggregation would be the most appropriate method to use.
Returning to the first example presented in this paper, purified and remade U630 particles, Fig. 14 shows a comparison of the properly aggregated model ages and the approximate WMexp aggregation using the mid68 estimators for each particle model age in each session. There was excellent agreement and no apparent bias in the WMexp method, with the slope and intercept being unity and zero within uncertainties: 0.99 ± 0.06 (1 σ) and -0.01 ± 0.09 (1 σ), respectively. The WMexp method remains an approximation, based only on the 68.3% most probable model age values and not the tails of the posterior distributions. As such, the absolute and relative uncertainties for each session are more often slightly larger when using WMexp than when aggregating counts. The WMexp method lowers the weight of larger particles with more precise particle ages, unlike aggregating by summing counts, which implicitly weights large particles more than small ones. Therefore, comparing the two methods can be useful for validating the assumption that the materials are from the same source, and that the mathematically proper aggregation method is not completely skewed toward, say, one large particle in a suite. These examples demonstrate that a reliable, though approximate, aggregation can be performed using only the mid68 “best estimator” values when the underlying count data or full posterior distributions are not available. These results increase the confidence that the mid68 estimator is meaningful and useful information for model age interpretation, in addition to a 95% CI and/or a full posterior probability distribution.
Conclusions
A robust method for age dating of U microparticles by LG-SIMS was recently introduced by Szakal et al.7 that addressed many of the associated analytical challenges. Most notable among these were potential causes of interferences, such as molecular isobars, abundance sensitivity (scattering from intense nearby peaks), and detector background. Also addressed was the evolution of the Th/U RSF during consumption of a particle. This method was amply demonstrated on numerous NIST/NBL CRMs and two unknown samples with known production dates. At the time of its writing, the youngest material analyzed was approximately 15 years old.In this study, we expanded upon the work of Szakal et al.,7 analyzing remade and radiochronometrically reset particles of CRM U630 from PNNL over the course of approximately 3.5 years to investigate the efficacy and potential bias present when analyzing extremely young material. We found no distinguishable bias present in the age dating analyses, as our model age predictions yielded a linear relationship with a slope of unity relative to the true age, within uncertainty. An offset was found in the model age regression indicating the initial presence of 230Th in the remade particles. Its magnitude was consistent with the purification of 99.3% ± 0.2% of the initially ingrown 230Th from CRM U630. We further explored the effects of detector background, ionization efficiency, and inter-element variability on age dating results. In general, it is extremely important to achieve the highest ion detection efficiency and to reduce the detector background to a minimum, i.e., to achieve the highest signal-to-noise ratio, especially for small, young, and/or low-enriched U particles. Mixed U–Th particles from SRNL with a nominally 6-order-of-magnitude range in Th contents were used to illustrate the effects of particle heterogeneity, RSF evolution, and substrate chemistry on age dating analyses. As demonstrated by Szakal et al.7 and confirmed here, it is important to consume at least 50% of each standard and unknown particle to achieve reproducible RSF and model age results. Plotting the integrated RSF or Th concentration with respect to analysis time (or cycle) can give an indication of how much of a particular type of particle to consume to achieve reliable results. Consuming less than 50% of a standard or unknown particle (or while the integrated RSF is varying cycle-to-cycle) can add unnecessary variance. On a related note, large-area scanning of planchets, such as by Cameca's automated particle measurements (APM) program, can be similarly impacted by these effects. Caution is warranted when analyzing mixed-element particles in this manner, since very little of each particle is consumed. The statistical precision of the measurement will be limited due to the dwell times per pixel utilized for scanning large areas, but the results will also be more representative of the transient period in RSF values and particle and substrate evolution. Therefore, single-particle microprobe measurements afterwards will likely remain necessary for inter-element accuracy. Due to the variety of surface chemistry effects present and the difficulty of exactly matching standard and unknown particle compositions, we recommend this “full consumption” method as opposed to other potential corrections.
In this study we also examined methods for aggregating U microparticle model ages to investigate potential causes bias. Using a Bayesian framework we demonstrated the validity and equality of three aggregation scenarios: using cycle-by-cycle counts as observations, using summed particle counts as observations, and using total summed counts as a single observation, all with different simulated detector background conditions. These results agree with the FC treatment suggested by Szakal et al. We also suggested a new estimator, the midpoint of the 68.3% CI with half-width uncertainty, called “mid68”, as the best model age estimator that adds value to a 95% CI. For analyses of particles with low 230Th counts in the presence of detector background, POE estimators are unsatisfactory, as they can cover nonphysical values. Likewise, the mean of the Bayesian posterior distribution can be overly influenced by large but very unlikely values, and it cannot be calculated using frequentist methods, such as FC. The mid68 estimator satisfies the desirable criteria specified in this study, adding value to a 2-point 95% CI estimate of a model age and providing a value with a symmetric uncertainty that can be easily used later for approximate aggregation or use in regressions. We found that a modification to the traditional arithmetic weighted mean, raising the inverse-variance weights to the power of (1/e), enabled the use of individual mid68 estimators to reproduce the aggregated model ages of both simulated and real-world particle sets. The new model age estimator and approximate aggregation method could be useful when a person evaluating the results does not have access to the underlying raw data and all associated correction factors.
Author contributions
EEG: wrote paper, developed methods, collected data, wrote software, performed analyses. TLW: developed methods, collected data, performed analyses. TRP: produced purified U630 particles. SMS: produced mixed U–Th particles. MW: produced mixed U–Th particles. MB: produced mixed U–Th particles.Data availability
The data supporting this article have been included as part of the ESI.† Data for this article, including spreadsheets, are also available at https://doi.org/10.18434/mds2-3692.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding for development and production of the mixed U–Th microparticles and purified CRM U630 microparticles was provided by the National Nuclear Security Administration of the Department of Energy, Office of International Nuclear Safeguards. This work was produced in conjunction with Battelle Savannah River Alliance, LLC under Contract No. 89303321CEM000080 with the U.S. Department of Energy. The Pacific Northwest National Laboratory is operated for the U.S. Department of Energy by Battelle Memorial Institute under Contract No. DE-AC05-76RL01830. We thank our colleagues for helpful discussions, guidance, manuscript reviews, and support, in particular Dave Simons (MELE Associates), Albert Fahey (Corning, Inc.), Travis Tenner (LANL), Ben Naes (LANL), Mindy Zimmer (PNNL), Steve Buntin (NIST), and Amanda Förster (NIST). We thank the NIST Editorial Review Board and anonymous external reviewers for their reviews.References
- A. Axelsson, D. M. Fischer and M. V. Peńkin, J. Radioanal. Nucl. Chem., 2009, 282, 725–729 CrossRef CAS.
- D. L. Donohue, J. Alloys Compd., 1998, 271, 11–18 CrossRef.
- D. L. Donohue and R. Zeisler, Anal. Chem., 2012, 65, 359A–368A CrossRef.
- M. J. Kristo, in Handbook of Radioactivity Analysis, ed. M. F. L'Annunziata, Academic Press, 4th edn, 2020, vol. 2, pp. 921–951. DOI:10.1016/B978-0-12-814395-7.00013-1.
- K. J. Moody, P. M. Grant and I. D. Hutcheon, Nuclear Forensic Analysis, CRC Press, 2005 Search PubMed.
- Research and Development Plan: Enhancing Capabilities for Nuclear Verification, Report STR-385,IAEA Safeguards, Vienna, Austria, 2018.
- C. Szakal, D. S. Simons, J. D. Fassett and A. J. Fahey, Analyst, 2019, 144, 4219–4232 RSC.
- K. J. Coakley, J. D. Splett and D. S. Simons, Meas. Sci. Technol., 2010, 21, 035102–035118 CrossRef.
- A. L. Faure and T. Dalger, Anal. Chem., 2017, 89, 6663–6669 CrossRef CAS PubMed.
- E. E. Groopman, T. L. Williamson and D. S. Simons, J. Anal. At. Spectrom., 2022, 37, 2089–2102 RSC.
- D. S. Simons and J. D. Fassett, J. Anal. At. Spectrom., 2017, 32, 393–401 RSC.
- P. M. L. Hedberg, P. Peres, F. Fernandes, N. Albert and C. Vincent, J. Vac. Sci. Technol., B:Nanotechnol. Microelectron.:Mater., Process., Meas., Phenom., 2018, 36, 03F108-1–03F108-5 Search PubMed.
- P. M. L. Hedberg, P. Peres, F. Fernandes and L. Renaud, J. Anal. At. Spectrom., 2015, 30, 2516–2524 RSC.
- Y. Ranebo, P. M. L. Hedberg, M. J. Whitehouse, K. Ingeneri and S. Littmann, J. Anal. At. Spectrom., 2009, 24, 277–287 RSC.
- A. J. Fahey, N. W. M. Ritchie, D. E. Newbury and J. A. Small, J. Radioanal. Nucl. Chem., 2010, 284, 575–581 CrossRef CAS.
- A. Benninghoven, F. G. Rüdenauer and H. W. Werner, Secondary ion mass spectrometry : basic concepts, instrumental aspects, applications, and trends, edA. Benninghoven, F. G. Rüdenauer and H. W. Werner, J. Wiley, New York, 1987 Search PubMed.
- R. G. Wilson, F. A. Stevie and C. W. Magee, Secondary Ion Mass Spectrometry: A Practical Handbook for Depth Profiling and Bulk Impurity Analysis, Wiley, 1989 Search PubMed.
- E. Zinner, Scanning, 1980, 3, 57–78 CrossRef CAS.
- E. E. Groopman, T. L. Williamson, K. M. Samperton, S. M. Scott, B. J. Foley, M. G. Bronikowski, G. S. King and M. S. Wellons, J. Anal. At. Spectrom., 2025 10.1039/d5ja00115c.
- C. D. Coath, R. C. J. Steele and W. F. Lunnon, J. Anal. At. Spectrom., 2013, 28, 52–58 RSC.
- R. C. Ogliore, G. R. Huss and K. Nagashima, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1910–1918 CrossRef.
- K. J. Coakley, D. S. Simons and A. M. Leifer, Int. J. Mass Spectrom., 2005, 240, 107–120 CrossRef CAS.
- N. Sharp, J. D. Fassett and D. S. Simons, J. Vac. Sci. Technol., B:Nanotechnol. Microelectron.:Mater., Process., Meas., Phenom., 2016, 34, 03H115-1–03H115-6 Search PubMed.
- K. Wittmaack, Surf. Interface Anal., 1996, 24, 389–398 CrossRef CAS.
- C. A. Barrett and N. C. Anheier, UO2 Particle Standards: Synthesis, Purification & Planchet Preparation, United States, 2016 Search PubMed.
- B. E. Naes, S. Scott, A. Waldron, S. Lawson, M. G. Bronikowski, L. I. Gleaton, R. J. Smith, K. N. Wurth, T. J. Tenner and M. Wellons, Analyst, 2023, 148, 3226–3238 RSC.
- C. Venchiarutti, Y. Aregbe, R. Middendorp and S. Richter, NUSIMEP-9 – Uranium isotope amount ratios and uranium mass in uranium micro-particles – Nuclear signatures inter-laboratory measurement evaluation programme, Publications Office, 2019 Search PubMed.
- P. Kegler and S. Neumeier, “Production, Analysis, and Application of Microparticulate Uranium Oxide-based Reference Materials” in Proceedings of the INMM & ESARDA - Joint Annual Meeting, May 22–26, Vienna, Austria, 2023.
- D. Mayberry, R. Stene, K. Koh, C. Awino, A. Albrecht and T. Pope, “Aspects of Crystal Growth and Atomic-Scale Characterization of Uranium Oxide Micro-Particles” in Proceedings of the INMM & ESARDA - Joint Annual Meeting, May 22–26, Vienna, Austria, 2023.
- S. Neumeier, P. Kegler, S. Richter, S. Hammerich, M. Zority, C. R. Hexel, B. T. Manard, A. K. Schmitt, M. Trieloff, S. K. Potts, D. Bosbach and I. Niemeyer, “Production and Analyses of Uranium Oxide Microparticulate Reference Standards: Current Status and Outlook” in Proceedings of the INMM & ESARDA - Joint Annual Meeting, May 22–26, Vienna, Austria, 2023.
- N. Gehrels, Astrophys. J., 1986, 303, 336–346 CrossRef CAS.
- B. P. Roe and M. B. Woodroofe, Phys. Rev. D, 2000, 63, 013009-1–013009-9 CrossRef.
- J. Conrad, Comput. Phys. Commun., 2004, 158, 117–123 CrossRef CAS.
- R. D. Cousins, K. E. Hymes and J. Tucker, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2010, 612, 388–398 CrossRef CAS.
- G. J. Feldman and R. D. Cousins, Phys. Rev. D, 1998, 57, 3873–3889 CrossRef CAS.
- R. P. Kraft, D. N. Burrows and J. A. Nousek, Astrophys. J., 1991, 374, 344–355 CrossRef.
- B. P. Roe and M. B. Woodroofe, Phys. Rev. D, 1999, 60, 053009-1–053009-5 CrossRef.
- R. Barlow, Asymmetric Statistical Errors, arXiv, 2004, preprint, arXiv:physics/0406120, DOI:10.48550/arXiv.physics/0406120.
- P. Croatto, U Series Reference Material Production, Age, and Sourcing, New Brunswick Laboratory, 2014 Search PubMed.
- H. Cheng, R. L. Edwards, C.-C. Shen, V. J. Polyak, Y. Asmerom, J. Woodhead, J. Hellstrom, Y. Wang, X. Kong, C. Spötl, X. Wang and E. C. Alexander, Earth Planet. Sci. Lett., 2013, 371–372, 82–91 CrossRef CAS.
- T. Williamson, E. Groopman and D. Simons, “Dual Chronometer Measurements of Uranium Particles by LG-SIMS” in Proceedings of the INMM & ESARDA-Joint Annual Meeting, Vienna, Austria, 2023.
- T. L. Williamson, D. S. Simons and J. D. Fassett, “Multi-Collector Configuration Considerations And Substrate Relative Sensitivity Factor Effects for Age-dating Measurements of Particles by Large Geometry Secondary Ion Mass Spectrometry” in Proceedings of the INMM & ESARDA-Joint Virtual Annual Meeting, 2021.
- E. E. Groopman, T. L. Williamson and D. S. Simons, “Recent Advances in Uranium Particle Analyses by LG-SIMS” in Proceedings of the INMM & ESARDA-Joint Annual Meeting, Vienna, Austria, 2023.
- Certain commercial equipment, instruments or materials are identified in this paper to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
- O. Abril-Pla, V. Andreani, C. Carroll, L. Dong, C. J. Fonnesbeck, M. Kochurov, R. Kumar, J. Lao, C. C. Luhmann, O. A. Martin, M. Osthege, R. Vieira, T. Wiecki and R. Zinkov, PeerJ Comput. Sci., 2023, 9, e1516 CrossRef PubMed.
- E. Groopman, FCpy (Version 0.1.3) [Computer Software], DOI:10.18434/mds2-2755, https://github.com/usnistgov/fcpy.
- D. York, Earth Planet. Sci. Lett., 1968, 5, 320–324 CrossRef.
- D. York, N. M. Evensen, M. L. Martinez and J. D. Delgado, Am. J. Phys., 2004, 72, 367–375 CrossRef.
- A. J. Fahey, Int. J. Mass Spectrom., 1998, 176, 63–76 CrossRef CAS.
- R. L. Hervig, F. K. Mazdab, P. Williams, Y. B. Guan, G. R. Huss and L. A. Leshin, Chem. Geol., 2006, 227, 83–99 CrossRef CAS.
- R. W. Hinton, Chem. Geol., 1990, 83, 11–25 CrossRef CAS.
- R. G. Wilson and S. W. Novak, J. Appl. Phys., 1991, 69, 466–474 CrossRef CAS.
- E. L. Lehmann, Testing statistical hypotheses, 2nd edn, 1986, Wiley, New York Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5an00249d |
| This journal is © The Royal Society of Chemistry 2025 |