 Open Access Article
Open Access ArticleSurface charge regulation mediates anomalous ion transport in silica nanochannels
Kaushik K.
Rangharajan
 and
Shaurya
Prakash
and
Shaurya
Prakash
 *
*
Department of Mechanical and Aerospace Engineering, The Ohio State University, 201 W. 19th Avenue, Columbus, OH 43210, USA. E-mail: prakash.31@osu.edu
First published on 13th May 2025
Abstract
A hybrid microfluidic–nanofluidic device was evaluated for the transport of a variety of ions with the purpose of enhancing the understanding of surface charge regulation for electrokinetic transport within silica nanochannels. A bank of three nanochannels at 16 nm depth connected two microfluidic channels that acted as fluid and electrolyte reservoirs for the experimental and modeling studies reported in this work. Surface charge regulation was noted to be dependent on the size of the hydrated cation, the type of anion, and the electrolyte concentration for the negatively charged silica nanochannels, with anomalous transport being observed. The results reported here provide new insight into the impact of surface charge regulation as a function of ion type and electrolyte concentration within nanochannels and subsequently raise the possibility of tuning electrolyte solution composition to manipulate surface charge and subsequent electroosmotic flow within nanochannels.
Introduction
Nanoscale conduits like nanochannels, nanopores, and nanotubes present important interfaces in biological1,2 and engineered systems3 for water desalination,4,5 energy generation,6–10 biosensors,11 or fluidic analogues of solid-state electronics.10,12–16 Essential for the viability of all these applications is a clear, complete, and mechanistic understanding of fundamental nanoconduit-surface–ion–water interactions, which vary significantly from bulk flows17,18 due to high surface area to volume ratios, with the nanoconduit surface charge having been identified as an essential variable impacting electrokinetic nanoscale flows.19,20Modulation of surface charge within nanoscale conduits is particularly important when the electrokinetic radius,21,22i.e., the ratio of nanoconduit size to electric double layer (EDL) thickness is O(1), as at these scales ionic selectivity and transport are governed by the surface charge. In this context, recent reports have highlighted the critical role of the phenomenon of surface charge regulation,23,24i.e., the change in surface charge due to ion or solute interactions with nanoconduit walls.25 Charge regulation has been shown to influence surface potentials within a nanofluidic device governed by characteristic length scales and geometries, the separation distance of electric double layers, the solution composition, or the applied voltages.26 Surface charge regulation27,28 has also been associated with reports of anomalous mole fraction effects due to nanoscale conduits presenting a lower ionic conductance with ion mixtures in solution in comparison with the same concentration of either ionic species by itself.27 The effect of charge regulation is significantly enhanced when working with dilute electrolyte solutions as the EDL occupies a significant fraction of nanoconduits. Moreover, recent work has also evaluated the regulation of surface charge leading to reversal of the native surface charge polarity due to excessive charge screening.29
Notably, the interaction of ions in solution with surface charges has been a topic of intense study for many years with the screening of surface charge being known to be highly dependent on the chemical structure of the entire solution.25 Theoretically, these investigations have largely focussed on the use of mean field theories such as the Poisson–Boltzmann equation; however, neither these theories work well in multivalent systems with strong ion–ion correlations, nor do these theories account for variations in ion and water densities near physical surfaces, discrete ionic and molecular sizes, and hydration of solvated ions.20,28 Therefore, advanced methods such as molecular dynamics simulations have been used to elucidate molecular details of ion–surface interactions.29
Previous studies have also reported surface charge regulation, including the phenomenon of charge inversion, as a key mediator of ion transport within nanoconduits.20,23,29–31 Yet, a key knowledge gap remains – there is a paucity of experimental data demonstrating charge regulation for a variety of cations and anions. Nearly all reported data remain limited to K+ with some emerging reports on Na+, Ca2+, and Mg2+ as other cations of interest.23,24,32,33 It is worth noting that there are no reports evaluating the effect of different anions in solution beyond the monovalent anion Cl−.
In this study, we report the experimental data on the transport of a broad array of both cations (Na+, K+, Ca2+, Mg2+, and Ba2+) and anions (Cl− and SO42−) through a parametric evaluation of valence and ion size (including hydrated ion radii) in slit-like (16 nm deep) silica nanochannels. Given the purpose of this work, that is, to report experimental data for ion transport in nanochannels, both cations and anions were chosen to reflect comparative analyses with known ions. Therefore, K+ and Cl− present validation to existing data. Mg2+ and Ca2+ complement the largely numerical work for additional ions, with new trends being reported that enhance some of the literature on divalent ion transport. Ba2+ is an emerging ion for a variety of applications such as water treatment of difficult-to-treat waters. Finally, the anion SO42− was chosen as a common divalent anion that complements the presence of chloride in applications such as water treatment.34 Our evaluation shows deviations from trends expected from the current state-of-the-art suggesting that surface charge regulation can lead to anomalous ion transport within nanochannels.
Methods
Nanofluidic device fabrication
The nanofluidic device uses two microfluidic channels (8 μm (H) × 50 μm (W) × 3 cm (L)) as fluidic reservoirs to connect a bank of three ultra-low aspect ratio (ULAR) nanochannels, 16 nm deep (30 μm (W) × 2.5 mm (L)). The fabrication process has been reported previously.35,36 Briefly, the micro- and nanofluidic channel network was patterned on a borosilicate glass substrate using standard UV lithography followed by wet etching using hydrofluoric acid (HF; Sigma-Aldrich). The top glass cover with holes drilled for fluidic access and the bottom glass slide comprising the etched channels were bonded using calcium-assisted glass bonding.37 The fabrication results in a hybrid microfluidic–nanofluidic device with fluorescence verification of flow in the nanochannels as shown in Fig. 1.Device operation
The microfluidic and nanofluidic channels were initially filled with various salt solutions prepared in de-ionized water to yield concentrations ranging from 0.001 to 10 mM. All salts (CaCl2, BaCl2, MgCl2, and CaSO4) were purchased from Sigma-Aldrich and used without modification. The pH of all solutions was monitored and maintained at 7.2 ± 0.2 with experiments conducted at room temperature. All nanochannel conductance measurements were conducted using methods previously reported and in an earth-grounded Faraday cage to minimize electrical interference.23,38 Briefly, the device testing setup included a power supply (Keithley 3390 function generator) used to apply a streamwise-axial (Va) potential with Va = 2 V. Current (I) through the nanochannels was monitored using a Keithley 6485 picoammeter. Devices were tested at each respective concentration to measure the intrinsic nanochannel conductance. Dedicated devices for each type of electrolyte were used to avoid contamination. Each device was initially tested with deionized (DI) water (18 MΩ, 10−7 M salt) to provide the same baseline for comparison between devices. Only devices with an initial DI water conductance within 0.15 ± 0.1 nS were used for comparison of results across devices as a function of ion type. The reported intrinsic DI-water conductance in the channels is similar to that reported in previous work39 and confirms the valid operation of our devices.Numerical modelling
The hybrid microfluidic–nanofluidic device can be modelled using well-known governing equations that have also been reported previously.13,40 Briefly, the nanochannel was modelled as a symmetric nanochannel with a total depth of 16 nm. The primary experimentally measured parameter is the electric current, arising from the flux of ions as given by eqn (1).
as given by eqn (1). | (1) |
 is the convective velocity. Ionic mobility is related to the diffusion coefficient as εi = eDi/kbT where e is the elementary charge, kb is the Boltzmann constant, and T is the absolute temperature.41 The summation of the ionic flux across all the species and subsequently integrating over the cross-section area and multiplying with the Faraday constant (F) and valence of each species then provides the total ionic current, I, which is typically measured.40 The steady-state flux continuity is given by
is the convective velocity. Ionic mobility is related to the diffusion coefficient as εi = eDi/kbT where e is the elementary charge, kb is the Boltzmann constant, and T is the absolute temperature.41 The summation of the ionic flux across all the species and subsequently integrating over the cross-section area and multiplying with the Faraday constant (F) and valence of each species then provides the total ionic current, I, which is typically measured.40 The steady-state flux continuity is given by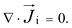 | (2) |
The model assumed an incompressible, isothermal fluid with the viscosity, density, and electrical permittivity of water remaining constant. The inlet and exit concentrations of ionic species were assumed to be the same as those of the bulk, defined by the experimental conditions. No ionic flux normal to nanochannel or microchannel walls was permitted.13 The equilibrium potential in the nanoscale conduit and the microchannel reservoirs is governed by the Poisson equation as follows:
 | (3) |
 | (4) |
Results and discussion
Context for results
Previous work on surface charge regulation has shown that at a particular electrolyte concentration, the surface charge polarity can change, i.e., for a negative surface, adsorption of cations causes the surface charge polarity to become positive leading to a phenomenon referred to as charge inversion (CI). We begin our reporting through evaluation of important previous results as there remain significant discrepancies between reported results for silica surfaces for similar ions.28,44 Towards the illustration of these discrepancies, a summary of key previous results is reported for both charge inversion and surface charge regulation in Fig. 2. It is worth noting that for a well-studied material like silica, there is no consensus on the surface charge or electrolyte concentration for charge inversion, despite testing under similar conditions by multiple researchers. For silica, much data are available on monovalent cations such as K+ (Fig. 2A). Fig. 2 shows that the range of surface charge values reported remains broad; however, as shown in Fig. 2B and C, respectively, the discrepancy in the reported values of surface charge for divalent cations, such as those evaluated herein, Ca2+ and Mg2+, is also significant while much less experimental data are available. Real-world systems in many applications such as water desalination or energy harvesting use complex mixtures of ions subject to nanoscale transport and the lack of available data continues to be a hindrance in the systematic design of new systems.Experimental evaluation of nanochannel conductance
Nanochannel transport data for electrokinetic flows are usually reported as nanochannel conductance (Fig. 3) to quantify the ion transport.20 Such an approach has led to the classification of two main transport regimes, where the bulk transport governed regime (BTGR) at higher ionic strengths shows an ohmic response with increasing electrolyte concentration while in the surface charge governed regime (SCGR) the nanochannel conductance is independent of the electrolyte concentration, typically at dilute electrolyte concentrations.19 To satisfy electroneutrality, the total space charge within the nanochannel volume must balance the total surface charge on the nanochannel walls. Ga is thus the summation of the SCGR and the BTGR conductance as shown in the equation below:20,28 | (5) |
 | ||
| Fig. 3 Measured ionic conductance in 16 nm deep silica nanochannels. (A) Conductance comparison between monovalent cations Na+ and K+; (B) conductance comparison between divalent cations Mg2+ and Ca2+; (C) conductance comparison between divalent cations Ba2+ and Ca2+; and (D) conductance comparison for different anions while keeping the cation as Ca2+. The dotted lines act as guides to the eye to show approximate regions for the SCGR and the BTGR.19 | ||
Notably, previous work has shown that the transition between the SCGR and the BTGR occurs approximately at 1 mM for silica nanochannels, regardless of the nanochannel size.12,15,20 As shown in Fig. 3, the trends reported here agree with previous reports12,15,20 meeting the two classifications of the SCGR and BTGR (dotted lines marked in Fig. 3 as visual guides). Fig. 3A shows that in the SCGR, Na+ conductance was higher than K+ conductance, within experimental error. However, in a new finding, the trend changes within the BTGR where K+ conductance was observed to be greater than Na+. In both cases, the anion was Cl−.
Comparing ion sizes, for a bare ion, the size of Na+ < K+; however, when comparing hydrated ion sizes,45 K+ < Na+. The change in measured nanochannel conductance is attributed to surface charge regulation and layering of ions due to differences in hydrated ion sizes.31,46–51 A similar evaluation for comparing divalent ions Mg2+ and Ca2+ with Cl− as the anion once again showed a similar trend, with Mg2+ conductance being higher than that with Ca2+ present within the nanochannels in the SCGR but the conductance of nanochannels with CaCl2 as the electrolyte was noted to be higher in the BTGR (Fig. 3B). Once again, it is noted that for bare ions,45 the size of Mg2+ < Ca2+ but for hydrated ions, the size of Ca2+ < Mg2+. Therefore, for these four cations, the larger hydrated cation dominates ion transport at higher concentrations and the smaller cation at lower concentrations, suggesting that in dilute solutions smaller cations may be more effective at screening surface charge.
To further evaluate the effect of ion sizes mediating surface charge regulation, the conductance of nanochannels was measured with Ba2+ as the cation while keeping the anion fixed as Cl−. Interestingly, the measured conductance for Ba2+ remains lower than that for Ca2+ across all tested concentrations (Fig. 3C) despite the fact that the size of a hydrated Ba2+ ion is smaller than that of a hydrated Ca2+ ion.45 Therefore, Ba2+-containing electrolyte solutions show anomalous transport with respect to Ca2+-containing electrolyte solutions.
The nanochannels in the experiments conducted here present a negative surface charge. Since these silica walls were negatively charged, at dilute concentrations exclusions of the co-ions (i.e., Cl− and SO42−) would be expected52 and therefore the nanochannel conductance should remain invariant with respect to anions in the solution. Given the emerging importance of Ca2+ in nanofluidic applications,4,53,54 we chose to test the validity of the anion independence by evaluating the electrokinetic transport of CaSO4 through the silica nanochannels (Fig. 3D; yellow bars). As seen in Fig. 3D, the CaSO4 containing nanochannels showed nearly concentration independent conductance, i.e., the presence of SO42− limits the transition from the SCGR to the BTGR. Moreover, in the entire concentration range tested, the measured conductance for CaSO4-containing nanochannels was lower than that for those containing CaCl2. Comparing anion sizes, as a bare ion the SO42− ion is approximately 60% larger than a Cl− ion, but is only ca. 14% larger in the hydrated state.45 However, some previous results have noted that unless specific ion–nanochannel wall interactions are accounted for, perfect permselectivity may not occur.40,52 Furthermore, the larger anion also exhibits a lower mobility and therefore the electrolyte transport presents a lower conductance.24 Taken together, these observations explain the difference in the conductances of CaCl2- and CaSO4-containing nanochannels. Therefore, a new observation from these data arises despite the prevailing view that co-ions are excluded from nanochannels and do not contribute to ion transport. Here, we show that the type of anion and the respective hydrated ion sizes limit cationic transport and can extend the concentration regime for surface-charge governed transport.
To place these results in the context of previous work, it is worth noting that ion transport within nanoarchitectures may also be impacted by the entrance of ions from a larger reservoir to the nanochannel. Previously, the role of net charge in the EDL near a pore surface as the source of the observed surface conductance has been evaluated. The authors identified leakage of surface electric potential from the nanopore into the reservoir using molecular dynamics simulations. In another report for conical nanopores, electric fields at the nanopore entrance and exit regions induce large surface charges generating non-uniform EDLs with accumulation of electrolyte ions at the orifice. Presumably, the distribution of charges limits the transfer of ions through these nanopores. These, and similar previous studies, emphasize that asymmetry in the nanoscale conduit geometry or small aspect ratio nanoscale conduits may significantly be impacted by the reservoir-entrance effects, including a role of counterions.50,51,55,56
Surface charge estimation
Using the well-known governing equations described above, the nanochannel conductance was used to compute the silica charge as reported previously.13 As the concentration of the bulk electrolyte increases and the transport of ions shifts from the SCGR to the BTGR, the surface charge for silica becomes progressively more positive indicating surface charge regulation due to likely cation adsorption. In this work, no charge inversion was observed. The lack of observed charge inversion agrees with previous reports that have identified significantly higher electrolyte concentrations for inversion than those evaluated here.29,44 In contrast, another study reported that charge inversion for divalent cations can occur at lower concentrations.28 Interestingly, the least negative surface charge was observed for Ba2+ as seen in Fig. 4A compared to Ca2+ and Mg2+ for the same anion (Fig. 4B and C, respectively). It is also worth noting that for the same anion Cl−, Mg2+, which presents the largest hydrated ion size among the three divalent cations, showed the largest range of surface charge (from ∼−0.2 C m−2 to −0.05 C m−2) as the bulk electrolyte concentration was varied. In contrast, when comparing against a fixed anion, Ca2+ showed more charge regulation for the larger anion SO42− (Fig. 4D). Therefore, for silica nanochannels, anions can also be used to modulate the cationic surface charge regulation in addition to known parameters such as pH or externally applied wall-electric potentials.18Surface charge regulation impacts electroosmotic flow
It is well-known that the electroosmotic flow (EOF) displays ion and electrolyte composition-dependent behaviour, including for nanofluidic devices.57 Using the surface charge density derived from the conductance measurements here, continuum modelling based on well-established theoretical models was implemented and the resulting velocities are shown in Fig. 5. Notably, the nanochannel was modelled as a symmetric channel with the centerline in the nanochannel being the location of the highest velocity. A no-slip boundary condition was imposed at the nanochannel wall indicated by the 8 nm channel height with the model geometry shown in Fig. 5A.Fig. 5B–D show the velocity profiles for each of the four electrolytes with divalent cations. As the bulk electrolyte concentration increased from 0.33 mM to 10 mM, the maximum EOF at the centerline was also noted to increase. Dilute solutions with electrolyte concentrations below 0.33 mM were not evaluated, as in the SCGR, the EOF velocity remains constant.15 Interestingly, while at the lowest concentration of 0.33 mM BaCl2 shows the highest EOF velocity of nearly 30 μm s−1, at 10 mM, the computed EOF for BaCl2 and that for CaSO4 were nearly identical and both electrolytes showed a much smaller EOF than the other two electrolytes, CaCl2 and MgCl2. Moreover, as can be seen from Fig. 5B–D, the maximum EOF for MgCl2 changes from ca. 5 μm s−1 to a highest EOF of ca. 70 μm s−1 at 3.33 mM and reduces to ca. 60 μm s−1 at 10 mM. On the other hand, CaCl2 shows a near monotonic increase with the computed EOF rising from 10 μm s−1 at 0.33 mM to 70 μm s−1 at 10 mM.
Ion-transport based on standard electromigration theories suggests that the EOF velocities should scale inversely with the size of the cation. The Pauli radii of the divalent cations follow the trend Mg2+ < Ca2+ < Ba2+. Therefore, the EOF is expected to follow the trend Ba2+ < Ca2+ < Mg2+ with Cl− as the anion. However, the calculated EOF that accounts for surface charge regulation shows a much more nuanced picture. Specifically, at the electrolyte concentration of 0.33 mM, the EOF trends follow the hydrated ion size trends (i.e., Ba2+ < Ca2+ < Mg2+ for EOFs being Mg2+ < Ca2+ < Ba2+), reflecting that in the SCGR the wall charge regulation controls the EOF, as expected. However, when the anion was changed with CaSO4 as the electrolyte, it was noted that the EOF of CaCl2 < CaSO4, suggesting that anions also play a role in surface charge regulation leading to unexpected changes in the EOF. When further exploring the nuances of the EOF in the transition region between the SCGR and the BTGR (i.e., 1 mM and 3.33 mM), additional anomalous transport was observed. At 1 mM, the EOF followed the trend MgCl2 ≈ CaCl2 ≤ CaSO4 < BaCl2, while at 3.33 mM the trend once again shifted to BaCl2 < CaSO4 < CaCl2 ≤ MgCl2. At 10 mM which falls within the BTGR, the EOF follows the trend BaCl2 < CaSO4 < MgCl2 < CaCl2.
The challenges with the use of PNP equations combined with Navier–Stokes equations in the absence of steric effects are worth noting, and the model presents validation of the device operation to add confidence in experimental data by showing the generally accepted trends for nanochannel conductance and EOF. Therefore, future work that accounts for steric effects with accurate hydration models for both the cationic and anionic species used in this primarily experimental report can likely elucidate the underlying mechanisms influencing the observed EOF trends.
Collectively, the change in EOF with ionic concentration with added dependence on the co-ion type is a new finding, especially for dilute electrolytes where the EDLs interact. To better understand the nuanced impact of charge regulation on the EOF, it is worth considering that in a recent modelling evaluation, the interplay between convection, surface-charge regulation, and slip length was evaluated for charged nanopores58 to enable future design guides for operation of electrokinetically driven nanofluidic devices. Moreover, Li et al. showed that in channels at 85 nm, the EOF for KCl and CaCl2 can be similar to charge regulation.31 Clearly, both cation and anion type along with electrolyte concentration can be used to regulate surface charge and thereby enhance control over the EOF.
Summary and conclusions
In this study, a hybrid microfluidic–nanofluidic device was evaluated for the transport of a variety of ions with the purpose of enhancing the understanding of surface charge regulation and electrokinetic transport within silica nanochannels. Surface charge regulation was noted to be dependent on the size of the hydrated cation for the negatively charged silica nanochannels. Furthermore, when exploring size-dependent ion transport, anomalous transport of Ba2+ as a divalent cation was noted when compared against the trends observed for Mg2+ and Ca2+. The size dependent ionic conductance trends were also verified for monovalent cations Na+ and K+. The surface charge regulation leads to the possibility of using an electrolyte solution's composition and concentration to manipulate the surface charge and the subsequent electroosmotic flow within nanochannels.Data availability
Data were acquired in the Microsystems and Nanosystems Laboratory at The Ohio State University and are archived as part of the dissertation of Dr Kaushik Rangharajan. The dissertation with supporting data is accessible through The Ohio State University Library System.Conflicts of interest
The authors do not have any competing conflicts of interest.Acknowledgements
The authors acknowledge the staff at Nanotech West Laboratories at The Ohio State University for assistance with equipment during fabrication and characterization of devices, Ohio Supercomputer for providing computational resources. The authors acknowledge partial financial support from the National Science Foundation (NSF) through grant CBET-1335946, the U.S. Department of Energy through grant DE-FE0024357, and the U.S. Department of Defense through grant CA210874.References
- A. Harsman, V. Kruger, P. Bartsch, A. Honigmann, O. Schmidt, S. Rao, C. Meisinger and R. Wagner, J. Phys.: Condens. Matter, 2010, 22, 454102 CrossRef PubMed.
- W. Wickner and R. Schekman, Science, 2005, 310, 1452–1456 CrossRef CAS PubMed.
- S. Prakash and J. Yeom, Nanofluidics and microfluidics: systems and applications, Elsevier, Norwich, MA, 2014 Search PubMed.
- S. J. Kim, S. H. Ko, K. H. Kamg and J. Han, Nat. Nanotechnol., 2010, 5, 297–301 CrossRef CAS.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS.
- S. K. Mehta, P. Padhi, S. Wongwises and P. K. Mondal, Microsyst. Technol., 2024, 1–10, DOI:10.1007/s00542-024-05763-3.
- S. K. Mehta, P. Padhi, S. Wongwises and P. K. Mondal, Langmuir, 2024, 40, 18750–18759 CrossRef CAS PubMed.
- S. K. Mehta, D. Deb, A. Nandy, A. Q. Shen and P. K. Mondal, Phys. Chem. Chem. Phys., 2024, 26, 20550–20561 RSC.
- S. K. Mehta, A. Ghosh, P. K. Mondal and S. Wongwises, Phys. Fluids, 2024, 36, 023101 CrossRef CAS.
- D. Pandey, P. K. Mondal and S. Wongwises, Soft Matter, 2023, 19, 1152–1163 RSC.
- M. A. Bakshloo, J. J. Kasianowicz, M. Pastoria-Gallego, J. Mathe, R. Daniel, F. Piguet and A. Oukhaled, J. Am. Chem. Soc., 2022, 144, 2716–2725 CrossRef.
- M. Fuest, C. Boone, K. K. Rangharajan, A. T. Conlisk and S. Prakash, Nano Lett., 2015, 15, 2365–2371 CrossRef CAS PubMed.
- W. Guan, R. Fan and M. A. Reed, Nat. Commun., 2011, 2, 506 CrossRef.
- R. Karnik, K. Castelino and A. Majumdar, Appl. Phys. Lett., 2006, 88, 123114 CrossRef.
- R. Karnik, R. Fan, M. Yue, D. Li, P. Yang and A. Majumdar, Nano Lett., 2005, 5, 943–948 CrossRef CAS PubMed.
- D. Pandey and P. K. Mondal, Phys. Fluids, 2023, 35, 082002 CrossRef CAS.
- C.-M. Kim, E. Yang, R. Karnik, R. W. Field, R. G. Fane, P. Wang and I. S. Kim, Chem. Eng. J., 2025, 505, 158366 CrossRef CAS.
- J. P. de Souza, C.-M. Chow, R. Karnik and M. Z. Bazant, Phys. Rev. E, 2021, 104, 04482 Search PubMed.
- S. Prakash and A. T. Conlisk, Lab Chip, 2016, 16, 3855–3865 RSC.
- R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 CrossRef CAS.
- D. Burgreen and F. R. Nakache, J. Phys. Chem., 1964, 68, 1084–1091 CrossRef.
- C. L. Rice and R. Whitehead, J. Phys. Chem., 1965, 69, 4017–4024 CrossRef CAS.
- M. Fuest, K. K. Rangharajan, C. Boone, A. T. Conlisk and S. Prakash, Anal. Chem., 2017, 89, 1593–1601 CrossRef CAS.
- P. Ramirez, J. A. Manzanares, J. Cervera, V. Gomez, M. Ali, S. Nasir, W. Ensinger and S. Mafe, Electrochim. Acta, 2019, 325, 134914 CrossRef CAS.
- J. Lyklema, Colloids Surf., A, 2006, 291, 3–12 CrossRef CAS.
- C.-Y. Lin, T. E. Acar, J. W. Polster, K. Lin, J.-P. Hsu and Z. S. Siwy, ACS Nano, 2019, 13, 9868–9879 CrossRef CAS.
- D. Gillespie, D. Boda, Y. He, P. Apel and Z. S. Siwy, Biophys. J., 2008, 95, 608–619 Search PubMed.
- S. X. Li, W. Guan, B. Weiner and M. A. Reed, Nano Lett., 2015, 15, 5046–5051 CrossRef CAS PubMed.
- A. Rojano, D. Becerra, J. H. Walther, S. Prakash and H. A. Zambrano, Phys. Fluids, 2024, 36, 102025 CrossRef CAS.
- S. H. Behrens and M. Borkovec, J. Chem. Phys., 1999, 111, 382–385 CrossRef CAS.
- J. Li, R. Peng and D. Li, Anal. Chim. Acta, 2019, 1059, 68–79 CrossRef CAS PubMed.
- Y. He, D. Gillespie, D. Boda, I. Vlassiouk, R. S. Eisenberg and Z. S. Siwy, J. Am. Chem. Soc., 2009, 131, 5194–5202 CrossRef CAS.
- T. Jain, B. C. Rasera, R. J. S. Guerrero, M. S. H. Boutilier, S. C. O’Hern, J. C. Idrobo and R. Karnik, Nat. Nanotechnol., 2015, 10, 1053–1057 CrossRef CAS.
- K. K. Rangharajan, P. M. Sundaram, A. T. Conlisk and S. Prakash, Analyst, 2018, 143, 4256–4266 RSC.
- M. Fuest, K. K. Rangharajan, C. Boone, A. T. Conlisk and S. Prakash, Anal. Chem., 2017, 89, 1593–1601 CrossRef CAS.
- M. Pinti, T. Kambham, B. Wang and S. Prakash, J. Nanotechnol. Eng. Med., 2013, 4, 020905 CrossRef.
- P. B. Allen and D. T. Chiu, Anal. Chem., 2008, 80, 7153–7157 CrossRef CAS PubMed.
- K. K. Rangharajan and S. Prakash, Analyst, 2022, 147, 3817–3821 RSC.
- C. Duan and A. Majumdar, Nat. Nanotechnol., 2010, 5, 848–852 CrossRef CAS PubMed.
- K. K. Rangharajan, M. Fuest, A. T. Conlisk and S. Prakash, Microfluid. Nanofluid., 2016, 20, 54 CrossRef.
- I. Vlassiouk, S. Smirnov and Z. S. Siwy, Nano Lett., 2008, 8, 1978–1985 CrossRef CAS.
- B. J. Kirby, Micro- and nanoscale fluid mechanics, Cambridge University Press, 2010 Search PubMed.
- A. T. Conlisk, Essentials of Micro-and Nanofluidics, Cambridge University Press, 2012 Search PubMed.
- F. H. J. van der Heyden, D. Stein, K. Besteman, S. G. Lemay and C. Dekker, Phys. Rev. Lett., 2006, 96, 224502 CrossRef.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- D. Gillespie, Microfluid. Nanofluid., 2015, 15, 717–738 CrossRef.
- J. Hoffman and D. Gillespie, Langmuir, 2013, 29, 1303–1317 CrossRef PubMed.
- S. Joseph and N. R. Aluru, Langmuir, 2006, 22, 9041–9051 CrossRef CAS PubMed.
- J. A. Rard and D. G. Miller, J. Chem. Eng. Data, 1980, 25, 211–215 CrossRef CAS.
- R. Qiao and N. Aluru, Langmuir, 2005, 21, 8972–8977 CrossRef CAS.
- R. Qiao, J. G. Georgiadis and N. R. Aluru, Nano Lett., 2006, 6, 995–999 CrossRef CAS PubMed.
- S. N. Bush, J. S. Ken and C. R. Martin, ACS Nano, 2022, 16, 8338–8346 CrossRef CAS.
- K. Lin, C.-Y. Lin, J. W. Polster, Y. Chen and Z. S. Siwy, J. Am. Chem. Soc., 2020, 142, 2925–2934 CrossRef CAS PubMed.
- J. Ma, Z. Zhang, X. Gu, K. Li, D. Li and Y. Chen, J. Phys. Chem. C, 2022, 126, 14661–14668 CrossRef CAS.
- A. Paul and N. R. Aluru, Phys. Rev. E, 2024, 025105 CrossRef CAS PubMed.
- R. Qiao and N. R. Aluru, Colloids Surf., A, 2005, 267, 103–109 CrossRef CAS.
- A. Alizadeh, W.-L. Hsu, M. Wang and H. Daiguji, Electrophoresis, 2021, 42, 834–868 CrossRef CAS PubMed.
- Y. Green, ACS Omega, 2022, 7, 36150–36156 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |




