DOI:
10.1039/D3YA00534H
(Paper)
Energy Adv., 2024,
3, 430-441
Untapped potential of scrap brass alloy: a new frontier in the use of brass-based photocathodes for stable and durable photoelectrochemical water splitting†
Received
3rd November 2023
, Accepted 17th January 2024
First published on 17th January 2024
Abstract
Photoelectrochemical (PEC) water splitting is a promising way to produce green hydrogen. However, one of the bottlenecks in realizing scalable green hydrogen production systems is the inability to identify and fabricate earth abundant, stable, and durable photocathodes. The main challenges with the reported photocathodes so far are their instability in aqueous solutions and the use of precious unabundant materials. To this end, the use of scrap materials to fabricate highly stable photocathodes would solve the two main challenges. Herein, scrap brass alloys with different zinc contents were used to fabricate photocathodes for photoelectrochemical green hydrogen production. The scrap brass alloy with 5% Zn showed enhancement in the photocurrent density of −0.26 mA cm−2 at 0.62 V vs. reversible hydrogen electrode (RHE), high long-term stability up to four hours under continuous illumination, high charge carrier density of 6.2 × 1021 cm−3 and less total resistance than the other brass samples. Through electrochemical impedance spectroscopy (EIS), the presence of surface states was verified. The 95Cu–5Zn sample showed an amount of evolved hydrogen of 0.2658 μmole after one hour of continuous illumination (area = 0.5 cm2), while the 100Cu sample only showed 3.965 nmole after 20 minutes of continuous illumination before being completely reduced to copper. Density functional theory (DFT) calculations were used to study the optical and electronic properties of the best-performing sample. This work is the first to systematically and fundamentally study scrap brass as a promising material for a more stable and durable PEC water splitting.
Introduction
The world's energy demand has been increasing rapidly. Developing clean, renewable, and environmental-friendly energy sources is indispensable to tackle the environmental crisis and meet human energy needs, especially due to the imminent depletion of fossil fuels. In this respect, hydrogen is a promising energy carrier, having a gravimetric energy density of 120 kJ g−1, which is 2.6 times that of gasoline.1,2 It is used in fuel cells and combustion engines without any pollutant generation.3 Currently, 95% of hydrogen is produced by fossil fuel reforming, which results in a high yield of hydrogen, yet this method is unsustainable due to its reliance on a non-renewable energy source.4,5 Thus, extensive efforts have been devoted to generating hydrogen via sustainable and renewable methods. Among various strategies, photoelectrochemical (PEC) water splitting is considered a promising one in the context of a carbon-neutral economy. Solar fuel production is a great example of the circular economy; a renewable energy source is used to split water into its main components; then, hydrogen can be used in combustion engines producing water as a by-product.6 A typical photoelectrochemical device consists of a photoanode or a photocathode, or both, in direct contact with an electrolyte, that is typically, water. In PEC, light is used to induce excitons that promote water dissociation into hydrogen and oxygen.7 Many semiconductors have been studied as photoanodes or photocathodes. The minority charge carriers in n-type and p-type semiconductors lead to the oxidation (reduction) of water resulting in the formation of oxygen (hydrogen).8 Even though PEC is an environmental-friendly method, the excessive mining of metals and the poor regulations in doing so lead to environmental and societal harm.9 Therefore, the usage of recycled photoelectrodes, whose source is scrap alloys, is of paramount importance, as this avoids mining and causing environmental harm that scientists try to avoid by using a technique like PEC.9
Researchers have worked on developing many photoanodes that can be used in PEC such as Ti2O, Fe2O3, and WO3, while the development of photocathodes is still lagging due to their instability in aqueous solutions.10 The lack of stable photocathodes for water reduction hinders the development of tandem photoelectrochemical water splitting cells.11 In this regard, cupric oxide (CuO) has attracted attention as an effective p-type semiconductor for PEC water splitting due to its availability, low cost, non-toxicity, narrow bandgap (1.44–1.68 eV), and band offsets that straddle the water reduction potential.12 However, the poor carrier mobility and photocorrosion instability of cupric oxide in aqueous solutions limit the feasible application of cupric oxide in PECs. The low carrier mobility leads to the accumulation of photogenerated electrons, thus reducing the cupric oxide to metallic copper instead of quickly transferring the carriers to the electrolyte to reduce water to hydrogen.13,14 Moreover, CuO has a thermodynamic reduction potential that lies below the water reduction potential making the electron transition to reduce itself more energetically favorable than reducing water.15,16 In addition, the performance of cupric oxide photocathodes can be rationalized by the presence of surface states. Even though surface states can work as recombination centers, when trapped holes recombine with trapped electrons, they can become an indirect pathway for charge transfer to the electrolyte, facilitating the process of water dissociation.17,18 The discussion of the role of surface states will be presented later in this manuscript.
For practical applications, several approaches have been applied to stabilize CuO photocathode and improve the charge transfer properties, one of them is coating the photocathode with a passivation layer protecting the photocathode against photocorrosion.19 Xing et al. stabilized CuO by using a TiO2 protective layer and Pt as a co-catalyst. The CuO/TiO2/Pt electrode showed PEC performance improvement compared to pristine CuO electrodes and CuO/TiO2 electrodes. That work proves that the combination of a protective layer and a cocatalyst improves the PEC performance.20 Another approach is to introduce graphene or other metals such as Li, Al, or Fe into CuO film.21,22 Constructing a p–n heterojunction with CuO that accelerates the transfer of photogenerated carriers and inhibits the recombination of electrons and holes. Another method to stabilize CuO is to alter the electrolyte environment and light intensity used with the CuO photocathode.23 However, all those attempts are either very complicated or come at the expense of the generated photocurrent.
Herein, cupric oxide was stabilized using zinc in scrap α-brass alloys. Alloying copper with different concentrations of zinc (5%, 15%, 30%) changes its chemical and physical properties. Incorporating Zn in the structure of CuO alters the electronic and optical properties of CuO. Of all metal ions, Zn has an ionic radius that is similar to Cu. Thus, Zn2+ ions can be easily incorporated into the CuO lattice without damaging the crystal structure.24,25 Characterization techniques such as SEM, XRD, Raman Spectroscopy, XPS, and UPS were used to study the properties of the anodized and annealed samples. In addition, photoelectrochemical measurements were employed to study the performance of the samples as photocathodes and to elucidate the role of surface states. Even though this study is not the first one reporting the use of α-brass in PEC, this study is the first to report the effect of different concentrations of Zn on the stability of cupric oxide, and the first one that fundamentally investigates the physical and chemical properties of the anodized and annealed brass samples.26 Density functional theory (DFT) calculations were employed to investigate the electronic and optical properties of the best performing α-brass sample in photoelectrochemical measurements. The properties of interest are band gap, dielectric constant, density of states, and band structure.27
Materials and methods
Alpha brass (95% Cu–5% Zn, 85% Cu–15% Zn, 70% Cu–30% Zn) samples were used throughout the experiment. For a fair comparison, a 100% Cu sample was also used. The samples were named 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu. Before anodization, the samples were mechanically polished using coarse, medium, and fine grinding papers. After that, the samples were ultrasonically cleaned using ethanol, acetone, and distilled water for 10 minutes each. The samples were anodized at room temperature according to the procedure described by Bahnasawy, et al. under a constant voltage of 4 V, and the anodization time was 5 minutes.28 After anodization, the samples were annealed at 350 °C in air for one hour with a heating/cooling rate of 5 °C min−1. The elemental analysis of the anodized and annealed samples was performed using energy dispersive X-ray (EDX) (EDX; Oxford ISIS 310, England). The morphology of the films was characterized using Zeiss SEM Ultra 60 field emission scanning electron microscopy (FESEM). The crystal structure of the annealed samples was determined using a PANalytical X-pert Pro PW3040 MPD X-ray diffractometer via monochromatic radiation (Cu-Kα, λ = 0.15406 nm, 50 mA, 40 kV) in the range of 5°–80° with a glancing angle of 2°. For Raman spectroscopy analysis, a Renishaw InVia dispersive Raman spectrometer equipped with a Leica DM microscope and a Renishaw HeNe 532 nm laser was used. X-Ray Photoelectron Spectroscopy (XPS) was used to analyze the surface composition of the as-anodized and as-annealed samples. Thermo Scientific Kα X-ray photoelectron spectrometer was used. The spectra were calibrated to C1s at 284.8 eV. Shimadzu UV-vis diffuse reflectance spectrometer was used to study the optical properties of the samples, and the band gap of the samples was calculated using Tauc plot. To determine the band offsets of the annealed samples, a Thermo Scientific, ESCALAB250 Xi ultraviolet photoelectron spectroscopy (UPS) was used.
Photoelectrochemical measurements were conducted in 0.1 M sodium carbonate (pH = 11.7) in a three-electrode cell configuration with Hg/HgO as a reference electrode, Pt as a counter electrode, and the annealed samples as the working electrode. The measurements were done using Bio-Logic SP 200 potentiostat equipped with a solar simulator (300 W Ozone-free Xenon lamp under 100 mW cm−2 illumination and with AM 1.5G filter). The scan rate was 10 mV s−1 for linear sweep voltammetry. Chronoamperometry under chopped and continuous illumination was performed to determine the stability of the sample at 0.62 V vs. RHE. Electrochemical impedance spectroscopy (EIS) was used to elucidate the role of surface states at 0.62 V vs. RHE with a frequency range from 1 MHz to 100 mHz in the dark and under illumination. Mott–Schottky analysis was performed to determine the charge carrier density of the samples in the dark. To quantify the amount of hydrogen produced using the 100Cu and 95Cu–5Zn samples, a 3-electrode cell was designed. Nitrogen gas was made to flow through the cell at a controlled rate. The outlet of the cell was directed towards the inlet of a gas chromatograph (GC), where the gas is analyzed at the set times of 20, 40, and 60 min. The applied voltage was 0.62 V vs. RHE throughout the measurements.
Computational methods
Computational calculations were conducted for 95Cu–5Zn sample. All calculations were based on a spin-polarized density functional theory and were performed using the standard Cambridge Serial Total Energy Package (CASTEP), as implemented in Materials Studio 2017.29 Generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional were used for geometry optimization, electronic properties calculations, and adsorption energy computations.30 The interaction between electrons and ions was represented using an OTFG ultrasoft pseudopotential, where the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm was utilized with a cutoff energy of 630 eV and a separation distance of 0.07 Å for the K-points. Convergence was ensured by relaxing the bulk structure of CuZnO, until it met the convergence criteria of less than 5.0 × 10−6 eV per atom, 0.01 eV Å−1, 0.02 GPa, and 5.0 × 10−4 Å for the energy, force, stress, and displacement, respectively.31 The optimized lattice constants for the bulk CuZnO were determined to be a = 7.21 Å, b = 5.38 Å, c = 9.63 Å, α = γ = 90°, and β = 89.81°, providing valuable insights into the structure of the material. The bulk structure is shown in Fig. 1a. To obtain a more accurate electronic band structure diagram, DFT+U calculations were performed to avoid the self-interaction error that often leads to a significant underestimation of the band gap. A Hubbard correction value of 9 eV was set for Cu's d orbitals, resulting in a band gap of 1.445 eV, which is in good agreement with the experimental band gap of 1.42 eV. Given that the hydrogen evolution reaction is most favorable on the (−111) facet, which is the dominant facet in our material, a cleaved surface of (−111) was utilized to build a bulk crystal with a vacuum of 15 Å in the Z direction. This approach prevented interaction between the periodic layers and allowed for an accurate analysis of the material's electronic properties.
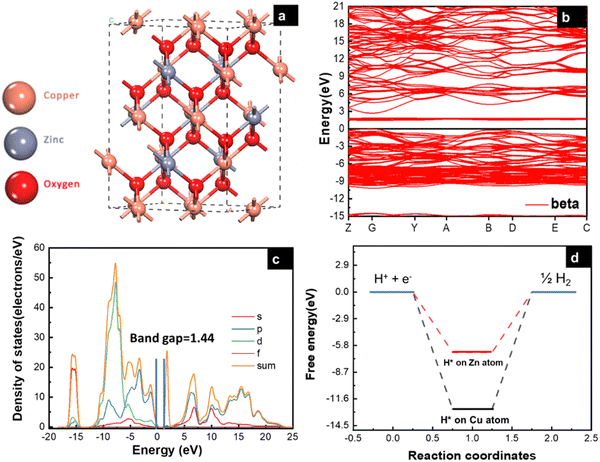 |
| | Fig. 1 (a) Side-view of CuZnO bulk (95% Cu, 5% Zn), (b) electronic band structure specified by the Fermi level with black line, (c) partial density of states (PDOS), and (d) free energy (eV) of H* adsorption on Cu and Zn atom. | |
Results and discussion
The electronic properties of the CuZnO (95% Cu, 5% Zn) material were investigated to gain a better understanding of its potential use in photoelectrochemical water splitting. The calculated electronic band structure (EBS) allows the estimation of the band gap energy and determination of the semiconductor type. The EBS calculation revealed a band gap of 1.445 eV and a shift of the Fermi level (0 eV) towards the valence band, as shown in Fig. 1b and c, indicating a p-type semiconducting behavior. Additionally, the partial density of states (PDOS) was computed to provide statistical insights into the role of each orbital in the number of occupied and unoccupied states as shown in Fig. 1c. While the region with low energy on the left side of the Fermi level represents the valence band, the region on the right represents the conduction band. Most of the state of the d orbital could be found in the valence band, which supports the hypothesis that the sample has a p-type semiconducting behavior.32 CuO is a p-type semiconductor with an indirect band gap.33 The band gap of CuO determines its electronic and optical properties and is an important characteristic for its potential application in optoelectronic devices.5 In our study, it was found that the band gap of CuO is 1.42 eV (experimentally), and 1.44 (computationally) due to the added Zn to the material. Specifically, the Zn d orbitals caused a slight shift in the energy of the conduction band away from the Fermi level, leading to a widening of the band gap. This finding could have implications for the development and optimization of CuO-based materials. Since the CuZnO structure is intended for use in photoelectrochemical water splitting, it is important to investigate its interaction with electromagnetic waves, specifically in the visible light region. The complex dielectric constant ε(ω) is a key factor in understanding this interaction. By analyzing the complex dielectric constant ε(ω) insights, the behavior of the CuZnO structure under different electromagnetic conditions can be obtained. Overall, these investigations into the electronic properties and electromagnetic interaction of the CuZnO structure provide a foundation for its potential use in PEC. In eqn (1), the real and imaginary parts of the dielectric constant represent the energy gain and energy loss by the material, respectively. Through eqn (1), the dielectric constant was computationally found to be 2.26. The dielectric function of CuZnO is shown in Fig. S1 (ESI†).The adsorption of hydrogen on the surface of the catalysts is a major step in the hydrogen evolution reaction (HER).34,35 HER is a two-electron transfer process with one catalytic intermediate, H*. HER occurs through two individual steps, either the Volmer–Heyrovsky step or the Volmer–Tafel step. If the surface coverage of H* is low, the Heyrovsky reaction would be favored. If the surface coverage of H* is high, the Tafel reaction would be favored.36
| (Volmer reaction): H+ + e− → H* |
| (Tafel reaction): 2H* → H2 |
| (Heyrovsky reaction): H* + H+ + e− → H2 |
The energy of hydrogen adsorption (Eads) is an important parameter in HER. A negative value means that H* binds favorably on the electrode surface making the Volmer reaction easy. However, if the value of adsorption energy is too negative, the next Tafel or Heyrovsky step would be difficult.37 To study the catalytic activity of a CuZnO surface towards HER, it is important to identify the most favorable adsorption site for hydrogen on the surface of the catalyst. In this study, the adsorption energy of hydrogen on the Cu and Zn atoms of the CuZnO catalyst was calculated as:| | 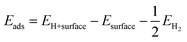 | (2) |
where EH+surface is the total energy of the hydrogen atom on the surface, Esurface is the total energy for the (−111) surface, and EH2 is the energy of the hydrogen molecule in vacuum. The calculations showed that the adsorption energy of H* on the Cu atom is lower than that on the Zn atom. This indicates that the adsorption of H* on the Cu atom is more favorable than that on the Zn as illustrated in Fig. 1d. The low Eads on the Cu atom can block the desorption of H2 molecules.38 Therefore, substituting zinc atoms in the cupric oxide lattice leads to increasing the value of Eads, implying that hydrogen will easily adsorb and desorb in the case of CuZnO structure more than mere CuO.39 In the work by Jiang et al., it was found by DFT calculations that doping CuO with 0.3% of Zn resulted in hydrogen adsorption free energy closer to 0 eV (−1.47 eV for bare CuO versus −0.95 eV for 0.3% Zn-doped CuO). This agrees well with our results that Zn alloying lowers the free energy of hydrogen adsorption closer to 0 eV to facilitate the adsorption and desorption of hydrogen, thus, improving the photoelectrochemical performance.25
The elemental analysis of the samples after anodization and after annealing shows a uniform distribution of Cu, Zn, and O throughout all the samples, as shown in Fig. S2 and S3 (ESI†). The morphology of as-anodized and as-annealed samples was characterized using SEM. The SEM images of the anodized samples are shown in Fig. S3 (ESI†). The SEM images of the as-annealed samples in Fig. 2 show a uniform and continuous distribution of the nanostructures over the brass substrates. Increasing zinc content leads to agglomeration, where the particles tend to lower their surface free energy. It is worth noting that after annealing the samples, some fusion of grain boundaries took place leading to larger particle size.40,41 The change in morphology between the 100Cu sample and other zinc alloyed samples may be due to the substitutional defects of zinc in the CuO lattice.42
 |
| | Fig. 2 Top-view SEM images of the anodically fabricated (a) 95Cu–5Zn, (b) 85Cu–15Zn, (c) 70Cu–30Zn, and (d) 100Cu samples after annealing at 350 °C in air for one hour with a heating/cooling rate of 5 °C min−1. | |
Fig. 3a depicts the XRD pattern of the annealed samples. The sharp XRD peaks imply that the samples are crystalline. The three main peaks in all the alloyed samples pattern are characteristic of the α-brass alloy (substrate) representing rhombohedral Cu–Zn at 42.83° (110), 43.82° (104), and 49.65° (112) (ICDD: 00-025-0322). The XRD pattern of sample 95Cu–5Zn shows peaks at 35.93°, 38.68°, 51.03°, and 61.86° attributed to the (−111) monoclinic CuO, (111) monoclinic CuO (ICDD: 01-080-0076), (200) cubic copper (ICDD: 00-003-1005), and (−113) monoclinic CuO (ICDD: 01-080-0076), respectively. Sample 85Cu–15Zn shows similar peaks to sample 95Cu–5Zn attributed to monoclinic CuO, rhombohedral Cu–Zn, and cubic copper. Sample 70Cu–30 Zn did not show peaks for monoclinic CuO, even though it showed a p-type semiconductor behavior, according to Mott–Schottky calculations that will be presented later. This might be because the metal oxide thin film on the brass substrate is too thin to be detected by XRD. Sample 100Cu showed peaks at 29.32°, 36.23°, 38.28°, 41.92°, 42.73°, and 60.76° attributed to (110) cubic Cu2O (ICDD: 01-078-2076), (111) cubic Cu2O, (111) monoclinic CuO, (200) cubic Cu2O, (111) cubic copper, and (−113) monoclinic CuO, respectively. It is worth noting that in samples (95Cu–5Zn, 85Cu–15Zn), a single phase of monoclinic CuO was formed implying that there is no phase segregation up to 30% alloying of copper when the samples are anodized and annealed, which means that zinc ions substituted copper ions in the lattice. This agrees well with the phase diagram of Cu–Zn alloy, which shows that Cu–Zn alloys exhibit a single α-phase below 35 wt% Zn, above which the intermetallic β-phase would be formed.43 Two phases of copper oxide were formed upon anodization and annealing of 100Cu sample. It is also noted that as the concentration of Zn increases, the intensity of copper oxide peaks decreases, even though there were no distinct peaks for ZnO. The average crystallite size and strain introduced in the samples can be calculated using Williamson–Hall (W–H) plots according to eqn (3).44,45
| | 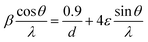 | (3) |
where
β is the half-width at half maximum,
ε is the lattice strain,
θ is the Bragg angle,
d is the average crystallite size, and
λ is the wavelength of the X-ray.
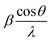
is plotted
vs.
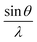
and fitted into a straight line, then the lattice strain can be obtained from the slope, and the average crystallite size from the intercept. The relationship between the zinc content
versus the lattice strain and average crystallite size is shown in Fig. S5 (ESI
†). As the zinc content increases, average crystallite size decreases and lattice strain increases, implying that increasing zinc content induces more lattice imperfections, which adversely affect the photoelectrochemical performance of the samples,
46,47 as will be discussed later.
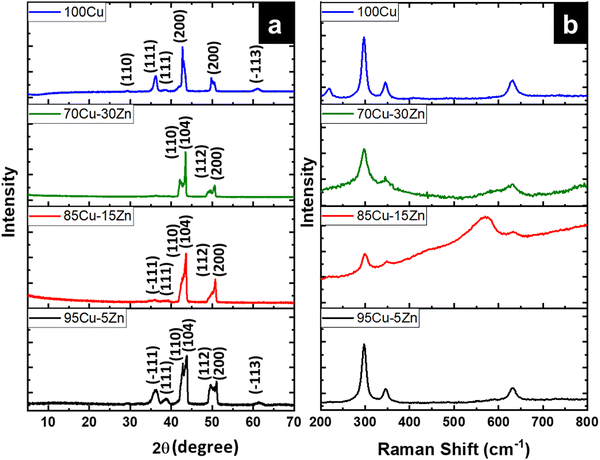 |
| | Fig. 3 (a) XRD patterns for the as-annealed 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu, (b) Raman Spectra of the 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu samples. | |
To further confirm the structural findings, Raman spectroscopy gives useful insights into whether secondary phases are formed for alloyed materials or not due to the introduction of foreign atoms in the host material. Fig. 3b shows the Raman spectra of the 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu samples. Copper oxide forms two different oxides; cupric oxide and cuprous oxide. Cupric oxide has twelve phonon modes. The zone center optical phonon modes for CuO are Γ = Ag + 2Bg + 4Au + 5Bu. Three of these phonon modes are Raman active (Ag, 2Bg) and the rest are infrared active.48 The symmetry of vibrational modes for Cu2O is Γ = A2u + Eu + 3T1u + T2u + T2g. The only Raman active mode is T2g symmetry.49,50 The remaining modes are either infrared active or silent modes. For sample 100Cu, the peaks at 217.13, 297.52, 345.01, and 630 cm−1 are attributed to Cu2O (Eu) silent mode, CuO (Ag), CuO (Bg) and CuO (Bg), which agrees with the XRD data. Sample 95Cu–5Zn shows the three Raman active phonon modes of CuO at 297.52, 345, and 630 cm−1. Sample 85Cu–15Zn shows the three Raman active phonon modes of CuO at 299.42, 348.79, and 633.66 cm−1. In addition, the T2g Raman active mode of Cu2O appears at 569.34 cm−1 proving that sample 85Cu–15Zn has a mixture of Cu2O and CuO, which was not obvious in XRD data.45,51,52 Sample 70Cu–30Zn shows Raman active modes of CuO at 297.52, 345, and 630 cm−1. Raman spectra were also used to calculate the phonon lifetime of the samples as shown in Table 1.53 The phonon lifetime can be calculated as the sum of a lifetime due to the harmonic process and due to the impurities present in the system as indicated by eqn (4):
| | 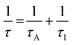 | (4) |
where
τA and
τl are the decay times due to the harmonic process and the impurities present, respectively. Phonon lifetime can be calculated in terms of energy-time uncertainty using
eqn (5):
| | 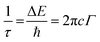 | (5) |
where
ℏ, Δ
E,
c, and
Γ are the reduced Planck constant, uncertainty in the phonon mode energy, velocity of light, and full width at half maximum obtained from Lorentzian fitting of Raman scattering curve, respectively. Sample 95Cu–5Zn showed the lowest phonon lifetime implying the decrease in electron–phonon coupling in this sample.
54 Thus, the sample showed the highest photocurrent as will be shown later.
55
Table 1 Calculated phonon lifetime in the samples
| Sample |
Phonon lifetime (ps) |
| 95Cu–5Zn |
37.29 |
| 85Cu–15Zn |
38.15 |
| 70Cu–30Zn |
40.09 |
| 100Cu |
41.11 |
X-ray photoelectron spectroscopy (XPS) was conducted to determine the chemical composition of the as-anodized and as-annealed samples. The XPS spectra of the 85Cu–15 Zn, 70Cu–30Zn, and 100Cu samples are shown in Fig. S6–S8 (ESI†). The XPS spectra of the as-anodized 95Cu–5Zn sample are depicted in Fig. 4a, revealing the presence of Cu+ at 931.96 eV and Cu2+ at 934.36 eV. The spin–orbit splitting for Cu+ spectra is 19.9 eV, and 19.8 eV for Cu2+. The peaks at 937.36, 941.16, and 960.16 eV are shake-up satellite peaks, which are characteristic of materials having d9 configuration in the ground state such as CuO.56,57Fig. 4b confirms the presence of Zn metal and Zn2+ in the anodized 95Cu–5Zn sample. The peaks at 1021.68 and 1023.78 eV correspond to Zn metal and Zn2+, respectively. The spin–orbit coupling for Zn metal is 23.3 eV and 23.6 eV for Zn2+.58Fig. 4c shows the oxygen peaks, where the peaks at 529.48, 531.58, and 533.88 eV are attributed to oxygen in CuO lattice, ZnO lattice, and adsorbed water, respectively.59,60Fig. 4d–f reveals the changes that occurred to the samples after annealing. In Fig. 4d, the sample is only composed of Cu2+ in CuO with satellite peaks that correspond to CuO. Zn metal no longer exists in sample 95Cu–5Zn after annealing due to the high oxidation affinity of Zn, which is even higher than Cu, as shown in Fig. 4e.61Fig. 4f shows that the amount of oxygen in the CuO lattice increased after annealing, as qualitatively proved, by the increase of the area under the graph of that peak. The amount of adsorbed water also decreased. Similar results were noted for the samples 85Cu–15Zn, 70Cu–30Zn, and 100Cu. It is worth noting that, even though ZnO peaks were not observed in XRD and Raman, there are peaks for Zn2+ and O in the ZnO lattice in XPS. This is due to the fact that XRD and Raman are mainly bulk techniques, while XPS is a surface technique. Therefore, XPS was able to detect ZnO that formed on the outermost layer of the surface. It is well known that the annealing of α-brass leads to further oxidation of the surface. When oxidation proceeds at high temperatures, the Zn diffusion coefficient increases, and Zn can diffuse through greater distances within a given time. The diffusion of Zn during the oxidation period thus proceeds directly from the bulk. The diffusion of Zn cation through the outermost CuO-rich layer results in a p-type layer combined with Zn.62,63
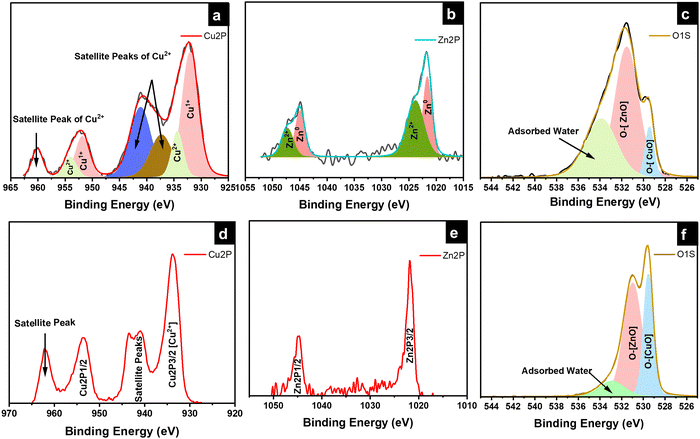 |
| | Fig. 4 High-resolution XPS spectra of the (a)–(c) as-anodized and (d)–(f) annealed 95Cu–5Zn sample. | |
The UV-Vis absorption spectra, Valence band XPS, and ultraviolet photoelectron spectroscopy (UPS) measurements were carried out to determine the band positions of 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu. The absorbance spectra can help determine the value of the optical bandgap of the sample using Tauc plot calculations, as shown in Fig. S9 (ESI†). Valence band XPS is a technique used to determine the energy difference between the valence band maximum position and the Fermi level position. UPS spectroscopy measurements help determine the electron affinity (χ) of the semiconductors according to eqn (6):
where
χ is the electron affinity,
hν is the excitation energy value of 21.2 eV used in UPS,
w is a constant obtained by subtracting the secondary energy cutoffs obtained from the UPS spectra, and
Eg is the bandgap of the material. The three measurements can be combined to determine the band positions of the samples with respect to vacuum energy levels.
Fig. 5 shows the absorbance spectra, UPS spectra, valence band XPS spectra, and band position of the samples with respect to vacuum. The band positions in
Fig. 5d indicate that the conduction band position of all the samples is more positive than the hydrogen evolution reaction potential, implying that the samples are suitable for water reduction. However, the valence band edge of the samples lies above the water oxidation potential, showing that the samples are not suitable for overall photoelectrochemical water splitting. Therefore, a photoanode needs to be used to create a tandem cell. The p-type behavior of the sample is evident, as the Fermi level (
Ef) of the samples lies close to the valence band, which agrees well with the DFT calculations.
64–67
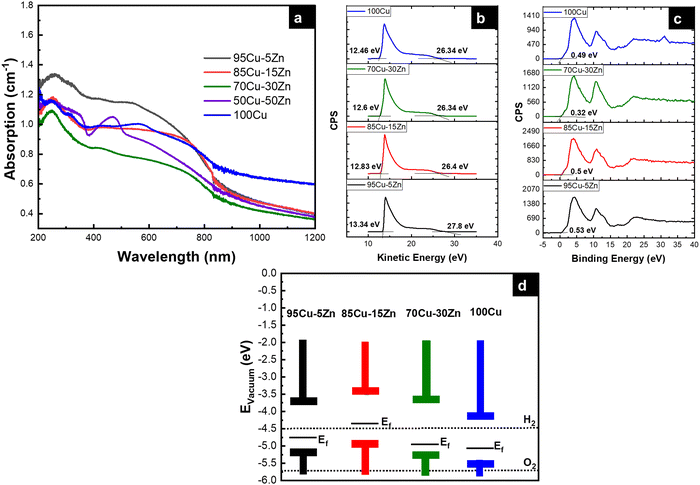 |
| | Fig. 5 (a) Absorbance spectra, (b) UPS spectra, (c) valence band XPS spectra, and (d) band positions of the samples with respect to vacuum. | |
The photoelectrochemical measurements were performed to assess the performance of the material for photoelectrochemical water reduction. The cyclic voltammetry (CV) was first recorded to evaluate the stability of the photocathode in the electrolyte, while performing a cathodic sweep, Fig. 6a. The first reduction peak is attributed to Cu2+ reduction to Cu+ and the second reduction peak is attributed to the reduction of Cu+ to Cu0.52–54 The intensity of the two reduction peaks decreased for the Zn-alloyed samples, proving that zinc alloying reduces the reduction of copper. When there is a high barrier to electron transfer, the electron transfer reactions are sluggish, therefore more negative potential is needed to observe reduction.68–70 As shown in Fig. 6a, alloying Cu with zinc gives rise to larger ΔEp meaning that the reduction of copper has become more sluggish, upon alloying with zinc, which is more beneficial in the PEC system in our study.71 To further investigate the sluggish kinetics of copper reduction for the zinc alloyed samples, Nicholson method was employed to calculate the rate constant (k°) for copper reduction using cyclic voltammetry in dark and under illumination.72,73 It was found that, as the zinc content increases, the rate constant decreases, to a certain limit, meaning that copper reduction is more sluggish whether in dark or under illumination, as shown in Table 2. Cyclic voltammetry was also beneficial to determine the working range of potential in linear sweep voltammetry. The potential range of 0.62 V to 1.2 V vs. RHE was chosen to ensure minimal copper reduction and make sure that the photocurrent is mostly due to hydrogen evolution reaction.74
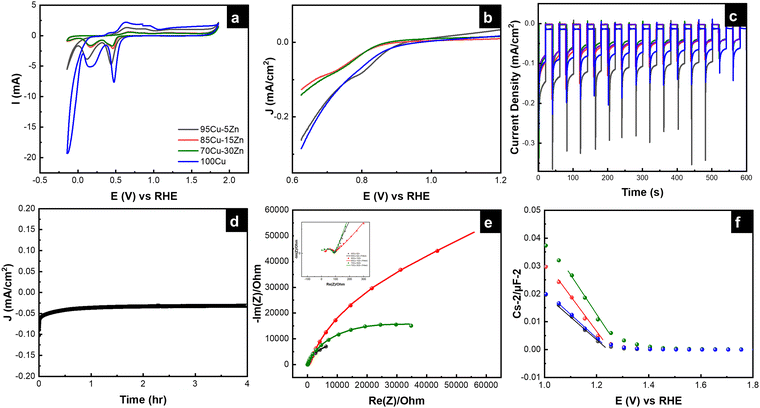 |
| | Fig. 6 (a) Cyclic voltammograms, (b) linear sweep voltammograms, (c) chronoamperometry graphs, (d) chronoamperometry graph under constant illumination for four hours, (e) electrochemical impedance spectra, and (f) Mott–Schottky plots of the tested samples. (Same color code is used for the samples, as in (a).) | |
Table 2 Rate constant in dark and under illumination for the samples
| Sample |
k° dark (cm s−1) |
k° light (cm s−1) |
| 95Cu–5Zn |
3.33 × 10−5 |
7.82 × 10−4 |
| 85Cu–15Zn |
1.81 × 10−5 |
2.07 × 10−5 |
| 70Cu–30Zn |
1.06 × 10−5 |
2.42 × 10−4 |
| 100Cu |
4.88 × 10−5 |
12.93 × 10−4 |
Linear sweep voltammetry (LSV) was performed to scan the photocurrent of the samples under dark and illumination conditions. Even though the 100Cu sample shows the highest current under illumination followed by the 95Cu–5Zn sample, the dark current of the 100Cu sample was the highest, as shown in Fig. S10 (ESI†). That is why we take into consideration the difference between the dark current and the current under illumination to judge the best sample in terms of photocurrent. Chronoamperometry was conducted to test the stability of the sample under chopped illumination. The initial spike upon light illumination is attributed to the rapid separation of photogenerated charge carriers in the space charge region, with electrons moving to the interface to charge the space charge capacitance and holes passing to the external circuit for p-type semiconductors. The following photocurrent decay is attributed to the accumulation of minority charge carriers (electrons) at the interface causing an increase in the flow of holes due to recombination. Then, a steady state is reached. The positive overshoot observed when the light is switched off is because the electron flux is interrupted revealing the mere hole flux.75 From the current–time graph, we were able to calculate the transient time constant, as shown in Table 3.76–79
Table 3 Transient time constant of the tested samples
| Sample |
The transient time constant (s) |
| 95Cu–5Zn |
5.78 |
| 85Cu–15Zn |
5.03 |
| 70Cu–30Zn |
5.128 |
The immediate photoresponse (Iin) is followed by an exponential decrease of the photocurrent until a stationary value is reached (Ist). A ratio (R) that correlates between the (Iin) and (Ist) is defined based on eqn (7):
| | 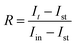 | (7) |
where
It is current at time
t, the photocurrent transient can be described by
eqn (8):
| | 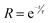 | (8) |
where
τ is the transient time constant. Therefore, the slope of ln(
R)
vs. time is the reciprocal of
τ.
It is worth mentioning that as the transient time constant increases, the recombination process gets delayed, as the charge carriers remain excited at the SEI for longer times. Sample 95Cu–5Zn shows the highest transient time constant compared to other samples. Thus, the photogenerated electrons will have more time to transfer to the interface initiating the water reduction reaction.80,81 The current–time graph also allowed calculating the retention current for the samples using eqn (9) as listed in Table 4. It is worth mentioning that sample 100Cu was exempted from the retention current calculations, transient time constant calculations, transient photovoltage calculations, long term stability measurements, and electrochemical impedance spectroscopy measurements, since the photocurrent results in cupric oxide reduction rather than hydrogen evolution, as will be shown by hydrogen quantification measurements.
| | 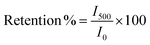 | (9) |
where
I500 is the current at 500 s, and
I0 is the initial current.
Table 4 Calculated retention current of the tested samples
| Sample |
Retention current (%) |
| 95Cu–5Zn |
66.53 |
| 85Cu–15Zn |
42.76 |
| 70Cu–30Zn |
46.93 |
Sample 95Cu–5Zn shows the highest retention current proving that the addition of Zn up to 5% has improved the stability of the sample. To get further insights into the trap states and the charge carriers recombination characteristics of the samples, the transient photovoltage decay behavior of the samples was studied using the open circuit potential switching response, as shown in Fig. S11 (ESI†). Sample 95Cu–5Zn shows the highest photovoltage change of 120 mV meaning that there will be a greater accumulation of photogenerated charge carriers. The recovery behavior of the photovoltage, when the light is terminated, can be due to trapping and recombination of charge carriers mediated by trap states.82 The decay lifetime was calculated for the samples and listed in Table 5. The decay lifetime was calculated from the V–t graphs by fitting it to a biexponential function with two time constants, according to eqn (10) and (11).
| | 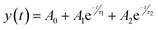 | (10) |
| | 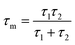 | (11) |
where
τ1 and
τ2 are two relaxation time constants representing two different recombination mechanisms during the decay process,
t is the time,
A0 is the initial photovoltage,
A1 and
A2 are two factors related to two different recombination mechanisms.
τ1 corresponds to the defect-related-recombination, and
τ2 is attributed to band-to-band recombination in the bulk.
τm is the harmonic mean lifetime and log(2
τm) is the total half-life.
Table 5 Calculated decay lifetime of the tested samples
| Sample |
Total half-life (s) |
| 95Cu–5Zn |
0.34 |
| 85Cu–15Zn |
0.56 |
| 70Cu–30Zn |
0.44 |
Sample 95Cu–5Zn showed the least decay lifetime implying that it has the least trap states.83 The transient time constant measurements, transient photovoltage decay measurements, and retention current calculations are in good agreement, showing that sample 95Cu–5Zn is the most stable one compared to the blank 100Cu sample. To elucidate the role of Zn on the stability of the 95Cu–5Zn sample, we have performed a chronoamperometric long-term stability test under constant illumination for four hours, as shown in Fig. 6d.
Electrochemical impedance spectroscopy (EIS) was used to reveal the interfacial interactions of the samples in the dark and under simulated sunlight illumination at an applied potential of 0.62 V vs. RHE. Previous studies only revealed the role of the space charge layer (SCL) in transferring the electrons from the bulk of the semiconductor to the electrolyte.84 However, a few studies focused on the role of surface states; illustrating their chemical capacitance related to the accumulation/transfer of charge through potential surface states at low frequencies. In this study, we propose using an equivalent circuit (EC) that considers the probable surface states to fit EIS data, as shown in Fig. S12 (ESI†). EIS data in the dark are shown in Fig. 6e. Two semicircles can be observed for each sample as shown in Fig. 6e and it is shown by the inset of the figure. EIS data under illumination are shown in Fig. S13 (ESI†). Illumination induces a decrease in the radius of the semicircle in Nyquist plot indicating a lower value of overall resistance due to the photoconductivity of all samples. It is also observed that sample 95Cu–5Zn has the lowest total resistance. More discussion regarding the role of surface states can be found in the ESI,† Fig. S14 and S15.85,86 Through that discussion, it is observed that surface states exist at around 0.8 V vs. RHE.
To study the relationship between the space charge layer capacitance Csc, the acceptor density (NA), and the flat band potential (VFB), Mott–Schottky measurements were conducted in the dark, as shown in Fig. 6f. The negative slopes of the plots indicate the p-type nature of the samples. Charge carrier density was calculated using eqn (12):
| | 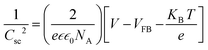 | (12) |
where
e is the electronic charge,
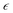
is the dielectric constant,
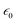
is the vacuum permittivity,
VFB is the flat-band potential of the electrode,
KB is Boltzmann constant, and
T is the temperature in Kelvin. The calculated charge carrier density for the samples is 6.2 × 10
21, 4.3 × 10
21, 3.9 × 10
21, and 6.1 × 10
21 cm
−3 for the 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu samples, respectively. Sample 95Cu–5Zn showed the highest charge carrier density, which might be the reason why it showed the highest photocurrent and the best performance among the samples.
The main challenge in using CuO-based photocathodes is ensuring that the photocurrent produced is resulting from HER and not from the self-reduction of the photocathode. Therefore, quantifying the amount of hydrogen produced is of paramount importance to ensure that the photocurrent is mainly from hydrogen production. In this regard, the 95Cu–5Zn sample showed an amount of hydrogen of 0.2658 μmole after 60 minutes of continuous illumination, as shown in Fig. S16 (ESI†). However, the 100Cu sample only showed 3.965 nmole after 20 minutes of illumination. After 20 minutes, it was observed that the sample was covered with a very shiny metal surface covering the area exposed to the light. These findings mean that most of the photocurrent resulting from the 100Cu sample in our chronoamperometry studies is due to the photoreduction of cupric oxide to copper and not from hydrogen production. Therefore, we can conclude that alloying of CuO with 5% Zn leads to improving the stability of the material in PEC application. Table S1 (ESI†) compares the amount of hydrogen gas obtained using Cu-based photocathodes under close conditions to those used in our study.
Conclusion
Scrap α-brass alloy can be nanostructured to work as a photocathode in PECs. This study showed that alloying copper with 5% zinc has excellent potential as a photocathode for green hydrogen production. Anodization and annealing of α-brass yield a nanostructured surface that contains zinc-doped cupric oxide through substitutional defects in the near-surface layer, and zinc oxide in the outermost layer. The XRD and Raman spectroscopy analyses showed the existence of copper oxides in different brass samples, while XPS analysis suggests the formation of both zinc-doped cupric oxide and zinc oxide. Bare copper and α-brass samples have an estimated optical bandgap in the range of 1.3–1.54 eV. UPS, valence band XPS, and absorption spectra are used to determine the valence band and conduction band offsets of the samples. All tested samples showed p-type behavior and band positions that straddle the water reduction potentials. Upon the use of the samples as photoelectrodes to split water under AM 1.5 illumination, the sample that contains 5% zinc showed a photocurrent density of −0.26 mA cm−2 at 0.62 V vs. RHE, a high long-term stability, a high charger carrier density, and low total resistance. The amount of hydrogen evolved upon the use of the 95Cu–5Zn photocathode was 0.2658 μmole after one hour of continuous illumination (area = 0.5 cm2), while the 100Cu sample could barely withstand 20 minutes of illumination producing only 3.965 nmole of hydrogen before being completely reduced into Cu metal. We hope this study will pave the way to explore other scrap alloys as photocathodes to achieve stable and durable solar fuel production.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
Special thanks to Ibrahim Badawy for his help with the hydrogen quantification measurements. The financial support of this work by the American University in Cairo is highly appreciated.
References
- S. Seethamraju and S. Bandyopadhyay, Clean Technol. Environ. Policy, 2023, 25, 755–756 CrossRef.
- N. K. Allam, C. W. Yen, R. D. Near and M. A. El-Sayed, Energy Environ. Sci., 2011, 4, 2909–2914 RSC.
- A. Boretti, Int. J. Hydrogen Energy, 2020, 45, 23692–23703 CrossRef CAS.
- C. Li, J. He, Y. Xiao, Y. Li and J. J. Delaunay, Energy Environ. Sci., 2020, 13, 3269–3306 RSC.
- M. Z. A. Khan, H. A. Khan, S. S. Ravi, J. W. Turner and M. Aziz, Renewable Sustainable Energy Rev., 2023, 183, 113483 CrossRef CAS.
- R. Seif, F. Z. Salem and N. K. Allam, Environ. Dev. Sustainable, 2023 DOI:10.1007/s10668-023-02925-7.
- W. Yang, R. R. Prabhakar, J. Tan, S. D. Tilley and J. Moon, Chem. Soc. Rev., 2019, 48, 4979–5015 RSC.
- J. Joy, J. Mathew and S. C. George, Int. J. Hydrogen Energy, 2018, 43, 4804–4817 CrossRef CAS.
- I. M. Badawy, A. M. Ismail, G. E. Khedr, M. M. Taha and N. K. Allam, Sci. Rep., 2022, 12, 13456 CrossRef CAS PubMed.
- D. R. Santos, S. Shukla and B. Vermang, J. Mater. Chem. A, 2023, 11, 22087–22104 RSC.
- S. M. Fawzy, M. M. Omar and N. K. Allam, Sol. Energy Mater. Sol. Cells, 2019, 194, 184–194 CrossRef CAS.
- Y. Li and K. Luo, RSC Adv., 2019, 9, 8350–8354 RSC.
- M. M. Hasan, G. E. Khedr, F. Zakaria, N. K. Allam and A. C. S. Appl, Energy Mater., 2022, 5, 9692–9701 CAS.
- H. Xing, L. E. Z. Guo, D. Zhao and Z. Liu, Chem. Eng. J., 2021, 409, 127237 CrossRef.
- H. Xing, E. Lei, Z. Guo, D. Zhao, X. Li and Z. Liu, Inorg. Chem. Front., 2019, 6, 2488–2499 RSC.
- C. Li, T. Hisatomi, O. Watanabe, M. Nakabayashi, N. Shibata, K. Domen and J. J. Delaunay, Appl. Phys. Lett., 2016, 109, 033902 CrossRef.
- S. M. Fawzy, G. E. Khedr and N. K. Allam, Int. J. Hydrogen Energy, 2023, 48, 33111–33118 CrossRef CAS.
- A. M. Elbanna, K. E. Salem, M. Ramadan and N. K. Allam, Energy Fuels, 2023, 37, 3942–3956 CrossRef CAS.
- H. Xing, E. Lie, D. Zhao, X. Li, M. Ruan and Z. Liu, Chem. Commun., 2019, 55, 15093–15096 RSC.
- H. Xing, L. E. Z. Guo, D. Zhao, X. Li and Z. Liu, Inorg. Chem. Front., 2019, 6, 2488–2499 RSC.
- G. K. Dalapati, S. Masudy-Panah, R. S. Moakhar, S. Chakrabortty, S. Ghosh, A. Kushwaha, R. Katal, C. S. Chua, G. Xiao, S. Tripathy and S. Ramakrishna, Global Challenges, 2020, 4, 1900087 CrossRef PubMed.
- A. Cots, P. Bonete and R. Gómez, J. Alloys Compd., 2021, 867, 158928 CrossRef CAS.
- Y. Li and K. Luo, RSC Adv., 2019, 9, 8350–8354 RSC.
- R. O. Yathisha and Y. Arthoba Nayaka, J. Mater. Sci., 2018, 53, 678–691 CrossRef CAS.
- T. Jiang, R. Zhang, Y. Zhang and J. Tian, J. Solid State Chem., 2020, 290, 121603 CrossRef CAS.
- D. S. Eissa, S. S. El-Hagar, E. A. Ashour and N. K. Allam, Int. J. Hydrogen Energy, 2019, 44, 14588–14595 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- N. Bahnasawy, A. M. Elbanna, M. Ramadan and N. K. Allam, Sci. Rep., 2022, 12, 16785 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- M. F. Sanad, A. R. Puente Santiago, S. A. Tolba, M. A. Ahsan, O. Fernandez-Delgado, M. Shawky Adly, E. M. Hashem, M. Mahrous Abodouh, M. S. El-Shall, S. T. Sreenivasan, N. K. Allam and L. Echegoyen, J. Am. Chem. Soc., 2021, 143, 4064–4073 CrossRef CAS PubMed.
- J. K. Cooper, Z. Zhang, S. Roychoudhury, C.-M. Jiang, S. Gul, Y.-S. Liu, R. Dhall, A. Ceballos, J. Yano, D. Prendergast and S. E. Reyes-Lillo, Chem. Mater., 2021, 33, 934–945 CrossRef CAS.
- N. R. Dhineshbabu, V. Rajendran, N. Nithyavathy and R. Vetumperumal, Appl. Nanosci., 2016, 6, 933–939 CrossRef CAS.
- V. Gorelov, D. M. Ceperley, M. Holzmann and C. Pierleoni, J. Chem. Phys., 2020, 153, 234117 CrossRef CAS PubMed.
- M. M. Hasan, G. E. Khedr and N. K. Allam, ACS Appl. Nano Mater., 2022, 5, 15457–15464 CrossRef CAS.
- M. Fang, G. Dong, R. Wei and J. C. Ho, Adv. Energy Mater., 2017, 7, 1700559 CrossRef.
- P. P. Patel, O. I. Velikokhatnyi, S. D. Ghadge, P. J. Hanumantha, M. K. Datta, R. Kuruba, B. Gattu, P. M. Shanthi and P. N. Kumta, Int. J. Hydrogen Energy, 2018, 43, 7855–7871 CrossRef CAS.
- H. Sun, I. H. Öner, T. Wang, T. Zhang, O. Selyshchev, C. Neumann, Y. Fu, Z. Liao, S. Xu, Y. Hou, A. Turchanin, D. R. T. Zahn, E. Zschech, I. M. Weidinger, J. Zhang and X. Feng, Angew. Chem., Int. Ed., 2019, 58, 10368–10374 CrossRef CAS PubMed.
- T. Jiang, R. Zhang, Y. Zhang and J. Tian, J. Solid State Chem., 2020, 290, 121603 CrossRef CAS.
- V. Cretu, V. Postica, A. K. Mishra, M. Hoppe, I. Tiginyanu, Y. K. Mishra, L. Chow, N. H. de Leeuw, R. Adelung and O. Lupan, J. Mater. Chem. A., 2016, 4, 6527–6539 RSC.
- A. Brudzisz, D. Giziński, J. Lee, M. Ibrahim, K. S. Gocman, J. Choi and W. J. Stępniowski, Electrochim. Acta, 2023, 471, 143353 CrossRef CAS.
- N. Jalalian Karazmoudeh, M. Soltanieh and M. Hasheminiasari, Ceram. Int., 2023, 49, 7768–7776 CrossRef CAS.
- M. Taunk and N. Singh, J. Electron. Mater., 2023, 52, 6888–6901 CrossRef CAS.
- A. Gaurav, R. Beura, J. S. Kumar and P. Thangadurai, Mater. Chem. Phys., 2019, 230, 162–171 CrossRef CAS.
- R. Lachhab, M. Galai, A. Ech-chebab, R. A. Belakhmima, M. E. Touhami and I. Mansouri, Ceram. Int., 2024, 50, 4282–4295 CrossRef CAS.
- V. Jagadeesan and V. Subramaniam, J. Mater. Sci.: Mater. Electron., 2019, 30, 1571–1578 CrossRef CAS.
- V. Jagadeesan, A. Rani Sangeetha and P. Anitha, IOP Conf. Ser.: Mater. Sci. Eng., 2021, 1166, 012047 CAS.
- V. Cretu, V. Postica, A. K. Mishra, M. Hoppe, I. Tiginyanu, Y. K. Mishra, L. Chow, N. H. de Leeuw, R. Adelung and O. Lupan, J. Mater. Chem. A, 2016, 4, 6527–6539 RSC.
- A. S. Zoolfakar, R. A. Rani, A. J. Morfa, A. P. O’Mullane and K. Kalantar-Zadeh, J. Mater. Chem. C, 2014, 2, 5247–5270 RSC.
- T. Sander, C. T. Reindl, M. Giar, B. Eifert, M. Heinemann, C. Heiliger and P. J. Klar, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045203 CrossRef CAS.
- B. P. Dhonge, S. S. Ray and B. Mwakikunga, RSC Adv., 2017, 7, 21703–21712 RSC.
- A. M. Koshy, A. Sudha, S. K. Yadav and P. Swaminathan, Phys. B, 2023, 650, 414452 CrossRef CAS.
- M. M. Sivalingam, J. A. Olmos-Asar, E. Vinoth, T. Tharmar, M. Shkir, Z. Said and K. Balasubramanian, ACS Appl. Nano Mater., 2021, 4, 12977–12985 CrossRef CAS.
- B. Karthikeyan, Appl. Phys. A Mater. Sci. Process., 2021, 127, 1–7 CrossRef.
- N. Ahmed, M. Ramadan, W. M. A. El Rouby, A. A. Farghali and N. K. Allam, Int. J. Hydrogen Energy, 2018, 43, 21219–21230 CrossRef CAS.
- Z. Zhang and P. Wang, J. Mater. Chem., 2012, 22, 2456–2464 RSC.
- F. Chen, J. He, C. Wang, N. Gao, C. Dong, M. Chen, Y. Wang and J. Chen, Microchem. J., 2023, 192, 108935 CrossRef CAS.
- N. T. Mai, T. T. Thuy, D. M. Mott and S. Maenosono, CrystEngComm, 2013, 15, 6606–6610 RSC.
- W. Z. Tawfik, M. A. Hassan, M. A. Johar, S.-W. Ryu and J. K. Lee, J. Catal., 2019, 374, 276–283 CrossRef CAS.
- T. J. Frankcombe and Y. Liu, Chem. Mater., 2023, 35, 5468–5474 CrossRef CAS.
- I. M. Badawy, A. M. Ismail, G. E. Khedr, M. M. Taha and N. K. Allam, Sci. Rep., 2022, 12, 13456 CrossRef CAS PubMed.
- S. Maroie, R. Caudano and J. Verbist, Surf. Sci., 1980, 100, 1–13 CrossRef CAS.
- T. Vanherwijnen, J. Catal., 1974, 34, 209–214 CrossRef CAS.
- S. S. Kalanur, Y. J. Lee and H. Seo, ACS Appl. Mater. Interfaces, 2021, 13, 25906–25917 CrossRef CAS PubMed.
- M. G. Helander, M. T. Greiner, Z. B. Wang and Z. H. Lu, Appl. Surf. Sci., 2010, 256, 2602–2605 CrossRef CAS.
- W. J. Chun, A. Ishikawa, H. Fujisawa, T. Takata, J. N. Kondo, M. Hara, M. Kawai, Y. Matsumoto and K. Domen, J. Phys. Chem. B, 2003, 107, 1798–1803 CrossRef CAS.
- P. Gupta and B. C. Joshi, Vacuum, 2023, 216, 112455 CrossRef CAS.
- C. Day, K. Greig, A. Massey, J. Eake, D. Crossley and R. A. W. Dryfe, ChemSusChem, 2020, 13, 1504–1516 CrossRef CAS PubMed.
- A. Jaikumar, K. S. V. Santhanam, S. G. Kandlikar, I. B. P. Raya and P. Raghupathi, ECS Trans., 2015, 66, 55–64 CrossRef CAS.
- Y. Li and K. Luo, RSC Adv., 2019, 9, 8350–8354 RSC.
- N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206 CrossRef CAS.
- I. Lavagnini, R. Antiochia and F. Magno, Electroanalysis, 2004, 16, 505–506 CrossRef CAS.
- X. Qiao, M. Arsalan, X. Ma, Y. Wang, S. Yang, Y. Wang, Q. Sheng and T. Yue, Anal. Bioanal. Chem., 2021, 413, 839–851 CrossRef CAS PubMed.
- Y. Yang, D. Xu, Q. Wu and P. Diao, Sci. Rep., 2016, 6, 35158 CrossRef CAS PubMed.
- L. M. Peter, A. B. Walker, T. Bein, A. G. Hufnagel and I. Kondofersky, J. Electroanal. Chem., 2020, 872, 114234 CrossRef CAS.
- F. Spadavecchia, S. Ardizzone, G. Cappelletti, L. Falciola, M. Ceotto and D. Lotti, J. Appl. Electrochem., 2013, 43, 217–225 CrossRef CAS.
- M. Radecka, M. Wierzbicka, S. Komornicki and M. Rekas, Phys. B, 2004, 348, 160–168 CrossRef CAS.
- Z. Yan, W. Wang, L. Du, J. Zhu, D. L. Phillips and J. Xu, Appl. Catal., B, 2020, 275, 119151 CrossRef CAS.
- Q.-L. Mo, S. Hou, Z.-Q. Wei, X.-Y. Fu, G. Xiao and F.-X. Xiao, Chem. Eng. J., 2022, 433, 133641 CrossRef CAS.
- A. M. Elbanna, K. E. Salem, A. M. Mokhtar, M. Ramadan, M. Elgamal, H. A. Motaweh, H. M. Tourk, M. A. H. Gepreel and N. K. Allam, J. Phys. Chem. C, 2021, 125, 12504–12517 CrossRef CAS.
- A. W. Amer, M. A. El-Sayed and N. K. Allam, J. Phys. Chem. C, 2016, 120, 7025–7032 CrossRef CAS.
- S. S. Yi, B. R. Wulan, J. M. Yan and Q. Jiang, Adv. Funct. Mater., 2019, 29, 1801902 CrossRef.
- J. Su, C. Liu, D. Liu, M. Li and J. Zhou, ChemCatChem, 2016, 8, 3279–3286 CrossRef CAS.
- F. Le Formal, N. Tétreault, M. Cornuz, T. Moehl, M. Grätzel and K. Sivula, Chem. Sci., 2011, 2, 737–743 RSC.
- L. Bertoluzzi, P. Lopez-Varo, J. A. Jiménez Tejada and J. Bisquert, J. Mater. Chem. A, 2016, 4, 2873–2879 RSC.
- M. S. Prévot, X. A. Jeanbourquin, W. S. Bourée, F. Abdi, D. Friedrich, R. van de Krol, N. Guijarro, F. Le Formal and K. Sivula, Chem. Mater., 2017, 29, 4952–4962 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: It includes EDX elemental analysis for the as-anodized and annealed samples, SEM images of the as-anodized samples, variation of the crystallite size and microstrain on the zinc content, XPS results of the as-anodized and annealed samples, Tauc plots, linear sweep voltammograms, open circuit potential measurements, EIS data analysis, and hydrogen quantification measurements. See DOI: https://doi.org/10.1039/d3ya00534h |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Sneha
Sreekumar
b,
Haydee
Pacheco
b,
Nada
Tarek
a,
Deirdre M.
O’Carroll
b,
Sneha
Sreekumar
b,
Haydee
Pacheco
b,
Nada
Tarek
a,
Deirdre M.
O’Carroll
 b and
Nageh K.
Allam
b and
Nageh K.
Allam
 *a
*a
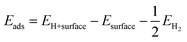
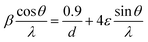
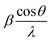 is plotted vs.
is plotted vs. 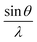 and fitted into a straight line, then the lattice strain can be obtained from the slope, and the average crystallite size from the intercept. The relationship between the zinc content versus the lattice strain and average crystallite size is shown in Fig. S5 (ESI†). As the zinc content increases, average crystallite size decreases and lattice strain increases, implying that increasing zinc content induces more lattice imperfections, which adversely affect the photoelectrochemical performance of the samples,46,47 as will be discussed later.
and fitted into a straight line, then the lattice strain can be obtained from the slope, and the average crystallite size from the intercept. The relationship between the zinc content versus the lattice strain and average crystallite size is shown in Fig. S5 (ESI†). As the zinc content increases, average crystallite size decreases and lattice strain increases, implying that increasing zinc content induces more lattice imperfections, which adversely affect the photoelectrochemical performance of the samples,46,47 as will be discussed later.

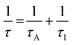
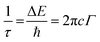

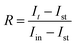
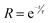
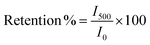
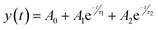
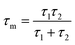
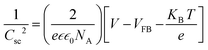
 is the dielectric constant,
is the dielectric constant, 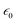 is the vacuum permittivity, VFB is the flat-band potential of the electrode, KB is Boltzmann constant, and T is the temperature in Kelvin. The calculated charge carrier density for the samples is 6.2 × 1021, 4.3 × 1021, 3.9 × 1021, and 6.1 × 1021 cm−3 for the 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu samples, respectively. Sample 95Cu–5Zn showed the highest charge carrier density, which might be the reason why it showed the highest photocurrent and the best performance among the samples.
is the vacuum permittivity, VFB is the flat-band potential of the electrode, KB is Boltzmann constant, and T is the temperature in Kelvin. The calculated charge carrier density for the samples is 6.2 × 1021, 4.3 × 1021, 3.9 × 1021, and 6.1 × 1021 cm−3 for the 95Cu–5Zn, 85Cu–15Zn, 70Cu–30Zn, and 100Cu samples, respectively. Sample 95Cu–5Zn showed the highest charge carrier density, which might be the reason why it showed the highest photocurrent and the best performance among the samples.




