Manipulating molecular orientation in vapor-deposited organic semiconductor glasses via in situ electric fields: a molecular dynamics study

Abstract

The manipulation of molecular orientation is a well established target in organic electronics and energy-harvesting applications since it may affect relevant parameters such as energy levels, electron transport, exciton recombination or light outcoupling. In vapor-deposited thin film organic glasses, thermal evaporation offers control of the molecular orientation by changing the deposition temperature or the deposition rate. However, the deposition conditions are strongly linked to other properties of the glass such as density and thermal stability. The deposition conditions that yield optimal orientation may result in poorly stable and low-density glasses, detrimental for device performance. Here, we use molecular dynamics simulations to investigate the possibility of manipulating molecular orientation of physicalvapor-deposited (PVD) glasses by applying external electric fields during the vapor deposition process. Our aim is to align the electric dipole moments of these molecules in the direction of the electric field, whether in-plane or out-of-plane. We consider three distinct molecules: TPD and two brominated TPD derivatives with larger intrinsic dipole moments. Our results demonstrate that the electric field effectively modifies the orientation polarization of the glass without modifying its density, opening a possible route to manipulate glass properties and device performance at will.

---

Introduction

The phenomenon of molecular anisotropy in thermally evaporated thin film organic glasses has captured considerable attention in recent years. Following the initial reports that detailed the anisotropic orientation of molecules within otherwise amorphous films,^1,2 there has been an increased interest in this topic. The manipulation of molecular orientation (MO) within a glassy layer holds the potential to significantly impact device performance by improving charge carrier transport through enhanced pi–pi interactions between neighboring molecules.³ MO is also being harnessed to enhance light outcoupling in OLEDs by promoting a horizontal orientation of the transition dipole moment (TDM) of the emitter with respect to the transparent substrate surface.^4–8

Molecular anisotropy in thin film vapor-deposited glasses can be attributed to both molecular shape and the inherently anisotropic nature of thermal evaporation. In contrast, organic glasses derived from liquid processing exhibit isotropic characteristics. The temperature of deposition plays a pivotal role in controlling the orientation of molecules within the film.^9–12 For rod-shaped molecules and at a given growth rate, lower deposition temperatures relative to the glass transition temperature (T_dep < 0.7 T_g) lead to a horizontal molecular orientation, where the long axis of the molecule aligns parallel to the substrate surface on average. As the deposition temperature increases, the layer becomes more isotropic or slightly vertically aligned, particularly in the deposition temperature range of 0.8–0.9 T_g. Deposition at temperatures exceeding 0.9 T_g results in nearly isotropic glasses. The observed enhanced stability and molecular anisotropy in vapor-deposited glasses can be attributed to surface equilibration,^13,14 underscoring its fundamental role in shaping these unique characteristics.^15,16

Besides temperature, the deposition rate is also a crucial factor as it dictates the residence time of each molecule on the surface before being overlaid by subsequent incoming molecules. Recent work by Bishop et al.^11,17 has shed light on the intertwined roles of growth rate and deposition temperature in molecular orientation, presenting a unified framework termed rate-temperature superposition (RTS). Lower deposition rates enable molecules more time to relax, leading to the adoption of equilibrated orientations that favor antiparallel dipole alignment and consequently reduce polarization. This effect is akin to employing high substrate temperatures, establishing a correlation between these two parameters, that in general cannot be independently tuned.

If the individual molecules have a permanent dipole moment (PDM) molecular anisotropy can result in significant average polarization and voltage drops across the vapor-deposited thin film.¹⁸ Most often this occurs in the direction perpendicular to the substrate due to growth constraints as stated above. The build-up of a large surface potential in vapor-deposited thin films glasses is known as spontaneous orientation polarization (SOP) and may have a tremendous impact on device performance. For instance, SOP can favor charge injection lowering the voltage threshold for the on-state of an OLED.¹⁹ In turn, polarization can induce surface charges at the interfaces between polar and non-polar materials reducing the power conversion efficiency of OLEDs due to an increased exciton-polaron quenching.²⁰ The exact influence of surface polarization on the various stacks of an OLED and its role on device performance is still to be fully understood. Recently, He et al. have used this formalism applied to SOP to engineer OLED devices maximizing their efficiency.²¹ Molecular orientation also plays a role in energy harvesting devices. Organic glassy layers of TPBi or Alq3 with SOP forming a plate-capacitor device have been shown to do work on an external circuit under a mechanical oscillation that induces electric currents.²²

While the presence of PDM in the individual molecule is a necessary condition for SOP the contrary is not true and there is not a clear trend between the permanent dipole moment of the molecules and the giant surface potential of the films, that is molecules with large PDM may result in films with small polarization. Most probably due to dipole/dipole interactions with a tendency to produce antiparallel orientation of neighbor molecules during growth. In addition, it is hard to find suitable molecules that upon vapor deposition show negative surface potential. Recently, several reports have proposed new molecular design rules to increase positive or negative giant surface potential (GSP) by adding functional groups to some organic molecules.^23,24

Besides molecular orientation thermal stability is also a relevant parameter for organic devices. Glasses with outstanding stability, known as ultrastable glasses, can be prepared by setting the deposition temperature at around 85% of the glass transition temperature of the conventional liquid-cooled glass, T_g.^25,26 Rafols et al.²⁷ have shown that OLED devices in which the electron transport layer and the emissive layers were grown at appropriate temperatures with respect to the T_g of the layers resulted in enhanced external quantum efficiency and larger operational lifetimes.

In general, OLED devices require of high stability and density for increasing their operational lifetime²⁷ and the temperatures at which the maximum stability is attained may not coincide with the required molecular orientation resulting in devices with lower performance. One of the persistent challenges to address in OLEDs is primarily related to the fact that their longevity correlates inversely to the brightness.^28,29 For this reason, high brightness applications still cannot be realized with OLEDs due to their insufficient stability^30–32 without compromising the optimal molecular orientation. Thus, efforts must be made towards decoupling the dependence of this trait on deposition temperature. This should be doable, as it has been demonstrated that anisotropy is not a condition for ultrastability.^33,34

The objective of this work is to investigate, by means of molecular dynamics simulations, alternative strategies – other than modifying deposition temperature and rate or molecular conformation – for manipulating the molecular orientation of vapor-deposited glasses. Specifically, we attempt to induce changes in the orientation of the molecular PDM, and therefore of the whole molecule, by applying an electric field during vapor deposition. Such a strategy has been successfully employed for organic liquid crystalline molecules,³⁵ showing a critical impact of the electric field on the corresponding optical properties and for metallo-phthalocyanines,^36,37 using electric fields in the order of 10⁵–10⁶ V m⁻¹. These molecules, however, crystallize during deposition and show a higher tendency to ordering than the molecules used for glassy organic electronics.

The molecules employed for this study are modified versions of TPD (N,N′-bis(3-methylphenyl)-N,N′-diphenylbenzidine), an organic semiconductor molecule widely used in the organic semiconductor industry and thoroughly characterized in terms of orientation and stability when vapor-deposited,^9,38 consisting in the inclusion of highly electronegative atoms in the structure of the molecule, allowing the increase of the total PDM of the molecule and a stronger interaction with the electric field.

We note that the ability to control and maximize both the thermal stability and the polarization of the organic layers may benefit other related fields such as organic memories and neuromorphics. We anticipate that using electric fields during vapor deposition may be an effective strategy to orient the PDM along the out-of-plane (positive or negative giant surface potentials) or in-plane directions while preserving the ultrastability of the amorphous layers.

Methods

DFT calculation of the electric dipole moment

To enhance the dipole moment of the TPD molecule while preserving its structural integrity, we investigated the effect of doping by means of a halogen atom. Accordingly, the Cartesian components of the electric dipole moment of the halogen-doped molecules have been estimated from density functional theory (DFT) calculations.

Halogens are characterized by a high electronegativity, which leads to an increase of the dipole moment by increasing the local electronic density near the addition site. Through optimization procedures conducted with the Gaussian package³⁹ at the ωb97Xd/cc-pVTZ level, various substitutional positions for halogenation on the TPD molecule were explored. Subsequently, frequency calculations were performed to assess the stability of each resulting structure.

The electric dipole moments of both the gas-phase isolated pristine TPD and the halogenated variants (with Cl, F, and Br atoms) were determined using this methodology. To validate the accuracy of our calculations, we employed the same functional and basis set to compare the experimental and DFT-calculated dipole moments of five reference heterocyclic molecules. These reference molecules were selected for their structural and electronic similarities to our target molecular systems (details provided in the ESI†). The computational results exhibit a minor deviation from the experimental values, yielding an overall root mean square (RMS) error of 0.09 D. This level of deviation is consistent with the latest advancements in such computational analyses.⁴⁰

Force field

The systems under study, both under and without the influence of the electric field, are simulated by molecular dynamics using AMBER force field,^41,42 which has been demonstrated to be effective in mimicking organic and biologic systems.^43,44 AMBER accounts for both intramolecular (bonded) and intermolecular (non-bonded) interactions: it includes three bonding terms (for the description of bonds, angles, and dihedrals) and two non-bonding terms (Coulomb and van der Waals). The internal energy of the unbiased system, U_AMBER, is expressed as:where r represents the interatomic distances, θ the angle formed by three bonded atoms and ϕ the dihedral angle between four bonded atoms. Subindex 0 indicates equillibrium positions. The atomic bonding terms in eqn (1) (K_r, K_θ, r₀, θ₀, V_n and γ) are taken from AMBER database.⁴¹ The last two summations in eqn (1) run over all i–j pairs of atoms in the system, and the involved parameters ( and σ_ij) are obtained by applying arithmetic mixing rules on σ_ii and 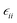, obtained from AMBER database too. It is important to remark that the actual values of the parameters depend on both the atomic species as well as on the chemical environment of the atom (i.e. the parameters for specific atoms are sensitive to the different bonding environment, as the sp²vs. sp³ hybridization). Thus, realistic atomic interactions are secured. Long-range Coulomb interactions were evaluated by using a particle mesh Ewald algorithm.⁴⁵ The last term in eqn (1), the Lennard-Jones term defined by the potential, is truncated by a cutoff set at 10 Å. The AMBER force field does not allow movements of the atomic partial charges, so electric field induced polarization of the charges is not included here. This approximation is supported by our DFT calculations (see ESI†), showing that both pristine and brominated TPD molecules exhibit sufficiently low polarizabilities to justify the use of a fixed charge treatment. We remark that the effect of an external electric field is introduced by adding an additional force to each atom that carries a point-like partial charge q_i. The resulting electrostatic force, acting in the direction of the electric field, is calculated internally by the LAMMPS package in the framework of classical electrostatics.

Classical molecular dynamics simulations

Molecular dynamics simulations are performed using LAMMPS package.⁴⁶ Newton equations of motion are integrated according to the velocity Verlet algorithm,⁴⁷ with a timestep of 0.5 fs. All simulations are performed in the canonical ensemble, coupling the system with a Nosé–Hoover thermostat and employing periodic boundary conditions. For simulations where molecules are deposited onto a substrate, the velocity of molecules during evaporation is calculated from the kinetic theory of gases, extracting values (such as the pressure and the temperature of the molecules) from the vapor deposition experimental conditions in the laboratory (see ESI†). The present computational setup has been validated by an estimate of the TPD glass transition temperature which is in reasonable agreement with the experiments⁴⁸ (see ESI† for a detailed description of the computational procedure).

In silico sample preparation

To assess the tendency of the molecules to align along the electric field, we considered at first an isolated molecule in vacuum. We performed NVT simulations both with and without an applied electric field spanning a total of 10⁷ timesteps. To simulate the deposition of the thin film glass, we initially prepared in silico a crystalline TPD substrate composed of four layers, each containing a grid of 6 × 4 molecules. Prior to the deposition process, we performed an amorphization of the top 2 layers to achieve a smooth surface for the incoming molecules. This approach enforces the stability of the organic substrate during vapor deposition and avoids deformations previously observed at the interface between organic molecules and inorganic Si substrates.⁴⁹ This deposition protocol, initially proposed by De Pablo,^34,49–51 was employed in our study with minor modifications. Molecules have been gradually deposited onto the substrate through an iterative process: at the onset of each iteration, 15 molecules are introduced approximately 70–90 Å above the substrate surface, with random positions and orientations. Next, the energy of the system (substrate & newly deposited molecules) was minimized through the Conjugate Gradients algorithm. Molecules approach the substrate with a temperature T_i = 400 K in in 2 × 10⁵ steps, and a translational velocity calculated according to the kinetic theory of gases (see ESI†). During deposition, the grown substrate (the substrate together with the previously deposited molecules) was kept at T_f = 300 K. Eventually, the newly-deposited molecules have been cooled down to T_f in 7 × 10⁵ steps, corresponding to a quenching rate of 3 × 10¹¹ K s⁻¹.

The iterative process is repeated 20 times creating a glass containing 300 molecules, as shown in Fig. 1.

Fig. 1 Representation of the creation of a 300 molecule TPD-Br1 glass on top of a pre-fabricated 4 layer crystal structure of the same molecule. Beside each snapshot is the number of molecules already deposited in the represented stages: 0, 75, 150, 225 and 300.

Results and discussion

Evaluation of the electric dipole moment by first principles DFT

DFT calculations yield a 0.41 D electric dipole moment for pristine TPD. The main objective of this study is to investigate the possible alignment patterns of the molecules’ dipole moments along the electric field lines, making molecules with a high permanent dipole moment (PDM) particularly suitable. DFT calculations allow us to investigate possible strategies to enhance the dipole moment of the TPD molecules through halogenation. Simulations involving various types of atoms (Br, Cl, and F) suggested that the addition of Br atoms into TPD resulted in the highest dipole moment enhancement (see ESI†). Electric dipole moments for TPD in its gas-phase before and after bromination are listed in Table 1. As anticipated, we observe a remarkable increase of the molecular dipole moment following halogenation with Br atoms. Moreover, the orientation of the dipole moment is greatly influenced by the relative positioning of the bromine atoms within the molecular geometry.

Table 1 Coordinates and modulus of the electric dipole moment of TPD, TPD-Br1 and TPD-Br2 derived from DFT calculations. Reference axes are represented in Fig. 2

Molecule	μ l (D)	μ t_1 (D)	μ t_2 (D)	μ (D)
TPD	0.04	0.26	−0.31	0.41
TPD-Br1	−0.06	4.05	0.12	4.05
TPD-Br2	2.77	0	0	2.77

---

We consider two distinct bromination configurations, both depicted in Fig. 2: one involving the addition of two Br atoms to the aromatic rings on opposing sides of the molecule (TPD-Br1), and the other with both Br atoms positioned at one end (TPD-Br2). Pristine TPD exhibits an electric dipole moment primarily directed perpendicular to the backbone of the molecule. Symmetric bromination in TPD-Br1 results in an electric dipole moment perpendicular to the long axis of the molecule (other dipole moment components are negligible), and it is 15 times larger than that of pristine TPD, measuring 4.05 D. Conversely, asymmetric bromination in TPD-Br2 yields a smaller dipole moment than TPD-Br1, measuring at 2.77 D, but still almost 7 times larger than that of pristine TPD. Notably, TPD-Br2 exhibits a distinctive feature: the direction of its electric dipole moment differs from the other two molecules, aligning along the long axis of the molecule, with zero components along the other directions. The variability in dipole moment orientations is of interest for identifying different molecular alignments in PVD glasses of these molecules, particularly when prepared under the same electric field direction.

Fig. 2 Chemical structure of TPD, TPD-Br1 and TPD-Br2 together with their electric dipole moment vector, μ (in green).

Single molecule in vacuum

We first carry out MD simulations of the dynamics of single TPD, TPD-Br1 and TDP-Br2 molecules under an electric field in vacuum (without interacting with any substrate). To elucidate the influence of thermal energy on the orientation of the molecular dipole with respect to the electric field, the simulations are performed at two distinct temperatures: T = 30 K and T = 300 K, see Fig. 3. For each temperature, we compare the behaviour of the molecules both in the absence and under the influence of an electric field set at 10⁹ V m⁻¹. The electric field remains constant and is directed along the ŷ direction, parallel to the substrate plane. Initially, the three molecules are placed with their long axis aligned in the same direction as the electric field. The permanent dipole moments (PDM) of TPD and TPD-Br1 are oriented perpendicular to the electric field, whereas the PDM of TPD-Br2 is aligned parallel to the field. To assess the degree of alignment of the total PDM, [small mu, Greek, vector], with the electric field, we analyze the evolution of the projection of [small mu, Greek, vector] onto different directions, namely, μ_x, μ_y and μ_z. In the event of perfect alignment between the permanent electric dipole moment and the electric field, the ŷ component of the dipole moment μ_y should be equal to the magnitude of the vector, μ.

Fig. 3 Time evolution of the modulus of the PDM (grey) and the projection towards the direction of the electric field lines, μ_y, for TPD, TPD-Br1 and TPD-Br2 molecules in vacuum at 30 K and at 300 K in the presence of an electric field of 10⁹ V m⁻¹. Time steps correspond to 0.5 fs. Units of the PDM are in Debye (D).

TPD, characterized by a lower electric dipole moment, shows minimal interactions with an applied electric field, a trait accentuated as the temperature rises up to 300 K. Even at a lower temperature, while subjected to an electric field, although TPD exhibits an oscillatory response it lacks an appreciable alignment of the dipole moment in any specific orientation. In contrast, TPD-Br1 and TPD-Br2 exhibit increased sensitivity to the electric field, evidenced by a damped oscillation of the ŷ component of the PDM towards the value of the total PDM of the molecule. This behaviour indicates a progressive alignment of the molecule, gradually orienting itself in the direction of the electric field. While this tendency is more pronounced at lower temperatures, the interaction between the dipole moment and electric field proves sufficiently robust to induce molecular reorientation even at higher temperatures, particularly evident in TPD-Br1. Notably, a distinct feature emerges in the behaviour of the total PDM of TPD-Br1 molecules at elevated temperatures. Regardless of the presence of an external electric field, the magnitude of the PDM undergoes abrupt fluctuations, oscillating between approximately 6 D and zero. This phenomenon is likely attributable to thermal energy enabling the molecule to explore various conformations. This occurs due to the flexibility of the molecule, which allows rotations around single carbon–carbon (C–C) and carbon–nitrogen (C–N) bonds, as well as inversions around the nitrogen center. These movements permit the benzene rings to change their relative orientations, contributing to the dynamic conformational behavior of the molecule. Consequently, the relative orientation of the Br atoms shifts, altering the orientation and overall value of the PDM. A notable configuration has the molecule twisted around its center of mass, bringing the two Br atoms on opposite sides of the molecule backbone. This results in a minimal PDM, making the TPD molecule non-polar and weakly interacting with the electric field. Similarly, albeit less pronounced, the fluctuations observed in the dipole moment evolution of TPD at higher temperatures are likely linked to the same underlying effect. In contrast, TPD-Br2, being an asymmetric molecule with both Br atoms situated on one side, remains immune to rotations around its long axis, thus preserving the modulus of its PDM. It is worth noting that the specific bending observed in simulations could be a consequence of the torsion angle parameters within the force field.

Molecular anisotropy on vapor-deposited glasses prepared under an electric field

vapor-deposited glasses of TPD-Br1 and TPD-Br2 have been prepared following the methodology described in Section 2.4. TPD is excluded from this part of the study, as we have previously seen that its small electric dipole moment barely aligns with the field. A sketch of the iterative process of vapor deposition is presented in Fig. 1, together with the direction of the electric field (applied in the ŷ direction).

One of the advantages of simulating glasses with molecular dynamics is the possibility of obtaining information about each molecule composing the film under study. This is something inaccessible in the laboratory, where averaged quantities are used to determine the properties of the glass. Here, we can plot the electric dipole moment of each molecule constituting the glass and thus determine the average change in molecular orientation as a function of the magnitude of the applied electric field. Fig. 4 shows the 3D plot of the electric dipole moment of the 300 molecules in the TPD-Br1 glass during the vapor deposition process under E = 0, 10⁸, and 10⁹ V m⁻¹ along ŷ and ẑ. The magnitude of such an electric field, based on the estimated DFT ionization potentials as large as 7 eV, should not lead to field-ionization phenomena (see ESI†). The coordinates of the electric dipole moments (μ_x, μ_y, μ_z) are represented with (0, 0, 0) as the starting coordinate for each vector. The plot clearly shows an isotropic glass in its as-deposited state without the presence of an external electric field. This is an expected result considering the rapid cooling rates employed during glass deposition. A similar isotropic distribution is observed for glasses prepared under E ≤ 10⁸ V m⁻¹. These electric fields do not induce any change in the molecular orientation of the glass, as the vectorial distribution remains identical to the case of zero electric field, and no preferential orientation of the electric dipole moment is observed (a representation of the vector distribution for 10⁵ and 10⁷ V m⁻¹ is provided in the ESI†).

Fig. 4 Representation of the normalized dipole moment components of the 300 molecules in the MD vapor-deposited glasses for TPD-Br1 prepared at 300 K and under 0, 10⁸ and 10⁹ V m⁻¹ electric fields along ŷ (in plane) and ẑ (out of plane) (direction of the field in yellow). The histograms show the counts of the normalized projections: μ_x/μ (in orange, vertical lines) μ_y/μ (in blue, horizontal lines) and μ_z/μ (in green, diagonal lines) of each specific case.

However, at E = 10⁹ V m⁻¹, the electric dipole moments tend to reorient towards the direction of the electric field. This observation is further supported by the histograms representing the normalized components of the electric dipole moment of the molecules in the glass (Fig. 4). The histograms for all components exhibit a flat profile, indicating random average orientation, except for μ_y and μ_z when the electric field is applied along the ŷ or ẑ directions at 10⁹ V m⁻¹, respectively. In these cases, the histograms shift towards higher values of dipole moment, approaching the modulus of the total electric dipole moment, indicating an alignment of the molecular dipoles with the electric field lines. Similar results have been obtained for TPD-Br2 glasses (refer to the ESI†).

Table 2 details the changes in the average molecular dipole moment within vapor-deposited glasses subjected to a 10⁹ V m⁻¹ electric fields, along the ŷ (in-plane) and ẑ (out-of-plane) directions. It allows us to derive values for the orientation polarization (OP) in each direction, reflecting the inherent orientation preference of the permanent dipole moment (PDM) within the glass.

Table 2 Normalized dipole moment components and OP associated to each direction of the MD vapor-deposited glasses for TPD-Br1 and TPD-Br2 samples prepared at E = 0 and 10⁹ V m⁻¹. Directions are indicated in Fig. 4. TPD-Br2 representation of the electric dipole moment vectors and histograms are displayed in ESI

	Field (V m^−1)	〈μx/μ〉	〈μy/μ〉	〈μz/μ〉	OPx (mV nm^−1)	OPy (mV nm^−1)	OPz (mV nm^−1)
TPD-Br1	0	0.01	−0.08	0.07	−0.46	−42.38	36.18
	10^9 in ŷ	0.02	0.38	0.06	10.71	197.4	31.76
	10^9 in ẑ	0.01	0.03	0.33	−4.42	18.06	169.99
TPD-Br2	0	−0.09	0.04	0.04	−47.69	18.30	22.05
	10^9 in ŷ	−0.03	0.32	0.03	−13.17	166.36	17.29
	10^9 in ẑ	−0.06	−0.02	0.18	−32.60	−11.10	92.48

---

The value of the OP per unit length for each direction d is shown in Table 2 and is given by:^18,52

where 〈μ_d〉 is the mean of the component of the electric dipole moment in the specific direction d; ε the relative permittivity (assumed to be ε = 3.5⁵³) and V the molecular volume (taken as 10⁻²⁷ m³).

First, we note that OPs around 160–190 mV nm⁻¹ are larger than those induced experimentally by spontaneous orientation polarization along the growth direction during thermal evaporation, even for molecules with larger PDM.⁵²Table 2 provides further insight, revealing that while TPD-Br1 exhibits a greater dipole moment than TPD-Br2, the alignment of the electric field in the ŷ direction does not yield significantly disparate values of orientation polarization. This phenomenon is attributed to the rotational dynamics of TPD-Br1 around the biphenyl core, shown in Fig. 2, an effect particularly relevant at elevated temperatures. Such rotations generally lead to a reduction in the overall dipole moment, consequently diminishing this molecule's contribution to the total OP. This deduction finds support in the considerable dispersion of the electric dipole moment modulus exhibited by TPD-Br1 compared to the more stable behaviour of TPD-Br2, as depicted in Fig. 5. The stability of TPD-Br2 PDM against rotation around the biphenyl core, owing to its asymmetric geometry, implies that its OP values only originate from molecular orientation, unlike TPD-Br1, whose OP is influenced by both orientation and conformation. Considering the relationship between molecular rotation and thermal energy, one plausible strategy to enhance OP in TPD-Br1 glasses could involve depositing vapor molecules at lower temperatures. Conversely, the lower OP value of TPD-Br2 in the z-direction (92 mV nm⁻¹) may stem from inherent challenges in aligning molecules with their long axis perpendicular to the substrate. Additionally, Fig. 5 illustrates a narrowing of the modulus distribution of TPD-Br1 when subjected to an electric field, a trend further supported by Fig. 6. Here, the plot showcases the mean modulus of the PDM of TPD-Br1 molecules along the field direction (ŷ) versus μ_y/μ. We attribute the less dispersed dipole distribution to the influence of molecular conformation. Higher temperatures activate certain conformations, which in turn result in stronger interactions with external electric fields. Previous studies have demonstrated a close correlation between stability and density.^13,25,54 This parameter can also serve as a useful metric for assessing whether the thermal stability of the glass is influenced by a change in molecular orientation. Therefore, we calculate the density of the glass to correlate stability and molecular orientation. To achieve this, we analyse the radial distribution function g(r) of our simulated PVD glasses, which is directly linked to the glass density. Fig. 7 presents a comparison of the radial distribution function of two TPD-Br1 glasses prepared at T_f = 300 K, one with (red lines) and one without (black lines) the effect of a 10⁹ V m⁻¹ field in the ŷ direction. Despite observable differences in the orientation of the molecules (as illustrated in Fig. 4), the radial distribution function remains unchanged for these two glasses. This observation suggests that the density of our glasses likely remains unaltered even in the presence of an applied electric field is applied, suggesting that stability remains unaffected. Such behaviour opens the possibility to an independent tuning of glass stability and molecular orientation in vapor-deposited glasses.

Fig. 5 Dispersion of the modulus of the electric dipole moment of molecules in TPD-Br1 and TPD-Br2 glasses prepared at 0 V m⁻¹ and 10⁹ V m⁻¹ in the plane of the substrate (ŷ).

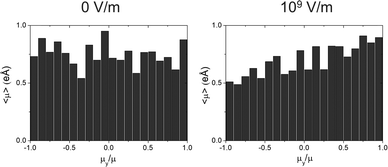Fig. 6 Mean value of the modulus of the electric dipole moment for the different values of the ŷ component of the dipole weighted by its modulus.

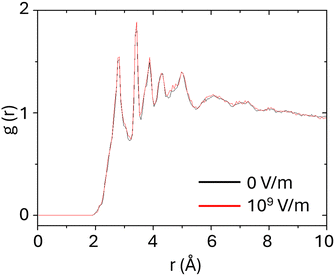Fig. 7 Radial distribution function for TPD-Br1 simulated vapor-deposited films deposited at T_f = 300 K with and without 10⁹ V m⁻¹ electric field in ŷ.

Conclusions

In this study we have used real-atomic molecules governed by the AMBER force field to explore how organic semiconductor glasses interact with electric fields through molecular dynamics simulations. Our results demonstrate the impact of external electric fields to actively control the orientation of the permanent dipole moments of the molecules along the direction of the electric field during the deposition process. The tunability of the average OP appears to be independent of the density of the glass. This strategy offers a promising avenue to produce a-la-carte highly stable glasses with tailored orientation, along in-plane or out-of-plane directions. Using adequate nanofabricated grids to implement appropriate in-plane or out-of-plane electric fields may help an experimental realization of this approach.

Author contributions

MGS, CM, LC and JRV designed, supervised and acquired the required funding for this research. MRL, RD, AC and CM designed the methodology and performed the calculations. All authors wrote, reviewed and edited the article.

Data availability

The code for classical molecular dynamics simulations can be found at DOI:10.1016/j.cpc.2021.108171. The version of the code employed for this study is 23Jun2022.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. R.-V., C. R.-T. and M. G.-S. acknowledge grants PID2020-117409RB-I00 from MICIU and 2021SGR-00644 funded by AGAUR. C.R.-T. is a Serra Hunter fellow. M. R.-L. was in receipt of a grant for the recruitment of research staff in training by Departament de Recerca i Universitats de la Generalitat de Catalunya. The ICN2 is funded by the CERCA programme/Generalitat de Catalunya and supported by the Severo Ochoa Centres of Excellence programme, grant no. CEX2021-001214-S, funded by grant no. MCIN/AEI/10.13039.501100011033. C. M, L. C., A. C. and R. D. acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support.

Notes and references

1. S. Berleb, W. Brütting and G. Paasch, Interfacial charges and electric field distribution in organic hetero-layer light-emitting devices, Org. Electron., 2000, 1, 41–47.
2. E. Ito, et al., Spontaneous buildup of giant surface potential by vacuum deposition of Alq3 and its removal by visible light irradiation, J. Appl. Phys., 2002, 92, 7306–7310.
3. D. Yokoyama, Y. Setoguchi, A. Sakaguchi, M. Suzuki and C. Adachi, Orientation Control of Linear-Shaped Molecules in Vacuum-Deposited Organic Amorphous Films and Its Effect on Carrier Mobilities, Adv. Funct. Mater., 2010, 20, 386–391.
4. T. Marcato and C. J. Shih, Molecular Orientation Effects in Organic Light-Emitting Diodes, Helv. Chim. Acta, 2019, 102, e1900048.
5. F. Tenopala-Carmona, et al., Identification of the Key Parameters for Horizontal Transition Dipole Orientation in Fluorescent and TADF Organic Light-Emitting Diodes, Adv. Mater., 2021, 33, 2100677.
6. A. Hofmann, M. Schmid and W. Brütting, The Many Facets of Molecular Orientation in Organic Optoelectronics, Adv. Opt. Mater., 2021, 9, 2101004.
7. M. Flámmich, et al., Orientation of emissive dipoles in OLEDs: Quantitative in situ analysis, Org. Electron., 2010, 11, 1039–1046.
8. D. Yokoyama, Molecular orientation in small-molecule organic light-emitting diodes, J. Mater. Chem., 2011, 21, 19187.
9. S. S. Dalal, D. M. Walters, I. Lyubimov, J. J. de Pablo and M. D. Ediger, Tunable molecular orientation and elevated thermal stability of vapor-deposited organic semiconductors, Proc. Natl. Acad. Sci., 2015, 112, 4227–4232.
10. A. Gujral, K. A. O’Hara, M. F. Toney, M. L. Chabinyc and M. D. Ediger, Structural characterization of vapor-deposited glasses of an organic hole transport material with X-ray scattering, Chem. Mater., 2015, 27, 3341–3348.
11. C. Bishop, A. Gujral, M. F. Toney, L. Yu and M. D. Ediger, Vapor-Deposited Glass Structure Determined by Deposition Rate-Substrate Temperature Superposition Principle, J. Phys. Chem. Lett., 2019, 10, 3536–3542.
12. J. Jiang, D. M. Walters, D. Zhou and M. D. Ediger, Substrate temperature controls molecular orientation in two-component vapor-deposited glasses, Soft Matter, 2016, 12, 3265–3270.
13. M. D. Ediger, Perspective: Highly stable vapor-deposited glasses, J. Chem. Phys., 2017, 147, 210901.
14. Y. Youn, et al., All-atom simulation of molecular orientation in vapor-deposited organic light-emitting diodes, J. Mater. Chem. C, 2018, 6, 1015–1022.
15. K. Bagchi and M. D. Ediger, Controlling Structure and Properties of Vapor-Deposited Glasses of Organic Semiconductors: Recent Advances and Challenges, J. Phys. Chem. Lett., 2020, 11, 6935–6945.
16. M. Shibata, Y. Sakai and D. Yokoyama, Advantages and disadvantages of vacuum-deposited and spin-coated amorphous organic semiconductor films for organic light-emitting diodes, J. Mater. Chem. C, 2015, 3, 11178–11191.
17. C. Bishop, Y. Li, M. F. Toney, L. Yu and M. D. Ediger, Molecular Orientation for Vapor-Deposited Organic Glasses Follows Rate-Temperature Superposition: The Case of Posaconazole, J. Phys. Chem. B, 2020, 124, 2505–2513.
18. Y. Noguchi, et al., Charge accumulation at organic semiconductor interfaces due to a permanent dipole moment and its orientational order in bilayer devices, J. Appl. Phys., 2012, 111, 114508.
19. G. Hong, et al., A Brief History of OLEDs—Emitter Development and Industry Milestones, Adv. Mater., 2021, 33, 2005630.
20. E. Pakhomenko, S. He and R. J. Holmes, Polarization-Induced Exciton–Polaron Quenching in Organic Light-Emitting Devices and Its Control by Dipolar Doping, Adv. Opt. Mater., 2022, 10, 2201348.
21. S. He, E. Pakhomenko and R. J. Holmes, Process Engineered Spontaneous Orientation Polarization in Organic Light-Emitting Devices, ACS Appl. Mater. Interfaces, 2023, 15, 1652–1660.
22. Y. Tanaka, N. Matsuura and H. Ishii, Self-Assembled Electret for Vibration-Based Power Generator, Sci. Rep., 2020, 101(10), 1–8.
23. M. Tanaka, M. Auffray, H. Nakanotani and C. Adachi, Spontaneous formation of metastable orientation with well-organized permanent dipole moment in organic glassy films, Nat. Mater., 2022, 21, 819–825.
24. W. C. Wang, K. Nakano, D. Hashizume, C. S. Hsu and K. Tajima, Tuning Molecular Conformations to Enhance Spontaneous Orientation Polarization in Organic Thin Films, ACS Appl. Mater. Interfaces, 2022, 14, 18773–18781.
25. C. Rodriguez-Tinoco, M. Gonzalez-Silveira, M. A. Ramos and J. Rodriguez-Viejo, Ultrastable glasses: new perspectives for an old problem, La Riv. del Nuovo Cimento, 2022, 45, 325–406.
26. S. F. Swallen, et al., Organic glasses with exceptional thermodynamic and kinetic stability, Science, 2007, 315, 353–356.
27. J. Ràfols-Ribé, et al., High-performance organic light-emitting diodes comprising ultrastable glass layers, Sci. Adv., 2018, 4, eaar8332.
28. S. J. Zou, et al., Recent advances in organic light-emitting diodes: toward smart lighting and displays, Mater. Chem. Front., 2020, 4, 788–820.
29. S. Sudheendran Swayamprabha, et al., Approaches for Long Lifetime Organic Light Emitting Diodes, Adv. Sci., 2021, 8, 2002254.
30. J. Lee, et al., Hot excited state management for long-lived blue phosphorescent organic light-emitting diodes, Nat. Commun., 2017, 8, 1–9.
31. J. Lee, et al., Deep blue phosphorescent organic light-emitting diodes with very high brightness and efficiency, Nat. Mater., 2015, 15, 92–98.
32. S. Reineke, et al., White organic light-emitting diodes with fluorescent tube efficiency, Nature, 2009, 459, 234–238.
33. K. Dawson, et al., Molecular packing in highly stable glasses of vapor-deposited tris-naphthylbenzene isomers, J. Chem. Phys., 2012, 136, 094505.
34. P. H. Lin, I. Lyubimov, L. Yu, M. D. Ediger and J. J. De Pablo, Molecular modeling of vapor-deposited polymer glasses, J. Chem. Phys., 2014, 140, 204504.
35. I. D. Karbovnyk, et al., Electric Field Oriented Nanostructured Organic Thin Films with Polarized Luminescence, Nanoscale Res. Lett., 2017, 12, 1–6.
36. T. V. Basova, et al., Orientation and morphology of chloroaluminum phthalocyanine films grown by vapor deposition: Electrical field-induced molecular alignment, Chem. Phys., 2011, 380, 40–47.
37. W. P. Hu, et al., Highly ordered vacuum-deposited thin films of copper phthalocyanine induced by electric field, Thin Solid Films, 1999, 347, 299–301.
38. D. M. Walters, R. Richert and M. D. Ediger, Thermal stability of vapor-deposited stable glasses of an organic semiconductor, J. Chem. Phys., 2015, 142, 134504.
39. M. J. Frisch, et al., Gaussian16 Revision C.01, 2016.
40. A. L. Hickey and C. N. Rowley, Benchmarking Quantum Chemical Methods for the Calculation of Molecular Dipole Moments and Polarizabilities, J. Phys. Chem. A, 2014, 118, 3678–3687.
41. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174.
42. R. Salomon-Ferrer, D. A. Case and R. C. Walker, An overview of the Amber biomolecular simulation package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210.
43. Y. Duan, et al., A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations, J. Comput. Chem., 2003, 24, 1999–2012.
44. C. Melis, A. Mattoni and L. Colombo, Atomistic investigation of Poly(3-hexylthiophene) adhesion on nanostructured titania, J. Phys. Chem. C, 2010, 114, 3401–3406.
45. M. P. Allen and D. J. Tildesley, Computer Simulations of Liquids, Clarendon Press, Oxford, 1987.
46. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19.
47. L. Verlet, Computer ‘Experiments’ on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules, Phys. Rev., 1967, 159, 98.
48. J. Ràfols-Ribé, et al., Evidence of thermal transport anisotropy in stable glasses of vapor deposited organic molecules, Phys. Rev. Mater., 2018, 2, 035603.
49. I. Lyubimov, M. D. Ediger and J. J. de Pablo, Model vapor-deposited glasses: growth front and composition effects, J. Chem. Phys., 2013, 139, 144505.
50. I. Lyubimov, et al., Orientational anisotropy in simulated vapor-deposited molecular glasses, J. Chem. Phys., 2015, 143, 094502.
51. S. Singh and J. J. De Pablo, A molecular view of vapor deposited glasses, J. Chem. Phys., 2011, 134, 194903-undefined.
52. Y. Noguchi, Y. Tanaka, H. Ishii and W. Brütting, Understanding spontaneous orientation polarization of amorphous organic semiconducting films and its application to devices, Synth. Met., 2022, 288, 117101.
53. P. Friederich, V. Rodin, F. Von Wrochem and W. Wenzel, Built-In Potentials Induced by Molecular Order in Amorphous Organic Thin Films, ACS Appl. Mater. Interfaces, 2018, 10, 1881–1887.
54. C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé, A. F. Lopeandía and J. Rodríguez-Viejo, Transformation kinetics of vapor-deposited thin film organic glasses: The role of stability and molecular packing anisotropy, Phys. Chem. Chem. Phys., 2015, 17, 31195–31201.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03271c

---