Rashba asymmetric topological insulator BiTeCl under compression: equation of state, vibrational features and electronic properties

Abstract

We present an in-depth characterization of the structural, vibrational, and electronic properties of the Rashba asymmetric topological insulator BiTeCl under high-pressure conditions (10 GPa) from an experimental and theoretical perspective. X-ray diffraction and Raman spectroscopy measurements reveal an incomplete and reversible phase transition to an allegedly less symmetric structure at a pressure above 5 GPa. The experimental equation of state and the axial compressibility of BiTeCl are reported and discussed, as well as a detailed analysis of the evolution of its vibrational features. The electronic band structure of BiTeCl is calculated and its behavior under compression is discussed, with emphasis on the behavior of the band gap and the increase of the Rashba splitting, which is found to be weakly anisotropic. An analysis of the electron density topology indicates that the low-pressure phase of BiTeCl is characterized by intralayer electron-deficient multicenter Bi–Te and Bi–Cl bonds and that interlayer bonds are not purely van der Waals in nature.

---

1. Introduction

Due to their wealth of fascinating physical features, bismuth tellurohalide compounds BiTeX (X = Cl, Br, I), have recently experienced a surge in popularity from the point of view of basic research and technological applications. The distinctive traits of this family of compounds comprise their anisotropic thermoelectric properties^1–3 as well as the presence of a Rashba spin–orbit splitting. Also known as the Bychkov–Rashba effect, Rashba splitting is a phenomenon observed in both bulk crystals and low-dimensional, layered compounds.⁴ It occurs when spin–orbit interaction plays a significant role in a material that lacks an inversion center. Rashba compounds show a momentum-dependent splitting of spin bands which can be used to manipulate electron spins using electric fields.^5,6 Consequently, compounds with this feature, such as bismuth tellurohalides, are highly relevant from the point of view of fundamental research and for a multitude of technological applications in the areas of spintronics, quantum computing, topological insulators, and spin–orbit torque devices.^7–13

Pressure is a potent tool for examining the behavior and properties of materials under extreme conditions. It can induce substantial changes in the structure, bonding, and electronic properties of crystalline compounds, often leading to the discovery of new phases and emergent phenomena. Bismuth tellurohalides, in particular, have shown intriguing behavior under compression. For instance, a structural phase transition for BiTeI (space group (S.G.) P3m1, No. 156) has been found experimentally at a moderately high pressure (HP) of about 9 GPa, leading to the closing of the band gap of this semiconductor and preventing the theoretically-predicted topological HP phase to occur.^14,15 Moreover, compression studies up to 30 GPa have highlighted the existence of two different HP orthorhombic phases, stable above 8.8 GPa (phase II) and 18.9 GPa (phase III), respectively, with phase III potentially showing a superconducting character.^16,17 Further, a topological quantum phase transition has been found in BiTeI from its pristine semiconducting character to a topological insulator at a pressure as low as 3 GPa.^17,18 On the other hand, BiTeBr (S.G. P3m1, No. 156) behaves similarly to BiTeI at HP, showing a topological quantum phase transition around 3 GPa,^19,20 with superconductivity being reported in its HP phase.¹⁸

Belonging to S.G. P6₃mc (No. 186), BiTeCl has a slightly different structure from BiTeI and BiTeBr at room pressure (RP) and was the first example of an inversion asymmetric topological insulator.²¹ In the last decade, evidence of the presence of surface and bulk topological states has been reported for BiTeCl^21–23 and its bulk topological character has been reported to be stable under compression up to at least 2.5 GPa.²⁴ Studies on the optical properties of single-crystal BiTeCl at HP have also shown the occurrence of a structural phase transition at a pressure above 6 GPa, leading to the closing of the band gap and reducing the infrared transmission of the samples.²⁵ Further, low-temperature and HP resistivity and Hall-effect measurements have confirmed the metallic behavior for BiTeCl at pressures below 0.8 GPa, with superconductivity arising above 6.8–13.0 GPa.^26,27 Interestingly, two structural HP phase transitions have been reported for BiTeCl in the range up to 55 GPa, one above 5.0–5.5 GPa, and a second one above 28.0–34.4 GPa.^26,27 Heuristic arguments (i.e., comparison with analog compounds) have been used to assign a Pnma structure to the intermediate-pressure phase, and a possible cubic symmetry to the highest-pressure structure.²⁶ However, to the best of our knowledge, the HP structures of BiTeCl are still unconfirmed, since lattice parameters and atomic positions of these phases have not been provided for verification.

To supply the lack of a comprehensive characterization of the low-pressure phase of BiTeCl under compression, in this work, we report HP powder and single crystal X-ray diffraction (XRD) and Raman spectroscopy (RS) measurements for a detailed study of the evolution of the structural, vibrational, and electronic properties of BiTeCl, up to 10 GPa. Besides accurately determining the bulk modulus of BiTeCl, we have found that BiTeCl has a marked anisotropic compressibility. A sluggish, reversible phase transition is found at a pressure above 5 GPa to an undetermined, but allegedly less symmetric new structure, as suggested by the increase in the number of XRD peaks and Raman modes. The evolution of the low-frequency Raman modes appears to be influenced by the strong polarity of the bonds in the Bi–Te–Cl monolayers. Theoretical calculations have also allowed us to explore in detail the electronic band structure of BiTeCl and its behavior under compression, up to 8 GPa. BiTeCl is found to be an indirect semiconductor with a calculated band gap of 0.41 eV at RP, which monotonically decreases upon compression in the studied pressure range. The pressure dependence of the Rashba splitting has been quantified, showing a weakly anisotropic behavior under compression. Additionally, the analysis of the topology of the electron density of BiTeX compounds has allowed us to find that these compounds are characterized by an intralayer electron-deficient multicenter bonding that affects the interlayer bonds, so they cannot be considered pure van der Waals compounds.

2. Methods

2.1. Experimental details

Single crystals of BiTeCl were grown by a gas-phase transport reaction in a temperature gradient from Bi, Te, and BiCl₃ (all with of them with 99.999% purity), as already reported.²⁸ The starting stoichiometric 2 : 3 : 1 mixture of the above materials was prepared in a glovebox into quartz glass ampoules and evacuated to pressure 1 × 10⁻³–2 × 10⁻³ Pa. The transport reaction was carried out in a horizontal furnace with a gradient 480–440 °C per 20 cm for 9 days, leading to plate-like single crystals with an area up to 100 mm². Before the crystal growth process, a heating of the ampoules in a reversed temperature gradient was employed, to purify the growth side of the ampoules.

Single crystal XRD (SC-XRD) measurements were performed at RP to analyze the sample quality and to obtain a reliable estimation of the unit-cell parameters. Data were collected using a SuperNOVA Rigaku diffractometer with an EoS2 CCD detector and measured using ω scans with Mo K_α radiation (λ = 0.71073 Å) at a maximum resolution of Θ = 28.2781 (0.75 Å). The program CrysAlisPro (Rigaku, V1.171.40.84a, 2020) was used to determine the total number of runs and images for the diffraction pattern as well as to index and refine it. A numerical absorption correction based on Gaussian integration over a multifaceted crystal model was performed using the Absorb software.²⁹

Powder HP-XRD measurements were conducted in nearly hydrostatic conditions on selected ground crystals of BiTeCl using diamond anvil cells (DACs) with 300 μm culets diamonds. Stainless steel gaskets with a 150 μm hole were used and a 4 : 1 methanol : ethanol mixture was employed as the pressure-transmitting medium.³⁰ The experiments were performed using monocromatic X-ray radiation (λ = 0.4246 Å) at the MSPD beamline of the ALBA Synchrotron (Spain),³¹ using Cu as the pressure gauge.³² A Rayonix CCD was used to recollect 2D images, which were subsequently integrated using the DIOPTAS software.³³ Structural analysis and Pawley/LeBail fits were performed using MAUD software.³⁴ The axial compressibility and the equation of state of our samples have been calculated using EoSFit7-GUI.³⁵ The software VESTA³⁶ has been used for the representation of the crystal structures and the calculation of the bond distances.

HP-RS measurements were performed employing a Horiba Jobin Yvon LabRAM HR UV microspectrometer equipped with a thermoelectric-cooled multichannel CCD detector and with a spectral resolution below 2 cm⁻¹. A HeNe laser (632.8 nm line) with power below 2 mW was used for excitation, to avoid sample heating. Measurements were conducted in a DAC in nearly hydrostatic conditions with a setup similar to that used for HP-XRD measurements. The ruby fluorescence was used as the pressure gauge.³⁷ In both HP-XRD and HP-RS measurements, the uncertainty on the pressure measurement inside the pressure chamber is 0.1 GPa.

2.2. Calculation details

First-principles calculations were carried out using the Vienna ab initio simulation package (VASP)^38,39 which is based on density functional theory (DFT).^40,41 The projector augmented wave (PAW) method^42,43 was used alongside plane-wave pseudopotentials to solve the Kohn–Sham equations and the exchange–correlation functional was described by the generalized gradient approximation (GGA) developed by Perdew, Burke, and Ernzerhof (PBE).⁴⁴ Dispersion correction of the Becke–Johnson damping function DFT-D3 approach was also considered, as these corrections showed the best agreement with structural experimental data.⁴⁵ The valence electrons 6s² 6p³, 5s² 5p⁴, and 3s² 3p⁵ were included in all calculations for Bi, Te, and Cl atoms, respectively. Structural optimization was performed using a cut-off energy of 600 eV to ensure convergence of the total energy within 10⁻⁵ eV per atom, until the Hellman–Feynman forces on each atom were less than 10⁻⁴ eV Å⁻¹. Fully relaxed crystal structures were obtained through the calculation of the forces on atoms and the stress tensor with a dense special k-point sampling Monkhorst–Pack grid (8 × 8 × 2).⁴⁶

Lattice dynamics calculations of the phonon modes were also performed for the P6₃mc phase at the BZ center (Γ point) with the direct force constant approach using the Phonopy package,⁴⁷ including the non-analytical corrections to obtain the LO/TO splitting. In addition, calculations of the electronic band structure were performed by including the spin–orbit coupling (SOC). To sample the first Brillouin zone (BZ), a dense gamma-centered k-point grid (15 × 15 × 4) was used for the density of states (DOS). The k-point path used to represent the electronic band structure calculations of BiTeCl was generated using VASPKIT program.⁴⁸

3. Results and discussion

3.1. Structural properties

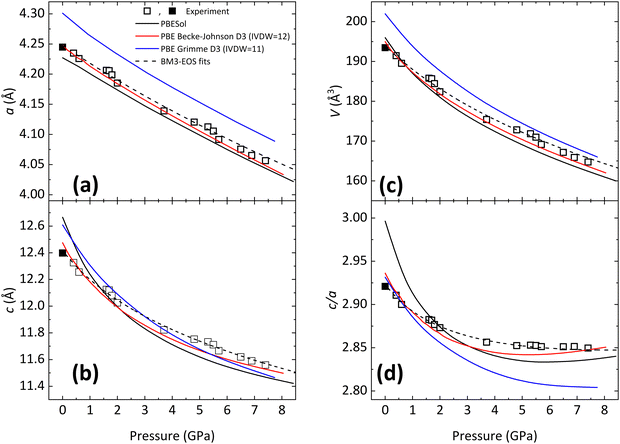
Since all BiTeX compounds are layered compounds, it is assumed that opposing X and Te atomic planes interact via weak van der Waals (vdW) forces, so that all BiTeX compounds are easily exfoliable materials, due to their weak interlayer bonds.⁴⁹ In all BiTeX compounds, Bi atoms are 6-fold coordinated and it is assumed that they are covalently linked with 3 Te and 3 X atoms in a quasi-regular octahedra. In particular, BiTeCl crystallizes at RP in the low-pressure (LP) phase within the hexagonal S.G. P6₃mc space group (No. 186, Z = 2) (Fig. 1). In this structure, Bi, Te (Cl) atoms occupy the 2b (2a) Wyckoff positions, with Bi–Te ≈ 3.02 Å and Bi–Cl ≈ 2.98 Å,²⁸ and neighbor octahedra share a Cl and a Te atom, thus forming planes perpendicular to the [001] direction. The cell parameters obtained for BiTeCl from a LeBail refinement of the XRD pattern of a powder sample in a DAC at a pressure as low as 0.4 GPa (Fig. S1 in the ESI†) are a = 4.23491(25) Å, c = 12.3261(19) Å, V = 191.44(3) ų. These values are in good agreement with our experimental data from SC-XRD measurements at RP (a₀ = 4.24470(10) Å, c₀ = 12.3987(3) Å, V₀ = 193.464(10) ų), from our theoretical calculations at RP (a₀ = 4.24848 Å, c₀ = 12.47487 Å, V₀ = 195 ų) and also with previous experimental studies at RP (a₀ = 4.2426(1) Å, c₀ = 12.397(1) Å, V₀ = 193.3(1) ų).²⁸ It can be observed that our calculations slightly overestimate the c₀ value of BiTeCl; a fact that, we will show later, comes into play when comparing the calculated and experimental c-axis compressibility.

Fig. 1 Crystalline structure of BiTeCl at RP. Pink, yellow, and green spheres represent Bi, Te and Cl, respectively (see legend). The coordination polyhedron of Bi is represented in pink. Cell parameters at RP as obtained by SC-XRD [theoretical calculations] are: a₀ = 4.24470(10) Å [4.24848 Å], c₀ = 12.3987(3) Å [2.47487 Å], V₀ = 193.464(10) ų [195 ų]. Atomic positions as obtained by SC-XRD [theoretical calculations] are: Bi (2/3, 1/3, 0.66424) [(2/3,13/, 0.63732)], Te (2/3, 1/3, 0.30415) [(2/3,1/3, 0.27874)], and Cl (0, 0, 0.52557) [(0, 0, 0.50205)] and Wyckoff positions 2b, 2b and 2a, respectively.

Under compression, the XRD patterns of BiTeCl show little changes up to 5 GPa, apart from the usual shift of the Bragg peaks due to the shrinking unit cell (Fig. 2). At a pressure of 5.7 GPa, subtle new features appear in the XRD patterns, as highlighted by the red arrows in Fig. 2. These features become more evident at 6.5 GPa and can be ascribed to a structural phase transition, in agreement with previous findings.^25,26 The transition is not abrupt, since the LP and HP phases coexist up to at least 10.3 GPa, the highest pressure achieved during our XRD experiment, with the relative intensity of the peaks of the HP phase increasing with pressure. This implies that the phase transition may be of first-order in character. Additionally, the transition appears to be completely reversible, as the XRD patterns upon pressure release, at 1.4 GPa, can be indexed in the original P6₃mc space group, with parameters a = 4.1879(3) Å, c = 12.139(4) Å and V = 184.38(3) ų (Fig. S2 in the ESI†). In the following, we will also see that the reversibility of the transition is confirmed by our HP-RS measurements. Interestingly, the broadening of the diffraction peaks in the recovered sample on pressure release seems to evidence the appearance of defects or disorder in the structure of the recovered LP phase. Although the HP phase could not be determined, the increase in the number of diffraction peaks points towards a lower symmetry of its structure with respect to the LP P6₃mc phase. This result seems to be consistent with our theoretical calculations, which suggest that the atomic positions for the LP phase, obtained at RP by SC-XRD measurements, do not change significantly with pressure in the studied pressure range (Fig. S3 in the ESI†), i.e., they do not tend towards values which could be typical of a HP phase with higher symmetry than the LP phase.

Fig. 2 HP-PXRD patterns for BiTeCl at selected pressure points (see legend) up to 10.3 GPa (black lines) and upon pressure release (blue lines). Red arrows indicate new features of the patterns due to the onset of a structural phase transition.

Le Bail fitting on the LP phase of BiTeCl could be reliably performed up to a pressure of 7.4 GPa. The axial compressibility χ is defined for each axis, namely x, as 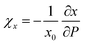, with x₀ being the value of x at RP. Fig. 3a and b show the experimental pressure dependence of the lattice parameters of the LP phase of BiTeCl and their comparison with theoretical calculations performed using different functionals and corrections. As mentioned before, simulations employing PBE functional with IVDW12 corrections, show the closest match with our experimental data. The values of the axial compressibility of the LP phase obtained from our experiments and calculations, estimated using an axial Birch-Murnaghan 3rd-order equation of state (BM3-EOS),³⁵ are shown in Table 1 and compared with the values for BiTeBr and BiTeI.^20,50 To allow a meaningful comparison, we have performed structural calculations for BiTeI and BiTeBr using the same functional and corrections used for BiTeCl (see section “Calculations Details” and Fig. S4 in the ESI†). It is important to mention that in ref. 20, the c-axis compressibility seems to be significantly overestimated. Therefore, the experimental data for BiTeBr presented in Table 1 were recalculated by re-fitting structural data from ref. 20 using a BM3-EOS. Finally, we have observed that a single BM3-EOS was unable to consistently fit our experimental and theoretical data for the BiTeX (X = Cl, I, Br) compounds across the entire pressure range (up to ca. 8 GPa), particularly for the c axis. This issue may arise from the unusual behavior of the c/a ratio in these compounds, which reverses its trend under compression (as discussed below). For this reason, BM3-EOS for axial and bulk compressibility were fitted for all BiTeX compounds only up to the pressures corresponding to the c/a trend inversion (i.e., to 5.3, 2.7, and 3.3 GPa, for BiTeCl, BiTeI, and BiTeBr, respectively^16,20). To correctly describe the strong initial reduction of the c axis at LP and to compensate for the reduced pressure range in the fitting of EOS, additional theoretical data points at pressure below those mentioned have been calculated.

Fig. 3 (a) Experimental and (b) calculated pressure dependence of the a and c lattice unit-cell parameters of the LP phase of BiTeCl; (c) pressure dependence of the unit-cell volume of the LP phase of BiTeCl; (d) pressure dependence of the c/a ratio of the LP phase of BiTeCl. In all plots, black open (closed) symbols represent the HP-XRD (SC-XRD) experimental data. Continuous lines indicate theoretical calculations using different functionals and corrections (see common legend in plot (a)). Black dashed lines represent the BM3-EOS fits of the experimental data for a (a), b (b), V (c) panels, and the c/a ratio from the lattice parameter fits for the (d) panel. As mentioned in the main text, only data up to 5.3 GPa have been used for the BM3-EOS fits.

Table 1 Experimental (Exp.) and theoretical (Th.) axial compressibility for the P6₃mc phase of BiTeCl and comparison with the calculated theoretical values for BiTeBr and BiTeI, as obtained in this work. Experimental data for BiTeBr have been calculated by re-fitting structural data given in ref. 20

	BiTeCl		BiTeBr		BiTeI
	Exp.	Th.	Exp.	Th.	Th.
χ a (10^−3 GPa^−1)	7.3(1.2)	7.98(13)	8.9(6)	9.51(14)	11.3(3)
χ c (10^−3 GPa^−1)	22(7)	33.5(8)	22.2(1.0)	36.0(1.1)	36(4)

---

Data in Table 1 show that the a-axis compressibility is similar for all the BiTeX compounds, with a fair agreement between experiments and calculations, at least for BiTeCl and BiTeBr (to the best of our knowledge, at the moment experimental data are not available for BiTeI). A comparison of the results available for BiTeCl and BiTeBr in Table 1 makes it clear that the slight overestimation of the calculated c parameter at RP leads to an overestimated calculated c-axis compressibility. This notwithstanding, calculations correctly describe the qualitative behavior of all BiTeX compounds. Generally speaking, the c axis of BiTeCl is found to be roughly thrice more compressible than the a axis, for experiments [calculations]. Similar results have been obtained for BiTeBr, with κ = 2.49(20) [3.78(13)] for experiments [calculations], and BiTeI, with a calculated κ = 3.19(9). From our results, it is reasonable to expect experimental values of the a- and c-axis compressibility for BiTeI similar to those observed for BiTeCl and BiTeBr, suggesting a uniform behavior of the axial compressibilities in BiTeX (X = Cl, I, Br) compounds.

The above results, with κ ≠ 1, confirm the pronounced anisotropic compressibility not only of BiTeCl but also of all BiTeX compounds. This behavior is commonly observed in other layered compounds with layers perpendicular to the c-axis and characterized by weak vdW-like interlayer interactions. The high c-axis compressibility of BiTeCl at low pressures is driven by the strong reduction of the interlayer distance, i.e., the distance of Te- and Cl-planes between adjacent layers. As shown in Fig. S5 in the ESI,† the interlayer Te–Cl distance varies about 0.5 Å (according to our theoretical calculations) up to 8 GPa, while the intralayer Te–Cl distance is almost constant in the same pressure range. In fact, there is a slight increase of the intralayer Te–Cl due to the pressure-induced symmetrization of the Bi octahedron (whose distortion index decreases from 7.36 × 10⁻³ at RP to 6.29 × 10⁻³ at 8 GPa, according to our calculations). In summary, according to data in Table 1, all BiTeX (X = Cl, I, Br) compounds show a marked anisotropic structural behavior under compression and a comparable a- and c-axis compressibility.

The analysis of the c/a ratio of BiTeCl under compression shows some differences with respect to BiTeI and BiTeBr. In these latter compounds, the experimental and theoretical c/a ratio exhibits pronounced local minima in the studied pressure range (Fig. S4d, ESI†). In BiTeCl, instead, just a weak local minimum is discernible in the theoretical data around 5.3 GPa (Fig. 3d and Fig. S4d, ESI†). This minimum of the c/a ratio is not clearly observed in our experimental measurements (Fig. 3d) despite the rather good correlation between experimental data and theoretical calculations below 5.3 GPa. We thus believe that the observed weak theoretical minimum around 5.3 GPa might be effectively related to the structural phase transition observed experimentally by HP-XRD measurements above 5.7 GPa (and above 5.1 GPa in HP-RS measurements, see next section). Therefore, our result suggests that, unlike in BiTeBr and BiTeI, there is no isostructural or topological electronic/quantum phase transitions in BiTeCl related to the change of slope of the c/a ratio with pressure that has been observed in other Bi and Sb compounds.^20,51,52 On the other hand, the total variation of the c/a ratio can be related to the polarity of the compound under examination, referred to as the polarity of the bonds in the Te–Bi–Cl monolayers.⁵³ In the case of BiTeCl, the experimental c/a ratio varies less than 0.1 across the studied pressure range, which may indicate a polarity comparable to (or even smaller than) that of BiTeBr.^20,53

Regarding the pressure dependence of the unit-cell volume (Fig. 3d), fitting a BM3-EOS to the experimental volume data of the LP phase of BiTeCl yields a zero-pressure unit-cell volume, V₀ = 193.9(1.0) ų, a zero-pressure bulk modulus, B₀ = 29(6) GPa, and a bulk modulus derivative, . These values compare nicely with our theoretical data (V₀ = 194.68(7) ų, B₀ = 22.3(3) GPa, ). Notice that a direct comparison is not straightforward, since the different values of 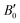affect to the values of B₀. In any case, the values obtained for BiTeCl are in line with (i) those obtained for BiTeBr in our theoretical calculations [experiments], V₀ = 102.84(5) ų [101.94(15) ų], B₀ = 21.3(5) GPa [28.30(1.9) GPa], , (ii) those obtained for BiTeI in our calculations (V₀ = 111.75(14) ų, B₀ = 22.1(7) GPa, ), and (iii) with those reported in previous works.^20,50 Noteworthy, when data for BiTeI⁵⁰ are fitted assuming a value of (close to our experimental and theoretical values for BiTeCl), we get B₀ = 28.3 GPa for BiTeI, a value that is almost identical to that obtained here for BiTeCl. It is worthwhile to note that the small value of B₀ for BiTeCl is mainly due to the strong initial reduction of the interlayer distance. Also, the relatively high value of B₀ for the Bi octahedra (B₀ = 74.6(7) GPa, see Fig. S6 in the ESI†) suggests that its compression has a negligible contribution to the overall compressibility of BiTeCl at RP. Incidentally, the Bi–Te bonds appear to be only slightly more compressible than Bi–Cl bonds (see Fig. S7 and related caption in the ESI†), thus these bonds contribute almost equally to the volume variation of the Bi octahedra.

3.2. Vibrational properties

According to group theory, the LP phase (S.G. P6₃mc) of BiTeCl has 18 vibrational modes (15 optical and 3 acoustic). The mechanical representation at the BZ center (Γ point) is: Γ = 3A₁(I,R) + 3E₁(I,R) + 3E₂(R) + 3B₁, where A₁ and E₁ modes are both (R) and infrared (I) active since they are polar modes, E modes are all doubly degenerated, B₁ modes are silent and 3 modes (E₁ + A₁) are acoustic.⁵⁴ In addition, in polar materials, such as BiTeCl, long-range electrostatic interactions make phonons both Raman and infrared-active, such as A₁ and E₁ modes, exhibit transverse optical (TO) and longitudinal optical (LO) components. As is typical for layered compounds, E modes correspond to atomic vibrations in the plane of the layers (perpendicular to the c axis), while A modes represent vibrations perpendicular to the layers (along the c axis).⁵⁵

The Raman spectrum of BiTeCl near RP (Fig. S8 in the ESI†) shows 4 out of the 12 non-silent expected Raman-active modes; more specifically, three E₂ modes and one A₁ mode. The calculated and experimental wavenumbers for all Raman-active modes at RP are shown in Table 2, together with their symmetry assignment. Numerical superindexes are used to order phonons of the same character, according to their increasing wavenumber. As shown in Table 2, the absolute wavenumbers at RP of the detected Raman modes agree within 10% with those obtained by theoretical calculations. Our Raman spectrum of the LP phase of BiTeCl is similar to those already reported at RP.^{25,27,49,56,57} Interestingly, a mode around 82–85 cm⁻¹ is reported experimentally for BiTeCl in ref. 27 and 56, which could not be detected neither in our Raman spectra nor in those from ref. 25, 49 and 57. On the other hand, most of the modes recently reported⁴⁹ agree with our calculations. Noteworthily, none of the reported Raman spectra show any signature of the TO/LO components of the A₁ mode of the highest wavenumber (A²₁, above 160 cm⁻¹). We have also to note that in our calculations the distribution of the vibrational modes at RP qualitatively agrees with those previously reported, although with a difference up to 10 cm⁻¹.⁵⁶

Table 2 Zero-pressure frequencies and pressure coefficients of the theoretical and experimental and theoretical Raman modes of BiTeCl when fitted to equation ω = ω₀ + aP + bP². The respective Grüneisen parameters, γ, are also given. For the calculation of the theoretical and experimental Grüneisen parameters, bulk moduli of 29.7 and 29 GPa have been used, respectively (see main text)

Mode	Theory				Experiment
	ω 0 (cm^−1)	a (cm^−1 GPa^−1)	b (cm^−1 GPa^−2)	γ	ω 0 (cm^−1)	a (cm^−1 GPa^−1)	b (cm^−1 GPa^−2)	γ
E^12	17.7	4.14	−0.243	6.95	17.6(1)	3.8(2)	−0.29(3)	6.20
B^11	32.7	7.5	−0.44	6.81	—	—	—
E^11(TO)	97.48	3.70	−0.094	1.13	—	—	—
E^22	107.4	6.7	−0.48	1.85	98.9(3)	9.3(3)	−0.85(6)	2.73
E^11(LO)	126.14	2.62	−0.076	0.62	—	—	—
E^21(TO)	129.46	3.31	−0.056	0.76	—	—	—
E^32	129.1	3.8	0.11	0.87	120.8(4)	4.6(4)	0.05(9)	1.10
A^11(TO)	147.42	3.60	−0.026	0.73	—	—	—
B^21	149.16	2.56	−0.031	0.51	—	—	—
A^11(LO)	155.19	5.75	−0.203	1.10	155.0(3)	6.0(3)	−0.36(5)	1.13
E^21(LO)	166.60	2.71	0.009	0.48	—	—	—
A^21(TO)	168.37	1.86	0.109	0.33	—	—	—
A^21(LO)	185.95	3.36	0.059	0.54	—	—	—
B^31	192.05	6.73	−0.125	1.04	—	—	—

---

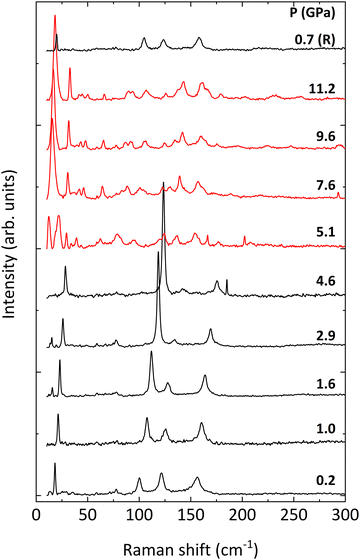
The evolution of the Raman spectra of BiTeCl with pressure is shown in Fig. 4, where spectra up to 5.1 GPa can be assigned to the P6₃mc phase. At a pressure of 5.1 GPa, the spectra undergo sudden changes which are consistent with the structural phase transition observed in our HP-XRD experiments at 5.7 GPa. These changes are completely reverted upon pressure release, confirming the reversibility of the phase transition (see Raman spectrum at 0.7 GPa in Fig. 4). The increase in the number of Raman modes above 5.1 GPa is compatible with the alleged lower symmetry of the HP phase mentioned in the previous section and with previous reports.^26,27

Fig. 4 Raman spectra of BiTeCl at selected pressures (indicated on the right). Black (red) lines represent spectra of the low (high) pressure phase. The R letter indicates the spectrum measured at pressure release. The small peaks close to 10 cm⁻¹ in the spectra at 1.6 GPa and 2.9 GPa are artifacts, likely due to the removal of the background in the proximity of the cut-off of the filter, while the narrow peaks at ∼175 cm⁻¹, ∼200 cm⁻¹, and ∼290 cm⁻¹ in the spectra at 4.6, 5.1, and 7.6 GPa are most likely uncorrected spikes.

Fig. 5 shows the pressure dependence of all the experimentally observed and calculated optical modes. First of all, we have to mention that all phonons harden upon compression with a monotonic increase, due to the shortening of the atomic bonds and interplanar distances. Moreover, the dependence of most modes on pressure is markedly nonlinear. Thus, a 2nd-order polynomial fit has been performed on both the calculated and experimental data to obtain the zero-pressure coefficient of all the optical modes, as well as their respective Grüneisen parameters- as shown in Table 2. The modes detected experimentally have been matched with those calculated theoretically by comparing the parameters of the 2nd-order polynomial fit. Due to the fair correspondence between the parameter of the fits obtained using the calculated and the experimental data, we will comment hereafter on the vibrational properties of BiTeCl relying on the calculated vibrational modes.

Fig. 5 Evolution of the Raman modes of BiTeCl with pressure. Symbols represent experimental measurements, while lines represent theoretical calculations (see legend). The measurements for the high-pressure phase (HP) are shown in red. Grey lines are guides to the eye.

In layered materials, with two or more layers per unit cell, the E mode of lowest wavenumber is commonly attributed to the atomic vibrations in which adjacent layers perpendicular to the c axis (in the a–b plane) vibrate one against the other, while the A or B mode of lowest wavenumber is related to vibrations of one layer against the other along the c axis.²⁰ These modes are known as rigid-layer modes: the shear rigid-layer mode (E-type) and the compressional rigid-layer mode (A or B-type).⁵⁸ In this respect, the E¹₂ mode measured (calculated) around 17.6 cm⁻¹ (17.7 cm⁻¹), which is also the most intense mode, can thus be attributed to the shear rigid-layer mode of the BiTeCl monolayers (neighbor layers vibrating almost rigidly out of phase in the a–b plane). Similarly, the silent B¹₁ mode calculated around 32.7 cm⁻¹ can be attributed to the compressional rigid-layer mode of the BiTeCl monolayers (neighbor layers vibrating almost rigidly out of phase in the c direction). This assignment is confirmed by the eigenvectors of both modes and is further supported by the much larger pressure coefficient of the B¹₁ mode than that of the E¹₂ mode since the compressional rigid-layer mode usually has a larger pressure coefficient than the shear rigid-layer mode.⁵⁹ This is due to the strong decrease of the interlayer spacing, that leads to the high compressibility of BiTeCl along the c-axis.

The rest of the E modes (E¹₁(TO), E¹₁(LO), E²₂, E²₁(TO), E³₂, and E²₁(LO)) have smaller pressure coefficients than E¹₂, except for the E²₂ mode. Similarly, the rest of A- and B-type modes (A¹₁(TO), B²₁, A¹₁(LO), A²₁(TO), A²₁(LO), and B³₁) have smaller pressure coefficients than the B¹₁ mode, except for the B³₁ mode. The large pressure coefficients of the E¹₂ and B¹₁ modes and their marked non-linear pressure dependences (see Table 2) can be attributed to the strong increase in the interlayer interaction between Te and Cl atoms of adjacent layers upon compression, favored by the strong reduction of the interlayer space in BiTeCl below 5 GPa (Fig. S5, ESI†).

In general, a larger pressure coefficient should be expected for low-wavenumber A or B modes, as observed in other layered vdW-like compounds, such as γ-InSe (S.G. R3m), ε-GaSe (S.G. P6̄m2) and also α- and β-GaGeTe (S.G. R3̄m and P6₃mc, respectively).^59–61 The situation is thus similar to what was already observed for BiTeBr and BiTeI,²⁰ in which the low-frequency E modes have all similar larger-than-expected pressure coefficients, which, in turn, are relatively small for the low-wavenumber A and B modes. This behavior is thus found to be typical of bismuth tellurohalides. In particular, it has been ascribed in BiTeI and BiTeBr to the intensity of interlayer forces in these compounds which, due to the strong polarity of their monolayers,⁵³ are much stronger than typical vdW forces in other layered materials.²⁰ In fact, the presence of an asymmetric layer in BiTeX compounds leads to uneven charges within the layer. Specifically, the electric charge in the Te plane differs from that in the Cl plane. This difference contributes to a partially ionic character of the interlayer forces, a feature not found in the families of layered materials with the same terminal atoms in the layers. In other words, the interlayer forces are stronger in the asymmetric polar bismuth tellurohalides compared to other layered semiconductor families with symmetrical layers. As a result of the stronger interlayer forces in BiTeX compounds than in the semiconductor families with symmetrical layers, the anisotropy (directional dependence) in bismuth tellurohalides is smaller than in the semiconductor families with symmetrical layers. As a confirmation of the sensitivity of the low-frequency E modes, it is interesting to note that the Grüneisen parameters of these phonons (in particular, of the E²₁ mode) are systematically higher or comparable to that of the A¹₁(TO), again due to the strong interlayer forces present in BiTeCl.

Noteworthy, the E²₂ mode (experimentally found at 98.9 cm⁻¹ at RP and theoretically predicted at 107.4 cm⁻¹) was not properly described in ref. 27. In that work, it was interpreted that the mode at 115 cm⁻¹ at 2.6 GPa corresponded to the mode at approximately 120 cm⁻¹ (the E³₂ mode), whose pressure coefficient was assumed to be negative. Indeed, we have shown that all vibrational modes of BiTeCl have a positive pressure coefficient and that the E²₂ mode has a very large pressure coefficient and is observed close to 115 cm⁻¹ at 2.6 GPa.

Concerning the high-wavenumber modes, i.e., above 140 cm⁻¹, these likely describe intralayer atomic vibrations dominated by the lighter Cl atoms.²⁰ There is only one E mode in this range, specifically the E²₁(LO) mode at 166.6 cm⁻¹, whose calculated pressure coefficient (2.71 cm⁻¹ GPa⁻¹) is among the lowest for E modes (see Table 2). Tentatively, this mode could be related to the in-plane and out-of-phase vibrations of the Cl and Te sublayers in the layer plane with respect to Bi atoms. It can be observed that all the pressure coefficients of the high-wavenumber A, B, and E modes in BiTeCl are much lower than those of BiTeBr, BiTeI, and β-GaGeTe (this latter in the same space group of BiTeCl),^20,59,62 and comparable or slightly higher than those of the α-phases of Bi₂Te₃, Sb₂Te₃, and Bi₂Se₃. It is worth noting, though, that for most high-wavenumber Raman modes the corresponding Grüneisen parameters γ are around 0.3–0.5 and at any rate much lower than the values around 0.7 found in BiTeBr, the values around 1.1 found in α-Bi₂Te₃, α-Sb₂Te₃ and α-Bi₂Se₃,²⁰ and the value slightly lower than 1 found for β-GaGeTe.⁵⁹ This finding confirms the marked differences in the anharmonicity of the intralayer forces between these families of compounds, which thus behave differently under compression.

Regarding the Raman modes above 5.1 GPa, in the absence of confirmation of the structure of the HP phase, we have tentatively highlighted in Fig. 5 the trends followed by the vibrational modes after the phase transition. As stated previously, an increase in the number of modes is noticeable in the HP phase, especially in the low-wavenumber range (below 100 cm⁻¹), which may be related to a transition to a less symmetric structure. A further indication in this regard is provided by the apparent splitting of some of the modes after the phase transition, e.g., the E²₂ mode. Additionally, at least two of the silent modes, B¹₁ and B³₁ seem to become Raman-active after the phase transition. Activation of silent modes in hexagonal structures (for instance, ZnO) has been attributed to disorder-activated Raman scattering (DARS), i.e., to the breakdown of the translation symmetry of a crystal due to the appearance of defects in the lattice or to impurities.⁶³ On the other hand, the activation of the B¹₁ mode at a pressure above 4 GPa is followed by a splitting of the now-active phonon, i.e., the B¹₁ mode originates a doublet which evolves with very small pressure coefficients (see Fig. 5). Therefore, we consider that the activation of these silent modes might be related to a phase transition to an HP phase having a structure with a lower symmetry than that of the LP phase. We want to stress here that we have simulated the theoretical Raman-active modes of the HP orthorhombic Pnma phase found in BiTeI and previously proposed as a possible HP phase in BiTeCl above 5 GPa (results not shown). The obtained frequencies and pressure coefficients for the Raman-active modes of the Pnma phase do not fit with those experimentally observed above 5 GPa in BiTeCl. Therefore, neither XRD nor RS measurements allow us to propose the HP Pnma phase found in BiTeI as the HP phase found in BiTeCl above 5 GPa.

3.3. Electronic properties

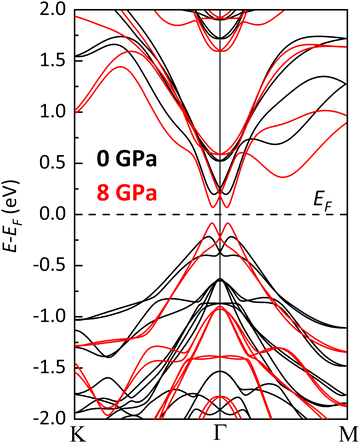
In the following, we will analyze in detail, from a theoretical perspective, the electronic properties of the LP phase of BiTeCl and their evolution with pressure. The indirect character of the bulk band gap of BiTeCl at RP is well established (along with those of BiTeI and BiTeBr⁶⁴), as well as its quantitative value E_g provided in the literature. Experimental values of E_g ≈ 0.7–0.8 eV have been reported independently by many authors.^11,21,65 Theoretical calculations of the band gap of BiTeCl usually give reasonable estimates of E_g, especially when SOC is taken into account, although they often are an underestimation of the experimental values. For BiTeCl at RP, theoretical values of E_g ranging from 0.2 to 0.5 eV have been reported.^11,21,64 In this work, SOC and vdW interactions have been taken into account to calculate the electronic band structure and the value of the band gap of BiTeCl. According to our PBE + SOC calculations, BiTeCl is a trivial indirect semiconductor at RP with a band gap E_g = 0.41 eV. At RP, the conduction band (CB) has an absolute minimum (CBM) situated at the Γ¹ point of the Brillouin zone (BZ) i.e., close to the Γ point but along the Γ–K direction. Meanwhile, the valence band (VB) has an absolute maximum (VBM) situated at the Γ² point, close to Γ point and also along the Γ–K path but slightly more shifted towards the K point (see Fig. 6a). Many larger secondary gaps are present, corresponding to local CBMs and VBMs (indicated by superscripts), such as a direct gap at Γ and various indirect gaps, A¹–A² (along the A–L path), L¹–L² along the L–H path, and a K¹–K² and M¹–M² gaps along K–M (Fig. 6a).

Fig. 6 Calculated electronic band structure of the LP phase of BiTeCl at (a) RP and (b) 8 GPa. The red (blue) oval indicates the CBM (VBM).

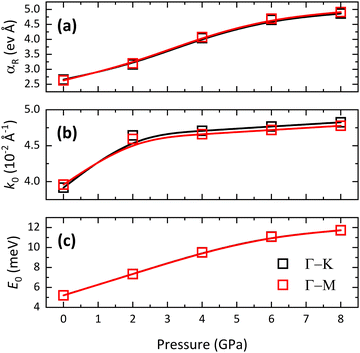
The Rashba splitting at the CB has been analyzed at RP along the Γ–K and Γ–M paths of the BZ quantifying the Rashba parameter α_R = 2E₀/k₀, where E₀ and k₀ are the energy difference of the split states (typically, the CBM) with respect to their crossing point and the shift of the split states from the symmetry point in the momentum space, respectively. According to our calculations, the Rashba parameter at the CB for bulk BiTeCl at RP is α_R = 2.66 eV Å (2.63 eV Å) along the Γ–K (Γ–M) path. These values nicely agree with the theoretical values obtained independently by Eremeev and coworkers (Fig. 7).⁶⁴

Fig. 7 Detail of the theoretical electronic band structure of BiTeCl along the Γ–K and Γ–M paths of the BZ, at 0 GPa (black lines) and 8 GPa (red lines), showing the effect of pressure on the Rashba splitting. The Rashba parameter α_R, calculated separately for the Γ–K and the Γ–M paths at 0 GPa (8 GPa) are α_R = 2.66 eV Å (4.86 eV Å) and α_R = 2.63 eV Å (4.91 eV Å).

The total and partial density of states (DOS and PDOS, respectively) of BiTeCl at RP are shown in Fig. 8a. The fundamental indirect gap at RP is dominated by the contributions of Bi and Te, with negligible contributions from the Cl atoms. Specifically, the CBM at RP (and almost the entire bulk of the CB) is mainly contributed by p_z orbitals of Bi that are slightly hybridized with p orbitals of Te, while the main contribution to the VBM at RP comes from all p (p_x, p_y, and p_z) orbitals of Te with minor contributions from Bi and negligible contributions from Cl. Interestingly, in BiTeBr and BiTeI the contribution of the p orbitals of the halide atoms to the VB in proximity of the VBM seems to be comparable to that of Te, unlike in BiTeCl, where the difference between these contributions is much more pronounced.⁶⁶ This result could likely be related to the similar mass and electronic structure of Te atoms to Br and I atoms than to Cl atoms, which in turn leads to a much similar Bi–Te, Bi–Br, and Bi–I bond strengths than to the Bi–Cl interaction. The bulk of the VB of the BiTeCl, on the other hand, gets populated mainly by the p states of the halide atom.

Fig. 8 Calculated total DOS and PDOS (projected on orbitals) for BiTeCl at 0 GPa (a) and 8 GPa (b). Contributions from each atom/orbital are shown in different colors (see common legend in (a)).

According to our calculations, BiTeCl retains the indirect character of the band gap upon compression up to at least 8 GPa (see Fig. 6b, Fig. 7 and Fig. S9 in the ESI†). The band gap closes with increasing pressure, in a markedly nonlinear fashion (Fig. 7 and 9), from 0.41 eV at RP to a value of approximately 0.15 eV at 8 GPa (the maximum pressure reached in our simulations). A 2nd-order polynomial fit yields a negative value of −46.7(2.2) meV GPa⁻¹ for the linear term of E_g(P) (see Fig. 9), which is roughly half than that reported for BiTeBr (−90 meV GPa⁻¹).²⁰ Our theoretical results on the decrease of the band gap with pressure in BiTeCl agree with the experimental results of infrared transmission measurements under compression.⁶⁷ In the studied pressure range, E_g is always strictly positive, suggesting the absence of a pressure-induced topological quantum phase transition in the LP phase.^67,68 The decrease in the band gap can be understood by analyzing the evolution of the DOS and PDOS at HP. Upon compression, the p states of Te shift to larger energies; i.e., the VBM receives an increasing contribution from the Te atoms (Fig. 8a, b and Fig. S10 in the ESI†), thus decreasing the band gap. An additional contribution to the closing of the band gap is brought by the reduction of Bi–Te atomic distance (Fig. S7, ESI†) and the subsequent increase in the SOC between Bi and Te, which inevitably leads to a decrease of E_g. This phenomenon has been observed, for instance, in bulk and monolayer BiTeBr.⁶⁹

Fig. 9 Theoretical indirect Γ¹–Γ² band gap E_g of BiTeCl as a function of pressure, calculated at different pressure points (open squares) and the respective quadratic fit (black line). The parameters of the fit are given in the legend.

The decrease of the band gap with increasing pressure is also associated with a change of shape of the dispersion of both the VBM and the CBM (see Fig. 7). At RP, the calculated VBM and CBM dispersion show a typical parabolic shape in the momentum space, while at 8 GPa the shape of VB and CB dispersion is much sharper and tends to a linear behavior. Therefore, the electronic dispersion in the momentum space of both the VBM and the CBM seems to gradually tend towards a linear relation on increasing pressure (see also Fig. S11 in the ESI†). This result is similar to what has been previously reported for BiTeI and BiTeBr,²⁰ and it is a characteristic feature of the approach to a topological quantum phase transition.⁶⁸ A consequence of the tendency to a linear dispersion around the VBM (CBM) is the decrease of the hole (electron) effective mass, , leading to a larger hole (electron) mobility. Therefore, a substantial increase of the electrical conductivity is expected for BiTeCl upon compression, due to the decrease in the band gap energy and carrier effective masses. This conclusion is at odds with conflicting available transport measurements for the LP phase of BiTeCl under compression which, in two different works, report an increase of the resistivity between RP and 6.5 GPa,²⁷ as well an increase of the resistivity between RP and 2.8 GPa followed by a decrease of the resistivity between 2.8 and 5.5 GPa.²⁶ As a comparison, transport measurements in BiTeI at RT confirm a weak decrease in the electrical resistivity under moderate pressure, with a minimum occurring between 2.4 and 3.6 GPa (in correspondence with the occurrence of the topological quantum phase transition).⁶⁸ A subsequent increment of the resistivity is observed in BiTeI up to 10 GPa followed by the appearance of superconductivity above 11 GPa.¹⁸ This complex scenario in BiTeI and the conflicting experimental results available for BiTeCl confirm that further work regarding transport measurements is needed to fully unravel the behavior of electrical conductivity in bismuth tellurohalides, and in BiTeCl in particular.

The Rashba effect is strongly influenced by pressure as well, due to the increase in the SOC caused by the contraction of the interatomic distances. The Rashba parameter α_R increases monotonically with pressure (see Fig. 7, 10a and Table 3). More specifically, two regimes can be identified in the pressure dependence of α_R: a quasi-linear increase up to 6 GPa followed by a plateauing trend above this pressure. It is interesting to note that the Rashba parameter evolves differently along the Γ–K and Γ–M paths of the BZ. In fact, for the quasi-linear pressure range (see Fig. 10a and related caption), the pressure coefficient of α_R(P) is 0.343(24) eV Å GPa⁻¹ (0.353(21) eV Å GPa⁻¹) along the Γ–K(Γ–M) path of the BZ. The Rashba splitting behavior in BiTeCl exhibits a weak, still detectable, anisotropy. An analysis of the dependence of E₀ and k₀ on pressure (Fig. 10b) reveals that, in contrast to E₀, k₀ is influenced by the chosen path across the BZ. This indicates that the behavior of k₀ is the source of the anisotropy in the dependence of α_R on pressure. Furthermore, the large pressure coefficient of α_R, especially at moderate pressure levels, indicates that the Rashba splitting can be readily tuned through compression. This feature makes BiTeCl particularly attractive for technological applications relying on the Rashba splitting phenomena.

Fig. 10 (a) Pressure dependence of the theoretical Rashba parameter α_R for BiTeCl calculated separately along the Γ–K and Γ–M paths of the BZ (black and red open squares, respectively). For the calculation of the pressure coefficient of α_R along Γ–K(Γ–M), the quasi-linear range between 0 and 6 GPa (2 and 8 GPa) has been used (see main manuscript). (b) The theoretical value of k₀ for the splitting of spin states with respect to the Γ point of the BZ, calculated separately along the Γ–K and Γ–M paths of the BZ (black and red open squares, respectively). (c) The theoretical value of E₀ along the Γ–K and Γ–M paths of the BZ (black and red open squares, respectively). In all plots, lines are a guide to the eye.

Table 3 Theoretical Rashba parameter (α_R), shift of the split states from the Γ point in the momentum space (k₀), and value of the energy term (E₀) for BiTeCl as a function of pressure, calculated along the Γ–K and Γ–M paths of the BZ (see also Fig. 10 and Fig. S11, ESI)

Pressure (GPa)	Γ–K			Γ–M
	α R (eV Å)	k 0 (10^−2 Å^−1)	E 0 (meV)	α R (eV Å)	k 0 (10^−2 Å^−1)	E 0 (meV)
0	2.66	3.917	52.072	2.63	3.959	52.039
2	3.16	4.643	73.431	3.20	4.594	73.422
4	4.04	4.707	95.163	4.08	4.660	95.002
6	4.65	4.767	110.900	4.69	4.719	110.704
8	4.86	4.826	117.282	4.91	4.777	117.320

---

In summary, BiTeCl is confirmed as an indirect semiconductor with Rashba splitting features and a calculated band gap around 0.41 eV at RP. The band gap decreases in a nonlinear fashion upon compression. This is the caused by the stronger increase in energy of the VBM than of the CBM, due to the strong increase in energy of the p levels of Te, consequence of the strong compression of the interlayer space. The increase of the SOC due to the contraction of atomic bonds also leads to a strong direct proportionality of the Rashba parameter with pressure. Additionally, the evolution of the Rashba parameter under compression is found to be weakly anisotropic in the momentum space.

4. Chemical bonding

To conclude this manuscript, we would like to comment on the different types of chemical bonding present in bismuth tellurohalides. As mentioned previously, there are two main types of chemical bonds in layered materials, the intralayer and the interlayer bonds. Intralayer (interlayer) bonds in layered materials have been usually considered to be strong (weak) bonds of covalent (vdW) type. These types of bonds are observed, for instance, in A^IIIX^VI layered compounds, such as InSe, GaSe, and GaS, and transition metal chalcogenides AX₂ (A = W, Mo; X = S, Se, Te).

Recent studies have evidenced that interlayer bonds in tetradymite-like A^V₂X^VI₃ sesquichalcogenides, such as Bi₂Se₃, Bi₂Te₃, Sb₂Te₃, and β-As₂Te₃, are much stronger than in the above-mentioned layered compounds, as reflected in the much smaller interlayer distance than the sum of the vdW radii of the terminal atoms. In fact, the stronger interlayer bonding is reflected in a smaller interlayer space in tetradymite-like compounds than what is expected for common vdW materials. This is reflected in the different regions and behaviors shown by tetradymite-like A^V₂X^VI₃ and A^IVB^V₂X^VI₄ compounds in Fig. 11, where interlayer spacing vs. intralayer spacing is plotted in different families of layered materials.^70–75

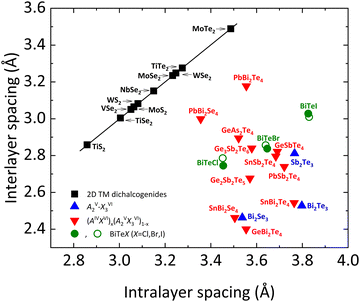Fig. 11 Comparison of the interlayer vs. intralayer spacing for 2D transition metal dichalcogenides (2D TM), layered A^V₂X^VI₃ compounds, (A^IVX^VI)_x (B^V₂X^VI₃)_1−x alloys and BiTeX (X = Cl, Br, I) (see legend). For the latter, green closed (open) symbols refer to experimental (theoretical) data. The position of BiTeX in this plot confirms that these are not pure vdW compounds, due to their relatively small interlayer spacing. The black line is a guide to the eye. Data for this plot have been extracted from ref. 72. Experimental data for BiTeBr and BiTeI have been obtained from ref. 28 and 76, respectively. Reproduced and updated from ref. 72 with permission from John Wiley and Sons, copyright 2018.

It has been suggested that the typical vdW interlayer bonding is strengthened in tetradymite-like A^V₂X^VI₃ and A^IVB^V₂X^VI₄ compounds, which are related to phase change materials, due to the presence of additional electronic charge in the interlayer space coming from the intralayer bonds. This extra interlayer charge is caused by the partial delocalization of electrons present in intralayer bonds and it is related to the unconventional character of the intralayer bonding in these and other phase change materials, such as rocksalt-like A^IVX^VI compounds.^70,77 This unconventional bonding in phase change materials has been discussed in the recent years to be explained by two models: the hypervalent and the metavalent bonding models.^78–80 However, it has been recently suggested that these materials feature an old kind of bond that was until now thought to be not possible in electron-rich elements, the electron-deficient multicenter bond (EDMB).^81–83

In bismuth tellurohalides, the interlayer distance is also much smaller than the sum of the vdW radii of the terminal atoms (see Table 4),⁷² so it is likely that a similar type of bonding as in tetradymite-like A^V₂X^VI₃ and A^IVB^V₂X^VI₄ compounds occurs, as it is reflected by the location of the BiTeX compounds in Fig. 11. Note that the interlayer distance in BiTeX compounds increases proportionally to the increase of the van der Waals radius of each X atom, but this does not preclude that the interlayer distance in all bismuth tellurohalides is much smaller than it should be if only interlayer vdW forces were present. Moreover, the sixfold coordination of Bi atoms and the strong p-type character of the Bi–Te and Bi–Cl bonds, commented on the previous section, also point to the presence of an unconventional type of bonding in BiTeX compounds.^{70,71,75,77–82}

Table 4 Theoretical lattice parameters, unit-cell volume, bond distances, Bader charges, and the corresponding number of electrons shared (ES) and electrons transferred (ET) values between two atoms for the three bismuth tellurohalides BiTeX (X = Cl, Br, I) at room pressure. The calculated interlayer (Te–X) distance is also compared with the sum of the vdW radii of Te and X atoms (from ref. 84). The three crystal structures were optimized using the PBE functional and applying the DFT-D3 Becke–Johnson method for van der Waals interactions (IVDW = 12)

	BiTeCl (sg. 186)	BiTeBr (sg. 156)	BiTeI (sg. 156)
a Ref. 76. b Ref. 28. c Ref. 84.
Unit cell param.
a/c (Å)	4.248/12.475	4.279/6.496	4.349/6.839
Volume (Å^3)	195	103	112
Bond distances (Å)
Bi–Te	3.021	3.029	3.044
Bi–X	2.977	3.108	3.278
Interlayer distance Te–X (Å)	2.786/2.745	2.856/2.838^a	3.010/3.028^b
Calculation/experiment
Sum of vdW radii (Å) Te–X^c	4.000	4.150	4.350
Bader charges
Bi, Te, X	+0.87, −0.27, −0.60	+0.79, −0.29, −0.50	+0.70, −0.33, −0.37
ES (Bi–Te)	1.18	1.33	1.29
ES (Bi–X)	0.63	0.92	0.95
ET (Bi–Te)	0.27	0.29	0.33
ET(Bi–X)	0.60	0.50	0.37

---

In order to show the EDMB nature of the intralayer bonding in bismuth tellurohalides, we have theoretically simulated the three BiTeX (X = Cl, Br, I) compounds at RP with the same methodology (see details in Table 4). According to the quantum theory of atoms in molecules,^70,81,82,85 we have calculated the Bader charges as well as the number of electrons shared (ES) and the normalized number of electrons transferred (ET) in the Bi–Te and Bi–X intralayer bonds (see Table 4). Since BiTeX compounds feature a single cation and two anions, the normalized ET values of the Bi–Te and Bi–X bonds are taken as the Bader charges of the anions divided by the oxidation state of the anion (2 for Te and 1 for X atoms).

The calculated ES and ET values for the intralayer Bi–Te and Bi–X bonds in BiTeX compounds have been plotted in the ES vs. ET map (Fig. 12). Since these intralayer bonds are located in the green region of the map, they can be catalogued as EDMBs according to recent works.^81,82 This result agrees with the EDMBs, previously considered metavalent bonds, observed in tetradymite-like A^V₂X^VI₃ and A^IVB^V₂X^VI₄ compounds.^70,75 As observed in the map, the electron-deficient character (ES ≈ 1) of the intralayer bonds in bismuth tellurohalides is reflected by the low ES values of the Bi–Te and Bi–X bonds as compared to covalent bonds (red region in Fig. 12). Moreover, the multicenter character of the intralayer bonds in bismuth tellurohalides is reflected in the hypercoordinated (sixfold) Bi cations and the linear Te–Bi–X bonds in three dimensions with rhombohedral-like structure.⁸¹ Notice that Bi cations tend to form hypercoordinated units even at RP not only in tetradymite-like Bi₂Te₃ and Bi₂Se₃, but also in Pnma-type Bi₂S₃, where one Bi is fivefold coordinated in a layered square pyramidal structure akin to that of TlI.^86,87 Note that in the square pyramidal structure of Pnma-type Bi₂S₃ there is a covalent Bi–S bond (d = 2.561 Å) which is perpendicular to two S–Bi–S EDMBs in which the Bi–S bond distance is d = 2.961 Å; i.e. ca. 0.3 Å longer than the covalent bond.

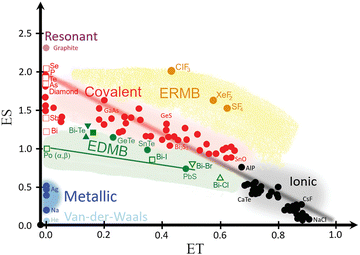Fig. 12 Revisited 2D map of the number of electrons shared (ES) vs. the normalized number of electrons transferred (ET), showing the chemical bond classification in materials. Besides the red, black, and blue regions corresponding to the classical covalent, ionic, and metallic bonds, respectively, the map shows the orange and green regions of materials with electron-rich multicenter bonds (ERMBs) and electron-deficient multicenter bonds (EDMBs). Closed and open symbols represent Bi–Te and Bi–X (X = Cl, Br, I) bonds for BiTeX compounds at RP, respectively. The Cl, Br, and I compounds are shown as upward triangles, downward triangles, and squares, respectively. The position of these evidence the EDMB nature of the intralayer bonds in BiTeX (X = Cl, Br, I). Reproduced and updated from ref. 82 with permission from Royal Society of Chemistry, copyright 2024.

Finally, it must be stressed that our calculations for BiTeX compounds do not show a significant change in the ES and ET values as pressure increases (up to 8 GPa) as long as the LP phase is maintained (data not shown). Therefore, we conclude that the main intralayer bonds in the LP phases of the layered bismuth tellurohalides are EDMBs irrespective to the pressure as long as they maintain the LP phase. In summary, the presence of intralayer bonds with EDMB character in bismuth tellurohalides explains the delocalized character of some electrons that contribute to strengthen the interlayer bonds in these layered materials in contrast to common layered vdW compounds with intralayer covalent bonds.^70,81,82 In other words, as shown in Fig. 11, the LP phases of BiTeX compounds, like those of tetradymite-like A^V₂X^VI₃ and A^IVB^V₂X^VI₄ compounds,^70,75 cannot be considered pure vdW compounds.

5. Summary

We have presented an exhaustive experimental and theoretical study of the layered Rashba-asymmetric topological insulator BiTeCl under high-pressure conditions, up to a maximum of 10 GPa. A sluggish, incomplete, and thus seemingly first-order structural phase transition appears above 5 GPa to an unconfirmed phase, likely of lower symmetry than the low-pressure phase. The transition is reversible, although the broad peaks of the XRD pattern obtained at pressure release may be correlated with the appearance of structural defects in the recovered structure. The axial compressibility and the bulk modulus of BiTeCl are comparable with analog compounds and the polarity of BiTeCl is found to be intermediate between those of BiTeI and BiTeBr. The peculiarities of the dependence on pressure of the vibrational modes of BiTeCl have been discussed as well, in comparison to BiTeI and BiTeBr. The distinct behavior has been attributed to the different strengths of the interlayer forces and the weaker interaction of the halide atom and the Te atom in BiTeCl, with respect to BiTeI and BiTeBr, as observed in the DOS of these compounds. The activation of silent vibrational modes at the phase transition and their dependence on pressure have been related to a phase transition, rather than to the appearance of structural defects induced by pressure.

Theoretical calculations confirm that BiTeCl is an indirect semiconductor with a band gap E_g = 0.41 eV situated in the proximity of the Γ point and dominated by p orbitals of Bi (CBM) and Te (VBM). The band gap closes upon compression, retaining its indirect character up to at least 8 GPa. No pressure-induced quantum topological phase transition occurs in the low-pressure phase. Therefore, its bulk topological character is retained up to structural phase transition above 5 GPa. Our calculations suggest a pressure-induced decrease in the resistivity that is at odds with the available experimental measurements, so more work is needed to solve this controversy. The calculated Rashba parameter α_R of BiTeCl at RP (ca. 2.63–2.66 eV Å) agrees with previous determinations. Noteworthy, α_R increases steadily with pressure due to the increase of SOC, plateauing in proximity of 6 GPa.

Finally, we have shown that the analysis of the electron topology and the comparison of the intralayer and interlayer spacings in bismuth tellurohalides suggest that these compounds show intralayer bonds that are electron-deficient multicenter bonds and interlayer bonds that are not pure vdW bonds.

Data availability

The data that support this study are available from the corresponding authors, E. B. and/or F. J. M., upon request.

Author contributions

E. B.: investigation, formal analysis, visualization, writing – original draft, writing – review & editing; H. H. O.: formal analysis, visualization, writing – review & editing; J. A. S.: investigation, formal analysis, writing – review & editing; P. R. H.: formal analysis, writing – review & editing; A. M.: formal analysis, writing – review & editing; J. G. P.: investigation, writing – review & editing; C. P.: investigation; E. G.: investigation, writing – review & editing; V. P.: investigation, writing – review & editing; C. D.: investigation, writing – review & editing; F. J. M.: resources, conceptualization, investigation, formal analysis, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This publication has been financed by the Spanish Research Agency (AEI) and Spanish Ministry of Science and Investigation (MCIN) under grants PID2021-125927NB-C21, PID2022-138076NB-C42/C44, and MALTA Consolider Team Network (RED2022-134388-T), co-financed by EU FEDER funds (DOI: 10.13039/501100011033). E. B. would like to thank the Generalitat Valenciana for the financial support from the ARCANGEL project (MFA/2022/025). We thank the Pittsburgh Supercomputer Center (Bridges2) and San Diego Supercomputer Center (Expanse) through allocation DMR140031 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants No. 2138259, No. 2138286, No. 2138307, No. 2137603, and No. 2138296. We also recognize the support of West Virginia High Education Policy Commission under the call Research Challenge Grand Program 2022 and NASA EPSCoR Award 80NSSC22M0173. Portions of this work were performed at GeoSoilEnviroCARS (The University of Chicago, Sector 13), Advanced Photon Source (APS), Argonne National Laboratory. GeoSoilEnviroCARS was supported by the National Science Foundation – Earth Sciences (EAR – 1634415). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.

References

1. J.-Z. Xin, C.-G. Fu, W.-J. Shi, G.-W. Li, G. Auffermann, Y.-P. Qi, T.-J. Zhu, X.-B. Zhao and C. Felser, Rare Met., 2018, 37, 274–281.
2. V. A. Kulbachinskii, V. G. Kytin, A. A. Kudryashov, A. N. Kuznetsov and A. V. Shevelkov, J. Solid State Chem., 2012, 193, 154–160.
3. L. Wu, J. Yang, S. Wang, P. Wei, J. Yang, W. Zhang and L. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195210.
4. A. Bordoloi, A. C. Garcia-Castro, Z. Romestan, A. H. Romero and S. Singh, J. Appl. Phys., 2024, 135, 220901.
5. D. Bercioux and P. Lucignano, Rep. Prog. Phys., 2015, 78, 106001.
6. S.-J. Gong, C.-G. Duan, Y. Zhu, Z.-Q. Zhu and J.-H. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035403.
7. L. Moreschini, G. Autès, A. Crepaldi, S. Moser, J. C. Johannsen, K. S. Kim, H. Berger, P. Bugnon, A. Magrez, J. Denlinger, E. Rotenberg, A. Bostwick, O. V. Yazyev and M. Grioni, J. Electron Spectrosc. Relat. Phenom., 2015, 201, 115–120.
8. S. Fiedler, T. Bathon, S. V. Eremeev, O. E. Tereshchenko, K. A. Kokh, E. V. Chulkov, P. Sessi, H. Bentmann, M. Bode and F. Reinert, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235430.
9. A. Crepaldi, L. Moreschini, G. Autès, C. Tournier-Colletta, S. Moser, N. Virk, H. Berger, P. Bugnon, Y. J. Chang, K. Kern, A. Bostwick, E. Rotenberg, O. V. Yazyev and M. Grioni, Phys. Rev. Lett., 2012, 109, 096803.
10. K. Ishizaka, M. S. Bahramy, H. Murakawa, M. Sakano, T. Shimojima, T. Sonobe, K. Koizumi, S. Shin, H. Miyahara, A. Kimura, K. Miyamoto, T. Okuda, H. Namatame, M. Taniguchi, R. Arita, N. Nagaosa, K. Kobayashi, Y. Murakami, R. Kumai, Y. Kaneko, Y. Onose and Y. Tokura, Nat. Mater., 2011, 10, 521–526.
11. M. Sakano, M. S. Bahramy, A. Katayama, T. Shimojima, H. Murakawa, Y. Kaneko, W. Malaeb, S. Shin, K. Ono, H. Kumigashira, R. Arita, N. Nagaosa, H. Y. Hwang, Y. Tokura and K. Ishizaka, Phys. Rev. Lett., 2013, 110, 107204.
12. J. Alicea, Y. Oreg, G. Refael, F. Von Oppen and M. P. A. Fisher, Nat. Phys., 2011, 7, 412–417.
13. C. Nayak, S. H. Simon, A. Stern, M. Freedman and S. Das Sarma, Rev. Mod. Phys., 2008, 80, 1083–1159.
14. M. K. Tran, J. Levallois, P. Lerch, J. Teyssier, A. B. Kuzmenko, G. Autès, O. V. Yazyev, A. Ubaldini, E. Giannini, D. Van Der Marel and A. Akrap, Phys. Rev. Lett., 2014, 112, 047402.
15. M. S. Bahramy, B. J. Yang, R. Arita and N. Nagaosa, Nat. Commun., 2012, 3, 679.
16. Y. Chen, X. Xi, W.-L. Yim, F. Peng, Y. Wang, H. Wang, Y. Ma, G. Liu, C. Sun, C. Ma, Z. Chen and H. Berger, J. Phys. Chem. C, 2013, 117, 25677–25683.
17. M. L. Jin, F. Sun, L. Y. Xing, S. J. Zhang, S. M. Feng, P. P. Kong, W. M. Li, X. C. Wang, J. L. Zhu, Y. W. Long, H. Y. Bai, C. Z. Gu, R. C. Yu, W. G. Yang, G. Y. Shen, Y. S. Zhao, H. K. Mao and C. Q. Jin, Sci. Rep., 2017, 7, 39699.
18. Y. Qi, W. Shi, P. G. Naumov, N. Kumar, R. Sankar, W. Schnelle, C. Shekhar, F. C. Chou, C. Felser, B. Yan and S. A. Medvedev, Adv. Mater., 2017, 29, 1605965.
19. A. Ohmura, Y. Higuchi, T. Ochiai, M. Kanou, F. Ishikawa, S. Nakano, A. Nakayama, Y. Yamada and T. Sasagawa, Phys. Rev. B, 2017, 95, 125203.
20. J. A. Sans, F. J. Manjón, A. L. J. Pereira, R. Vilaplana, O. Gomis, A. Segura, A. Muñoz, P. Rodríguez-Hernández, C. Popescu, C. Drasar and P. Ruleova, Phys. Rev. B, 2016, 93, 024110.
21. Y. L. Chen, M. Kanou, Z. K. Liu, H. J. Zhang, J. A. Sobota, D. Leuenberger, S. K. Mo, B. Zhou, S. L. Yang, P. S. Kirchmann, D. H. Lu, R. G. Moore, Z. Hussain, Z. X. Shen, X. L. Qi and T. Sasagawa, Nat. Phys., 2013, 9, 704–708.
22. F. X. Xiang, X. L. Wang and S. X. Dou, arXiv, 2014, preprint, arXiv:1401.6732 DOI:10.48550/ARXIV.1401.6732.
23. Y. J. Yan, M. Q. Ren, X. Liu, Z. C. Huang, J. Jiang, Q. Fan, J. Miao, B. P. Xie, F. Xiang, X. Wang, T. Zhang and D. L. Feng, J. Phys.: Condens. Matter, 2015, 27, 475004.
24. D. VanGennep, D. E. Jackson, D. Graf, H. Berger and J. J. Hamlin, J. Phys.: Condens. Matter, 2017, 29, 295702.
25. I. Crassee, F. Borondics, M. K. Tran, G. Autès, A. Magrez, P. Bugnon, H. Berger, J. Teyssier, O. V. Yazyev, M. Orlita and A. Akrap, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 045201.
26. M. L. Jin, S. J. Zhang, L. Y. Xing, W. M. Li, G. Q. Zhao, X. C. Wang, Y. W. Long, X. D. Li, H. Y. Bai, C. Z. Gu and C. Q. Jin, J. Phys. Chem. Solids, 2019, 128, 211–217.
27. J. J. Ying, V. V. Struzhkin, Z. Y. Cao, A. F. Goncharov, H. K. Mao, F. Chen, X. H. Chen, A. G. Gavriliuk and X. J. Chen, Phys. Rev. B, 2016, 93, 100504.
28. A. V. Shevelkov, E. V. Dikarev, R. V. Shpanchenko and B. A. Popovkin, J. Solid State Chem., 1995, 114, 379–384.
29. R. J. Angel, J. Appl. Crystallogr., 2004, 37, 486–492.
30. S. Klotz, J.-C. Chervin, P. Munsch and G. Le Marchand, J. Phys. D: Appl. Phys., 2009, 42, 075413.
31. F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360–S370.
32. A. Dewaele, P. Loubeyre and M. Mezouar, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094112.
33. C. Prescher and V. B. Prakapenka, High Press. Res., 2015, 35, 223–230.
34. L. Lutterotti, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 334–340.
35. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49, 1377–1382.
36. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
37. A. D. Chijioke, W. J. Nellis, A. Soldatov and I. F. Silvera, J. Appl. Phys., 2005, 98, 114905.
38. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
41. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
43. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
46. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
47. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
48. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
49. W. Zhou, J. Lu, G. Xiang and S. Ruan, J. Raman Spectrosc., 2017, 48, 1783–1788.
50. S. Güler-Kiliç and Ç. Kiliç, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245204.
51. A. L. J. Pereira, L. Gracia, D. Santamaría-Pérez, R. Vilaplana, F. J. Manjón, D. Errandonea, M. Nalin and A. Beltrán, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174108.
52. A. L. J. Pereira, J. A. Sans, R. Vilaplana, O. Gomis, F. J. Manjón, P. Rodríguez-Hernández, A. Muñoz, C. Popescu and A. Beltrán, J. Phys. Chem. C, 2014, 118, 23189–23201.
53. Y. Ma, Y. Dai, W. Wei, X. Li and B. Huang, Phys. Chem. Chem. Phys., 2014, 16, 17603–17609.
54. E. Kroumova, M. L. Aroyo, J. M. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transitions, 2003, 76, 155–170.
55. S. Gallego-Parra, E. Bandiello, A. Liang, E. Lora da Silva, P. Rodríguez-Hernández, A. Muñoz, S. Radescu, A. H. Romero, C. Drasar, D. Errandonea and F. J. Manjón, Mater. Today Adv., 2022, 16, 100309.
56. I. Y. Sklyadneva, R. Heid, K. P. Bohnen, V. Chis, V. A. Volodin, K. A. Kokh, O. E. Tereshchenko, P. M. Echenique and E. V. Chulkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 094302.
57. A. Akrap, J. Teyssier, A. Magrez, P. Bugnon, H. Berger, A. B. Kuzmenko and D. Van Der Marel, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035201.
58. R. Zallen and M. Slade, Phys. Rev. B: Solid State, 1974, 9, 1627–1637.
59. E. Bandiello, S. Gallego-Parra, A. Liang, J. A. Sans, V. Cuenca-Gotor, E. Lora da Silva, R. Vilaplana, P. Rodríguez-Hernández, A. Muñoz, D. Diaz-Anichtchenko, C. Popescu, F. G. Alabarse, C. Rudamas, C. Drasar, A. Segura, D. Errandonea and F. J. Manjón, Mater. Today Adv., 2023, 19, 100403.
60. C. Ulrich, M. A. Mroginski, A. R. Goñi, A. Cantarero, U. Schwarz, V. Muñoz and K. Syassen, Phys. Status Solidi B, 1996, 198, 121–127.
61. A. M. Kulibekov, H. P. Olijnyk, A. P. Jephcoat, Z. Y. Salaeva, S. Onari and K. R. Allakhverdiev, Phys. Status Solidi B, 2003, 235, 517–520.
62. Y. S. Ponosov, T. V. Kuznetsova, O. E. Tereshchenko, K. A. Kokh and E. V. Chulkov, JETP Lett., 2014, 98, 557–561.
63. F. J. Manjón, B. Marí, J. Serrano and A. H. Romero, J. Appl. Phys., 2005, 97, 053516.
64. S. V. Eremeev, I. A. Nechaev, Y. M. Koroteev, P. M. Echenique and E. V. Chulkov, Phys. Rev. Lett., 2012, 108, 246802.
65. J. Jacimovic, X. Mettan, A. Pisoni, R. Gaal, S. Katrych, L. Demko, A. Akrap, L. Forro, H. Berger, P. Bugnon and A. Magrez, Scr. Mater., 2014, 76, 69–72.
66. S. Zhou, J. Long and W. Huang, Mater. Sci. Semicond. Process., 2014, 27, 605–610.
67. I. P. Rusinov, T. V. Menshchikova, I. Y. Sklyadneva, R. Heid, K.-P. Bohnen and E. V. Chulkov, New J. Phys., 2016, 18, 113003.
68. V. Rajaji, F. J. Manjón and C. Narayana, J. Phys.: Condens. Matter, 2022, 34, 423001.
69. S.-D. Guo and H.-C. Li, Comput. Mater. Sci., 2017, 139, 361–367.
70. Y. Cheng, O. Cojocaru-Mirédin, J. Keutgen, Y. Yu, M. Küpers, M. Schumacher, P. Golub, J. Raty, R. Dronskowski and M. Wuttig, Adv. Mater., 2019, 31, 1904316.
71. R. Vilaplana, S. Gallego-Parra, E. Lora Da Silva, D. Martínez-García, G. Delaizir, A. Muñoz, P. Rodríguez-Hernández, V. P. Cuenca-Gotor, J. A. Sans, C. Popescu, A. Piarristeguy and F. J. Manjón, J. Mater. Chem. C, 2023, 11, 1037–1055.
72. R. Wang, F. R. L. Lange, S. Cecchi, M. Hanke, M. Wuttig and R. Calarco, Adv. Funct. Mater., 2018, 28, 1705901.
73. B. J. Kooi and M. Wuttig, Adv. Mater., 2020, 32, 1908302.
74. E. L. Da Silva, M. C. Santos, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón, Crystals, 2023, 13, 498.
75. J. A. Sans, R. Vilaplana, E. L. Da Silva, C. Popescu, V. P. Cuenca-Gotor, A. Andrada-Chacón, J. Sánchez-Benitez, O. Gomis, A. L. J. Pereira, P. Rodríguez-Hernández, A. Muñoz, D. Daisenberger, B. García-Domene, A. Segura, D. Errandonea, R. S. Kumar, O. Oeckler, P. Urban, J. Contreras-García and F. J. Manjón, Inorg. Chem., 2020, 59, 9900–9918.
76. A. Zeugner, J. Teichert, M. Kaiser, T. V. Menshchikova, I. P. Rusinov, A. V. Markelov, E. V. Chulkov, T. Doert, M. Ruck and A. Isaeva, Chem. Mater., 2018, 30, 5272–5284.
77. M. Wuttig, V. L. Deringer, X. Gonze, C. Bichara and J.-Y. Raty, Adv. Mater., 2018, 30, 1803777.
78. M. Wuttig, C. Schön, J. Lötfering, P. Golub, C. Gatti and J. Raty, Adv. Mater., 2023, 35, 2208485.
79. M. Wuttig, C. Schön, D. Kim, P. Golub, C. Gatti, J. Raty, B. J. Kooi, Á. M. Pendás, R. Arora and U. Waghmare, Adv. Sci., 2024, 11, 2308578.
80. J. Hempelmann, P. C. Müller, L. Reitz and R. Dronskowski, Inorg. Chem., 2023, 62, 20162–20171.
81. H. H. Osman, A. Otero-de-la-Roza, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón, ChemRxiv, 2023, preprint DOI:10.26434/chemrxiv-2023-pv66p-v2.
82. H. H. Osman, A. Otero-de-la-Roza, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón, J. Mater. Chem. C, 2024, 12, 10447–10474.
83. F. J. Manjón, H. H. Osman, M. Savastano and Á. Vegas, Materials, 2024, 17, 2840.
84. C. E. Housecroft and A. G. Sharpe, Inorganic chemistry, Pearson Prentice Hall, Upper Saddle River, NJ, 2nd edn, 2005.
85. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford, 1990.
86. V. Kupik and L. Veseli-Novikovi, TMPM, Tschermaks Mineral. Petrogr. Mitt., 1970, 14, 55–59.
87. L. Helmholz, Z. Kristallogr., 1936, 95, 129–137.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03027c

‡ Present address: Soreq Nuclear Research Center, Applied Physics Department, Yavne, Israel.

---