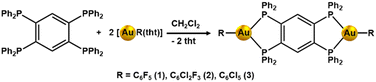Improving the quantum yield of luminescence for three-coordinated gold(I) TADF emitters by exploiting inversion symmetry and using perhaloaryl ligands

Abstract

Herein, we report the synthesis of a new family of extremely efficient TADF three-coordinated gold(I) emitters based on the chelating and bridging abilities of the 1,2,4,5-tetrakis(diphenylphosphino)benzene (tpbz) ligand and the neutral gold(I) [AuR] fragments (R = C₆F₅ (1), C₆Cl₂F₃ (2), C₆Cl₅ (3)). Their emission energies appear in the orange range of the spectrum. The quantum yields of the emissions are directly related to the electronegativity of the perhalophenyl groups bonded to the metal center, even when they are not directly involved in the orbitals responsible for the luminescence. DFT and TD-DFT calculations suggest that the symmetry of the solid-state structures facilitates the coupling of the transition dipole moments, which leads to a drastic increase in their quantum yields as the electronic accepting abilities of the perhalophenyl groups decreases.

---

Introduction

The evolution of materials used in the development of organic light-emitting diodes (OLEDs) or in light emitting electrochemical cells has been very rapid and has taken place during the past few years.^1–5 Light emitters have evolved from the primitive purely fluorescent organic molecules to phosphorescent transition metal compounds of high-cost heavy metals (Ir and Pt), and more recently, to those displaying thermally activated delayed fluorescence (TADF).^6,7 The development has been mainly motivated by the search for a higher efficiency, which is not always easy to achieve. Thus, the evolution has taken place from pure fluorescent compounds that harvest 25% of the excitons,^6–9 to the next generation phosphorescent emitters that through intersystem crossing (ISC) utilize all singlet and triplet excitons for generating light (the triplet harvesting mechanism).^10–13 Nevertheless, these emitters have several undesired properties such as high cost, toxicity, and problems with blue-light emission. TADF emitters, as an alternative to phosphorescent ones, also allow for harvesting all generated singlet and triplet excitons, but in this case, the emission stems from the lowest singlet excited state (the singlet harvesting mechanism) leading to a shorter lifetime and thereby avoiding undesired effects of the longer emission time such as device stability problems due to the decomposition or roll-off effects.¹⁴ Another advantage of the TADF mechanism is the possibility of using lighter metal (first- and second-row elements) complexes or purely organic molecules. Among them, copper(I) complexes have been extensively studied,^15–20 while silver(I) complexes have been examined to a lesser extent.^21–25

There are strict requirements that the complexes must fulfil to exhibit the TADF behaviour. Basically, short decay times require a small energy gap (ΔE(S₁–T₁)) between the lowest excited singlet (S₁) and triplet (T₁) states, preferably small enough that the gap can be surpassed at room temperature, along with a fast radiative rate constant between the S₁ state and the ground state (S₀).^20,24,26 The simultaneous appearance of these two conditions in a single molecule may be challenging. A small ΔE(S₁–T₁) can be achieved with small exchange interactions, i.e., a small HOMO–LUMO overlap, usually resulting in charge-transfer transitions.^20,24,27,28 It may also lead to small transition-dipole moments and, consequently, to small radiative rate constants k(S₁ → S₀).^20,24 In addition, a metal such as copper(I) has weak spin–orbit coupling and a marked tendency to oxidize, whereas silver(I) is more inert to oxidation but it often exhibits photosensitivity and limited luminescence properties.²⁹

To overcome these problems, one can use a double strategy consisting of a rational choice of ligands and metals. Recently, we reported the synthesis and photophysical studies of gold(I) complexes with a stoichiometry of [AuR(dppBz)] (R = C₆F₅, C₆Cl₂F₃, C₆Cl₅, C₆BrF₄, C₆F₄I; dppBz = 1,2-bis(diphenylphosphino)benzene).^30,31 These complexes show TADF behaviour originating from metal–ligand to ligand charge transfer states (MLL’CT) with small ΔE(S₁–T₁) energy gaps resulting in an efficient TADF mechanism at room temperature with a maximum quantum yield of luminescence of around 70%. The dppBz ligand in these complexes has two phosphorus centers allowing a chelate coordination to the metal atom, which leads to a rigid geometry that precludes non-radiative deactivation channels and provides energetically accessible π* orbitals that can act as electron acceptors. Gold has a large SOC, thanks to its heavy metal character. However, its contribution to the frontier orbitals is not significant, which allows transitions with distinct spatial separations of the HOMO and LUMO, resulting in small exchange interactions and, consequently, a small ΔE(S₁–T₁) energy gap. Moreover, gold(I) is inert towards oxidation under normal ambient conditions, and it is not toxic.

Nevertheless, despite all these advantages, the obtained values, although promising, are not spectacular. An essential parameter that influences the rate of the radiative S₁ → S₀ transition is the value of the transition dipole moment, which is small in these complexes, reducing the efficiency of the TADF process due to the competing phosphorescence at higher temperatures.

A very clever strategy, which was originally used in a dinuclear copper complex,³² was inspired by the Davidov model.^33–36 The tpbz ligand (tpbz = 1,2,4,5-tetrakis(diphenylphosphino)benzene) coordinates to two metal fragments, which doubles the number of transition dipole moments between the S₁ state and S₀ as compared to a dppBz complex with the ligand coordinated to only one metal. According to this model, the coupling between two individual transition dipole moments results in their two linear combinations. The first one of ungerade parity corresponds to the sum of the individual transition dipoles in an antiparallel orientation, giving rise to an almost vanishing transition moment. The second linear combination that has gerade parity leads to a transition dipole moment that is approximately twice that of the monomer. Thus, one expects a considerable increase in the radiative transition rate from S₁ and, therefore, a much more efficient TADF process. The changes in the energy of T₁ are also expected to be small,^33–36 which retains the small ΔE(S₁–T₁) energy gap.

In this work, we experimentally and computationally study the photophysical properties of gold-containing dinuclear complexes with a stoichiometry of [(Au–C₆X₅)₂(tpbz)] and compare them with the ones for the corresponding mononuclear [(Au–C₆X₅)(dppBz)] complexes. We show computationally that an adequate combination of gold and ligands may give rise to a TADF efficiency of almost 100% at room temperature. The studied dinuclear complexes may be ideal candidates as dopants in OLED devices and the strategy is useful for the design of emitter molecules.

Results and discussion

Synthesis and characterization

The reaction of [AuR(tht)] with tpbz (R = C₆F₅, C₆Cl₂F₃, C₆Cl₅; tht = tetrahydrothiophene; tpbz = 1,2,4,5-tetrakis(diphenylphosphino)benzene) in a 2 : 1 (Au : tpbz) molar ratio in dichloromethane leads to products with a stoichiometry [(AuR)₂(tpbz)] (R = C₆F₅ (1), C₆Cl₂F₃ (2), C₆Cl₅ (3)) in high yields (78% (1), 73% (2), 75% (3)) as orange solids (see Scheme 1).

Scheme 1 Synthesis of complexes 1–3.

The complexes show analytical and spectroscopic data in accordance with the proposed formulation. In the ³¹P{¹H} NMR spectra, they display a single resonance at 15.4 (1), 15.1 (2) and 16.5 (3) ppm, respectively, indicating the equivalence of the four phosphorus of the phosphine. Complexes 1 and 2 show the expected resonances in their ¹⁹F NMR spectra. Complex 1 has three signals at −113.98 (m, 2F, F_o), −159.03 (m, 1F, F_p) and −162.36 (m, 2F, F_m), and for complex 2, two resonances appear at −87.91 (m, 2F, F_o) and −112.38 (m, 1F, F_p) corresponding to the different types of F nuclei of the pentaflourophenyl or dichlorotrifluorophenyl groups that occupy similar positions at the two sides of the tetraphosphine, respectively. The IR spectra of the complexes display absorptions at ν = 1634, 954, 790 (1), 1591, 1573, 1564 (2) and 840, 620 (3) cm⁻¹ due to the [Au^I–R] groups, and those corresponding to the tpbz ligand appear around 1435 and 1100 cm⁻¹ for the three complexes (see ESI†).

Crystal structures

The crystal structures of 1·C₆H₁₂ and 3 were unequivocally determined via X-ray diffraction studies from single crystals obtained by slow evaporation of saturated cyclohexane solutions. Complex 1 crystallizes in the C2/c space group of the monoclinic system with one molecule of cyclohexane per molecule of compound, while 3 crystallizes in the P1̄ space group of the triclinic system (see ESI† and Fig. S12).

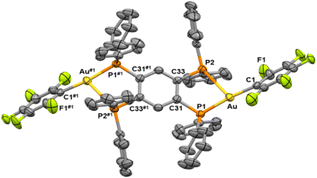
The two structures show similarities, and they can be described as two neutral [AuR] fragments asymmetrically bonded to the tpbz tetraphospane bridging ligand through its phosphorus atoms (Fig. 1 and 2). The gold atoms are three-coordinated in a very distorted trigonal geometry defined by the perhalophenyl terminal group (Au–C = 2.047(9) Å (1) and 2.042(5) Å (3)) and two phosphorus from the tpbz ligand. A marked asymmetry in the Au–P bond lengths is observed in the two complexes [2.275(2)–2.897(3) Å (1) and 2.2758(14)–2.8442(15) Å (3)]. This asymmetry also affects the C–Au–P angles [170.2(3)–111.9(2)° (1) and 162.55(15)–119.34(15)° (3)], leading to the nonequivalence of the phosphorus atoms of the tpbz ligand in the solid state. Therefore, the environment of the gold(I) centres could be better described as a distorted T-shaped geometry rather than a trigonal planar one (Fig. 3(a)–(b)). Thus, the phosphorus involved in the wider C–Au–P angle also displays the shortest Au–P distance, while the one with a narrower C–Au–P angle is further away from the gold atom. Similar distorted structures have been reported for three-coordinated Au(I) complexes with dppBz (1,2-bis(diphenylphosphino)benzene) and perhalophenyl groups (C₆F₅, C₆Cl₂F₃, C₆Cl₅, o-C₆BrF₄) as aryl ligands to gold.^30,31 The latter complexes could be defined as monomers, while complexes 1–3 could be named dimers according to the R-Au-diphosphino twin fragments. Comparison of the molecular structures of the monomers and dimers reveals some interesting differences. For the [(Au–C₆F₅)(dppBz)] (1m)³¹ monomer and the [(Au–C₆F₅)₂(tpbz)] (1) dimer, the shortest Au–P bonds are very similar with lengths of 2.2774(14) Å and 2.275(2) Å, respectively. However, when the longest Au–P distances are compared, an important shortening from 3.3461(14) Å to 2.895(3) Å is observed for the dimer (1). By contrast, the [(Au–C₆Cl₅)₂(tpbz)] (3) dimer undergoes a slight lengthening of the longest Au–P bond from 2.673(2) Å to 2.8435(18) Å in the [(Au–C₆Cl₅)(dppBz)](3m)³⁰ monomer.

Fig. 1 The molecular structure of 1·C₆H₁₂ (50% probability ellipsoids) with the labelling scheme adopted for the atom positions. Selected bond lengths (Å) and angles (deg): Au–C(1) 2.047(9), Au–P(1) 2.275(2), Au–P(2) 2.897(3), C(1)–Au–P(1) 170.2(3), C(1)–Au–P(2) 111.9(2), P(1)–Au–P(2) 76.97(8). The solvent molecule and H atoms are omitted for clarity. Symmetry transformations are used to generate equivalent atoms. #1 − x + 1, −y + 1, −z + 1.

Fig. 2 The molecular structure of 3 (50% probability ellipsoids) with the labelling scheme adopted for the atom positions. Selected bond lengths (Å) and angles (deg): Au–C(1) 2.042(5), Au–P(1) 2.2758(14), Au–P(2) 2.8442(15), C(1)–Au–P(1) 162.55(15), C(1)–Au–P(2) 119.34(15), and P(1)–Au–P(2) 78.10(5). H atoms are omitted for clarity. Symmetry transformations are used to generate equivalent atoms. #1 −x + 1, −y + 1, −z + 1.

Fig. 3 The coordination environment for the gold(I) centers of complexes 1 (A) and 3 (B); the core topology of complex 1 (C).

The coordination of the gold centers does not lead to any significant configurational changes of the ligand. The distances between the phosphorus atoms remain very similar upon coordination, being 3.224 Å for the free tpbz³⁷ and 3.255 Å for complexes 1 and 3. The coplanar eclipse-type configuration with a centroid distance of 4.110 Å for two phenyl rings at the adjacent P centers of the free tetraphosphine ligand is also observed in the gold(I) complexes. The near-lying phenyl rings lead to intramolecular π···π stacking interactions with ring distances of 3.769 Å (1) and 3.972 Å (3). (see ESI† and Fig. S13).

The central aromatic ring and the four phosphorus atoms of the ligand are essentially planar (Fig. 3(c)). The two Au(I) atoms in each molecule are located above and below the plane of the central ring, respectively, leading to the formation of a chair-like conformation. This kind of disposition has been previously reported for other [M₂tpbz] complexes containing d¹⁰ Ag(I) and Cu(I) coinage metals.^21,32,38,39

The chelating and bridging coordination abilities of the tpbz ligand with other metals such as Ni, Pd, Pt, Mo, W and Fe have also been reported.^37,40–42 However, to the best of our knowledge, this is the first time that this disposition has been obtained for gold(I). In fact, Au(I) compounds bearing the tpbz ligand have previously displayed a structure in which each phosphorus atom is coordinated to one gold center leading to a tetranuclear [Au₂tpbzAu₂] core, whose Au(I) ions are two-coordinated with aurophilic interactions between the adjacent gold atoms.^43–46

Photophysical properties

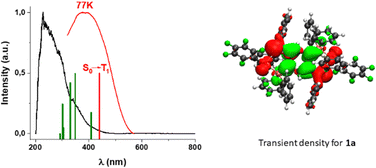
The three complexes show very interesting optical properties in the solid state. They absorb at high energy (200–300 nm) in the UV region that matches those observed for the precursor gold complexes [AuR(tht)] (R = C₆F₅, C₆Cl₂F₃, C₆Cl₅) and the tetraphosphine. These bands are therefore assigned to the same origin, i.e., to π → π* transitions located in the perhalophenyl groups and in the tpbz ligand. However, charge-transfer (Au → π*) transitions cannot be excluded. Long absorption tails down to 500 nm that are absent in the precursors [AuR(tht)] and tpbz appear in the spectra of the complexes. The absorption band of the precursors ends at 400 nm suggesting that there are charge-transfer transitions, probably of forbidden nature, between the donor (Au^I-R) and acceptor (phosphine) parts of the complexes.

Powder samples of the three complexes display a very intense orange luminescence at room temperature (RT) and at 77 K when they are irradiated with UV-Vis light (Fig. 4 and Fig. S17–S20, ESI†). Complex 1 emits at 645 nm (exc. 375 nm, RT) with a quantum yield of luminescence (ϕ₁) of 24% and at 661 nm (exc. 400 nm, 77 K), complex 2 at 638 nm (exc. 365 nm, RT) (ϕ₂ = 46%), and 667 nm (exc. 400 nm, 77 K) and complex 3 at 682 nm (exc. 450 nm, RT) (ϕ₃ = 61%) and 707 nm (exc. 430 nm, 77 K). The observed red-shift of the emissions of complexes 1–3 upon cooling would be related to the fact that the sample cooling produces a contraction of the interatomic bonds, leading to a shortening of the energy difference between the frontier molecular orbitals.

Fig. 4 The emission spectra in the solid state of complexes [(Au₂(C₆F₅)₂(tpbz))] (1) (maroon), [(Au₂(C₆Cl₂F₃)₂(tpbz))] (2) (red) and [(Au₂(C₆Cl₅)₂(tpbz))] (3) (orange) measured at room temperature. The FWHM values for the emission bands at RT are 3599 (1), 3707 (2) and 3396 cm⁻¹ (3).

The lifetimes of 3.93 μs (RT) and 41.20 μs (77 K) for 1, 0.90 μs (RT) and 27.83 μs (77 K) for 2, and 2.50 μs (RT) and 60.78 μs (77 K) for 3 suggest that the lowest triplet state in each case is involved in the emissions. The emission bands are unstructured even at low temperature, which is typical for charge-transfer transitions. The difference in the energy of the emission bands for complexes 1–3 does not show remarkable shifts when varying the temperature. In addition, the emission lifetimes are in the microsecond range, and they are also significantly shorter at RT. Thermally activated delayed fluorescence (TADF) processes are therefore most likely responsible for the emission of the studied complexes at RT. The adjustment of the emission decay at RT and at 77 K gives a mono-exponential function in the whole temperature range (see ESI,† Fig. S21–S23), suggesting a fast thermal equilibrium process. Plots of the lifetime versus the temperature follow Boltzmann-type expressions for the three complexes (ESI,† Fig. S24–S26). The data obtained for complex 3 are given in Fig. 5.

Fig. 5 Top: The emission decay times of complex (3) versus temperature. The solid line represents a fit of the experimental data to a Boltzmann-type expression. Middle: The emission intensity of complex 3 stemming from S₁ (delayed fluorescence), and from T₁ (phosphorescence) as a function of the temperature according to eqn (2) and (3). Bottom: Schematic energy level diagram and decay times of complex (3).

The analysis of the data of these representations gives small energy differences of 416 (1), 395 (2) and 530 (3) cm⁻¹ between the S₁ and T₁ states. The complexes are likely to have mainly phosphorescent emissions at 77 K, whereas the population of S₁ increases at higher temperature. This leads to shorter decay times at RT, which most likely corresponds to emissions mainly from S₁ to S₀ at RT.

The reported ΔE(S₁–T₁) values of the monomers (656, 966, 1165 cm⁻¹) for the C₆F₅ (1m), C₆Cl₂F₃ (2m) and C₆Cl₅ (3m), respectively, are larger than those of the corresponding dimers. The lifetime at room temperature is longer. The radiative rate constants obtained from the expression k_r = ϕ τ⁻¹, for the dimers are 6.33 × 10⁴ (1), 51.12 × 10⁴ (2) and 24.52 × 10⁴ s⁻¹ (3). This leads to faster radiative constant for the dimers by a factor of two for the pentafluorophenyl, a factor of sixty six for the dichlorotrifluorophenyl and a factor of forty six for the pentachlorophenyl.³¹ (see ESI† and Table S2).

In metal complexes with TADF behavior, the emission at RT usually contains non-negligible contributions from phosphorescent transitions, resulting in a mixture of fluorescence and phosphorescence. To determine the phosphorescence contribution to the TADF at a given temperature, we use eqn (1) where we assume that the populations of S₁ and T₁ follow a Boltzmann distribution and where g(S₁) and g(T₁) represent the degeneracy of the two states.

Considering equal quantum yields for both processes when they are pure (S₁ → S₀ and T₁ → S₀), and the total luminescence intensity as the sum of the partial intensities from the radiative emissions of the singlet and triplet excited states, we can simplify eqn (1) to

By considering that I_tot = I(S₁) + I(T₁) one obtains

where τ is the decay time at each temperature.

Using the fitted parameters (ΔE(S₁–T₁): 530 (1), 416 (2) and 395 (3) cm⁻¹; τ (S₁): 3.9 μs (1), 0.9 μs (2), 2.50 (3) μs; and τ (T₁): 41.2 μs (1), 27.8 μs (2) and 60.8 μs (3)), we can calculate the temperature-dependent ratio between the TADF and the phosphorescence intensities at a given temperature (see Fig. 5(b) and Fig. S27, S28, ESI†). When the temperature increases from 77 K to RT, the relative emission intensity from T₁ (phosphorescences) decreases rapidly, while the emission intensity from S₁ increases. For the three dimers (1–3), the temperature at which the TADF process begins to dominate is lower than for monomers (below 150 K for the dimers and around 250 K for the monomers). The TADF contribution dominates at RT with a very small phosphorescence contribution of 8% (1), 5% (2) and 7% (3), respectively, whereas the monomers (ESI,† Fig. S29–S31) have TADF contributions of 68%, 73% and 65% at 300 K for the C₆F₅ (1m), C₆Cl₂F₃ (2m) and C₆Cl₅ (3m) derivatives, respectively.

We calculated the rate constants of the individual processes from the fitted data (Fig. 5(c) and Fig. S27–S31, ESI†) using eqn (4)^47–49

k(combined) = k(TADF) + k(T₁) (4)

and obtained k(combined) values of 26.7 × 10⁴ (1), 1.1 × 10⁴ (2) and 401.2 × 10⁴ (3) s⁻¹ at 300 K when k(T₁) rate constants are 2.7 × 10⁴ (1), 4 × 10⁴ (2) and 1.7 × 10⁴ (3) s⁻¹, respectively, and k(TADF) values are 24 × 10⁴ (1), 107 × 10⁴ (2) and 38.5 × 10⁴ (3) s⁻¹.

These data show that the double coordination in the dimers induces an increase in the TADF rate by a factor of 3.5, 31 and 12 for 1, 2 and 3, respectively, as compared to the ones for the corresponding monomers.

Computational studies

Absorption–excitation. The photophysical properties were calculated for the model systems 1a–3a at the density functional theory (DFT), time-dependent DFT (TD-DFT), and the second-order algebraic diagrammatic construction (ADC(2)) levels of theory. The model systems represent the experimentally studied complexes 1–3 (see Computational details).

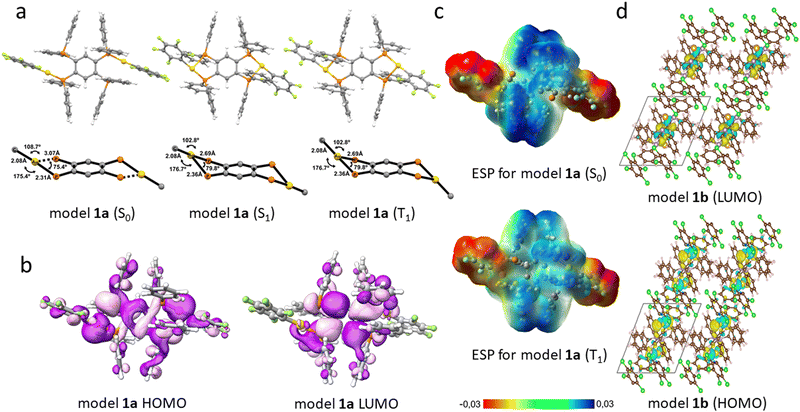
The molecular structures of the ground-state (S₀) were optimized at the DFT level. The vertical excitation energies were calculated at the TD-DFT level. The first excited singlet (S₁) and triplet (T₁) states of 1a–3a were fully optimized at the TD-DFT level. The molecular structures of the S₁ and T₁ states differ significantly from the S₀ ones, whereas the optimized S₁ and T₁ are almost identical. The Au(I) coordination changes significantly when the molecules are excited from S₀ to S₁ or T₁. (see Fig. 6(a) and ESI,† Table S3 and Fig. S32, S33). The gold atoms are asymmetrically coordinated to the atoms of the P donor of the tetraphosphine in the S₀ state. The Au–P1 bond of 2.33 Å is short in the S₁ state of 1a–3a, whereas the Au–P2 distance of 2.52 (2.54) Å is longer for 1a and 2a. For 3a, it is 2.50 (2.52) Å. The corresponding distances for the T₁ state are given in parenthesis. The asymmetric coordination is also observed in the experimental structures. Previously, it was reported that for the dppBz mononuclear complexes,^30,31 the Au–P2 distance of the T₁ state is 2.70 Å for 1a and 2a, and 2.68 Å for 3a. Structural changes upon the S₀ → T₁ excitation involve the C–C distances of the phenylene ring (see Table S3, ESI†), leading to an expansion of the ring, which suggests that the π* orbital in the aromatic ring is occupied in the T₁ state.

Fig. 6 (a) The optimized molecular structure of 1a in the ground (S₀) and lowest singlet (S₁) and triplet (T₁) excited state; (b) the frontier molecular orbitals (HOMOs and LUMOs) of the S₀ state; (c) the ESP surfaces of the S₀ and T₁ states of 1a; (d) the frontier MOs of the solid-state material of 1b obtained using periodic DFT calculations.

The structural distortions observed in the S₀ → T₁ transition suggest that there is a charge transfer from the electron-rich Au–P2 atoms to the phenylene moiety of the tpbz ligand (vide infra). Calculated ESP surfaces for 1a–3a in the S₀ and T₁ states show that the molecules are very polarized in the S₀ state, whereas they are less polarized in the T₁ state due to the charge transfer from the electron-rich R–Au–P2 fragment to the electron-deficient phenylene group (see Fig. 6(c) and Fig. S41, ESI†). We also computed the frontier molecular orbitals (HOMO and LUMO for S₀ as well as SOMO and SOMO−1 for T₁) (see Fig. 6(b) and Fig. S34, S35, ESI†). The shape and population analysis of the frontier orbitals show that the origin of the emission is the SOMO → HOMO transition, which agrees well with the metal–ligand (Au–P2) to ligand (phenylene) charge transfer transition MLL’CT discussed above (see Tables S4–S6, ESI†).

The electronic structure of the solid state of 1 (1b) was obtained using periodic DFT calculations, which confirm that the frontier orbitals of the solid-state structure are the same as those obtained in gas-phase calculations. Analysis of the density of states (DOS) shows that the higher energy states of the valence band have mainly Au d character, whereas the lower energy states of the conduction band have mainly carbon p character (see Fig. 6(d) and Fig. S37, ESI†).

The excitation energies of the 10 lowest S_n and T_n states of the A_u and A_g irreducible representations were calculated at the time-dependent density-functional theory (TD-DFT) level using the PBE0 functional and the molecular structure of the ground state. The obtained excitation energies are compared with the experimental absorption spectra. The calculated excitation energies of the singlet states agree with the low energy part of the absorption band of the solid-state material of 1–3. The transitions with larger oscillator strengths correspond to metal–ligand (Au–P2) to ligand (phenylene or PPh₂) charge transfer transitions (see Fig. 7, Fig. S42–S43 and Tables S7–S9, ESI†). The calculated excitation energy of the lowest triplet state agrees well with the experimental excitation spectra of 1–3, which are red shifted as compared to the absorption spectra. The frontier orbitals are involved in the lowest S₀ → T₁ transition, leading to a metal–ligand (Au–P2) to ligand (phenylene) charge transfer transition (³MLL’CT), which is also the origin of the observed luminescence, i.e., the phosphorescence at 77 K and the TADF at RT (see Fig. 7 and ESI,† Fig. S38–S40).

Fig. 7 (left) Comparison of solid-state absorption spectra (black), excitation spectra (red), the calculated singlet excitation energies (green), and the calculated excitation energy of the T₁ state (red line). (right) The transition density of the S₀ → T₁ excitation calculated at the TD-DFT level. The excitation increases the electron density in the green areas and decreases it in the red ones.

The Davidov model

Structurally, complexes 1–3 have inversion symmetry (I) with respect to the center of the phenylene ring, leading to two photophysically active units (quasi-monomers) with their corresponding transition-dipole moments ([small mu, Greek, vector](mon)). Each quasi-monomer has an allowed metal–ligand (Au–P) to ligand (phenylene) charge-transfer transition to the S₀ state (¹MLL′CT → S₀). The transition-dipole moments ([small mu, Greek, vector](mon)) couple in either parallel or antiparallel fashion, leading to two total transition-dipole moments ([small mu, Greek, vector](dim)). The addition of the transition dipole moment vectors leads to the S₂ state, while their subtraction leads to the S₁ state. The transition dipole moment for the S₁ state is approximately twice that of the monomer, while for the S₂ state, it is approximately zero (see Fig. 8). These resulting transition dipole moments are related to the radiative constants (k_r) and oscillator strengths (f), being four times larger than those for the monomers (1m–3m) (see Fig. 8).^30,31 This four-fold increase of the oscillator strength can be directly related to the experimental trend in quantum yield of 1, 2, and 3 (ϕ₁ < ϕ₂ < ϕ₃).

Fig. 8 Schematic representation of the emission properties of 1–3 as compared to the corresponding monomers (1m–3m). We analysed the experimentally observed quantum yields trend at the TD-DFT level.

Table 1 shows the computed data for models 1a–3a and 1m–3m. The TD-DFT calculations provide very good results and confirm that the Davidov model can be applied to these dinuclear Au(I) TADF emitters 1a–3a. An almost four-fold f(dim)/f(mon) ratio and radiative rate constant are obtained in the calculations since ([small mu, Greek, vector]₁(dim)) is about twice larger than ([small mu, Greek, vector](mon)).

Table 1 Oscillator strengths (f) of the S_n → S₀ transitions for 1a–3a and 1m–3m calculated at the TD-DFT level using the optimized molecular structures of T₁

Aryl	Molecule	Osc. strength^a	f(dim)/f(mon)//[small mu, Greek, vector](dim)/[small mu, Greek, vector](mon)^b
a The oscillator strengths of the vertical excitations calculated at the TD-DFT level using the optimized T1 geometries of 1a–3a. b Ratio between the oscillator strengths of the dimers and monomers, and ratio between the transition-dipole moments of the dimers and monomers.
C6F5	1a	S1 → S0: 0.1022 S2 → S0: 0.00	3.4//1.8
	1m	S1 → S0: 0.0302
C6Cl2F3	2a	S1 → S0: 0.1093 S2 → S0: 0.00	3.6//1.9
	2m	S1 → S0: 0.0305
C6Cl5	3a	S1 → S0: 0.1392 S2 → S0: 0.00	4.9//2.2
	3m	S1 → S0: 0.0283

---

The values of quantum yields depend on the perhalophenyl groups bound to gold(I) as observed experimentally. Computationally, the oscillator strengths follow the same trend. This result is to some extent surprising because the ligands are not directly involved in the electronic transition that is responsible for the luminescence. The different donor properties of the perhalophenyl ligands probably influence the MLL’CT leading to different transition dipole moments. The smallest oscillator strength is obtained for 1, with C₆F₅ ligands, while the largest one is obtained for 3 having C₆Cl₅ groups. The smallest oscillator strength is probably obtained when the aryl groups have more electronegative substituents such as fluorine, whereas the fastest radiative rate and largest quantum yield of luminescence are obtained when the aryl groups have less electronegative chlorine atoms.

We have also calculated the excitation energies of the S₁, S₂, T₁, and T₂ states at the TD-DFT level that yielded the energy differences ΔE(S₁–S₂) and ΔE(S₁–T₁) in Table 2. The spin–orbit coupling (SOC) matrix elements 〈S₁|H_SO|T₁〉 calculated at the TD-DFT level were used for calculating rate constants for intersystem crossing (k_ISC) and reverse intersystem crossing (k_RISC) between S₁ and T₁ of 1a–3a.

Table 2 The excitation energies (eV) of the S₁, S₂ and T₁ states and the energy differences ΔE(S₁–S₂) and ΔE(S₁–T₁) (cm⁻¹) calculated using the molecular structure of the S₁ state; the SOC matrix elements 〈S₁|H_SO|T₁〉 (cm⁻¹); the rate constants k_ISC (s⁻¹) and k_RISC (s⁻¹) between S₁ and T₁ of 1a–3a calculated at the TD-DFT level; excitation energies (eV) of the S₁, S₂ and T₁ states calculated using the molecular structure of the S₁ and the T₁ states

	1a	2a	3a
T1	1.50	1.50	1.51
S1	1.65	1.65	1.66
S2	1.89	1.89	1.88
ΔE(S1–S2)	0.24	0.24	0.22
〈S1|HSO|T1〉	70.8	70.7	68.2
k ISC(S1 →T1)	2.3 × 10^12	2.3 × 10^12	2.1 × 10^12
k RISC(T1 → S1)	2.3 × 10^9	2.3 × 10^9	2.1 × 10^9
k IC(S1 → S0)	3.3 × 10^8	3.2 × 10^8	1.8 × 10^8

---

Calculations of vertical excitation energies at the TD-DFT level yielded ΔE(S₁–T₁) energy splittings of 2175, 2179 and 2049 cm⁻¹ for 1a–3a, respectively, when using the molecular structure of the S₀ state. Since TADF occurs when the ΔE(S₁–T₁) energy gap is less than 1000 cm⁻¹,^50–53 the ΔE(S₁–T₁) values obtained at the TD-DFT level are slightly too large for an efficient TADF process at RT. The corresponding ΔE(S₂–S₁) values for 1a–3a calculated at the TD-DFT level are 2894, 2878 and 2606 cm⁻¹, respectively. The Davidov model is valid when the energy difference between S₁ and S₂ is small. More accurate ΔE(S₁–T₁) values of 1234, 1258 and 1210 cm⁻¹ are obtained for 1a–3a by calculating the excitation energies using the molecular structures optimized for the S₁ state. At the TD-DFT level, the ΔE(S₂–S₁) energy gaps are 1928, 1928 and 1766 cm⁻¹ for 1a–3a when using the molecular structure optimized for the S₁ state.

Since the luminescence energies obtained at the TD-DFT level are smaller than the experimental ones and the energy splittings are slightly too large, we also performed calculations at the ab initio correlated ADC(2) level. In the ADC(2) calculations of the lowest singlet and triplet excitation energies, we used the optimized molecular structures of the S₁ and T₁ states. The obtained excitation energies are given in Table 3. The ADC(2) calculations yielded significantly smaller ΔE(S₁–T₁) values of 202, 194 and 161 cm⁻¹ for 1a–3a, respectively, when using the optimized molecular structure of the S₁ states. When using the optimized molecular structure of the T₁ state, the ΔE(S₁–T₁) values of 476, 347 and 278 cm⁻¹ for 1a–3a are slightly larger. The ΔE(S₁–T₁) values calculated at the ADC(2) level agree well with the energy differences deduced from the experiment. At the ADC(2) level, the ΔE(S₂–S₁) energy gaps are 1914, 1906 and 1706 cm⁻¹ for 1a–3a when using the molecular structure optimized for the S₁ state.

Table 3 The excitation energies (eV) of the S₁, S₂ and T₁ states and the energy differences ΔE(S₁–S₂) and ΔE(S₁–T₁) (cm⁻¹) calculated using the molecular structure of the S₀ state; the SOC matrix elements 〈S₁|H_SO|T₁〉 (cm⁻¹); the rate constants k_ISC (s⁻¹) and k_RISC (s⁻¹) between S₁ and T₁ of 1a–3a calculated at the ADC(2) level; excitation energies (eV) of the S₁, S₂ and T₁ states calculated using the molecular structure of the S₁ and T₁ states

	1a	2a	3a
T1	2.09	2.06	2.04
S1	2.11	2.09	2.06
S2	2.35	2.33	2.27
ΔE(S1–S2)	0.24	0.24	0.21
ΔE(S1–T1)	0.03	0.03	0.02
〈S1|HSO|T1〉	71.6	71.5	68.2
k ISC(S1 →T1)	5.5 × 10^12	5.5 × 10^12	5.1 × 10^12
k RISC(T1 → S1)	8.4 × 10^11	5.4 × 10^11	7.8 × 10^11
k IC(S1 → S0)	3.7 × 10^7	4.1 × 10^7	2.7 × 10^7

---

The RISC rate constants k_RISC(T₁ → S₁) of 2.3 × 10⁹ (1a), 2.3 × 10⁹ s⁻¹ (2a) and 2.1 × 10⁹ s⁻¹ (3a) calculated at the TD-DFT level, and the RISC rate constants k_RISC(T₁ → S₁) of 8.4 × 10¹¹ (1a), 5.4 × 10¹¹ (2a) and 7.8 × 10¹¹ s⁻¹ (3a) calculated at the ADC(2) level are of the same size as previously obtained for mononuclear gold(I) complexes with the diphosphine ligand dpbz.^30,31 The RISC rate constants calculated at the ADC(2) level are two-orders of magnitude larger than the ones obtained at the TD-DFT level because ΔE(S₁–T₁) is much smaller at the ADC(2) level. The ΔE(S₁–T₁) splitting is overestimated at the TD-DFT level because double excitations are not explicitly considered at that level of theory.⁵⁴ The calculated SOC matrix elements of 71.6 (1a), 71.5 (2a), and 68.2 cm⁻¹ (3a) are larger than the ones previously reported for mononuclear complexes.^30,31

Experimental section

General

The starting products [AuR(tht)] (R = C₆F₅, C₆Cl₂F₃, C₆Cl₅; tht = tetrahydrothiophene)^55–57 and the ligand 1,2,4,5-tetrakis((diphenylphosphino)benzene)⁴⁵ (tpbz), were prepared according to the literature. All solvents used for the synthesis of the new complexes were obtained from commercial sources and were used without further purification.

Materials and physical measurements

Infrared spectra were recorded in the 2000–450 cm⁻¹ range on a PerkinElmer FT-IR Spectrum Two with an ATR accessory. ¹H, ¹⁹F and ³¹P{¹H} NMR spectra were recorded on a Bruker Avance 400 MHz spectrometer in toluene-d₈ solutions. Chemical shifts are quoted relative to SiMe₄ (¹H external), CFCl₃ (¹⁹F external) and H₃PO₄ (³¹P, external). The C, H, N analyses were carried out with a C.E. Instrument EA-1110 CHNSO microanalyzer. Diffuse reflectance UV-vis spectra of the pressed powder samples diluted with KBr were recorded using a Shimadzu UV-3600 spectrophotometer (with a Harrick Praying Mantis accessory) and recalculated following the Kubelka–Munk function. Excitation and emission spectra in the solid state were recorded using an Edinburgh FLS 1000 fluorescence spectrometer. Luminescence lifetime was measured on an Edinburgh FLS 1000 fluorescence spectrometer. Quantum yields were measured in the solid state using a Hamamatsu Quantaurus-QY C11347-11 integrating sphere with excitation at 375 nm (1), 365 nm (2) and 450 nm (3).

Synthesis and characterization

Complexes [Au₂R₂(tpbz)] (R = C₆F₅ (1), C₆Cl₂F₃ (2) and C₆Cl₅ (3)). To a dichloromethane solution (20 mL) of [Au(C₆F₅)(tht)] (0.222 g, 0.491 mmol) (1), [Au(C₆Cl₂F₃)(tht)] (0.238 g, 0.491 mmol) (2), and [Au(C₆Cl₅)(tht)] (0.262 g, 0.491 mmol) (3) was added 1,2,4,5-tetrakis(diphenylphosphanyl)benzene (tpbz) (0.200 g, 0.245 mmol) (1), (0.200 g, 0.245 mmol) (2) and (0.200 g, 0.245 mmol (3)) in a 2 : 1 molar ratio. After 30 min of stirring at room temperature, the solvent was evaporated under a vacuum to ca. 5 mL. Finally, addition of n-hexane (15 mL) led to the precipitation of products 1 (0.591 g, 0.383 mmol), 2 (0.573 g, 0.356 mmol) and 3 (0.628 g, 0.368 mmol), all as orange solids. Yield: 78% (1), 73% (2) and 75% (3).

Experimental data for 1. Anal (%) calcd for 1: (C₆₆H₄₂P₄Au₂F₁₀): C, 51.38; H, 2.74. Found: C, 50.15; H, 2.57. ¹H (298 K, toluene-d₈): δ 7.73–6.72 (m, 42H, H_Ar). ¹⁹F (298 K, toluene-d₈): δ −113.98 (m, 2F, F_o), δ −159.03 (m, 1F, F_p), δ −162.36 (m, 2F, F_m). ³¹P{¹H} (298 K, toluene-d₈): δ 15.36 (m, 4P). MS(ESI⁻): m/z 531.00 [Au–(C₆F₅)₂]⁻. ESI(+): m/z 1543.18 [C₆₆H₄₃P₄Au₂F₁₀]⁺. ATR-IR: ν 1101, 1436 cm⁻¹ (tpbz); ν 790, 954, 1634 cm⁻¹ (Au–C₆F₅).

Experimental data for 2. Anal (%) calcd for 2: (C₆₆H₄₂P₄Au₂Cl₄F₆): C, 49.28; H, 2.63. Found: C, 50.02; H, 2.71. ¹H (298 K, toluene-d₈): δ 7.31–6.73 (m, 42H, H_Ar). ¹⁹F (298 K, toluene-d₈): δ −87.91 (m, 2F, F_o), δ −112.38 (m, 1F, F_p). ³¹P{¹H} (298 K, toluene-d₈): δ 15.12 (m, 4P). MS(ESI⁻): m/z 596.88 [Au–(C₆Cl₂F₃)2]⁻. ESI(+): m/z 1609.06 [C₆₆H₄₃P₄Au₂Cl₄F₆]⁺. ATR-IR: ν 1098, 1434 cm⁻¹ (tpbz); ν 1564, 1573, 1591 cm⁻¹ (Au–C₆Cl₂F₃).

Experimental data for 3. Anal (%) calcd for 3: (C₆₆H₄₂P₄Au₂Cl₁₀): C, 46.43; H, 2.48. Found: C, 47.38; H, 2.36. 1H (298 K, toluene-d₈): δ 7.37–6.67 (m, 42H, H_Ar). ³¹P{¹H} (298 K, toluene-d₈): δ 16.52 (m, 4P). MS(ESI⁻): m/z 694.69 [Au–(C₆Cl₅)₂]⁻. ESI(+): m/z 1708.77 [C₆₆H₄₃P₄Au₂Cl₁₀]⁺. ATR-IR: ν 1091, 1435 cm⁻¹ (tpbz); ν 620, 840 cm⁻¹ (Au-C₆Cl₅).

Crystallography

The crystals were mounted in inert oil on a MiteGen MicroMount™ and transferred to the cold gas stream of a Bruker APEX-II CCD diffractometer equipped with an Oxford Instruments low-temperature controller system. Data were collected using monochromated Mo Kα radiation (λ = 0.71073 Å). Scan type: ω and ϕ. Absorption corrections: semiempirical (based on multiple scans). The structures were solved with the XT structure solution program using Intrinsic Phasing and refined with the SHELXL refinement package using Least Squares minimization and refined on F₀² using the program SHELXL-97.⁵⁸ Hydrogen atoms were included using a riding model. CCDC 2303804 and 2303805 contain the supplementary crystallographic data for this article.†

Computational details

The molecular structures of the ground state (S₀) of 1a–3a were optimized at the density functional theory (DFT) level using the B3LYP functional,^59–61 the def2-TZVP basis sets⁶² and the semiempirical D3(BJ) term to account for van der Waals interaction.^63,64 The molecular structures of the lowest excited singlet state (S₁) and the lowest excited triplet state (T₁) were optimized at the time-dependent DFT (TD-DFT)⁶⁵ level using the PBE0 functional,⁶⁶ the def2-TZVP basis sets and the D3(BJ) van der Waals term.^63,64 The molecular structures are given in the ESI.† The Gaussian 16 program package⁶⁷ was used for calculating the ESP surfaces, the transient density isosurfaces, and for investigating the validity of the Davidov model.

The Turbomole program package was used in the optimization of structures and in the calculations of the excitation energies at the TD-DFT level.^68,69 The energies of the S₁ and T₁ states were also calculated at the algebraic diagrammatic construction of second order (ADC(2)) level^70,71 using the spin-opposite-scaling approximation^72,73 and the Laplace transformation (LT) approach as implemented in Turbomole.^74,75 Split-valence polarization (def2-SVP) quality basis sets⁷⁶ were used in the ADC(2) calculations. The LT-SOS-ADC(2)/def2-SVP level of theory can be applied to large molecules when using the reduced virtual space (RVS) approach where all virtual orbitals above a given orbital-energy level are omitted in the correlation calculation.^77,78 Here, we freeze all virtual orbitals with an orbital energy larger than 50 eV (RVS-50) in addition to the core orbitals that Turbomole freezes as default.

The molecular structures of S₀ of 1a–3a optimized at the DFT level using the PBE0⁶⁶ functional and the def2-TZVP⁶² basis sets were used in the calculations of the spin–orbit coupling (SOC) matrix elements 〈S₁|H_SO|T_n〉 and the rate constants of intersystem crossing k_ISC and reverse intersystem crossing k_RISC between the S₁ state and the two lowest triplet states (T₁ and T₂). The excitation energies of the 10 lowest S_n and T_n states of the A_u and A_g irreducible representations were calculated at the time-dependent density-functional theory (TD-DFT) level using the PBE0 functional and the molecular structure of the S₀ state. The spin–orbit coupling (SOC) matrix elements 〈S_n|H_SO|T_n〉 were calculated at the TD-DFT/PBE0 level using the MOLSOC⁷⁹ program. The rate constant of reverse intersystem crossing (k_RISC) at room temperature T = 298 K was estimated as proposed in ref. 30 and 80–82.

Periodic DFT calculations were performed using Quantum Espresso 7.0⁸³ using pseudopotentials for plane-wave calculations.⁸⁴

Conclusions

The new tetraphosphine perhalophenyl gold(I) complexes reported in this work constitute an improved designed set of compounds that display a very efficient TADF behaviour. A detailed photophysical study of the three dinuclear complexes revealed that the observed emission at room temperature (RT) stems from an almost pure TADF phenomenon (92–95%), which is a higher percentage than that estimated for the corresponding quasi-monomers (ca. 70%). The emission wavelengths of the new compounds do not depend significantly on the nature of the perhalophenyl group bonded to the gold(I) center since all complexes display an orange emission at room temperature and at 77 K. The experimental and computational studies reveal that there is a relationship between the efficiency of the emission at RT and the electron withdrawing ability of the aryl groups. Application of the Davidov model on the complexes 1–3, which is possible thanks to the inversion symmetry of the molecular structures, provides a relationship between the radiative rate constants, the oscillator strengths and the transition dipole moments of the monomer and the dimer. The transition dipole moment of S₁ → S₀ of the dinuclear complexes with inversion symmetry (1–3) is about twice that of the corresponding monomer. The larger transition dipole moments lead to four times larger oscillator strengths (f) and radiative rates (k_r) of the S₁ → S₀ transition of the dimer complexes. Therefore, the quantum yields obtained for 1–3 are much higher than those for the monomers.

The calculations show that the perhalophenyl groups bearing more electronegative substituents, such as fluorine (1), give rise to a smaller transition dipole moment than those bearing less electronegative atoms such as chlorine (2 and 3). By adjusting the withdrawing ability of the perhalophenyl groups, one can control the quantum yield of the complexes. The larger transition dipole moment of 3 results in a faster radiative rate and consequently an enhanced quantum yield of emission as compared to those of 1 and 2. This study gives a new clue to design complexes that show more efficient TADF behaviour at room temperature and, hence, suggest promising candidates for use as emitter molecules in OLEDs. New studies of this kind are currently in progress.

Author contributions

The manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript. The experimental studies were performed by IS, AGEH MEO, MM, MRC and JMLL, whereas most of the computational studies was performed by RR, RRV and DS.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the DGI MICINN/FEDER (project number PID2022-139739NB-I00 (AEI/FEDER, UE)) and “ERDF A way of making Europe”. The authors would also like to acknowledge the Spanish network, Organometallic Chemistry for Sustainable Solutions–OASIS (RED2022-134074-T). I. S. also acknowledges CAR-UR for a FPI grant and A. G. E.-H. for a María Zambrano post-doctoral scholarship from the MU and the EU-Next Generation program. This work has also been supported by the Academy of Finland through projects 340582 (RRV) and 340583 (DS).

References

1. C. Bizarri, E. Spuling, D. M. Knoll, D. Volz and S. Bräse, Sustainable metal complexes for organic light-emitting diodes (OLEDs), Coord. Chem. Rev., 2018, 373, 49–82.
2. J. Bauri, R. B. Choudhary and G. Mandal, Recent advances in efficient emissive materials-based OLED applications: a review, J. Mater. Sci., 2021, 56, 18837–18866.
3. C. Zhang, R. Liu, D. Zhang and L. Duan, Progress on Light-Emitting Electrochemical Cells toward Blue Emission, High Efficiency, and Long Lifetime, Adv. Funct. Mater., 2020, 30, 1907156.
4. M. D. Weber, E. Fresta, M. Elie, M. E. Miehlich, J.-L. Renaud, K. Meyer, S. Gaillard and R. D. Costa, Rationalizing Fabrication and Design Toward Highly Efficient and Stable Blue Light-Emitting Electrochemical Cells Based on NHC Copper(I) Complexes, Adv. Funct. Mater., 2018, 28, 1707423.
5. B. N. Bideh and H. Shahroosvand, New moleculary engineered binuclear ruthenium(II) complexes for highly efficient near-infrared light emitting electrochemical cells (NIR-LECs), Dalton Trans., 2022, 51, 3652–3660.
6. Highly efficient OLEDs-Materials based on Thermally Activated Delayed Fluorescence, ed. H. Yersin, Wiley-VCH, Weinheim, Germany, 2019.
7. Handbook of Organic-Light-Emitting Diodes, ed. C. Adachi, R. Hattori, H. Kaji and T. Tsujimura, Springer, Tokyo, Japan, 2022.
8. H. Yersin and U. Monkowius, Komplexe mit kleinen Singulett-Triplett-Energie-Abständen zur Verwendung in opto-elektronischen Bauteilen (Singlett-Harvesting-Effekt). Internal patent filing, University of Regensburg, 2006. German Pat., DE 10 2008 033563 A1, 2008.
9. R. Czerwieniec, J. Yu and H. Yersin, Blue-Light Emission of Cu(I) Complexes and Singlet Harvesting, Inorg. Chem., 2011, 50, 8293–8301.
10. S. Lamansky, P. I. Djurovich, D. Murphy, F. Abdel-Razzaq, H.-E. Lee, C. Adachi, P. E. Burrows, S. R. Forrest and M. E. Thompson, Highly Phosphorescent Bis-Cyclometalated Iridium Complexes: Synthesis, Photophysical Characterization, and Use in Organic Light Emitting Diodes, J. Am. Chem. Soc., 2001, 123, 4304–4312.
11. H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, The triplet state of organo-transition metal compounds. Triplet harvesting and singlet harvesting for efficient OLEDs, Coord. Chem. Rev., 2011, 255, 2622–2652.
12. C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, Nearly 100% internal phosphorescence efficiency in an organic light emitting devices, J. Appl. Phys., 2001, 90, 5048–5051.
13. H. Yersin and W. J. Finkenzeller, Triplet Emitters for Organic Light-Emitting Diodes: Basic properties, in Highly Efficient OLEDs with Phosphorescent Materials, Wiley-VCH Verlag, ed. H. Yersin, 2008, pp.1–97.
14. H. Noda, H. Nakanotani and C. Adachi, Excited state engineering for efficient reverse intersystem crossing, Sci. Adv., 2018, 4, eaao6910.
15. C. E. Housecroft and E. C. Constable, TADF: Enabling luminescent copper(I) coordination compounds for light-emitting electrochemical cells, J. Mater. Chem. C, 2022, 10, 4456–4482.
16. A. Y. Baranov, A. S. Berezin, D. G. Samsonenko, A. S. Mazur, P. M. Tolstoy, V. F. Plyusnin, I. E. Kolesnikov and A. V. Artem’ev, New Cu(I) halide complexes showing TADF combined with room temperature phosphorescence: the balance tuned by halogens, Dalton Trans., 2020, 49, 3155–3163.
17. A. Alconchel, O. Crespo, P. García-Orduña and M. C. Gimeno, Closo- or Nido-Carborane Diphosphene as Responsible for Strong Thermochromism or Thermally Activated Fluorescence (TADF) in [Cu(N^N)(P^P)]^0/+, Inorg. Chem., 2021, 60, 18521–18528.
18. A. Alconchel, O. Crespo and M. C. Gimeno, Thermally Activated Fluorescence in Neutral and Cationic Copper(I) Complexes with the 2-(4-Thiazolyl)benzimidazole Ligand, Inorg. Chem., 2023, 62, 10431–10439.
19. H. Yersin, R. Czerwieniec, U. Monkowius, R. Ramazanov, R. Valiev and M. Shafikov, Intersystem crossing, phosphorescence, and spin-orbit coupling. Two contrasting Cu(I)-TADF dimers investigated by milli- to micro-second phosphorescence, femto-second fluorescence, and theoretical calculations, Coord. Chem. Rev., 2023, 478, 214975.
20. R. Czerwieniec, M. J. Leitl, H. H. H. Homeier and H. Yersin, Cu(I) complexes-Thermally activated delayed fluorescence. Photophysical approach and material design, Chem. Rev., 2016, 325, 2–28.
21. M. Z. Shafikov, A. F. Suleymanova, A. Schinabeck and H. Yersin, Dinuclear Ag(I) Complex Designed for Highly Efficient Thermally Activated Delayed Fluorescence, J. Phys. Chem. Lett., 2018, 9, 702–709.
22. J.-H. Jia, D. Liang, R. Yu, X.-L. Chen, L. Meng, J.-F. Chang, J.-Z. Liao, M. Yang, X.-N. Li and C.-Z. Lu, Coordination-Induced Thermally Activated Delayed Fluorescence: From Non-TADF Donor-Acceptor-Type Ligand to TADF-Active Ag-Based Complexes, Chem. Mater., 2020, 32, 620–627.
23. Z. Han, X.-Y. Dong and S.-Q. Zang, Crystalline Metal–Organic Materials with Thermally Activated Delayed Fluorescence, Adv. Opt. Mater., 2021, 9, 2100081.
24. H. Yersin, R. Czerwieniec, M. Z. Shafikov and A. F. Suleymanova, TADF Material Design: Photophysical Background and Cases Studies Focusing on Cu^I and Ag^I Complexes, ChemPhysChem, 2017, 18, 3508–3535.
25. T. Teng, K. Li, G. Cheng, Y. Wang, J. Wang, J. Li, C. Zhou, J. Liu, T. Zou, J. Xiong, C. Wu, H.-X. Zhang, C.-M. Che and C. Yang, Lighting Silver(I) Complexes for Solution Processed Organic Light-Emitting Diodes and Biological Applications via Thermally Activated Delayed Fluorescence, Inorg. Chem., 2020, 59, 12122–12131.
26. X.-K. Chen, D. Kim and J.-L. Brédas, Thermally Activated Delayed Fluorescence (TADF) Path towards Efficient Electroluminescence in Purely Organic Materials: Molecular Level Insight, Acc. Chem. Res., 2018, 51, 2215–2224.
27. J. A. Barltrop and J. D. Coyle, Excited states in organic chemistry, Wiley, New York, 1975.
28. P. W. Atkins, Quanta: A Handbook of Concepts, Oxford University Press, Oxford, U.K., 1991.
29. M. Hashimoto, S. Igawa, M. Yashima, I. Kawata, M. Hoshino and M. Osawa, Highly Efficient Green Organic Light-Emitting Diodes Containing Luminescent Three-Coordinate Copper(I) Complexes, J. Am. Chem. Soc., 2011, 133, 10348–10351.
30. J. M. López-de-Luzuriaga, M. Monge, M. E. Olmos, M. Rodríguez-Castillo, I. Soldevilla, D. Sundholm and R. R. Valiev, Perhalophenyl Three-coordinate Gold(I) Complexes as TADF Emitters: A Photophysical Study from Experimental and Computational Viewpoints, Inorg. Chem., 2020, 59, 14236–14244.
31. I. Soldevilla, A. García-Camacho, R. T. Nasibullin, M. E. Olmos, M. Monge, D. Sundholm, R. R. Valiev, J. M. López-de-Luzuriaga and M. Rodríguez-Castillo, Influence of perhalophenyl groups in the TADF mechanism of diphosphino gold(I) complexes, J. Mater. Chem. C, 2022, 10, 4894–4904.
32. A. Schinabeck, J. Chen, L. Kang, T. Teng, H. H. H. Homeier, A. F. Suleymanova, M. Z. Shafikov, R. Yu, C.-Z. Lu and H. Yersin, Symmetry-Based Design Strategy for Unprecedentedly Fast Decaying Thermally Activated Delayed Fluorescence (TADF). Application to Dinuclear Cu(I) Compounds, Chem. Mater., 2019, 31, 4392–4404.
33. A. S. Davydov, The Theory of Molecular Excitons, Sov. Phys. Usp., 1964, 7, 145–178.
34. M. Hesse, H. Meier and B. Zeeh, Spectroscopic Methods in Organic Chemistry, Thieme, 2nd edn, 2007.
35. H. Yersin and G. Gliemann, Spectroscopic Studies of M_x[Pt(CN)₄]·yH₂O, Ann. N. Y. Acad. Sci., 1978, 313, 539–559.
36. P. Day, Excitons in one-dimensional tetracyanoplatinate salts, J. Am. Chem. Soc., 1975, 97, 1588–1589.
37. G. Hogarth and T. Norman, Zero-valent Group 6 complexes of 1,2,4,5-tetrakis(diphenylphosphino)benzene, Inorg. Chim. Acta, 1996, 248, 167–174.
38. J. Chen, T. Teng, L. Kang, X.-L. Chen, X.-Y. Wu, R. Yu and C.-Z. Lu, Highly Efficient Thermally Activated Delayed Fluorescence in Dinuclear Ag(I) Complexes with a Bis-Bidentate Tetraphosphane Bridging Ligand, Inorg. Chem., 2016, 55, 9528–9536.
39. J. Chen, T. Teng, J.-Y. Wang, L. Kang, X.-L. Chen, L.-J. Xu, R. Yu and C.-Z. Lu, Synthesis, Structure, and Characterization of Emissive Neutral Dinuclear Cu^I Complexes with a Tetraphosphane Bridging Ligand, Eur. J. Inorg. Chem., 2016, 3036–3041.
40. K. Arumugam, M. Selvachandran, A. Obanda, M. C. Shaw, P. Chandrasekaran, S. L. Caston Good, J. T. Mague, S. Sproules and J. P. Donahue, Redox-Active Metallodithiolene Groups Separated by Insulating Tetraphosphinobenzene Spacers, Inorg. Chem., 2018, 57, 4023–4038.
41. K. Arumugam, M. C. Shaw, J. T. Mague, E. Bill, S. Sproules and J. P. Donahue, Long-Range Spin Coupling: A Tetraphosphine-Bridged Palladium Dimer, Inorg. Chem., 2011, 50, 2995–3002.
42. G. Hogarth, Synthesis and X-ray crystal structure of [{(CO)₃Fe}₂{μ-η²-η²-(Ph₂P)₂C₆H₂(PPh₂)₂}], J. Organomet. Chem., 1991, 406, 391–398.
43. V. W.-W. Yam, S. W.-K. Choi and K.-K. Cheung, Synthesis and Design of Novel Tetranuclear and Dinuclear Gold(I) Phosphine Acetylide Complexes. First X-ray Crystal Structures of a Tetranuclear ([Au₄(tppb)(C≡CPh)₄]) and a Related Dinuclear ([Au₂(dppb)(C≡CPh)₂]) Complex, Organometallics, 1996, 15, 1734–1739.
44. F. K.-W. Hau, K.-L. Cheung, N. Zhu and V. W.-W. Yam, Calixarene-based alkynyl-bridged gold(I) isocyanide and phosphine complexes as building motifs for the construction of chemosensors and supramolecular architectures, Org. Chem. Front., 2019, 6, 1205–1213.
45. M. Ferrer, L. Giménez, A. Gutiérrez, J. C. Lima, M. Martínez, L. Rodríguez, A. Martín, R. Puttreddy and K. Rissanen, Polypyridyl-functionalizated alkynyl gold(I) metallaligands supported by tri- and tetradentate phosphanes, Dalton Trans., 2017, 46, 13920–13934.
46. N. Glebko, T. M. Dau, A. S. Melnikov, E. V. Grachova, I. V. Solovyev, A. Belyaev, A. J. Karttunen and I. O. Koshevoy, Luminescence Thermochromism of Gold(I) Phosphane-Iodide Complexes: A Rule or an Exception?, Chem. – Eur. J., 2018, 24, 3021–3029.
47. A. Schinabeck, N. Rau, M. Klein, J. Sundermeyer and H. Yersin, Deep blue emitting Cu(I) tripod complexes. Design of high quantum yield materials showing TADF-assisted phosphorescence, Dalton Trans., 2018, 47, 17067–17976.
48. J. Toigo, G. Farias, C. A. M. Salla, L. G. T. A. Duarte, A. J. Bortoluzzi, T. D. Z. Atvars, B. de Souza and I. H. Bechtold, Speeding-up Thermally Activated Delayed Fluorescence in Cu(I) Complexes Using Aminophosphine Ligands, Eur. J. Inorg. Chem., 2021, 3177–3184.
49. A. Y. Baranov, A. S. Berezin, D. G. Samsonenko, A. S. Mazur, P. M. Tolstoy, V. F. Plyusnin, I. E. Kolesnikov and A. V. Artem’ev, New Cu(I) halide complexes showing TADF combined with room temperature phosphorescence: the balance tuned by halogens, Dalton Trans., 2020, 49, 3155–3163.
50. C. J. Chiang, A. Kimyonok, M. K. Etherington, G. C. Griffiths, V. Jankus, F. Turksoy and A. P. Monkman, Ultrahigh Efficiency Fluorescent Single and Bi-Layer Organic Light Emitting Diodes: The Key Role of Triplet Fusion, Adv. Funct. Mater., 2013, 23, 739–746.
51. T. J. Penfold, F. B. Dias and A. P. Monkman, The Theory of Thermally Activated Delayed Fluorescence for Organic Light Emitting Diodes, Chem. Commun., 2018, 54, 3926–3935.
52. R. M. Gadirov, R. R. Valiev, L. G. Samsonova, K. M. Degtyarenko, N. V. Izmailova, A. V. Odod, S. S. Krasnikova, I. K. Yakushchenko and T. N. Kopylova, Thermally activated delayed fluorescence in dibenzothiophene sulfone derivatives: Theory and experiment, Chem. Phys. Lett., 2019, 717, 53–58.
53. R. R. Valiev, B. F. Minaev, R. M. Gadirov, E. N. Nikonova, T. A. Solodova, S. Y. Nikonov, M. B. Bushuev and T. N. Kopylova, Electroluminescence of Halogen Complexes with Monovalent Copper: OLED Devices and DFT Modeling, Russ. Phys. J., 2016, 58, 1205–1211.
54. L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, On the origin of the inverted singlet–triplet gap of the 5th generation light-emitting molecules, Phys. Chem. Chem. Phys., 2022, 24, 18713–18721.
55. A. L. Casado and P. Espinet, A novel reversible aryl Exchange involving two organometallics: mechanism of the gold(I)-catalyzed isomerization of trans-[PdR₂L₂] complexes (R = aryl, L = SC₄H₈), Organometallics, 1998, 17, 3677–3683.
56. R. Usón, A. Laguna, J. Vicente, J. García and B. Bergareche, Preparation of pentahalophenyl p-tolylisocyanide complexes of gold(I) and their reactions with amines, ammonia and alcohols, J. Organomet. Chem., 1979, 173, 349–355.
57. R. Usón, A. Laguna and J. Vicente, Preparation and Properties of Stable Salts Containing Mono- or Bis-(pentafluorophenyl)aurate(I) and Mono-, Tris-, or Tetrakis-(pentafluorophenyl)aurate(III) Ions, Chem. Commun., 1976, 353–354.
58. G. M. Sheldrick, SHELXL-97, Program for Crystals Structure Refinement, University of Göttingen, Germany, 1997.
59. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behaviour, At., Mol., Opt. Phys., 1988, 38, 3098–3100.
60. A. D. Becke, Density-functional thermochemistry. III: The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
61. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
62. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
63. S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, Consistent an Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
64. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
65. M. E. Casida and M. Huix-Rotllant, Progress in time-dependent density-functional theory, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
66. C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158–6170.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision G.01., Gaussian, Inc., Wallingford CT, 2016.
68. TURBOMOLE V7.7.1. 2023, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; Available from https://www.turbomole.org (accessed January 2024).
69. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, TURBOMOLE: Modular Program Suite for Ab Initio Quantum-Chemical and Condensed-Matter Simulations, J. Chem. Phys., 2020, 152, 184107.
70. J. Schirmer, Beyond the random-phase approximation: A new approximation scheme for the polarization propagator, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
71. A. Dreuw and M. Wormit, The algebraic diagrammatic construction scheme for the polarization propagator for the calculation of excited states, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95.
72. Y. Jung, R. C. Lochan and A. D. Dutoi, Scaled opposite-spin second order Møller-Plesset correlation energy: an economical electronic structure method, J. Chem. Phys., 2004, 121, 9793–9802.
73. Y. M. Rhee and M. Head-Gordon, Scaled Second-Order Perturbation Corrections to Configuration Interaction Singles:  Efficient and Reliable Excitation Energy Methods, J. Phys. Chem. A, 2007, 111, 5314–5326.
74. N. O. C. Winter and C. Hättig, Scaled opposite-spin CC2 for ground and excited states with fourth order scaling computational costs, J. Chem. Phys., 2011, 134, 184101.
75. N. O. C. Winter and C. Hättig, Quartic scaling analytical gradients of scaled opposite-spin CC2, Chem. Phys., 2012, 401, 217–227.
76. A. Schäfer, H. Horn and R. Ahlrichs, Fully Optimized Contracted Gaussian-Basis Sets for Atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577.
77. R. Send, V. R. I. Kaila and D. Sundholm, Reduction of the virtual space for coupled-cluster excitation energies of large molecules and embedded systems, J. Chem. Phys., 2011, 134, 214114.
78. C. M. Suomivuori, N. O. C. Winter, C. Hättig, D. Sundholm and V. R. I. Kaila, Exploring the Light-Capturing Properties of Photosynthetic Chlorophyll Clusters Using Large-Scale Correlated Calculations, J. Chem. Theory Comput., 2016, 12, 2644–2651.
79. S. G. Chiodo and M. Leopoldini, MolSOC: A Spin–Orbit Coupling Code. Comput, Phys. Commun., 2014, 185, 676–683.
80. R. M. Gadirov, R. R. Valiev, L. G. Samsonova, K. M. Degtyarenko, N. V. Izmailova, A. V. Odod, S. S. Krasnikova, I. K. Yakushchenko and T. N. Kopylova, Thermally activated delayed fluorescence in dibenzothiophene sulfone derivatives: Theory and experiment, Chem. Phys. Lett., 2019, 717, 53–58.
81. R. R. Valiev, V. N. Cherepanov, R. T. Nasibullin, V. Y. Arthuhov, D. Sundholm and T. Kurtén, Calculating rate constants for intersystem crossing and internal conversion in the Franck–Condon and Herzberg-Teller Approximations, Phys. Chem. Chem. Phys., 2019, 21, 18495–18500.
82. D. Blasco, R. T. Nasibullin, R. R. Valiev and D. Sundholm, Gold(I)-Containing Light-Emitting Molecules with an Inverted Singlet–Triplet Gap, Chem. Sci., 2023, 14, 3873–3880.
83. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr., A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, R. Gerstmann, E. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Advanced capabilities for materials modelling with QUANTUM ESPRESSO, J. Phys.: Condens. Matter., 2017, 29, 465901.
84. N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2303804 and 2303805. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc02133a

---