 Open Access Article
Open Access ArticleToward high-power terahertz radiation sources based on ultrafast lasers
Won Jin
Choi
 *a,
Michael R.
Armstrong
a,
Jae Hyuck
Yoo
a and
Taeil
Lee
b
*a,
Michael R.
Armstrong
a,
Jae Hyuck
Yoo
a and
Taeil
Lee
b
aPhysical and Life Sciences Directorate, Lawrence Livermore National Laboratory, USA. E-mail: choi21@llnl.gov
bMaterials Science and Engineering Department, Gachon University, Republic of Korea
First published on 30th May 2024
Abstract
The development of new photon sources has propelled scientific and technological breakthroughs across disciplines, ranging from atomic physics and quantum technology to optoelectronics, chemistry, and biomedical devices. This is particularly evident with emerging photon sources of previously unattainable high power, allowing for the clear deconvolution of semiconductor energy states and the elucidation of the dynamics of quasi-particles and molecular vibrations. Terahertz (THz) radiation, once considered a gap in the electromagnetic spectrum, has become readily accessible with advancements in ultrafast optics. While various sources and detectors are available, their output intensity based on typical femtosecond lasers remains still limited to approximately 0.5 mW at 1 THz, constraining their widespread applications. In this review, we explore the main mechanisms and recent advancements in THz radiation generation using nonlinear optics, optoelectronics, and plasma. We summarize their characteristics by examining their performance across different optical configurations. Additionally, we review a novel approach utilizing acoustic waves, initially proposed approximately 15 years ago, but only limited subsequent progress has been made. We delineate the challenges associated with this approach and propose potential solutions, highlighting the significance of further investigation and improvement, which could potentially catalyze a breakthrough in this field.
Introduction
Terahertz (THz) radiation has been attracting significant interest in quantum science, optical spectroscopy, and emerging material sciences. One of the main reasons for this is that THz photon energies, ranging from 0.001 to 0.01 eV, overlap with fundamental motions of spins, electrons, and quasi-particles in all states of matter (gas, liquids, solids, and plasma).1,2 For example, THz radiation offers precise probing capabilities down to the Rydberg energy states in atomic and semiconducting physics,3,4 as well as the fundamental studies of dynamics of phonons, excitons, and magnons.1,5 Moreover, THz radiation holds immense potential applications in chemistry and biomedicine too.6,7 Serving as non-destructive, non-ionizing, and remote analytical spectroscopies, THz waves are capable of capturing vibrations and phonon modes present in crystalline molecules and biomolecular assemblies.3,8,9Although many physical and chemical phenomena have been revealed by the continuous development of THz spectroscopies and technology over the last decade, the average radiation power of THz sources remains relatively weak, typically a few milliwatts. This limitation significantly restricts their current applications to only probing the linear response of materials.1 There is a pressing need for high-power THz sources to advance further in areas where the strong-field of THz waves can lead to the modification of states of matter, such as switching magnetic order, spin–lattice coupling, and parametric amplification of optical phonons.1,10,11 Furthermore, high-power THz waves are necessary to penetrate objects like human hands and tissues, even those several centimetres thick with high absorption coefficients, particularly in blood and water.12 These bodily fluids, which initially limit THz transparency, can be leveraged for imaging purposes.13 They naturally act as high-contrast agents for fine vessels that intricately spread throughout tissues, thus offering new possibilities for medical diagnostics and imaging.14
The THz frequency range lies between the microwave and infrared regions in the electromagnetic (EM) spectrum, where electronics-based techniques (e.g., impact ionization avalanche diodes, magnetrons) are pushed to their upper frequency limits, and optical techniques (e.g., nonlinear frequency mixing, optical parametric oscillators) are pushed to their longer wavelength limits to generate THz radiation.15–17 In this intermediate range, some of optical components for THz such as lenses, mirrors, waveplates, can be adopted from well-known infrared optics and microwave electronics. In addition, metamaterials, artificial arrays of subwavelength structures, or antennas mostly designed for microwave and radiofrequencies (RF) have been able to replicate similar THz optical components by applying simple scaling laws after considering the resonance frequency and its dimension.8,18 However, this has not been the case for THz emitters and detectors. It should be noted that RF vacuum electronics, such as magnetrons used in typical household microwave ovens, can now generate more than 800 W of power.19 However, similar magnetrons with electron cavity designs intended for THz frequencies only emit a few milliwatts, and only up to approximately 300 GHz due to a significant drop in efficiency at higher frequencies.16,20
A breakthrough to achieve high-power THz sources is needed. In this review, we review some of the recent advancements focused on laser-based THz generation, specifically using ultrafast lasers. Ultrafast lasers provide significant advantages over continuous wave lasers for THz radiation generation due to their ability to produce high peak power, enabling efficient nonlinear interactions, broad spectral content, and precise temporal control, all of which are crucial for generating and studying THz radiation effectively. We discuss their advantages and limitations, along with their main mechanisms. Following this, we will explore future directions aimed at achieving high-power THz generation.
Generation of THz radiation
The emission of electromagnetic waves at THz frequencies requires oscillation of current density, ‘jTHz’, i.e., time-varying currents at the corresponding picosecond time scale.1 One can imagine dipolar directional THz radiation occurring when localized current density, akin to the Hertzian dipole model, oscillates at THz frequency. Generally, four major categories have been developed for generating THz waves, with some extensively studied while others remain largely open: (1) electro-optic, (2) photoconductive antenna, (3) plasma, and (4) acoustic wave (Fig. 1). While the fundamental mechanisms of each category could vary, one commonality exists: the key element in all these mechanisms involves time-varying current density, jTHz. The only difference lies in the element that causes the source current distribution; for some cases, it is free electrons (for example, carriers in semiconductors or photo-conducting antennas), while for others, it is the displacement of the charge density of bound electrons and/or ions (for example, induced dipole moment of crystals).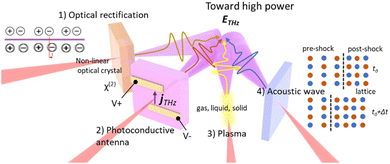 | ||
| Fig. 1 Different methods of terahertz generation using femtosecond lasers: (1) electro-optic, (2) photoconductive antenna, (3) plasma, and (4) acoustic wave. | ||
(1) THz generation based on optical rectification
One of the most common methods of THz generation leverages the nonlinear optical process in non-centrosymmetric optical crystals with femtosecond lasers. This process, known as optical rectification, is the inverse electro-optic second-order phenomenon that occurs in nonlinear crystals such as inorganic crystals of ZnTe (zinc telluride), LiNbO3 (lithium niobate), GaP (gallium phosphide), GaAs (gallium arsenide), and organic crystals such as DAST (4-N,N-dimethylamino-4′-N′-methyl-stilbazolium tosylate), DSTMS (4-N,N-dimethylamino-4′-N′-methyl-stilbazolium 2,4,6-trimethylbenzenesulfonate), OH1 (2-[3-(4-hydroxystyryl)-5,5-dimethylcyclohex-2-enylidene] malononitrile), BNA (N-benzyl-2-methyl-4-nitroaniline), and HMQ-TMS (2-(4-hydroxy-3-methoxystyryl)-1-methilquinolinium-2,4,6 trimethylbenzenesulfonate).1,2 Along with these, metal–organic hybrid perovskite crystals such as MAPbX3 (methylammonium lead halide) and CsPbX3 (cesium lead halide) are also suitable for THz emission.Optical rectification phenomena can be interpreted as difference-frequency generation (DFG) within the intra-pulse of the femtosecond laser pulses, resulting in a mixed THz wave with a frequency, ΩTHz. Note that since the bandwidth of typical femtosecond optical laser pulses spans the THz range (from tens of femtoseconds to a few picoseconds), the resulting frequency, ΩTHz, falls within the THz frequency range.
When a laser is incident into a nonlinear crystal and DFG occurs, the induced polarization in the nonlinear optical medium can be calculated as follows:
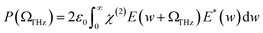 | (1) |
The phase matching condition is one of the main factors necessary to achieve high efficiency in this process and consequently generate high-power THz fields. The nonlinear optical crystals listed above are selected empirically and theoretically based on this criterion. However, the efficiency remains relatively low, typically ranging from 10−4 to 10−6 of the optical pump energy converted to THz output energy.2 The efficiency of energy conversion, when phase matched and pump absorption is ignored, can be described as follows:
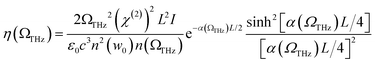 | (2) |
Through optical rectification, many attempts have been made to achieve so-called high-power milliwatt-class THz sources.21–23 The central wavelength for pumping (between 800 to 1600 nm of wavelength) was selected considering broad velocity matching, and high pulse energy with short pulse duration were utilized. For example, milliwatt THz generation has been reported using HMQ-TMS and BNA organic crystals with a 10 MHz Yb-doped fiber laser. In the case of BNA, heatsinking the crystal to a diamond substrate was employed to manage the thermal issues.22 While suppressing the temperature rise of the organic crystal is ideal, cooling it with a cryostat or other devices should also be approached carefully, as changes in their crystal structure and thus many optical properties can occur.
New inorganic/organic optical crystals are currently under development for high-power THz generation with higher efficiency, through both computational and/or experimental approaches.24–26 Phase matching conditions are essential requirements for materials development. However, we can also explore noncollinear geometries, such as tilted-pulse-front-pumping (TPFP),27,28 utilizing materials like LiNbO3 which are difficult to phase-match using a typical collinear configuration. Another recent trend to achieve high power with increased efficiency is pumping at longer infrared wavelengths from 1.6 to 2.5 μm. In this case, high order (three- or more) photon absorption (3PA or 4PA) is effective, which can obtain higher pumping intensity with higher conversion efficiency (Fig. 2(a) and (b)).29,30
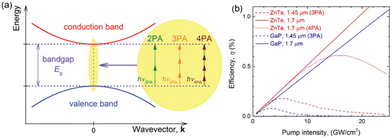 | ||
| Fig. 2 (a) Schematic of band structures depicting multiphoton absorption of two to four orders. (b) Calculated THz conversion efficiency with 3PA and 4PA for ZnTe and GaP crystals, with respect to the pump intensity. Reproduced from ref. 29 with permission from Optica, copyright 2016. | ||
The THz field strength can be further enhanced by micro- to nano-patterning of nonlinear optical crystals. One such method is the so-called contact grating technique,31 where, for example, the 1-micron line-and-space of monolithically patterned ZnTe has resulted in as high as 3% efficiency and 3.9 μJ THz pulse energy (Fig. 3(a)). Additionally, subwavelength nanopatterned metasurfaces with semiconductors (e.g., InAs, GaAs) have also recently been reported to demonstrate high-efficiency generation by suppressing photo-Dember and supporting resonant electric dipole mode (Fig. 3(b)). High-power THz generation can be achieved by focusing THz pulses, leveraging the capabilities of these monolithically formed binary-phase THz metasurfaces.
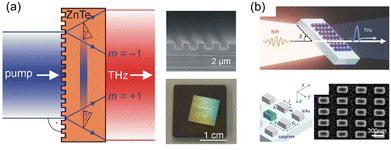 | ||
| Fig. 3 (a) Diagram illustrating the contact grating THz source with collinear geometry, utilizing two diffraction orders fabricated by monolithic etching. Shown are scanning electron microscopy and photographic images. Reproduced from ref. 31 with permission from Optica, copyright 2016. (b) Nanopatterned metasurfaces designed for resonant electric dipole mode to enhance THz pulse generation efficiency. Reprinted with permission from ref. 32. Copyright 2022 American Chemical Society. | ||
Emerging two-dimensional materials, including graphene and their plasmon-enhanced versions, can also be candidates for high-power THz emission through enhanced optical rectification and/or the photon drag effect.33–36 Their high carrier mobility, linear energy dispersion, and relatively low momentum relaxation rate, combined with a large variety of chemical compositions, doping and 3D nanostructures,36 could be advantageous.
Future work entails exploring non-centrosymmetric crystals with higher nonlinear coefficients (>300 pm V−1), high damage thresholds, thermal robustness, and the capability of large sizes, especially through sophisticated crystallization processes. Regarding the principles of development, there is an effort to accelerate crystal development by using data mining from crystal databases such as the Cambridge Structural Database.24 Researchers are scrutinizing the non-centrosymmetric lattice packing among the crystals and identifying properties such as hyperpolarizability from new materials. Some crystals face issues such as scaling the crystal size and having a low damage threshold, which can be mitigated by developing improved growth techniques and/or alloying/doping.37 Engineering crystal structures and orientations to enhance nonlinear optical effects, as well as ensuring stability, reliability, and scalability, is crucial for THz sources based on these materials for practical applications. This could represent a breakthrough, particularly as pump laser systems are being developed and optimized to achieve high power (>50 W) and MHz repetition rate femtosecond lasers.38
(2) THz generation based on transient current of photoconductive antenna
Typical photoconductive antennas (PCAs) consist of a semiconducting material with two metallic contacts. THz generation using PCAs involves the following steps: (i) when the gap between the two metallic contacts is illuminated by an ultrafast laser pulse with photon energy greater than the bandgap of the semiconductor, free carriers are created in the channel. (ii) Since an electric field between the electrodes is applied, the generated carriers are rapidly accelerated toward opposite electric field gradient and then captured by carrier recombination and/or defects. (iii) Upon acceleration and subsequent recapture of the free carriers, an electromagnetic pulse is radiated. Here, the propagation direction of the generated EM wave is perpendicular to the acceleration direction, and the characteristic time scale of the EM pulse, and therefore its frequency, lies in the THz range, resulting in the generation of a THz pulse from a PCA.39,40In a typical THz pulse, there are two major peaks with opposite polarities. The shape of the first peak is determined by the free carrier generation and acceleration process, while the shape of the second peak is determined by the carrier recombination or defect-assisted capture process. The characteristics of these processes are governed by the laser pulse wavelength and duration, the associated optoelectronic properties of the semiconductor channel material, and the electrode geometry. For example, the band gap of the semiconductor material determines the excitation energy and the absorption depth of the laser pulse, and therefore the optimal channel thickness. Also, the electrode geometry affects the electric field distribution, guiding the acceleration process, along with the intrinsic substrate channel properties such as carrier mobility, lifetime, dark resistance, and breakdown voltage. In general, high carrier mobility, high dark resistance, high breakdown voltage, and short carrier lifetime are desirable for THz PCAs as these are strongly related to the efficiency of THz generation.34 GaAs and its variations, such as low-temperature (LT)-GaAs and semi-insulating (SI)-GaAs, are the most widely utilized substrate materials for PCAs. This is due, for example, to their ability to suppress the broadening of the peak by taking advantage of their subpicosecond carrier lifetime.39,40
Recent developments in ultrafast amplified laser systems have brought the opportunity for PCAs to achieve high-power THz generation. By increasing the interaction volume for the free carrier generation/acceleration,41 higher THz field are obtained. Early demonstrations to scale up the interaction volume were carried out by having a large gap (>1 mm) between the metallic contacts, operating under a large bias voltage (∼10 kV). Another scaling approach without the requirement of a large bias voltage is to design the array of interdigitated electrodes with a small gap (<50 μm) over a large area (∼1 cm2) in conjunction with shadow masks to selectively generate the free carriers in the same acceleration direction.42 However, the obtained field amplitudes were not simply scaled up by the interaction volume. The performance discrepancy is attributed to space-charge screening that is more pronounced with smaller gaps.
Apart from the scaling up approach, there have been studies to improve an optical-to-THz conversion efficiency to obtain high-power THz generation. Plasmonic nanostructures have been employed between the electrode gap to enhance the absorption in the semiconductor substrate (Fig. 4(a)–(c)).43
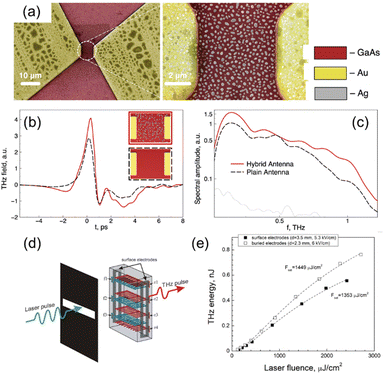 | ||
| Fig. 4 (a) THz PCA with plasmonic Ag nanostructures. (b) Time-domain THz spectra obtained from the same PCA without (black dotted line) and with (red solid line) Ag nanostructures. (c) Their corresponding spectra in frequency domain are illustrated. Reproduced from ref. 43 with permission from Springer Nature, copyright 2018. (d) A schematic of electrically conductive graphite buried 3D electrodes formed inside diamond crystal. (e) THz pulse energy versus laser fluence for 3D graphite electrodes of diamond. Reproduced from ref. 44 with permission from MDPI, copyright 2023. | ||
A broadband THz spectrum was achieved by using a germanium (Ge) substrate, which does not have phonon modes in the THz region, and the intrinsically long carrier lifetime was reduced by adding Au deep traps.45 Buried graphite electrodes in a diamond substrate to create a homogeneous bias field to address the large absorption depth associated with the diamond substrate (Fig. 4(d) and (e)).44 Three-dimensional electrode structures have been demonstrated for efficient transport of the free carriers.46
(3) THz generation based on plasma
Plasma is a quasi-neutral medium composed of electrons and positive ions, exhibiting long-range collective behavior.47 It has garnered significant attention as a promising source for generating THz electromagnetic wave, primarily due to the ease with which its free charge particles can be readily accelerated by external electric or magnetic fields. Considering plasma as a source for electromagnetic radiation with a specific frequency would probably not be that surprising, as Hertz's experiment confirmed the existence of EM wave from spark-discharge plasmas a long time ago, in 1887.48 However, it can be asserted that pulsed laser-based plasma in the realm of THz EM wave generation undeniably possesses novelty.Hamster et al.49,50 have achieved successful generation of THz EM waves from high-density plasma (1018–1023 cm−3) generated by femtosecond pulse lasers in 1993. The interaction of intense femtosecond pulse lasers with materials, at intensities typically exceeding 1012 W cm−2, results in the ionization of the material, transitioning it into a is damage-free plasma state. This process leads to the generation of THz radiation through the interaction between the generated plasma and the incident laser. It showcases the success achieved through the creation of high-density plasma by intense lasers and the acceleration of free electrons up to the THz frequency via femtosecond pulses. Following the success of Hamster et al., numerous studies have reported on the generation of THz radiation through femtosecond pulse laser–plasma interactions.51–57
As summarized in Fig. 5, research so far has predominantly classified the state of the laser target medium—gas, liquid, or solid. Various mechanisms for THz generation via the interaction between plasma and lasers have been proposed depending on the nature of the target medium. For gas plasma, direct THz generation is attributed to electron acceleration by laser ponderomotive force and wakefield effects.49,58,59 In the case of liquid media, THz generation is interpreted through the formation of electric dipoles between electrons and ionized liquid molecules under laser ponderomotive force and space charge field.60–62 In solid plasma, THz generation is explained by transient dipoles induced by transient currents of sideband electrons at the incident surface and forward transient electron bunch currents,63–65 as well as ion acceleration in the plasma sheath formed by electron bunches exiting the rear side.66 While diverse mechanisms are proposed based on different media, they can all still be understood from a classical electromagnetic wave generation point of view, such as transient currents of free electrons, jTHz, or electric displacement.
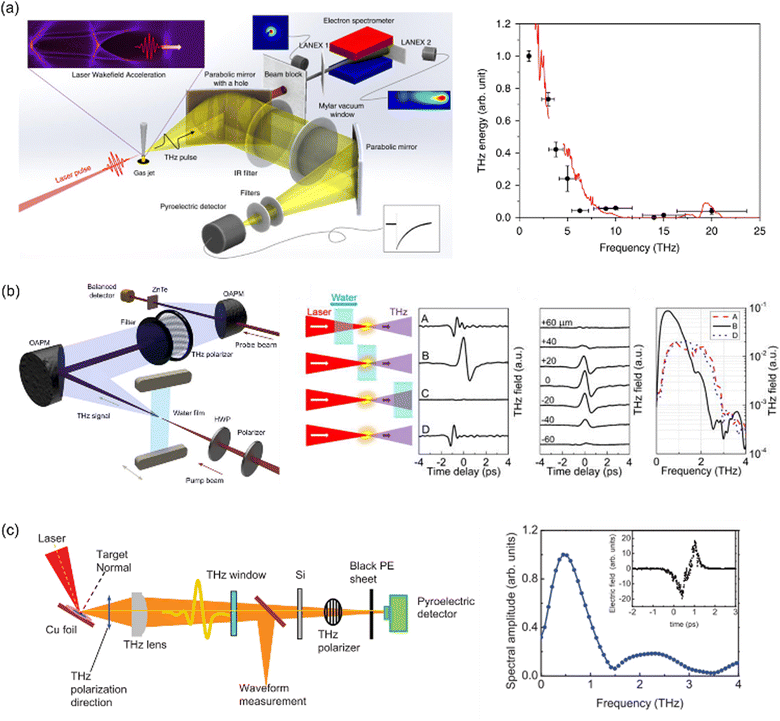 | ||
| Fig. 5 (a) The laser pulse ionizes a gas jet and accelerates plasma electrons via a laser wakefield accelerator, simultaneously generating THz radiation and discrete THz spectrum characterized with bandpass filters for the pure nitrogen gas target. Reproduced from ref. 59 with permission from Springer Nature, copyright 2023. (b) Broadband THz wave is generated by tightly focusing the optical laser beam into a gravity-driven wire-guided free-flowing water film and measurements of the THz fields when the water film is translated along the direction of laser propagation. Reproduced from ref. 62 with permission from AIP publishing, copyright 2017. (c) Schematic experiment set up of the THz generation from relativistic laser focused solid target and normalized spectrum of the THz radiation. The inset is the temporal waveform measured by a single-shot electric-optic sampling method. Reproduced from ref. 64 with permission from AIP publishing, copyright 2012. | ||
To obtain high-energy THz from the interaction between plasma and laser, the formation of a high-density plasma is first required, necessitating the use of intense lasers and preferably solid media over low-density gases. While gas targets have reported up to ∼0.185 mJ of THz emission,52 employing ultra-high-intensity femtosecond pulse lasers on solid targets has yielded around ∼55 mJ of THz emission.55 However, using solid targets for plasma generation poses challenges due to target destruction from intense laser irradiation, resulting in unstable plasma states, which hinders reliable THz generation. In contrast, while gas targets offer lower density, their refreshability allows for the formation of stable plasma, ensuring consistent reliability in THz emission. As a compromise between the advantages and disadvantages of gas and solid targets, liquid targets with higher density and potentially improved plasma stability have been considered. Yet, current efficiency levels of THz generation from liquid targets stand at around 0.08 mJ,54 highlighting the need for further enhancements in efficiency.
Moving towards high-power THz emission, solid plasma sources are preferable as they produce high plasma density. However, for stability and fidelity, gaseous sources have advantages. In between them lie liquid sources, and an optimized design would involve a mixture of gas and liquid or liquid and solid.
Recent reports have introduced the generation of THz radiation from plasma sources beyond the traditional pulse laser-induced plasma. L. H. Cao et al.67 theoretically proposed that by applying a rotational motion akin to cyclotron motion to a cylindrical plasma via radial electric fields and axial magnetic fields, THz generation could be achievable. Additionally, M. S. Nikoo et al.68 reported that 0.1 THz pulses, reaching 600 mW, were emitted from nano-plasmas formed when gases undergo insulator breakdown in nano-gaps.
(4) THz generation by laser-induced acoustic wave
Theoretically proposed and experimentally realized about 15 years ago by scientists from Lawrence Livermore National Laboratory (LLNL), the coherent generation of THz waves from crystalline polarizable materials via a compressive shock wave has not yet been thoroughly investigated after its initial observation.69–71 Here, in this review, we revisit this mechanism of THz generation, which is distinct from others, leveraging the nonlinear mechanical acoustic response of a material, i.e., not relying on optical excitation.Strong dynamic compression over long (>ns time scales) typically destroys the compressed material subsequent to release, via dissipative heating, phase transitions (where possible), and disassembly.72 For shock wave compression, strong anisotropically applied stress and associated elastic strain exceeds the yield strength and plastic deformation occurs. Dissipative energy is generated by plastic work, heating the material, and the interaction of release waves internal to the material leads to regions of tension and material disassembly (spall). On picosecond time scales, kinetics may limit the plastic work which can happen over the time scale of compression. In this case, compression stress/strain may substantially exceed the static yield strength without generating dissipation, up to strains of at least 1%.73 Similarly, coherent phase transitions (such as the martensitic phase transition in Fe) have been observed to recover to the initial state even subsequent to strong shock compression.74
When a shock wave impacts materials, it is often considered a destructive process that endangers atomic and molecular bonding.71 However, it could be reversible, i.e., materials remain undamaged after the shock, maintaining their original crystal structures if the shock wave process involves small strain amplitudes, less than 1%, and occurs in very short durations, on the order of a few picoseconds. These requirements of amplitudes and durations are difficult to control using other means such as bullets and cannons. However, femtosecond lasers with short pulses of millijoules can sufficiently generate shock waves in materials under control, providing a potential pathway for the continuous generation of THz waves. It is important to note that femtosecond lasers are not strictly necessary for generation; rather, they are convenient due to their initially fast rise times and suitability for electro-optic sampling techniques.
When a charged particle traverses an interface between two dielectric materials, a coherent EM wave can be generated. This phenomenon is known as transition radiation. Similarly, when a shock wave crosses an interface between materials with two different piezoelectric coefficients (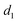 and
and 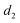 ), ‘acoustic transition radiation’ can be generated. This phenomenon was theoretically predicted using molecular dynamic simulations with the AlN/GaN system and experimentally verified through pump–probe measurements. Here, polarization currents are directly associated with the stress profile,
), ‘acoustic transition radiation’ can be generated. This phenomenon was theoretically predicted using molecular dynamic simulations with the AlN/GaN system and experimentally verified through pump–probe measurements. Here, polarization currents are directly associated with the stress profile, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) zz = (w,
zz = (w, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) l), and thus, the generated far-field electric field also has direct relevance, as follows:
l), and thus, the generated far-field electric field also has direct relevance, as follows:
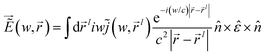 | (3) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) at point
at point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) l on the interface.70Fig. 6(a) shows good agreement between strain rate and simulated electric field. This was calculated for a flat 25 μm diameter shock front under the assumption of no effect of acoustic wave propagation at the GaN/AlN interface, which is quite valid when it is sufficiently thin and atomically sharp. One of the most notable highlights of this simulation is that the emitted terahertz radiation can contain spectral information with atomic-scale resolution of the wave, as indicated by the signal around the fundamental frequency of 4 THz and its harmonics around 8 THz (Fig. 6(b)).
l on the interface.70Fig. 6(a) shows good agreement between strain rate and simulated electric field. This was calculated for a flat 25 μm diameter shock front under the assumption of no effect of acoustic wave propagation at the GaN/AlN interface, which is quite valid when it is sufficiently thin and atomically sharp. One of the most notable highlights of this simulation is that the emitted terahertz radiation can contain spectral information with atomic-scale resolution of the wave, as indicated by the signal around the fundamental frequency of 4 THz and its harmonics around 8 THz (Fig. 6(b)).
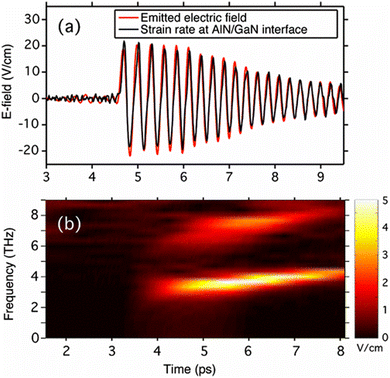 | ||
| Fig. 6 (a) The strain rate observed in a simulation at an AlN/GaN interface is compared to the electric field. (b) The frequency of electromagnetic radiation is plotted against time. Reproduced from ref. 70 with permission from American Physical Society, copyright 2008. | ||
Not only theoretically, but experimentally, the generation of THz radiation was observed using a pump–probe measurement setup (Fig. 7(a)) employing femtosecond lasers and electro-optic sampling with a 〈110〉 ZnTe crystal.69 Here, the sample is Al-coated GaN/AlN, which is tilted 45 degrees to both the pump and probe beams. The pump beam is incident on the Al-coated side, and the acoustic wave is generated by the fast (∼3.5 ps) thermal expansion of Al, with a maximum strain of ∼0.01. As predicted, when the acoustic wave crosses the interfaces (Al/GaN and GaN/AlN), THz radiation generation was observed, which was readily confirmed by simulation of the acoustic profile (Fig. 7(b)). It should be noted that since the experiments were conducted below the damage threshold, this is a non-destructive method, and the data were obtained by averaging multiple shots.
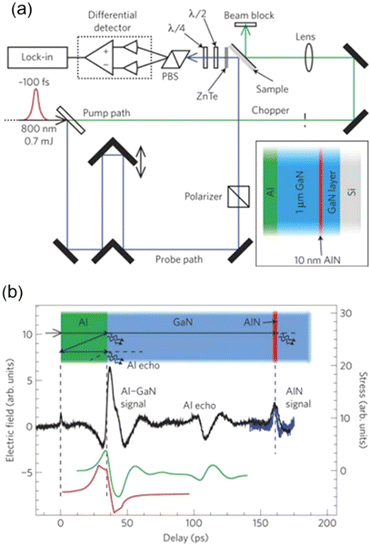 | ||
| Fig. 7 (a) Schematic diagram illustrating the THz experimental setup employing acoustic pump–probe measurement. (b) Measured electric field by electro-optic sampling (black), and stress calculated from the electric field (green) compared to the stress from a simulation of the acoustic profile (red). Reproduced from ref. 69 with permission from Springer Nature, copyright 2009. | ||
The coupling between radiation modes and induced polarization currents is one of the most important factors that should be considered for practical applications. To achieve sufficient results, the higher piezoelectric tensor direction of the materials and compressive strain should be matched. Additionally, an angled incident pump beam would be required for directional THz radiation. As predicted, hundreds of V cm−1 of electric field could be emitted, which is far higher than in the case of normal incidence pump beam, where it is only on the order of tens of V cm−1.
Conclusion and future work
In this review, we examine several important and distinct mechanisms for generating THz electromagnetic waves from femtosecond lasers.Over the past few decades, significant advancements in efficiency have been made in nonlinear optics, achieving up to three orders of magnitude improvement using various techniques such as TPFP, contact gratings, metasurfaces, and novel organic/inorganic crystals or emerging semiconductors. Additionally, the development of long-wavelength infrared lasers has contributed to enhancing the THz field strength, showing huge potential for high-power THz sources.
Efforts have also been focused on comprehending the behaviour of time-transient photocurrent in semiconductors for THz antennas, employing 3D electrodes, and designing various resonant subwavelength structural antennas to achieve enhanced performance.
The femtosecond laser-based pulse plasma technology has offered a versatile means of generating high-output THz electromagnetic waves from any medium capable of attaining a plasma state, irrespective of the material's electronic and crystal structure. Nonetheless, this technology encounters challenges in achieving high-output THz EM waves due to the low efficiency of plasma generation via laser and the consequential damage to the target material under high-energy laser irradiation. Hence, it appears necessary to integrate well-developed, high-efficiency plasma generation technologies such as magnetron plasma or hollow cathode plasma with it. Another approach would be to increase the plasma volume within which electron acceleration should occur in picosecond time scales. To achieve this, two methods could be considered for implementation: (1) micro-lens array and (2) beam shaping. The strength of the THz output should linearly increase as the number of plasma filaments increases.75 Programmable modulation of the phase distribution and spatial distribution using a spatial light modulator (SLM) will also enable optimized manipulation of the length, position, and electron density of the plasma filament to improve terahertz output.76
Acoustic transient radiation represents an intriguing area that utilizes lasers without direct optical excitation. In this exemplary work, only piezoelectric materials have been investigated; however, other strongly correlated materials such as ferroelectrics, ferromagnets, superconductors, and/or superlattice structures could be of interest, offering the potential for breakthroughs.77,78
Furthermore, emerging technologies with high potential include a quantum cascade mid-infrared laser-pumped molecular THz laser employing methyl fluoride gas in a cavity.79 This could be exploited for optical rectification or other categories of THz sources with a synergistic effect. Quantum cascade lasers in the THz range themselves would also be quite promising if they are well equipped with a wide range of frequency tunability.
Author contributions
WJC managed the project administration. WJC, MRA, JHY, and TIL participated in writing the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. W. J. C. gratefully acknowledge the LLNL LDRD Programs for funding support of this project under no. 22-ERD-056 and 24-LW-035.References
- J. A. Fülöp, S. Tzortzakis and T. Kampfrath, Adv. Opt. Mater., 2020, 8, 1900681, DOI:10.1002/adom.201900681.
- S. Mansourzadeh, T. Vogel, A. Omar, T. O. Buchmann, E. J. R. Kelleher, P. U. Jepsen and C. J. Saraceno, Opt. Mater. Express, 2023, 13, 3287 CrossRef CAS.
- W. J. Choi, S. H. Lee, B. C. Park and N. Kotov, J. Am. Chem. Soc., 2022, 144(50), 22789–22804, DOI:10.1021/jacs.2c04817.
- C. G. Wade, N. Šibalić, N. R. de Melo, J. M. Kondo, C. S. Adams and K. J. Weatherill, Nat. Photonics, 2017, 11, 40–43 CrossRef CAS.
- C. Meineke, J. Schlosser, M. Zizlsperger, M. Liebich, N. Nilforoushan, K. Mosina, S. Terres, A. Chernikov, Z. Sofer, M. A. Huber, M. Florian, M. Kira, F. Dirnberger and R. Huber, Nano Lett., 2024, 24(14), 4101–4107, DOI:10.1021/acs.nanolett.3c05010.
- X. Yang, X. Zhao, K. Yang, Y. Liu, Y. Liu, W. Fu and Y. Luo, Trends Biotechnol., 2016, 34, 810 CrossRef CAS PubMed.
- Q. Sun, Y. He, K. Liu, S. Fan, E. P. J. Parrott and E. Pickwell-MacPherson, Quant. Imaging Med. Surg., 2017, 7, 345 CrossRef PubMed.
- W. J. Choi, G. Cheng, Z. Huang, S. Zhang, T. B. Norris and N. A. Kotov, Nat. Mater., 2019, 18, 820–826, DOI:10.1038/s41563-019-0404-6.
- J. Xu, G. J. Ramian, J. F. Galan, P. G. Savvidis, A. M. Scopatz, R. R. Birge, S. J. Allen and K. W. Plaxco, Astrobiology, 2003, 3, 489 CrossRef CAS PubMed.
- P. Salén, M. Basini, S. Bonetti, J. Hebling, M. Krasilnikov, A. Y. Nikitin, G. Shamuilov, Z. Tibai, V. Zhaunerchyk and V. Goryashko, Phys. Rep., 2019, 1, 836–837 Search PubMed.
- S. F. Maehrlein, I. Radu, P. Maldonado, A. Paarmann, M. Gensch, A. M. Kalashnikova, R. V. Pisarev, M. Wolf, P. M. Oppeneer, J. Barker and T. Kampfrath, Sci. Adv., 2018, 4, eaar5164, DOI:10.1126/sciadv.aar5164.
- O. A. Smolyanskaya, N. V. Chernomyrdin, A. A. Konovko, K. I. Zaytsev, I. A. Ozheredov, O. P. Cherkasova, M. M. Nazarov, J.-P. Guillet, S. A. Kozlov, Yu. V. Kistenev, J.-L. Coutaz, P. Mounaix, V. L. Vaks, J.-H. Son, H. Cheon, V. P. Wallace, Yu Feldman, I. Popov, A. N. Yaroslavsky, A. P. Shkurinov and V. V. Tuchin, Prog. Quantum Electron., 2018, 62, 1–17 CrossRef.
- O. P. Cherkasova, D. S. Serdyukov, E. F. Nemova, A. S. Ratushnyak, A. S. Kucheryavenko, I. N. Dolganova, G. Xu, M. Skorobogatiy, I. V. Reshetov, P. S. Timashev, I. E. Spektor, K. I. Zaytsev and V. V. Tuchin, J. Biomed. Opt., 2021, 26, 090902 Search PubMed.
- Z. Zang, J. Wang, H.-L. Cui and S. Yan, Plant Methods, 2019, 15, 106 CrossRef PubMed.
- M. R. Armstrong, E. J. Reed, K.-Y. Kim, J. H. Glownia, W. M. Howard, E. L. Piner and J. C. Roberts, Nat. Phys., 2009, 5, 285 Search PubMed.
- M. Mukherjee, N. Mazumder, S. K. Roy and K. Goswami, Semicond. Sci. Technol., 2007, 22, 1258 CrossRef CAS.
- A. Acharyya and J. P. Banerjee, Appl. Nanosci., 2014, 4, 1 CrossRef CAS.
- Y. He, Y. Chen, L. Zhang, S.-W. Wong and Z. N. Chen, China Commun., 2020, 17, 124 Search PubMed.
- Vacuum Electronics, ed. J. A. Eichmeier, M. K. Thumm, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008 Search PubMed.
- R. K. Verma, S. Maurya and V. V. P. Singh, J. Electromagn. Waves Appl., 2018, 32, 113 CrossRef.
- S. Mansourzadeh, T. Vogel, A. Omar, M. Shalaby, M. Cinchetti and C. J. Saraceno, APL Photonics, 2023, 8, 011301, DOI:10.1063/5.0126367.
- S. Mansourzadeh, T. Vogel, M. Shalaby, F. Wulf and C. J. Saraceno, Opt. Express, 2021, 29, 38946 CrossRef CAS PubMed.
- T. O. Buchmann, E. J. Railton Kelleher, M. Jazbinsek, B. Zhou, J.-H. Seok, O.-P. Kwon, F. Rotermund and P. U. Jepsen, APL Photonics, 2020, 5, 106103, DOI:10.1063/5.0022762.
- G. A. Valdivia-Berroeta, Z. B. Zaccardi, S. K. F. Pettit, (Enoch) S.-H. Ho, B. W. Palmer, M. J. Lutz, C. Rader, B. P. Hunter, N. K. Green, C. Barlow, C. Z. Wayment, D. J. Ludlow, P. Petersen, S. J. Smith, D. J. Michaelis and J. A. Johnson, Adv. Mater., 2022, 34, 2107900, DOI:10.1002/adma.202107900.
- S.-J. Kim, I. C. Yu, J.-A. Lee, W. T. Kim, M. Jazbinsek, W. Yoon, H. Yun, F. Rotermund and O.-P. Kwon, Dyes Pigm., 2021, 192, 109433 CrossRef CAS.
- I. E. Ilyakov, G. K. Kitaeva, B. V. Shishkin and R. A. Akhmedzhanov, Laser Phys. Lett., 2018, 15, 125401 CrossRef CAS.
- A. G. Stepanov, J. Hebling and J. Kuhl, Appl. Phys. Lett., 2003, 83, 3000 CrossRef CAS.
- K. H. Yang, P. L. Richards and Y. R. Shen, Appl. Phys. Lett., 1971, 19, 320 CrossRef CAS.
- Gy Polónyi, B. Monoszlai, G. Gäumann, E. J. Rohwer, G. Andriukaitis, T. Balciunas, A. Pugzlys, A. Baltuska, T. Feurer, J. Hebling and J. A. Fülöp, Opt. Express, 2016, 24, 23872 CrossRef PubMed.
- C. Gollner, M. Shalaby, C. Brodeur, I. Astrauskas, R. Jutas, E. Constable, L. Bergen, A. Baltuška and A. Pugžlys, APL Photonics, 2021, 6, 046105 CrossRef CAS.
- J. A. Fülöp, Gy Polónyi, B. Monoszlai, G. Andriukaitis, T. Balciunas, A. Pugzlys, G. Arthur, A. Baltuska and J. Hebling, Optica, 2016, 3, 1075 CrossRef.
- H. Jung, L. L. Hale, S. D. Gennaro, J. Briscoe, P. P. Iyer, C. F. Doiron, C. T. Harris, T. S. Luk, S. J. Addamane, J. L. Reno, I. Brener and O. Mitrofanov, Nano Lett., 2022, 22, 9077 CrossRef CAS PubMed.
- H. Wang, Y. Zhou, Z. Yao, L. Zhu, Y. Huang, X. Xu and Z. Ren, Carbon N. Y., 2018, 134, 439 CrossRef CAS.
- J. Maysonnave, S. Huppert, F. Wang, S. Maero, C. Berger, W. de Heer, T. B. Norris, L. A. De Vaulchier, S. Dhillon, J. Tignon, R. Ferreira and J. Mangeney, Nano Lett., 2014, 14, 5797 CrossRef CAS PubMed.
- Y.-M. Bahk, G. Ramakrishnan, J. Choi, H. Song, G. Choi, Y. H. Kim, K. J. Ahn, D.-S. Kim and P. C. M. Planken, ACS Nano, 2014, 8, 9089 CrossRef CAS PubMed.
- L. Zhu, Y. Huang, Z. Yao, B. Quan, L. Zhang, J. Li, C. Gu, X. Xu and Z. Ren, Nanoscale, 2017, 9, 10301 RSC.
- B. W. H. Palmer, C. Rader, E. S.-H. Ho, Z. B. Zaccardi, D. J. Ludlow, N. K. Green, M. J. Lutz, A. Alejandro, M. F. Nielson, G. A. Valdivia-Berroeta, C. C. Chartrand, K. M. Holland, S. J. Smith, J. A. Johnson and D. J. Michaelis, ACS Appl. Electron. Mater., 2022, 4, 4316 CrossRef CAS.
- C.-L. Tsai, F. Meyer, A. Omar, Y. Wang, A.-Y. Liang, C.-H. Lu, M. Hoffmann, S.-D. Yang and C. J. Saraceno, Opt. Lett., 2019, 44, 4115 CrossRef CAS PubMed.
- N. M. Burford and M. O. El-Shenawee, Opt. Eng., 2017, 56, 010901 CrossRef.
- D. R. Bacon, J. Madéo and K. M. Dani, J. Opt., 2021, 23, 064001 CrossRef.
- E. Budiarto, J. Margolies, S. Jeong, J. Son and J. Bokor, IEEE J. Quantum Electron., 1996, 32, 1839 CrossRef CAS.
- T. Hattori, K. Egawa, S. Ookuma and T. Itatani, Jpn. J. Appl. Phys., 2006, 45, L422 CrossRef CAS.
- S. Lepeshov, A. Gorodetsky, A. Krasnok, N. Toropov, T. A. Vartanyan, P. Belov, A. Alú and E. U. Rafailov, Sci. Rep., 2018, 8, 6624 CrossRef PubMed.
- T. V. Kononenko, K. K. Ashikkalieva, V. V. Kononenko, E. V. Zavedeev, M. A. Dezhkina, M. S. Komlenok, E. E. Ashkinazi, V. V. Bukin and V. I. Konov, Photonics, 2023, 10, 75 CrossRef CAS.
- A. Singh, A. Pashkin, S. Winnerl, M. Welsch, C. Beckh, P. Sulzer, A. Leitenstorfer, M. Helm and H. Schneider, Light: Sci. Appl., 2020, 9, 30 CrossRef CAS PubMed.
- S.-H. Yang, M. R. Hashemi, C. W. Berry and M. Jarrahi, IEEE Trans. Terahertz Sci. Technol., 2014, 4, 575 Search PubMed.
- A. Piel, Plasma Physics: An Introduction to Laboratory, Space, and Fusion Plasmas, Springer Science & Business Media, 2010 Search PubMed.
- H. R. Hertz, Untersuchungen Ueber Die Ausbreitung Der Elektrischen Kraft, Johann Ambrosius Barth, 1892 Search PubMed.
- H. Hamster, A. Sullivan, S. Gordon, W. White and R. W. Falcone, Phys. Rev. Lett., 1993, 71, 2725 CrossRef CAS PubMed.
- H. Hamster, A. Sullivan, S. Gordon and R. W. Falcone, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 671 CrossRef CAS PubMed.
- K. Y. Kim, A. J. Taylor, J. H. Glownia and G. Rodriguez, Nat. Photonics, 2008, 2, 605 CrossRef CAS.
- A. D. Koulouklidis, C. Gollner, V. Shumakova, V. Yu Fedorov, A. Pugžlys, A. Baltuška and S. Tzortzakis, Nat. Commun., 2020, 11, 292 CrossRef CAS PubMed.
- A. Pukhov, A. Golovanov and I. Kostyukov, Phys. Rev. Lett., 2021, 127, 175001 CrossRef CAS PubMed.
- I. Dey, K. Jana, V. Yu Fedorov, A. D. Koulouklidis, A. Mondal, M. Shaikh, D. Sarkar, A. D. Lad, S. Tzortzakis, A. Couairon and G. R. Kumar, Nat. Commun., 2017, 8, 1184 CrossRef PubMed.
- G. Liao, Y. Li, H. Liu, G. G. Scott, D. Neely, Y. Zhang, B. Zhu, Z. Zhang, C. Armstrong, E. Zemaityte, P. Bradford, P. G. Huggard, D. R. Rusby, P. McKenna, C. M. Brenner, N. C. Woolsey, W. Wang, Z. Sheng and J. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3994 CrossRef CAS PubMed.
- Z. Jin, H. B. Zhuo, T. Nakazawa, J. H. Shin, S. Wakamatsu, N. Yugami, T. Hosokai, D. B. Zou, M. Y. Yu, Z. M. Sheng and R. Kodama, Phys. Rev. E, 2016, 94, 033206 CrossRef CAS PubMed.
- Y. Zeng, C. Zhou, L. Song, X. Lu, Z. Li, Y. Ding, Y. Bai, Y. Xu, Y. Leng, Y. Tian, J. Liu, R. Li and Z. Xu, Opt. Express, 2020, 28, 15258 CrossRef CAS PubMed.
- W. P. Leemans, C. G. R. Geddes, J. Faure, Cs Tóth, J. van Tilborg, C. B. Schroeder, E. Esarey, G. Fubiani, D. Auerbach, B. Marcelis, M. A. Carnahan, R. A. Kaindl, J. Byrd and M. C. Martin, Phys. Rev. Lett., 2003, 91, 074802 CrossRef CAS PubMed.
- T. Pak, M. Rezaei-Pandari, S. B. Kim, G. Lee, D. H. Wi, C. I. Hojbota, M. Mirzaie, H. Kim, J. H. Sung, S. K. Lee, C. Kang and K.-Y. Kim, Light: Sci. Appl., 2023, 12, 37 CrossRef CAS PubMed.
- H. Wang and T. Shen, Appl. Phys. Lett., 2020, 117, 131101 CrossRef CAS.
- Y. E, Q. Jin, A. Tcypkin and X.-C. Zhang, Appl. Phys. Lett., 2018, 113, 181103 CrossRef.
- Q. Jin, Y. E, K. Williams, J. Dai and X.-C. Zhang, Appl. Phys. Lett., 2017, 111, 071103 CrossRef.
- C. Li, G.-Q. Liao, M.-L. Zhou, F. Du, J.-L. Ma, Y.-T. Li, W.-M. Wang, Z.-M. Sheng, L.-M. Chen and J. Zhang, Opt. Express, 2016, 24, 4010 CrossRef CAS PubMed.
- Y. T. Li, C. Li, M. L. Zhou, W. M. Wang, F. Du, W. J. Ding, X. X. Lin, F. Liu, Z. M. Sheng, X. Y. Peng, L. M. Chen, J. L. Ma, X. Lu, Z. H. Wang, Z. Y. Wei and J. Zhang, Appl. Phys. Lett., 2012, 100, 254101 CrossRef.
- Y. T. Li, X. H. Yuan, M. H. Xu, Z. Y. Zheng, Z. M. Sheng, M. Chen, Y. Y. Ma, W. X. Liang, Q. Z. Yu, Y. Zhang, F. Liu, Z. H. Wang, Z. Y. Wei, W. Zhao, Z. Jin and J. Zhang, Phys. Rev. Lett., 2006, 96, 165003 CrossRef CAS PubMed.
- A. Macchi, M. Borghesi and M. Passoni, Rev. Mod. Phys., 2013, 85, 751 CrossRef CAS.
- L. H. Cao, W. Yu, M. Y. Yu and C. Y. Yu, Laser Part. Beams, 2021, 2021, e17, DOI:10.1155/2021/6666760.
- M. Samizadeh Nikoo, A. Jafari, N. Perera, M. Zhu, G. Santoruvo and E. Matioli, Nature, 2020, 579, 534 CrossRef CAS PubMed.
- M. R. Armstrong, E. J. Reed, K.-Y. Kim, J. H. Glownia, W. M. Howard, E. L. Piner and J. C. Roberts, Nat. Phys., 2009, 5, 285 Search PubMed.
- E. J. Reed, M. R. Armstrong, K.-Y. Kim and J. H. Glownia, Phys. Rev. Lett., 2008, 101, 014302 CrossRef PubMed.
- E. J. Reed, M. R. Armstrong, K. Kim, M. Soljačić, R. Gee, J. H. Glownia and J. D. Joannopoulos, Mater. Today, 2007, 10, 44 CrossRef CAS.
- W. J. Nellis, Rep. Prog. Phys., 2006, 69, 1479 CrossRef CAS.
- J. C. Crowhurst, M. R. Armstrong, K. B. Knight, J. M. Zaug and E. M. Behymer, Phys. Rev. Lett., 2011, 107, 144302 CrossRef PubMed.
- D. H. Kalantar, J. F. Belak, G. W. Collins, J. D. Colvin, H. M. Davies, J. H. Eggert, T. C. Germann, J. Hawreliak, B. L. Holian, K. Kadau, P. S. Lomdahl, H. E. Lorenzana, M. A. Meyers, K. Rosolankova, M. S. Schneider, J. Sheppard, J. S. Stölken and J. S. Wark, Phys. Rev. Lett., 2005, 95, 075502 CrossRef CAS PubMed.
- K. Bai, Y. Gou and X.-Y. Peng, AIP Adv., 2022, 12, 095113 CrossRef.
- Y. Feng, R. Wang, M. Gao, X. Qu, H. Ruan and Z. Zhang, Infrared, Millimeter-Wave, and Terahertz Technologies X, ed. Y. E., M. Tani, C. Zhang, SPIE, 2023, vol. 12776, p. 47 DOI:10.1117/12.2685819.
- R. Cattaneo, E. A. Borodianskyi, A. A. Kalenyuk and V. M. Krasnov, Phys. Rev. Appl., 2021, 16, L061001 CrossRef CAS.
- Y. Okamura, H. Handa, R. Yoshimi, A. Tsukazaki, K. S. Takahashi, M. Kawasaki, Y. Tokura and Y. Takahashi, npj Quantum Mater., 2022, 7, 91 CrossRef CAS.
- A. Amirzhan, P. Chevalier, J. Rowlette, H. T. Stinson, M. Pushkarsky, T. Day, H. O. Everitt and F. Capasso, APL Photonics, 2022, 7, 016107, DOI:10.1063/5.0076310.
| This journal is © The Royal Society of Chemistry 2024 |

