Decoding the domain dynamics of polycrystalline 0.7BiFeO₃–0.3BaTiO₃

Abstract

Despite the extraordinary significance of high-temperature piezoelectric ceramics in engineered systems, understanding their macroscopic electromechanical response in terms of local underlying phenomena, in particular the domain dynamics at elevated temperatures that directly influence the stability of device performance, remains a significant challenge. Here, we investigate the relationship between domain evolution with temperature and its piezoelectric response utilizing 0.7Bi_1.05FeO₃–0.3BaTiO₃ (BF30BT), a critical alternative to lead-based ferroelectrics for high-temperature applications. By analyzing the frequency and loading amplitude-dependent Rayleigh behavior, we are able to demonstrate the importance of the intrinsic contributions in piezoelectric response. The re-entrant relaxor nature of BF30BT results in active locally heterogeneous nanodomains that display reversible rapid response contributions rather than typical extrinsic contributions due to their low activation energy. Decoding the complicated domain dynamics of BF30BT allows for the further integration of microstructures and macroscopic characteristics, guiding the design and utilization of further high-temperature piezoelectric ceramics.

---

1. Introduction

Due to their electromechanical coupling and fast reaction time to an applied electric or stress field, piezoelectric and ferroelectric materials are frequently used as enabling components in a variety of electronic devices. With increasing technical demands, including sustainable development, piezoelectric materials are exposed to more extreme conditions during their use in various applications, especially for stable performance in high-temperature environments, such as aerospace, energy, tool manufacturing, and other industrial applications.^1–3 To date, due to excellent temperature stability and high Curie temperature as well as good electromechanical response, lead-based piezoelectric ceramics dominate the market. However, because of the lack of efficient lead recycling and reuse technology for electronic materials, as well as potential health and environmental hazards of lead, there has been a concerted effort to develop lead-free piezoelectric materials as an alternative to lead-based ceramics. Although much focus has been placed on optimizing and understanding the small- and large-signal piezoelectric response, one area in which lead-free ferroelectrics have excelled in comparison to lead-containing systems is in high temperature stability.⁴ Among the various lead-free candidates, bismuth-layered materials have been widely studied because of their extremely high Curie temperature T_C (∼900 °C) and outstanding temperature-stable electromechanical response, although the relatively small piezoelectric coefficient (∼15 pC N⁻¹) significantly hinders its use in applications.^5,6 A more extreme example is Nd₂Ti₂O₇, which possesses a Curie temperature of up to 1482 °C, possibly the highest of any currently accessible material. However, its complex synthesis process and 2.6 pC N⁻¹ piezoelectric coefficient are severe limitations.⁷ On the other hand, for systems with large piezoelectric signals, such as niobate systems represented by (K,Na)NbO₃, Wu et al. induced a relaxor slush polar state near room temperature by multicomponent doping, which enhanced the piezoelectric performance to as high as 650 pC N⁻¹ but substantially deteriorated the T_C (∼190 °C).⁸ Obviously, achieving high piezoelectricity and Curie temperature simultaneously remains a significant challenge.

Bismuth ferrite (BiFeO₃, BF) has received considerable interest as an end member in high-temperature piezoelectric material systems because of the high T_C (∼830 °C) and large spontaneous polarization P_s (∼100 μC cm⁻²).^9,10 In order to overcome the limitations of high coercive field and electrical conductivity found in BiFeO₃,³ binary solid solutions with other perovskite ferroelectrics, such as barium titanate (BaTiO₃, BT), have been introduced.^11,12 BaTiO₃ displays a lower spontaneous polarization that can effectively reduce the energy difference between the ferroelectric phase and the paraelectric phase, which will enhance the electromechanical constitutive behavior while simultaneously decreasing the ferroelectric–paraelectric phase transition temperature and reducing the thermal stability. As such, BiFeO₃–BaTiO₃ (BF–BT) can achieve performance modulation by adjusting the proportion of BT.¹³ Using this concept and with the aid of quenching, Lee et al. reported excellent piezoelectric performance (d₃₃ ∼402 pC N⁻¹) and a high T_C ∼454 °C.¹⁴

Although numerous researchers have tried various methods to further optimize the properties of BF–BT ceramics, one of the effective methods is the regulation of relaxor characteristics,^15,16 which is usually achieved by different types of substitutions, such as A- and B-site dopants (Sm, Nd, La, etc.^17–19), ABO₃-type ((Na_1/2Bi_1/2)TiO₃, NaTaO₃, etc.^20,21), and simple oxides (ZnO₂, MnO₂, TiO₂, etc.^22–24). Such substitutions are understood to break the long-range-ordered ferroelectric structure (LRO) and result in a relaxor ferroelectric structure. Typical relaxor ferroelectrics may be divided into three regions with an increasing temperature: nonergodic state (NE), ergodic state (E), and nonpolar state.^25–27 Here, the Burns temperature T_B separates the nonpolar and ergodic regions, below which the active polar nanoregions (PNRs) will appear. Upon further cooling, the freezing temperature T_f separates the ergodic and nonergodic regions, and PNRs rapidly transform into static ferroelectric domains below T_f.^26,28,29 Therefore, the stability of PNRs is the most significant indicator for distinguishing different relaxor states.

It is worth noting that due to the mismatch of valence and ionic radii between A and B site cations, local nanoscale heterogeneity in the relaxor BF–BT ceramic system is observed,^30,31 primarily manifested as heterogeneous polar regions (NHPRs) represented by nanodomains. It should be emphasized that here, we use nanoscale heterogeneous polar regions (NHPRs) instead of polar nanoregions (PNRs) to describe the local heterogeneity formed by nanoscale chemical and structural heterogeneity.^32,33 The reason is that the concept of PNRs is derived from glass-like materials, which means that the polar regions are embedded in the “nonpolar” matrix. While in many cases, PNRs are embedded in long-range ordered ferroelectric structures, for example, according to TEM observation³⁴ and molecular dynamics (MD) simulations,³⁵ relaxor-PbTiO₃ exhibits significant polarization with a small nonpolar area near room temperature. Based on this, Li et al. previously proposed the concept of NHPRs to predict and explain the high performance of 2.5 mol% Sm-doped 0.71PMN–0.29PT and 0.69PMN–0.31PT ceramics, which seems to be a more appropriate way to describe the local heterogeneity in these systems.³⁶ Numerous investigations have shown that local nanoscale heterogeneity can help to reduce the energy difference between different polarization states and promote the transformation of relaxor ferroelectrics (RFE) into LRO ferroelectrics (FE), which can result in enhanced performance in PMN–PT³⁶ and BNT³⁷ ceramic systems. Interestingly, Kim et al. demonstrated using high-energy synchrotron radiation X-ray diffraction that the nanodomain structure of BF–BT originates from the disordered arrangement of Bi³⁺, which is helpful for domain reorientation.³⁸ Importantly, since Bi³⁺ disorder cannot be completely eliminated by poling, the existence of nanodomains is observed in poled³⁰ and unpoled³¹ systems. In addition, because BF–BT has various potential applications at high temperatures, it is important to study the dynamics of such a domain structure as a function of temperature, but there is currently no relevant published investigation.

Furthermore, from a macroscopic perspective, high-temperature domain dynamics account for just a fraction of the performance of piezoelectric ceramics. The piezoelectric response of multiphase coexisting perovskite ceramics, as is well known, comprises intrinsic and extrinsic contributions. The former can be attributed to lattice contributions in reaction to applied external fields, whereas the latter is caused by domain wall motion or phase boundary motion, which consists of reversible and irreversible elements.³⁹ Under subcoercive external forces, such as electric field and stress, the domain walls are reversibly and irreversibly displaced, without a change in domain wall density expected for large-signal loading. As a result of external field effects, the direct piezoelectric response of ferroelectric materials is often nonlinear and hysteretic under a subcoercive field. This hysteresis follows the Rayleigh relationship with distinct reversible and irreversible coefficients, allowing the proportion of each contribution to be determined by fitting,^40,41 as demonstrated for K_0.5Na_0.5NbO₃,⁴² Bi_1/2K_1/2TiO₃,⁴³ Pb(Zr,Ti)O₃³⁹ as well as other high-performance ceramics.

Therefore, we have investigated the origin of the piezoelectric response at high temperatures in polycrystalline BF-–BT by characterizing the temperature-dependent Rayleigh behavior to better understand how the domain dynamics change with increasing temperature. In this work, polycrystalline 0.7Bi_1.05FeO₃–0.3BaTiO₃ was prepared using the solid-state reaction method with 5 mol% excess Bi to compensate for volatilization during sintering.⁴⁴ This research directly addresses the origins of the electromechanical response in an important high-temperature piezoelectric material, which is critical for implementation in applications, as their temperature-dependent performance determines device stability and reliability. Macroscopic experimental data are contrasted with in situ temperature-dependent X-ray diffraction to evaluate domain morphology and analyze changes in the powder structure throughout the heating process. The combination of studies at different scales is conducive to a more in-depth and thorough analysis of materials, which is critical for the preparation of high-performance BF–BT ceramics and their practical applications.

2. Experimental methodology

Polycrystalline 0.7Bi_1.05FeO₃–0.3BaTiO₃ (BF30BT) ceramics were synthesized by a solid-state reaction method. Analytically pure powders of Bi₂O₃ (99%, Alfa Aesar, Germany), Fe₂O₃ (99.9%, ThermoFisher GmbH, Germany), TiO₂ (99.6%, Alfa Aesar, Germany), and BaCO₃ (99.8%, Alfa Aesar, Germany) were dried overnight in an oven at 120 °C to remove moisture, weighed, and then mixed with the required stoichiometric ratio in a glove box with a relative humidity of <10%. Previous studies have reported on the utilization of Bi₂O₃ with purities ranging from 99% to 99.99% in the synthesis of BF–BT ceramics, with a large portion of the ceramics exhibiting second phase Bi₂₅FeO₄₀. Perhaps, after the purity of Bi₂O₃ reached a certain level, impurity elements like Si and Al did not play a significant role in the emergence of the secondary phase.^3,45 Raw material powders were subsequently ball-milled for 24 h using zirconia balls (5 mm) in absolute ethanol, dried using a rotary evaporator, and calcined at a heating rate of 5 K min⁻¹ at 700 °C for 2 h. Following this, the calcined powders were ball-milled in ethanol for an additional 24 h. After drying, the powders were uniaxially pressed to form cylinders with a diameter of 10.2 mm and a height of 10 mm and then cold isostatically pressed at 180 MPa. The cylinders were sintered at 980 °C for 3 h at a heating rate of 5 K min⁻¹ and a cooling rate of 1 K min⁻¹. During sintering, the BF–BT sample was embedded in sacrificial calcinated BF–BT powder. The sintered samples were ground into cylinders with a diameter of 5.8 mm (±0.02 mm) and a height of 6 mm (±0.02 mm) using a surface grinder. An annealing step at 450 °C for 2 h, with a heating and cooling rate of 5 K min⁻¹, was used after sample preparation to relieve the residual stresses induced by machining. Subsequently, Pt electrodes were sputtered on both circular faces of the cylinder, and the samples were poled in silicone oil (AK200, Wacker) under a DC electric field of 2.5 kV mm⁻¹ for 30 min at 100 °C, followed by field cooling to room temperature.

Density was measured using Archimedes’ method with distilled water, and the three samples were weighed under the same conditions. Scanning electron microscopy (SEM, Quanta 200, FEI) was used to determine the microstructures of the sectioned samples. The average grain size was calculated by characterizing the grain area to obtain the equivalent grain diameter. For this purpose, five images were considered, and at least 500 grains were measured.

After crushing the sintered bulk ceramics into powder and annealing at 500 °C for 2 h, diffraction data were collected for crystal structure analysis using an X’ Pert Pro MPD (DY120 PANalytical) equipped with a Cu X-ray source (λKα₁/λKα₂ = 1.540598/1.544426). Diffraction data were collected in the 2θ range of 10° to 70° with a step size of 0.01° and a counting time of 10 s per step. The same measurement parameters were used for the in situ temperature-dependent measurements. A heating rate of 10 K min⁻¹, and a temperature stabilization time of 5 min were used at each target temperature. The MAUD program was employed to refine XRD data.⁴⁶

The temperature-dependent dielectric properties were measured on the cylindrical samples from room temperature to 550 °C (2 K min⁻¹ heating and cooling rate) over a frequency range from 100 Hz to 1 MHz in an oven (LE 4/11/3216, Nabertherm) equipped with a custom-built sample holder and an LCR meter (Keysight 4980 AL, USA) controlled by a custom LabView control and analysis program.

Piezoelectric force microscopy (PFM) measurements were performed using an atomic force microscope (MFP-3D, Asylum Research, Goleta, CA) in out-of-plane mode with a scanning speed of f = 1 Hz and a scanning AC voltage of 3 V.

The room-temperature piezoelectric constant (d₃₃) was measured 24 h after poling with a Berlincourt meter (PiezoMeter System PM300, Piezotest Ltd) using a bias mechanical force of 10.2 N and a frequency of 110 Hz. Temperature-dependent d₃₃ and permittivity measurements were carried out from −150 °C to 400 °C with frequencies ranging from 0.5–140 Hz and 100 Hz to 1 MHz, respectively, using a custom-built setup comprised of a modified screw-type load frame (5967, Instron) and a thermal chamber cooled with liquid nitrogen.⁴⁷ Inside the chamber, samples were placed on polished tungsten carbide bearings that allow electrical contact, and a piezoelectric stack actuator (P-025.80, PI Ceramics GmbH) was used to apply a constant stress amplitude of ±0.5 MPa at different frequencies ranging from 0.5 to 140 Hz. Rayleigh behavior was measured by varying the stress amplitude between ±0.5 and ±5 MPa with a pre-stress of −15 MPa from 25 °C to 400 °C and a constant frequency of 10 Hz. A preload was required in order to ensure that mechanical and electrical contacts were maintained throughout the measurements for all applied stress amplitudes.

3. Results and discussion

To ensure the reliability and repeatability of the experimental results, the room-temperature structure of BF30BT was characterized using XRD to assess the quality of samples, as shown in Fig. 1a. The diffraction patterns are in good agreement with the perovskite structure, but a minor Bi₂O₃-rich impurity phase Bi₂₅FeO₄₀ (ICSD#62719) was observed, which has been mentioned in other studies.^48,49 Typically, the structure of BF–BT is characterized by distinctive peaks at 110_pc, 111_pc, and 200_pc, where cluster peaks rather than clear peak splitting indicate a multiphase state. To explore the phase composition of BF30BT ceramics, the R_BF phase (ICSD#15299, R3c) and T_BT phase (ICSD#23758, P4mm) were used to fit powder XRD. The results of sigma value (sig) ≈ 1.37 and weighed pattern R-factor (R_wp) ≈ 4.3 show that the refinement process is reliable.⁵⁰ The phase structure of BF–BT ceramics has been debated, with researchers proposing various phase compositions such as R3c + P4mm (R + T),¹⁴R3c + Pm3̄m (R + PC),¹³R3c (R),⁵¹ and P4mm + Pm3̄m (T + PC)⁵² to model the diffraction data. The origin of such discrepancies is possibly related to the processing conditions, i.e., Bi volatilization and the associated existence of secondary phases as well as the core–shell microstructure. Moreover, similar to other Bi-based perovskite oxides,^53,54 BF–BT may also exhibit local-scale variation in Bi-displacement, making the investigation of the average structure more challenging. Nevertheless, different combinations of space groups, i.e., R3c + P4mm, R3c + Pm3̄m, R3c, and P4mm + Pm3̄m were employed to model the room-temperature diffraction data presented in Fig. 1 and Fig. S1 and Table S1 (ESI†). Our data can be best modeled using a combined R3c + P4mm space group. Here, the lattice parameters obtained from refinements are a = b = 5.6439 Å and c = 13.8192 Å for rhombohedral (63%), and a = b = 3.9962 Å and c = 4.0189 Å for tetragonal (32%), confirming that the polycrystalline BF30BT displays a coexistence of rhombohedral and tetragonal phases at room temperature. Recently, Chen et al. and Wang et al. respectively investigated the local structure of BF–BT ceramics using TEM and observed considerable P4mm symmetry, which may support the practicality of this fitting conclusion.^55,56 It is, therefore, understood to be located in the morphotropic phase boundary (MPB) region associated with high piezoelectricity performance.^3,14

Fig. 1 (a) Rietveld refinement XRD patterns in the 2θ range of 10°–90°; enlarged XRD peaks (b₁) 31.2°–32°, (b₂) 38°–40° and (b₃) 44.8°–46° of BF30BT.

The surface microstructures of BF30BT ceramics were investigated using SEM. The polished and thermally etched samples were used to further reveal their microstructure, as shown in Fig. 2 and Fig. S2 (ESI†). The prepared polycrystalline ceramics present a homogeneous and dense microstructure, with a comparatively bright area indicating the existence of a Bi-rich phase, identified as Bi₂₅FeO₄₀.^49,57 According to the statistical analysis of the surface SEM images (Fig. S2a, ESI†), the grain size had an average diameter of 6.9 μm with a standard deviation of ±1.7 μm. Here, the density measured by the Archimedes method is ≈7.265 g cm⁻³, reaching approximately 95% of the theoretical density,⁵⁸ indicating that the sintering conditions are suitable for electromechanical investigations.

Fig. 2 SEM images of the polished and thermally etched BF30BT ceramics.

Under certain conditions, the application of an electric field and/or mechanical stress can induce an irreversible relaxor-to-ferroelectric transformation in nonergodic relaxor ferroelectrics, improving the overall small signal piezoelectric response.^8,15,16,59 However, the relaxor state of ergodic relaxor ferroelectrics is stable, i.e., the relaxor phase returns to the disordered state after the external electric field is removed, resulting in a low small-signal piezoelectric response¹⁶ but potentially an enhanced large-signal unipolar strain response.^31,60,61 One important factor controlling this state change is the critical relaxor-to-ferroelectric temperature, which can be seen in the temperature-dependent dielectric response. As such, relative permittivity was characterized as a function of temperature (25–700 °C) to investigate the phase transition temperature and relaxor characteristics of BF30BT ceramics (Fig. 3).

Fig. 3 (a) Temperature-dependent cooling curve of permittivity of BF30BT ceramic; (b) enlarged view at 25–200 °C.

The dielectric response shows that the dielectric peak at T_m gradually moves to a higher temperature with increasing frequency, displaying a broadening that is characteristic of a relaxor ferroelectric,^15,16 analogous to the canonical relaxor ferroelectric Pb(Mg_1/3Nb_2/3)O₃–PbTiO₃ (PMN–PT).⁶² Meanwhile, the rapid increase in dielectric loss is attributed to the significant enhancement in the conductivity of BF–BT ceramics above 200 °C.^19,63,64 To characterize the relaxor characteristics of the BF30BT ceramic, the modified Curie–Weiss law was applied using eqn (1) and (2):

ε = C/(T − T_o) (1)

where γ is the diffuseness degree, and C is the Curie-like constant. T* denotes the temperature at which ε_(T) begins to follow the Curie–Weiss law with γ = 1,^15,16,65 and ε_m is the highest value of the relative permittivity ε_(T). Conventional ferroelectrics and ideal relaxor ferroelectrics are represented by γ = 1 and 2, respectively, whereas the diffuse phase transition of ferroelectrics is represented by 1 < γ < 2.⁵⁰γ = 1.65 is obtained by fitting the data at 100 kHz, indicating that BF30BT ceramics exhibit relaxor behavior. Since Ba²⁺ (CN = 12, 1.61 Å) and Ti⁴⁺ (CN = 6, 0.61 Å) occupy the A- and B-sites previously occupied by Bi³⁺ (CN = 12, 1.45 Å) and Fe³⁺ (CN = 6, 0.65 Å),⁶⁶ respectively, the mismatch between the radius and the valence state leads to the random distribution of the local elastic and electric field in the solid solution, possibly breaking the LRO structure and generating NHPRs.^32,36 The local structural heterogeneity is considered to be conducive to eliminating the discontinuity between different polarization states, leading to the enhancement of piezoelectricity.^36,59 Additionally, the earliest evidence for PNRs and Burns temperatures came from the temperature dependence of the optical index of refraction,⁶⁷ which was verified by elastic neutron and X-ray scattering around the reciprocal lattice.^16,68,69 Since the difference between T_B and T* is understood to be relatively small, T* has been frequently employed to evaluate the value of T_B in recent studies.⁷⁰

To better understand the relaxor characteristics of the BF30BT ceramic, the empirical Vogel–Fulcher law is used to fit the experimental data with eqn (3):

where f is the driving frequency, f₀ is the Debye frequency, E_a is the average activation energy, k is the Boltzmann constant, and T_f is the freezing temperature.^28,71 The freezing temperature was found to be 470 °C (Fig. 4c), implying that BF30BT is in a nonergodic state near room temperature with NHPRs.^72–74 It is worth noting that an abnormal peak around 75 °C can be clearly observed in the enlarged inset of Fig. 3, which can be considered as an indication of re-entrant relaxor behavior.^75–77 Typically, the ceramic undergoes a cooling process from the paraelectric state to the ferroelectric state, accompanied by the freezing of active nanoclusters from the paraelectric state,⁷⁵i.e., paraelectric state → ferroelectric state + nanoclusters → ferroelectric state. However, in the case of the re-entrant relaxor phenomenon, the freezing behavior results from the ferroelectric state rather than the paraelectric phase, suggesting that the ceramic undergoes the following processes: paraelectric state → ferroelectric state → ferroelectric state + nanoclusters, which usually lead to the coexistence of the ferroelectric and relaxor states at room temperature.^15,75,78 Interestingly, for most ferroelectrics with re-entrant behavior, the re-entrant temperature is generally higher than the freezing temperature, whereas BF30BT and (1 − x)BaTiO₃–xBiScO₃ are the few systems with a re-entrant behavior in the NE state at T < T_f.^78–80 Based on the previous analysis, we can infer that BF30BT is a nonergodic relaxor ferroelectric (NE-RFE) and is likely accompanied by NHPRs at room temperature.

Fig. 4 (a) Relationship between and inverse dielectric permittivity 10 000/ε_r of BF30BT ceramics; (b) Curie–Weiss fitting line of BF30BT ceramics; and (c) Vogel–Fulcher fitting curves of BF30BT ceramics.

To investigate these effects further, PFM was employed to study the domain configurations of the unpoled BF30BT ceramic at room temperature. As shown in Fig. 5a, the domain morphology of the ceramic includes heterogeneous structures of island-like and stripe domains. Furthermore, as an enlarged view of Fig. 5a (block, white dashed lines), Fig. 5b clearly demonstrates the coexistence of typical herringbone domains and nanodomains, which always exhibit a relatively strong piezoelectric response to tip voltage. It should be emphasized that in the KNN⁸¹ and BF⁸² systems, herringbone domains are usually connected with 90° domain walls, which is related to the T phase in the BF–BT ceramic systems. Interestingly, meandering striped domains were observed in small grains of the same ceramic sample (Fig. 5c). This domain structure is somewhat blurry and shows a weak polar state in response to the tip, which is very similar to the PFM response of nanoscale heterogeneity in NBT–BT,⁸³ and it has been broadly defined as a nanodomain structure with symmetry of the underlying crystal symmetry in BNT⁸⁴ and KNN⁸⁵. Such nanoscale heterogeneity is usually sensitive to external electric fields, and the coexistence of large-sized domains and nanodomains can result in some nanodomains being clamped by large-sized domains after poling and failing to return to their initial state after the external electric field is removed.⁸⁶ This phenomenon is also confirmed by the PFM morphology of the poled sample (Fig. S3, ESI†), which showed a strong piezoelectric response and much lower domain wall density than the unpoled samples.⁸⁷ Simultaneously, as stated previously, certain nanoscale domains have not been merged into the large-domain structure, corresponding to local heterogeneity, which is difficult to completely eliminate via poling.

Fig. 5 (a)–(d) Amplitude and corresponding phase pattern of unpoled BF30BT ceramics with different areas; and (b) and (d) enlarged views of (a) and (c).

Furthermore, as the temperature-dependent phase structure is the foundation for evaluating the domain dynamics and piezoelectric contributions, in situ XRD measurements were employed to analyze the structural transition of both poled and unpoled samples from room temperature to 450 °C (Fig. 6a and c). Within the testing temperature range, BF30BT displayed a perovskite structure with characteristic peaks that gradually moved towards lower angles due to the thermal expansion of the lattice. It is worth mentioning that poled BF30BT displays a modest low-angle shift in 2θ. This phenomenon is primarily driven by the crystal structural distortion attributed to external electric fields,^60,88 resulting in variations of lattice parameters such as an increase in tetragonality and the rhombohedral tilting angle of 90° − α, which is consistent with the refinement results in Fig. 7a and b. In general, the ferroelectric space group R3c can be regarded as the ideal paraelectric cubic phase Pm3̄m frozen by two lattice distortion modes: (i) polar displacements of Bi³⁺ and Fe³⁺ along the [001] direction and (ii) antiferrodistortive distortion rotation of the oxygen octahedron around the [001] axis. These distortions are most noticeable at the characteristic 111_pc peak of R3c.^48,89,90 As illustrated in Fig. 6b and d, the 111_pc peak progressively weakens and moves to a lower angle with increasing temperature, suggesting that R3c eventually converts into R3m, and the total fraction of the rhombohedral phase decreases.

Fig. 6 In situ XRD patterns of BF30BT ceramics with unpoled and poled states measured at different temperatures within (a) and (c) 2θ = 10°–80° and (b) and (d) 2θ = 38.5°–39.5°.

Fig. 7 (a) and (b) Crystal structure distortion of BF30BT ceramics with η_T = c_T/a_T and ; and (c) schematic phase diagram of BF30BT ceramics.

To further investigate the phase structure, we used several phase combinations (R3m + P4mm, R3c + P4mm, R3m + Pm3̄m, and R3c + Pm3̄m, modes) for XRD refinement. It should be emphasized that R3c and R3m cannot be reliably differentiated in proportion due to the structural similarities and resolution of the measurement method used here. Typically, lattice distortion can be estimated using ,^61,91 as illustrated in Fig. 7a, b and Tables S2, S3 (ESI†). During heating, the lattice progressively expanded, and the distortion gradually decreased, indicating a transition from a low- to a high-symmetry phase. Furthermore, as the temperature increases, the template combination fitting results for R3m + P4mm increasingly outperform those for R3c + P4mm (see Tables S1 and S2, ESI†), which is consistent with the conclusion that the fraction of the R3m phase fraction increases. This transition also occurs in other BF–BT²⁰ ceramic systems, particularly in pure BF systems.⁹⁰ The oxygen octahedron's tilt state changes due to thermal vibration at high temperatures, but the polarization direction remains stable. Since several experimental studies and first-principle calculations indicate that the tilt of the oxygen octahedron suppresses the ferroelectric polarization,^92,93 the R3m phase without the tilt of the oxygen octahedron is more favorable in lowering the polarization rotation barrier and enhancing the piezoelectric performance, which results in the improvement of piezoelectric performance within a certain temperature range.²⁰ Based on the above-refined results and analysis, the phase diagrams of poled and unpoled BF30BT are shown in Fig. 7c. The fraction of R3c changes from 62% to 72% due to the poling process. The energy provided by the electric field during the poling process helps the ground state of the tetragonal phase overcome the energy barrier and transform into a low-symmetry rhombohedral phase. Increasing the temperature generates larger and more frequent thermal fluctuations, which lead to the high symmetry of tetragonal phase within the whole system, while within the rhombohedral phase, it also undergoes a transformation from R3c to R3m. As the temperature approaches the Curie temperature, the entire system gradually transitions into a state dominated by the paraelectric cubic phase.

In general, compared to ergodic RFE, NHPRs in nonergodic RFE will not entirely revert to the unoriented state after removing the external electric field,^32,36 especially in poled BF–BT, where NHPRs and LRO structures coexist at room temperature. The behavior of such a complicated system at high temperatures directly affects the device's dependability. To understand the domain dynamics during the heating process, temperature-dependent dielectric and small-signal piezoelectric coefficients were investigated from −150 to 450 °C under a constant −15 MPa uniaxial preload as a function of frequency from 0.5 Hz to 140 Hz (Fig. 8). The applied stress does not significantly change the domain wall density and structure within the range of the sub-coercive field for Rayleigh analysis,³⁹ as the −15 MPa preload used in our experiment is far lower than the −500 MPa coercive field of BF–BT ceramics reported in the literature.⁹⁴ Here, the dielectric anomaly corresponding to the re-entrant temperature of around 75 °C is more visible in Fig. 8b, indicating that the effect of re-entrant behavior on the direct piezoelectric effect cannot be disregarded. In general, the temperature increase leads to a d₃₃ enhancement, which subsequently decreases at high temperatures due to the loss of electric field-induced macroscopic polarization. Usually, the following equation is employed to estimate the piezoelectric response of ferroelectrics:

d₃₃ = 2QεP (4)

where Q is the electrostrictive coefficient, which is usually considered to be temperature-independent.⁹⁵ As demonstrated in Fig. S4 and Table S4 (ESI†), since P_r and E_c of the BF30BT ceramic exhibit a significant upward and downward trend within the measurement range of 20 °C–100 °C,¹³ respectively, the peak found in the d₃₃ curve at approximately 75 °C may correlate with the peak of re-entrant behavior in the dielectric constant curve. Furthermore, the frequency dispersion of d₃₃ increases with temperature, most notably above 100 °C up to the depolarization temperature. It is worth noting that the frequency dispersion of the piezoelectric response is typically directly related to the dynamics of the hysteretic extrinsic contributions in response to an external field, such as non-180° domains.^39,96 Domain walls can overcome local barriers generated by pinning under the operation of alternating current (AC) fields, boosting their contribution to piezoelectric characteristics. The d₃₃ values show low-frequency dispersion at low temperatures because the lower thermal energy reduces the domain activity and suppresses the mobility of the domain walls.^97,98 The domain and domain wall motions become active with an increase of temperature, which renders the d₃₃ dispersion behavior more visible. Nevertheless, due to thermal excitation, conductivity also increases at higher temperatures, leading to a rapid decrease of the low-frequency piezoelectric response at 0.5 Hz and 1 Hz beyond 350 °C, which corresponds to the rapid increase in dielectric losses.⁹⁹

Fig. 8 (a) Temperature-dependent d₃₃ and (b) enlarged dielectric permittivity of BF–BT with different frequencies under uniaxial compressive stress of −15 MPa.

Here, frequency-dependent Rayleigh behavior is employed to further investigate the piezoelectric response, as follows:

d₃₃ = d₀ + βω_A (5)

where d₀ is the static piezoelectric coefficient, ω_A is the measurement frequency, and β is the Rayleigh coefficient that quantifies the frequency dependence of d₃₃, which is generally related to the activity of the domain and the motion of the non-180° domain walls.^39,97,98 Fig. S5 (ESI†) illustrates the fitting curve based on a plot of the frequency-dependent d₃₃ for the selected temperature. A larger β coefficient indicates greater sensitivity to frequency.^40,97,98 Although numerous contributions, such as phase transitions and defects, may contribute to the observed behavior, the main mechanism of ferroelectric materials is understood to be domain wall nucleation and motion.^96,97

The Rayleigh parameters d₀ and β reveal different regions throughout the heating process for BF30BT (Fig. 9). Initially, within the low-temperature range (−150–0 °C), both the frequency-independent contribution component d₀ and frequency-dependent contribution β increase. This phenomenon has also been observed in PZT and Bi_1/2K_1/2TiO₃ systems,^43,98 where the increase of d₀ is primarily due to the activation and expansion of the lattice, and the enhancement of frequency-dependent contribution β is likely attributed to the thermal activation of frozen macro- and nanodomains, resulting in the enhancement of the domain wall motion.^97,98 Upon further heating to the temperature range of 0–100 °C, d₀ continues to increase with a small peak near 75 °C, while β exhibits a modest decreasing trend despite the enhanced thermal energy, which should increase domain activation and enhance domain wall motion. It should be noted that the dielectric and piezoelectric responses of the BF–BT ceramics show an apparent decoupling with frequency near room temperature¹⁰⁰; hence, variations in this temperature range may be mainly ascribed to the impact of re-entrant behavior. In general, NHPRs will transform into LRO structures around the re-entrant temperature,^19,75,78,101i.e., nanodomains will transform into macrodomains near 75 °C, thereby reducing the domain wall density. This phenomenon is common in other ferroelectric materials with re-entrant behavior, such as (1 − x)BaTiO₃–xBiScO₃⁷⁸ and (Ba_0.925Bi_0.05)(Ti_1−xSn_x)O₃.¹⁰¹ On the one hand, the large domains may interact and potentially clamp small domains during the heating process, causing a decrease in their mobility.^102–104 The above two factors are suggested to decrease the frequency-dependent β and result in a peak of d₀ near the re-entrant temperature of 75 °C. Usually, local heterogeneity is mainly caused by A- and B-site atom disorder, which can be aligned when an electric field is applied but returns to its disordered state when the electric field is removed. This rapid response to external electric fields that nanodomain activity is more likely to be estimated in the frequency-independent response d₀ rather than frequency-dependent β within the test frequency.³⁸

Fig. 9 (a) Temperature-dependent variation in d₀ and (b) frequency Rayleigh coefficient β for the BF30BT ceramics under a pre-stress of −15 MPa.

Within the temperature range of 100–200 °C, β increases, although the underlying mechanism is unclear. It is suggested that increasing the temperature may increase β through enhanced activation of non-180° domain wall motion, which in turn boosts the frequency dispersion of the piezoelectric response.^42,43,97,98 Furthermore, as shown by in situ XRD, increasing the temperature encourages the conversion of R3c to R3m, leading to an enhancement of the piezoelectric performance, which is a component of the frequency-independent response d₀.^20,90 When the temperature increases to 200–350 °C, thermally activated defect dipoles¹⁰⁵ may reduce the pinning effect on the domain wall, allowing non-180° domain walls to move faster, ultimately reducing the frequency dispersion. Within this temperature range, lattice deformations caused by heating, such as symmetry, lattice expansion, and reduced distortion, dominate the contribution of d₀, which is also observed in materials Bi_1/2K_1/2TiO₃⁴³ and Pb(Zr,Ti)O₃.³⁹ After the temperature exceeds 350 °C, BF30BT begins to lose its polarization state, resulting in a drop in d₀ and β.¹⁰⁶

In addition to the frequency, the intrinsic and extrinsic contributions to the piezoelectric response are significantly influenced by the applied stress amplitude. The former refers to crystal lattice deformation caused by external fields, such as electric fields and pressure, while the latter comes from other effects, such as the movement of domain walls or interphase boundaries. The intrinsic contribution is generally reversible, while the extrinsic contribution can include both reversible and irreversible components.³⁹ The stress amplitude-dependent measurement of d₃₃ with a fixed frequency (10 Hz) was used to investigate the domain dynamics with the Rayleigh model, which is commonly used to identify reversible and irreversible piezoelectric responses.³⁹ It should be noted that the measurement of stress amplitude-dependent Rayleigh behavior starts at room temperature since the freezing of the lattice and domain wall motion at low temperatures results in little difference in the piezoelectric response under different amplitudes. As shown in Fig. 10, the trend with low stress is comparable to the previous frequency-dependent data shown in Fig. 8a. Notably, stress amplitude dependence is not observed until above approximately 200 °C, indicating that irreversible contributions such as domain wall motion start accumulating, which corresponds well with previous observations.

Fig. 10 Temperature-dependent d₃₃ with varying amplitudes for BF30BT at 10 Hz under a pre-stress of −15 MPa.

Additionally, the stress-dependent Rayleigh behavior was used to fit the experimental data in order to determine the reversible and irreversible contributions as a function of temperature, as follows:

d₃₃ = d_init + ασ_A (6)

where d_init represents the initial contribution from lattice deformation and reversible domain wall motion at a pre-stress of −15 MPa, σ_A is the stress amplitude, and α is the Rayleigh coefficient, which describes the change in the piezoelectric response as a function of stress amplitude.^39,98 Fig. S6 (ESI†) illustrates the fitting based on a plot of the stress amplitude-dependent d₃₃ for the selected temperature. Despite the re-entrant relaxor behavior and expected enhanced nanodomain activation occurring at 25–150 °C, which should result in major changes to the irreversible contribution (Fig. 11), the α value remarkably remains nearly zero, indicating limited extrinsic contributions. This indicates that the piezoelectric response in this temperature region is dominated by reversible contributions, such as lattice deformation and nanodomains with reversible domain wall motion. On the other hand, due to the R3c to R3m transition and the activated domain wall motion with increasing temperature, d_init and α were found to simultaneously increase between 150 and 350 °C. Eventually, both d_init and α decrease beyond 350 °C due to the loss of polarization orientation at high temperatures, resulting in a ferroelectric to paraelectric transition.

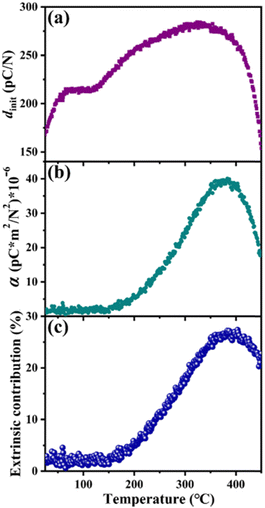Fig. 11 (a) Temperature-dependent variation in d_init, (b) Rayleigh coefficient α, and (c) estimated extrinsic contribution at BF30BT ceramics at 10 Hz under a pre-stress of −15 MPa.

Based on the data presented in this work, Fig. 12 is proposed to depicts the possible domain dynamic stages in BF30BT with variations in temperature. The initial state consists of randomly oriented long-range ordered macrodomains (illustrated by the thick arrow) and local heterogeneous nanodomains (illustrated by the thin arrow). After electrical poling, the macrodomains tend to orient with the applied field, resulting in the coalescence of smaller polar regions into larger domains, thereby lowering the domain wall density. The nanodomains reorient arbitrarily once the external electric field is removed due to their high activity. Moreover, as the temperature changes, the evolution of domain dynamics will likely undergo the following five stages:

Fig. 12 Schematic representation of the possible stages of temperature-dependent domain dynamics in BF30BT ceramics contributing to the microscopic piezoelectric response.

Stage I (−150 to 0 °C): when the poled ceramic is at a low temperature, both macro- and nanodomains freeze. With increasing temperature, the domains become progressively more active with increasing thermal activation, resulting in a temperature-dependent piezoelectric response. Here, piezoelectric characteristics are mostly derived from the intrinsic contribution of the macrodomain lattice response.

Stage II (0–100 °C): when the temperature increases, nanodomains tend to orient with the polarization direction of the macrodomain, forming LRO structures due to the influence of re-entrant relaxor behavior. It should be noted that because macrodomains do not fully recover from the frozen state within this stage, the piezoelectric properties are more likely to originate from rapid lattice responses, nanodomains, and reversible domain wall motion.

Stage III (100–200 °C): the behavior of the grains is transitional when the temperature reaches this stage, which involves a mixed active and normal state of the macrodomain, leading to fluctuations in the piezoelectric response. The apparent frequency dispersion of the piezoelectric characteristics shows that extrinsic contributions, such as domain wall motion, become active.

Stage IV (200–350 °C): all domains become active, and the piezoelectric frequency dispersion is slightly decreased compared to the previous stage. Although extrinsic contributions, including domain wall motion, play an essential role at this stage, the piezoelectric response is still dominated by the lattice contributions.

Stage V (350–400 °C): above 350 °C, the LRO structure inside the ceramic grains begins to break, thereby increasing the domain wall density (both macro- and nanodomains) while decreasing the overall piezoelectric response. It is expected that the ceramics will finally completely depolarize as the temperature increases (>450 °C). Furthermore, in situ temperature-dependent TEM and local structural analysis are required to validate the proposed domain dynamics model.

4. Conclusions

The domain dynamics of high-temperature piezoelectric ceramic BF30BT were investigated through a combination of temperature-dependent structural analysis as well as dielectric and piezoelectric properties. Based on an analysis of its relaxor properties and microstructure, we found that BF30BT ceramics coexist in the R-T phase at room temperature and contain both macro- and nanodomains. Surprisingly, during the subsequent characterization of the Rayleigh behavior, we observed that nanodomains primarily demonstrate an intrinsic and reversible contribution because of their rapid reaction in the low-temperature region, which has received limited attention in previous investigations. As detailed in this work, we also discovered that the enhancement of high-temperature piezoelectric characteristics is primarily due to the reversible contribution of lattice deformation, with the remainder attributed to irreversible contributions such as active domain wall motion. We believe that decoding the domain dynamics and the mechanism of piezoelectric contributions can provide a more in-depth understanding of the physical properties of high-temperature ferroelectrics and piezoelectric materials, which are meaningful for further research and applications.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. H. K., A. G. and K. G. W. gratefully acknowledge the financial support for this work by the Deutsche Forschungsgemeinschaft (DFG) under GRK2495/H. L. X. X., T. Z., and J. G. Z. acknowledge the support of the National Natural Science Foundation of China (52032007), the Sichuan Science and Technology Program (23ZDYF0173), the Natural Science Foundation of Sichuan Province (24NSFSC5385 and 2024NSFSC1383), and the China Scholarship Council (No. 20200624013). We also appreciate Ms. Hui Wang from the Analytical & Testing Center of Sichuan University for help with SEM characterization.

References

1. J. Rödel, W. Jo, K. T. P. Seifert, E.-M. Anton, T. Granzow and D. Damjanovic, J. Am. Ceram. Soc., 2009, 92, 1153–1177.
2. J. Rödel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura and D. Damjanovic, J. Eur. Ceram. Soc., 2015, 35, 1659–1681.
3. D. Wang, G. Wang, S. Murakami, Z. Fan, A. Feteira, D. Zhou, S. Sun, Q. Zhao and I. M. Reaney, J. Adv. Dielectr., 2019, 08.
4. T. R. Shrout and S. Zhang, J. Electroceram., 2007, 19, 113–126.
5. W. Shi, S. Guan, X. Li, J. Xing, F. Zhang, N. Chen, Y. Wu, H. Xu, Y. Xu and Q. Chen, J. Eur. Ceram. Soc., 2022, 42, 6968–6976.
6. C. Long, W. Zhou, W. Ren, Y. Zhang, K. Zheng and L. Liu, Scr. Mater., 2021, 204, 114102.
7. H. Yan, H. Ning, Y. Kan, P. Wang and M. J. Reece, J. Am. Ceram. Soc., 2009, 92, 2270–2275.
8. H. Tao, H. Wu, Y. Liu, Y. Zhang, J. Wu, F. Li, X. Lyu, C. Zhao, D. Xiao, J. Zhu and S. J. Pennycook, J. Am. Chem. Soc., 2019, 141, 13987–13994.
9. T. Mondal, S. Das, T. Badapanda, T. P. Sinha and P. M. Sarun, Phys. B, 2017, 508, 124–135.
10. J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Science, 2003, 299, 1719–1722.
11. H. Zhang, W. Jo, K. Wang and K. G. Webber, Ceram. Int., 2014, 40, 4759–4765.
12. S. O. Leontsev and R. E. Eitel, J. Mater. Res., 2011, 26, 9–17.
13. C. Li, T. Zheng and J. Wu, Acta Mater., 2021, 206, 116601.
14. M. H. Lee, D. J. Kim, J. S. Park, S. W. Kim, T. K. Song, M. H. Kim, W. J. Kim, D. Do and I. K. Jeong, Adv. Mater., 2015, 27, 6976–6982.
15. A. A. Bokov and Z.-G. Ye, J. Adv. Dielectr., 2012, 02, 1241010.
16. A. A. Bokov and Z.-G. Ye, J. Mater. Sci., 2006, 41, 31–52.
17. Z. Chen, X. Bai, H. Wang, J. Du, W. Bai, L. Li, F. Wen, P. Zheng, W. Wu, L. Zheng and Y. Zhang, Ceram. Int., 2020, 46, 11549–11555.
18. C. Zhou, H. Yang, Q. Zhou, Z. Cen, W. Li, C. Yuan and H. Wang, Ceram. Int., 2013, 39, 4307–4311.
19. Z. Yang, B. Wang, T. Brown, S. J. Milne, A. Feteira, A. Wohninsland, K. V. Lalitha, Y. Li and D. A. Hall, J. Mater. Chem. C, 2023, 11, 2186–2195.
20. L. Xie, M. Mo, H. Chen, Y. Xie, Y. Cheng, C. Shu, Q. Chen, J. Xing, Z. Tan, J. Zhu and H. Zhu, J. Mater. Chem. A, 2022, 10, 22540–22550.
21. S. Cheng, B.-P. Zhang, L. Zhao and K.-K. Wang, J. Am. Ceram. Soc., 2019, 102, 7355–7365.
22. S. O. Leontsev and R. E. Eitel, J. Am. Ceram. Soc., 2009, 92, 2957–2961.
23. Y. Zhang, R. Huang, F. Zhang, Z. Liang, T. Xie, H.-T. Lin and Y. Dai, J. Am. Ceram. Soc., 2023, 106, 2384–2392.
24. X. Chen, H. Qin, H. Li, Y. Du, S. Wang, P. Li, Y. Hu, L. Liu, J. Zhao and D. Wang, J. Am. Ceram. Soc., 2024, 107, 4232–4241.
25. L. Wu, X. Wang and L. Li, RSC Adv., 2016, 6, 14273–14282.
26. Z. Yang, H. Du, L. Jin, Q. Hu, H. Wang, Y. Li, J. Wang, F. Gao and S. Qu, J. Mater. Chem. A, 2019, 7, 27256–27266.
27. X. Dong, X. Li, X. Chen, J. Wu and H. Zhou, Chem. Eng. J., 2021, 409, 128231.
28. D. Viehland, S. J. Jang, L. E. Cross and M. Wuttig, J. Appl. Phys., 1990, 68, 2916–2921.
29. H. Li, J. Zhao, Y. Li, L. Chen, X. Chen, H. Qin, H. Zhou, P. Li, J. Guo and D. Wang, ACS Appl. Mater. Interfaces, 2024, 16, 9078–9087.
30. F. Zeng, C. Zhou, C. Zhang, L. Jiang, J. Zhang, H. Guo, Y. Chen, W. Lu, W. Cai, G. Zhang, Y. Hu and G. Fan, Ceram. Int., 2022, 48, 10539–10546.
31. G. Wang, Z. Fan, S. Murakami, Z. Lu, D. A. Hall, D. C. Sinclair, A. Feteira, X. Tan, J. L. Jones, A. K. Kleppe, D. Wang and I. M. Reaney, J. Mater. Chem. A, 2019, 7, 21254–21263.
32. F. Li, S. Zhang, D. Damjanovic, L.-Q. Chen and T. R. Shrout, Adv. Funct. Mater., 2018, 28, 1801504.
33. Y. Imry and S.-k Ma, Phys. Rev. Lett., 1975, 35, 1399–1401.
34. K.-H. Kim, D. A. Payne and J.-M. Zuo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 184113.
35. H. Takenaka, I. Grinberg, S. Liu and A. M. Rappe, Nature, 2017, 546, 391–395.
36. F. Li, D. Lin, Z. Chen, Z. Cheng, J. Wang, C. Li, Z. Xu, Q. Huang, X. Liao, L.-Q. Chen, T. R. Shrout and S. Zhang, Nat. Mater., 2018, 17, 349–354.
37. J. Yin, X. Shi, H. Tao, Z. Tan, X. Lv, X. Ding, J. Sun, Y. Zhang, X. Zhang, K. Yao, J. Zhu, H. Huang, H. Wu, S. Zhang and J. Wu, Nat. Commun., 2022, 13, 6333.
38. S. Kim, R. Miyauchi, Y. Sato, H. Nam, I. Fujii, S. Ueno, Y. Kuroiwa and S. Wada, Adv. Mater., 2023, 35, 2208717.
39. D. Damjanovic, J. Appl. Phys., 1997, 82, 1788–1797.
40. D. Damjanovic, J. Am. Ceram. Soc., 2005, 88, 2663–2676.
41. J. J. Prejean and J. Souletie, J. Phys., 1980, 41, 1335–1352.
42. A. Gadelmawla, U. Eckstein, K. Riess, Y.-X. Liu, K. Wang, J.-F. Li, K.-I. Kakimoto, N. H. Khansur and K. G. Webber, J. Am. Ceram. Soc., 2023, 106, 2326–2337.
43. G. E. Eyoum, U. Eckstein, K. Riess, A. Gadelmawla, E. Springer, K. G. Webber and N. H. Khansur, J. Mater. Sci.: Mater. Electron., 2022, 57, 15843–15861.
44. C. Zhou, H. Yang, Q. Zhou, G. Chen, W. Li and H. Wang, J. Mater. Sci.: Mater. Electron., 2013, 24, 1685–1689.
45. Y. Yin, Y. Tang, W. Pan, A. Song, J. Yu and B. Zhang, Ceram. Int., 2021, 47, 9486–9494.
46. J. Xing, Z. Tan, X. Chen, L. Jiang, W. Wang, X. Deng, B. Wu, J. Wu, D. Xiao and J. Zhu, Inorg. Chem., 2018, 58, 428–438.
47. F. H. Schader, D. Isaia, M. Weber, E. Aulbach and K. G. Webber, J. Mater. Sci., 2018, 53, 3296–3308.
48. S. Cheng, L. Zhao, B. Zhang and K. Wang, Ceram. Int., 2019, 45, 10438–10447.
49. B. Xun, N. Wang, B. Zhang, X. Chen, Y. Zheng, W. Jin, R. Mao and K. Liang, Ceram. Int., 2019, 45, 24382–24391.
50. J. Xing, Z. Tan, L. Xie, L. Jiang, J. Yuan, Q. Chen, J. Wu, W. Zhang, D. Xiao and J. Zhu, J. Am. Ceram. Soc., 2018, 101, 1632–1645.
51. Y. Yoneda, K. Yoshii, S. Kohara, S. Kitagawa and S. Mori, Jpn. J. Appl. Phys., 2008, 47, 7590.
52. L.-F. Zhu, X.-W. Lei, L. Zhao, M. I. Hussain, G.-Z. Zhao and B.-P. Zhang, Ceram. Int., 2019, 45, 20266–20275.
53. Y. Kuroiwa, S. Kim, I. Fujii, S. Ueno, Y. Nakahira, C. Moriyoshi, Y. Sato and S. Wada, Commun. Mater., 2020, 1, 71.
54. I. Levin, D. S. Keeble, G. Cibin, H. Y. Playford, M. Eremenko, V. Krayzman, W. J. Laws and I. M. Reaney, Chem. Mater., 2019, 31, 2450–2458.
55. T. Liu, W. Qian, Y. Jiang, J. Xing, W. Xuan, J. Chen, J. Cheng and H. Gu, J. Eur. Ceram. Soc., 2023, 44, 2866–2873.
56. G. Wang, T. Hu, W. Zhu, Z. Lu, A. Kleppe, M. Diaz Lopez, A. Feteira, D. C. Sinclair, Z. Fu, H. Huang, D. Wang and I. M. Reaney, Phys. Rev. Lett., 2023, 130, 076801.
57. I. Calisir and D. A. Hall, J. Mater. Chem. C, 2018, 6, 134–146.
58. B.-W. Xun, Y.-C. Tang, J.-Y. Chen and B.-P. Zhang, J. Eur. Ceram. Soc., 2019, 39, 4085–4095.
59. F. Li, M. J. Cabral, B. Xu, Z. Cheng, E. C. Dickey, J. M. LeBeau, J. Wang, J. Luo, S. Taylor, W. Hackenberger, L. Bellaiche, Z. Xu, L.-Q. Chen, T. R. Shrout and S. Zhang, Science, 2019, 364, 264–268.
60. J. Chen, J. E. Daniels, J. Jian, Z. Cheng, J. Cheng, J. Wang, Q. Gu and S. Zhang, Acta Mater., 2020, 197, 1–9.
61. N. H. Khansur, M. Hinterstein, Z. Wang, C. Groh, W. Jo and J. E. Daniels, Appl. Phys. Lett., 2015, 107, 242902.
62. C. J. Stringer, N. J. Donnelly, T. R. Shrout, C. A. Randall, E. F. Alberta and W. S. Hackenberger, J. Am. Ceram. Soc., 2008, 91, 1781–1787.
63. B. Li, T. Zheng and J. Wu, ACS Appl. Mater. Interfaces, 2021, 13, 37422–37432.
64. K. H. Härdtl, Ceram. Int., 1982, 8, 121–127.
65. Z.-G. Ye and A. A. Bokov, Ferroelectrics, 2004, 302, 227–231.
66. R. D. Shannon and C. Prewitt, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
67. G. Burns and F. H. Dacol, Solid State Commun., 1983, 48, 853–856.
68. S. B. Vakhrushev, B. E. Kvyatkovsky, A. A. Naberezhnov, N. M. Okuneva and B. P. Toperverg, Ferroelectrics, 1989, 90, 173–176.
69. S. Tsukada and S. Kojima, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 144106.
70. D. Viehland, S. J. Jang, L. E. Cross and M. Wuttig, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 8003–8006.
71. X. Dong, X. Li, H. Chen, Q. Dong, J. Wang, X. Wang, Y. Pan, X. Chen and H. Zhou, J. Adv. Ceram., 2022, 11, 729–741.
72. H. Yang, J. Zhao, J. Zhuang, M. Hinterstein, W. Ren, Z.-G. Ye and N. Zhang, J. Eur. Ceram. Soc., 2023, 43, 3289–3296.
73. A.-K. Fetzer, A. Wohninsland, K. Lalitha and H.-J. Kleebe, Phys. Rev. Mater., 2022, 6, 064409.
74. K. Dey, A. Ahad, K. Gautam, A. Tripathy, S. S. Majid, S. Francoual, C. Richter, M. N. Singh, A. Sagdeo, E. Welter, N. Vittayakorn, V. G. Sathe, R. Rawat and D. K. Shukla, Phys. Rev. B, 2021, 103, L100205.
75. V. V. Shvartsman and D. C. Lupascu, J. Am. Ceram. Soc., 2012, 95, 1–26.
76. B. Wang, C. Fu, X. Liu, B. Xie and D. A. Hall, Open Ceram., 2023, 13, 100322.
77. H. Yang, X. Wang, X. Yang, S. Guan, F. Huang, H. Zhang, H. Tan and Q. Chen, J. Eur. Ceram. Soc., 2024, 44, 3247–3257.
78. H. Y. Guo, C. Lei and Z.-G. Ye, Appl. Phys. Lett., 2008, 92, 172901.
79. I. Levin, V. Krayzman, J. C. Woicik, F. Bridges, G. E. Sterbinsky, T. M. Usher, J. L. Jones and D. Torrejon, Phys. Rev. B, 2016, 93, 104106.
80. M. Alguero, J. M. Gregg and L. Mitoseriu, Nanoscale Ferroelectrics and Multiferroics: Key Processing and Characterization Issues, and Nanoscale Effects, Wiley, vol. 2, 2016.
81. R. López-Juárez, O. Novelo-Peralta, F. González-García, F. Rubio-Marcos and M.-E. Villafuerte-Castrejón, J. Eur. Ceram. Soc., 2011, 31, 1861–1864.
82. T. Zhao, A. Scholl, F. Zavaliche, K. Lee, M. Barry, A. Doran, M. P. Cruz, Y. H. Chu, C. Ederer, N. A. Spaldin, R. R. Das, D. M. Kim, S. H. Baek, C. B. Eom and R. Ramesh, Nat. Mater., 2006, 5, 823–829.
83. D. Gobeljic, V. V. Shvartsman, A. Belianinov, B. Okatan, S. Jesse, S. V. Kalinin, C. Groh, J. Rödel and D. C. Lupascu, Nanoscale, 2016, 8, 2168–2176.
84. J. Yin, H. Tao, G. Liu and J. Wu, J. Am. Ceram. Soc., 2020, 103, 1881–1890.
85. C. Hu, X. Meng, M.-H. Zhang, H. Tian, J. E. Daniels, P. Tan, F. Huang, L. Li, K. Wang, J.-F. Li, Q. Lu, W. Cao and Z. Zhou, Sci. Adv., 2020, 6, eaay5979.
86. T. Zheng and J. Wu, Adv. Electron. Mater., 2020, 2000079.
87. J. Chen, C. Chen, S. Chang, C. Zhao and X. Jiang, Ceram. Int., 2024, 50, 11022–11031.
88. Z. Ning, Y. Jiang, J. Jian, J. Guo, J. Cheng, H. Cheng and J. Chen, J. Eur. Ceram. Soc., 2020, 40, 2338–2344.
89. J. Chen, J. Cheng, J. Guo, Z. Cheng, J. Wang, H. Liu and S. Zhang, J. Am. Ceram. Soc., 2019, 103, 374–381.
90. J.-P. Zhou, R.-L. Yang, R.-J. Xiao, X.-M. Chen and C.-Y. Deng, Mater. Res. Bull., 2012, 47, 3630–3636.
91. H. D. Megaw and C. N. W. Darlington, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 161–173.
92. J. B. Neaton, C. Ederer, U. V. Waghmare, N. A. Spaldin and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014113.
93. X. Dai, Z. Xu, J. F. Li and D. Viehland, Appl. Phys. Lett., 1995, 77, 3354–3360.
94. N. H. Khansur, J. Glaum, O. Clemens, H. Zhang, J. E. Daniels and K. G. Webber, Ceram. Int., 2017, 43, 9092–9098.
95. K. Uchino, S. Nomura, L. E. Cross, R. E. Newnham and S. Jang, J. Mater. Sci., 1981, 16, 569–578.
96. T. Rojac, A. Bencan, G. Drazic, M. Kosec and D. Damjanovic, J. Appl. Phys., 2012, 112, 064114.
97. D. Damjanovic, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R649–R652.
98. B. Kaeswurm, F. H. Schader and K. G. Webber, Ceram. Int., 2018, 44, 2358–2363.
99. Y. Li, T. Zheng, B. Li and J. Wu, J. Am. Ceram. Soc., 2023, 106, 2393–2406.
100. Z. Yang, Y. Li, B. Wang, J. Pan, A. K. Kleppe and D. A. Hall, J. Materiomics, 2023, 10, 57–69.
101. M. Fang, Y. Ji, Z. Zhang, Y. Yang, C. Liu, D. Wang, L. Zhang, J. Gao and X. Ren, NPG Asia Mater., 2018, 10, 1029–1036.
102. C. A. Randall, N. Kim, J.-P. Kucera, W. Cao and T. R. Shrout, J. Am. Ceram. Soc., 1998, 81, 677–688.
103. M. E. Drougard and D. R. Young, Phys. Rev., 1954, 94, 1561–1564.
104. X. Lv, J. Wu, J. Zhu, D. Xiao and X. Zhang, J. Am. Ceram. Soc., 2018, 38, 85–94.
105. B. Li, C. Li, T. Zheng and J. Wu, Adv. Electron. Mater., 2022, 8, 2200609.
106. Y. Cui, X. Zhang, X. Lei, T. Yan, X. Chen, B. Peng, P. Ren, C. Li and L. Liu, J. Mater. Chem. C, 2022, 10, 8301–8309.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc01199f

---