Unexpected p-type thermoelectric transport arising from magnetic Mn substitution in Fe₂V_1−xMn_xAl Heusler compounds

Abstract

p-Type Fe₂VAl-based thermoelectrics have been much less investigated compared to their respective n-type counterparts. Thus, it is crucial to identify novel doping strategies to realize enhanced p-type Fe₂VAl Heusler compounds. In the current study, the effect of Mn substitution in Fe₂V_1−xMn_xAl is investigated with respect to temperature-dependent electronic transport as well as temperature- and field-dependent magnetic properties. We find an anomalous and unexpected p-type Seebeck coefficient for nominally n-doped Fe₂V_1−xMn_xAl over an extremely large range of concentrations up to x = 0.6. Using density functional theory (DFT) calculations, this is traced back to distinct modifications of the electronic structure, i.e., localized magnetic defect states (m = 2.43μ_B) at the valence and conduction band edges, and a concomitant pinning of the Fermi level within the pseudogap. Furthermore, we were able to further optimize the thermoelectric properties by co-doping Al antisites in off-stoichiometric Fe₂V_0.9Mn_0.1Al_1+y, yielding sizeable values of the power factor, PF = 2.2 mW K⁻² m⁻¹ in Fe₂V_0.9Mn_0.1Al_1.1 at 350 K, and figure of merit, ZT ∼ 0.1 for highly off-stoichiometric Fe₂V_0.9Mn_0.1Al_1.5 at T = 500 K. Our work underlines the prospect of engineering Fe₂VAl-based Heusler compounds via magnetic doping to realize enhanced p-type thermoelectris and encourages studies involving other types of co-substitution for Mn-substituted Fe₂V_1−xMn_xAl.

---

Introduction

Thermoelectric (TE) materials can convert waste heat into electric energy, or vice versa, by utilizing the Seebeck effect, thus representing a viable option for generating eco-friendly energy to address the current energy crisis.^1–4 A crucial task, however, lies in further improving the conversion efficiency of thermoelectric materials.^5,6 The efficiency of TE materials is determined by a dimensionless figure of merit (ZT) = (S²/ρκ) × T, where S is the Seebeck coefficient, ρ the electrical resistivity, κ = (κ_elec+ κ_ph) the thermal conductivity, consisting of electron and lattice contributions, and T the temperature. These key properties have tradeoffs that limit progress in enhancing ZT, and it is necessary to develop new enhancement principles.^7–9 Among several material classes, the Heusler-type intermetallic compound Fe₂VAl is a promising candidate for thermoelectric power generation near room temperature.^10,11 This alloy has the cubic L2₁-ordered crystal structure and exhibits a high thermoelectric power factor PF = S²/ρ near room temperature.¹² Fe₂VAl shows a semiconductor-like temperature dependence of the electrical resistivity in a wide temperature range up to 1200 K or above.¹⁰ The electronic structure of stoichiometric Fe₂VAl suggests a deep pseudogap at the Fermi level.¹³ Stoichiometric Fe₂VAl is a nonmagnetic, low carrier, and compensated semimetal.^13–18 Recently, it was shown that rational co-substitution can tune the band gap and therefore significantly improve the thermoelectric properties, yielding high power factors up to around 10.3 mW K⁻² m⁻¹.^19–22 However, the lattice thermal conductivity of Fe₂VAl is about one order of magnitude larger than that of other high-performance thermoelectric materials, resulting in much smaller ZT values compared to the best-performing systems at room temperature like Bi₂Te₃ or Mg₃Sb₂-based compounds.^6,23–28

In order to further increase ZT of Fe₂VAl-based systems, various strategies have been employed already, including elemental substitution at all lattice sites, tuning the microstructure and grain size as well as thin film deposition.^29–50 Particularly, B. Hinterleitner et al. reported an ultrahigh power factor, above 45 mW K⁻² m⁻¹, and ZT around 5 at 350 K for Fe₂V_0.8W_0.2Al metastable thin films.⁵⁰ Also, doping of Fe₂VAl p-type Heusler compounds with various elements, such as Ti and Zr, has been studied to understand the effects of different dopants on the thermoelectric performance.^40,51,52 However, the performance of p-type Fe₂VAl-based thermoelectrics remains still far below those of the best n-type compounds. Therefore, it is crucial to identify novel p-type candidate materials and doping elements.

Furthermore, it has been demonstrated that spin fluctuations can contribute significantly to optimize the power factor (PF = 1.2 mW K⁻² m⁻¹ at 400 K) in weakly ferromagnetic Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 and Fe_2.2V_0.8Al_0.6Si_0.4.⁵³ That being said, likewise to spin fluctuations, the usage of magnetism in different forms to enhance the Seebeck coefficient is also rapidly increasing; for example, spin Seebeck effect, anomalous Nernst effect, magnon drag, paramagnon drag, spin entropy, etc.^54–61 are most recently studied instances.

Thus, magnetic doping can be a useful strategy in improving thermoelectric properties. In the case of Fe₂VAl-based compounds, however, the effect of magnetic element doping with respect to thermoelectric properties, has not been well studied. This motivated us to substitute V/Mn in Fe₂V_1−xMn_xAl. We observed a unusual hole-dominated Seebeck coefficient in nominally n-doped Fe₂V_1−xMn_xAl, which increases with increasing Mn content up to x = 0.2. Employing first principles electronic structure calculations within the framework of the density functional theory⁶² and the coherent potential approximation,⁶³ used to model the effects of the substitutional atomic disorder, we trace this back to a severe modification of the electronic structure, wherein magnetic impurity states are formed by Mn atoms, leading to a pinning of the Fermi energy near the valence band edge and within the pseudogap.

Moreover, we additionally co-substituted Al antisites at the Fe and V sites in Al-rich Fe₂V_0.9Mn_0.1Al_1+y samples to further optimize the thermoelectric performance. Since p-type Fe₂VAl Heusler compounds have been reported to a lesser content compared to n-type systems, we systematically studied the effect of combined Al off-stoichiometry and Mn co-substitution in p-type Fe₂V_1−xMn_xAl_1+y. As an extra finding, the thermal conductivity is substantially suppressed already in single-substituted Fe₂V_1−xMn_xAl and even further by introducing additional Al off-stoichiometry in Fe₂V_1−xMn_xAl_1+y. Moreover, the latter shows a sizeable enhancement of the thermopower and a shift of the maximum towards higher temperatures, together with an unexpectedly low electrical resistivity. It is crucial to focus on and optimize p-type full-Heusler systems suitable for applications in thermoelectric power generation, because the well-studied n-type material must be paired with a p-type counterpart to assemble efficient thermoelectric modules.

Experimental & computational details

High-purity elements of Fe (99.98%), Mn (99.99%), V (99.9%), and Al (99.999%), were weighted in the stoichiometric ratio and were arc-melted in Ar atmosphere on a water-cooled copper hearth. The ingots were turned over on the copper hearth and were re-melted for four times to ensure homogeneity. The obtained ingots were loaded to a tungsten carbide jar in the glove box under an Ar atmosphere and milled to a fine powder in a planetary ball mill at a speed of 200 rpm for 5 hours. The obtained fine powders were loaded in a graphite die and consolidated by spark plasma sintering (SPS, SPS-1080 System, SPS SYNTEX INC) under a pressure of 40 MPa at 1273 K for 10 minutes under static vacuum (2 × 10⁻² Pa). We performed post-annealing for all the samples after the SPS sintering the samples were sealed in quartz tubes for high-temperature annealing at 1273 K for 24 hours and then slowly cooled down to 673 K in 48 hours, where the samples were further annealed for 48 hours and finally naturally cooled to room temperature.

Powder X-ray diffraction measurements were performed to check the phase purity and lattice parameters of the cubic Heusler compounds using a RINT TTR-3 diffractometer (Rigaku Co., Akishima, Tokyo, Japan) and employing Cu K_α radiation. Experimental data were further analyzed by the Rietveld refinement method using the program RIETAN-FP.⁶⁴ Finally, bar-shaped samples were cut out of the disk samples and used to measure the Seebeck coefficient and electrical resistivity. Measurements were done with a four-probe method on a commercial system ZEM3 (Advance Riko Inc.). The thermal conductivity κ was calculated by using κ = DC_pd, where D is the thermal diffusivity, C_p is heat capacity, and d is density. The thermal diffusivity coefficient (D) and the heat capacity (C_p) of bulk material were concurrently measured for the disk sample on a xenon laser flash system (Netzsch LFA 467, Germany) with a pyro Ceram disk as a reference sample. Magnetization measurements were performed by using a superconducting quantum interference device magnetometer from Quantum Design.

Density functional theory calculations of the electronic structure of Fe₂V_1−xMn_xAl were performed using the coherent potential approximation (CPA) in the framework of the Korringa–Kohn–Rostoker (KKR) method and the atomic sphere approximation (ASA).^65,66 In our KKR–ASA calculations the partial wave functions were expanded in a spdf-basis (up to l = 3) and the effects of exchange and correlation are treated within the density functional theory using standard PBE exchange–correlation functionals.⁶² To model thermal magnetic disorder above the magnetic ordering temperature, we employed the disordered local moments (DLM) formalism.⁶⁷

Results and discussion

Fig. 1(a) and (c) shows the powder X-ray diffraction patterns for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y samples, respectively. All the samples crystallize in the Heusler (L2₁) type structure; no impurity peak or secondary phase has been observed. The (111) peak at around 27° is not very pronounced and is further suppressed with increasing Mn or Al concentration in Fe₂V_1−xMn_xAl or Fe₂V_0.9Mn_0.1Al_1+y [see Fig. S1(a) and (b) in the ESI†]. The suppressing of the (111) peak suggests that disorder in the Fe₂VAl compound becomes more significant with doping. Because the 111 peak is mainly due to the difference in the scattering factors of the Al and the V-sites, our findings indicate that an inter-atomic B2-type disorder exists between the two sites. The (220) peak at around 44.5° for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y is shown in Fig. 1(b) and (d), indicating a steady increase in the lattice parameter with increasing Mn/Al concentration. The broadening of (220) peak with increasing Mn concentration indicates that disorder is increasing in Mn-doped Fe₂VAl compounds. Also, the grain size reduction is another possibility of broadening of (220) peak. Moreover, the lattice parameter was obtained by Rietveld analysis for all samples. Fig. 1(e) and (f) exhibits the lattice parameters as a function of the concentration x and y for the Mn-doped and Al-rich samples, respectively. The increase in the lattice parameter with Mn doping is basically in line with Vegard's law. Also, we observed a slight deviation from Vegard's law for high Mn concentration, i.e., x = 0.6.⁶⁸ Furthermore, we found that the lattice parameter for Al-rich Fe₂V_0.9Mn_0.1Al_1+y is increasing with increasing Al doping. The increase of the lattice parameter with y in Fe₂V_0.9Mn_0.1Al_1+y does not follow Vegard's law. Moreover, the lattice parameter increases rapidly for y = 0.5, which deviates from previously reported results for the Al-rich Fe₂VAl_x.⁶⁹ Nonetheless, the overall tendency of an increasing lattice parameter is consistent with that reported on Al-rich Fe₂VAl_x, although the absolute values are smaller compared to those reported previously. The linear trend observed in the lattice parameter indicates that Mn atoms successfully substitute the V site; the solubility limit of Al in Al-rich Fe₂V_0.9Mn_0.1Al_1+y is y = 0.5. In comparison, the solubility limit of Al in pure Fe₂VAl_x was found to be x = 2 in ref. 64. For Al-rich Fe₂V_0.9Mn_0.1Al_1+y, the off-stoichiometry manifests itself through the presence of Al antisites on the Fe and V sites.⁶⁹ Overall, the crystallographic site occupancies can considerably affect the physical properties of Heusler compounds.⁷⁰

Fig. 1 (a) XRD patterns for Fe₂V_1−xMn_xAl sintered samples, with the numbers in the XRD pattern indicating Miller indices. (b) Zoomed view of (220) peak at around 44.5° for Fe₂V_1−xMn_xAl. (c) XRD patterns for Fe₂V_0.9Mn_0.1Al_1+y sintered samples. (d) Zoomed view of (220) peak at around 44.5° for Fe₂V_0.9Mn_0.1Al_1+y. (e) The lattice parameter was obtained by a refinement using the Rietveld method with RIETAN-FP⁶⁴ of Fe₂V_1−xMn_xAl as a function of concentration x of Mn, and the solid line represents the linear Vegard's law. (f) Lattice parameter obtained by a refinement of Fe₂V_0.9Mn_0.1Al_1+y as a function of y.

Fig. 2 depicts the temperature-dependent thermoelectric properties of Fe₂V_1−xMn_xAl. Firstly, the electrical resistivity at T = 300 K shows a slight increase as x increases up to x = 0.1, then gradually decreases with further increasing the Mn concentration in Fe₂V_1−xMn_xAl [Fig. 2(a)]. We note that the Seebeck coefficient for stoichiometric Fe₂VAl (x = 0) is slightly negative in this study, whereas usually sizeable positive values have been reported for samples synthesized via arc or induction melting.^45,71 This discrepancy can likely be explained by off-stoichiometry or antisite disorder induced during the synthesis via ball milling and has been found by other groups as well.^72,73 However, the Seebeck coefficient becomes p-type upon substituting Mn at the V site in Fe₂V_1−xMn_xAl, even though n-type doping would be expected from a simple estimation of the effective valence electron concentration per atom, indicating non-rigid band doping behavior. The absolute value of the Seebeck coefficient reaches S = 64 μV K⁻¹ at 300 K for Fe₂V_1−xMn_xAl with x = 0.2 [Fig. 2(b)]. For higher Mn-doped samples, the Seebeck coefficient decreases down to S = 16 μV K⁻¹ at 300 K for Fe₂V_1−xMn_xAl (x = 0.6). For non-doped Fe₂VAl, the Seebeck coefficient is almost temperature-independent, and the absolute value is near to zero. Again, these results deviate significantly from those obtained in melted samples and suggest the presence of defects such as antisites in the present sample. The highest value of the power factor PF = 0.8 mW K⁻² m⁻¹ [Fig. 2(c)] is obtained for Fe₂V_0.8Mn_0.2Al and peaks near room temperature, like all the other samples from Fe₂V_1−xMn_xAl.

Fig. 2 Thermoelectric properties of Fe₂V_1−xMn_xAl (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6) (a)–(d) temperature dependence of electrical resistivity ρ, Seebeck coefficient S, power factor PF, and total thermal conductivity κ, respectively.

The total thermal conductivity of Fe₂V_1−xMn_xAl [Fig. 2(d)], κ, is nearly temperature-independent, and the values decrease substantially upon Mn doping in Fe₂V_1−xMn_xAl. The total thermal conductivity at room temperature for stoichiometric Fe₂VAl is 16 W m⁻¹ K⁻¹, which is significantly lower than for melted samples (∼25–30 W m⁻¹ K⁻¹),^74,75 again indicating an increased number of defects such as antisite disorder, lattice strain, and grain boundaries that likely arise from the synthesis via ball milling. For Fe₂V_1−xMn_xAl (x = 0.6), the thermal conductivity further decreases down to 9 W m⁻¹ K⁻¹. In general, the total thermal conductivity κ for ordinary metals and semimetals is the sum of electronic and phonon terms, which can be specified as κ = κ_elec+ κ_ph, where κ_ph is the lattice thermal conductivity and κ_elec is the electronic contribution, although a bipolar share should be expected when minority carriers actively contribute to transport. Since previous studies on Fe₂VAl-based systems have neglected the bipolar contribution, we align our investigation with those works and only distinguish between lattice and electron contributions, where κ_el is related to the electrical resistivity ρ as given by the Wiedemann–Franz law κ_el = L₀T/ρ, where L₀ = 2.45 × 10⁻⁸ WΩ K⁻² is the Lorenz number, and ρ is the electrical resistivity. The lattice thermal conductivity (κ_ph) can be obtained by subtracting κ_el from the total thermal conductivity (κ). Fig. 3(a) shows κ_ph as a function of temperature. At room temperature, κ_ph drops from 14 to 7.5 W m⁻¹ K⁻¹ due to the Mn substitution, which is a significant reduction compared to previously reported values for doped Fe₂VAl systems,^{12,30,74,76–78} considering that there are no significant differences in atomic mass and size between Mn and V atoms. Meanwhile, it is obvious that κ_elec is smaller than κ_ph for all the studied compounds, which signifies that the total thermal conductivity is dominated by lattice phonons rather than charge carriers. This implies that a substantial further enhancement can be achieved by further suppressing heat conduction through phonons, e.g. by tuning the microstructure or via co-substitution as employed in the second part of this study. The dimensionless figure of merit, ZT, was determined and reaches its highest value ZT = 0.025, for Fe₂V_1−xMn_xAl (x = 0.4) at about T = 350 K [Fig. 3(b)].

Fig. 3 (a) Temperature dependence of lattice thermoelectric conductivity for Fe₂V_1−xMn_xAl. (b) The thermoelectric performance, ZT values vs. temperature for Fe₂V_1−xMn_xAl.

In order to further improve the TE properties of Mn-substituted Fe₂V_1−xMn_xAl, additional co-substitution/off-stoichiometry with Al at the Fe and V sites has been performed. This type of off-stoichiometry has been previously shown to not only significantly increase the p-type Seebeck coefficient of Fe₂VAl-based thermoelectrics but also greatly reduces the lattice thermal conductivity via substitutions on different sublattices.⁶⁹Fig. 5 demonstrates the temperature-dependent thermoelectric properties of Al-rich Fe₂V_0.9Mn_0.1Al_1+y. Indeed, within this study we have observed that ρ decreases with increasing Al concentration (see Fig. 5(a)). Furthermore, the temperature-dependent behavior of ρ(T) changes from semiconductor-like, dρ/dT < 0, towards metallic-like, dρ/dT > 0. It is interesting to note, however, that ρ reaches its lowest values for Fe₂V_0.9Mn_0.1Al_1.3 (y = 0.3) and increases again dramatically as y further rises up to y = 0.5, concomitant with an unexpected decrease of the carrier concentration. This indicates peculiar changes in the electronic structure and clearly shows that such Al off-stoichiometry cannot be regarded as a conventional doping mechanism.

Regarding the Seebeck coefficient, the additional off-stoichiometry clearly has a beneficial effect and not only increases the absolute values of the Seebeck coefficient but also modifies the overall temperature-dependent behavior such that S stays large over a broader temperature interval (see Fig. 5(b)). Upon increasing the amount of Al in Fe₂V_0.9Mn_0.1Al_1+y, the maximum of |S| shifts from below room temperature up to almost 500 K for Fe₂V_0.9Mn_0.1Al_1.5 (y = 0.5). Moreover, the peak value S = 82 μV K⁻¹ for Fe₂V_0.9Mn_0.1Al_1.5 (y = 0.5) is about 20% larger than the maximum value of the Fe₂V_1−xMn_xAl series, S = 61 μV K⁻¹ for x = 0.2 (shown in Fig. 3(b)). Hence, as expected, the Al-excess in terms of antisites on Fe and V sublattices has brought an enhancement in the Seebeck coefficient, consistent with findings in ref. 69. The value S = 82 μV K⁻¹ is comparable to the largest ones in the p-type Fe₂VAl-based systems^{12,19,44–49,69,74} and establishes such type of Al-off stoichiometry and concomitant co-substitution, e.g., with V/Mn, as a desirable route to improve the ZT of p-type full-Heusler systems. The temperature dependence of the Seebeck coefficient shows a maximum at around T = 350 K for y = 0.1 and 0.2, and around T = 450 K for x = 0.3 and 0.5. The maximum for y = 0 is not seen in Fig. 4(b), but is expected below T = 300 K. Thus, the maximum temperature systematically increases with increasing y. This reflects the increase in the hole carrier concentration by extra Al doping and also hints at a possible expansion of the band gap.

Fig. 4 Thermoelectric properties of Fe₂V_0.9Mn_0.1Al_1+y (y = 0, 0.1, 0.2, 0.3 and 0.5) (a)–(d) temperature dependence of electrical resistivity ρ, Seebeck coefficient S, power factor PF, and total thermal conductivity κ, respectively.

Compared to the single substitution series Fe₂V_1−xMn_xAl, where the power factor peaks at 0.8 mW K⁻² m⁻¹, PF is significantly improved up to 2.0 mW K⁻² m⁻¹ for Fe₂V_0.9Mn_0.1Al_1.1. However, the power factor decreases with increasing Al concentration in Fe₂V_0.9Mn_0.1Al_1+y, hovering around PF = 1.6–1.8 mW K⁻² m⁻¹ at 450–500 K for y = 0.3 and 0.5. The thermal conductivity of Fe₂V_0.9Mn_0.1Al_1+y shows only weak temperature dependence for the measured temperature range 300–550 K (see Fig. 5(d)). The thermal conductivity at room temperature for stoichiometric Fe₂V_0.9Mn_0.1Al, is 12.1 W m⁻¹ K⁻¹, while it decreases monotonically as a function of y down to 9 W m⁻¹ K⁻¹ for Fe₂V_0.9Mn_0.1Al_1+y (y = 0.5). We observed an almost 40% drop in thermal conductivity for Fe₂V_0.9Mn_0.1Al_1+y (y = 0.5) compared to the stoichiometric Fe₂VAl compound, despite the lack of any heavy element substitution in the investigated samples. The significant decreases in thermal conductivity with increasing Al in Fe₂V_0.9Mn_0.1Al_1+y is consistent with the findings in ref. 69 and is assumed to be stemming from the sizeable atomic disorder and point defects brought about by the large number of Al/Fe and Al/V antisites.

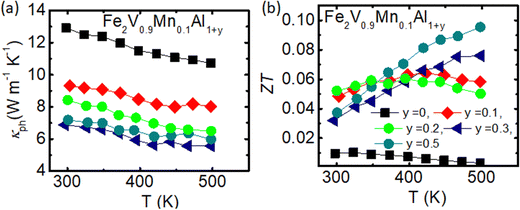Fig. 5 (a) Temperature dependence of lattice thermoelectric conductivity for Fe₂V_0.9Mn_0.1Al_1+y. (b) The thermoelectric performance, ZT values vs. temperature for Fe₂V_0.9Mn_0.1Al_1+y.

Fig. 6 (a) The Seebeck coefficient as a function of valence electron concentration (VEC) at 300 K. The dotted lines are doped off-stoichiometric Fe₂VAl data taken from ref. 78. (b) The Seebeck coefficient as a function of hole carrier concentration p estimated at T = 300 K for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y with Ioffe–Pisarenko cure.

The temperature dependence of κ_ph is shown in Fig. 5(a), which was again obtained by applying the Wiedemann–Franz law to estimate the electronic contribution from the experimental electrical resistivity. Overall, the thermal conductivity is phonon-driven, while the κ_elec contribution increases for Al-rich samples. As discussed in the previous section, the electrical resistivity was further decreased, and the Seebeck coefficient enhanced for the Al-rich Fe₂V_0.9Mn_0.1Al_1+y samples, Consequently, the power factor has improved, and thermal conductivity decreased for Al-rich Fe₂V_0.9Mn_0.1Al_1+y samples. Moderately, the ZT values have been improved for Fe₂V_0.9Mn_0.1Al_1+y (y = 0.5), with the highest ZT value 0.1 achieved for Fe₂V_0.9Mn_0.1Al_1+y (y = 0.5) at around T = 500 K [Fig. 5(b)].

Furthermore, we have investigated the valence electron concentration (VEC) dependence of the Seebeck coefficient (S) at T = 300 K for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y. Fe₂VAl has 24 valence electrons per formula unit, thereby VEC = 6.⁴⁰ As aliovalent elements are doped in the Fe₂VAl system, the VEC deviates from 6, which affects largely the Seebeck coefficient. For Mn-doped Fe₂V_1−xMn_xAl, the VEC scenario is not in agreement with the behavior observed within the majority of single-element doping studies reported in the literature so far; rather, we have observed a p-type Seebeck coefficient for the VEC > 6.0 (see Fig. 7(a)). The universal curve based on the VEC is only valid for the rigid band case.⁴⁰ However, substitutions on the Fe- or V-sites with certain transition metals, can cause significant changes in the electronic band structure; thereby, the simple VEC rule is no longer valid. For instance, off-stoichiometric Heusler alloys, Fe_2−xV_1+x−yTi_yAl (p-type Seebeck coefficient), have been investigated using soft X-ray photoelectron spectroscopy.⁷⁹ The electronic structure near the Fermi level is found to be drastically altered by off-stoichiometry, while doping with Ti has a more moderate effect in a rigid-band-like manner.⁷⁹ In the case of off-stoichiometric Fe_2−xV_1+x Al-based Heusler alloys, Soda et al. proposed that the excess V or Fe (antisite) defects may induce impurity states near the valence band edge, resulting in a potential enhancement of the Seebeck coefficient.⁸⁰ To elucidate the anomalous p-type Seebeck coefficient in nominally n-doped Fe₂V_1−xMn_xAl, we have performed extensive density functional theory calculations of the alloy-averaged densities of states of substituted Fe₂V_1−xMn_xAl, which are summarized in the subsequent section. Our theoretical investigations reveal that the Fermi level remains pinned near the valence band edge inside the pseudogap, owing to the creation of additional electronic states below E_F, which balances the chemical potential.

Fig. 7 The Seebeck effective mass () as a function of hole carrier concentration p estimated at T = 300 K for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y. The dotted line represents a linear trend in with increasing Mn doping in Fe₂V_1−xMn_xAl.

To further shed light on the anomalous doping dependence of Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y, we have measured the Hall resistivity to estimate the carrier concentration.

The magnetic field-dependent Hall resistivity for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y at T = 300 K is shown in the ESI† [see Fig. S7]. A linear magnetic field dependence ρ_xy was observed for all samples. The Hall coefficient R_H was then determined from the slope of ρ_xyversus the applied magnetic field B. The carrier concentration (p) was estimated using the simple equation p = 1/eR_H. All the samples (except for x = 0 and y = 0) are p-type, and the hole carrier concentration appears to increase monotonically with doping, except for y = 0.5.

The Seebeck coefficient as a function of carrier concentration at room temperature, known as the Ioffe–Pisarenko plot, is shown in Fig. 7(b). The results here deviate from the Ioffe–Pisarenko curve, especially in the heavily doped region. Although a general trend with a maximum is similar, a clear difference is that the peak is much wider than the normal IP curve, with a shift of maximum to higher carrier concentrations. This is consistent with an increase of the density of states effective mass. Indeed, DFT calculations reveal that rather localized electronic states are formed at both sides of the Fermi level and that the slope of the energy-dependent density of states is enhanced, which is in good agreement with experimental findings. Similar features were reported by Parzer et al. for the Al-rich Fe₂VAl system, where they suggested that a shift in a maximum of S vs. carrier concentration occurs due to resonant states located close to the Fermi level.⁶⁹ Therefore, Mn- and extra Al-doping can be a very fast and effective way to increase the Seebeck coefficient through disorder-related resonant levels in the Heusler compounds. In the present case, the Mn- and Al-doping provoked too much hole carriers, thereby the enhancement in the Seebeck coefficient was just moderate. It should also be stressed that thermally quenched samples of Fe₂VAl showed only n-type behavior and an effective strategy for enhancing the p-type Heusler compound has not been reported. The present findings, Mn- and/or excess Al-doping induced disorder may cast a new way for achieving p-type high power factor.

The Hall mobility was derived using μ_H = ρ_xy/(ρ_xxB) [see Table S2, ESI†]. μ_H decreases by increasing the Mn doping concentration in Fe₂V_1−xMn_xAl or increasing Al in Fe₂V_0.9Mn_0.1Al_1+y due to the increasing charge carrier density and/or increasing static disorder in the crystalline unit cell.

Fig. 7 shows the Seebeck effective mass () as a function of hole carrier concentration p estimated at T = 300 K for Fe₂V_1−xMn_xAl and Fe₂V_0.9Mn_0.1Al_1+y. 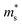was estimated using eqn (S1) (ESI†), where the values are directly proportional to the Seebeck coefficient and the carrier concentration (p).⁸¹ The formula used was taken from ref. 81 where it is suggested that there are two classes of effective masses; one describes an inertial effective mass that is relevant to a specific electron, and the other one depends more on the density of the electron states (DOS), and is hence called a DOS mass, 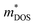. Further, 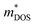can be directly calculated from the Seebeck coefficient employing eqn (S2) (ESI†); thus, 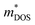can be considered as Seebeck effective mass (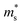). We found that with increasing carrier concentration, the Seebeck effective mass increases linearly in the case of Fe₂V_1−xMn_xAl, while for the Fe₂V_0.9Mn_0.1Al_1+y, it slightly deviates from linearity. According to literature, the tendencies of the Seebeck effective mass 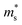at room temperature and above upon doping are straightforwardly explained by changes in the band structure, e.g., band convergence or changes in the dominant scattering mechanism. In fact, it has been mentioned for Al-rich Fe₂VAl_x systems that a local distortion of the electronic density of states arises for very large Al concentrations.⁶⁹ Again, the increase of 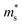is fully consistent with first-principles calculations, revealing a modification of the alloy-averaged densities of states, where both conduction and valence band edges become more steep. Thus, the density of states effective mass increases due to the rather localized impurity states by Mn, which spawn at both sides of the Fermi energy.

As can be seen in Fig. 6(a), p-type full Heusler materials have a smaller absolute value of the Seebeck coefficient compared to n-type materials. Additionally, it's challenging to obtain p-type materials due to a more restricted number of doping elements. Mn doping Al-rich Fe₂VAl could lead to improved thermoelectric properties in p-type materials near room temperature. The achieved power factor around 2.2 mW K⁻² m⁻¹ at T = 350 K, involving a Mn-doped Al-rich Fe₂VAl strategy, is larger than Ta-doped or Al-rich Fe₂VAl systems, while it is lower than for off-stoichiometric and Ti-doped samples, reaching up to ∼4 mW K⁻² m⁻¹.^12,52 In the present cases, the highest ZT value of 0.05 was achieved for Fe₂V_0.9Mn_0.1Al_1+y (y = 0.1, 0.2) near room temperature. The value of power factor for Mn-doped Al-rich Fe₂V_0.9Mn_0.1Al_1+y (y = 0.1) around 2.2 mW K⁻² m⁻¹ is a relatively high value for p-type Heusler compound near room temperature. The explored compounds could be useful for applications in thermoelectric power generation.

The magnetic properties of selected samples were also investigated. Fig. 8(a) depicts the temperature-dependent magnetization M under an applied external magnetic field B = 1 T for the Fe₂V_1−xMn_xAl (x = 0, 0.1, 0.2, 0.4) samples in the temperature range 2–300 K. We fitted the inverse of the magnetic susceptibility H/M vs. temperature measured at B = 1 T for x = 0, 0.1, 0.2 and 0.4 in the paramagnetic region above 200 K employing the Curie–Weiss function, H/M = (T − θ)/C, where C and θ are the Curie constant and Weiss temperature, respectively [see Fig. 8(b)]. From least squares fit, the obtained values of parameters C, and θ are summarized in Table 1. Because of the decreasing Curie constants upon an increasing Mn content, the overall susceptibility decreases. The value of θ can be seen as a measure of the inter-site magnetic interaction in the case of a molecular-field approximation. Thus, the samples with x = 0 and 0.1 are weakly ferromagnetic, with a Weiss temperature θ = 35 K and θ = 50 K, respectively, which can most likely be attributed to intrinsic antisite defects involving the Fe sublattices.

Fig. 8 (a) The temperature dependence of magnetization M for Fe₂V_1−xMn_xAl (x = 0, 0.1, 0.2, 0.4), (b) The inverse of magnetic susceptibility H/M vs. T for Fe₂V_1−xMn_xAl (x = 0, 0.1, 0.2, 0.4). The dotted line shows the fitting to the Curie–Weiss function H/M = (T − θ)/C with C = NP_eff²/3k_B, where P_eff, N, and k_B are the effective magnetic moment, number of magnetic ions and the Boltzmann constant, respectively. (c) and (d) The magnetization M vs. B curves for Fe₂V_1−xMn_xAl (x = 0, 0.1, 0.2, 0.4) at 2.0 K and 300 K.

Table 1 Obtained results from Curie–Weiss function H/M = (T − θ)/C for the Fe₂V_1−xMn_xAl samples

Samples	C (K emu mol^−1)	μ eff (μB per atoms)	θ (K)
x = 0	5.88	3.44	35
x = 0.1	4.05	2.87	50
x = 0.2	3.59	2.69	−2.5
x = 0.4	2.46	1.85	−14.6

---

A further increase of x, however, causes a crossover of θ to negative values (x = 0.4: θ ∼ −16 K), indicating that the growing Mn content triggers eventually antiferromagnetic interactions. This is very much in line with our first-principles calculations of the exchange interactions between Mn atoms shown in the ESI† (Table S7).

The derivative of magnetization dM/dT vs. T shows a peak at around 16 K for undoped Fe₂VAl and 30 K for x = 0.1, which suggests a Curie temperature T_C ∼ 16 K for x = 0 and T_C ∼ 30 K for x = 0.1 [see ESI,† Fig. S6(a)]. The isothermal magnetization at T = 2 K decreases rapidly with increasing Mn concentration in Fe₂V_1−xMn_xAl for x ≥ 0.2. This decrease in magnetization is expected due to the antiferromagnetic correlation between Mn atoms. The higher Mn concentration, for example, the x ≥ 0.2 samples, probably shows a ferrimagnetic nature, which is analogous to the ferrimagnetism reported in the Fe₂MnAl compound.⁸² However, above the Curie point, the inverse magnetic susceptibility is no longer following the Néel hyperbola. This deviation is due to the limitations of magnetization measurements in the paramagnetic state of the alloys without perfect atomic ordering. The effective magnetic moments evaluated from the respective Curie constants C are μ_eff = 3.44μ_B per atoms for x = 0, μ_eff = 2.87μ_B per atoms for x = 0.1, μ_eff = 2.69μ_B per atoms for x = 0.2, and μ_eff = 1.85μ_B per atoms for x = 0.4. The μ_eff values for x ≤ 0.2 are close to those calculated for Fe₂V_0.9Cr_0.1Al and other Fe₂VAl-based full-Heusler compounds etc.^31,53,83

Beyond that, it is interesting to point out that the Seebeck coefficient of the Mn-doped Fe₂V_1−xMn_xAl exhibits its maximum value of about 60 μV K⁻¹ at 300 K for a wide range of Mn concentrations, x = 0.1 to 0.4, as seen in Fig. 2(b). This plateau-like behavior cannot be explained by a normal doping dependence (see Fig. 6(a)). In addition, the magnetic interaction is also found to be reduced by Mn-doping, as is seen in Fig. 8. The undoped Fe₂VAl shows large effective magnetic moment μ_eff = 3.44μ_B per atoms, which suggests off-stoichiometry or Fe antisite defects is present in the sample. The values of effective magnetic moments decrease with increasing Mn doping levels in Fe₂V_1−xMn_xAl. We can assume that at low Mn doping level, isolated magnetic ions might act as local perturbations, but their influence on the overall magnetic interaction might be minimal. As the Mn doping level increases, the competing interactions could become more pronounced, potentially leading to a more significant reduction in magnetic interaction. Consequently, the Mn-doped samples need to assume other changes in the electronic structure emerging from the substitution of Mn atoms at the V sublattice that cause an enhancement of the Seebeck coefficient.

The magnetization (M) as a function of applied magnetic field (B) for Fe₂V_1−xMn_xAl (x = 0.1, 0.2, 0.4) is shown in Fig. 8(c) and (d) at 2.0 K and 300 K, respectively. The magnetization curves up to B = 5 T reveal a gradual change, from ferromagnetic-like features (x = 0.1) towards a paramagnetic behaviour for x = 0.4. Most importantly, the magnetization decreases with increasing Mn concentration. It might be possible that introducing Mn magnetic ions at the V site in Fe₂VAl could create several competing magnetic interactions. Depending on the specific magnetic ion and its interactions with Fe and Al, these competing interactions might partially cancel out the ferromagnetic order between Fe atoms, leading to a net reduction in the overall magnetic interaction strength. Also, we have studied magnetic properties for Al-rich Fe₂V_0.9Mn_0.1Al_1+y compounds [see ESI,† Fig. S5(a)–(d)].

Density functional theory calculations

To further elucidate the anomalous behavior of Mn substitution in Fe₂V_1−xMn_xAl, both with respect to the thermoelectric transport and magnetic properties, we performed extensive density functional theory (DFT) calculations on substituted Fe₂V_1−xMn_xAl Heusler compounds across different concentrations x. Our calculations indicate that Mn atoms, when substituted at the V site, exhibit a large local magnetic moment of around 2.43μ_B, while they stay non-magnetic, when substituted at the Fe sites.

To simulate the true paramagnetic state with thermally disordered magnetic moments at high temperatures, calculations were performed within the framework of the disordered local moment (DLM) approximation.⁶⁷ Moreover, the substitutional alloy disorder due to Mn atoms randomly replacing V atoms in the unit cell, is fully accounted for in the calculations of the electronic structure by making use of the Coherent Potential Approximation (CPA).⁶³Fig. 9(a) shows the atom-projected and spin-polarized density of states of a single Mn atom in Fe₂V_0.9Mn_0.1Al. A sizeable splitting between majority and minority spin channels is obvious, resulting in a large magnetic moment of around 2.43μ_B. Interestingly, both minority- and majority-spin contributions exhibit a gap at the Fermi energy. Moreover, rather sharp and localized features in the electronic density of states occur at both sides of the Fermi level for the majority-spin bands. These impurity states contribute to the total DOS of Fe₂V_1−xMn_xAl at the conduction and valence band edge as shown in Fig. 10(b), effectively narrowing the pseudogap of pristine Fe₂VAl with increasing Mn substitution.

Fig. 9 (a) Spin-polarized density of states of a single Mn atom in Fe₂V_0.9Mn_0.1Al, showing a sizeable splitting between majority and minority contributions, yielding a large magnetic moment m ∼ 2.43μ_B for Mn atoms substituted at the V site. (b) Partial atom-projected density of states of Fe₂V_0.9Mn_0.1Al.

Fig. 10 (a) Total density of states (DOS) of Fe₂V_1−xMn_xAl calculated in the disordered local moment (DLM) theory. (b) DOS around the Fermi energy, featuring contributions from rather localized Mn impurity states at the valence and conduction band edges, as well as a pinning of the Fermi level within the pseudogap. To indicate the energy range, relevant for thermoelectric transport, the derivative of the Fermi–Dirac distribution at 300 K is shown in grey.

Fig. 9(b) displays the atom-projected partial DOS of Fe₂V_0.9Mn_0.1Al in the paramagnetic state with the respective contributions from all atoms. We point out that, despite the large electron doping concentration of 0.2 e per formula unit upon substituting 10% Mn at the V site, the Fermi level remains virtually unaffected and stays within the pseudogap. This becomes even more evident in Fig. 10, where the total DOS of Fe₂V_1−xMn_xAl is shown for various Mn concentrations in the paramagnetic state, matching our experimentally investigated samples. Even for Mn substitutions as high as x = 0.5, corresponding to an entire additional electron, the Fermi level remains pinned within the pseudogap and does not get shifted into the conduction band. The anomalous doping behavior can be traced back to Mn forming magnetic impurity states below the Fermi energy (see Fig. 10(a)), which can accommodate the additional electrons doped by Mn in Fe₂V_1−xMn_xAl. Thus, although the valence electron concentration increases, the total number of states below E_F increases as well, rendering an unchanged position of E_F. This readily explains the unconventional VEC dependence of the Seebeck coefficient in Fig. 7(a), where S retains positive values even for VEC ≫ 6.

We also studied the effect of substituting Mn at the Fe site, i.e., considering that Mn may occupy the Fe site with Fe atoms simultaneously occupying the vacant V positions as antisite defects (Fe_1.9Mn_0.1V_0.9Fe_0.1Al), which cannot be ruled out by our standard X-ray diffraction experiments due to the very similar atomic scattering factors of Mn, Fe and V. However, the electronic density of states of Fe_1.9Mn_0.1V_0.9Fe_0.1Al (see ESI,† Fig. S8) indicates that this seems very unlikely, since a metallic ground state with a very large DOS at E_F emerges, which contradicts the experimental Seebeck coefficient and its VEC dependence.

Conclusion

Overall, p-type Fe₂VAl compounds are less developed compared to n-type ones. Here, we performed a systematic experimental and theoretical study of the thermoelectric properties of Mn-doped Fe₂V_1−xMn_xAl Heusler compounds across a wide range of Mn concentrations x = 0 – 0.6. We found an unexpected hole-dominated Seebeck coefficient in nominally n-doped Fe₂V_1−xMn_xAl. Using DFT calculations, the origin for this unconventional doping behavior was found to be rooted in distinct modifications of the electronic density of states upon Mn substitution. More specifically, Mn atoms at the V site form magnetic impurity states with a large local magnetic moment (m ∼ 2.43μ_B) and antiferromagnetic exchange interactions. The additional electronic states contributed below E_F exactly balance the chemical potential, such that E_F remains pinned at the valence band edge, within the pseudogap, even for very large Mn concentrations up to x = 0.6. Moreover, rather localized Mn states spawn at both sides of the pseudogap, yielding an increase of the DOS effective mass, albeit a narrowing of the pseudogap is triggered as well. Consequently, relatively large p-type Seebeck coefficients and an anomalous doping/VEC dependence emerges in Fe₂V_1−xMn_xAl.

The thermoelectric properties could be further improved by co-substituting Al antisites at the Fe and V sublattices in Al-rich Fe₂V_0.9Mn_0.1Al_1+y compounds. Fe₂V_0.9Mn_0.1Al_1.1 exhibits the largest Seebeck coefficient (S = 75 μV K⁻¹) and PF = 2.2 mW K⁻² m⁻¹ at T = 350 K. Also, the thermal conductivity decreased to 9 W m⁻¹ K⁻¹ for Fe₂V_0.9Mn_0.1Al_1.5 (y = 0.5). Consequently, the largest ZT value, ∼0.1, was found for Fe₂V_0.9Mn_0.1Al_1.5 (y = 0.5), at T = 500 K. Our study motivates further investigations and optimization studies of Fe₂VAl-based Heusler compounds, co-substituted with Mn at the V site, to realize high-performance p-type thermoelectrics, which are relevant for technological applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was mainly supported by JST Mirai Program Grant JPMJMI19A1. N. T. has been supported by JSPS KAKENHI, 22H01761.

References

1. L. E. Bell, Science, 2008, 321, 1457.
2. J. Heand and T. M. Tritt, Science, 2017, 357, eaak9997.
3. N. Nandihalli, C.-J. Liu and T. Mori, Nano Energy, 2020, 78, 105186.
4. I. Petsagkourakis, K. Tybrandt, X. Crispin, I. Ohkubo, N. Satoh and T. Mori, Sci. Technol. Adv. Mater., 2018, 19, 836.
5. T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Adv. Mater., 2017, 29, 1605884.
6. Z. Liu, N. Sato, W. Gao, K. Yubuta, N. Kawamoto, M. Mitome, K. Kurashima, Y. Owada, K. Nagase, C.-H. Lee, J. Yi, K. Tsuchiya and T. Mori, Joule, 2021, 5, 1196.
7. T. Mori, Small, 2017, 13, 1702013.
8. J. Mao, Z. Liu, J. Zhou, H. Zhu, Q. Zhang, G. Chen and Z. Ren, Adv. Phys., 2018, 67, 69–147.
9. T. Hendricks, T. Caillat and T. Mori, Energies, 2022, 15, 7307.
10. Y. Nishino, M. Kato, S. Asano, K. Soda, M. Hayasaki and U. Mizutani, Phys. Rev. Lett., 1997, 79, 1909.
11. H. Kato, M. Kato, Y. Nishino, U. Mizutani and S. Asano, J. Jpn. Inst. Met., 2001, 65, 652.
12. Y. Nishino and Y. Tamada, J. Appl. Phys., 2014, 115, 123707.
13. G. Y. Guo, G. A. Botton and Y. Nishino, J. Phys.: Condens. Matter, 1998, 10, L119.
14. D. J. Singh and I. I. Mazin, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 14352.
15. R. Weht and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6855.
16. A. Laila, M. Nanko and M. Takeda, Mater. Trans., 2020, 61, 2216.
17. M. Weinert and R. E. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 9732.
18. H. Okamura, J. Kawahara, T. Nanba, S. Kimura, K. Soda, U. Mizutani, Y. Nishino, M. Kato, I. Shimoyama, H. Miura, K. Fukui, K. Nakagawa, H. Nakagawa and T. Kinoshita, Phys. Rev. Lett., 2000, 84, 3674.
19. F. Garmroudi, A. Riss, M. Parzer, N. Reumann, H. Muller, E. Bauer, S. Khmelevskyi, R. Podloucky, T. Mori, K. Tobita, Y. Katsura and K. Kimura, Phys. Rev. B, 2021, 103, 085202.
20. F. Garmroudi, M. Parzer, A. Riss, A. V. Ruban, S. Khmelevskyi, M. Reticcioli, M. Knopf, H. Michor, A. Pustogow, T. Mori and E. Bauer, Nat. Commun., 2022, 13, 3599.
21. F. Garmroudi, M. Parzer, A. Riss, N. Reumann, B. Hinterleitner, K. Tobita, Y. Katsura, K. Kimura, T. Mori and E. Bauer, Acta Mater., 2021, 212, 116867.
22. F. Garmroudi, M. Parzer, A. Riss, S. Beyer, S. Khmelevskyi, T. Mori, M. Reticcioli and E. Bauer, Materials Today, Physics, 2022, 27, 100742.
23. Z. Liu, W. Gao, H. Oshima, K. Nagase, C.-H. Lee and T. Mori, Nat. Commun., 2022, 13, 1120.
24. K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965–971.
25. L. Wang, N. Sato, Y. Peng, R. Chetty, N. Kawamoto, D. H. Nguyen and T. Mori, Advanced Energy, Materials, 2023, 13, 2301667.
26. Y. C. Lan, B. Poudel, Y. Ma, D. Z. Wang, M. S. Dresselhaus, G. Chen and Z. F. Ren, Nano Lett., 2009, 9, 1419.
27. Y.-Z. Li, Q. Zhang, K. Liu, Y.-J. Lin, N. Lin, Y. Yu, F. Liu, X.-B. Zhao, B.-H. Ge, O. Cojocaru-Mirédin, C.-G. Fu and T.-J. Zhu, Materials Today, NANO, 2023, 22, 100340.
28. J. Pei, B. Cai, H.-L. Zhuang and J.-F. Li, Natl. Sci. Rev., 2020, 7, 1856–1858.
29. Y. Feng, J. Y. Rhee, T. A. Wiener, D. W. Lynch, B. E. Hubbard, A. J. Sievers, D. L. Schlagel, T. A. Lograsso and L. L. Miller, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 165109.
30. K. Soda, H. Murayama, K. Shimba, S. Yagi, J. Yuhara, T. Takeuchi, U. Mizutani, H. Sumi, M. Kato, H. Kato, Y. Nishino, A. Sekiyama, S. Suga, T. Matsushita and Y. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 245112.
31. M. Kato, Y. Nishino, U. Mizutani and S. Asano, J. Phys.: Condens. Matter, 2000, 12, 1769–1779.
32. T. Naka, K. Sato, M. Taguchi, T. Nakane, F. Ishikawa, Y. Yamada, Y. Takaesu, T. Nakama and A. Matsushita, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085130.
33. S. Jemima, A. Mani, A. Bharathi, N. Ravindran and Y. Hariharan, J. Alloys Compd., 2001, 326, 183–187.
34. E. P. Amaladass, A. T. Satya, S. Sharma, K. Vinod, V. Srinivas, C. S. Sundar and A. Bharathi, J. Alloys Compd., 2015, 648, e34–e38.
35. O. Nashima, T. Kanomata, Y. Yamaguchi, S. Abe, T. Harada, T. Suzuki, H. Nishihara, K. Koyama, T. Shishido, K. Watanabe and T. Kaneko, J. Alloys Compd., 2004, 383, 298–301.
36. M. Mikami, Y. Kinemuchi, K. Ozaki, Y. Terazawa and T. Takeuchi, J. Appl. Phys., 2012, 111, 093710.
37. R. Jha, N. Tsujii, C. Bourgès, W. Gao, E. Bauer and T. Mori, Z. Anorg. Allg. Chem., 2022, 648, e202200058.
38. W. Lu, W. Zhang and L. Chen, J. Alloys Compd., 2009, 484, 812–815.
39. F. Kobayashi, N. Ide and Y. Nishino, J. Jpn. Inst. Met., 2007, 71, 208.
40. Y. Nishino, IOP Conf. Ser.: Mater. Sci. Eng., 2011, 18, 142001.
41. T. Sugiura and Y. Nishino, J. Jpn. Inst. Met., 2009, 73, 846.
42. Y. Sandaiji, N. Ide, Y. Nishino, T. Owada, S. Harada and K. Soda, J. Jpn. Soc. Powder Powder Metall., 2010, 57, 207.
43. I. Knapp, B. Budinska, D. Milosavljevic, P. Heinrich, S. Khmelevskyi, R. Moser, R. Podloucky, P. Prenninger and E. Bauer, Phys. Rev. B, 2017, 96, 045204.
44. K. Iwase, Y. Nishino, H. Miyazaki and K. Soda, J. Jpn. Inst. Met., 2008, 72, 464.
45. Y. Nishino, H. Kato, M. Kato and U. Mizutani, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 233303.
46. Y. Hanada, R. O. Suzuki and K. Ono, J. Alloys Compd., 2001, 329, 63.
47. C. S. Lue and Y.-K. Kuo, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 085121.
48. T. Nakama, Y. Takaesu, K. Yagasaki, T. Naka, A. Matsushita, K. Fukuda and Y. Yamada, J. Phys. Soc. Jpn., 2005, 74, 1378.
49. Y. Nishino, S. Kamizono, H. Miyazaki and K. Kimura, AIP Adv., 2019, 9, 125003.
50. B. Hinterleitner, I. Knapp, M. Poneder, Y. Shi, H. Müller, G. Eguchi, C. Eisenmenger-Sittner, M. Stöger-Pollach, Y. Kakefuda, N. Kawamoto, Q. Guo, T. Baba, T. Mori, S. Ullah, X.-Q. Chen and E. Bauer, Nature, 2019, 576, 85–90.
51. H. Matsuura, Y. Nishino, U. Mizutani and S. Asano, J. Jpn. Inst. Met., 2002, 66, 767.
52. H. Miyazaki, S. Tanaka, N. Ide, K. Soda and Y. Nishino, Mater. Res. Express, 2014, 1, 015901.
53. N. Tsujii, A. Nishide, J. Hayakawa and T. Mori, Sci. Adv., 2019, 5, eaat5935.
54. R. Ang, A. U. Khan, N. Tsujii, K. Takai, R. Nakamura and T. Mori, Angew. Chem., Int. Ed., 2015, 54, 12909.
55. F. Ahmed, N. Tsujii and T. Mori, J. Mater. Chem. A, 2017, 5, 7545.
56. Y. Zheng, T. Lu, Md. M. H. Polash, M. Rasoulianboroujeni, N. Liu, M. E. Manley, Y. Deng, P. J. Sun, X. L. Chen, R. P. Hermann, D. Vashaee, J. P. Heremans and H. Zhao, Sci. Adv., 2019, 5, eaat9461.
57. J.-B. Vaney, S. Aminorroaya Yamini, H. Takaki, K. Kobayashi, N. Kobayashi and T. Mori, Mater. Today Phys., 2019, 9, 100090.
58. S. Hebert, R. Daou, A. Maignan, S. Das, A. Banerjee, C. Bourgès, N. Tsujii and T. Mori, Sci. Technol. Adv. Mater., 2021, 22, 583.
59. W. L. Lee, S. Watauchi, V. L. Miller, R. J. Cava and N. P. Ong, Phys. Rev. Lett., 2004, 93, 226601.
60. R. Ramos, M. H. Aguirre, A. Anadon, J. Blasco, I. Lucas, K. Uchida, P. A. Algarabel, L. Morellón, E. Saitoh and M. R. Ibarra, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054422.
61. H. Matsuura, M. Ogata, T. Mori and E. Bauer, Phys. Rev. B, 2021, 104, 214421.
62. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
63. B. L. Gyorffy, Phys. Rev. B: Solid State, 1972, 5, 2382.
64. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15.
65. I. A. Abrikosov and H. L. Skriver, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16532.
66. A. V. Ruban and H. L. Skriver, Comput. Mater. Sci., 1999, 15, 199.
67. B. L. Gyorffy, A. J. Pindor, J. Staunton, G. M. Stocks and H. Winter, J. Phys. F: Met. Phys., 1985, 15, 1337.
68. A. Denton and N. Ashcroft, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 3161.
69. M. Parzer, F. Garmroudi, A. Riss, S. Khmelevskyi, T. Mori and E. Bauer, Appl. Phys. Lett., 2022, 120, 071901.
70. F. Garmroudi, M. Parzer, A. Riss, A. Pustogow, T. Mori and E. Bauer, Phys. Rev. B, 2023, 107, L081108.
71. B. Hinterleitner, F. Garmroudi, N. Reumann, T. Mori, E. Bauer and R. Podloucky, J. Mater. Chem. C, 2021, 9, 2073–2085.
72. K. Kurosaki, H. Muta, Y. Endo, A. Charoenphakdee, M. Uno and S. Yamanaka, J. Alloys Compd., 2009, 486, 507–510.
73. Y. Takagiwa and Y. Iwasaki, ACS Appl. Energy Mater., 2023, 6(15), 8256–8265.
74. Y. Nishino, S. Deguchi and U. Mizutani, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115115.
75. B. Hinterleitner, P. Fuchs, J. Rehak, F. Garmroudi, M. Parzer, M. Waas, R. Svagera, S. Steiner, M. Kishimoto, R. Moser, R. Podloucky and E. Bauer, Phys. Rev. B, 2020, 102, 075117.
76. Y. Nishino, H. Sumi and U. Mizutani, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 094425.
77. C. S. Lue, C. F. Chen and K. Kuo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064204.
78. M. Mikami and K. Kobayashi, J. Alloys Compd., 2008, 466, 530–534.
79. K. Soda, S. Harada, M. Kato, S. Yagi, M. Inukai, H. Miyazaki, Y. Sandaiji, Y. Tamada, S. Tanaka, T. Sugiura and Y. Nishino, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 236.
80. K. Soda, S. Harada, M. Kato, S. Yagi, Y. Sandaiji and Y. Nishino, IOP Conf. Ser.: Mater. Sci. Eng., 2011, 18, 142004.
81. G. J. Snyder, A. Pereyra and R. Gurunathan, Adv. Funct. Mater., 2022, 32, 2112772.
82. N. I. Kourov, V. V. Marchenkov, A. V. Korolev, L. A. Stashkova, S. M. Emelyanova and H. W. Weber, Phys. Solid State, 2015, 57, 700–708.
83. K. Sato, T. Naka, M. Taguchi, T. Nakane, F. Ishikawa, Y. Yamada, Y. Takaesu, T. Nakama, A. de Visser and A. Matsushita, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104408.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc00779d

---