Tuning quantum interference through molecular junctions formed from cross-linked OPE-3 dimers

Abstract

This study highlights a novel strategy for tuning the electrical conductance of single molecules by cross linking the molecules to form a dimer. By studying the electrical conductance of dimers formed by cross linking OPE monomers, we demonstrate that the appearance of destructive or constructive quantum interference in cross-linked OPE-based dimers is independent of the nature of the molecular cross link. Instead, the type of the interference is controlled by the connectivity to external electrodes and is determined by the presence or otherwise of meta-connected phenyl rings in the transport path. This is expected to be an important design feature, when synthesising molecules with cross links of different stiffnesses for thermoelectric energy harvesting, since it shows that the stiffness (and hence phonon transport properties) can be tuned without affecting the nature of the electronic quantum interference.

---

Comprehending charge transport through single molecules or self-assembled monolayers (SAMs), is an essential goal of molecular electronics research.^1–3 To realize this target, various strategies have been developed to measure the conductance, current–voltage characteristics, inelastic electron tunneling spectra, transition voltage spectra (TVS), and current-induced local heating of single molecules located between two electrodes.^4–7 Theories of electron transport in single-molecule junctions are built on the concept that electrons passing through a molecule from a source electrode to a drain electrode are phase coherent and that the energy E of the electron does not change during the passage.^8–10 Consequently, if the source–drain voltage is small, the electrical conductance G of the molecular junction is given by the Landauer formula G = G₀T(E_F), where G₀ is the quantum of conductance and T(E_F) is the transmission coefficient, evaluated at the Fermi energy E_F of the electrodes.

Typically, E_F lies within the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the molecule and consequently certain simplifications arise, which would not occur if E_F coincided with either of the HOMO or LUMO energy levels. For example, the electrical conductance of OPE-like molecules is measured to be proportional to the cosine-squared of the dihedral angle between neighbouring phenyl rings⁸ and theory shows that this occurs, because E_F lies within the HOMO–LUMO gap.^11,12 We have chosen OPE3 dimers as examples of cross-linked molecules, because their monomer counterparts have been studied extensively in the literature, both for their quantum-interference-derived properties^13–18 and their thermal properties.^19,20

In the current work, we address the question of how electrical conductances of linear molecules change when a chemical cross link is introduced between pairs of molecules to form dimers. We study the conductance of molecular dimers composed of a series of cross-linked OPE3 molecules, and we derive useful rules for predicting their transport properties, based on identification of the dominant transport paths for electrons passing through the dimers. These transport properties are also rationalised by identifying quantum interference features associated with frontier orbitals, taking into account their energy level spacings and degeneracies.

To form a cross-linked dimer, we started from the well-studied oligophenyleneethynylene (OPE3) molecule, which is known to be a highly conjugated molecular conductor. Next, we linked two OPE3s together by bridges formed from either an alkane chain to create 1 or a highly conjugated phenyleneethynylenechain to create 2, as shown in Fig. 1.

Fig. 1 Two OPE3 molecules cross-linked by two different bridges to form molecules 1 and 2. Each molecule possesses four thiol terminal end-groups (SH).

Computational methods

All the theoretical simulations were carried out using the density functional (DFT) code SIESTA.²¹ The optimised geometries of isolated cross-linked dimers were obtained by relaxing the cross-link dimers until all forces on the atoms were less than 0.01 eV Å⁻¹ (for more detail see optimised DFT structures of isolated structures see Fig. S1, ESI†). We used a double-zeta plus polarization orbital basis set, norm-conserving pseudopotentials, the local density approximation (LDA) exchange correlation functional, and to define the real space grid, an energy cutoff of 250 Rydbergs. We also computed results using GGA and found that the resulting structures were comparable,^22–24 with those obtained using LDA. The electronic properties of the cross-linked (C-L), dimers were modelled using a combination of DFT and quantum transport theory. We are interested in computing the electrical conductance of each dimer when a source electrode makes contact with one of the thiols and a second (drain) electrode makes contact with a different thiol. Since these C-L dimers (labelled 1 and 2 in Fig. 2), possess four terminal thiol end-groups, we computed transport properties with 6 distinct pairs of contacts to electrodes. For each of the two C-L dimers, the highest occupied molecular orbital (HOMO), lowest unoccupied orbital (LUMO), and their neighbours (i.e., HOMO−1, LUMO+1 etc), along with their energies are shown in Fig. S3 and S4 (ESI†). In the absence of the bridges, since two isolated OPE3s each possess identical orbital energy levels, the energy levels of the decoupled dimer are doubly degenerate. In the presence of a bridge, each degenerate pair is weakly coupled and the degeneracy is slightly lifted. Consequently, as shown in Fig. S3 and S4 (ESI†), the LUMO and LUMO+1 of each dimer are almost degenerate and similarly the HOMO and HOMO−1 are almost degenerate.

Fig. 2 Four different sulphur atoms can connect to external electrodes as 6 different pairs, namely 1–3, 2–4, 1–2, 3–4, 1–4, 2–3. 1–3 = 2–4: para–para (P–P), 1–2 = 3–4: ortho–meta (O–M), 1–4: ortho–ortho (O–O), and 2–3: meta–meta (M–M).

Our aim is to compute the electrical conductances of these OPE3 dimers (1–2), when only two of the four thiols are contacted to two metal electrodes and the current passes from one electrode to another via the dimer. As shown in Fig. 2, if the thiols are labelled 1 to 4, then there are 6 choices of thiol pairs, namely 1–3, 2–4, 1–2, 3–4, 1–4 and 2–3. To anticipate the role of quantum interference, we note that the triple bond labelled ‘a’ is para connected to triple bond ‘b’, and following the discussion in ref. 25 since para (and ortho) connectivity corresponds to constructive quantum interference (CQI), electrons travelling from thiol 1 to thiol 3 are expected to experience CQI and the corresponding electrical conductance is expected to be high. Similarly, since triple bond ‘e’ is para connected to triple bond ‘f’, electrons travelling from thiol 2 to thiol 4, or from thiol 1 to thiol 3 are expected to experience CQI, leading to high electrical conductance. On the other hand, triple bond ‘a’ is ortho connected to triple bond ‘c’, and triple bond ‘e’ is meta connected to triple bond ‘d’. Since meta connectivity corresponds to destructive quantum interference (DQI), electrons travelling from thiol 1 to thiol 2, or from thiol 3 to thiol 4, or from thiol 1 to thiol 2 are expected to experience DQI, leading to low electrical conductance. It should be noted that electrons travelling from thiol 1 to thiol 2 pass through the ortho path ‘a’–‘c’, and the meta path ‘d’–‘e’. Similarly, from thiol 3 to thiol 4, there is a meta path ‘b’-‘c’ and an ortho path ‘d’-‘f’. Since the meta paths leads to DQI the conductance of molecules connected to electrodes via the thiol pairs 1–2 or 3–4 is expected to be low up to this point four thiol pairs are explored 1–3, 2–4, 1–2, 3–4 and the predicted trend is either CQI (1–3 and 2–4) or DQI (1–2 and 3–4). Next we consider the electrical conductance when electrodes are connected to thiols 1 and 4 or 2 and 3. Since the 1–4 path includes ortho ‘a’–‘c’ and ortho ‘d’–‘f’, we expect it to exhibit CQI and high electrical conductance. In contrast, the 2–3 connectivity to electrodes involves the meta-connected paths ‘e’–‘d’ and ‘c’–‘d’, leading to DQI and therefore low electrical conductance is anticipated.

To examine the above quantum interference predictions, we construct a Hückel (i.e., tight binding, TB) Hamiltonian,^26–37 which captures the dependence of the conductance for the two cross-linked dimers on their connectivity to electrodes. The Hamiltonian matrix comprises of diagonal elements H_jj = ε_j, which describe the energy ε_j of an electron on site j and nearest neighbour off-diagonal elements H_ij, which describe hopping integrals between neighbouring sites l and j. All other matrix elements are set to zero. If all the sites were identical, then the simplest model would be obtained by setting all ε_j = 0 (which defines the zero of energy) and all nearest neighbour coupling equal to −1, which sets the energy scale. Such a Hamiltonian is a simple connectivity table, whose entries H_ij are equal to −1 when two atoms i and j are connected and are zero otherwise.

When semi-infinite one-dimensional crystalline leads are coupled to sites 1 and 3, the resulting transmission coefficient T(E) is shown as the red-solid curve in Fig. 3. The smooth nature of this curve near the middle of the HOMO–LUMO gap (E = 0) indicates the presence of CQI. Similarly, coupling to sites 2 and 4, leads to CQI, as indicated by the smooth nature of the red-dotted curve near E = 0. On the other hand, when electrodes are linked to sites 1 and 2 or 3 and 4, the green-solid/-dotted curves are produced. These curves possess sharp dips near E = 0, signaling the presence of DQI.^38–44 For electrodes connected to sites 1 and 4 the purple-sold curve is produced and exhibits CQI, whereas for electrodes connected to sites 2 and 3, the light green-sold curve is produced, which possesses a DQI dip. These results for a tight binding model with a single bond H_ij forming the bridge between the monomers, which is the simplest model of 1, in which an alkane chain bridges the dimer. Tight binding transmission coefficients of cross-linked dimers 1 and 2 demonstrate that the bridging linker has no influence on the presence of CQI or DQI in the transmission curves, because the two dimers exhibit roughly the same curves for the 6 different pairs of contacts, as demonstrated in Fig. S5 and S6 (ESI†).

Fig. 3 Transmission coefficients, obtained from the tight binding model (TBM), for 6 different connectivities to electrodes (see Fig. 2) tp cross-linked, dimer 1. Curves for the para connected junctions 1–3 and 2–4 (red-solid and red-dotted lines) are identical, as are the curves for ortho connected and meta connected junctions 1–2 and 3–4 (green-solid and green-dotted lines). Transmission coefficients of the ortho–ortho connected and meta–meta connected junctions 1–4 and 2–3 are purple-solid and light green-solid lines. Note: TBM detail, the coupling parameter γ = −1 and on energy sites of carbon and sulphur are ε_C = 0 and ε_S = 0.

To compare with the TBM results we performed DFT transport simulations for the two C-L dimers, each with 6 different pairs of connectivities to electrodes. To simulate the likely contact configuration during a break-junction experiment, we employed gold metal electrodes constructed from 6 layers of Au (111), each containing 30 gold atoms and further terminated with a pyramid of gold atoms. After relaxing each molecular junction, we calculated the transmission coefficient for each of the two molecules shown in Fig. 1, using the Gollum quantum transport code³⁶ (for more details, see DFT-based transport simulations section in the ESI†).

Fig. 4, shows zero bias transmission coefficients T(E), obtained from density functional theory, for 6 different electrode connectivities to dimer 1. This figure displays 6 transmission functions; three of them show CQI, while the other three show DQI. In agreement with the tight binding results and the above discussion, these show that DQI arises when the transport path contains one of more meta connected phenyl rings.

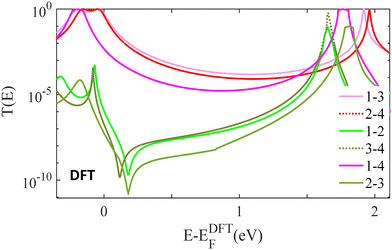Fig. 4 Zero bias transmission coefficients T(E), obtained from density functional theory (DFT), in 6 different possible pairs contact points (see Fig. 2). Cross-linked, dimer 1: para connected junctions 1–3 and 2–4 (red-solid and red-dotted lines), ortho connected + meta connected junctions 1–2 and 3–4 (green-solid and green-dotted lines), ortho connected + ortho connected and meta connected + meta connected junctions 1–4 and 2–3 (purple-solid and light green-solid lines).

TBM results are in qualitative agreement with the DFT transmission coefficients of the studied molecules, as shown in Fig. S5 of the ESI.† Both TBM and DFT approaches demonstrate that in the presence of the 1–3, 2–4 and 1–4 connectivities, there is no signature of a DQI. However, the same dimers with 1–2, 3–4 and 2–3 connectivities switch from CQI to DQI regardless to the bridging linker chemical structure. The main qualitative difference between the DFT results and the TBM results arise from the fact that the tight-binding model is a nearest-neighbour bipartite lattice, in which atoms can be labelled, such that odd numbered atoms interact with even numbered atoms only and vice versa. This chiral symmetry guarantees that the transmission coefficient is a symmetric function of the electron energy E. In the DFT simulation, this symmetry is not present, because next-nearest-interactions are present. The DFT results (S7–S20, ESI†) demonstrate that the presence or otherwise of DQI is insensitive to the nature of the bridging linker and confirm that 1–3, 2–4 and 1–4 are high conductance connectivities due to CQI, whereas 1–2, 3–4 and 2–3 are low-conductance connectivities, due to the presence of DQI.^37–42

In summary, using density functional theory and a tight-binding model, we have demonstrated that the appearance of destructive or constructive quantum interference in cross-linked OPE-based dimers is independent of the nature of the nature of the molecular cross link. Instead, the nature of the interference is controlled by the connectivity to external electrodes and is determined by the presence or otherwise of meta-connected phenyl rings on the transport path. This is expected to be an important design feature, when synthesising molecules with cross links of different stiffnesses, because it means that the stiffness and hence phonon transport properties can be tuned, whilst maintaining CQI or DQI.

In the literature, and as discussed in a recent textbook,⁸ there are many demonstrations of quantum interference effects in monomer molecules, starting with the first demonstration DQI⁴² in 2011 and including more recent demonstrations of QI, such as ref. 43–45 switching in ref. 46–49 and QI in graphene junctions.^50–52 In contrast, the present paper breaks new ground, by investigating and demonstrating quantum interference effects in cross-linked dimers. These results have several experimental consequences. For example, when applied for experimental systems based on break junction experiments, where all connectivities would be sampled, our calculations lead to the prediction that conductance histograms with multiple peaks would be measured, corresponding to both CQI (high conductances) and DQI (low conductances). In addition, in a break junction experiment, they predict the appearance of qualitatively distinct pulling curves. In one type of a curve, electrodes will maintain e.g., a 1–3 connectivity and the junction will break cleanly, leading to a single dominant conductance plateau. In another, the junction may jump from a 1-3 connectivity to a 3-2 connectivity before breaking, leading to two distinct plateaus in a pulling curve.

In the case of SAMs, if both thiols 3 and 4 are initially bound to a substrate and a top contact such as graphene is added, then the 1–3, 2–4 connectivities will act in parallel, leading to CQI and high conductance. In contrast, if the staggered conformations in Fig. 1 are realised, then only the 3-2 connectivity will be relevant, leading to CQI and low conductance. This leads to a new strategy for achieving novel memristive switching behaviour in SAMs, in which a functional cross-linker is employed, whose rigidity can be switched in response to an external stimulus, which in turn causes the molecule to switch between a staggered and non-staggered conformation. The associated switching from a high to low electrical conductance, with an on–off ratio of up to 6 orders of magnitude (see Fig. 4) would be ideal for in-memory, vector-matrix multiplication in deep neural networks.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Leverhulme Trust for Early Career Fellowship ECF-2020-638 and the Engineering and Physical Sciences Research Council of UK (QMol project EP/X026876/1). B. A. is grateful for financial assistance from Northern Border University (Saudi Arabia), and the Saudi Ministry of Education. A. A. is grateful to the Deanship of Scientific Research at Prince Sattam bin Abdulaziz University, Al-Kharj. A. K. I. and A. A. are grateful for financial assistance from Tikrit and Anbar Universities (Iraq), and the Iraqi Ministry of Higher Education (SL-20).

References

1. A. Nitzan and M. A. Ratner, Electron transport in molecular wire junctions, Science, 2003, 300(5624), 1384–1389.
2. N. J. Tao, Electron transport in molecular junctions, Nat. Nanotechnol., 2006, 1(3), 173–181.
3. R. L. McCreery, Molecular electronic junctions, Chem. Mater., 2004, 16(23), 4477–4496.
4. J. Hihath, C. Bruot, H. Nakamura, Y. Asai, I. Díez-Pérez, Y. Lee, L. Yu and N. Tao, Inelastic transport and low-bias rectification in a single-molecule diode, ACS Nano, 2011, 5(10), 8331–8339.
5. S.-Y. Jang, P. Reddy, A. Majumdar and R. A. Segalman, Interpretation of stochastic events in single molecule conductance measurements, Nano Lett., 2006, 6(10), 2362–2367.
6. M. T. González, S. Wu, R. Huber, S. J. Van Der Molen, C. Schönenberger and M. Calame, Electrical conductance of molecular junctions by a robust statistical analysis, Nano Lett., 2006, 6(10), 2238–2242.
7. X. Wang, A. Ismael, B. Alanazi, A. Al-Jobory, J. Wang and C. J. Lambert, High Seebeck coefficient from isolated oligo-phenyl arrays on single layered graphene via stepwise assembly, J. Mater. Chem. C, 2023, 11(42), 14652–14660.
8. C. J. Lambert, Quantum transport in nanostructures and molecules, IOP Publishing, 2021.
9. L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Dependence of single-molecule junction conductance on molecular conformation, Nature, 2006, 442, 904.
10. S.-X. Liu, A. K. Ismael, A. Al-Jobory and C. J. Lambert, Signatures of Room-Temperature Quantum Interference in Molecular Junctions, Acc. Chem. Res., 2023, 4193–4201.
11. C. M. Finch, S. Sirichantaropass, S. W. Bailey, I. M. Grace, V. M. Garcia-Suarez and C. J. Lambert, Conformation dependence of molecular conductance: chemistry versus geometry, J. Phys.: Condens. Matter, 2007, 20(2), 022203.
12. A. K. Ismael and C. J. Lambert, Molecular-scale thermoelectricity: a worst-case scenario, Nanoscale Horiz., 2020, 5(7), 1073–1080.
13. Y. Fan, S. Tao, S. Pitié, C. Liu, C. Zhao, M. Seydou, Y. J. Dappe, P. J. Low, R. J. Nichols and L. Yang, Destructive quantum interference in meta-oligo(phenyleneethynylene) molecular wires with gold–graphene heterojunctions, Nanoscale, 2024, 16, 195–204.
14. E. Gorenskaia, J. Potter, M. Korb, C. J. Lambert and P. J. Low, Exploring relationships between chemical structure and molecular conductance: from α,ω-functionalised oligoynes to molecular circuits, Nanoscale, 2023, 15, 10573.
15. E. Gorenskaia, M. Naher, L. Daukiya, S. A. Moggach, D. Costa Milan, A. Vezzoli, C. J. Lambert, R. J. Nichols, T. Becker and P. J. Low, Experimental validation of quantum circuit rules in molecular junctions, Aust. J. Chem., 2021, 74, 806–818.
16. D.-Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, M. R. Bryce and C. J. Lambert, A quantum circuit rule for interference effects in single-molecule electrical junctions, Nat. Commun., 2015, 6, 6389.
17. W. Haiss, C. Wang, I. Grace, A. S. Batsanov, D. J. Schiffrin, S. J. Higgins, M. R. Bryce, C. J. Lambert and R. J. Nichols, Precision control of single-molecule electrical junctions, Nat. Mater., 2006, 5, 995–1002.
18. V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, Correlations between Molecular Structure and Single-Junction Conductance: A Case Study with Oligo(phenylene-ethynylene)-Type Wires, J. Am. Chem. Soc., 2012, 134(11), 5262–5275.
19. H. Dekkiche, A. Gemma, F. Tabatabaei, A. S. Batsanov, T. Niehaus, B. Gotsmann and M. R. Bryce, Electronic conductance and thermopower of single-molecule junctions of oligo(phenyleneethynylene) derivatives, Nanoscale, 2020, 12, 18908.
20. A. Gemma, F. Tabatabaei, U. Drechsler, A. Zulji, H. Dekkiche, N. Mosso, T. Niehaus, M. R. Bryce, S. Merabia and B. Gotsmann, Full thermoelectric characterization of asingle molecule, Nat. Commun., 2023, 14, 3868.
21. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745.
22. R. J. Davidson, D. C. Milan, O. A. Al-Owaedi, A. K. Ismael, R. J. Nichols, S. J. Higgins, C. J. Lambert, D. S. Yufit and A. Beeby, Conductance of ‘bare-bones’ tripodal molecular wires, RSC Adv., 2018, 8(42), 23585–23590.
23. A. Markin, A. K. Ismael, R. J. Davidson, D. C. Milan, R. J. Nichols, S. J. Higgins, C. J. Lambert, Y.-T. Hsu, D. S. Yufit and A. Beeby, Conductance Behavior of Tetraphenyl-Aza-BODIPYs, J. Phys. Chem. C, 2020, 124(12), 6479–6485.
24. A. Alshehab and A. K. Ismael, Impact of the terminal end-group on the electrical conductance in alkane linear chains, RSC Adv., 2023, 13(9), 5869–5873.
25. C. J. Lambert, Basic concepts of quantum interference and electron transport in single-molecule electronics, Chem. Soc. Rev., 2015, 44(4), 875–888.
26. S. Grimme, C. Bannwarth and P. Shushkov, A robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent interactions of large molecular systems parametrized for all spd-block elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13(5), 1989–2009.
27. M. T. González, A. K. Ismael, M. Garcia-Iglesias, E. Leary, G. Rubio-Bollinger, I. Grace, D. Gonzalez-Rodriguez, T. Torres, C. J. Lambert and N. Agrait, Interference Controls Conductance in Phthalocyanine Molecular Junctions, J. Phys. Chem. C, 2021, 125(27), 15035–15043.
28. A. K. Ismael, 20-State Molecular Switch in a Li@ C60 Complex. ACS Omega 2023.
29. C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Signatures of Quantum Interference Effects on Charge Transport Through a Single Benzene Ring, Angew. Chem., Int. Ed., 2013, 52(11), 3152–3155.
30. A. A. Al-Jobory and A. K. Ismael, Controlling quantum interference in tetraphenyl-aza-BODIPYs, Curr. Appl. Phys., 2023, 54, 1–4.
31. S. V. Aradhya and L. Venkataraman, Single-molecule junctions beyond electronic transport, Nat. Nanotechnol., 2013, 8(6), 399–410.
32. J. Ye, A. Al-Jobory, Q.-C. Zhang, W. Cao, A. Alshehab, K. Qu, T. Alotaibi, H. Chen, J. Liu and A. K. Ismael, Highly insulating alkane rings with destructive σ-interference, Sci. China: Chem., 2022, 65(9), 1822–1828.
33. T. Kim, P. Darancet, J. R. Widawsky, M. Kotiuga, S. Y. Quek, J. B. Neaton and L. Venkataraman, Determination of energy level alignment and coupling strength in 4, 4′-bipyridine single-molecule junctions, Nano Lett., 2014, 14(2), 794–798.
34. X. Wang, A. Ismael, A. Almutlg, M. Alshammari, A. Al-Jobory, A. Alshehab, T. L. Bennett, L. A. Wilkinson, L. F. Cohen and N. J. Long, Optimised power harvesting by controlling the pressure applied to molecular junctions, Chem. Sci., 2021, 12(14), 5230–5235.
35. M. Alshammari, T. Alotaibi, M. Altoaibi and A. K. Ismael, Influence of Charge Transfer on Thermoelectric Properties of Endohedral Metallofullerene (EMF) Complexes, Energies, 2023, 16(11), 4342.
36. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. Bailey and K. Gillemot, GOLLUM: a next-generation simulation tool for electron, thermal and spin transport, New J. Phys., 2014, 16(9), 093029.
37. G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Exploring local currents in molecular junctions, Nat. Chem., 2010, 2(3), 223–228.
38. A. Ismael, A. Al-Jobory, X. Wang, A. Alshehab, A. Almutlg, M. Alshammari, I. Grace, T. L. Benett, L. A. Wilkinson and B. J. Robinson, Molecular-scale thermoelectricity: as simple as ‘ABC’, Nanoscale Adv., 2020, 2(11), 5329–5334.
39. D. Miguel, L. Alvarez de Cienfuegos, A. Martín-Lasanta, S. P. Morcillo, L. A. Zotti, E. Leary, M. Bürkle, Y. Asai, R. Jurado and D. J. Cárdenas, Toward multiple conductance pathways with heterocycle-based oligo (phenyleneethynylene) derivatives, J. Am. Chem. Soc., 2015, 137(43), 13818–13826.
40. L. Herrer, A. Ismael, S. Martin, D. C. Milan, J. L. Serrano, R. J. Nichols, C. Lambert and P. Cea, Single molecule vs. large area design of molecular electronic devices incorporating an efficient 2-aminepyridine double anchoring group, Nanoscale, 2019, 11(34), 15871–15880.
41. A. K. Ismael and C. J. Lambert, Single-molecule conductance oscillations in alkane rings, J. Mater. Chem. C, 2019, 7, 6578–6581.
42. T. L. Bennett, M. Alshammari, S. Au-Yong, A. Almutlg, X. Wang, L. A. Wilkinson, T. Albrecht, S. P. Jarvis, L. F. Cohen and A. Ismael, Multi-component self-assembled molecular-electronic films: towards new high-performance thermoelectric systems, Chem. Sci., 2022, 13(18), 5176–5185.
43. W. Hong, H. Valkenier, G. Mészáros, D.-Z. Manrique, A. Mishchenko, A. Putz, P. Moreno García, C. J. Lambert, J. Hummelen and T. Wandlowski, An MCBJ case study: The influence of π-conjugation on the single-molecule conductance at a solid/liquid interface, Beilstein J. Nanotechnol., 2011, 2, 699–713.
44. H. E. Skipper, B. Lawson, X. Pan, V. Degtiareva and M. Kamenetska, Manipulating Quantum Interference between σ and π Orbitals in Single-Molecule Junctions via Chemical Substitution and Environmental Control, ACS Nano, 2023, 17, 16107.
45. A. Daaoub, L. Ornago, D. Vogel, P. Bastante, S. Sangtarash, M. Parmeggiani, J. Kamer, N. Agraït, M. Mayor, H. van der Zant and H. Sadeghi, Engineering Transport Orbitals in Single-Molecule Junctions, J. Phys. Chem. Lett., 2022, 13, 9156.
46. B. Zhang, M. H. Garner, L. Li, L. M. Campos, G. C. Solomon and L. Venkataraman, Destructive quantum interference in heterocyclic alkanes: the search for ultra-short molecular insulators, Chem. Sci., 2021, 12, 10299.
47. C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, Q. Xu, A. Nitzan and X. Guo, Covalently bonded single-molecule junctions with stable and reversible photoswitched conductivity, Science, 2016, 352, 1443.
48. H.-Y. Gao, P. A. Held, M. Knor, C. Mück-Lichtenfeld, J. Neugebauer, A. Studer and H. Fuchs, Decarboxylative Polymerization of 2,6-Naphthalenedicarboxylic Acid at Surfaces, J. Am. Chem. Soc., 2014, 136, 9658–9663.
49. L. Xie, T. Chen, X. Dong, H. Wang, L. Xu and G. Zhou, Multifunctional spin transport behaviors of biphenyl-molecule-based nanodevices, Vacuum, 2023, 214, 112233.
50. X. Q. Deng and R. Q. Sheng, Electronic and thermal spin effect of molecular nanowires between graphene electrodes, RSC Adv., 2018, 8, 34182.
51. C. Luo, T. Chen, X. Dong, L. Xie, D. Qin, L. Huang, H. Lic and X. Xiao, Theoretical insight into the intrinsic electronic transport properties of graphene–biphenylene–graphene nanosheets and nanoribbons: a first-principles study, J. Mater. Chem. C, 2023, 11, 9114–9123.
52. Z.-K. Ding, Y.-J. Zeng, H. Pan, N. Luo, J. Zeng, L.-M. Tang and K.-Q. Chen, Edge states of topological acoustic phonons in graphene zigzag nanoribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 106, L121401.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc00611a

---