Electron-deficient multicenter bonding in pnictogens and chalcogens: mechanism of formation

Abstract

Phase change materials (PCMs), which bear a strong relationship with pnictogens (group V or 15) and chalcogens (group VI or 16), are mostly chalcogens related to A^IVB^VI and A^V₂B^VI₃ families. The exceptional properties and technological applications of PCMs have sparked interest in the nature of the unconventional chemical bonding present in the crystalline phases of PCMs, which has been reported as resonant, hypervalent, electron-rich multicenter, three-center-four-electron, and metavalent bonding along the last seventy years. This unconventional bond is also expected to occur at high pressure in most pnictogens, chalcogens, and A^IVB^VI and A^V₂B^VI₃ compounds that are not PCMs at room pressure. These compounds are characterized at room pressure by a mixture of primary covalent ppσ-bonds and secondary bonds in which the lone electron pairs (LEPs) are involved. In this work, we provide evidence of the existence of an unconventional bonding (similar to that of PCMs) in the highpressure phases of pnictogens and chalcogens using theoretical simulations. We also unravel the mechanism of its formation and how it depends on the type of LEP present in secondary bonds. Moreover, we show that the unconventional bond of PCMs is the electron-deficient multicenter bond. This comprehensive understanding of chemical bonding in pnictogens and chalcogens, which can be extrapolated to advanced materials, such as PCMs, will play a crucial role in explaining the structure and properties of advanced materials as well as in enhancing their applications.

---

1. Introduction

The concept of chemical bonding is commonly used to understand key features of the structures and properties of molecules and solids. The prototypical bonding types, like covalent, ionic, and metallic bonds, are widely discussed in the textbooks; however, several other interactions, including hypervalent, donor–acceptor, pnictogen, chalcogen, halogen, and multicenter (both electron-rich and electron-deficient) bonding interactions, have also been found beyond such idealized bonding descriptions.^1–3 Since chemical bonding is an elusive and controversial concept and it is not directly given by a quantum-mechanical operator,^4,5 several approaches have been developed over the last few decades to analyze the different types of chemical bonds in solids based on quantum-mechanical wavefunctions and electron densities. In this regard, chemically meaningful entities, such as bonding electron pairs (Lewis pairs) and lone electron pairs (LEPs), can be analyzed using natural bond orbitals,⁶ Wannier functions,^7,8 the electron localization function (ELF),⁹ and the chemical-pressure formalism,^10,11 among others.

A great deal of attention has been recently devoted to the analysis of the unconventional chemical bonding in phase change materials (PCMs) consisting of binary chalcogenides of the A^IVB^VI and A^V₂B^VI₃ families, such as GeTe, SnTe, Sb₂Te₃, and their related ternary compounds, such as Ge₂Sb₂Te₅ (GST). The crystalline phases of PCMs have exceptional properties including: (i) hypercoordination (violation of the 8-N rule), i.e. a higher atomic coordination than that expected for compounds with covalent ppσ-bonds that obey the 8-N rule, (ii) relatively low band gaps and shiny metallic luster, (iii) moderate electrical conductivity, (iv) extremely high optical dielectric constants and Born effective charges, (v) low-frequency optical phonons and high Grüneisen parameters, (vi) low thermal conductivity, and (vii) brittleness and high probability of multiple emission events in laser-assisted field evaporation measurements, which has been attributed to the softer character of their bonds than that of the covalent ones.^12,13 Thanks to the significant changes in the properties of the amorphous and crystalline phases of PCMs, they have a wide range of applications, such as re-writable data storage in DVDs, phase change RAMs, and thermal energy storage systems.^14–17 Moreover, many PCMs also show highly efficient thermoelectric and exceptional topological properties.^18–20

Until the last decade, the unconventional chemical bonding in the crystalline phases of PCMs was considered to be a kind of resonant bonding related to the single covalent (two-center two-electron, 2c-2e) bond.^21–24 This bonding was similar to that suggested by Pauling for benzene and graphite (later extended to metals)^25–27 with the possible participation of d orbitals. However, from the 1980 decade onwards, it was noted that: (i) the contribution of d orbitals to the unconventional bonding in PCMs is minor,²⁸ (ii) the influence of s–p mixing, related to the LEP stereoactivity, on the bonding of PCMs is essential,^29–33 and (iii) the properties of PCMs are completely different from those of benzene and graphite.^13,34

Although the concepts of resonance and resonant bonding have been widely used and discussed to explain the unconventional bonding in the crystalline phases of PCMs, as recently reviewed,^35,36 two alternative chemical bonding models (hypervalent and metavalent) have rivaled for explaining their exceptional properties in the last decade. On the one hand, several groups, including Kolobov and coworkers,^37,38 Dronskowski and coworkers,^39–41 and Lee and Elliot,^42–44 have considered that PCMs feature hypervalent bonding based on electron-rich multicenter bonds (ERMBs). The ERMB is considered to be the generalization and extension of the three-center four-electron (3c-4e) bond, proposed by Rundle and Pimentel for molecules such as I₃⁻ and XeF₂,^45,46 and is also related to the concepts of donor–acceptor bonds⁴⁷ and hypervalent bonds.^48–51 Notably, Dronskowski and coworkers have suggested the electron delocalization and multicenter character of bonding in PCMs by calculations of the projected force constants along several atoms and of the crystal-orbital bond index (COBI), together with its integrated values for two-center and three-center bonds, ICOBI(2c) and ICOBI(3c), respectively.^39–41 Moreover, the multicenter character (presence of three-center interactions) of bonding in crystalline PCMs has also been recently suggested.⁵²

On the other hand, Wuttig and coworkers have proposed that crystalline PCMs feature metavalent bonding, i.e., a new unconventional bonding characterized by a mixture of localized electrons (as in covalent materials) and delocalized electrons (as in metals). In other words, PCMs show two-center one-electron (2c-1e) bonds that are intermediate between the simple covalent 2c-2e bonds and the metallic bonds.^12,13,34 Consequently, these authors considered the materials with this type of bonding as incipient metals. Interestingly, they located incipient metals in an intermediate position between covalent and metallic materials in a 2D map showing the number of electrons shared (ES) vs. the normalized number of electrons transferred (ET), i.e. two values that are defined using Bader's integrated atomic charges and delocalization indices from the quantum theory of atoms in molecules (QTAIM).⁵³

The two alternative chemical bonding models for incipient metals have been recently reviewed³⁶ and it has been concluded that both hypervalent and metavalent models describe the same bonding scenario. Both models agree that some electrons are localized, i.e. shared between two atoms, and some are delocalized. The two models also agree that the unconventional bonding in crystalline PCMs is characterized by sharing less than two electrons per atom pair. In this sense, the supporters of the hypervalent model assume that ERMBs have only two bonding electrons shared between three centers, as was suggested for the Rundle–Pimentel 3c-4e model.⁵⁴ Consequently, Jones has proposed that, although terms like resonant bonding and hypervalent bonding are well extended in the scientific literature and the term metavalent bonding has become popular in the last five years, the unconventional bonding in incipient metals should be called electron-rich multicenter bonding³⁶ since the existence of multicenter bonds was already postulated in the early days of quantum mechanics.^55–57

In 2023, the two current bonding models of crystalline PCMs have been defended by their supporters.^58–61 On one hand, Wuttig and coworkers⁵⁸ have suggested that metavalent bonds cannot be ERMBs, as suggested by Jones.³⁶ Wuttig and coworkers have calculated the ES value between two atoms, as two times the delocalization index,⁵³ in molecules with well-known 3c-4e bonds, such as XeF₂ and SF₄, and have evidenced that they present ES values between 1.5 and 2, i.e. similar to those of covalent bonds. This result differs from the ES values obtained for incipient metals (ES ≈ 1), so they have shown that molecules with ERMBs are located in a different position than incipient metals in Wuttig's ES vs. ET map,⁵⁸ thus concluding that the unconventional bond in incipient metals cannot be of ERMB type. In this context, Wuttig and coworkers have left open the door for metavalent bonds to be equivalent to charge-shift bonds,⁶² or even to electron-deficient multicenter bonds (EDMBs). In this context, it has been recently demonstrated by two groups in an independent way that metavalent bonding is equivalent to electron-deficient bonding.^60,63 Contrarily, Jones et al.⁵⁹ have insisted that crystalline PCMs feature ERMBs and that the ES value is not a good parameter to characterize bonding. These authors argue that Wuttig's ES vs. ET map is not useful for materials with different kinds of bonds in their crystalline structures,⁴⁴e.g. the case of the amorphous phases of PCMs and crystalline A^IVB^VI and A^V₂B^VI₃ materials showing a mixture of conventional 2c-2e bonds and unconventional bonds at room pressure (RP). Finally, Dronskowski et al.⁶¹ have recently commented on the similarity of the chemical bonding in a PCM, such as rocksalt GeTe, and polyiodides. In summary, the dispute regarding the nature of the unconventional bonding in crystalline PCMs is unresolved.

In order to understand the different points of view of the two groups, it is worth noting that supporters of the two different bonding models in incipient metals usually work with different methodologies, which explains in large part their conflicting views. Researchers working with the metavalent bonding model have mainly adopted a phenomenological view and focused on the different properties of the materials, such as electrical and thermal conductivities, optical dielectric constant, Born effective charges, and phonon anharmonicity. Moreover, they have used density-based theoretical methods, such as QTAIM methodology, to analyze the topology of the electron density and evaluate the ES and ET values.^{12,13,24,34,64–68} Alternatively, researchers supporting the hypervalent bonding model have paid more attention to the projected force constants between atoms, the chemical interactions between LEPs and antibonding orbitals σ* of covalent ppσ-bonds and the associated electronic band structure of the materials.^29,39–44 To understand the chemical bonding in PCMs, these researchers have analyzed chemical interactions through the charge density, ρ, and its Laplacian, ∇²ρ, at bond critical points (BCPs), the electronic density of states (DOS), and the ELF and have used theoretical orbital-based methods, such as the crystal-orbital overlap population (COOP), the projected crystal-orbital Hamiltonian population (pCOHP) along the different bonds between two atoms and their integrated values, IpCOHP(2c) and COBI (including ICOBI(2c) and ICOBI(3c)). Furthermore, the supporters of the hypervalent bonding model have proposed an explanation for the linear bonding configurations present in PCMs based on the valence shell electron repulsion (VSEPR) theory, taking into account that these linear bonding configurations have been observed in many molecules with ERMBs.^43,44 In particular, they have classified the molecular units in amorphous and crystalline phases of GST depending on whether they violate or not the octet rule, with the molecular units obeying the octet rule composed of pure ordinary covalent bonds and LEPs and the molecular units violating the octet rule composed of at least one ERMB in addition to other possible covalent bonds or LEPs.^43,44

In the present manuscript, we analyze the pros and cons of the two above-commented bonding models for PCMs and work with tools already used by the supporters of the two mentioned models. Given the present controversy and the merits of the two current bonding models, we rename the unconventional bond in crystalline PCMs as the “electron-deficient multicenter bond (EDMB)”. We consider that these two terms (electron-deficient and multicenter) characterize bonds in incipient metals as will be discussed later in detail. On the one hand, the terms electron-deficient and metavalent are equivalent,^60,63 as we have just commented, and will be discussed later; on the other hand, the multicenter character of the bond in PCMs has been already suggested^39–41 and will be further substantiated later on. Due to the excessive length of our original manuscript,⁶³ we have decided to split it into two parts. This paper corresponds to the first part of ref. 63 in which we comment on the mechanism of EDMB formation. In particular, we will show in Sections 2 and 3 of this manuscript that the term multicenter means that the bond is not isolated (multicenter bonds always come in pairs) as will be proved by the mechanism of EDMB formation. The second part of our original manuscript,⁶³ to be published elsewhere, will be devoted to the discussion of the different types of the EDMBs and ERMBs with examples of different materials, and the geometries of these two different bond types, and will also provide additional justification of the EDMB nature of the bonding in incipient metals.

It must be noted that the dispute regarding the metavalent and hypervalent bonding models in crystalline PCMs started much earlier than shown in the preceding paragraphs. With the change of the millennium, Hoffmann and coworkers studied several Sb-based molecules and compounds with linear bonds in one (1D), two (2D), and three dimensions (3D).^49,50 In particular, they suggested that the simple cubic (sc) phase of Sb should show ERMBs.⁵¹ This claim is in line with the views of Kolobov and coworkers,^37,38 Dronskowski and coworkers,^39–41 Lee and Elliot,^42–44 and Jones,^36,59 and against the position of Wuttig and coworkers, who considered that sc-Sb shows the same metavalent – previously resonant – bonds as incipient metals.^68–70 To this dispute, we can also add the contribution of Lubchenko and coworkers, who suggested the presence of multicenter bonds in Bi₂Te₃.³¹ This position is in contrast to the position of Wuttig and coworkers, who later considered the presence of metavalent bonds in all tetradymite-like V₂–VI₃ chalcogenides.⁶⁷ In other words, the dispute regarding the nature of the unconventional bonding in incipient metals goes beyond the two current research teams that have supported their claims in 2023 and the controversy about the bonding in these materials can be traced back to the 1950s.^21–24

Remarkably, Hoffmann and coworkers came up with several interesting ideas that are worth exploring. One is the idea that the multicenter bonds in several materials, such as sc-Sb,^50,51 had their origin in secondary bonds or backbonds,⁷¹i.e. bonds present in rhombohedral Sb at RP and, in general, in materials showing a mixture of covalent ppσ-bonds and LEPs. Since sc-Sb has been considered a high-pressure (HP) phase of Sb,⁷² the above idea suggests that there is a mechanism of multicenter bond formation in sc-Sb as pressure increases. By this mechanism, we mean the transformation path from the original primary covalent bonds and secondary bonds in rhombohedral Sb at RP to the final multicenter bonds in sc-Sb at HP. One of the main objectives of this work is to analyze the mechanism of formation of the unconventional EDMB in the sc phase of pnictogens to resolve the dispute regarding the bonding in all incipient metals. Another idea of Hoffmann and coworkers was to suggest that secondary bonds, also known as donor–acceptor bonds, charge-transfer bonds,⁴⁷ or σ-hole bonds,^73,74 are similar if not equal to ERMBs.⁴⁹ Nowadays, several types of secondary bonds, such as hydrogen, triel, tetrel, pnictogen, chalcogen, and halogen bonds, are considered just different types of σ-hole bonds in line with Hoffmann's view.^75–79 It is well known that secondary bonds are, in fact, some of the workhorses in supramolecular chemistry.^80,81 Therefore, the study of the mechanism of formation of the unconventional bond in the sc phase of pnictogens could shed light on these bond types and could be of utmost importance not only for solid-state chemistry but also for supramolecular chemistry. Finally, the third idea of Hoffmann and coworkers^31,42,50 (later adopted by other authors^31,42,50) was that it is very difficult to distinguish between the scenario with primary and secondary bonds involving LEPs and the scenario with multicenter bonds because secondary bonds and multicenter bonds seem to be the extremes of a single type of interaction with a continuous degree of strength. In this regard, we will show in this work that three stages can be clearly distinguished between the pre-EDMB and EDMB scenarios as well as between pre-ERMB and ERMB scenarios.

A very useful tool to produce continuous degrees of strength is pressure since it allows altering interatomic distances with much better accuracy and precision than changing the atomic composition. Pressure is the perfect tool to distinguish between the pre-EDMB and EDMB scenarios and its importance has been highlighted in several works related to PCMs.^13,31,34,52 Unfortunately, the important role of pressure has still not been fully exploited to help understand the bonding in PCMs, despite examples of the pressure-induced metavalent bond –now EDMB– formation in A^IVB^VI and A^V₂B^VI₃ chalcogenides, such as GeSe, SnSe, GeTe, and As₂S₃, have been recently published.^82–85 In particular, those works have shown how the change from the pre-EDMB scenario to the EDMB scenario proceeds as octahedral coordination is approached at HP. In this context, it has been stressed that more HP studies, in particular the computational ones, are needed to understand the effect of pressure on these unconventional bonds, exploring the bond strength–bond length relationship and how pressure affects the deviation from octahedral coordination in the pre-EDMB scenario.^86,87 Notwithstanding, a systematic study of the pressure-induced EDMB formation in elemental pnictogens and A^IVB^VI and A^V₂B^VI₃ chalcogenides has not been undertaken yet.

The lack of HP studies involving pnictogens and chalcogens will be fulfilled by the present study, which can be extrapolated to PCMs of A^IVB^VI and A^V₂B^VI₃ chalcogenides. One way of addressing the controversy regarding the nature of bonding in PCMs is to study materials at HP from both real (bond) and reciprocal (band) perspectives.⁸⁸ In particular, it is interesting to study simple p-type elements of groups 15 and 16, which show homoatomic/homonuclear linkages and are much simpler systems than binary and ternary PCMs.⁸⁹ In this work, we follow this approach to illustrate the pressure-induced mechanism of EDMB formation in elemental pnictogens and chalcogens. The reasons to study these elements are: (i) they are the simplest known materials characterized by a mixture of original primary covalent ppσ-bonds and secondary bonds (related to LEPs) at RP, i.e. they are LEP-based semiconductors at RP⁹⁰ and (ii) they have been predicted to show unconventional bonds (as those of PCMs) at HP as they approach octahedral coordination, e.g. the HP phase of sc-Sb.⁷² In this context, it is well known that the crystalline structures of pnictogens and chalcogens at RP display a small atomic coordination that satisfies the 8-N rule, except Po, and it is known that the octahedral distortion decreases as pressure increases.^51,91,92 In addition, the crystalline structures of pnictogens (As, Sb, and Bi) and chalcogens (Se and Te) at RP are considered Jones-Peierls distorted structures of the octahedrally coordinated sc phase, in the same way as the crystalline structures at RP of most A^IVB^VI and A^V₂B^VI₃ chalcogens (not PCMs) that have been considered to be Jones-Peierls distorted structures of the octahedrally coordinated cubic rock-salt (rs) phase present in many PCMs.^24,93–95 Therefore, there is a clear relationship between the crystalline phases of PCMs and pnictogens and chalcogens, so the results obtained in this work for pnictogens and chalcogens can be applied to PCMs.

This paper is divided into two sections. In Section 2, we analyze the effect of pressure on the structural, vibrational, and electronic properties of the crystalline structures of pnictogens (As, Sb, and Bi) and chalcogens (Se, Te, and Po) using density functional theory (DFT) calculations, although our results can be extended to the rest of the group-15 and -16 elements. Using theoretical bonding descriptors previously used by the proponents of the hypervalent and metavalent bonding models of PCMs, we obtain evidence for the EDMB formation in the octahedrally coordinated phases of these two elemental families, which can be extended to all A^IVB^VI and A^V₂B^VI₃ PCMs. We will also show that the existence of EDMBs in these elements and crystalline PCMs is consistent with the most recent Wuttig's 2D map showing ES vs. ET.^67,68 Finally, in Section 3, we describe the mechanism of the pressure-induced transformation from the pre-EDMB scenario to the EDMB scenario in pnictogens and chalcogens using both the real-space (bond) and the reciprocal-space (band) pictures. We will show that the mechanism of EDMB formation is similar but proceeds through different stages for both elemental families. This mechanism of EDMB formation is expected to apply also to PCMs and it is different from the mechanism of formation of ERMBs (although they share a common origin). Details of the ab initio simulations for most of the materials studied in this work are given in Section 1 of the ESI.†

2. Unconventional bonding in pnictogens and chalcogens at high pressure

In this section, we perform a systematic theoretical DFT study of the two families of p-type elements at HP, paying special attention to the effect of pressure on the distortion from the octahedral coordination in the low-coordinated trigonal R3̄m and P3₁21 structures of pnictogens (As, Sb, Bi) and chalcogens (Se, Te) at RP, respectively (Strukturbericht types A7 and A8, respectively), as well as on the high-coordinated (octahedral) Pm3̄m (sc) and R3̄m structures of α-Po and β-Po at RP, respectively (Strukturbericht types A_h and A_i, respectively).

To check the goodness of our theoretical simulations, we compare the pressure-induced, simulated changes in the structural and vibrational properties of the low-coordinated A7 (As, Sb, Bi) and A8 (Se, Te) phases with available experimental results. The relatively good agreement with experimental results using the PBEsol functional allows us to extrapolate our results to the less well-known HP phases of these two elemental families in order to study the pressure-induced bonding transformation.

First, we will prove that pnictogens tend to undergo a pressure-induced A7-to-A_h phase transition (PT) as schematized in Fig. 1a, while chalcogens tend to undergo a pressure-induced A8-to-A_i PT as schematized in Fig. 1b. These results are in line with the observation of the A_h and A_i phases either at RP or HP in many of these elements. Second and most importantly, we will prove that the unconventional bonding, typical of PCMs at RP, also occurs in the A_h and A_i phases of Po at RP and of As, Sb, Bi, Se, and Te at HP. For this purpose, we will calculate several quantum-mechanical bonding descriptors with physical and chemical meanings for the studied phases. In particular, we will use descriptors extensively used by Wuttig and coworkers and Manjón and coworkers,^12,13,85,96 such as the optical phonon frequencies, ω_i, and the corresponding Grüneisen parameters, γ_i, which can give evidence of soft bonds and lattice anharmonicity, the average of the diagonal components of the Born effective charge tensor, Z*, which accounts for the bond polarizability, and the ES and ET values, which allow understanding the degree of bond covalency and ionicity, respectively. We will also use other bonding descriptors used by Lee and Elliott, Dronkowski and coworkers, and Manjón and coworkers,^39,40,42,85 such as ρ, ∇²ρ at the BCP, and the pCOHP, IpCOHP(2c), and ICOBI(3c) parameters. The latter parameters will help us to describe the evolution of the different atomic interactions as pressure increases. All these parameters, previously used for binary and ternary PCMs, as already remarked, will show us how physical and chemical worlds can be made compatible to provide a richer perspective of the unconventional bonds present in the octahedrally coordinated phases of pnictogens and chalcogens. More specifically, the existence of EDMBs will be evidenced by the small ω_i, soft-mode behavior, and large γ_i for optical phonons, the extremely high values of Z*, and the ES values close to 1. Precisely, an ES value of the order of 1 is what accounts for the electron-deficient nature of the bond in PCMs.^60,63 This is in good agreement with the picture provided by the analogous bonding descriptor 2·ICOBI(2c),^60,97 and so we will use the ES value from now on in this manuscript. In addition, the existence of EDMBs will be supported by: (i) the very small value of ∇²ρ,^42,96 which is intermediate between the negative values, typical for the covalent bond, and the positive values, typical for the metallic bond⁹⁸ and (ii) a value of ICOBI(3c) different from zero, which gives account for the multicenter character of the bond.⁴² Moreover, the multicenter character of the bond will be further evidenced by the inverse pressure-dependent relationship between different magnitudes (bond lengths, ρ and ∇²ρ at BCPs, ELF, and ES) of the primary and secondary bonds in the low-coordinated phases of pnictogens and chalcogens.

Fig. 1 Phase transition sequence studied in group-15 and -16 elements. Pnictogens crystallizing in the rhombohedral A7 phase tend at HP to the cubic A_h phase. Chalcogens crystallizing in the hexagonal A8 phase tend at HP to the rhombohedral A_i phase. The short intralayer (intrachain) d₁ bond distance and the long interlayer (interchain) d₂ bond distance of the A7 (A8) phases in group-15 (16) elements are represented by solid and dashed orange lines, respectively. A_h and A_i phases only feature a single bond distance, d.

2.1. Pnictogens

The relaxation of the structural parameters of pnictogens (As, Sb, and Bi) in the A7 phase at different pressures evidences a decrease in the octahedral distortion of the A7 structure at HP until a final octahedrally coordinated A_h (sc) structure is reached (see Fig. 1a and Table S1 in the ESI†). This is evidenced by the decrease of the quadratic elongation of the distorted octahedron around each atom in the A7 structure and the increase of the effective coordination number (see Fig. S1c, S2c, and inset of S4a in the ESI†). In particular, a progressive change in the effective coordination number from the trigonally coordinated A7 structure, characterized by three primary short covalent bonds plus three long secondary bonds (related to LEPs), towards the octahedrally coordinated A_h structure, characterized by six equal bonds each at 90°, is observed. These results are consistent with previous expectations^51,91,92 and with the observation of the sc structure in P and As at HP.⁹⁹

Since the best and simplest example to show the pressure-induced changes in pnictogens is provided by arsenic, with an A7-to-A_h phase transition (PT) theoretically predicted at a transition pressure (P_t) of 25 GPa in good agreement with experimental results (see the inset of Fig. S1a in the ESI†),⁹¹ we will mainly comment the results for As in the present work. Most of the results on other pnictogens (Sb and Bi) will be provided in the ESI† to complement those of As.

The optimized simulated atomic volume and lattice parameters for the As-I (A7) and As-II (A_h) phases at different pressures exhibit a nice agreement with available experimental data⁹¹ and previous simulations^100,101 (see Fig. S1 in the ESI†). Remarkably, the structural relaxations of the trigonal A7 phase do not reach the perfect A_h phase except for very high pressures (e.g. our calculations for As just above 25 GPa show a residual trigonal distortion of the sc phase). This result agrees with the most recent and accurate experimental measurements on phosphorus, in which a distorted sc phase (pseudo-sc), as an intermediate phase between the A7 and the A_h phases, has been reported.¹⁰²

A characteristic experimental feature of A^IVB^VI and A^V₂B^VI₃ chalcogenides, such as GeSe, GeTe, SnTe, and As₂S₃ that are not PCMs at RP but become PCMs at HP, is the softening of some optical phonon frequencies at the pre-EDMB scenario (low-pressure phase) and hardening of these optical phonon frequencies at the EDMB scenario (high-pressure phase). This means that there is a change in the sign of the pressure coefficient of the frequency in some optical modes at the pre-EDMB-to-EDMB transition.^13,82–85 A similar feature is experimentally found in As⁹¹ and nicely reproduced by our calculations (Fig. 2a). The small values of the frequencies of the Raman-active phonons in As at RP (below 300 cm⁻¹) compared to those of Ge (above 300 cm^−1 103) and the soft behavior of the optical phonons of As at HP compared to their increase in Ge¹⁰³ clearly suggest that the bonds in the A7 structure of As are quantitatively and qualitatively different than those of the zinc blende structure of Ge. This result is contrary to expectations since both elements are close in the periodic table and have similar masses, which could suggest similar phonon frequencies and pressure behaviors.

Fig. 2 Pressure dependence of the properties of the As-I (A7, red) and As-II (A_h, blue) phases of As. (a) Calculated (lines) and experimental⁹¹ (circles) phonon frequencies, ω, correspond to Raman-active modes A_1g and E_g of As-I. Solid and dashed red lines above 25 GPa correspond to the first and second-order (overtone) modes of the distorted sc phase of As-I, respectively. (b) Calculated average Born effective charge, Z*. The inset shows the absolute Grüneisen parameter, |γ_i|, of the A_1g mode of As-I. (c) Laplacian of the charge density at the BCP, ∇²ρ, where e is the electron charge and a₀ is the Bohr radius, in primary and secondary bonds of As-I (red) and the EDMB of As-II (blue). The three stages of the mechanism of EDMB formation are separated by vertical black dashed and red dotted lines. The latter corresponds to the calculated A7-to-A_h phase transition pressure, P_t.

Curiously, our calculated Raman frequencies for As-I soften under compression above 10 GPa at a much higher rate than the experimental ones. More specifically, the calculated Raman frequencies of As-I tend to zero at P_t, unlike the experimental ones. According to the Landau theory of PTs, the tendency of soft phonons to exhibit zero frequency means that our simulations for As indicate that the A7-to-A_h PT is of second-order character.^104,105 This result is similar to that of the most extensive theoretical work performed on As.¹⁰⁰ Therefore, the simulated results contrast with the apparent first-order character of the experimental PT.⁹¹ The disagreement could likely be caused by anharmonic effects that have not been included in the simulations yet. In this context, it is well known that anharmonic effects are notable in PCMs and important for the description of the vibrational properties as the formation of unconventional bonds is approached.^{13,52,83,84,106,107} In fact, the presence of strong anharmonic interactions in As-I close to P_t is also evidenced by the large values of the absolute phonon Grüneisen parameter, |γ_i|, of the A_1g mode (inset of Fig. 2b).

It must be stressed that while optical phonons in PCMs soften upon crystallization, i.e. when EDMBs are formed, hardening of the low-energy acoustic phonons is experimentally observed.¹⁰⁶ The soft (hard) behavior of optical (acoustic) phonons has been also experimentally reported in pnictogens at HP.^108,109 This different behavior of acoustic and optical phonons in pnictogens can be understood in light of a recently published simple model of three-center interactions,⁵² which suggests that bonding in incipient metals has a multicenter character.

As regards the A_h phase of As (As-II) above 25 GPa, it exhibits only acoustic phonon modes (see the blue line in Fig. 2a); however, our calculations provide non-zero optical phonon modes above 25 GPa (red line) due to the presence of a residual trigonal distortion of the sc structure, as already commented. These forbidden simulated optical phonons for the A_h phase (also found for the A_h phases of Sb and Bi in Fig. S2d and S4c in the ESI† and in the rs phase of PCMs^13,52) seem to be indeed experimentally observed in As-II above 25 GPa with a positive pressure coefficient once the EDMBs are formed (see open circles in Fig. 2a).⁹¹ The positive pressure coefficient of the frequency of the only mode observed in As-II shows a relatively good agreement with the pressure coefficient of the frequency corresponding to the second-order mode we obtain as the overtone of the simulated first-order phonon (see the dashed red line above 25 GPa in Fig. 2a). Therefore, our simulations seem to reproduce well the experimental observations above 25 GPa, thus suggesting that the experimental phonons observed in As-II might be caused by a distortion of the sc structure similar to that recently reported for phosphorus at HP.¹⁰² It could also be speculated that the observation of such forbidden mode comes from an anomalously enhanced second-order Raman scattering, as recently predicted to occur in incipient metals.¹¹⁰

The presence of EDMBs in As-II is not only supported by the simulated change of the pressure coefficient of the optical phonon frequencies and the high value of |γ_i| near P_t, but also by the simulated high Z* value (Fig. 2b). The high Z* values for As (much higher than the nominal valence (0) of pure As) are observed for As-I near P_t and also for As-II. It has been shown that such high Z* values are also observed for A^IVB^VI and A^V₂B^VI₃ PCMs.^13,67 Additional confirmation of EDMB formation in As-II comes from the pressure dependence of ∇²ρ along the main bonds in the A7 and A_h phases (Fig. 2c). As expected, ∇²ρ is negative for the strong primary covalent intralayer bond (d₁ bond distance) and positive for the weak secondary interlayer bond (d₂ bond distance) in As-I. Both ∇²ρ values tend to equalize, especially above 15 GPa, until they reach a value close to zero above P_t. The occurrence of a simultaneous relatively large value of ρ at BCP and a relatively small (close to zero) value of ∇²ρ at BCP is unusual and characteristic of EDMB in elemental solids, where no polar covalent or ionic bonds can occur and only intermediate bonds between covalent and metallic bonds can justify the existence of a value of ∇²ρ close to zero.¹¹¹ This seems to happen only for the EDMB, as it was already shown for Sb–Te2 and Sn–Te2 bonds in crystalline SnSb₂Te at RP⁹⁶ and for Sb–Te and Ge–Te bonds in crystalline GST.⁴² We must stress that the inverse relationship observed between the pressure dependence of ∇²ρ for both primary and secondary bonds, especially between 15 and 25 GPa, can be considered new solid proof of the multicenter interaction taking place in this pressure region that results in the multicentre character of the unconventional bond (EDMB) formed above 25 GPa in As.

Significantly, the similarity of the EDMBs present in sc-As and those present in the rs phase of A^IVB^VI PCMs can be understood since both are isoelectronic (10-electron) materials.²⁴ In particular, As and α-GeTe show a rather close behavior because α-GeTe has a layered R3m structure at RP with primary ppσ-bonds and secondary bonds (including LEPs) similar to those of As-I. Furthermore, α-GeTe undergoes a pressure-induced PT to the rs phase (β-GeTe), in which EDMBs similar to those of As-II have been identified.^13,112,113

Following the same strategy as with elemental As, we have simulated the effect of pressure on the A7 phases of Sb (Sb-I) and Bi (Bi-I) (see all information in the ESI†). As already mentioned, the A7 phases of Sb and Bi also tend to transform into the A_h phase. Interestingly, this phase has not been observed in Bi at HP, although the monoclinic Bi-II phase is a slightly distorted sc phase, and it remains uncertain whether it exists or not in Sb (see discussion in Section 2 of the ESI†). In any case, we have calculated the A7-to-A_h PT in both elements because it provides valuable insight into the decrease of the polyhedral distortion with respect to the octahedral coordination and to clarify the various stages of the pre-EDMB to EDMB transformation to be discussed in the next section. The presence of EDMBs in the hypothetical A_h phases in Sb and Bi is suggested by the change in the sign of the simulated pressure coefficients of the optical phonon frequencies at P_t, the high value of |γ_i| near P_t, the increase of the value of Z* in the A7 phase and its high value in the octahedrally coordinated A_h phase, and the negligible value of ∇²ρ in the A_h phase (see Section 3 in the ESI†). Therefore, despite the fact that the A_h phase could not be experimentally observed in Sb and Bi at HP (see discussion in the ESI†), it can be concluded that both Sb and Bi tend to exhibit EDMBs as pressure increases and octahedral coordination is approached.

Experimentally, the pressure-induced EDMB formation in pnictogens can be evidenced by a sign change in the pressure coefficients of the optical phonon frequencies that occurs at 25, 9, and 3 GPa in As, Sb, and Bi, respectively (see Fig. S2d and S4c in the ESI† for Sb and Bi).^102,114,115 Our simulated P_t values of pnictogens (for the A7-to-A_h PT), which mark the onset of the octahedral coordination, agree with experimental values for As (25 GPa) and Sb (7 GPa) but not for Bi (14 GPa). Since the P_t value is expected to decrease along the series P–As–Sb–Bi, in agreement with recent experimental results for phosphorus,¹⁰² the larger value for Bi than that for Sb suggests that the PBEsol functional does not work well for Bi (see discussion in Section 3 of the ESI†). Better calculations for Bi-I can be performed with the AM05 functional (pink line in Fig. S4a–c), which was already used for Bi₂S₃;^102,114,115 however, we will show here the results obtained using the PBEsol functional for Bi for the sake of comparison with As and Sb under similar conditions.

To conclude this subsection, we can summarize that our simulations predict a transformation of the chemical bonding in pnictogens as pressure increases. The A7 phase at RP features a mixture of primary covalent ppσ-bonds plus secondary bonds (related to LEPs), whereas the octahedrally coordinated HP phases, such as the A_h structure and its slightly distorted structures, feature EDMBs. These EDMBs of pnictogens in the A_h structure show a cubic geometry similar to that of the rs phase of PCMs of the heavy A^IVB^VI family and have similar properties.^24,93,94,116

2.2. Chalcogens

Now, we present the results of theoretical simulations of the A8 phase of Se (Se-I) and Te (Te-I) as well as of the A_h and A_i phases of α-Po and β-Po, respectively, at different pressures. As expected, the octahedral distortion, measured by the quadratic elongation of the distorted octahedron around each atom of the trigonal A8 phase in Se and Te, decreases as pressure increases (see Fig. S7c and S9c in the ESI†). However, the relaxation of the A8 structure at HP results in a final octahedrally coordinated rhombohedral A_i phase instead of the previously assumed cubic A_h phase^24,93,94,116 (see Fig. 1b and Table S2 in the ESI† for the structural parameters of the A8 and A_i phases at different pressures). Our simulated results agree with the experimental observation of the A_i phase at HP in several chalcogens, e.g. S-V (above 150 GPa¹¹⁷), Se-V (above 40–60 GPa^118,119), and Te-IV (above 10 GPa^120,121), although the structure of Te-IV has been recently questioned.¹²² Noteworthily, the experimental P_t values at which the A_i phase is observed decrease along the series S–Se–Te–Po. This result is well reproduced in our calculations for Se (23 GPa), Te (7 GPa), and Po (RP).

The simulated optimized atomic volume and lattice parameters of the A8 and A_i phases of Se and Te at different pressures agree nicely with available experimental data and previous calculations (see Fig. S7 and S9 in the ESI†).^{92,120,121,123–129} A progressive change occurs in the effective coordination number from the twofold-coordinated A8 structure, characterized by two primary short covalent p-type bonds plus four long secondary bonds (related to LEPs), towards the octahedrally coordinated A_i structure of β-Po, characterized by six equal bonds. It must be noted that our structural relaxations of the trigonal A8 phase of Se and Te do not reach the A_i phase, except for very high pressures, so our calculations always show a residual bond distortion of the A_i structure in the pressure range discussed here (see data in Table S2 of the ESI†). This residual structural distortion of chalcogens at HP with respect to the A_i phase is similar to that previously found for pnictogens at HP with respect to the A_h phase.

Regarding the vibrational properties, the trigonal phase of Se-I and Te-I has three Raman active modes: A₁ and two double degenerated, E′ and E′′ modes (see Fig. 3a). Both Se-I and Te-I exhibit a considerable experimental softening of the A₁ mode corresponding to the A8 phase, whose frequency pressure coefficient changes above ca. 18 and 7 GPa, respectively.¹²⁹ These results are well reproduced by our simulations (Fig. 3a and Fig. S9d, ESI†), except near P_t, where our simulations predict a second-order PT, similar to that found for pnictogens in the previous subsection. Again, the disagreement is likely caused by the lack of anharmonic interactions (that seem to be only significant near P_t) in our simulations. Note that the A_i phase should not exhibit optical Raman-active modes (only acoustic phonon modes), but our calculations provide non-zero optical phonon frequencies above 23 GPa in Se and Te due to the remaining distortion of the trigonal A_i phase. All the calculated optical phonon frequencies in the distorted A_i phase of Se and Te harden with increasing pressure, as expected once EDMBs are formed. As for pnictogens, the formation of EDMBs in the A_i phases of Se and Te is indicated by the hardening of the optical modes in the distorted A_i phases (Fig. 3a and Fig. S9d, ESI†), the high values of Z* and |γ_i| for the A₁ mode of the A8 phase (Fig. 3b and Fig. S9e, ESI†), and the negligible value of ∇²ρ (Fig. 3c and Fig. S9f, ESI†). Hence, we conclude that EDMBs are formed in Se and Te at HP as they approach the octahedral coordination typical of the A_i phase.

Fig. 3 Pressure dependence of the properties of the Se-I (A8, red) and A_i (blue) phases of Se. (a) Calculated (lines) and experimental⁹¹ (circles) phonon frequencies, ω, correspond to Raman-active modes A₁, E′, and E′′ of Se-I and their corresponding modes in HP phases. (b) Calculated average Born effective charge, Z*. The inset shows the absolute Grüneisen parameter, |γ_i|, of the A_1g mode of As-I. (c) Laplacian of the charge density at the BCP, ∇²ρ, where e is the electron charge and a₀ is the Bohr radius, in primary and secondary bonds of Se-I (red) and the EDMB of the A_i phase (blue). The two stages of the mechanism of EDMB formation are separated by a vertical red dotted line. The latter corresponds to the calculated A8-to-A_i phase transition pressure, P_t.

Our theoretical results for Se and Te can be compared with experiments. Soft phonons are not only observed in the A8 phase (Se-I and Te-I) but also in the Se-II and Se-III phases (below 28 GPa) as well as in the Te-II phase (below 8 GPa). The hardening of soft optical phonons in Se occurs experimentally between 18 and 28 GPa (Fig. 3a), i.e. upon transition from Se-II to Se-III, and especially to the Se-IV phase.¹²⁹ Similarly, the hardening of optical phonons in Te occurs experimentally above 7 GPa,^128,129i.e. upon transition to Te-III.^{120–122,128,129} Notably, these changes in Se and Te are also related to their decrease in resistivity.¹³⁰ Therefore, it can be concluded that all these experimental features in Se and Te provide additional support to the presence of asymmetric EDMBs in Se-IV (Te-III) as suggested by our calculations above 23 (7) GPa. It must be stressed that the presence of asymmetric EDMBs in these intermediate phases of Se and Te, as already suggested to be present in Bi-II in the previous subsection, likely occurs before reaching the perfect A_i structure of Se-V and Te-IV phases that are experimentally found at slightly higher pressures.^128,129

A paradigmatic example of EDMB formation occurs in Po at RP. Po is the only chalcogen that shows octahedral coordination at RP, either in the cubic A_h structure (α-Po) at RP and room temperature or in the rhombohedral A_i phase (β-Po) at RP and high temperature. Our calculations show that β-Po at RP features a quasi-cubic arrangement of Po atoms, i.e. β-Po shows a very small distortion with respect to α-Po since all six bond distances are equal in both phases and only a small deviation of the rhombohedral bond angle from 90° occurs in β-Po at RP. This deviation disappears at HP, thus leading to a PT to α-Po below 2 GPa (see Fig. S11 in the ESI†). As regards the vibrational properties, both phases of Po have only acoustic phonons and the presence of EDMBs in Po is here only evidenced by the high (negligible) values of Z* (∇²ρ) at all calculated pressures (see Fig. 4a and b).

Fig. 4 Pressure dependence of several physical parameters of α-Po (blue) and β-Po (green). (a) Average of the diagonal components of the Z* tensor. (b) Laplacian of the charge density at the BCP, ∇²ρ. (c) Bond distance and charge density at the BCP, ρ. e is the electron charge and a₀ is the Bohr radius.

All in all, our calculations on chalcogens (Se, Te) show that a bonding change occurs in these elements as pressure increases. The A8 phase at RP features a mixture of primary covalent ppσ-bonds plus secondary bonds (related to LEPs), whereas the octahedrally coordinated HP phases, such as the A_i structure and its slightly distorted structures, feature EDMBs. The EDMBs in the A_i structure show a rhombohedral geometry similar to that of the tetradymite phase of PCMs made of heavy A^V₂B^VI₃ chalcogenides.^128,129 Notice that both chalcogens and A^V₂B^VI₃ chalcogenides are almost isoelectronic. Polonium is the only chalcogen (in both α and β phases) with all bonds being symmetric EDMBs at RP.

2.3. Electron-deficient character of bonds in PCMs: ES vs. ET map

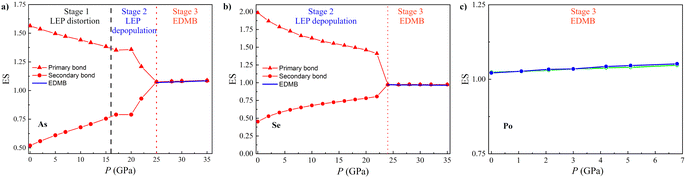
Once established that EDMBs occur in the octahedrally coordinated crystalline phases of pnictogens and chalcogens either by increasing pressure or by changing composition due to substitution by heavier elements of the same group, we will show now that the change from the pre-EDMB scenario to the EDMB scenario can be traced by the change in the number of electrons shared (ES) and the normalized number of electrons transferred (ET) in the two-center bonds of materials, as obtained from QTAIM methodology. As already mentioned, the ES and ET parameters of a two-center bond provide an estimation of the degree of bond covalency and ionicity, respectively, and have been previously used by Wuttig and coworkers to study PCMs.^12,58,67,68

In contrast to previous studies, we have calculated the pressure dependence of the ES and ET values in the A7 (A8) phases of group-15 (-16) elements not only for the primary covalent bond (with the d₁ length and plotted with solid lines in Fig. 1) but also for the secondary bonds of those phases (with the d₂ length and plotted with dashed lines in Fig. 1). Similarly, we have calculated the ES and ET values of the only bond present in the A_h and A_i phases of these two elemental families. In this way, we can see the evolution of the number of electrons shared by two atoms for the different bonds present in the A7 and A8 structures as EDMB formation proceeds at HP. It must be noted here that since we are dealing with pure elements with a unique Wyckoff site at each crystalline structure, the values of ET for the primary and secondary bonds are necessarily zero; thus, we only need to calculate the values of ES for bonds in pnictogens and chalcogens at different pressures.

As examples of both families, Fig. 5 shows the pressure dependence of the ES value in As and Se, as well as in α-Po and β-Po. The ES values of the primary covalent bonds in As-I and Se-I at RP are between 1.5 and 2, which are typical for strong primary covalent bonds, while the ES values of the secondary bonds at RP (around 0.5) are typical for relatively weak secondary donor–acceptor bonds.¹³¹ Remarkably, the ES value of the only bond present in the A_h and A_i phases of As, Se, and Po is close to 1.0. This means that an ES value close to 1.0 is characteristic of the octahedral coordination in As (Se) above 25 (23) GPa as well as of the two phases of Po at RP. In other words, bonds between two centers in these phases are 2c-1e bonds characterized by sharing one electron between two atoms, as already suggested for PCMs.^58,68 Therefore, the ES values close to 1.0 indicate the presence of EDMBs in the octahedrally coordinated phases of pnictogens and chalcogens. In this context, it must be stressed that they are not isolated 2c-1e bonds but interacting 2c-1e bonds, as suggested by the multicenter character of this unconventional bond.^39–41,52 We want to note that the pressure dependence of the ES values shown in Fig. 5 for the ES values obtained from QTAIM in pnictogens and chalcogens is confirmed by the ES values obtained as 2 × ICOBI(2c) using the LOBSTER program (not shown). Therefore, the picture we have described in Fig. 5 is consistent with both density-based and orbital-based methods. Importantly, the inverse relationship observed between the pressure dependence of ES values for both primary and secondary bonds in As and Se in Fig. 5 means that there is a charge redistribution, as already found in the formation of ERMBs, such as in HF₂⁻ (or [F–H–F]⁻).¹³² Therefore, this inverse relationship of ES values can be considered solid proof of the multicenter character of the interaction occurring in the A7 and A8 phases of As and Se, respectively, leading to the formation of multicenter bonds in the octahedrally coordinated α-Po and β-Po phases of As and Se at HP. Note that the equalization of ES values in the octahedrally coordinated α-Po and β-Po phases of pnictogens and chalcogens means that the electrons shared in the new bonds of these phases come from the original covalent bonds in the low-coordinated phases, thus showing the connection (multicenter character) between the weakened covalent bond and the new bond when the pressure-induced EDMB is formed.

Fig. 5 Pressure dependence of the calculated number of electrons shared (ES) between two adjacent atoms along the primary (triangles) and secondary (circles) bonds in (a) As: A7 (red) and A_h (blue), (b) Se: A8 (red) and A_i (blue), and (c) Po: A_h (blue) and A_i (green).

It has been suggested that ES and ET values calculated for primary bonds in materials can be used in a 2D map that allows a classification of the different types of materials and the definition of metavalency, i.e. a region between the covalency and metallicity.^12,67,68 We have used the ES vs. ET plot (see Fig. 6) to locate the different phases of pnictogens and chalcogens at different pressures. As expected, the ES values of the primary bonds in As, Sb, Se, and Te at RP are between 1.4 and 2.0, thus corresponding to classical covalent bonds. Note that a pure covalent bond with ET = 0 would have ca. ES = 2, and thus Sb and Te cannot be considered to feature pure covalent bonds but weakened covalent bonds. Meanwhile, the ES value of the primary bond in Bi at RP is 1.2. This value is close to 1.0, which corresponds to materials showing EDMBs, like α-Po and β-Po. This is also the case for many PCMs with rs structure, such as β-GeTe, SnTe, and PbS, despite in these cases ES being different from 1 due to the larger value of ET.⁶⁸ Consequently, our result for Bi-I at RP suggests that this element is characterized by bonds that are intermediate between covalent bonds and EDMBs. This result is consistent with the appearance of asymmetric EDMBs in Bi-II above 2.5 GPa (the smallest pressure of all pnictogens), as already commented. Finally, the ES values of the sixfold-degenerated bonds in α-Po and β-Po at RP, as well as in the HP phases of the other elements (As-II, sc-Sb, Bi-II, and β-Po phases of Se and Te) are all around 1.0 (see Fig. 6 and Fig. S12, ESI†). These results evidence that all the latter phases show EDMBs that are in good agreement with their positions in the 2D map.⁶⁸

Fig. 6 Revisited 2D map of the number of electrons shared (ES) vs. the normalized number of electrons transferred (ET) showing the chemical bond classification in materials. Besides the red, black, and blue regions corresponding to the classical covalent, ionic, and metallic bonds, respectively, the map shows the orange and green regions of materials with electron-rich multicenter bonds (ERMBs) and electron-deficient multicenter bonds (EDMBs). Red (blue) dashed arrows indicate how pure covalent (ionocovalent) p-type materials are affected by pressure or by composition (substitution by a heavier element). Circles correspond to materials studied in previous studies.^60,63,68 Pnictogens and chalcogens here studied at different pressures are shown as open squares. As observed, the structures of pnictogens and chalcogens with octahedral coordination are located in the green region of EDMBs as well as PCMs, such as cubic GeTe, SnTe, and PbS. Reproduced with permission.⁶⁸ Copyright 2021, Wiley-VCH.

At this point, it is worth pointing out that EDMBs (with ES ≈ 1) are an intermediate step between ionocovalent bonds (with ES ≈ 2) and metallic bonds (with ES → 0). Since pressure tends to increase atomic coordination, the octahedral coordination will be surpassed at high enough pressures and there will be an increase in the number of delocalized electrons relative to localized electrons. This means that the EDMB will tend to become a metallic bond at HP, as suggested by Wuttig and coworkers.^13,34

The tendency of materials with p-type bonds to change from ionocovalent bonds to EDMBs and finally to metallic bonds upon the change in pressure or composition (substitution by a heavier element within a group), is indicated by arrows for pure covalent and ionocovalent p-type materials in Fig. 6. It can be speculated that the fully metallic bond will occur in pnictogens and chalcogens as well as in A^IVB^VI and A^V₂B^VI₃ chalcogens when the eightfold-coordinated body-centered cubic (bcc, Strukturbericht type A2) phase is reached since the A2 phase is a common HP phase to all of them.^99,121,133 This hypothesis seems to agree with the results of Häuserman and coworkers,¹³⁴ who commented (later discussed) the notable differences between the electronic band structure and DOS in the A2 HP phase and previous phases at lower pressures in Bi. However, the hypothesis of metallic bonding in the bcc phase is contrary to the claim of Lubchenko and coworkers, who consider that this phase is still characterized by multicenter bonds.³¹ Further work in this direction must be done that is outside the scope of the present manuscript.

It is important to stress that the usefulness of the ES vs. ET map has been recently questioned.⁵⁹ It has been stated that this map should not be used to understand the origin of EDMBs in PCMs because it is impossible to locate in this map materials with more than a single type of bond. We consider that this is true and that is likely the case why Wuttig et al. only locate materials through their principal bond. Moreover, we believe that even though the ES vs. ET map cannot be used to univocally characterize materials, it is quite valid to characterize bonds in materials. We find that the ES vs. ET map is equivalent to the map already published by Mori-Sánchez et al. to classify bonding types with two parameters, the electron density flatness, f, and the global charge-transfer index, c. In fact, the map of Mori-Sánchez et al. has been suggested to be equivalent to the van Arkel–Ketelaar diagram.¹¹¹ The flatness is equivalent to metallicity and therefore is inverse to ES, while the charge-transfer index is similar to ET. According to our calculations, As-II and α-Po (with sc structures) and PbS (with rs structure) show f values close to 0.1, i.e. intermediate between those of materials with covalent bonding, like Ge and GaAs, and materials with metallic bonding, such as Al and Cu. These results indicate that the region of metavalency, intermediate between covalent and metallic regions, can also be placed in the f vs. c map, and correspondingly in the equivalent van Arkel–Ketelaar diagram. All in all, this means that the ES vs. ET map seems to be equivalent to the f vs. c map of Mori-Sánchez et al. and the classic van Arkel–Ketelaar diagram. Thus, our results support Wuttig's claim about the validity of the ES magnitude for locating the metavalency region between the covalent and metallic regions.^12,13,34 It must be mentioned that these results differ from those of Lubchenko and coworkers, who suggest that the multicenter bond is only intermediate between ionic and metallic bonds.³¹ On the other hand, our results agree with the claim of Lubchenko and coworkers³¹ that multicenter bonds are promoted with increasing density since the changes in pressure and composition (going down within a group) allow for increasing the electronic density of the material. Finally, we have to mention that after the first submission of this version of the manuscript to publication on December 1st, 2023,⁶³ a new paper from Wuttig and coworkers has been published that shows that the ES vs. ET map, which is based on electron density methods, is equivalent to the map of 2 × ICOBI vs. normalized Löwdin charge, which is based on orbital methods.⁶⁰ In a similar way, a new paper from Dronskowski and coworkers has been just accepted for publication that in our opinion reinforces the similarity of both maps.⁹⁷ In conclusion, we consider that the ES vs. ET map is valid to characterize bonds in materials as it has been assessed by different groups with different methodologies. This map provides evidence for the electron-deficient nature of bonds in the octahedrally coordinated crystalline phases of pnictogens, chalcogens, and binary PCMs.

2.4. Multicenter character of bonds in the crystalline phases of PCMs

Once confirming the electron-deficient (metavalent) character of EDMBs in the octahedrally coordinated crystalline phases of pnictogens and chalcogens, to finish this section, we want to remark that the multicenter character of the unconventional bond in the A_h and A_i phases of group-15 and -16 elements is consistent with previous calculations of PCMs characterized by the IpCOHP(2c) and the ICOBI(3c) values reported by Dronskowski and coworkers.^39,40 For this purpose, we have analyzed the values of the IpCOHP(2c) along the primary and secondary bonds of the A7 and A8 structures in pnictogens and chalcogens, respectively, at different pressures and also the ICOBI(3c) along the two bonds.

As an example, we will comment on the data for As. As exhibits a decrease (increase) of IpCOHP(2c) along the primary d₁ (secondary d₂) bonds in As-I from −3.451 (−0.835) at 0 GPa to −3.135 (−2.733) at 35 GPa. This trend is indicative of the decrease (increase) of the strength of the primary (secondary) bond until both bonds reach the same value once the As-II structure is attained. This pressure-induced “trans influence”, i.e. the influence of the secondary bond on the primary bond, is evidenced for As in Fig. 5a by the inverse pressure dependence of the ES values of both primary and secondary bonds. On the other hand, the increase of the absolute value of ICOBI(3c) from −0.046 at 0 GPa to −0.076 at 35 GPa is indicative of the increase of the multicenter (in this case three-center) interaction as one goes from As-I to As-II. According to Dronkowski and coworkers, the negative value of ICOBI(3c) indicates that these multicenter bonds are ERMBs;³⁹ however, we think that this interpretation of the value of ICOBI(3c) should be revisited. In any case, the trans influence of the secondary bond on the primary bond in pnictogens and chalcogens, substantiated in the inverse behavior under pressure of many parameters related to these two bonds, evidences that there is a secondary multicenter interaction that ends with the formation of a multicenter bond (EDMB) at HP above a certain pressure, i.e. the EDMB that comes from the original primary and secondary bonds at RP in the Peierls distorted phase (A7 in pnictogens and A8 in chalcogens). This result agrees with the previous suggestion of the multicenter character of this bond in PCMs.³⁹

As a kind of conclusion for this section, we can comment that we have shown that the A_h and A_i phases of group-15 and -16 elements feature the same type of unconventional bond as PCMs, which have been catalogued as incipient metals. These unconventional bonds and phases are mainly observed in pnictogens and chalcogens at HP, except for polonium. Our results show that this unconventional bond is an EDMB, which is an intermediate bond between covalent and metallic bonds characterized by localized electrons (typically one) between two atoms and delocalized electrons over more than two atoms. This result agrees with both the hypervalent and metavalent bonding models, which have already proved the partial delocalized nature of electrons in the unconventional bonding of PCMs using the projected force constants³⁹ and the ES values.³⁴ In this context, we have chosen to use the ES values in Fig. 5. On the other hand, our view has some agreement and some disagreement with the previous hypervalent and metavalent bonding models of crystalline PCMs. We agree with the hypervalent model in the multicenter character of the unconventional bonds but disagree with the electron-rich character of this bond. On the other hand, we agree with the metavalent model that the electron delocalization in EDMBs is responsible for the sharing of ca. one electron (ES ≈ 1) between every two atoms; i.e. the bond is electron-deficient in character. However, we consider that the metavalent bonding has a multicenter character. Therefore, we consider that the unconventional bond in PCMs is not a new-brand bond (the metavalent bond) but the old-known electron-deficient multicenter bond present in boron and boranes.^12,67,135

The lower ES value in the EDMBs than in covalent bonds indicates that the electronic charge shared between two atoms in EDMBs is smaller than in covalent bonds. Consequently, EDMBs are softer bonds than covalent bonds, as confirmed by lattice dynamics studies.¹³⁶ In fact, EDMBs are half bonds, i.e. one electron bonds that are well known to be softer and longer than covalent bonds.^12,67,135 The high probability of multiple events observed in laser-assisted field evaporation experiments of PCMs using atomic force microscopy has also been correlated to the softness of EDMBs;^12,67,135 however, we consider that it could also be correlated to the multicenter character of the unconventional bonds in PCMs. The transformation of the strong covalent p-type bonds into the softer EDMBs in group-15 and -16 elements at HP, marked by the progressive softening of the covalent bonds as atomic coordination increases at HP, accounts for the softening of the optical phonon frequencies in their covalent p-type crystalline phases at low pressures, as already proved,⁵² and for the lower melting points of Bi and Po than those of Sb and Te at RP and of Sb and Te than those of As and Se, respectively.¹¹⁶ In the next section, we will explore in more detail the transformation process from the strong covalent bonds to the soft EDMBs to unveil the mechanism of such transformation.

3. Mechanism of EDMB formation in pnictogens and chalcogens

The magnitude of pressure allows fine-tuning of interatomic interactions by the gradual change in interatomic distances; consequently, the analysis of the pressure dependence of the parameters related to the primary and secondary bonds in the A7 (A8) phases of pnictogens (chalcogens) could allow us to delve deeper into the mechanism of their pressure-induced pre-EDMB-to-EDMB transformation. For this purpose, we will make use of several theoretical bond descriptors, such as ES and ET, ρ and ∇²ρ, ELF, DOS, COOP, pCOHP, IpCOHP, and ICOBI, that have been previously used to describe the unconventional bonds in PCMs.^{12,34,39–44,57} In particular, we will analyze here the pressure dependence of the primary and secondary bond distances, d₁ and d₂, and their corresponding values of charge densities, ρ_d1 and ρ_d2, and ELF, ELF_d1, and ELF_d2 at the BCPs for the A7 (A8) phase of group-15 (16) elements. We will also analyze the evolution of the pCOHP and COBI parameters and their integrated values along the two distances d₁ and d₂. These values will help us to understand the bonding, nonbonding, or antibonding character of the different orbitals involved in the different bonds.^{39–41,137–139} The same calculations will be here also performed for the only bond distance present in the A_h and A_i phases of Po. Finally, we will analyze the behavior of the ELF isosurfaces of all these phases at different pressures.¹⁴⁰ This information will allow us to determine the evolution of the LEPs of the A7 (A8) phase of group-15 (-16) elements at HP when they undergo the PT to the A_h (A_i) phase and to understand the mechanism of the transformation from the pre-EDMB scenario to the EDMB one.

Before analyzing the precise mechanism of the transformation from the pre-EDMB scenario to the EDMB one in pnictogens and chalcogens, we want to stress that the basics of this transformation, either by the change in pressure or composition, proceed according to the sequence from left to right displayed in Fig. 7a–c. In this section, we will show that the pressure-induced transformation from the pre-EDMB scenario to the EDMB one in group-15 and -16 elements (and by extension in PCMs) proceeds via several stages: three stages (Fig. 7a–c) in pnictogens and two stages (Fig. 7b and c) in chalcogens. The only exception is Po, which is already in stage 3 at RP (Fig. 7c). It must be stressed that the appearance of up to three stages in the formation of EDMBs is no surprise since it is related to the formation of multicenter bonds. Notice that the same three stages have been observed in the formation of ERMBs, such as those of HF₂⁻ (or [F–H–F]⁻).¹³²

Fig. 7 Graphical representation of the mechanism of EDMB formation under the effect of pressure, P, or change in chemical composition, X (substitution of atoms by their heavy analogues). (a) and (b) Stages 1 and 2 correspond to classical primary covalent ppσ-bonds plus secondary bonds in pnictogens (As, Sb, and Bi) and chalcogens (Se and Te) at RP, respectively. (c) Stage 3 represents the EDMBs that are present in α-Po and β-Po at RP as well as in the octahedrally coordinated HP phases of As, Sb, Bi, Se, and Te. Blue isosurfaces correspond to the bonding orbital of the covalent A–B bond, as well as the EDMB. Pink isosurfaces represent the antibonding orbital of the covalent A–B bond and the LEP of atom C. The color intensity of different interactions reflects the bond strength at the different stages. (d)–(f) Projected crystal-orbital Hamilton populations (pCOHPs) for the As-I phase at 0, 20, and 35 GPa corresponding to the three stages, respectively. The colored regions in the pCOHP panels illustrate the LEP and its interactions. Vertical dashed lines indicate the limits of the stages that we have noted as LEP distortion, LEP depopulation, and LEP delocalization.

It is important to note that a similar plot to Fig. 7a–c was schematized by Lee and Elliott for the crystallization of GST,^42–44 which was based on the progressive formation of hypervalent ERMBs in molecules, as already commented by Hoffmann and coworkers,^{29,49,50,141,142} and recently reviewed.⁸¹ However, the scheme for ERMB formation is slightly different to that for EDMB formation. In other words, both multicenter bonds share some features of the scheme but not all. Let us briefly comment on their similarities and differences.

The similarities between the two types of multicenter bonds can be understood if we consider that the formation of ERMBs and EDMBs occurs due to the existence of a mixture of strong primary bonds and weak secondary (noncovalent) interactions that show a multicenter interaction. Precisely, secondary bonding, multicenter bonding, and the trans influence of the secondary bond on the primary bond, which is characteristic of multicenter interactions, are key concepts of supramolecular chemistry that have been extensively revisited in the last two decades.⁸¹ These secondary interactions, apart from van der Waals interactions between LEPs of different atoms and other possible minor interactions, are traditionally considered to be caused by the interaction of the LEP (donor or Lewis base) of atom C in Fig. 7a and b and the antibonding orbital (σ*, acceptor or Lewis acid) associated with the primary covalent ppσ-bond between A and B atoms in Fig. 7a and b. This is the donor–acceptor charge transfer model of secondary bonding.⁸¹

The common features of multicenter (ERMB and EDMB) bond formation concerning Fig. 7a and c can be summarized as follows. For both multicenter bonds, Fig. 7a represents the case of a B atom showing a strong primary covalent ppσ-bond with the A atom (both separated a short distance d₁) and a weak secondary bond with the C atom (both separated a large distance d₂) in which a LEP is involved. This case corresponds to d₂/d₁ ≫ 1. Fig. 7b represents the case of a B atom showing a weakened primary covalent ppσ-bond with the A atom and a strengthened secondary bond with the C atom. We will show that this case corresponds to d₂/d₁ > 1. It has been reported that the strength of the secondary interactions is determined by the appropriate alignment of the directions of the LEP and σ*, which in turn depends on the d₂/d₁ ratio. In this way, the closer the A–B–C angle to 180° and the smaller the d₂/d₁ ratio the stronger the LEP–σ* interaction. This consideration suggests that, in general, the strength of the secondary bond is higher in stage 2 (Fig. 7b) than in stage 1 (Fig. 7a). Finally, Fig. 7c represents the case of a B atom showing a multicenter bond (either an ERMB or EDMB, at least in electron-rich elements) with A and C atoms. Ideally, a fully symmetric, linear multicenter bond occurs when A and C atoms are exactly at the same distance from the B atom (d₂/d₁ = 1). We will show in this section that: (i) Fig. 7a is the typical case of pnictogens at RP; (ii) Fig. 7b is the typical case of chalcogens at RP and of As above 16 GPa; and (iii) Fig. 7c is the typical case of Po at RP and of As, Sb, Bi, Se, and Te when they reach the octahedral coordination at HP.

Let us comment now on the differences between the mechanism of ERMB and EDMB formation. The above-described model for secondary LEP-σ* donor–acceptor interaction (also noted as n → σ*) has been usually considered for the formation of hypervalent molecules, i.e. with ERMBs.⁸¹ Traditionally, the LEP–σ* interaction has been explained as a charge-transfer model in which part of the charge is transferred from the LEP donor to the σ* acceptor. This trans influence of the secondary bond on the primary bond, characteristic of multicenter bonds, is accompanied by an increase in the bond distance and a weakening of the primary covalent bond and it is related to the formation of the molecular orbital in the secondary interaction.¹³² This model of secondary donor–acceptor bonding can be considered to be due to the interaction of two antibonding orbitals since the LEP participates in an orbital, with assumed nonbonding character, but that has a certain antibonding character due to s–p mixing.^29,33 In our work, there is no donor and acceptor roles for different atoms since all pnictogen (chalcogen) atoms in A7 (A8) phases have LEPs and associated σ*, i.e. the roles of atoms in Fig. 7a–c could be reversed because the B atom also has a LEP and the C atom also has an antibonding orbital. This suggests that the n → σ* model is not valid to describe the EDMB formation in incipient metals.

The secondary noncovalent interaction has been reinterpreted in the last few decades in light of the σ-hole concept.^{73,74,76–79,81} According to the σ-hole bond model, the secondary donor–acceptor bond consists of an electrostatic interaction between an electrophilic (acceptor) moiety and a nucleophilic (donor) moiety. This Coulombic interaction is related to the more electropositive potential and smaller electronic density of the acceptor moiety (σ-hole) and the more electronegative potential and larger electronic density of the donor moiety (σ-bump). In our work, the σ-hole could be considered to be located at both ends of the primary covalent ppσ-bond (e.g. As–As) and would correspond to the antibonding orbital, while the σ-bump could be considered to be located at the LEP of each atom. A key difference between the n →σ* and σ-hole bond models is that there is a net charge transfer from the donor to the acceptor in the n →σ* model, while there is no net charge transfer from the donor to the acceptor in the σ-hole bond model, but a polarization or charge shift in the acceptor moiety, which is induced by the proximity of the donor moiety. Therefore, it has been considered that the σ-hole model corresponds to an early stage of the supramolecular interaction (weak secondary bonding), while the n →σ* model corresponds to a more developed stage of this interaction (strong secondary bonding), i.e. closer to the multicenter bond formation.^{73,74,76–79,81}

A full discussion of the two models (ERMB and EDMB) for secondary bonding in molecules and solids, including group-15 and -16 elements, in the light of the σ-hole bond model is out of the scope of the present manuscript and will be provided in the second, forthcoming paper derived from ref. 63. Now we are only interested in pointing out that the ERMB is typically a 3c-4e bond in which there are three molecular levels: one bonding, one nonbonding (slightly antibonding), and one antibonding.⁸¹ In the ERMB formation, the LEP contributes two electrons to populate the medium nonbonding orbital. This means that the LEP, either transferred or not according to the n → σ* or σ-hole bond models of secondary bonding, respectively, provides the charge needed to form the ERMB. In other words, the two nonbonding electrons initially associated with the (donor) LEP in the secondary interaction partly become bonding electrons (i.e. participate in the bonding) when the ERMB is formed. This is the case of the pictures plotted by Lee and Elliot when discussing the mechanism of 3c-4e hyperbond formation in crystalline GST.^42–44

The situation is completely different in the process of EDMB formation that we plot in Fig. 7a–c. In the EDMB formation, the trans influence of the secondary bond on the primary bond leads to a charge transfer from the primary covalent bond towards the secondary noncovalent interaction. This is evidenced by the inverse relationship between the ES values of the primary and secondary bonds exemplified in Fig. 5. We will see next that in the process of EDMB formation the LEP plays a minor and different role than in the process of ERMB formation. Notice that all pnictogen (chalcogen) atoms have LEPs in the A7 (A8) structure, so the real situation is more symmetric than plotted in Fig. 7a–c and one cannot talk about donor and acceptor roles of different atoms as in the case of ERMB formation. We will see that the two nonbonding electrons initially associated with the LEP remain as nonbonding electrons in the EDMB (in this case forming part of a delocalized LEP).

In summary, EDMBs and ERMBs are two types of multicenter bonds that can be formed from original primary (covalent) and secondary (noncovalent) interactions. In ERMBs, the ES values are larger than the values of typical covalent bonds with similar ET values,^31,42,50 because the original nonbonding electrons of the stereoactive LEP in the secondary (donor–acceptor) interaction partly transform into bonding electrons of the newly formed 3c-4e bonds. In EDMBs, the ES values are smaller than the values of typical covalent bonds with similar ET values,^31,42,50 because the original nonbonding electrons of the stereoactive LEP in the secondary noncovalent interaction remain as nonbonding electrons of the inactive and delocalized LEP. In other words, most of the p-type electrons needed to form EDMBs that are interacting 2c-1e bonds come from the original primary covalent bonds because the s-type electrons of the original LEP do not participate in the formation of the EDMBs. Now let us analyze in more detail the mechanism of EDMB formation in pnictogens and chalcogens, the different stages of the pre-EDMB-to-EDMB transformation in these two elemental families, and the way how the LEPs of these elements become delocalized as the EDMBs are formed upon increasing pressure.

3.1. Pnictogens

Experimental⁹¹ and theoretical data for As show that the pressure-induced A7-to-A_h PT is characterized by the equalization of the (three) short primary intralayer, d₁, and the (three) large secondary interlayer, d₂, bond distances in As-I as pressure increases (Fig. 8a). Concomitantly, an equalizing trend is observed for ρ_d1 and ρ_d2 (Fig. 8b) and for ELF_d1 and ELF_d2 at BCPs (see Fig. S12 in the ESI†). Remarkably, both ρ and ELF values of the EDMBs in As-II at P_t are smaller than those of the covalent bonds in As-I at RP. Similar trends also occur in Sb and Bi during the A7-to-A_h PT and in Se and Te during the A8-to-A_i PT (see Fig. S3, S5, S8, and S10 in the ESI†). Furthermore, similar trends have also been reported in A^IVB^VI and A^V₂B^VI₃ compounds.^{42,82,85,96,143} Therefore, our results suggest that EDMBs at P_t in group-15 and -16 elements are weaker than covalent bonds at RP, as already commented at the end of the previous section. In this context, it is worth noting that the covalent character previously attributed by many researchers to the EDMBs in Bi-III and PCMs of the A^IVB^VI family^52,134 is likely due to the relatively high values of ρ and ELF found for EDMBs, but they are typically somewhat smaller than those found for covalent bonds (ρ_d1 and ELF_d1). Since both ρ and ELF values show similar trends hereon we will comment only those of ρ values.

Fig. 8 Theoretical physical properties of As-I (A7, red) and As-II (sc, blue) as a function of pressure. (a) Calculated (line) and experimental (circles)⁹² first- and second-nearest neighbor distances, d₁ and d₂, respectively, in As-I and As-II crystals. (b) Charge density at the BCP along the different bond distances, ρ_d1 and ρ_d2, respectively, in As-I and As-II. (c) Evolution of d₁vs. d₂ for As-I. (d) Evolution of ρ_d1vs. ρ_d2 for As-I. Arrows in (c) and (d) indicate the direction of increasing pressure. e is the electron charge and a₀ is the Bohr radius. The three stages of the pre-EDMB-to-EDMB transformation are separated by vertical dashed and dotted lines.

The most important point in Fig. 8a and b is that three distinct stages occur in As between 0 and 35 GPa. These three stages correspond to stages 1 to 3 in Fig. 7a–c. In stage 1 (up to 16 GPa), there is a small (strong) decrease of d₁ (d₂) as well as a correspondingly small (large) increase of ρ_d1 (ρ_d2). In stage 2 (from 16 to 25 GPa), there is a decrease of d₂ and an anomalous increase of d₁ as well as a corresponding decrease (increase) of ρ_d1 (ρ_d2). Again, we have to stress that the inverse pressure dependence of d₁ and d₂ as well as of ρ_d1 and ρ_d2 in stage 2 evidences the trans influence of the secondary bond on the primary bond that accounts for the multicenter interaction present in this stage and that ends with the multicenter character of the EDMB in As-II. Finally, stage 3 is reached once both primary and secondary bonds equalize (above 25 GPa) in the A_h phase. This stage is characterized by linear EDMBs that show the normal decrease of the bond distance and increase of the bond charge density as pressure increases. A clearer picture of the three stages along the A7-to-A_h PT in As can be noted by the S-like behavior of d₁vs. d₂ and ρ_d1vs. ρ_d2 in As (see Fig. 8c and d) since d₂ (ρ_d2) always decreases (increases) with increasing pressure.

As commented in the Introduction section, it has been traditionally considered that no clear distinction could be made between secondary bonds and multicenter bonds.^31,42,50 However, a clear difference between stages 1 and 2 in As is provided by the sign change in the pressure coefficient of d₁ and ρ_d1 around 16 GPa (Fig. 8a and b) due to the simulated anomalous increase (decrease) of d₁ (ρ_d1) that occurs in stage 2 above that pressure. These anomalous trends agree with the results of previous calculations of the effect of pressure on As-I¹⁰⁰ and on As trimers,³¹ which left unnoticed. Unfortunately, the simulated increase of d₁ has still not been experimentally confirmed in pure As due to the limited resolution of the only published results based on a lab-based diffractometer⁹¹ and the lack of more accurate results coming from synchrotron-based X-ray diffraction measurements. In any case, it must be pointed out that our results for As are also consistent with the increase of the short intrachain d₁ distance in Se at low pressures (see Fig. S8a in the ESI†),¹⁴⁴ with the equalization of bonds at HP and the anomalous increase of the short bond distance at HP experimentally reported along the A7-to-A_h PT in elemental phosphorus,¹⁰² and with the anomalous increase of the short covalent bond experimentally reported for the Pnma–Cmcm (or Bbmm) PT in SnSe around 10 GPa.¹⁴³

Interestingly, the equalization of bond distances between strong primary covalent bonds and weak secondary closed-shell interactions upon the increase of pressure or density were already reported in the formation of multicenter bonds in molecules.^31,50 Moreover, an anomalous increase in the covalent bond distance was observed in the region close to the formation of the multicenter bond in different systems.^31,50 Additionally, simulations of the effect of pressure on elemental nitrogen have reported an anomalous increase in the intramolecular N–N bond distance at HP.⁸⁶ Simulating the evolution of the trimer (N₂)₃ system at HP, in which there is a coexistence of triple intramolecular N≡N bonds in N₂ and secondary intermolecular N₂ interactions at RP, it was found that the triple bond is destroyed at HP and single N–N bonds are formed.⁸⁶ An equalization of intramolecular and intermolecular N–N distances in this system occurs at HP, together with an anomalous increase of the intramolecular N–N bond distance, until both bond distances reach similar values at HP. Similarly, an equalization of intramolecular and intermolecular H–H distances occurs in elemental hydrogen at HP together with an anomalous increase of the intramolecular bond distance above 100 GPa.^145–148 Simulating the ring (H₂)₃ system, the equalization of distances in hydrogen has been understood as due to the progressive charge transfer from the primary, covalent, intramolecular H–H bonds to the secondary (noncovalent) intermolecular H–H bonds due to the trans influence between the primary and the secondary bonds.¹⁴⁸

For many years, the trans influence in the A7 structure of pnictogens was supposed to exist and invoked to explain the decrease of the frequencies of the optical phonons as well as the increase in the acoustic phonon frequencies and, consequently, the increase of the elastic constants at HP.^108,109 The inverse behavior of the simulated ρ_d1 and ρ_d2 in As at stage 2 (above 16 GPa) as well as of the ES values (Fig. 5a) of both primary and secondary bonds confirms the existence of the trans influence that results in a charge transfer from the primary covalent bond to the secondary bond as pressure increases until they reach the same value at P_t (once the EDMBs are formed).

As regards stage 3 in As (As-II), the normal decrease (increase) of the interatomic bond distance (bond charge density) of EDMBs in this stage is a common behavior of covalent materials with sp³ geometry and no secondary bonding, such as zinc blende Si and Ge.¹⁴⁹ This normal behavior of the bond distances and the charge densities of EDMBs is consistent with the experimentally and theoretically observed hardening of all phonons in As-II (Fig. 2a), as it occurs for Si and Ge.^103,150 This normal behavior of phonon modes at the EDMB scenario in As-II (also in rs-GeTe¹³) contrasts with the soft optical phonons in the pre-EDMB scenario in As-I (also in the R3m phase in GeTe).¹³ The normal behavior in sc-As and zinc blende Si and Ge is the result of the lack of trans influence due to the lack of secondary bonds in these crystalline structures. In other words, there is only a single type of bond in these crystalline structures. This normal behavior of EDMBs under pressure makes it difficult to distinguish these unconventional bonds from conventional covalent bonds. Based on the above observations regarding phonons, we tentatively conclude that the existence of soft optical phonons in materials with primary covalent ppσ-bonds and secondary bonds is a clear fingerprint for the previously suggested instability of these primary bonds at HP.^151–154 The softening of optical phonons in p-type covalent materials with secondary bonds, as shown by a recent three-center interaction model,⁵² can be understood as an instability of the structure due to the transformation of covalent bonds into EDMBs at HP. This instability of covalent p-type materials is analogous to the instability of tetrahedrally coordinated sp³ ionocovalent materials, such as zinc blende Si and Ge, whose soft acoustic modes at the Brillouin zone edges are signatures of the instability of the sp³ σ-bonds against octahedral coordination at HP.¹⁵⁵

3.1.1. Band picture analysis of the EDMB formation in pnictogens. A deeper understanding of chemical bonding in As can be obtained from the reciprocal-space (band) picture,^156,157 since the three stages of As can be distinctively characterized by orbital-based methods. The electronic bands and DOS of As-I at 0 GPa have been thoroughly discussed in the literature and are briefly commented on in Section 6 of the ESI.† Here we analyze the pCOHP (Fig. 6d–f) and COBI (Fig. S13 in the ESI†) as well as their integrated values (IpCOHP, ICOBI(2c), and ICOBI(3c)) along the d₁ and d₂ bonds in As-I at 0, 20, and 35 GPa that correspond to stages 1, 2, and 3, respectively.

The most important point in our calculations for As is that bands with antibonding character (a positive value of pCOHP¹³⁷) appear below the Fermi level both along d₁ and d₂ at RP. A similar feature was already reported in previous simulations of Te-I.¹³⁹ These bands come from the interaction between the LEP and the bonding orbital of the covalent bond (along d₁) and between the LEP and the antibonding orbital of the covalent bond (along d₂), as already discussed by Hoffmann and coworkers.⁴⁹ The antibonding character of these bands, in which LEPs are involved, comes from the s–p mixing, i.e. the mixing of the s-type electrons of the LEP and the p-type electrons of the bonding and antibonding orbitals of the covalent bond.^29,33

In stage 1 of As-I at 0 GPa (Fig. 7d), the larger pCOHP absolute values of the bonding bands (negative values of pCOHP¹³⁷) as well as the larger IpCOHP and ICOBI(2c) values along d₁ than along d₂ indicate a much stronger bonding in primary than in secondary bonds, as already commented at the end of Section 2. In addition, since negative (positive) values of ICOBI(3c) are interpreted to correspond to electron-rich or 3c-4e (electron-deficient or 3c-2e) interactions,^39,40 the small negative ICOBI(3c) value compared to the high positive ICOBI(2c) value along d₁ seems to indicate that three-center interactions are negligible in As-I at 0 GPa.

In stage 2 of As-I at 20 GPa (Fig. 7e), the profiles of the pCOHP along d₁ and d₂ become more similar (both above and below the Fermi level). The decrease (increase) of the strength of primary (secondary) interactions due to the trans influence is reflected in the smaller (larger) values of the pCOHP than at 0 GPa. Moreover, the antibonding bands below the Fermi level along d₁ (d₂) show a smaller (larger) value of the pCOHP in comparison to As-I at 0 GPa. This could be interpreted as if the LEP in this stage experiences a much larger interlayer interaction (LEP-σ*) than intralayer interaction. We interpret this feature as the signature that the LEP starts to become inactive (non-stereoactive) with increasing pressure due to LEP delocalization. The smaller and weaker (larger and stronger) primary (secondary) bonds in stage 2 than in stage 1 due to the trans influence are also reflected in the smaller (larger) values of IpCOHP(2c) and ICOBI(2c) along d₁ (d₂).^39,40 Moreover, the ICOBI(3c) value at 20 GPa is a much larger negative value than at 0 GPa, which seems to be consistent with the process of multicenter bond formation in As at HP.

Finally, pCOHP profiles are similar for the primary and secondary bonds in As-I at 35 GPa (Fig. 7f) as expected for EDMBs in stage 3. The slightly different profiles for both bonds are due to the slight distortion of the simulated A7 phase above 25 GPa with respect to the cubic symmetry, as already mentioned (both pCOHP profiles are exactly equal in As-II at 35 GPa when the cubic symmetry is forced, as shown in Fig. S13d in the ESI†). The most representative feature of stage 3 in As (As-II) is that an intense, broad antibonding band appears in the pCOHP just below the Fermi level. Unlike in the pre-EDMB scenario, this band overlaps with the antibonding orbitals of the conduction band, and so the value (negative) of the pCOHP at the Fermi level is different from zero. This result is the same as previously obtained for Te-II¹³⁹ and the antibonding character at the Fermi energy in As-II (Te-II) is clearly due to the repulsion between the inactive (weakly active) LEPs at reduced interlayer (interchain) distances.¹³⁹

At this point, we want to stress that our pCOHP results for As between stages 1 and 3 are fully consistent with the pCOHP results previously reported for Te, where completely different pCOHP profiles for the two different bonds in Te-I contrast with the similar profiles of the two different bonds in Te-II.¹³⁹ The similarity of the bonding orbitals along d₁ and d₂ in stage 3 of As (also in Te-II in ref. 139) indicates that p-type orbitals contribute equally to all bonds since they are of similar length, while s electrons forming part of the LEP are inactive in As-II and very weakly active in Te-II. Note that there is a small distortion of the triclinic structure of Te-II with respect to the cubic A_h structure,¹³⁹ which is similar to the distortion of the HP A_i phase of Te that we have simulated. Moreover, the weak LEP stereoactivity or even inactivity due to the LEP delocalization in stage 3 is consistent with the non-layered 3D structures of As-II and Te-II (as well as the other phases of As and Te at higher pressures). Noteworthily, the loss of the LEP stereoactivity and the occurrence of a flat/steep band near the Fermi level in Te-II have been postulated as signatures of superconductivity in the HP phases of group-15 and -16 elements¹³⁹ and also for the transition between trivial- and topological-insulating phases in the same materials.¹⁵⁸

We have to comment that the absolute value of ICOBI(3c) for As–As–As interaction in elemental As gradually increases (in the negative value) over the three stages (Fig. 7d–f), with the ICOBI(3c) value at stage 3 in As-II being similar to that recently reported for β-GeTe, in which ERMB formation was suggested.³⁹ However, we have already commented that bonds in As-II must be electron-deficient and not electron-rich, as suggested by the ES values and the charge transfer from the primary bond to the secondary one. In this context, we consider that there must be an unfortunate misinterpretation of the ICOBI(3c) value. Note that the negative values of ICOBI(3c) found in EDMBs, such as those of As-II and β-GeTe, are close to zero, i.e. much smaller in absolute value than those reported for molecules with ERMBs, such as XeF₂.³⁹

To conclude this subsection, we have to comment that our simulations on Sb and Bi also provide evidence of the presence of the three stages of the mechanism of EDMB formation along the A7-to-A_h PT (see discussion in Section 3 in the ESI†). As already commented, these three stages seem to be characteristic of the process of multicenter bond formation, as confirmed by the work of Espinosa et al.¹³² In this context, we observe a progressive decrease of the pressure range of stages 1 and 2 on going from As (stage 1: 0–15 GPa; stage 2: 15–25 GPa) to Sb (stage 1: 0–3.5 GPa; stage 2: 3.5–7 GPa) and Bi (stage 1: 0–2.5 GPa; stage 2: 2.5–2.7 GPa).

3.2. Chalcogens

Experimental and theoretical data show that the pressure-induced A8-to-A_i PT in Se and Te is characterized by the equalization of the (two) short primary intrachain (d₁) and the (four) large secondary interchain (d₂) bond distances as pressure increases (Fig. S8a and S10a in the ESI†). Concomitantly, an equalizing trend is observed for ρ_d1 and ρ_d2 (Fig. S8b and S10b, ESI†) and for ELF_d1 and ELF_d2 at BCPs (Fig. S12d and e in the ESI†). The most important point is that the two stages that occur in Se and Te at HP in the above-mentioned figures correspond to stages 2 and 3 in Fig. 7b and c. In stage 2 (near RP), there is a strong decrease of d₂ and an anomalous increase of d₁ that matches with available experimental values for Se (see Fig. S8a, ESI†).¹⁴⁴ This anomalous increase of d₁ is similar to that previously commented for As in stage 2 above 16 GPa. Correspondingly, there is an increase (decrease) of ρ_d2 (ρ_d1) and of ELF_d2 (ELF_d1) at BCPs in Se and Te, respectively. Finally, in stage 3, the A_i phase is reached and both primary and secondary bonds of Se and Te become EDMBs that show a normal decrease (increase) of the bond distance (bond charge density) at HP. Again, the partial S-like behavior of d₁vs. d₂ (Fig. S8c and S10c, ESI†) and ρ_d1vs. ρ_d2 (Fig. S8d and S10d, ESI†) provides a clearer picture of the two stages present in Se and Te at HP. Regarding the two mentioned stages of the pressure-induced pre-EDMB to EDMB transformation in Se and Te, it is worth noting that the behavior of bond distances and bond charge densities in stage 2 of Se and Te is similar to that previously found in stage 2 in pnictogens. The inverse behavior of ρ_d2 and ρ_d1 in elemental chalcogens at HP is caused by the trans influence between primary and secondary bonds (see ES in Se Fig. 5b), as already mentioned for pnictogens in stage 2, and gives support to the multicenter character of the EDMBs formed at HP.

As for pnictogens, the trans influence in elemental chalcogens was invoked a long time ago to explain the strong softening of the A₁ mode of the A8 phase as well as the increase of the frequencies of the acoustic phonons and the values of the elastic constants in Se-I and Te-I at HP.^151,159,160 In fact, the softening of the A₁ mode was attributed to the negative contribution of the intrachain bond stretching force constant, indicating a weakening of the intrachain covalent bonds.¹⁶⁰ On the other hand, the normal decrease of the interatomic bond distance and the increase of the bond charge density of EDMBs in stage 3 are consistent with the hardening of all phonons in the distorted A_i phase (Fig. S7d and S9d, ESI†). Again, it is interesting to remark that the pressure range of stage 2 decreases in group-16 elements from Se (0–23 GPa) to Te (0–7 GPa), i.e. it decreases for heavier cations, as already observed for group-15 elements.

A completely different behavior from pnictogens and chalcogens is found for both phases of Po. The normal, slight decrease (increase) of the bond distance (charge density) in both phases of Po at HP (Fig. 4c) clearly evidences that both phases of Po do not show several stages at HP. The reason is that they are already in stage 3 at RP because they show fully symmetric EDMBs at RP. The pCOHP features of α-Po and β-Po at RP (Fig. S11d, ESI†) are very similar and show similar values of IpCOHP(2c) to those found in As-II at 35 GPa (Fig. S13d, ESI†). Again, the negative value of ICOBI(3c) suggests the presence of ERMBs according to Dronskowski and coworkers,^39,40 although we consider that this interpretation should be revisited. In this context, we must stress that, although the value of ICOBI(3c) in Po is smaller than in As-II, the ratio ICOBI(3c)/IpCOHP(2c) is larger in Po than in As-II. This picture is also consistent with the pressure dependence of the ES (Fig. 5c) and ELF (Fig. S12f, ESI†). Notice that both phases of Po have ES ≈ 1 and a negligible increase of ES with pressure. This is an expected result for the EDMBs in stage 3 since there is no trans influence in this stage and bonds show no gain or loss of charge at HP, just a monotonous decrease (increase) of the bond distance (charge density) similar to that of materials with four ionocovalent bonds distributed in an sp³ geometry, such as Si and Ge.

A clearer comparison among all the studied pnictogens and chalcogens regarding the process of pressure-induced EDMB formation can be seen by plotting d₁ and ρ_d1vs. normalized d₂ and normalized ρ_d2, respectively (Fig. 9). This figure nicely shows the three (two) stages of the mechanism of EDMB formation in group-15 (16) elements. Moreover, the strength of the secondary interaction along the three stages can be traced by the change in the background color (from light blue to pink). The comparison of all elements in normalized values allows us to observe the decrease in the pressure range of stages 1 and 2 in pnictogens and of stage 2 in chalcogens upon moving down the group (from As to Bi and from Se to Po), with the only exception of Bi due to the issue of the PBEsol functional above 6 GPa commented in Section 2. Therefore, we conclude that the pressure-induced transformation from the pre-EDMB scenario to the EDMB scenario in group-15 (16) elements proceeds via three (two) stages, with Po being the only element of these two families whose two crystalline structures feature EDMBs at RP.

Fig. 9 Calculated primary bond distance, d₁, vs. the normalized secondary bond distance, d₂, in group-15 (a) and -16 (c) elements. Calculated charge density at BCP of the primary bond, ρ_d1, vs. the normalized charge density for the secondary bond, ρ_d2, in group-15 (b) and -16 (d) elements, where e is the electron charge and a₀ is the Bohr radius. Normalization is performed with respect to the corresponding values at P_t. The stages for each group of elements are separated by vertical dashed and dotted lines. The gradual change in the background color reflects the strength of the secondary bonds until the EDMB is formed at the normalized value of 1.

3.3. Bond vs. band analysis in the mechanism of EDMB formation

At this point, we want to stress that several questions regarding the mechanism of EDMB formation are still not clearly understood and need further exploration: Why do pnictogens show a three-stage mechanism and chalcogens only a two-stage one? Why is the A_h phase preferred by pnictogens at HP, while the A_i phase is preferred by chalcogens at HP? What is the relationship between stage 2 in group-15 and -16 elements? To provide an answer to these questions, here we study the mechanism of EDMB formation through the real-space (bond) picture that is complementary to the previously commented reciprocal-space (band) picture.¹⁴⁰

Since the analysis of the ELF topology is a good tool for understanding the formation of secondary bonds, as already shown for CO₂,¹⁶¹ we have analyzed the ELF isosurfaces corresponding to the values of the secondary bonds in which LEPs for the studied elements at different pressures are involved (Fig. 10). In group-15 elements, each atom in the layered A7 structure at RP (stage 1) is characterized by a single ELF attractor perpendicular to the layers corresponding to the LEP (Fig. 10a). This single-basin LEP is formed by s-type orbitals, and it is not aligned along any of the three secondary bonds of the A7 structure. At a certain pressure, the s-type LEP dissociates or splits into three similar lobes (onset of stage 2) that appropriately align with the directions of the three secondary bonds (Fig. 10b). At P_t (upon the A7-to-A_h PT), three new lobes along the primary bonds appear that become equal to those of the secondary bonds. This final LEP delocalization marks the onset of stage 3. At this stage, six lobes can be observed around each atom corresponding to the three pairs of EDMBs in the A_h phase (Fig. 10c). Noteworthily, six ELF attractors of similar size to those of the A_h phase in As are also observed in Bi-II (Fig. S6f, ESI†), thus indicating that Bi-II already exhibits asymmetric EDMBs. It is important to mention that six equal ELF lobes are also present in α-Po at RP; thus, we conclude that six equal ELF attractors are characteristic of fully symmetric EDMBs with cubic symmetry in electron-rich elements.

Fig. 10 ELF isosurfaces of elemental pnictogens (a)–(c) and chalcogens (d) and (e) at the three possible stages of the mechanism of EDMB formation at different pressures. RP and HP stand for room and high pressures, respectively. The LEP basins are defined by an ELF isosurface (yellow color) arbitrary choice for the element/stage. At RP, As, Sb, and Bi are located in stage 1, Se and Te are located in stage 2, and Po is located in stage 3.

Considering the LEP picture, the results in Fig. 10a–c for pnictogens can be understood in the following way: in stage 1, the single-basin LEP found at RP suffers a considerable distortion due to the increasing interlayer interaction as pressure increases, which is caused by the strong compression of the interlayer distance. At the same time, the trans influence in stage 1 slightly increases the charge of the secondary bond at the expense of the primary covalent ppσ-bond. The LEP distortion ends with the splitting of the single ELF basin into three ELF basins (onset of stage 2), which are aligned along the three secondary bonds. Upon further increase of pressure, the LEP starts to become inactive due to a gradual decrease in the LEP charge and an increase in the LEP delocalization. The lack of LEP stereoactivity is evidenced in As by the decrease of the strength of the band located below the Fermi level in the pCOHP profile along the primary bond (Fig. 7d–f). In other words, the LEP becomes increasingly depopulated and delocalized in stage 2 as pressure increases, as already reported in Te at HP.¹⁵⁸ These results are consistent because the decrease of the LEP stereoactivity at HP is a well-known phenomenon in many materials, e.g. β-Bi₂O₃.¹⁰⁵ Concomitantly, a much larger trans influence occurs in stage 2 than in stage 1 (Fig. 5a), which is consistent with the strong decrease of phonon frequencies in As and Sb above 16 and 4 GPa, respectively. The trans influence ends at P_t when both the primary and secondary bonds acquire the same charge (onset of stage 3). In this stage, six lobes or basins are observed around each pnictogen atom that correspond to the three pairs of orthogonal EDMBs in the A_h phase.

A similar interpretation of the ELF isosurfaces can be made for chalcogens. Each Se and Te atom in the A8 structure at RP (stage 2) is characterized by two ELF attractors or lobes that are already aligned in the directions of two of the four secondary bonds, i.e. they form an angle of nearly 180° with the nearest covalent bond (Fig. 10d). These features agree with previous calculations,^139,158 and are typical of p-type LEPs. In other words, there is a p-type LEP distributed along two (of the four) secondary bonds of each atom of Se and Te at RP, and no LEP lobe pointing along the other two secondary bonds of the same atom. As pressure increases, the two LEP lobes become severely distorted and spread over the four secondary bonds. Finally, upon the A8-to-A_i PT at P_t (stage 3), an ELF attractor with a toroidal shape is observed around each atom (Fig. 10e). This toroidal shape of the ELF is also found in β-Po at RP; thus, we conclude that a toroidal ELF attractor is characteristic of EDMBs with rhombohedral symmetry in electron-rich elements.

The results in Fig. 10d and e for chalcogens can be understood in the following way: in stage 2, the p-type LEP of Se and Te at RP shows two ELF basins that are aligned along two of the four secondary bonds. This stage of chalcogens mirrors stage 2 of pnictogens, where the lobes are also appropriately aligned along the secondary bonds. Therefore, it seems that group-15 and -16 elements show a different number of stages that are related to the different LEP spatial distributions (or a kind of LEP) involved in the secondary bonds. This allows us to understand the relationship between stage 2 in both pnictogens and chalcogens and why the short primary bond distance (charge density) shows an anomalous increase (decrease) with increasing pressure at this stage in both elemental families. The reason is the strong trans influence present in this stage of the pre-EDMB to EDMB transformation, which is also responsible for the strong decrease of the A₁ phonon frequencies in Se and Te already at RP. All the above results are consistent with previous results for Te at HP.^139,158 Finally, the trans influence ends at P_t when both the primary and secondary bonds acquire the same charge (onset of stage 3). In this stage, a toroidal lobe or basin is observed around each chalcogen atom that corresponds to the weakly active LEP in the A_i phase.

As previously mentioned for pnictogens, the p-type LEP of chalcogens in stage 2 becomes gradually inactive as pressure increases due to the LEP depopulation and delocalization; however, we have to stress that the behavior of the LEP of chalcogens at this stage is different from that of pnictogens. In stage 2, the ELF basins of the p-type LEPs in chalcogens become increasingly distorted with increasing pressure and become elongated towards the direction of the two secondary bonds with no ELF attractor at RP. This behavior is consistent with the electron transfer of the p-type LEP to the antibonding orbitals in Te-I at HP proposed in ref. 158 and also with the breakdown and delocalization of the LEP in Te-I at HP, so that one of the p-type electrons becomes itinerant in Te-II as suggested in ref. 139. These results contrast with the behavior of s-type LEPs in stage 2 of pnictogens that barely change their profiles as they become progressively inactive. Due to the itinerant p-type electron, the ELF isosurface of Se and Te at the end of stage 2 shows a toroidal shape around each atom that is maintained in stage 3 and is characteristic of the A_i phase and different from that of the A_h phase, where no itinerant electrons are observed. This itinerant electron in the A_i phase can be ascribed to the extra valence electron present in group-16 elements as compared to group-15 elements. Therefore, it is clear why group-15 elements (with five valence electrons) tend to the A_h phase at HP, as rationalized by Papoian and Hoffmann,⁵¹ and why group-16 elements (with six valence electrons) tend to the A_i phase at HP.

Now we are in a better position to show the correlation between the three (two) stages found in group-15 (-16) elements with the three stages represented in Fig. 7a–c and their extension to A^IVB^VI and A^V₂B^VI₃ compounds related to PCMs. Stage 1 in Fig. 7a corresponds to a material with primary, short, and strong covalent 2c-2e ppσ-bonds (distance d₁) between A and B atoms and secondary, large, and weak bonds to atom C (distance d₂), which usually correspond to a ratio d₂/d₁ ≫ 1. This stage seems to occur in materials showing a single-basin-type LEP, such as pnictogens at RP. Therefore, we can speculate that this situation could also be found in isoelectronic A^IVB^VI compounds showing no rs structure at RP (GeS, GeSe, α-GeTe, SnS, and SnSe) as well as A^V₂B^VI₃ compounds showing no tetradymite-like structure at RP (As₂S₃, As₂Se₃, α-As₂Te₃, Sb₂S₃, Sb₂Se₃, and Bi₂S₃). The step going from stage 1 to stage 2 is characterized by the single-basin-type LEP dissociation or splitting, i.e. the LEP in stage 1 splits into several basins aligned along the directions of the secondary bonds. Therefore, stage 2 (Fig. 7b) corresponds to a material with weakened primary covalent ppσ-bonds and strengthened secondary bonds caused by the charge transfer (trans influence) from the primary bonds to the secondary bonds. This stage occurs upon the decrease of the d₂/d₁ ratio (d₂/d₁ > 1) and it is caused by either the effect of pressure or composition (substitution by a heavier element). Stage 2 is the prior step to the EDMB formation, and so asymmetric EDMBs could be likely formed in stage 2 for values of d₂/d₁ close to 1 (tentatively below 1.05–1.10). Stage 2 is observed at RP in materials with p-type LEPs, such as Se and Te, and also at HP in materials with single-basin-type LEPs, such as pnictogens and perhaps the above commented A^IVB^VI and A^V₂B^VI₃ materials. The step going from stage 2 to stage 3 is characterized by the disappearance (or almost) of the LEP stereoactivity, due to a progressive LEP depopulation and delocalization, which finally leads to octahedral coordination in materials with p-type bonds. Curiously, the decrease of the LEP stereoactivity in group-15 and -16 elements at HP upon approaching the octahedral coordination is related to the appearance of superconductivity in all these elements at HP, except for Bi, which already shows superconductivity at RP.^139,162,163

The ideal stage 3 (Fig. 7c) corresponds to a material with fully developed and symmetric EDMBs and with equal A–B and B–C bonds. This stage occurs for d₂/d₁ ≈ 1. For instance, stage 3 occurs in the A_h and A_i phases of Po at RP and octahedrally coordinated pnictogens and chalcogens at HP. This stage with EDMBs is also observed at RP in the rs phase of A^IVB^VI PCMs and of related ternary compounds, such as GeSb₂Te₄ and GST. Moreover, stage 3 can be considered to be also present at RP in the tetradymite-like phases of A^V₂B^VI₃ PCMs (Bi₂Se₃, β-As₂Te₃, Sb₂Te₃, and Bi₂Te₃)⁶⁸ and of ternary A^IVB₂^VC₄^VI compounds (GeSb₂Te₄ and SnSb₂Te₄),⁹⁶ although not all atoms in the tetradymite-like phases show EDMBs due to their layered crystalline structures.⁵¹ The above observations support the idea already mentioned that the LEP stereoactivity decreases at HP and on going down a group in the periodic table. A total disappearance of the LEP stereoactivity is noticed in stage 3 if a cubic phase is obtained, such as in the A_h structure (of P, As, and α-Po) or the rs structure (of A^IVB^VI PCMs). However, a residual LEP stereoactivity is observed in stage 3 if a distorted cubic phase is obtained, such as distorted sc phases (Bi-II and Bi-III) and rhombohedral phases (chalcogens and tetradymite-like A^V₂B^VI₃ PCMs). Finally, it must be mentioned that EDMBs can be formed in one, two, or three directions. In this manuscript, we have only commented on the case of EDMBs in three directions and the cases of EDMBs along one and two directions will be commented on in the second paper derived from ref. 63.

The unanswered question regarding LEP stereoactivity, already posed by Papoian and Hoffmann more than 20 years ago,⁵¹ is why α-Po crystallizes in the A_h phase at RP and low temperatures if chalcogens have an extra electron that tends to distort the sc structure typical of pnictogens with five valence electrons. As we have already commented, this distortion causes chalcogens to crystallize in the rhombohedral A_i phase of β-Po at HP. Papoian and Hoffmann suggested that the sixth electron of α-Po could be divided over the three p-bands (1/3 to each p_x, p_y, and p_z); therefore, the extra electron in chalcogen atoms would be shared with the neighbors. However, our results show that the extra electron is not shared between the chalcogen atoms in the EDMBs since the values of electrons shared (ES) between two atoms are similar in both phases of Po (Fig. 5c) and are even slightly smaller than those of the A_h phase of As-II (Fig. 5a). Instead, our results suggest that the extra electron in α-Po resonates between the six lobes of the ELF of the A_h phase since the values of the ELF isosurfaces showing the inactive LEP in the A_h phase are smaller for As-II (0.825) than for α-Po (0.875). In other words, there is a larger charge density at the inactive LEP in α-Po than in As-II. Therefore, it looks like that low temperature helps to freeze the extra p-type electron of Po into the six lobes of the inactive LEP. It remains to be seen if this effect also occurs in Se and Te at HP and low temperatures or if it is only possible in Po due to the secondary periodicity caused by the strong spin–orbit interaction (relativistic effect).¹⁶⁴

Before finishing this manuscript, it must be commented that our observation of three (two) stages in group-15 (16) elements, which are characterized by the progressive equalization of primary and secondary bonds at HP and include the anomalous increase of the covalent bond lengths in stage 2, also seems to be consistent with the experimental observation of bond equalization and anomalous elongation of short covalent bonds in trimers during the process of ERMB formation. These features were observed in molecules forming trimers of Sb and Te with halogen atoms by Hoffmann and coworkers and later replotted by Lubchenko and coworkers.^31,50 They attributed the anomalous increase of the short covalent bond to the trans influence corresponding to stage 2, despite the fact that no critical bond distance was noted by those authors. Therefore, our proposal for the existence of up to three stages during the EDMB formation in pnictogens and chalcogens agrees with the three stages found during the ERMB formation.¹³² Further support for the existence of the proposed stages in ERMB formation has been recently provided by the existence of critical points marking regions separating the continuum between supramolecular bonds and covalent bonds in molecules.⁸⁰ Therefore, it can be concluded that the presence of three stages seems to be characteristic of the process of multicenter bond formation.

At this point, we consider it interesting to comment that the three-stage mechanism observed during the pressure-induced EDMB formation in pnictogens and the ERMB formation in different compounds¹³² shows a parallelism with the molecular, semimolecular, and atomic/polymeric stages that have been suggested but not fully explained in nitrogen and hydrogen at HP.^86,145–148 As previously remarked, the pressure dependence of the intramolecular and intermolecular bond distances in N₂ and H₂ seems to show different stages between the pure covalent molecular stage and the HP metallic atomic stage. A deep analysis of these systems would require future calculations that are out of the scope of the present paper. In any case, the three-stage mechanism we propose for pnictogens seems to be consistent with the simulations of the (N₂)₃ system at HP carried out by Hoffmann and coworkers.⁸⁶ They pointed out that there is a significant contraction of the intermolecular distance (contraction of the van der Waals region between N₂ molecules) and a corresponding negligible change of the intramolecular distance at low pressures (molecular regime, stage 1). This stage is followed by a pressure region in which there is an anomalous increase of the intramolecular distance once the intermolecular distance decreases below 1.6 Å (semimolecular regime, stage 2). Finally, a third pressure region was found where there is a normal contraction of both intramolecular and intermolecular bond distances once all single N–N bonds are formed (atomic/polymeric regime, stage 3). Interestingly, a similar behavior has been observed in hydrogen at HP.^145–148 A normal decrease of both intramolecular and intermolecular H–H distances up to 100 GPa (stage 1) is followed by an anomalous increase (decrease) of the intramolecular (intermolecular) distances as pressure increases (stage 2), which is caused by the charge transfer from intramolecular to intermolecular bonds.^145–148 The trans influence ends once both bond distances equalize and each bond has a single electron per atom pair, i.e. all H–H bonds are 2c-1e bonds (stage 3). This seems to be the case above 500 GPa once the atomic/polymeric phases of hydrogen (that are expected to show metallic conductivity) appear.^145–148 In other words, we believe that EDMBs can be formed in elemental nitrogen and hydrogen at HP. Moreover, we can speculate that no metallic conductivity is going to appear in the phases of hydrogen that form close to 500 GPa. The reason is that the 2c-1e bonds that are going to appear in hydrogen around this pressure are EDMBs that correspond to directed bonds. These directed bonds feature a moderate electrical conductivity, as already commented concerning incipient metals,⁵⁸ but not a full metallic electrical conductivity. The lack of true metallicity in hydrogen around 500 GPa due to EDMB formation could explain recent results of electrical measurements that consider that elemental hydrogen behaves as a semimetal in this pressure range,¹⁶⁵ just as is the case of incipient metals, such as Bi close to RP. Moreover, the pressure-induced formation of EDMBs in nitrogen is further supported by the recent discovery of the black phosphorus phase in nitrogen around 140 GPa.¹⁶⁶ Note that the A_h phase has been observed in phosphorus at a pressure larger than that for the formation of the black phosphorus phase.¹⁰² Therefore, it could be expected that the A_h phase or a slightly distorted one with sixfold coordination could be observed in elemental nitrogen well above 140 GPa.

4. Conclusions

We have performed systematic HP theoretical work on pnictogens and chalcogens intending to study the mechanism of EDMB formation. The reason to study these elements is that they are the simplest materials that undergo a change from the pre-EDMB scenario to the EDMB one, either by the effect of pressure or the change in the composition by heavier analog elements. We have used bond descriptors previously used by researchers defending either the metavalent (electron-deficient) or hypervalent (electron-rich multicenter) bonding models in PCMs as well as the bond and band pictures. In particular, we have deeply studied how pressure decreases the octahedral distortion of the trigonal R3̄m (A7) and trigonal P3₁21 (A8) crystalline structures of group-15 and -16 elements at RP, respectively, and the A_h (sc) and A_i phases of α-Po and β-Po, respectively. As a result, we conclude that:

(1) The A7 structure of group-15 (As, Sb, Bi) elements tends at HP towards the A_h phase of α-Po at RP, while the A8 phase of group-16 (Se, Te) elements tends at HP towards the A_i phase of β-Po at RP. These results are consistent with the observation of α-Po and β-Po as HP phases in several pnictogens (P, As) and chalcogens (S, Se, Te), respectively. This finding agrees with the electron count of Papoian and Hoffmann in the formation of hypercoordinated units⁵¹ since the formation of the cubic α-Po structure in group-15 elements is favored by their five valence electrons, while the formation of the rhombohedral β-Po structure in group-16 elements with six valence electrons occurs because the extra valence electron avoids the complete inactivation of the LEP at HP and induces a distortion in the cubic structure.

(2) With the use of different techniques, we have shown that EDMBs, i.e. electron-deficient bonds with multicenter character, are present in both the HP octahedrally coordinated A_h and A_i phases of pnictogens (As, Sb, and Bi) and chalcogens (Se and Te), respectively. Since these HP phases are not experimentally found in some of these elements, our results must be reinterpreted in a more general way: group-15 and -16 elements change in bonding from covalent ppσ-bonds plus secondary bonds to EDMBs as the octahedral atomic coordination is approached upon increasing pressure. In particular, we propose that fully developed EDMBs occur in As-II above 25 GPa, in Sb-II above 8 GPa, in Bi-III above 2.7 GPa, in Se-V above 40 GPa, and in Te-III above 8 GPa. Additionally, we propose that a mixture of covalent bonds and EDMBs or even asymmetric EDMBs could also occur in intermediate HP phases, such as in Bi-II above 2.5 GPa, in Se-III and Se-VI above 23 GPa, and in Te-II above 4 GPa.

(3) Polonium, in its two polymorphs at RP (α-Po and β-Po), is the only element, together with tetragonal boron,²⁷ that exhibits EDMBs at RP. Remarkably, Po is the only element with all bonds being fully EDMBs at RP, unlike tetragonal boron, which exhibits a mixture of EDMBs and covalent bonds. Since EDMBs are softer than covalent bonds, one can understand the low melting temperature of Po, which has been considered a common metal or semimetal, despite displaying the octahedral coordination of incipient metals.¹³

(4) The formation of EDMBs in group-15 and -16 elements either at RP or at HP is in good agreement with the 2D map showing the number of electrons shared (ES) vs. the normalized number of electrons transferred (ET) used by Wuttig and coworkers to classify bonds in materials.⁶⁸ In addition, the ES vs. ET map can be used to follow the changes in bonding upon changes in pressure and/or composition.

Moreover, by working with elemental solids exhibiting pure covalent bonds, we have shown that EDMBs can occur between purely covalent and metallic bonds. This is in contrast to a previous claim that considered that the formation of multicenter bonds could only occur between ionic and metallic bonds.³¹ It can be concluded that EDMBs are unconventional 2c-1e bonds that are characterized by ES ≈ 1, i.e. half the value expected for a pure covalent bond. In conclusion, the EDMB is a directional bond intermediate between ionocovalent p-type bonds (with fully localized electrons) and metallic bonds (with fully delocalized electrons), where the number of electrons shared between two atoms is around one instead of two as in ionocovalent bonds or in ERMBs. In other words, the EDMB is an intermediate bond between covalent and metallic bonds, which is characterized by localized electrons (typically one) between two atoms and delocalized electrons over more than two atoms.

(5) In general, EDMBs occur at smaller pressures along the series Se–Te–Po and As–Sb–Bi. This means that the effect of pressure is equivalent to the substitution of the composition of elements by their heavy analogues. This result is consistent with the larger distortion of octahedral coordination for the lighter elements. In other words, the result is consistent with the smaller structural distortion of Bi-I (Te-I) than Sb-I and As-I (Se-I) with respect to the A_h (A_i) phase. This result agrees with previous studies that relate the stronger structural distortion in different materials with larger s–p mixing and consequently with stronger LEP stereoactivity.^29–33 Our result is also consistent with the well-known rule that pressure is equivalent to going down the group in the periodic table since pressure induces a decrease of the LEP stereoactivity in the same way as going down the group to heavier elements.^29–33 Therefore, both pressure and composition tend to transform covalent ppσ-bonds into EDMBs and finally into metallic bonds. Interestingly, both pressure and composition lead to an increase in mass density, which in turn results in an increase in electronic density. Therefore, other ways of increasing electronic density could also lead to a decrease in the LEP stereoactivity and the formation of EDMBs. Two examples are chemical pressure¹⁶⁷ and reduction, i.e. providing electrons to the system.⁵¹

(6) Using the bond and band pictures, we have shown that the formation of EDMBs with increasing electronic density proceeds in a similar gradual way in both group-15 and -16 elements. This result is in line with previous suggestions that proposed the formation of multicenter bonds by the increase in mass density, e.g. by increasing pressure.^31,87 This result is in contrast to the sudden change in coordination and properties between materials with covalent bonds and EDMBs previously reported by Wuttig and coworkers upon a change in composition between PCMs and non-PCMs of the A^IVB^VI and A^V₂B^VI₃ families.⁶⁸

(7) Unlike what was previously assumed,^31,42,50 we have shown that the transformation process from secondary bonds towards multicenter bonds involves several intermediate stages until fully (or almost fully) symmetrical EDMBs are formed. Notably, we have shown that the mechanism of EDMB formation proceeds via different stages that depend on the type of LEP involved in the secondary bonds. In group-16 elements (with a p-type LEP involved in secondary bonds), the mechanism of EDMB formation comprises two stages, while in group-15 elements (with an s-type LEP involved in secondary bonds) the mechanism comprises three stages. Therefore, we conclude that the LEP stereoactivity, related to the s–p mixing, is the primary factor that rules the EDMB formation in group-15 and -16 elements, extending to binary A^IVB^VI and A^V₂B^VI₃ chalcogenides and other related complex chalcogenides. This result agrees with previous works that reflect the importance of s–p mixing in these elemental families.^29–33 In other words, we suggest that the unveiled mechanism of EDMB formation could be universal, at least, in p-type elements, and that all materials undergoing a bonding change from a covalent ppσ-bond plus a secondary bond to an EDMB upon increase of electronic density will follow a two- or three-stage mechanism depending on the type of LEP involved in secondary bonds.

(8) EDMBs and ERMBs are two types of multicenter bonds that can be formed from original primary (covalent) and secondary (noncovalent) interactions and the process of multicenter bond formation comprises three stages. In ERMBs, the ES values are larger than the values of typical covalent bonds with similar ET values,^31,42,50 because the original nonbonding electrons of the stereoactive LEP in the secondary donor–acceptor interaction transform into bonding electrons of the newly formed 3c-4e bonds. In EDMBs, the ES values are smaller than the values of typical covalent bonds with similar ET values,^31,42,50 because the original nonbonding electrons of the stereoactive LEP in the secondary donor–acceptor interaction remain as nonbonding electrons of the inactive and delocalized LEP. In other words, the electrons needed to form EDMBs that are 2c-1e bonds come mainly from the original primary covalent bonds.

(9) EDMBs in solids will be easily recognized by the scientific community if clear observables are defined for incipient metals. We have proposed two measurable magnitudes to identify EDMB formation: (i) the change (from a negative to a positive pressure coefficient) in the optical phonon frequencies, i.e. a sign change in Grüneisen parameters and (ii) the increase of the average Born effective charge. These are some of the easiest ways to evidence the change from the pre-EDMB scenario to the EDMB scenario at HP. This will occur simultaneously with a pressure-induced change from an anomalous increase to a normal decrease in the short bond distances. In this context, we have come up with the idea that soft optical modes of high frequency in p-type materials are the signatures of the instability of the ionocovalent ppσ-bonds at HP. This situation is similar to that of soft acoustic modes at the Brillouin zone edges that are the signatures of the instability of ionocovalent sp³σ-bonds.

Both ERMBs and EDMBs are longer than covalent bonds. It has been estimated that they are between 1.1 and 1.3 times longer than covalent bonds under the same pressure/temperature conditions. Unlike ERMBs, EDMBs have ca. half the electronic charge of covalent bonds since they have ca. half ES and ELF values, and thus EDMBs should have typical charge densities 60 to 65% smaller than covalent bonds. These descriptors can help researchers identify EDMBs in solids. For instance, the formation of EDMBs is expected to occur in iodates at HP since recent studies have evidenced the equalization of the short and long I–O bonds with increasing pressure, which is concomitant with the softening of high-frequency optical phonons.^168–171

As a final remark, we want to stress that the results of this work have very far-reaching consequences for the broad scientific community, especially for chemists and condensed matter scientists. This work provides a comprehensive framework to understand how EDMBs are formed in solid elemental and complex materials (from primary ionocovalent ppσ-bonds plus secondary bonds involving LEPs). We have provided several descriptors that can be used to identify EDMBs at RP and HP in a wide variety of materials from simple elements to complex materials, such as PCMs, topological insulators, superconductors, highly efficient thermoelectrics, and highly efficient photovoltaic materials. Therefore, this work opens the door for a better understanding of the chemical bonding mechanisms in the above-commented advanced materials for improving their performance.¹⁵⁷ We hope that this work will promote further studies to understand EDMBs in solids and their associated exceptional properties.

5. Future perspectives

This work allows us to predict that EDMBs can be potentially observed at HP in all materials that show at RP a mixture of primary covalent ppσ-bonds and secondary bonds in which LEPs are involved. Consequently, our results can be readily extrapolated to all group-15, -16, and -17 elements (including N, O, and F). In particular, EDMB formation is expected to occur in phosphorus at the A7-to-A_h PT experimentally reported at HP,^102,172 and N could form EDMBs at pressures higher than those for which the black phosphorus structure is found.¹⁶⁶ Finally, sulfur will start showing some EDMBs in S-III or S-IV phases above 30 GPa since these phases exhibit positive pressure coefficients of all Raman-active modes,¹²⁷ although the A_i phase is reported in S-V above 150 GPa.¹¹⁷ In addition, the observation of EDMBs is also expected in hydrogen above 500 GPa. In this context, it must be mentioned that since EDMBs are characterized by a mixture or coexistence of localized and delocalized electrons, in general, EDMBs are expected to be found in many materials at sufficiently high pressures as a prior step to full electron delocalization corresponding to the metallic bond.

Our results can be also extrapolated to other families of materials with covalent ppσ-bonds and LEPs, such as binary A^IVB^VI and A^V₂B^VI₃ families and related ternary compounds that are, in turn, related to PCMs. Moreover, we propose that EDMBs could also be found in compounds with p-type covalent bonds in which cations show the presence of LEPs (typical of elements at their smallest valence state), such as Cl⁵⁺, Br⁵⁺, I⁵⁺, S⁴⁺, Se⁴⁺, Te⁴⁺, As³⁺, Sb³⁺, Bi³⁺, Ge²⁺, Sn²⁺, Pb²⁺, Ga⁺, In⁺, and Tl⁺. The EDMB formation in these compounds at different pressures will depend on the strength of the LEP stereoactivity at a given electronic density. EDMBs will be formed at RP when LEP stereoactivity is negligible at RP, but they will not be formed when LEP stereoactivity is strong. In such a case, HP will help to promote the appearance of EDMBs. This consideration agrees with the results of Waghmare et al.³⁰ and is also consistent with the decrease of LEP stereoactivity for a given cation, e.g., Sn²⁺, Sb³⁺, when linked to chalcogen atoms in the series S–Se–Te.¹⁷³ This explains why PCMs at RP are observed mainly in Te-based compounds, e.g., in SnTe and Sb₂Te₃ at RP, and not in SnS, SnSe, Sb₂S₃, and Sb₂Se₃ at RP. In the latter compounds, EDMBs are expected to be formed at HP, as already proved for GeSe, which is isostructural to SnS and SnSe.⁸² It is also well known that cation LEP stereoactivity decreases along a group, e.g. along the series Ge–Sn–Pb or As–Sb–Bi. Therefore, EDMBs are only encountered, for instance, in Se-based compounds PbSe and Bi₂Se₃ at RP and not in GeSe, SnSe, As₂Se₃, and Sb₂Se₃ at RP. In the latter compounds, EDMBs are expected to be formed at HP, as already proved for GeSe⁸² and As₂S₃ (isostructural to As₂Se₃).⁸⁵

In addition, we predict that either a two or three-stage process for EDMB formation at HP is likely to occur in other group-15 (N, P) and -16 (O, S) elements, also in group-17 elements (Br, I), and in A^IVB^VI and A^V₂B^VI₃ compounds that are not PCMs at RP. A more detailed discussion of the different stages of EDMB formation in A^IVB^VI and A^V₂B^VI₃ chalcogenides that are not PCMs at RP will be published elsewhere. In these more complex binary compounds than elemental pnictogens and chalcogens, the presence of two or three stages must be further clarified in a future paper, but a hint of these stages has been already observed in GeSe and As₂S₃ at HP.^82,85 We have also shown that these stages show a parallelism with the molecular, semimolecular, and atomic/polymeric stages in nitrogen and hydrogen at HP, with EDMBs likely being present in nitrogen and hydrogen above 140 and 500 GPa, respectively. Since both ERMBs and EDMBs are multicenter bonds and have a similar process of formation, we have proposed that three stages could also be found in the mechanism of ERMB formation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is financed by the Spanish Ministerio de Ciencia e Innovación and the Agencia Estatal de Investigación MCIN/AEI/10.13039/501100011033 as part of the project MALTA Consolider Team network (RED2022-134388-T) and I+D+i projects PID2019-106383GB-42/43, PGC2021-125518NB-I00, and PID2022-138076NB-C42/C44 co-financed by EU FEDER funds, by the project PROMETEO CIPROM/2021/075 (GREENMAT) financed by Generalitat Valenciana, and by the project AYUD/2021/51036 financed by Principality of Asturias (FICYT) and co-financed by EU FEDER. This study also forms part of the Advanced Materials programme supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1), by Generalitat Valenciana through the project MFA/2022/025 (ARCANGEL), and by the Principality of Asturias (FICYT) through the project TED2021-129457B-I00. AOR also thanks the Spanish MINECO for a Ramón y Cajal fellowship (RyC-2016-20301). We would like to express our gratitude to Jose Manuel Recio, Juan Ángel Sans, Álvaro Lobato, Julia Contreras-García, David Santamaría-Pérez, Maria Consuelo Jiménez-Molero, Matteo Savastano, and Ángel Vegas for their insightful and engaging discussions on our findings. Their input and feedback greatly enriched the development of this article. Particularly, we want to acknowledge Álvaro Lobato and Julia Contreras-García, who called our attention to the hypercoordination in the atomic/polymeric phases of nitrogen and hydrogen at HP, respectively.

References

1. J. K. Burdett, Chemical Bonding in Solids, Oxford University Press, New York, 1995.
2. P. Ball, Nature, 2011, 469, 26.
3. G. Frenking and S. Shaik, The Chemical Bond, Wiley-VCH Verlag, Weinheim, Germany, 2014.
4. S. Alvarez, R. Hoffmann and C. Mealli, Chem. – Eur. J., 2009, 15, 8358–8373.
5. P. Needham, Stud. Hist. Philos. Sci. A., 2014, 45, 1–13.
6. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
7. G. H. Wannier, Phys. Rev., 1937, 52, 191–197.
8. N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475.
9. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
10. A. Lobato, H. H. Osman, M. A. Salvadó, M. Taravillo, V. G. Baonza and J. M. Recio, Phys. Chem. Chem. Phys., 2019, 21, 12585–12596.
11. H. H. Osman and F. J. Manjón, Phys. Chem. Chem. Phys., 2022, 24, 9936–9942.
12. Y. Cheng, S. Wahl and M. Wuttig, Phys. Status Solidi RRL, 2021, 15, 2000482.
13. M. Wuttig, V. L. Deringer, X. Gonze, C. Bichara and J.-Y. Raty, Adv. Mater., 2018, 30, 1803777.
14. M. Wuttig and N. Yamada, Nat. Mater., 2007, 6, 824–832.
15. S. Raoux, F. Xiong, M. Wuttig and E. Pop, MRS Bull., 2014, 39, 703.
16. S. Raoux, Annu. Rev. Mater. Res., 2009, 39, 25–48.
17. K. Pielichowska and K. Pielichowski, Prog. Mater. Sci., 2014, 65, 67–123.
18. M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045–3067.
19. I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904.
20. Y. Yu, M. Cagnoni, O. Cojocaru-Mirédin and M. Wuttig, Adv. Funct. Mater., 2020, 30, 1904862.
21. H. Krebs, Z. Elektrochem. Ber. Bunsenges. Phys., 1957, 61, 925–934.
22. H. Krebs, Acta Cryst., 1956, 9, 95–108.
23. G. Lucovsky and R. M. White, Phys. Rev. B: Solid State, 1973, 8, 660–667.
24. P. B. Littlewood, Crit. Rev. Solid State Mater. Sci., 1983, 11, 229–285.
25. L. Pauling, Phys. Rev., 1938, 54, 899–904.
26. L. Pauling, Proc. R. Soc. London, Ser. A, 1949, 196, 343–362.
27. L. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crys- Tals: An Introduction to Modern Structural Chemistry, Cornell University Press, Ithaca, New York, 1960.
28. W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295.
29. M. L. Munzarová and R. Hoffmann, J. Am. Chem. Soc., 2002, 124, 4787–4795.
30. U. V. Waghmare, N. A. Spaldin, H. C. Kandpal and R. Seshadri, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125111.
31. J. C. Golden, V. Ho and V. Lubchenko, J. Chem. Phys., 2017, 146, 174502.
32. D.-K. Seo and R. Hoffmann, J. Solid State Chem., 1999, 147, 26–37.
33. A. Ienco, R. Hoffmann and G. Papoian, J. Am. Chem. Soc., 2001, 123, 2317–2325.
34. J.-Y. Raty, M. Schumacher, P. Golub, V. L. Deringer, C. Gatti and M. Wuttig, Adv. Mater., 2019, 31, 1806280.
35. R. O. Jones, J. Phys.: Condens. Matter, 2018, 30, 153001.
36. R. O. Jones, J. Phys.: Condens. Matter, 2022, 34, 343001.
37. A. V. Kolobov, P. Fons, J. Tominaga and S. R. Ovshinsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165206.
38. A. V. Kolobov, P. Fons and J. Tominaga, Sci. Rep., 2015, 5, 13698.
39. J. Hempelmann, P. C. Müller, C. Ertural and R. Dronskowski, Angew. Chem., Int. Ed., 2022, 61, e202115778.
40. P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, J. Phys. Chem. C, 2021, 125, 7959–7970.
41. J. Hempelmann, P. C. Müller, P. M. Konze, R. P. Stoffel, S. Steinberg and R. Dronskowski, Adv. Mater., 2021, 33, 2100163.
42. T. H. Lee and S. R. Elliott, Adv. Mater., 2020, 32, 2000340.
43. T. H. Lee and S. R. Elliott, Phys. Status Solidi Rapid Res. Lett., 2021, 15, 2000516.
44. T. H. Lee and S. R. Elliott, Nat. Commun., 2022, 13, 1458.
45. R. J. Hach and R. E. Rundle, J. Am. Chem. Soc., 1951, 73, 4321–4324.
46. G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448.
47. H. A. Bent, Chem. Rev., 1968, 68, 587–648.
48. J. I. Musher, Angew. Chem., Int. Ed. Engl., 1969, 8, 54–68.
49. G. A. Landrum, N. Goldberg and R. Hoffmann, J. Chem. Soc., Dalton Trans., 1997, 3605.
50. G. A. Landrum and R. Hoffmann, Angew. Chem., Int. Ed., 1998, 37, 1887–1890.
51. G. A. Papoian and R. Hoffmann, Angew. Chem., Int. Ed., 2000, 39, 2408–2448.
52. J.-P. Gaspard, Phys. Status Solidi Rapid Res. Lett., 2022, 16, 2200111.
53. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990.
54. R. L. DeKock and W. B. Bosma, J. Chem. Educ., 1988, 65, 194.
55. F. Hund, Z. Phys., 1928, 51, 759–795.
56. F. Bloch, Z. Phys., 1929, 52, 555–600.
57. E. Hückel, Z. Phys., 1931, 70, 204–286.
58. M. Wuttig, C.-F. Schön, J. Lötfering, P. Golub, C. Gatti and J.-Y. Raty, Adv. Mater., 2023, 35, 2208485.
59. R. O. Jones, S. R. Elliott and R. Dronskowski, Adv. Mater., 2023, 35, 2300836.
60. M. Wuttig, C. Schön, D. Kim, P. Golub, C. Gatti, J. Raty, B. J. Kooi, Á. M. Pendás, R. Arora and U. Waghmare, Adv. Sci., 2023, 35, 2308578.
61. J. Hempelmann, P. C. Müller, L. Reitz and R. Dronskowski, Inorg. Chem., 2023, 62, 20162–20171.
62. S. Shaik, D. Danovich, J. M. Galbraith, B. Braïda, W. Wu and P. C. Hiberty, Angew. Chem., Int. Ed., 2020, 59, 984–1001.
63. H. H. Osman, A. Otero-de-la-Roza, P. Rodríguez-Hernández, A. Muñoz and F. J. Manjón, ChemRxiv, 2023 DOI:10.26434/chemrxiv-2023-Pv66p-V2.
64. D. Lencer, M. Salinga, B. Grabowski, H. Tilmannand, J. Neugebauer and M. Wuttig, Nat. Mater., 2008, 7, 972–977.
65. B. Huang and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 81204.
66. M. Esser, S. Maintz and R. Dronskowski, J. Comput. Chem., 2017, 38, 620–628.
67. Y. Cheng, O. Cojocaru-Mirédin, J. Keutgen, Y. Yu, M. Küpers, M. Schumacher, P. Golub, J.-Y. Raty, R. Dronskowski and M. Wuttig, Adv. Mater., 2019, 31, 1904316.
68. L. Guarneri, S. Jakobs, A. von Hoegen, S. Maier, M. Xu, M. Zhu, S. Wahl, C. Teichrib, Y. Zhou, O. Cojocaru-Mirédin, M. Raghuwanshi, C.-F. Schön, M. Drögeler, C. Stampfer, R. P. S. M. Lobo, A. Piarristeguy, A. Pradel, J.-Y. Raty and M. Wuttig, Adv. Mater., 2021, 33, 2102356.
69. K. Shportko, S. Kremers, M. Woda, L. Dominicand, J. Robertson and M. Wuttig, Nat. Mater., 2008, 7, 653–658.
70. M. Wuttig, Phys. Status Solidi B, 2012, 249, 1843–1850.
71. N. W. Alcock, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus, A. G. Sharpe, Academic Press, 1972, pp. 1–58.
72. The hypothetical sc phase of Sb at HP (see discussion in Section 2 of the ESI†) has been suggested to feature either ERMBs or resonant/metavalent bonds in several papers (see ref. 51, 68, 69 and 70). However, systematic studies of group-15 and -16 elemental families to prove the unconventional character of the bonds in the sc phase of the different elements, the nature of the bond and the mechanism of the bond transformation have never been performed to the best of our knowledge.
73. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
74. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
75. A. Varadwaj, P. R. Varadwaj, H. M. Marques and K. Yamashita, Molecules, 2022, 27, 3421.
76. S. J. Grabowski, Phys. Chem. Chem. Phys., 2013, 15, 7249–7259.
77. S. J. Grabowski, Science, 1979, 4(2022), 17.
78. B. Silvi, E. Alikhani and H. Ratajczak, J. Mol. Model., 2020, 26, 62.
79. S. J. Grabowski, Molecules, 2021, 26, 4939.
80. D. K. Miller, I. Yu. Chernyshov, Y. V. Torubaev and S. V. Rosokha, Phys. Chem. Chem. Phys., 2022, 24, 8251–8259.
81. R. H. Crabtree, Chem. Soc. Rev., 2017, 46, 1720–1729.
82. M. Xu, S. Jakobs, R. Mazzarello, J.-Y. Cho, Z. Yang, H. Hollermann, D. Shang, X. Miao, Z. Yu, L. Wang and M. Wuttig, J. Phys. Chem. C, 2017, 121, 25447–25454.
83. A. Pawbake, C. Bellin, L. Paulatto, K. Béneut, J. Biscaras, C. Narayana, D. J. Late and A. Shukla, Phys. Rev. Lett., 2019, 122, 145701.
84. C. Bellin, A. Pawbake, L. Paulatto, K. Béneut, J. Biscaras, C. Narayana, A. Polian, D. J. Late and A. Shukla, Phys. Rev. Lett., 2020, 125, 145301.
85. V. P. Cuenca-Gotor, J. Á. Sans, O. Gomis, A. Mujica, S. Radescu, A. Muñoz, P. Rodríguez-Hernández, E. L. da Silva, C. Popescu, J. Ibañez, R. Vilaplana and F. J. Manjón, Phys. Chem. Chem. Phys., 2020, 22, 3352–3369.
86. W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, Angew. Chem., Int. Ed., 2007, 46, 3620–3642.
87. A. Zhugayevych and V. Lubchenko, J. Chem. Phys., 2010, 133, 234503.
88. R. Hoffmann, Solids and Surfaces: A Chemist's View of Bonding in Extended Structures, Wiley-VCH, 1988.
89. H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1981, 20, 33–51.
90. M. Kastner, Phys. Rev. Lett., 1972, 28, 355–357.
91. H. J. Beister, K. Strössner and K. Syassen, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 5535–5543.
92. H. C. Hsueh, C. C. Lee, C. W. Wang and J. Crain, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3851–3856.
93. J.-P. Gaspard, A. Pellegatti, F. Marinelli and C. Bichara, Philos. Mag. B, 1998, 77, 727–744.
94. J.-P. Gaspard, C. R. Phys., 2016, 17, 389–405.
95. The above consideration is not surprising because the crystalline structures at RP of most group-15 and -16 elements as well as most A^IVB^VI and A₂^VB₃^VI compounds feature a mixture of a primary covalent ppσ-bond and a secondary LEP-based bond [ref. 24 and 121]. In addition, both group-15 and A^IVB^VI compounds are all 10-electron materials [ref. 24].
96. J. A. Sans, R. Vilaplana, E. L. da Silva, C. Popescu, V. P. Cuenca-Gotor, A. Andrada-Chacón, J. Sánchez-Benitez, O. Gomis, A. L. J. Pereira, P. Rodríguez-Hernández, A. Muñoz, D. Daisenberger, B. García-Domene, A. Segura, D. Errandonea, R. S. Kumar, O. Oeckler, P. Urban, J. Contreras-García and F. J. Manjón, Inorg. Chem., 2020, 59, 9900–9918.
97. P. C. Müller, S. R. Elliott, R. Dronskowski and R. O. Jones, J. Phys.: Condens. Matter, 2024, 36, 325706.
98. D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628.
99. O. Degtyareva, M. I. McMahon and R. J. Nelmes, High Press. Res., 2004, 24, 319–356.
100. P. Silas, J. R. Yates and P. D. Haynes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174101.
101. C. R. S. da Silva and R. M. Wentzcovitch, Comput. Mater. Sci., 1997, 8, 219–227.
102. D. Scelta, A. Baldassarre, M. Serrano-Ruiz, K. Dziubek, A. B. Cairns, M. Peruzzini, R. Bini and M. Ceppatelli, Angew. Chem., Int. Ed., 2017, 56, 14135–14140.
103. D. Olego and M. Cardona, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 1151–1160.
104. M. T. Dove, Am. Mineral., 1997, 82, 213–244.
105. A. L. J. Pereira, J. A. Sans, R. Vilaplana, O. Gomis, F. J. Manjón, P. Rodríguez-Hernández, A. Muñoz, C. Popescu and A. Beltrán, J. Phys. Chem. C, 2014, 118, 23189–23201.
106. T. Matsunaga, N. Yamada, R. Kojima, S. Shamoto, M. Sato, H. Tanida, T. Uruga, S. Kohara, M. Takata, P. Zalden, G. Bruns, I. Sergueev, H. C. Wille, R. P. Hermann and M. Wuttig, Adv. Funct. Mater., 2011, 21, 2232–2239.
107. S. Lee, K. Esfarjani, T. Luo, J. Zhou, Z. Tian and G. Chen, Nat. Commun., 2014, 5, 3525.
108. J. S. Lannin, J. M. Calleja and M. Cardona, Phys. Rev. B: Solid State, 1975, 12, 585–593.
109. W. Richter, T. Fjeldly, J. Renucci and M. Cardona, in Proceedings of the International Conference on Lattice Dynamics, ed. M. Balkanski, Flammarion, Paris, 1978.
110. R. Arora, U. V. Waghmare and C. N. R. Rao, Adv. Mater., 2023, 35, 2208724.
111. P. Mori-Sánchez, A. M. Pendás and V. Luaña, J. Am. Chem. Soc., 2002, 124, 14721–14723.
112. A. M. Redon and J. M. Leger, High Press. Res., 1990, 4, 315–317.
113. A. Onodera, I. Sakamoto, Y. Fujii, N. Môri and S. Sugai, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 7935–7941.
114. X. Wang, K. Kunc, I. Loa, U. Schwarz and K. Syassen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 134305.
115. Y. Zhao, S. Clément, J. Haines and R. Viennois, J. Phys. Chem. C, 2020, 124, 26659–26669.
116. A. von Hippel, J. Chem. Phys., 1948, 16, 372–380.
117. O. Degtyareva, E. Gregoryanz, H. K. Mao and R. J. Hemley, High Press. Res., 2005, 25, 17–33.
118. Y. Akahama, M. Kobayashi and H. Kawamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 20–26.
119. T. Krüger and W. B. Holzapfel, Phys. Rev. Lett., 1992, 69, 305–307.
120. J. C. Jamieson and D. B. McWhan, J. Chem. Phys., 1965, 43, 1149–1152.
121. G. Parthasarathy and W. B. Holzapfel, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 8499–8501.
122. C. Hejny and M. I. McMahon, Phys. Rev. Lett., 2003, 91, 215502.
123. S. Minomura, K. Aoki, N. Koshizuka and T. Tsushima, The Effect of Pressure on The Raman Spectra in Trigonal Se and Te, ed. K. D. Timmerhaus, M. S. Barber, Springer US, Boston, MA, 1979.
124. G. Parthasarathy and W. B. Holzapfel, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 10105–10108.
125. O. Yoshinori, Y. Itsuro, Y. Makoto and E. Hirohisa, J. Phys. Soc. Jpn., 1995, 64, 4766–4789.
126. A. K. Bandyopadhyay and D. B. Singh, Pramana, 1999, 52, 303–319.
127. O. Degtyareva, E. R. Hernández, J. Serrano, M. Somayazulu, H. Mao, E. Gregoryanz and R. J. Hemley, J. Chem. Phys., 2007, 126, 84503.
128. C. Marini, D. Chermisi, M. Lavagnini, D. Di Castro, C. Petrillo, L. Degiorgi, S. Scandolo and P. Postorino, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 64103.
129. X. Li, X. Huang, X. Wang, M. Liu, G. Wu, Y. Huang, X. He, F. Li, Q. Zhou, B. Liu and T. Cui, Phys. Chem. Chem. Phys., 2018, 20, 6116–6120.
130. Y. Akahama, M. Kobayashi and H. Kawamura, Solid State Commun., 1992, 84, 803–806.
131. J.-Y. Raty, C. Gatti, C.-F. Schön and M. Wuttig, Phys. Status Solidi RRL, 2021, 15, 2000534.
132. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
133. Y. Akahama, M. K. M. Kobayashi and H. K. H. Kawamura, Jpn. J. Appl. Phys., 1992, 31, L1621.
134. U. Häussermann, K. Söderberg and R. Norrestam, J. Am. Chem. Soc., 2002, 124, 15359–15367.
135. M. Zhu, O. Cojocaru-Mirédin, A. M. Mio, J. Keutgen, M. Küpers, Y. Yu, J.-Y. Cho, R. Dronskowski and M. Wuttig, Adv. Mater., 2018, 30, 1706735.
136. P. Bauer Pereira, I. Sergueev, S. Gorsse, J. Dadda, E. Müller and R. P. Hermann, Phys. Status Solidi B, 2013, 250, 1300–1307.
137. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
138. V. L. Deringer, R. P. Stoffel, M. Wuttig and R. Dronskowski, Chem. Sci., 2015, 6, 5255–5262.
139. S. Deng, J. Köhler and A. Simon, Angew. Chem., Int. Ed., 2006, 45, 599–602.
140. B. Silvi, J. Mol. Struct., 2002, 614, 3–10.
141. R. Hoffmann, J. M. Howell and E. L. Muetterties, J. Am. Chem. Soc., 1972, 94, 3047–3058.
142. M. M. L. Chen and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1647–1653.
143. I. Loa, R. J. Husband, R. A. Downie, S. R. Popuri and J.-W. G. Bos, J. Phys.: Condens. Matter, 2015, 27, 072202.
144. T. Masaharu and N. Kiyofumi, J. Phys. Soc. Jpn., 2007, 76, 17–18.
145. V. Labet, R. Hoffmann and N. W. Ashcroft, J. Chem. Phys., 2012, 136, 074503.
146. V. Labet, R. Hoffmann and N. W. Ashcroft, J. Chem. Phys., 2012, 136, 074502.
147. V. Labet, P. Gonzalez-Morelos, R. Hoffmann and N. W. Ashcroft, J. Chem. Phys., 2012, 136, 074501.
148. V. Riffet, V. Labet and J. Contreras-García, Phys. Chem. Chem. Phys., 2017, 19, 26381–26395.
149. A. Mujica, A. Rubio, A. Muñoz and R. J. Needs, Rev. Mod. Phys., 2003, 75, 863–912.
150. B. A. Weinstein and G. J. Piermarini, Phys. Rev. B: Solid State, 1975, 12, 1172–1186.
151. R. M. Martin, T. A. Fjeldly and W. Richter, Solid State Commun., 1976, 18, 865–869.
152. R. M. Martin, G. Lucovsky and K. Helliwell, Phys. Rev. B: Solid State, 1976, 13, 1383–1395.
153. K. J. Chang and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7371–7374.
154. A. Minelli, S. M. Souliou, T. Nguyen-Thanh, A. H. Romero, J. Serrano, W. I. Hernandez, M. J. Verstraete, V. Dmitriev and A. Bosak, Phys. Rev. B, 2019, 100, 104305.
155. B. A. Weinstein, Phys. Rev. B, 2021, 104, 54105.
156. M. H. Cohen, L. M. Falicov and S. Golin, IBM J. Res. Dev., 1964, 8, 215–227.
157. J. F. Khoury and L. M. Schoop, Trends Chem., 2021, 3, 700–715.
158. L. A. Agapito, N. Kioussis, W. A. Goddard and N. P. Ong, Phys. Rev. Lett., 2013, 110, 176401.
159. W. Richter, J. B. Renucci and M. Cardona, Phys. Status Solidi B, 1973, 56, 223–229.
160. A. Katsutoshi, S. Osamu, M. Shigeru, K. Naoki and T. Tachiro, J. Phys. Soc. Jpn., 1980, 48, 906–911.
161. J. Contreras-García, Á. M. Pendás, B. Silvi and J. M. Recio, J. Phys. Chem. B, 2009, 113(4), 1068–1073.
162. C. Buzea and K. Robbie, Supercond. Sci. Technol., 2004, 18, R1.
163. O. Prakash, A. Kumar, A. Thamizhavel and S. Ramakrishnan, Science, 1979, 355(2017), 52–55.
164. R. O. Jones, Phys. Rev. B, 2020, 101, 24103.
165. M. I. Eremets, A. P. Drozdov, P. P. Kong and H. Wang, Nat. Phys., 2019, 15, 1246–1249.
166. D. Laniel, B. Winkler, T. Fedotenko, A. Pakhomova, S. Chariton, V. Milman, V. Prakapenka, L. Dubrovinsky and N. Dubrovinskaia, Phys. Rev. Lett., 2020, 124, 216001.
167. E. O. Gomes, A. F. Gouveia, L. Gracia, Á. Lobato, J. M. Recio and J. Andrés, J. Phys. Chem. Lett., 2022, 13, 9883–9888.
168. A. Liang, S. Rahman, P. Rodriguez-Hernandez, A. Muñoz, F. J. Manjón, G. Nenert and D. Errandonea, J. Phys. Chem. C, 2020, 124, 21329–21337.
169. A. Liang, C. Popescu, F. J. Manjon, P. Rodriguez-Hernandez, A. Muñoz, Z. Hebboul and D. Errandonea, Phys. Rev. B, 2021, 103, 054102.
170. B. B. Sharma, P. S. Ghosh, A. K. Mishra and H. K. Poswal, Vib. Spectrosc., 2021, 117, 103318.
171. D. Errandonea, H. H. Osman, R. Turnbull, D. Diaz-Anichtchenko, A. Liang, J. Sanchez-Martin, C. Popescu, D. Jiang, H. Song, Y. Wang and F. J. Manjon, Mater. Today Adv., 2024, 22, 100495.
172. H. Iwasaki and T. Kikegawa, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 353–357.
173. A. Walsh and G. W. Watson, J. Phys. Chem. B, 2005, 109, 18868–18875.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc00604f

---