Open Access Article
Open Access ArticleAcoustic emissions from spin crossover complexes†
Sarah M.
Kamel
 ab,
Lajos
Daróczi
ab,
Lajos
Daróczi
 a,
László Z.
Tóth
a,
László Z.
Tóth
 a,
Dezső L.
Beke
a,
Dezső L.
Beke
 *a,
Gerardo Gutiérrez
Juárez
c,
Saioa
Cobo
d,
Lionel
Salmon
*a,
Gerardo Gutiérrez
Juárez
c,
Saioa
Cobo
d,
Lionel
Salmon
 d,
Gábor
Molnár
d,
Gábor
Molnár
 *d and
Azzedine
Bousseksou
*d
*d and
Azzedine
Bousseksou
*d
aDepartment of Solid State Physics, Doctoral School of Physics, University of Debrecen, P.O. Box 2, H-4010 Debrecen, Hungary. E-mail: dbeke@science.unideb.hu
bPhysics Department, Faculty of Science Ain Shams University, Abbassia, 11566, Cairo, Egypt
cDepartamento de Ingeniería Física, División de Ciencias e Ingenierías, Universidad de Guanajuato-Campus León, Loma del Bosque 103, Loma del Campestre, 37150, León, Gto., Mexico
dLCC, CNRS & University of Toulouse, 205 route de Narbonne, 31077 Toulouse, France. E-mail: gabor.molnar@lcc-toulouse.fr; azzedine.bousseksou@lcc-toulouse.fr
First published on 19th March 2024
Abstract
Acoustic emission from the compounds [Fe(HB(tz)3)2] and [Fe(Htrz)(trz)2]BF4 was detected during the thermally induced spin transition and is correlated with simultaneously recorded calorimetric signals. We ascribe this phenomenon to elastic waves produced by microstructural and volume changes accompanying the spin transition. Despite the perfect reversibility of the spin state switching (seen by the calorimeter), the acoustic emission activity decreases for successive thermal cycles, revealing thus irreversible microstructural evolution of the samples. The acoustic emission signal amplitude and energy probability distribution functions followed power-law behavior and the characteristic exponents were found to be similar for the two samples both on heating and cooling, indicating the universal character, which is further substantiated by the well scaled average temporal shapes of the avalanches.
Introduction
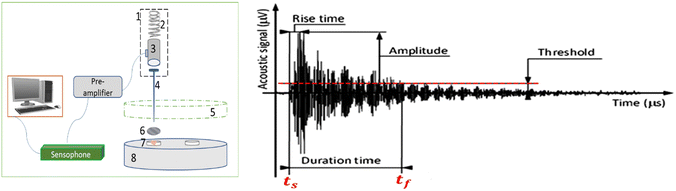
The molecular spin crossover (SCO) phenomenon exhibited by certain 3d4–3d7 (pseudo)octahedral transition metal complexes refers to the reversible switching of the compound between its high spin (HS) and low spin (LS) electronic configurations upon external stimulation (temperature, pressure, light irradiation, etc.)1,2 In the past decades, considerable efforts have been devoted to exploring the possibility of using SCO molecules as ‘active materials’ in a range of technological applications,3,4 including display and memory devices,5,6 mechanical actuators,7 photonic switches,8 gas sensors,9 and thermal management systems.10 In this context, the notions of stability and endurance have also received increasing attention.11–13 On the one hand, the issues of chemical stability and stability against environmental factors (oxygen, humidity, UV light, etc.) depend on the specific compound and can be alleviated in many cases by encapsulation.14 Another efficient strategy for ensuring high reliability uses closed-loop control of device operation.15 On the other hand, the structural and mechanical stability associated with repeating switching events remains relatively ill understood in these compounds. Indeed, the electronic spin state change is strongly coupled to changes in the molecular geometry, crystal lattice and materials microstructure.16–19 At the molecular level, the population of antibonding 3dz2 and 3dx2−y2 orbitals in the HS state is concomitant with an elongation of the metal–ligand bond lengths. For the most studied FeIIN6 coordination complexes, this represents typically 10% increase in the Fe–N distance and a swelling of 25% of the coordination octahedron.20 This characteristic modification of the coordination sphere is accompanied by other changes of the molecular structure (angles and distances), intermolecular interactions, crystal packing and, obviously, that of the lattice parameters.16,21 These effects are rather dissimilar from one compound to another, but are usually well established from X-ray diffraction measurements. Notably, the lattice volume typically increases by 1–10% in the HS state. In contrast, much less is known about the microstructural changes associated with the SCO, such as the variation of the size and shape of crystalline domains, the mosaicity in crystals, micro-constraints and grain boundaries in powder samples and, in general, about the formation of structural defects.22–26 One of the most spectacular examples for microstructural changes was reported for the compound [Fe(DAPP)(abpt)](ClO4)2 (DAPP = bis(3-aminopropyl)(2-pyridylmethyl)amine, abpt = 4-amino-3,5-bis(pyridin-2-yl)-1,2,4-triazole), whose crystals were literally pulverized by thermal cycling around the spin transition (ca. 20 cycles).27 Even if such drastic effects remain uncommon, it is clear that the exploration of microstructural phenomena in SCO samples is necessary for a deeper understanding of their physical properties and, eventually, for their use in practical applications.In this context, here we present investigations of two benchmark SCO compounds [Fe(HB(tz)3)2] (1) (tz = 1,2,4-triazol-1-yl) and [Fe(Htrz)(trz)2]BF4 (2) (trz = 1,2,4-triazolato) using an acoustic emission (AE) technique. Since the SCO in the selected two materials is accompanied by a first-order phase transition with a thermal hysteresis, it is expected that during this transformation, the intermittent character of the interface motions will lead to AE signals. Indeed this non-destructive method is particularly well suited to detect reversible or irreversible changes of the structural integrity of samples associated with sudden, discontinuous local changes (cracks, jump of phase boundaries, delamination, etc.) Notably, during first-order phase transitions, the time evolution of the system, under smooth driving, results in a sequence of discontinuous jumps (avalanches) of the interphase boundaries, which are separated by inactive periods. The avalanches of this so-called “crackling noise”,28 are usually very fast as compared to the rate of the external field, and an adiabatic limit can be a good description (the driving rate is close to zero). The advance of an interface produces elastic waves, which propagate through the material and can be recorded at the surface with an appropriate transducer (Fig. 1). Thus, AE events are inherently related to elementary steps of the phase transition or any structural changes producing elastic waves. The local strain field changes caused by individual local interface shifts with a certain velocity, v, are proportional to the voltage signal, V, detected by a piezoelectric sensor. For more details on the intermittent character of the transformations and of AE experiments, we refer to studies in ref. 28–31.
Below, we provide the results of experimental investigation on statistics of AE avalanches, measured simultaneously with differential scanning calorimetry (DSC) signals during the spin transition in compound 1. Similar results obtained for compound 2 are provided in the ESI.† It is to be noted that the AE method has been already used to study crackling noise in a few molecular crystals displaying solid–liquid or solid–solid phase transitions.32–35 Here we not only extend the scope of AE studies to spin crossover molecules, but importantly we show that despite the relatively soft nature of such molecular crystals, it is possible to detect AE avalanches in sufficiently high number to conduct a statistical analysis of the crackling noises. In addition, we also provide the averaged temporal shape of avalanches of fixed area, which will be compared to theoretical predictions.
Experimental
Samples of the well-known SCO compounds 1 and 2 were synthesized and characterized as described in previous reports.36,37 Compound 1 was obtained as a batch of single crystals with lateral sizes of ca. 100–150 μm. On the other hand, samples of compound 2 were powders of much smaller sized crystals with elongated shape of ca. 1 μm in length and 60 nm in diameter. Thus, for compound 1 we could carry out the measurements directly (by putting ca. 1 mg of the crystals into the DSC aluminium pan and pressing by a silicon wafer), while for compound 2 we were obliged to compress the powder into pellets in order to increase the AE signal intensity (see the ESI† for more details).The simultaneous AE and calorimetric measurements and their evaluations were carried out, similar to the conventional procedure described in ref. 38 and 39. DSC thermograms were acquired by means of a PerkinElmer DSC7 device (PerkinElmer Inc., Waltham, MA, USA), using 10 K min−1 scanning rate. The calibration was made with the melting transitions of pure indium and tin. The AE measurements were carried out in the modified DSC device, enabling simultaneous DSC and AE measurements (Fig. 1).38,39
The mass of samples of compound 1 was 1.2 and 0.9 mg for the hit and streaming mode of AE data acquisition, respectively. The streaming mode was used only for the construction of the temporal shape of avalanches (vide infra). For AE measurements the Sensophone AED404 Acoustic Emission Diagnostic Equipment (Geréb and Co.,Ltd, Budapest, Hungary) equipped with a piezoelectric sensor (MICRO-100S from Physical Acoustic Corporation, Princeton junction, NJ, USA) was used. The microphone had a good frequency response between 100 kHz and 1 MHz, which is nearly flat in the range between 0.2 and 1 MHz (at −75 dB in average) with maximum ± 10 dB deviation (1 V reference value). The sensor was coupled to the sample via a 18 mm long steel waveguide (with 1 mm diameter), in order to provide thermal isolation from the sample when its temperature was widely varied. The analog-to-digital converter sampling rate was 16 MHz, and the setup had a band-pass from 30 kHz to 1 MHz (hit-mode). A 30 dB preamplifier and a main amplifier (logarithmic gain) with 90 dB dynamic range were used. The threshold levels were determined from measurements carried out in the high-temperature state for cooling and the low-temperature state for heating (where no AE due to structural changes is present), respectively. The amplitude, A, area, S, and energy, E, of acoustic avalanches were calculated from the detected voltage, V(t) (temporal avalanche shape) according to their usual definitions38,39 (see also Fig. 1): A is the maximum value, 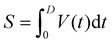 , and
, and 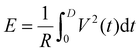 , where R is an arbitrarily chosen resistance (1 Ohm) and D is the duration time of the avalanche.
, where R is an arbitrarily chosen resistance (1 Ohm) and D is the duration time of the avalanche.
Results and discussion
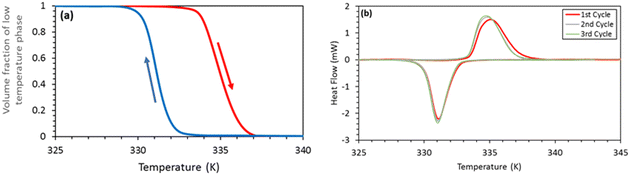
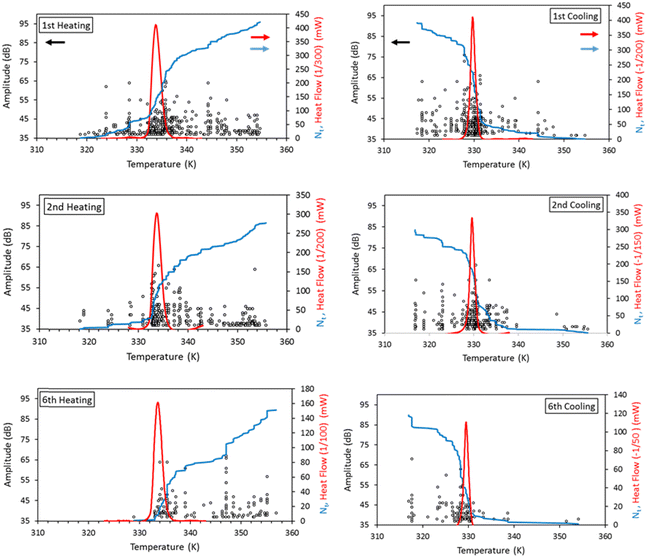
Fig. 2 displays the DSC thermograms recorded for compound 1 over three thermal cycles. Although the first heating is usually anomalous to some extent,13 the transition is very well reproducible, the peak positions and area showed only a minor change after the first cycle and were constant during the successive cycles (vide infra). The associated heat of transformation (Q = 16 kJ mol−1, measured in a closed DSC pan) is comparable with previously reported values for the same compound.36 The hysteresis loop constructed from the first DSC run is also shown. These were obtained by taking the ratio of the partial integral and the full integration of the dQ/T ratio, which is in fact the fraction of the transformed entropy.40 It can be noted that the deviation of the slope of the hysteresis loop from that of the vertical line for cooling and heating is a measure of the stored/released elastic energy by the transformed volume fraction,41 which is small in this case. This indicates that the stored elastic energy, which can be expected to be large due to the relatively large volume change (ca. 4.6% in 136), is mostly relaxed, either by emission of elastic waves or by other mechanisms (e.g. crack formations, plastic deformation).In the next step, we acquired simultaneously measured DSC and AE signals, which are displayed in Fig. 3 for compound 1 (similar results were obtained for compound 2, which are shown in Fig. S1 in the ESI†). Remarkably, most of the AE events (an AE event is a signal like the one shown in Fig. 1) appear in the same temperature interval, where the DSC peaks are observed, denoting a clear correlation between the spin transition and the number of AE events. This is also supported by the fact that the curves of the cumulative number of hits indeed have the largest slope around the DSC peaks. In other words, these results show that acoustic emissions from compound 1 originate primarily from microstructural and volume changes associated with the spin transition. Nevertheless, one can note some increased numbers of hits above the DSC peaks for heating as well (see for example the high numbers of hits between 344 and 348 K in Fig. 3). We attribute these events to crack formations, which was indeed visually observed on pellets of compound 2. Another important observation concerns the fact that the number of hits (number of dots in the figure) gradually decreases for successive thermal cycles for both samples (see red and blue dots in Fig. 4 and Fig. S2 in the ESI†). This finding contrasts with the perfect reversibility of the transformation heat associated with the spin crossover in these compounds (see grey dots in Fig. 4 and Fig. S2, ESI†). Indeed, both complexes are known for their very robust SCO properties.11,42 In particular, single crystals of compound 1 were cycled across the spin transition for more than 10 thousand times without any noticeable change in the SCO behaviour.13 We can thus conclude that the irreversible variation of the AE signal must be linked to changes in the sample microstructure upon thermal cycling, which do not appreciably influence the SCO itself. This observation can be compared with previous powder X-ray diffraction experiments on 2, conducted over 50 thermal cycles, revealing a clear structural fatigability through the continuous decrease of the size of the coherent diffracting domains, without altering the SCO properties.24 Structural fatigability in a nanocrystalline sample of 2 has been also inferred from in situ atomic force microscopy and electron diffraction imaging experiments.23,26 These measurements revealed significant, partially reversible changes of grain boundary morphologies as well an irreversible degradation of the particles manifested by the “peeling” of their surface layer.
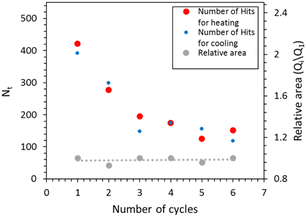 | ||
| Fig. 4 Cumulative number of AE events (red and blue dots) and the relative value of the transformation heat (compared to the first cycle) as a function of the number of cycles. | ||
Besides first-order phase transformations, quite a large number of phenomena are known to produce crackling noises such as earthquakes, sand-piles, plastic deformation, Barkhausen noise, ferroelastic or porous materials. The most important general feature of crackling noises is that they show similar statistics, which is a consequence of their self-similar behaviour.43 Indeed, the avalanches are jerky responses to the slowly changing driving force or field and are fingerprints of the so-called driven (tuned) criticality, resulting in a truncated power-law behaviour28,44,45 for the probability distribution density P(x):
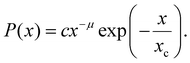 | (1) |
In the literature, several well-known power law relationships are given between the measured exponents.28,46 In particular, the following relationship can be obtained:
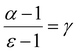 | (2) |
Fig. 5 shows, as an illustration, typical examples of probability distribution density functions for the amplitude, A, energy, E, and area, S, as well as typical power law relations between E and A, S and A, as well as between S and the duration time, D. The latter exponent (γ) plays a central role in the theory, since all the other characteristic exponents can be expressed by γ.46–50
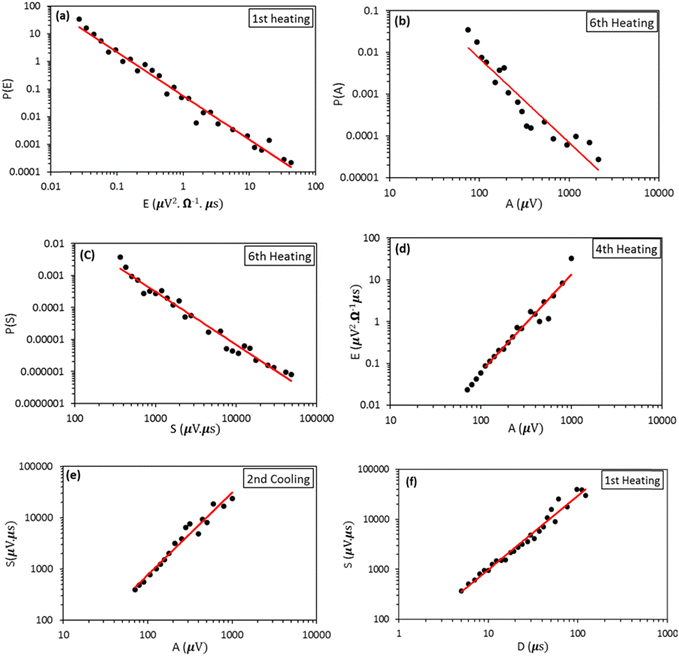 | ||
| Fig. 5 Examples of probability distribution density functions of (a) energy, (b) amplitude and (c) area as well as illustrations of (d) energy–amplitude, (e) area–amplitude and (f) area–duration power relations for compound 1. The fitted straight lines are the results of fits according to eqn (1) (see also the text and ESI†) as well as of fits according to the power relations between E and A as well as S and A. | ||
It can be seen in Fig. 5 that a nice linear fit can be made over ca. three orders of magnitude for the energy distributions and the cut-off is practically not visible in the experimentally attainable parameter ranges. Table 1 contains the corresponding calculated exponents (mean value of six runs and standard deviation) for both heating and cooling (see Table S1 in the ESI† for compound 2). Thanks to the relatively high numbers of hits, we were able to determine the characteristic exponents, according to eqn (1) for A, E and S. Their average values for both compounds fall in the range α = 2.2 ± 0.2, ε = 1.5 ± 0.1, and τ = 1.7 ± 0.1 (see also the ESI† for alternative strategies for the analysis of the exponents and the estimations of error bars) i.e. α and ε approximately fulfil the scaling relation in eqn (2). Importantly, we found that the exponents in the P(x) probability distribution density functions are (i) independent of the number of thermal cycles, (ii) have the same values for heating and cooling, (iii) have comparable values for samples 1 and 2, and (iv) fulfil the scaling relation.
| Energy exponent, ε | Area exponent, τ | Amplitude exponent, α | E ∼ A exponent, y | S ∼ A exponent, x | S ∼ D exponent, γ | |
|---|---|---|---|---|---|---|
| Heating | 1.5 (1) | 1.8 (1) | 2.3 (2) | 2.4 (1) | 1.6 (1) | 1.4 (1) |
| Cooling | 1.5 (1) | 1.7 (1) | 2.1 (2) | 2.2 (1) | 1.5 (1) | 1.5 (1) |
The average values of α, ε and τ suggest that the crackling noise, measured here, most probably belongs to the universality class with long range elastic interactions,43 for which the more sophisticated renormalization group calculations, going beyond the MFT approximation, predict γ = 1.79, α = 2.3, ε = 1.72 and τ = 1.5 for long range interactions, as well as γ = 1.56, α = 1.60, ε = 1.37 and τ = 1.50 for short range interactions, respectively48,52 (note that in MFT:43γ = 2, α = 2.34, ε = 1.67 and τ = 2). It can be seen from Table 1 (see also Tables S1, S2 in the ESI†) that our data are closer to the predicted values for long-range interactions. Before continuing the comparison of our experimental data with the theoretical predictions, it is worth making three important comments.
First, the predictions of the parameter values for the two universality classes are rather close to each other and to the experimental numbers, they change only slightly for different interaction mechanisms.
Secondly, in some martensitic systems (e.g. in shape memory alloys) it was observed that the exponents for heating and cooling could be different, and this phenomenon is called “asymmetry” in the emitted noise.53,54 This gave hints about the different accumulation/relaxation mechanisms of elastic energy during the strain jumps and AE activities for the forward or backward transitions.41,53 Visibly, this is not the case in the present SCO systems, which suggests similar statistics of local elastic energy changes for both directions (i.e. HS to LS and LS to HS).
Thirdly, usually there is a serious problem regarding the transfer of the source signal by the detection system, which can lead to deviations from the expected (true) values of the exponents.51,55 This is illustrated in Fig. 6. As a consequence, exponents such as x and y can also deviate from the theoretical prediction and indeed the experimental observations showed that in AE experiments x ≅ 1 and y ≅ 2 (instead of x = 2 and y = 3), which was called as “enigma for acoustic emission”.55 It was shown that this phenomenon is indeed due to the above distortion effect and while the exponents in the probability density distribution of A, E and S are only moderately distorted, this is not true for the duration time distribution (and this is why we did not show this from our data). In addition, in the power relations between the measured parameters, this effect is manifested in an approximate behaviour: the theoretically predicted exponents can be obtained only in the limit when the duration time is much larger than the characteristic attenuation time describing the exponential decay of the elastic wave (see Fig. 6). It was also shown that while in some cases this limit could be well reached, frequently, this is not the case; e.g. for the S∼Dγ power relation, the experimentally obtained power exponent was smaller even in the experimentally attainable long time limit.48
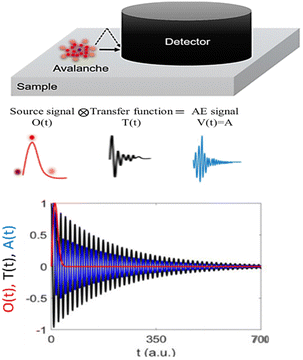 | ||
| Fig. 6 Schematic representation of the composition of an avalanche signal in acoustic emission experiments (reprinted with permission from ref. 55). During local switching, an avalanche with V(t) emits a strain signal (i.e. the source function) which propagates through the sample and is eventually measured by the detector. During the propagation and attenuation, the signal also generates the ringing of the sample. The profile of a source delta function would generate T(t), the so-called transfer function. The distortion is manifested on the time scale in a long exponential decay tail at the end of the avalanche. Thus, the duration of the avalanche is heavily distorted, while the amplitude and rising time are less influenced. | ||
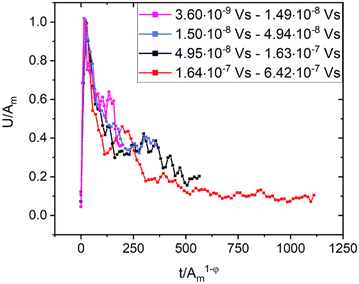
The above problem is also manifested in the difficulty of achieving universal temporal avalanche shapes at fixed area. It was obtained from the theory that, in mean field approximation:50
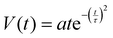 | (3) |
Conclusions
We show that during the first order phase transformation of the spin crossover complexes [Fe(HB(tz)3)2] and [Fe(Htrz)(trz)2]BF4 a large number of acoustic emission avalanches could be detected allowing the statistical analysis of AE signals. The temperature range of the detected acoustic signals and the SCO peaks in the DSC runs are in very good overlap with each other, allowing us to clearly conclude on the origin of AE events. Nevertheless, AE peaks due to crack formation during heating were also detected. The statistical analysis of the AE signal reveals that the characteristic exponents of the amplitude, energy and area distributions, as well as the power relations between E and A, as well as S and A fall in a range, which is typical for many crackling noises with long range interaction between the propagating interface and the pinning points. In addition, well-scaled average temporal shapes of avalanches, as expected from the self-similarity of the crackling noises, were obtained for several fixed area bins, similarly to those obtained during martensitic phase transformation of shape memory alloys. This first statistical analysis of AE avalanches of SCO complexes opens thus interesting perspectives for studying both reversible and irreversible microstructural phenomena in these materials (e.g. HS/LS interface motion, crack formation). Of particular interest would be to conduct simultaneous optical microscopy and AE measurements on large single crystals, which could provide scope for a deeper understanding of the spatio-temporal dynamics of the SCO phenomenon.60 In addition, it would be useful to correlate the decay of the AE signal intensity upon thermal cycling with microstructural changes inferred from crystallography and microscopy analysis. Eventually, this could allow one to use the AE technique as a simple and fast tool to detect structural fatigability in SCO materials.Author contributions
SMK: investigation, data curation, formal analysis, and writing – original draft; LD: investigation and methodology; LZT: software, formal analysis, and validation; DLB: conceptualization, supervision, validation, and writing – original draft; GGJ: conceptualisation and preliminary investigation; SC: sample synthesis and characterization; LS: sample synthesis and characterization; GM: methodology, validation, and writing – original draft; AB: conceptualization, preliminary investigation, validation, and funding acquisition. All authors have contributed to the data analysis and manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 101019522) and from the from the French-Mexican International Research Project (IRP, CNRS) ‘‘Molecular Chemistry with Applications in Materials and Catalysis’’.Notes and references
- P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024 CrossRef.
- Spin-Crossover Materials: Properties and Applications, ed. M. A. Halcrow, John Wiley & Sons Ltd, Oxford, UK, 2013 Search PubMed.
- K. S. Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176 CrossRef.
- G. Molnar, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 1703862 CrossRef PubMed.
- O. Kahn, J. Kröber and C. Jay, Adv. Mater., 1992, 4, 718 CrossRef CAS.
- O. Kahn and C. J. Martinez, Science, 1998, 279, 44 CrossRef CAS.
- H. J. Shepherd, I. A. Gural'skiy, C. M. Quintero, S. Tricard, L. Salmon, G. Molnár and A. Bousseksou, Nat. Commun., 2013, 4, 2607 CrossRef PubMed.
- P. Mounaix, E. Freysz, J. Degert, N. Daro, J.-F. Létard, P. Kužel, V. Vigneras and L. Oyenhart, Appl. Phys. Lett., 2006, 89, 174105 CrossRef.
- M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4767 CrossRef CAS PubMed.
- K. G. Sandeman, APL Mater., 2016, 4, 111102 CrossRef.
- K. Ridier, A.-C. Bas, Y. Zhang, L. Routaboul, L. Salmon, G. Molnar, C. Bergaud and A. Bousseksou, Nat. Commun., 2020, 11, 3611 CrossRef PubMed.
- S. Liu, K. Zhou, T. Yuan, W. Lei, H.-Y. Chen, X. Wang and W. Wang, J. Am. Chem. Soc., 2020, 142, 15852 CrossRef CAS PubMed.
- Y. Zhang, L. Zhang, K. Ridier, L. Salmon, I. Séguy, G. Molnár and A. Bousseksou, Mater. Adv., 2022, 3, 8193 RSC.
- Y. Zhang, I. Seguy, K. Ridier, V. Shalabaeva, M. Piedrahita-Bello, A. Rotaru, L. Salmon, G. Molnar and A. Bousseksou, J. Phys.: Condens. Matter, 2020, 32, 214010 CrossRef CAS PubMed.
- M. Piedrahita-Bello, J. E. Angulo-Cervera, A. Enriquez-Cabrera, G. Molnar, B. Tondu, L. Salmon and A. Bousseksou, Mater. Horiz., 2021, 8, 3055 RSC.
- M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119 RSC.
- P. Guionneau, Dalton Trans., 2014, 43, 382 RSC.
- E. Collet and P. Guionneau, C. R. Chim, 2018, 21, 1133 CrossRef CAS.
- S. Pillet, J. Appl. Phys., 2021, 129, 181101 CrossRef CAS.
- P. Guionneau, M. Marchivie, G. Bravic, J.-F. Létard and D. Chasseau, Top. Curr. Chem., 2004, 234, 97 CrossRef CAS.
- J. A. Real, A. B. Gaspar and M. C. Muñoz, Dalton Trans., 2005, 2062 RSC.
- A. Grosjean, P. Négrier, P. Bordet, C. Etrillard, D. Mondieig, S. Pechev, E. Lebraud, J.-F. Létard and P. Guionneau, Eur. J. Inorg. Chem., 2013, 796 CrossRef CAS.
- M. D. Manrique-Juarez, I. Suleimanov, E. M. Hernandez, L. Salmon, G. Molnar and A. Bousseksou, Materials, 2016, 9, 537 CrossRef PubMed.
- A. Grosjean, N. Daro, S. Pechev, L. Moulet, C. Etrillard, G. Chastanet and P. Guionneau, Eur. J. Inorg. Chem., 2016, 1961 CrossRef CAS.
- S. Lakhloufi, E. Tailleur, W. Guo, F. Le Gac, M. Marchivie, M. H. Lemée-Cailleau, G. Chastanet and P. Guionneau, Crystals, 2018, 8, 363 CrossRef.
- H. Mba, M. Picher, N. Daro, M. Marchivie, P. Guionneau, G. Chastanet and F. Banhart, J. Phys. Chem. Lett., 2023, 14, 8100 CrossRef CAS PubMed.
- Y. Miyazaki, T. Nakamoto, S. Ikeuchi, K. Saito, A. Inaba, M. Sorai, T. Tojo, T. Atake, G. S. Matouzenko, S. Zein and S. A. Borshch, J. Phys. Chem. B, 2007, 111, 12508 CrossRef CAS PubMed.
- J. P. Sethna, K. A. Dahmen and C. R. Myers, Nature, 2001, 410, 242 CrossRef CAS PubMed.
- M. L. Rosinberg and E. Vives, Metastability, Hysteresis, Avalanches, and Acoustic Emission: Martensitic Transitions in Functional Materials, in Disorder and Strain Induced Complexity in Functional Materials, ed. T. Kakeshita, T. Fukuda, A. Saxena and A. Planes, Springer Series in Materials Science, Springer, Berlin, Germany, 2012, vol. 148, pp. 249–272. ISBN 978-3-642-20943-7 Search PubMed.
- J. P. Sethna, K. Dahmen and O. Perkovic, Random-Field Ising Models of Hysteresis, in The Science of Hysteresis, ed. G. Berttoti and I. Mayergoyz, Academic Press, Amsterdam, The Netherlands, 2006, vol. II, pp. 107–179. ISBN 9780080540788 Search PubMed.
- L. Mañosa, A. Planes, D. Rouby and J. L. Macqueron, Acta Metall. Mater., 1635, 1990, 38 Search PubMed.
- O. Lee, Y. Koga and A. P. Wade, Talanta, 1990, 37, 861 CrossRef CAS PubMed.
- M. K. Panda, M. Etter, R. E. Dinnebier and P. Naumov, Angew. Chem., Int. Ed., 2017, 56, 8104 CrossRef CAS PubMed.
- S. S. Azimov, V. N. Petukhov, A. N. Lakaev and A. B. Leksovskii, Tech. Phys., 2016, 61, 635 CrossRef CAS.
- T. Sawada, Y. Gohshi, C. Abe and K. Furuya, Anal. Chem., 1985, 57, 1743 CrossRef CAS.
- S. Rat, K. Ridier, L. Vendier, G. Molnar, L. Salmon and A. Bousseksou, CrystEngComm, 2017, 19, 3271 RSC.
- J. Kröber, J. P. Audière, R. Claude, E. Codjovi, O. Kahn, J. G. Haasnoot, F. Grolière, C. Jay, A. Bousseksou, J. Linarès, F. Varret and A. Gonthier-Vassal, Chem. Mater., 1994, 6, 1404 CrossRef.
- M. K. Bolgár, L. Z. Tóth, S. Szabó, S. Gyöngyösi, L. Daróczi, E. Y. Panchenko, Y. I. Chumlyakov and D. L. Beke, J. Alloys Compd., 2016, 658, 29 CrossRef.
- L. Z. Tóth, L. Daróczi, S. Szabó and D. L. Beke, Phys. Rev. B, 2017, 93, 144108 CrossRef.
- D. L. Beke, L. Daróczi and T. Y. Elrasasi, Determination of elastic and dissipative energy contributions to martensitic phase transformation in shape memory alloys, in Shape Memory Alloys-Processing, Characterization and Applications, ed. F. Fernandes, InTech, London, UK, 2013, p. 167. ISBN 978-953-51-1084-2 Search PubMed.
- D. L. Beke, L. Daróczi, N. M. Shamy, L. Z. Tóth and M. K. Bolgár, Acta Mater., 2020, 200, 490 CrossRef CAS.
- C. Lefter, R. Tan, S. Tricard, J. Dugay, G. Molnar, L. Salmon, J. Carrey, A. Rotaru and A. Bousseksou, Polyhedron, 2015, 102, 434 CrossRef CAS.
- E. K. Salje and K. A. Dahmen, Annu. Rev. Condens. Matter Phys., 2014, 5, 233 CrossRef CAS.
- L. Carrillo and J. Ortín, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 11508 CrossRef CAS.
- M. C. Kuntz and J. P. Sethna, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11699 CrossRef CAS.
- M. LeBlanc, L. Angheluta, K. Dahmen and N. Goldenfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022126 CrossRef PubMed.
- S. Papanikolaou, F. Bohn, R. L. Sommer, G. Durin, S. S. Zapperi and J. P. Sethna, Nat. Phys., 2011, 7, 316 Search PubMed.
- L. Laurson, X. Illa, S. Santucci, K. T. Tallakstad, K. J. Maloy and M. J. Alava, Nat. Commun., 2013, 4, 2927 Search PubMed.
- A. Planes, L. Manosa and E. Vives, J. Alloys Compd., 2013, 577, S699 CrossRef CAS.
- A. Dobrinevski, P. Le Doussal and K. J. Weise, EPL, 2015, 108, 66002 CrossRef.
- S. M. Kamel, N. M. Samy, L. Z. Tóth, L. Daróczi and D. L. Beke, Materials, 2022, 15, 4556 CrossRef CAS PubMed.
- G. Durin and S. Zapperi, Phys. Rev. Lett., 2000, 84, 4705 CrossRef CAS PubMed.
- D. L. Beke, M. K. Bolgár, L. Z. Tóth and L. Daróczi, J. Alloys Compd., 2018, 741, 106 CrossRef CAS.
- D. L. Beke, L. Daróczi, L. Z. Tóth, M. K. Bolgár, N. M. Samy and A. Hudák, Metals, 2019, 9, 58 CrossRef CAS.
- B. Casals, K. A. Dahmen, B. Gou, S. Rooke and E. K. H. Salje, Sci. Rep., 2021, 11, 5590 CrossRef CAS PubMed.
- V. Chi-Cong and J. Weiss, Phys. Rev. Lett., 2020, 125, 105502 CrossRef PubMed.
- G. Spark and R. Maas, Acta Mater., 2018, 152, 86 CrossRef.
- J. Antonaglia, W. J. Wright, X. Gu, R. R. Byer, T. C. Hufnagel, M. LeBlanc, J. T. Uhl and K. A. Dahmen, Phys. Rev. Lett., 2014, 112, 1555501 CrossRef PubMed.
- L. Z. Tóth, E. Bronstein, L. Daróczi, D. Shilo and D. L. Beke, Materials, 2023, 16, 2089 CrossRef PubMed.
- K. Ridier, G. Molnár, L. Salmon, W. Nicolazzi and A. Bousseksou, Solid State Sci., 2017, 74, A1 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional acoustic emission data. See DOI: https://doi.org/10.1039/d4tc00495g |
| This journal is © The Royal Society of Chemistry 2024 |