Multiferroicity in 2D MSX₂ (M = Nb and Zr; X = Cl, Br, and I)

Abstract

Recently, two-dimensional (2D) multiferroic materials have aroused intensive interest owing to the combination of ferroelectric and magnetic properties. In this work, we design a family of 2D MSX₂ (M = Zr and Nb; X = Cl, Br, and I) and investigated their structural, mechanical, magnetic, electronic, ferroelectric, and piezoelectric properties based on first-principles calculations. We find that ferroelectric (FE) ZrSX₂, paraelectric (PE) ZrSX₂ and FE NbSX₂ are stable. ZrSX₂ materials are nonmagnetic, while NbSX₂ materials have antiferromagnetic (AFM) ground states. NbSX₂ materials demonstrate multiferroic behaviors, which can be explained by the pseudo Jahn–Teller distortion (PJTE) mechanism. Our work reveals the intrinsic multiferroicity of MSX₂, which may provide a guidance on the design of 2D functional materials.

---

1. Introduction

2D multiferroics have been attracting much attention due to their promising properties such as high spontaneous FE polarization,^1–4 photovoltaic effects,^5–8 and high-temperature magnetism.⁹ FE materials, such as BiFeO₃¹⁰ and BaTiO₃,^11–13 have demonstrated outstanding potential for memory storage and integrated microelectrons. 2D GeS showed a tunable Curie temperature and spontaneous polarization of 1 C m⁻², and mutliferroic behaviors under small strain provided high freedom for modulating ferroelectric devices.³ 2D CrI₃-based magnetic tunneling junctions exhibit layered-dependent magnetism, in which an outstanding magnetoresistance was reported.^14,15 Commonly, there is an off-center displacement in FE phases other than the PE phase, indicating the break of symmetry for FE polarization.^10,16–18 Taking 2D VOCl₂ as an example, the off-center displacement of V ions contributes to FE characteristics, and the energy barrier of the FE flip is 0.18 eV, which stabilizes the ferroelectricity.¹⁹ 2D TiOBr₂ exhibits significant piezoelectricity with d₁₁ = 37.758 pm V⁻¹, resulting from low in-plane elastic constants and atomic sensitivity to an applied strain.⁴ Young's moduli (C_ij) reflect the ability to stretch and deform. The structures also have large piezoelectric strain coefficients (d_ij) because of their large piezoelectric stress coefficients (e_ij) and low Young's moduli. The CrOF₂ monolayer exhibits a half-metallic nature with intrinsic ferromagnetism (FM) and a high phase transition temperature. The Pmna-MnOCl₂ monolayer is an FM-stabilized semiconductor with an indirect band gap of 0.152 eV, while the Pmmn-MnOCl₂ monolayer is an FM Dirac semimetal with a Curie temperature of 910 K.²⁰ Uniaxial strain drives the magnetic phase transition in CrOF₂, resulting in a high phase transition temperature.²¹ 2D NbOX₂ materials possess suitable conduction band minimums (CBMs) and valence band maximums (VBMs) for photocatalytic water splitting, which can be further tuned by stacking.²² Furthermore, the proper built-in electric field, high carrier mobility, and suitable band edges in 2D NbOXY make it a potential candidate for overall water splitting.²³ 2D MoOCl₂ has hyperbolic optical properties with two wide hyperbolic windows from 0.41 to 2.90 eV and from 3.63 to 5.54 eV.²⁴

Compared with bulk counterparts, 2D materials can be modified by various methods, such as surface engineering,^25,26 defect engineering,²⁷ strain engineering,²⁸ heterostructure engineering,^29,30 and composition engineering,³¹ to achieve ideal properties for targeted applications. Although numerous investigations have been carried out on 2D metal oxide dihalides,^22,32–34 studies on the ferroelectricity of 2D metal sulfide dihalides are limited. In this work, we present a systematic study of 2D MSX₂ based on first-principles calculations. We reveal the intrinsic ferroelectricity in MSX₂ and piezoelectric effects vary with tension.

2. Methods

All calculations were performed by the Vienna ab initio simulation package (VASP) with the projector augmented wave (PAW) potential and Perdraw–Burke–Ernzerhof (PBE) energy functional.^35–39 A vacuum slab of 15 Å along the c-axis was used to avoid interactions between neighboring layers, which has been tested (Fig. S1, ESI†). The cut-off energy for the plane-wave basis set was 550 eV, and the convergence threshold and residual forces were 1 × 10⁻⁷ eV and 1 × 10⁻³ eV Å⁻¹, respectively.^36,40,41 A 2 × 2 × 1 supercell was used to study magnetic properties. The Γ-centered k-meshes for sampling the Brillouin zone (BZ) were 12 × 12 × 1, 6 × 6 × 1, and 3 × 3 × 1 for structural relaxation, electronic structures, and phonon calculations, respectively.⁴² The Γ-only grid was used for the AIMD simulation. The Heyd–Scuseria–Ernzerhof hybrid functional (HSE06) was used to calculate band structures accurately.⁴³ The climbing image nudged elastic band (CI-NEB)⁴⁴ method was implemented to determine the energy barrier of the ferroelastic phase transition. To describe the Coulomb interaction among partially occupied d-electrons of transition metals, the GGA+U⁴⁵ method was adopted in our calculations. The various values of 1, 2, and 3 eV elucidate the effects of Hubbard U on structural and electronic properties.

The density-functional perturbation theory⁴⁶ (DFPT) was used to calculate the phonon dispersion with the Phonopy⁴⁷ code; 3 × 3 × 1 supercells were used for the phonon calculations as well as AIMD simulations. The Γ-centered k-meshes were 18 × 18 × 1 for the calculations of piezoelectric parameters via the DFPT. To study the thermodynamic stability, the ab initio molecular dynamic (AIMD) simulation⁴⁸ was performed. The simulated temperature, time step, and time period in AIMD were 300 K, 1 fs, and 8 ps, respectively. VASPKIT⁴⁹ was used as the post-processing tool for data analysis.

To determine Néel temperatures (T_N), Monte Carlo (MC) simulations⁵⁰ were performed based on the Wolff algorithm of the classical Heisenberg model using the MCSOLVER code.^51,52 In the MC simulations, a 100 × 100 square supercell containing 10 000 local magnetic moments was adopted; 40 000 MC steps were performed at each temperature, and the calculations lasted for 6.4 × 10⁹ loops at each temperature.

3. Results and discussion

3.1 Structural properties

MSX₂ has four atoms in a unit cell, including one metal atom (M = Zr and Nb), one sulfur atom and two halogen atoms (X = Cl, Br, and I). Similar to 2D TiOX₂, VOX₂, and VOXY,^4,53 in-plane off-center displacement of metal atoms leads to multiferroic behavior. The FE phases with the space group of Pmm2 (No. 25) and PE phases with the space group of Pmmm (No. 47) were investigated. The FE structures have two kinds of M–S bond lengths (d_M–S2 and d_M–S1) and two kinds of S–M–X bond angles (Fig. 1). The differences between θ₁ and θ₂ decrease as X changes from Cl to I. In contrast, the lengths of M–S bonds are the same in the PE phases, and the bond angles of S–M–X remain 90° (Table S1, ESI†). Moreover, two kinds of X–M–X angles are found in the structures. The polar displacement (P.D.) leads to in-plane ferroelectricity, which can be defined as follows:⁵³

P.D. = |d_M–S2 − d_M–S1|/2, (1)

where d_M–S2 indicates the long bond length between metal and sulfur atoms, and d_M–S1 is the short one.

Fig. 1 (a) Top and (b) and (c) side views of a 2 × 2 × 1 supercell of FE MSX₂ and (d) top and (e) side views of PE MSX₂. M–S2 indicates the long bond length between metal and sulfur atoms, M–S1 is the short counterpart, and the black arrow indicates the direction of FE polarization.

The P.D. decreases dramatically with the increase in U in ZrSX₂. In contrast, the P.D. varies slightly with U in NbSX₂ (Fig. S2 and Table S2, ESI†). There are imaginary optical phonon modes at the Γ point for PE ZrSX₂ and little imaginary frequency for FE counterparts, suggesting spontaneous symmetry breaking and off-center displacements of metal atoms^4,54 (Fig. S3 and S4, ESI†). The negligible imaginary dispersions of the FE phases may be induced by the calculation accuracy and lattice instabilities related to long wave undulations, which have been reported in other 2D materials.^55,56 Correspondingly, the lattice parameter b in the FE phase is larger than that in the PE phase because of the off-center displacements of metal atoms in MSX₂ (Table S1, ESI†). Furthermore, PE ZrSX₂ materials with U = 3 eV are dynamically stable with negligible imaginary frequencies (Fig. S4, ESI†). NbSX₂ materials are dynamically unstable without U, while exhibiting similar FE phenomena with U = 3 eV (Fig. 2a and Fig. S5, S6, ESI†). NbSCl₂ shows a weak tolerance to tension (Fig. S6, ESI†). All of the ZrSX₂ materials exhibit dynamically stable FE phases without U and PE phases with U = 3 eV. MSCl₂ and MSBr₂ are unstable with U = 1 eV and 2 eV, but have stable FE phases with U = 3 eV (Fig. S3–S8, ESI†). Previous reports indicate that NbSX₂ and VOX₂ exhibited varied polarizations with U.^4,57 Therefore, ZrSX₂ without and with U (3 eV) and NbSX₂ with U = 3 eV were investigated.

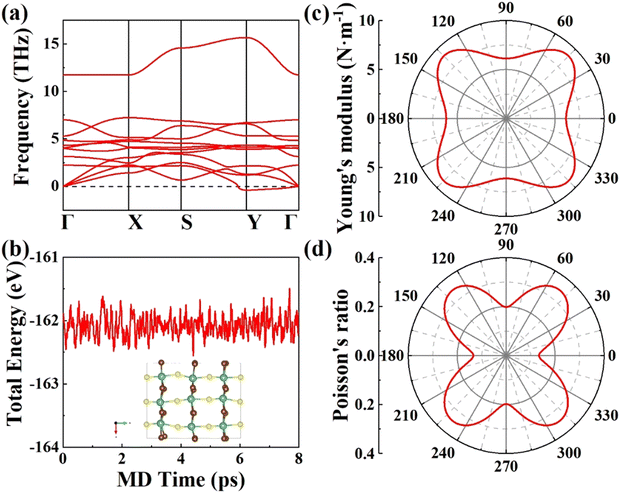Fig. 2 (a) Phonon spectrum, (b) AIMD simulation, (c) Young's moduli, and (d) Poisson's ratio of FE NbSBr₂ with U = 3 eV.

3.2 Structural stability

To ensure thermodynamic and mechanical stabilities, we carried out AIMD simulations and calculated mechanical parameters. The AIMD simulations show that the total energies of the structures have little fluctuations over time, and the mean squared displacement (MSD) was defined aswhere x(t) and x(0) is the position of atom i at a time of t and 0, respectively, and N stands for the total number of atoms.

The MSDs are less than 0.6 Ų, indicating thermodynamic stability (Fig. 2b and Fig. S9 and S10, ESI†).⁵⁸ Stable FE phases are supposed to retain positive elastic constants restricted by the Born–Huang criteria:⁵⁹

C₁₁C₂₂ − C₁₂² > 0 (3)

C₆₆ > 0 (4)

We see that FE ZrSX₂, ZrSX₂ with U = 3 eV, and FE NbSX₂ with U = 3 eV are mechanically stable as obtained elastic constants satisfy the Born–Huang criteria. Their Young's moduli (E_x and E_y), Poisson's ratios (ν_x and ν_y) and shear moduli (G) are also obtained (Table 1). Thus, we confirm that MSX₂ materials are dynamically, thermodynamically, and mechanically stable. In addition, the distorted shapes of Young's moduli and Poisson's ratios reflect their anisotropic nature (Fig. 2c and d and Fig. S11–S15, ESI†). Previous studies have indicated that the mechanical and piezoelectric properties may be enhanced under tension along polarization.^60,61 Thus, we also obtained the corresponding parameters at a tension of 5% along b-axes. With the tension along the b-axis, C₂₂ drops significantly, leading to a lower E_y and a higher ν_x. Conversely, C₂₂ soars with a larger U in ZrSX₂, resulting in higher E_y and smaller Poisson's ratios.

Table 1 Mechanical parameters of the structures

MSX2	Tension (%)	U (eV)	Stiffness tensor (GPa)					Young's modulus E (GPa)		Poisson's ratio		Shear modulus G (GPa)
			C 11	C 12	C 22	C 66	C 11 C 22 − C12^2 (±)	X	y	X	y	G
ZrSCl2	0	0	18.569	3.606	23.747	4.577	+	18.021	23.047	0.152	0.194	7.482
ZrSCl2	5	0	17.766	2.839	4.957	3.582	+	16.140	4.503	0.573	0.160	7.464
ZrSCl2	0	3	18.877	0.959	57.459	4.926	+	18.861	57.410	0.017	0.051	8.959
ZrSBr2	0	0	16.083	3.192	24.629	4.485	+	15.669	23.995	0.130	0.198	6.446
ZrSBr2	5	0	15.621	2.633	4.936	3.577	+	14.216	4.492	0.533	0.169	6.494
ZrSBr2	0	3	16.102	0.926	57.017	4.762	+	16.087	56.964	0.016	0.058	7.588
ZrSI2	0	0	13.550	2.554	27.386	4.361	+	13.312	26.905	0.093	0.188	5.498
ZrSI2	5	0	13.424	2.196	5.582	3.524	+	12.560	5.223	0.393	0.164	5.614
ZrSI2	0	3	13.479	0.895	56.740	4.491	+	13.465	56.681	0.016	0.066	6.292
NbSCl2	0	3	18.943	4.931	15.986	6.013	+	17.422	14.702	0.308	0.260	7.006
NbSCl2	5	3	20.242	1.481	3.439	4.898	+	19.604	3.331	0.431	0.073	9.381
NbSBr2	0	3	17.985	3.562	26.608	6.122	+	17.508	25.903	0.134	0.198	7.212
NbSBr2	5	3	17.967	3.455	2.784	5.000	+	13.679	2.120	1.241	0.192	7.256
NbSI2	0	3	16.385	3.088	31.860	6.024	+	16.086	31.278	0.097	0.188	6.649
NbSI2	5	3	16.659	3.050	3.551	5.027	+	14.039	2.993	0.859	0.183	6.805

---

The formation energies were also obtained to demonstrate their possibility for experimental realization:⁶²

E_f = (E_MSX2 − E_M − E_S − 2E_X)/4, (5)

where E_MSX2 is the ground state energy of MSX₂ per chemical formula, and E_M, E_S, and E_X are the chemical potentials of metal, sulfur and halogen atoms calculated from their elemental forms, respectively. The calculated formation energies are negative (Table S3, ESI†), indicating that they are possible to be achieved experimentally. Moreover, other phases, including MS and X₂, as well as MX₂ and S, were considered to calculate the formation energy of MSX₂. Their formation energies are obtained as follows:

E_f1 = (E_MSX2 − E_MS − 2E_X) (6)

E_f2 = (E_MSX2 − E_S − E_MX2), (7)

where E_MS and E_MX2 are the energies of bulk MS and MX₂, respectively. The results indicate that MSI₂ may decompose into MS and I₂ and others may not (Table S4, ESI†). We find that energy barriers between FE and AFE structures are 19, 17, 8, 60, 52, and 38 meV per unit cell for ZrSCl₂, ZrSBr₂, ZrSI₂, NbSCl₂, NbSBr₂, and NbSI₂, respectively (Fig. S16, ESI†), which are much lower than those of the VOCl₂ monolayer¹⁹ and LiNbO₃ perovskite.⁶³ FE polarizations are switchable, and the energy barriers for FE-AFE switches in NbSX₂ are higher than the thermal energy at room temperature (∼26 meV), indicating stable FE states (Fig. S16, ESI†).

3.3 Magnetic properties

FE ZrSX₂ materials do not show magnetism as the energies do not change with spin (Table S5, ESI†). In contrast, the FE NbSX₂ materials demonstrate magnetic behaviors. To determine the magnetic ground states of NbSX₂, one FM state and three AFM states were studied in a 2 × 2 × 1 supercell (Fig. S17, ESI†). The exchange energy per unit cell is the energy difference between stable AFM and FM states:^62,64

E_ex = (E_AFM − E_FM)/N, (8)

where E_AFM is the energy of the most stable AFM state, E_FM is the energy of the FM state, and N is the number of unit cells inside a supercell (N = 4). The exchange energies are −226, −36, and −17 meV per unit cell for NbSCl₂, NbSBr₂, and NbSI₂, respectively, illustrating the AFM3 ground state (Table 2 and Table S6, ESI†). The exchange energy of NbSCl₂ is much higher than that of VTe₂.⁶⁴ Compared with FM-stabilized materials, AFM-stabilized ones do not have redundant magnetic fields and are significantly insensitive to external magnetic fields due to their zero total magnetization. Moreover, 2D AFM structures have fast spin dynamics and high packing density, making them potential candidates for fostering innovation in spin-based devices.^65–68

Table 2 Exchange energies (E_ex), magnetic moments, exchange coupling parameters, and Néel temperatures

NbSX2	U (eV)	E ex (meV per unitcell)	Nb (μB)	S (μB)	X (μB)	J a (meV)	J b (meV)	J ab (meV)	T N (K)
NbSCl2	3	−226	±0.863	±0.072	0	−28.593	0.328	0.218	25
NbSBr2	3	−36	±0.870	±0.069	0	−4.618	0.099	0.116	4.5
NbSI2	3	−17	±0.868	±0.063	0	−2.356	0.203	0.194	2

---

Magnetic anisotropy describes the preferred orientations of magnetic moment vectors.⁶⁹ The magnetic anisotropy energies (MAEs) in xOz, yOz, and xOy planes for NbSCl₂, NbSBr₂ and NbSI₂, respectively, are investigated by including the spin–orbital coupling (SOC) effect, which is defined as^70–72

MAE = E_‖ − E_⊥, (9)

where E_‖ and E_⊥ are energies per chemical formula with the in-plane and out-of-plane spins with respect to the easy axes, respectively.

The angular dependent results show that easy magnetization axes are [100], [001], and [010], and the MAEs are 0.073, 0.050 and 0.036 meV per unit for NbSCl₂, NbSBr₂ and NbSI₂, respectively (Fig. S18, ESI†), which are much higher than those of cubic Fe⁷³ and Ni.⁷⁴ As X changes from Cl to I, the easy magnetization axes are altered, and the MAEs decrease. Specifically, the total energy varies significantly with the magnetization direction in the xOy and yOz planes. The significant the MAEs of NbSX₂ make them potential candidates for nanoscale devices such as magnetic recording media.⁷⁵

The magnetic moments of niobium atoms are close to 1μ_B per Nb. The nearest–neighbor (NN) and next–nearest–neighbor (NNN) exchange interactions are considered to determine the exchange parameters of NbSX₂.^19,54 The NN exchange coupling parameters along the a- and b-directions are J_a and J_b, and the NNN exchange coupling parameter is J_ab (Fig. S17, ESI†).^76,77 The Hamiltonian is written as

where H₀ is the nonmagnetic Hamiltonian, M_i is the net magnetic moment at site i, 〈ij〉_a is nearest Nb atoms along the a-direction, and 〈〈kl〉〉 stands for NNN Nb atoms. The NN and NNN exchange coupling parameters can be solved by the energies of one FM state and three AFM states. The total energies of the four magnetic states are calculated as¹⁹

E_FM = E₀ − 4M² (J_a + J_b + 2J_ab) (11)

E_AFM1 = E₀ − 4M² (−J_a + J_b − 2J_ab) (12)

E_AFM2 = E₀ − 4M² (J_a − J_b − 2J_ab) (13)

E_AFM3 = E₀ − 4M² (−J_a − J_b − 2J_ab) (14)

After obtaining the MAEs and exchange parameters, the T_N can be determined by the MCSOLVER code. The T_N of NbSCl₂ is higher than that of VOF₂⁷⁸ and VOI₂⁷⁹ (Table 3 and Fig. S19, ESI†).

Table 3 Piezoelectric parameters of the structures

MSX2	Tension (%)	U (eV)	e 21 (10^−10 C m^−1)	e 22 (10^−10 C m^−1)	d 21 (pm V^−1)	d 22 (pm V^−1)
ZrSCl2	0	0	1.754	−19.836	0.264	−0.875
ZrSCl2	5	0	0.530	−11.489	0.441	−2.570
ZrSBr2	0	0	1.476	−19.387	0.255	−0.820
ZrSBr2	5	0	0.401	−10.965	0.440	−2.456
ZrSI2	0	0	1.236	−21.474	0.243	−0.807
ZrSI2	5	0	0.234	−10.551	0.349	−2.027
NbSCl2	0	3	4.379	−37.886	0.922	−2.654
NbSBr2	0	3	0.537	−13.883	0.137	−0.540
NbSBr2	5	3	0.159	−9.832	0.904	−4.653
NbSI2	0	3	0.356	−13.069	0.101	−0.420
NbSI2	5	3	0.000	−8.951	0.548	−2.991

---

3.4 Electronic properties

The band structures and densities of states (DOSs) were calculated based on the magnetic ground states to uncover the mechanism of FE switching and magnetism. FE ZrSX₂ are direct bandgap semiconductors with flat bands around the CBMs (Fig. S20 and Table S7, ESI†). FE NbSX₂ are indirect bandgap semiconductors (Fig. 3, Fig. S21 and Table S7, ESI†). PE ZrSX₂, PE NbSCl₂, and PE NbSBr₂ have small direct bandgaps with the CBM and VBM at Γ points (Fig. 3, Fig. S21 and Table S7, ESI†). Moreover, the FE ZrSX₂ materials are direct bandgap semiconductors according to the HSE06 method, whose CBMs and VBMs meet the requirements of photocatalysts (Fig. S22 and Table S7, ESI†).

Fig. 3 Band structures of (a) FE and (b) PE NbSBr₂, PDOSs of (c) FE and (d) PE NbSBr₂, PDOSs of Nb atoms in (e) FE and (f) PE NbSBr₂, and PDOSs of S atoms in (g) FE and (h) PE NbSBr₂ with U = 3 eV.

The partial density of states (PDOSs) illustrate the hybridization between metal and non-metal atoms (Fig. S23–S27, ESI†). Around the CBMs, the spin-polarizations dominantly originate from the d-orbitals of metal atoms, while the p-electrons of non-metal atoms contribute mostly to the VBMs of ZrSX₂ (Fig. S23 and S24, ESI†). Differently, the d-electrons of niobium atoms dominate the states near the VBMs of NbSCl₂ and NbSBr₂. Furthermore, the spin-polarizations near the CBMs in ZrSX₂ mainly originate from the d_z² orbital. In contrast, significant spin-splitting around the VBMs induced by the d_z² orbitals and CBMs by the d_xy and d_yz orbitals leads to magnetic moments of 0.863, 0.870, and 0.868μ_B per Nb for NbSCl₂, NbSBr₂, and NbSI₂, respectively. The charge distribution reflects the bonding among atoms. The ELF contour around the center of M–X bonds is near 0, revealing ionic interaction (Fig. S25 and S26, ESI†). According to Goodenough–Kanamori–Anderson rules,^80–83 the super-exchange usually leads to AFM characteristics in FE NbSX₂ when the average angles of cation–anion–cation bond angles are around 90°. The average angles of θ₁ and θ₂ as well as α₁ and α₂ are 90° (Fig. 1 and Table S1, S8, ESI†), confirming the AFM nature. Therefore, the super-exchange is responsible for the AFM state observed in NbSX₂ because of their semiconducting nature.^84–87

Similar to metal oxide dihalides, the off-center displacements of metal atoms give rise to multiferroic characters. The bandgaps of the FE phases are much larger than their PE counterparts (Table S7, ESI†), and a similar trend has been reported in 2D VOCl₂.¹⁹ We find that the energy levels of the d_xz orbitals are much lower in the FE phases than those in the PE phases, leading to d electrons with low energies (Fig. 3e, f and Fig. S27, S29, and S30, ESI†). The energies of FE phases are lower than those of the PE phases, which can be elucidated by the PJTE mechanism.⁸⁸ According to the PJTE mechanism, similar to Ti⁴⁺, Zr⁴⁺ exhibits a d⁰ configuration. In contrast, Nb⁴⁺ demonstrates a d¹ configuration like Ti³⁺ and V⁴⁺.⁸⁹ Zr⁴⁺ leads to a zero magnetic moment, whereas Nb⁴⁺ is endowed with magnetism, leading to multiferroic characteristics in NbSX₂. Unpaired electrons are found in Nb⁴⁺, whereas all the electrons are paired in Zr⁴⁺, causing the spin-splitting in Nb⁴⁺. There is spin-splitting in the t_1u orbitals of S atoms in FE NbSX₂, leading to magnetic moments of over 0.06μ_B per sulfur. However, the magnetic moments are 0 in ZrSX₂ and PE NbSX₂.

3.5 Piezoelectric properties

To further investigate the FE switching in ZrSX₂, the piezoelectric parameters were obtained. The piezoelectric strain coefficients are defined as^53,90

d₂₁ = (e₂₁C₂₂ − e₂₂C₁₂)/(C₁₁C₂₂ − C₁₂²) (15)

d₂₂ = (e₂₂C₁₁ − e₂₁C₁₂)/(C₁₁C₂₂ − C₁₂²), (16)

where e_ij is piezoelectric stress coefficients and C_ij is stiffness tensors. Due to smaller C₂₂ and larger off-center displacement of metal atoms, the strain coefficients become significant under tension along the direction of FE switching (Table 3). The piezoelectric stress coefficients are much higher than those of some 2D Janus transition metal dichalcogenides,⁹¹ as well as the h-BN monolayer.⁹² At a tension of 5%, the Poisson's ratios along the [010] axes are much lower than those along the [100] axes. Consequently, negative Poisson's ratios are found in NbSX₂ (Fig. S14, ESI†). Moreover, the variations of X–M–X angles are more significant than those of S–M–X angles at a tension (Table S8, ESI†), leading to higher Poisson's ratios along the [100] axes rather than the [010] axes. Similar trends are found in penta-BCP because of the major fluctuation of bond angles.⁹⁰ By considering FE switching stability, piezoelectric stress and strain coefficients, we see that NbSX₂ can be applied for sensors and energy conversion.^93,94

4. Conclusions

In summary, we propose a 2D family MSX₂ (M = Zr and Nb; X = Cl, Br, and I) and investigate their stability, magnetic, electronic, and piezoelectric properties on the basis of the first-principles calculations for multiferroicity. We find that FE ZrSX₂, PE ZrSX₂, and FE NbSX₂ are stable, and the FE switching of NbSX₂ is stable at room temperature. The off-center displacements of M ions induce differences between the electronic structures of the FE and PE phases. It is expected that designed structures can be applied to nanoscale spintronic devices. This work may provide guidance on the design of 2D materials with promising multiferroicity.

Conflicts of interest

There is no conflict to declare.

Acknowledgements

This work was supported by the Science and Technology Development Fund (FDCT) from Macau SAR (0050/2023/RIB2, 0023/2023/AFJ, 006/2022/ALC, and 0111/2022/A2), Multi-Year Research Grants (MYRG-GRG2023-00010-IAPME and MYRG2022-00026-IAPME) from the Research & Development Office at the University of Macau, and the Shenzhen-Hong Kong-Macao Science and Technology Research Programme (Type C) (SGDX20210823103803017) from Shenzhen.

References

1. D. Sando, Y. Yang, E. Bousquet, C. Carretero, V. Garcia, S. Fusil, D. Dolfi, A. Barthelemy, P. Ghosez, L. Bellaiche and M. Bibes, Nat. Commun., 2016, 7, 10718.
2. Y. Zhai, A. Fan, K. Zhong, D. V. Karpinsky, Q. Gao, J. Yi and L. Liu, J. Eur. Ceram. Soc., 2024, 44, 224–232.
3. R. Fei, W. Kang and L. Yang, Phys. Rev. Lett., 2016, 117, 097601.
4. A. Alam, M. Noor and M. Nolan, Nanoscale, 2022, 14, 11676–11683.
5. A. Bhatnagar, Y. Kim, D. Hesse and M. Alexe, Nano Lett., 2014, 14, 5224–5228.
6. G.-L. Yuan and J. Wang, Appl. Phys. Lett., 2009, 95, 252904.
7. K. M. Batoo, M. F. Ijaz, A. Imran and S. Pandiaraj, Chemosphere, 2024, 346, 140410.
8. Q. Sun, Y. Fang, S. Wang, W. Ma, Q. Zhang, J. Wang, Y. Wang, J. Lang, J. Zhang, Y. Liu and J. Yang, Mater. Sci. Eng. B, 2024, 299, 116921.
9. N. Zhang, J. Ding, Y. Wang, X. Liu, Y. Li, M. Liu, Z. Fu, Y. Yang, J. Su, G. Song, F. Yang, Y. Guo and J. Liu, J. Phys.: Condens. Matter, 2021, 33, 135803.
10. H. Yamada, V. Garcia, S. Fusil, S. Boyn, M. Marinova, A. Gloter, S. Xavier, J. Grollier, E. Jacquet, C. Carretero, C. Deranlot, M. Bibes and A. Barthelemy, ACS Nano, 2013, 7, 5385–5390.
11. L. Bocher, A. Gloter, A. Crassous, V. Garcia, K. March, A. Zobelli, S. Valencia, S. Enouz-Vedrenne, X. Moya, N. D. Mathur, C. Deranlot, S. Fusil, K. Bouzehouane, M. Bibes, A. Barthelemy, C. Colliex and O. Stephan, Nano Lett., 2012, 12, 376–382.
12. J. Y. Son, J. H. Lee, S. Song, Y. H. Shin and H. M. Jang, ACS Nano, 2013, 7, 5522–5529.
13. Z. Yu, B. Li, H. Bai and H. Pan, J. Mater. Chem. A, 2023, 11, 19074–19082.
14. J. Chu, Y. Wang, X. Wang, K. Hu, G. Rao, C. Gong, C. Wu, H. Hong, X. Wang, K. Liu, C. Gao and J. Xiong, Adv. Mater., 2021, 33, e2004469.
15. T. Song, X. Cai, M. W. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Science, 2018, 360, 1214–1218.
16. H. Bai, D. Liu, P. Zhou, J. Feng, X. Sui, Y. Lu, H. Liu and H. Pan, J. Mater. Chem. A, 2022, 10, 25262–25271.
17. W. Song, R. Fei and L. Yang, Phys. Rev. B, 2017, 96, 235420.
18. H. Li, S. Ruan and Y. J. Zeng, Adv. Mater., 2019, 31, e1900065.
19. H. Ai, X. Song, S. Qi, W. Li and M. Zhao, Nanoscale, 2019, 11, 1103–1110.
20. G. Song, C. Zhang, T. Xie, Q. Wu, B. Zhang, X. Huang, Z. Li, G. Li and B. Gao, Phys. Chem. Chem. Phys., 2022, 24, 20530–20537.
21. X. Gu, X. Li, Y. Diao, Z. Lu, Z. Dong, H. Fu and C. Zhong, Comput. Mater. Sci., 2023, 228, 112311.
22. B. Mortazavi, M. Shahrokhi, B. Javvaji, A. V. Shapeev and X. Zhuang, Nanotechnology, 2022, 33, 275701.
23. T. Su, C. H. Lee, S.-D. Guo, G. Wang, W.-L. Ong, L. Cao, W. Zhao, S. A. Yang and Y. S. Ang, Mater. Today Phys., 2023, 31, 101001.
24. J. Zhao, W. Wu, J. Zhu, Y. Lu, B. Xiang and S. A. Yang, Phys. Rev. B, 2020, 102, 245419.
25. F. Zhou, S. Yan, F. Yang, X. Liao, S. Lin, M. Liao, S. Lou, Y. Liu, Z. Gong, K. B. Tom, Y. Deng, X. Wang, Y. Huang, J. Zhu and J. Yao, ACS Nano, 2020, 14, 15544–15551.
26. J. Huang, M. Li, J. Chen, Y. Cheng, Z. Lai, J. Hu, F. Zhou, N. Qu, Y. Liu and J. Zhu, Surf. Interfaces, 2023, 38, 102825.
27. J. Huang, J. Xue, M. Li, J. Chen, Y. Cheng, Z. Lai, J. Hu, F. Zhou, N. Qu, Y. Liu and J. Zhu, Appl. Surf. Sci., 2023, 635, 157757.
28. F. Li, H. Ai, D. Liu, K. H. Lo and H. Pan, J. Mater. Chem. A, 2021, 9, 17749–17759.
29. H. Bai, D. Liu and H. Pan, Mater. Horiz., 2023, 10, 5126–5132.
30. J. Xue, J. Huang, M. Li, J. Chen, Z. Wei, Y. Cheng, Z. Lai, N. Qu, Y. Liu and J. Zhu, Metals, 2023, 13, 1690.
31. N. Qu, M. Chen, M. Liao, Y. Cheng, Z. Lai, F. Zhou, J. Zhu, Y. Liu and L. Zhang, Materials, 2023, 16, 2633.
32. J. Zhao, W. Wu, J. Zhu, Y. Lu, B. Xiang and S. A. Yang, Phys. Rev. B, 2020, 102, 245419.
33. Y. Jia, M. Zhao, G. Gou, X. C. Zeng and J. Li, Nanoscale Horiz., 2019, 4, 1113–1123.
34. C. Liu, X. Zhang, X. Wang, Z. Wang, I. Abdelwahab, I. Verzhbitskiy, Y. Shao, G. Eda, W. Sun, L. Shen and K. P. Loh, ACS Nano, 2023, 17, 7170–7179.
35. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
36. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
38. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
41. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
42. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
43. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
44. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
45. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
46. S. Baroni, S. d Gironcoli and A. D. Corso, Rev. Mod. Phys., 2001, 73, 515–562.
47. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Solid State, 2008, 78, 134106.
48. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
49. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
50. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092.
51. L. Liu, S. Chen, Z. Lin and X. Zhang, J. Phys. Chem. Lett., 2020, 11, 7893–7900.
52. L. Liu, X. Ren, J. Xie, B. Cheng, W. Liu, T. An, H. Qin and J. Hu, Appl. Surf. Sci., 2019, 480, 300–307.
53. A. Mahajan and S. Bhowmick, J. Phys. Chem. C, 2023, 127, 11407–11418.
54. H. Ai, F. Li, H. Bai, D. Liu, K. H. Lo, S. A. Yang, Y. Kawazoe and H. Pan, npj Comput. Mater., 2022, 8, 60.
55. S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
56. H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
57. H. P. You, N. Ding, J. Chen and S. Dong, Phys. Chem. Chem. Phys., 2020, 22, 24109–24115.
58. Z. Gao, M. Wang, H. Zhang, S. Chen, C. Wu, I. D. Gates, W. Yang, X. Ding and J. Yao, Sol. Energy Mater. Sol. Cells, 2021, 233, 111401.
59. B. Li, J. Geng, H. Ai, Y. Kong, H. Bai, K. H. Lo, K. W. Ng, Y. Kawazoe and H. Pan, Nanoscale, 2021, 13, 8038–8048.
60. Y. Chen, X. Pu, X. Xu, M. Shi, H. J. Li and D. Wang, Sensors, 2022, 23, 91.
61. X. Liang and C. Wang, Acta Mater., 2022, 241, 118406.
62. J. Geng, I. N. Chan, H. Ai, K. H. Lo, Y. Kawazoe, K. W. Ng and H. Pan, Phys. Chem. Chem. Phys., 2020, 22, 17632–17638.
63. M. Ye and D. Vanderbilt, Phys. Rev. B, 2016, 93, 134303.
64. H. Pan, J. Phys. Chem. C, 2014, 118, 13248–13253.
65. X. Lan, Y. Gao, Y. Ge, W. Wan and Y. Liu, AIP Adv., 2023, 13, 125014.
66. M. Fiebig, N. P. Duong, T. Satoh, B. B. Van. Aken, K. Miyano, Y. Tomioka and Y. Tokura, J. Phys. D: Appl. Phys., 2008, 41, 164005.
67. S. Rahman, J. F. Torres, A. R. Khan and Y. Lu, ACS Nano, 2021, 15, 17175–17213.
68. T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Nat. Nanotechnol., 2016, 11, 231–241.
69. D. Yi, C. L. Flint, P. P. Balakrishnan, K. Mahalingam, B. Urwin, A. Vailionis, A. T. N'Diaye, P. Shafer, E. Arenholz, Y. Choi, K. H. Stone, J. H. Chu, B. M. Howe, J. Liu, I. R. Fisher and Y. Suzuki, Phys. Rev. Lett., 2017, 119, 077201.
70. G. H. O. Daalderop, P. J. Kelly and M. F. H. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11919–11937.
71. X. Wang, D. S. Wang, R. Wu and A. J. Freeman, J. Magn. Magn. Mater., 1996, 159, 337–341.
72. H. S. Sarmah and S. Ghosh, J. Phys. D: Appl. Phys., 2023, 56, 345002.
73. Y. Sun, Z. Zhuo, X. Wu and J. Yang, Nano Lett., 2017, 17, 2771–2777.
74. G. H. Daalderop, P. J. Kelly and M. F. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 11919–11937.
75. H. L. Zhuang, P. R. C. Kent and R. G. Hennig, Phys. Rev. B, 2016, 93, 134407.
76. C. Ederer and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 024102.
77. J. He, P. Lyu, L. Z. Sun, Á. M. Garcíaa and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 6500–6509.
78. H. You, N. Ding, J. Chen and S. Dong, Phys. Chem. Chem. Phys., 2020, 22, 24109–24115.
79. N. Ding, J. Chen, S. Dong and A. Stroppa, Phys. Rev. B, 2020, 102, 165129.
80. Y. Guo, Y. H. Zhang, S. J. Yuan, B. Wang and J. L. Wang, Nanoscale, 2018, 10, 18036–18042.
81. J. B. Goodenough and A. L. Loeb, Phys. Rev., 1955, 98, 391–408.
82. P. W. Anderson, Phys. Rev., 1959, 115, 2–13.
83. J. Kanamori, Prog. Theor. Phys., 1963, 30, 275–289.
84. H. Pan, J. Phys. Chem. C, 2014, 118, 13248–13253.
85. C. Song, K. W. Geng, F. Zeng, X. B. Wang, Y. X. Shen, F. Pan, Y. N. Xie, T. Liu, H. T. Zhou and Z. Fan, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 024405.
86. H. Pan, Sci. Rep., 2014, 4, 7524.
87. R. A. De. Groot and F. M. Mueller, Phys. Rev. Lett., 1983, 50, 2024–2027.
88. I. B. Bersuker, Phys. Rev. Lett., 2012, 108, 137202.
89. Y. Zhang, L. Lin, A. Moreo, G. Alvarez and E. Dagotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, L121114.
90. C. Hou, Y. Shen, W. Sun, Y. Chen, D. Ni and Q. Wang, J. Mater. Chem. C, 2022, 10, 10302–10309.
91. W. Chen, X. Hou, X. Shi and H. Pan, ACS Appl. Mater. Interfaces, 2018, 10, 35289–35295.
92. K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876.
93. W. Wu, L. Wang, Y. Li, F. Zhang, L. Lin, S. Niu, D. Chenet, X. Zhang, Y. Hao, T. Heinz, J. Hone and Z. Wang, Nature, 2014, 514, 470–474.
94. H. Zhu, Y. Wang, J. Xiao, M. Liu, S. Xiong, Z. Wong, Z. Ye, Y. Ye, X. Yin and X. Zhang, Nat. Nanotechnol., 2015, 10, 151–155.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc00463a

---