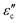Establishing the correlation of negative permittivity and AC conductivity of La2−xSrxNiO4 (x = 0, 0.1, 0.3, 1.0) for microwave shielding applications
Tarun
Katheriya
a,
Gurudeo
Nirala
ab and
Shail
Upadhyay
 *a
*a
aDepartment of Physics, Indian Institute of Technology (BHU), Varanasi-221005, India
bDepartment of Basic Science and Humanities, Government Polytechnic, Munger 811213, India. E-mail: supadhyay.app@itbhu.ac.in
First published on 16th May 2024
Abstract
Negative permittivity, a phenomenon observed in certain materials, has attracted considerable interest because of its significant implications in various fields of physics and engineering. Herein, from the perspective of intrinsic properties of single-phase materials, a few compositions of the La2−xSrxNiO4 system (x = 0, 0.1, 0.3, 1.0) were synthesized using the solid-state reaction method. XRD studies showed that the solubility limit of Sr in the lattice of La2NiO4 is limited (0.3 < x < 1.0). Morphological studies have revealed that average grain size and density increase with increasing Sr content. Dielectric/electrical properties were studied across a wide frequency range (20 Hz–2 MHz) and at higher temperatures (30–600 °C). All the samples have negative dielectric constant and this is attributed to plasma oscillation. The Drude model was fitted to experimental data and parameters like plasma frequency (ωp) and relaxation frequency (ωτ) were determined. The low value of activation energy (<0.05 eV) for direct current (D.C.) conduction and an increasing trend in relaxation time (τ) with temperature suggest a “small-polaron hopping conduction” mechanism. Studies on complex plane impedances have shown positive reactance and increased inductance with Sr-doping. Microwave shielding analysis revealed reflection as the primary shielding mechanism. The composition with x = 0.30 having high dielectric constant and conductivity shows the best shielding capabilities. These findings highlight the ability to tune the negative dielectric properties of La2NiO4 through compositional adjustments, which is significant for applications such as microwave shielding and coil-less inductive materials for future devices.
1. Introduction
Negative permittivity materials belong to the class of metamaterials, which are artificially engineered materials exhibiting some unique properties not present in natural materials. They can influence electromagnetic waves in ways that ordinary materials cannot.1–4 Earlier, properties of metamaterials were controlled by engineering complex geometric structures, rather than depending merely on material composition and microstructure. Many efforts have been made so far to realize negative permittivity in real materials so that properties can be controlled by compositional modifications and microstructure. A review article published in 2021 by Kai et al. highlighted the latest developments in the field of negative permittivity in composites called metacomposites.5 The negative permittivity in these composites appears when the concentration of metals exceeds a specific threshold, creating a percolating conducting path. However, these composites have limitations in low-dimensional applications, mainly due to their heterogeneous and non-uniform composition. To address these limitations, researchers have shifted their focus toward exploring negative permittivity in homogeneous or single-phase materials. Negative permittivity has been reported in various single-phase materials: Sr-doped LaMnO3,6–8 Mn-doped Sr2SnO4,9 Nb-doped Sr2MnO4,10 Sb-doped SnO2,11 and Sn-doped In2O3.12 We have put continuous efforts into exploring single-phase materials to achieve negative permittivity at room temperature in pristine (undoped) compounds. We have recently observed negative permittivity at and above room temperature in La2NiO4.13La2NiO4 nickelate with the K2NiF4-type structure is an important dielectric material that has received increasing attention due to its application as cathode material in solid oxide fuel cells (SOFCs).14–17 There is growing interest among researchers in exploring its dielectric and electrical conductivity properties for other applications such as microwave shielding. It is reported that Sr doping at the La site can modify the electrical and dielectric characteristics of La2NiO4. This highlights the fundamental role of the dielectric response and electrical conductivity of La2NiO4 in influencing its microwave shielding capabilities.18 While current reports mostly focus on measuring the electrical properties of materials at low temperatures and their microwave shielding properties at very high frequencies (GHz), it is acknowledged that, for most device applications, the properties of materials should be characterized at and above room temperature.
The aforementioned gap has motivated us to conduct a systematic detailed experimental investigation to understand the effect of Sr-doping on the structural, micro-structural, electrical properties, dielectric properties, and microwave shielding properties of La2NiO4. To achieve the objective, compositions with x = 0, 0.1, 0.3, and 1.0 of the system La2−xSrxNiO4 have been synthesized by the solid-state reaction method. The dielectric and electrical properties of the synthesized samples have been studied in the radio-frequency range (20 Hz–2 MHz) and a wide temperature range (RT–600 °C) using an LCR meter. Microwave shielding effectiveness has been measured in two different frequency bands of 1–2 MHz and 8–13 GHz.
2. Sample preparation
The compositions with x = 0, 0.1, 0.3, and 1.0 of La2−xSrxNiO4 were synthesized by the solid-state reaction method. For convenience, these compositions have been referred to by code name LN0 (x = 0.0), LN1 (x = 0.1), LN2 (x = 0.3) and LN3 (x = 1.0) henceforth. Spectroscopically pure La2O3 (Alfa Assar, purity >99.9%), NiCO3·2Ni(OH)2·xH2O (Sigma Aldrich, purity >99.9%) and SrCO3 (Alfa Assar, purity > 99.9%) were taken in a stoichiometric ratio and crushed in a planetary ball mill (Retsch PM 200, Germany) using an agate jar and balls (milling vessel is 250 ml, and the diameter of the balls is 10.2 mm) for 15 h at 200 rpm taking acetone as the mixing medium. During the mixing period, a ball-to-powder ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (by weight) was fixed. To prevent the heating and sticking of the powder to the container walls and balls, and agglomeration, the milling sequence was selected, such as 15 min of milling followed by 5 min of stop period. The prepared mixtures were dried for a long period (24 h) at 80 °C in a conventional oven. The calcination of the mixtures was performed at 1200 °C (optimized) in a platinum crucible for 12 h in an ambient atmosphere. The powders thus obtained were reground with 2% PVA, pressed into cylindrical pellets (10.0 × 2.0 mm), and sintered at 1500 °C for 12 h with the heating rate of 4 °C min−1 and 2 °C min−1 in cooling.
1 (by weight) was fixed. To prevent the heating and sticking of the powder to the container walls and balls, and agglomeration, the milling sequence was selected, such as 15 min of milling followed by 5 min of stop period. The prepared mixtures were dried for a long period (24 h) at 80 °C in a conventional oven. The calcination of the mixtures was performed at 1200 °C (optimized) in a platinum crucible for 12 h in an ambient atmosphere. The powders thus obtained were reground with 2% PVA, pressed into cylindrical pellets (10.0 × 2.0 mm), and sintered at 1500 °C for 12 h with the heating rate of 4 °C min−1 and 2 °C min−1 in cooling.
For the microwave shielding measurement, the powder of sintered pellets was dispersed in clear epoxy and dried overnight. The weight ratio of powder/epoxy for each composite was maintained at 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (each sample contained 80 wt% powder). The samples were cut into the desired rectangular shape waveguide adapters.
1 (each sample contained 80 wt% powder). The samples were cut into the desired rectangular shape waveguide adapters.
3. Characterization
The phase purity of the samples was confirmed by recording the X-ray diffraction pattern using CuKα (λ = 1.5406 Å) radiation with the help of a diffractometer (Rikagu X'PERT PRO MPD). The room temperature XRD patterns were collected in the range of 20–80° with a step size of 0.02°. The structure was analyzed by the Rietveld refinement method using the “FullProf program” and a pseudo-Voigt profile function with preferred orientation correction. The microstructure was studied by using a bench-top scanning electron microscope (Nova Nano SEM450, USA) at room temperature. The dielectric and electrical properties of the samples were investigated and measured using an inductance–capacitance–resistance (LCR) meter (Keysight E-4980A, USA) in a wide range of temperature (40–600 °C) and frequency (20 Hz–2 MHz) with a heating rate of 4 °C min−1 in cooling. Silver wires were used as electrodes in the sample holder. Conducting paste was not applied on the surface of the pellets for electrical measurements, as the samples were already conducting. Valence states of the constituent elements La, Sr, Ni, and O were studied by recording the core spectra of these elements employing an X-ray photoelectron spectrometer (Thermo Fisher Scientific K-Alpha, USA), operating at a high pressure of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
× ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11 Torr.
10−11 Torr.
Rectangular-shaped samples (length a = 23.86 mm and width b = 10.05 mm) were fit into the wave-guide adapter, with the whole assembly connected to a vector network analyzer (Agilent N5230c, USA) using co-axial cables for microwave property measurements. Full two-port calibration was performed to remove errors. Two coaxial rectangular wave-guide adapters, filling the fixture cross-section, were used to determine the S-parameters and study the microwave shielding properties of undoped and doped La2NiO4, i.e. LN0, and LN2, for comparative study.
4. Results and discussion
4.1. Phase analysis and crystal structure
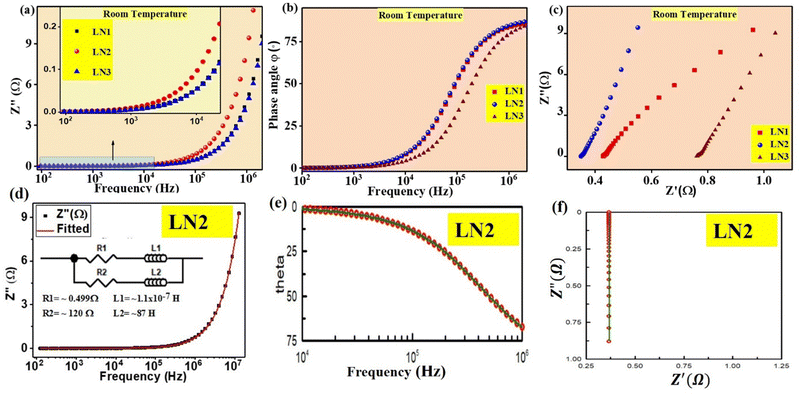
It is well known that calcination temperature has a determinant role in the phase purity and morphology of the powders. Mixtures of raw materials were subjected to calcination at 1200 °C for 8 h. The room temperature diffraction pattern of calcined powders was recorded and is shown in Fig. 1(a). The peaks observed in the XRD pattern of the samples have been indexed using the COD (crystallographic open database) file (1533571) of La2NiO4. Apart from the La2NiO4 peaks, there are a few peaks of very low intensities of raw materials, and a peak of secondary phase LaNiO3 was also observed (at 32°). To eliminate the impurity phases and get the desired single-phase materials, pellets of calcined powders were obtained using a stainless steel die and a hydraulic press. | ||
| Fig. 1 X-ray diffraction patterns of samples LN0–LN3: (a) calcined powders and (b) sintered pellets. In the inset, the magnified view of the highest-intensity peaks is shown. | ||
Pellets made from the calcined powders were sintered at 1500 °C for 12 h. Sintered pellets were cleaned and polished, and their diffraction pattern is shown in Fig. 1(b). Upon comparison with the COD file 1533571 (for La2NiO4), it was found that the peaks corresponding to raw materials and secondary phases have disappeared. Only the peaks of La2NiO4 are present, except for the composition with x = 1.0 (LN3).
In sample LN3 (x = 1.0), impurity peaks of very low intensity of SrCO3 suggest that the solubility limit of Sr in the lattice of La2−xSrxNiO4 solid solution is x < 1.0 under the chosen experimental parameters.
We used the ‘FullProf suite Programme’ to analyze X-ray diffraction patterns using the Rietveld refinement method to determine lattice parameters. For comparing the form of diffraction peaks, we used the pseudo-Voigt function. Furthermore, the background is represented by interpolation between collections of background points up to refinable heights. Throughout the process of refinement, important variables were methodically improved. A number of variables have been refined, including lattice dimensions (a, b, c), thermal attributes (B), scale factor, background properties, half-width parameters, zero correction, and positional coordinates (x, y, z) while the occupancy parameters of all ions remained constant during the process of refinement. For the refinement, a tetragonal crystal structure within the space group (I4/mmm) as reported for La2NiO4 was adopted. In this structure, La/Sr atoms are situated at the 4e (0, 0, z) sites, oxygen atoms O1 and O2 occupied positions at 4c (0.5, 0, 0) and (0, 0.5, 0), and Ni atoms at the 2a (0, 0, 0) position. The refinement pattern was in good agreement with the calculated and experimental diffraction patterns as reported previously.19 The structural parameters obtained after final refinement are presented in Table 1.
| S.N. | Composition | Sample code | Lattice parameters (Å) | c/a | Volume (Å3) | Density ρtheoretical (g cm−3) |
|---|---|---|---|---|---|---|
| 1 | La2NiO4 | LN0 | a = b = 3.851 | 3.269 | 186.697 | 6.934 |
| c = 12.589 | ||||||
| 2 | La1.9Sr0.1NiO4 | LN1 | a = b = 3.855 | 3.286 | 188.304 | 7.135 |
| c = 12.671 | ||||||
| 3 | La1.7Sr0.3NiO4 | LN2 | a = b = 3.866 | 3.292 | 190.247 | 7.228 |
| c = 12.729 | ||||||
| 4 | LaSrNiO4 | LN3 | a = b = 3.867 | 3.289 | 190.196 | 6.955 |
| c = 12.719 | ||||||
From Table 1 it is noticed that the lattice parameters increase with increasing doping concentration, i.e. x. A linear increase in unit cell volume is also observed. A magnified view of the most intense diffraction peaks (013) and (110) is shown in the inset of Fig. 1(b). The position of the peaks shifts towards lower angles with increasing doping concentration (x). This shift signifies an expansion of the unit cell. The reason for the expansion of unit cell volume lies in the comparison of atomic radii of dopant Sr2+ and host La3+ in the same coordination number. The ionic radius of Sr2+ is 1.31 Å whereas that of La3+ is 1.06 Å. Due to the larger atomic radius of Sr2+ in comparison to La3+, the incorporation of Sr2+ ions in the lattice of La2NiO4 at the La3+ ion's site leads to an expansion in the unit cell volume. This result becomes evident through the shift of the diffraction peak towards lower angles, as clearly demonstrated in Fig. 1(b).
For perovskite structures, Goldschmidt's tolerance factor, denoted as “t”, is an indicator of the stability and distortion of crystal structures. The tolerance factor, for A2BO4 structures, is defined as follows:9
 | (1) |
We have calculated the tolerance factor using eqn (1). In the La2−xSrxNiO4 system, the tolerance factor is found within the range of 0.88 (LN0) to 0.97 (LN3), increasing with increasing Sr doping concentration.
4.2. Microstructure analysis
The microstructure and surface morphology of sintered pellets were examined using a bench-top scanning electron microscope (BT-SEM). Fig. 2(a–d) display micrographs of the fractured surfaces at a magnification of 5000×. These micrographs reveal the presence of well-developed grains with cuboidal shapes. Materials of the RP (rock salt and perovskite) type have a unit cell structure in which one dimension, responsible for the stacking of perovskite [ABO3] and rock salt [A–O] structures, is longer than the other two dimensions. In the lattice of the current RP phase of La2−xSrxNiO4, anisotropic thermal expansion is evident, resulting in varying degrees of dilation along different axes, with a more pronounced expansion along the c-axis. This behavior is attributed to the structural diversity of the material. Consequently, the sintering process, involving thermal cycling, can lead to a combination of grain development and anisotropic modifications, potentially resulting in the formation of micro-pores.20,21 From samples LN1 to LN3, upon Sr substitution, there is a significant reduction in pore size, leading to improved structural density and denser ceramics. We have calculated the experimental densities of sintered samples at room temperature with the help of a pycnometer (25 ml capacity), using Archimedes’ principle. The experimental densities for x = 0, 0.1, 0.3, and 1.0 samples were 89.7% (±0.023%), 91.2% (±0.061%), 93% (±0.049%), and 92.7% (±0.095%) respectively. The density values may initially appear similar, however, a visible increase is evident upon incorporation of Sr. | ||
| Fig. 2 SEM images of fractured surfaces of sintered pellets. The amount of Sr-dopant for (a)–(d) is 0, 0.1, 0.3, and 1.0 respectively. | ||
5. Electrical properties
The variation in the negative permittivity in Sr-doped lanthanum nickelate (La2−xSrxNiO4) with changes in temperature and frequency can be understood and explained by analyzing various electrical parameters such as conductivity (σtotal), permittivity ( ), conduction-loss (
), conduction-loss (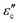 ), and impedance (Z), along with calculated parameters such as carrier concentration (neff) and plasma frequency (ωp). We have described these parameters in detail in the following sections.
), and impedance (Z), along with calculated parameters such as carrier concentration (neff) and plasma frequency (ωp). We have described these parameters in detail in the following sections.
5.1. Negative dielectric constant
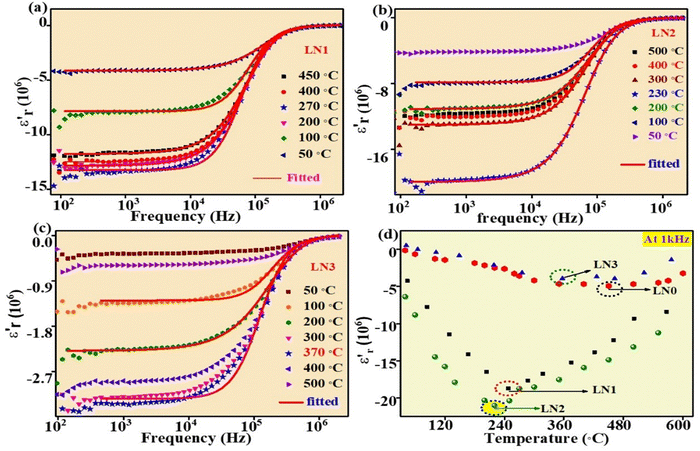
The relative permittivity or dielectric constant ( ) of the samples was measured over a wide range of temperatures, from 30 °C to 600 °C, and frequencies ranging from 20 Hz to 2 MHz as shown in Fig. 3(a–d). It has been observed that the absolute value of the dielectric constant increases with increasing temperature up to a certain point, after which it decreases for all samples. This temperature, where the trend changes, is known as the transition temperature. Additionally, with increasing Sr doping concentration (x), the transition temperature decreases. For the undoped LNO sample (x = 0), the transition temperature was found to be 450 °C. However, in the LN2 sample (x = 0.3), the transition temperature has significantly dropped to 230 °C. In contrast, the magnitude of the dielectric constant increases with increasing doping concentration. These findings demonstrate the influence of Sr doping on the dielectric properties of La2NiO4. In Fig. 3(d) this influence can be further verified by re-plotting the dielectric constant with temperature at a frequency of 1 kHz, which shows a clear trend of decreasing transition temperature with increasing Sr doping. In addition, as the temperature rises, we observe an increase in the dispersion of
) of the samples was measured over a wide range of temperatures, from 30 °C to 600 °C, and frequencies ranging from 20 Hz to 2 MHz as shown in Fig. 3(a–d). It has been observed that the absolute value of the dielectric constant increases with increasing temperature up to a certain point, after which it decreases for all samples. This temperature, where the trend changes, is known as the transition temperature. Additionally, with increasing Sr doping concentration (x), the transition temperature decreases. For the undoped LNO sample (x = 0), the transition temperature was found to be 450 °C. However, in the LN2 sample (x = 0.3), the transition temperature has significantly dropped to 230 °C. In contrast, the magnitude of the dielectric constant increases with increasing doping concentration. These findings demonstrate the influence of Sr doping on the dielectric properties of La2NiO4. In Fig. 3(d) this influence can be further verified by re-plotting the dielectric constant with temperature at a frequency of 1 kHz, which shows a clear trend of decreasing transition temperature with increasing Sr doping. In addition, as the temperature rises, we observe an increase in the dispersion of  (real part of permittivity) with frequency. This trend closely resembles previously reported observations, indicating that the temperature-dependent variations in dielectric constant and dispersion are inherent characteristics of the samples and are not attributable to any artifacts stemming from the sample-electrode contribution.
(real part of permittivity) with frequency. This trend closely resembles previously reported observations, indicating that the temperature-dependent variations in dielectric constant and dispersion are inherent characteristics of the samples and are not attributable to any artifacts stemming from the sample-electrode contribution.
In prior studies, two theoretical models, namely the Drude and Drude–Lorentz models, have been used to fit the experimental data concerning negative permittivity. Researchers have mostly used the Drude model to elucidate the behavior of negative permittivity in metals and semiconductors.22,23
According to this model, the real part of the complex permittivity ( ) is expressed as (2)
) is expressed as (2)
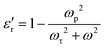 | (2) |
In this equation, ωτ represents the damping factor, which signifies the collision frequency of electrons. On the other hand, ωp stands for the Drude plasma frequency,11 and it is correlated to parameters such as carrier concentration (neff), effective mass (m*), and electronic charge (e) as indicated below:
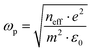 | (3) |
The Drude model (eqn (2)) was fitted to the experimental data points shown in Fig. 3(a–c). The solid line represents the data generated by eqn (2), while the symbols are the experimental data points. The fitting curves closely align with the experimental data points, indicating a good agreement between the experimental and theoretical data points. This suggests that negative permittivity arises from the plasma oscillation of free (delocalized) electrons, a phenomenon typically observed in metals and semiconductors. The values of ωτ and ωp obtained through the fitting process at various temperatures are given in Table 2.
| T (°C) | LN1 | LN2 | LN3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ω τ (MHz) | ω P (GHz) | n eff (m−3) | ω τ (MHz) | ω P (GHz) | n eff (m−3) | ω τ (MHz) | ω p (GHz) | n eff (m−3) | |
| 50 | 1.586 | 20.36 | ∼1.72 × 1017 | 1.359 | 23.69 | ∼1.92 × 1017 | 2.601 | 24.65 | ∼2.11 × 1017 |
| 100 | 1.382 | 20.72 | 0.940 | 24.66 | 2.457 | 24.4 | |||
| 150 | 1.177 | 21.72 | 0.796 | 24.60 | 2.298 | 25.11 | |||
| 200 | 0.986 | 21.77 | 0.736 | 22.71 | 1.870 | 24.77 | |||
| 250 | 0.816 | 22.15 | 0.731 | 22.42 | 1.664 | 22.44 | |||
| 300 | 0.803 | 22.35 | 0.730 | 22.37 | 1.560 | 22.51 | |||
| 350 | 0.851 | 22.18 | 0.756 | 22.21 | 1.4.95 | 21.7 | |||
| 400 | 0.869 | 21.07 | 0.768 | 22.24 | 1.444 | 20.40 | |||
| 500 | 1.002 | 21.43 | 0.899 | 22.14 | 1.513 | 26.32 | |||
| 600 | 1.072 | 20.01 | 1.242 | 22.65 | 1.560 | 26.19 | |||
In the Drude model, ωτ is related to relaxation time, τ (ω = 2π, f = 2π/τ), of the charge carriers. In metals, ωτ increases (τ decreases) with temperature, i.e. it leads to an increase in resistance as temperature rises. However, for the synthesized samples, ωτ is decreasing (τ is increasing) with increasing temperature. The mobility of the electrons is directly proportional to the relaxation time of the electron. The increasing value of τ with temperature indicates an increase in mobility with temperature. In the case of band conduction, mobility decreases with increasing temperature, whereas in the case of hopping conduction, mobility (μ) increases with increasing temperature. Thus, a decreasing value of ωτ with increasing temperature suggests hopping-type conduction in the samples.
With the presumption that m* = m, the values of neff were computed by applying eqn (3) and are given in Table 2. The value of neff is found to increase slowly as the amount of doping increases. An increase in neff eventually leads to an increase in conductivity. The conduction loss (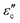 ) is related to direct current conductivity (σdc) by the relation
) is related to direct current conductivity (σdc) by the relation  = σdc/ωεo. At room temperature, the variation of
= σdc/ωεo. At room temperature, the variation of  against frequency for samples is shown in Fig. 4. We can see that on increasing Sr concentration,
against frequency for samples is shown in Fig. 4. We can see that on increasing Sr concentration,  increases.
increases.
Table 3 summarizes the value of  at two different frequencies. The values reported in Table 3 are approximately 5 orders by magnitude higher than the values reported in the literature.4 Cheng et al. reported strong electromagnetic shielding properties in carbon/Si3N4 due to huge impedance mismatching caused by the high value of negative permittivity and dielectric loss.24,25 High values of
at two different frequencies. The values reported in Table 3 are approximately 5 orders by magnitude higher than the values reported in the literature.4 Cheng et al. reported strong electromagnetic shielding properties in carbon/Si3N4 due to huge impedance mismatching caused by the high value of negative permittivity and dielectric loss.24,25 High values of 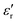 and
and  make these materials suitable for electromagnetic shielding and microwave absorption applications.
make these materials suitable for electromagnetic shielding and microwave absorption applications.
| Samples | Frequency | |
|---|---|---|
| 1 kHz | 1 MHz | |
| LN1 | 0.6 × 1010 | 2 × 107 |
| LN2 | 11 × 1010 | 7 × 107 |
| LN3 | 3 × 1010 | 2.1 × 107 |
The observed values of  mentioned in Table 3 are further confirmed by the study of electrical conductivity, discussed in the subsequent section.
mentioned in Table 3 are further confirmed by the study of electrical conductivity, discussed in the subsequent section.
5.2. Electrical conductivity
AC conductivity (σac) has been calculated using the measured values of capacitance (C) and dissipation factor (D) in the temperature and frequency ranges that are mentioned above. The relationship between σac and frequency at some distinct temperatures is presented in Fig. 5(a–c). At low frequencies (up to 100 kHz), σac remains constant and independent of frequency. However, at higher frequencies, σac diminishes with increasing frequency. This phenomenon is primarily attributed to the skin effect observed, particularly in metallic materials. The skin effect is a phenomenon that arises at high frequencies, in which alternating current (AC) mostly flows in the outermost layer of a conductor. As the frequency increases, resistance also increases. This happens as a consequence of the AC-inducing self-generated magnetic fields, which lead to electron concentration close to the surface of the conductor. Hence, at higher frequencies, electric current flows near the surface of the conductor. This results in an increase in resistance and a decrease in the effective cross-sectional area available for current conduction. The penetration of the current at the surface is known as the “skin depth”. The skin depth is inversely proportional to the square root of the frequency and directly proportional to the square root of the resistivity of the material.According to the Drude model, AC conductivity of metals can be expressed as13
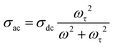 | (4) |
By fitting eqn (4) to the experimental points in Fig. 5, we have determined the values of DC conductivity (σdc) and ωτ at different temperatures for all the samples. These results are shown in Table 4.
| Temperature (°C) | LN1 | LN2 | LN3 | |||
|---|---|---|---|---|---|---|
| σ dc (S m−1) | ω τ (MHz) | σ dc (S m−1) | ω τ (MHz) | σ dc (S m−1) | ω τ (MHz) | |
| 100 | 62 | 0.837 | 54 | 0.98 | 17 | 2.54 |
| 200 | 67 | 0.705 | 77 | 0.94 | 21 | 2.29 |
| 300 | 66 | 1.44 | 75 | 0.799 | 24 | 1.87 |
| 400 | 65 | 0.869 | 70 | 0.760 | 23 | 1.74 |
| 500 | 63 | 1.38 | 64 | 0.898 | 20 | 1.55 |
From Table 4 it is clear once again that ωτ decreases with increasing temperature as reported in Table 3. DC conductivity increases with increasing temperature up to a particular temperature (transition temperature) and above this temperature it starts decreasing. Every composition displays an obvious transition in electrical conduction characteristics from semiconductor-type to metal-type, which is similar to previously reported results.26 The electrical conductivity increases with measuring temperature through a maximum transition temperature and then decreases with the further increase of temperature.
In Fig. 6, a graph depicting the log of σdc plotted against 1000/T shows a linear increase in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σdc with the inverse of temperature. This linear behaviour suggests that conductivity obeys the Arrhenius relation as given below:
σdc with the inverse of temperature. This linear behaviour suggests that conductivity obeys the Arrhenius relation as given below:
| σdc = Ae−Ea/kBT | (5) |
 | ||
| Fig. 6 (a–c) Variation of the logarithm of DC conductivity with the inverse of temperature. The activation energy (Ea) of the samples was calculated from the slope of the straight-line fit. | ||
For all compositions, using linear fitting of the measured data (below the transition temperature) the value of the slope was computed, and hence the activation energy. The value of the activation energy for all the samples is shown in their respective plot. The value of activation energy, i.e., the energy needed for the charge carrier to pass through the energy barriers caused by the defects, was minimum for sample LN2 and maximum for LN3. The observed activation energy aligns with values reported by other researchers, suggesting that the “small-polaron hopping mechanism” may be possible in La2NiO4 oxide.27,28 For the composition LN2, we have observed the maximum conductivity of about ∼79 Ω−1 m−1 at 230 °C (transition temperature) which is at least three times higher than that of the undoped LN0. A similar behavior is observed for other compositions as well at different transition temperatures, confirming the intrinsic behavior of Sr doped and undoped layered lanthanum necklets.
According to defect chemistry, the replacement of La by a lower valence element such as Sr would result in either the generation of electron/holes at the nickel site or the change in oxygen content or change in the valence state of nickel,20,29 as described by the below equations:
 | (6) |
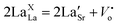 | (7) |
 | (8) |
It is reported that La2NiO4 is a p-type conductor.27 If charge compensation occurs according to eqn (6), doping of Sr will generate more charge carriers, and hence conductivity will increase. On the other hand, a decrease in the activation energy with increasing Sr content is possible due to an increase in the number of hopping sites. An increase in the hopping sites may be possible on partial oxidation of Ni2+ to Ni3+.
6. XPS analysis
To reveal valence states for the constituent elements (La, Ni, Sr, and O) in La2−xSrxNiO4, X-ray photoelectron spectroscopy (XPS) was used. The survey scan data for La2NiO4 are presented in Fig. 7(a), revealing particular peaks corresponding to the elements La (3d), Ni (2p), Sr (3d), and O (1s) only. To establish binding energies, the C 1s peak at 285 eV was employed as a reference. Core level spectra for Ni 2p, La 3d, Sr 3d, and O 1s are depicted in Fig. 7(b–e). These core level peaks were fitted using the Shirley function. | ||
| Fig. 7 The XPS spectrum: (a) survey scan, (b) core level spectra of Ni (2p), (c) core level spectra of La (3d), (d) core level spectra of Sr (3d), and (e) core level spectra of O (1s). | ||
In Fig. 7(b), the XPS spectra of Ni for various compositions reveal two distinct peaks at 855.2 eV and 851.6 eV. These peaks can be attributed to the characteristic peaks of Ni 2p3/2 and the satellite peak, respectively. This observation suggests that the chemical state of nickel is predominantly Ni2+ in LN0, in agreement with previous reports.6 However, for LN1 and LN2, the presence of Ni3+ is confirmed, as indicated by the presence of two peaks around 872 eV, corresponding to Ni3+ states. As Sr increases, the concentration of Ni3+ increases.
The XPS spectra of La 3d for LN0, LN1, and LN2 are presented in Fig. 7(c) and they primarily exhibit the spin–orbit splitting of La 3d5/2 and 3d3/2, as previously reported.30 In the synthesized samples, the characteristic peaks of 3d5/2 are centered at 834.28 eV and 838.29 eV, while the peaks of 3d3/2 are located around 851.53 eV and 855.14 eV. These findings strongly suggest that lanthanum in all the samples is predominantly in the La3+ state.
The core–shell XPS spectrum of Sr 3d is shown in Fig. 7(d) and it mainly consists of the spin–orbit splitting of Sr 3d into Sr 3d5/2 and Sr 3d3/2 respectively. For both the samples LN1 and LN2, the representative peaks of Sr 3d5/2 are around 133 eV and for Sr 3d3/2 around 134 eV respectively confirming that the valence state of Sr is +2 in both the samples.31
Conversely, in the XPS spectra of O (1s) depicted in Fig. 7(e), a single peak is discerned, which can be further deconvoluted into three distinct peaks. These peaks have been attributed to different oxygen species. The lower binding energy peak, located at approximately 528.3 eV, corresponds to OH− adsorption, whereas the peak at 531 eV belongs to lattice oxygen. The increase in the intensity of the peak corresponding to OH− adsorption on increasing the concentration of Sr at 528 eV is because Sr2+ is more prone to OH− adsorption than La3+. These results show that charge compensation on doping Sr at the La site is occurring by conversion of a partial amount of Ni2+ into Ni3+ state, according to eqn (8).
7. Impedance analysis
The “reactance” is a key parameter that helps us understand the phase relationships between current and voltage when an alternating electric field is applied. Based on the sign of the reactant, we can differentiate a capacitor and an inductor. When voltage lags behind the current, we observe a negative reactance, indicating the capacitive nature of the material. Conversely, a positive reactance suggests inductive characteristics, where the current phase lags behind the voltage phase. This subtle polarity in reactance holds significance for comprehending and utilizing material electrical properties, making it relevant in various research and technological applications.11,13,32,33There was a corresponding relation between permittivity and reactance:
 | (9) |
Fig. 8(a) shows the frequency dependence of reactance for samples with different amounts of Sr-dopant at room temperature. The reactance displayed an escalating trend with the increase in frequency. For La2−xSrxNiO4 ceramics (where x varies from 0 to 1), it was observed that the reactance remained consistently positive across the entire range of test frequencies. Furthermore, the corresponding real permittivity exhibited a negative value, attributed to the occurrence of plasmonic oscillations. A similar behavior was observed by many researchers.34
Meanwhile, Fig. 8(b) gives the frequency dependence of the impedance phase angle for samples with different Sr-dopants. The positive phase angle suggests that the phase relationship between voltage and current in epsilon-negative samples is different from that in positive permittivity materials. With Sr-dopant increasing, the ceramics exhibit a higher phase angle.
As indicated in Fig. 8(c), the variation of Z′′ with Z′ also confirms that the reactance is positive. The value of Z′ at the lowest frequency (represented by the intercept on the x-axis) decreases as the Sr concentration increases. It is important to clarify that Z′ signifies DC resistance, and this decrease in the value with increasing Sr concentration suggests that the samples are exhibiting a more pronounced inductive behavior. In other words, the inductive characteristic was responsible for negative permittivity from the perspective of impedance property.11
Here, it is important to note that the possibility of stray inductance provided by the sample holder and its connecting wires may unwittingly contribute to the experimentally observed impedance values since the total measured impedance values are small in magnitude. Therefore, it is necessary to take this into account and separate the unintentional contribution caused by the sample holder's impedance from experimentally collected data before analyzing the reactance behavior of the synthesized samples.
For this purpose, different combinations of resistors and inductors were tried to model and simulate the experimentally measured impedance data using Z-view simulation software. For sample LN2, the equivalent circuit as shown in the inset of Fig. 8(d) is found to be the most suitable circuit to represent the experimentally measured impedance data. Further, the obtained results were validated through complex fitting in Origin Pro17. In Fig. 8(d), the values of R1, R2, L1, and L2 were obtained from complex impedance data fitting of the equivalent circuit. Fig. 8(e and f) is the simulated version of the same data using Z-View software.
For other samples, similar processes were used and the findings are summarized in Table 5. It is observed that the values of R1 and L1 are very small compared to R2 and L2 values. Therefore we have assigned R1 and L1 to the contribution from the wires and sample holder and R2 and L2 to the contributions from our samples. Negative dielectric behavior is caused by plasmonic oscillations of free charge carriers. The plasmonic oscillation of these charge carriers in an applied sinusoidal electric field gives rise to surface current. The origin of the sample's inductive behavior (L2) can be attributed to this current on the surface of the sample. The resistance (R2) can be attributed to the resistance offered to this circulating current on the grains’ surface and/or resistance offered to the conduction current within/through the grains.
| Sample | R1 (mΩ) | L1 (μH) | R2 (Ω) | L2 (H) |
|---|---|---|---|---|
| LN1 | 4.23 | 10 | 191 | 62 |
| LN2 | 4.17 | 11 | 120 | 87 |
| LN3 | 4.11 | 11 | 147 | 23 |
Furthermore, our materials with negative permittivity offer significantly higher inductance (∼87 H) compared to conventional wire-wound inductors. Therefore, exploring negative permittivity materials holds great research potential for developing coil-less electric inductors.35
8. Microwave shielding effectiveness analysis
The effectiveness of electromagnetic interference (EMI) shielding relies on three primary mechanisms: reflection, absorption, and multiple internal reflection.36 EMI shields primarily reflect radiation, utilizing charge carriers that interact with EM fields, thus requiring high electrical conductivity. Absorption of electromagnetic radiation is facilitated by interactions with electric/magnetic dipoles, electrons, and phonons. Multiple internal reflections within the material significantly contribute to EMI shielding effectiveness, stemming from scattering centers, interfaces, or defect sites, resulting in multiple scattering and EM wave absorption. The total shielding effectiveness (SET) includes shielding due to reflection (SER) arising from an impedance mismatch between air and the shielding material, while shielding due to absorption (SEA) dissipates electromagnetic microwaves in the shield. The absorption of EM energy (SEM) correlates with multiple internal reflections.The total shielding effectiveness (SET) would be given by37
| SET = SEA + SER + SEM | (10) |
When the total shielding effectiveness of the material is more than 10 dB, then loss due to multiple reflections (SEM) becomes negligible and can be neglected.38
Thus, the total shielding effectiveness (SET) now can be expressed as
| SET = SEA + SER | (11) |
 | (12) |
 | (13) |
Fig. 9(a) represents the material under test (MUT). Fig. 9(b–d) illustrates the variation of different microwave shielding parameters SER, SEA, and SET in the frequency range of 8–13 GHz. Fig. 9(b) reveals that the reflection phenomena dominate the shielding mechanism. The total shielding effectiveness (SET) is approximately −15 dB for sample LN0 and about −47 dB for sample LN2, i.e. 99.99% microwave absorption at 8.54 GHz with a matching thickness of only 2 mm, which is higher than previously reported data.18
This increase in SER or the total effective shielding parameter, SET (=SEA + SER), for the LN2 sample in comparison with LN0 may be attributed to the higher conductivity, resulting from the presence of higher density of plasmons (surface delocalized electrons). The high conductivity of the material results in a significant impedance mismatch with the surrounding air,25 and reduces the skin depth  of the material. The combination of high impedance mismatch at the interface with incident electromagnetic fields and reduced skin depth enhances the material's ability to effectively reflect and attenuate microwave radiation.
of the material. The combination of high impedance mismatch at the interface with incident electromagnetic fields and reduced skin depth enhances the material's ability to effectively reflect and attenuate microwave radiation.
Similarly, to provide an inclusive understanding of the shielding effectiveness of the samples at lower frequencies as well, Fig. 10 further examines their total shielding effectiveness in the 1–2 MHz region. SET for sample LN0 is about −11 dB to –15 dB and for LN2 is between −41 and −45 dB. These frequency ranges are crucial for assessing the effectiveness of the shield in practical electromagnetic interference shield developments.
 | ||
| Fig. 10 Variation of total microwave shielding effectiveness (SET) with frequency (1–2 MHz) of LN0 and LN2 samples. | ||
It is important to mention that the desired EMI shielding effectiveness for commercial applications is approximately 20 dB, which corresponds to equal to or less than 1% transmittance of electromagnetic waves. Hence, there is an expectation that our improved material could be more suitable for various commercial applications.
9. Conclusion
In this paper, we have tried to establish the correlation between electrical conductivity and negative dielectric constant. Single-phase Sr-doped La2NiO4 was successfully synthesized using the solid-state reaction method. Examination of the SEM image verified the irregular growth of cuboidal-shaped grains. The real part of permittivity consistently exhibited negative values across all tested frequencies and temperatures. The experimental data points were well-fitted by the Drude model, and this negative permittivity behavior was attributed to the plasma oscillation of free charge carriers. The lower activation energy (Ea) for DC conduction indicated a small polaron hopping conduction mechanism. Positive values of the imaginary part of impedance (Z′′) confirmed inductive behavior across the entire range of temperature and frequency measurements. The microwave studies indicate a prominent rise in total shielding effectiveness (SET) upon the incorporation of Sr (LN2) compared to the undoped sample (LN0).It can be inferred from the observations that a higher magnitude of electrical conductivity leads to a larger negative permittivity, which in turn causes a stronger impedance mismatch. This results in an increase in the total shielding effectiveness (SET) value of the samples. This outcome signifies the potential to tune and modify the microwave shielding properties by compositional modification for a variety of applications.
Data availability
The raw/processed data required to reproduce these findings cannot be shared at this time as the data also form part of an ongoing study.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors are grateful to the Head, Department of Physics, and the Coordinator, CIFC, IIT(BHU), Varanasi, for providing experimental facilities. The author Mr Tarun Katheriya is also thankful to the Ministry of Education and the Council of Scientific & Industrial Research (CSIR) for the fellowship to carry out this work, which are bodies of the Government of India, New Delhi, India.References
- V. G. Veselago, Phys.-Usp., 1968, 10, 509–514 CrossRef.
- P. Xie, Z. Shi, M. Feng, K. Sun, Y. Liu, K. Yan, C. Liu, T. A. A. Moussa, M. Huang, S. Meng, G. Liang, H. Hou, R. Fan and Z. Guo, Adv. Compos. Hybrid Mater., 2022, 5, 679–695 CrossRef.
- G. Fan, P. Xie, Z. Wang, Y. Qu, Z. Zhang, Y. Liu and R. Fan, Ceram. Int., 2017, 43, 16980–16985 CrossRef CAS.
- K. L. Yan, R. H. Fan, M. Chen, K. Sun, L. W. Yin, H. Li, S. B. Pan and M. X. Yu, J. Alloys Compd., 2015, 628, 429–432 CrossRef CAS.
- G. Fan, K. Sun, Q. Hou, Z. Wang, Y. Liu and R. Fan, EPJ Appl. Metamater., 2021, 8 DOI:10.1051/epjam/2021005.
- X. Ye, S. Dong, X. Jin, J. Wei, L. Wang and Y. Zhang, Coatings, 2022, 12 DOI:10.3390/coatings12111739.
- K. Sun, P. Yang, Q. He, R. Fan, Z. Wang, J. Tian, X. Yang, W. Duan, X. Wu and Z. Wang, Ceram. Int., 2022, 48, 8417–8422 CrossRef CAS.
- K. Yan, L. Shen, R. Fan and N. Bao, J. Mater. Sci., 2021, 56, 10183–10190 CrossRef CAS.
- G. Nirala, D. Yadav, T. Katheriya and S. Upadhyay, J. Eur. Ceram. Soc., 2022, 42, 453–461 CrossRef CAS.
- S. Mno, J. Mater. Sci., 2022, 57, 15862–15875 CrossRef.
- G. Fan, Z. Wang, K. Sun, Y. Liu and R. Fan, J. Mater. Chem. C, 2020, 8, 11610–11617 RSC.
- G. Fan, Z. Wang, K. Sun, Y. Liu and R. Fan, J. Mater. Sci. Technol., 2021, 61, 125–131 CrossRef CAS.
- T. Katheriya and S. Upadhyay, Phys. Scr., 2023, 98 DOI:10.1088/1402-4896/acf967.
- V. V. Kharton, A. P. Viskup, E. N. Naumovich and F. M. B. Marques, J. Mater., 1999, 9, 2623–2629 RSC.
- V. V. Vashook, I. I. Yushkevich, L. V. Kokhanovsky, L. V. Makhnach, S. P. Tolochko, I. F. Kononyuk, H. Ullmann and H. Altenburg, Solid State Ionics, 1999, 119, 23–30 CrossRef CAS.
- K. Zakharchuk, A. Bamburov, E. N. Naumovich, M. A. Vieira and A. A. Yaremchenko, Processes, 2021, 10, 82 CrossRef.
- A. R. Gilev, E. A. Kiselev, D. M. Zakharov and V. A. Cherepanov, J. Alloys Compd., 2018, 753, 491–501 CrossRef CAS.
- S. Liu, Y. Cheng, J. He, S. Yan, H. Luo and L. Deng, Front. Mater., 2020, 7 DOI:10.3389/fmats.2020.00271.
- M. Saleem, D. Singh, A. Mishra and D. Varshney, Mater. Res. Express, 2018, 6 DOI:10.1088/2053-1591/aaecf7.
- K. Zakharchuk, A. Kovalevsky and A. Yaremchenko, Materials, 2023, 6(4), 1755 CrossRef.
- G. Nirala, D. Yadav and S. Upadhyay, J. Adv. Ceram., 2020, 9, 129–148 CrossRef CAS.
- P. Drude, Ann. Phys., 1900, 306, 566–613 CrossRef.
- X. Yao, X. Kou, J. Qiu and M. Moloney, J. Phys. Chem. C, 2016, 120, 4937–4944 CrossRef CAS.
- C. Cheng, K. Yan, R. Fan, L. Qian, Z. Zhang, K. Sun and M. Chen, Carbon, 2016, 96, 678–684 CrossRef CAS.
- C. Cheng, R. Fan, Z. Wang, Q. Shao, X. Guo, P. Xie, Y. Yin, Y. Zhang, L. An, Y. Lei, J. E. Ryu, A. Shankar and Z. Guo, Carbon, 2017, 125, 103–112 CrossRef CAS.
- K. Ishikawa, W. Shibata, K. Watanabe, T. Isonaga, M. Hashimoto and Y. Suzuki, J. Solid State Chem., 1997, 131, 275–281 CrossRef CAS.
- W.-H. Jung, J. Mater., 2013, 1–6 CrossRef.
- X. Ma, Y. Gao, B. Yang, X. Lou, J. Huang, L. Ma and D. Jing, Nanoscale, 2022, 7083–7095 CAS.
- D. H. Hop, R. B. K. Chung, Y. W. Heo, J. J. Kim and J. H. Lee, J. Korean Ceram. Soc., 2020, 57, 416–422 CAS.
- P. Swetha, R. Aswini, M. Binesh, M. S. Muhammed, K. Sridharan and S. Swaminathan, Mater. Today Commun., 2023, 34, 105287 CrossRef.
- J. L. Ortiz-Quiñonez, L. García-González, F. E. Cancino-Gordillo and U. Pal, Mater. Chem. Phys., 2020, 246 DOI:10.1016/j.matchemphys.2020.122834.
- Z. Wei, Z. Wang, G. Fan, C. Xu, G. Shi, G. Zhang, Y. Liu and R. Fan, Ceram. Int., 2021, 47, 2208–2213 CrossRef CAS.
- C. Deng, Y. Li, H. Wang, Y. Qu, X. Qi, Z. Peng, Z. Chen, H. Shen, K. Sun and R. Fan, Ceram. Int., 2023, 49, 16149–16155 CrossRef CAS.
- Y. Wu, Z. Wang, X. Liu, X. Shen, Q. Zheng, Q. Xue and J. K. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 9059–9069 CrossRef CAS PubMed.
- G. Nirala, T. Katheriya, D. Yadav, H. Verma and S. Upadhyay, Emergent Mater., 2023, 6, 1951–1962 CrossRef CAS.
- G. Kulkarni, P. Kandesar, N. Velhal, V. Phadtare, A. Jatratkar, S. K. Shinde, D. Y. Kim and V. Puri, Chem. Eng. J., 2019, 355, 196–207 CrossRef CAS.
- S. W. Phang, T. Hino, M. H. Abdullah and N. Kuramoto, Mater. Chem. Phys., 2007, 104, 327–335 CrossRef CAS.
- T. K. Gupta, B. P. Singh, V. N. Singh, S. Teotia, A. P. Singh, I. Elizabeth, S. R. Dhakate, S. K. Dhawan and R. B. Mathur, J. Mater. Chem. A, 2014, 2, 4256–4263 RSC.
- C. Y. Tsay, Y. H. Huang and D. S. Hung, Ceram. Int., 2014, 40, 3947–3951 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |