Mechanism of isosymmetric polar order–disorder phase transition in pyroelectric [CH₃CH₂NH₃]₂NaGa(HCOO)₆ double perovskite

Abstract

Recently, hybrid double-perovskite structures have attracted attention due to their versatile multifunctional properties originating from the variety of different constituent units in these materials. Here, we report the synthesis and comprehensive multitechnique characterization of a novel hybrid double-perovskite formate-based material [CH₃CH₂NH₃]₂NaGa(HCOO)₆. The heat capacity measurements indicate that this compound has a structural phase transition at 379 K. In the low-temperature phase, the compound crystallizes in the non-centrosymmetric polar Pn structure, which exhibits a long-range order of ethylammonium (EA⁺) cations. Surprisingly, the Pn space group is not affected by the transition to the high-temperature disordered phase, which indicates that the transitions are isosymmetric making this compound a unique member of the formate-based double-perovskite family. The presence of the second-harmonic generation response in both phases confirms their non-centrosymmetric nature, while the dielectric spectroscopy experiments reveal that the transitions have a continuous order–disorder character. The observation of the pyroelectric current, but the absence of the electric polarization switching indicate that this compound is not properly ferroelectric. The electron paramagnetic resonance experiments of a compound slightly doped with paramagnetic Fe³⁺ impurities confirm the continuous character of the transition and allow us to probe the EA⁺ cation and framework dynamics in this system. The vibrational spectroscopy data confirm that the phase transition is primarily driven by the progressive ordering of EA⁺ cations and the resulting changes in the hydrogen bond strength. The temperature-dependent luminescence studies show that the [EA]₂NaCr_0.931Ga_0.069(HCOO)₆ perovskite is a promising material for noncontact temperature monitoring.

---

Introduction

Recently, three-dimensional (3D) hybrid organic–inorganic perovskite materials with the formula AM^IIX₃ (A⁺ denotes a protonated amine, M^II – a divalent metal ion, and X⁻–a small organic linker) have gained significant attention due to their structure-based multifunctionalities.^1–5 In some hybrid perovskites, a few intriguing physical phenomena can simultaneously coexist making them appealing for a wide range of applications.^2,5–7 In particular, the simplest halide 3D lead-based perovskites comprising the smallest organic cations, including methylammonium (MA⁺),^8–10 fluoromethylammonium (FMA⁺),¹¹ formamidinium (FA⁺),^12–14 methylhydrazinium (MHy⁺),^15,16 and aziridinium (AZR⁺),¹⁷ exhibit excellent optical properties for optoelectronic photovoltaic, light emitting, and lasing applications, including tuneable bandgaps, second-harmonic generation (SHG), excitonic emission, long carrier diffusion lengths, high mobility, and high absorption coefficients.^1,5,18,19 Due to a rather scarce choice of molecular cations forming 3D lead halide perovskites and lead toxicity, perovskites with other metal ions and longer organic linkers, such as formates, hypophosphites, azides, cyanides, and dicyanamides, are of considerable relevance.^6,20

Order–disorder phase transitions (PT) are a common feature in these materials, and they are usually connected with the emergence of phenomena related to the loss of the inversion centre.^21–26 The organic cation A⁺ is often involved in the ordering due to the interaction with the 3D framework via a network of N–H⋯X hydrogen bonds (HBs).^20,21,23

Because of their remarkable ferroelectric, multiferroic, dielectric, magnetic, and optical properties, formate perovskites containing divalent metal ions M^II are the most researched group.^6,20–26 Only formates, azides, and cyanides are capable of forming the A₂M^IM^IIIX₆ double-perovskite structure, which is comprised of an equimolar ratio of monovalent (M^I) and trivalent (M^III) metal ions arranged into an alternately propagating 3D framework of ligand-connected octahedra.^27,28

There are several members of the A₂M^IM^III(HCOO)₆ family, where A⁺ = ammonium (AM⁺), hydrazinium (Hy⁺), MA⁺, dimethylammonium (DMA⁺), ethylammonium (EA⁺), imidazolium (IM⁺), and guanidinium (GA⁺) cations, M^I = Na⁺, K⁺, and M^III = Al³⁺, Cr³⁺, and Fe³⁺.^27–32 Order–disorder PTs have only been reported for DMA⁺ and EA⁺ analogues, and the latter compounds have received significant attention due to the density functional theory (DFT) calculations and experimental findings suggesting the presence of ferroelectricity²⁹ and polarization enhancement under high pressure.^33,34 Its existence, however, has never been proven experimentally for double-perovskite formates.

All known [EA]₂NaM^III(HCOO)₆ members (M^III = Al³⁺, Cr³⁺, and Fe³⁺) exhibited PT in the 361–369 K range when heated from the low-temperature (LT) non-centrosymmetric and polar phase Pn to the high-temperature (HT) centrosymmetric phase P2₁/n. In the HT phase, the EA⁺ cations are disordered, and the arrangement of dipole moments prevents the occurrence of polar order.^28–30 Furthermore, the presence of Cr³⁺ ions in the structure predisposes the aforementioned materials to be used as luminescent thermometers, with the crystal field strength being dependent on the applied metal ion ratio.²⁷ We recently demonstrated [EA]₂NaCr(HCOO)₆ as a sensitive thermometer with low operating temperatures.²⁷

This work is focused on the structural, dielectric, electric, optical, and phonon properties of a novel analogue, [EA]₂NaGa(HCOO)₆. We show that, despite various similarities, the physicochemical properties of this compound stand out in the group, primarily because the HT phase is also polar. As an outcome, the compound displays an extremely rare order–disorder polar–polar PT, which has been reported among formate perovskites only for the subgroup of [MHy]M^II(HCOO)₃ (M^II = Fe, Mg, Mn, and Zn).³⁵ The mechanism of this unusual PT is discussed. The investigated perovskite can be used as a non-linear optical switch and a luminescent thermometer.

Experimental

Materials and synthesis

The crystals of [EA]₂NaGa(HCOO)₆ (1) were synthesized using the solvothermal method described earlier for [EA]₂NaCr_xAl_1−x(HCOO)₆.²⁷ All chemicals were purchased and used without further purification. To synthesize 1, a mixture of ca. 4 mmol (ca. 1.5 g) of Ga(NO₃)₃·XH₂O (Sigma Aldrich, 99.9%), 4 mmol (0.3262 g) of ethylamine hydrochloride (Sigma Aldrich, 98%), and 8 mmol (0.5441 g) of sodium formate (Sigma Aldrich, 99%) was dissolved in 10 mL of distilled water. Next, 25 mL of N-ethylformamide (Sigma Aldrich, 99%) and 5 mL of concentrated formic acid (Avantor Poland, 98–100%) were added. The solution was sealed in a Teflon-line autoclave and heated at 140 °C for 24 hours. The obtained liquid was then allowed to slowly evaporate at room temperature (RT). After two days, the crystals were separated, washed with 10 mL of anhydrous methanol (Sigma-Aldrich, 99.8%), and dried in air.

Despite attempts to synthesize a mixed sample with a composition of 25 mol% Cr³⁺ and 75 mol% Ga³⁺, a sample with much more chromium crystallized. The EDS tests confirmed that we were only able to synthesize a sample composed of ca. 6.9 mol% Ga³⁺ and 93.1 mol% Cr³⁺ ions, namely [EA]₂NaCr_0.931Ga_0.069(HCOO)₆ (2).

To get more information on the framework contribution to the mechanism of PT, an additional sample comprising a small amount (ca. 0.01 mol%) of paramagnetic Fe³⁺ ions (3) was prepared in the same manner.

X-ray diffraction

The single crystal of 1 was mounted on a CCD Xcalibur diffractometer (graphite monochromatic, MoKα radiation, λ = 0.71073 Å) at 293(2) K and 391(2) K. The corrections to the Lorentz and polarization factors were applied to the reflection intensities. The structures were solved by direct methods applying the SHELX program. The H atoms were determined from the geometric concepts and refined in a riding model with isotropic temperature factors 1.2 times the U_eq value of the parent atom. All non-hydrogen atoms were located from difference Fourier synthesis and refined by the least squares method in the full-matrix anisotropic approximation. The crystallographic data for 1 and details of the X-ray experiment are collected in Table S1 (ESI†). The structure drawings in the ESI† were prepared by using OLEX program.³⁶

The CCDC deposits 2254366 (293 K) and 2254367 (391 K) contain the supplementary crystallographic data for 1.† These data can be obtained free of charge at https://www.ccdc.cam.ac.uk/structures.

Powder X-ray diffraction patterns of 1, 2, and 3 were collected using an X’Pert Pro X-ray diffraction system fitted with a PIXcel detector, a focusing mirror, and Soller slits for CuKα radiation (λ = 1.54056 Å). Fig. S1 (ESI†) presents a comparison of experimental patterns with a simulated pattern based on structure refinement for 1 at 293 K.

Differential scanning calorimetry (DSC)

The heat capacity of 1 was measured from RT to 400 K using a Mettler Toledo DSC-1 calorimeter with a high resolution of 0.4 μW. Nitrogen was used as a purging gas, and the heating and cooling rates were 5 K min⁻¹. The mass of the measured sample was 6.1 mg. The excess heat capacity associated with the PT was calculated by subtracting from the data a baseline representing the system variation in the absence of PTs.

Second harmonic generation (SHG)

SHG properties were studied using a laser system Coherent Astrella Ti:Sapphire regenerative amplifier providing femtosecond laser pulses (800 nm, 75 fs) at a 1 kHz repetition rate. The laser fluence at the sample was set to 0.28 mJ cm⁻². The single crystals of 1 were crushed with a spatula and sieved through an Aldrich mini-sieve set, collecting a microcrystal size fraction of 88–125 μm. Next, size-graded sample of 1 was fixed in-between microscope glass slides to form a tightly packed layer, sealed, and mounted to the horizontally aligned sample holder. No refractive index matching oil was used. The employed measurement setup operates in the reflection mode. Specifically, the laser beam was directed onto the sample at 45 degrees to its surface. Emission collecting optics consisted of a Ø25.0 mm plano-convex lens of focal length 25.4 mm mounted on the 400 μm 0.22 NA glass optical fiber and was placed along the normal to the sample surface. The distance between the collection lens and the sample was equal to 30 mm. The spectra of SHG responses were recorded using an Ocean Optics Flame T XR fiber-coupled CCD spectrograph with 200 μm entrance slit. Scattered pumping radiation was suppressed with the use of a Thorlabs 700 nm hard-coated short-pass dielectric filter. The temperature-dependent SHG study was performed in the 353–403 K range using a Linkam LTS420 Heating/Freezing Stage. Temperature stability was equal to 0.1 K. Kurtz–Perry powder tests were performed at 293 K, using potassium hydrogen phosphate of the same particle size as the SHG reference.

Electronic paramagnetic resonance (EPR) studies

The X-band (9.5 GHz) EPR experiments of the sample 3 were performed using a Bruker ELEXSYS E580 EPR spectrometer. For the EPR measurements, the crystal samples of [EA]₂NaGa(HCOO)₆:Fe were ground into a fine powder. For the continuous-wave (CW) EPR experiments, we used 8 G and 100 kHz field modulation. The microwave power was adjusted to avoid saturation of the EPR signal. The pulsed EPR experiments were performed using 32 ns π-pulse duration. The echo-detected field sweep (EDFS) spectra were recorded using a Hahn echo pulse sequence (π/2–τ–π–τ–echo) with an interpulse delay τ of 200 ns and two-step phase cycling. The three-pulse electron spin echo envelope (ESEEM) time traces were obtained by integrating the echo obtained using the stimulated echo pulse sequence (π/2–τ–π/2–τ′–π/2–τ–echo) with the four-step phase cycling, where the interpulse delay τ′ was incremented by a time step of 8 ns. A stretched exponential function was used for background correction.

Dielectric measurements

Dielectric spectroscopy experiments of single crystal and pressed pellet samples of 1 were performed in the 20–10⁶ Hz frequency range using an HP4284A LCR meter. The flat capacitor model was used to calculate the complex dielectric permittivity from the measured capacitance and dielectric loss tangent. Silver paste was used for sample electrodes. Temperature-dependent dielectric spectra were measured on cooling at a rate of 1 K min⁻¹.

Pyrocurrent measurements

For the pyrocurrent measurements, the pellet sample of 1 was poled with 50 VDC and cooled down through the PT from 400 K to RT. Afterwards, the poling voltage was removed and the sample was shorted. The pyrocurrent was measured using a 6514 Keithley electrometer during heating at a rate of 1 K min⁻¹.

Electric polarization measurements

An Aixact instrument was used to measure the electric field-dependent electric polarization of a pellet sample of 1. A periodic triangular signal with a frequency of 100 Hz was used for the measurements. A high voltage was obtained using a Trek 609E6 voltage amplifier.

Vibrational measurements

RT Raman spectra in the range of 3600–80 cm⁻¹ of 1 and 2 were measured using a Bruker FT-Raman RFS 100/S spectrometer with a 1064 nm excitation line (YAG:Nd).

The temperature-dependent IR spectra of 1 in the 3250–675 cm⁻¹ range were measured using a Nicolet iN10 FTIR microscope and a Linkam THMS600 stage equipped with ZnSe windows.

Optical measurements

The diffuse reflectance spectra of 1 and 2 were collected in the back-scattering geometry using an Agilent Cary 5000 spectrophotometer.

A Hamamatsu PMA-12 photonic multichannel analyzer paired with a BT-CCD sensor was employed to obtain temperature-dependent emission spectra of 2. As an excitation source, a 405 nm laser diode was used. A Linkam THMS600 stage was employed to regulate the temperature.

Energy-dispersive X-ray spectroscopy (EDS)

The chemical composition of 2 was determined using a FEI NOVA NanoSEM 140 scanning electron microscope.

Results and discussion

Thermal properties

The acquired DSC curve, shown in Fig. S2 (ESI†), demonstrates that 1 undergoes PT at T_C = 379 and 376 K during heating and cooling, respectively. A small temperature hysteresis of 2 K as well as the lambda-shaped change in ΔC_p and a gradual change in ΔS associated with this PT shown in Fig. 1 imply that this transformation has a second-order (continuous) nature. The estimated value of change in entropy ΔS (3.5 J mol⁻¹ K⁻¹) is similar to that reported for the [EA]₂NaM^III(HCOO)₆ (M^III = Al³⁺, Cr³⁺, Fe³⁺) analogues (2.0–5.0 J mol⁻¹ K⁻¹),^29,30 indicating a similar order–disorder mechanism of PTs (see the comparison of thermal parameters in Table S2, ESI†).

Fig. 1 (a) Temperature dependence of the excess heat capacity (ΔC_p) and change in entropy (ΔS) obtained for 1.

Assuming that ΔS = R ln N, where R denotes the gas constant, and N specifies the ratio of disordered states in the HT and LT phases, respectively, the calculated N for 1 is 1.6. This value is slightly lower than that obtained from our X-ray diffraction data (see below), revealing that EA⁺ cations in 1 display two-fold disorder in the HT phase and become ordered below the T_C (N = 2). This mismatch indicates that the deformation of the metal-formate framework triggered by the ordering of EA⁺ cations is equally significant.

Single-crystal X-ray diffraction

The structure of 1 has been determined at 293 and 391 K. Both, the HT and LT phases belong to the monoclinic system, non-centrosymmetric and polar space group Pn at 293 and 391 K. Table S1 (ESI†) contains the experimental data regarding the single-crystal structure determination. Table S3 (ESI†) provides the geometrical parameters for both phases.

In the HT phase, the asymmetric part of the unit cell consists of two metal ions (Ga³⁺ and Na⁺) surrounded by six formate (HCOO⁻) linkers and two protonated EA⁺ cations (see Fig. 2 and Fig. S3, ESI†). The metal centres are connected through formate linkers in the anti–anti mode configuration forming a 3D network with pseudo-cubic voids. The cavities are occupied by EA⁺ cations joined to the framework by stronger N–H⋯O and weaker C–H⋯O HBs (Table S4, ESI†). The organic cations are dynamically disordered in two positions (Fig. 2a and Fig. S3 and S4, ESI†). The crystal structure is very similar to previously studied [EA]₂NaM^III(HCOO)₆ (M^III = Al³⁺, Cr³⁺, Fe³⁺) members with disordered HT phases, in which dipole moment alignment leads to the disappearance of polar properties in the HT centrosymmetric P2₁/n phase.^29,30 In contrast, the HT phase of 1 remains non-centrosymmetric despite the similar disorder of EA⁺ cations.

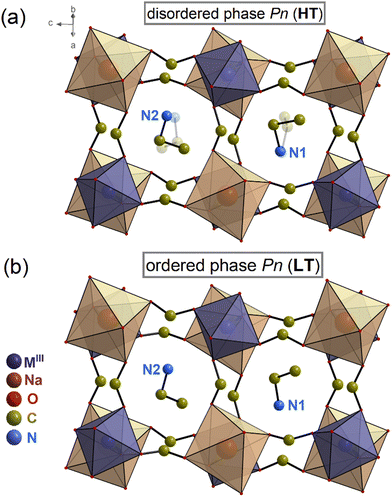Fig. 2 Structures of 1 at (a) 391 K (disordered phase) and (b) 293 K (ordered phase). The M^III label stands for Ga³⁺/Fe³⁺/Cr³⁺.

Lowering the temperature below 377 K causes the organic cations to order. The asymmetric unit in the LT phase has remained mostly unaltered. However, the PT strongly affects the HB network, as the donor–acceptor distances (D⋯A) are in the 2.865(5)–3.277(5) Å range for the LT phase and 2.85(4)–3.444(19) Å range for the HT phase (see Table S4, ESI†).

The distortion of octahedral coordination in both phases is depicted in bond lengths and valence angles (see Tables S2 and S3, ESI†). At 293 K, the Ga–O distances range from 1.965(3) Å to 1.987(3) Å, while the Na–O from 2.385(5)–2.531(4) Å, resulting in the bond length distortion indexes Δ of 0.0040 and 0.0196 for the GaO₆ and NaO₆ octahedra, respectively. The corresponding bond angle variances σ² are equal to 1.77 and 17.04 deg², respectively, implying that the NaO₆ octahedra are more distorted in the LT phase compared to the GaO₆ ones. The increase of temperature to 391 K results in a decrease of Δ (0.0027) and σ² (1.42 deg²) for GaO₆, making it less distorted. In contrast, for NaO₆ the Δ parameter slightly increases to 0.0231, while σ² is decreased to 12.06 deg². Taking into account the Δ and σ² parameters for all members of the [EA]₂NaM^III(HCOO)₆ family, the crystals of 1 are composed of the most distorted NaO₆ and M^IIIO₆ octahedra (Table S2, ESI†).

Second harmonic generation

Temperature-dependent SHG study was performed by illumination of 1 with 800 nm femtosecond laser pulses in the 354–403 K temperature range. The temperature plot of integral intensities of the SHG signal of 1 is shown in Fig. 3, while the experimental spectra are provided in Fig. S5 (ESI†). It is apparent that both LT and HT phases show the SHG response, confirming a non-centrosymmetric nature of these phases. Moreover, one also sees a gradual decrease in the SHG intensity with increasing temperature (LT phase) with an inflection at around 387 K, above which the SHG response stays flat (HT phase). There is also a negligible temperature hysteresis for heating and cooling runs. These features indicate the continuous character of the transition between the two acentric phases, in line with the DSC studies. From the quantitative perspective, the amplitude of the SHG response is rather moderate. A Kurtz–Perry powder test³⁷ using a size-graded sample of 1 at 293 K shows that the SHG response is 0.01 versus a KDP reference of the same particle size, see Fig. S6 (ESI†).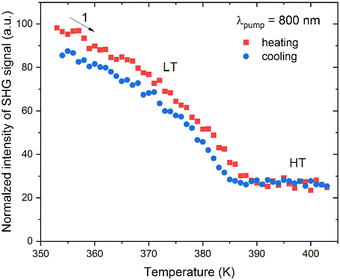

Fig. 3 Integral intensities of the SHG signal of 1 for heating (red squares) and cooling (blue squares) runs.

Dielectric properties

The temperature dependence of the real ε′ and imaginary ε′′ parts of the complex dielectric permittivity (ε* = ε′ − iε′′) a single crystal sample of 1 is presented in Fig. 4. A sharp anomalous increase of ε* can be observed at 380 K (Fig. 4) due to the isosymmetric phase transition in good agreement with the DSC and SHG results. A similar anomalous behaviour is also observed for the pressed pellet sample (see Fig. S7a, ESI†). Note that we did not observe any additional dielectric anomalies, which can be associated with the phase transitions down to 5 K temperature (Fig. S7b, ESI†). The overall dielectric response is similar to that of the related [EA]₂NaFe(HCOO)₆ compound.²⁹

Fig. 4 Temperature dependence of the (a) real and (b) imaginary parts of the complex dielectric permittivity of a single crystal sample of 1 obtained at selected frequencies. The inset in (a) shows the 1/ε′ vs. temperature plot, where the linear fits (solid lines) correspond to the Curie–Weiss fits above and below the phase transition point.

We analysed the dielectric anomaly using the Curie–Weiss law ε′ = C/(T − T_C), where C is the Curie–Weiss constant and T_C denotes the phase transition temperature.³⁸ It follows from this equation that 1/ε′ should linearly depend on temperature, which is indeed observed in our dielectric data (see inset in Fig. 4a). The values of the determined Curie–Weiss constants in the ordered and disordered phases are 101 K and 195 K, respectively. Both values are close to the value of the transition temperature confirming the order–disorder nature of the transition.³⁸ In addition, the ratio of the Curie–Weiss constants C(T > T_C)/C(T < T_C) is very close to 2 indicating a second-order (continuous) phase transition in agreement with the DSC and SHG results.³⁸

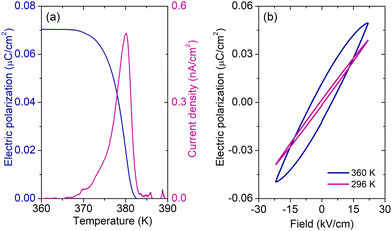
Pyrocurrent and polarization measurements

The temperature-dependent pyrocurrent density of a pellet sample of 1 obtained after the background correction (see Fig. S8, ESI†) is presented in Fig. 5a. A clear maximum at the phase transition point can be observed, which indicates the pyroelectric nature of the compound. The corresponding electric polarization is also presented in Fig. 5a showing a typical behaviour at the phase transition point observed in other formate-based hybrid perovskites.^39–41

Fig. 5 (a) Temperature dependence of the pyrocurrent and corresponding electric polarization of a pellet sample of 1. (b) Electric field dependence of the electric polarization of 1 pellet sample obtained at 296 and 360 K.

The pyrocurrent response shows that the studied system is pyroelectric, but it is not sufficient to prove the ferroelectric behaviour. A ferroelectric compound should exhibit a ferroelectric hysteresis loop, i.e. switching of the electric polarization with the external electric field.³⁸ The obtained electric field dependent polarization of a pellet sample of 1 at 296 and 360 K is presented in Fig. 5b showing typical ‘banana’ loops of a slightly conducting compound⁴² and the absence of ferroelectric switching. This indicates that the studied compound is not ferroelectric or that the moderate amplitude of the driving field (22 kV cm⁻¹) is insufficient to switch the polarization.

EPR

We further employed CW and pulsed EPR spectroscopy on the sample doped with a small amount of paramagnetic Fe³⁺ ions to further probe the phase transition and dynamic properties of [EA]₂NaGa(HCOO)₆. The measured EDFS (10 K) and CW EPR spectra a sample of 3 show a typical powder pattern of high-spin Fe³⁺ ions⁴³ (Fig. 6a). The Fe³⁺ centre has 3d⁵ electronic configuration and, in the high-spin state, it has five unpaired electrons leading to the total electron spin of S = 5/2. In a non-cubic environment, this ion is expected to have a substantial zero-field splitting providing a complicated fine structure pattern observed in the measured spectra of 3.

Fig. 6 (a) EDFS (10 K) and CW (200, 270, and 400 K) EPR spectra of the Fe³⁺ centres in 3. (b) Temperature dependence of the CW EPR linewidth (at 70 mT) of the Fe³⁺ centres in 3 indicating the phase transition at 377 K (arrow). Inset in (b) shows the Arrhenius-type temperature dependence of the EPR linewidth. Error bars in (b) are about the size of the data points.

The temperature dependence of the CW EPR linewidth of Fe³⁺ centres in 3 is presented in Fig. 6b. Upon temperature increase in the low-temperature phase, the linewidth exhibits a significant broadening and peaks at 377 K indicating the structural phase transition in agreement with other methods. Similar behaviour of the EPR linewidth was observed in a number of different systems (including hybrid perovskites) exhibiting ferroelectric and related structural phase transitions, and it was assigned to the critical dynamics of the order parameter fluctuations.^44–47 The measured anomaly also indicates that the Fe³⁺ ions are susceptible to the local changes of the [EA]₂NaGa(HCOO)₆ lattice occurring during the phase transition, which confirms the successful incorporation of these ions in this material.

We analysed the temperature dependence of the CW EPR linewidth in the low-temperature phase in more detail assuming that the broadening process follows the Arrhenius law: Γ − Γ₀ = Γ_∞e^−E_a/kT. Here, E_a is the activation energy of a dynamic process, k is the Boltzmann constant, and Γ₀ and Γ_∞ denote the linewidth in the low and high temperature limits, respectively. Using Γ₀ = 1.2 mT (low temperature limit), our analysis provides E_a = 204(12) meV (see the inset in Fig. 6b), which is in the range of typical values for molecular cation motion observed in different hybrid perovskites such as [DMA]Zn(HCOO)₃ (266 meV)⁴⁸ and MAPbI₃ (80 meV).⁴⁹ Thus, the broadening of the Fe³⁺ signal with increasing temperature may be related to the enhanced EA⁺ cation motion, as it directly couples to the inorganic framework via the H-bonds.

We used pulsed EPR spectroscopy to further investigate the local Fe³⁺ ion environment in 3. The magnetic field dependence of the three-pulse ESEEM spectrum in the low-frequency region is presented in Fig. 7 revealing a well-resolved peak with frequency linearly dependent on the magnetic field. Such a signal belongs to a nucleus with non-zero nuclear spin in close vicinity of the Fe³⁺ centre. The slope of the signal occurring corresponds to the gyromagnetic ratio of ²³Na nucleus. ³⁸We have not detected any ESEEM signals from ⁶⁹Ga and ⁷¹Ga isotopes indicating that Ga³⁺ ions are significantly more distant than Na⁺ from the iron impurity. Based on the crystal structure of 1, these results confirm that Fe³⁺ substitutes Ga³⁺ in the lattice and forms FeO₆ octahedra.

Fig. 7 Colour plot of the three-pulse ESEEM spectrum vs. magnetic field of 3 obtained at 10 K and τ = 130 ns. The field-dependent signal of ²³Na is indicated in the plot. The field-independent signal at about 0.6 MHz is assigned to methyl group quantum rotational tunnelling of the EA⁺ cation.

Fig. 7 also shows a couple of ESEEM signals below 1 MHz, which are independent of the magnetic field. The origin of the weaker signal at about 0.61 MHz can be assigned to the quantum rotational tunneling of methyl groups of the EA⁺ molecular cation. Note that such a field-independent ESEEM effect has recently been observed in Mn- and Co-doped [DMA]Zn(HCOO)₃,^50,51 and Mn-doped [DMA]Cd(N₃)₃⁵⁰ hybrid perovskites, as well as nitroxide radicals.⁵² The current work provides the first signatures of this effect detected with a paramagnetic Fe³⁺ centre. The stronger signal occurring at much lower frequency of 0.1 MHz may originate from the NH₃ group tunneling, as, due to the stronger H-bonds, these groups are expected to have a higher rotational barrier (lower tunneling frequency) compared to the CH₃ groups. Note that we also cannot rule out that the origin of this low frequency signal is imperfect background correction of the time-domain ESEEM data. The EPR measurements of the samples containing partially deuterated EA⁺ cations are needed to unambiguously determine the origin of these field-independent signals.

The frequency at which the tunnelling signal appears can be used to estimate the rotation barrier of the CH₃ and NH₃ groups in [EA]₂NaGa(HCOO)₆ by diagonalizing the rotational Hamiltonian on the basis of the free quantum rotor.⁵³ The obtained barrier for the CH₃ group is 12.1 kJ mol⁻¹, which is similar in value to the energies obtained for methyl group rotation in DMA-containing hybrid perovskites.^50,51 Assuming that the low-frequency signal originates from the NH₃ groups, a rough estimate for the NH₃ group rotational barrier gives ∼18 kJ mol⁻¹. In the calculations, we used rotational constants B(CH₃) = 0.655 meV and B(NH₃) = 0.782 meV.⁵⁴

Phonon properties

We further used vibrational spectroscopy to study the phonon properties of [EA]₂NaGa(HCOO)₆. Fig. S9 (ESI†) compares the Raman spectra of 1 and 2 obtained at room temperature. Table S5 (ESI†) includes Raman band assignment based on published data for [EA]₂NaM^III(HCOO)₆ (M^III = Al³⁺, Cr³⁺, and Fe³⁺).^29,30 Because the doping level of Ga³⁺ in 2 is as low as 6.9 mol%, the Raman spectrum is roughly comparable to that reported earlier for the pure [EA]₂NaCr(HCOO)₆ compound.³⁰

When Cr³⁺ ions are replaced with Ga³⁺ ions, a number of bands move due to differences in weights and electronegativity; gallium ions are approximately 34% heavier at almost the same ionic radius, and Ga–O bonds are more ionic than Cr–O bonds. The most significant change among internal vibrations is 5 cm⁻¹, whereas the highest shift among the lattice modes involving M^III translations is up to 12 cm⁻¹.

IR spectra were obtained as a function of temperature to better understand the mechanism of the PT occurring in 1 (see Fig. 8 and Fig. S10, ESI†). The assignments of IR bands at 80 and 400 K are summarized in Table S6 (ESI†). As shown by the results, the number of observed bands at 80 K is significantly higher than those at room temperature and at temperatures corresponding to the HT phase (above 380 K). Since for both phases, the space group symmetry of the cell does not vary, the number of expected phonon modes for the crystal 1 also remains the same. Thus, the large number of bands at low temperatures can only be attributable to strong narrowing and better separation of closely laid bands. Such narrowing is a common effect observed for order–disorder transformations, and it confirms the nature of the observed PT.^55,56

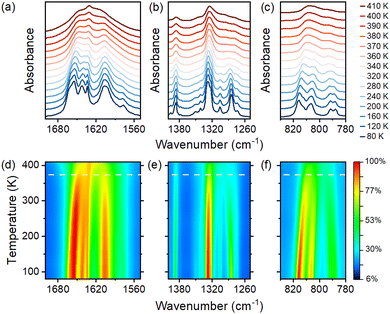Fig. 8 Temperature-dependent IR spectra measured for 1 (a)–(c) and the corresponding contour maps of intensity (d)–(f). Horizontal dashed lines in (d)–(f) correspond to the PT temperature.

Fig. 8a and d present the temperature evolution of bands corresponding to bending modes of NH₃ groups that coincide with antisymmetric OCO stretching. In the HT phase, all bands in this range merge into a very broad contour. The map presented in Fig. 8d exhibits that the intensity decreases quicker above the PT temperature. The disorder of HBs in the HT phase also contributes to the severe half-width of the bands. Similar substantial broadening is also observed for IR bands in the 1250–1400 cm⁻¹ range, which correspond to alkyl chain bending modes and formate ligand stretching vibrations. (Fig. 8b).

Fig. 8c and f present the thermal evolution of bands that result from the OCO bending vibrations. Fig. S11a (ESI†) depicts the fitting of those bands. The abrupt shifts and the disappearance of bands in the HT phase are caused by the fitting procedure, in which the usage of the same number of bands in both phases fails to produce satisfactory results. Nonetheless, significant shifts in maxima and differences in the intensity of band contours imply a more deformed metal-formate framework in the LT phase.

The structural, thermal, dielectric, and EPR data demonstrate that the spectral changes are continuous (Fig. 8 and Fig. S10 and S11, ESI†). As a result, cation ordering does not occur abruptly but rather is a gradual process that still occurs below the PT temperature. This behavior can be demonstrated by thermal changes in bands corresponding to rocking modes of protonated amine groups and alkyl chain vibrations (Fig. S11b, ESI†). They remain quite broad (Fig. S11c, ESI†) at the PT temperature, and their narrowing upon cooling is still observed down to 80 K. The corresponding intensity changes are also continuous over the entire range of measured temperatures (Fig. S11d, ESI†).

Optical properties

Finally, we investigated the optical properties of [EA]₂NaGa(HCOO)₆. Fig. S12 (ESI†) presents the absorption spectra of crystals of 1 and 2. As can be seen, the spectrum of the sample containing Cr³⁺ ions consists of two broad bands centered at around 17 265 cm⁻¹ (579 nm) and 24 035 cm⁻¹ (416 nm) attributed to spin-allowed ⁴A_2g → ⁴T_2g and ⁴A_2g → ⁴T_1g transitions, respectively. The low intense and narrow band localized at 14 571 cm⁻¹ (686 nm) is characteristic of the R₁ line of the spin-forbidden ⁴A_2g → ⁴T_2g transition. The sample of 1 does not contain any absorption bands in the given range.

Using the diffuse reflectance spectrum, it is possible to determine the energy band gap (E_g) of investigated samples by applying the Kubelka–Munk relation.⁵⁷ The E_g for 1 equals 5.04 eV and is comparable with the band gap (5.09 eV) of the recently reported [EA]₂NaAl(HCOO)₆ (Fig. S13, ESI†).²⁷ The analogue comprising Cr³⁺ ions 2 has a much lower E_g of 4.71 eV. The decreasing energy band gap with increasing concentrations of Cr³⁺ has been reported lately for similar compounds.^27,58

In sample 2, Cr³⁺ ions are positioned in the octahedral sites. The low-temperature (80 K) emission spectrum contains a few sharp and narrow bands that span from 679 nm to 778 nm (Fig. S14, ESI†). The most intense line centered at 686 nm (14 577 cm⁻¹) is attributed to the spin-forbidden ²E_g → ⁴A_2g transition and is called the R line.^32,58,59 The band localized at 697 nm (14 347 cm⁻¹) belongs to the N line and can be assigned to the Cr³⁺–Cr³⁺ pair line.^30,32,59 Moreover, some anti-Stokes phonon side bands of the R line are visible in the range of 707–778 nm.⁶⁰ Similar behavior has been reported recently for other formate analogues with Cr³⁺ ions.^32,58,59 Careful analysis shows a less intense and wide emission band extending up to 1000 nm, which can be attributed to the spin-allowed ⁴T_2g → ⁴A_2g transition (Fig. S14, ESI†).

Based on the absorption and emission spectra, the crystal field (D_q) and Racah parameters (B and C) were calculated according to the previously applied methodology.^30,59,61 The calculated values are presented in Table 1. The ratio of D_q/B = 2.35 indicates that Cr³⁺ ions are positioned in a strong crystal field. This value is very close to the 2.3 point on the Tanabe–Sugano diagram for the d³ configuration, where the ²E_g and ⁴T_2g levels overlap and separate the areas of D_q/B < 2.3 and D_q/B > 2.3 corresponding to weak and strong crystal fields, respectively. The obtained values as well as the experimental data show that the ²E_g energy level is located below the ⁴T_2g state (Fig. 9a and b), and the energy separation between these two levels is not large. It was mentioned that even at 80 K, residual emission from the ⁴T_2g level is visible and becomes stronger upon heating. Careful analysis showed that the intensity of the spin-forbidden transition decreases significantly with rising temperature, while the broad emission associated with the ⁴T_2g → ⁴A_2g transition becomes stronger up to 190 K (Fig. 9a–c). This phenomenon is related to the temperature-stimulated energy transfer from the lower ²E_g level to the ⁴T_2g higher state. Above 190 K, the regular temperature quenching process occurs via the intercrossing of the ⁴T_2g excited state with the ⁴A_2g ground state parabolas (Fig. 9d).

Table 1 Energy band gap and crystal field parameters of the investigated formate perovskites

Sample	E g (eV)	D q/B	B (cm^−1)	C (cm^−1)	C/B
1	5.04	—	—	—	—
2	4.71	2.35	689	3157	4.6

---

Fig. 9 (a) Temperature-dependent emission spectra of 2, (b) thermal evolution of the measured intensity at various temperatures, (c) integrated emission intensity of the spin-forbidden and spin-allowed transitions, and (d) the schematic energy level diagram of Cr³⁺ ions.

The significant changes in the emission intensity of both spin-forbidden and spin-allowed transitions can be an attractive feature for luminescence thermometry applications. Recently, the potential of hybrid organic–inorganic compounds with a perovskite-type architecture containing Cr³⁺ ions for temperature detection based on the fluorescence intensity ratio (FIR) of two emission bands was reported.^27,62 In the investigated Cr³⁺-doped perovskite, FIR parameter Δ can be defined as a ratio of the ²E_g → ²A_2g (660–718 nm) to the ⁴T_2g → ⁴A_2g (718–970 nm) (Fig. S15, ESI†) transitions of the Cr³⁺ ions. It is not surprising that FIR decreases with an increase in temperature (Fig. S16, ESI†). To further compare the luminescence thermometry performance, the absolute (S_a) and relative (S_r) sensitivities, as well as the temperature uncertainty (δT) were calculated as follows: S_a = |∂Δ/∂T|, S_r = 1/Δ| ∂Δ/∂T|, and δT = 1/S_r|δΔ/Δ|, where ∂Δ symbolizes the changes of Δ at ∂T temperature change.

The fluorescence intensity ratio curve was fitted using the following equation: ΔT = A/(1 + αexp(–ΔE/k_BT) (Fig. S15, ESI†). The temperature dependencies of S_a and S_r are presented in Fig. 10. First, upon heating, the sensitivity increases with temperature and reaches the maximum S_r value of 2.11% K⁻¹ at 150 K (Fig. 10b). Then capability of temperature readout decreases as the temperature increases. However, the sensitivity above 0.5% K⁻¹ can be achieved in the broad temperature range from 90 to 280 K. The sensitivity of perovskite 2 is comparable with the S_r parameter obtained for other formate analogues with the EA⁺ and GA⁺ cations.^27,62 The summary of the S_r parameters of various luminescent thermometers is shown in Table 2.

Fig. 10 (a) The absolute sensitivity (S_a) and (b) relative sensitivity (S_r) of optical thermometer 2. The temperature uncertainty (δT) is presented on the graph (b) as error bars.

Table 2 Comparison of the highest relative sensitivity (S_r) at operating temperature (T) of selected luminescent thermometers

Compound	S r (% K^−1)	T (K)	Ref.
Coordination polymers
[EA]2NaCr0.21Al0.79(HCOO)6	2.84	160	27
2	2.11	150
[GA]Mg(HCOO)3:1% Cr^3+	2.08	90	62
[GA]Mn(HCOO)3:3% Cr^3+	1.20	100	62
[GA]Zn(HCOO)3:1% Cr^3+	1.08	90	62
Inorganic compounds
ZnGa2O4:Cr^3+	2.8	310	65
La2MgTiO6:Cr^3+, V^4+	1.96	165	66
La2MgTiO6:Cr^3+, Mn^4+	1.74	220	67
Sr2MgAl22O36:Cr^3+	1.7	310	68
Bi2Al4O9:Cr^3+	1.24	290	69
MgTiO3:Mn^4+	1.2	93	70
SrAl12O19:Mn^4+	0.27	393	71

---

The thermometric performance of the Cr³⁺-based materials might also be extended by combining the presented approach with the SHG signal. Such a strategy of temperature sensing has been successfully used for lanthanide-based nanoparticles and MOFs.^63,64 However, due to the overlap of the SHG excitation wavelength with Cr³⁺ emission bands, this particular method has not been applied in this study.

Conclusions

A solvothermal method has been employed to successfully synthesize a novel double perovskite [CH₃CH₂NH₃]₂NaGa(HCOO)₆. Our multitechnique characterization approach revealed that this compound exhibits a phase transition at about 379 K. We also synthesized its analogues doped with approximately 0.1 mol% Fe³⁺ ions to study the effects of phase transition on the metal-formate framework and those doped with roughly 93.1 mol% Cr³⁺ to estimate the usefulness for non-contact temperature sensing. The powder X-ray diffraction, Raman and EPR studies confirmed the phase purity and that the dopant ions are located at expected sites in the crystal structure.

The single-crystal X-ray diffraction studies of [CH₃CH₂NH₃]₂NaGa(HCOO)₆ revealed that the high-temperature phase comprises disordered EA⁺ cations in two different positions. Below the phase transition temperature, they start to order, resulting in a modification of the H-bond network and deformation of the metal-formate framework. According to the XRD results, both phases are represented by a non-centrosymmetric and polar Pn monoclinic space group. Such an isosymmetric order–disorder polar phase transition is extremely unusual among formates. The SHG measurement confirmed the continuous character of the transition and the acentric nature of both phases.

The dielectric spectroscopy experiments revealed that the phase transition is of the order–disorder character. The pyrocurrent and electric polarization loop measurements demonstrated that [CH₃CH₂NH₃]₂NaGa(HCOO)₆ is pyroelectric, but not a proper ferroelectric, as we did not observe polarization switching (polarization hysteresis). We note that such a behavior is rather typical for formate-based perovskites.

We also employed EPR spectroscopy to probe the phase transition and dynamic effects in [CH₃CH₂NH₃]₂NaGa(HCOO)₆ enriched with a tiny amount of paramagnetic Fe³⁺ ions. Our CW EPR experiments confirmed the continuous character of the phase transition and allowed us to probe the dynamics of the inorganic framework. The pulsed EPR ESEEM experiments confirmed that the iron ions were successfully incorporated at the Ga³⁺ sites in the lattice. We also observed ESEEM signals independent of the magnetic field, which were assigned to the quantum rotational tunneling dynamics of the CH₃ and NH₃ groups of the EA⁺ cation. This allowed us to estimate the rotational barriers of these rotors in [CH₃CH₂NH₃]₂NaGa(HCOO)₆.

IR investigations confirmed the nature of the observed phase transition and helped to clarify that the EA⁺ cation ordering does not occur abruptly but rather is a gradual process that still occurs below the phase transition temperature. The narrowing of IR bands corresponding to vibrations of atoms involved in H-bonding demonstrated that there is still some degree of disorder at 80 K.

The linear optical results revealed that [CH₃CH₂NH₃]₂NaGa(HCOO)₆ has a wide bandgap of 5.04 eV. The analogue, composed mainly of Cr³⁺ ions, exhibited a substantially lower bandgap value of 4.71 eV. The estimated Racah parameters showed that Cr³⁺ ions are positioned in a strong crystal field, which was applied to evaluate the utility of the Cr-doped material for non-contact temperature monitoring. Based on the temperature-dependent luminescence, the maximum relative sensitivity (2.11% K⁻¹) was reached at 150 K, and this value is comparable to other hybrid and inorganic materials.

Author contributions

Conceptualization, M. P., A. K., and M. S.; formal analysis, M. P., A. K., B. D., S. B., G. U., M. S., and D. S.; funding acquisition, D. S. and M. S.; investigation, M. P., A. K., B. D., S. B., G. U., J. K. Z., M. S., and A. S.; methodology, M. P. and M. S.; project administration, D. S. and M. S.; resources, M. S., D. S.; supervision, J. B., D. S., and M. S.; validation, M. P., M. S., and D. S.; visualization, M. P., A. K., B. D., S. B., G. U., M. S., and D. S.; writing – original draft, M. P., A. K., B. D., S. B., G. U., J. K. Z., M. S., A. S., and D. S.; writing – review & editing, M. P. and M. S.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was founded by the National Science Centre, Poland, under project no. UMO-2020/39/D/ST5/01289. This project was funded by the Research Council of Lithuania (LMTLT) (agreement no. S-MIP-22-73). The authors would like to thank Dr Damian Szymański for performing the EDS tests, Ewa Bukowska for measurements of powder XRD patterns, and Dr Bogusław Macalik for measurements of diffuse reflectance spectra. JKZ acknowledges support from Academia Iuvenum, Wroclaw University of Science and Technology. For the purpose of open access, the author has applied a CC-BY public copyright license to any Author Accepted Manuscript (AAM) version arising from this submission.

References

1. X. Zhao, J. D. A. Ng, R. H. Friend and Z. K. Tan, Opportunities and Challenges in Perovskite Light-Emitting Devices, ACS Photonics, 2018, 5, 3866–3875,  DOI:10.1021/acsphotonics.8b00745.
2. B. Saparov and D. B. Mitzi, Organic-Inorganic Perovskites: Structural Versatility for Functional Materials Design, Chem. Rev., 2016, 116, 4558–4596,  DOI:10.1021/acs.chemrev.5b00715.
3. W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Chemically Diverse and Multifunctional Hybrid Organic-Inorganic Perovskites, Nat. Rev. Mater., 2017, 2, 1–18,  DOI:10.1038/natrevmats.2016.99.
4. J. Y. Kim, J. W. Lee, H. S. Jung, H. Shin and N. G. Park, High-Efficiency Perovskite Solar Cells, Chem. Rev., 2020, 120, 7867–7918,  DOI:10.1021/acs.chemrev.0c00107.
5. F. Wang, Y. Cao, C. Chen, Q. Chen, X. Wu, X. Li, T. Qin and W. Huang, Materials toward the Upscaling of Perovskite Solar Cells: Progress, Challenges, and Strategies, Adv. Funct. Mater., 2018, 28, 1803753,  DOI:10.1002/adfm.201803753.
6. H. L. B. Boström, M. S. Senn and A. L. Goodwin, Recipes for Improper Ferroelectricity in Molecular Perovskites, Nat. Commun., 2018, 9(1), 1–7,  DOI:10.1038/s41467-018-04764-x.
7. J. Huang, Y. Yuan, Y. Shao and Y. Yan, Understanding the Physical Properties of Hybrid Perovskites for Photovoltaic Applications, Nat. Rev. Mater., 2017, 2, 1–19,  DOI:10.1038/natrevmats.2017.42.
8. A. Capitaine and B. Sciacca, Monocrystalline Methylammonium Lead Halide Perovskite Materials for Photovoltaics, Adv. Mater., 2021, 33, 1–38,  DOI:10.1002/adma.202102588.
9. Y. He, K. Zheng, P. F. Henry, T. Pullerits and J. Chen, Direct Observation of Size-Dependent Phase Transition in Methylammonium Lead Bromide Perovskite Microcrystals and Nanocrystals, ACS Omega, 2022, 7, 39970–39974,  DOI:10.1021/acsomega.2c04503.
10. K. Schötz, A. M. Askar, A. Köhler, K. Shankar and F. Panzer, Investigating the Tetragonal-to-Orthorhombic Phase Transition of Methylammonium Lead Iodide Single Crystals by Detailed Photoluminescence Analysis, Adv. Opt. Mater., 2020, 17, 1–9,  DOI:10.1002/adom.202000455.
11. S. Huang, P. Huang, L. Wang, J. Han, Y. Chen and H. Zhong, Halogenated-Methylammonium Based 3D Halide Perovskites, Adv. Mater., 2019, 31, 1–5,  DOI:10.1002/adma.201903830.
12. Z. A. Nan, L. Chen, Q. Liu, S. H. Wang, Z. X. Chen, S. Y. Kang, J. B. Ji, Y. Y. Tan, Y. Hui, J. W. Yan, Z. X. Xie, W. Z. Liang, B. W. Mao and Z. Q. Tian, Revealing Phase Evolution Mechanism for Stabilizing Formamidinium-Based Lead Halide Perovskites by a Key Intermediate Phase, Chem, 2021, 7, 2513–2526,  DOI:10.1016/j.chempr.2021.07.011.
13. S. Jiang, Y. Luan, J. I. Jang, T. Baikie, X. Huang, R. Li, F. O. Saouma, Z. Wang, T. J. White and J. Fang, Phase Transitions of Formamidinium Lead Iodide Perovskite under Pressure, J. Am. Chem. Soc., 2018, 140, 13952–13957,  DOI:10.1021/jacs.8b09316.
14. N. Pellet, P. Gao, G. Gregori, T. Y. Yang, M. K. Nazeeruddin, J. Maier and M. Grätzel, Mixed-Organic-Cation Perovskite Photovoltaics for Enhanced Solar-Light Harvesting, Angew. Chem., Int. Ed., 2014, 53, 3151–3157,  DOI:10.1002/anie.201309361.
15. M. Maczka, M. Ptak, D. L. M. Vasconcelos, L. Giriunas, P. T. C. Freire, M. Bertmer, J. Banys and M. Simenas, NMR and Raman Scattering Studies of Temperature-and Pressure-Driven Phase Transitions in CH₃NH₂NH₂PbCl₃ Perovskite, J. Phys. Chem. C, 2020, 124, 26999–27008,  DOI:10.1021/acs.jpcc.0c07886.
16. M. Maczka, M. Ptak, A. Gagor, D. Stefanska, J. K. Zareba and A. Sieradzki, Methylhydrazinium Lead Bromide: Noncentrosymmetric Three-Dimensional Perovskite with Exceptionally Large Framework Distortion and Green Photoluminescence, Chem. Mater., 2020, 32, 1667–1673,  DOI:10.1021/acs.chemmater.9b05273.
17. H. R. Petrosova, O. I. Kucheriv, S. Shova and I. A. Gural'skiy, Aziridinium Cation Templating 3D Lead Halide Hybrid Perovskites, Chem. Commun., 2022, 58, 5745–5748,  10.1039/d2cc01364a.
18. M. Pitaro, E. K. Tekelenburg, S. Shao and M. A. Loi, Tin Halide Perovskites: From Fundamental Properties to Solar Cells, Adv. Mater., 2022, 34, 1–47,  DOI:10.1002/adma.202105844.
19. M. Maczka, A. Gagor, J. K. Zareba, D. Stefanska, M. Drozd, S. Balciunas, M. Simenas, J. Banys and A. Sieradzki, Three-Dimensional Perovskite Methylhydrazinium Lead Chloride with Two Polar Phases and Unusual Second-Harmonic Generation Bistability above Room Temperature, Chem. Mater., 2020, 32, 4072–4082,  DOI:10.1021/acs.chemmater.0c00973.
20. M. Ptak, A. Sieradzki, M. Simėnas and M. Maczka, Molecular Spectroscopy of Hybrid Organic–Inorganic Perovskites and Related Compounds, Coord. Chem. Rev., 2021, 448, 1–51,  DOI:10.1016/j.ccr.2021.214180.
21. P. Jain, V. Ramachandran, R. J. Clark, D. Z. Hai, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, Multiferroic Behavior Associated with an Order-Disorder Hydrogen Bonding Transition in Metal-Organic Frameworks (MOFs) with the Perovskite ABX3 Architecture, J. Am. Chem. Soc., 2009, 131, 13625–13627,  DOI:10.1021/ja904156s.
22. M. Sanchez-Andujar, S. Presedo, S. Ya Nez-Vilar, S. Castro-García, J. Shamir and M. A. Senaris-Rodriguez, Characterization of the Order-Disorder Dielectric Transition in the Hybrid Organic-Inorganic Perovskite-like Formate Mn(HCOO)₃[(CH₃)₂NH₂], Inorg. Chem., 2010, 49, 1510–1516,  DOI:10.1021/ic901872g.
23. Y. Imai, B. Zhou, Y. Ito, H. Fijimori, A. Kobayashi, Z. M. Wang and H. Kobayashi, Freezing of Ring-Puckering Molecular Motion and Giant Dielectric Anomalies in Metal-Organic Perovskites, Chem. – Asian J., 2012, 7, 2786–2790,  DOI:10.1002/asia.201200673.
24. W. Li, Z. Zhang, E. G. Bithell, A. S. Batsanov, P. T. Barton, P. J. Saines, P. Jain, C. J. Howard, M. A. Carpenter and A. K. Cheetham, Ferroelasticity in a Metal-Organic Framework Perovskite; Towards a New Class of Multiferroics, Acta Mater., 2013, 61, 4928–4938,  DOI:10.1016/j.actamat.2013.04.054.
25. Z. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Anionic NaCl-Type Frameworks of [MnII(HCOO)_3-], Templated by Alkylammonium, Exhibit Weak Ferromagnetism, Dalton Trans., 2004, 2209–2216,  10.1039/B404466E.
26. S. Chen, R. Shang, K. L. Hu, Z. M. Wang and S. Gao, [NH₂NH₃][M(HCOO)₃] (M = Mn²⁺, Zn²⁺, Co²⁺ and Mg²⁺): Structural Phase Transitions, Prominent Dielectric Anomalies and Negative Thermal Expansion, and Magnetic Ordering, Inorg. Chem. Front., 2014, 1, 83–98,  10.1039/c3qi00034f.
27. A. Kabanski, M. Ptak and D. Stefanska, Metal-Organic Framework Optical Thermometer Based on Cr³⁺ Ion Luminescence, ACS Appl. Mater. Interfaces, 2023, 15, 7074–7082,  DOI:10.1021/acsami.2c19957.
28. Y. Yu, R. Shang, S. Chen, B. W. Wang, Z. M. Wang and S. Gao, A Series of Bimetallic Ammonium AlNa Formates, Chem. – Eur. J., 2017, 23, 9857–9871,  DOI:10.1002/chem.201701099.
29. M. Ptak, M. Mączka, A. Gagor, A. Sieradzki, A. Stroppa, D. Di Sante, J. M. Perez-Mato and L. Macalik, Experimental and Theoretical Studies of Structural Phase Transition in a Novel Polar Perovskite-like [C₂H₅NH₃][Na_0.5Fe_0.5(HCOO)₃] Formate, Dalton Trans., 2016, 45, 2574–2583,  10.1039/c5dt04536c.
30. M. Ptak, M. Maczka, A. Gagor, A. Sieradzki, B. Bondzior, P. Deren and S. Pawlus, Phase Transitions and Chromium(III) Luminescence in Perovskite-Type [C₂H₅NH₃][Na_0.5Cr_xAl_0.5-x(HCOO)₃] (x = 0, 0.025, 0.5), Correlated with Structural, Dielectric and Phonon Properties, Phys. Chem. Chem. Phys., 2016, 18, 29629–29640,  10.1039/c6cp05151k.
31. M. Ptak, A. Gagor, A. Sieradzki, B. Bondzior, P. Deren, A. Ciupa, M. Trzebiatowska and M. Maczka, The Effect of K⁺ Cations on the Phase Transitions, and Structural, Dielectric and Luminescence Properties of [Cat][K_0.5Cr_0.5(HCOO)₃], Where Cat Is Protonated Dimethylamine or Ethylamine, Phys. Chem. Chem. Phys., 2017, 19, 12156–12166,  10.1039/c7cp01336a.
32. M. Ptak, B. Zarychta, D. Stefanska, A. Ciupa and W. Paraguassu, Novel Bimetallic MOF Phosphors with an Imidazolium Cation: Structure, Phonons, High- Pressure Phase Transitions and Optical Response, Dalton Trans., 2019, 48, 242–252,  10.1039/C8DT04246B.
33. M. Ptak, I. E. Collings, K. L. Svane, A. Sieradzki, W. Paraguassu and M. Maczka, Pressure-Enhanced Ferroelectric Polarisation in a Polar Perovskite-like [C₂H₅ NH₃]Na_0.5Cr_0.5(HCOO)₃ Metal-Organic Framework, J. Mater. Chem. C, 2019, 7, 8660–8668,  DOI:10.5281/zenodo.2608304.
34. D. Di Sante, A. Stroppa, P. Jain and S. Picozzi, Tuning the Ferroelectric Polarization in a Multiferroic Metal-Organic Framework, J. Am. Chem. Soc., 2013, 135, 18126–18130,  DOI:10.1021/ja408283a.
35. M. Maczka, A. Gagor, M. Ptak, W. Paraguassu, T. A. Da Silva, A. Sieradzki and A. Pikul, Phase Transitions and Coexistence of Magnetic and Electric Orders in the Methylhydrazinium Metal Formate Frameworks, Chem. Mater., 2017, 29, 2264–2275,  DOI:10.1021/acs.chemmater.6b05249.
36. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: A Complete Structure Solution, Refinement and Analysis Program, J. Appl. Crystallogr., 2009, 42, 339–341,  DOI:10.1107/S0021889808042726.
37. S. K. Kurtz and T. T. Perry, A Powder Technique for the Evaluation of Nonlinear Optical Materials, J. Appl. Phys., 1968, 39, 3798–3813,  DOI:10.1063/1.1656857.
38. M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Clarendon Press, Oxford, 1977, ISBN: 9780198507789.
39. M. Simenas, S. Balciunas, M. Maczka, J. Banys and E. E. Tornau, Structural Phase Transition in Perovskite Metal-Formate Frameworks: A Potts-Type Model with Dipolar Interactions, Phys. Chem. Chem. Phys., 2016, 18, 18528–18535,  10.1039/c6cp03414d.
40. W. Wang, L. Q. Yan, J. Z. Cong, Y. L. Zhao, F. Wang, S. P. Shen, T. Zou, D. Zhang, S. G. Wang, X. F. Han and Y. Sun, Magnetoelectric Coupling in the Paramagnetic State of a Metal-Organic Framework, Sci. Rep., 2013, 3, 1–5,  DOI:10.1038/srep02024.
41. Y. Tian, A. Stroppa, Y. Chai, L. Yan, S. Wang, P. Barone, S. Picozzi and Y. Sun, Cross Coupling between Electric and Magnetic Orders in a Multiferroic Metal-Organic Framework, Sci. Rep., 2014, 4, 1–5,  DOI:10.1038/srep06062.
42. J. F. Scott, Ferroelectrics Go Bananas, J. Phys. Condens. Matter, 2008, 20, 1–3,  DOI:10.1088/0953-8984/20/02/021001.
43. F. Gheorghiu, M. Simenas, C. E. Ciomaga, M. Airimioaei, V. Kalendra, J. Banys, M. Dobromir, S. Tascu and L. Mitoseriu, Preparation and Structural Characterization of Fe-Doped BaTiO₃ Diluted Magnetic Ceramics, Ceram. Int., 2017, 43, 9998–10005,  DOI:10.1016/j.ceramint.2017.05.013.
44. W. C. Phillips, W. C. Phillips, R. J. Weiss, P. B. Rev, T. Paakori, S. Manninen, O. Inkinen, R. Currat, P. D. DeCicco, A. Harvey, W. A. Rachinger, J. Sci, R. E. Watson, T. von Waldkirch, K. A. Muller and W. Berlinger, Fluctuations in SrTi0₃ near the 105-K Phase Transition, Phys. Rev. B: Solid State, 1972, 7, 1052–1066,  DOI:10.1103/PhysRevB.7.1052.
45. K. Nishimura and T. Hashimoto, ESR Investigation of TGS Doped with Cr³⁺ Ions, J. Phys. Soc. Japan, 1973, 35, 1699–1703,  DOI:10.1143/JPSJ.35.1699.
46. M. Simenas, A. Ciupa, G. Usevicius, K. Aidas, D. Klose, G. Jeschke, M. Maczka, G. Volkel, A. Poppl and J. Banys, Electron Paramagnetic Resonance of a Copper Doped [(CH₃)₂NH₂][Zn(HCOO)₃] Hybrid Perovskite Framework, Phys. Chem. Chem. Phys., 2018, 20, 12097–12105,  10.1039/c8cp01426d.
47. M. Simenas, A. Ciupa, M. Mączka, G. Volkel, A. Poppl and J. Banys, EPR of Structural Phase Transition in Manganese- and Copper-Doped Formate Framework of [NH₃(CH₂)₄NH₃][Zn(HCOO)₃]₂, J. Phys. Chem. C, 2016, 120, 19751–19758,  DOI:10.1021/acs.jpcc.6b07389.
48. M. Simenas, S. Balciunas, A. Ciupa, L. Vilciauskas, D. Jablonskas, M. Kinka, A. Sieradzki, V. Samulionis, M. Maczka and J. Banys, Elucidation of Dipolar Dynamics and the Nature of Structural Phases in the [(CH₃)₂NH₂][Zn(HCOO)₃] Hybrid Perovskite Framework, J. Mater. Chem. C, 2019, 7, 6779–6785,  10.1039/c9tc01275c.
49. M. Simenas, S. Balciunas, J. N. Wilson, S. Svirskas, M. Kinka, A. Garbaras, V. Kalendra, A. Gagor, D. Szewczyk, A. Sieradzki, M. Maczka, V. Samulionis, A. Walsh, R. Grigalaitis and J. Banys, Suppression of Phase Transitions and Glass Phase Signatures in Mixed Cation Halide Perovskites, Nat. Commun., 2020, 11, 5103,  DOI:10.1038/s41467-020-18938-z.
50. M. Simenas, D. Klose, M. Ptak, K. Aidas, M. Mączka, J. Banys, A. Poppl and G. Jeschke, Magnetic Excitation and Readout of Methyl Group Tunnel Coherence, Sci. Adv., 2020, 6, 1–7.
51. G. Usevicius, A. Eggeling, I. Pocius, V. Kalendra, D. Klose, M. Mączka, A. Poppl, J. Banys, G. Jeschke and M. Simenas, Probing Methyl Group Tunneling in [(CH₃)₂NH₂][Zn(HCOO)₃] Hybrid Perovskite Using Co²⁺ EPR, Molecules, 2023, 28, 1–13,  DOI:10.3390/molecules28030979.
52. J. Soetbeer, L. F. Ibanez, Z. Berkson, Y. Polyhach and G. Jeschke, Regularized Dynamical Decoupling Noise Spectroscopy-a Decoherence Descriptor for Radicals in Glassy Matrices, Phys. Chem. Chem. Phys., 2021, 23, 21664–21676,  10.1039/d1cp03103a.
53. R. M. Dimeo, Visualization and Measurement of Quantum Rotational Dynamics, Am. J. Phys., 2003, 71, 885–893,  DOI:10.1119/1.1538575.
54. M. Prager and A. Heidemann, Rotational Tunneling and Neutron Spectroscopy: A Compilation, Chem. Rev., 1997, 97, 2933–2966,  DOI:10.1021/cr9500848.
55. M. Maczka, A. Pietraszko, B. Macalik and K. Hermanowicz, Structure, Phonon Properties, and Order-Disorder Transition in the Metal Formate Framework of [NH₄][Mg(HCOO)₃], Inorg. Chem., 2014, 53, 787–794,  DOI:10.1021/ic4020702.
56. M. Trzebiatowska-Gusowska and A. Gagor, The Order-Disorder State of Diaminoalkanes in Cu-Based Metal-Organic Materials, J. Coord. Chem., 2017, 70, 1536–1547,  DOI:10.1080/00958972.2017.1305109.
57. P. Kubelka and F. Munk, Ein Beitrag Zur Optik Der Farbanstriche, Z. Tech. Phys., 1931, 12, 593–601.
58. M. Ptak, B. Dziuk, D. Stefanska and K. Hermanowicz, The Structural, Phonon and Optical Properties of [CH₃NH₃]M_0.5Cr_xAl_0.5-x(HCOO)₃ (M = Na, K; X = 0, 0.025, 0.5) Metal-Organic Framework Perovskites for Luminescence Thermometry, Phys. Chem. Chem. Phys., 2019, 21, 7965–7972,  10.1039/c9cp01043b.
59. M. Maczka, B. Bondzior, P. Deren, A. Sieradzki, J. Trzmiel, A. Pietraszko and J. Hanuza, Synthesis and Characterization of [(CH₃)₂NH₂][Na_0.5Cr_0.5(HCOO)₃]: A Rare Example of Luminescent Metal-Organic Frameworks Based on Cr(III) Ions, Dalton Trans., 2015, 44, 6871–6879,  10.1039/c5dt00060b.
60. W. Dai, F. Chi, B. Lou, X. Wei, J. Cheng, S. Liu and M. Yin, Temperature-Dependent Luminescent Properties of Cr³⁺ Doped ZnGa₂O₄ Far-Red Emitting Phosphor, Opt. Mater., 2021, 116, 1–8,  DOI:10.1016/j.optmat.2021.111104.
61. M. Ptak, D. Stefanska, A. Gagor, K. L. Svane, A. Walsh and P. Waldeci, Heterometallic Perovskite-Type Metal–Organic framework with an Ammonium Cation: Structure, Phonons, and Optical Response of [NH₄]Na_0.5Cr_xAl_0.5-x(HCOO)₃ (X = 0, 0.025 and 0.5), Phys. Chem. Chem. Phys., 2018, 20, 22284–22295,  10.1039/c8cp03788d.
62. D. Stefańska, A. Kabański, T. H. Q. Vu, M. Adaszyński and M. Ptak, Structure, Luminescence and Temperature Detection Capability of [C(NH₂)₃]M(HCOO)₃ (M = Mg²⁺, Mn²⁺, Zn²⁺) Hybrid Organic–Inorganic Formate Perovskites Containing Cr³⁺ Ions, Sensors, 2023, 23, 6259,  DOI:10.3390/s23146259.
63. M. Runowski, P. Woźny, I. R. Martín, K. Soler-Carracedo, T. Zheng, H. Hemmerich, F. Rivera-López, J. Moszczyński, P. Kulpiński and S. Feldmann, Multimodal Optically Nonlinear Nanoparticles Exhibiting Simultaneous Higher Harmonics Generation and Upconversion Luminescence for Anticounterfeiting and 8-Bit Optical Coding, Adv. Funct. Mater., 2023, 34, 2307791,  DOI:10.1002/adfm.202307791.
64. M. Runowski, D. Marcinkowski, K. Soler-Carracedo, A. Gorczyński, E. Ewert, P. Woźny and I. R. Martín, Noncentrosymmetric Lanthanide-Based MOF Materials Exhibiting Strong SHG Activity and NIR Luminescence of Er³⁺: Application in Nonlinear Optical Thermometry, ACS Appl. Mater. Interfaces, 2023, 15, 3244–3252,  DOI:10.1021/acsami.2c22571.
65. J. Ueda, M. Back, M. G. Brik, Y. Zhuang, M. Grinberg and S. Tanabe, Ratiometric Optical Thermometry Using Deep Red Luminescence from 4T2 and 2E States of Cr³⁺ in ZnGa₂O₄ Host, Opt. Mater., 2018, 85, 510–516,  DOI:10.1016/j.optmat.2018.09.013.
66. D. Stefanska, B. Bondzior, T. H. Q. Vu, M. Grodzicki and P. J. Deren, Temperature Sensitivity Modulation through Changing the Vanadium Concentration in a La2MgTiO6: V5 +, Cr3+ Double Perovskite Optical Thermometer, Dalton Trans., 2021, 50, 9851–9857,  10.1039/d1dt00911g.
67. D. Stefanska, T. H. Q. Vu and P. J. Deren, Multiple Ways for Temperature Detection Based on La₂MgTiO₆ Double Perovskite Co-Doped with Mn⁴⁺ and Cr³⁺ Ions, J. Alloys Compd., 2023, 938, 1–10,  DOI:10.1016/j.jallcom.2022.168653.
68. Q. Wang, Z. Liang, J. Luo, Y. Yang, Z. Mu, X. Zhang, H. Dong and F. Wu, Ratiometric Optical Thermometer with High Sensitivity Based on Dual Far-Red Emission of Cr³⁺ in Sr₂MgAl₂₂O₃₆, Ceram. Int., 2020, 46, 5008–5014,  DOI:10.1016/j.ceramint.2019.10.241.
69. M. Back, J. Ueda, J. Xu, K. Asami, M. G. Brik and S. Tanabe, Effective Ratiometric Luminescent Thermal Sensor by Cr³⁺ -Doped Mullite Bi₂Al₄O₉ with Robust and Reliable Performances, Adv. Opt. Mater., 2020, 8, 1–10,  DOI:10.1002/adom.202000124.
70. E. Glais, V. Dordevic, J. Papan, B. Viana and M. D. Dramicanin, MgTiO₃:Mn⁴⁺ a Multi-Reading Temperature Nanoprobe, RSC Adv., 2018, 8, 18341–18346,  10.1039/c8ra02482k.
71. S. H. Yang, Y. C. Lee and Y. C. Hung, Thermometry of Red Nanoflaked SrAl₁₂O₁₉:Mn⁴⁺ Synthesized with Boric Acid Flux, Ceram. Int., 2018, 44, 11665–11673,  DOI:10.1016/j.ceramint.2018.03.242.

---

Footnote

† Electronic supplementary information (ESI) available: Fig S1–S16: powder XRD, DSC curve, asymmetric parts and packing diagrams, SHG traces, dielectric permittivity, current density, room-temperature Raman spectra, temperature-dependent IR spectra, thermal evolution of selected IR bands, absorption spectra, Tauc plots, emission spectra, FIR ratio; Tables S1–S6: XRD experimental data, selected geometric and hydrogen bond parameters, and assignment of Raman bands. See DOI: https://doi.org/10.5281/zenodo.10624656 (link will be given upon acceptance). CCDC 2254366 and 2254367. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc04529c

---