Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Triphasic circularly polarized luminescence switch quantum simulation of a topologically chiral catenane†
Giovanni
Bella
 *,
Marco
Milone
,
Giuseppe
Bruno
and
Antonio
Santoro
*,
Marco
Milone
,
Giuseppe
Bruno
and
Antonio
Santoro
Department of Chemical, Biological, Pharmaceutical and Environmental Sciences, University of Messina, Viale F. Stagno d’Alcontres 31, 98166 Messina, Italy. E-mail: gbella@unime.it
First published on 18th January 2024
Abstract
The realm of molecular topology has witnessed a profound paradigm shift with the emergence of chiral catenanes, and their interactions with circularly polarized light are opening new perspectives in the study of chirality. Recently, the first mechanically interlocked platform based on catenane architecture acting as a multi-sequence switch of circularly polarized luminescence (CPL) was expertly designed. This unique chiral luminophore offered us the opportunity to survey the connection between the topological features and its chiral emission properties. In these terms, a theoretical DFT protocol for this CPL spectral prediction is urgent. Herein, we present a robust but accessible computational workflow able to accurately predict a triple-responsive CPL switch (on, off, and boosted signals). Taking advantage of a preliminary DFT benchmark, we decided to use the LC-wHBPE functional to realize a conformational analysis of the pyrene excimer installed in the catenane structure (for the three switchable forms) in the first excited state by means of Born–Oppenheimer molecular dynamics. Consequently, an exhaustive TD-DFT treatment demonstrated the PW6B95D3/6-311G(d,p) level to be the most valuable method to capture skillfully both the band positions and intensities for the on, off and enhanced CPL outputs generated by the interlaced molecular system.
Introduction
Mechanically interlocked molecules (MIMs) have long captured chemists’ imaginations, culminating in the 2016 Nobel prize,1–3 and through the decades, MIMs have evolved from simple structural curiosities into sophisticated molecular machines.4–6 Among the MIMs, catenane structures undoubtedly occupy a leading position, due to their higher-level spatial orientation.7 These extraordinary molecular structures, although composed of intrinsically achiral components, exhibit a remarkable chirality that challenges conventional notions of asymmetry in chemistry.8 Chirality, the property of non-superimposability of an object onto its mirror image, is ubiquitous in the natural world and plays a fundamental role in many biochemical, chemical, and material phenomena.9–15 Traditional chiral molecules, such as amino acids and sugars, derive their chirality from the spatial arrangement of atoms in their structures.16–19 However, chiral catenanes defy this conventional wisdom by showcasing chirality without any inherent molecular asymmetry in their loops.20–22 In this context, the emergence of a chiral topology in these entangled molecules offers the possibility to study the intricate interplay between the topological features and the circularly polarized luminescence (CPL). Notwithstanding the burgeoning of MIMs in many research articles,23–26 their use as chiral emitters is still extremely limited: in fact, very few examples of CPL-active mechanically interlocked molecules are reported in the literature27–30 and just one in this chemical elite is a catenane.31 This unicum exploits the excimer nature of pyrene units to create a CPL multistate switch based on a mechanically interlaced platform as excellently described in a recent article by Yang et al.31 In this unexplored landscape, a theoretical treatment of a CPL-switch is still missing, and to the best of our knowledge, quantum simulation of chiral emission spectra generated by MIMs has never been reported. With this in mind, we propose a computational protocol in order to capture the fascinating relationship between the conformational topology and the different CPL outputs in the molecular systems presented in Fig. 1. Specifically, this multiphasic chiroptical switch shows three stimulus-responsive states: on, off and enhanced. Our theoretical workflow is composed of some preliminary steps. (1) DFT analyses for finding the more suitable functional in order to energy-minimize the different forms of catenane in the ground state (S0). (2) The time-dependent density functional theory (TD-DFT) was used to follow the interlocked system in its excited state (S1), by paying attention to the diverse co-conformations that cause the cycling CPL process. (3) TD-DFT benchmark with the aim of obtaining final interpretable CPL spectra along the tri-directional chiral outputs. On these grounds, a single level of theory was finally defined to achieve an excellent level of accuracy between the three states of CPL source chirality.Results and discussion
For the purpose of accessing immediately to the theoretical focus of this study, Fig. 1 provides a complete overview of the whole chiroptical switching process, the target molecule (central part in Fig. 1, closed form) is a catenane formed by two macrocycles bearing two pyrene fragments. Ideally, it is possible to consider this supramolecular architecture as a combination of two modules: (1) the mechanically interlocked scaffold acts as a topologically chiral platform necessary to guarantee an efficient switch between the various co-conformations; (2) the pyrene units in the role of luminophores to activate the CPL emission mechanism through the excimer formation. On this basis, the introduction of external chemical stimuli can strategically orient the catenated moiety to favour a specific topological arrangement in order to modulate directly the CPL signal. On account of this situation, the closed form can undergo a bidirectional fashion: (1) the addition of acid induces the protonation of the amine sites producing the biprotonated form which provokes a boosted CPL signal (top part of Fig. 1); (2) the use of alkali metal ions (like sodium cations) triggers the entrapping by the oligo-ethylene glycol portion causing a remarkable disarticulation of the whole system which in turn destroys the pyrene stacking (open form, silent CPL signal, bottom part of Fig. 1).From a computational point of view, taking note of this precise dynamism between the three co-conformations, it intuitively emerges that the chiroptical properties are greatly dependent on the location of the molecular system within the hypersurface of potential energy.32,33 In density functional theory, the quality of the energy-optimized conformations is significantly affected by the choice of the exchange–correlation functionals,34,35 whose performances are generally ranked by virtue of benchmarks targeting the accurate prediction of X-ray preferential conformations.36–38 As a consequence of the lack of the single crystal X-ray data for the catenane depicted in Fig. 1, we decided to use its precursor whose structure was deposited in CSD,39 for our DFT benchmark (Fig. 2). We believe that this choice represents a good compromise, because this parent catenane has the same concatenated skeleton, and the absence of rigid fused rings like pyrene arms should not induce noteworthy differences in the DFT functionals’ performance.
 | ||
| Fig. 2 Chemical structure of the parent catenane; for convenience of easy drawing, only the (S) configuration is reported. | ||
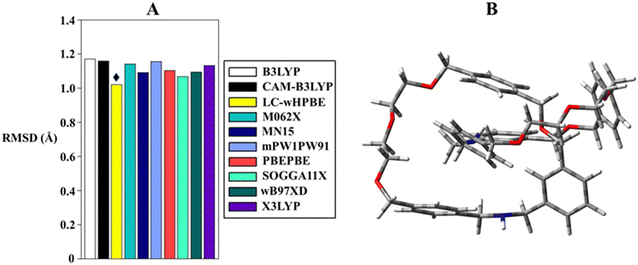
Taking into consideration the lack of bibliographic proliferation of DFT benchmarks for MIM optimization, we chose to construct our DFT set following two criteria: the selection of functionals recommended for predicting properties in MIMs40,41 and the inclusion of convenient functionals for organic molecules.42,43 With this premise, B3LYP, CAM-B3LYP, LC-wHPBE, M062X, MN15, mPW1PW91, PBEPBE, SOGGA11X, ωB97XD and X3LYP were tested in the gas phase in order to allow meaningful comparisons with X-ray crystal coordinates. The Pople basis set was adopted as it has been proven to be quite valid in modelling the second-period elements.44–46 Faced with the wealth of structural information offered by the calculations, a statistical analysis becomes appropriate to democratize which functional acts better in imitating the crystallographic structure. To accomplish this task, the root-mean-square deviation (RMSD) of all non-hydrogen atoms was assessed between the calculated 3D structure and the crystallographic atomic positions. The results shown in Fig. 3 and Table 1 indicate that the agreement between experimental and calculated geometries does not substantially vary between the tested computational methods, and just a modest fluctuation is outlined. In favour of the latter, the RMSD values span from 1.02 to 1.172 Å, and within this interval, LC-wHPBE cropped up as the best candidate to clone the X-ray molecular structure. A reasonable conclusion can be drawn focusing on the intimate nature of the mechanical bond, which can be characterized by through-space interactions, and under such circumstances, a long-range-corrected functional (LC-wHPBE) succeeds in the geometrical simulation.
| Functional | RMSD (Å) |
|---|---|
| B3LYP | 1.172 |
| CAM-B3LYP | 1.160 |
| LC-wHPBE | 1.020 |
| M062X | 1.141 |
| MN15 | 1.092 |
| mPW1PW91 | 1.156 |
| PBEPBE | 1.103 |
| SOGGA11X | 1.069 |
| ωB97XD | 1.093 |
| X3LYP | 1.134 |
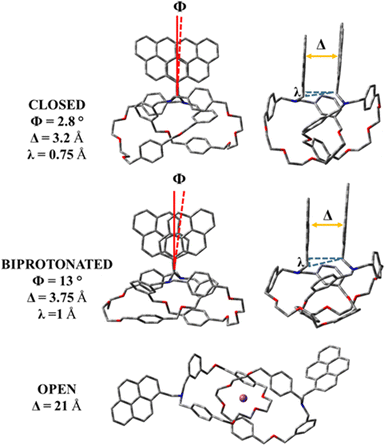
Once the leading functional was determined, based on its transferability performance, we optimized the three switchable forms (closed, biprotonated and open) at the LC-wHPBE/6-311G(d,p) level in the ground state (S0). The outcomes of the optimization jobs are summarised in Fig. 4 and clearly reveal notable differences in the catenane backbone dispositions that directly influence the pyrene stacking (responsible for the CPL signal). In these terms, the relaxed closed form exhibits an antiparallel stacked pyrene assembling with an almost imperceptible in-plane rotation (Φ ∼ 2.8°), an equilibrium layer-to-layer distance of about 3.2 Å and a vertical translation of ∼0.75 Å. A more slipped translation is recognized for the biprotonated system, the twist angle increased until 13° and the pyrene interspaced length reached 3.75 Å. This change in structural pyrene assembling parameters can be justified by concentrating on the protonated amine groups that try to minimize the coulombian repulsion by spacing out their positively charged sites (higher value for Δ). A larger value for the twist angle and the vertical translation (λ ∼ 1 Å) is due to the hydrogen bonds involving the protonated nitrogen atoms and the benzyloxy groups (see Fig. S1, ESI†), that differently set the interlocked macrocycles. Lastly, the minimum found for the open status oppositely redistributes the polyarene portions in a cryptand-like fashion implying that the sodium cations and two couples of pseudo-axial and pseudo-equatorial oxygen atoms belong to the cyclic polyether fractions (see Fig. S2, ESI†). In this specific case, the towering value of 21 Å between the pyrene components prevents any excimer intra-catenane aggregation.
The previous conformational investigation of the three possible exchangeable states constituted an indispensable starting point to explore accurately the chiral luminescence outputs along such a cyclic process. In fact when a chiroptical event such as circularly polarized luminescence regards highly flexible molecules as the presented systems, the thermal movements become important (especially in the solvent phase) and surely impact the final spectral signatures of the reversible CPL. In view of this, the topological asymmetry associated with the different excimer interactions was examined by combining thermal-dependent fluctuations with the light irradiation along the excited photochemical pathway. For the purposes hereof, ab initio excited molecular dynamics (Born–Oppenheimer molecular dynamics, BOMD) for the three separate forms (closed, biprotonated and open) in the solvent phase helped us to perform an appropriate phase space conformational sampling of the first excited state, permitting the collection of an ensemble of statistically relevant conformers. The final CPL spectra were thus simulated as a weighted sum of the spectra calculated at the TD-DFT level on temporally equispaced molecular conformation snapshots extracted from BOMD trajectories. In this way, the time-dependent formalism becomes essential to compute two decisive ingredients to recreate the chiral emission profile: the emission wavelengths (band position) and the rotatory strengths (intensity of the signal).47 Motivated by the evidence from the preliminary DFT benchmark and convinced by previous theoretical studies on pyrene excimers,48 we opted to utilize LC-wHPBE for an adequate description of the excited potential energy surfaces over time (picosecond scale). First, the scrutiny of the excited state trajectories spotlighted significant insights into the excimer interactions between S0 and S1 for closed and biprotonated forms. Given this framework, a solid discrepancy in the spatial proximity between the two pyrene layers was detected; in fact, the normalized distribution of Δ for the closed form in S1 confirms that the pyrene–pyrene distance is on average more compact than in S0 (see Fig. S3C, ESI†). An opposite trend was noticed for the biprotonated form that is inclined to separate the pyrene stacking with the aim of mitigating the electrostatic repulsion in S1 (positive charges on nitrogen atoms) as illustrated in Fig. S3C (ESI†). Curiously, in both cases, the magnitude of the pyrene–pyrene displacement is the same, 0.2 Å (3.2–3.0 Å for S0/S1 closed form, 3.7–3.9 Å for S0/S1 biprotonated one). Finally, it is obvious that in S1, the pyrene interdistance in the open form is unable to support an excimer assembly.
Once the three S1 trajectories were inspected, a salient list of exchange–correlation functionals at the TD-DFT level was trialed to quantify realistically the chiroptical responses for the three status in the CPL switch. In order to duplicate appropriately the experimental CPL spectra, APFD, B97D3, M06L, MN15, B3LYP, B98, PW6B95D3, PBEPBE, CAM-B3LYP and ωB97XD were evaluated. It must be emphasized that our primary intention aims to identify a unique functional able to emulate exquisitely the multi-state chiral emissive conditions of the switch in Fig. 1. For this reason, our modus operandi started with the selection of the closed form as our initial reference to test the performance of the aforementioned functionals with the goal of guaranteeing the best DFT-performance for the more tricky CPL spectra (biprotonated and open forms).
At first glance in Fig. 5, it is worth noting that the bisignate nature of CPL and the relative asymmetrical pseudo-Gaussian lineshape are well reproduced, highlighting proper sampling in the conformer populations. Beyond these preliminary spectral features, Fig. 5A gives an advantageous picture of the functional diversification in the ability to capture the exact band position of the experimental CPL spectrum. Remembering that the experimental CPL maximum is at 480 nm (Fig. 5B), it is virtually possible to split the collection of theoretical spectra (Fig. 5A) into three segments. (1) a section at lower wavelengths (300–400 nm) populated by the CPL maxima of CAM-B3LYP, ω-B97XD and MN15, which also fail in the computation of the intensity of the peaks (especially CAM-B3LYP and ω-B97XD). (2) A central region around 500 nm (intermediate wavelengths) crowded by PW6B95D3, PBEPBE, B98, APFD and B3LYP. In this sense, their CPL maxima are grouped between 484 nm and 505 nm, with B98 and B3LYP that moderately underestimate the band intensity. (3) A higher wavelength interval (550–650 nm) characterized by M06L and B97D3 functionals whose CPL bands suffer from an excessive red shift.
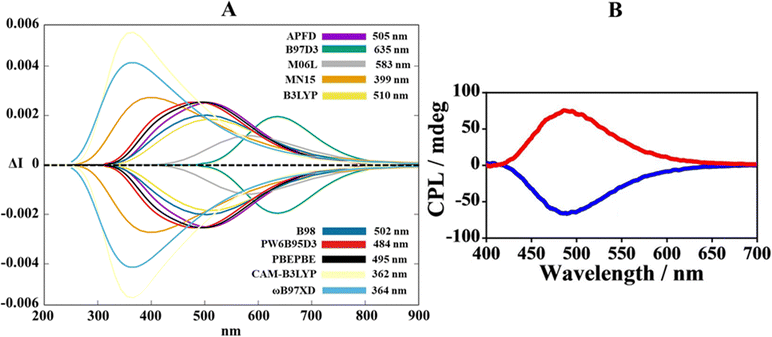 | ||
| Fig. 5 (A) Overview of TD-DFT calculated CPL spectra at the functional/6-311G(d,p) level along the MD trajectory for the closed form in CH2Cl2. (B) Experimental CPL spectrum of the closed configuration in dichloromethane. Adapted with permission from ref. 31 © 2022 Wiley-VCH Verlag GmbH & Co. KGaA. | ||
Summarizing the previous spectroscopic considerations, it distinctly appears that PW6B95D3 is the dominant functional, with an error of just 2 nm compared to the experimental maximum (but also PBEPBE could be a valid alternative), confirming its capability in determining the pyrene excimer chiral luminescence for the closed form. Persuaded by the promising vertical emission energies of PW6B95D3, we applied this functional to both biprotonated and open forms. The experimental CPL profile of the biprotonated form was amplified owing to turning off of the photo induced electron transfer (PET),49 that usually quenches the emissive process in the pyrene excimers due to the lone pairs of amines.50 The theoretical CPL spectrum delineated in Fig. 6B (blue line) managed to replicate meticulously both the intensification (supported by higher values of the rotatory strengths compared to those of the closed form, see Table S1, ESI†) and the mild red-shift of the CPL response for the biprotonated form. In contrast, TD-DFT calculations for the forbidden-excimer open form produced silent rotatory strengths all along the 25 scanned configurations (see Table S1, ESI†), expressing a CPL off signal (grey line, Fig. 6B).
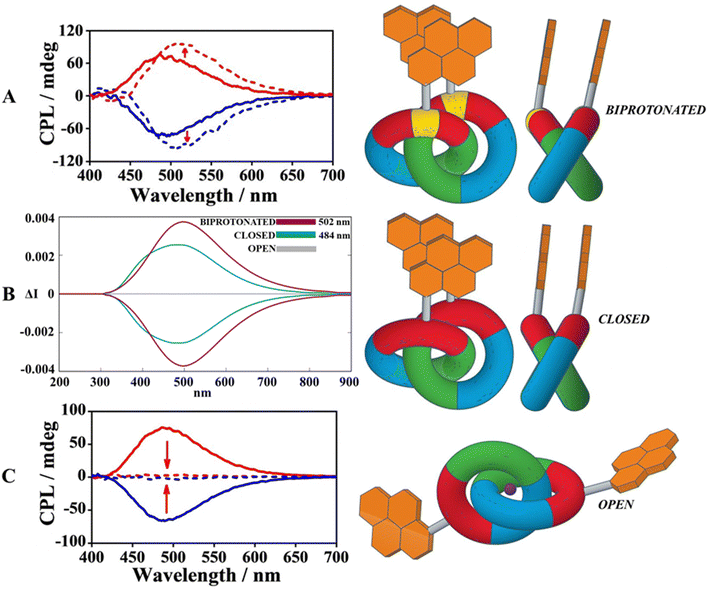 | ||
| Fig. 6 (A) Comparison between the experimental CPL spectra for closed and biprotonated (dashed profile) forms in CH2Cl2. Adapted with permission from ref. 31 © 2022 Wiley-VCH Verlag GmbH & Co. KGaA. (B) Collection of boosted (biprotonated form, blue lineshape), on (closed form, green lineshape) and off (open form, grey lineshape) CPL spectra calculated at the TD-DFT PW6B95D3/6-311G(d,p) level in CH2Cl2. (C) Comparison between the experimental CPL spectra for closed and open (dashed profile) forms in CH2Cl2. Adapted with permission from ref. 31 © 2022 Wiley-VCH Verlag GmbH & Co. KGaA. | ||
Computational details
The crystallographic structure of the parent catenane was recovered from the Cambridge Structural Database (CCDC: 1918124) and optimized in the gas phase by employing the following functionals for the DFT benchmark: B3LYP, CAM-B3LYP, LC-wHPBE, M062X, MN15, mPW1PW91, PBEPBE, SOGGA11X, ωB97XD and X3LYP coupled with 6-311G(d,p) basis set, using a superfine grid and a tight criterion for energy and geometry optimization convergence. As a consequence of the previous DFT benchmark, the minima of the closed, biprotonated and open forms of the pyrene-functionalized catenane were found at the LC-wHPBE/6-311G(d,p) level in the gas phase. For each switchable status (closed, biprotonated and open) Born–Oppenheimer molecular dynamic (BOMD) productions were run at 298 K in the first electronic state (S1) at the LC-wHPBE/6-311G(d,p) level of theory in the solvent phase (dichloromethane), with a total simulation time of 1 ps and a step size of 2 fs. The solvation environment was modelled by using the integral equation formalism for the polarizable continuum model (IEF-PCM); the default parameters of Gaussian16 were used for the construction of the cavity, built as the envelope of interlocked spheres centered on each atom of the solute (dichloromethane: ε = 8.93). Preliminarily, for the closed form, 25 equidistant configurations (every 40 fs) were obtained from the BOMD and TD-DFT subjected to extract rotatory strengths, excitation energies and oscillator strengths at APFD, B97D3, M06L, MN15, B3LYP, B98, PW6B95D3, PBEPBE, CAM-B3LYP and ωB97XD/6-311G(d,p) levels considering the first excited state (solvent phase, dichloromethane). For the biprotonated and open forms, TD-DFT calculations (for the 25 configurations) were carried out adopting the PW6B95D3/6-311G(d,p) protocol as a result of the previous analyses (same solvent conditions). The CPL intensities (ΔI) were determined as follows:51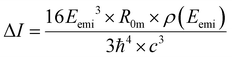 | (1) |
Conclusions
This research, based on the unique CPL emitting catenane derivative presented in the literature, made it possible to define a theoretical protocol to connect the topological chiral features with circularly polarized luminescence. For the first time, the CPL spectrum of a mechanically interlocked molecule was successfully constructed with a cheap yet accurate quantum modelling. This encouraged us to extend our simulation workflow to replicate ingeniously an unprecedented multistate CPL switch (closed, biprotonated and open) supported by mechanical bonded platforms. An initial DFT benchmark targeting the parent catenane allowed us to individuate the correct exchange–correlation functional to precisely describe the flexibility of the backbone rings; hence, LC-wHPBE was chosen as the best performer. For the CPL treatment, the computational strategy started with a Born–Oppenheimer molecular dynamic in the first excited state at the LC-wHPBE/6-311G(d,p) level to analyze the thermally dependent fluctuations that impact the excimer interactions for the three possible forms. To acquire a balanced picture of the TD-DFT performance in this specific CPL prediction, a group (10) of exchange–correlation functionals was scanned for the closed form (adopted as a “computational probe”). After thorough screening, the PW6B95D3/6-311G(d,p) level was authenticated as the first-rate method for this CPL spectral simulation and was designated to computationally recreate the different CPL outputs of the whole chiral emissive cycle. Finally, the same level of theory was shown to be extraordinarily responsive and accurate to emulate the reversible CPL intensities between on (closed), off (open) and enhanced (biprotonated) signals. In conclusion, our study intend to be a theoretical starting point for the in silico identification of the spectral chiral emission of switchable mechanically interlocked architectures.Author contributions
Giovanni Bella: conceptualization, methodology, software, validation, investigation, project administration, writing – original draft. Marco Milone: resources, writing – review & editing. Giuseppe Bruno: resources, supervision, writing – review & editing. Antonio Santoro: supervision, writing – review & editing visualization, resources, cata curation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The ISCRA (CINECA) supercomputing initiative is acknowledged for computational time provided.Notes and references
- B. L. Feringa, Angew. Chem., Int. Ed., 2017, 56, 11060–11078 CrossRef CAS PubMed.
- J.-P. Sauvage, Angew. Chem., Int. Ed., 2017, 56, 11080–11093 CrossRef CAS PubMed.
- J. F. Stoddart, Angew. Chem., Int. Ed., 2017, 56, 11094–11125 CrossRef CAS PubMed.
- S. Kassem, T. van Leeuwen, A. S. Lubbe, M. R. Wilson, B. L. Feringa and D. A. Leigh, Chem. Soc. Rev., 2017, 46, 2592–2621 RSC.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- I. Aprahamian, ACS Cent. Sci., 2020, 6, 347–358 CrossRef CAS PubMed.
- G. Gil-Ramírez, D. A. Leigh and A. J. Stephens, Angew. Chem., Int. Ed., 2015, 54, 6110–6150 CrossRef PubMed.
- J. R. J. Maynard, P. Gallagher, D. Lozano, P. Butler and S. M. Goldup, Nat. Chem., 2022, 14, 1038–1044 CrossRef CAS PubMed.
- Q. Sallembien, L. Bouteiller, J. Crassous and M. Raynal, Chem. Soc. Rev., 2022, 51, 3436–3476 RSC.
- P. Peluso and B. Chankvetadze, Chem. Rev., 2022, 122, 13235–13400 CrossRef CAS PubMed.
- J. R. Brandt, F. Salerno and M. J. Fuchter, Nat. Rev. Chem., 2017, 1, 0045 CrossRef CAS.
- F. Zaera, Chem. Soc. Rev., 2017, 46, 7374–7398 RSC.
- A. Pietropaolo, A. Mattoni, G. Pica, M. Fortino, G. Schifino and G. Grancini, Chem, 2022, 8, 1231–1253 CAS.
- P. Wu, A. Pietropaolo, M. Fortino, M. Bando, K. Maeda, T. Nishimura, S. Shimoda, H. Sato, N. Naga and T. Nakano, Angew. Chem., Int. Ed., 2023, 62, e202305747 CrossRef CAS PubMed.
- A. Giannetto, F. Nastasi, F. Puntoriero, G. Bella, S. Campagna and S. Lanza, Dalton Trans., 2021, 50, 1422–1433 RSC.
- Y.-P. Xue, C.-H. Cao and Y.-G. Zheng, Chem. Soc. Rev., 2018, 47, 1516–1561 RSC.
- A. C. Evans, C. Meinert, C. Giri, F. Goesmann and U. J. Meierhenrich, Chem. Soc. Rev., 2012, 41, 5447–5458 RSC.
- A. J. Wagner, D. Y. Zubarev, A. Aspuru-Guzik and D. G. Blackmond, ACS Cent. Sci., 2017, 3, 322–328 CrossRef CAS PubMed.
- J. E. Hein and D. G. Blackmond, Acc. Chem. Res., 2012, 45, 2045–2054 CrossRef CAS PubMed.
- E. M. G. Jamieson, F. Modicom and S. M. Goldup, Chem. Soc. Rev., 2018, 47, 5266–5311 RSC.
- A. Rodríguez-Rubio, A. Savoini, F. Modicom, P. Butler and S. M. Goldup, J. Am. Chem. Soc., 2022, 144, 11927–11932 CrossRef PubMed.
- N. H. Evans, Chem. – Eur. J., 2018, 24, 3101–3112 CrossRef CAS PubMed.
- N. Hoyas Pérez and J. E. M. Lewis, Org. Biomol. Chem., 2020, 18, 6757–6780 RSC.
- J. Yu, M. Gaedke and F. Schaufelberger, Eur. J. Org. Chem., 2023, e202201130 CrossRef CAS.
- J. Riebe and J. Niemeyer, Eur. J. Org. Chem., 2021, 5106–5116 CrossRef CAS.
- B. Taghavi Shahraki, S. Maghsoudi, Y. Fatahi, N. Rabiee, S. Bahadorikhalili, R. Dinarvand, M. Bagherzadeh and F. Verpoort, Coord. Chem. Rev., 2020, 423, 213484 CrossRef CAS.
- A. H. G. David, R. Casares, J. M. Cuerva, A. G. Campaña and V. Blanco, J. Am. Chem. Soc., 2019, 141, 18064–18074 CrossRef CAS PubMed.
- W.-J. Li, Q. Gu, X.-Q. Wang, D.-Y. Zhang, Y.-T. Wang, X. He, W. Wang and H.-B. Yang, Angew. Chem., Int. Ed., 2021, 60, 9507–9515 CrossRef CAS PubMed.
- X. Song, X. Zhu, S. Qiu, W. Tian and M. Liu, Angew. Chem., Int. Ed., 2022, 61, e202208574 CrossRef CAS PubMed.
- Z. Peng, P.-P. Jia, X.-Q. Wang, X.-L. Zhao, H.-B. Yang and W. Wang, Research Square, 2023 DOI:10.21203/rs.3.rs-2597765/v1.
- Y. Wang, J. Gong, X. Wang, W.-J. Li, X.-Q. Wang, X. He, W. Wang and H.-B. Yang, Angew. Chem., Int. Ed., 2022, 61, e202210542 CrossRef CAS PubMed.
- G. Bella, G. Bruno and A. Santoro, FlatChem, 2023, 40, 100509 CrossRef CAS.
- G. Bella, G. Bruno and A. Santoro, J. Mol. Liq., 2023, 391, 123268 CrossRef CAS.
- C. Zhao, R. Wu, S. Zhang and X. Hong, J. Phys. Chem. A, 2023, 127, 6791–6803 CrossRef CAS PubMed.
- J. Sharma and P. A. Champagne, J. Comput. Chem., 2022, 43, 2131–2138 CrossRef CAS PubMed.
- É. Brémond, M. Savarese, N. Q. Su, Á. J. Pérez-Jiménez, X. Xu, J. C. Sancho-García and C. Adamo, J. Chem. Theory Comput., 2016, 12, 459–465 CrossRef PubMed.
- G. Bella, A. Santoro, F. Nicolò, G. Bruno and M. Cordaro, ChemPhysChem, 2021, 22, 593–605 CrossRef CAS PubMed.
- G. Bella, M. Milone, G. Bruno and A. Santoro, Phys. Chem. Chem. Phys., 2022, 24, 26642–26658 RSC.
- T.-Y. Tai, Y.-H. Liu, C.-C. Lai, S.-M. Peng and S.-H. Chiu, Org. Lett., 2019, 21, 5708–5712 CrossRef CAS PubMed.
- D. Benitez, E. Tkatchouk, I. Yoon, J. F. Stoddart and W. A. Goddard, III, J. Am. Chem. Soc., 2008, 130, 14928–14929 CrossRef CAS PubMed.
- R. P. Orenha, G. F. Caramori, R. L. T. Parreira and A. Munoz-Castro, Phys. Chem. Chem. Phys., 2023, 25, 19409–19421 RSC.
- C. Liang, J. Yang, G. Luo and Y. Luo, Comput. Theor. Chem., 2020, 1187, 112942 CrossRef CAS.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- B. C. Ferrari and C. J. Bennett, J. Phys.: Conf. Ser., 2019, 1290, 012013 CrossRef CAS.
- G. Bella, A. Santoro, M. Cordaro, F. Nicolò and G. Bruno, Chin. J. Chem., 2020, 38, 163–168 CrossRef CAS.
- G. Bella and A. Rotondo, Chem. Phys. Lipids, 2020, 232, 104973 CrossRef CAS PubMed.
- M. Fortino, G. Schifino and A. Pietropaolo, Chirality, 2023, 35, 673–680 CrossRef CAS PubMed.
- M. Kołaski, C. R. Arunkumar and K. S. Kim, J. Chem. Theory Comput., 2013, 9, 847–856 CrossRef PubMed.
- A. Santoro, G. Bella, A. M. Cancelliere, S. Serroni, G. Lazzaro and S. Campagna, Molecules, 2022, 27, 2713 CrossRef CAS PubMed.
- S. H. Lee, S. H. Kim, S. K. Kim, J. H. Jung and J. S. Kim, J. Org. Chem., 2005, 70, 9288–9295 CrossRef CAS PubMed.
- G. Longhi, E. Castiglioni, S. Abbate, F. Lebon and D. A. Lightner, Chirality, 2013, 25, 589–599 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc04491b |
| This journal is © The Royal Society of Chemistry 2024 |