Surface and volume energies of α-, β-, and κ-Ga₂O₃ under epitaxial strain induced by a sapphire substrate

Abstract

In order to understand the competition among α, β, and κ phases in Ga₂O₃ deposition on sapphire substrates, particularly the easy appearance of the orthorhombic κ phase in MOCVD experiments, we calculated the volume and the surface energies under misfit strain relative to the experimental orientations of the three phases. This applies to the early stages of growth, indicating that the energetic advantage of the β-(−201) film is no longer present on the sapphire substrate. In optimizing the atomistic structure of the strained surfaces, we also discovered a very effective and intriguing reconstruction of the κ phase for the (001) and (00−1) surfaces, which is the lowest in energy among the low-Miller indexes surfaces of this phase, even at zero strain.

---

Introduction

β-Ga₂O₃ is a very promising material for high-power electronics,^1–3 beyond the present dominance of 4H-SiC, due to the larger bandgap (4.9 eV) and a moderate thermal budget in the epitaxial growth (usually, 700–800 °C by MOCVD), potentially allowing integration with the Si technology. Still, in addition to the stable β phase, which is monoclinic in structure, four different allotropic phases can be obtained through epitaxy, and the most interesting ones for power electronics, i.e. the α phase (rhombohedral, as corundum) and the κ phase (orthorhombic, formerly indicated as ε-hexagonal^4,5), display a tight competition in free energy with the β phase.^6,7 In addition to a lower degree of anisotropy with respect to the monoclinic structure, the former one displays an even larger bandgap (5.3 eV, which means a higher electric breakdown voltage), while the latter one exhibits a spontaneous polarization along the 〈001〉 direction, which is predicted to allow the formation of a two-dimensional electron gas on GaN, with a high carrier density.^8,9

For several reasons, the usual substrate in the heteroepitaxial growth of Ga₂O₃ phases is sapphire, i.e. Al₂O₃ in the α phase, oriented as (0001) when considering the conventional hexagonal cell out of the unit rhombohedral one. This is clearly one advantage in targeting the deposition of the isostructural α-Ga₂O₃, but for a sizeable lattice misfit.^10,11 Moreover, the monoclinic β phase and the orthorhombic κ phase easily grow in domains, due to the peculiar arrangement in layers of the oxygen atoms along the (−201) plane of the former and the (001) plane of the latter, which nearly matches in symmetry the oxygen network of the Al₂O₃ α phase,^12,13 but with a large anisotropic lattice misfit. Despite a poor thermal conductance, a common problem with Ga₂O₃, the sapphire substrates are reasonably cheap: this is one good reason to use Al₂O₃ in attempting the deposition of monocrystalline Ga₂O₃ films, although two structural issues hinder such a target. The first one is the misfit in lattice parameters with the substrate (see Table 4, in the following): it is some percent for the α phase, still isotropic in the (0001) plane, whereas it is larger and anisotropic for the 〈001〉 orientation of the κ phase and, particularly, for the 〈−201〉 orientation of the β phase. This calls for interfacial strategies in relieving the strain: while the common plastic relaxation by dislocations is demonstrated in the case of α-Ga₂O₃,^10,11 rotational domains appear to mitigate the elastic energy in case of anisotropic strain, and this is the second problem. In addition to this, buffer layers of non-stoichiometric phases, or the relaxed α phase, are reported for the κ¹³ and the β phases,¹² respectively.

The role of the interface and the related kinetic issues are evidenced by the fact that various growth methods (mist-CVD, MOCVD, High-Vacuum VPE, MBE, PLD, Halide-VPE) and diverse growth conditions^14–17 lead to different phases. The situation is rather complex, but some trends are sufficiently clear: low temperatures (and/or high growth rates) favor the α phase, intermediate values the κ phase, whereas conditions closer to equilibrium induce the stable β phase. Due to the large misfit strain, it appears that epitaxy in the initial stage should proceed via island formation, particularly in the case of the β phase, where a 3-D configuration is evident.^18,19 This suggests that a longer surface diffusion length (as obtained closer to equilibrium conditions) promotes the 3-D accumulation of the stable β structure, whereas a ready incorporation at the 2-D interface sites favors the epitaxial lock-in of the other two metastable phases.^17,20

In order to make some quantitative predictions/interpretations, the adoption of the nucleation and growth model by 3-D islands has been recently suggested for the competition between the κ and the β phase in MOCVD experiments.²¹ Rather than focusing on the complex kinetic barriers in surface diffusion, this consolidated approach to the kinetic issues of the epitaxial growth considers thermodynamic parameters, such as the surface energies of the islands in different phases, their volumetric energies under a biaxial strain with respect to the chemical potential in the gas phase, and the interface energies. It is clear that, even considering these thermodynamic parameters, comparing different low-symmetry binary structures is a formidable task, when the degree of experimental information on the island faceting with strain is by far lower to what has been achieved in the simple and prototypical case of Ge–Si islands on Si.^22,23 Moreover, the interface of the different Ga₂O₃ phases with the sapphire substrate poses a more fundamental problem for a computational analysis: do the buffer layers of a different phase (α dislocated, γ non-stoichiometric, or composition of them^4,13,14,17) appear at the growth front, or are they produced at some critical thickness, as for the case of the plastic relaxation?

Aiming at setting some quantitative background for the nucleation and growth modelling of ref. 21, at least for the early growth stages, we present here a comparison of the volume and surface energies for three different phases of Ga₂O₃, namely α, β, and κ, as calculated by density functional theory (DFT) and including the strain produced by the sapphire substrate. Actually, the estimate of the surface energies for the κ-Ga₂O₃ (001) free surfaces is still not present in the literature, probably due to the lack of a mirror symmetry between the top and the bottom surfaces in a slab configuration. The elastic contribution of the lattice misfit with the sapphire substrate (and with a plastically relaxed α-Ga₂O₃ buffer layer) was calculated by imposing the matching between the planar network of oxygen atoms of the film and the one of the substrate, specifically for the surface orientations that have been experimentally observed at the growth front. The interesting variation with strain in the hierarchy of the Ga₂O₃ phases, both in volume and in surface energies, will be discussed, and some preliminary considerations to an island modelling will be presented. In particular, the fact that the oxygen layers are bridging the films with the substrate (or with a buffer layer) points out that the main issue is the physical strain to (nearly) accommodate the misfit in the two networks, more than a different chemical bonding at the interface. For such a reason, in addition to the complexity of buffer layers described above, the interface energies are still not explicitly considered here and will be the subject of a work in progress.

Computational methods for volume energies

As shown in Fig. 1, the three phases are characterized by a different Ga–O coordination. While in the α-Ga₂O₃ all Ga atoms are coordinated with six O atoms forming octahedral cages, in β and κ phases 50% and 25% of Ga atoms are four-coordinated, respectively, forming tetrahedral complexes. The vertical axis in Fig. 1 indicates the actual growth direction and the alternate layers of oxygen atoms (in red) are evident.

Fig. 1 Optimized structures of the conventional cell of bulk α- (a), β- (b) and κ-(c) Ga₂O₃. Ga and O atoms are shown with grey and red spheres, respectively; solid black lines show the cell structure. Tetrahedral and octahedral Ga–O coordination structures are shown as well, through orange and blue surfaces. The vertical direction of the image is aligned with the normal of the surfaces discussed below, i.e. the (001) (a), (−201) (b) and the (001) (c) planes, respectively.

It is known in literature that the hierarchy in cohesion energy (E_coh) of Ga₂O₃ polymorphs at T = 0 K is sensitive to the choice of the exchange and correlation functional, since in some cases the α phase is found to be slightly more stable than the κ one.^6,7,24–26 This is not surprising on qualitative grounds: while Al ions are smaller and α-Al₂O₃ is clearly the most stable phase,⁷ due to a larger Madelung contribution provided by the octahedral cages, the Ga ions are larger and the steric repulsion favors the more open β phase, with 50% of tetrahedral sites. The κ and the α phases compete tightly in steric and Madelung contributions for the case of Ga₂O₃. Anyhow, we started our analysis by performing the bulk calculations with two GGA functional,^27,28 the AM05 functional²⁹ and a meta-GGA functional³⁰ (see Tables S1 and S2, ESI†). Our results are in good agreement with those reported in the literature and the PBEsol functional reproduces the same hierarchy in E_coh (β < α < κ) of the more sophisticated SCAN functional, being also more suitable for the surface energy calculations.

Therefore, we performed all calculations within the DFT framework using the VASP software,^31–33 using the Perdew–Burke–Ernzerhof exchange–correlation functional revised for solids (PBEsol).²⁸

We employed pseudopotentials with 6 and 13 electrons in the valence states for O and Ga atoms, respectively. To obtain strain-free structures for the bulk cases, both the ionic coordinates and the cell parameters have been optimized by a plane waves cut-off of 850 eV: still, the calculation of E_coh did not change appreciably setting the energy cut-off for the plane waves basis set to 500 eV, and such a value was used for the energies, due to computational speed reasons. The Brillouin zone was sampled through 10 × 10 × 5, 11 × 11 × 11 and 10 × 10 × 5 unshifted Monkhorst–Pack k-point meshes for the unit cells of α (triclinic), β (monoclinic) and κ (orthorhombic) phases, respectively, and suitably reduced in the case of larger supercells.

Results for volume energies

We report in Table 1 the values of the cohesive energy E_coh, calculated for the three different Ga₂O₃ polymorphs. The β phase is the most stable one, while the κ and the α polymorphs are very close, with the former having the higher energy, in agreement with ref. 25 (see Table S1 in the ESI†). With respect to the competition between steric repulsion and Madelung energy, we also display the atomic density and the charge partitioning between the two constituent atoms, as calculated by the Bader criterion^34,35 which is not sensibly different between tetrahedral and octahedral sites (the number of neighbors makes the difference), and in agreement to the large electronegativity difference between Ga and O. Finally, it is fair to say that our results are obtained at T = 0 K, i.e. we deal with cohesion energy, not the free energy, which includes the entropic contribution provided by the phonon population. Actually, the MOCVD growth temperatures are 600–800 °C and in such conditions the κ phase is predicted to come very close to the β one, due to a larger phonon density of states at low energies.⁶

Table 1 Difference of the cohesive energy with respect to the β polymorph ΔE_β, atomic density ρ and charge partitioning calculated for the optimized bulk of different Ga₂O₃ phases

Phase	ΔEβ (meV per atom)	ρ (atoms per Å^3)	Valence electrons
			Gaoct	Gatetra	Omin–Omax
β	0	0.095	11.12	11.19	7.24–7.22
κ	+13	0.098	11.14	11.18	7.22–7.26
α	+9	0.103	11.15	—	7.23

---

Computational methods for surface energies

After confirming the validity of our results by the PBEsol functional for strain-free bulk structures, we move now to the surfaces. In this case, we exploited the slab construction by inserting a vacuum region of at least 13 Å in the supercell along the direction perpendicular to the surfaces, avoiding interactions between the two terminating surfaces of the periodically repeated slabs.

We first investigated the (001), (100) and (012)§ surfaces of the α phase and the (001), (11−2) and (−201)¶ surfaces of the β phase: their surface energies (γ) have already been reported in different works,^36–41 as these surfaces are quite competitive in γ for each phase. Still, we add a graphical discussion of the changes in coordination of the surface atoms, to help with the interpretation of the γ values, by moving from “as-cut” surfaces to those obtained after ionic relaxation (named as “relaxed”), or after forcing the reconstruction of the terminations (named as “reconstructed”, if any). This approach is rather useful in discussing the unprecedented calculations for the (001), (010) and (100) surfaces of the κ phase, where one unexpected reconstruction occurs for the (001) one. Lacking most of the experimental data on the surface reconstructions, we considered only the γ of stoichiometric slabs. Actually, the (001) surfaces of the α and κ phases and the (−201) of the β phase are the ones observed at the growth front for Ga₂O₃ films on the sapphire substrate,^{11–13,18,42,43} so that they will also be investigated in the case of misfit strain in the next section.

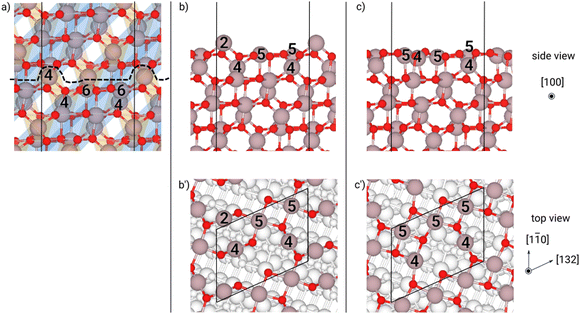
While cleaving the surfaces out of the bulk configuration, we chose those terminations minimizing the number of dangling bonds, because the cost of exposing a surface is roughly proportional to the broken bonds (see the sketches in panel (a) of (Fig. 2–11). We label such cleaved surfaces “as-cut” that can be seen by a side and top view in panel (b–b′) of Fig. 2–11. We then optimized the atomic coordinates only, keeping the in-plane cell parameters of the slab fixed to the corresponding bulk-like values (reported in Table S3, ESI†): we label these structures “relaxed”, as seen from side and top view, in panel (c–c′) of Fig. 2–11. In two cases, we also took into account low-γ reconstructions: the one for the β (−201) surface, which has already been reported in the literature as being more stable than the relaxed one,⁴¹ and the one for the κ-{001} surface, which we identified as particularly low in γ, during the optimization of our slabs (see Fig. 10(d) and 11(d)). The latter reconstruction spontaneously occurred in our relaxation procedure only with the misfit-strained slab, as described in the following sections (see also Fig. S12 in the ESI†). In the unstrained case, we optimized an initial structure placing the atoms in a configuration corresponding to the strained result but adapting the cell parameters to the unstrained case. The resulting strain free configuration had a lower surface energy with respect to the relaxed case.

Fig. 2 Structures of the (−201) β-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab, (c)–(c′) “relaxed” slab and (d)–(d′) “reconstructed” geometry. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. In panels a and d, the two Ga atoms added to the “as-cut” slab to obtain the “reconstructed” structure are marked with black circles. Ga and O atoms are shown with grey and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 3 Structures of the (11−2) β-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 4 Structures of the (100) β-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 5 Structures of the (001) α-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 6 Structures of the (100) α-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 7 Structures of the (012) α-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 8 Structures of the (100) κ-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 9 Structures of the (010) κ-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab and (c)–(c′) “relaxed” slab. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 10 structures of the (001) κ-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab, (c)–(c′) “relaxed” slab and (d)–(d′) “reconstructed” geometry. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. In panels b–d′, the major displacements of O and Ga atoms are marked with black, green and blue arrows. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

Fig. 11 Structures of the (00−1) κ-Ga₂O₃ surface at different optimization steps: (a) cleaving the bulk, (b)–(b′) “as-cut” slab, (c)–(c′) “relaxed” slab and (d)–(d′) “reconstructed” geometry. In the bulk (a), orange/blue polyhedra highlight tetrahedral/octahedral coordination cages. For selected Ga atoms, the number of first neighbors is reported. In panels b–d′, the major displacements of O and Ga atoms are marked with black, green and blue arrows. Ga and O atoms are shown with gray and red spheres, respectively; the supercell is shown by the black solid line and the cleaving termination with the dashed line.

All the corresponding results for the surface energies in meV Å⁻² are reported in Table 3, but before coming to a detailed discussion some peculiar issues of our calculations need to be reported.

By definition, γ can be calculated from the total energy of the slab, subtracting the bulk contribution E_coh for all its constituent atoms: a tiny difference is therefore estimated by subtracting two much larger quantities. The value E_coh, therefore, should be carefully evaluated, taking the same unit cell and k-grid of the slab for a periodic crystal, in order to avoid a systematic error. Thus, we chose the linear extrapolation method reported in ref. 7 where γ is obtained through the linear relationship between the total energy E of two slabs with different thickness and their number of atoms N as follows (given the surface area A):

For the β- and α-Ga₂O₃ surfaces, we chose a slab thickness already tested in literature to provide reliable calculations, usually expressed in terms of the number of the multi-atomic layers to replicate the structure of the bulk. For the surfaces of the κ phase, we maintained a similar number of layers: to provide an easier comparison among the different phases we report in Table 2 the slab thicknesses in Å.

Table 2 Thickness (reported in Å) of the slabs investigated in this work for the calculation of the surface energies

	β			α			κ
	(−201)	(11−2)	(100)	(001)	(100)	(012)	(100)	(010)	(00±1)
Thin	17.7	16.8	39.8	30.8	17.3	27.4	12.4	20.4	22.4
Thick	22.4	18.9	45.7	39.7	21.6	31.3	16.7	29.9	31.6

---

We would like to emphasize that all the surfaces possess mirror symmetry along the direction perpendicular to the surfaces, except the {001} slabs of κ-Ga₂O₃. In such a case, the slab has a net surface dipole, because the (001) surface exposed on top is not equivalent to the (00−1) one cleaved at the bottom of the same slab. For example, looking along the direction perpendicular to the cutting plane in Fig. 10(a), the tetrahedra on the two sides have a different orientation. Hence, the Ga atoms on the two facets have a slightly different coordination towards the bulk side (see the analysis of the coordination in Fig. S9 and S10, ESI†). Although we corrected the artificial potential due to the asymmetric slab by inserting a dipole correction in the vacuum region, we deemed crucial to assess the separate energy contribution of the two surfaces. Therefore, we adopted the “simultaneous equations method” described in ref. 44, which exploits the linear system defined by the total energies of the same slab with four different configurational constraints: both surfaces “as-cut”, both surfaces relaxed, top surface relaxed and bottom surface “as-cut”, top surface “as-cut” and bottom surface relaxed (see the discussion in the ESI†). We report the two values of γ calculated with this approach for the {001} surfaces in Table 3 for the “as-cut” and “relaxed” slabs. We notice that, independently from the optimization step, the results are not equal, yet rather similar, at least within the scope of the thermodynamic stability of the different phases. Hence, we can assume that neither of the two terminations has a γ remarkably different from the other and should be treated as an additional surface. Therefore, in the rest of our work we will not perform this additional analysis. We anticipate, however, that the differences between the (001) and (00−1) surface regions, particularly concerning few layers below, where tetrahedral rather than octahedral sites are present, cannot be completely neglected, and will be affected by the new reconstruction, driving the slab towards a common, more-symmetric structure, as we will discuss later on.

Table 3 Surface energies γ calculated for different Ga₂O₃ phases and facets. The reference values, in square brackets, are calculated using the³⁹ HSE,^36,38 B3LYP or³⁷ PBE exchange and correlation functionals

Phase-surface		Geometry	γ (meV Å^−2)
β	(−201)	As-cut	146 [166^39]
		Relaxed	58 [60,^39 58^38]
		Reconstructed	50 [47^41]
	(11−2)	As-cut	162
		Relaxed	65 [60,^39 62^41]
	(100)	Aas-cut	52 [37,^39 60^36]
		Relaxed	37 [21,^39 42,^36,39 40^38]
α	(001)	As-cut	157
		Relaxed	70 [60^37]
	(100)	As-cut	162
		Relaxed	100 [89]
	(012)	As-cut	115
		Relaxed	88 [59^37]
κ	(100)	As-cut	175
		Relaxed	100
	(010)	As-cut	145
		Relaxed	101
	(001)/(00−1)	As-cut	164/160
		Relaxed	80/84
		Reconstructed	53

---

With the aim of providing a facile descriptor for the chemical environment of each atom, we calculated the number of first neighbors (N_f) by integrating its pair distribution function within a radius of 2.5 Å. We take such a cutoff since it preserves the topology of the coordination cage of the Ga species, i.e. tetrahedral/octahedral, within the different phases. The comparison of the whole pair distribution functions is reported for all our slabs in Fig. S1–S10 (ESI†).

Results and discussion of surface energies

The comparison between the values of γ for different phases and surfaces confirms some trends present in literature and adds new results for the κ phase. The relaxed surfaces of the β phase generally display the lower values in energy, probably due to the fact that the inward displacement of Ga surface atoms, partially recovering the bulk coordination (see the coordination numbers in (Fig. 2–4) is favored by a more open structure compared with the other phases. For a graphical representation of the atomic displacements, see Fig. S1–S3 in the ESI.†

This effect generates the large decrease in γ between the “as-cut” and the “relaxed” configuration, while the reconstruction of the (−201) further lowers the surface energy by a moderate amount. In Fig. 2(d), the additional formula unit providing the reconstruction is indicated by the two top Ga atoms fourfold coordinated.

Interestingly, the β-(100) surface (which corresponds to the termination with lowest γ labelled “B” in ref. 36, 38 and “A” in ref. 41) has a much lower γ than the (−201), since the number of dangling bonds is quite small already in the “as-cut” configuration, and the relaxation mostly acts on the electronic transfer,^39,45 rather than a recovery in coordination (see Fig. 4). However, this orientation is not the one eventually observed during the growth of a film on sapphire, probably due to the different symmetry in the network of oxygen atoms at the interface (compare Fig. 4(c′) with e.g.Fig. 2(c′)): still, these facets are likely to appear in the early nucleation of 3-D islands. All our results are in good agreement with the literature results, as obtained with the same and other exchange–correlation functionals (see Table 3).

For what concerns the α phase, the one with a larger atomic density provided by all octahedral sites, the lowering of γ from the “as-cut” configuration to the “relaxed” one is minor and remains quite high, with no recovery in surface atom coordination (see Fig. 5–7 and Fig. S4–S6, ESI†).

A sizeable decrease in energy is seen just in the case of the (001) surface, and this corresponds to a larger inward motion of one Ga surface atom (see Fig. 5(c)), probably corresponding to a more suitable distribution of electrons from the dangling bonds of the Ga to the O atoms.³⁹ In the case of the α-Ga₂O₃ surfaces, the agreement of our numerical results with literature data (see Table 3) is less satisfactory, still preserving the hierarchy. We ascribe this discrepancy to the different exchange–correlation functional used in our calculations (PBEsol vs. PBE), since we found similar energy variations in the bulk (see Table S1, ESI†).

Finally, we come to the unprecedented results of the κ phase: the surface energies for the (100) and (010) orientations display large values even for the “relaxed” configurations, comparable to the ones of the α phase, suggesting that the inward motion of the Ga surface atoms is hindered by the structure, in some cases compensating the increase in coordination of one atom in the surface cell with a decrease in coordination of another one in the same cell (see Fig. 8 and 9).

It is true that these orientations do not appear in the growth front of a film on sapphire and that (001)-oriented 2-D islands are visible in the experiments,²¹ rather than 3-D islands. Actually, the most interesting results come from (001) and (00−1) surfaces: in both cases a large decrease in γ from the “as-cut” configuration to the “relaxed” one appear, in a way similar to the β case. In Fig. 10, 11 and Fig. S9, S10 (ESI†), it is apparent that a large inward motion of two Ga atoms in the surface unit cell occurs with relaxation, even recovering a coordination 4 in the case of the (00−1) surface. Still, the subsurface configuration of the two orientations is different (Ga atoms in octahedral sites rather than tetrahedral ones) and this may explain why the two γ values are slightly different, even after the relaxation. However, the lowest surface energy for the two opposite surfaces is attained by a relevant reconstruction, which involves not only the first Ga layer, but also the ones below, leading to a situation very similar for the two opposite surfaces (see Fig. 10(d) and 11(d)). In both cases, one surface Ga atom deeply dips to the second Ga layer (see the green arrows) and change coordination from 3 to 6, whereas the consequent structural rearrangement in the layers below turns to have one Ga atom with coordination 4 and one with coordination 6 (see the blue arrows), starting from two Ga atoms with coordination 6 in the (00−1) surface, or two Ga atoms with coordination 4 in the (001) surface. This kind of “symmetrisation” of the two opposite surfaces actually leads to a γ value practically equal one to another and fully comparable to the reconstructed (−201) surface of the β phase.

Computational methods for volume and surface energies with misfit strain

In this section we evaluate the role of the strain induced by the interface lattice misfit to volume energy of the three phases, and to selected surface energies. In order to perform a comparison with growth conditions, we considered the relevant β (−201), κ (001) and α (001) orientations of the Ga₂O₃ film with respect to two substrates: the actual pattern of the sapphire and the relaxed (001) α-Ga₂O₃. The latter case displays a less severe lattice misfit, sometimes providing a relaxed buffer layer for the growth of the other polymorphs.^10,11

Since each oxygen layer provides a chemical bridge between the substrate and the film, and since the coordination of this planar network is the same in both cases (see Fig. 12), we decided to estimate the misfit strain of the film by imposing a global minimization of the differences of the in-plane positions of the O atoms of the film (red dots) with respect to the ones of the substrate (blue dots), under the independent variation of two perpendicular lattice sides. In particular, we constructed rectangular conventional cells, including both the planar periodicity of the film and the one of the substrate, when the two oxygen layers are nearly coincident by variation of the rectangular sides for the film. We illustrate this procedure for the case of the (−201) β-Ga₂O₃ and the (001) κ-Ga₂O₃ on (001) α-Al₂O₃ in Fig. 12(a)–(d), respectively. This procedure is intended to mimic the actual process occurring during the early stages of deposition.¹² Then, we define the misfit parameter between the growing crystalline phase and the substrate along either directions as f_i = (a^film_i − a^sub_i)/a^film_i and we report the values in Table 4. Our values of the lattice misfit are in good agreement with those available in the literature. In the case of the (−201) surface of β-Ga₂O₃, the result reported in ref. 12 is just a mean value, calculated taking an average in-plane O–O distance. In the case of κ and α phases, the difference is due to relying on the calculated lattice parameters rather than the experimental ones (especially for the Al₂O₃ substrate, since a_expt = 4.76 Å⁴⁶vs. a_theor = 4.80 Å).

Fig. 12 Matching of the in-plane coordinates of O atoms at the surface for the (−201) β-Ga₂O₃ (panels a and b) and (001) κ-Ga₂O₃ (panels c and d) surfaces on the (001) α-Al₂O₃ substrate. Panels a–c or b–d show the overlap of the two structures before or after the deformation of the Ga₂O₃ overlayer, respectively. In panels a–c, the semi-opaque areas mark the in-plane unit cell of the different elements, i.e. with the gray or orange box the Ga₂O₃ or Al₂O₃ in-plane cells. In panels b and d the strained cells of Ga₂O₃ are show through the light-orange box, while the difference with the un-strained cell is shown by the thick orange region. The O atom taken as a reference for straining the Ga₂O₃ structure is indicated by a black circle.

Table 4 Cohesive energy differences ΔE_β and ΔE^opt_β reported with respect to the β phase (calculated with fixed and optimized atomic coordinates, respectively) and the corresponding elastic energy contributions ΔE_el and ΔE^opt_el of the strained polymorphs of Ga₂O₃. The values of the bi-axial strain are equal to the misfit parameter f calculated for different reference planes on different substrates. The x/y axis is aligned with the [100]/[−120] direction of the c-sapphire. The corresponding crystal directions for each phase are reported as well

Bulk		β			α			κ
Plane		(−201)			(001)			(001)
vs. (001) α-Al2O3	f x (%)	[102]	2.4	6.6^12	[100]	3.9	4.5^13	[100]	5.1	5.3^13,19
	f y (%)	[0−10]	8.9		[−120]		4.7^42	[010]	4.1
	ΔEβ (meV per atom)	0			−97			−74
	ΔEel (meV per atom)	158			52			72
	ΔE^optβ (meV per atom)	0			−52			−46
	ΔE^optel (meV per atom)	109			48			50
vs. (001) α-Ga2O3	f x (%)	[102]	−1.6		—			[100]	1.2
	f y (%)	[0−10]	5.3		—			[010]	0.2
	ΔEβ (meV per atom)	0			−30			−24
	ΔEel (meV per atom)	39			0			3
	ΔE^optβ (meV per atom)	0			−22			−16
	ΔE^optel (meV per atom)	30			0			2

---

We approach first the case of the bulk, and we focus our attention on the changes in E_coh under an anisotropic deformation. Starting from the already optimized strain-free bulk structures, we constructed conventional unit cells in which the z axis is along the direction normal to the surface of interest (see Table S3, ESI† for additional details on these unit cells), and the strain corresponding to the misfit is applied to the in-plane orthogonal sides of this conventional cell. Along the z direction, the cell parameter is optimized to get the minimum cohesion energy, calculated by varying the height of the cell, starting from values close to the simulated Poisson ratios, which are reported in the literature.⁴⁷ We investigated two limiting cases: in the first one, we kept the fractional coordinates of the atoms fixed to those in the unstrained geometry, in order to evaluate a purely elastic contribution.

In the second case, we re-optimized the atomic coordinates within the cells, in order to include possible rearrangements of the atomic positions. The resulting values of E_coh under strain, and the elastic contributions ΔE_el and ΔE^opt_el are reported in Table 4.

In the case of the surfaces under strain, we started from the “as-cut” configuration, then we applied the misfit strain to the slab, and finally we relaxed the structure. For the reconstructed β (−201), we started from the strain-free configuration of the reconstruction reported in literature,⁴¹ we applied the biaxial strain, and then we relaxed the structure. The same holds for κ-(00±1) with a misfit strain corresponding to the α-Ga₂O₃ buffer layer (reduced misfit), while for the misfit strain corresponding to the α-Al₂O₃ the reconstruction spontaneously appears with relaxation (see Fig. S12 in the ESI†). In all these cases, the Poisson deformation is naturally fulfilled by the free surfaces. We report the resulting values of γ in Table 5.

Table 5 Surface energy γ for different strained surfaces of Ga₂O₃, given the epitaxial match with the two substrates

Phase-surface	With strain – on α (001)-Al2O3			With strain – on α (001)-Ga2O3
	γ as-cut (meV Å^−2)	γ relaxed (meV Å^−2)	γ reconstructed (meV Å^−2)	γ as-cut (meV Å^−2)	γ relaxed (meV Å^−2)	γ reconstructed (meV Å^−2)
a This structure spontaneously optimizes in the reconstructed geometry when the applied strain corresponds to the misfit with the sapphire substrate.
β-(−201)	158	85	57	146	63	53
α-(001)	156	88	—	—
κ-{001}	179	86^a	86	168	87	53

---

Results and discussion for volume and surface energies with misfit strain

The strain induced in the β phase by the substrate is obviously larger and more anisotropic on c-sapphire than on a relaxed α-Ga₂O₃ buffer layer. Still, by considering the cohesion energies, in both cases the sizeable anisotropic strain is sufficient to alter the hierarchy in energy: the α and the κ phases are favored, and the difference between the latter ones remains small, even on c-sapphire, when the atomic positions inside the cell are optimized under misfit strain. Interestingly, a more general calculation of E_coh as a function of the strain reveals that the ordering of the polymorphs is driven mainly by the strain along the 〈−120〉 directions of (001) α-Al₂O₃ (see Fig. S11, ESI†). Finally, our calculations are performed at zero temperature and the additional extra gain due to the vibrational entropy, predicted in literature for the κ phase over the α phase at zero strain and finite temperatures,^6,48 should be re-calculated in such conditions and included.

As far as the surface energies are concerned, it appears that the clear hierarchy in the values for relaxed surfaces at zero strain (β < α < κ) is no longer present with c-sapphire misfit, as the three values are very close, in the range 85–88 meV Å⁻², probably within the computational resolution, including the spontaneous reconstruction of the κ-(001). It is fair to say that the β (−201) reconstruction provides a sensible lowering in surface energy, but as soon as substrate is the α-Ga₂O₃ buffer layer, then surface energies for the reconstructed β (−201) and κ (001) become fully degenerate, similar to the strain-free case.

Conclusions

In this work we aimed at setting some quantitative information concerning the competition among three Ga₂O₃ phases during epitaxial deposition on sapphire. Actually, the κ phase is frequently appearing in MOCVD experiments when the surface diffusion length is hindered by lower temperatures and/or larger growth rates. Starting from the early deposition stages, when the misfit strain is dominant and no plastic/elastic relaxation already occurred, the volume energy of the β phases is no longer the lowest in energy and the α, κ values are very close, at least at zero temperature. The surface energies of the relaxed surfaces are also very close and the only way to elastically relax the extra misfit cost for the β is to generate 3-D island, provided the surface diffusion is promoted by higher temperatures and lower growth rates. As the misfit strain is released, either by plastic relaxation by extended defects, or by buffer not-stoichiometric phases, the volume energy of the β phase is more favourable with respect to the other two phases (only at zero temperature), but the surface energies of the reconstructed β-(−201) orientation and of the new configuration of the κ-(001) orientation are very close, one to another. Fig. 3 of ref. 21 is the most pertinent experimental reference to our results, as it is clear how the comparable surface energies of the reconstructed surfaces (and predicted volume free energies at growth temperature), especially when the misfit strain is released at sufficient MOCVD deposition thickness, are producing a tight competition between the β and the κ phases, favoring the former at low growth rates and higher temperatures. It is worth mentioning how the amorphous phase appears at very low temperatures, e.g. below 200 °C in plasma-enhanced ALD,⁴⁹ turning to the α phase as the growth temperature is raised at some 250–350 °C, and to a mixture of the α and the κ phases, as the temperature is above 350 °C. This indicates that the large lattice misfit between the two oxides requires a minimum surface diffusion length in order nucleate some local portions of crystalline phase: below such threshold, no structural surface lock-in of the substrate plays a role in nucleating the preferred α-phase.

Finally, it is an open question to debate if the surface reconstruction of the β-(−201) is relevant during the dynamical growth, as it is based on the addition of a stoichiometric unit of atoms at the surface, whereas the new configuration for the κ (001) reconstruction relies on surface and sub-surface rearrangement, the kinetic barrier of which is not present for misfit-strained structure, as shown in Fig. S12 at the end of the ESI.† The interface energies are still missing in this picture and are to be calculated with care: it appears, however, that the misfit-strain contributions are important in changing the energetic hierarchy, probably more than the chemical bonding across the similar oxygen network between the two crystalline sides.

Author contributions

I. B. investigation, formal analysis, visualization; A. U. investigation, validation, formal analysis, writing original draft; E. S. methodology, validation, formal analysis, resources; L. M. conceptualization, formal analysis, writing original draft, supervision, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was carried out within the MOST–Sustainable Mobility Center and received funding from the European Union Next-GenerationEU (PIANO NAZIONALE DI RIPRESA E RESILIENZA (PNRR)–MISSIONE 4 COMPONENTE 2, INVESTIMENTO 1.4 – D.D. 1033 17/06/2022, CN00000023). The authors thank Prof. Roberto Fornari and colleagues (Department of Mathematical, Physical and Computer Sciences of Parma University) for discussions and for reading our manuscript in advance.

Notes and references

1. S. J. Pearton, J. Yang, H. I. V. Cary Patrick, F. Ren, J. Kim and M. J. Tadjer, et al., A review of Ga₂O₃ materials, processing, and devices, Appl. Phys. Rev., 2018, 5(1), 11301,  DOI:10.1063/1.5006941.
2. A. J. Green, J. Speck, G. Xing, P. Moens, F. Allerstam and K. Gumaelius, et al., β-Gallium oxide power electronics, APL Mater., 2022, 10(2), 29201,  DOI:10.1063/5.0060327.
3. M. Biswas and H. Nishinaka, Thermodynamically metastable α-, ε- (or κ-), and γ-Ga₂O₃: From material growth to device applications, APL Mater., 2022, 10(6), 60701,  DOI:10.1063/5.0085360.
4. I. Cora, F. Mezzadri, F. Boschi, M. Bosi, M. Čaplovičová and G. Calestani, et al., The real structure of ε-Ga₂O₃ and its relation to κ-phase, CrystEngComm, 2017, 19(11), 1509–1516,  10.1039/C7CE00123A.
5. H. Nishinaka, H. Komai, D. Tahara, Y. Arata and M. Yoshimoto, Microstructures and rotational domains in orthorhombic ε-Ga₂O₃ thin films, Jpn. J. Appl. Phys., 2018, 57(11), 115601,  DOI:10.7567/JJAP.57.115601.
6. S. Yoshioka, H. Hayashi, A. Kuwabara, F. Oba, K. Matsunaga and I. Tanaka, Structures and energetics of Ga₂O₃ polymorphs, J. Phys.: Condens. Matter, 2007, 19(34), 346211,  DOI:10.1088/0953-8984/19/34/346211.
7. Y. Hinuma, T. Gake and F. Oba, Band alignment at surfaces and heterointerfaces of Al₂O₃, Ga₂O₃, In₂O₃, and related group-III oxide polymorphs: A first-principles study, Phys. Rev. Mater., 2019, 3(8), 84605,  DOI:10.1103/PhysRevMaterials.3.084605.
8. F. Mezzadri, G. Calestani, F. Boschi, D. Delmonte, M. Bosi and R. Fornari, Crystal Structure and Ferroelectric Properties of ε-Ga(2)O(3) Films Grown on (0001)-Sapphire, Inorg. Chem., 2016, 55(22), 12079–12084.
9. S. Leone, R. Fornari, M. Bosi, V. Montedoro, L. Kirste and P. Doering, et al., Epitaxial growth of GaN/Ga₂O₃ and Ga₂O₃/GaN heterostructures for novel high electron mobility transistors, J. Cryst. Growth, 2020, 534, 125511.
10. K. Kaneko, H. Kawanowa, H. Ito and S. Fujita, Evaluation of Misfit Relaxation in α-Ga₂O₃ Epitaxial Growth on α-Al₂O₃ Substrate, Jpn. J. Appl. Phys., 2012, 51(2R), 20201,  DOI:10.1143/JJAP.51.020201.
11. J. G. Hao, T. C. Ma, X. H. Chen, Y. Kuang, L. Li and J. Li, et al., Phase tailoring and wafer-scale uniform hetero-epitaxy of metastable-phased corundum α-Ga₂O₃ on sapphire, Appl. Surf. Sci., 2020, 513, 145871.
12. S. Nakagomi and Y. Kokubun, Crystal orientation of β-Ga₂O₃ thin films formed on c-plane and a-plane sapphire substrate, J. Cryst. Growth, 2012, 349(1), 12 8.
13. Y. Xu, J. H. Park, Z. Yao, C. Wolverton, M. Razeghi and J. Wu, et al., Strain-Induced Metastable Phase Stabilization in Ga₂O₃ Thin Films, ACS Appl. Mater. Interfaces, 2019, 11(5), 5536–5543,  DOI:10.1021/acsami.8b17731.
14. Y. Yao, S. Okur, L. A. M. Lyle, G. S. Tompa, T. Salagaj, N. Sbrockey, R. F. Davis and L. M. Porters, Growth and characterization of α-, β-, and ε-phases of Ga₂O₃ using MOCVD and HVPE techniques, Mater. Res. Lett., 2018, 6(5), 268–275,  DOI:10.1080/21663831.2018.1443978.
15. M. Bosi, P. Mazzolini, L. Seravalli and R. Fornari, Ga₂O₃ polymorphs: tailoring the epitaxial growth conditions, J. Mater. Chem. C, 2020, 8(32), 10975–10992,  10.1039/D0TC02743J.
16. B. R. Tak, S. Kumar, A. K. Kapoor, D. Wang, X. Li and H. Sun, et al., Recent advances in the growth of gallium oxide thin films employing various growth techniques—a review, J. Phys. D: Appl. Phys., 2021, 54(45), 453002,  DOI:10.1088/1361-6463/ac1af2.
17. K. Kaneko, K. Uno, R. Jinno and S. Fujita, Prospects for phase engineering of semi-stable Ga₂O₃ semiconductor thin films using mist chemical vapor deposition, J. Appl. Phys., 2022, 131(9), 90902,  DOI:10.1063/5.0069554.
18. Y. Lv, J. Ma, W. Mi, C. Luan, Z. Zhu and H. Xiao, Characterization of β-Ga₂O₃ thin films on sapphire (0001) using metal-organic chemical vapor deposition technique, Vacuum, 2012, 86(12), 1850–1854.
19. Y. Zhuo, Z. Chen, W. Tu, X. Ma, Y. Pei and G. Wang, β-Ga₂O₃ versus ε-Ga₂O₃: Control of the crystal phase composition of gallium oxide thin film prepared by metal-organic chemical vapor deposition, Appl. Surf. Sci., 2017, 420, 802–807.
20. H. Sun, K. H. Li, C. G. T. Castanedo, S. Okur, G. S. Tompa and T. Salagaj, et al., HCl Flow-Induced Phase Change of α-, β-, and ε-Ga₂O₃ Films Grown by MOCVD, Cryst. Growth Des., 2018, 18(4), 2370–2376,  DOI:10.1021/acs.cgd.7b01791.
21. M. Bosi, L. Seravalli, P. Mazzolini, F. Mezzadri and R. Fornari, Thermodynamic and Kinetic Effects on the Nucleation and Growth of ε/κ- or β-Ga₂O₃ by Metal–Organic Vapor Phase Epitaxy, Cryst. Growth Des., 2021, 21(11), 6393–6401,  DOI:10.1021/acs.cgd.1c00863.
22. F. Montalenti, P. Raiteri, D. B. Migas, H. von Känel, A. Rastelli and C. Manzano, et al., Atomic-Scale Pathway of the Pyramid-to-Dome Transition during Ge Growth on Si(001), Phys. Rev. Lett., 2004, 93(21), 216102,  DOI:10.1103/PhysRevLett.93.216102.
23. R. Gatti, F. Pezzoli, F. Boioli, F. Montalenti and L. Miglio, Assessing the composition of hetero-epitaxial islands via morphological analysis: an analytical model matching GeSi/Si(001) data, J. Phys.: Condens. Matter, 2012, 24(10), 104018,  DOI:10.1088/0953-8984/24/10/104018.
24. J. Furthmüller and F. Bechstedt, Quasiparticle bands and spectra of Ga₂O₃ polymorphs, Phys. Rev. B, 2016, 93(11), 115204,  DOI:10.1103/PhysRevB.93.115204.
25. Y. Hinuma, H. Hayashi, Y. Kumagai, I. Tanaka and F. Oba, Comparison of approximations in density functional theory calculations: Energetics and structure of binary oxides, Phys. Rev. B, 2017, 96(9), 094102,  DOI:10.1103/PhysRevB.96.094102.
26. J. B. Varley, First-principles calculations of structural, electrical, and optical properties of ultra-wide bandgap (Al_xGa_1−x)₂O₃ alloys, J. Mater. Res., 2021, 36(23), 4790–4803,  DOI:10.1557/s43578-021-00371-7.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
28. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria and L. A. Constantin, et al., Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100(13), 136406,  DOI:10.1103/PhysRevLett.100.136406.
29. R. Armiento and A. E. Mattsson, Functional designed to include surface effects in self-consistent density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(8), 85108,  DOI:10.1103/PhysRevB.72.085108.
30. J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115(3), 36402,  DOI:10.1103/PhysRevLett.115.036402.
31. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1103/PhysRevB.47.558.
32. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
33. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
34. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36(3), 354–360.
35. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134(6), 64111,  DOI:10.1063/1.3553716.
36. V. M. Bermudez, The structure of low-index surfaces of β-Ga₂O₃, Chem. Phys., 2006, 323(2), 193–203.
37. X. Zhou, E. J. M. Hensen, R. A. van Santen and C. Li, DFT Simulations of Water Adsorption and Activation on Low-Index α-Ga₂O₃ Surfaces, Chem. – Eur. J., 2014, 20(23), 6915–6926,  DOI:10.1002/chem.201400006.
38. R. Schewski, K. Lion, A. Fiedler, C. Wouters, A. Popp and S. V. Levchenko, et al., Step-flow growth in homoepitaxy of β-Ga₂O₃ (100)—The influence of the miscut direction and faceting, APL Mater., 2018, 7(2), 22515,  DOI:10.1063/1.5054943.
39. S. Mu, M. Wang, H. Peelaers and C. G. de Walle, First-principles surface energies for monoclinic Ga₂O₃ and Al₂O₃ and consequences for cracking of (Al_xGa_1−x)₂O₃, APL Mater., 2020, 8(9), 91105,  DOI:10.1063/5.0019915.
40. D. Yang, B. Kim, T. H. Lee, J. Oh, S. Lee and W. Sohn, et al., Selective Area Growth of Single-Crystalline Alpha-Gallium Oxide on a Sapphire Nanomembrane by Mist Chemical Vapor Deposition, ACS Appl. Electron Mater., 2021, 3(10), 4328–4336,  DOI:10.1021/acsaelm.1c00512.
41. Y. Hinuma, T. Kamachi, N. Hamamoto, M. Takao and T. Toyao, Shimizu K ichi. Surface Oxygen Vacancy Formation Energy Calculations in 34 Orientations of β-Ga₂O₃ and θ-Al₂O₃, J. Phys. Chem. C, 2020, 124(19), 10509–10522,  DOI:10.1021/acs.jpcc.0c00994.
42. Z. Cheng, M. Hanke, P. Vogt, O. Bierwagen and A. Trampert, Phase formation and strain relaxation of Ga₂O₃ on c-plane and a-plane sapphire substrates as studied by synchrotron-based x-ray diffraction, Appl. Phys. Lett., 2017, 111(16), 162104,  DOI:10.1063/1.4998804.
43. I. Cora, Z. S. Fogarassy, R. Fornari, M. Bosi, A. Rečnik and B. Pécz, In situ TEM study of κ → β and κ → γ phase transformations in Ga₂O₃, Acta Mater., 2020, 183, 216–227.
44. N. M. Stuart and K. Sohlberg, A method of calculating surface energies for asymmetric slab models, Phys. Chem. Chem. Phys., 2023, 25(19), 13351–13358,  10.1039/D2CP04460A.
45. M. D. Pashley, Electron counting model and its application to island structures on molecular-beam epitaxy grown GaAs(001) and ZnSe(001), Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(15), 10481–10487,  DOI:10.1103/PhysRevB.40.10481.
46. M. Lucht, M. Lerche, H. C. Wille, V. Shvyd’ko Yu, H. D. Rüter and E. Gerdau, et al., Precise measurement of the lattice parameters of α-Al₂O₃ in the temperature range 4.5–250 K using the Mössbauer wavelength standard, J. Appl. Crystallogr., 2003, 36(4), 1075–1081,  DOI:10.1107/S0021889803011051.
47. J. Su, J. Zhang, R. Guo, Z. Lin, M. Liu and J. Zhang, et al., Mechanical and thermodynamic properties of two-dimensional monoclinic Ga₂O₃, Mater. Des., 2019, 184, 108197.
48. F. Al-Quaiti, P. Y. Chen, J. G. Ekerdt and A. A. Demkov, Contributions of bulk and surface energies in stabilizing metastable polymorphs: A comparative study of group 3 sesquioxides La₂O₃, Ga₂O₃, and In₂O₃, Phys. Rev. Mater., 2022, 6(4), 43606,  DOI:10.1103/PhysRevMaterials.6.043606.
49. J. W. Roberts, P. R. Chalker, B. Ding, R. A. Oliver, J. T. Gibbon and L. A. H. Jones, et al., Low temperature growth and optical properties of α-Ga₂O₃ deposited on sapphire by plasma enhanced atomic layer deposition, J. Cryst. Growth, 2019, 528, 125254.

---

Footnotes

† Electronic supplementary information (ESI) available: Comparison of the bulk crystal structure, valence charges and cohesive energies calculated with different functionals, in-plane lattice structure of the slabs, additional information about the methodology of surface energy calculations, analysis of the strain-dependent cohesive energies. See DOI: https://doi.org/10.1039/d3tc04284g

‡ These authors contributed equally.

§ Given the different symmetries of the structures we deal with in this work, we assume crystal coordinates referred to the conventional bulk unit cell of each phase (see Table S1, ESI†). In the case of the α phases (both for Ga₂O₃ and Al₂O₃), the Miller–Bravais indices are frequently used: the (001), (100) and (012) surfaces of this phase can also be reported as (0001), (2−1−10) and (01−12), respectively.

¶ The (−201) surface of β-Ga₂O₃, due to its symmetry, is equivalent to the (20−1) one and as such it has been reported in ref. 41.

---