 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluation of Li2SnO3:Cr3+, Mn4+ as a dual-emitter luminescence sensor for cryogenic temperatures†
V.
Mykhaylyk
 *a,
Y.
Zhydachevskyy
*a,
Y.
Zhydachevskyy
 bc,
H.
Kraus
d,
V.
Stasiv
b,
G.
Leniec
bc,
H.
Kraus
d,
V.
Stasiv
b,
G.
Leniec
 e,
V.
Hreb
e,
V.
Hreb
 f,
L.
Vasylechko
f,
L.
Vasylechko
 f,
V.
Sydorchuk
g and
A.
Suchocki
f,
V.
Sydorchuk
g and
A.
Suchocki
 b
b
aDiamond Light Source, Harwell Campus, Didcot, OX11 0DE, UK
bInstitute of Physics, Polish Academy of Sciences, aleja Lotników 32/46, Warsaw 02-668, Poland. E-mail: vitaliy.mykhaylyk@diamond.ac.uk
cBerdyansk State Pedagogical University, Shmidta Str. 4, Berdiansk 71100, Ukraine
dUniversity of Oxford, Department of Physics, Denys Wilkinson Building, Keble Road, Oxford, OX1 3RH, UK
eWest Pomeranian University of Technology in Szczecin, al. Piastów 48, Szczecin 70-311, Poland
fLviv Polytechnic National University, S. Bandera Str. 12, Lviv 79013, Ukraine
gInstitute for Sorption and Problems of Endoecology, NAS of Ukraine, Henerala Naumova Str. 13, 03164 Kyiv, Ukraine
First published on 22nd December 2023
Abstract
The sensitivity of luminescence properties in materials doped with transition metal (TM) ions to changes of temperature makes them particularly promising for thermometric applications. Designing and optimizing such materials requires a deep understanding of their structure, local environment of emission centres, and luminescence processes. In this work, we investigate the potential of Li2SnO3 doped with Cr3+ and Mn4+ as a dual-emitting luminescence temperature sensor. Li2SnO3 was chosen as the host material due to it being able to host both Cr3+ and Mn4+ at Sn octahedral positions. As a result, Mn4+ ions exhibit a distinctive 2E → 4A2 line emission due to a strong crystal field, and Cr3+ ions experience an intermediate crystal field strength resulting in both, 2E → 4A2 and 4T2 → 4A2 emissions. Through thorough examination, using powder X-ray diffraction (XRD), electron paramagnetic resonance (EPR) and photoluminescence techniques we identified two distinct types of [SnO6] octahedral centers that correspond to two types of slightly different Cr3+ and Mn4+ emission centers in the Li2SnO3 structure. The high sensitivity of the decay time constant for the 2E → 4A2 emission of Li2SnO3–Cr3+, Mn4+ to temperature changes (2.0%/K at 190 K and 5.8%/K at 220 K for Cr3+ and Mn4+, respectively) positions the material as an attractive non-contact temperature sensor. Furthermore, application of such a dual-emitter luminescence material as a temperature sensor expands its sensitivity across a broader temperature range and offers the additional advantage of cross-checking measurements compared to materials solely doped with Cr3+ or Mn4+.
Introduction
The electronic configuration of excited states of transition metal (TM) ions with an unfilled 3d shell provides the basis for a unified methodology of interpreting their optical properties within the framework of crystal field theory.1,2 This method has been successfully applied towards understanding the nature of the luminescence of Cr3+ and Mn4+ in different hosts.3–8 These ions are typically stabilized in octahedral or distorted octahedral environments, coordinated by six oxygen ions, where the energy structure of 3d states and their dependence on crystal field strength are well explained by the classical Tanabe–Sugano diagram.1,2,7,8 The diagram shows that the energy of most multiplets except 2T1 and 2Eg are strongly dependent on the crystal field strength, which has a decisive impact on luminescence. Mn4+ ions doped in various hosts always experience a strong crystal field which gives rise to emission lines from 2E → 4A2 transitions, aided by lattice vibrations.5 In contrast, the effect of the surrounding crystal field on Cr3+ ions can vary from weak to strong as established through relevant luminescence spectra. Specifically, a broad emission band due to 4T2 → 4A2 transitions and sharp 2E → 4A2 lines are simultaneously observed in intermediate crystal fields, while in weak crystal fields the line emission disappears.8 This dependence of the emission properties of Cr3+ and Mn4+ on the strength of the local crystal field enables customization and fine-tuning of the emission characteristics for specific applications.In this regard, of particular interest is the case when both Cr3+ and Mn4+ can occupy the same crystallographic position. This may occur in the same host despite of the different valence states of the ions. In such a case the needs to compensate a local charge disparity may create additional perturbations of the crystal field surrounding the impurity, resulting in changes of the emission properties. To date only characteristic sharp emission peaks due to spin-forbidden transitions 2E → 4A2 of Cr3+ and Mn4+ have been reported in several hosts, indicating that both ions are experiencing a strong crystal field effect.9–13 It should be noted that such materials with two types of emission centers are particularly interesting for application as multimodal luminescence sensors of temperature.14 The dual-emitter sensor allows to extend the temperature range of operation and improves the reliability of the technique. It would be interesting therefore to investigate a material where in addition to the spin-forbidden transitions of Mn4+ and Cr3+ the spin-allowed transitions 4T2 → 4A2, yielding broadband emission, can also occur. Due to the coexistence of two radiative channels, the luminescence characteristics of such a material may exhibit enhanced sensitivity to changes of temperature that can be exploited for temperature monitoring.
To test this idea we turned our attention to Li2SnO3, a material currently being investigated for its potential as an electrode in lithium batteries15–18 and light emitting devices (LED).19 Li2SnO3 has a honeycomb layered monoclinic structure that contains octahedral sites SnO6 which are suitable for accommodating Mn4+ and Cr3+ ions with smaller ionic radius (r = 0.54 and 0.61 Å, respectively) in place of the larger Sn4+ ion (r = 0.69 Å). Previous research has shown that Li2SnO3 doped with Mn4+ exhibits strong red luminescence originating from 2E → 4A2 transitions.20,21 However, to the best of our knowledge no studies have been conducted on Cr-doped Li2SO3. We successfully synthesized the material using a hydrothermal method22 and preliminary examinations have indicated that Cr3+ ions occupy the octahedrally-coordinated Sn4+ sites in the Li2SnO3 host, experiencing a crystal field of intermediate strength (Dq/B = 2.48). This field is responsible for the characteristic room temperature luminescence of Cr3+i.e. a broad luminescence band spanning the range from 650 to 850 nm with a narrow and sharp emission line at 700 nm. These originate from spin-allowed 4T2 → 4A2 and spin-forbidden 2E → 4A2 transitions of the Cr3+ ion, respectively. In this study we conducted a detailed characterization of Li2SnO3 co-doped with Cr3+and Mn4+ in the temperature range from 4 to 300 K, aiming to establish the potential of this dual-emitter phosphor for application as non-contact luminescence sensor of temperature.
Experimental methods
The Li2SnO3–Cr3+, Mn4+ nanocrystalline phosphor was synthesized as described in ref. 22. In particular, the material studied in the present work has been calcined at 1200 °C. The photoluminescence (PL) and the photoluminescence excitation (PLE) spectra were measured using a Horiba/Jobin-Yvon Fluorolog-3 spectrofluorometer with a 450 W continuous spectrum xenon lamp for excitation. The emission was detected by a Hamamatsu R928P photomultiplier operating in a photon counting mode. The PL spectra were corrected for the spectral response of the used system. The luminescence decay kinetics were measured using the same Fluorolog-3 spectrofluorometer with the excitation light modulated by a mechanical chopper. The spectroscopic measurements in the temperature range of 4.2–330 K were carried out in a Janis continuous-flow liquid helium cryostat using a Lake Shore 331 temperature controller. The studies in the temperature range of 300–600 K were done using a Linkam THMS600 temperature stage.Electron paramagnetic resonance (EPR) spectra were recorded at a magnetic induction in the range of B = 10–1400 mT on a conventional X-band Bruker ELEXSYS E 500 CW-spectrometer, operating at 9.5 GHz with 100 kHz magnetic induction modulation and microwave power of P = 2.002 mW. The temperature dependence of the EPR spectrum was analysed using a nitrogen-flow cryostat (Oxford Instruments ESP) in the nitrogen temperature range. The position of the EPR line is determined by the formula geff = 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 773 fez(GHz)/Brez(mT), where frez is the microwave frequency and Brez is the position of the resonance line in the magnetic induction. The EPR/NMR program was used to find local symmetry and Spin-Hamiltonian (SH) parameters of the chromium ions.23 The optimization and normalization of the above parameters was performed using a root-mean-square deviation method.
773 fez(GHz)/Brez(mT), where frez is the microwave frequency and Brez is the position of the resonance line in the magnetic induction. The EPR/NMR program was used to find local symmetry and Spin-Hamiltonian (SH) parameters of the chromium ions.23 The optimization and normalization of the above parameters was performed using a root-mean-square deviation method.
Results and discussion
Crystal structure
The crystal structure of Li2SnO3 doped with Cr3+ was studied recently by X-ray powder diffraction and application of full profile Rietveld refinement. Comprehensive details of the refinement procedure along with a complete set of structural data including unit cell dimension, coordinates, and displacement parameters of atoms can be found in ref. 22. The Li2SnO3 structure belonging to space group C2/c, Z = 4 can be visualised as stacked slabs comprising interconnected [SnO6] and [LiO6] octahedra in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. These are interleaved with layers consisting of Li+ ions (see Fig. 1). A distinctive feature of the Li2SnO3 host structure is the presence of three different octahedral positions of Li+ ions, located at the 4d, 4e and 8f Wyckoff sites. Furthermore, the structure boasts two non-equivalent four-fold 4e sites, which are occupied by Sn atoms in an octahedral oxygen environment. The octahedral coordination of Sn4+ ions in both sites provides a conducive environment for accommodating Cr3+ and Mn4+ cations.
1 ratio. These are interleaved with layers consisting of Li+ ions (see Fig. 1). A distinctive feature of the Li2SnO3 host structure is the presence of three different octahedral positions of Li+ ions, located at the 4d, 4e and 8f Wyckoff sites. Furthermore, the structure boasts two non-equivalent four-fold 4e sites, which are occupied by Sn atoms in an octahedral oxygen environment. The octahedral coordination of Sn4+ ions in both sites provides a conducive environment for accommodating Cr3+ and Mn4+ cations.
An examination of the nearest interatomic distances in the Li2SnO3:Cr3+ structure, calculated from the atomic coordinates reported in ref. 22, reveals a difference in the configuration of [SnO6] octahedra around Sn1 and Sn2 atoms. Specifically, the distribution of the six nearest Sn–O distances inside [Sn1O6] and [Sn2O6] polyhedra (as listed in Table 1) indicates that the [Sn1O6] octahedron with a volume of 12.57 Å3 exhibits significantly greater distortion compared to the [Sn2O6] octahedron which has a volume of 11.28 Å3 (see Fig. 1). Given that dopant ions can incorporate into both of these Sn sites, it is anticipated that there will be two different types of Cr3+ and Mn4+centres in the Cr- and Mn-doped Li2SnO3 materials. It is worth noting that this peculiarity of the host lattice, namely the existence of two different octahedral Sn sites was not identified in recent publications that studied luminescence properties of Li2SnO3:Mn4+ phosphors.20,21
| Polyhedron, atoms | Distances in Å | Polyhedron, atoms | Distances in Å | Polyhedron, atoms | Distances in Å |
|---|---|---|---|---|---|
| [Li1O6] | [Li2O6] | [Sn1O6] | |||
| Li1–O3 | 2.02(5) | Li2–O3 | 2 × 2.02(2) | Sn1–O3 | 2 × 2.04(2) |
| Li1–O1 | 2.17(5) | Li2–O2 | 2 × 2.16(2) | Sn1–O1 | 2 × 2.12(2) |
| Li1–O3 | 2.25(5) | Li2–O1 | 2 × 2.28(2) | Sn1–O2 | 2 × 2.19(2) |
| Li1–O2 | 2.32(5) | Li2–Oave | 2.15 | Sn1–Oave | 2.12 |
| Li1–O2 | 2.32(5) | [Li3O6] | [Sn2O6] | ||
| Li1–O1 | 2.47(5) | Li3–O2 | 2 × 2.06(2) | Sn2–O2 | 2 × 2.00(2) |
| Li1–Oave | 2.25 | Li3–O1 | 2 × 2.19(2) | Sn2–O1 | 2 × 2.03(2) |
| Li3–O3 | 2 × 2.19(2) | Sn2–O3 | 2 × 2.10(2) | ||
| Li3–Oave | 2.15 | Sn2–Oave | 2.04 |
Electron paramagnetic resonance studies
EPR allows detection of even small amounts of paramagnetic ions within the studied materials. It aids in discerning key structural properties such as the local symmetry of paramagnetic ions and their interactions. In the case of Li2SnO3 doped with Cr3+ ions and Mn4+ ions, we expect to observe a distinct EPR signal from these dopants. Cr3+ ions are paramagnetic ions with an electron configuration of 3d3 and an electron spin S = 3/2. Similarly, Mn4+ ions are paramagnetic ions with an electron configuration of 3d3 and electron spin S = 3/2. Additionally, for Mn4+ ions, we expect an EPR signal arising from the 55Mn isotope (100% abundance) possessing a nuclear spin S = 5/2. It is worth noting that the position of the signal is strongly influenced by the local environment of the paramagnetic ions. This feature enables us to ascertain the local symmetry of these dopants. Fig. S1 (ESI†) showcases the EPR spectra for the Li2SnO3:Cr3+, Mn4+ recorded at temperatures T = 80 K and T = 300 K.The EPR spectra recorded at room temperature exhibit three distinct lines emerging from two magnetic centres. Specifically, the EPR line with geff = 1.999 can be attributed to the Mn4+ ion while the lines with geff = 3.649 and geff = 1.38 are characteristic of Cr3+ ions within an octahedral environment; notably these two EPR lines corresponds to a single Cr3+ centre,24.25 As temperature drops, the components of the EPR lines originating from Cr3+ ions become more discernible along with the hyperfine interactions of Mn4+ ions. To delve further into ion symmetry, we selected the lowest temperature of T = 80 K as this provides a clearer understanding of the structural arrangement of the ions in question.
The spin Hamiltonian (SH) parameters for ions with spin S = 3/2 were determined using the EPR/NMR programme through the following system of equations:
 | (1) |
For single Cr3+ ions the following values were calculated: gx = gy = 1.998(2), gz = 1.997(2), and D = 0.252(5) cm−1 (E = 0). These parameters suggest an axially symmetric site for the Cr3+ ions with insignificant distortions of an octahedra. Similarly, for single Mn4+ ions the values are: gx = gy = 1.985(3), gz = 1.980(3), D = 0.006(1) cm−1, E = 0, Ax = Ay = 0.0030(2) cm−1, Az = 0.0029(2) cm−1. These parameters affirm an axially symmetric site for the Mn4+ ions. The spin Hamiltonian parameters were obtained from the best fit of the experimental EPR spectra to the simulated spectra generated using the spin Hamiltonian. Fig. 2(a) and (b) illustrate the experimental spectra and simulated spectra, derived from the above equations and SH parameters.
It is worth noting that at temperatures below T < 120 K the signal at geff ∼ 3.6 apparently consists of two EPR lines (inset of Fig. S1, ESI†) of the same intensity. This may indicate that the signal from Cr3+ ions originates from two Cr3+ centres (Cr3+ → [Sn1O6] and [Sn2O6]) with different distortions. EPR studies do not confirm the presence of two different Mn4+ centres, but it should be borne in mind that the EPR signal from Mn4+ ions consists of many lines originating from fine and hyperfine interactions, meaning that two Mn4+ ions with the same symmetry but different distortion cannot be distinguished.
Effect of temperature on the luminesce properties
Previous studies of Li2SnO3 doped with Cr3+ or Mn4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19–22 provide some insight into the expected emission properties of this material when co-doped with both ions. Given that the concentration of the impurity ions is maintained at low level (<0.1%) and there is no spectral overlap between the emission and excitation spectra of different impurities, no energy transfer is expected between the two emitters. Consequently, the luminescence of Li2SnO3:Cr3+, Mn4+ represents a superposition of emissions from individual ions resulting in a combined spectrum as depicted in Fig. 3.
19–22 provide some insight into the expected emission properties of this material when co-doped with both ions. Given that the concentration of the impurity ions is maintained at low level (<0.1%) and there is no spectral overlap between the emission and excitation spectra of different impurities, no energy transfer is expected between the two emitters. Consequently, the luminescence of Li2SnO3:Cr3+, Mn4+ represents a superposition of emissions from individual ions resulting in a combined spectrum as depicted in Fig. 3.
 | ||
| Fig. 3 Luminescence spectrum of Li2SnO3:Cr3+, Mn4+ measured at 480 nm excitation (T = 40 K, (a) and excitation spectra monitored at Cr3+ and Mn4+ emission peaks at T = 4.2 K, (b). | ||
The configuration coordinate model offers an innate way towards understanding the emission properties of Cr3+ and Mn4+ ions (see Fig. 4). The vertical blue arrows indicate excitation transitions that promote electrons from the ground state to the 4T1g and 4T2g states via parity-allowed transitions. The luminescence excitation bands due to these transitions are clearly seen in the luminescence excitation spectra displayed in Fig. 3(b). Subsequently, the electrons promptly relax along the parabola to 2Eg and 4T2g states. At this stage the splitting of the subsequent relaxation pathway becomes apparent.
 | ||
| Fig. 4 Energy diagram of Mn4+ and Cr3+ ions showing excitation (blue), emission (red) and thermally activated (black dotted) transitions. | ||
The strong crystal field experienced by Mn ions shifts the 4T2g states above the 2Eg levels, leaving only one channel for radiative recombination through the spin-forbidden transitions 2E → 4A2, giving rise to the sharp emission lines (red arrow). In contrast, the weaker crystal field experienced by Cr3+ places the 4T2g states at lower energy, thus opening an additional channel for the radiative recombination through the spin-allowed 4T2g → 4A2 transitions, as shown in Fig. 4. Hence in addition to the line emission due to 2E → 4A2 transitions, broad band emission occurs when the temperature rises, and the 4T2g states are populated by thermally induced transitions from the 2Eg levels (black dotted arrow). The positions of the main excitation bands and emission peaks of Cr3+ and Mn4+ observed at low temperature are listed in Table 2. The subsequent studies of the luminescence of Li2SnO3:Cr3+, Mn4+ have revealed the influence of temperature.
| Ion, (position) | Ē → 4A2 (R1-line), nm | 2Ā → 4A2 (R2-line), nm | R 1 – R2 gap, meV | 4A2 → 4T2g, nm | 4A2 → 4T1g, nm |
|---|---|---|---|---|---|
| a The high energy excitation band 4A2 → 4T1g of Mn4+ is not resolved due to overlap with the excitation band, resulting from the charge-transfer transitions O2− → Mn4+. | |||||
| Mn4+(I) | 655.9 | 654.4 | 4.0 | 473 | (Not detected)a |
| Mn4+(II) | 656.4 | 655.6 | 2.4 | ||
| Cr3+(I) | 699.0 | 698.5 | 1.7 | 617 | 440 |
| Cr3+(II) | 699.1 | 698.5 | 1.6 | ||
Initially, our study focussed on temperature-induced variations of the narrow band emissions of Mn4+ and Cr3+ caused by the 2E → 4A2 transitions in the Li2SnO3. Fig. 5(a) shows that with rising temperature the intensity of the emission lines experiences a gradual reduction with increasing temperature. High-resolution low-temperature photoluminescence measurements revealed that the zero-phonon (R1) line of Cr3+ appears as two closely spaced lines which merge into a single line above 100 K while the R2 line of Cr3+ remains unsplit even at the lowest temperatures. In the case of Mn4+ a pair of R1 and R2 lines is clearly visible in low-temperature spectra as illustrated in Fig. 5(b). This dual set of R-lines for both Cr3+ and Mn4+ centers implies the existence of two distinct types of these centers, originating from the substitution of TM ions for two different sites occupied by Sn4+ cations in the host lattice. It is pertinent to remark that incorporation of TM ions at different crystallographic sites is a common feature observed in complex oxides.26–28
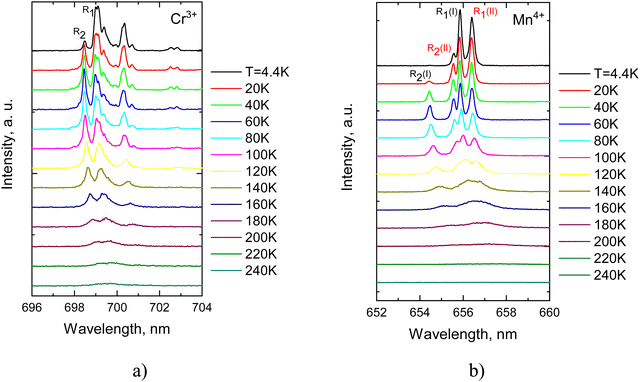 | ||
| Fig. 5 Temperature evolution of ZPL emission (2E → 4A2) for Cr3+ (a) and Mn4+ (b) in Li2SnO3–Cr3+, Mn4+. | ||
The observed temperature dependencies offer insight into the dynamics governing the population of excited states within the emission centres under consideration. To attain a more comprehensive understanding of this behaviour, we examined the normalized intensity of various emissions, presented as a function of temperature (see Fig. 6). As it is seen, the 2E → 4A2 emission of Cr3+ and Mn4+ is significantly affected by thermal quenching. Our finding suggests that the measured temperature dependence cannot be adequately modelled by a canonical Mott–Seitz type expression which is typically employed to describe thermal quenching as a single step deactivation process.29,30
 | ||
| Fig. 6 Normalized intensity of the narrow-line (2E → 4A2) emissions of Mn4+ (blue) and Cr3+ black) and broadband (4T2 → 4A2) emission of Cr3+ (green) with temperature. Red lines show the fitting of experimental results by eqn (2) and (3). | ||
Aiming to address this behaviour comprehensively, we adopted an approach previously validated in ref. 31 using an equation designed to accommodate the presence of two distinct pathways for thermal deactivation:
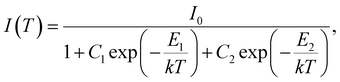 | (2) |
In this equation, I0 is the total emission intensity at zero temperature, C1 and C2 are the transition rate constants, E1 and E2 are the activation energies for the non-radiative quenching, k is the Boltzmann constant. Using this equation, we achieved a very good agreement of the theoretical curve (the solid red line in Fig. 6) with the experimental data. The parameters of the fit are summarized in Table 3.
A prominent feature of the luminescence in Li2SnO3 is a broad band emission associated with the 4T2g → 4A2 transitions of Cr3+ which becomes prominent with increasing temperature, peaking at ca. 225 K as displayed in Fig. 7. Subsequently, it undergoes a gradual decline, disappearing above 500 K. This type of temperature dependence, referred to as negative thermal quenching, has been observed in the luminescence of some materials,32,33 including phosphors doped with TM ions.34 The phenomenon is explained by considering two main processes that govern the population of the emitting state (i) thermally activated population of the emitting centres that lead to an increase of the luminescence and (ii) the quenching of the emission intensity due to the non-radiative decay of emission centres. In the framework of the model developed by Shibata35 the observed temperature behaviour of broadband emission can be readily understood, considering that the 4T2g state is being populated through the thermally activated crossover transition from the metastable 2E levels of Cr3+ as illustrated in Fig. 4. This process is responsible for the emergence of this band with heating with the decrease of the emission intensity occurring above 225 K, the result of thermal quenching. It should be noted that the increase in intensity of this band coincides with a simultaneous decrease in the intensity of the 2E → 4A2 emission intensity of Cr3+, also evident in Fig. 7. To account for this activation process within the model, an additional term is introduced in the numerator of eqn (2) which leads to the following expression for the temperature dependence of the emission intensity:35
 | (3) |
In this formula, the additional parameters A1 and  are the transition rate constant and the activation energy necessary to promote the charged electrons from the metastable to the emission state respectively. Consequently, the expression in the numerator is responsible for the rise of emission due to the thermally activated population of the emitting transition 4T2g states. Conversely, the denominator of the equation encompasses processes related to thermally activated non-radiative quenching of the emitting state. The measured temperature dependence of the integrated luminescence intensity of the broad band emission of Cr3+ was fitted using this equation over the entire temperature range confirming validity of the model used (see Fig. 6). The best fit was achieved using parameters collated in Table 3. The value for energy
are the transition rate constant and the activation energy necessary to promote the charged electrons from the metastable to the emission state respectively. Consequently, the expression in the numerator is responsible for the rise of emission due to the thermally activated population of the emitting transition 4T2g states. Conversely, the denominator of the equation encompasses processes related to thermally activated non-radiative quenching of the emitting state. The measured temperature dependence of the integrated luminescence intensity of the broad band emission of Cr3+ was fitted using this equation over the entire temperature range confirming validity of the model used (see Fig. 6). The best fit was achieved using parameters collated in Table 3. The value for energy  obtained from the fit (
obtained from the fit ( ) corresponds to the energy barrier of the thermal activation of 2E→ 4T2g transitions in the Cr3+ ion.
) corresponds to the energy barrier of the thermal activation of 2E→ 4T2g transitions in the Cr3+ ion.
Finally, the photoluminescence quantum yield of Cr3+ emission in Li2SnO3 at room temperature was determined to be 4.5 ± 0.4%. Notably the room-temperature intensity is approximately 0.4 in comparison to that at 4.2 K leading us to deduce an approximate quantum efficiency of 11% at lower temperature that is deemed satisfactory for thermometry measurements.
Temperature-induced shift and intensity ratio of R-lines
Next, we analyze the temperature-induced changes in the spectra of the spin-forbidden 2E → 4A2 transitions as illustrated in Fig. 5, where the changes in the narrow emission line's shape or position are evident. These changes primarily originate from the change in the population of emitting states Ē and 2Ā and from their interaction with lattice vibrations, resulting in a noticeable variation of the intensity ratio of the R-lines and shifts in their position. Therefore, these two spectroscopic characteristics form the basis for two modes of operation which are frequently utilised in non-contact luminescence measurements of temperature. The temperature dependencies of the intensity ratio (F = IR2/IR1) for Cr3+ and Mn4+ lines in Li2SnO3 are displayed in Fig. 8, and the variations of peak positions of the R-lines with temperature are shown in Fig. 9.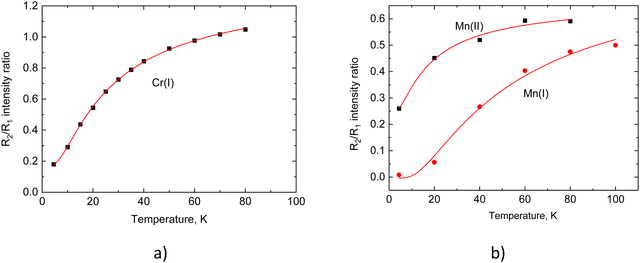 | ||
| Fig. 8 The intensity ratio (IR2/IR1) as a function of temperature for Cr3+ (a) and Mn4+ centers (b) in Li2SnO3. The red lines display the best fitting of experimental data (dots) to eqn (4) using the value of the energy gap D as shown in Table 4. | ||
 | ||
| Fig. 9 Variation of the position of R-lines with temperature observed for different emission centers of Cr3+ (a) and Mn4+ (b) in Li2SnO3. The red lines show the best fit of experimental results (dots) to eqn (5) using the parameters presented in Table 4. | ||
It is important to note that the presence of two slightly different types of emission centres adds complexity to the interpretation of spectroscopic data. The first issue we encountered was identification of the R-lines of Cr3+. The R1 lines attributed to Cr(I) and Cr(II) centres are distinguishable only below 100 K, as can be seen in Fig. 5, while the R2 lines are not resolved at all. Therefore, we derived only one temperature dependence of the intensity ratio for the Cr(I) centre displayed in Fig. 6(a). This dependence was fitted using Boltzmann statistics, which describes the population variation of two emitting levels with temperature:
 | (4) |
In this equation, A is a constant, D denotes the energy difference between the two emitting levels, k stands for the Boltzmann constant, T is absolute temperature and B accounts for an offset. The fitting resulted in very good agreement with the experimental data as illustrated in Fig. 8(a). It yielded an energy gap value of D = 1.9 meV which aligns well with the energy difference between the R1 and R2 lines obtained from the spectroscopic data.
The second complication arose in assigning two pairs of R-lines to the appropriate emission centres of Mn4+, namely Mn(I) and Mn(II). Fortunately, at low temperatures all the individual lines are fully resolved allowing us to apply eqn (4) for verification of their pairing. The best fit was achieved using the values of energy gaps shown in Table 4 which correlates with the results obtained from the spectroscopic measurements (refer to Table 2). This finding also affirms the suggested assignment of the lines to the specific emission centres of Mn4+. It is worth noting that an alternative pairing of R-lines results in values of energy gaps that significantly deviate from the experimentally determined ones.
| Emission center | D, meV | α 1, cm−1 | α 2, cm−1 | T D, K |
|---|---|---|---|---|
| Cr(I) | 1.9 ± 0.1 | −705 | −678 | 738 |
| Mn(I) | 3.9 ± 0.4 | −437 | −596 | 510 |
| Mn(II) | 1.2 ± 0.3 | −215 | −257 | 413 |
Following this we examined the temperature-induced changes in the spectral positions of R-lines measured in Li2SnO3:Cr3+, Mn4+ (see Fig. 9) using the model developed in ref. 36 In the framework of this model the observed shift of the lines, denoted as Δν, originates from the electron–phonon interaction between the excited states of impurity ions and the lattice vibrations of the host material. This phenomenon can be quantified by the formula:
 | (5) |
These findings allow us to evaluate the potential use of the spectroscopic characteristics of Li2SnO3:Cr3+, Mn4+ for temperature monitoring. Upon inspecting the two temperature dependences displayed in Fig. 8 and 9 a noteworthy shortcoming become apparent: both methods of temperature sensing, whether based on intensity ratio or R-line shift, are effective within a relatively narrow temperature range. The operational range of the intensity ratio method is limited to 80 K, while discernible changes in the position of the Cr3+ peak can be detected within the temperature range 100–200 K. This inherent limitation of these two methods has already been noticed in previous studies.14 However, with Li2SnO3:Cr3+, Mn4+ this constraint is more pronounced, limiting the application of two method based on spectroscopic data in non-contact temperature measurements.
Temperature dependence of the luminescence decay time
The change of decay time constant of the R-lines is yet another feature of emission of TM ions that is regularly applied for temperature monitoring.26,37–39 To verify the merit of these characteristics we measured the variation of luminescence decay time constants of the R-lines in Li2SnO3. Fig. 10 shows the temperature dependence of decay time constants for 2E → 4A2 transitions of Cr3+ and Mn4+.Both measured dependences τ(t) exhibit similar qualitative behaviour. Starting at the lowest temperature, the decay time constant initially increases but after reaching a maximum begins to decrease. The main difference lies in the rate of this reduction: it occurs swiftly in case of Cr3+, while in case of Mn4+ one can see a levelled-off part in the τ(t) graphs followed by a rapid decrease in the decay time constant above 170 K. The observed decrease of the decay time constant at higher temperature is commonly observed in luminescence materials.40 It has the same origin as the temperature quenching, which is caused by an increase of the probability for non-radiative de-excitation of the emitting level of TM ions.30,41,42 The rise of the decay time constant with heating at low temperature is an interesting feature that has been previously documented in a few systems doped with Cr3+.38,43 More recently we observed this phenomenon for both ions in Al2O3 co-doped with Cr3+ and Mn4+.14 This behaviour is explained by considering different radiative transition probabilities from the Ē and 2Ā levels, which together constitute the emitting 2E state. The likelihood of radiative decay from the upper level 2Ā is lower compared to that for Ē, i.e. 1/τ2 < 1/τ1. At very low temperature the upper level remains unpopulated, and consequently, the single R1 line observed in the emission is predominantly a result of radiative transition from the low-lying level Ē which has a shortened decay time τ1. As the temperature increases the upper level gradually becomes populated, as indicated by the emergence of the R2 line, and it starts to contribute to the emission process. This leads to the gradual increase of the measured decay time constant of the R-emission with heating.
To analyse the relaxation dynamics of 2E emitting states in Li2SnO3–Cr3+, Mn4+, we applied a model developed in ref. 38 that provides a comprehensive interpretation of the observed behavior of the decay time constant of TM ions over a wide temperature range. The model offers a highly accurate quantitative description of all features of τ = f(T) characteristic of Cr3+ and Mn4+ emissions. It takes into consideration the primary processes influencing the dynamics of radiative transitions, which encompass thermalisation between the Ē and 2Ā levels, phonon-assisted relaxation, and depopulation of the levels due to thermally induced transitions from 2E to an upper 4T2 state. It is pertinent to remark that the upper state may subsequently play a different role. For instance, in case of Cr3+ it actively participates in luminescence giving rise to broadband emission, whereas in the case of Mn4+ it undergoes non-radiative decay through the crossover process. Regardless of these nuances the dependence of the decay time constant of the 2E → 4A2 transitions in Li2SnO3 on temperature is described by the following relation:
 | (6) |
This equation has been used to model the temperature dependence of the luminescence decay time constants of R-lines of both Cr3+ and Mn4+ in Li2SnO3–Cr3+, Mn4+. The curves displayed in Fig. 10 exhibit an excellent agreement with the experimental results, as substantiated by a high correlation coefficient (>0.998). The fitting parameters are summarized in Table 5.
 | ||
| Fig. 10 Temperature dependence of the luminescence decay time constant of Cr3+ (a) and Mn4+ (b) R-lines in Li2SnO3–Cr3+, Mn4+. The solid lines show the best fit of eqn (6) to the experimental results (dots) using the parameters summarized in Table 5. | ||
| Parameter | Cr3+ | Mn4+ |
|---|---|---|
| a The value of D is fixed to be equal to the average energy splitting of the 2E level. | ||
| τ 1, ms | 1.95 ± 0.01 | 0.55 ± 0.01 |
| τ 2, ms | 2.03 ± 0.01 | 0.57 ± 0.01 |
| E p, meV | 25.4 ± 0.2 | 35.3 ± 0.1 |
| D , meV | 1.7 | 3.2 |
| τ 3, μs | 5.8 ± 0.2 | 5.5 ± 0.5 × 10−5 |
| ΔE, meV | 103.8 ± 0.7 | 292 ± 16 |
| R 2 | 0.999 | 0.998 |
Upon examining the fitting parameters, it becomes evident that for the 2E → 4A2 transitions of both Cr3+ and Mn4+ the decay time constants of the lower level (τ1) is shorter than that of the upper level (τ2), which is in line with the reasoning proposed here for the interpretation of the observed behaviour of the luminescence decay time constant at very low temperatures. It is worth noting that the values of activation energies ΔE obtained here are similar to those derived from fitting the temperature dependence of the emission intensity of R-lines. This correspondence is expected given that temperature changes of both intensity and radiative decay are controlled by the same mechanism of non-radiative quenching.
Thermometric performance
The observed substantial changes in the decay time constant of R-lines of Cr3+ and Mn4+ in Li2SnO4 with changing temperature serve as strong indicators that this property can be readily utilized for temperature monitoring. The assessment of efficiency of a measured quantity Q for temperature sensing is done using the quality indicators such as relative sensitivity (Sr) and the temperature uncertainty or resolution (δT) determined using the following equations.44,45 | (7) |
 | (8) |
Fig. 11 shows the calculated quality indicator parameters for the thermometer based on the measurements of the decay time constants in Li2SnO3–Cr3+, Mn4+ along with pertinent data for the reference sample Ga2O3–Cr3+.38 Upon close examination of the plots in Fig. 11 it becomes evident that the efficiency of temperature sensing using the Cr3+-emission of Li2SnO4 is very comparable to that of Ga2O3–Cr3+. The difference lies in a slight shift of the peak sensitivity from 160 to 190 K and an increase of the relative sensitivity from 1.7 to 2.0%/K. This leads to modest enhancement of the best achievable temperature uncertainty of Li2SnO3–Cr3+ compared to the reference Ga2O3–Cr3+, from 0.3 to 0.25 K. Assuming an uncertainty ±1 K as an upper limit for practical application of a temperature sensor, it is evident that this material exhibits resolution ±1 K or better over a broad temperature range (100–350 K) surpassing that of Ga2O3–Cr3+.
Finally, the maximum sensitivity of temperature sensing using Mn4+ emission of Li2SnO3 is nearly three times better, resulting in an impressive resolution δT = 0.08 K at 220 K. While this performance competes with the best uncertainties achieved by non-contact luminescence decay time sensors (refer to Table 6), it is effective merely within a narrow range (180–250 K).
| Material | Temperature | Relative sensitivity, %/K | Temperature uncertainty, K | Ref. |
|---|---|---|---|---|
| Ga2O3–Cr3+ | 165 | 1.7 | 0.3 | 38 |
| Mg2SiO4–Cr3+ | 240 | 0.92 | 0.2 | 46 |
| ZnGa2O4–Cr3+ | 200 | 1.9 | <2 | 47 |
| MgTiO4–Mn4+ | 277 | 4.1 | 0.025 | 48 |
| Li2TiO3–Mn4+ | 332 | 3.2 | 0.031 | 49 |
| LaTiSbO6–Mn4+ | 298 | 3.0 | 0.05 | 50 |
| Li2SnO3–Cr3+ | 190 | 2.0 | 0.25 | This work |
| Li2SnO3–Mn4+ | 220 | 5.8 | 0.08 | This work |
Summary
Due to their high sensitivity to temperature changes, oxides doped with TM ions find extensive use in non-contact luminescence thermometry. In most cases, temperature sensing relies on monitoring the luminescence properties of a single TM ion. However, it has been demonstrated that employing two TM ions can extend the sensor sensitivity to a wider temperature range and add redundancy. Inspired by this concept, our work focuses on exploring the potential of Li2SnO3 co-doped with Cr3+ and Mn4+ as a non-contact temperature sensor.To comprehend the relationship between the structure and luminescence properties of TM ions in this compound, we conducted examinations using X-ray diffraction, electron paramagnetic resonance, and luminescence techniques. Our structural studies revealed two types of distinct [SnO6] octahedral centres in Li2SnO3, both suitable for incorporating TM ions. This finding was further confirmed by EPR and luminescence spectroscopy. Notably, high-resolution, low-temperature photoluminescence measurements distinctly revealed two pairs of R-lines attributed to the 2E → 4A2 transitions in Mn4+ in Li2SnO3. The energy gap between the R-lines of Cr3+ remains distinguishable but is significantly smaller, while the separation of R-lines resulting from two different Cr3+ centres is very small. All of this indicates a reduced strength of the local crystal field compared to that experienced by Mn4+ ions.
To evaluate the material suitability for non-contact luminescence thermometry, we investigated the temperature behaviour of the luminescence spectra and decay time constant of Li2SnO3 co-doped with Cr3+ and Mn4+. The results were analysed within the framework of relevant theoretical models, which explain the observed temperature dependences arising from various mechanisms affecting the dynamics of exited states due to thermalization, electron–phonon interaction, non-radiative decay, and thermally-activated depopulation. Following this analysis, we found that spectroscopic techniques for temperature monitoring based on measurements of the intensity ratio of R-lines or their spectral shift in Li2SnO3–Cr3+, Mn4+ are effective only within a relatively narrow temperature range, limiting their practical application. In contrast, we discovered that thermometry based on measurements of the decay time constant of the 2E → 4A2 transitions of TM ions in Li2SnO3 shows great promise, as this luminescence parameter exhibits high sensitivity to temperature changes.
The relative sensitivity of Cr3+ emission, equal to 2.0%/K at 190 K, is comparable to that demonstrated by Ga2O3–Cr3+ taken as reference. This translates to an expected temperature resolution of measurements better than ±1 K over a broad temperature range from 100 to 350 K. The emission of Mn4+ exhibits even higher sensitivity at 220 K, with a value of 5.8%/K. However, due to steep thermal quenching, practical temperature measurements are only possible within a narrow range of temperatures. Nevertheless, this emission may be very useful for cross-verifying results of temperature measurements obtained from the Cr3+ emitter. This added feature enhances the potential of Li2SnO3–Cr3+, Mn4+ as a non-contact luminescence sensor for temperature.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the Polish National Science Centre (project no. 2018/31/B/ST8/00774 and 2021/40/Q/ST5/00336) and by the National Research Foundation of Ukraine (grant no. 2020.02/0373 “Crystalline phosphors’ engineering for biomedical applications, energy saving lighting and contactless thermometry”).References
- S. Sugano, Y. Tanabe and H. Kamimura, Multiplets of Transition-Metal Ions in Crystals, Academic Press, New York and London, 1970 Search PubMed.
- M. G. Brik and A. M. Srivastava, Review-A Review of the Electronic Structure and Optical Properties of Ions with d(3) Electron Configuration (V2+, Cr3+, Mn4+, Fe5+) and Main Related Misconceptions, ECS J. Solid State Sci. Technol., 2018, 7, R3079–R3085 CrossRef CAS.
- M. G. Brik, S. J. Camardello, A. M. Srivastava, N. M. Avram and A. Suchocki, Spin-Forbidden Transitions in the Spectra of Transition Metal Ions and Nephelauxetic Effect, ECS J. Solid State Sci. Technol., 2016, 5, R3067–R3077 CrossRef CAS.
- S. Adachi, Photoluminescence properties of Mn4+-activated oxide phosphors for use in white-LED applications: A review, J. Lumin., 2018, 202, 263–281 CrossRef CAS.
- S. Adachi, Review-Mn4+-Activated Red and Deep Red-Emitting Phosphors, ECS J. Solid State Sci. Technol., 2020, 9, 016001 CrossRef CAS.
- S. Adachi, Mn4+ and Cr3+ ions in red and deep red-emitting phosphors: Spectral analysis and Racah parameter determination, J. Lumin., 2020, 223, 117217 CrossRef CAS.
- S. Adachi, Review – Mn4+vs. Cr3+: A Comparative Study as Activator Ions in Red and Deep Red-Emitting Phosphors, ECS J. Solid State Sci. Technol., 2020, 9, 026003 CrossRef CAS.
- S. Adachi, Review-Photoluminescence Properties of Cr3+-Activated Oxide Phosphors, ECS J. Solid State Sci. Technol., 2021, 10, 026001 CrossRef CAS.
- E. Jara, R. Valiente, J. Gonzalez, J. I. Espeso, N. Khaidukov and F. Rodriguez, Optical spectroscopy of the Sr4Al14O25:Mn4+,Cr3+ phosphor: pressure and temperature dependences, J. Mater. Chem. C, 2022, 10, 6380–6391 RSC.
- M. Yuan, X. L. Yang and S. G. Xiao, Photoluminescence Properties of Mn4+, Cr3+ co-doped BaMgAl10O17 Phosphor, ECS J. Solid State Sci. Technol., 2020, 9, 126002 CrossRef CAS.
- W. C. Zheng, B. X. Li, G. Y. Feng and H. G. Liu, Research on the thermal shifts and electron–phonon coupling parameters of R-line for Cr3+ and Mn4+ ions in YAlO3 crystals, J. Lumin., 2013, 138, 214–217 CrossRef CAS.
- J. H. Ou, X. L. Yang and S. G. Xiao, Luminescence performance of Cr3+ doped and Cr3+, Mn4+ co-doped La2ZnTiO6 phosphors, Mater. Res. Bull., 2020, 124, 110764 CrossRef CAS.
- T. J. Chen, X. L. Yang, W. B. Xia, W. Li and S. G. Xiao, Deep-red emission of Mn4+ and Cr3+ in (Li1−xAx)2MgTiO4 (A = Na and K) phosphor: Potential application as W-LED and compact spectrometer, Ceram. Int., 2017, 43, 6949–6954 CrossRef CAS.
- V. B. Mykhaylyk, H. Kraus, L. I. Bulyk, I. Lutsyuk, V. Hreb, L. Vasylechko, Y. Zhydachevskyy, A. Wagner and A. Suchocki, Al2O3 co-doped with Cr3+ and Mn4+, a dual-emitter probe for multimodal non-contact luminescence thermometry, Dalton Trans., 2021, 50, 14820–14831 RSC.
- N. Musa, H. J. Woo, L. P. Teo and A. K. Arof, Optimization of Li2SnO3 Synthesis for Anode Material Application in Li-ion Batteries, Mater. Today: Proc., 2017, 4, 5169–5177 Search PubMed.
- Y. Zhao, X. F. Li, B. Yan, D. B. Xiong, D. J. Li, S. Lawes and X. L. Sun, Recent Developments and Understanding of Novel Mixed Transition-Metal Oxides as Anodes in Lithium Ion Batteries, Adv. Energy Mater., 2016, 6, 1502175 CrossRef.
- N. Kuganathan, A. Kordatos and A. Chroneos, Li2SnO3 as a Cathode Material for Lithium-ion Batteries: Defects, Lithium Ion Diffusion and Dopants, Sci. Rep., 2018, 8, 12621 CrossRef PubMed.
- Y. A. Zulueta, M. T. Nguyen and J. A. Dawson, Boosting Li-Ion Transport in Transition-Metal-Doped Li2SnO3, Inorg. Chem., 2020, 59, 11841–11846 CrossRef CAS PubMed.
- M. Garcia-Tecedor, J. Bartolome, D. Maestre, A. Trampert and A. Cremades, Li2SnO3 branched nano- and microstructures with intense and broadband white-light emission, Nano Res., 2019, 12, 469 CrossRef.
- R. P. Cao, W. D. Wang, J. L. Zhang, S. H. Jiang, Z. Q. Chen, W. S. Li and X. G. Yu, Synthesis and luminescence properties of Li2SnO3:Mn4+ red-emitting phosphor for solid-state lighting, J. Alloys Compd., 2017, 704, 124–130 CrossRef CAS.
- L. Yuanyuan, Y. Jiuhong, W. Kun-Yao, W. Ya-Nan and L. Zhao, Energy transfer and luminescent properties of Li2SnO3:Mn4+ phosphors, Ferroelectrics, 2023, 606, 187–198 CrossRef.
- L. Vasylechko, V. Sydorchuk, V. Hreb, S. Ubizskii, S. Khalameida, A. Luchechko and Y. Zhydachevskyy, Hydrothermal Synthesis, Structure, and Luminescence of Cr3+-Doped Li2SnO3 and Na2SnO3 Stannates, Acta Phys. Pol., A, 2022, 141, 241–246 CrossRef CAS.
- M. J. Mombourquette, J. A. Weil and D. G. McGavi, EPR-NMR User's Manual, University of Saskatchewan, Department of Chemistry, Canada, 1999 Search PubMed.
- G. Leniec, Electron Paramagnetic Resonance: A Technique to Locate the Nearest Environment of Chromium Luminescent Centers, ACS Appl. Opt. Mater., 2023, 1, 1114–1121 CrossRef CAS.
- V. Rajendran, K.-C. Chen, W.-T. Huang, N. Majewska, T. Leśniewski, M. Grzegorczyk, S. Mahlik, G. Leniec, S. M. Kaczmarek, W. K. Pang, V. K. Peterson, K.-M. Lu, H. Chang and R.-S. Liu, Pentavalent Manganese Luminescence: Designing Narrow-Band Near-Infrared Light-Emitting Diodes as Next-Generation Compact Light Sources, ACS Energy Lett., 2023, 8, 289–295 CrossRef CAS.
- L. Vasylechko, V. Stadnik, V. Hreb, Y. Zhydachevskyy, A. Luchechko, V. Mykhaylyk, H. Kraus and A. Suchocki, Synthesis, Crystal Structure and Photoluminescent Properties of Red-Emitting CaA4O7:Cr3+ Nanocrystalline Phosphor, Inorganics, 2023, 11, 205 CrossRef CAS.
- P. Rodionovs, M. Kemere, A. Antuzevics, U. Rogulis, A. Sarakovskis and A. Fedotovs, Multi-site incorporation of Cr3+ in CaAl12O19, Materialia, 2023, 32, 101927 CrossRef CAS.
- H. Zeng, T. Zhou, L. Wang and R.-J. Xie, Two-Site Occupation for Exploring Ultra-Broadband Near-Infrared Phosphor—Double-Perovskite La2MgZrO6:Cr3+, Chem. Mater., 2019, 31, 5245–5253 CrossRef CAS.
- R. W. Gurney and N. F. Mott, Luminescence in solids, Trans. Faraday Soc., 1939, 35, 69–73 RSC.
- M. Grinberg and T. Lesniewski, Non-radiative processes and luminescence quenching in Mn4+ doped phosphors, J. Lumin., 2019, 214, 116574 CrossRef CAS.
- Y. Zhydachevskyy, V. Mykhaylyk, V. Stasiv, L. I. Bulyk, V. Hreb, I. Lutsyuk, A. Luchechko, S. Hayama, L. Vasylechko and A. Suchocki, Chemical Tuning, Pressure, and Temperature Behavior of Mn4+ Photoluminescence in Ga2O3–Al2O3 Alloys, Inorg. Chem., 2022, 61, 18135–18146 CrossRef CAS PubMed.
- L. Swiderski, K. Brylew, W. Drozdowski, M. Grodzicka-Kobylka, L. Janiak and M. Moszynski, LuAG:Pr, LuAG:Pr,Mo and LuYAG:Pr relative light yield measured at wide temperature range with MPPC readout, Nucl. Instrum. Methods Phys. Res., Sect. Ad, 2022, 1021, 165924 CrossRef CAS.
- A. Hrytsak, M. Rudko, V. Kapustianyk, L. Hrytsak and V. Mykhaylyk, X-Ray Luminescence and Thermally Stimulated Processes in Cesium Iodide Crystal, Phys. Status Solidi B, 2023, 260, 2300289 CrossRef CAS.
- S. Adachi, Review-Temperature Dependence of Luminescence Intensity and Decay Time in Cr3+-Activated Oxide and Fluoride Phosphors, ECS J. Solid State Sci. Technol., 2022, 11, 066001 CrossRef.
- H. Shibata, Negative thermal quenching curves in photoluminescence of solids, Jpn. J. Appl. Phys., 1998, 1(37), 550–553 CrossRef.
- D. E. McCumber and M. D. Sturge, Linewidth and Temperature Shift of the R Lines in Ruby, J. Appl. Phys., 1963, 34, 1682–1684 CrossRef CAS.
- Z. Y. Zhang, K. T. V. Grattan, A. W. Palmer, V. Fernicola and L. Crovini, Temperature-Dependence of the YAG-Cr3+ Fluorescence Lifetime over the Range 77 to 900 K, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 2656–2660 CrossRef CAS PubMed.
- V. Mykhaylyk, H. Kraus, Y. Zhydachevskyy, V. Tsiumra, A. Luchechko, A. Wagner and A. Suchocki, Multimodal Non-Contact Luminescence Thermometry with Cr-Doped Oxides, Sensors, 2020, 20, 5259 CrossRef CAS PubMed.
- L. Marciniak, K. Kniec, K. Elzbieciak-Piecka, K. Trejgis, J. Stefanska and M. Dramicanin, Luminescence thermometry with transition metal ions. A review, Coordin, Chem. Rev., 2022, 469, 214671 CAS.
- N. Ahmed, H. Kraus, H. J. Kim, V. Mokina, V. Tsiumra, A. Wagner, Y. Zhydachevskyy and V. B. Mykhaylyk, Characterisation of tungstate and molybdate crystals ABO4 (A = Ca, Sr, Zn, Cd; B = W, Mo) for luminescence lifetime cryothermometry, Materialia, 2018, 4, 287–296 CrossRef CAS.
- W. H. Fonger and C. W. Struck, Temperature Dependences of Cr+3 Radiative and Nonradiative-Transitions in Ruby and Emerald, Phys. Rev. B: Solid State, 1975, 11, 3251–3260 CrossRef CAS.
- T. Senden, R. J. A. van Dijk-Moes and A. Meijerink, Quenching of the red Mn4+ luminescence in Mn4+-doped fluoride LED phosphors, Light: Sci. Appl., 2018, 7, 8 CrossRef PubMed.
- Z. Y. Zhang, K. T. V. Grattan and A. W. Palmer, Temperature Dependences of Fluorescence Lifetimes in Cr3+-Doped Insulating Crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 7772–7778 CrossRef CAS PubMed.
- C. D. S. Brites, S. Balabhadra and L. D. Carlos, Lanthanide-Based Thermometers: At the Cutting-Edge of Luminescence Thermometry, Adv. Opt. Mater., 2019, 7, 1801239 CrossRef.
- M. Back, J. Ueda, M. G. Brik and S. Tanabe, Pushing the Limit of Boltzmann Distribution in Cr3+-Doped CaHfO3 for Cryogenic Thermometry, ACS Appl. Mater. Interfaces, 2020, 12, 38325–38332 CrossRef CAS PubMed.
- Z. Risti, V. Dordevic, M. Medic, S. Kuzman, M. Sekulic, Z. Antic and M. D. Dramicanin, Triple-temperature readout in luminescence thermometry with Cr3+-doped Mg2SiO4 operating from cryogenic to physiologically relevant temperatures, Meas. Sci. Technol., 2021, 32, 054004 CrossRef.
- E. Glais, M. Pellerin, V. Castaing, D. Alloyeau, N. Touati, B. Viana and C. Chanéac, Luminescence properties of ZnGa2O4:Cr3+,Bi3+ nanophosphors for thermometry applications, RSC Adv., 2018, 8, 41767–41774 RSC.
- E. Glais, V. Dordevic, J. Papan, B. Viana and M. D. Dramicanin, MgTiO3:Mn4+ a multi-reading temperature nanoprobe, RSC Adv., 2018, 8, 18341–18346 RSC.
- M. D. Dramićanin, B. Milićević, V. Đorđević, Z. Ristić, J. Zhou, D. Milivojević, J. Papan, M. G. Brik, C.-G. Ma, A. M. Srivastava and M. Wu, Li2TiO3:Mn4+ Deep-Red Phosphor for the Lifetime-Based Luminescence Thermometry, Chemistry, 2019, 4, 7067–7075 Search PubMed.
- H. Luo, X. Li, X. Wang and M. Peng, Highly thermal-sensitive robust LaTiSbO6:Mn4+ with a single-band emission and its topological architecture for single/dual-mode optical thermometry, Chem. Eng. J., 2020, 384, 123272 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03913g |
| This journal is © The Royal Society of Chemistry 2024 |





