The interplay of intersystem crossing and internal conversion in quadrupolar tetraarylpyrrolo[3,2-b]pyrroles

Abstract

Adding nitro groups to aromatic compounds usually quenches their fluorescence via intersystem crossing (ISC) or internal conversion (IC). Herein, we investigated centrosymmetric 1,4-dihydropyrrolo[3,2-b]pyrroles linked to variously substituted nitro-heteroaryls. A 1,4-orientation of the nitro substituent versus the electron rich 1,4-dihydropyrrolo[3,2-b]pyrrole core invokes a strong fluorescence in non-polar solvents and intense two-photon absorption while a 1,3-orientation of push–pull substituents results in a dramatic hypsochromic shift of absorption, weak, bathochromically shifted emission and weak two-photon absorption. The combined experimental and computational study indicates that the primary responsible factors are: (1) the difference in electron density distribution in the LUMO; (2) the difference in μ₁₀. IC is a dominant mechanism of non-radiative dissipation of energy in all these dyes but as long as the distribution of electron density within the HOMO and LUMO is delocalized on the 1,4-dihydropyrrolo[3,2-b]pyrrole core as well as on the nitroaromatic moieties its rate is slower than the fluorescence rate in non-polar solvents.

---

Introduction

During the last five years, the question of why and when nitro-aromatics become fluorescent has attracted strong attention,^1–10 whereas in the past the focus was on explaining the lack of fluorescence.^11–16 This paradigm shift resulted in generalizing the observation of nitroaromatics’ emission followed by attempts to rationalize such behaviour. The drawback of nitroaromatics is that their electronically excited singlet states usually exhibit very short lifetimes (sub-ns and often sub-ps time range).^6,7,10 The long-standing presumption that they are effectively non-fluorescent was reinforced by these short lifetimes, although for some of them fluorescence was detected, albeit with fluorescence quantum yields (Φ_fl) that are often smaller than about 10⁻³.^6,10 Interestingly however, already early on, amine derivatives of nitrobenzoxadiazole were found to possess sufficiently strong fluorescence to be widely used as fluorescence probes in molecular biology.⁸ The most typical and efficient way by which nitro groups quench fluorescence is intersystem crossing (ISC) leading to triplet formation.^6,10 Consequently, introducing charge-transfer (CT) character in the excited states which decreases spin orbit coupling (SOC) can increase lifetimes of the S₁ states of nitroaromatics rendering them fluorescent. On the other hand however, polar solvents stabilize such polarized states, bringing them closer to the ground state, resulting in opening the pathways for efficient internal conversion (IC) via back CT. Accordingly, in polar media, emission of fluorescent nitroaromatics possessing push–pull architecture is typically quenched.¹⁰ For now several guiding principles were formulated e.g. (1) lowering the energy level of the S₁ state below that of T₂ and the other upper triplet states; (2) ensuring that the energy levels of the lowest ¹ππ* and ¹nπ* excited states are well separated; (3) suppressing the electronic coupling with the nitro group, e.g., placing –NO₂ at a node of the frontier orbitals. Notwithstanding the achieved breakthroughs, an enormous complexity of various effects on the excited-state dynamics of nitroaromatics is the reason why further progress can be achieved only by studying suitable model systems enabling probing the effect of small structural changes on the fate of the molecules in their excited states. In this context, centrosymmetric 1,4-dihydropyrrolo[3,2-b]pyrroles (DHPPs) have garnered significant attention.^17–23 Studies have revealed that placing NO₂ groups on phenyl substituents attached to positions 2 and 5 of DHPP ensures electronic coupling that is (1) sufficiently weak to ensure slow intersystem crossing and intense fluorescence, and (2) sufficiently strong to introduce substantial charge-transfer character that controls the excited-state dynamics. The multicomponent nature of the reaction leading to this heterocycle^24,25 combined with their strong electronic communication at positions 2 and 5 offers a unique vehicle to study the effects of the structural parameters on the fate of the molecule in the excited state.^26,27 We believed that a further in-depth study on the influence of the relative arrangement of the core and NO₂ groups, embracing both five-membered and six-membered heterocycles as substituents, will enable deeper understanding of how to modulate a pronounced CT character of the excited states of dyes bearing the strongly electron-withdrawing nitro substituents.

Results and discussion

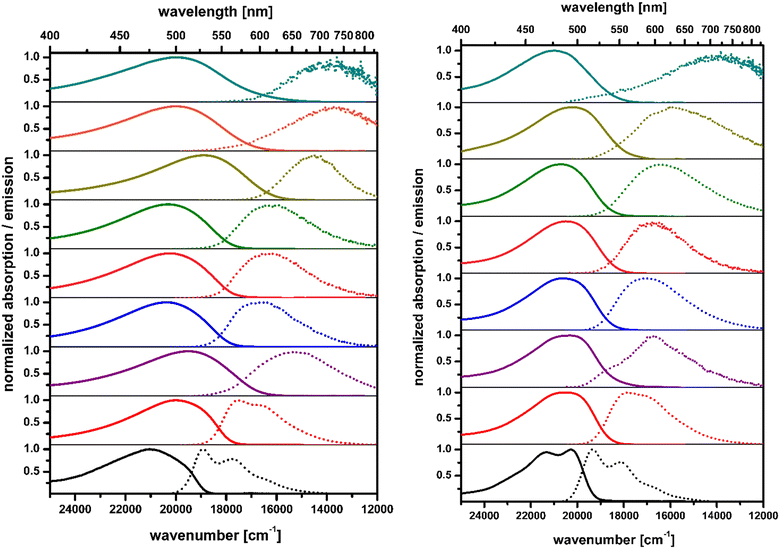
We have chosen aromatic five-membered heterocycles possessing one heteroatom as substituents at positions 2 and 5 as our models. This choice was dictated by the novelty factor and the fact that thiophene and pyrrole offer different electronic interactions between NO₂ groups and the DHPP core compared with benzene. To cover a reasonable chemical space, we have selected dyes possessing heterocyclic substituents connected at position 2 of pyrrole and the NO₂ group at positions 4 and 5. Further diversification comes from a connection at position 3 of thiophene with the nitro group at position 5. Finally, we have also employed a 4-nitro-2-pyridinyl substituent leading to dye being a direct analog of 2,5-di(4-nitrophenyl)pyrrolo[3,2-b]pyrrole (DNPP) possessing basic nitrogen atom. All four quadrupolar centrosymmetric tetraaryl-pyrrolo[3,2-b]pyrroles (TAPPs) 1–4 possessing both nitro groups and heterocyclic aromatic substituents at positions 2 and 5 were synthesized in yields 20–59% directly from the corresponding aldehydes (Fig. 1 and Scheme S1, ESI†). The comparison of the absorption spectrum of dye 1 in toluene with those of previously described analogues possessing 5-nitrofuryl and 5-nitrothienyl groups²² correlates with the effect of electron richness of the five-membered heterocycles. Pyrrole is the most electron-rich and both absorption and emission of 1 are hypsochromically shifted vs. that of the analogues,²² whereas the emission intensity stays at the same level. On the other hand, comparison of dye 3 with 2,5-di(4-nitrophenyl)pyrrolo[3,2-b]pyrrole (DNPP) enables us to see the exact effect of increased electron-withdrawing strength of the 5-nitropyrid-2-yl moiety. In toluene, there is an approx. 20 nm bathochromic shift of absorption, the same for emission, accompanied by a rapid fluorescence quantum yield decrease upon increasing the solvent polarity, analogously to DNPP.

Fig. 1 Structures of TAPPs 1–4 and reaction yields.

Analyzing the spectroscopic properties, we can distinguish the two groups among investigated quadrupolar dyes. Furthermore, the molecular structure analysis indicates that this division is directly correlated with the orientation of the nitro group in relation to the 1,4-dihydropyrrolo[3,2-b]pyrrole core. The first set of compounds is represented by TAPPs 1 and 3 that strongly absorb in the visible spectrum range (λ_max ≈ 490–500 nm, Fig. 3). The broad absorption spectrum of dyes 1 and 3 slightly changes with solvent polarity, indicating a rather nonpolarized character of the ground state, which stands in line with the centrosymmetric architecture of these quadrupolar dyes. The nitro groups in 1 and 3 are strongly conjugated with the central electron-rich DHPP, thus significantly affecting the electronic structure of the investigated compounds. The distribution of electron density within the HOMO and LUMO, for both compounds, is delocalized on the 1,4-dihydropyrrolo[3,2-b]pyrrole core as well as on the nitroaromatic moieties (Fig. 2). For this reason, the transition S₀ → S₁ for 1 and 3 is characterized by a high oscillator strength, f ≈ 1.5, regardless of the solvent (Tables S1 and S5, ESI†), indicating the strongly allowed nature of the first electronic transition leading to intense visible range absorption. On the other hand, for higher electron transitions falling in the UV range, a more than 25-times drop of oscillator strength is observed. The clearly forbidden character of these transitions is reflected in the experimental results, showing residual absorption in the UV range. For both compounds in hexane, the emission spectra exhibit a distinct oscillation pattern, which is lost in favor of a broad band upon rising solvent polarity, accompanied by solvatofluorochromism, originating from the excited state symmetry breaking.²⁸ Both TAPPs 1 and 3 demonstrate yellow fluorescence in nonpolar solvents (λ_max ≈ 528 nm and 517 nm, respectively), reaching a quantum yield of 96% for 3 in hexane, which is a relatively rare value for nitroaromatics (Fig. 3). Nevertheless, increasing solvent polarity enhances the Stokes shift, up to ≈7000 cm⁻¹ and ≈6000 cm⁻¹ for 1 and 3 respectively, shifting emission maximum up to 725 nm in acetonitrile. However, the fluorescence is quenched in analogy to some other quadrupolar centrosymmetric TAPPs.¹⁷

Fig. 2 Optimized ground state (S₀) structures and frontier molecular orbitals (FMOs) of quadrupolar dyes.

Fig. 3 Absorption (solid) and emission (dot) spectra of 1 (left) and 3 (right) in hexane (black), toluene (red), n-octanol (purple), propyl butyrate (blue), tetrahydrofuran (pink), ethyl acetate (green), butyl acetate (gold), acetonitrile (cyan).

The second set of discussed dyes is represented by TAPPs 2 and 4, that exhibit broad, small (2, λ_max ≈ 406 nm) or negligible (4, λ_max ≈ 431 nm) absorption within the visible range (Fig. S9, ESI†) practically doesn’t affected by solvent polarity. Indeed the absorption spectrum of TAPP 2 resembles spectrum of 2,5-di(3-nitrophenyl)pyrrolo[3,2-b]pyrrole.¹⁷ In these systems, the nitro group is weakly conjugated to the electron-rich 1,4-dihydropyrrolo[3,2-b]pyrrole core. A clear isolation of the donor–acceptor subunits manifests in the electron density distribution, which in the HOMO is located mainly in the 1,4-dihydropyrrolo[3,2-b]pyrrole subunit, while in the LUMO it is localized only at the nitroaromatic moiety (Fig. 2). The lack of overlap of the electron density distribution at both levels results in low oscillator strength of S₀ → S₁ transition, equal f ≈ 0.2 and f ≈ 0.03, for 2 and 4 respectively (Tables S3 and S7, ESI†). The clearly forbidden nature of the first electronic transition leads to weak visible range absorption. On the other hand, both dyes exhibit intense absorption within the UV range which, according to TD-DFT calculations, corresponds to S₀ → S₃ and S₀ → S₅ transitions for 2 (λ_max > 350 nm) and 4 (λ_max ≈ 350 nm), respectively. The strong charge separation in S₁ leads to symmetry breaking²² causing a significant increase of excited state dipole moment, which in turn is responsible for a clear shift in the emission spectra up to 10 300 cm⁻¹ for 2 (λ_max ≈ 729 nm) and in the case of 4 more than 10 000 cm⁻¹ (Table 2 and Fig. S9, ESI†) up to the near infrared range (NIR) in acetonitrile. However, due to the forbidden character of the S₁ → S₀ transition, the observed fluorescence quantum yields in most solvents are markedly below 1%, for both 2 and 4. Due to low Φ_fl we were unable to estimate the emission maximum for TAPP 4 in ethyl acetate, butyl acetate and acetonitrile.

To get deeper insight into the photophysics of the obtained TAPPs we performed quantum chemical calculations. The DFT/B3LYP/6-31G(d,p) theory level optimized ground state (S₀) structures of studied dyes 1–4 are presented in Fig. 2. As described in the ESI,† the S₀ geometry optimizations include the GD3 empirical dispersion correction for consideration of dispersive interactions. The dispersion correction to DFT along with the 6-31G(d,p) basis function successfully explained the ground state geometrical properties. For a better agreement between the experiment and computational simulations of photophysical properties, we implemented higher percentage of Hartree–Fock exchange i.e. 37% in B3LYP functional (henceforth called B3LYP-37) for TDDFT simulations. The same B3LYP-37/6-31G(d,p) method has also been successfully used in our previous report (ref. 27). The calculated highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are presented in Fig. 2, and other molecular orbitals like HOMO−1 and LUMO+1 are provided in ESI† (Fig. S17).

The effects of the intersystem crossing (ISC), internal conversion (IC) rate constants and the radiative decay rate (k_r) on the fluorescence quantum yield (Φ^theor_fl) for the studied dyes are discussed below. We have elaborated the theoretical methodologies for the nonradiative (ISC and IC) and radiative rate constants in the ESI.† The calculated singlet and triplet states excitation energies, SOCMEs, and k_ISC are listed in Table 1. We should note that, for all of the investigated dyes, in all solvents, we found triplet states T₁ and T₂ are below the singlet S₁ level (see Table 1), and we considered them as only possible states for ISC quenching of the S₁ state. The combination of ΔE_ST and SOCME parameters plays an important role in determining the ISC rate. For example, the large ΔE_S1T2 > 1 eV, ΔE_S1T2 > 0.4 eV and small SOCME between these states for dye 1 led to a small k_ISC rates of order about 10⁵ s⁻¹. For 2, the ΔE_S1T1 remains considerably large (>0.6 eV), but ΔE_S1T2 becomes smaller (up to 0.2 eV in polar solvents), while SOCME_S1T2 is higher than for compound 1. This finally results in a k_ISC rate for compound 2 of about 10⁶ s⁻¹ order. For dyes 3 and 4, the SOCME_S1T2 is even higher than for TAPPs 1 and 2, while the ΔE_S1T2 remains small, that results in a k_ISC rate for both 3 and 4 of about 10⁷–10⁸ s⁻¹. We should note here that we do not observe a clear dependence of k_ISC on solvent polarity in contrast to experimental observations. Particularly, compound 1 demonstrates significant quenching of fluorescence with an increase in solvent polarity (Table 2).

Table 1 Calculated singlet, triplet excited state energies, perturbative spin–orbit coupling matrix elements (SOCMEs) values, intersystem crossing (ISC), radiative rate constants, internal conversion (IC) rates, and fluorescence quantum yields of 1–4 in solution

Dye	Solvent	S1 (eV)	T1 (eV)	T2 (eV)	SOCMES1T1 (cm^−1)	SOCMES1T2 (cm^−1)	k ISC (s^−1)	k r ^a (s^−1)	k IC × 10^8 ^b (s^−1)	Φ ^theorfl
1	Toluene	2.40	1.11	1.93	0.18	0.03	3.00 × 10^5	3.0 × 10^8	0.70	0.73
	Tetrahydrofuran	2.20	1.00	1.80	0.18	0.03	5.50 × 10^5	3.5 × 10^8	1.00	0.77
	Ethyl acetate	2.23	1.02	1.84	0.18	0.02	6.00 × 10^5	4.0 × 10^8	1.00	0.78
	Acetonitrile	2.10	0.95	1.76	0.17	0.02	1.00 × 10^6	3.0 × 10^8	5.00	0.37
2	Toluene	2.17	1.53	1.73	0.02	0.07	5.00 × 10^5	4.0 × 10^5	5.00	0.0008
	Tetrahydrofuran	2.03	1.41	1.75	0.03	0.08	1.00 × 10^6	1.0 × 10^6	7.00	0.0014
	Ethyl acetate	2.05	1.43	1.76	0.03	0.08	4.00 × 10^6	8.0 × 10^5	6.00	0.0014
	Acetonitrile	1.97	1.35	1.77	0.04	0.08	1.00 × 10^7	1.5 × 10^6	10.0	0.0015
	Methanol	1.97	1.35	1.78	0.03	0.08	7.00 × 10^6	1.0 × 10^6	1.50	0.007
3	Toluene	2.33	1.29	2.27	0.06	0.36	9.00 × 10^7	3.0 × 10^8	0.30	0.69
	Tetrahydrofuran	2.16	1.21	2.06	0.06	0.10	6.00 × 10^7	3.0 × 10^8	0.70	0.69
	Ethyl acetate	2.19	1.22	2.06	0.06	0.10	7.00 × 10^7	3.0 × 10^8	0.70	0.73
	Acetonitrile	2.07	1.18	2.05	0.06	0.10	1.00 × 10^8	—	—	—
4	Toluene	1.81	1.40	1.70	0.28	1.22	3.00 × 10^8	7.0 × 10^3	10.0
	Tetrahydrofuran	1.82	1.28	1.50	0.30	1.00	1.00 × 10^8	6.5 × 10^3	30.0
	Ethyl acetate	1.70	1.25	—	0.30	—	5.00 × 10^5	—	—	—
	Acetonitrile	1.60	1.23	—	0.30	—	1.00 × 10^7	—	—	—

---

Table 2 Photophysical data of dyes 1–4 measured in solution and compared to theoretical calculations

Dye	Solvent	λ ^maxabs (nm)	λ ^maxem (nm)	Φ fl [%]	Δν [cm^−1]
a Rh6G in EtOH as a standard, QY = 94%.^49 b Rh101 in MeOH as a standard, QY = 100%.^49 c Coum153 in EtOH as a standard, QY = 38%.^49 d PCM/B3LYP-37/6-31G(d,p) theory level. e Results obtained in propyl ethanoate.
1	n-Hexane	474 [461]^d	528 [504]^d	21.5^a	2200
	Toluene	499 [468]^d	569 [516]^d	28^a	2500
	Propyl butyrate	490 [473]^d^e	591 [553]^d^e	6.1^a	3500
	THF	494 [473]^d	604 [562]^d	5.2^a	3700
	Ethyl acetate	494 [471]^d	609 [555]^d	3.9^a	3800
	n-Octanol	513 [475]^d	639 [570]^d	1.1^a	3800
	n-Butyl acetate	530 [470]^d	684 [549]^d	0.63^a	4200
	Acetonitrile	501 [475]^d	697 [590]^d	0.26^a^b	5600
2	Toluene	406 [385]^d	603 [570]^d	1.03^c	8000
	Propyl butyrate	403 [398]^d^e	627 [602]^d^e	0.33^c	8900
	THF	411 [400]^d	642 [609]^d	0.24^c	8800
	Ethyl acetate	405 [398]^d	630 [604]^d	0.17^c	8800
	n-Octanol	420 [403]^d	637 [615]^d	0.102^c	8100
	n-Butyl acetate	417 [396]^d	637 [599]^d	0.108^c	8300
	Acetonitrile	417 [407]^d	729 [629]^d	0.039^c	10300
	Methanol	410 [407]^d	552 [628]^d	0.011^c	6300
3	n-Hexane	493 [468]^d	517 [516]^d	96^a	950
	Toluene	488 [474]^d	558 [528]^d	77^a	2600
	THF	488 [477]^d	604 [572]^d	1.3^a	3900
	Ethyl acetate	483 [475]^d	599 [566]^d	0.81^a	4000
	Propyl butyrate	486 [475]^d^e	580 [563]^d^e	7.5^a	3300
	n-Octanol	492 [478]^d	578 [579]^d	2.9^a	3000
	n-Butyl acetate	495 [475]^d	623 [560]^d	0.49^a	4150
	Acetonitrile	478 [477]^d	— [597]^d	0.02^a	—
4	n-Hexane	431 [473]^d	600 [664]^d	0.67^b	6500
	Toluene	453 [478]^d	719 [678]^d	0.27^b	8200
	Propyl butyrate	451 [489]^d^e	765 [716]^d^e	0.019^b	9100
	THF	460 [491]^d	822 [725]^d	0.010^b	9600
	Ethyl acetate	462 [489]^d	— [719]^d	0.002^b	—
	n-Octanol	450 [493]^d	700 [732]^d	0.06^b	7900
	n-Butyl acetate	468 [488]^d	740 [712]^d	0.04^b	7900
	Acetonitrile	467 [496]^d	— [750]^d	0.011^b	—

---

It is worth pointing out, that the calculated ISC rates do not have a significant effect on the low Φ_fl for the emissive dyes 1 and 3 because k_r is 10⁸ s⁻¹ higher than the k_ISC rates for these molecules. Thus, we calculated the internal conversion (IC) rates for all of the studied dyes and found solvent-dependent IC rates are 0.7–5.0 × 10⁸ s⁻¹ and 0.3–0.7 × 10⁸ s⁻¹ for TAPPs 1 and 3, respectively. Taking in to account the k_IC values, we estimated the solvent dependent fluorescence quantum yield (Φ_fl) of 37–78% for 1 and 69–73% for 3, respectively (Table 1) in good agreement with the experimental values (Table 2). Thus, the strong fluorescence of dyes 1 and 3 in non-polar solvents originates from the fact of weak contribution from both ISC and IC quenching channels.

At the same time, higher solvent polarity induces the red shift of fluorescence that subsequently increases the internal conversion rate and IC becomes a significant fluorescence quenching channel. For NIR-emissive dye 2, though the calculated k_r is in-line with the k_ISC values, we predicted k_IC about 10² s⁻¹ higher. This is the origin of its very low fluorescence quantum yield (0.1–0.7%). Similarly, the Φ_fl for 4 is calculated to be nearly zero because of the very small radiative decay rate (about 10⁵ s⁻¹ order smaller than k_ISC and k_ISC) (Table 1).

Here, we note that, for decay rate constants as well as fluorescence quantum yields theoretical calculations (mentioned in Table 1), we considered experimental S₁ emission energy and theoretically calculated S₁ → S₀ oscillator strength. This is because we noticed significant overestimation in S₁ energy with the TD-DFT/B3LYP-37 theory. Additionally, because we lack the experimental measurements, we could not reproduce the photophysical properties in some solvents for compounds 3 and 4.

Two-photon absorption. While many molecular architectures exhibit two-photon absorption (TPA),^29–39 the centrosymmetric quadrupolar structures are the most common motif known for strong nonlinear responses.^40–45 We employed the open-aperture Z-scan method to characterize their TPA properties. The obtained spectra in chloroform solution are shown in Fig. 4.

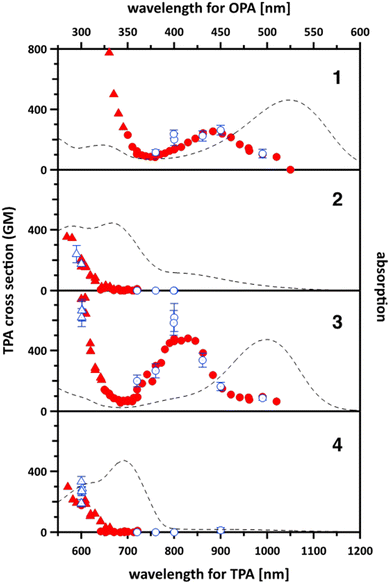Fig. 4 Two-photon absorption (TPA) spectra of the quadrupolar dyes 1–4 (circles and triangles) in chloroform to bottom and left axes. The data shown with triangle were affected by the saturable absorption (SA) and analysed by considering it. The filled symbols are the data measured with a single incident power (WL-scan), and the open symbols with error bars are those measured by varying the incident power (power scan). See Experimental in ESI† for the details on these modes of measurements. The one-photon absorption spectra (to right and top axes) also shown with the scale where the transition energies of TPA and OPA locate to the same horizontal position. The data points out of the vertical range are displayed in Fig. S15 in ESI.†

It was found that TAPPs 1 and 3 have spectra with a similar shape. They both have a broad TPA peak in the near infrared wavelength range with relatively large TPA cross sections (σ⁽²⁾ = 260 ± 30 GM at 900 nm for 1 and σ⁽²⁾ = 620 ± 90 GM at 800 nm for 3). At wavelengths shorter than 700 nm, the cross section rapidly increases. At this region, the tail of the linear absorption (i.e., one-photon absorption, OPA) could not be ignored (Fig. S15 in ESI†) and the saturable absorption (SA) of OPA was observed (shown with triangle in Fig. 4 and Fig. S15, ESI†). The largest value observed was 3900 GM at 620 nm for 1 and 1010 GM at 600 nm for 3 after the correction for SA (see Experimental in ESI†). The drastic increase of the TPA cross section was matched in wavelength with the OPA tail, suggesting the strong influence of the resonance enhancement.⁴⁶

On the other hand, TAPPs 2 and 4, exhibit very different two-photon absorption spectra. The TPA starts at 700 nm and gradually increases as the wavelength decreases. At the shortest wavelength (570 nm), the observed TPA cross section was around σ⁽²⁾ = 350 GM for 2 and 300 GM for 4. Contrary to TAPPs 1 and 3, no detectable TPA signal was observed in the NIR wavelength range for dyes 2 and 4. In all these cases however Laporte rules for centrosymmetric molecules are obeyed.

We also employed DFT calculations to simulate the TPA spectra and to understand the nature of the transitions (see Experimental for the detailed methods). The simulated spectra (Fig. S16, ESI†) were qualitatively reproduced. Many features of the experimental spectra such as the transition energy and TPA cross section were overestimated. Compounds 1 and 3 were found to have a strong TPA peak assigned to the S₀ → S₂ transition. Dyes 2 and 4 also had a TPA peak of the S₀ → S₂ transition, but one to two orders of magnitude smaller than those of 1 and 3. (Please note that S₁ and S₂ are degenerate in the case of 4 and they have the same orbital nature. So, the S₀ → S₁ peak of 4 in Fig. S16 (ESI†) means the same as S₀ → S₂.) TPA bands observed for 2 and 4 at 700 nm or shorter are assigned to the higher excited states (S₀ → S₇, S₁₁, S₁₃, S₁₅ for 2 and S₀ → S₇, S₂₀ for 4) as suggested by the experimental results.

To understand the prominent difference in non-linear optical properties between the two sets of TAPPs (1, 3 and 2, 4) we focused on the S₀ → S₂ TPA transition, for which the largest contributing intermediate state is S₁. Thus, the transition path is represented as S₀ → S₁ → S₂ and the corresponding orbital transition path is HOMO → LUMO → LUMO+1 from the electronic configuration of each state. The related transition dipole moments are summarized in Table 3. The transition dipole moment between the excited state μ₂₁ is similar among all TAPPs (19–25 D), which can be understood from the good overlap between LUMO and LUMO+1 for all dyes. Meanwhile, μ₁₀ differs significantly (13 D for 1, 3versus 2–6 D for 2, 4) as discussed on the overlap between HOMO and LUMO above. TPA cross section at the peak of S₀ → (S₁) → S₂ transition can be written by the three-state approximation for the centrosymmetric molecules as,^47,48

where θ is the angle between μ₂₁ and μ₁₀, E₂₀ and E₁₀ are the transition energies of S₁ → S₂ and S₀ → S₁, Γ₂₀ is the relaxation constant of S₂ → S₀, c is the speed of light, and n is the refractive index.

Table 3 Transition dipole moments (μ₂₁ for S₁ → S₂ and μ₁₀ for S₀ → S₁), the angle between the moments (θ), and the detuning factor (D.F.) calculated at the TDA-CAM-B3LYP/6-31+G(d) level. Solvent effect was considered by using PCM (chloroform)

Compound	μ 21/D	μ 10/D	θ/°	D.F.
1	18.5	13.7	178	2.28
2	22.5	5.6	16	2.86
3	21.5	13.5	176	2.58
4	24.7	2.3	97	1.00

---

The two transition dipole moments are almost parallel to each other (θ ≈ 180°) in the case of TAPPs 1 and 3, resulting in the maximum value in the angle factor 1 + 2 cos² θ ≈ 3 while it deviated from the maximum for TAPPs 2 and 4. As for the detuning factor, D.F. = (1/4) (E₁₀/E₂₀ − 1/2)⁻², the value is similar to each other (2.3–2.9) for all studied dyes except for 4 (1.0), but it further acts to decrease the cross section for 4. Therefore, the difference in μ₁₀, which is the common parameter with OPA, is the dominant factor responsible for large differences in TPA strength. As discussed above, the difference in electron density distribution in the LUMO within this set of dyes governs the optical properties of the quadrupolar dyes not only for OPA but also for TPA.

Conclusions

Placing NO₂ groups in non-conjugated positions versus 1,4-dihydropyrrolo[3,2-b]pyrrole core leads to tremendous differences in photophysical properties compared to analogous TAPPs with more conjugated nitro group. The differences originate from the electron density distribution i.e. HOMO is located mainly in the 1,4-dihydropyrrolo[3,2-b]pyrrole subunit, while LUMO is located on nitroaryl substituents. The bis-nitro-TAPP possessing 5-nitro-thiophen-3-yl substituent studied herein represents an exceptional case as a result of linking DHPP core with thiophene at less conjugated position 3. Our study demonstrates that this combination leads to very small fluorescence quantum yields regardless the solvents polarity and negligibly weak absorption beyond 400 nm. Decreasing the ISC rates for the bis-nitro-TAPPs makes them fluorescent in non-polar solvents, but it also allows the effects from IC to emerge and dominate their photophysics in polar media. This is a rationale behind strong fluorescence of TAPP possessing 5-nitropyrrol-2-yl and 5-nitropyridin-2-yl substituents. Parallel analysis of linear and two-photon absorption reveal that the underlying key factor governing the photophysical properties of these quadrupolar dyes, is the difference in electron density distribution in the LUMOs. If LUMO does not spread beyond nitroaryl substituents emission is weak across the solvents polarity scale and TAPPs do not possess distinct TPA peak in the NIR region. The TPA simulation clarified that the change in the oscillator strength of the HOMO → LUMO transition also determines the two-photon absorption. Furthermore, our combined study has shown that, for cases where the radiative rate constant is small (less than 10⁸ s⁻¹ order of magnitude) intersystem crossing is another efficient process responsible for fluorescence quenching in addition to internal conversion.

Author contributions

Conceptualization: D. T. G.; investigation: K. G., D. K., S. O., M. B., R. V., S. R. S.; supervision: D. T. G., G. B., K. K.; visualization: K. G., D. K., S. O., M. B.; writing – original draft: K. G., D. K., G. B., K. K.; writing – review & editing: D. T. G.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Foundation for Polish Science (TEAM POIR.04.04.00-00-3CF4/16-00). We also thank the National Science Centre, Poland, under QuantERA programme, project 2017/25/Z/ST2/03038 and OPUS 2020/37/B/ST4/00017. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowka-Curie grant agreement no. 101007804. This work was partially supported by JSPS KAKENHI Grant Number 21H01887(KK). G. B. thank the Ministry of Education and Science of Ukraine for support (Project No. 0121U107533). R. V. thanks the Academy of Finland through project 346369. The quantum-chemical calculations were performed with computational resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS 2023/5-77) at the National Supercomputer Centre (NSC) at Linköping University partially funded by the Swedish Research Council through grant agreement no. 2022-06725. G. B. thanks the support by the Swedish Research Council through starting grant no. 2020-04600. G. B. and S. R. S. also thanks for support from Olle Engkvists Stiftelse (Sweden), project number 212-0136.

Notes and references

1. H. Görner, M. Megyesi, Z. Miskolczy and L. Biczók, J. Photochem. Photobiol., A, 2010, 214, 188–193.
2. K. Rybicka-Jasińska, E. M. Espinoza, J. A. Clark, J. B. Derr, G. Carlos, M. Morales, M. K. Billones, O. O’Mari, H. Ågren, G. V. Baryshnikov and V. I. Vullev, J. Phys. Chem. Lett., 2021, 12, 10295–10303.
3. K. Skonieczny, I. Papadopoulos, D. Thiel, K. Gutkowski, P. Haines, P. M. McCosker, A. D. Laurent, P. A. Keller, T. Clark, D. Jacquemin, D. M. Guldi and D. T. Gryko, Angew. Chem., Int. Ed., 2020, 59, 16104–16113.
4. J. S. Siddle, R. M. Ward, J. C. Collings, S. R. Rutter, L. Porrès, L. Applegarth, A. Beeby, A. S. Batsanov, A. L. Thompson, J. A. K. Howard, A. Boucekkine, K. Costuas, J. F. Halet and T. B. Marder, New J. Chem., 2007, 31, 841–851.
5. M. Chen, Y. Lee, Z. Huang, D. Chen and P. Chou, Chem. – Eur. J., 2020, 26, 7124–7130.
6. W. Rodríguez-Córdoba, L. Gutiérrez-Arzaluz, F. Cortés-Guzmán and J. Peon, Chem. Commun., 2021, 57, 12218–12235.
7. B. Sadowski, M. Kaliszewska, Y. M. Poronik, M. Czichy, P. Janasik, M. Banasiewicz, D. Mierzwa, W. Gadomski, T. D. Lohrey, J. A. Clark, M. Łapkowski, B. Kozankiewicz, V. I. Vullev, A. L. Sobolewski, P. Piatkowski and D. T. Gryko, Chem. Sci., 2021, 12, 14039–14049.
8. Y. M. Poronik, B. Sadowski, K. Szychta, F. H. Quina, V. I. Vullev and D. T. Gryko, J. Mater. Chem. C, 2022, 10, 2870–2904.
9. S. Saha and A. Samanta, J. Phys. Chem. A, 1998, 102, 7903–7912.
10. M. Chen, D. Chen and P. Chou, ChemPlusChem, 2021, 86, 11–27.
11. R. Arce, E. F. Pino, C. Valle, I. Negrón-Encarnación and M. Morel, J. Phys. Chem. A, 2011, 115, 152–160.
12. J. P. Zobel, J. J. Nogueira and L. González, Chem. – Eur. J., 2018, 24, 5379–5387.
13. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032.
14. R. Arce, E. F. Pino, C. Valle and J. Ágreda, J. Phys. Chem. A, 2008, 112, 10294–10304.
15. A. K. Mora, S. Murudkar, P. K. Singh, N. S. K. Gowthaman, T. Mukherjee and S. Nath, J. Photochem. Photobiol., A, 2013, 271, 24–30.
16. S. Murudkar, A. K. Mora, P. K. Singh and S. Nath, J. Phys. Chem. A, 2011, 115, 10762–10766.
17. Y. M. Poronik, G. V. Baryshnikov, I. Deperasińska, E. M. Espinoza, J. A. Clark, H. Ågren, D. T. Gryko and V. I. Vullev, Commun. Chem., 2020, 3, 190.
18. Ł. G. Łukasiewicz, H. G. Ryu, A. Mikhaylov, C. Azarias, M. Banasiewicz, B. Kozankiewicz, K. H. Ahn, D. Jacquemin, A. Rebane and D. T. Gryko, Chem. – Asian J., 2017, 12, 1736–1748.
19. S. Stecko and D. T. Gryko, JACS Au, 2022, 2, 1290–1305.
20. M. Krzeszewski, D. Gryko and D. T. Gryko, Acc. Chem. Res., 2017, 50, 2334–2345.
21. D. H. Friese, A. Mikhaylov, M. Krzeszewski, Y. M. Poronik, A. Rebane, K. Ruud and D. T. Gryko, Chem. – Eur. J., 2015, 21, 18364–18374.
22. Ł. G. Łukasiewicz, M. Rammo, C. Stark, M. Krzeszewski, D. Jacquemin, A. Rebane and D. T. Gryko, ChemPhotoChem, 2020, 4, 508–519.
23. G. Sanil, B. Koszarna, Y. M. Poronik, O. Vakuliuk, B. Szymański, D. Kusy and D. T. Gryko, Adv. Heterocycl. Chem., 2022, 138, 335–409.
24. A. Janiga, E. Glodkowska-Mrowka, T. Stoklosa and D. T. Gryko, Asian J. Org. Chem., 2013, 2, 411–415.
25. M. Tasior, O. Vakuliuk, D. Koga, B. Koszarna, K. Górski, M. Grzybowski, Ł. Kielesiński, M. Krzeszewski and D. T. Gryko, J. Org. Chem., 2020, 85, 13529–13543.
26. B. Dereka, A. Rosspeintner, M. Krzeszewski, D. T. Gryko and E. Vauthey, Angew. Chem., Int. Ed., 2016, 55, 15624–15628.
27. K. Górski, I. Deperasińska, G. V. Baryshnikov, S. Ozaki, K. Kamada, H. Ågren and D. T. Gryko, Org. Lett., 2021, 23, 6770–6774.
28. B. Dereka, A. Rosspeintner, R. Stężycki, C. Ruckebusch, D. T. Gryko and E. Vauthey, J. Phys. Chem. Lett., 2017, 8, 6029–6034.
29. K. Górski, J. Mech-Piskorz and M. Pietraszkiewicz, New J. Chem., 2022, 46, 8939–8966.
30. C. Le Droumaguet, O. Mongin, M. H. V. Werts and M. Blanchard-Desce, Chem. Commun., 2005, 2802–2804.
31. A. Charbonnier and D. Clement, Acta Gastroenterol. Belg., 1952, 15, 235–236.
32. L. Porrès, O. Mongin, C. Katan, M. Charlot, T. Pons, J. Mertz and M. Blanchard-Desce, Org. Lett., 2004, 6, 47–50.
33. O. Varnavski, X. Yan, O. Mongin, M. Blanchard-Desce and T. Goodson, J. Phys. Chem. C, 2007, 111, 149–162.
34. M. Williams-Harry, A. Bhaskar, G. Ramakrishna, T. Goodson, M. Imamura, A. Mawatari, K. Nakao, H. Enozawa, T. Nishinaga and M. Iyoda, J. Am. Chem. Soc., 2008, 130, 3252–3253.
35. Y. Z. Cui, Q. Fang, G. Xue, G. B. Xu, L. Yin and W. T. Yu, Chem. Lett., 2005, 34, 644–645.
36. C. Katan, S. Tretiak, M. H. V. Werts, A. J. Bain, R. J. Marsh, N. Leonczek, N. Nicolaou, E. Badaeva, O. Mongin and M. Blanchard-Desce, J. Phys. Chem. B, 2007, 111, 9468–9483.
37. L. Beverina, J. Fu, A. Leclercq, E. Zojer, P. Pacher, S. Barlow, E. W. Van Stryland, D. J. Hagan, J. L. Brédas and S. R. Marder, J. Am. Chem. Soc., 2005, 127, 7282–7283.
38. S. J. Chung, K. S. Kim, T. C. Lin, G. S. He, J. Swiatkiewicz and P. N. Prasad, J. Phys. Chem. B, 1999, 103, 10741–10745.
39. R. Kannan, G. S. He, T. C. Lin, P. N. Prasad, R. A. Vaia and L. S. Tan, Chem. Mater., 2004, 16, 185–194.
40. S. J. K. Pond, M. Rumi, M. D. Levin, T. C. Parker, D. Beljonne, M. W. Day, J. L. Brédas, S. R. Marder and J. W. Perry, J. Phys. Chem. A, 2002, 106, 11470–11480.
41. J. Arnbjerg, M. Johnsen, P. K. Frederiksen, S. E. Braslavsky and P. R. Ogilby, J. Phys. Chem. A, 2006, 110, 7375–7385.
42. L. Ventelon, S. Charier, L. Moreaux, J. Mertz and M. Blanchard-Desce, Angew. Chem., Int. Ed., 2001, 40, 2098–2101.
43. O. Mongin, L. Porrès, M. Charlot, C. Katan and M. Blanchard-Desce, Chem. – Eur. J., 2007, 13, 1481–1498.
44. S. J. Chung, S. Zheng, T. Odani, L. Beverina, J. Fu, L. A. Padilha, A. Biesso, J. M. Hales, X. Zhan, K. Schmidt, A. Ye, E. Zojer, S. Barlow, D. J. Hagan, E. W. Van Stryland, Y. Yi, Z. Shuai, G. A. Pagani, J. L. Brédas, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 2006, 128, 14444–14445.
45. J. Arnbjerg, A. Jiménez-Banzo, M. J. Paterson, S. Nonell, J. I. Borrell, O. Christiansen and P. R. Ogilby, J. Am. Chem. Soc., 2007, 129, 5188–5199.
46. K. Kamada, K. Ohta, Y. Iwase and K. Kondo, Chem. Phys. Lett., 2003, 372, 386–393.
47. K. Kamada, Disp. Imag., 2014, 1, 107–130.
48. K. Ohta, S. Yamada, K. Kamada, A. D. Slepkov, F. A. Hegmann, R. R. Tykwinski, L. D. Shirtcliff, M. M. Haley, P. Sałek, F. Gel’mukhanov and H. Ågren, J. Phys. Chem. A, 2011, 115, 105–117.
49. A. M. Brouwer, Pure Appl. Chem., 2011, 83, 2213–2228.

---

Footnote

† Electronic supplementary information (ESI) available: Quantum chemical calculation and experimental data, synthetic procedures as well as, ¹H and ¹³C{¹H} NMR spectra. See DOI: https://doi.org/10.1039/d3tc03851c

---