Effects of Al concentration on the structure and conductivity of lithium lanthanum zirconium oxide

Abstract

Cubic Li_7−3xAl_xLa₃Zr₂O₁₂ (LLZO) is a promising, next-generation solid electrolyte due to its stability with Li-metal and high bulk conductivity (∼1 mS cm⁻¹). However, the source of the high conductivity is not completely understood. In this work, we address this key knowledge gap through the integration of elemental analysis, neutron diffraction sensitive to Li and O atoms, and impedance spectroscopy to understand the structure–property correlations for LLZO. We show the metal–oxygen framework structure remains constant with variation in Al substitution, resulting in a constant activation energy of ∼0.35 eV and little effect on the bulk conductivity. Instead, Li concentration, Al blocking and trapping of mobile defects, and Li–Li nearest neighbor interactions largely control the Al substituted LLZO bulk conductivity, resulting in decreases from 0.73 to 0.22 mS cm⁻¹ as the Al concentration increases from 0.17 to 0.32 mol. These results differ from those of Ta substituted LLZO, where the framework structure and Li–Li site distances play large roles in controlling the conductivity. The increased understanding of the controlling factors of conductivity allows for greater ability to tailor the design of and substitution into the LLZO structure for improved conductivity.

---

1. Introduction

Cubic Li₇La₃Zr₂O₁₂ (LLZO) is a promising electrolyte for next-generation batteries, due to its high conductivity (∼1 mS cm⁻¹),¹ chemical stability against Li metal,^2,3 wide electrochemical window (∼6 V),⁴ and high fracture strength (∼100 MPa) to resist dendrite propagation through the electrolyte,⁵ though challenges remain in achieving coherent electrode interfaces and conductivities comparable to liquid electrolytes.^1,6–9 LLZO exists in two polymorphs, the low conductivity (10⁻⁴ S cm⁻¹ bulk conductivity) tetragonal phase and the high conductivity (10⁻³ S cm⁻¹ bulk conductivity) cubic phase.^5,10 The tetragonal phase, with the theoretical composition of Li₇La₃Zr₂O₁₂, is the room temperature stable polymorph. In this phase, the Li-ions are fully ordered into their three low energy sites, creating a broken chain in the Li-ion pathway.¹¹ This full ordering requires fully collective motion of Li-ions for conduction to occur, leading to high activation energies and the observed low conductivity.¹² In contrast, the cubic form of LLZO (as shown in Fig. 1) has two Li-ion sites, both of which are partially occupied (disordered), leading to a continuous 3D conduction pathway, as is illustrated in Fig. 1a and b. In Fig. 1, these sites are the 24d/Li1 site (in the yellow tetrahedra) and the 96h/Li2 site (two sites in each blue octahedra).^13–21 In the transition from tetragonal to cubic, the two tetragonal tetrahedral sites, one of which is fully occupied and one that is empty, become the partially occupied cubic 24d/Li1 site while two fully occupied distorted octahedra sites transform into the cubic 96h/Li2 sites.^22–24 The 3D network consists of Li1 sites connecting four Li2 sites, each of which can only be occupied by one Li-ion at a time due to coulombic repulsion.¹⁸ The partially colored spheres illustrate the partial occupancy of each site in Fig. 1. The partial occupancy and presence of mobile Li vacancies lead to a change in conduction mechanism upon the tetragonal to cubic transition. Rather than the fully synchronous, collective motion, which Meier, et al. observed in tetragonal LLZO, the vacancies and disorder in the cubic garnet system allows for single ion hops paired with cooperative motion of a few Li-ions.¹² This mechanism decreases the activation energy, leading to the observed increase in conductivity. Theoretical work by He, et al. corroborates this finding.²⁵ Other works have suggested that the cooperative motion may also be initiated through Li–Li interactions or Li-site instabilities, as observed by the increased likelihood for Li-ions to hop from the Li1 site.^26–28 As shown in Fig. 1c, there are two main proposed paths for conductivity in the cubic garnet structure: (1) the Li2–Li1–Li2/96h–24d–96h path and (2) the Li2–Li2/96h–96h path, where the Li⁺ moves either through the shared edge of the Li1 or through the interstitial space between the octahedra.^{12,14,16–18,20,27–31}

Fig. 1 (a) Representation of the cubic LLZO-Al garnet structure. Zr octahedra are black and La dodecahedra are grey. The partially filled circles represent partial occupation of the Li sites. The size of the colored wedge in the partially filled circles defines the approximate fraction the element defined by that color is predicted to sit on that site. Li is blue, Al is purple, and vacancies (v) are white. Overlapping atoms are the two Li2 sites, of which only one of the two 96h sites can be occupied at the time. Oxygen atoms are located at the polyhedra corners and Li polyhedra were omitted for clarity. (b) A partial slice of the Li sublattice. Yellow tetrahedra have the Li1/24d site while the blue distorted octahedra house the two Li2/96h sites. The inset is a zoomed section of the two polyhedra. The red arrow shows the two sites that are measured to determine the Li1–Li2 site distance. It also intersects the plane of the Li1–Li2 bottleneck. The green arrow shows the two sites that are measured to determine the Li2–Li2 site distance. The arrow intersects the planes of the Li2–Li2 bottleneck. (c) The theoretically predicted Li conduction pathways. Path 1 is the Li2–Li1–Li2 (96h–24d–96h) path. Path 2 is the Li2–Li2 (96h–96h path).

While early works suggested that a cubic phase with fully occupied Li-sites is possible at room temperatures,^13,22,32 later experimental and computational works suggest it is possible that the cubic phase stabilized through unintentional Al substitution onto the Li1/24d site.^19,33–41 It has been hypothesized that the introduction of the Al into the structure created a sufficient number of vacancies to induce Li-site disorder and stabilize the high conductivity cubic phase. Since this finding, Al has remained one of the popular substitution options due to its low cost and high abundance and the cubic LLZO-Al's high conductivity (∼0.5 mS cm⁻¹) and stability with Li metal.^2,3 Al has been hypothesized to affect the structure beyond stabilization of the cubic phase. First, Al is considered located in the 24d site, shown as the purple wedge in the partially occupied 24d site in Fig. 1a and b. While the Li⁺ is mobile in the LLZO interstitial sublattice, the Al is considered immobile. The blocked Li-ion conduction pathway is thought to impede conductivity. In addition to blocking the 24d site, the Al ion may cause mobile defect trapping in its neighboring sites, further decreasing conduction through the lattice.^17,18,31,38 In a study of single crystal LLZO-Al, Posch, et al. suggested a second NMR peak with an increased Li⁺ conductivity activation energy of 0.38 eV (as compared to 0.30 eV) could be due to sluggish mobility of Li-ions in the vicinity of Al substitution sites.¹⁷ However, they did not rule out the possibility of the Li2–Li2 path as the source of this higher activation energy. García Daza, et al., using a variety of computational methods, observed the Al³⁺ substitute trapping Li⁺ and vacancies in the surrounding tetrahedral and octahedral sites, decreasing Li⁺ diffusivity.³¹ They also determined that the effect of trapping increased when multiple Al ions were in the vicinity of each other. In a combination of the above studies, Chen, et al. suggested that the vacancy trapping in the surrounding 96h sites of the Al substitute limited the number of active vacancies that were involved in conduction.³⁸ Finally, Parascos, et al., in examining a range of Al substitution concentrations, surmised that the maximum active vacancy density at the octahedral sites maximizes the conductivity.⁴² Therefore, Al concentration defines the mobile octahedral vacancies and, thus, the conductivity. In summary, the Al seems to play a major role in defining conductivity by blocking the conductivity path and decreasing the mobility and availability of charge carriers. However, the role of the introduction of Al on the framework structure and its corresponding impact on conductivity has not been investigated.

Previous work analyzing the relationship between substitution concentration, structure, and conductivity has largely focused on different garnet systems, such as cubic Li₇La₃Zr₂O₁₂ substituted on the Zr or La site or Li_5+xBa_xLa_3−xTa₂O₁₂. It may be anticipated that the role of the Al substitution may be quite different than the roles of the previous substitutes studied, primarily due to the difference in substitution site, i.e. the garnet framework vs. a Li-ion interstitial site. However, in all cases, they have been theorized to stabilize the cubic phase by introducing Li-site disorder, so results from these studies may offer some clues as to the potential role Al may be playing in the structure beyond that of mobile ion/defect trapping. Using ab initio molecular dynamics and topological analysis, Miara, et al. found that the largest contribution to conductivity in the Ta substituted LLZO was a maximized Li concentration (up to 6.75 mol Li) and that the substitution did not seem to largely affect the bottleneck radius (∼1.32 Å from 0.25–1 mol Ta), migration pathway (96h–24d–96h hopping from 0.25–1 mol Ta), or activation energy (0.20 eV from 0.25–1 mol Ta).²⁸ They also found that the Li concentration controlled the conductivity in Rb substituted LLZO. However, in this case over-substitution beyond 7.25 mol Li led to significant decreases in the concentration of vacancies, thereby decreasing the conductivity. While Thompson, et al. observed a change in bulk activation energy from 0.435 to 0.536 eV when increasing from 0.5 to 1.5 mol Ta, they otherwise had similar findings to Miara, et al.^28,43 They determined that the number of “effective charge carriers” was the most important contributing factor to bulk conductivity and that the number of effective charge carriers was controlled by the decreasing 24d–96h site distances from 1.64 to 1.61 Å as Ta substitution decreased from 1.5 to 0.5 mol. Kataoka, et al. also attributed a maximum conductivity of 1.10 mS cm⁻¹ in LLZO-Ta to the substitution content (0.4 mol Ta) with the shortest Li1–Li2 site distance of 1.59 Å.⁴⁴ However, they acknowledged that the decreasing lattice parameters (12.94–12.91 Å) with an increasing Ta content of 0.2–0.8 mol contributed to the decreasing conductivity through the decrease in migration pathways which increased the activation energies from 0.39 to 0.47 eV. Similarly, in substituting with Nb or co-substituting with Nb and Ca or Nb and Sr, Kihira, et al. observed a peak in the conductivity from 12.94 Å to 12.96 Å.⁴⁵ However, they only observed a maximum conductivity below 6.5 mol Li per formula unit.⁴⁵ Zhang, et al., in co-substitution with Ca and Ta to maintain a constant Li concentration of 5.8 mol Li, also found a peak in the conductivity when the lattice parameters were between 12.935 Å and 12.961 Å.⁴⁶ However, Chen, et al. has suggested that the lattice parameters are not a direct reflection of the framework parameters that determine the Li-ion conductivity and activation energy.⁴⁷ Works where the effect of substitutions on the M–O bond length and the conductivity were examined had conflicting results.^48,49 Wang, et al. predicted that the maximum bulk conductivity found in their previous study of 0.96 mS cm⁻¹ was due to high Li concentrations of 6.7 mol (0.3 mol Ta).^21,50 However, instead of the close Li–Li site distances cited by Kataoka, et al. and Thompson, et al. or ideal lattice parameters cited by Zhang, et al. and Kihira, et al., they cited a large number of close Li–Li pairs (<2.5 Å proximity) and maximized concentrations of octahedral vacancy–occupied tetrahedral–octahedral vacancy Li-ion arrangements as drivers for the heightened conductivity at that substitution concentration.^43–46 O'Callaghan and Cussen observed majority occupation of both the octahedral (∼83%) and tetrahedral (56.8%) sites once more than 6.5 mol Li content was reached on Li_5+xBa_xLa_3−xTa₂O₁₂, with 57% of the octahedra having neighboring occupied tetrahedra and a Li–Li distance of 2.47 Å.¹⁵ They surmised that the combination of >50% occupation of both sites paired with the short distances between them could lead to Li⁺ destabilization and the increased ion mobility/conductivity observed generally in garnet structures. Summarizing, previous research on the substitution–structure–conductivity relationship with different substitutes emphasized the importance of the effect of substitution on the Li–Li site distance, either in decreasing the minimum site distance between the ions/ion-pairs or in increasing the number of nearest neighbor Li-ions. However, disagreements remain as to the effects of the M–O bond length and framework structure in these systems. Additionally, these parameters have not been investigated in the Al substituted system, leaving an open question as to their applicability in LLZO-Al.

As can be seen above, conductivity of the LLZO is strongly dependent on the composition. However, none of the previous studies are known to have simultaneously characterized the composition and the crystal structure as a function of substitution and Li concentration. The lack of such simultaneous compositional and structural characterization leaves open questions into the precise role of the composition on the Li-site disorder and occupation, Al trapping, Li–Li distance, and mobile charge carrier concentration on the conductivity of LLZO.

To clarify the role of Al and Li in the structure, we synthesized a series of LLZO substituted with x = 0.17, 0.28, and 0.32 mol of Al, hereto referred to as LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32, respectively. We performed neutron powder diffraction as a function of Al concentration and temperature to accurately characterize the structure of the LLZO and its effect on conductivity. Through this work, we have succeeded in clarifying the role of the framework structure, Li1/Li2 site occupancy, and Li–Li site distance on the conductivity of LLZO-Al.

2. Experimental

2.1. Sample preparation

Li_7−3xAl_xLa₃Zr₂O₁₂ samples were synthesized with nominal x values of 0.25, 0.35, or 0.45 mol. This range was selected as it was sufficient to stabilize the cubic phase (∼0.25 mol Al) and approached the Al solubility window (∼0.40 mol Al) in the garnet Ia3̄d space group. Intervals of 0.1 mol Al were chosen so compositions would remain distinct even within the range of error in weighing the precursors. The powder was prepared via solid-state reaction. Samples were prepared from precursors of ⁷Li₂CO₃ (Sigma-Aldrich, ≥99% purity), La₂O₃ (Pacific Industrial Development Corporation), ZrO₂ (Inframat Advanced Materials, 99.9% purity), and Al₂O₃ (Mager Scientific Inc.). Precursors were combined in stoichiometric quantities with 20 wt% excess ⁷Li₂CO₃ to make up for lithium loss during processing. ⁷Li₂CO₃ was used to decrease the effect of the large neutron absorption of ⁶Li. Precursors were ball milled (Labmill 8000 Jar Mill Machine, Gardco) in ethanol with 2 mm yttria stabilized zirconia milling media in a polypropylene bottle for 20 hours then dried under infrared heat lamps for 6 hours. The resulting powders were pressed into 25.4 mm pellets using a stainless-steel die (MTI Corporation) at 2 tons. The pellets were then put in a magnesia boat and calcined for 4 hours at 1000 °C in a tube furnace (STT-1700C-2.5-12, Sentrotech) under flowing dry air. The calcined pellets were then ground and sieved to pass through a 200 mesh.

The powders were hot-pressed at 47 MPa and 1225 °C for 40 minutes using rapid induction hot-pressing (RIHP) in a flowing argon atmosphere. After hot-pressing each billet (∼12.7 mm diameter, ∼8 mm height) was cut into pellets (∼1.0 mm thick) using a diamond saw. Pellets for neutron and X-ray powder diffraction were pulverized and immediately brought into the glove box to minimize atmospheric exposure and the resulting Li⁺/H⁺ exchange. Total exposure time to air is anticipated to lead to minimal Li⁺/H⁺ exchange (∼0.07 mol Li) which is within the inductively coupled plasma optical emission spectroscopy detection limits, limiting the effect on the analysis of the composition and structure.^51,52 The pellets for electrochemical measurements proceeded to facing and polishing steps. The pellets were ground to achieve parallel faces by using 400 grit sandpaper and a lapping fixture (PELCO 15000 micrometer-controlled lapping fixture, Ted Pella), then ground using 600 grit and 1200 grit sandpaper. After, the pellets were polished using 15 mm, 6 mm, 1 mm, 0.5 mm, and 0.1 mm diamond polishing compounds with a glycol-based diamond extender (EcoMET 300 Pro, Buehler). For each polishing step, 10 N of force was applied to each pellet and the head and base were rotated at 210 rpm and 60 rpm, respectively. All samples were stored in an argon-filled glove box (Omni-Lab, VAC) with less than 1 ppm of oxygen to minimize atmospheric exposure.

2.2. Characterization – structural, electrochemical, and chemical

2.2.1. X-ray diffraction. Powder X-ray diffraction (XRD) (Miniflex 600, Rigaku) was used to determine the crystalline phases present after hot-pressing. Cu Kα radiation was used to collect XRD patterns within the 15 to 60° 2θ at 4° min⁻¹ scanning rate. This range was selected as it includes the most prominent peaks for the cubic phase LLZO as well as those of the most common secondary phases. The sample was not rotated during pattern collection as grinding of the samples provided sufficient randomization of the grain orientations. Diffraction of powders was collected in air, though at time frames (<15 minutes) that would minimize the effects of Li⁺/H⁺ exchange on the structure and phase purity of the LLZO as predicted by previous works.^51,52

2.2.2. Neutron diffraction. Time-of-flight neutron powder diffraction (NPD) data were collected for each composition at the POWGEN beamline at the Spallation Neutron Source, Oak Ridge National Laboratory with a center wavelength of 1.5 Å at 20 K, 180 K, 220 K, 260 K, and 300 K. Approximately 4 grams of sample were placed into 6 mm diameter vanadium cans under argon and loaded in the POWGEN automatic changer to minimize air exposure to the samples. The measurement time was approximately 2 hours. Rietveld refinements of the neutron diffraction data were performed using GSAS-II.^53–55 While cross section of Al is smaller than the other elements with positive cross sections (i.e. La, Zr, and O), we believe it is sufficient for obtaining the structural information we are interested in combined with the known lattice site occupancy and the compositional analysis.

2.2.3. Electrochemical characterization. After polishing, the pellets were heat treated at 400 °C for 4 hours in an argon-filled glove box to remove any Li₂CO₃ and LiOH contamination layers that remained after polishing. After the heat treatment, a 0.75 mm thick Li foil (Alfa Aesar, Ward Hill, MA) was scraped then pressed at 66.7 N onto each side of the pellet with a Ni foil (Targray). The pellet was then heated to ∼170 °C for ∼6 hours to achieve <20 Ω cm² interfacial resistance between the Li foil and the LLZO.

Electrochemical impedance spectroscopy (EIS) was performed on three hot-pressed pellets at each composition at nominal temperatures of 22 °C, 10 °C, 0 °C, −10 °C, −20 °C, and −30 °C to determine the bulk activation energy. To perform low temperature measurements, samples were placed in an environmental chamber (ESPEC, SU 642). Thermocouples were attached in four corners of the chamber. The resulting temperatures as read from the thermocouples were averaged together to determine the temperature at which the EIS was performed. The error of the temperature readings was ∼±1.9 °C. The room temperature EIS measurement was used to calculate the room temperature bulk conductivity for each composition and averaged over the three samples. EIS measurements were performed from 7 MHz to 1 Hz using a perturbation amplitude of 50 mV. A Bio-Logic VMP300 and EC-Lab V11.33 software were used to conduct the EIS measurements and perform equivalent circuit fitting. An equivalent circuit was used for modeling the data and determining the bulk resistance. Bulk conductivity was calculated using the bulk resistance from the EIS measurements, specific specimen thickness, and electrode area.

Arrhenius fits were performed to determine the bulk activation energy for each composition from three samples measured at all 6 nominal temperatures. The bulk conductivity activation energy was calculated from the following equation:⁵⁶

ln(σ_bT) = ln(σ₀) − E_b/kT (1)

where σ_b is the bulk conductivity, σ₀ is a constant, E_b is the bulk activation energy, T is the temperature in degrees Kelvin, and k is the Boltzmann's constant.

2.2.4. Inductively coupled plasma optical emission spectroscopy (ICP-OES). To prepare the sample for compositional analysis, LLZO pellets of each composition were ground using a mortar and pestle. 11.25 mL of a 25 : 25 : 50 ratio of H₂SO₄ : HNO₃ : H₂O was combined with 0.75 mL of 30% H₂O₂ to digest ∼36 mg of the pulverized LLZO pellet. The powder and liquids were combined in a standard 50 mL Teflon vessel which was then placed into a microwave digester (CEM MARS 6 Microwave) at 260 °C for 35 minutes.⁵⁷ The resulting contents were then diluted at a 1 : 5 ratio of contents to deionized water. Compositional make-ups of the digested powders were confirmed via ICP-OES using an iCAP 7400 ICP-OES (Thermo Fisher Scientific). Concentrations were normalized to Zr values of 1.98 to account for Hf impurities. Composition of the elements in the LLZO phase was adjusted based on the Rietveld refinement determined weight percentage of the phase.

2.2.5. X-ray photoelectron spectroscopy (XPS). A SPECS Enviro-ESCA utilizing a monochromatic Al Kα X-ray source (1486 eV, 15 kV) was used in ultra-high vacuum mode for the X-ray Photoelectron Spectroscopy (XPS) studies. The pass energy was 100 eV. A survey spectra was obtained to determine the presence of the different elements. No charge neutralizer was used during the measurements. Charge correction was performed using adventitious carbon (285.0 eV) to accommodate the charging on the yttria stabilized zirconia milling media and polypropylene milling bottle.

3. Results and discussion

3.1. Synthesis and processing

Three samples of Al substituted LLZO (Li_7−3xAl_xZr₂La₃O₁₂) with different Al concentrations were prepared. The nominal Al concentrations were chosen to be 0.25 mol, 0.35 mol, and 0.45 mol of Al, as these have previously been found to fall within the cubic phase stability window.⁵⁸ Therefore, the nominal concentrations of Li are 6.25 mol, 5.95 mol, and 5.65 mol. However, insufficient amounts of Li have previously been observed to lead to the formation of La₂Zr₂O₇ rather than LLZO. To prevent the formation of La₂Zr₂O₇, 20 wt% excess ⁷Li₂CO₃ was added above the stoichiometric levels of Li to account for Li-loss during the high temperature (>1000 °C) processes of calcination and hot-pressing. Hot-pressing was used as the method for densification to create samples with nearly 100% relative density, eliminating the effects of porosity on the phase purity and electrochemical properties of the material.⁵⁹

3.2. Compositional analysis

ICP was performed on hot-pressed pellets of each of the LLZO compositions. The nominal compositions were Li_6.25Al_0.25La₃Zr₂O₁₂, Li_5.95Al_0.35La₃Zr₂O₁₂, and Li_5.65Al_0.45La₃Zr₂O₁₂. However, the compositions as obtained from ICP, shown in Table 1, are Li_6.43Al_0.171La_2.90Zr_1.93O_12−δ, Li_6.18Al_0.286La_2.92Zr_1.95O_12−δ, and Li_5.93Al_0.323La_2.93Zr_1.93O_12−δ. Since ICP results include all impurity phases present, the initial compositions as determined by ICP were adjusted to reflect the weight fractions of the LLZO as determined by Rietveld refinement. This is further supported by the near perfect charge neutrality achieved (average 2.3% deviation from neutral) across the three compositions, when assuming 12 mol of O per formula unit. When comparing the nominal to the actual compositions, the most notable attribute is that the Li and Al concentrations are different from intended (Tables 1 and S1†). In all cases, there is ∼0.23 mol more Li than the nominal amount. The higher than intended Li concentrations are likely due to the 20 wt% excess ⁷Li₂CO₃ added to the precursors, which was originally intended to compensate for Li-losses associated with the high temperature calcination (1000 °C) and densification (1225 °C) processes. Assuming there are no Li-losses during processing, the precursors of the LLZO with the 20 wt% excess ⁷Li₂CO₃ would create LLZO with compositions of Li_7.51Al_0.25La₃Zr₂O₁₂, Li_7.08Al_0.35La₃Zr₂O₁₂, and Li_6.79Al_0.45La₃Zr₂O₁₂ (Table S1†). Rather than the 1.2 mol of Li anticipated to be lost in synthesis and densification, ∼80% of that value is lost, leading to an increased amount of Li in the final structure than originally intended. As it has previously been suggested that 6.5–6.6 mol of Li is the maximum Li concentration before Li site ordering occurs and the cubic structure transitions to the tetragonal polymorph,^23,60 we report as high as 6.43 mol of Li, suggesting that we are nearing the maximum Li concentration for cubic LLZO stability.

Table 1 ICP derived compositions of hot-pressed LLZO pellets^a

Composition	Li [mol]	Al [mol]	La [mol]	Zr [mol]
a Nominal concentrations for each element are included in parentheses.
LLZO-Al0.17	6.43 (6.25)	0.171 (0.25)	2.90 (3)	1.93 (2)
LLZO-Al0.28	6.18 (5.95)	0.286 (0.35)	2.92 (3)	1.95 (2)
LLZO-Al0.32	5.93 (5.65)	0.323 (0.45)	2.93 (3)	1.93 (2)

---

There is also a decrease in Al as compared to the nominal concentration by ∼0.1 mol Al in each composition. While it has been suggested by Parascos, et al. that decreases in Al could occur in the bulk LLZO due to Al-rich secondary phase evolution, our samples have <0.6 wt% Al-rich secondary phases, at their highest amounts.⁴² As will be discussed below, only the LLZO-Al0.32 sample has any Al-rich secondary phases. When both phases are accounted for, the Al concentration is 0.344 mol Al, still representing a loss of ∼0.1 mol Al. Therefore, the formation of Al-rich secondary phases cannot explain most of the Al loss from the system. To determine the source of the decreased Al, first the alumina precursor was checked. A thorough discussion on this step is included in the ESI,† with the conclusion that it does not seem likely that impurities in the Al₂O₃ precursor are the reason for the observed decrease in Al concentration. Next, the media and milling bottle were examined using X-ray Photoelectron Spectroscopy (XPS) to determine if the Al₂O₃ precursor was left behind in the milling process. XPS was used as it probes the surface of the yttria-stabilized zirconia milling media and milling jar to look for Al₂O₃ as opposed to the bulk. Results are shown in Fig. S1.† Compared to the LLZO-Al powder, the peak in the 2s and 2p Al are decreased, suggesting that this was not the main driver for the loss in Al. Therefore, the decrease in Al may be due to losses associated with calcination or hot-pressing steps. The lithia-alumina phase diagram has a liquid eutectic point at 1055 °C which corresponds to the onset of liquid phase sintering in Al substituted LLZO.^61,62 Therefore, it may be possible that during the hot-pressing step, this Li- and Al-rich liquid is lost to gaps in the die, causing the 0.1 mol decrease in Al and potentially also contributing to the 1 mol decrease in Li. After hot-pressing, it is common to observe solidified ceramic on the outsides of the anvil and plunger where there was no direct contact with LLZO powder, further suggesting that some liquid phase may be forming during the processing of the LLZO that is lost from the LLZO billet.

The off-stoichiometry of La has been observed in ICP digestion before.^35,57 Malkowski, et al. consistently observed approximately a 10% increase in the La than compared to the expected, resulting in ∼3.2 mol of La while Shimonishi, et al. observed ∼3.1 mol La rather than the expected 3 mol.^35,57 Since our samples were made with a 6% La deficiency,⁶³ we would expect to see ∼3.1 mol of La with a similar increase. In all three samples we see only ∼2.9 mol of La. The decrease in La concentration from the expected may indicate a lower La concentration stability in the cubic LLZO structure than the anticipated stoichiometric concentration, potentially leading to some La losses in processing. This lower concentration may be related to the loss of the La-rich intermediary phase La₂Li_0.5Al_0.5O₄ during hot-pressing.⁶⁴ Like the Al-rich phase, previous work has suggested that this phase forms a liquid during sintering at 1200 °C.^42,62 Therefore, some of this La-rich liquid phase may also be lost to gaps in the die, resulting in lower than expected La concentrations. Interestingly, the total La concentration in the LLZO-Al0.32 sample, when including the LaAlO₃ secondary phase, is the expected 3.1 mol of La. Unlike La₂Li_0.5Al_0.5O₄, the melting temperature of LaAlO₃ is well above that of the sintering temperature (∼2100 °C vs. 1225 °C), suggesting that over all La loss from the system is mitigated by the stabilization of a La- and Al-rich solid phase above the Al solubility limit.

3.3. Electrochemical properties

Fig. 2 shows bulk conductivity of the LLZO-Al samples as a function of Li concentration. LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32 have average bulk conductivity values of 0.73 ± 0.09, 0.28 ± 0.03, and 0.22 ± 0.01 mS cm⁻¹, respectively. Bulk conductivity is obtained by measuring the EIS at room temperature (∼23 °C), then fitting the equivalent circuit in Fig. S2† to deconvolute the bulk and grain boundary resistance. A representative fit of a Nyquist plot is in the ESI (Fig. S2).† EIS spectra from representative samples of each composition are also given in the ESI (Fig. S3).† As the concentration of Li increases and the Al decreases, the conductivity increases correspondingly. It is interesting to note that the bulk conductivity does not increase linearly as a function of Li concentration. This was also observed by Thompson, et al. for the case of Ta substitution.⁴³ Between the LLZO-Al0.17 and LLZO-Al0.28 concentrations, the conductivity decreases by 0.45 mS cm⁻¹ while between the LLZO-Al0.28 and LLZO-Al0.32 there is only a 0.06 mS cm⁻¹ decrease. According to the conductivity equation,^56,65

σ_i = γ(Nq_i²/T)c(1 − c)a²v₀ exp(−E_a/kT) (2)

where γ is the correlation factor, N is the charge carrier density, q_i is the charge of the carrier ion, T is the temperature in K, c is the fraction occupied, a is the hop distance, v₀ is the attempt frequency, E_a is the activation energy for Li-ion hopping, and k is the Boltzmann constant, bulk conductivity is proportional to the number of charge carriers. Therefore, if the decrease in bulk conductivity were only to be due to the number of charge carriers, as was predicted by previous works to be the largest contribution to bulk conductivity,^28,59 there should be a linear decrease in the bulk conductivity as a function of Al/Li concentration. However, that is not the case, indicating another component, either the activation energy or a structural component, is playing a role in determining the bulk conductivity. These factors will be explored further below.

Fig. 2 Bulk conductivity (σ_b) as a function of Li concentration. Open circles are from previous works in the literature. Purple lines and circles indicate samples where compositional analysis was not performed. Black dashed lines indicate samples where compositional analysis was completed. Data from this work is shown in black squares with black dashed lines and is labelled with the corresponding bulk conductivity.

In addition to the data from this study, the bulk conductivity as a function of Li concentration from previously available works on LLZO-Al is also plotted (open circles, Fig. 2). Studies, such as this one that included ICP of the final material, are drawn with black lines. Studies that only reported nominal compositions are plotted in purple. The bulk conductivity of LLZO-Al0.17 (0.73 mS cm⁻¹) is comparable to the highest values previously reported by Han, et al. and Ashuri, et al. of 0.75 mS cm⁻¹ and 0.74 mS cm⁻¹.^5,66 However, the Li concentrations are reported with only 6.25 mol and 6.1 mol of Li, respectively, while this work reports a Li concentration of 6.43 mol Li.^5,66 These two works were among those reported that did not determine actual Li composition. As stated above, the total Li concentration in our samples was ∼0.23 mol higher than the nominal amounts. Adding 0.23 mol to the nominal reported values of Han, et al. and Ashuri, et al. brings them to 6.48 mol and 6.33 mol of Li, respectively, much closer to the 6.43 mol reported in our work. The closer values of Han, et al. and our work compared to Ashuri, et al. and our work may be due to the similarity of the processing. Both this work and that of Han, et al. used solid-state reaction and hot-pressing to synthesize the samples where Ashuri, et al. used sol–gel synthesis and conventional sintering.^5,66 The amount of Li-loss during processing, therefore, may shift depending on the synthesis procedure, suggesting different optimal Li-excess levels for different processes. The similarities in the adjusted Li contents in the former works to ours suggests that the ideal Li amount for conductivity may have been previously underestimated. Therefore, our understanding of the ideal composition for bulk conductivity is shifted towards higher Li concentrations than previously believed and highlights the importance of knowing the precise compositions of the grains of the materials under observation. Additionally, in the present work the maximum conductivity value is obtained with 6.43 mol of Li, falling at the higher end of the 6.5–5.95 mol Li previously cited or predicted to be the optimal Li conductivity targets,^{13,26,67–69} suggesting that ideal values for conductivity maximize Li concentration in this range.

The optimum Al concentration of 0.17 mol Al, the substitution concentration with the highest conductivity, also aligns well with previous work that completed Al compositional analysis: Parascos, et al. reported 0.18 mol as the ideal concentration of Al for maximizing total conductivity in LLZO.⁴² These Al concentration values are nearly the same as the minimum reported values for cubic phase stability in LLZO by Rangasamy, et al., Düvel, et al., Sudo, et al., and Bernstein, et al. with values of 0.204 mol, 0.20 mol, 0.201 mol, and 0.2 mol Al, respectively.^23,58,68,70 All of these works either performed compositional analysis or were computational. Combined, these findings confirm previous hypotheses that the optimum conductivity is achieved at the minimum substitution concentration to stabilize the cubic phase. Interestingly, this is similar to findings in oxygen ion conducting oxides that stabilize into the cubic fluorite phase with substitutions, such as CeO₂, ThO₂, and stabilized ZrO₂.⁵⁶ Similarly, maximum conductivity is frequently observed to be at the minimum substitution concentration necessary to stabilize the cubic phase. Therefore, minimized substitutions for high conductivity may be more generally applicable to systems where high conductivity phase stability depends on substitution and vacancy concentration.

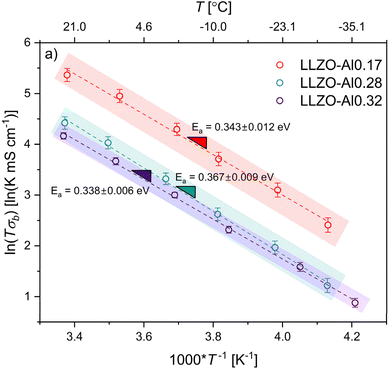
To explain the conductivity mechanism, EIS was performed at six temperature values from ∼23 down to −35 °C. Representative EIS spectra for each composition at each temperature can be found in Fig. S3.† Temperatures were decreased rather than increased to amplify both the bulk and grain boundary contributions to the resistance and allow for their deconvolution. Bulk resistance was determined using the equivalent circuit shown in Fig. S2† to fit each of the resulting Nyquist plots. The natural log of bulk conductivity times the temperature is plotted as a function of the inverse temperature in Fig. 3. The slope of the plot can be used to find the activation energy for bulk Li-ion conduction using the Arrhenius equation shown in the experimental section. The shaded areas are considered reasonable estimates for the regions that the slopes could shift given the standard deviations of each of the conductivity values. The average bulk activation energy of the LLZO-Al0.17 and LLZO-Al0.32 are 0.343 eV and 0.338 eV, respectively, while for the LLZO-Al0.28 a slightly elevated value of 0.367 eV is found. These are within the expected range of previous works and follow trends predicted by Miara, et al.^{17,19,20,28,59,69,71–74} Within 3 standard deviations, or 99.7% confidence, all of these points overlap, indicating that there is no significant difference between the activation energies of each of the compositions. The activation energy is determined by the mechanism for Li⁺ conductivity, which is partially controlled by factors such as cooperative/coordinated motion, bottleneck sizes, M–O bond lengths, and charge carrier trapping. The consistent bulk activation energy suggests that the mechanism for Li⁺ conductivity is the same between all compositions and that the variables controlling the activation energy do not change significantly.

Fig. 3 Activation energy from each composition. The red is the LLZO-Al0.17 composition, blue is the LLZO-Al0.28 composition, and purple is the LLZO-Al0.32 composition. The activation energy is derived from the slope of the log of the temperature times the conductivity plotted as a function of 1/T. The dotted lines are the best fit lines and the shaded rectangles are approximate areas for where the lines may fall given the standard deviations on each point in the line.

3.4. Crystal structure

XRD (Fig. S4†) was used to confirm cubic phase stability as well as to identify secondary phases. XRD peak matching with the ICSD 422259 cubic LLZO pattern confirms cubic phase stability in samples from all compositions. The secondary phase, Li₂ZrO₃, is also present in all three compositions and can be observed most prominently at ∼27.3° 2θ (circle, Fig. S4†). Additionally, it appears that LaAlO₃ is present in the LLZO-Al0.32 sample, which can be observed at ∼23.9° 2θ (square, Fig. S4†). The La₂Zr₂O₇ phase was not detected in any of the samples, suggesting a sufficient amount of excess Li was added to prevent its formation.

To quantify the phase fractions and determine the structural parameters, we use the refinement results of the neutron powder diffraction of samples taken at 20 K. In fitting each of the NPD patterns, we confirmed the cubic garnet structure (space group Ia3̄d, IT # 230) at 97.7 wt%, 98.5 wt%, and 96.8 wt% for the LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32 compositions, respectively. There is no evidence, such as peak splitting or anomalous anisotropic broadening, which might indicate the presence of significant levels of secondary tetragonal garnet phase in our samples, as further confirmed by good Rietveld fits in a cubic structural model (see below). There is also no evidence of the La₂Zr₂O₇ phase, aligning with the observations of the XRD. In all cases, Li₂ZrO₃ peaks were present in the structure (Fig. 5 and S7–S20†). Its refined weight fractions are 2.3 wt%, 1.5 wt%, and 2.6 wt% for LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32, respectively. Li₂ZrO₃ is commonly found as a secondary phase in cubic LLZO. It is hypothesized to be one of the intermediate phases in the solid-state reaction between the precursors and the final LLZO and is hypothesized to react with La₂O₃ and the La intermediary product La₂Li_0.5Al_0.5O₄ to form LLZO-Al.⁶⁴ Since our synthesis is La-deficient compared to the amount needed to achieve 3 mol of La in the LLZO, it may be that there was an insufficient concentration of La phases present to fully react all of the Li₂ZrO₃, leading it to remain in the sample. The depleted La may also be due to the loss of some liquid phase La₂Li_0.5Al_0.5O₄ during hot-pressing, as discussed above. LaAlO₃ was present in only the LLZO-Al0.32 samples and had a phase fraction at 0.6 wt% The presence of this Al-rich phase confirms previous findings that the Al solubility limit falls approximately between 0.35-0.45 mol of Al.^{34,42,58,59,70} The refined lattice parameters of the main (garnet) phase at 20 K are 12.93669(13) Å, 12.93508(7) Å, and 12.93389(7) Å for LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32, respectively. These values are reported in Fig. S5, Tables 2, S2 and S3 (ESI).† This is similar to the 12.9438(2) Å reported by Buschmann, et al. for LLZO-Al0.28 at 4 K.¹⁹ To compare better to other literature, neutron diffraction was also performed at 300 K. The refined lattice parameters at room temperature are 12.96027(4) Å, 12.95997(6) Å, and 12.95858(6) Å for LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32, respectively. Similar lattice parameter values in the range of 12.96–12.99 Å were reported by several groups,^{5,19,22,32,42,59,68,75} though slightly higher lattice parameters of 13.0791 Å were reported by Hubaud, et al. at comparable substitution amounts.⁷⁶ In our work, at both room temperature and 20 K, there is a slight decrease in lattice parameters as the Al concentration increases. While there is no consistent trend observed by Sudo, et al. the decrease in lattice parameter with increasing Al concentration is observed by both Parascos, et al. and Moy, et al.^42,59,68 This decrease could be expected as the Al³⁺ ion is slightly smaller than the Li⁺ ion it is substituting for, with ionic radii of 0.39 Å and 0.59 Å, respectively.⁷⁷ The replacement of Li-ions with a smaller ion likely causes the decrease in lattice parameter with increased Al. However, since the Al- and Li-ions reside on interstitial sites and because of their similar sizes, it is expected that this change in lattice parameter with substitution should be small, as is observed.

Table 2 Structural refinement 20 K LLZO-Al0.17^a

Element	Wyckoff position	x	y	z	Fraction	100 × Uiso
a R wp = 4.778%, lattice parameter a = 12.93669(13) Å. Since the Li1 and Li2 fractions were manually input and defined by the minimum Rwp their errors are not included in Table 2 or in the below discussion.
Li1	24d	0.375	0	0.25	0.4500	2.24(13)
Al1	24d	0.375	0	0.25	0.0570	2.24(13)
Li2	96h	0.09648(24)	0.18701(27)	0.42532(26)	0.4233	0.83(6)
La1	24c	0.125	0	0.25	0.9979(18)	0.465(8)
Zr1	16a	0	0	0	0.9939(22)	0.379(10)
O1	96h	0.09991(4)	0.19583(4)	0.28217(4)	0.9968(17)	0.776(8)

---

The accurate determination of site occupancies is especially important for LLZO-Al as there are some discrepancies in the literature with Li1 occupancy reported anywhere between 0.35 and 0.65 and Li2 occupancy reported between 0.26 and 0.46.^{13,18,19,34,38,42,43} The site occupancies and atomic displacement parameters (ADP, U_iso) of the Li1/Al and Li2 sites (Fig. 4) are difficult to determine unambiguously from Rietveld refinement because of the inevitable strong correlation between these parameters caused by their shared contribution to the Bragg peak intensities. To obtain a reasonable estimate for the site occupancies, the following procedures were taken to deconvolve these contributions. First, the actual compositions as defined by the ICP and adjusted for by the Rietveld refinement derived weight fractions are fixed. Having an accurate account of the total Al³⁺ and Li⁺ in the structure will give a more accurate representation of the actual occupancies of the Li1 and Li2 sites. In this work, the Al occupation was exclusively fixed to the 24d/Li1 site as suggested by previous works.^33,41 The adjusted sum (accounting for the difference in site multiplicity) of the Li occupations of the Li1 and Li2 sites was fixed to the total Li concentration from ICP. Next, Rietveld analysis of neutron diffraction data collected at 20 K was performed to minimize the effect of thermal motion. To further separate the effects of occupancy and thermal motion, a procedure developed by Lobanov, et al. was followed.⁷⁸ The occupancy of the Li in the Li1 site was fixed at several values and the goodness of fit (R_wp) obtained from Rietveld refinements was plotted as a function of that Li1 occupancy (Fig. 4). Since R_wp is a measure of how well the model fits to the diffraction pattern, the minimum value of R_wp is assumed to be the actual fraction occupied. Additionally, the U_iso of both the Li1 and Li2 sites is plotted as a function of the fraction of Li in the Li1 site. Since the Li1 and Li2 sites are similar in that they both have partial Li occupancy and similar coordination environments,²² it would be expected that their U_iso values would be similar. However, as these sites do vary in energy and Al occupation, it would be reasonable to take the R_wp minimum as the most probable fraction occupied while the U_iso intersection could indicate that, if anything, the Li1 site occupancy may be slightly below this value.

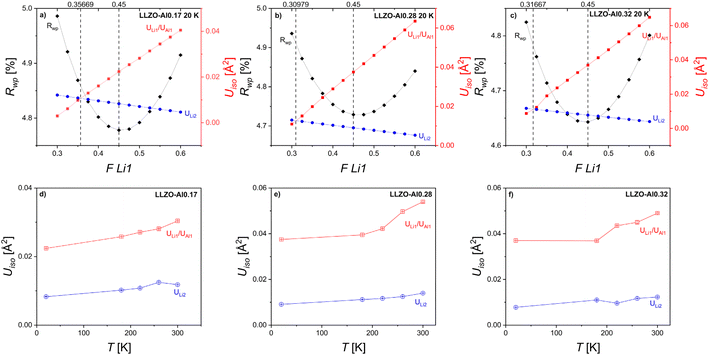Fig. 4 (a)–(c) show R_wp as a function of Li occupation of the Li1/24d site and atomic displacement parameters for LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32, respectively. Black vertical lines denote the Li occupation fraction of the Li1 site where R_wp is at a minimum and where the atomic displacement parameters (U_iso) for Li1/24d and Li2/96h sites intercept. The Li1 and Li2 sites are the two Li sites in the LLZO as defined in Fig. 1b (d)–(f) show the evolution of the atomic displacement parameters of the Li1 (red squares) and Li2 sites (blue circles) as a function of temperature.

To attempt to separate the static vs. dynamic contributions to the ADP, U_iso was also plotted as a function of temperature in Fig. 4d–f.⁷⁹U_iso values from higher temperatures were obtained using the same procedure as was performed at 20 K, i.e. by taking the values as defined by the R_wp minimum. Theoretically, at sufficiently high temperatures, a linear increase in the U_iso is expected with increasing temperature. Additionally, as the temperature approaches 0 K, the U_iso values should approach low values (though non-zero due zero point/quantum vibrations). It can be observed in Fig. 4 that neither the high temperature linearity nor the approaching of the ADP values to nearly 0 at 0 K is consistently true. This finding indicates that there is a substantial contribution to the ADP from static disorder. This is similar to findings made by Wang, et al. in the neutron diffraction Rietveld refinement of LLZO-Ta samples.²¹ When comparing the two Li sites, the U_iso value is higher in the Li1/Al site compared to that of the Li2 site. Specifically, at 20 K, the U_iso for the Li1/Al and Li2 are 0.0224(13) Ų and 0.0083(6) Ų, 0.0375(24) Ų and 0.0091(4) Ų, 0.0370(24) Ų and 0.0078(6) Ų for LLZO-Al0.17, LLZO-Al0.28, and LLZO-Al0.32, respectively. The observed 2- to 5-fold increase in ADP is likely to reflect the effect of mixed occupancy, i.e. that the local positions of each species are slightly different due to the different sizes and valences of the Al and Li ions at the Li1 site. Chen, et al. attributed the increased U_iso to the fast diffusion pathways, however, that effect should be limited here due to the extremely low temperatures (20 K) that the measurement was taken.³⁸ Tian, et al. and Wang, et al. observed a broadened Li density distribution on each site using a combination of X-ray and neutron total scattering and molecular dynamics and neutron diffraction and atomistic simulations, respectively.^20,21 Their findings are consistent with our observations of static disorder components at both the Li1 and Li2 sites.

The final refinement fit for the LLZO-Al0.17 at 20 K is shown in Fig. 5 and Table 2, all others are provided in the ESI.† The open black circles represent the observed diffraction pattern from the neutron diffraction. The red curve is the calculated diffraction as defined by the Rietveld refinement model discussed above. The yellow line is the difference curve. The green and blue dashed lines represent the expected locations for cubic LLZO and Li₂ZrO₃ intensity peaks, respectively. The inset is the close-up of the 0.5–1.5 Å d-spacing range. A more zoomed in range of 1–1.5 Å is provided in the ESI† for each composition at 20 K. The fit quality is good, as reflected in the low R_wp values (4.778%, 4.729%, and 4.643% at 20 K, see Tables 2, S2 and S3†) and lack of systematic discrepancies between observed and calculated patterns. Low R_wp values below 5% are also obtained in the Rietveld refinement of the 180, 220, 260, and 300 K datasets for each composition (Tables S4–S15†), indicating that the model is good across all temperatures and conditions.

Fig. 5 Rietveld refinement results and NPD for LLZO-Al0.17 at 20 K. Open circles are the observed neutron diffraction intensities in arbitrary units. The red line is the pattern calculated using the refined model calculated from Rietveld refinement. The yellow line is the difference curve. The green dashes are the expected locations for cubic LLZO intensity peaks. The blue dashes are the expected locations for Li₂ZrO₃ intensity peaks. The inset is a close-up of the 0.5–1 Å d-spacing range. The NPD obtained from the other compositions and temperatures can be viewed in the ESI.†

Across all three compositions the location of the minimum of the R_wp remains constant, indicating that the Li1/24d site has the same Li occupancy (∼0.450) as the Al concentration increases from 0.17 to 0.32 mol and the Li concentration decreases from 6.43 to 5.93 mol. Since the Li1 and Li2 fractions were manually input and defined by the minimum R_wp their errors are not included in Table 2 or in the below discussion. A similar trend was reported by Miara, et al., who calculated that the Li1 site occupancy of Ta and Rb substituted garnets remained at ∼0.5 between 6 and 7 mol Li.²⁸ However, this is contrary to findings in other garnet systems where the Li1 site occupation is observed to decrease as the Li concentration increases.^{14,15,21,24,26,43} In the one other known work on Al concentration variation, Parascos, et al. observed a decrease in Li1 site Li occupancy from 0.505(18) to 0.495(12) as the content of Al changed from 0.18 to 0.24 mol.⁴² Generally, in previous works, additional Li is not only preferentially placed on the Li2 octahedral sites, but Li also displaces from the Li1 tetrahedral sites to the Li2 octahedral sites. Combined, these phenomena lead to a simultaneous decrease in Li1 occupation and increase in Li2 occupation. In LLZO-Al, both Li and Al reside on the Li1 site. Combined, it is observed that the Li and Al on the Li1 lead to an increase in Li1 total occupancy, since the Li occupation remains constant and the Al occupation increases. In our case, and in previous works, there is an increase in 96h/Li2 vacancy fraction as the substitution concentration increases. We observe a decrease in Li2 occupation from 0.4233 to 0.3817 from LLZO-Al0.17 to LLZO-Al0.32. It may be the case that the Al plays a role in this trend in occupancy. Unlike other garnet structures where the substitution is on the La or Zr site, the substitution in this case occupies the Li 24d/Li1 site, as is shown schematically in Fig. 1, where the purple sphere represents the Al-ion on the 24d/Li1 site. The increased charge on the site causes preferable vacancy formation and trapping on the immediate Li2 sites around it, as is shown by the white spheres trapped in the surrounding Li2 sites.^{17,31,38,56,65} García Daza, et al. used molecular dynamics to determine that there were two trapped Li2 vacancies while Chen, et al. hypothesized that all four Li2 sites that surround each Li1 site are sites with trapped vacancies, as depicted in Fig. 7 and 8.^31,38 Using NMR, Posch, et al. hypothesized that their increase in local activation energy for Li⁺ diffusion from the global 0.3 to the local 0.38 eV may be an indication of the vacancy trapping, however, they did not determine a specific number of trapped vacancies.¹⁷ Therefore, in LLZO-Al it may be more preferable for the Li2 site to form vacancies than the Li1 site to accommodate for the increased charge substituted onto the Li1 site. In the case of other garnet systems, like Li_7−xLa₃Zr_2−xTa_xO₁₂ and Li_5+xBa_xLa_3−xTa₂O₁₂, where there is no substitution in the Li1 site, the drive for vacancy formation in Li2 would not be as pronounced, allowing for the change in Li1 site Li occupancy.^15,21,43 The difference between our results and the previous works may also originate from differences in the refinement procedures and structural models and/or a lack of compositional analysis of the Li concentration in the previous publications, all of which could distort the results of the site occupancies.^{15,21,42–44}

3.5. Structure–conductivity relationship

3.5.1. Li sublattice occupancy. The linear dependence of bulk conductivity as a function of Li content would be expected if the number of charge carriers determined the bulk conductivity, as has previously been hypothesized.^28,59 However, we observed an apparent non-linearity (Fig. 2 and 6). To identify its origin bulk conductivities as a function of variation in the Li1 and Li2 site occupancies has been plotted (Fig. 6).

Fig. 6 Bulk conductivity (σ_b) plotted as a function of Li concentration (lower x-axis, yellow squares), 96h fraction occupied (upper x-axis, blue triangles), 24d vacancy fraction (upper x-axis, green circles), and “active” 96h vacancy fraction (upper x-axis, purple diamonds).

The bulk conductivity as a function of the Li1 site vacancy occupation and Li concentration share a trend, suggesting that the number of Li1 site vacancies affects the bulk conductivity. As the composition changes from Li_5.93Al_0.323La_2.93Zr_1.93O_12−δ to Li_6.18Al_0.286La_2.92Zr_1.95O_12−δ to Li_6.43Al_0.171La_2.90Zr_1.93O_12−δ, the bulk conductivity increases from 0.22 ± 0.01 mS cm⁻¹ to 0.28 ± 0.03 mS cm⁻¹ to 0.73 ± 0.09 mS cm⁻¹ and the 24d/Li1 vacancy fraction increases from 0.4423 to 0.4547 to 0.4930. The bulk conductivity as a function of Li concentration is shown in the yellow curve in Fig. 6 and the bulk conductivity as a function of Li1 vacancy fraction is shown in the green curve. Since the Li1 fractions were manually input and defined by the minimum R_wp, their errors are not included. As shown in Fig. 4, the Li occupation remains constant at 0.450 as the Li increases from 5.93 to 6.43 mol Li. Therefore, the variation in Li1 vacancy occupation must be due to the variation in Al content on the Li1 site. As the conductivity increases, the Al fraction on the Li1 site decreases from 0.1077 to 0.0570. As shown in Fig. 7, when Al enters the structure, it occupies the Li1 sites, preventing Li-ion conduction through that path. As the amount of Al increases in the structure, more sites are blocked, creating a more tortuous path for Li-ion motion and decreasing the Li-ion conductivity. This blocking phenomena correlates to the z(1 − c) term in eqn (2), which is defined as the fraction of empty nearest neighbor sites. According to this term, as the fraction of empty nearest neighbor sites increases, it is expected that the bulk conductivity will correspondingly increase. Therefore, the observation of the increase in conductivity with a decrease in Al concentration and occupancy aligns well with the exponential pre-factor term of eqn (2). Additionally, as detailed above, the presence of Al³⁺ in the site is believed to cause vacancy trapping in the nearest Li2 sites as well as potentially the nearest Li1 sites.^17,31,38 In Fig. 7, this is represented by the four white vacancies surrounding the purple Al-ion. As the amount of Al increases in the structure, more vacancies are trapped around the Al-ions. With molecular dynamics García Daza, et al. predicted that Al-ions in close vicinity further increases the tortuosity for the Li-ion path, thereby decreasing the bulk conductivity (see the increase in the Li-ion path length in Fig. 7).³¹ Additionally, Chen, et al. introduced the concept of “active” 96h/Li2 vacancies. These “active” vacancies are those that are not trapped by the Al-ion and are free and able to participate in conduction of the Li-ions.³⁸ The “active” vacancies would be related to the z(1 − c) term, or fraction of empty nearest neighbors term, as it determines the effective concentration of nearest neighbor sites that are actually available for Li-ion conduction. To assess this theory, the bulk conductivity was plotted as a fraction of “active” Li2 vacancies. To calculate the fraction of “active” vacancies, the number of trapped vacancies was subtracted from the total number of 96h vacancies then divided by the total number of Li2 sites. Since there is no consensus on the number of trapped vacancies per Al-ion, the number that was proposed by Chen, et al. (four) was used in this work and shown in Fig. 7.^17,31,38 When the bulk conductivity is plotted as a fraction of “active” vacancies in the Li2 site in Fig. 6 (purple curve), the trend as the bulk conductivity as a function of Li concentration varies from what was previously observed. As the composition changes from Li_5.93Al_0.323La_2.93Zr_1.93O_12−δ to Li_6.18Al_0.286La_2.92Zr_1.95O_12−δ to Li_6.43Al_0.171La_2.90Zr_1.93O_12−δ, the bulk conductivity increases from 0.22 ± 0.01 mS cm⁻¹ to 0.28 ± 0.03 mS cm⁻¹ to 0.73 ± 0.09 mS cm⁻¹ and the “active” vacancy fraction on the 96h/Li2 site changes from 0.5106 to 0.5022 to 0.5197. The “active” vacancy fraction was determined from the manually input Al and Li2 fractions as defined by the minimum R_wp, so they also do not have errors associated with the individual values and are not included. While the highest conductivity of 0.73 mS cm⁻¹ does correlate to the greatest number of active vacancies of 0.5197, as predicted by Chen, et al., the lowest conductivity does not have the lowest number of active vacancies (0.5106 vacancy fraction for 0.22 mS cm⁻¹vs. 0.5022 vacancy fraction for 0.28 mS cm⁻¹).³⁸ This discrepancy may be related to the compounding effect of vacancy trapping with increasing Al ions that was predicted by García Daza, et al. that would result in a non-linear correlation between trapped vacancies and Al occupancy.³¹ Additionally, since there is no consensus in the literature for the number of trapped vacancies, it may be that there is not a consistent number for each Al ion in the structure.^17,31,38 The inconsistencies between the trends of active vacancies, Li concentration and bulk conductivity suggest that while active vacancies are likely involved in determining the bulk conductivity, their contribution may be more complex than the simple linear relationship modelled in Fig. 6.

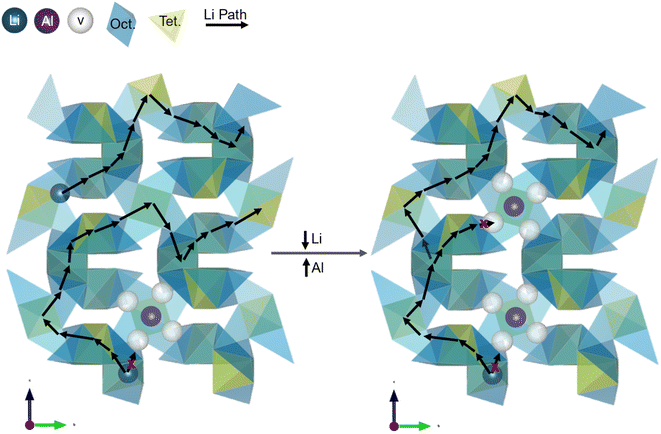Fig. 7 Representation of the impact of Al substitution into the Li1 site. Both figures are an extended version of the Li sublattice shown in Fig. 1. The yellow tetrahedra are the polyhedra with the 24d/Li1 site, the blue distorted octahedra are the polyhedra each with the two Li2/96h split sites, the blue spheres are the Li-ions, the purple spheres are the Al-ions, the white spheres are the vacancies, the black arrows show the Li path from polyhedra to polyhedra, and the red x's show inaccessible path directions. As the Al concentration increases, the number of Li-ions in the structure decrease, decreasing the bulk conductivity. As Al-ions substitute in the Li1 sites, they trap vacancies in the surrounding sites (here approximated as the four surrounding sites), preventing Li-ion conduction through both the local Li1 and Li2 surrounding sites. As the Al- concentration increases, the pathways for Li-ion conduction become more tortuous, decreasing the bulk conductivity.

The bulk conductivity also appears to be influenced by the occupancy of the Li on the Li2 site (Fig. 6, blue curve), following a trend observed by several previous works on various garnet systems.^15,42,43 As the Li2/96h site occupancy increases from 0.3817 to 0.4025 to 0.4233, the bulk conductivity correspondingly increases from 0.22 ± 0.01 mS cm⁻¹ to 0.28 ± 0.03 mS cm⁻¹ to 0.73 ± 0.09 mS cm⁻¹. Since the Li2 fractions were manually input and defined by the minimum R_wp, they do not have errors associated with the individual values, so they are not included. Since the Li1 site maintains a constant occupation at 0.450 as the Li concentration increases in the LLZO-Al, all additional Li is added to the 96h/Li2 site. Since only one 96h site can be simultaneously occupied in an octahedra, this translates in an increase from ∼76% to ∼85% Li2 octahedra occupation between the lowest and highest Li concentrations. Fig. 8 shows a schematic of the likely Li-ion sublattice as the Li concentration increases. An increase in Li2 occupancy with constant Li1 Li occupancy forces more neighboring polyhedra to be occupied, leading to an increase in nearest neighbor Li-ions. In the case of both the nearest neighbor Li2–Li2 distance (between the centers of the atoms indicated by the green arrow in Fig. 1b) and the Li1–Li2 distance (between the Li1 and either of the Li2 sites in the neighboring octahedra), the distance between the atoms are <2.5 Å. O'Callaghan and Cussen hypothesized that this closeness in distance, in their case 2.47 Å, leads to increases in conductivity.¹⁵ They believed that the increased coulombic repulsions linked to the close proximity of the charged ions cause the Li-ions to become unstable in their sites, increasing their mobility. This is shown in Fig. 8 by the increase in the number of Li-ions with black curves around them. Therefore, the observed increase in close Li-ion neighbors may lead to increased propensity or ease of hopping of these less stable Li-ions, thereby increasing the bulk conductivity. Other previous work has suggested that an increase in Li2 occupation would lead to an increase in conductivity by initiating correlated motion and decreasing the activation energy.²⁵ However, in our system, the activation energy does not change. Therefore, the increase in bulk conductivity from increased Li2 occupation is likely not due to this mechanism. It may be that throughout this concentration range of 0.17 to 0.34 mol Al, each motion is already associated with correlated motion, leaving the activation energy unaffected. However, by increasing the number of Li-ions with nearest neighbors, a higher fraction of Li may be participating in this correlated motion or in hopping, leading to the increase in conductivity. This increased fraction in conducting Li ions is most likely associated with the attempt frequency, ν₀, term of eqn (2). As an increasing number of Li-ions become nearest neighbors, they are more likely to be affected by coulombic effects and initiate correlated motion and low activation energy conduction. It may also be that the 96h occupation is not the main trigger for decreased activation energy. Chen, et al. concluded that a minimum number of active 96h vacant sites are necessary for high Li conductivity.³⁸ It appears that even with a Li2 occupancy fraction as high as 0.4233, there is a sufficient number of 96h site vacancies to allow for high Li-ion conduction. Notably, the constant occupation of the Li in the Li1 site has been observed for the first time in LLZO-Al to be a contributing factor in controlling the Li ion conductivity. Combined, the increase in Li2 occupation and number of Li nearest neighbors as well as the decrease in Al effects on Li-ion path blocking and vacancy trapping leads to more Li moving through the lattice, increased Li–Li instabilities, and an increase in the available pathways for conduction.

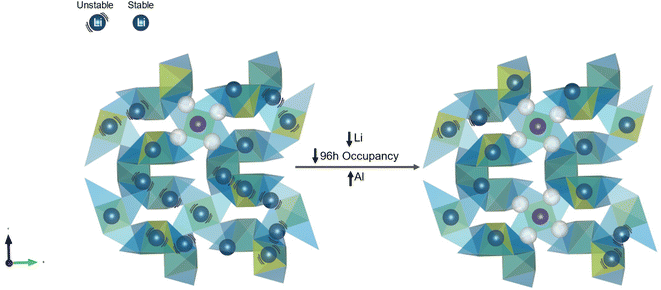Fig. 8 Representation of the impact of increased Li2 occupancy on conductivity. All symbols are the same as in Fig. 7 except that black lines represent Li-ions with nearest neighbor Li-ions (≤2.5 Å apart). These close ions have strong coulombic interactions causing them to become less stable in their sites and more likely to induce conduction. As the amount of Al increases and Li decreases in the structure, the number of Li-ions on the Li2/96h site decreases, decreasing the total number of Li-ions with nearest neighbors, which contributes to the decrease in bulk conductivity.

3.5.2. Framework structure. The red curves in Fig. 9(c)–(g) are a compilation of the framework structure data from the structure model as determined by the Rietveld refinement at 20 K. We define the framework structure as the portions of Fig. 1 that do not focus on the occupancy of the Li sublattice. As far as the authors know, most of this structural data has not been previously published as a function of Al concentration, specifically with respect to the M–O bond lengths and bottleneck areas. As previously discussed, as the Li concentration increases from 5.93 to 6.43 mol Li, the bulk conductivity increases from 0.22 to 0.73 mS cm⁻¹ and the activation energy remains constant at ∼0.35 eV. As the Li concentration increases from 5.93 to 6.43 mol, the framework structure remains largely constant. In this Li concentration range, the M–O bond length and lattice parameters remain constant at ∼2.105 Å and ∼12.94 Å, respectively. The M–O bond length is the distance between the Zr-ion and the oxygen and defines the distance between the metal framework ion and the Li-ion conduction pathway. The bottleneck areas are the areas that the Li-ions must pass between to conduct through either path 1 or path 2 shown in Fig. 1c. The 24d–96h or the Li1–Li2 bottleneck constrains path 1 and is the area of the triangle defined by oxygen vertices that the Li-ion hops through. The triangle is intercepted by the black arrow in Fig. 1d in path 1. The 96h–96h (Li2–Li2) bottleneck area is defined by either triangle in the distorted octahedra that the Li-ion must pass through and is, likewise, intercepted by the black arrow in Fig. 1d, path 2. In both the case of the 24d-96h bottleneck (Fig. 9f) and the 96h–96h bottleneck (Fig. 9e), areas are very similar between Al concentrations. From 5.93 to 6.43 mol Li content, the 24d–96h bottleneck area changes from 4.134 to 4.140 Ų and the 96h–96h bottleneck changes from 4.166 to 4.162 Ų. In both cases, the change is restricted to thousandths of an Å as the Al range changes. Finally, the Li–Li jump distance is calculated and plotted as a function of the Li concentration. Li1–Li2 distance is shown in Fig. 1b as the distance between the centers of the Li-sites pointed out by the red arrow, more specifically the 24d/Li1 site and the nearest 96h/Li2 site. The Li2–Li2 distance is the distance between the centers of the Li-ion sites pointed out by the green arrow, more specifically the closest 96h/Li2 sites in adjacent octahedra. The Li1–Li2 distance is the jump distance needed for path 1 and the Li2–Li2 distance is the jump distance needed for path 2, both shown in Fig. 1c. Again, there is little change in these parameters as well. As the Li increases from 5.93 to 6.43 mol, the Li1–Li2 distance changes from 1.631(4) to 1.627(4) Å and the Li2–Li2 distance changes from 2.482(6) to 2.478(6) Å. Overall, while there is an increase in bulk conductivity with respect to increasing Li concentration, the structural parameters and activation energy remain fairly constant. This further iterates the above points that the conductivity is largely controlled by the Li concentration and the Li1/Li2 Al and Li occupancies.

Fig. 9 Comparison between the electrochemical properties and the framework structure of LLZO-Al (this work) and LLZO-Ta (previous works). Structural data from these works were obtained from both the manuscripts as well as the published structural cif files in the Inorganic Crystal Structure Database (collection code numbers 239663 and 239664 for Thompson, et al. and 22956, 22957, 22958, and 22959 for Kataoka, et al.)^43,44 (a) bulk conductivity, (b) activation energy, (c) lattice parameters, (d) M–O bond length, (e) 96h–96h bottleneck area, (f) 24d–96h bottleneck area, and (g) Li–Li distances as a function of Li concentration. M–O bond length is the average bond length of the Zr/Ta to O over the structure.

3.5.2.1. Comparison to LLZO-Ta. To determine the effect that different site substitutions have on the conductivity (Fig. 9a) and activation energy (Fig. 9b), LLZO-Ta is compared to LLZO-Al via structural data from Thompson, et al. and Kataoka, et al.^43,44 and included in each of the plots in Fig. 9. Structural framework parameters from these works on LLZO-Ta as well as this work are also included in Table 3. Since no compositional analysis data was reported by these authors, nominal Li concentrations as reported were plotted. Similar to LLZO-Al, the conductivity increases as the Li concentration increases and substitution concentration decreases for the LLZO-Ta. Kataoka, et al. observed an increase from 0.59 to 1.1 mS cm⁻¹ as the Li concentration increased from 6.2 to 6.6 mol of Li and the Ta concentration decreased from 0.8 to 0.4 mol.⁴⁴ Thompson, et al. reported an increase in the bulk conductivity from 0.103 to 0.903 mS cm⁻¹ as the concentration increased from 5.5 to 6.5 mol Li and decreased from 1.5 to 0.5 mol Ta.⁴³ However, rather than a constant activation energy, both the LLZO-Ta series had a decrease in activation energy from 0.47 to 0.42 eV (Kataoka, et al.) and 0.536 to 0.435 eV (Thompson, et al.) as the Li concentration increased.^43,44 The LLZO-Ta values reported showed greater changes in the framework structure parameters than the LLZO-Al reported in this work. In the case of lattice parameters and M–O bond lengths, the distances increased from 12.9071 to 12.9375 Å and 2.089 to 2.094 Å, respectively, for Kataoka, et al. and 12.84 to 12.93 Å and 2.023 to 2.085 Å, respectively, for Thompson, et al. as the Li concentration increased.^43,44 Similarly, the Li2–Li2 and Li1–Li2 bottleneck areas calculated from their reported structures had larger changes in size compared to LLZO-Al with 4.119 to 4.161 Ų and 4.258 to 4.193 Ų, respectively, for Thompson, et al. and 4.156 to 4.176 Ų and 4.165 and 4.186 Ų, respectively, for Kataoka, et al. with the increase in Li concentration.^43,44 Finally, for the Li1–Li2 and Li1–Li1 site distances, Thompson, et al. observed a decrease from 1.64 to 1.61 Å and 2.475 to 2.431 Å, respectively, and Kataoka, et al. observed a decrease from 1.66 to 1.59 Å and 2.54 to 2.45 Å, respectively, as the Li concentration increased.^43,44 In all, while the framework structure and activation energy remain roughly constant as the substitution concentration changes in the LLZO-Al, the LLZO-Ta does see variation in both aspects.

Table 3 Summary of framework structure parameters from this work, Thompson, et al., and Kataoka, et al. shown in Fig. 9.^43,44

Ref.	Sample	M–O bond length [Å]	96h–96h bottleneck [Å^2]	24d–96h bottleneck [Å^2]	Li1–Li2 distance [Å]	Li2–Li2 distance [Å]
This work	Li6.43Al0.171La2.90Zr1.93O12−d	2.106	4.162	4.140	1.627(4)	2.478(6)
	Li6.18Al0.286La2.92Zr1.95O12−d	2.105	4.164	4.134	1.633(4)	2.487(6)
	Li5.93Al0.323La2.93Zr1.93O12−d	2.105	4.166	4.134	1.631(4)	2.482(6)
34	Li6.5La3Zr1.5Ta0.5O12	2.085	4.161	4.193	1.61	2.431(9)
	Li6.25La3Zr1.25Ta0.75O12	2.070	—	—	1.62	—
	Li5.5La3Zr0.5Ta1.5O12	2.023	4.119	4.258	1.64	2.475(11)
35	Li6.6La3Zr1.6Ta0.4O12	2.094	4.176	4.186	1.59(4)	2.45(7)
	Li6.5La3Zr1.5Ta0.5O12	2.091	4.165	4.176	1.59(4)	2.44(6)
	Li6.4La3Zr1.4Ta0.6O12	2.089	4.157	4.168	1.67(4)	2.56(6)
	Li6.2La3Zr1.2Ta0.8O12	2.089	4.156	4.165	1.66(5)	2.54(8)

---

The activation energy is partially controlled by structural factors, such as the bottleneck size and M–O bond length. In the case of bottleneck size, a smaller bottleneck requires more energy for the Li-ion to migrate between sites as compared to a larger bottleneck, leading to a corresponding increase in activation energy.⁴⁷ In M-site substitutions (LLZO-Ta), the change in bottleneck area involved in both hopping paths (Li2–Li1–Li2 and Li2–Li2) as the substitution concentration increases is over an order of magnitude greater than that observed in LLZO-Al (∼0.02–0.06 Ųvs. 0.004 Ų). Thompson, et al. reported an increase in bottleneck size for the 24d–96h bottleneck, however Kataoka, et al. reported a decrease for this bottleneck size and both reported decrease in the Li2–Li2 bottleneck area.^43,44 Therefore, it appears that the constant activation energy observed in the LLZO-Al as a function of substitution corresponds to the relatively constant bottleneck sizes while the increase in activation energy in the LLZO-Ta is related to the decrease in bottleneck size with substitution concentration.

Additionally, the M-site substitution seems to affect the activation energy through the M–O bond lengths. The M–O bond length is likely to affect the activation energy through the bottleneck size and coulombic forces between the M-ion and the Li-ion conduction path. As the M–O bond length decreases, the bottleneck size increases, decreasing the activation energy.⁴⁸ Simultaneously, as the M–O bond length decreases, the distance between the Li conduction path and the M-ion decreases, increasing the activation energy.⁴⁸ In LLZO-Al, the constant M–O bond length (∼2.105 Å) is likely unaffected by the substitution as the metal is not varied, thereby maintaining the framework structure and constant activation energy (∼0.35 eV). However, in M-site substituted LLZO-Ta, the M–O bond length decreases between 0.005–0.062 Å, suggesting that in this substitution range, the increase in Ta concentration and change in M–O bond length leads to the increase in activation energy by 0.043–0.101 eV, clarifying the effect of M–O bond length in controlling the conductivity in these systems.^43,44 The M–O bond length is also expected to affect the lattice parameters.^48,49 As lattice parameters are a reflection of changes in the M–O bond lengths and bottleneck sizes, it is not surprising that the lattice parameter in LLZO-Al stays constant at ∼12.94 Å. Meanwhile, since the M–O bond length decreases in LLZO-Ta as the Ta content increases, the lattice parameter correspondingly decreases 0.0304–0.09 Å.^43,44 However, lattice parameters themselves are not anticipated to affect the conductivity.⁴⁷ Therefore, the constant M–O bond length and bottleneck size contributes to the constant activation energy as a function of Li concentration in the case of LLZO-Al.

According to the conductivity equation, the Li–Li hopping distance (a in eqn (2)) plays a role in determining bulk conductivity. Above, the nearest Li site distances between separate polyhedra are plotted, since their proximity would suggest that they are the most likely jumping sites for conduction between the tetrahedra and octahedra and the two separate octahedra. In the case of both potential pathways for LLZO conduction (Li2–Li1–Li2, Fig. 1c pathway 1, or Li2–Li2, Fig. 1c pathway 2), the Li–Li site distances remains constant at ∼1.63 Å and ∼2.48 Å as the Al concentration changes, likely due to the lack of change in the framework structure of the garnet. This constant Li–Li site distance would suggest that the distance is not the main defining factor of conductivity in LLZO-Al. However, in the case of the LLZO-Ta, the Li1–Li2 and Li2–Li2 distances vary by 0.07 Å and 0.03 Å, respectively, for Kataoka, et al. and for 0.03 Å and 0.044 Å, respectively, for Thompson, et al. with the shortest site distances leading to their highest reported conductivities of 1.1 mS cm⁻¹ and 0.903 mS cm⁻¹.^43,44 Due to this correlation, they cite the decreased Li–Li site distances with decreased substitution as the reason for the increase in conductivity. The findings above suggest that while the framework structure and Li–Li site distances alter the conductivity of M-substituted LLZO, they do not have an effect on the LLZO-Al conductivity. Overall, though they play an important role in LLZO with other substitutes, it appears that the structural parameters that define the framework of the garnet do not control the LLZO-Al conductivity, leaving the Li concentration and Al and Li occupancies as the main determinants of the conductivity.

4. Conclusion

In this work, we synthesized a series of LLZO-Al compositions and identified the structure–conductivity relationships. Through compositional analysis, Rietveld refinement of the LLZO neutron powder diffraction data, and conductivity measurements, we were able to identify the main contributors to LLZO-Al conductivity. In addition to providing for highly reliable Rietveld refinements, we found that elemental analysis is instrumental in defining the optimal composition for conductivity. The maximum conductivity was observed at 6.43 mol Li and 0.17 mol Al. Interestingly, it appears that the highest conductivity was observed at the minimum Al concentration required to stabilize the cubic structure and at the higher end of Li levels previously reported. Additionally, it is observed that the framework structure (M–O bond length, bottleneck size, lattice parameters, and Li–Li site distances) remains roughly constant as the Al concentration varies, leading to the constant activation energy of Li-ion conduction through the LLZO-Al series. Consequently, the LLZO conductivity is predominantly controlled by Li concentration, Li2 occupancy, and Li1 site vacancies, likely acting through Al blocking, vacancy trapping, and nearest neighbor Li–Li site interactions. This finding brings to light a new understanding of the mechanisms controlling the bulk conductivity of Al substituted LLZO. Additionally, these controlling mechanisms are contrasted to those of LLZO-Ta, where the conductivity is influenced by decreased Li–Li site distances and changes in the framework structure.^43,44 By gaining a greater understanding of the levers that control Li-ion conduction, we can more specifically tailor the design of LLZO-Al for improved Li-ion conductivity while maintaining the advantages of using Al as a substitute by minimizing the Al concentration to that necessary for the cubic phase transition and maximizing the Li concentration of the cubic phase. Additionally, findings may encourage further future investigation of substitution or co-substitution schemes that use informed alteration of the lattice framework and Li concentration to maximize conductivity. For example, one future design may include substituting onto the M-site to increase the bottleneck size while simultaneously maintaining heightened Li concentrations and cubic phase stability, allowing for a decrease in activation energy and trapping paired with the benefits of increased mobile ions and Li–Li site interactions. Given the vast number of potential substitutions that are possible in the garnet structure,^1,80 computational screening of ideal substitutions and co-substitutions based on their coulombic interactions, effects on the framework structure, and thermodynamic stability is suggested to guide future experimental work.

Data availability

Data supporting this article have been included as part of the ESI.†

Author contributions

A. C. M. – conceptualization, data curation, formal analysis, funding acquisition, investigation, visualization, writing – original draft, writing – review and editing A. M. S. – data curation, formal analysis, investigation, writing – review and editing T. C. C. – investigation, writing – review and editing M. V. L. – formal analysis, writing – review and editing G. M. V. – conceptualization, funding acquisition, resources, supervision, writing – review and editing J. S. – conceptualization, funding acquisition, resources, supervision, writing – review and editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

A. C. M. would like to thank Jeffrey Einkauf and Diana Stamberga in ORNL's Chemical Separations Group for repeated access to the ICP used in this work and Amanda Musgrove for assistance in performing the ICP measurements. A. C. M would also like to thank Nicola Ashcroft and Brian Toby for helpful discussions. M. L. is grateful to Takeshi Egami for helpful discussions. This work was part of the US-German joint collaboration on “Interfaces and Interphases in Rechargeable Li-Metal Based Batteries” supported by the US Department of Energy (DOE) and the German Federal Ministry of Education and Research (BMBF) under DOE grant number DE-ACO5-000R22275 is acknowledged. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists, Office of Science Graduate Student Research (SCGSR) program. The SCGSR program is administered by the Oak Ridge Institute for Science and Education for the DOE under contract number DE-SC0014664. A. C. M. would like to thank the Rackham Graduate School at the University of Michigan for support through the Rackham Pre-Doctoral Fellowship. A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by Oak Ridge National Laboratory (IPTS-27340.1 for POWGEN experiment) for supporting this research through its user program. A portion of this work (ICP, data analysis) was performed at the Oak Ridge National Laboratory (G. M. V.) and supported by U.S. Department of Energy's Vehicle Technologies Office under the US-Germany Consortium Project, directed by Tien Duong. This manuscript has been authored in part by UT-Battelle, LLC, under contract DEAC05-00OR22725 with the U.S. Department of Energy (DOE). The publisher, by accepting the article for publication, acknowledges that the U.S. government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for U.S. government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doepublic-accessplan).

References

1. A. Junio Samson, K. Hofstetter, S. Bag and V. Thangadurai, Energy Environ. Sci., 2019, 12, 2957–2975.
2. J. G. Connell, T. Fuchs, H. Hartmann, T. Krauskopf, Y. Zhu, J. Sann, R. Garcia-Mendez, J. Sakamoto, S. Tepavcevic and J. Janek, Chem. Mater., 2020, 32, 10207–10215.
3. C. Ma, Y. Cheng, K. Yin, J. Luo, A. Sharafi, J. Sakamoto, J. Li, K. L. More, N. J. Dudney and M. Chi, Nano Lett., 2016, 16, 7030–7036.
4. T. Thompson, S. Yu, L. Williams, R. D. Schmidt, R. Garcia-Mendez, J. Wolfenstine, J. L. Allen, E. Kioupakis, D. J. Siegel and J. Sakamoto, ACS Energy Lett., 2017, 2, 462–468.
5. G. Han, B. Kinzer, R. Garcia-Mendez, H. Choe, J. Wolfenstine and J. Sakamoto, J. Eur. Ceram. Soc., 2020, 40, 1999–2006.
6. Y. Ren, T. Danner, A. Moy, M. Finsterbusch, T. Hamann, J. Dippell, T. Fuchs, M. Müller, R. Hoft, A. Weber, L. A. Curtiss, P. Zapol, M. Klenk, A. T. Ngo, P. Barai, B. C. Wood, R. Shi, L. F. Wan, T. W. Heo, M. Engels, J. Nanda, F. H. Richter, A. Latz, V. Srinivasan, J. Janek, J. Sakamoto, E. D. Wachsman and D. Fattakhova-Rohlfing, Adv. Energy Mater., 2022, 2201939.
7. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162.
8. J. Janek and W. G. Zeier, Nat. Energy, 2023, 1–11.
9. T. Krauskopf, H. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2019, 11, 14463–14477.
10. J. Wolfenstine, E. Rangasamy, J. L. Allen and J. Sakamoto, J. Power Sources, 2012, 208, 193–196.
11. J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, J. Solid State Chem., 2009, 182, 2046–2052.
12. K. Meier, T. Laino and A. Curioni, J. Phys. Chem. C, 2014, 118, 6668–6679.
13. H. Xie, J. A. Alonso, Y. Li, M. T. Fernández-Díaz and J. B. Goodenough, Chem. Mater., 2011, 23, 3587–3589.
14. E. J. Cussen, Chem. Commun., 2006, 412–413.
15. M. P. O'Callaghan and E. J. Cussen, Chem. Commun., 2007, 2048–2050.
16. M. P. O'Callaghan, A. S. Powell, J. J. Titman, G. Z. Chen and E. J. Cussen, Chem. Mater., 2008, 20, 2360–2369.
17. P. Posch, S. Lunghammer, S. Berendts, S. Ganschow, G. J. Redhammer, A. Wilkening, M. Lerch, B. Gadermaier, D. Rettenwander and H. M. R. Wilkening, Energy Storage Mater., 2020, 24, 220–228.
18. S. Adams and R. Prasada Rao, J. Mater. Chem., 2012, 22, 1426–1434.
19. H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392.
20. H. Tian, G. Cai, L. Tan, H. Lin, A. E. Phillips, I. Abrahams, D. A. Keen, D. S. Keeble, A. Fiedler, J. Zhang, X. Yang Kong and M. T. Dove, J. Mater. Chem. A, 2023, 11, 25516–25533.
21. Y. Wang, A. Huq and W. Lai, Solid State Ionics, 2014, 255, 39–49.
22. J. Awaka, A. Takashima, K. Kataoka, N. Kijima, Y. Idemoto and J. Akimoto, Chem. Lett., 2011, 40, 60–62.
23. N. Bernstein, M. D. Johannes and K. Hoang, Phys. Rev. Lett., 2012, 109, 205702.
24. F. Chen, J. Li, Z. Huang, Y. Yang, Q. Shen and L. Zhang, J. Phys. Chem. C, 2018, 122, 1963–1972.
25. X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893.
26. B. Kozinsky, S. A. Akhade, P. Hirel, A. Hashibon, C. Elsässer, P. Mehta, A. Logeat and U. Eisele, Phys. Rev. Lett., 2016, 116, 055901.
27. R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430.
28. L. J. Miara, S. P. Ong, Y. Mo, W. D. Richards, J.-M. Lee, H. S. Lee and G. Ceder, Chem. Mater., 2013, 25, 3048–3055.
29. J. Han, J. Zhu, Y. Li, X. Yu, S. Wang, G. Wu, H. Xie, S. C. Vogel, F. Izumi, K. Momma, Y. Kawamura, Y. Huang, J. B. Goodenough and Y. Zhao, Chem. Commun., 2012, 48, 9840–9842.
30. M. Xu, M. S. Park, J. M. Lee, T. Y. Kim, Y. S. Park and E. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 052301.
31. F. A. García Daza, M. R. Bonilla, A. Llordés, J. Carrasco and E. Akhmatskaya, ACS Appl. Mater. Interfaces, 2019, 11, 753–765.
32. R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781.
33. S. Vema, A. H. Berge, S. Nagendran and C. P. Grey, Chem. Mater., 2023, 35, 9632–9646.
34. C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2011, 50, 1089–1097.
35. Y. Shimonishi, A. Toda, T. Zhang, A. Hirano, N. Imanishi, O. Yamamoto and Y. Takeda, Solid State Ionics, 2011, 183, 48–53.
36. D. Rettenwander, P. Blaha, R. Laskowski, K. Schwarz, P. Bottke, M. Wilkening, C. A. Geiger and G. Amthauer, Chem. Mater., 2014, 26, 2617–2623.
37. D. O. Shin, K. Oh, K. M. Kim, K.-Y. Park, B. Lee, Y.-G. Lee and K. Kang, Sci. Rep., 2015, 5, 18053.
38. Y. Chen, E. Rangasamy, C. Liang and K. An, Chem. Mater., 2015, 27, 5491–5494.
39. J.-M. Lee, T. Kim, S.-W. Baek, Y. Aihara, Y. Park, Y.-I. Kim and S.-G. Doo, Solid State Ionics, 2014, 258, 13–17.
40. D. Rettenwander, J. Langer, W. Schmidt, C. Arrer, K. J. Harris, V. Terskikh, G. R. Goward, M. Wilkening and G. Amthauer, Chem. Mater., 2015, 27, 3135–3142.
41. B. Karasulu, S. P. Emge, M. F. Groh, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2020, 142, 3132–3148.
42. K. Parascos, J. L. Watts, J. A. Alarco, Y. Chen and P. C. Talbot, Ceram. Int., 2023, 49(14), 23082–23090.
43. T. Thompson, A. Sharafi, M. D. Johannes, A. Huq, J. L. Allen, J. Wolfenstine and J. Sakamoto, Adv. Energy Mater., 2015, 5, 1500096.
44. K. Kataoka and J. Akimoto, J. Ceram. Soc. Jpn., 2019, 127, 521–526.
45. Y. Kihira, S. Ohta, H. Imagawa and T. Asaoka, ECS Electrochem. Lett., 2013, 2, A56.
46. Y. Zhang, F. Chen, R. Tu, Q. Shen, X. Zhang and L. Zhang, Solid State Ionics, 2016, 284, 53–60.
47. F. Chen, L. Xu, J. Li, Y. Yang and Q. Shen, Ionics, 2020, 26, 3193–3198.
48. X. Xiang, F. Chen, W. Yang, J. Yang, X. Ma, D. Chen, K. Su, Q. Shen and L. Zhang, J. Am. Ceram. Soc., 2020, 103, 2483–2490.
49. Y. Zhang, F. Chen, J. Li, L. Zhang, J. Gu, D. Zhang, K. Saito, Q. Guo, P. Luo and S. Dong, Electrochim. Acta, 2018, 261, 137–142.
50. Y. Wang and W. Lai, Electrochem. Solid-State Lett., 2012, 15, A68.
51. A. Sharafi, S. Yu, M. Naguib, M. Lee, C. Ma, H. M. Meyer, J. Nanda, M. Chi, D. J. Siegel and J. Sakamoto, J. Mater. Chem. A, 2017, 5, 13475–13487.
52. Z. F. Yow, Y. L. Oh, W. Gu, R. P. Rao and S. Adams, Solid State Ionics, 2016, 292, 122–129.
53. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
54. A. Huq, M. Kirkham, P. F. Peterson, J. P. Hodges, P. S. Whitfield, K. Page, T. Hűgle, E. B. Iverson, A. Parizzi and G. Rennich, J. Appl. Crystallogr., 2019, 52, 1189–1201.
55. A. Huq, J. P. Hodges, O. Gourdon and L. Heroux, in European Powder Diffraction Conference; August 2010, Oldenbourg Wissenschaftsverlag, 2011, Darmstadt, Germany, pp. 127–136.
56. H. L. Tuller, J. Phys. Chem. Solids, 1994, 55, 1393–1404.
57. T. F. Malkowski, E. D. Boeding, D. Fattakhova-Rohlfing, N. Wettengl, M. Finsterbusch and G. M. Veith, Ionics, 2022, 28, 3223–3231.
58. E. Rangasamy, J. Wolfenstine and J. Sakamoto, Solid State Ionics, 2012, 206, 28–32.
59. A. C. Moy, G. Häuschen, D. Fattakhova-Rohlfing, J. B. Wolfenstine, M. Finsterbusch and J. Sakamoto, J. Mater. Chem. A, 2022, 10(41), 21955–21972.
60. T. Thompson, J. Wolfenstine, J. L. Allen, M. Johannes, A. Huq, I. N. David and J. Sakamoto, J. Mater. Chem. A, 2014, 2, 13431–13436.
61. L. P. Cook, E. R. Plante, R. S. Roth and J. W. Hastie, Phase Equilibria of Stored Chemical Energy Reactants, National Bureau of Standards Gaithersburg Md Inorganic Materials Div, 1984.
62. Y. Jin and P. J. McGinn, J. Power Sources, 2011, 196, 8683–8687.
63. J. M. Valle and J. Sakamoto, Solid State Ionics, 2020, 345, 115170.
64. Y. Chen, E. Rangasamy, C. R. dela Cruz, C. Liang and K. An, J. Mater. Chem. A, 2015, 3, 22868–22876.
65. J. B. Goodenough, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1984, 393, 215–234.
66. M. Ashuri, M. Golmohammad, A. Soleimany Mehranjani and M. Faghihi Sani, J. Mater. Sci. Mater. Electron., 2021, 32, 6369–6378.
67. L. Zhuang, X. Huang, Y. Lu, J. Tang, Y. Zhou, X. Ao, Y. Yang and B. Tian, Ceram. Int., 2021, 47(16), 22768–22775.
68. R. Sudo, Y. Nakata, K. Ishiguro, M. Matsui, A. Hirano, Y. Takeda, O. Yamamoto and N. Imanishi, Solid State Ionics, 2014, 262, 151–154.
69. Z. Hu, H. Liu, H. Ruan, R. Hu, Y. Su and L. Zhang, Ceram. Int., 2016, 42, 12156–12160.
70. A. Düvel, A. Kuhn, L. Robben, M. Wilkening and P. Heitjans, J. Phys. Chem. C, 2012, 116, 15192–15202.
71. M. Wang, J. B. Wolfenstine and J. Sakamoto, Electrochim. Acta, 2019, 296, 842–847.
72. W. E. Tenhaeff, E. Rangasamy, Y. Wang, A. P. Sokolov, J. Wolfenstine, J. Sakamoto and N. J. Dudney, Chemelectrochem, 2014, 1, 375–378.
73. L. Cheng, W. Chen, M. Kunz, K. Persson, N. Tamura, G. Chen and M. Doeff, ACS Appl. Mater. Interfaces, 2015, 7, 2073–2081.
74. W. Xia, B. Xu, H. Duan, X. Tang, Y. Guo, H. Kang, H. Li and H. Liu, J. Am. Ceram. Soc., 2017, 100, 2832–2839.
75. C. Im, D. Park, H. Kim and J. Lee, J. Energy Chem., 2018, 27, 1501–1508.
76. A. A. Hubaud, D. J. Schroeder, B. J. Ingram, J. S. Okasinski and J. T. Vaughey, J. Alloys Compd., 2015, 644, 804–807.
77. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
78. M. V. Lobanov, S. Li and M. Greenblatt, Chem. Mater., 2003, 15, 1302–1308.
79. M. V. Lobanov, M. Greenblatt, E. N. Caspi, J. D. Jorgensen, D. V. Sheptyakov, B. H. Toby, C. E. Botez and P. W. Stephens, J. Phys. Condens. Matter, 2004, 16, 5339.
80. S. Ramakumar, C. Deviannapoorani, L. Dhivya, L. S. Shankar and R. Murugan, Prog. Mater. Sci., 2017, 88, 325–411.

---

Footnote

† Electronic supplementary information (ESI) available: Additional ICP, XPS results and explanation, representative Nyquist plots with equivalent circuit fitting and for activation energy calculation, additional neutron powder diffraction and Rietveld refinement results. See DOI: https://doi.org/10.1039/d4ta04862h

---