Mechanisms of Li deposition on graphite anodes: surface coverage and cluster growth

Abstract

Li plating on the anode is a side reaction in Li-ion batteries which competes with Li intercalation and leads to loss of capacity. Growth of Li clusters into dendrites is a potential safety hazard for batteries which can lead to internal short-circuit and fires. We consider two possibilities of Li deposition on the surface of graphite anode: deposition of Li⁺ ions uniformly on the surface and deposition of clusters of metallic Li. Using ab initio simulations, we predict the operating voltage for the occurrence of the above processes and safety measures to prevent dendrite growth in batteries. We find that Li deposition occurs in the following stages: at positive voltages vs. Li, surface deposition of Li⁺ ions is the dominant process. Below a critical cross-over voltage, the process of reduction of aggregated Li⁺ ions and the formation of metallic Li clusters takes over. This cross-over voltage is found to be −12 mV on the basal plane of unlithiated graphite and −29 mV on lithiated graphite. To prevent formation of Li clusters and for safe operation of Li-ion batteries, the voltage on the graphite anode should be kept above the cross-over value.

---

1 Introduction

Progress in the electrification of vehicles critically depends upon the performance of the energy storage device, which is primarily a Li-ion battery (LIB).^1–3 Desirable criteria of LIBs in electric vehicles are safety, lifetime and fast charging, which depend upon the materials used in the LIB. Graphite, the most commonly used anode material in the LIB is vulnerable to Li plating, which leads to loss of capacity, and is a potential safety hazard.⁴ The causes, mechanism, and mitigation strategies of Li plating are being intensively studied in order to address this important safety concern.^5,6

The thermodynamic condition for Li nucleation occurs when the graphite anode is at a lower voltage with respect to a standard Li metal reference electrode.^7,8 Nucleation is defined here and elsewhere as the first step in the conversion of a metastable phase into a stable form, e.g. the formation of dendritic crystals of snow during supercooling of water vapour. Gao et al. demonstrated that the Li-ion diffusion limitation in a single graphite particle can also lead to saturation of Li at the graphite edges causing Li nucleation to occur.⁸ A recent study by Lu et al. explores lithiation in multi-particle graphite electrodes, showing that Li plating and stripping depend on both intra-particle as well as inter-particle diffusion.⁹ Several studies have tried to suppress formation of dendrites of metallic Li on graphite anode during fast charging,¹⁰e.g. with carbon nanotubes on graphite anode,¹¹ aligned graphene arrays,¹² coating an ultra-thin layer of gold on separator,¹³ potassium electrolyte additives,¹⁴ a localized high-concentration electrolyte,¹⁵etc.

Multiscale modelling techniques have also been applied to design safe and fast charging batteries.^16,17 Atomistic computational simulation studies have revealed important insights into the nucleation of Li clusters.^17–19 The binding energy of Li clusters on a graphene surface has been found to be higher than on the surface of Li metal suggesting a plausible cause for the Li nucleation reaction.²⁰ The energy barrier for the Li nucleation reaction has been found to depend upon the state of charge, voltage, and can be altered in the presence of functional groups.^21,22

In our previous work, we simulated the faradaic deposition and dissolution of Li nanoclusters on graphite, predicting the formation and dissolution of clusters, as a function of the applied negative overpotential vs. a standard lithium reference electrode.²³ We were able to predict the voltage, state of charge and location for growth of Li clusters on graphite anode in good agreement with experimental measurements. Using the concept of the potential of zero nucleation energy (U_PZN), we calculated the overpotentials required for the deposition of Li_n clusters from n = 1 to 65. Simulations predicted nucleation and growth of small clusters at negative overpotentials, reversibly with varying potential up to a critical cluster size; however, beyond a critical size and potential, the growth would be uncontrollable, with important implications for subsequent dendrite growth.

The present work adds the parallel reaction of double layer charging that occurs at all potentials, due to adsorbed Li⁺ ions balanced by electrons beneath the surface, similar to supercapacitors. As before, we used the standard thermodynamic model of nucleation and growth with the concept of the potential of zero nucleation energy (U_PZN). By contrast with Li clusters quantified by size, double layer charge is better quantified by surface charge density i.e. charge per surface area, assuming uniform surface coverage by equally spaced Li⁺ ions due to electrostatic repulsion, as depicted in Fig. 1 of the results section. It also assumes a substrate-layer registration as noted for other examples of electro-adsorption on single crystal surfaces e.g. H⁺ adsorption on Pt.²⁴

Fig. 1 Atomic Mulliken charges on the Li-graphite system during surface coverage (a) unlithiated graphite (b) lithiated graphite.

Finally, we note that the two processes of Li⁺ ion adsorption and faradaic deposition of Li clusters can occur simultaneously like charging of two capacitors connected in parallel. Gao et al. visualized colour changes in graphite and recorded growth of large dendrites via operando optical imaging during the experiment using a stereomicroscope and digital camera.⁸ Experimental observation of formation of small clusters could require very sophisticated techniques such as in situ microscopy at atomic resolution. However, the formation of two-dimensional surface crystals in regular patterns on the basal plane could be amenable to diffraction analysis, revealing nearest-ion distances decreasing as the potential drops to zero. Moreover, Slow Scan Cyclic Voltammetry (SSCV) and the Potential Intermittent Titration Technique (PITT) could be used to confirm the potentials (vs. a Li reference electrode) at which step changes in the total charge passed occur (cf.Fig. 6 of results section). We now present methods, results and discussion followed by conclusions, as predictions, with an open challenge for experimental electrochemists to verify such phenomena.

2 Methods

The nucleation reaction of Li on a graphite anode can be written as nLi + G → Li_n|G, where G represents the graphite and Li_n|G represents n atoms of lithium nucleated on graphite either spread uniformly on the surface or clustered together. The grand free energy change of the above reaction or the nucleation energy (ΔΩ) governs the thermodynamic feasibility of the Li nucleation at an applied voltage (U), which is calculated in the same way as in ref. 23:

ΔΩ(U) = Ω_Lin|G(U) − Ω_G(U) − n × [small mu, Greek, tilde]^ref_Li(U = 0), (1)

where [small mu, Greek, tilde]^ref_Li(U = 0) is the electrochemical potential of Li at the reference electrode, which is calculated from the change in the free energy of the Li reference electrode slab with respect to the number of Li atoms in the slab. From the calculation of nucleation energy at different applied voltages (U), one can find the voltage at which nucleation energy reaches zero, or the voltage below which Li nucleation becomes thermodynamically feasible. This voltage is called the potential of zero nucleation energy (U_PZN).

To calculate the grand free energy Ω, we use density functional theory (DFT), a popular method for modelling the electronic structure of materials.^25,26 We use the ONETEP DFT program which has a linear-scaling computational cost with the system size.^27,28 The kinetic energy cutoff of 1000.0 eV is used for the basis set consisting of psinc functions which are equivalent to plane waves.²⁹ A radius of 8.0 a₀ is used for the localized orbitals which are non-orthogonal generalized Wannier functions (NGWFs).³⁰ Perdew Burke Ernzerhof (PBE) generalized gradient approximation is used for the exchange correlation functional.³¹ Van der Waals interactions are represented using a D2 dispersion model.³²

The simulations under applied voltage (U) are performed using DFT in a grand canonical ensemble.³³ Within this framework, the calculated chemical potential of electrons (μ^ref_e) in the Li reference electrode is found to be −4.42 eV. Calculations on the graphite electrode are performed under an applied potential of U = −0.1, 0.0, 0.1 V with respect to the Li reference electrode. In this way, the chemical potential of electrons on the graphite anode is constrained at μ_e = μ^ref_e − e × U, and the number of electrons is allowed to vary, which leads to the development of a net charge on the electrode. The charged electrode is neutralized by the build-up of oppositely charged ions of the electrolyte near the interface.^34,35 The electrolyte is described by the Poisson–Boltzmann equation, which is solved using the DL_MG multigrid solver.^36,37 The electrolyte is 1.0 M LiPF₆ in ethylene carbonate solvent (EC). The accessibility function for the electrolyte is described as a product of soft spheres of error functions around atom centres.³⁵ The size of the soft spheres is determined by an isoradius of radial electronic density for an isolated atom at a value of 0.001 e/a₀³ and a solvation shell radius of 3.0 a₀, which are obtained by calibrating computed activity coefficients of electrolytes with experiments.³⁵ The EC solvent is also described via the soft-sphere model,³⁸ with a dielectric permittivity of 90.7 at 298.15 K,³⁹ and a surface tension of 0.0506 N/m.⁴⁰ The structural geometries for Li clusters and graphite electrodes have been obtained using ab initio molecular dynamics (AIMD) simulations from our previous paper.¹⁸ For larger Li clusters included in this study, additional AIMD has been performed using the same methodology. Li clusters of different size are carved from a Li bulk body-centred cubic (BCC) structure and placed on the graphite surface. AIMD is performed for 6 ps with a time step of 0.5 fs. Three low-energy configurations from AIMD simulation are chosen and the structural geometry is optimized. The lowest energy structure is chosen for calculations of nucleation energy. During the course of AIMD simulations, the large Li clusters changed from a crystalline to an amorphous-like structure. Although Li prefers a BCC structure at room temperature, the transformation to an amorphous-like cluster may be indicative of the Ostwald mechanism.⁴¹ All input, output and structural files are provided for reproduction of results.

3 Results and discussion

3.1 Structural models and oxidation states

The structures and the corresponding oxidation state of the Li-graphite system is shown via Mulliken charges on a colour scale in Fig. 1 and 2 for the two mechanisms of Li deposition, which are uniform surface coverage and cluster growth, respectively. We consider Li deposition at two states of charge of the graphite anode: Li deposition on a graphite electrode which has no intercalated Li (called unintercalated or unlithiated graphite) shown in (a) and Li deposition on a graphite electrode which is fully intercalated with Li (called intercalated or lithiated graphite) shown in (b). Note that even though Li gets deposited on unlithiated graphite, it still remains ‘unlithiated’ (as no Li is intercalated). Unlithiated graphite has AB stacking, whereas lithiated graphite has AA stacking. There are 256 carbon atoms in each layer of graphite. The number of deposited Li can be normalized per surface carbon hexagon corresponding to Li_xC₆. Note that ‘x’ denotes amount of deposited Li and not the intercalated Li. We consider the entire range 0 ≤ x ≤ 3. The clean surface corresponds to x = 0, while the fully covered surface corresponds to x = 3.

Fig. 2 Atomic Mulliken charges on the Li-graphite system during cluster growth (a) unlithiated graphite (b) lithiated graphite.

As seen in Fig. 1(a), uniform surface coverage on unlithiated graphite leads to a positive charge on the lithium in the form of Li⁺ ions and a slightly negative charge on the carbon atoms underneath. Full surface coverage shows reduction in the oxidation state of lithium close to that of metallic plated Li. Uniform surface coverage on the lithiated graphite in Fig. 1(b) shows similar adsorption of Li⁺ ions and a slightly negative charge on the carbon atoms underneath. The intercalated Li⁺ ions have a higher positive charge than the Li⁺ ions deposited on the surface. Similar to the unlithiated graphite, full surface coverage on lithiated graphite also shows reduction in the oxidation state of surface lithium close to that of metallic plated Li. Fig. 2(a) shows that the oxidation state of lithium during cluster growth on unlithiated graphite is more similar to metallic Li and decreases with the distance of the Li atom from the surface. A similar trend is seen for the oxidation state of clusters deposited on lithiated graphite, shown in Fig. 2(b). The oxidation state shows that the intercalated lithium are Li⁺ ions, unlike Li clusters deposited on the surface.

3.2 Nucleation energy

The thermodynamic feasibility of nucleation at a particular voltage (U) can be calculated from the nucleation energy, ΔΩ(U) in eqn (1). Li nucleation is energetically favorable if the nucleation energy ΔΩ(U) < 0, while it is thermodynamically unfavorable if the nucleation energy ΔΩ(U) > 0. In Fig. 3, we show the nucleation energy at different applied voltages (U = −0.1, 0.0, 0.1 V) on the graphite electrode with respect to the Li reference electrode calculated using the grand canonical ensemble DFT method.³³ The abscissa shows the amount of Li deposited (x) in Li_xC₆. As the applied voltage (U) is reduced, the nucleation energy becomes lower, and the thermodynamic favorability of Li nucleation on graphite increases. Comparing the two different mechanisms, the nucleation energy for deposition of Li⁺ ions uniformly covering the surface is initially lower than for the deposition of Li clusters, suggesting that surface coverage will be more thermodynamically favorable and dominate at lower amounts of deposited Li(x). However, at higher Li deposition (x), the cluster growth has a lower nucleation energy than surface coverage, suggesting the cluster growth mechanism to take over.

Fig. 3 Energy required for nucleation of (a) Li⁺ ions uniformly on graphite surface and (b) Li cluster on graphite surface. The simulations were performed under potential control at different voltages (U = −0.1, 0.0, 0.1 V).

3.3 Potential of zero nucleation energy (U_PZN)

To quantify the exact voltage below which the nucleation process becomes thermodynamically favorable, we calculate the potential of zero nucleation energy ΔΩ(U_PZN) = 0, shown in Fig. 4. We see a cross-over in U_PZN after a certain amount of Li has been deposited (x_cr). Below this cross-over point, or at x < x_cr, the mechanism of uniform surface coverage is thermodynamically more favorable and occurs at higher voltages than the mechanism of cluster growth. This suggests that the bare graphite surface is more prone to be uniformly covered by surface Li⁺ ions before nucleation of Li clusters. When the amount of deposited lithium goes above the cross-over point, or at x > x_cr, the mechanism of cluster growth takes over, suggesting that only after certain amount of surface has been uniformly covered by Li⁺ ions, does the process of nucleation of Li clusters become thermodynamically more favorable. At this point the required potential, U_PZN(x_cr) has already fallen below zero volts, which explains experimental observations of dendrite growth only at negative voltages on graphite.⁸ Although the mechanism of cluster growth leading to dendrites takes over only when U < U_PZN(x_cr), uniform surface coverage occurs even at higher voltages U > U_PZN(x_cr) and precedes growth of Li clusters.

Fig. 4 The potential of zero nucleation energy, U_PZN(V) for surface coverage and cluster growth on (a) unlithiated graphite and (b) lithiated graphite.

The cross-over voltage is found to be −12 mV on unlithiated graphite and −29 mV on lithiated graphite. Above, the cross-over voltage, the higher stability of uniformly adsorbed Li⁺ ions as compared to deposition of Li clusters may be attributed to the energy required to bring Li ions together overcoming the electrostatic repulsion. The fully covered surface has a Li above every hexagonal ring of carbon. The Li⁺ ions are reduced, similar to clusters. So now the cohesive energy of a cluster dominates over a flat surface. Therefore, below the cross-over voltage, we can see the higher stability of clusters over the completely covered surface. The overpotential required for complete surface coverage on graphite electrode is found to be −123 mV on unlithiated graphite and −138 mV on lithiated graphite. The deposition of a complete Li surface on a Li reference electrode would occur at zero volts; however, a sufficient overpotential is required for complete surface coverage on graphite due to the different hexagonal surface adsorption lattice of graphite as compared to the surface of a Li electrode.

3.4 Charge transfer

During Li nucleation, the Li⁺ ions (Q_ion) are transferred internally via electrolyte to the graphite electrode and electrons are transferred externally via the electrical circuit (Q_el). Some of the Li⁺ ions are deposited on the graphite surface (Q_Li) and the electrolyte surrounding the graphite electrode develops a net charge (Q_dl). These forms of charge transfer are quantitatively shown in Fig. 5 with respect to U_PZN for all the four cases considered. We see that the total number of electrons passed in the external circuit is equal to the charge transferred in the form of Li deposition and the electrolyte double layer, Q_ion = Q_Li + Q_dl = −Q_el. Or in other words, Q_ion + Q_el = 0 at all potentials, in accordance with the principle of charge conservation and global electroneutrality. We see that the amount of charge transferred due to uniform surface coverage increases gradually as the U_PZN is decreased. However, the charge transfer due to cluster growth is small at larger potentials and increases abruptly in the form of a spike close to U_PZN dropping below zero volts. The slope of these curves (dQ/dU) predicts the differential capacitance of these processes.

Fig. 5 The amount of charge transfer via Li deposition, electrolyte double-layer charging and electronic current during Li deposition via two mechanisms: (a) uniform surface coverage and (b) cluster growth.

3.5 Charge transferred vs. potential

The comparison of charge–potential curves for the two mechanisms of Li nucleation is further shown in Fig. 6. Here, one can clearly see the cross-over between the mechanisms of uniform coverage of graphite surface by Li⁺ ions and growth of Li clusters on graphite with voltage. The curves predict that during an experiment, as the potential on graphite is reduced, initially a gradual current would be observed owing to the nucleation of Li⁺ ions in the form of uniform surface coverage. At potentials close to the cross-over point, an abrupt spike is observed owing to the large amount of electrons transferred to deposit Li clusters on graphite. The process of deposition of Li⁺ ions uniformly on the graphite surface is reversible, which means that if the potential is increased, the deposited Li⁺ ions would dissolve back into the electrolyte. After the cross-over point, the Li⁺ ions reduce to metallic Li clusters. If these clusters lose contact with the electrode, it leads to an irreversible loss of capacity, and if these clusters remain connected to the electrode, they have the potential of growing into dendrites, posing a hazard to safety of the battery. Therefore for the safe operation of Li-ion batteries, the voltage on graphite anode should not be allowed to fall below the cross-over point.

Fig. 6 Charge–potential curves for Li deposition via surface coverage and cluster growth on unlithiated and lithiated graphite.

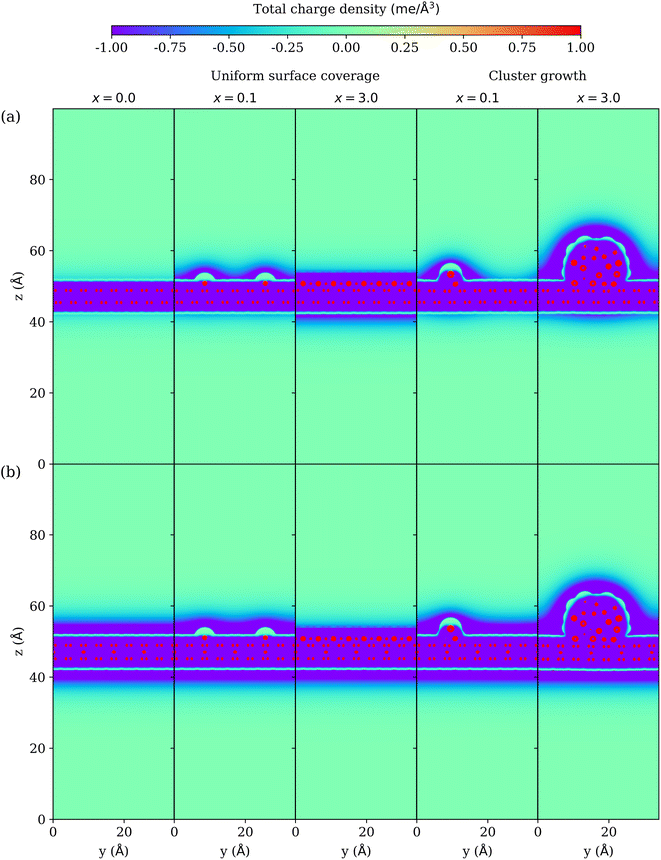
3.6 Charge density

The total charge density due to electrons, nuclei and electrolyte is shown in Fig. 7 for both mechanisms of surface coverage and cluster growth on (a) unlithiated and (b) lithiated graphite at U = 0.0 V. On the electrode, the positive nuclei of carbon and lithium can be seen as red dots, while negative electrons can be seen in purple. The quantum electrode (consisting of nuclei and electrons) is surrounded by the continuum solvent and electrolyte. The net charge on the electrode is neutralized by the opposite charge on the electrolyte. The Pauli repulsion of the continuum electrolyte is modelled by a steric potential, which creates a sharp (green) boundary around the electrode, which is devoid of electrolyte. x = 0.0 represents clean graphite surface with no lithium deposition. At x = 0.0, the unlithiated graphite has a charge of 1.3 e, while the lithiated graphite has a charge of 9.6 e. As a result, a much thinner tint of electrolyte layer can be seen around the unlithiated graphite, while a much thicker dense electrolyte layer can be seen around the lithiated graphite to neutralize the large positive charge. In the process of Li deposition, the charge on the unlithiated graphite during uniform surface coverage is 4.3 e at x = 0.1 and 3.5 e at x = 3.0, while during cluster growth it is 3.5 e at x = 0.1 and 17.9 e at x = 3.0. The charge on the lithiated graphite during uniform surface coverage is 11.3 e at x = 0.1 and 5.9 e at x = 3.0, while during cluster growth it is 10.7 e at x = 0.1 and 30.1 e at x = 3.0. The net charge on the electrode is positive, and is neutralized by a buildup of a negative charge density on the electrolyte side. Thus, the system behaves as an electrical double layer capacitor. For the case of Li deposition on unlithiated graphite, the majority of the electrolyte charge is above the surface adsorbed by lithium because the positive lithium attracts more negative electrolyte charge than carbon, except the fully covered surface at x = 3.0, where Li are reduced to neutral metallic state and have extra electrons. The fully covered surface at x = 3.0 does not have a distinctly visible green region around Li unlike other cases as it is filled by these extra electrons. For the case of Li deposition on lithiated graphite the negatively charged electrolyte layer also builds up on the unadsorbed side (below the electrode) unlike for unlithiated graphite because of the attraction of the electrolyte to intercalated Li⁺ ions.

Fig. 7 Total charge density due to the electrons, nuclei and electrolyte at different amounts of Li deposition (x) in a plane perpendicular to the graphite surface at U = 0 V on (a) unlithiated graphite and (b) lithiated graphite.

4 Conclusions

We have studied mechanisms of Li deposition and charge transfer on the surface of the graphite anode in Li-ion batteries under potential control. Using ab initio calculations, we found that the graphite surface is covered uniformly by adsorbed Li⁺ ions even at positive potentials (in the range studied) with respect to the Li reference electrode. As the potential applied on graphite is reduced, the surface coverage of adsorbed Li⁺ ions increases gradually. At slightly negative potentials, after certain surface coverage has been achieved, the process of Li plating and cluster growth takes over. This critical potential is found to be −12 mV on unlithiated graphite and −29 mV on lithiated graphite. Below this critical potential, there will be a visible growth of clusters on a graphite anode. The clusters can potentially grow into dendrites, which can cause internal short-circuit of the battery and pose a hazard for safety. Therefore for safe operation of Li-ion batteries, the voltage on graphite anode should be kept above this critical value. We encourage experimentalists to reproduce our predictions of the competition between uniform Li coverage and cluster growth. The exploration of effects such as current density, temperature and mechanical pressure on Li nucleation with multiscale modelling requires further research.

Data availability

The data that supports the findings of this study is available with the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out with the funding from the Faraday Institution (https://www.faraday.ac.uk/; EP/S003053/1), grant numbers FIRG025 and FIRG059. The calculations presented in this work were performed on the Iridis5 and Iridis6 supercomputers at the University of Southampton, HSUper facility at the Helmut Schmidt University, the tryton+ facility at the CI TASK Centre of Informatics in Gdańsk, Poland, and the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk; via the UKCP HEC Consortium, EPSRC grant number: EP/X035956/1).

Notes and references

1. J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
2. V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262.
3. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
4. J. Vetter, P. Novák, M. R. Wagner, C. Veit, K. C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269–281.
5. D. Hu, L. Chen, J. Tian, Y. Su, N. Li, G. Chen, Y. Hu, Y. Dou, S. Chen and F. Wu, Chin. J. Chem., 2021, 39, 165–173.
6. T. Waldmann, B. I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2018, 384, 107–124.
7. P. Arora, M. Doyle and R. E. White, J. Electrochem. Soc., 1999, 146, 3543–3553.
8. T. Gao, Y. Han, D. Fraggedakis, S. Das, T. Zhou, C. N. Yeh, S. Xu, W. C. Chueh, J. Li and M. Z. Bazant, Joule, 2021, 5, 393–414.
9. X. Lu, M. Lagnoni, A. Bertei, S. Das, R. E. Owen, Q. Li, K. O'Regan, A. Wade, D. P. Finegan, E. Kendrick, M. Z. Bazant, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2023, 14, 5127.
10. S. Liu, B. Gu, Z. Chen, R. Zhan, X. Wang, R. Feng and Y. Sun, J. Energy Chem., 2024, 91, 484–500.
11. G. Yeo, J. Sung, M. Choi, N. Kim and M. Ko, J. Mater. Chem. A, 2022, 10, 12938–12945.
12. C. Zhang, L. Dong, N. Zheng, H. Zhu, C. Wu, F. Zhao and W. Liu, Energy Storage Mater., 2021, 37, 296–305.
13. S. Yan, X. Chen, P. Zhou, P. Wang, H. Zhou, W. Zhang, Y. Xia and K. Liu, J. Energy Chem., 2022, 67, 467–473.
14. S. Moharana, G. West, M. Walker, X. S. Yan and M. Loveridge, ACS Appl. Mater. Interfaces, 2022, 14, 42078–42092.
15. X. Yue, J. Zhang, Y. Dong, Y. Chen, Z. Shi, X. Xu, X. Li and Z. Liang, Angew. Chem., Int. Ed., 2023, 62, e202302285.
16. A. Tomaszewska, Z. Chu, X. Feng, S. O'Kane, X. Liu, J. Chen, C. Ji, E. Endler, R. Li, L. Liu, Y. Li, S. Zheng, S. Vetterlein, M. Gao, J. Du, M. Parkes, M. Ouyang, M. Marinescu, G. Offer and B. Wu, eTransportation, 2019, 1, 100011.
17. L. M. Morgan, M. P. Mercer, A. Bhandari, C. Peng, M. M. Islam, H. Yang, J. Holland, S. W. Coles, R. Sharpe, A. Walsh, B. J. Morgan, D. Kramer, M. S. Islam, H. E. Hoster, J. S. Edge and C.-K. Skylaris, Prog. Energy, 2022, 4, 012002.
18. C. Peng, A. Bhandari, J. Dziedzic, J. R. Owen, C.-K. Skylaris and D. Kramer, J. Mater. Chem. A, 2021, 9, 16798–16804.
19. X. Chen, X. R. Chen, T. Z. Hou, B. Q. Li, X. B. Cheng, R. Zhang and Q. Zhang, Sci. Adv., 2019, 5, eaau7728.
20. X. Fan, W. T. Zheng, J. L. Kuo and D. J. Singh, ACS Appl. Mater. Interfaces, 2013, 5, 7793–7797.
21. M. Liu, A. Kutana, Y. Liu and B. I. Yakobson, J. Phys. Chem. Lett., 2014, 5, 1225–1229.
22. J. Cui, S. Yao, M. Ihsan-ul haq, J. Wu and J.-k. Kim, Adv. Energy Mater., 2019, 9, 1802777.
23. A. Bhandari, C. Peng, J. Dziedzic, J. R. Owen, D. Kramer and C.-K. Skylaris, J. Mater. Chem. A, 2022, 10, 11426–11436.
24. E. Herrero, L. J. Buller and H. D. Abruña, Chem. Rev., 2001, 101, 1897–1930.
25. R. O. Jones, Rev. Mod. Phys., 2015, 87, 897–923.
26. W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980.
27. J. C. A. Prentice, J. Aarons, J. C. Womack, A. E. A. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M.-M. Dubois, K. K. B. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. O'Regan, M. J. S. Phipps, L. E. Ratcliff, Ã. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. M. Hine, A. A. Mostofi, M. C. Payne and C.-K. Skylaris, J. Chem. Phys., 2020, 152, 174111.
28. C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119.
29. A. A. Mostofi, P. D. Haynes, C.-K. Skylaris and M. C. Payne, J. Chem. Phys., 2003, 119, 8842–8848.
30. C.-K. Skylaris, A. A. Mostofi, P. D. Haynes, O. Diéguez and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035119.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
33. A. Bhandari, C. Peng, J. Dziedzic, L. Anton, J. R. Owen, D. Kramer and C.-K. Skylaris, J. Chem. Phys., 2021, 155, 024114.
34. A. Bhandari, L. Anton, J. Dziedzic, C. Peng, D. Kramer and C.-K. Skylaris, J. Chem. Phys., 2020, 153, 124101.
35. J. Dziedzic, A. Bhandari, L. Anton, C. Peng, J. C. Womack, M. Famili, D. Kramer and C.-K. Skylaris, J. Phys. Chem. C, 2020, 124, 7860–7872.
36. J. C. Womack, L. Anton, J. Dziedzic, P. J. Hasnip, M. I. J. Probert and C.-K. Skylaris, J. Chem. Theory Comput., 2018, 14, 1412–1432.
37. http://www.dlmg.org .
38. G. Bramley, M.-T. Nguyen, V.-A. Glezakou, R. Rousseau and C.-K. Skylaris, J. Chem. Theory Comput., 2020, 16, 2703–2715.
39. D. S. Hall, J. Self and J. R. Dahn, J. Phys. Chem. C, 2015, 119, 22322–22330.
40. R. Naejus, C. Damas, D. Lemordant, R. Coudert and P. Willmann, J. Chem. Thermodyn., 2002, 34, 795–806.
41. W. Ostwald, Z. fur Phys. Chem, 1897, 22U, 289–330.

---

Footnote

† Electronic supplementary information (ESI) available: All calculation input and output files are provided for reproduction of results. See DOI: https://doi.org/10.1039/d4ta04834b

---