Mesomeric control of the optoelectronic properties of polymerized small molecule acceptors

Abstract

Organic photovoltaics based on polymer blends have the potential for flexible solar cells with superior mechanical and thermal resiliency. Recently, regioregular polymerized small molecule acceptors (PSMAs) were synthesized and utilized as active acceptor materials to achieve record-breaking all-polymer solar cells with power conversion efficiency approaching 20%. The reported experimental studies show a systematic correlation between polymerization sites and the properties of the PSMA, where one of the regioisomers (γ-PSMA) displays more favorable optoelectronic and photovoltaic properties compared to the other (δ-PSMA). However, these experimental observations have not yet been rationalized. Here, we used first-principles calculations to reveal that the substituents on the cross-conjugated terminal unit of the SMA core are responsible for improving the optoelectronic properties of γ-PSMAs, by extending the conjugation length and enhancing favorable mesomeric effects. Importantly, we demonstrate that these effects can be exploited as a universal molecular design principle, and we predict that functionalizing PSMAs in selected positions with electron-withdrawing groups can further improve their optoelectronic properties. Our study provides a quantitative framework for understanding and rationalizing the relationship between polymerization sites and optoelectronic properties in regioregular PSMAs; in addition, our results pave the way for a rational design principle to further improve the properties of these conjugated polymers and, in turn, the efficiency of all-polymer solar cells.

---

Introduction

All-polymer solar cells (all-PSCs) with an n-type conjugated polymer as the electron acceptor (A) and a p-type conjugated polymer as the electron donor (D) are emerging as promising candidates for highly efficient organic photovoltaics. They feature low costs of production, light weight, and solution processability. Furthermore, compared to solar cells with non-fullerene small molecule acceptors (SMAs), the polymeric nature of both donor and acceptor species enables higher tolerance towards the donor/acceptor ratio in the devices, improved solution processability, better scalability and higher mechanical flexibility.^1–4 However, commonly used polymeric acceptors usually exhibit low electron mobility, low electron affinity, and a weak light harvesting ability, leading to low power conversion efficiencies (PCEs) of the corresponding all-PSCs.^5–7

Hence, improving the performance of all-PSCs requires new design strategies at the molecular level to finely tune the photovoltaic properties of polymeric acceptors. To this end, in 2017 Li et al. introduced the so-called polymerized small molecule acceptor (PSMA) strategy to obtain efficient functional n-type conjugated polymers for all-PSCs. Starting from the fused-ring A–D–A-type non-fullerene SMA IDIC-16,⁸ they polymerized the core unit with a thiophene π-linker obtaining the PZ1 acceptor polymer (Fig. 1).⁹

Fig. 1 Chemical structure of PZ1 as a representative polymerized non-fullerene small molecule acceptor. Different colors are used for highlighting the different constituting units of a PSMA, i.e. the non-fullerene SMA core (orange) and the π-linker (cyan). Closeup: schematic structure of the 1,1-dicyanomethylene-3-indanone (IC) SMA terminal group with the γ and δ polymerization sites indicated in red.

The PSMA strategy leads to functional acceptors that retain the finely tuned optoelectronic and photovoltaic properties of non-fullerene SMAs,^10,11 while simultaneously taking advantage of the stability of polymers under light irradiation, and of their good film-forming properties, as well as improving the morphology of the active layer.^12–14 For PZ1, this strategy resulted in an improved PCE of 9.18% for the PZ1-based device compared to the SMA-based one (3.96%).⁹ This promising result prompted the exploration of the chemical space of available SMA building blocks and π-conjugated linkers for the synthesis of novel efficient acceptor polymers. This strategy led to a rapid increase of the efficiency of PSMA-based all-PSCs, reaching PCEs of over 18%,^15,16 a value comparable to that of SMA-based devices.

The vast majority of the SMAs used as building blocks for PSMAs (i.e. A–D–A′–D–A or A–D–A-type molecular architectures)¹⁴ feature the strongly electron-withdrawing 1,1-dicyanomethylene-3-indanone (IC) as terminal acceptor group (closeup Fig. 1).¹⁷ In isolated SMAs this unit yields favorable energy levels and improved intramolecular charge transfer.¹⁸ In addition, as a building block of PSMAs, this unit provides regioregularity control as an additional design variable, since both γ and δ sites on the indanone backbone represent viable polymerization sites. In general, previous studies showed that controlling the regioselectivity of the polymerization process improves the intrinsic properties of the polymers, and, in turn, their efficiency as conducting units in organic electronics.¹⁹ In this context, PSMAs are no exception. Indeed, it has been reported that with no regioregularity control upon polymerization, one obtains PSMAs with a regiorandom polymer backbone, thus negatively affecting their intrinsic optoelectronic and photovoltaic properties, including charge mobility and transport, light absorption efficiency, intermolecular π–π stacking and, ultimately, the device performance.^12,13,19,20 Additionally, regiorandom PSMAs affect the batch-to-batch reproducibility of the synthetic procedures.^20–22 For all these reasons, regioregularity control is rapidly emerging as an important design strategy to obtain highly efficient PSMA-based devices and several efforts have been made to ensure regioregularity within polymerization, resulting in enhanced PCEs of the related solar cells.^19,20

Interestingly, several studies revealed a consistent trend between the polymerization site and the optoelectronic and photovoltaic properties of regioregular PSMAs. In all the cases presented in the literature, γ-PSMAs display more favorable optical and electronic properties compared to δ-PSMAs, often leading to a remarkably higher PCE of the γ-based devices.^{20,21,23–28} Spectroscopical, morphological and computational investigations revealed that, compared to δ-PSMAs, γ-PSMAs have lower-lying and more delocalized lowest unoccupied molecular orbitals (LUMOs), increased extended conjugation, higher electron transport and absorption wavelength red-shifted towards the near-infrared region.^20,23,25 All these factors, combined with improved morphological features, play a fundamental role in boosting the PCE of γ-PSMA-based devices.

Even though recent results highlight remarkable improvements of the efficiency of regioregular PSMA-based devices, the microscopic origin of the relationship between polymerization sites and their optoelectronic properties in regioregular PSMAs has neither been elucidated nor systematically investigated. In this work, we provide a quantitative framework to understand and rationalize how regioregularity affects the properties of PSMAs. Using Density Functional Theory (DFT) and Time-Dependent Density Functional Theory (TDDFT) calculations, we study the electronic structure and optical properties of several experimentally reported PSMAs. We evaluate the effect of the substituents in the IC unit on conjugation length and mesomeric effects, by comparing the properties of realistic IC-based regioisomers with those bearing symmetric indandione (IND) SMA end groups,²⁹ where the dicyanomethylene group is replaced by a keto group. Our results show that, upon symmetrization, the properties of γ and δ isomers become quantitatively indistinguishable, demonstrating that the optoelectronic properties of γ-PSMAs are controlled and enhanced by the presence of the dicyanomethylene group in the IC unit. Furthermore, we show that the optoelectronic properties of γ-PSMAs can be further improved by, for instance, vicinal functionalization of the IC unit with an electron-withdrawing substituent, which we predict will further enhance the properties of γ-PSMAs via favorable mesomeric effects.

Results and discussion

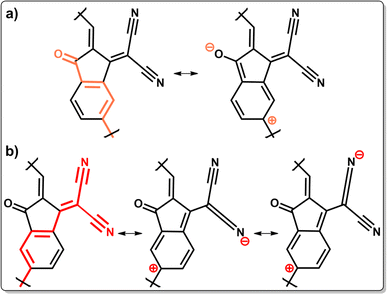
As mentioned in the Introduction, most of the SMA cores in PSMAs feature terminal IC units. In this molecular scaffold, the electron-withdrawing dicyanomethylene and keto groups exert simultaneously negative inductive (−I) and negative mesomeric (−M) effects, rendering the IC unit electron-deficient. As shown in Fig. 1, the IC unit is cross-conjugated: both the keto and dicyanomethylene unsaturated groups on the cyclopentene moiety of IC are conjugated to a third unsaturated center (the fused phenyl double bond); however they are not conjugated to each other.^30,31 Cross-conjugation is ubiquitous in organic conjugated polymers³² and, in this specific case, it has two important effects on the electronic properties of PSMAs. Firstly, it preserves conjugation in the polymers without full single-double bond alternation patterns (formally associated to extended conjugation). Secondly, because of IC's cross-conjugation, the extended conjugation patterns at the two polymerization sites are different, depending on the IC substituents (see Scheme 1).

Scheme 1 Schematic representation of the extended conjugation patterns along the terminal IC group for δ- (a) and γ-PSMAs (b), together with representative Lewis resonance structures along the pattern induced by the −M effect of the keto and dicyanomethylene groups, respectively. In the δ isomer the −M effect of the electron-withdrawing keto group leads to the delocalization of a positive charge along the δ conjugation pattern and, as a result, a Lewis structure is formed, with the positive charge localized at the δ site, enabling further delocalization towards the conjugated π-linker. In the case of the γ isomer, the −M effect of the dicyanomethylene group leads to delocalization of two positive charges along the γ conjugation pattern and, as a result, two Lewis structures with the positive charge localized at the γ site are present, namely twice the number of those associated with the mesomeric effect of the keto substituent along the δ conjugation pattern.

As shown in Scheme 1a, the extended conjugation pattern through the δ site of the IC group (i.e. the one relevant for conjugation in δ-PSMAs) is controlled directly by the keto group, whereas the conjugation pattern at the γ site is controlled by the dicyanomethylene group (Scheme 1b). Hence, one relevant difference between the two polymerization sites is that γ-PSMAs have a longer conjugation length than δ-PSMAs. A longer conjugation length in narrow band gap conjugated polymers is usually associated with smaller fundamental and optical gaps,³³ and hence it is reasonable to expect it may contribute to the red-shifted optical absorption revealed experimentally for γ-PSMAs.

Additionally, the keto and dicyanomethylene groups have a different structure, and therefore they exert a quantitatively different negative mesomeric effect on the two isomers, as can be inferred by applying classical mesomerism theory on the extended conjugation patterns in the IC end group (Lewis resonance structures in Scheme 1). The comparison of the Lewis resonance structures reported in Scheme 1a and 1b (and of all the relevant resonance structures reported in Schemes S1 and S2 in the ESI† for the δ and γ isomers, respectively) reveals that the branched nature of the dicyanomethylene group induces an enhanced negative mesomeric effect along the γ conjugation pattern. In fact, each of the cyano groups of the dicyanomethylene substituent can independently induce positive charge delocalization along the conjugation pattern and, as a result, twice the number of Lewis structures representing positive charge delocalization along the γ conjugation pattern are obtained. This effect is associated with the lowering of the frontier energy levels and of the HOMO–LUMO and optical gaps of the molecular unit; it is also associated with an increased LUMO delocalization and enhanced π-conjugation resulting from increased π-delocalization.³⁴

The qualitative analysis reported above suggests that the optoelectronic properties of γ-PSMAs are controlled (and enhanced) by the nature of the dicyanomethylene substituent. To verify quantitatively this hypothesis derived from our analysis, we carry out (TD)DFT calculations at the B3LYP level of theory (see Computational Details for the full computational protocol) on the eleven experimentally reported PSMAs shown in Fig. 2.

Fig. 2 Chemical structures of the eleven PSMAs featured in this study. The experimental studies where each regiorandom (top line) and/or regioregular PSMA (bottom line, when applicable) has been experimentally characterized are listed. We use PY-T (i.e. Y-type core with a thiophene linker)²³ as a PSMA featuring Y-series A–D–A′–D–A core units; we consider core-fused rings modifications by including PZT,²⁵ and terminal group functionalization by including PY-T-F.²⁶ We include PSMAs with Y-type cores polymerized with bithiophene (PY-2T),^35,36 selenophene (PY-Se), biselenophene (PY-BiSe),²⁷ fluorinated bithiophene (PY-2F2T),²¹ as well as the efficient PY-BTz we recently reported,³⁷ featuring a dialkoxy-bithiazole linker. Finally, we consider PSMAs with A–D–A-type cores, such as PZ1,⁹ MBTI,³⁸ which also contains a functionalized bithiophene diimide linking group, and the recently reported non-fused core-based PBTO.²⁸Inset: schematic structure of the 1,1-dicyanomethylene-3-indanone (IC) and indandione (IND) terminal groups used in this study.

The chosen computational protocol yields good agreement with previously reported experimental results for optical and electronic properties (see Computational Methods section for details). The selected PSMAs sample a relatively large chemical space, thus providing a general set of results. For each PSMA we optimize the structure of both δ and γ isomers and we compute several key optoelectronic properties related to their performance in all-PSCs. Then, for each PSMA and each isomer we substitute the IC unit with a symmetric indandione (IND) terminal unit (see inset Fig. 2) and repeat all our calculations. When replacing the dicyanomethylene group with a keto group in IND, we obtain PSMAs with identical mesomeric effects and conjugation length at the γ and δ sites. Therefore, the hypothesis discussed above—that the optoelectronic properties of γ-PSMAs are controlled by the nature of the dicyanomethylene substituent—will be verified if, after the IC group replacement, γ- and δ-PSMAs exhibit qualitatively similar optoelectronic properties. We show below that this is indeed the case.

We start our analysis by considering the extent of the backbone delocalization of the LUMOs in the two isomers, using PY-2T as a representative case. The extent of the LUMO delocalization in PSMAs is a relevant property, since it impacts the intramolecular charge transfer along the polymer backbone and, in turn, enhances the charge transport and helps suppressing charge recombination in the related solar cell devices. Furthermore, the LUMO delocalization is tightly connected to the mesomeric model discussed earlier. It is known that enhanced mesomeric effects in the π-conjugated building blocks of semiconducting polymers are accompanied by an increased delocalization of the LUMO towards the neighboring conjugated units.³⁴ Therefore, the increased −M effect in γ-PSMAs should be accompanied by an increased LUMO delocalization (and π-conjugation) along the polymer backbone, compared to δ-PSMAs. Indeed, we find that the LUMO is more efficiently delocalized in the IC unit of γ-PY-2T, following the pattern dictated by the respective resonance structures (see Fig. S3 in the ESI† and discussion therein). Upon inspection of the LUMO isosurfaces (Fig. 3a–d) for the PY-2T isomers, we find them to be consistent with the mesomeric control of the LUMO delocalization along the polymer backbone. We indeed observe a clear difference between IC-terminated δ- and γ-PY-2T: while the LUMO of the latter (Fig. 3b) is fully delocalized on the whole molecular unit, that of δ-PY-2T is only localized on the two Y5 units with no LUMO localization on the linker (Fig. 3a). This effect can be quantified by computing the reduced atomic LUMO populations on the atoms of the π-linker (p), which give a measure (in percentage) of the extent of the LUMO localization on the bithiophene linker. Indirectly, p values allow to infer quantitatively the extent of LUMO delocalization on the molecular units of δ and γ isomers: negligible p values suggest poor LUMO delocalization, whereas higher p values indicate that the LUMO is fully delocalized on the polymer backbone. As shown in Fig. 3a and b, the p values we find for δ- and γ-PY-2T are consistent with the conclusions inferred from the LUMO isosurfaces: 6.7% of the LUMO is localized on the linker of γ-PY-2T, while only 0.6% of the LUMO is localized on the bithiophene unit of δ-PY-2T. Notably, for IND-terminated PY-2T isomers, the LUMOs of δ- and γ-PY-2T-IND are similarly delocalized over the respective molecular units (Fig. 3c and d). Accordingly, the LUMOs of δ- and γ-PY-2T-IND feature practically identical p values (4.4% and 4.6%, respectively).

Fig. 3 LUMO isosurfaces (isodensity value: 10 me/a₀³) for IC-terminated δ- and γ-PY-2T (a and b) and IND-terminated δ- and γ-PY-2T-IND (c and d). For each isosurface, the percentage of LUMO localization on the linker unit (p) is reported. (e) Effect of regioregularity on the LUMO localization on the linker unit (Δp) for IC- (red) and IND-terminated (blue) δ- and γ-PSMAs.

To verify the generality of the descriptor used above, we computed the p values and LUMO isosurfaces for all IC- and IND-terminated δ and γ isomers of the PSMAs reported in Fig. 2, and we quantified the effect of regioregularity on p for IC- and IND-terminated PSMAs as follows:

Δp = p^γ − p^δ (1)

where p^γ and p^δ are atomic LUMO populations on the atoms of the π-linker for γ and δ isomers, respectively.

The computed Δp values for IC-terminated PSMAs (red bars in Fig. 3e) are consistent with the trend discussed for PY-2T. In all cases, δ isomers feature negligible p values (no linker LUMO localization and poor backbone LUMO delocalization) and γ isomers have higher p values (increased linker localization and more efficient backbone delocalization). As a result, Δp values are positive throughout the series of IC-terminated PSMAs, with an average value of 5.5 ± 3.0%. Instead, upon introduction of the symmetric IND group, Δp values are considerably smaller for all IND-terminated PSMAs (blue bars in Fig. 3e) with an average of 0.4 ± 3.0%, indicating a similar extent of LUMO delocalization (and π-delocalization) along the backbone of the two isomers. A comparison between the LUMO isosurfaces of IC- and IND-terminated PSMAs supports the conclusions drawn from the computed Δp. Despite the localization patterns of the LUMO of the δ-PSMAs may appear at first sight different, we note that the LUMO and LUMO+1 are quasi-degenerate orbitals (see Fig. S5 in the ESI† and discussion therein); hence one should consider their linear combination to analyze localization patterns. Such linear combination yields an effective LUMO. By doing so, we observe that the effective LUMOs are poorly delocalized on all δ-PSMAs but fully delocalized on all γ-PSMAs, while the character of the LUMOs of IND-terminated γ- and δ-PSMAs becomes indistinguishable (see Fig. S4 and S6 in the ESI†).

These results provide a proof of concept of the mesomeric effect on the electronic structure of regioregular PSMAs. In essence, as a direct consequence of the enhanced −M effect on the γ conjugation pattern, a more delocalized LUMO is found for all γ-PSMAs. This result highlights the connection of our mesomeric model with a distinctive feature of the electronic structure of the polymers; we can expect that, at least qualitatively, the different nature of the LUMOs of δ- and γ-PSMAs may also impact some of their optoelectronic properties. For instance, we can expect that, due to an increased LUMO delocalization, γ-PSMAs display LUMO levels at lower energies, leading to lower fundamental and possibly optical gaps.

Hence, we quantitatively evaluate the extent of the mesomeric control of some key optoelectronic properties of regioregular PSMAs such as the HOMO–LUMO (E_HL) and the optical (E_g) gaps, vertical electron affinities (VEA) and exciton binding energies (E_b). To do so, we compute these properties for IC- and IND-terminated γ- and δ-PSMAs and we evaluate the regioregularity effect as follows:

ΔE_HL = E^δ_HL − E^γ_HL (2)

ΔE_g = E^δ_g − E^γ_g (3)

ΔVEA = VEA^δ − VEA^γ (4)

ΔE_b = E^δ_b − E^γ_b (5)

where “γ” and “δ” superscripts refer to properties computed for γ and δ isomers, respectively.

The quantities defined above are reported in Fig. 4. The ΔE_HL values are always positive throughout the series for IC-terminated PSMAs (red bars in Fig. 4a), with an average value of 43 ± 22 meV, indicating that the fundamental gap of γ-PSMAs is always smaller than that of δ-PSMAs, in agreement with previous theoretical and experimental findings.^{19–21,23,26,27} Interestingly, the replacement of the dicyanomethylene with the keto substituent in the IND group leads to ΔE_HL values that are consistently smaller throughout the series (blue bars in Fig. 4a). The average value of ΔE_HL is approximately one order of magnitude smaller (5 ± 4 meV) than that of IC-PSMAs; this result indicates that IND-terminated γ- and δ-PSMAs have similar HOMO–LUMO gaps, due to the identical mesomeric effect exerted by the two keto groups on the IND unit. We also evaluated the effect of regioregularity on the absolute HOMO and LUMO energies of regioregular PSMAs separately (Fig. S7 in the ESI†). Our results indicate that IC-terminated γ-PSMAs have lower-lying HOMO and LUMO levels (negative ΔE_H and ΔE_L values); however, the effect of regioregularity on the two molecular orbitals is quantitatively different. As can be inferred from Fig. S7a,† for each IC-terminated PSMA the absolute value of ΔE_L is larger than ΔE_H. Upon symmetrization, we find that ΔE_H and ΔE_L values are similar for each IND-terminated PSMA (see Fig. S7b†). These results are consistent with those of Fig. 4a, and, most importantly, with the known relationship between mesomeric effects and energy levels, where −M effects are expected to lower LUMO energies to a bigger extent compared to HOMO energies. Overall, our results indicate that the energy levels of PSMAs are modulated by the substituents on the IC terminal group and that the enhanced −M effect of dicyanomethylene group lowers the LUMO energy (and, likely, to a lesser extent the HOMO energy) of γ-PSMAs, hence reducing their HOMO–LUMO gap.

Fig. 4 Effect of regioregularity on fundamental (ΔE_HL, a) and optical (ΔE_g, b) gaps, vertical electron affinities (ΔVEA, c) and exciton binding energies (ΔE_b, d) for IC- (red) and IND-terminated (blue) PSMAs. The average value of each quantity for IC- and IND-terminated PSMAs is reported.

We turn to analyzing the optical properties of the PSMAs. We find that the qualitative features of the computed absorption spectra are not affected by regioregularity (see Fig. S8 in the ESI† and discussion therein). Our calculations, however, show a clear regioregularity effect on the optical gaps of all PSMAs (Fig. 4b). Consistent with experimental data from UV-vis spectroscopy,^{19–21,23,26,27} we find that ΔE_g is positive throughout the series, indicating a smaller optical gap (and thus a bathochromic shift of the absorption wavelength) for γ-PSMAs, with an average value of 68 ± 15 meV. Upon end-group symmetrization, all IND-terminated PSMAs feature much smaller ΔE_g values (average of 7 ± 4 meV), indicating that the increased mesomeric effect of the dicyanomethylene groups also controls the optical gap of γ-PSMAs, further shifting their absorption wavelengths towards the near-infrared region. This result is particularly significant, indicating that enhanced −M effects in γ-PSMAs are a crucial factor for controlling the enhancement of the photon absorption range, which is key to improve the performance of the related all-PSCs.

Interestingly, −M effects impact significantly vertical electron affinities as well. Both δ- and γ-PSMAs have negative VEAs but the electron affinity of γ-PSMAs is lower than that of δ-PSMAs (see red bars in Fig. 4c). This result is interesting, as a high electron affinity is crucial for high-performing acceptors in all-PSCs to ensure high electron mobility and charge separation. Our data indicate that the enhanced electron affinity of γ-PSMAs could be one of the factors that boost the performance of γ-based devices. Furthermore, end-group symmetrization indicates that −M effects are likely the origin of the improved electron affinity: ΔVEA values are sizably smaller for IND-terminated PSMAs (blue bars in Fig. 4c). On average, ΔVEA decreases by roughly one order of magnitude from IC- (59 ± 17 meV) to IND-terminated (6 ± 6 meV) PSMAs, indicating that their electron affinity is controlled by conjugation length and negative mesomeric effects.

Notably, the trend observed for exciton binding energies is not as simple as that of the other optoelectronic properties. Firstly, since lower exciton binding energies are associated with an increased photovoltaic performance, allowing for a reduction of energy losses and favoring charge separation, one would expect that the more efficient γ-PSMAs exhibit smaller E_b values compared to δ-PSMAs. However, ΔE_b values for IC-terminated PSMAs (red bars, Fig. 4d) are negative in most cases, indicating on average slightly lower E_b values for δ isomers. The only exception is γ-MBTI, featuring a slightly smaller E_b value compared to δ-MBTI. End-group symmetrization affects ΔE_b (blue bars, Fig. 4d): for most acceptors its value decreases for IND-terminated PSMAs. However, this effect is not systematic: PY-Se-IND, for instance, has a higher |ΔE_b|, and ΔE_b values for MBTI and MBTI-IND are very similar. These heterogeneous trends found for the exciton binding energies may be caused by several factors. Several physical phenomena that are not accounted for in our calculations (e.g. electron–phonon coupling) can sizably affect the computed values of E_b and modify the trends reported in Fig. 4d.^39–41 Furthermore, E_b is related to the dielectric constant of the material (ε), where higher ε values correspond to lower exciton binding energies. It has been shown that, for non-fullerene SMAs, ε is linearly related to the ratio between the isotropic polarizability (α) and the molecular volume of the acceptor.⁴² We computed α for IC- and IND-terminated δ and γ isomers and we evaluated the effect of regioregularity on its value (Δα). As shown in Fig. S9 in the ESI,† while no strong correlation between Δα and ΔE_b is found, the two quantities seem to be at least qualitatively related, indicating that the isotropic polarizability of regioregular PSMAs is likely one of the factors controlling their exciton binding energy; however, the latter is affected by a multitude of factors that go beyond just mesomeric effects and are therefore difficult to disentangle and rationalize within the model discussed in the present work.

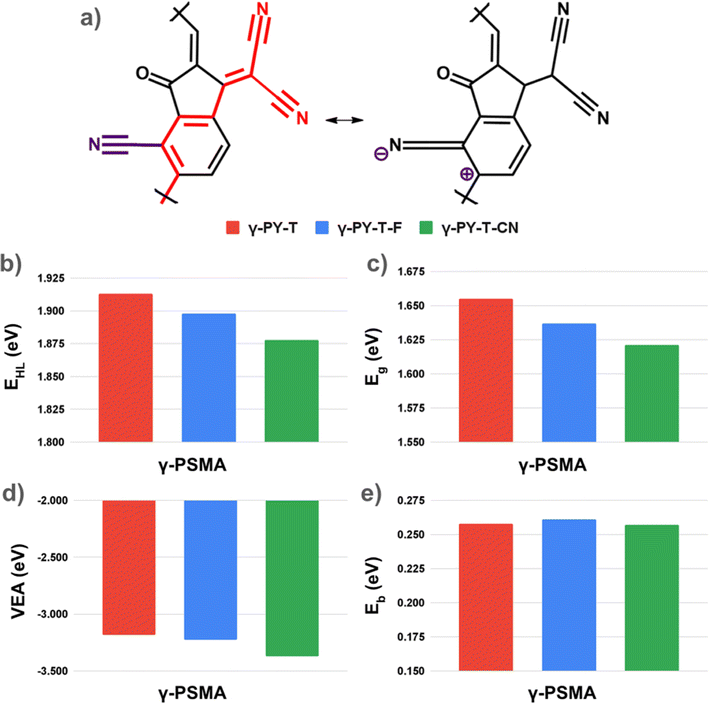
The results discussed so far establish a clear relationship between favorable mesomeric effects and the enhanced properties of γ-PSMAs, relative to δ-PSMAs, naturally raising the question of how to identify design rules and strategies for the selective functionalization of acceptor polymers, so as to enhance −M effects in the IC unit. It has been recently suggested that the engineering of the IC terminal SMA group could potentially represent a strategy to further improve the properties of functional regioregular PSMAs. So far, the main efforts in terminal group engineering consist of end-group halogenations.²⁰ In fact, halogens (e.g. fluorine), with their high electronegativity, induce a negative inductive effect that makes the terminal IC unit even more electron-deficient, thus favoring intra-molecular charge transfer in the polymeric acceptor and overall enhancing the properties of the PSMA. PY-T-F (see Fig. 2) is an example of this type of functionalization in regioregular PSMAs, where the “parent” PY-T has been fluorinated at the β-position of the terminal IC unit. Based on the results discussed in the previous section, end-group functionalization could simultaneously favor a negative inductive effect and a negative mesomeric effect, thus leading to a more efficient tuning of the optoelectronic properties of PSMAs. Halogens, however, induce a positive mesomeric (+M) effect due to their lone pair, indicating that fluorinated PSMAs exclusively take advantage of −I effects. Electron-withdrawing groups such as the cyano group are highly electronegative (thus exerting a −I effect) and, as shown in Fig. 5a, they can also exert a favorable −M effect when the IC group is functionalized in a vicinal (ortho) position with respect to the polymerization site (for instance the β position of the IC unit in γ-PSMAs).

Fig. 5 (a) Representative Lewis resonance structures showing the favorable −M effect of the cyano group in the β position of the IC unit of γ PSMAs. (b–e) Comparison of the fundamental gap, optical gap, vertical electron affinity and exciton binding energy of γ-PY-T (red), γ-PY-T-F (cyan) and γ-PY-T-CN (green).

A comparison between γ-PY-T, γ-PY-T-F (i.e. fluorination at the IC β position inducing favorable −I and unfavorable +M effects) and γ-PY-T-CN (i.e. cyanation at the IC β position inducing favorable −I and −M effects) reveals that indeed the properties of γ-PSMAs could be further improved by simultaneously accounting for −I and −M effects. As shown in Fig. 5b–d, the fundamental and optical gaps and the vertical electron affinities of γ-PY-T-CN are systematically improved upon β-cyanation not only compared with “parent” PY-T, but also compared with PY-T-F. Interestingly, once again, controlling the exciton binding energies via IC functionalization appears to be a less straightforward strategy, as indicated by the only marginal improvement of E_b upon β-cyanation (Fig. 5e). Ultimately, it is worth noting that β-cyanation and β-fluorination appear to have a comparable effect on the backbone coplanarity of the PSMAs. As shown in Fig. S10,† γ-PY-T-F, which has been experimentally reported and integrated in a high-PCE device,²⁶ displays a linker-SMA dihedral angle of 19.0°. Notably, γ-PY-T-CN, despite the bigger size of the cyano substituent, displays a very similar linker-SMA dihedral angle (23.8°), suggesting that β-cyanation could be a viable functionalization strategy also from a morphological standpoint.

To evaluate the generality of the design principle identified here, all IC-terminated γ-PSMAs shown in Fig. 2 have been functionalized with a cyano group at the β position of the IC unit and the effect of β-cyanation on their optoelectronic properties has been evaluated as follows:

ΔE^CN_HL = E^γ-CN_HL − E^γ_HL (6)

ΔE^CN_g = E^γ-CN_g − E^γ_g (7)

ΔVEA^CN = VEA^γ − VEA^γ-CN (8)

ΔE^CN_b = E^γ-CN_b − E^γ_b (9)

where the “γ” and “γ-CN” superscripts refer to real and β-functionalized γ isomers.

As expected, the data reported in Fig. 6 indicate that the effect of β-cyanation is beneficial for all γ-PSMAs. Both the fundamental and optical gaps (Fig. 6a and b, respectively) of γ-PSMAs are found to be sensitive to the β-cyano functionalization of the IC unit. The fundamental gaps of all PSMAs are smaller upon cyanation, with negative ΔE^CN_HL values throughout the series (average value of −52 ± 23 meV). We also find that LUMO energies are more sensitive than HOMO energies to the introduction of a cyano group in the β position (Fig. S11 in the ESI†), consistent with the simultaneous −I and −M effect exerted by the cyano group, which lowers the LUMO energy more than the HOMO energy. Similarly, we predict smaller optical gaps upon functionalization, with ΔE^CN_g values negative throughout the series (average value of −39 ± 25 meV). This indicates that the vicinal functionalization of the IC terminal unit is potentially able to and tune the energy levels of the acceptor, and, as a result, to further shift the light absorption region towards longer wavelengths.

Fig. 6 Effect of cyano-functionalization at the β position of the IC unit of γ-PSMAs on fundamental (a) and optical (b) gaps, vertical electron affinities (c) and exciton binding energies (d). The average value of each property is reported.

We find that the β-functionalization has a highly beneficial effect on vertical electron affinities (Fig. 6c): we computed positive ΔVEA^CN values for all γ-PSMAs, indicating a noticeable enhancement of their electron affinity upon functionalization with a cyano substituent. On average, the electron affinity of PSMAs is sensibly improved by 174 ± 16 meV. Again, in general, these results indicate that tackling simultaneously both −I and −M effects by selective end-group functionalization of γ-PSMAs can systematically improve the electron affinity of the polymeric acceptors and, in turn, their efficiency in all-PSCs.

Finally, we evaluated the effect of cyano functionalization on the exciton binding energies of γ-PSMAs (Fig. 6d). Notably, we find a smaller exciton binding energy for cyano-functionalized PSMAs, with ΔE^CN_b values consistently negative throughout the series. This result is consistent with the increased electron-withdrawing ability of the cyanated IC unit, which has been shown to be beneficial to lower E_b.⁴² However, the complexity of the trends discussed earlier for the exciton binding energies is reflected in a high variability of the magnitude of ΔE^CN_b along the series, where in several instances the −I/−M effect of the cyano group is only marginally beneficial for lowering E_b. Hence, we conclude that the selective IC functionalization combining −M and −I effects may be a viable strategy to lower the exciton binding energies of regioregular PSMAs, to extents that vary with the molecular structure of the PSMA.

Conclusions

In this work, using DFT and TDDFT simulations, we investigated the influence of regioregularity on the optoelectronic properties of experimentally reported polymerized small molecule acceptors for all-polymer solar cells. We showed that the optical and electronic properties of δ- and γ-PSMAs are controlled by the conjugation length and mesomeric effects of the substituents on the cross-conjugated terminal 1,1-dicyanomethylene-3-indanone group of the SMA core, i.e. the keto and dicyanomethylene groups, respectively. Specifically, we found that the dicyanomethylene group extends the conjugation length of the IC unit and induces stronger negative mesomeric effects along the extended conjugation pattern of γ-PSMAs, thus improving their optoelectronic properties. We computed several properties of δ- and γ-PSMAs, considering IC- and IND-terminated isomers; these properties include the extent of LUMO delocalization over the polymer backbone, fundamental and optical gaps, vertical electron affinities, and exciton binding energies. Our findings show that IC-terminated γ-PSMAs have a more delocalized LUMO, and increased π-delocalization, smaller fundamental and optical gaps, and higher vertical electron affinities compared to δ-PSMAs. For IND-terminated PSMAs, where the dicyanomethylene group is replaced by another keto group, the properties of δ- and γ-PSMAs become quantitatively undistinguishable, confirming the essential role of the dicyanomethylene group in boosting the optoelectronic properties of γ-PSMAs via favorable enhanced mesomeric effects.

Based on these results, we proposed design rules to further boost the optoelectronic properties of regioregular γ-PSMAs. Our calculations indicate that vicinal functionalization on the β position of the terminal IC unit with an electron-withdrawing group (e.g. cyano substituent) is a potentially effective way to improve the optoelectronic properties of regioregular PSMAs, including smaller optical and fundamental gaps, higher electron affinities and lower exciton binding energies. Our results also suggest that functionalizing regioregular PSMAs by simultaneously enhancing negative inductive and mesomeric effects allows for a desirable control of several of their optoelectronic and photovoltaic properties, thus providing an effective design principle to further enhance their efficiency in all-PSCs.

It is worth emphasizing that the β-cyanation of the IC unit of γ-PSMAs is the most immediate and effective way of realizing functionalization strategies that can boost the properties of PSMAs via mesomeric control. However, the principle described here is general, and it could be exploited in a multitude of different ways accessible via molecular design. For instance, a very large number of available SMAs featuring various IC derivatives have been reported in the literature.⁴³ Among those, SMAs with π-extended IC units (for instance where the phenyl group of IC is replaced with a naphthyl group),^44–48 would offer an ideal platform to tailor the properties of the resulting γ-PSMAs via mesomeric control. In fact, the π-extension offers a larger number of viable sites along the γ conjugation pattern to be favorably functionalized with electron-withdrawing substituents, thus providing multiple possibilities to boost their optoelectronic properties via joint and tunable −I/−M effects. Similarly, π-linkers, whose molecular design remains relatively unexplored, could be functionalized following an analogous principle. For instance, functionalizing the 3-position of commonly used thiophene linkers with a cyano substituent would, in principle, enable favorable and simultaneous −I/−M effects along the polymer backbone. Notably, selectively cyano-functionalized dialkoxy-bithiophene linkers have been reported to yield functional n-type conjugated polymers featuring a low-lying LUMO as a consequence of the mesomeric control exerted by the cyano group.^49–51 Ultimately, it is worth noting that cross-conjugation is ubiquitous in π-conjugated polymers: notable examples include the p-type donor polymer PM6 (ref. 52) and the n-type acceptor polymer P(NDI2OD-T2).⁵³ Since the design principles discussed here are derived from the general framework of classical mesomerism theory, we expect that analogous design strategies based on mesomeric control can be directly extended to tune the properties of a broader class of conjugated polymers for applications in organic electronics.

In sum, in this study we elucidate the systematic effect of regioregularity on the optoelectronic properties of regioregular PSMAs, while also providing practical suggestions on their molecular engineering of regioregular PSMAs. We foresee that by integrating a rational design principle based on mesomeric control with the vast library of reported building blocks, the optoelectronic properties of PSMAs may be substantially improved, paving the way for an efficiency boost of PSMA-based devices.

Computational methods

Computational protocol

All DFT calculations have been carried out with the ORCA quantum chemistry program package (5.0.3 version).⁵⁴ All geometry optimizations have been carried out in vacuo using the B3LYP hybrid exchange–correlation functional,^55–57 the double-zeta quality def2-SVP basis set,⁵⁸ and the D3 atom-pairwise dispersion correction with the Becke–Johnson damping scheme (D3BJ).^59,60 All PSMAs (i.e. δ and γ isomers, IC-terminated, IND-terminated and cyano-functionalized structures) have been simplified as dimers and the different alkyl side chains have been replaced with methyl groups to ensure the computational feasibility of the calculations. HOMO and LUMO energies have been evaluated by carrying out a single point calculation on the optimized structures using the same computational protocol but using a larger triple-zeta quality def2-TZVPP basis set. Vertical electron affinities have been calculated at the same level of theory as the energies associated to the PSMA + e⁻ → PSMA⁻ process. Optical gaps have been computed with TDDFT, by carrying out calculations on optimized structures at the same level of theory described above. For consistency with experimentally determined optical gaps in solution from previous works, the conductor-like polarizable continuum model (CPCM)⁶¹ has been used to account for solvent effects. For each PSMA, implicit solvation accounting for the solvent used experimentally for UV-vis spectra has been chosen. As a result, TDDFT calculations for IC-terminated, IND-terminated and cyano-substituted isomers of PY-2T and PY-BTz have been computed using CPCM settings for toluene, whereas all the other TDDFT calculations have been carried out using CPCM settings for chloroform.

From TDDFT and DFT data, exciton binding energies have been computed as follows:

E_b = E_HL − E_g (10)

Validation of the chosen computational setup

To ensure that the chosen computational setup and that the structural approximations introduced do not affect the accuracy of the results reported, the computed optical gaps have been compared to available literature data from UV-vis spectroscopy for regioregular PSMAs. As shown in Fig. S1 in the ESI,† the optical gaps computed well compare with experimental ones: TDDFT data are found to only slightly overestimate E_g values systematically. We also compared ΔE_g values with available experimental ones and the results indicate a qualitative agreement with similarly small variations (Fig. S2 in the ESI†), capturing the sign of the variations, which is central to the discussion here reported.

Additionally, the B3LYP functional suffers from high self-interaction error, which can lead to over-delocalization of the frontier molecular orbitals wavefunctions and errors in the estimation of fundamental gaps.^62,63 This has been reported to be detrimental for the study of optoelectronic properties of low-bandgap conjugated organic polymers, whereas gap-tuned long-range corrected hybrid functionals have been suggested for minimizing all these sources of error and obtaining more accurate results.^64–66

To ensure that the chosen setup does not affect the consistency of the results discussed, we compare the performance of B3LYP with the ω*B97XD gap-tuned long-range corrected exchange-correlation functional⁶⁷ (for which the range–separation parameter ω has been optimized via a non-empirical gap tuning procedure,⁶⁸ see the ESI for more information and Table S1† for optimal ω* values). We compared the performance of the two functionals for representative IC- and IND-terminated δ- and γ-PY-2T. As shown in Table S2,† both B3LYP and ω*B97XD capture the same relative trends upon isomerization and symmetrization, with E_HL and E_g values being smaller for γ-PY-2T compared to δ-PY-2T and predicting very close values for symmetrized δ- and γ-PY-2T-2CO. Most importantly, B3LYP and ω*B97XD predict analogous values and trends for p (i.e. the extent of LUMO delocalization along the backbone), meaning that the high self-interaction error in B3LYP does not affect the extent of LUMO delocalization along the backbone and therefore the related discussion on the relationship between mesomeric effects and electronic structure of regioregular PSMAs. Notably, however, B3LYP outperforms ω*B97XD in absolute terms: the latter predicts very large E_HL, E_g and E_b values, yielding a notably worse agreement with the available experimental data. This is most likely due to error compensation between the approximations in B3LYP and the structural approximations used in this work (i.e. using dimers models with methyl side chains). We also note that the effect of the basis set on the computed optoelectronic properties is small (less than 0.1 eV) for both functionals (see Table S3 in the ESI†). Therefore, comparative analyses with both available experimental data and long-range corrected hybrid functionals reveal that the chosen computational protocol is accurate and predictive to describe the phenomena discussed in this work for this class of polymers.

Author contributions

Diego Sorbelli: conceptualization, investigation, project administration, formal analysis, visualization, validation, writing – original draft; Yilei Wu: conceptualization, writing – review & editing; Zhenan Bao: conceptualization, writing – review & editing; Giulia Galli: conceptualization, supervision, funding acquisition, project administration, resources, writing – original draft.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The authors acknowledge the Office of Naval research under Award N00014-19-1-2453 for the financial support and the computational resources of the University of Chicago Research Computing Center. The authors thank Prof. Enrique Gomez for many useful discussions.

Notes and references

1. S. Chen, S. Jung, H. J. Cho, N. H. Kim, S. Jung, J. Xu, J. Oh, Y. Cho, H. Kim, B. Lee, Y. An, C. Zhang, M. Xiao, H. Ki, Z. G. Zhang, J. Y. Kim, Y. Li, H. Park and C. Yang, Angew. Chem., Int. Ed., 2018, 57, 13277–13282.
2. J. Choi, W. Kim, S. Kim, T. S. Kim and B. J. Kim, Chem. Mater., 2019, 31, 9057–9069.
3. C. Lee, S. Lee, G. U. Kim, W. Lee and B. J. Kim, Chem. Rev., 2019, 119, 8028–8086.
4. G. Wang, F. S. Melkonyan, A. Facchetti and T. J. Marks, Angew. Chem., Int. Ed., 2019, 58, 4129–4142.
5. Z. Genene, W. Mammo, E. Wang and M. R. Andersson, Adv. Mater., 2019, 31, 1807275.
6. B. Fan, W. Zhong, L. Ying, D. Zhang, M. Li, Y. Lin, R. Xia, F. Liu, H. L. Yip, N. Li, Y. Ma, C. J. Brabec, F. Huang and Y. Cao, Nat. Commun., 2019, 10, 1–8.
7. C. Gu, X. Su, Y. Li, B. Liu, Y. Tian, W. Tan, J. Ma and X. Bao, Mol. Syst. Des. Eng., 2022, 7, 1364–1384.
8. Y. Lin, Q. He, F. Zhao, L. Huo, J. Mai, X. Lu, C. J. Su, T. Li, J. Wang, J. Zhu, Y. Sun, C. Wang and X. Zhan, J. Am. Chem. Soc., 2016, 138, 2973–2976.
9. Z. G. Zhang, Y. Yang, J. Yao, L. Xue, S. Chen, X. Li, W. Morrison, C. Yang and Y. Li, Angew. Chem., Int. Ed., 2017, 56, 13503–13507.
10. J. Wang, P. Xue, Y. Jiang, Y. Huo and X. Zhan, Nat. Rev. Chem, 2022, 6, 614–634.
11. J. Wang, Y. Xie, K. Chen, H. Wu, J. M. Hodgkiss and X. Zhan, Nat. Rev. Phys., 2024, 6, 365–381.
12. Z. G. Zhang and Y. Li, Angew. Chem., Int. Ed., 2021, 60, 4422–4433.
13. Y. Kong, Y. Li, J. Yuan and L. Ding, InfoMat, 2022, 4, e12271.
14. W. Khelifi and C. K. Luscombe, Chem. Phys. Rev., 2023, 4, 41307.
15. T. Zhang, Y. Xu, H. Yao, J. Zhang, P. Bi, Z. Chen, J. Wang, Y. Cui, L. Ma, K. Xian, Z. Li, X. Hao, Z. Wei and J. Hou, Energy Environ. Sci., 2023, 16, 1581–1589.
16. J. Wang, Y. Cui, Y. Xu, K. Xian, P. Bi, Z. Chen, K. Zhou, L. Ma, T. Zhang, Y. Yang, Y. Zu, H. Yao, X. Hao, L. Ye and J. Hou, Adv. Mater., 2022, 34, 2205009.
17. Y. Lin, J. Wang, Z. G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, Adv. Mater., 2015, 27, 1170–1174.
18. H. Bai, Y. Wang, P. Cheng, J. Wang, Y. Wu, J. Hou and X. Zhan, J. Mater. Chem. A, 2015, 3, 1910–1914.
19. Y. Kim, H. Park, J. S. Park, J. W. Lee, F. S. Kim, H. J. Kim and B. J. Kim, J. Mater. Chem. A, 2022, 10, 2672–2696.
20. C. Gu, Y. Zhao, B. Liu, Y. Tian, Y. Li, S. Wang, S. Wen, J. Ma and X. Bao, J. Mater. Chem. C, 2023, 11, 9082–9092.
21. H. Wang, H. Chen, W. Xie, H. Lai, T. Zhao, Y. Zhu, L. Chen, C. Ke, N. Zheng and F. He, Adv. Funct. Mater., 2021, 31, 2100877.
22. C. Sun, J. W. Lee, S. Seo, S. Lee, C. Wang, H. Li, Z. Tan, S. K. Kwon, B. J. Kim and Y. H. Kim, Adv. Energy Mater., 2022, 12, 2103239.
23. Z. Luo, T. Liu, R. Ma, Y. Xiao, L. Zhan, G. Zhang, H. Sun, F. Ni, G. Chai, J. Wang, C. Zhong, Y. Zou, X. Guo, X. Lu, H. Chen, H. Yan and C. Yang, Adv. Mater., 2020, 32, 2005942.
24. T. Jia, J. Zhang, H. Tang, J. Jia, K. Zhang, W. Deng, S. Dong and F. Huang, Chem. Eng. J., 2022, 433, 133575.
25. H. Fu, Y. Li, J. Yu, Z. Wu, Q. Fan, F. Lin, H. Y. Woo, F. Gao, Z. Zhu and A. K. Y. Jen, J. Am. Chem. Soc., 2021, 143, 2665–2670.
26. H. Yu, M. Pan, R. Sun, I. Agunawela, J. Zhang, Y. Li, Z. Qi, H. Han, X. Zou, W. Zhou, S. Chen, J. Y. L. Lai, S. Luo, Z. Luo, D. Zhao, X. Lu, H. Ade, F. Huang, J. Min and H. Yan, Angew. Chem., Int. Ed., 2021, 60, 10137–10146.
27. S. Seo, C. Sun, J.-W. Lee, S. Lee, D. Lee, C. Wang, T. Ngoc-Lan Phan, G.-U. Kim, S. Cho, Y.-H. Kim, B. J. Kim, S. Seo, J. Lee, S. Lee, T. N-L Phan, G. Kim, B. J. Kim, C. Sun, Y. Kim, D. Lee, S. Cho and C. Wang, Adv. Funct. Mater., 2022, 32, 2108508.
28. C. Wang, J. Fang, C. Guan, T. Wu, X. Liu, F. Liu, C. Xiao and W. Li, ACS Appl. Mater. Interfaces, 2023, 15, 13363–13370.
29. K. N. Winzenberg, P. Kemppinen, F. H. Scholes, G. E. Collis, Y. Shu, T. B. Singh, A. Bilic, C. M. Forsyth and S. E. Watkins, Chem. Commun., 2013, 49, 6307–6309.
30. N. F. Phelan and M. Orchin, J. Chem. Educ., 1968, 45, 633–637.
31. P. A. Limacher and H. P. Lüthi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 477–486.
32. M. Gholami and R. R. Tykwinski, Chem. Rev., 2006, 106, 4997–5027.
33. M. C. Scharber and N. S. Sariciftci, Adv. Mater. Technol., 2021, 6, 2000857.
34. K. Takimiya, I. Osaka and M. Nakano, Chem. Mater., 2014, 26, 587–593.
35. Y. Li, M. Wang, Q. Zhang, Z. Wu, H. Lim, Y. Wang, H. Qin, J. Yang, C. Gao, H. Young Woo and J. Yuan, Chem. Eng. J., 2022, 428, 131232.
36. H. Yu, Y. Wang, H. K. Kim, X. Wu, Y. Li, Z. Yao, M. Pan, X. Zou, J. Zhang, S. Chen, D. Zhao, F. Huang, X. Lu, Z. Zhu and H. Yan, Adv. Mater., 2022, 34, 2200361.
37. Y. Wu, Y. Yuan, D. Sorbelli, C. Cheng, L. Michalek, H. W. Cheng, V. Jindal, S. Zhang, G. LeCroy, E. D. Gomez, S. T. Milner, A. Salleo, G. Galli, J. B. Asbury, M. F. Toney and Z. Bao, Nat. Commun., 2024, 15, 2170.
38. H. Sun, B. Liu, Y. Ma, J.-W. Lee, J. Yang, J. Wang, Y. Li, B. Li, K. Feng, Y. Shi, B. Zhang, D. Han, H. Meng, L. Niu, B. J. Kim, Q. Zheng, X. Guo, H. Sun, B. Zhang, D. Han, L. Niu, B. Liu, J. Yang, J. Wang, Y. Li, B. Li, K. Feng, Y. Shi, X. Guo, H. Meng, Y. Ma, Q. Zheng, J. Lee and B. J. Kim, Adv. Mater., 2021, 33, 2102635.
39. B. M. Savoie, N. E. Jackson, L. X. Chen, T. J. Marks and M. A. Ratner, Acc. Chem. Res., 2014, 47, 3385–3394.
40. L. Zhu, Z. Wei and Y. Yi, J. Phys. Chem. C, 2022, 126, 14–21.
41. S. Kashani, J. J. Rech, T. Liu, K. Baustert, A. Ghaffari, I. Angunawela, Y. Xiong, A. Dinku, W. You, K. Graham and H. Ade, Adv. Energy Mater., 2024, 14, 2302837.
42. L. Zhu, Y. Yi and Z. Wei, J. Phys. Chem. C, 2018, 122, 22309–22316.
43. J. Huang, H. Tang, C. Yan and G. Li, Cell Rep. Phys. Sci., 2021, 2, 100292.
44. S. M. Swick, T. Gebraad, L. Jones, B. Fu, T. J. Aldrich, K. L. Kohlstedt, G. C. Schatz, A. Facchetti and T. J. Marks, ChemPhysChem, 2019, 20, 2608–2626.
45. S. Li, L. Ye, W. Zhao, X. Liu, J. Zhu, H. Ade and J. Hou, Adv. Mater., 2017, 29, 1704051.
46. H. Feng, Y. Q. Q. Yi, X. Ke, Y. Zhang, X. Wan, C. Li and Y. Chen, Sol. RRL, 2018, 2, 1800053.
47. X. Wang, J. Han, H. Jiang, Z. Liu, Y. Li, C. Yang, D. Yu, X. Bao and R. Yang, ACS Appl. Mater. Interfaces, 2019, 11, 44501–44512.
48. H. Feng, N. Qiu, X. Wang, Y. Wang, B. Kan, X. Wan, M. Zhang, A. Xia, C. Li, F. Liu, H. Zhang and Y. Chen, Chem. Mater., 2017, 29, 7908–7917.
49. J. Huang, Y. Tang, K. Gao, F. Liu, H. Guo, T. P. Russell, T. Yang, Y. Liang, X. Cheng and X. Guo, Macromolecules, 2017, 50, 137–150.
50. H. Wang, J. Huang, M. A. Uddin, B. Liu, P. Chen, S. Shi, Y. Tang, G. Xing, S. Zhang, H. Y. Woo, H. Guo and X. Guo, ACS Appl. Mater. Interfaces, 2019, 11, 10089–10098.
51. K. Yang, Z. Chen, Y. Wang and X. Guo, Acc. Mater. Res., 2023, 4, 237–250.
52. M. Zhang, X. Guo, W. Ma, H. Ade, J. Hou, M. Zhang, X. Guo, J. Hou, W. Ma and H. Ade, Adv. Mater., 2015, 27, 4655–4660.
53. R. Steyrleuthner, R. Di Pietro, B. A. Collins, F. Polzer, S. Himmelberger, M. Schubert, Z. Chen, S. Zhang, A. Salleo, H. Ade, A. Facchetti and D. Neher, J. Am. Chem. Soc., 2014, 136, 4245–4256.
54. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
56. K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089–10094.
57. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
58. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
59. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
60. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
61. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
62. A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 194112.
63. P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 201102.
64. N. Kuritz, T. Stein, R. Baer and L. Kronik, J. Chem. Theory Comput., 2011, 7, 2408–2415.
65. L. Pandey, C. Doiron, J. S. Sears and J. L. Brédas, Phys. Chem. Chem. Phys., 2012, 14, 14243–14248.
66. T. Körzdörfer and J. L. Brédas, Acc. Chem. Res., 2014, 47, 3284–3291.
67. Y. S. Lin, G. De Li, S. P. Mao and J. Da Chai, J. Chem. Theory Comput., 2013, 9, 263–272.
68. T. Stein, H. Eisenberg, L. Kronik and R. Baer, Phys. Rev. Lett., 2010, 105, 266802.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04192e

---