Understanding the swelling behavior of Ti₃C₂T_x MXene membranes in aqueous media

Abstract

Two-dimensional (2D) lamellar MXene membranes have demonstrated ultrafast water permeance and outstanding ion rejection performance, thus showing great potential for water purification. However, as typical 2D lamellar structures, MXene membranes tend to swell in aqueous media caused by increased d-spacing, leading to deteriorated mechanical stability and reduced ion sieving efficiency. Despite several chemical and physical confinement attempts to obtain stable ion sieving performance of the membranes, there is still limited knowledge of the main cause of this swelling problem. In this systematic study, the interlayer spacing of the MXene membrane lamellar sheets was altered by intercalating different valence ions (Na⁺, Ca²⁺, and Al³⁺), then we used simultaneous in situ environmental scanning electron microscopy and in situ XRD to investigate the root cause of the swelling phenomenon of pristine and ion-intercalated Ti₃C₂T_x MXene membranes under different environmental conditions. Molecular dynamics simulations were used to fundamentally understand the structure and mobility of water in the MXene channel. As predicted using the theoretical model, the d-space decreases by increasing the charge of the ions in the solution. Trivalent cation intercalated membranes were found to collapse more easily at high temperatures, which could make such membranes suitable for water desalination membranes and temperature sensor applications. Ca and Al intercalation in the MXene membrane have provided more stability to interlayer spacing, hence causing less swelling and improved rejection of ions and other molecules. On the other hand, monovalent cation intercalated membranes were substantially more sensitive to relative humidity increase, making them less suitable for water treatment but rather attractive for humidity sensor applications. This work contributes to the rational design of stable 2D membranes for water purification and sensing applications.

---

1 Introduction

Two-dimensional (2D) nanomaterial-based membranes have attracted growing interest in many fields, including the separation of isotopes, gases, organic solvents, and charged molecules, as well as in water purification applications.^1,2 These 2D nanomaterial membranes consist of layered sheet-like structures that vary from one atom thickness up to a few micrometers in lateral dimensions and 2D channels.³ As a result, several separation applications have been improved by deploying 2D nanomaterials in high-performance membrane fabrication.

A newly emerging 2D membrane architecture is represented by 2D transition metal carbides and carbonitrides (MXenes). Generally, MXenes (M_n+1X_nT_x, where M is a transition metal, X is either carbon and/or nitrogen, and T_x is a termination group (OH⁻, O⁻, F⁻, or other groups); n = 1, 2, or 3) can be produced by selective acid etching of the group A layer from the MAX phase (where M is an early transition metal, A is an A-group element and X is C, N, B and/or P), followed by a delamination process, to create 2D sheets with a varied lateral dimension and thickness by tuning the intercalation and delamination processes.⁴ The unique properties of MXene membranes, ranging from hydrophilicity, lamellar structure, ion intercalation capacity to high surface functionality, make them attractive for aqueous phase applications, including gas separation and water purification.^2,5–8 A typical lamellar MXene membrane is usually prepared from a colloidal solution via vacuum-assisted filtration (VAF) to produce stacked sheets with controllable interlayer spacing.

Graphene oxide (GO) membranes, on the other hand, have been an ideal model for 2D membranes consisting of sub-micrometer-thick laminar structures, which are usually produced via coating or filtration processes.⁹ GO membranes can selectively permeate specific ions based on size exclusion. GO membranes primarily consist of oxygen-rich functional groups like hydroxyl (–OH), carboxyl (–COOH), and epoxy groups. These functional groups attract water molecules but do not bind them as tightly as MXene's surface terminations.

In this regard, MXene membranes are superior in the sense that a slit-like channel system acts as a pathway for charge- and size-selective ion sieving processes.^10–12

The molecular separation or ion sieving mechanism through 2D nanomaterial membranes is mainly governed by size exclusion, due to the well-defined pore sizes, lamellar arrangement, and unique mechanical properties.¹² However, in the pressure-driven filtration process, progressive intercalation of water molecules enlarges the spacing between the layers, resulting in membrane swelling and subsequent failure of the ion sieving efficiency.^13,14 A number of attempts have been realized to resolve the swelling issue of 2D membranes such as cross-linking,^15,16 building multilayer architectures,^17,18 and controlling the surface charge of the membranes.¹⁹ The last approach was achieved by coating the membrane surface with selected polyelectrolytes that exert repulsion and suppression forces against doubly charged and singly charged counter-ions, respectively, while maintaining water permeation through the membrane.¹⁹

The swelling phenomenon of 2D GO membranes was investigated by Daio et al., who observed a thickness change in the multilayered membranes using an in situ environmental scanning electron microscope (ESEM) in a humidity-controlled environment and examined the effect of water intercalation. There is a direct relationship between relative humidity and membrane thickness, the relative humidity (RH) increases as the thickness increases, and vice versa.²⁰ GO membranes are known to swell excessively, often leading to a reduction in ion rejection performance, particularly under high relative humidity as the water molecules easily penetrate between the graphene oxide layers, expanding the interlayer spacing.

In MXene membranes, the ion intercalation mechanism involves the expansion of interlayer spacing, solvent insertion, and subsequent intercalation of ions between the MXene layers. Specifically, when MXene membranes come in contact with water, they tend to swell due to the interaction between water molecules and the functional groups of the MXene lamellas.^21–23 The swelling leads to increased interlayer spacing, allowing for enhanced solvent penetration and subsequent ion intercalation. Water molecules act as a medium for the transport of ions, facilitating their movement into the MXene interlayers. Moreover, pristine MXene is susceptible to oxidation in aqueous media, which can degrade its structure and properties.

The in situ XRD of MXene intercalated with different cations showed a discontinuous d-space variation upon changing the relative humidity, as a single or a bi-layer of intercalated water molecules.²⁴ Another report proved that over a wide range of relative humidity values, the hydration process seems to have a heterogeneous water distribution between the layers even at high relative humidity. Moreover, the transition between one water and two water layers does not happen abruptly as seen in many other studies but occurs rather progressively.²⁵ Recently, the group of Balke reported a computational/experimental study to track the intercalation of aqueous Li⁺, Na⁺, K⁺, Cs⁺, and Mg²⁺ ions into Ti₃C₂ MXene, to understand their positioning between the MXene layers and their effect on capacitive energy storage.²⁶ Despite the considerable amount of research conducted on Ti₃C₂T_x MXene and its micro-scale d-space variations, there is a lack of studies examining the effect of ion intercalation on MXene membranes at the macroscale.

Herein, we investigate the effect of temperature and relative humidity (RH) changes on the stability of cation (Na⁺, Ca²⁺, and Al³⁺, respectively) intercalated Ti₃C₂T_x MXene membranes, using in situ Environmental Scanning Electron Microscopy measurement and in situ XRD. We supported our conclusions by performing first-principles molecular dynamics (FPMD) simulation of intercalated 2D MXene layers in aqueous solutions, indicating a link between the stability and membrane thickness of 2D MXene layers and the cavity radius of the intercalated ion in solution.

2 Materials and methods

2.1 Materials

Sodium chloride (NaCl), calcium chloride (CaCl₂·6H₂O), aluminum chloride (AlCl₃), hydrochloric acid (HCl), rhodamine B (RhB), methyl green zinc chloride salt, bovine serum albumin lyophilized powder, ≥96%, and lithium fluoride (LiF) and polyvinylidene fluoride (PVDF) substrates (47 mm diameter, Millipore) were purchased from Sigma-Aldrich. Ti₃AlC₂ was purchased from Y-Carbon, Ltd., Ukraine. Other chemicals were of analytical grade and used as received. Deionized (DI) water was used in all experiments.

2.2 Synthesis of delaminated (DL)-Ti₃C₂T_x MXene nanosheets

Ti₃AlC₂ (MAX) was etched using a HCl/LiF (1 g, ≥99%, Sigma) mixture to obtain multi-layered (ML) MXene following a previously reported procedure with some minor modifications.⁴ Typically, 800 mg of LiF was mixed with 10 mL of 9 M HCl under stirring, followed by a gradual addition of 500 mg of MAX powder over one hour, and the final mixture was allowed to react at 40 °C for 1 day. The resulting mixture was purified by multiple centrifugation and washing steps until a pH of 5–6 was reached. Preparation of large sheets of DL-Ti₃C₂T_x was done as described previously.²⁷ Briefly, the solution was sonicated in a water bath for an hour, then centrifuged at 3500 rpm for 1 h, followed by careful decantation to isolate the supernatant containing the colloidal DL-Ti₃C₂T_x from residual precipitate impurities.

2.3 Fabrication of free-standing ion intercalated Ti₃C₂T_x MXene membranes

Pristine and intercalated lamellar membranes were prepared by the VAF process from Ti₃C₂T_x (MXene) colloidal solutions. Typically, DL-Ti₃C₂T_x solution (20 mL, 2 mg mL⁻¹) was further diluted to 500 mL and filtered through a VAF setup on a 0.22 μm hydrophilic polyvinylidene fluoride (PVDF) substrate (47 mm diameter, Millipore) to obtain the Li-Ti₃C₂T_x lamellar membrane. Similarly, the same colloidal DL-Ti₃C₂T_x solution was diluted with 500 mL solution of 0.001 M NaCl, CaCl₂, and AlCl₃, respectively, and kept on a shaker for 1 h to allow the ions to intercalate between MXene nanosheets. Then, (Na⁺, Ca²⁺, and Al³⁺)-intercalated MXene membranes were prepared by VAF. Finally, membranes were washed 3–5 times with DI water to remove the excess salt. Finally, all prepared membranes were dried at room temperature for 24 h and labeled as Ti₃C₂T_x, Na-Ti₃C₂T_x, Ca-Ti₃C₂T_x, and Al-Ti₃C₂T_x, respectively.

2.4 Characterization

An X-Ray Diffractometer (XRD) with a Differential Scanning Calorimeter (DSC) attachment (Bruker SmartLab, Tokyo, Japan) was utilized for the in situ XRD analysis (Cu Kα radiation was used as a source of radiation). All the samples were scanned at a step size of 0.02° with a speed of 3 deg min⁻¹ at variable temperatures with no humidity control. The in situ measurement was done at 50 °C, 100 °C, 150 °C, 200 °C, 250 °C, and 300 °C. Each measurement was preconditioned for 1 h equilibration time at each temperature and 3 °C min⁻¹ ramp for stabilization.

An Environmental Scanning Electron Microscope (ESEM) 650FEG from FEI – Quanta, Brno, Czech Republic was used to examine the morphological changes in the intercalated Ti₃C₂T_x membranes with respect to temperature and relative humidity (RH). The supplied ESEM's hot and cold stages were employed for the temperature experiment from room temperature to 300 °C, and the relative humidity experiment was done from 40% to 90% RH, respectively. The samples were fixed to the stage using a Cu tape. Further, Energy-Dispersive Spectroscopy (EDS) was used for elemental mapping from Bruker.

The X-ray photoelectron spectroscopy (XPS) measurement was performed on the standard Thermo Fisher ESCALAB 250XI type XSP platform. A monochromatic Ag Kα anode X-ray beam was used with a beam energy of 1486.6 eV and an energy resolution greater than 100 meV. The XPS spectra are acquired with a 180° hemispherical electron energy analyzer with a normal emission angle and a beam incident angle of 45° to the surface normal. High-resolution Ti 2p, C 1s, O 1s, F 1s, Ca 2p, Na 1s, and Cl 2p core level spectra were taken with a pass energy of 20 eV and a step size of 0.02 eV. Sample spectra were also collected after an etching process using an Ar⁺ beam under an ion energy of 4000 kV and a raster size of 1.5 mm. The energy positions were calibrated with respect to the Fermi level at 0 eV. All the measurements were conducted at room temperature in a UHV chamber of 10⁻¹⁰ mbar. The integration of the Na⁺ peak was done by a proper fitting procedure as the Na 1s signal (Na(OH) at 1073.2 eV and NaF/NaCl at 1071.6 eV)^28,29 partially overlapped with the Ti–O₂ and Ti–C LMM Auger features.³⁰ A Talos 200X Transmission Electron Microscope (TEM) from FEI was used for characterization of the samples.

UV-vis absorption spectra were obtained using a Jasco V-670 spectrophotometer. The maximum absorption was recorded at λ_max = 554 nm, 630 nm, and 280 nm for RhB, MG, and BSA respectively. Inductively coupled plasma-optical emission spectrometry (ICP-OES) (Agilent, USA) was employed to detect cationic species, while ion chromatography (Thermo Scientific, USA) was utilized for the detection of anionic species.

2.5 First-principles molecular dynamics simulation of MXene layers in aqueous solution

First-Principles Molecular Dynamics (FPMD) simulations were performed to obtain a molecular picture of the intercalation of MXene layers with an aqueous solution of different salts. In FPMD simulations, forces are calculated on-the-fly using quantum mechanical methods to provide accurate description of the interactions in the system. Contrary to other more standard approaches based on classical and empirical force fields, FPMD grants an accurate description of both the electronic structure and forces between the crystal substrate and water.^31,32 However, FPMD comes with a computational cost that limits the time and space scales that can be addressed compared to classical MD. Two parallel MXene sheets (Ti₃C₂) were created with the exposed Ti and C terminated by –OH and –H groups, respectively. The horizontal dimensions of the MXene layers were 16.7 Å and 10.5 Å in the X and Y directions, respectively. Each MXene layer counts 248 atoms. In the case of two MXene layers in pure water, the system was solvated in a box of initial dimensions of 30, 10.64, and 40 Å in the X, Y, and Z directions, respectively, for a final total number of 1528 atoms in the system. The simulation box is periodic in all three dimensions: this creates a water channel between the two MXene layers along the X-direction, resembling 2D infinite parallel slabs along the Y-axis. Fig. S1† displays this initial configuration. Afterward, this initial structure was relaxed by geometry and cell dimension optimization. The final optimized configuration, with an initial d-space of ∼0.9 nm, was used as a starting configuration for constant pressure (1 atm) and temperature (300 K) (NpT) MD simulations. For the NpT simulations with Na⁺, Ca²⁺, and Al³⁺ solutions, the starting configurations were prepared by taking the initial snapshot of the pure water case and replacing three water molecules between the MXene layers with three cations of the same species. The cations were placed in three different locations: one fully surrounded by water molecules within the two MXene layers, one in proximity, and one separated by one water layer from the MXene hydroxylated surface: this was done in order to have three different scenarios for the cation solvation in the same (computationally expensive) FPMD run. Similar to the water run, also in the cation case, the initial structures were relaxed by geometry and cell dimension optimization. Finally, three additional and independent NpT production runs, one for each cationic species (i.e., Na⁺, Ca²⁺, and Al³⁺), were performed. During the MD production runs, the simulations box dimensions and the distance between the two MXene layers were recorded to assess the convergence of the runs.

All the FPMD runs were performed using BLYP^33–36 density functional theory as implemented in the CP2K code.³⁷ Grimme's dispersion (D3) correction was exploited,³⁸ and the TZV2P basis set was truncated at 300 Ry. While the valence electrons were explicitly considered, Goedecker–Teter–Hutter pseudopotentials were used to model core electrons. A Nose–Hoover thermostat³⁹ with a time constant of 50 femtoseconds (fs) was used to keep the temperature at 300 K, while the pressure was controlled to 1 bar with a time constant of 100 fs.

2.6 Membrane flux and rejection measurements

A dead-end filtration setup (Sterlitech, USA) with an effective filtration area of 14.6 cm² was used to measure the membrane flux and rejection at 1–12 bar. The water flux (J_w) was computed using eqn (1):where V represents the permeate volume, A represents the membrane effective area, t is the operation time, and P stands for the applied pressure.

The rejection performance of the prepared membranes was assessed using feed solutions having 50 ppm of rhodamine B (RhB), methyl green (MG), bovine serum albumin (BSA), NaCl, CaCl₂, and AlCl₃, respectively. In each filtration experiment, we used a consistent feed volume of 50 mL. This volume was selected to ensure that there was sufficient feed solution for accurate measurement of the permeated flux and rejection performance. The collected permeate volume varied slightly depending on the membrane type and its performance but generally ranged between 40 and 45 mL, and the duration of each filtration experiment was 15 minutes on average.

The rejection was computed using eqn (2):

where C_f is the feed concentration and C_p is the permeate concentration.

3. Results and discussion

3.1 Structural characterization

The structure of the as-prepared pristine and intercalated membranes was investigated by spectroscopy and microscopy analyses. The SEM image of the as-prepared DL-Ti₃C₂T_x showed a wrinkled, sheet-like structure (Fig. S1a and c†). The TEM image of DL-Ti₃C₂T_x exhibited a flat, exfoliated structure with few-layer MXene flakes (Fig. S1b†). Fig. S1d† shows the XRD pattern of DL-Ti₃C₂T_x. Acid etching of aluminum was confirmed by the disappearance of the most intense peak at 2θ = ∼39°, typical of Ti₃AlC₂ MAX (Fig. S1(e),† JCPDS number: 52-0875), in DL-Ti₃C₂T_x. Furthermore, the shift of the (002) peak to a lower angle (2θ = 6.7°) and broadening of the peak confirmed the successful formation of DL-Ti₃C₂T_x. Also, characteristic peaks of DL-Ti₃C₂T_x such as (004), (006), (008), (0010), and (0012) were observed.⁴⁰

The cross-sectional SEM image and EDS mapping of the resulting free-standing DL-Ti₃C₂T_x and ion intercalated membrane are shown in Fig. 1a–d. The flexibility of the membrane was demonstrated by mechanical folding of the film several times without breaking (see the inset of Fig. S1(c)†). EDS mapping confirms the presence of well-distributed Na⁺, Ca²⁺, and Al³⁺ cations on the surface and in between the Ti₃C₂T_x lamellar sheets. The effect of ion intercalation on the interlayer spacing of pristine DL-Ti₃C₂T_x was examined for Na-Ti₃C₂T_x, Ca-Ti₃C₂T_x, and Al-Ti₃C₂T_x membranes. XRD patterns of Ti₃C₂T_x, Na-Ti₃C₂T_x, Ca-Ti₃C₂T_x, and Al-Ti₃C₂T_x sheets are shown in (Fig. 1e). Cations can intercalate the MXene c-lattice due to the electrostatic force between the positive ions and the negatively charged MXene sheets.^24,26,41 It is important to highlight that cation intercalation is affected by different factors, such as the hydration energy, ionic radius, and water coordination number.^26,41–46 The (002) peak has shifted to lower 2θ angles, suggesting a significant expansion in the interlayer spacing of Ti₃C₂T_x in the presence of ions in between the layers in the following pattern Na-Ti₃C₂T_x < Ca-Ti₃C₂T_x < Al-Ti₃C₂T_x, indicating d-spacing with increasing ion valence and the corresponding hydration radius.

Fig. 1 SEM with superimposed EDS mapping of (a) DL-Ti₃C₂T_x, (b) Na-Ti₃C₂T_x, (c) Ca-Ti₃C₂T_x, and (d) Al-Ti₃C₂T_x. The used coloring code is for the ease of observation only. (e) XRD patterns of DL-Ti₃C₂T_x upon intercalation with Na⁺, Ca²⁺, and Al³⁺.

XPS measurement was used to probe the cation intercalation in between the sheets by recording the corresponding Na 1s, Ca 2p, and Al 2p core levels. An Ar⁺ based etching process was applied to ensure removing the physisorbed layer from the top surface, and the XPS spectra were recorded before and after the etching process (see Fig. S3, S4 and Table S1,† for the atomic percentage of different elements and the corresponding deconvolution). As indicated in Fig. S3† (left panel), the samples before etching show considerable variation in the Ti 2p, O 1s, and C 1s spectra, which is expected due to the different surface termination groups. After imposing sufficient Ar⁺ etching on the surface, the resulting XPS spectra show almost identical patterns for all the studied membranes. In particular, C 1s shows various components C–Ti, C–C/C=C, C–O and C=O before etching for all samples. While, after etching, the C=O and C–C disappeared with only a major C–Ti peak. This reflects the high purity of the inner Ti₃C₂T_x sheets that is not affected by the type of intercalated ions. Fig. 2a–c show the deconvolution of Na 1s, Ca 2p and Al 2p before and after sufficient etching, and by integration of the spectral area after appropriate Shirley background subtraction, the cation concentration was quantitatively estimated. Following an adequate etching process, the cation concentrations within the layers were determined to be 2.9% for Na⁺, 0.74% for Ca²⁺, and 0.96% for Al³⁺. These findings provide additional evidence of ion intercalation occurring between the layers and of their consistent concentration. By looking at the time evolution of the etching process in Fig. 2d–f, we notice that the cation signals mainly attenuate during the initial 40 s of the etching process and become constant during subsequent cycles, which indicate that the quantity of intercalated cations is homogeneous across the membrane's sheets.

Fig. 2 XPS measurement of the intercalated MXene membranes before and after etching. Deconvolution of (a) Na 1s, (b) Ca 2p and (c) Al 2p spectra are shown after appropriate Shirley background subtraction. A Voigt type line profile (convolution of Gaussian and Lorentzian distributions) was applied. Variation of the amount of intercalated (d) Na⁺, (e) Ca²⁺, and (f) Al³⁺ as a function of etching time, as measured by XPS.

3.2 Effect of relative humidity on membrane swelling

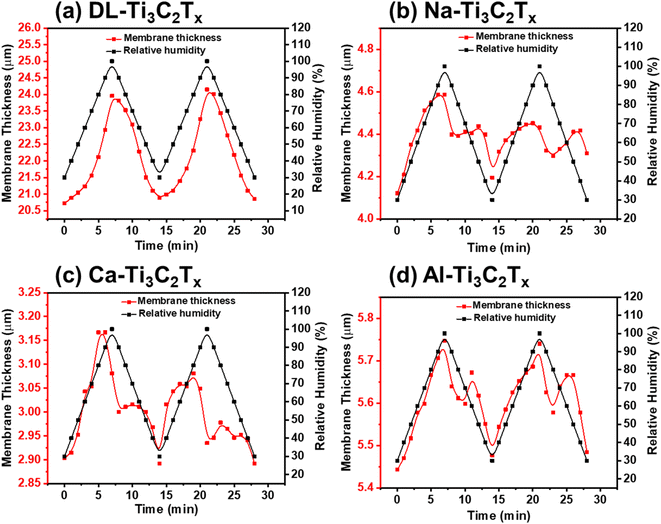
In situ scanning electron microscopy (SEM) has emerged as a powerful technique for studying materials and processes with high spatial resolution. One area of significant interest is the investigation of the behavior and performance of membranes under varying relative humidity (RH) conditions. Understanding how membranes respond to changes in RH is essential for optimizing their functionality and designing advanced materials with enhanced performance. In this context, in situ SEM coupled with controlled RH environments offers a unique opportunity to visualize and analyze the structural, morphological, and dynamic properties of membranes in real time at a micro-scale level.

In situ ESEM was used to measure the effect of RH changes on the stability of pristine DL-MXene, Na-MXene, Ca-MXene, and Al-MXene membranes, as shown in Fig. 3. Accurate measurement was achieved by fixing the focus conditions and the point of measurement on the cross-section as a reference area at different relative humidity (RH) levels. Two cycles of RH were performed, starting from 40% to 90% with 10% interval and 60 second delay to allow the saturation of the membrane between each step.

Fig. 3 In situ SEM for different intercalated MXene membranes under relative humidity from 40% (left panel) to 90% (right panel). The thickness increase values are (a) 9.8% for DL-Ti₃C₂T_x, (b) 14.0% for Na-Ti₃C₂T_x, (c) 8.6% for Ca-Ti₃C₂T_x, and (d) 4.3% for Al-Ti₃C₂T_x.

All membranes showed an increase in the interlayer spacing due to the introduction of water molecules with increasing RH. The thickness of the pristine and ion intercalated MXene membranes, as shown in Fig. 3, has increased by 9.8%, 14.0%, 8.6%, and 4.3% for DL-Ti₃C₂T_x, Na-Ti₃C₂T_x, Ca-Ti₃C₂T_x, and Al-Ti₃C₂T_x, respectively, when the RH was increased from 40% to 90%. Na-Ti₃C₂T_x reported the highest thickness increase, followed by Ti₃C₂T_x, Ca-Ti₃C₂T_x, and Al-Ti₃C₂T_x in the 40–90% RH range.

This trend could be attributed to two main reasons: first, the hydration enthalpy of the intercalated cations between the MXene layers, as the Na⁺ cation has the least hydration enthalpy (Table S5†), followed by Li⁺, Ca²⁺, and Al³⁺ cations.⁴² Secondly, higher valence cations have higher intercalation capacity due to their van der Waal bonds with surface termination between the MXene membrane layers allowing only high-ordered stable water layers to be intercalated, stabilizing the MXene membrane under varying RH.^25,47 Moreover, the adsorbed anion can also play an important role in the swelling of all membranes.⁴⁸ As is seen from other studies, the GO membrane thickness increase was much higher (18% and 14.9%) within the same relative humidity range as compared with our results for the pristine MXene membrane.^20,24,49

Our observation has been supported by other studies, indicating that cations with varying sizes and charges (such as Na⁺, K⁺, NH⁴⁺, Mg²⁺, and Al³⁺) can intercalate between Ti₃C₂T_x layers,^45,46 which can lead to the contraction or expansion of the layers under varying relative humidity, depending on the charge and hydrodynamic radius of the cation.⁴⁴ Single-valent Na⁺ can readily migrate into the interlayer of the Ti₃C₂T_x membrane and form weak intercalation with the sheets or an electrical double layer allowing for more free water molecules to seep in between the layers and thereby increase the membrane swelling. In the case of multivalent cations, Ca²⁺ and Al³⁺ have a strong tendency to intercalate with MXene sheets due to their higher electrostatic attraction. This will reduce the available space for water molecules to enter between the membrane layers, thereby reducing the membrane swelling potential.^10,26,32

The thickness variation of the membrane with RH for pristine and intercalated MXene membranes is plotted in Fig. 4.

Fig. 4 Variation of membrane thickness in response to two cycles of relative humidity for (a) DL-Ti₃C₂T_x, (b) Na-Ti₃C₂T_x, and (c) Ca-Ti₃C₂T_x, and (d) Al-Ti₃C₂T_x. All measured thickness data points are within ±0.01 μm error.

By comparing the two cycles of in situ ESEM relative humidity, an oscillation behavior is seen for all intercalated membrane sheets supporting the hydration heterogeneity theory explained by Stéphane et al.,^25,50 where layers with different hydration states coexist within the same crystals. However, the two cycles for Ca²⁺ and Al³⁺ intercalated cations have a higher hysteresis, which could be related to the small initial thickness of the corresponding membranes compared to DL-Ti₃C₂T_x and Na-Ti₃C₂T_x membranes. In order to observe the membrane's thickness variation, a video has been recorded of each of these membranes (see the ESI†).

3.3 Effect of temperature on the membrane swelling

The in situ XRD equipped with a DSC was used to correlate the changes in the (002) peak corresponding to d-spacing changes for DL-Ti₃C₂T_x, Na-Ti₃C₂T_x, Ca-Ti₃C₂T_x, and Al-Ti₃C₂T_x with temperature variation. The temperature was increased from 50 °C to 300 °C with a 50 °C step and a 1 h equilibration time at each temperature step. The XRD patterns of the MXene samples show how the 2θ values of the 002 reflection at around 5.6 and 7.4 for pristine and cation intercalated Ti₃C₂T_x represent the structural changes between mono- and double-layer hydration patterns at the nano-scale, corresponding to different c lattice (c-L) parameter patterns of pristine and ion intercalated MXene films. The (002) peak at around 2θ = 7.01 for all intercalated membranes shifts continuously to the right with the broadening of the peak as the temperature increases, indicating the loss of interlayer water molecules and consequently a decrease of the c-parameter of MXene.^24,51

It is well established that the (002) peak of MXene shifts when temperature changes, corresponding to a d-space decrease from its initial state, indicating a loss of water layers from MXene sheets.²⁵ As shown in Fig. 5, Al-Ti₃C₂T_x and Ca-Ti₃C₂T_x membranes shows the highest d-space decrease of 2.29 Å and 2.07 Å, respectively, compared to those of Na-Ti₃C₂T_x and DL-Ti₃C₂T_x membranes of 1.85 Å and 1.09 Å, when the temperature is increased from 50 °C to 300 °C. This behavior is a consequence of the valence of the intercalated cations.⁴² In fact, high valence cations are characterized by a high hydration number, hence they tend to accommodate a higher number of water molecules in their coordination shell.^52,53 Therefore, when the temperature is increased up to 100 °C, free water molecules get released from the intercalated membranes, followed by the release of coordinated water molecules at temperatures above 100 °C. Since the high valence cations exhibit stronger intercalation with the negatively charged functional groups between the layers of the MXene membrane as compared with low valence cations, the loss of coordination water causes the interlayer spaces to collapse more predominately in the case of Al-Ti₃C₂T_x and Ca-Ti₃C₂T_x membranes.⁵⁴

Fig. 5 XRD patterns of in situ XRD, where the temperature has been varied from 50 °C to 300 °C for as-prepared (a) DL-Ti₃C₂T_x, (b) Na-Ti₃C₂T_x, (c) Ca-Ti₃C₂T_x, and (d) Al-Ti₃C₂T_x membranes.

In Fig. 5, distinct and sharper peaks are observed for DL-Ti₃C₂T_x and Na-Ti₃C₂T_x membranes at 50 °C, while the peaks for Ca-Ti₃C₂T_x and Al-Ti₃C₂T_x membranes appear less defined. This observation suggests a correlation between the presence of monovalent cations and enhanced homogeneity of the MXene membrane, when compared to membranes with higher valence cations.^24,41,43 As illustrated in Fig. 6, generally, the d-spacing decreases in a similar fashion for the three cations intercalated membranes, although it seems to follow a trend based on the cationic valence (Na⁺ < Ca²⁺ < Al³⁺), which was observed in another study related to relative humidity.^24,55

Fig. 6 d-Space (calculated from XRD analysis) variation between 50 and 300 °C.

The effect of increasing temperature on the pristine and intercalated MXene membranes was investigated using in situ ESEM with temperature stage, keeping the same measuring conditions used in the in situ ESEM measurement with RH, with temperature ranging from 50 °C to 300 °C, at 50 °C steps with a 60 second delay to stabilize at each step. The membranes were kept at room temperature in a dry environment for 24 hours before the experiment. As observed in Fig. 7, the cross-sectional shrinkage percentage for the Al-Ti₃C₂T_x membrane between 50 °C and 300 °C was the highest among other intercalated MXene membranes with a value of 17.5%. Na-Ti₃C₂T_x was found to be the most stable membrane at high temperatures, followed by the DL-Ti₃C₂T_x membrane, Ca-Ti₃C₂T_x membrane, and Al-Ti₃C₂T_x membrane with percentages of 4.13%, 4.8%, 7.07%, and 17.5%, respectively. These results are in good agreement with the in situ XRD heating experiment, where the trend of d-space decrease was Al-Ti₃C₂T_x > Ca-Ti₃C₂T_x > DL-Ti₃C₂T_x > Na-Ti₃C₂T_x. Therefore, a high valence intercalated MXene membrane could be suitable for high temperature sensing applications.

Fig. 7 In situ SEM for different intercalated MXene membranes at temperatures from 50 to 300 °C. The thickness decrease values are (a) −16.08% for DL-Ti₃C₂T_x, (b) −4.13% for Na-Ti₃C₂T_x, (c) −7.07% for Ca-Ti₃C₂T_x, and (d) −17.53% for Al-Ti₃C₂T_x.

3.4 Computational simulations

FPMD simulations provide a molecular picture for the 2D MXene layers intercalated with different cations in aqueous media (Fig. 8). As described in the Methodology section, for each cation, a separate FPMD was performed placing three identical cations in three different starting locations, which are indicated in yellow in Fig. 8a, maximizing the number of solvation scenario observable within the same FPMD runs. During the limited time scale of 3 ps, ions did not diffuse significantly from their initial position. However, Fig. 8b shows the d-space between the two MXene layers as a function of time for the 4 FPMD runs (one with no ion and the other three with Na⁺, Ca²⁺ and Al³⁺ in solution, respectively), and all the profiles equilibrate within ∼2 ps. In the case of Ca²⁺ and Al³⁺, there is an initial transient oscillation of ∼0.2 nm height: this was due to the initial configurations in which water molecules were replaced by (three) di- or (three) tri-valent ions, perturbing the system. As observed in Fig. 8b, the contraction (or expansion) of the d-space equilibrates quite rapidly. This implies that, in the case of ion diffusion from the bulk solution into the water channel formed by the two MXene layers, the shirking or swelling of the layers is expected to be quite instantaneous, i.e., within 2 ps.

Fig. 8 Panel (a): Initial snapshot from the FPMD trajectory of Na⁺ solution. Atom color code: Na⁺(blue), Ti (pink), C (gray), O (red) and H (white). Identical snapshots, but with Ca²⁺ and Al³⁺ ions, were used for the simulations with other cations. The intercalated ions are labelled 1, 2, and 3, respectively, in yellow. Panel (b): d-space between the two MXene layers in the pure water case (blue line) and in the case of Na⁺, Ca²⁺ and Al³⁺ aqueous solutions (red, green and blue lines, respectively) as a function of the simulation time. The vertical orange dashed line indicates the 2 ps time, from which statistics is collected.

The average d-spacing observed from the FPMD runs after equilibration (i.e., 2 ps) is reported in Table 1. The d-space decreases by increasing the charge of the ions in solution, with differences among the cations that are larger than the statistical uncertainties. It is difficult to make a quantitative comparison between experimental and FPMD results because water between the membranes is not homogeneously distributed in the experimental case, plus the ion concentration is different. Moreover, it is difficult to map experimental RH with an exact number of water molecules in the simulation box. Nevertheless, it is encouraging to see the experimental trend for membrane thicknesses at high RH, which more closely resemble the computational starting conditions in Fig. 8a, somehow matching the computational d-space trend as a function of the cationic valence in Fig. 8b. A recent computational/experimental study also revealed a stronger interaction, hence a smaller d-space, for polyvalent cations (e.g., Mg²⁺) with respect to monovalent cations (Li⁺, Na⁺, K⁺, and Cs⁺).²⁶ Interestingly, solvated magnesium and cesium cations had the tendency to stay halfway between the MXene sheets, whereas smaller cations partially dehydrated and adhered to one surface of the MXene.

Table 1 Distance between the two MXene layers (i.e., d-space) and distance from the ions to the nearest water oxygen, d_ion–O (nm), observed in the FPMD simulations for each of the cations labelled in Fig. 8a. Experimental values were obtained from Marcus ion compilation⁵⁶

	d-Space (nm)	d ion–O (nm)
Na^+	0.8188 ± 0.0086	(1) 0.2254 ± 0.0065
		(2) 0.2202 ± 0.0042
		(3) 0.2214 ± 0.0077
Ca^2+	0.7927 ± 0.0113	(1) 0.2307 ± 0.0037
		(2) 0.2305 ± 0.0043
		(3) 0.2260 ± 0.0044
Al^3+	0.7729 ± 0.0060	(1) 0.1781 ± 0.0030
		(2) 0.1711 ± 0.0020
		(3) 0.1810 ± 0.0035

---

The FPMD trajectories can provide more physicochemical insights for the observed d-space with different cations. Table 1 reports the average distance, d_ion–Ow, between the three intercalated ions labeled in Fig. 8a and the nearest oxygen (i.e., water oxygen or the oxygen belonging to the hydroxylated MXene surface), which defines a radius for a cavity region around the ion where water is excluded.⁵⁷

Results shown in Fig. 8 suggest the contribution of an entropic term driving the membrane shirking, which complements the literature showing an enthalpic contribution originating from the electrostatic attraction between the negatively charged MXene surface and the highly charged cations leading to the compression of interlayer spacing and shrinkage of the membrane in the z-direction.¹⁰ Both entropic and enthalpic terms govern the d-space between MXene layers intercalated in saline solutions, but the relative importance of one term over the other likely depends on the environmental conditions, such as the amount of water present in the system. The correlation between the amount of water contained and the hydration enthalpy of the intercalated cations has been experimentally observed by the group of Barsoum.²⁴ Whereas, under wet conditions, the solvent shields the electrostatic interaction between cations and the negatively charged MXene surface, so the cost of solvent re-organization may be dominant. Under dry or low humidity conditions, a direct interaction between the cations and the surface of MXene is mostly driven by enthalpic contribution. Whereas under wet conditions, the solvent re-organization energy may be dominant, most likely because the solvent shields the electrostatic interaction between cations and the negatively charged MXene surface. Notably the ionic hydration enthalpies for the cations studied in this work follow the trend: Al³⁺ > Ca²⁺ > Na⁺.⁴²

3.5 Ion rejection performance

The above results suggest that multivalent cations intercalated in the MXene membrane are better suited for applications that require low swelling and stable MXene films under high RH, such as membrane desalination and water dialysis.³² On the other hand, monovalent Na-Ti₃C₂T_x combines high water intake capacity with stable response to RH variation, which makes such membranes good candidates for sensor applications⁴³ and more conveniently humidity sensors benefiting from the electric properties of MXene.^58,59 As shown in another report, when K⁺ and Mg²⁺ are intercalated between the MXene layers, the water intake was increased significantly, making the K-intercalated MXene membrane an excellent model for humidity sensor applications.⁴⁷ To validate this hypothesis, we have tested the membranes for sieving of organic molecules and ions.

Organic fouling is one of the main challenges in the membrane separation process caused by the adsorption of organic molecules on the membrane surface. The prepared membranes (pristine MXene, Na-MXene, Ca-MXene, and Al-MXene) were tested for the rejection of different single-solute feed solutions, including RhB, MG, and BSA, as well as NaCl, CaCl₂, and AlCl₃ salts. RhB, MG, and BSA were used to determine the molecular weight cut-off (MWCO) of the membranes. As seen in Fig. S56,† the MWCO values of pristine Ti₃C₂T_x and Na-Ti₃C₂T_x are above 480 Da, while those of Ca-Ti₃C₂T_x and Al-Ti₃C₂T_x are below 380 Da. The rejection of BSA was almost 100% for all tested membranes, as shown in Fig. 9a. Interestingly, the highest rejection of RhB and MG was achieved by the Al-Ti₃C₂T_x membrane with 94% and 97%, while those achieved by the Na-Ti₃C₂T_x membrane were only 72% and 79%, respectively. Also, the rejection of different ions was studied, as shown in Fig. 9c. The Al-Ti₃C₂T_x membrane showed the highest rejection of 14%, 59%, and 70% for NaCl, CaCl₂, and AlCl₃ salts, respectively. The rejection of all the membranes against cations increases in the order of Na-Ti₃C₂T_x < pristine DL-Ti₃C₂T_x < Ca-Ti₃C₂T_x < Al-Ti₃C₂T_x membranes. This trend supports the discussed mechanism for cation permeation between the MXene layers, where Na⁺ causes MXene layers to expand in the Na-MXene membrane leading to a lower rejection, while the presence of intercalated cations in Ca-Ti₃C₂T_x and Al-Ti₃C₂T_x provides more stability to interlayer spacing, hence causing less swelling and therefore improving the rejection performance of the membranes. Non-swelling MXene membranes prepared by the intercalation of Al³⁺ ions have been previously reported in the literature, demonstrating excellent stability in aqueous solutions and high rejection of NaCl (∼89.5–99.6%) with fast water fluxes.³²

Fig. 9 (a) Rejection percentage of RhB, MG, and BSA; (b) permeance of water, RhB, MG, and BSA solutions; (c) rejection percentage of NaCl, CaCl₂, and AlCl₃; (d) permeance of water, NaCl, CaCl₂, and AlCl₃ solutions.

The membrane flux measured during the rejection of RhB, MG, and BSA ranges from 246 to 302 L m⁻² h⁻¹ bar⁻¹, with the highest flux for Na-Ti₃C₂T_x and the lowest for Al-MXene. In general, the water permeance of the membranes increases in the order of Al-Ti₃C₂T_x < Ca-Ti₃C₂T_x < pristine MXene < Na-Ti₃C₂T_x membranes. A similar pattern was observed during the sieving of salt ions (NaCl, CaCl₂, and AlCl₃). Na-Ti₃C₂T_x shows the highest permeance values, with 371 L m⁻² h⁻¹ bar⁻¹ for NaCl, 369 L m⁻² h⁻¹ bar⁻¹ for CaCl₂, and 339 L m⁻² h⁻¹ bar⁻¹ for AlCl₃. For the pristine MXene membrane, the high permeance values are as follows: approximately 342 L m⁻² h⁻¹ bar⁻¹ for NaCl, 335 L m⁻² h⁻¹ bar⁻¹ for CaCl₂, and 311 L m⁻² h⁻¹ bar⁻¹ for AlCl₃ against 345 L m⁻² h⁻¹ bar⁻¹ for deionized water. Moreover, Ca-Ti₃C₂T_x and Al-Ti₃C₂T_x follow a similar trend with permeance values of approximately 290 and 273 L m⁻² h⁻¹ bar⁻¹ for NaCl, 282 and 265 L m⁻² h⁻¹ bar⁻¹ for CaCl₂, and 273 and 248 L m⁻² h⁻¹ bar⁻¹ for AlCl₃, respectively. These results indicate that all types of MXene membranes maintain high permeance for NaCl, with slightly reduced values for CaCl₂ and further reduced values for AlCl₃, reflecting the increasing ion charge and its impact on membrane performance, in good agreement with the ion rejection performances discussed above.

The membrane flux measurements further support the proposed membrane swelling behavior. Indeed, the Na⁺ in the Na-MXene membrane is responsible for the expansion of the MXene layers, hence the highest permeance, whereas the superior stability demonstrated for Ca-Ti₃C₂T_x, and in particular Al-Ti₃C₂T_x membranes is responsible for the lower permeance against the tested salts. The same trend has been reported by Ren et al., where the permeation rate of cations through Ti₃C₂T_x membranes followed the order Na⁺ > Ca²⁺ > Al³⁺.¹⁰ We further evaluated the stability of Al-Ti₃C₂T_x at different times and pressures. As seen in Fig. S6a,† the rejection variation was stable over 72 h, within 4%, and 9% fluctuation for Ca²⁺ and BSA, respectively. This is in agreement with the previously reported observation by Ding et al., where Al-intercalated MXene showed rejection performance for up to 400 h.³² The Al-Ti₃C₂T_x membrane also demonstrated stable flux with pressure up to 7 bar in the dead-end setup, after which a 3-fold increase was observed most likely due to mechanical damage to the membrane (see Fig. S6b†). This highlights the need to improve the mechanical strength of MXene membranes at higher pressures. Stabilizing the interlayer spacing with conjugated nanosheets⁶⁰ or metal–polymer coordination^61,62 is another tactic to regulate the nanosheet spacing for controlling the interlayer spacing in the membranes and enforcing mechanical stability. Comparatively, the flux for our intercalated membranes ranged between 294 and 377 L m⁻² h⁻¹, with Ca²⁺ and Al³⁺ showing a slightly reducing flux due to stronger ion interactions, similar to the literature trends for high-valence ions (see Table S6†).

MXene membranes exhibit higher selectivity for multivalent ions (Mg²⁺ and Al³⁺) over monovalent ions (Na⁺) due to strong electrostatic interactions and their narrower tunable interlayer spacing compared to GO membranes.^10,63 GO membranes display moderate selectivity between monovalent and divalent ions due to the size exclusion mechanism but struggle with fine-tuning ion sieving compared to MXenes. GO membranes exhibit high Na⁺/Mg²⁺ and Na⁺/Ca²⁺ selectivity due to their layered structure, but the lack of tunability in interlayer spacing limits their performance in high-salinity environments.⁶⁴ Nevertheless, studies demonstrated that fixing the nanochannel diameters of conjugated 2D materials like MXene and GO led to improved ion pair selectivity, particularly for Na⁺/Ca²⁺, Li⁺/Mg²⁺, and Na⁺/Mg²⁺, which can optimize the selectivity and flux in desalination processes.^65,66

4 Conclusions

In this study, we have employed in situ environmental scanning electron microscopy, in situ XRD, and molecular dynamics simulations to explore the swelling behavior and mechanical stability of pristine and intercalated Ti₃C₂T_x MXene. Our findings indicated that intercalation with multivalent cations (Ca²⁺ and Al³⁺) significantly enhances the stability of the MXene membranes by reducing the interlayer spacing, thus mitigating swelling. This stabilization is crucial for applications requiring consistent ion-sieving performance and mechanical integrity, such as water desalination and dialysis. In contrast, monovalent cation (Na⁺) intercalated membranes exhibited higher water intake and sensitivity to humidity changes. Na-Ti₃C₂T_x had the highest swelling of +14.0%, followed by Ca-Ti₃C₂T_x and Al-Ti₃C₂T_x in the 40–90% RH range, making them more suitable for humidity sensor applications.

The rejection performance tests demonstrated that Al-MXene membranes achieved the highest rejection rates for organic molecules (RhB and MG) and salts (NaCl, CaCl₂, and AlCl₃), correlating with their improved structural stability. These findings suggest that the swelling of MXene membranes can be effectively controlled through selective ion intercalation, rendering this class of 2D-nanomaterial membranes more efficient for water purification and sensor technologies.

While these structural observations are important, we understand that correlating this with membrane performance (i.e., water flux and ion rejection) under high-temperature filtration conditions would significantly enhance the study. In particular, the stability of the membranes at elevated temperatures suggests potential for filtration applications in thermally challenging environments, such as high-temperature desalination.

In summary, this study can guide the rational design of ion-intercalated 2D MXene membranes toward understanding the membrane behavior in aqueous environments and provide a foundation for engineering application-specific 2D membranes.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Qatar Environment and Energy Research Institute (QEERI, at Hamad Bin Khalifa University) for supporting this research. The authors would also like to thank Dr Ravi Pandey for technical support and the core lab staff at the Qatar Energy and Environment Research Institute (QEERI), namely, Mr Janarthanan Ponraj for material characterization support. For HPC resources and services, we acknowledge the Research Computing group in Texas A&M University at Qatar, founded by the Qatar Foundation for Education, Science and Community Development, and the use of Qatar Environment and Energy Research Institute (QEERI) HPC under Project ID HPC-P21003.

References

1. Z. Ahmed, F. Rehman, U. Ali, A. Ali, M. Iqbal and K. H. Thebo, ChemBioEng Rev., 2021, 8, 110–120.
2. Y. A. J. Al-Hamadani, B.-M. Jun, M. Yoon, N. Taheri-Qazvini, S. A. Snyder, M. Jang, J. Heo and Y. Yoon, Chemosphere, 2020, 254, 126821.
3. H. Zhang, ACS Nano, 2015, 9, 9451–9469.
4. M. Ghidiu, M. R. Lukatskaya, M. Q. Zhao, Y. Gogotsi and M. W. Barsoum, Nature, 2014, 516, 78–81.
5. C. F. Carolin, P. S. Kumar, A. Saravanan, G. J. Joshiba and M. Naushad, J. Environ. Chem. Eng., 2017, 5, 2782–2799.
6. L. Huang, L. Ding and H. Wang, Small Sci., 2021, 1, 2100013.
7. O. Kwon, Y. Choi, J. Kang, J. H. Kim, E. Choi, Y. C. Woo and D. W. Kim, Desalination, 2022, 522, 115448.
8. S. Hong, F. Al Marzooqi, J. K. El-Demellawi, N. Al Marzooqi, H. A. Arafat and H. N. Alshareef, ACS Mater. Lett., 2023, 5, 341–356.
9. G. Liu, W. Jin and N. Xu, Chem. Soc. Rev., 2015, 44, 5016–5030.
10. C. E. Ren, K. B. Hatzell, M. Alhabeb, Z. Ling, K. A. Mahmoud and Y. Gogotsi, J. Phys. Chem. Lett., 2015, 6, 4026–4031.
11. L. Ding, Y. Wei, Y. Wang, H. Chen, J. Caro and H. Wang, Angew Chem. Int. Ed. Engl., 2017, 56, 1825–1829.
12. G. Liu, J. Shen, Q. Liu, G. Liu, J. Xiong, J. Yang and W. Jin, J. Membr. Sci., 2018, 548, 548–558.
13. S. Zheng, Q. Tu, J. J. Urban, S. Li and B. Mi, ACS Nano, 2017, 11, 6440–6450.
14. O. Alnoor, T. Laoui, A. Ibrahim, F. Kafiah, G. Nadhreen, S. Akhtar and Z. Khan, Membranes, 2020, 10, 292.
15. W.-S. Hung, C.-H. Tsou, M. De Guzman, Q.-F. An, Y.-L. Liu, Y.-M. Zhang, C.-C. Hu, K.-R. Lee and J.-Y. Lai, Chem. Mater., 2014, 26, 2983–2990.
16. S. Zheng, Q. Tu, M. Wang, J. J. Urban and B. Mi, ACS Nano, 2020, 14, 6013–6023.
17. Y. Zhao, C. Zhou, J. Wang, H. Liu, Y. Xu, J. W. Seo, J. Shen, C. Gao and B. Van der Bruggen, J. Mater. Chem. A, 2018, 6, 18859–18864.
18. Y. Zhao, W. Shi, B. Van der Bruggen, C. Gao and J. Shen, Adv. Mater. Interfaces, 2018, 5, 1701449.
19. M. Zhang, K. Guan, Y. Ji, G. Liu, W. Jin and N. Xu, Nat. Commun., 2019, 10, 1253.
20. T. Daio, T. Bayer, T. Ikuta, T. Nishiyama, K. Takahashi, Y. Takata, K. Sasaki and S. Matthew Lyth, Sci. Rep., 2015, 5, 11807.
21. A. Iakunkov, U. Lienert, J. Sun and A. V. Talyzin, Adv. Sci., 2024, 11, 2307067.
22. A. Iakunkov, A. Nordenström, N. Boulanger, C. Hennig, I. Baburin and A. V. Talyzin, Nanoscale, 2022, 14, 10940–10949.
23. X. Liu, N. Graham, W. Yu, Y. Shi, K. Sun and T. Liu, J. Membr. Sci., 2022, 654, 120469.
24. M. Ghidiu, J. Halim, S. Kota, D. Bish, Y. Gogotsi and M. W. Barsoum, Chem. Mater., 2016, 28, 3507–3514.
25. S. Célérier, S. Hurand, C. Garnero, S. Morisset, M. Benchakar, A. Habrioux, P. Chartier, V. Mauchamp, N. Findling, B. Lanson and E. Ferrage, Chem. Mater., 2018, 31, 454–461.
26. Q. Gao, W. Sun, P. Ilani-Kashkouli, A. Tselev, P. R. C. Kent, N. Kabengi, M. Naguib, M. Alhabeb, W.-Y. Tsai, A. P. Baddorf, J. Huang, S. Jesse, Y. Gogotsi and N. Balke, Energy Environ. Sci., 2020, 13, 2549–2558.
27. M. Alhabeb, K. Maleski, B. Anasori, P. Lelyukh, L. Clark, S. Sin and Y. Gogotsi, Chem. Mater., 2017, 29, 7633–7644.
28. P. H. Citrin, Phys. Rev. B: Solid State, 1973, 8, 5545–5556.
29. V. I. Nefedov, Y. V. Salyn, G. Leonhardt and R. Scheibe, J. Electron Spectrosc. Relat. Phenom., 1977, 10, 121–124.
30. J. E. Castle, Surf. Interface Anal., 1984, 6, 302.
31. D. Marx and J. Hutter, Ab Initio Molecular Dynamics, Cambridge University Press, Cambridge, 2009.
32. L. Ding, L. Li, Y. Liu, Y. Wu, Z. Lu, J. Deng, Y. Wei, J. Caro and H. Wang, Nat. Sustainability, 2020, 3, 296–302.
33. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
34. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
35. R. Lang, X. Du, Y. Huang, X. Jiang, Q. Zhang, Y. Guo, K. Liu, B. Qiao, A. Wang and T. Zhang, Chem. Rev., 2020, 120, 11986–12043.
36. F. Pietrucci and A. M. Saitta, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15030.
37. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
39. S. NosÉ, Mol. Phys., 2002, 100, 191–198.
40. G. Zou, Z. Zhang, J. Guo, B. Liu, Q. Zhang, C. Fernandez and Q. Peng, ACS Appl. Mater. Interfaces, 2016, 8, 22280–22286.
41. N. C. Osti, M. Naguib, A. Ostadhossein, Y. Xie, P. R. Kent, B. Dyatkin, G. Rother, W. T. Heller, A. C. van Duin, Y. Gogotsi and E. Mamontov, ACS Appl. Mater. Interfaces, 2016, 8, 8859–8863.
42. D. W. Smith, J. Chem. Educ., 1977, 54, 540.
43. H. J. Koh, S. J. Kim, K. Maleski, S. Y. Cho, Y. J. Kim, C. W. Ahn, Y. Gogotsi and H. T. Jung, ACS Sens., 2019, 4, 1365–1372.
44. J. Come, J. M. Black, M. R. Lukatskaya, M. Naguib, M. Beidaghi, A. J. Rondinone, S. V. Kalinin, D. J. Wesolowski, Y. Gogotsi and N. Balke, Nano Energy, 2015, 17, 27–35.
45. O. Mashtalir, M. Naguib, V. N. Mochalin, Y. Dall'Agnese, M. Heon, M. W. Barsoum and Y. Gogotsi, Nat. Commun., 2013, 4, 1716.
46. M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall'Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Science, 2013, 341, 1502–1505.
47. E. S. Muckley, M. Naguib, H. W. Wang, L. Vlcek, N. C. Osti, R. L. Sacci, X. Sang, R. R. Unocic, Y. Xie, M. Tyagi, E. Mamontov, K. L. Page, P. R. C. Kent, J. Nanda and I. N. Ivanov, ACS Nano, 2017, 11, 11118–11126.
48. C. A. Voigt, M. Ghidiu, V. Natu and M. W. Barsoum, J. Phys. Chem. C, 2018, 122, 23172–23179.
49. T. Bayer, S. R. Bishop, M. Nishihara, K. Sasaki and S. M. Lyth, J. Power Sources, 2014, 272, 239–247.
50. M. S. Whittingham, Mater. Res. Bull., 1974, 9, 1681–1689.
51. Z. Lin, P. Rozier, B. Duployer, P.-L. Taberna, B. Anasori, Y. Gogotsi and P. Simon, Electrochem. Commun., 2016, 72, 50–53.
52. G. A. Moldoveanu and G. P. Demopoulos, J. Chem. Technol. Biotechnol., 2015, 90, 686–692.
53. M. Khorshidi, N. Lu and A. Khorshidi, Vadose Zone J., 2016, 15, 1–12.
54. M. Seredych, C. E. Shuck, D. Pinto, M. Alhabeb, E. Precetti, G. Deysher, B. Anasori, N. Kurra and Y. Gogotsi, Chem. Mater., 2019, 31, 3324–3332.
55. N. Shpigel, M. D. Levi, S. Sigalov, T. S. Mathis, Y. Gogotsi and D. Aurbach, J. Am. Chem. Soc., 2018, 140, 8910–8917.
56. Y. Marcus, Biophys. Chem., 1994, 51, 111–127.
57. T. T. Duignan, D. F. Parsons and B. W. Ninham, J. Phys. Chem. B, 2013, 117, 9421–9429.
58. Z. Wang, H. Kim and H. N. Alshareef, Adv. Mater., 2018, 30, e1706656.
59. E. S. Muckley, M. Naguib and I. N. Ivanov, Nanoscale, 2018, 10, 21689–21695.
60. Y. Zong, Q. Long, L. Chen, A. Samadi, H. Luo, K. Liang, X. Wan, F. Liu, Y. Chen, Z. Zhang and S. Zhao, J. Membr. Sci., 2024, 693, 122328.
61. R. Hardian, P. Pogany, Y. M. Lee and G. Szekely, J. Mater. Chem. A, 2021, 9, 14400–14410.
62. L. Wang, R. Zhang, X. Tian, J. Ye, J. Dai and J. Pan, J. Membr. Sci., 2024, 695, 122454.
63. F. Shi, J. Sun, J. Wang, M. Liu, Z. Yan, B. Zhu, Y. Li and X. Cao, J. Membr. Sci., 2021, 620, 118850.
64. R. K. Joshi, P. Carbone, F. C. Wang, V. G. Kravets, Y. Su, I. V. Grigorieva, H. A. Wu, A. K. Geim and R. R. Nair, Science, 2014, 343, 752–754.
65. J. Wang, Z. Zhang, J. Zhu, M. Tian, S. Zheng, F. Wang, X. Wang and L. Wang, Nat. Commun., 2020, 11, 3540.
66. S. Hong, M. Di Vincenzo, A. Tiraferri, E. Bertozzi, R. Górecki, B. Davaasuren, X. Li and S. P. Nunes, Nat. Commun., 2024, 15, 3160.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04079a

‡ These authors contributed equally.

---