Mechanistic insights into the origin of the oxygen migration barrier

Abstract

Oxygen ion conductors require high temperatures to exhibit the high ion conductivity needed for practical use. In this work, we related oxygen vacancy formation energy and migration barrier to the electronic structure of perovskites using ab initio simulations. The vacancy formation energy increases with the increasing energy penalty for transferring electrons from oxygen to the highest filled metal states. On the other hand, the migration barrier increases with larger electronic energy penalty for screening the charge that accumulates around the oxygen vacancy. Bringing localized filled electronic states associated with the oxygen vacancy closer to the conduction band or increasing the metal–oxygen band overlap can decrease charge accumulation in the oxygen vacancy and reduce the migration barrier. By investigating the changes in the electronic structure during oxygen migration, the critical role of increasing the charge screening capability of the host lattice local environment in decreasing the migration barrier was further highlighted. Our findings provide new insights into lowering the migration barrier in oxygen ion conductors and trends towards accelerating their discovery.

---

Introduction

Oxygen ion conductors are central to numerous electrochemical devices ranging from solid oxide fuel cells^1,2 and electrolyzers,³ to sensors^4,5 and separation membranes.⁶ Unfortunately, the majority of the commercially available oxygen ion conductors such as Yttria-stabilized zirconia (YSZ)⁷ and Sr-, Mg-substituted LaGaO₃ (LSGM)^8,9 exhibit high oxygen ion conductivity (e.g., >0.1 S cm⁻¹) only at high temperatures (>1000 °C for YSZ⁷ and >800 °C for LSGM^8,9). As a result, solid oxide electrochemical cells must operate at high temperatures (>800 °C), which cause material degradation, difficulty in sealing, and other technological challenges that ultimately lead to high costs and reduced lifetime.^10–13 Achieving an oxygen ion conductivity of 0.1 S cm⁻¹ at lower temperatures would increase the durability and lower the cost of electrochemical devices and hence render them more viable technological solutions. Several new families of oxygen ion conductors have been reported with promising values of oxygen ion conductivity, including lanthanum-molybdenum oxides (LAMOX) (La₂Mo₂O₉, 6 × 10⁻² S cm⁻¹ at 800 °C (ref. 14)), Dion-Jacobson phases (CsBi₂Ti₂NbO_10−x, ∼0.1 S cm⁻¹ at 800 °C (ref. 15)), apatite (La_9.50(Ge_0.916Al_0.083O₄)₆O_2.0, 0.16 S cm⁻¹ at 800 °C (ref. 16)), layered strontium silicates (Sr_0.8K_0.2Si_0.5Ge_0.5O_2.9, 7.4 × 10⁻³ S cm⁻¹ at 600 °C (ref. 17)), perovskites derived from Na_0.5Bi_0.5TiO₃ (approaching 10⁻² S cm⁻¹ at 600 °C (ref. 18)), melilites (La_1.54Sr_0.46Ga₃O_7.27, 2 × 10⁻² S cm⁻¹ at 600 °C (ref. 19)), and bismuth-vanadium oxides with substituent metals BIMEVOX²⁰ (Bi₂V_1.9Cu_0.1O_5.35, ∼0.1 S cm⁻¹ at 600 °C (ref. 21)). However, even in these families of oxygen ion conductors, an oxygen ion conductivity of 0.1 S cm⁻¹ is only accessible at temperatures greater than 600 °C. Reaching an oxygen ion conductivity of 0.1 S cm⁻¹ at lower temperatures (closer to 400 °C) demands a fundamental understanding of the factors governing oxygen ion migration.

Oxygen ion migration within solid lattices can occur via various mechanisms based on oxygen vacancies or interstitials for sub-stoichiometric or super-stoichiometric materials, respectively.^22,23 The prevalent mechanism in perovskite materials, which are the focus of this study, is vacancy-mediated,^24–28 with oxygen ions diffusing through the solid lattice by hopping across vacant oxygen lattice sites.^23,27 The type and quantity of oxygen vacancies in a material result from the equilibrium between oxygen desorption and vacancy formation mechanisms, with vacancies possessing the lowest migration barriers being more inclined to engage in transport. As such, fast vacancy-mediated oxygen ion transport requires low oxygen vacancy formation energy and migration barrier.^27,29 Decreasing vacancy formation energy and migration barrier has been the focus of a notable number of existing studies.^30–53 The oxygen vacancy formation energy in transition metal oxides has been shown to decrease with descriptors of weaker bond strength such as lower bond dissociation energy,³³ M ionization potential,³⁰ enthalpy of formation,³¹ and Madelung potential,³² as well as lower reduction potential³³ and band gap.³¹ By tuning the position of the O 2p band center closer to the Fermi level,³⁴ lower M–O bond strength and redox energy can be achieved,³⁶ leading to low vacancy formation energy penalty.^33,34,36 Beyond transition metal oxides, similar physics-based descriptors (i.e., band gap and formation energy) have been combined in multi-variate linear models³⁶ or crystal graph convolutional neural networks⁵⁴ showing good predictions of vacancy formation energy for non-transition metal oxides. However, to our knowledge, a single fundamental descriptor that comprehensively rationalizes trends in vacancy formation energy with different charge states and across oxides with and without transition metals has not been proposed, which is addressed in this work.

While the oxygen migration barrier can be correlated to the geometry, lattice dynamics, or electronic structure of the crystal, the physical origin of the oxygen migration barrier is not understood clearly. Regarding the geometry of the crystal, increasing the size of the lattice bottleneck,^39,40 and free volume in the lattice,^37,38 or minimizing the size mismatch between different cations in equivalent sites^41–43 (i.e., substituents) have been correlated with decreasing migration barrier^38,39 and increasing ionic conductivity.^40–43 However, these geometric properties are often intercorrelated,^43–45 and are thus difficult to generalize as descriptors for migration barriers across different oxygen ion conductors. In addition, lattice dynamics have been correlated with oxygen ion migration,⁴⁸ where reduced migration barrier and increased conductivity are linked to lower force constants for lattice moiety rotation in Ruddlesden–Popper oxides,⁴⁴ and lower energy of phonon modes in Brownmillerites.^46,47 In addition to the crystal structure and lattice dynamics, several studies have found a correlation between the migration barrier and the electronic structure of the material.^49–53 Specifically, a closer O 2p band center to the Fermi level,⁴⁹ and lower vacancy formation energy penalty,^49,50,53 have been shown to decrease the oxygen migration barrier of perovskites. The origin of vacancy formation energy penalty has been attributed to bond strength,⁴⁹ or the extent of charge transfer between metal and oxygen ions,^48,51,54 which can be connected by the required redox energy to fill d band orbitals at higher energy in transition metal oxides upon vacancy formation.^33,35 On the other hand, the physical origin of the oxygen migration barrier and its link to the electronic structure requires further understanding. The migration barrier decreases with weaker M–O bond strength at increasing ionization potential of the metal,³⁰ lattice volume,^37,38 tensile strain,⁵⁴ or minimized binding energy between defects of opposite charge.⁵⁵ Additionally, the migration barrier can increase with increasing charge transfer between metal and oxygen ions^51,52 or with more densely localized charge (i.e., Co 3⁺ in high spin state,⁵² Fe cations with higher valence,⁵¹ or F centers in SrTiO_3−x (ref. 56)). Unfortunately, descriptors for the migration barrier valid across oxides with and without transition metal ions remain elusive. In this work, density functional theory (DFT) simulations are performed to seek an understanding of the oxygen migration barrier in oxygen conductors. Over 70 perovskites with and without transition metals (a complete list in Table S1, ESI†) are examined, where electronic structure changes upon the introduction of oxygen vacancies are correlated with vacancy formation and migration barrier energetics. In the presence of a large band gap, such as in the case of oxides with zero or ten stoichiometric d electron count, localized electronic states associated with oxygen vacancies can be observed in the electronic density of state (DOS) between the valence and conduction bands. By relating the position of these localized electronic states with respect to the valence and conduction bands, the physical origin of vacancy formation energy and migration barrier is decoupled. Building on previous work,³⁴ the vacancy formation energy is related to the energy of the highest filled metal states with respect to the O 2p band center. On the other hand, higher migration barriers are correlated with increasingly localized electronic states of oxygen vacancies being formed at lower energies below the lowest unoccupied metal states in the conduction band. Leaving localized states unfilled or increasing the charge screening capability of the host lattice can lower the migration barrier. Moreover, by analyzing the changes of electronic structure during oxygen migration, we further show that changes in the energy of vacancy states from the equilibrium to the transition state, which depend on the charge screening capability of the local host lattice, regulate oxygen ion migration barrier. Our observations related to the interconnectedness of the electronic structure and the migration barrier not only establish the increased charge screening capability of the local host lattice environment as a design guideline to decrease the oxygen migration barrier but also facilitate the discovery of fast oxygen ion conductors.

Results and discussion

Relating the electronic structure of oxygen vacancies to oxygen migration barriers

Oxygen ion migration barriers were computed for perovskites with non-computationally compensated (NCC) oxygen vacancies and computationally compensated (CC) oxygen vacancies, as shown in Fig. 1a. NCC oxygen vacancies were created as neutral oxygen vacancies by removing an oxygen atom from the perfect structure and leaving behind two electrons that the host lattice needs to compensate for, as indicated by the left black arrow in Fig. 1a. On the other hand, CC oxygen vacancies were created as charged oxygen vacancies by removing an oxygen atom along with two electrons from the perfect structure, as indicated by the right black arrow in Fig. 1a, without the need for the host lattice to compensate for the two electrons left behind by the oxygen atom. Other studies have created similar NCC and CC oxygen vacancies to investigate oxygen ion transport in perovskites⁴⁹ or rocksalt MgO_1−x.⁵⁷ Although there are different pathways for oxygen hopping,^32,49 we considered two typical in-plane (ipv) and out-of-plane (opv) oxygen migration pathways in Fig. 1b, which were examined across a library of perovskites (full list in Table S1, ESI†) with and without transition metal ions (detailed in the Methods sections). The trends observed in the computed migration barriers for ipv (Fig. S1a, ESI†) and opv (Fig. S1b, ESI†) pathways were similar. In Fig. 1c migration barriers of transition-metal-containing perovskites having non-zero stoichiometric d electron count for transition metal ions (with d electrons) and with NCC (blue open circles) and CC (orange open circles) oxygen vacancies are comparable, both of which decrease with the O 2p band center moving closer to the Fermi level. This trend agrees with previous computational work,⁴⁹ and our computed migration barrier values agree reasonably with experimental results,^{24,28,39,58–66} showing a mean absolute error of 0.087 eV for (La,Sr)BO_3−x (B = Mn, Fe, Co) perovskites in Fig. S2 of the ESI.† For (La,Sr)CrO_3−x a lower barrier (highest is NCC LaCrO_3−x with a migration barrier of 1.44 eV) than La_0.9Ca_0.12CrO_3−x (1.74 eV)⁵⁹ was found in Fig. S2,† which we attribute to the difference between experimental and simulated composition. NCC and CC migration barriers of oxides with d electrons show similar degree of correlation with the position of the O 2p band center relative to the Fermi level (r-value = −0.78 in Fig. 1c) and the energy of the metal band relative to the O 2p band center (r-value = 0.75 in Fig. S3, ESI†). These correlations can be observed by noting that oxides with early transition metals having high metal d states far from the O2p band center, such as La_0.75Sr_0.25TiO_2.875 and La_0.75Sr_0.25VO_2.875 (NCC migration barriers of 1.70 eV and 1.38 eV and CC migration barriers of 1.61 eV and 1.14 eV) have higher migration barrier compared to oxides with late transition metals having low metal d states close to the O2p band center, such as La_0.75Sr_0.25CoO_2.875 and La_0.75Sr_0.25NiO_2.875 (NCC migration barriers of 0.76 eV and 0.77 eV and CC migration barriers of 0.77 eV and 0.74 eV). In addition, substituting cations with lower valence on the A-site to increase the oxidation state of transition metals lowers the Fermi level and the energy of the metal states relative to the O2p band center,⁶⁷ which also decreases the migration barrier. For example, the migration barrier can decrease from LaTiO_2.875 (1.54 eV for NCC and 1.48 eV for CC) and La_0.75Sr_0.25TiO_2.875 (1.70 eV for NCC and 1.61 eV for CC) to SrTiO_2.875 (0.65 eV for NCC and 0.46 eV for CC), from LaCoO_2.875 (0.80 eV for NCC 0.69 eV for CC) and La_0.75Sr_0.25CoO_2.875 (0.76 eV for NCC and 0.77 eV for CC) to SrCoO_2.875 (0.64 eV for NCC), and from LaNiO_2.875 (0.88 eV for NCC and 0.78 eV for CC) and La_0.75Sr_0.25NiO_2.875 (0.77 eV for NCC and 0.74 eV for CC) to SrNiO_2.875 (0.48 eV for NCC). In contrast, perovskites with stoichiometric d electron count equal to zero or ten (without d electrons) and with NCC vacancies (blue solid circles) can exhibit larger calculated migration barriers than those with CC oxygen vacancies (orange solid circles) in Fig. 1c and reported experimental values of activation energy^{24,28,39,60–63} shown in Fig. S4 (ESI†). Specifically, the migration barriers of perovskites without d electrons and with NCC oxygen vacancies (ranging from 0.31 eV for CaTiO_2.875 to 3.08 eV for ErAlO_2.875) and are much higher than their CC migration barriers (ranging from 0.11 eV for CaTiO_2.875 eV to 0.62 eV for LaAlO_2.875). Computed NCC and CC migration barrier values for oxides with and without d electrons are in agreement with previously reported computed migration barriers showing a mean absolute error of 0.117 eV in Fig. S5 of the ESI.†^32,39,49 The CC migration barriers of oxides without d electrons may appear to fall on the orange line in Fig. 1c. However, these CC migration barriers of perovskites without d electrons show poor correlation with the O 2p band center as reflected by a Pearson correlation coefficient (r-value) of 0.45. These migration barriers also show an r-value of 0.69 with the energy of the metal band relative vs. the O 2p band center in Fig. S3 of the ESI.† The fundamentals behind these apparent correlations are not well understood. Additionally, while some NCC migration barriers of oxides without d electrons may also appear to correlate with the O 2p band center, the large differences in the NCC and CC migration barriers of oxides without d electrons found for similar values of O 2p band center are also not understood. Therefore, while the O 2p band center is a useful descriptor, we lack an understanding of the physical origin behind correlations and different trends in migration barriers, which is addressed in this work. By simulating NCC and CC oxygen vacancies in different materials, we can uncover trends in migration barriers ranging from a few eV to units of eV to establish a general framework for all types of oxygen vacancies. Next, we examine the electronic structure changes associated with the formation of NCC and CC vacancies of perovskites with and without d electrons.

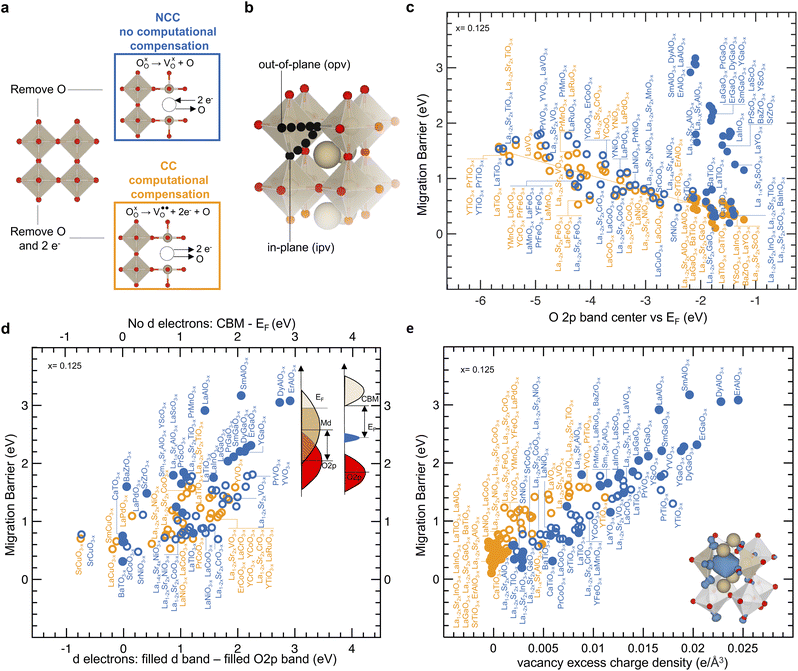Fig. 1 Electronic descriptors of NCC and CC oxygen migration barriers. (a) Formation of a non-computationally compensated (NCC in blue) and a computationally compensated (CC in orange) oxygen vacancy. (b) Computed migration pathways towards an in-plane-vacancy (ipv) and an out-of-plane vacancy (opv), as detailed in the Methods section. (c) Comparison between migration barrier and the energy of the O 2p band center vs. Fermi level descriptor computed on the perfect structure without oxygen vacancies. Fitted orange line has R² = 0.82. (d) Comparison between NCC migration barrier and the energy of lowest unoccupied vs. highest occupied states for oxides without d electrons (top x-axis and right schematic). Also, comparison between the migration barrier and the energy of filled metal d states vs. the filled O 2p states for oxides with d electrons (bottom x-axis and left schematic). (e) Correlation between migration barrier and vacancy excess charge density. Computation of vacancy excess charge density considered redistribution of Bader charge on the first neighbors of the oxygen vacancy highlighted in the bottom right schematic (2 B-site, and 4 A-site cations), and is further detailed in the ESI.† For panels (c–e), and throughout the manuscript solid and open circles correspond to oxides with zero or then stoichiometric d electron count (without d electrons), and with stoichiometric d electron count greater than zero and lower than ten (with d-electrons), respectively. Data are tabulated in Tables S2 and S3 of the ESI.†

Introducing NCC and CC oxygen vacancies in transition-metal-containing perovskites (with d electrons) results in similar electronic structure changes, as shown in Fig. 2 for (La,Sr)TiO_3−x, Fig. S6 (ESI†) for (La,Sr)CoO_3−x and Fig. S7 (ESI†) for (La,Sr)NiO_3−x. For example, creating NCC and CC oxygen vacancies in LaTiO₃ (Fig. 2a) to generate LaTiO_2.875 is accompanied by the emergence of new electronic states below the minimum of the conduction band in Fig. 2b and c, respectively. These new states can be attributed to symmetry breaking^68,69 and the lowering of the energy of the metal states as M–O bonds are broken.^69,70 During the formation of oxygen bonds, electrons are transferred from the metal (M) to oxygen, resulting in positively charged cations surrounded by oxygen anions. In this process, the energy of metal states is raised higher than the energy of O 2p states, and bands are formed based on the translational symmetry of the oxide crystal⁷¹ with M band higher in energy than O 2p band. When an oxygen atom is removed to create an oxygen vacancy, the energy of metal states is locally brought down near the vacancy site, resulting in states that appear below the conduction band. Accordingly, the new electronic states below the conduction band of LaTiO_2.875 predominantly have metal d character (Fig. S8, ESI†) and belong to Ti ions surrounding the vacancy, as evidenced by the computed orbitals and site-projected DOS for CC and NCC LaTiO_2.875 (Fig. S9, ESI†). La_0.75Sr_0.25TiO_2.875 with both NCC (Fig. 2d) and CC (Fig. S10, ESI†) oxygen vacancies shows similar electronic structure changes but downshifted Fermi level towards the O 2p band center, consistent with the reduced d band filling of La_0.75Sr_0.25TiO_2.875 than LaTiO_2.875. The vacancy electronic state observed for CC LaTiO_2.875 and NCC La_0.75Sr_0.25TiO_2.875 (with Ti³⁺ ions) appear closer to the minimum of the conduction band than in NCC LaTiO_2.875 (with Ti²⁺ ions), as the higher oxidation state leads to higher energy level for electrons in localized d orbitals near the oxygen vacancy. These new localized electronic states for LaTiO_2.875 and La_0.75Sr_0.25TiO_2.875 appear below the Fermi level and are filled, resulting in localized charge accumulation in the proximity of oxygen vacancies in these perovskites (Fig. S11a–c, ESI†). Both NCC (1.54 eV), CC LaTiO_2.875 (1.48 eV), and La_0.75Sr_0.25TiO_2.875 (1.70 eV) have comparable migration barriers (Fig. 2e), where NCC vacancy formation does not cause a significant increase in the Fermi level (Fig. 2a–d, and S10 of the ESI†) and in the localized charge density (Fig. S11a–c, ESI†) upon the formation of oxygen vacancies relative to CC. In addition, bringing the Fermi level or the highest filled metal states closer to the O 2p band reduces localized charge accumulation in the proximity of oxygen vacancies in LaNiO_2.875 (Fig. S11d, ESI†) and La_0.75Sr_0.25NiO_2.875 (Fig. S11e, ESI†) compared to LaTiO_2.875 (Fig. S11a, ESI†) and La_0.75Sr_0.25TiO_2.875 (Fig. S11c, ESI†), and is correlated with much smaller migration barriers (i.e., 0.92 eV lower for NCC La_0.75Sr_0.25NiO_2.875 than NCC La_0.75Sr_0.25TiO_2.875), in line with previous studies.^50,72 Moreover, replacing La³⁺ in LaTiO₃ (Fig. 2a) with Sr²⁺ to form SrTiO₃ (Fig. 2f) results in the Fermi level closer to the O2p band and lower charge densities in the oxygen vacancies of SrTiO_2.875 (Fig. S11f, ESI†) than LaTiO_2.875 (Fig. S11a, ESI†), which reduces migration barriers for NCC (0.65 eV) and CC (0.46 eV) SrTiO_2.875 compared to NCC (1.54 eV) and CC (1.48 eV) LaTiO_2.875, as shown in Fig. 2e. Therefore, similar NCC and CC migration barriers of transition metal containing perovskites with d electrons are correlated with comparable electronic structure changes resulting from NCC and CC oxygen vacancies. We will further seek electronic signatures of oxygen vacancies responsible for the migration barrier and oxygen vacancy formation energy penalty in later sections.

Fig. 2 Electronic signatures of oxygen vacancies and migration barriers in (La,Sr)TiO_3−x. Computed electronic DOS of (a) LaTiO₃, LaTiO_2.875 with (b) NCC and (c) CC oxygen vacancies, and (d) La_0.75Sr_0.25TiO_2.875 with NCC oxygen vacancies (CC in Fig. S10, ESI†). The red and brown areas correspond to oxygen 2p and metal orbitals in the electronic DOS, respectively. The Fermi level and the O 2p band center are indicated by the black dotted and red horizontal lines, respectively. Filled states, which emerged in the DOS of LaTiO_2.875 with NCC and CC oxygen vacancies, are highlighted by the blue and orange arrows in panels (b) and (c), respectively. (e) NCC (blue) and CC (orange) energy landscapes of (La,Sr)TiO_3−x. Computed electronic DOS of (f) SrTiO₃, SrTiO_2.875 with (g) NCC and (h) CC oxygen vacancies referenced to the valence band maximum (VBM) of the perfect structure (SrTiO₃).

Unlike perovskites with d electrons, NCC and CC oxygen vacancies in perovskites without d electrons result in different electronic structure changes, as shown in Fig. 3 for (La,Sr)GaO_3−x, Fig. S12 (ESI†) for (La,Sr)AlO_3−x, and Fig. S13 (ESI†) for (La,Sr)InO_3−x. Introducing oxygen vacancies in LaGaO₃ (Fig. 3a) leads to the emergence of new electronic states in the band gap for both NCC (Fig. 3b) and CC (Fig. 3c) LaGaO_2.875. The new electronic states have localized character⁷¹ and originate largely from empty low-energy orbitals of the metal occupying the B-site (i.e., Ga s for (La,Sr)GaO_3−x) as well as high energy O 2p orbitals, which is shown by the orbital-projected DOS of LaGaO_2.875 (Fig. S14, ESI†). These localized states of NCC LaGaO_2.875 (blue arrow in Fig. 3b) are filled, resulting in large charge accumulation in the proximity of the vacancy (Fig. S15a, ESI†) and higher Fermi level compared to LaGaO₃ (Fig. 3a) and CC LaGaO_2.875 (Fig. 3c). On the other hand, localized states of CC LaGaO_2.875 (orange arrow in Fig. 3c), as well as NCC (blue arrow in Fig. 3d) and CC (Fig. S16, ESI†) La_0.75Sr_0.25GaO_2.875, are unfilled, resulting in insignificant charge accumulation near oxygen vacancies (Fig. S15b and c, ESI†) and no change in the Fermi level. These observed densities of states are in agreement with previous work.^73–75 The larger migration barrier of NCC LaGaO_2.875 (2.04 eV) than CC LaGaO_2.875 (0.33 eV) and La_0.75Sr_0.25GaO_2.875 (0.32 eV for NCC and 0.43 eV for CC) in Fig. 3e is accompanied by higher energy of the highest filled states and more localized charge accumulation upon the formation of oxygen vacancies. We further seek electronic structure signatures associated with oxygen vacancies responsible for the larger NCC migration barriers as compared to CC migration barriers for perovskites without d electrons.

Fig. 3 Electronic signatures of oxygen vacancies and migration barriers in (La,Sr)GaO_3−x. Computed electronic DOS of (a) LaGaO₃, LaGaO_2.875 with (b) NCC and (c) CC oxygen vacancies, and (d) La_0.75Sr_0.25GaO_2.875 with NCC oxygen vacancies (CC in Fig. S16, ESI†). The DOS are referenced to the valence band maximum (VBM) of LaGaO₃. (e) NCC (blue) and CC (orange) energy landscapes of (La,Sr)GaO_3−x.

Of significance to note is that increasing NCC migration barriers for oxides without d electrons (blue solid) largely correlate with greater energy differences between the conduction band minimum (CBM) and the localized states that emerged with oxygen vacancies, as shown by the top axis in Fig. 1d. This correlation is supported by the observation of the NCC LaBO_2.875 (B = Al, Ga, In, Tl) series in Fig. 4, where introducing more polarizable ions from Al to Tl brings localized filled electronic states closer to the conduction band, which decreases the migration barriers. Qualitatively, more localized electronic states of NCC oxygen vacancies are seen for more unfavorable oxidation states of the B-site with uncoordinated B₂O₅ polyhedral units. Leaving these localized states empty can reduce migration barriers, as shown by CC oxygen vacancies (orange) as well as A-site substitution. For example, substituting A-site cations with lower valence leaves these localized states empty, as illustrated by NCC La_0.75Sr_0.25GaO_2.875 (Fig. 3d) as well as NCC La_0.75Sr_0.25AlO_2.875 (Fig. S12d, ESI†), which is associated with reduced migration barriers comparable to CC migration barriers (Fig. 4e). Therefore, greater NCC than CC migration barriers for perovskites without d electrons can be attributed to the larger electronic energy penalty arising from localized filled states of NCC oxygen vacancies, when the excess charge was not compensated by A-site substitution. On the other hand, increasing NCC (open blue) and CC (open orange) migration barriers for oxides with d electrons largely correlate with greater energy differences between the filled metal d band and the O2p band center for the bottom axis, as shown in Fig. 1d. The apparent correlation results from a number of oxides with unfavorable oxidation states for transition metal ions (e.g., 2+ for the B-site upon the formation of oxygen vacancies), which have migration barriers greater than 1 eV. Beyond these oxides, there is no clear correlation between migration barriers and the filled metal d band relative to the O2p band center. Going beyond thermodynamic energetic descriptors for migration barriers, we show that computed NCC and CC migration barriers in perovskites increase with localized charge density associated with the formation of oxygen vacancies, as shown in Fig. 1e (r-value = 0.84). The vacancy excess charge density in Fig. 1e was computed based on Bader charge analyses,⁷⁶ with positive values corresponding to net electronic charge accumulation on the first neighbor to the vacancy as detailed in the supplementary computational methods (ESI†). Localized states upon the formation of NCC oxygen vacancies are accompanied by considerable excess charge (Fig. S11 and S15, ESI†), which is supported by the correlation between increasing vacancy excess charge density and greater difference between unfilled metal states and filled localized states (r-value = 0.92 top axis in Fig. S17, ESI†). Introducing more polarizable ions on the B-sites (i.e., going from Al to Tl in the LaBO_2.875, having B = Al, Ga, In, Tl) can increase the charge screening capability of the local environments by having localized filled electronic states closer to the conduction band minimum (Fig. 4a–d), and decrease excess charge and migration barriers in Fig. 4e. These observations are in agreement with previous work showing that moving filled localized states of oxygen vacancies closer to CBM can decrease the accumulation of charge.^77,78 In addition, the excess charge associated with the formation of oxygen vacancies can be compensated through A-site substitution such as La_0.75Sr_0.25GaO_2.875 (Fig. 3d), La_0.75Sr_0.25AlO_2.875 (Fig. S12d, ESI†), and La_0.75Sr_0.25InO_2.875 (Fig. S13d, ESI†) or via computational compensation in CC LaGaO_2.875 (Fig. 3c), LaAlO_2.875 (Fig. S12c, ESI†), and LaInO_2.875 (Fig. S13c, ESI†), rendering empty localized states and lower migration barriers. Interestingly, the computed migration barriers of the A-site substituted (La_0.75Sr_0.25BO_2.875) and CC LaBO_2.875 series (B = Al, Ga, In, Tl) follow the same trend where increasing charge screening capability of the host lattice decreases migration barrier from Al to Tl in Fig. 4e, in agreement with previous experimental reports.⁶⁰ On the other hand, larger excess charge density and NCC migration barriers (Fig. 1e) were found for perovskites with d electrons and unfavorable oxidation states for B-site ions such as Ti²⁺ ions in LaTiO_2.875 (unable to screen excess charge in Fig. S11a of the ESI†) than others with favorable oxidation states for B-site ions such as Ti³⁺ ions in ATiO_2.875 (A = Ca, Sr, Ba), which are able to screen excess charge in Fig. S11f (ESI†). Additionally, decreasing vacancy excess charge density correlates with the O 2p band center closer to the Fermi level (highest filled M d orbital) in oxides with d electrons (bottom axis in Fig. S17, ESI†) with r-values equal to 0.82 and 0.75 for NCC and CC, respectively, highlighting that moving the O 2p band center closer to the Fermi level increases the charge screening capability of the local environment. We also tested the correlation between decreasing migration barriers and decreasing vacancy excess charge density for selected 3d transition metal oxides (list in Table S4†) using PBE + U formalism,^79,80 which is further detailed in the Methods section. Vacancy excess charge densities at the PBE and PBE + U level showed a similar trend (Fig. S18a†) and decreasing migration barriers were correlated with decreasing vacancy excess charge densities at the PBE + U level (r-value = 0.82 in Fig. S18b†). Therefore, excess charge density associated with the formation of oxygen vacancies is proposed as one general descriptor for migration barriers of oxygen ions in perovskites, and increasing the charge screening capability of local environments can promote ion migration. Next, we discuss how the electronic structure of an oxygen vacancy governs the oxygen vacancy formation energetics and further investigate the connection between the charge screening capability of the local environment and the electronic states of oxygen vacancies during ion migration.

Fig. 4 Trends in electronic signatures of NCC oxygen vacancies, vacancy excess charge densities, and migration barriers in the LaBO_2.875 (B = Al, Ga, In, Tl) series. (a) LaAlO_2.875, (b) LaGaO_2.875, (c) LaInO_2.875, and (d) LaTlO_2.875. The highest energy of the filled electronic states and the lowest unoccupied metal orbitals are indicated by the blue and brown horizontal lines, respectively. Crystal structures are reported below each DOS plot where the iso-surface represents eigenstates of the filled vacancy electronic states and is color coded based on the values of vacancy excess charge density. Values are 0.166 e Å⁻³ for LaAlO_2.875 (blue isosurface) and 0.085 e Å⁻³ for LaTlO_2.875 (white isosurface). (e) Computed migration barriers for the NCC LaBO_2.875 (blue), La_0.75Sr_0.25BO_2.875 (blue), and CC ABO_2.875 (orange) series (B = Al, Ga, In, Tl). Experimental migration barriers for La_0.9Sr_0.1BO_2.95 (ref. 60) are also included (brown).

Electronic structure descriptors of oxygen vacancy energetics

The difference between NCC and CC migration barriers was found to increase with NCC vacancy formation energetics for perovskites with no d electrons for B-site ions (Fig. 5a), where the excess charge was not compensated computationally nor by substitution of cations with lower valence. Such a finding is in line with simple classical chemistry arguments where unfavorable uncoordinated B-sites would be associated with higher NCC migration barrier. On the other hand, no significant difference between NCC and CC migration barriers was found for perovskites with d electrons for B-site ions when excess charge coming from oxygen vacancy was screened. For example, introducing Sr substituents can stabilize unfavorable B₂O₅ polyhedral units lowering the migration barrier and the vacancy formation energy, as shown in Fig. 5a for La_0.75Sr_0.25GaO_2.875. Therefore, the difference between NCC and CC migration barriers can have a similar origin to that of the oxygen vacancy formation energy penalty, which comes from the energy penalty associated with screening excess charge during oxygen ion migration and oxygen vacancy formation, respectively. This hypothesis is supported by the black line fitted (R² = 0.96) on perovskites without transition metals and showing a slope of 0.42 in Fig. 5a, which is close to ½ and can be explained by the fact that the migration barrier is defined by energy penalty per unit charge migrated, where the value of the oxygen ion charge is 2. Perovskites with zero-d electrons but with transition metals (highlighted in gray) do not fall on the same fitted line, which can be due to the different character of the conduction band. The energy of the highest filled metal states relative to the O 2p band center was found to correlate with the computed energy penalty for the formation of NCC and CC oxygen vacancies in all the perovskites with (open) and without (solid) d electrons, as shown in Fig. 5b. The energy of the highest filled metal states is the Fermi level, which coincides with metal d states for oxides with d electrons (top right schematics in Fig. 5b) and with VBM or the filled localized states (bottom right schematics in Fig. 5b) for oxides without d electrons. Our computed vacancy formation energies are in close agreement with previous work (Fig. S19, ESI†).^32,49,81 For example, the vacancy formation energy penalty of NCC and CC LaTiO_2.875 (5.97 eV and 5.88 eV), and NCC and CC La_0.75Sr_0.25TiO_2.875 (5.98 eV and 5.97 eV) are comparable, but much greater than those of NCC and CC LaNiO_2.875 (2.15 eV and 1.89 eV) or NCC and CC La_0.75Sr_0.25NiO_2.875 (1.40 eV and 1.11 eV), attributable to the much higher energy of filled Ti 3d (Fig. 2a–d, and S10 of the ESI†) than the one for Ni 3d (Fig. S7a–e, ESI†) states. The slope from the correlation of perovskites with d electrons was close to 2 in Fig. 5b (fitted slope of 1.9), which can be interpreted as the transfer of two electrons (for each oxygen vacancy) from oxygen states to the highest filled metal states based on a rigid band model.³⁵ These findings are in agreement with previous work that shows correlations between the oxygen vacancy formation energetics and the oxygen p band center³⁴ as well as the metal–oxygen valency for oxides with d electrons.^31,51,67,82 On the other hand, NCC and CC oxygen vacancy formation penalty of SrTiO_2.875 is different. Creating NCC oxygen vacancies in SrTiO_2.875 (Fig. 2g) raises the Fermi level (2.26 eV up) to the bottom of the conduction band, consistent with previously reported DOS,^83,84 and reflects in high vacancy formation energy penalty (5.22 eV). In contrast, the Fermi level is kept pinned at the VBM creating CC oxygen vacancies in SrTiO_2.875 (Fig. 2h), which reflects in lower vacancy formation energy (0.83 eV). The higher NCC than CC vacancy formation energy of SrTiO_2.875 is consistent with previous theoretical work³¹ and these NCC and CC vacancy formation energies are in agreement with experiments where the vacancy formation energy is evaluated in the n-type (5.8 eV at 800 °C and 1 atm (ref. 85)) and p-type (1.3 eV at 800 °C and 1 atm (ref. 85)) regime, respectively.⁸⁶ Similarly, increasing NCC vacancy formation energies of other oxides without d electrons were also correlated with the filled (localized) states formed higher energy relative to the VBM (r-value = 0.93 in Fig. S20, ESI†). The energy of the highest filled metal states can coincide with the conduction band edge (i.e., for BaTiO_2.875 in Fig. 2g) or can be lower than the conduction band edge (i.e., for LaGaO_2.875 in Fig. 3b). Therefore, the electronic energy penalty associated with transferring electrons from oxygen to metal states was found to regulate oxygen vacancy formation energetics, in line with previous work,³⁵ which is governed by the highest filled metal states or filled localized states above the VBM created with oxygen vacancies. We further examine the relationship between the migration barrier and the energy of electronic states of oxygen vacancies through analyzing the changes in the electronic structure from equilibrium to the transition state during oxygen ion migration.

Fig. 5 Electronic descriptors of vacancy formation energy penalty. (a) Comparison between the difference in migration barrier (NCC vs. CC) and the NCC vacancy formation energy. The black fitted line has R² = 0.96 and the dotted line represents y = 0. (b) Correlation between the vacancy formation energy and the energy difference between the Fermi level and the O 2p band center. For oxides with d electrons, the Fermi level corresponds to the highest filled metal d states (schematics at the top right of the graph). For oxides without d electrons, the Fermi level can correspond to the VBM or the top of the filled localized states (schematics at the bottom right of the graph). Data are tabulated in Tables S2 and S3 (ESI†).

Relating the electronic structure of the transition state to migration barriers

We first investigate how the energy of filled localized states of oxygen vacancies observed between conduction and valence band for oxides without d electrons (e.g., LaGaO_2.875 with NCC oxygen vacancies in Fig. 3c) as well as other oxides with d electrons (e.g., LaTiO_2.875 with both CC in Fig. 2b or NCC in Fig. 2c oxygen vacancies) changes during oxygen migration. As oxygen ions migrate from the equilibrium (initial) to the transition state, filled localized states associated with oxygen vacancies increase in energy (e.g., 1.23 eV up for NCC LaGaO_2.875 as indicated by E_1NCC in Fig. 6a) while the lowest unoccupied metal states decrease in energy (e.g., 0.32 eV down for NCC LaGaO_2.875 as indicated by E_2NCC in Fig. 6a). Similarly, the filled localized states of LaTiO_2.875 with CC (Fig. S21a, ESI†) and NCC (Fig. S21b, ESI†) oxygen vacancies raise in energy closer to the conduction band minimum from the equilibrium to the transition state. These changes in the electronic structure during migration result in a decreased energy gap between filled localized states and unoccupied metal states at the transition state. We argue that the migration barrier correlates with the energy needed to oxidize/reduce the charge localized in the oxygen vacancy during oxygen ion migration, which can be described by the energy difference from the filled localized states to the lowest unoccupied metal states between the equilibrium position (Fig. 6a left and right) and the transition state (Fig. 6a center). This hypothesis is supported by previous studies that have shown that localized electrons can impede oxygen ion transport by locally raising the migration barrier.^52,56,57 For instance, F centers in MgO_1−x are oxygen vacancies with localized electrons,⁸⁷ which exhibit a higher migration barrier (3.4 eV (ref. 88)) than oxygen vacancies without localized electrons (1.9–2.7 eV (ref. 57 and 89)) according to density functional theory (DFT) calculations⁸⁹ and experimental measurements.^57,88 In addition, the visualization of the filled localized states associated with the NCC oxygen vacancy of LaGaO_2.875 shows the movement of charge occurring in the opposite direction of oxygen ion migration (Fig. 6b). Similarly, the decrease in energy gap for LaTiO_2.875 is also accompanied by the movement of charge occurring in the opposite direction of oxygen ion migration (Fig. S21c, ESI†), consistent with previous reports on other transition metal oxides with d electrons.^32,51 Other examples of zero-d-electron perovskites with a decreased energy gap between filled localized states and unoccupied metal states at the transition state than the equilibrium state (NCC and ErAlO_2.875), can be found in Fig. S22 (ESI†). The sum of E_1NCC and E_2NCC is correlated nearly 1 : 1 with the NCC migration barrier (r-value = 0.93 and fitted slope of 0.97) and the difference between the NCC and CC migration barrier (r-value = 0.91 and fitted slope of 0.89) for perovskites without d electrons, as shown in Fig. 6c. Moreover, the sum of E_1NCC and E_2NCC is also correlated with the amount of charge that is screened out of the oxygen vacancy as the oxygen ion moves from the equilibrium position to the saddle point (transition state), approaching the oxygen vacancy (r-value = 0.90 in Fig. S23a, ESI†). Additionally, increasing migration barriers of oxides without d electrons (solid) having filled localized states as well as oxides with d electrons (open) are strongly correlated with increasing excess charge that is screened out of the oxygen vacancy as the oxygen ion moves from the equilibrium position to the saddle point (r-value = 0.82 in Fig. S23b, ESI†), consistent with the hypothesis of increasing migration barrier with increasing energy for oxidation/reduction of the localized charge. These trends of migration barriers with electronic signatures of ion migration going from equilibrium to transition state further support the correlations in Fig. 1d and e highlighting linear free energy relationships between thermodynamic (relative to equilibrium) and kinetic (relative to changes from equilibrium to transition state) quantities and providing a more insightful mechanistic picture. Therefore, the physical origin of the migration barrier could be connected to the electronic structure of the transition state and the energy penalty required to screen the charge that accumulates in oxygen vacancies. Decreasing oxygen migration barrier of perovskite oxides have been suggested to correlate with lower vacancy formation energy penalty,^49,50,53 which may resemble the Brønsted–Evans–Polanyi (BEP) principle. However, the correlation between NCC migration barrier and NCC vacancy formation is poor, which can be seen by the light blue datapoint Fig. 6c. For instance, the NCC migration barrier of LaGaO_2.875 (2.04 eV) is much higher than that of BaTiO_2.875 (0.75 eV) while the NCC vacancy formation energy of LaGaO_2.875 (5.10 eV) is comparable to that of BaTiO_2.875 (5.23 eV). Additionally, BaTiO_2.875 has higher NCC than CC (4.51 eV difference) vacancy formation energy but a similar NCC and CC (0.17 eV difference) migration barrier in Fig. 6c. On the other hand, LaGaO_2.875 has higher NCC than CC vacancy formation energy (4.94 eV difference) and migration barrier (1.71 eV difference) in Fig. 6c. Such differences in the energetics of migration barrier and vacancy formation energy cannot be explained by the BEP principle and suggest that the fundamental descriptor associated with migration barrier is fundamentally different from vacancy formation energy, which is governed by energy of O 2p band center relative to the Fermi level.

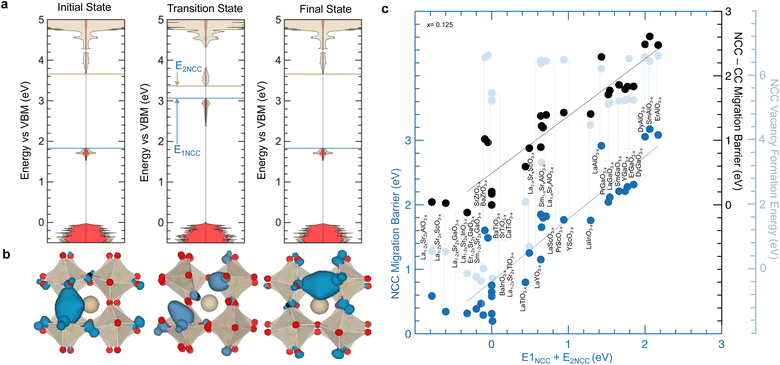Fig. 6 Electronic structure changes during oxygen migration in perovskites without d electrons (NCC). (a) Computed DOS for NCC LaGaO_2.875 at different stages of oxygen migration: initial (left), transition (center), and final (right) states. E_1NCC (blue arrow) represents the Fermi level change from initial to transition state, and E_2NCC (brown arrow) indicates the energy change of the lowest unoccupied metal state from initial to transition state. (b) Visualization of oxygen ion transport in NCC LaGaO_2.875. Eigenstates associated with filled localized states are shown as a blue iso-surface for the initial (left), transition (center) and final (right) states during oxygen ion migration. The hopping oxygen atom is highlighted in black. (c) Comparison between the NCC migration barrier and the change in energy E_1NCC + E_2NCC (as highlighted in panel a). The difference between NCC and CC migration barriers and NCC vacancy formation energies (right vertical axes) are also shown by the black and light blue datapoint, respectively, in comparison with E_1NCC + E_2NCC. The black and blue fitted lines have R² = 0.83 and 0.87, respectively. Data are tabulated in Tables S2 and S5 (ESI†).

Upon oxygen ion migration from the equilibrium (initial) to the transition state, empty localized states associated with oxygen vacancies (charge compensated by computation or substitution) increase from the initial state to the transition state (e.g., 0.34 eV up for CC LaGaO_2.875 as indicated by E_1CC in Fig. 7a). These arising empty localized states belong to the cation on the B-site that is being approached by the oxygen ion during migration (e.g., Ga ion in CC LaGaO_2.875 as shown by the site-projected DOS in Fig. S24 of the ESI†). Notably, increasing migration barriers are correlated with higher energy differences of empty localized states from equilibrium to transition state in Fig. 7b (r-value = 0.86), which can be attributed to reduced charge screening of the migrating oxygen ion by the local environments. This hypothesis is supported by the observations that the energy difference of empty localized states from the initial to the transition state increases with that of these empty localized states relative to the VBM at the transition state (Fig. S25a, ESI†), which also increases linearly with that in the equilibrium state (Fig. S25b, ESI†). Moreover, decreasing energy differences of empty localized states from equilibrium to transition state are also found with metal states closer to O 2p states at the transition state (Fig. S26a, ESI†), which is indicative of reduced charge screening capability of the local environments, as supported by correlations between O 2p states closer to Fermi level and reduced excess charge density in oxygen vacancies (Fig. S17, ESI†). Within this physical picture, the migration barrier of perovskites without (Fig. S26b, ESI†) and with (Fig. S26c, ESI†) d electrons can be decreased by moving the energy of metal states closer to O 2p states at the transition state by promoting the charge screening capability of the host lattice to reduce excess charge associated with oxygen migration. Therefore, the energy of oxygen vacancy states closer to the conduction band edge, is indicative of higher charge screening capability of the local environment and proposed as a descriptor for low oxygen migration barrier in perovskites.

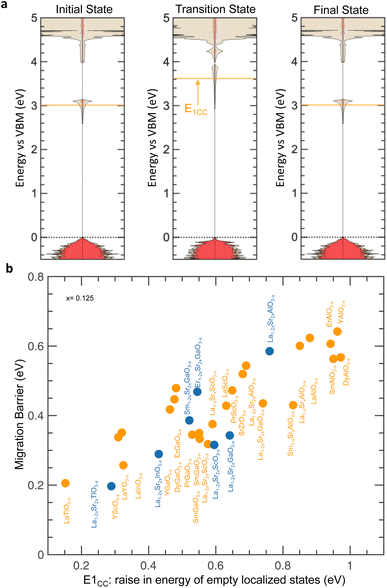Fig. 7 Electronic structure changes during oxygen migration in perovskites without d electrons (CC or with substitution). (a) Computed DOS of CC LaGaO_2.875 at different stages of oxygen migration: initial (left), transition (center), and final (right) states. E_1CC (orange arrow), represents the energy increase of the lowest unoccupied metal states from initial to transition state. (b) Comparison between the migration barrier and E_1CC (as highlighted in panel a). Data are tabulated in Tables S2 and S5 (ESI†).

To demonstrate the practical use of our results, we searched the literature for experimentally reported oxides and using the identified one promising but untested oxygen ion conductor. Considering that having the energy of vacancy electronic states near the conduction band is an indication of low migration barriers, we note that BaSnO₃ (ref. 90 and 91) and SrSnO₃ (ref. 92–94) have reported oxygen vacancy states close to the conduction band edge. One study has investigated BaSn_1−yY_yO_3−y/2 reporting a barrier for oxygen transport between 0.96 eV and 1.32 eV,⁹⁵ while derivatives of SrSnO₃ are still non explored to our knowledge. Starting from SrSnO₃ (electronic structure in Fig. S27a, ESI†) compensated oxygen vacancies were created by computational compensation in CC SrSnO_2.875 (electronic structure in Fig. S27b, ESI†) or by substituting K in Sr sites to form Sr_0.75K_0.25SnO_2.875 (electronic structure in Fig. S27c, ESI†), which showed non localized energy states of oxygen vacancies being formed close to the conduction band edge. Furthermore, the migration barriers of CC SrSnO_2.875 (0.62 eV) and of NCC Sr_0.75K_0.25SnO_2.875 (0.54 eV and 0.62 eV for pathways in Fig. S27d, ESI†) were computed and found comparable to those of state of art oxygen ion conductors such as (La,Sr)(Ga,Mg)O_3−x (ranging from 0.59 eV to 1.18 eV)⁹ or Na_0.5Bi_0.5TiO₃ (0.86 eV and 0.44 eV at a temperature below and above 320 °C, respectively).¹⁸ Therefore, Sr_0.75K_0.25SnO_2.875 can be a promising oxygen ion conductor, worthy of in-depth investigations in future studies. While we explored the substitution of K in Sr sites to create oxygen vacancies, future studies should also explore other substituents to optimize the different local environments within the crystal lattice, which can be done by leveraging our proposed framework and descriptors, as shown next.

To support that the proposed descriptors can be used in different local environment of the same crystal lattice, oxygen transport was investigated in different local environments of Na_0.5Bi_0.5TiO₃ perovskite, where fast conductive pathways result from local chemical environments rich in Bi,⁹⁶ such as BiO⁺ layers having lower migration barrier than NaO⁻ layers.^96,97 Na_0.5Bi_0.5TiO₃ was simulated with (100) ordering and alternating NaO⁻, TiO₂ and BiO⁺ layers as shown in Fig. 8a. Na_0.5Bi_0.5TiO₃ showed metal states closer to the O 2p band center (gap of 4.23 eV in Fig. 8b) compared to other titanates such as LaTiO₃ (Fig. 2a) or SrTiO₃ (Fig. 2f), which can be attributed to the inductive effect coming from electronegative Bi³⁺ ions.⁹⁸ Oxygen vacancy states are created close to the conduction band minimum as they are not localized within the bandgap (Fig. S28a, ESI†).⁹⁵ Migration barriers were computed along 4 different pathways (shown in Fig. 8c) giving lower values in the BiO⁺ layer (0.37 eV and 0.48 eV in gold in Fig. 8c), than the NaO⁻ layer (0.66 eV and 0.75 eV, pathways in light blue in Fig. 8c). These trends of migration barriers agree with those reported by de Souza and co-workers (0.4 eV (ref. 97) and 0.93 eV (ref. 97) for the BiO⁺ and NaO⁻ layers, respectively) and Dawson et al.⁹⁶ (0.63 eV and 0.77 eV for the BiO⁺ and NaO⁻ layers, respectively). Lower migration barrier is correlated with increased charge screening capability of BiO⁺ layers (excess charge density of −6 × 10⁻⁴ e Å⁻³) compared to NaO⁻ layers (excess charge density of +7 × 10⁻⁴ e Å⁻³). Through analyzing the site-projected DOS, it is found that the O 2p band center is closer to the VBM in the BiO⁺ (Fig. 8d) than the NaO⁻ layer (Fig. 8e), leading to a decreased gap between Ti 3d and O 2p states in the BiO⁺ (4.08 eV, as shown by the site-projected DOS in Fig. S28b and c, ESI†) than the NaO⁻ (4.42 eV, as shown by the site-projected DOS in Fig. S28b and d, ESI†) layer. Therefore, we propose that locally increased charge screening capability coming from having a metal band closer in energy to the O 2p band is the origin of fast oxygen ion transport in Bi-rich environments of Na_0.5Bi_0.5TiO₃. Our interpretation is also supported by previously reported correlation between decreasing migration barrier and shorter A–O bond length in Bi-rich environments,⁹⁶ where stronger bonding interactions found at decreasing Bi–O bond strength may lead to weaker Ti–O bonds based on inductive effects⁹⁹ and metal band closer to O 2p band. Therefore, our proposed descriptors can explain trends of migration barriers across different local environments of Na_0.5Bi_0.5TiO₃.

Fig. 8 Electronic origin of fast oxygen transport in Na_0.5Bi_0.5TiO₃. (a) Structure of Na_0.5Bi_0.5TiO₃ with alternating BiO⁺ (magenta), TiO₂ and NaO⁻ (green) layers. (b) Computed electronic DOS of Na_0.5Bi_0.5TiO₃. (c) Energy landscape of four different migration pathways: two in the BiO⁺ layer (magenta) and two in the NaO⁻ layer (green) layers, as shown in the top left schematic. Projected O 2p DOS below the Fermi level in the (d) BiO⁺ and (e) NaO⁻ layers with the O 2p band center marked by a red horizontal line.

Beyond perovskite oxides, the descriptors were assessed by introducing oxygen vacancies and computing NCC and CC migration barriers for ipv and opv pathways in rutile (Fig. S29a, ESI†) and fluorite (Fig. S29b, ESI†) crystal structures. Starting with rutile GeO₂ (Fig. S30a, ESI†), NCC GeO_1.9583 showed filled vacancy states (Fig. S30b, ESI†) and a higher migration barrier (3.26 eV for ipv and 2.47 eV for opv) compared to CC GeO_1.9583 with empty vacancy states (Fig. S30c, ESI†) and lower barrier (2.82 eV for ipv and 1.59 eV for opv). Similarly, starting with fluorite ThO₂ (Fig. S31a, ESI†), NCC ThO_1.96875 showed filled vacancy states (Fig. S31b, ESI†) and a higher migration barrier (2.05 eV for ipv and 2.04 eV for opv) than CC ThO_1.96875 with empty vacancy states (Fig. S31c, ESI†) and lower barrier (0.76 eV for ipv and 0.73 eV for opv). Vacancy states closer to the conduction band edge were correlated with lower vacancy excess charge density (r-value = 0.84) for rutile and fluorite (squares and diamonds in Fig. S32, ESI,† respectively) structures, indicative of higher charge screening capability of the host lattice. Substituting more polarizable elements from Ge to Pb in rutile BO₂ (B = Ge, Sn, Pb) brought oxygen vacancy states closer to the conduction band edge (Fig. S32, ESI†). Such a trend is consistent with previously reported oxygen vacancy states⁷⁷ (organized in Fig. S33, ESI†) moving closer to the conduction band upon substitution of more polarizable elements from Al to In in B₂O₃ (B = Al, Ga, In) or from Si to Sn in BO₂ (B = Si, Ge, Sn). These findings support the hypothesis that the energy of vacancy states relative to the conduction band edge is a descriptor of the oxygen migration barrier, consistent with the expectation that bigger and more polarizable cations decrease the migration barrier.^48,100 Additionally, in rutile (diamonds) and fluorite (squares) structures, decreasing NCC migration barriers for ipv (Fig. S34a, ESI†) and opv (Fig. S34b, ESI†) pathways as well as CC migration barriers for ipv (Fig. S34c, ESI†) or opv (Fig. S34d, ESI†) pathways were also found to decrease with energy of vacancy states closer to the conduction band edge. Migration barriers in rutile structures were higher in ipv pathways (NCC in Fig. S34a and CC Fig. S34c†) than opv pathways (NCC in Fig. S34b and CC Fig. S34d†). Conversely, in fluorite structures, migration barriers were comparable between ipv pathways (NCC in Fig. S34a and CC Fig. S34c†) and opv pathways (NCC in Fig. S34b and CC Fig. S34d†). Furthermore, the oxides with reported vacancy states well below the conduction band⁷⁷ in Fig. S33† are also reported to have high migration barriers, such as MgO (1.9–2.7 eV (ref. 57 and 89)), SiO₂ (2.0–4.6 eV (ref. 101)) and Al₂O₃ (6.3–6.9 eV (ref. 102)). On the other hand, the oxides with vacancy states reported to be closer to the conduction band edge⁷⁷ in Fig. S33 (ESI†) have documented low energy barriers of oxygen transport, such as Pb(Ti,Zr)O₃ (0.56–0.91 eV (ref. 27)), and TiO₂ (1.05–1.15 eV (ref. 103 and 104)), or have been successfully integrated in solid oxide fuel cells applications, such as SnO₂ (ref. 105) and In₂O₃.^106,107 While these preliminary data are promising to generalize the proposed descriptors beyond perovskite oxides, future in-depth investigations can be useful to draw stronger conclusions. Therefore, the energy of oxygen vacancy states relative to the conduction band edge is proposed as a promising descriptor of a low migration barrier and increasing the charge screening capability of the local environment can lower the migration barrier beyond perovskite oxides.

Our calculated trends are in good agreement with experimental results. For example, Fig. S2 (ESI†) reveals experimentally observed trends of decreasing migration barriers from early transition metal perovskites like La_0.9Ca_0.12CrO_3−x (with a migration barrier of 1.74 eV)⁵⁹ to later ones like LaCoO_3−x (with a migration barrier of 0.80 eV).²⁸ Additionally, experimental data⁶⁰ demonstrate a decrease In migration barriers for the series La_0.9Sr_0.1BO_2.95 (B = Al, Ga, In) going from Al to In (Fig. 4e). When we compare our CC migration barriers with the previously reported experimental data^{24,28,39,58–65} (Table S6, ESI†) we find a correlation coefficient of 0.84 and a mean squared error of 0.10 eV. However, differences exist between ‘microscopic’ migration barriers obtained from computational simulations^32,39,49 (Fig. S5, ESI†) and ‘macroscopic’ migration barriers from experiments (Fig. S2,^28,58,59 and S4,^{24,28,39,60–65} ESI†), which can be attributed, to the presence of substituents, defects, grain boundaries, leading to different local environments. The ‘macroscopic’ migration barrier measured in experiments arises from diverse hopping pathways and different ‘microscopic’ barriers.^108–110 In this work, we limited substituents and resorted to computational compensation. Future work will further focus on exploring descriptors for different local environments in highly substituted materials to bridge the gap between ‘microscopic’ and ‘macroscopic’ migration barriers. While this paper focuses on oxygen ion conductors, we believe that increasing the charge screening capability of the host lattice is an effective design strategy to decrease the ion migration barrier for other crystal structures and mobile species such as Li⁺ ions, which is supported by decreasing migration barriers with substitution of more polarizable anions in Lithium superionic conductors (LISICONs).¹¹¹ Work is ongoing to provide more concrete results for the generalization of our proposed descriptors to other mobile species. Similarly, while our results are focused on the vacancy formation mechanism, investigating other defects such as interstitials can help to further generalize the concepts presented in this work. Additionally, while the paradigm of decreasing migration barrier to increase conductivity is widely leveraged in the search for faster ion conductors,^112,113 the conductivity should not be always expected to increase with decreasing migration barrier,¹¹⁴ which can be seen by looking at the trend of measured conductivities in Fig. S4 (ESI†).^{24,28,39,60–65} Following the Arrhenius type expression of conductivity,¹¹⁵ a dependence of the pre-exponential factor is also to be expected, which can lead to large changes in conductivity due to (for example) migration entropy.⁴⁸ Along these lines, decreasing the migration barrier typically leads to increasing pre-exponential factors in oxygen^9,116 and other ionic conductors^48,117 due to enthalpy-entropy compensation law.¹¹⁸ Thus, to accelerate the discovery of materials with high oxygen ion conductivities, future work should also be directed towards increasing our understanding of the pre-exponential of Arrhenius law and the entropy of migration.

Conclusions

To gain a better understanding of the origin of oxygen migration barrier, we examined NCC and CC oxygen vacancies for a range of perovskites with and without d electrons, which allowed us to establish correlations between the electronic structure of oxygen vacancies with their vacancy formation and migration energetics. We found that the electronic structures resulting from the introduction of NCC and CC oxygen vacancies in oxides with d electrons were similar, with regards to the filled localized states, relative positions of the highest filled metal states, and O 2p band center. The similarity between electronic structures led to similar NCC and CC oxygen vacancy formation energies and migration barriers. On the other hand, after the introduction of NCC and CC oxygen vacancies in zero-d-electrons perovskites different electronic structures were obtained. Specifically, localized states were filled (empty) and the position of the highest filled metal states relative to O 2p band center was (was not) raised for NCC (CC) oxygen vacancies. The different electronic structures led to higher NCC oxygen vacancy formation energies and migration barriers than the CC ones.

Through analyzing trends in electronic structure across different perovskites, we could correlate the increasing vacancy formation energy with the increasing energy of the highest filled metal states compared to the O 2p band center. The slope of this correlation could be interpreted based on the electronic energy penalty required to transfer electrons from oxygen to higher energy metal states. For oxides without d electrons, such energy penalty was regulated by the energy of the filled vacancy electronic states relative to the VBM.

We also found that the migration barrier increased with the increasing accumulation of localized charge near oxygen vacancies coming from filled localized states. For perovskites without d electrons, increasing such localized charge was correlated with an increased energy gap between the CBM and the filled vacancy electronic states. For perovskites with d electrons, increasing such localized charge was correlated with metal d band closer to the O 2p band. Furthermore, we analyzed how the electronic structure varies during ion migration and found that the localized states and unfilled metal states moved closer in energy from the equilibrium state to the transition state. The magnitude of the decrease in the energy gap was correlated with the oxygen migration barrier. This observed correlation supports the idea that the migration barrier is regulated by the electronic energy penalty to screen the localized charge associated with the oxygen ion during migration and that increasing the charge screening capability of the host lattice can effectively decrease the migration barrier. In addition, we analyzed oxides where localized states were left empty by substitution with lower valence cations or computation compensation and could correlate the increasing migration barrier with the increasing raise in energy of these empty localized states from the equilibrium to the transition state. Based on the link between the energy of empty localized states and M–O bond strength, this observed correlation also supports the idea that increasing the charge screening capability of the host lattice can effectively decrease the migration barrier.

Derivatives of SrSnO₃ were identified as potential oxygen ion conductors with low migration barriers, based on oxygen vacancy states being reported close to the conduction band edge,^92–94 which was tested by introducing oxygen vacancies by K substitution in Sr sites and computing migration barriers in CC SrSnO_2.875 (0.62 eV) and NCC Sr_0.75K_0.25SnO_2.875 (0.54 eV and 0.62 eV). We further tested the significance of our proposed framework in aiding oxygen ion conductor designs by using it to understand the fast oxygen transport in Na_0.5Bi_0.5TiO₃ and the lower migration barriers in BiO⁺ layers compared to NaO⁻ layers. We could relate the fast oxygen ion transport of Na_0.5Bi_0.5TiO₃ in the BiO⁺ layer based on an increased charge screening capability of the host lattice in the BiO⁺ layer than the NaO⁻ layer, highlighting possibilities to use our proposed descriptors for computational designs based on optimizing different local environments in the same crystal structure. The energy of oxygen vacancy was tested as a descriptor of oxygen migration barrier beyond perovskite structures, considering two different pathways for a series of rutile and fluorite structures, and previously reported data,⁷⁷ highlighting its significance in aiding the search for promising oxides. Our observations on the interconnectedness of the electronic structure and the migration barrier not only establish the increased charge screening capability of the host lattice as a design guideline for decreasing the oxygen migration barrier, but they also deepen our understanding of the oxygen migration barrier.

Methods

The simulations of oxygen ion migration were performed using DFT and the exchange-correlation was treated based on the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA)¹¹⁹ as implemented in the VASP package.¹²⁰ The core electrons were treated within the projector augmented wave (PAW) formalism.¹²¹ We elected the GGA level of theory with PBE exchange functionals as the most efficient compromise of efficiency and accuracy. While SCAN functionals have been proposed to yield higher accuracy,¹²² they have shown slower convergence and lower completion rate for high-throughput solid calculations,¹²³ which would have increased the computational cost and the required human intervention in our study. As the GGA formalism can introduce self-interaction errors when modeling oxides with d electrons,¹²⁴ we conducted simulations on selected oxides with d electrons (complete list and computed energetics provided in Table S4†) using Hubbard correction with rotationally invariant approach.⁷⁹ The U correction values utilized were sourced in the Materials Project and are calibrated based on formation enthalpies of transition metal oxides.⁸⁰

The workflow was automated and executed using the MAST¹²⁵ and Pymatgen¹²⁶ Python libraries. Perovskite calculations used a 2 × 2 × 2 (40 atoms) supercell and a 4 × 4 × 4 k points grid in a Monkhorst–Pack scheme.¹²⁷ Previous studies have also used 40 atoms supercell to analyze trends in migration barrier⁵⁴ and vacancy formation energy⁵¹ across perovskites. In GGA and GGA + U formalisms energies are typically converged below 3 meV (ref. 128) and migration barriers are typically converged below 20 meV relative to our choice of k-point mesh.⁵⁴ All the structures in this work were obtained starting from the ideal perovskite structure and relaxing prior to the introduction of oxygen vacancies (stoichiometric ABO₃ structure), converging forces to 10⁻⁴ eV Å⁻¹. The symmetry of the resulting ABO₃ structures is reported in Table S1 (ESI†). All calculations were spin polarized and initialized in ferromagnetic states with initial guesses for the magnetic moments being +1μ_B, +5μ_B, and +1μ_B for A-site, B-site and O ions, respectively. While some perovskites can be antiferromagnetic at room temperature, they typically become paramagnetic at typical operative temperatures for solid oxide electrochemical cells (above 400 °C), which is seen for LaMnO₃,¹²⁹ LaFeO₃,¹³⁰ LaCoO₃,¹³¹ and LaNiO₃.¹³¹ Following previous high-throughput computations of vacancy formation energy¹³² and migration barrier⁵⁴ in perovskite oxides, we have initialized ferromagnetic structures as a cost-effective yet accurate strategy to approximate paramagnetism. Exploring the effect of different magnetic configurations is something that can be investigated in future studies. Our computed magnetic moments align with previously reported trends across oxides, as evidenced in Table S1 (ESI†). Calculations for non-perovskite structures used 3 × 2 × 2 and 2 × 2 × 2 supercells of 72 and 96 atoms for rutile and fluorite structures, respectively. All other settings were analogous to perovskite calculations.

After the introduction of the vacancy, the atomic positions were further relaxed to establish the minimum energy structure converging energies to 10⁻⁵ eV. A energy cutoff 150 eV higher than the suggested value in the pseudopotential was used for lattice relaxations. Additionally, Gaussian smearing with a width of 0.05 eV was employed in lattice relaxations. By introducing an oxygen vacancy in our supercells, non-stoichiometry values of 1/24 were obtained leading to structures with ABO_2.875 reduced chemical formula. To investigate the effect of vacancy electronic states on vacancy formation and migration barrier energetics, we created NCC and CC defected structures starting from the same stoichiometric ABO₃ structure as shown in Fig. 1a. Starting from the obtained NCC and CC non-stoichiometric ABO_2.875 structures, the corresponding NCC and CC vacancy formation energies and migration barriers were computed.

The vacancy formation energies were computed by comparing the energies of structures with and without oxygen vacancies according with previously reported formalism¹³³ and as further detailed in the ESI.† For all relaxations, the cutoff energies were set to 150 eV above the default values in the pseudopotential files to increase the accuracy. The migration barrier was determined using the climbing-image nudged elastic band method.¹³⁴ For each perovskite, the migration barrier was computed along two different migration pathways pointing at two different crystallographic directions in-plane (ipv) and out-of-plane (opv), shown in Fig. 1b. The considered migration path was a curved trajectory around the B-site,⁴³ and the ipv and opv pathways corresponded to the oxygen atom moving along two different edges of a BO₆ octahedron. The comparison between ipv (Fig. S1a, ESI†) and opv (Fig. S1b, ESI†) migration barriers generally showed small differences. The observed variability between ipv and opv migration barriers can be attributed to the anisotropy of oxygen ion diffusion in perovskites, which has been reported along different crystallographic directions^135,136 depending on crystal symmetry,³² or local magnetic moment.⁵² To analyze trends of migration barrier across different perovskites, we reported the minimum migration barrier among ipv (Fig. S1a, ESI†) and opv (Fig. S1b, ESI†). The vacancy formation energies and migration barriers of different perovskites are tabulated in Table S2 (ESI†).

All the descriptors were computed on the defected structures unless otherwise specified. All the transition state simulations and descriptors are reported for the specific pathway for which the migration barrier was selected. Before extracting descriptors based on electronic DOS and Bader charge analyses,⁷⁶ the electronic structure and charge densities were computed using a 8 × 8 × 8 k points grids, a cutoff of 850 eV and a fine FFT grid with 250 × 250 × 250 points. Moreover, the tetrahedron method with Blöchl corrections¹³⁷ was employed to improve the accuracy of zero-d-electron perovskite calculations. The O 2p band center was calculated as the centroid of the DOS below Fermi level projected onto the 2p orbitals of the O atoms. Similarly, the position of metal bands was computed as the centroid of the DOS projected onto their orbitals. The vacancy excess charge density was computed by dividing the atomic excess charge of first neighbors of an oxygen vacancy (2 B-site and 4 A-site cations as shown in Fig. 1e) by their Bader volume, as further detailed in the ESI.† Filled electronic states associated with NCC oxygen vacancies in oxides without d electrons represented the highest occupied orbital and their energy was identified by the Fermi level. The energy of empty electronic states associated with CC oxygen vacancies or A-site substituted perovskites was evaluated as the centroid of their DOS. The descriptors hereby reported have been tabulated in Tables S3 and S5 (ESI†).

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Conceptualization: D. V., K. G., and Y. S. H. Methodology: D. V., K. G., and Y. S. H. Investigation: D. V., and K. G. Data Curation: D. V., K. G., R. M., and S. R. Writing: D. V., K. G., and Y. S. H. Review and editing: D. V., K. G., R. M., S. R., and Y. S. H. Supervision: Y. S. H. Funding acquisition: Y. S. H.

Conflicts of interest

The authors do not have any conflict of interest do declare.

Acknowledgements

The authors thank Prof. Livia Giordano and Dr Karthik Akkiraju for fruitful discussions. This work was supported by ExxonMobil Technology and Engineering Company. D. V. was also financially supported by the Warren M. Roshenow Fellowship fund and the MathWorks Mechanical Engineering Fellowship. This research used the resources of the National Energy Research Scientific Computing Center (NERSC). This research also made use of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (NSF) grant number ACI-1548662, and SDSC through DMR160163 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by NSF grants #2138259, #2138286, #2138307, #2137603, and #2138296.

References

1. A. Orera and P. R. Slater, New chemical systems for solid oxide fuel cells, Chem. Mater., 2010, 22, 675–690.
2. N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Progress in material selection for solid oxide fuel cell technology: a review, Prog. Mater. Sci., 2015, 72, 141–337.
3. M. Chatenet, et al., Water electrolysis: from textbook knowledge to the latest scientific strategies and industrial developments, Chem. Soc. Rev., 2022, 51, 4583–4762.
4. D. R. Miller, S. A. Akbar and P. A. Morris, Nanoscale metal oxide-based heterojunctions for gas sensing: a review, Sens. Actuators, B, 2014, 204, 250–272.
5. T. Liu, X. Zhang, L. Yuan and J. Yu, A review of high-temperature electrochemical sensors based on stabilized zirconia, Solid State Ionics, 2015, 283, 91–102.
6. G. Chen, et al., Roadmap for Sustainable Mixed Ionic-Electronic Conducting Membranes, Adv. Funct. Mater., 2022, 32, 2105702.
7. O. H. Kwon and G. M. Choi, Electrical conductivity of thick film YSZ, Solid State Ionics, 2006, 177, 3057–3062.
8. T. Ishihara, Development of new fast oxide ion conductor and application for intermediate temperature Solid Oxide Fuel Cells, Bull. Chem. Soc. Jpn., 2006, 79, 1155–1166.
9. K. Huang, R. S. Tichy and J. B. Goodenough, Superior Perovskite Oxide-Ion Conductor; Strontium- and Magnesium-Doped LaGaO3: I, Phase Relationships and Electrical Properties, J. Am. Ceram. Soc., 1998, 75, 2565.
10. D. J. L. Brett, A. Atkinson, N. P. Brandon and S. J. Skinner, Intermediate temperature solid oxide fuel cells, Chem. Soc. Rev., 2008, 37, 1568–1578.
11. E. D. Wachsman and K. T. Lee, Lowering the temperature of solid oxide fuel cells, Science, 2011, 334, 935–939.
12. A. Hauch, et al., Recent advances in solid oxide cell technology for electrolysis, Science, 2020, 370, eaba6118.
13. Y. Song, X. Zhang, K. Xie, G. Wang and X. Bao, High-temperature CO2 electrolysis in solid oxide electrolysis cells: developments, challenges, and prospects, Adv. Mater., 2019, 31, 1902033.
14. P. Lacorre, F. Goutenoire, O. Bohnke, R. Retoux and Y. Laligant, Designing fast oxide-ion conductors based on La2Mo2O9, Nature, 2000, 404, 856–858.
15. W. Zhang, et al., Oxide-ion conduction in the Dion–Jacobson phase CsBi2Ti2NbO10− δ, Nat. Commun., 2020, 11, 1–8.
16. L. León-Reina, et al., High oxide ion conductivity in Al-doped germanium oxyapatite, Chem. Mater., 2005, 17, 596–600.
17. P. Singh and J. B. Goodenough, Sr 1− x K x Si 1− y Ge y O 3− 0.5 x: a new family of superior oxide-ion conductors, Energy Environ. Sci., 2012, 5, 9626–9631.
18. M. Li, et al., A family of oxide ion conductors based on the ferroelectric perovskite Na0. 5Bi0. 5TiO3, Nat. Mater., 2014, 13, 31–35.
19. X. Kuang, et al., Interstitial oxide ion conductivity in the layered tetrahedral network melilite structure, Nat. Mater., 2008, 7, 498–504.
20. F. Abraham, J. C. Boivin, G. Mairesse and G. Nowogrocki, The bimevox series: A new family of high performances oxide ion conductors, Solid State Ionics, 1990, 40–41, 934–937.
21. S. J. Skinner and J. A. Kilner, Oxygen ion conductors, Mater. Today, 2003, 6(3), 30–37.
22. H. Mehrer, Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer Science & Business Media, 2007, vol. 155.
23. A. Chroneos, B. Yildiz, A. Tarancón, D. Parfitt and J. A. Kilner, Oxygen diffusion in solid oxide fuel cell cathode and electrolyte materials: Mechanistic insights from atomistic simulations, Energy Environ. Sci., 2011, 4, 2774–2789.
24. M. Kessel, R. A. De Souza and M. Martin, Oxygen diffusion in single crystal barium titanate, Phys. Chem. Chem. Phys., 2015, 17, 12587–12597.
25. R. A. De Souza, V. Metlenko, D. Park and T. E. Weirich, Behavior of oxygen vacancies in single-crystal SrTiO 3: Equilibrium distribution and diffusion kinetics, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–11.
26. T. Ishigaki, S. Yamauchi, J. Mizusaki, K. Fueki and H. Tamura, Tracer diffusion coefficient of oxide ions in LaCoO3 single crystal, J. Solid State Chem., 1984, 54, 100–107.
27. R. A. De Souza, Oxygen Diffusion in SrTiO3 and Related Perovskite Oxides, Adv. Funct. Mater., 2015, 25, 6326–6342.
28. T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, Diffusion of oxide ion vacancies in perovskite-type oxides, J. Solid State Chem., 1988, 73, 179–187.
29. J. B. Goodenough, Review Lecture-Fast ionic conduction in solid, Proc. R. Soc. London, Ser. A, 1984, 393, 215–234.
30. M. Pavone, A. M. Ritzmann and E. A. Carter, Quantum-mechanics-based design principles for solid oxide fuel cell cathode materials, Energy Environ. Sci., 2011, 4, 4933–4937.
31. A. M. Deml, V. Stevanović, C. L. Muhich, C. B. Musgrave and R. O'Hayre, Oxide enthalpy of formation and band gap energy as accurate descriptors of oxygen vacancy formation energetics, Energy Environ. Sci., 2014, 7, 1996–2004.
32. Y.-S. Zheng, et al., Electronic origin of oxygen transport behavior in La-based perovskites: a density functional theory study, J. Phys. Chem. C, 2018, 123, 275–290.
33. R. B. Wexler, G. S. Gautam, E. B. Stechel and E. A. Carter, Factors governing oxygen vacancy formation in oxide perovskites, J. Am. Chem. Soc., 2021, 143, 13212–13227.
34. Y. L. Lee, J. Kleis, J. Rossmeisl, S. H. Yang and D. Morgan, Prediction of solid oxide fuel cell cathode activity with first-principles descriptors, Energy Environ. Sci., 2011, 4, 3966–3970.
35. L. Giordano, et al., Electronic Structure-Based Descriptors for Oxide Properties and Functions, Acc. Chem. Res., 2022, 55, 298–308.
36. A. M. Deml, A. M. Holder, R. P. O'Hayre, C. B. Musgrave and V. Stevanović, Intrinsic material properties dictating oxygen vacancy formation energetics in metal oxides, J. Phys. Chem. Lett., 2015, 6, 1948–1953.
37. R. Gao, et al., Designing optimal perovskite structure for high ionic conduction, Adv. Mater., 2020, 32, 1905178.
38. R. L. Cook and A. F. Sammells, On the systematic selection of perovskite solid electrolytes for intermediate temperature fuel cells, Solid State Ionics, 1991, 45, 311–321,  DOI:10.1016/0167-2738(91)90167-A.
39. J. A. Kilner and R. J. Brook, A study of oxygen ion conductivity in doped non-stoichiometric oxides, Solid State Ionics, 1982, 6, 237–252.
40. T. Famprikis, et al., Under pressure: mechanochemical effects on structure and ion conduction in the sodium-ion solid electrolyte Na3PS4, J. Am. Chem. Soc., 2020, 142, 18422–18436.
41. V. Butler, C. R. A. Catlow, B. E. F. Fender and J. H. Harding, Dopant ion radius and ionic conductivity in cerium dioxide, Solid State Ionics, 1983, 8, 109–113,  DOI:10.1016/0167-2738(83)90070-X.
42. F. Giannici, et al., Structure and oxide ion conductivity: local order, defect interactions and grain boundary effects in acceptor-doped ceria, Chem. Mater., 2014, 26, 5994–6006.
43. M. Cherry, M. S. Islam and C. R. A. Catlow, Oxygen ion migration in perovskite-type oxides, J. Solid State Chem., 1995, 118, 125–132.
44. J. R. Tolchard, P. R. Slater and M. S. Islam, Insight into doping effects in apatite silicate ionic conductors, Adv. Funct. Mater., 2007, 17, 2564–2571.
45. A. F. Sammells, R. L. Cook, J. H. White, J. J. Osborne and R. C. MacDuff, Rational selection of advanced solid electrolytes for intermediate temperature fuel cells, Solid State Ionics, 1992, 52, 111–123.
46. C. A. Fuller, et al., Brownmillerite-Type Sr2ScGaO5 Oxide Ion Conductor: Local Structure, Phase Transition, and Dynamics, Chem. Mater., 2019, 31, 7395–7404.
47. W. Paulus, et al., Lattice dynamics to trigger low temperature oxygen mobility in solid oxide ion conductors, J. Am. Chem. Soc., 2008, 130, 16080–16085.
48. S. Muy, R. Schlem, Y. Shao-Horn and W. G. Zeier, Phonon–ion interactions: Designing ion mobility based on lattice dynamics, Adv. Energy Mater., 2021, 11, 2002787.
49. T. T. Mayeshiba and D. D. Morgan, Factors controlling oxygen migration barriers in perovskites, Solid State Ionics, 2016, 296, 71–77.
50. M. M. Kuklja, E. A. Kotomin, R. Merkle, Y. A. Mastrikov and J. Maier, Combined theoretical and experimental analysis of processes determining cathode performance in solid oxide fuel cells, Phys. Chem. Chem. Phys., 2013, 15, 5443–5471.
51. A. M. Ritzmann, A. B. Muñoz-García, M. Pavone, J. A. Keith and E. A. Carter, Ab initio DFT+ U analysis of oxygen vacancy formation and migration in La1-xSr x FeO3-δ (x= 0, 0.25, 0.50), Chem. Mater., 2013, 25, 3011–3019.
52. A. M. Ritzmann, M. Pavone, A. B. Muñoz-García, J. A. Keith and E. A. Carter, Ab initio DFT+U analysis of oxygen transport in LaCoO3: The effect of Co3+ magnetic states, J. Mater. Chem. A, 2014, 2, 8060–8074.
53. Y. A. Mastrikov, R. Merkle, E. A. Kotomin, M. M. Kuklja and J. Maier, Formation and migration of oxygen vacancies in La 1− x Sr x Co 1− y Fe y O 3− δ perovskites: insight from ab initio calculations and comparison with Ba 1− x Sr x Co 1− y Fe y O 3− δ, Phys. Chem. Chem. Phys., 2013, 15, 911–918.
54. T. Mayeshiba and D. Morgan, Strain effects on oxygen migration in perovskites, Phys. Chem. Chem. Phys., 2015, 17, 2715–2721.
55. M. S. Islam, Computer modelling of defects and transport in perovskite oxides, Solid State Ionics, 2002, 154, 75–85.
56. J. Carrasco, et al., First-principles calculations of the atomic and electronic structure of F centers in the bulk and on the (001) surface of SrTi O3, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(6), 064106.
57. A. I. Popov, E. A. Kotomin and J. Maier, Basic properties of the F-type centers in halides, oxides and perovskites, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 3084–3089.
58. A. Belzner, T. M. Gür and R. A. Huggins, Oxygen chemical diffusion in strontium doped lanthanum manganites, Solid State Ionics, 1992, 57, 327–337.
59. I. Yasuda, K. Ogasawara and M. Hishinuma, Oxygen tracer diffusion in polycrystalline calcium-doped lanthanum chromites, J. Am. Ceram. Soc., 1997, 80, 3009–3012.
60. K. Nomura and S. Tanase, Electrical conduction behavior in (La0.9Sr0.1)MIIIO3-δ (MIII = Al, Ga, Sc, In, and Lu) perovskites, Solid State Ionics, 1997, 98, 229–236.
61. R. A. De Souza, V. Metlenko, D. Park and T. E. Weirich, Behavior of oxygen vacancies in single-crystal SrTiO 3: Equilibrium distribution and diffusion kinetics, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–11.
62. S. A. Hayward, et al., Transformation processes in la al o 3: Neutron diffraction, dielectric, thermal, optical, and raman studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 054110.
63. T.-Y. Chen and K.-Z. Fung, Comparison of dissolution behavior and ionic conduction between Sr and/or Mg doped LaGaO3 and LaAlO3, J. Power Sources, 2004, 132, 1–10.
64. T. Takahashi and H. Iwahara, Ionic conduction in perovskite-type oxide solid solution and its application to the solid electrolyte fuel cell, Energy Convers., 1971, 11, 105–111.
65. T. Ishihara, et al., Oxide Ion Conductivity in Doubly Doped PrGaO3 Perovskite-Type Oxide, J. Electrochem. Soc., 1999, 146, 1643.
66. G. B. Zhang and D. M. Smyth, Defects and transport of the brownmillerite oxides with high oxygen ion conductivity—Ba2In2O5, Solid State Ionics, 1995, 82, 161–172.
67. W. T. Hong, et al., Toward the rational design of non-precious transition metal oxides for oxygen electrocatalysis, Energy Environ. Sci., 2015, 8, 1404–1427.
68. S. A. Prosandeyev, N. M. Teslenko and A. V. Fisenko, Breaking of symmetry of one-electron orbitals at oxygen vacancies in perovskite-type oxides, J. Phys.: Condens. Matter, 1993, 5, 9327.
69. W.-J. Yin, S.-H. Wei, M. M. Al-Jassim and Y. Yan, Origin of the diverse behavior of oxygen vacancies in A B O 3 perovskites: A symmetry based analysis, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 201201.
70. W. J. Yin, S. H. Wei, M. M. Al-Jassim and Y. Yan, Prediction of the chemical trends of oxygen vacancy levels in binary metal oxides, Appl. Phys. Lett., 2011, 99, 10–13.
71. R. Hoffmann, How chemistry and physics meet in the solid state, Angew. Chem., Int. Ed. Engl., 1987, 26, 846–878.
72. A. B. Munoz-Garcia, A. M. Ritzmann, M. Pavone, J. A. Keith and E. A. Carter, Oxygen transport in perovskite-type solid oxide fuel cell materials: insights from quantum mechanics, Acc. Chem. Res., 2014, 47, 3340–3348.
73. M. S. Khan, M. S. Islam and D. R. Bates, Dopant substitution and ion migration in the LaGaO3-based oxygen ion conductor, J. Phys. Chem. B, 1998, 102, 3099–3104.
74. M. Kajitani, et al., Doping effect on crystal structure and conduction property of fast oxide ion conductor LaGaO3-based perovskite, J. Phys. Chem. Solids, 2007, 68, 758–764.
75. M. Gambino, et al., Defect interaction and local structural distortions in Mg-doped LaGaO3: a combined experimental and theoretical study, J. Chem. Phys., 2017, 147, 144702.
76. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
77. C. Linderalv, A. Lindman and P. Erhart, A unifying perspective on oxygen vacancies in wide band gap oxides, J. Phys. Chem. Lett., 2018, 9, 222–228.
78. M. S. Malghani and D. Y. Smith, Physical basis of the Mollwo-Ivey relation between lattice constant and optical absorption of defects in ionic crystals, Phys. Rev. Lett., 1992, 69, 184.
79. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
80. M. Wang and A. Navrotsky, Enthalpy of formation of LiNiO2, LiCoO2 and their solid solution, LiNi1− xCoxO2, Solid State Ionics, 2004, 166, 167–173.
81. M. T. Curnan and J. R. Kitchin, Effects of concentration, crystal structure, magnetism, and electronic structure method on first-principles oxygen vacancy formation energy trends in perovskites, J. Phys. Chem. C, 2014, 118, 28776–28790.
82. E. A. Kotomin, et al., First principles calculations of oxygen vacancy formation and migration in mixed conducting Ba0. 5Sr0. 5Co1− yFeyO3− δ perovskites, Solid State Ionics, 2011, 188, 1–5.
83. C. Mitra, C. Lin, J. Robertson and A. A. Demkov, Electronic structure of oxygen vacancies in SrTiO 3 and LaAlO 3, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 1–8.
84. C. Ricca, I. Timrov, M. Cococcioni, N. Marzari and U. Aschauer, Self-consistent DFT+ U+ V study of oxygen vacancies in SrTiO 3, Phys. Rev. Res., 2020, 2, 023313.
85. G. M. Choi and H. L. Tuller, Defect structure and electrical properties of single-crystal Ba0. 03Sr0. 97TiO3, J. Am. Ceram. Soc., 1988, 71, 201–205.
86. N. G. Eror and D. M. Smyth, Nonstoichiometric disorder in single-crystalline BaTiO3 at elevated temperatures, J. Solid State Chem., 1978, 24, 235–244.
87. J. H. Schulman and W. D. Compton, Color Centers in Solids, Pergamon, 1962, vol. 2.
88. A. I. Popov, M. A. Monge, R. Gonzalez, Y. Chen and E. A. Kotomin, Dynamics of F-center annihilation in thermochemically reducedMgO single crystals, Solid State Commun., 2001, 118, 163–167.
89. A. I. Popov, E. A. Kotomin and M. M. Kuklja, Quantum chemical calculations of the electron center diffusion in MgO crystals, Phys. Status Solidi B, 1996, 195, 61–66.
90. H. M. Jaim, S. Lee, X. Zhang and I. Takeuchi, Stability of the oxygen vacancy induced conductivity in BaSnO3 thin films on SrTiO3, Appl. Phys. Lett., 2017, 111, 172102.
91. M. Kim, et al., Oxygen-vacancy-introduced BaSnO3− δ photoanodes with tunable band structures for efficient solar-driven water splitting, Adv. Mater., 2019, 31, 1903316.
92. Q. Gao, H. Chen, K. Li and Q. Liu, Band gap engineering and room-temperature ferromagnetism by oxygen vacancies in SrSnO3 epitaxial films, ACS Appl. Mater. Interfaces, 2018, 10, 27503–27509.
93. N. Zidi, et al., Transport properties and photo electrochemical characterization of oxygen-deficient ASnO3− δ (A= Ca, Sr and Ba), Phys. B, 2010, 405, 3355–3359.
94. L. Chantelle, et al., Probing the site-selective doping in SrSnO3: Eu oxides and its impact on the crystal and electronic structures using synchrotron radiation and DFT simulations, Inorg. Chem., 2020, 59, 7666–7680.
95. K. S. Belthle, et al., Quantitative Determination of Native Point-Defect Concentrations at the ppm Level in Un-Doped BaSnO3 Thin Films, Adv. Funct. Mater., 2022, 32, 2113023.
96. J. A. Dawson, H. Chen and I. Tanaka, Crystal structure, defect chemistry and oxygen ion transport of the ferroelectric perovskite, Na 0.5 Bi 0.5 TiO 3: insights from first-principles calculations, J. Mater. Chem. A, 2015, 3, 16574–16582.
97. H. Zhang, A. H. H. Ramadan and R. A. De Souza, Atomistic simulations of ion migration in sodium bismuth titanate (NBT) materials: towards superior oxide-ion conductors, J. Mater. Chem. A, 2018, 6, 9116–9123.
98. D. A. Kuznetsov, J. Peng, L. Giordano, Y. Román-Leshkov and Y. Shao-Horn, Bismuth substituted strontium cobalt perovskites for catalyzing oxygen evolution, J. Phys. Chem. C, 2020, 124, 6562–6570.
99. D. A. Kuznetsov, et al., Tuning redox transitions via inductive effect in metal oxides and complexes, and implications in oxygen electrocatalysis, Joule, 2018, 2, 225–244.
100. Z. W. B. Iton and K. A. See, Multivalent Ion Conduction in Inorganic Solids, Chem. Mater., 2022, 34, 881–898.
101. M. S. Munde, D. Z. Gao and A. L. Shluger, Diffusion and aggregation of oxygen vacancies in amorphous silica, J. Phys.: Condens. Matter, 2017, 29, 245701.
102. T. Nabatame, et al., Comparative studies on oxygen diffusion coefficients for amorphous and γ-Al2O3 films using 18O isotope, Jpn. J. Appl. Phys., 2003, 42, 7205.
103. G. G. Marmitt, et al., Oxygen diffusion in TiO2 films studied by electron and ion Rutherford backscattering, Thin Solid Films, 2017, 629, 97–102.
104. Z. Zhang, et al., Imaging intrinsic diffusion of bridge-bonded oxygen vacancies on TiO 2 (110), Phys. Rev. Lett., 2007, 99, 126105.
105. H. Cai, et al., Diverse functions of oxygen vacancies for oxygen ion conduction, ACS Appl. Energy Mater., 2022, 5, 11122–11132.
106. K. Sasaki, M. Gödickemeier, P. Bohac, A. Orliukas and L. J. Gauckler, Microstructure design of mixed-conducting solid oxide fuel cell cathodes, in Proc 5th IEA Workshop on SOFC Materials, Process Engineering and Electrochemistry, Forschungszentrum Jülich, Germany, 1993, pp. 187–196.
107. D. Xiang, et al., High-Performance Fuel Cells Based on In2O3–La/Pr-Doped Ceria Semiconductor–Ionic Conductor Materials Electrolyte, Energy Technol., 2020, 8, 1900753.
108. A. Kushima and B. Yildiz, Oxygen ion diffusivity in strained yttria stabilized zirconia: Where is the fastest strain?, J. Mater. Chem., 2010, 20, 4809–4819.
109. B. P. Uberuaga and G. Pilania, Effect of cation ordering on oxygen vacancy diffusion pathways in double perovskites, Chem. Mater., 2015, 27, 5020–5026.
110. J. Koettgen, et al., Understanding the ionic conductivity maximum in doped ceria: trapping and blocking, Phys. Chem. Chem. Phys., 2018, 20, 14291–14321.
111. S. Muy, et al., Tuning mobility and stability of lithium ion conductors based on lattice dynamics, Energy Environ. Sci., 2018, 11, 850–859.
112. Y. Wang, et al., Design principles for solid-state lithium superionic conductors, Nat. Mater., 2015, 14, 1026–1031.
113. J. Lee, N. Ohba and R. Asahi, Design rules for high oxygen-ion conductivity in garnet-type oxides, Chem. Mater., 2020, 32, 1358–1370.
114. Y. Gao, N. Li, Y. Wu, W. Yang and S. Bo, Rethinking the design of ionic conductors using Meyer–Neldel–conductivity plot, Adv. Energy Mater., 2021, 11, 2100325.
115. J. B. Goodenough, Oxide-ion conductors by design, Nature, 2000, 404, 821–823.
116. A. V. Berenov, J. L. MacManus-Driscoll and J. A. Kilner, Observation of the compensation law during oxygen diffusion in perovskite materials, Int. J. Inorg. Mater., 2001, 3, 1109–1111.
117. S. Gelin, A. Champagne-Ruel and N. Mousseau, Enthalpy-entropy compensation of atomic diffusion originates from softening of low frequency phonons, Nat. Commun., 2020, 11, 3977.
118. A. Yelon, B. Movaghar and R. S. Crandall, Multi-excitation entropy: Its role in thermodynamics and kinetics, Rep. Prog. Phys., 2006, 69, 1145–1194.
119. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
120. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
121. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
122. J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly constrained and appropriately normed semilocal density functional, Phys. Rev. Lett., 2015, 115, 036402.
123. R. Kingsbury, et al., Performance comparison of r 2 SCAN and SCAN metaGGA density functionals for solid materials via an automated, high-throughput computational workflow, Phys. Rev. Mater., 2022, 6, 013801.
124. L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA+ U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
125. T. Mayeshiba, et al., The MAterials Simulation Toolkit (MAST) for Atomistic Modeling of Defects and, Comput. Mater. Sci., 2017, 126, 90–102.
126. S. P. Ong, et al., Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319,  DOI:10.1016/j.commatsci.2012.10.028.
127. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
128. R. Jacobs, T. Mayeshiba, J. Booske and D. Morgan, Material discovery and design principles for stable, high activity perovskite cathodes for solid oxide fuel cells, Adv. Energy Mater., 2018, 8, 1702708.
129. J.-S. Zhou and J. B. Goodenough, Paramagnetic phase in single-crystal LaMnO 3, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R15002.
130. D. Treves, M. Eibsch tz and P. Coppens, Dependence of superexchange interaction on Fe 3+? O 2?? Fe 3+ linkage angle, Phys. Lett., 1965, 18, 216–217.
131. J. B. Goodenough and P. M. Raccah, Complex vs band formation in perovskite oxides, J. Appl. Phys., 1965, 36, 1031–1032.
132. Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Ab initio energetics of La B O 3 (001)(B= Mn, Fe, Co, and Ni) for solid oxide fuel cell cathodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101.
133. C. Freysoldt, et al., First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305.
134. G. Henkelman, B. P. Uberuaga and H. Jónsson, Climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
135. M. Burriel, et al., Anisotropic oxygen diffusion properties in epitaxial thin films of La 2 NiO 4+ δ, J. Mater. Chem., 2008, 18, 416–422.
136. J.-M. Bassat, et al., Anisotropic oxygen diffusion properties in Pr2NiO4+ δ and Nd2NiO4+ δ single crystals, J. Phys. Chem. C, 2013, 117, 26466–26472.
137. P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223.

---

Footnote

† Electronic supplementary information (ESI) available: Electronic DOS, tabulated data and additional figures and analyses. See DOI: https://doi.org/10.1039/d4ta04049j

---