 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Differentiating ion transport of water-in-salt electrolytes within micro- and meso-pores of a multiporous carbon electrode†
M. Tauhidul
Islam
 a,
Bernhard
Gollas
a,
Bernhard
Gollas
 a and
Qamar
Abbas
a and
Qamar
Abbas
 *ab
*ab
aInstitute for Chemistry and Technology of Materials, Graz University of Technology, Stremayrgasse 9, 8010 Graz, Austria. E-mail: qamar.abbas@tugraz.at
bInstitute of Chemistry and Technical Electrochemistry, Poznan University of Technology, Berdychowo 4, 60965 Poznan, Poland
First published on 22nd August 2024
Abstract
Understanding ion transport in porous carbon electrodes is crucial for enhancing the performance of electrochemical energy storage devices. However, for systems using carbon electrodes and water-in-salt electrolytes, this is not generally understood. Here, two salts with different ionic interactions in water, lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) or choline chloride (ChCl), were utilized at concentrations up to 20 mol kg−1 to explore the ion transport behavior. We report a new method for calculating the ion diffusion coefficient in carbon pores, considering the diffusivity of the bulk electrolyte, as well as the tortuosity and porosity of the carbon electrode. Accuracy is validated by comparing data with bulk electrolyte diffusivity reported from PFG-NMR in the literature, which is further used together with porosity estimated with nitrogen gas adsorption and tortuosity from electrochemical impedance spectroscopy. This technique effectively distinguishes between tortuosity in micro- and meso-pores by considering their volume and surface area. The different ion hydration patterns of ChCl and LiTFSI at concentrations above 10 mol kg−1 influence the ion transport and the tortuosity to different extents. This is confirmed by changes in hydrogen bonding observed in the Raman water bands. Lastly, we introduce a relationship between tortuosity, in-pore ion diffusivity and capacitance to distinguish the charge distribution within micro- and meso-pores at open circuit voltage as well as under applied bias voltages. Our findings reveal the degree of ion dissociation in concentrated aqueous electrolytes as a key parameter determining the charging/discharging rate performance of carbon electrode based capacitors. This study helps develop carbon materials and compatible electrolytes to ensure that the capacitor meets the desired performance criteria while being reliable and efficient.
Introduction
Electrochemical capacitors play a vital role in hybrid electric vehicles, where rapid charging and discharging are crucial. In both electric double-layer capacitors (EDLCs) and hybrid capacitors, the power performance of the device primarily arises from the charge stored in the EDL electrode.1 Nanoporous carbon stands out as a typical electrode material for EDL charge storage, wherein ionic charges are physically stored through electrosorption at the electrode/electrolyte interface and efficiently released during discharge. The energy density E of an EDLC is directly proportional to the capacitance C and the square of the voltage U (E = ½CU2). Consequently, achieving superior performance (power and cycle life of electrochemical capacitors) involves customizing the pore morphology of carbon electrodes and utilizing electrolytes with high electrochemical stability.Non-aqueous electrolytes have been shown to withstand high voltages of up to 3 V.2–4 However, these electrolytes require strictly moisture-free processing, resulting in high costs, and pose safety and environmental risks.5–7 On the other hand, aqueous electrolytes possess high ionic conductivity while being safe and inexpensive, avoiding the above-mentioned drawbacks.5 In order to avoid water oxidation/reduction reactions that limit the stability of classical aqueous electrolytes, Suo et al. in 2015 proposed water-in-salt electrolytes. In lithium bis(trifluoromethanesulfonyl)imide based electrolyte at high concentrations up to 21 mol kg−1, the salt fraction exceeds the solvent in both volume and mass, which enabled a battery operating at 2.3 V with Mo6S8 as the anode and LiMn2O4 as the cathode.7 Following this initial demonstration, LiTFSI-based water-in-salt electrolytes have undergone extensive research for their applicability in various energy storage devices, including EDLCs8–10 and hybrid capacitors.11 More recently, cost-effective and environmentally friendly alternatives, such as choline chloride, choline nitrate, and choline iodide, have also been investigated as potential water-in-salt electrolytes for high-energy electrochemical hybrid capacitors.12,13 However, using water-in-salt electrolytes leads to certain challenges, such as restricted ion transport, insufficient wetting of carbon electrodes,14 and unsatisfactory low-temperature performance. For example, Lannelongue et al. reported a decrease in capacitance of around 15% and 33% after 2000 charge/discharge cycles with a current loading of 0.8 A g−1 for 7 mol kg−1 and 31.3 mol kg−1 LiTFSI, respectively. They suggested a compromise between voltage, power density, energy density, and stability to address these effects.6 Hence, investigating the ion dynamics of water-in-salt electrolytes both in bulk solution and within the pores of carbon electrodes is essential for unlocking their full potential and expanding their range of applications.
Several research groups have reported the ion dynamics in bulk water-in-salt electrolytes of LiTFSI using PFG-NMR.15–18 Abbas et al. compared the ion diffusivity and dissociation of bulk water-in-choline fluoride with water-in-LiTFSI and found enhanced ionicity for the choline salts.13 Mangiacapre et al. measured the diffusivity of choline ions in aqueous bulk ChCl solution using PFG-NMR.19 Unfortunately, due to the rapid relaxation of the 35Cl nucleus, the diffusivity of chloride ions could not be determined by PFG-NMR.20 These reports primarily focus on the diffusivity of bulk water-in-salt electrolytes prepared from LiTFSI and ChCl, without providing information on ion hydration. To comprehend device performance fully, it is crucial to interpret the complex phenomena of ion transport within the networks of nanoscale carbon pores characterized by different diameters, porosity, tortuosity, permeability, and bottlenecks.21–24 To the best of our knowledge, only Moreno-Fernández et al. have offered insights into the in-pore transport of LiTFSI water-in-salt electrolytes based on the relaxation time of 19F and 7Li nuclei in solid-state NMR during electrolyte diffusion.23
Various electrochemical methods, including cyclic voltammetry (using the Randles–Ševčík equation),25,26 electrochemical impedance spectroscopy (using the Randles–Warburg model, electrode thickness and knee frequency),27–29 galvanostatic and intermittent titration techniques30 or step potential electrochemical spectroscopy,31 have been used to determine the in-pore ion diffusivity of various classical electrolytes. Although a similar trend was found, conflicting diffusivity values have been determined with these techniques.32 On the other hand, solid-state NMR,23in situ PFG-NMR,22,24 EQCM (electrochemical quartz microbalance),33 small-angle X-ray and neutron scattering (SAXS and SANS),34in situ IR spectroscopy,35 and computer simulations36 are frequently utilized for a more precise analysis of the ion transport properties of organic electrolytes within carbon nanopores. These techniques are sophisticated and expensive and come with a few technical limitations. For example, not all electrolyte ions may possess NMR-active nuclei, and the resolution of in-pore NMR peaks has been reported to be low, particularly for water-in-salt electrolytes, owing to the high proportion of inaccessible sub-nanometer carbon pores.23 Furthermore, commercially available carbons used for supercapacitors typically encompass sub-nanometer micro-, meso-, and macro-pores, making it challenging for the aforementioned techniques to efficiently probe and differentiate ion transport behavior in multiporous carbons.22–24
Here, we studied the effective ion diffusivity of water-in-salt electrolytes based on ChCl and LiTFSI in the micro- and meso-pores of commercially available carbon YP80 F. To comprehend in-pore ion dynamics, we explored the relationship between bulk electrolyte diffusivity, porosity, and tortuosity. The average bulk electrolyte diffusivity based on PFG-NMR has been obtained from several references, while the porosity was estimated from N2 gas adsorption. The electrode's tortuosity was determined from electrochemical impedance spectroscopy (EIS), considering parameters such as maximum capacitance, knee frequency, in-pore ionic resistance, pore volume fraction, and surface area fraction.32,37,38 To this end, EIS is used as a preferred technique, as it is non-invasive and inexpensive compared to other techniques with the additional feature of being able to distinguish between diffusivities within a range of pore sizes of the same carbon electrode. By considering the micro- and/or meso-pores as inter- and intra-connected series capacitors, the total equivalent capacitance has been calculated as the sum of the reciprocals of the individual capacitances in these pores. Finally, we correlated the energy efficiency of capacitors with different concentrations of water-in-salt electrolytes to the diffusion of ions, ionicity, and hydration behavior.
Experimental
Electrolytes
Lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) and (2-hydroxyethyl)trimethylammonium chloride (choline chloride, labelled here as ChCl) were procured from IoLiTec (Heilbronn, Germany) and Sigma-Aldrich (Germany), respectively, to prepare a range of electrolytes with concentrations of 1, 5, 10, 15 and 20 mol kg−1. The salt-to-water volume ratio, salt-to-water weight ratio, and water-to-salt molar mass ratio for different concentrations of electrolytes are given in Table S1 and Fig. S1 (ESI).†Characterization electrolytes
The dynamic viscosity (η) of the bulk electrolyte solutions was determined with a Modular Compact Rheometer (MCR 502 SN 82231668 with a cone plate system, Anton Paar, Graz, Austria) by adopting a standard protocol at 25 °C. A two-electrode Swagelok cell with a cylindrical PTFE (polytetrafluoroethylene) ring spacer positioned between two metallic current collectors (Fig. S2†) was utilized for measuring the electrolyte resistance R by potentiostatic electrochemical impedance spectroscopy (PEIS). Ni-alloy (C22) and stainless-steel rods (1.2 cm diameter) were employed as current collectors for choline chloride and LiTFSI solutions, respectively. PEIS was performed over the frequency range of 100 kHz to 1 mHz with a single sine sinusoidal signal at open circuit voltage using a BioLogic VMP-300 Potentiostat (Paris, France). The ionic conductivity σ of the electrolyte is calculated with eqn (1). | (1) |
Electrochemical capacitor cell assembly and characterization
Activated porous carbon sheets used as electrodes in capacitor cells were fabricated from a mixture of 90 wt% YP80 F commercial carbon, 5 wt% carbon black SUPER C65 (Imerys) as a conductive additive, and 5 wt% polytetrafluoroethylene (60 wt% suspensions in water, Sigma-Aldrich) as a binder. The components were mixed in isopropanol using a material to solvent ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 and the mixture was stirred at 70 °C until a homogeneous dough was obtained. Subsequently, the dough was rolled onto a glass plate to produce a ∼140 μm thick sheet. The carbon sheet was dried at 80 °C overnight and was used as positive and negative electrodes in the two-electrode symmetric Swagelok-type capacitor cells described above. 1.0 cm diameter working and counter electrode disks made from the prepared carbon sheet sandwiched a 1.2 cm diameter glass microfiber separator (Whatman GF/A, 260 μm thick). Water-in-salt electrolyte solutions consisted of concentrated ChCl or LiTFSI. Electrochemical impedance spectra were collected in the frequency range of 1 MHz to 1 mHz using a single sinusoidal signal at open circuit voltage as well as at 0.4 V, 0.8 V and 1.2 V. A single data point was obtained by averaging five measurements at each frequency. Capacitance, power, and energy values were normalized against 90 wt% YP80 F, considering the total mass of both electrodes. The porosity data for the carbon were assessed from nitrogen (N2) adsorption and desorption at −196 °C, utilizing a Micromeritics ASAP 2020 surface area and porosity analyser (Georgia, U.S.A). Prior to isotherm determination within the relative pressure range of 0.1 < P/P0 < 1.0, the sample was degassed at a temperature of 140 °C for a period of 12 hours.
20 and the mixture was stirred at 70 °C until a homogeneous dough was obtained. Subsequently, the dough was rolled onto a glass plate to produce a ∼140 μm thick sheet. The carbon sheet was dried at 80 °C overnight and was used as positive and negative electrodes in the two-electrode symmetric Swagelok-type capacitor cells described above. 1.0 cm diameter working and counter electrode disks made from the prepared carbon sheet sandwiched a 1.2 cm diameter glass microfiber separator (Whatman GF/A, 260 μm thick). Water-in-salt electrolyte solutions consisted of concentrated ChCl or LiTFSI. Electrochemical impedance spectra were collected in the frequency range of 1 MHz to 1 mHz using a single sinusoidal signal at open circuit voltage as well as at 0.4 V, 0.8 V and 1.2 V. A single data point was obtained by averaging five measurements at each frequency. Capacitance, power, and energy values were normalized against 90 wt% YP80 F, considering the total mass of both electrodes. The porosity data for the carbon were assessed from nitrogen (N2) adsorption and desorption at −196 °C, utilizing a Micromeritics ASAP 2020 surface area and porosity analyser (Georgia, U.S.A). Prior to isotherm determination within the relative pressure range of 0.1 < P/P0 < 1.0, the sample was degassed at a temperature of 140 °C for a period of 12 hours.
Results and discussion
Ion mobility in bulk water-in-salt electrolyte
Fig. 1 presents the dependency of physicochemical electrolyte properties on their concentration. An increase in concentration leads to enhanced viscosity for both ChCl and LiTFSI (Fig. 1a and b) caused by increasing electrostatic interactions. Fig. 1c illustrates the relationship between electrolyte concentration and ionic conductivity. It shows that the maximum values are 50 mS cm−1 and 100 mS cm−1 at 5 mol kg−1 for LiTFSI and ChCl, respectively. However, the maximum conductivity is the result of a trade-off between the number of ionic charge carriers and their mobility, which directly depends on the viscosity.18 The viscosity and ionic conductivity of electrolytes based on choline chloride and LiTFSI align with trends highlighted in prior research, as illustrated in Fig. 1a–c. Since superconcentrated electrolytes have almost saturated salt contents, their physicochemical character is expected to differ from that of diluted electrolytes.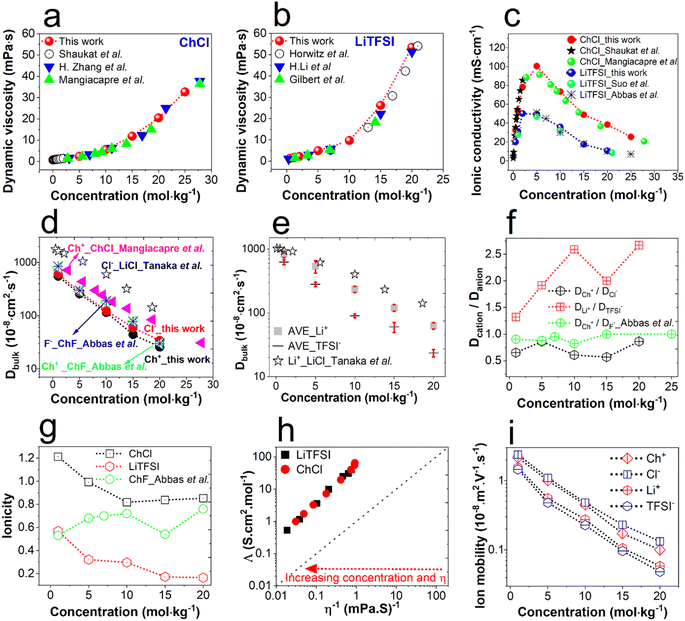 | ||
| Fig. 1 Effect of concentration on the transport properties of bulk ChCl and LiTFSI solutions at 25 °C. (a) The viscosity of aqueous ChCl and literature values from ref. 19, 39 and 40; (b) the viscosity of aqueous LiTFSI and literature values from ref. 16, 41 and 42; (c) ionic conductivity of ChCl and LiTFSI with relevant literature values from ref. 7, 13, 19 and 39; (d) calculated ion diffusivity of ChCl and literature values of diffusivity of choline fluoride,13 diffusivity of Ch+ from ChCl (PFG-NMR),19 and diffusivity of Cl− from LiCl (diaphragm cell);43 (e) average ion diffusivity of LiTFSI from PFG-NMR studies13,16–18 and diffusivity of Li+ from LiCl from the diaphragm cell method;43 (f) diffusivity ratio of cations to anions for ChCl, LiTFSI, and choline fluoride;13 (g) ionicity of ChCl, LiTFSI, and choline fluoride;13 (h) modified Walden plot of ChCl and LiTFSI; (i) mobility of Ch+, Cl−, Li+, and TFSI−. The dotted lines serve as a guide to the eye. | ||
In order to comprehend the EDL charging phenomena occurring in the porous carbon electrodes, it is essential to investigate the ionic interactions in both ChCl and LiTFSI electrolytes and express them in terms of ion transport parameters. For estimating the transport parameters of the bulk electrolytes, the average ion diffusivity values of bulk LiTFSI were taken from previous PFG-NMR studies.13,16–18 Mangiacapre et al. measured the diffusivity of choline ions in aqueous bulk ChCl solution using PFG-NMR.19 Unfortunately, due to the rapid relaxation of the 35Cl nucleus, the diffusivity of chloride ions could not be obtained by PFG-NMR.20 Tanaka et al. described the tracer diffusivity of Li+ and Cl− in concentrated aqueous LiCl (up to 18.6 mol kg−1) using a diaphragm cell method.43 Here, we measured the viscosity η of choline fluoride and LiCl by maintaining the concentrations specified in the literature to obtain the hydrodynamic radii of Ch+ and Cl− using the Stokes–Einstein equation (eqn (2)).44
 | (2) |
The dynamic viscosity, diffusivity, and hydrodynamic radii of LiCl and ChF are listed in Tables S2 and S3.† Subsequently, the hydrodynamic radii of Ch+ (from ChF) and Cl− (from LiCl) together with the viscosity of choline chloride solutions were used in the Stokes–Einstein eqn (2) to calculate the diffusivity of both Ch+ and Cl−. From the calculated diffusivity and measured viscosity of ChCl, the hydrodynamic radii of Ch+ and Cl− were determined. The calculated and average diffusivity values of both electrolytes are shown in Fig. 1d and e, with an expected declining trend with increasing salt concentration. Further, the calculated diffusivities of Ch+ and Cl− and the values from both the diaphragm cell method and PFG-NMR are listed together with the diffusivities from the literature in Tables S2 and S3.† Notably, the calculated diffusivities of Ch+ follow the same trend as the PFG-NMR-based diffusivities of Ch+ in choline chloride with small deviations for each concentration. The order of the molecular weight and viscosity of these four salts is LiCl < ChF < ChCl < LiTFSI. Hence, the diffusivity trend can be anticipated as LiCl > ChF > ChCl > LiTFSI. In the case of the diaphragm cell method, the highest diffusivity of Li+ and Cl− was found for the lowest viscosity of LiCl, and an identical trend was obtained with PFG-NMR studies (Fig. 1d and e).43 Hence, the calculated diffusivities of Ch+ and Cl− were confidently utilized in further analyses.
The diffusivity ratio of cations to anions is shown in Fig. 1f, to correlate the ion dissociation phenomena. The DLi+/DTFSI− increases from 1.2 to 2.4 with increasing salt concentration, suggesting a diminishing hydration of the Li+ ion. In the case of DCh+/DCl−, the diffusivity ratio is found to be almost concentration-independent up to 10 mol kg−1. This behavior is comparable to that of ChF, where DCh+/DF− being around 1 and independent of salt concentration indicates a weak interaction of F− and Ch+ with water13. In such a case, the ionicity (degree of ion dissociation) can be an effective parameter for understanding the ionic association at higher concentrations. Ionicity is the ratio of theoretical molar ionic conductivity to experimental molar ionic conductivity. According to the Nernst–Einstein equation, the molar ionic conductivity ∧NE can be derived from eqn (3), which is applicable for any ideal electrolyte solution (infinite dilution) free of ion–ion association.44
 | (3) |
 | (4) |
Overall, the calculated conductivities were higher than those found experimentally (Table S4†). Fig. 1g shows a declining trend of ionicity for both ChCl and LiTFSI. The ionicity of LiTFSI monotonically decreases from ≈0.6 to 0.2, indicating ion-paring with increasing salt concentration. Interestingly, at 1 mol kg−1 the ionicity of ChCl is higher than 1 indicating superionic behavior. Nürnberg et al. also reported an ionicity >1, suggesting superionicity in Li-coordinating cation based ionic liquids for uncorrelated ion motion.45 Above a concentration of 10 mol kg−1, ChCl exhibited an almost constant ionicity of around 0.8. The superionic behavior of ChCl was additionally corroborated by the fractional Walden plot shown in Fig. 1h. Liquids above and below the ideal line are termed ‘superionic’ and ‘subionic’, respectively. This phenomenon has also been observed in water-in-ChCl19 and water-in-LiTFSI.46 In superionic solutions, ions have greater mobility than in a classical solution. The ionicity exceeding 1 for 1 mol kg−1 ChCl suggests that Ch+ and Cl− ions are efficiently transported, rendering the electrolyte highly conductive. The fractional Walden plot in Fig. 1h indicates all concentrations of ChCl and LiTFSI as superionic, whereas the ionicity plot in Fig. 1g shows only 1 mol kg−1 ChCl as superionic, which could be due to considering different phenomena in those analyses. The overall ion dissociation of the choline salts was found with both methods to be higher than that of LiTFSI (Fig. 1g and h), which is also reflected in the ionic mobility μ (Fig. 1i) and ion transference number in a similar fashion (Fig. S3 and Method S1†). Ionic mobilities were determined by employing the relationship in eqn (5).47
 | (5) |
Hydration in water-in-salt electrolytes
The hydration of ions and their effect on the water structure have been studied to further understand the ion dissociation behavior of ChCl and LiTFSI. The hydration number Ns was obtained by using eqn (6).46,47 Several radii and Ns values are presented in Fig. 2a–c. | (6) |
In principle, RS must be higher than the ionic radius (RCRY) (Fig. 2d), but the observed trend was opposite. In Stokes's law, the hydrodynamic radii are often calculated to be inappropriately small, because water is not a continuous medium and the radii of the hydrated ions are usually not sufficiently large compared with that of a water molecule for the conditions of viscous flow to be fulfilled.50 Closely related to the hydration number is the effective radius or hydrodynamic radius (denoted as RH throughout the manuscript) of an ion in water, which is larger than its crystallographic radius (RCRY). However, for a better understanding and comparison, the hydration numbers were estimated using both RS and RH values and are presented in Table S5.†
Rs values resulted in an unrealistic trend, giving negative hydration numbers. As the salt concentration increased, the hydrodynamic radii and hydration numbers of Li+, TFSI−, and Cl− showed a decreasing trend (except at 20 mol kg−1), as depicted in Fig. 2c using RH. This trend is apparently similar to that in a relevant study by Borodin et al.18 Except for Ch+ above 10 mol kg−1, the values of RH and NS for all other ions can be explained by the respective charge densities. For instance, due to its small RCRY, Li+ has a higher charge density than the other ions and thus attracts more water molecules to its hydration shell, consequently showing a bigger RH and NS (Fig. 2c). The resulting RH values of Li+ and TFSI− were found to be comparable with the values reported by Moreno-Fernández et al. using solid-state NMR.10Fig. 2e shows the characteristic patterns of the hydration sheath of Ch+ and Cl− from diluted to water-in-salt choline chloride solutions. Similarly, it illustrates the typical configurations of the hydration sheath of Li+ and TFSI− from diluted to water-in-salt LiTFSI solutions. At low concentrations, the number of available water molecules surrounding each ion is large, resulting in a large RH and NS. In other words, at low concentrations, the ions are dissociated with weak ion–ion interactions. By contrast, at high concentrations, the number of available water molecules per ion is smaller, leading to a decrease of RH and NS. In particular, the smaller distance between Li+ and TFSI− in 20 mol kg−1 LiTFSI leads to stronger electrostatic interactions and the formation of ion pairs via coulombic interactions. Han et al. also reported the reduction of the average size of water clusters with increasing concentration of LiTFSI, supporting the overall trend of RH and NS found in our study.17 Exceptionally, the high hydrated ion volume for 15 or 20 mol kg−1 ChCl in Fig. 2c does not support the presence of a large number of water molecules given a very low molar ratio. This behavior rather suggests choline–choline association via hydrogen bonding at 15 and 20 mol kg−1 choline chloride (Fig. 2e).
For a better understanding of hydration and ion dissociation behavior, Raman spectroscopy of both water-in-salt bulk solutions has been performed. For different concentrations of ChCl, the major bands between 4000 and 120 cm−1 and their assignment are presented in Fig. S4 and Table S6.† For different concentrations of LiTFSI, the major bands between 4000 and 120 cm−1 are shown in Fig. S5.† Peak assignments and a detailed understanding of the ion aggregation behavior in water-in-LiTFSI have been reported by Suo et al. and Borodin et al.7,18,54 Here, H2O bands at wavelengths of 1640 cm−1, 3220 cm−1, 3430 cm−1, and 3610 cm−1 were mainly used to extract information on hydrogen bonding for both ChCl and LiTFSI-based water-in-salt electrolytes. Changes in the water band intensity at 1640 cm−1 for different concentrations of ChCl and LiTFSI are presented in Fig. S6.† Upon adding ChCl to water, initially a blue-shift compared to deionized water was noticed (Fig. S6a and Table S7†). However, for 25 mol kg−1, 30 mol kg−1, and crystalline ChCl, no pronounced band was observed at 1640 cm−1, indicating almost complete absence of partially hydrogen-bonded water and therefore negligible hydration.55 Compared to DI water (1637.33 cm−1), successive blue-shifts up to 10 mol kg−1 (1 mol kg−1: 1643.68 cm−1 > 5 mol kg−1: 1651.82 cm−1 > 10 mol kg−1: 1653.04 cm−1) were noted, followed by a red-shift for 15 mol kg−1 (1651.65 cm−1) and 20 mol kg−1 (1651.58 cm−1), in agreement with the trend of ionicity, effective hydrodynamic radii and hydration numbers. Higher ChCl content results in a characteristic blue shift with initially increasing band intensity, indicating that ChCl acts as a hydrogen donor.56
The Raman water band at 1640 cm−1 assigned to the partially hydrogen-bonded water in the second or third hydration shell corresponds to the symmetric bending mode of water. The vibrational properties of the O–H bonds and the frequency of this symmetric bending mode are directly governed by the hydrogen bonding configuration of ChCl solutions. Stronger hydrogen bonding in water-in-ChCl provides a higher vibrational frequency for the O–H stretching mode, leading to a characteristic blue shift. A high blue shift of 14.32 cm−1 and 14.25 cm−1 for 15 and 20 mol kg−1 ChCl solutions, respectively, compared to only 6.35 cm−1 for 1 mol kg−1 ChCl indicates a specific combination of the hydrogen bond donor56 and acceptor.57 For example, the hydroxyl group of the choline cation could participate in the formation of new hydrogen bonds with limited water molecules and with other choline chloride molecules promoting co-ion association as depicted in Fig. 2e. This could result in exceptionally high hydrodynamic radii calculated for Ch+ and Cl− at these particular concentrations.
In the case of aqueous LiTFSI, except for 1 mol kg−1 concentration, no water band was observed at 1640 cm−1 (Fig. S6b†). To verify this observation, we recorded the Raman spectra of more diluted aqueous LiTFSI solutions of 0.01 and 0.1 mol kg−1 concentrations, where this band was confirmed (Fig. S7†). The absence of the band above 5 mol kg−1 salt concentration could be due to the robust hydration of Li+, which extensively reduces the extent of partially hydrogen bonded55 water to a level too low for being detectable with Raman and consequently generates ion aggregates.7,18,54
In order to compare the hydration behavior of ChCl with that of LiTFSI, the water bands at 3220 cm−1, 3430 cm−1, and 3610 cm−1 were analysed (Fig. 3a and b). These bands are assigned to the symmetric stretching vibration of –OH, the asymmetric stretching vibration of –OH, and the vibration of free –OH, respectively.55,58 The band at 3220 cm−1 is assigned to fully hydrogen-bonded water (FHW), i.e. a well-structured, strongly connected network of water molecules, whereas the bands at 3430 and 3610 cm−1 are due to partially hydrogen-bonded water (PHW), i.e. weaker and less stable hydrogen bonds.55,58 In our study, we consider the water molecules in the primary hydration shell as fully hydrogen-bonded water, whereas the water in the second or third hydration shell is supposed to be partially hydrogen-bonded water.
In order to distinguish those bands efficiently, we deconvoluted the selected regions of all spectra using the Gaussian function of OriginPro 2021b software, as shown in Fig. S8 and S9.† The wavelength shifts, the intensity, and the width of the bands are presented in Tables S8 and S9.† The FHW band of ChCl solutions at 3220 cm−1 showed a monotonically declining trend in both intensity and width, as well as a blue shift. A less pronounced blue shift of this band with a higher intensity and lower width was found for crystalline ChCl, indicating that the salt possesses intrinsic hydrogen bonds in its structure. For the PHW bands at 3430 and 3610 cm−1, a similar trend of blue and red shifts was found, as previously discussed for the band at 1640 cm−1. Both salts were extensively dried before the Raman measurements, but they quickly absorbed moisture under ambient conditions during the measurement, giving rise to a band near 3400 cm−1, while no band was observed for crystalline ChCl at 3610 cm−1, indicating the absence of free –OH. For LiTFSI on the other hand, the –OH stretching vibration bands were significantly altered, with successive fading of the broad band, accompanied by the appearance of a new band at ∼3560 cm−1, which is known from other water-in-salts, including NaCF3SO3 and NaClO4.59 This new sharp band at 3560 cm−1 can be ascribed to the Raman signature of crystalline hydrates of LiTFSI. In such a case, most of the H2O molecules participate in ion coordination with Li+ and TFSI− with negligible hydrogen bonding among them. The band intensity ratio of PHW to FHW indicates the hydrogen bond situation as a function of salt concentration in the electrolytes and was calculated with eqn (7). This ratio describes the hydration behavior of both salts and is shown in Fig. 3c.
 | (7) |
For ChCl, this ratio is mainly dominated by the FHW band, as the intensities of the PHW bands were not altered that much. Although both PHW band intensities for LiTFSI changed significantly, the sum of I3440 and I3610 did not change a lot. So, for LiTFSI, the PHW/FHW ratio was also dominated by the FHW band intensity. The declining intensity of FHW with increasing concentrations of ChCl and LiTFSI indicates a weakening hydrogen bond interaction. The higher I3610, on the other hand, suggests that a higher proportion of water molecules is involved in these weaker hydrogen bond environments. As such, the higher PHW/FHW ratio would indicate an overall less ordered hydrogen bond environment in the salt solutions. The resulting plot of PHW/FHW reached a maximum at 10 mol kg−1 for ChCl and a minimum for crystalline ChCl. The PHW/FHW ratio for LiTFSI shows a monotonically increasing trend, reaching a maximum for the crystalline salt, which suggests a weaker hydrogen bond configuration. The hydrogen bond strength as a function of salt concentration was further elucidated using the –OH stretching ratio I3220/I3440 (Fig. S10†). I3220/I3440 for both salts also showed a trend similar to that of the previously discussed bands. The higher I3220/I3440 ratio points at a higher proportion of fully hydrogen-bonded water, implying a well-ordered hydrogen bond configuration. By contrast, a lower ratio could indicate a larger fraction of partially hydrogen-bonded water, suggesting a less structured, more dynamic hydrogen bond arrangement.
Upon increasing ChCl concentration, the presence of all four water bands above 10 mol kg−1 concentration indicates different hydrogen bond networks between the chloride ions and water molecules, because it can simultaneously act as both a hydrogen bond donor and acceptor. Furthermore, multiple choline chloride molecules formed hydrogen bonds with each other, promoting the formation of choline–choline co-ion associations. On the other hand, with increasing LiTFSI concentration, the solvation structure around Li+ changes from solvent-separated ion pairs to the coexistence of solvent-separated ion-pairs, contact ion pairs and ionic aggregates via coulombic interactions. In the forthcoming section, these characteristics of bulk water-in-salt electrolytes are correlated with the capacitor performance.
Effect of salt concentration on impedance behavior
Ion transport parameters within the micro- and meso-pores of carbon electrodes were first investigated by electrochemical impedance spectroscopy of symmetric capacitor cells at open circuit voltage. Fig. 4a presents the Nyquist plots of capacitor impedance data for different concentrations of ChCl and LiTFSI. Overall, the cells assembled with ChCl electrolyte showed nearly 50% lower resistance than those assembled with LiTFSI and reached their minimum resistance at a concentration of 5 mol kg−1. The variation in salt concentration leads to a trend in resistance change that is in line with the bulk ionic conductivities outlined in the previous section.In the mid-frequency range between 1 and 100 Hz, the resistance and capacitance are frequency-dependent and diffusion processes have a strong influence.60 This region appears as a slope in the Nyquist plots (Fig. 4a), which can be used to derive the diffusion properties of the ions. The transition between intermediate and low-frequency domains is characterized by a so-called knee-frequency (F), which separates dominantly resistive and capacitive behavior.61,62 At the highest frequency, the first intersection with the real axis is equivalent series resistance (ESR), which is mainly associated with the electric resistance of all the connections, particularly the measurement connections, the contact resistance between the activated carbon electrodes and the current collectors and the ionic conductivity of the bulk electrolyte.63,64
The diameter of the semicircle in the high frequency range is known as charge transfer resistance (CTR), which is attributed to the resistance of the interface between the porous surface of the carbon electrode and the electrolyte.63–65 In the very low-frequency range, the intercept of the linear extrapolation of the vertical portion of the Nyquist plot with the real axis is named equivalent distribution resistance (EDR).63,66 At lower frequencies just after the semicircle, the ions are able to access the bulk electrode and deep pores. At these frequencies, the ion diffusion resistance (IDR) can be obtained by subtracting the resistance at the low frequency endpoint of the semicircle from the resistance at the knee frequency.67,68 The dependence of the ESR, CTR, EDR, and IDR at OCP for selected salt concentrations of ChCl and LiTFSI is shown in Fig. 4b, and for all other concentrations in Fig. S11 and Table S10.† The trends of resistance as a function of salt concentration match those of bulk ionic conductivities discussed in the previous section.
The frequency dependence of the complex capacitance was used to study the in-pore ion dynamics and to correlate the overall energy storage behavior of the electrodes. At high frequencies, both the imaginary and the real part of the capacitance are negligible, since the resistive processes dominate. At low frequencies, the capacitive processes dominate. The real part of the capacitance C′ contains information about the capacitance of the whole system, while the imaginary part C′′ quantifies the loss of energy. Several parameters including angular frequency (ω), the real part of the dielectric permittivity (ε′) and the imaginary part of the dielectric permittivity (ε′) were calculated to obtain C′ and C′′ with eqn (S1) to (S6) as mentioned in Method S3.†Fig. 4c shows the characteristic imaginary capacitance C′′ at OCP for selected concentrations of ChCl and LiTFSI. C′ and C′′ for all concentrations are presented in Fig. S12 and S13.†C′′ reaches a maximum at a characteristic knee-frequency (F) due to the simultaneous effects of resistive components, which dissipate energy through ohmic loss, and capacitive components, which store electric energy. Fig. 4d indicates the knee-frequency shift as a function of salt concentration for ChCl and LiTFSI. The dispersed energy drastically increases when approaching F, since only a few electric charges are stored at the electrode surface and resistive behavior dominates. After reaching the maximum, these losses decrease rapidly towards lower frequencies and the system becomes more capacitive. Specifically, the relaxation time, which is also termed the cell-time constant, indicates how fast a capacitor can be charged or discharged. This is expressed as the inverse of the characteristic knee-frequency (1/2πF), at which the resistive and capacitive components of the capacitor cells are equal, corresponding to a phase angle φ of −45° for ideal behavior shown in the impedance Bode plots in Fig. S14.† This value can be easily obtained from the maximum of C′′ corresponding to the maximum loss of energy by ohmic dissipation. With increasing salt concentration, C′′ for both ChCl and LiTFSI is shifted to higher frequencies reaching a maximum for 5 mol kg−1 ChCl confirming important ion association contributions. The active power P′ was calculated with eqn (8) to correlate several in-pore ion transport properties.60 The P′ values are shown in Fig. S15.†
| P′ = C′′|ΔVrms|2 | (8) |
 , where Vmax is the maximum AC potential amplitude of 5 mV. Ion transport parameters within the carbon pores and the power performance of the capacitor cells are broadly correlated and discussed in the following section.
, where Vmax is the maximum AC potential amplitude of 5 mV. Ion transport parameters within the carbon pores and the power performance of the capacitor cells are broadly correlated and discussed in the following section.
Ion transport within the micro- and meso-pores of carbon electrodes
The in-pore ionic resistance Rin-pore was calculated from C′′ and F with eqn (9) (Fig. 4d). | (9) |
 | (10) |
 | (11) |
The pore configurations of the carbon electrode (YP80 F) were determined from N2 gas adsorption and desorption isotherms (Fig. S16†). The specific surface area and the pore size distribution of the carbon were estimated by applying the QS-DFT adsorption model for slit, cylindrical-shaped pores.22 The total cumulative surface area, total BET surface area, and volume of the micropores (<2 nm), and the volume of the mesopores (2–50 nm) were determined to be 1735 m2 g−1, 2307 m2 g−1, 0.80 cm3 g−1, and 0.23 cm3 g−1, respectively (Fig. 5a). The volume fraction of micro- and meso-pores was found to be 85.3% and 14.7%, whereas the surface area fraction was 89.9% and 10.1%, respectively. The porosity ∅ was estimated from the ratio of any pore volume to the total pore volume.
The impedance of the two-electrode symmetric capacitor cells was measured as the sum of both electrodes and thus the overall C′′ of the full cells was obtained. For the calculation of tortuosity, the pore surface area fractions were used in order to distinguish micro-/meso-pore regions, which is termed effective tortuosity. Measurements of two-electrode symmetric cells cannot distinguish the electrochemical behavior of the positive and negative electrodes. Hence, the modified Darken's relationship of binary diffusivity was utilized as proposed by Krachkovskiy et al. for obtaining bulk ion-pair (mutual) diffusivity values DChCl and DLiTFSI from their self-ion diffusivity (see details in Method S4†).70
The effective tortuosity and ion diffusivity within micro- and meso-pores for different salt concentrations are shown in Fig. 5b and listed in Table S12.† For all salt concentrations, the tortuosity of the micropores is around fifty times higher than that of the mesopores. For ChCl, the tortuosity of both meso- and micro-pores decreased up to a concentration of 10 mol kg−1 and then increased for 15 and 20 mol kg−1, consistent with the hydrodynamic radii and hydration behavior. In the case of LiTFSI, on the other hand, the tortuosity decreased linearly with concentration. The tortuosity of YP80 F affects the pathways and transport rate of ions within the electrode. High tortuosity means longer and more convoluted pathways for ion confinement and desolvation, resulting in reduced screening of charge. The tortuosity of mesopores tends to be lower, because they provide shorter pathways. The more complex hydration structure of the ions at concentrations above 10 mol kg−1 ChCl or LiTFSI affects the interaction between the ions and the carbon surface, and thus also ion transport and the degree of tortuosity. High tortuosity consequently hinders the ions from reaching deep into the pores and accessing the full surface area of the carbon electrode, which can be empirically correlated with the in-pore diffusivity.
The diffusivity of ChCl and LiTFSI is denoted as DChCl and DLiTFSI, respectively. The Din-pore values decrease monotonically with increasing salt concentration, reflecting the tendency of bulk DChCl and DLiTFSI (Fig. 5b). The effective diffusion of water-in-salt electrolytes in micropores Dmicro and in mesopores Dmeso resembles the results of several in situ NMR studies, as shown in Table S13.†22,24 Borchardt et al.22 followed three assumptions and models from liteartures27–29 based on EIS to compare their in situ NMR diffusivity values within micro-, meso-, and hierarchical pores. Among them, the diffusivities based on the model of Armstrong et al.29 and Ahuja et al.27 showed coherence with the in situ NMR data. However, the assumption of van Aken et al.28 leads to a difference of about four orders of magnitude although the substrate was identical (Table S13†). Xu et al. also found a different order of diffusivities for chloroaluminate intercalation into graphite electrodes in rechargeable aluminium batteries using EIS and the galvanostatic intermittent titration technique and recommended taking porosity and tortuosity into account to obtain reliable diffusivities.32 We have considered DChCl and DLiTFSI, whereas the in situ NMR study provides information on the self-diffusion of ions. Additionally, acetonitrile has a small ionic interaction and a very low viscosity of 0.3 mPa s, which is 70% smaller than that of water. Thus, a solution of 1 M TEABF4 in acetonitrile exhibits viscosities almost 60 and 166 times lower than those of aqueous solutions containing 20 mol kg−1 ChCl and LiTFSI, respectively.22 The empirical Din-pore values exhibited a slight variation but maintained a consistent pattern. Notably, despite variations in the type of cation, anion, solvent, salt concentration, and electrolyte viscosity in previous literature (Table S13†), the diffusivity ratio trend between the bulk electrolyte and in-pore was highly comparable to the results of the in situ NMR study of micro- and meso-pores.22,24 This confirms that the method used here based on bulk electrolyte diffusivity, porosity, and tortuosity can accurately estimate in-pore diffusivities.
The ion diffusion of water-in-salt electrolytes inside carbon micropores is significantly slower than in the bulk due to the dominance of the close packing and passage through the porous network, as shown in Fig. 5b. This type of diffusivity is described as ‘configurational’ diffusion and is a result of an activated hopping path in the force field of confinement within the micropores.22 The Dbulk/Din-pore of ChCl initially shows higher values at diluted (1 mol kg−1) solutions, which then decreases until 10 mol kg−1 and subsequently increases again at 15 and 20 mol kg−1 concentrations. This trend directly correlates with the Raman water band analysis, specifically the PHW to FHW ratio as discussed previously. ChCl solutions exhibit higher Dbulk/Din-pore values compared to those of LiTFSI solutions, attributed to the stronger hydrogen bond strength in ChCl compared to LiTFSI. The overall dependency of Dbulk/Din-pore on salt concentrations can be correlated with ion desolvation and confinement, which is attributed to a few phenomena, as explained in previous reports.71–73 The characteristic charge distributions of 5 and 20 mol kg−1 ChCl and LiTFSI within the positive and negative carbon nanopores are visualized in Scheme 1.
To deepen our understanding of how pore confinement affects the ion transport of both salts at varying concentrations, we have considered the size of the ion pairs. This includes estimation of the size for cation–cation, anion–anion, and cation–anion pairs, using the effective hydrated radii RH. The CSA% for the corresponding cumulative surface area fraction was measured by considering the pore width that is similar to the ion pair size. The data in Table S14† show that ions placed side-by-side have sizes ranging from approximately 0.6 nm to 1.0 nm, corresponding to about 15% and 49%, respectively, of the cumulative surface area of the micropores in YP80 F, impeding the mutual transport of ions within the pores. Expectedly, the trends of Dbulk/Din-pore values for both ChCl and LiTFSI are directly correlated with the size of their hydrated cation–cation and anion–anion pairs placed side-by-side. Thus, the ions in the diluted solutions will partially dehydrate/desolvate their outer shell in these microporous regions. Such partial de-solvation and ion sieving effects are also reported by Eliad et al.74 Therefore, a hydrated cation in typical diluted solutions will experience hindered diffusion and partial desolvation in the case of pore widths less than RH. Meanwhile, pore widths equal to or greater than the RH of cation–cation or anion–anion pairs allow effective and facile ion diffusion. In the case of mesopores, the dominance of ion-entrapping/confinement decreases, resulting in lower ion diffusion resistance and enhanced ionic transport (Dbulk/Dmeso < Dbulk/Dmicro), as shown in Fig. 5c. In the case of concentrated 20 mol kg−1 LiTFSI, stronger coulombic attraction between Li+ and TFSI− hinders the screening of partially hydrated ions within pores. Meanwhile, relatively weak hydrogen bonds in choline–choline co-associated ions or within choline and chloride in 20 mol kg−1 ChCl are likely to break under the potential difference of carbon electrodes.
Expectedly, the ratio of bulk ionic conductivity to in-pore ionic conductivity (σbulk/σin-pore) or the ratio of in-pore ionic resistance to bulk ionic resistance exhibits a trend comparable to Dbulk/Din-pore (Table S12†). The in-pore ionic conductivity was calculated as the reciprocal of Rin-pore with eqn (9). In the case of σbulk/σin-pore, the overall electrode porosity was considered, thereby leading to values lower than Dbulk/Dmicro and values higher than Dbulk/Dmeso. As such, Dbulk/Din-pore, σbulk/σin-pore, and Rin-pore to Rbulk can be used as indicators of the ionic transport resistance. Hence, the relationships between Din-pore and Rin-pore as well as between Din-pore and C′′ were established. The effect of pore confinement was considered for extracting Rmico, Rmeso,  , and
, and  from Dmicro and Dmeso using eqn (12)–(17) by merging eqn (9)–(11). To do so, the τ′ values were determined with eqn (12) and (13), respectively.
from Dmicro and Dmeso using eqn (12)–(17) by merging eqn (9)–(11). To do so, the τ′ values were determined with eqn (12) and (13), respectively.
 | (12) |
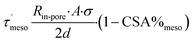 | (13) |
 | (14) |
 | (15) |
 | (16) |
 | (17) |
 and
and  are the tortuosity considering micro- and meso-pore confinement effects, respectively. The subscript ‘in-pore’ refers to parameters for all pores combined. Rmico, Rmeso,
are the tortuosity considering micro- and meso-pore confinement effects, respectively. The subscript ‘in-pore’ refers to parameters for all pores combined. Rmico, Rmeso,  , and
, and  values are shown in Table S12† for all salt concentrations. Due to their higher tortuosity, micropores exhibit resistance values Rmicro almost nine times lower than mesopores (Rmeso). However, because of their higher surface area and porosity fraction, micropores accommodate more ions, resulting in higher capacitance compared to mesopores. As expected, the sum of Rmicro and Rmeso equals the total Rin-pore (Table S12† and Fig. 4d).
values are shown in Table S12† for all salt concentrations. Due to their higher tortuosity, micropores exhibit resistance values Rmicro almost nine times lower than mesopores (Rmeso). However, because of their higher surface area and porosity fraction, micropores accommodate more ions, resulting in higher capacitance compared to mesopores. As expected, the sum of Rmicro and Rmeso equals the total Rin-pore (Table S12† and Fig. 4d).| Rin-pore,EIS = Rmicro + Rmeso | (18) |
 | (19) |
This indicates that inter- and intra-connected micro- or meso-pores can be treated as a series of capacitors. Furthermore, it has been verified that the sum of the inverse micro- and meso-pore capacitances contributes to the overall capacitance, as evidenced by the total capacitance obtained from EIS (eqn (19)), supporting the validity of our estimation.
Finally, the time constant and power density  of the capacitor are plotted together as a function of salt concentration in Fig. 5d to demonstrate how the above discussed ion transport parameters affect the charge/discharge rate performance of the capacitor cells. At a concentration of 1 mol kg−1, the cell-time constant was found to be high for both ChCl and LiTFSI. They show a minimum of 167 ms and 421.9 ms for 5 mol kg−1 ChCl and 10 mol kg−1 LiTFSI, respectively. Above 10 mol kg−1, the time constant monotonically increases for both salts, which is in line with the bulk ionic conductivity trends mentioned in the previous section. A higher electrolyte concentration can generally lead to faster charging and discharging rates up to 5 mol kg−1, but there are different practical limits for ChCl and LiTFSI with increasing concentration. For example,
of the capacitor are plotted together as a function of salt concentration in Fig. 5d to demonstrate how the above discussed ion transport parameters affect the charge/discharge rate performance of the capacitor cells. At a concentration of 1 mol kg−1, the cell-time constant was found to be high for both ChCl and LiTFSI. They show a minimum of 167 ms and 421.9 ms for 5 mol kg−1 ChCl and 10 mol kg−1 LiTFSI, respectively. Above 10 mol kg−1, the time constant monotonically increases for both salts, which is in line with the bulk ionic conductivity trends mentioned in the previous section. A higher electrolyte concentration can generally lead to faster charging and discharging rates up to 5 mol kg−1, but there are different practical limits for ChCl and LiTFSI with increasing concentration. For example,  for the capacitor cell was found with 5 mol kg−1 LiTFSI and higher concentrations of LiTFSI result in diminishing power performance. For ChCl, P′ was high at 5 mol kg−1, declining at 10 and 15 mol kg−1 and
for the capacitor cell was found with 5 mol kg−1 LiTFSI and higher concentrations of LiTFSI result in diminishing power performance. For ChCl, P′ was high at 5 mol kg−1, declining at 10 and 15 mol kg−1 and  was found for 20 mol kg−1. As discussed in the previous section, a small hydration number of Li+ and TFSI− results in ion association. This causes slower transport of Li+ within the carbon pores above a concentration of 5 mol kg−1. On the other hand, ChCl shows an exceptional rearrangement of its hydrogen bond network at 20 mol kg−1 (Fig. 5c), ultimately leading to
was found for 20 mol kg−1. As discussed in the previous section, a small hydration number of Li+ and TFSI− results in ion association. This causes slower transport of Li+ within the carbon pores above a concentration of 5 mol kg−1. On the other hand, ChCl shows an exceptional rearrangement of its hydrogen bond network at 20 mol kg−1 (Fig. 5c), ultimately leading to  at this high concentration.
at this high concentration.
To explore the electrode–electrolyte interface phenomena for different electrolyte systems under applied bias voltage, the electrochemical impedance spectra of the capacitor cells were recorded at 0.4 V, 0.8 V and 1.2 V and are shown in Fig. S17.† The narrow voltage range was selected to avoid any unwanted faradaic contribution related to the oxidation/reduction of the electrolyte. When voltage is applied, electrolyte ions are accumulated at the EDL and electro-adsorbed. Higher voltage increases the charge screening density at the EDL, storing more charge in the electrode, as evidenced in Table S15,† an apparent monotonic declining trend of ESR, CTR, IDR and EDR values for all electrolyte systems (except for the IDR of 5 and 10 mol kg−1 ChCl). The carbon pores attract ions, and higher voltages drive more ions to form an electric double layer, further increasing the stored charge as corroborated by the trend of C′′ and P′ (Fig. S18 and S19†). The maximum energy performance, for instance  and
and  , was recorded at a medium concentration of 5 mol kg−1 at 1.2 V. For ascribing this trend, the data related to the effect of salt concentration and voltage on Rin-pore, tortuosity, in-pore ion diffusivity, and charge discharge time constant are listed in Table S16.† The Rmicro and Rmeso values decreased monotonically with increasing applied voltage, reflecting the behavior of bulk electrolyte resistivity.
, was recorded at a medium concentration of 5 mol kg−1 at 1.2 V. For ascribing this trend, the data related to the effect of salt concentration and voltage on Rin-pore, tortuosity, in-pore ion diffusivity, and charge discharge time constant are listed in Table S16.† The Rmicro and Rmeso values decreased monotonically with increasing applied voltage, reflecting the behavior of bulk electrolyte resistivity.
In principle, higher voltages can promote the migration of ions, potentially leading to reduced tortuosity as ions move more freely through the carbon structure, thereby resulting in higher in-pore ion diffusivity, i.e. quicker charging–discharging. However, for concentrations higher than 5 mol kg−1, the performance of the two electrolytes starts to differ. The disrupted order of in-pore ion transport parameters was evident as a function of applied bias voltage. With a higher electric field strength, the attraction of Ch+ and Li+ ions into the EDL increases, as shown in Table S17.† The higher voltage can disrupt the ion association and influence the hydration of Ch+ and Li+ ions. Also, the orientation and dynamics of water molecules in the hydration shell can be affected, potentially leading to either a more ordered or a disrupted hydration shell. These observations support the in situ NMR study on the dehydration of NaF ions in voltage-gated carbon nanopores by Luo et al.75 and time-resolved IR absorption measurements of the hydrated Na+ or tetrapropylammonium cation (Pr4N+) by Yamakata et al.76 In addition, the effect of voltage on tortuosity may also depend on the size and geometry of the carbon pores. Under applied voltage, ions with an appropriate size can enter the micropores more easily, even if the pores are smaller than RH. This can result in enhanced ion transport through micropores. Mesopores being larger than micropores do not exhibit the same level of the ion sieving effect.74 Instead, applied voltage facilitates ion transport through mesopores due to the larger pore size. The voltage drives ions into the mesopores, reducing the tortuosity of the pathways and increasing the rate of ion diffusion (Table S16†). These observations are consistent with the study of voltage-assisted in-pore ion dynamics by in situ PFG-NMR.22,24
As such, at concentrations above 10 mol kg−1, significant differences in the charging behaviour of the two electrolytes start to appear. As shown in Fig. S18,† the capacitance linearly increases with applied voltage for 1 and 5 mol kg−1 concentrations of both electrolytes. This trend is absent in 10 mol kg−1 LiTFSI and concentrations above due to very strong ion association, which prevents the increase of capacitance by the applied voltage (also proved by equivalent circuit analysis in Fig. S20, S21 and Table S18†). On the other hand, the capacitance increases in the case of ChCl with higher concentration and at higher voltages. This is due to the weaker hydrogen bond mediated choline–choline co-ionic associations that are prone to easy breaking under applied bias voltage, thereby facilitating quicker ion transport to the electric double layer. Overall, the electrostatic attraction/association in LiTFSI limits the screening of charges at the EDL, while ions in highly concentrated ChCl show an enhanced degree of dissociation in carbon pores, resulting in increased charge screening.
Conclusions
This work explored the interplay between the diffusivity of bulk electrolyte and the porosity and tortuosity of carbon electrodes to understand the ion transport behavior of LiTFSI and ChCl water-in-salt electrolytes. An effective strategy to investigate and differentiate ion diffusivity within the micro- and meso-pores of multiporous carbon has been demonstrated. The charge screening in porous carbon electrodes operating in electrolytes of low and medium concentrations occurs according to the classical concepts of de-solvation and ion re-arrangement. A deviation from this trend has been observed for concentrated electrolytes above 10 mol kg−1. This is explained via altered ion hydration of ChCl and strongly associated ions in LiTFSI at concentrations above 10 mol kg−1, which affect the tortuosity and rate of ion transport to different degrees. The hydration behaviour of ions in the bulk electrolyte affects their transport within the carbon pores. Desolvation and confinement are important parameters for ion transport in relatively diluted electrolytes. However, ion association/dissociation is the determining factor for the performance of supercapacitors in highly concentrated electrolytes. To distinguish the distribution of charges within micro- and meso-pores, a new relationship has been established based on parameters from both the bulk electrolyte and the carbon electrode, including tortuosity, in-pore ion diffusivity, and cell capacitance. Taking these parameters into account, new types of carbon electrodes can be developed with compatible electrolytes to create high-performance electrochemical energy storage systems.Data availability
The data supporting the results of this study have been included in the ESI,† and additional data are available from the corresponding authors upon reasonable request.Author contributions
MTI: conceptualization; data curation; formal analysis; investigation; methodology; software; validation; visualization; writing – original draft. BG: supervision; writing – review & editing; project administration; resources. QA: conceptualization; supervision; funding acquisition; project administration; resources; writing – review & editing.Conflicts of interest
The authors have no financial and personal relationships with other people or organizations that could inappropriately influence their work.Acknowledgements
The Austrian Research Promotion Agency (FFG) is gratefully acknowledged for funding this research under the ECOCAPs project # 39966764. The authors thank Dr Harald Fitzek from the Institute of Electron Microscopy and Nanoanalysis, Graz University of Technology for providing Raman spectroscopy facilities.Notes and references
- Y. Shao, M. F. El-Kady, J. Sun, Y. Li, Q. Zhang, M. Zhu, H. Wang, B. Dunn and R. B. Kaner, Chem. Rev., 2018, 118, 9233–9280 CrossRef CAS PubMed.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- K. Xu, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed.
- L. Hu and K. Xu, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3205–3206 CrossRef CAS PubMed.
- X. Tian, Q. Zhu and B. Xu, ChemSusChem, 2021, 14, 2501–2515 CrossRef CAS.
- P. Lannelongue, R. Bouchal, E. Mourad, C. Bodin, M. Olarte, S. le Vot, F. Favier and O. Fontaine, J. Electrochem. Soc., 2018, 165, A657–A663 CrossRef CAS.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943 CrossRef CAS PubMed.
- D. Xiao, Q. Wu, X. Liu, Q. Dou, L. Liu, B. Yang and H. Yu, ChemElectroChem, 2019, 6, 439–443 CrossRef CAS.
- K. Mahankali, N. K. Thangavel, Y. Ding, S. K. Putatunda and L. M. R. Arava, Electrochim. Acta, 2019, 326, 134989 CrossRef CAS.
- G. Moreno-Fernández, R. Mysyk, N. Díez, D. Carriazo and J. M. López del Amo, Electrochim. Acta, 2022, 404, 139716 CrossRef.
- M. Zhang, S. Makino, D. Mochizuki and W. Sugimoto, J. Power Sources, 2018, 396, 498–505 CrossRef CAS.
- P. Przygocki, Q. Abbas, B. Gorska and F. Béguin, J. Power Sources, 2019, 427, 283–292 CrossRef CAS.
- Q. Abbas, P. Nürnberg, R. Ricco, F. Carraro, B. Gollas and M. Schönhoff, Adv. Energy Sustainability Res., 2021, 2, 2100115 CrossRef CAS.
- A. Brandt and A. Balducci, J. Power Sources, 2014, 250, 343–351 CrossRef CAS.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. B, 2021, 125, 13246–13254 CrossRef CAS PubMed.
- Z. Li, R. Bouchal, T. Mendez-Morales, A. L. Rollet, C. Rizzi, S. Le Vot, F. Favier, B. Rotenberg, O. Borodin, O. Fontaine and M. Salanne, J. Phys. Chem. B, 2019, 123, 10514–10521 CrossRef CAS PubMed.
- K. S. Han, Z. Yu, H. Wang, P. C. Redfern, L. Ma, L. Cheng, Y. Chen, J. Z. Hu, L. A. Curtiss, K. Xu, V. Murugesan and K. T. Mueller, J. Phys. Chem. B, 2020, 124, 5284–5291 CrossRef CAS PubMed.
- O. Borodin, L. Suo, M. Gobet, X. Ren, F. Wang, A. Faraone, J. Peng, M. Olguin, M. Schroeder, M. S. Ding, E. Gobrogge, A. Von Wald Cresce, S. Munoz, J. A. Dura, S. Greenbaum, C. Wang and K. Xu, ACS Nano, 2017, 11, 10462–10471 CrossRef CAS PubMed.
- E. Mangiacapre, F. Castiglione, M. D'Aristotile, V. Di Lisio, A. Triolo and O. Russina, J. Mol. Liq., 2023, 383, 122120 CrossRef CAS.
- C. D'Agostino, L. F. Gladden, M. D. Mantle, A. P. Abbott, E. I. Ahmed, A. Y. M. Al-Murshedi and R. C. Harris, Phys. Chem. Chem. Phys., 2015, 17, 15297–15304 RSC.
- A. C. Forse, C. Merlet, J. M. Griffin and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 5731–5744 CrossRef CAS PubMed.
- L. Borchardt, D. Leistenschneider, J. Haase and M. Dvoyashkin, Adv. Energy Mater., 2018, 8, 1800892 CrossRef.
- G. Moreno-Fernández, R. Mysyk, N. Díez, D. Carriazo and J. M. López del Amo, Electrochim. Acta, 2022, 404, 139716 CrossRef.
- A. C. Forse, J. M. Griffin, C. Merlet, J. Carretero-Gonzalez, A. R. O. Raji, N. M. Trease and C. P. Grey, Nat. Energy, 2017, 2, 16216 CrossRef.
- B. Dyatkin, E. Mamontov, K. M. Cook and Y. Gogotsi, Prog. Nat. Sci.: Mater. Int., 2015, 25, 631–641 CrossRef CAS.
- J. K. McDonough, A. I. Frolov, V. Presser, J. Niu, C. H. Miller, T. Ubieto, M. V. Fedorov and Y. Gogotsi, Carbon, 2012, 50, 3298–3309 CrossRef CAS.
- P. Ahuja, V. Sahu, S. K. Ujjain, R. K. Sharma and G. Singh, Electrochim. Acta, 2014, 146, 429–436 CrossRef CAS.
- K. L. Van Aken, J. K. McDonough, S. Li, G. Feng, S. M. Chathoth, E. Mamontov, P. F. Fulvio, P. T. Cummings, S. Dai and Y. Gogotsi, J. Phys.: Condens. Matter, 2014, 26, 284104 CrossRef PubMed.
- R. D. Armstrong, J. Electroanal. Chem., 1986, 198, 177–180 CrossRef CAS.
- J. Wang, E. Pameté, S. Yan, W. Zhao, J. Zhang, X. He, Z. Supiyeva, Q. Abbas and X. Pan, Electrochem. Commun., 2023, 150, 107488 CrossRef CAS.
- M. F. Dupont and S. W. Donne, Electrochim. Acta, 2015, 167, 268–277 CrossRef CAS.
- J. H. Xu, T. Schoetz, J. R. McManus, V. R. Subramanian, P. W. Fields and R. J. Messinger, J. Electrochem. Soc., 2021, 168, 060514 CrossRef CAS.
- W. Y. Tsai, P. L. Taberna and P. Simon, J. Am. Chem. Soc., 2014, 136, 8722–8728 CrossRef CAS PubMed.
- S. Boukhalfa, D. Gordon, L. He, Y. B. Melnichenko, N. Nitta, A. Magasinski and G. Yushin, ACS Nano, 2014, 8, 2495–2503 CrossRef CAS PubMed.
- F. W. Richey, B. Dyatkin, Y. Gogotsi and Y. A. Elabd, J. Am. Chem. Soc., 2013, 135, 12818–12826 CrossRef CAS PubMed.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, B. Daffos, P. L. Taberna, P. Simon and M. Salanne, Nat. Commun., 2013, 4, 2701 CrossRef CAS PubMed.
- J. Landesfeind, J. Hattendorff, A. Ehrl, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, A1373–A1387 CrossRef CAS.
- N. Ogihara, Y. Itou and S. Kawauchi, J. Phys. Chem. Lett., 2019, 10, 5013–5018 CrossRef CAS PubMed.
- S. Shaukat and R. Buchner, J. Chem. Eng. Data, 2011, 56, 4944–4949 CrossRef CAS.
- H. Zhang, M. L. Ferrer, M. J. Roldán-Ruiz, R. J. Jiménez-Riobóo, M. C. Gutiérrez and F. Del Monte, J. Phys. Chem. B, 2020, 124, 4002–4009 CrossRef CAS PubMed.
- G. Horwitz, C. R. Rodríguez, P. Y. Steinberg, G. Burton and H. R. Corti, Electrochim. Acta, 2020, 359, 136915 CrossRef CAS.
- W. J. R. Gilbert, J. Safarov, D. L. Minnick, M. A. Rocha, E. P. Hassel and M. B. Shiflett, J. Chem. Eng. Data, 2017, 62, 2056–2066 CrossRef CAS.
- K. Tanaka and M. Nomura, J. Chem. Soc., Faraday Trans., 1987, 83, 1779–1782 RSC.
- O. Nordness and J. F. Brennecke, Chem. Rev., 2020, 120, 12873–12902 CrossRef CAS.
- P. Nürnberg, J. Atik, O. Borodin, M. Winter, E. Paillard and M. Schönhoff, J. Am. Chem. Soc., 2022, 144, 4657–4666 CrossRef PubMed.
- M. Becker, R. S. Kühnel and C. Battaglia, Chem. Commun., 2019, 55, 12032–12035 RSC.
- P. W. Atkins, J. D. Paula and J. Keeler, Chapter 8: Atomic structure and spectra, in Atkins' Physical Chemistry, Oxford University Press, 11 edn, 2014, pp. 323–325 Search PubMed.
- Y. Matsuda, H. Nakashima, M. Morita and Y. Takasu, J. Electrochem. Soc., 1981, 128, 12552 CrossRef.
- N. G. Tsierkezos and A. I. Philippopoulos, Fluid Phase Equilib., 2009, 277, 20–28 CrossRef CAS.
- E. R. Nightingale, J. Phys. Chem., 1959, 63, 1381–1387 CrossRef CAS.
- N. Q. Khuyen, Z. Zondaka, M. Harjo, J. Torop, T. Tamm and R. Kiefer, Polymers, 2019, 11, 849 CrossRef CAS PubMed.
- Y.-J. Kim, Y. Matsuzawa, S. Ozaki, K. C. Park, C. Kim, M. Endo, H. Yoshida, G. Masuda, T. Sato and M. S. Dresselhaus, J. Electrochem. Soc., 2005, 152, A710 CrossRef CAS.
- A. P. Abbott, D. Boothby, G. Capper, D. L. Davies and R. K. Rasheed, J. Am. Chem. Soc., 2004, 126, 9142–9147 CrossRef CAS PubMed.
- L. Suo, D. Oh, Y. Lin, Z. Zhuo, O. Borodin, T. Gao, F. Wang, A. Kushima, Z. Wang, H. C. Kim, Y. Qi, W. Yang, F. Pan, J. Li, K. Xu and C. Wang, J Am Chem Soc., 2017, 139, 18670–18680 CrossRef CAS PubMed.
- D. M. Carey, J. Chem. Phys., 1998, 108, 2669–2675 CrossRef CAS.
- R. Stefanovic, M. Ludwig, G. B. Webber, R. Atkin and A. J. Page, Phys. Chem. Chem. Phys., 2017, 19, 3297–3306 RSC.
- C. R. Ashworth, R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2016, 18, 18145–18160 RSC.
- Q. Hu, X. Lü, W. Lu, Y. Chen and H. Liu, J. Mol. Spectrosc., 2013, 292, 23–27 CrossRef CAS.
- M. H. Lee, S. J. Kim, D. Chang, J. Kim, S. Moon, K. Oh, K. Y. Park, W. M. Seong, H. Park, G. Kwon, B. Lee and K. Kang, Mater. Today, 2019, 29, 26–36 CrossRef CAS.
- P. L. Taberna, P. Simon and J. F. Fauvarque, J. Electrochem. Soc., 2003, 150, A292 CrossRef CAS.
- J. Chmiola, G. Yushin, R. Dash and Y. Gogotsi, J. Power Sources, 2006, 158, 765–772 CrossRef CAS.
- J. Gamby, P. L. Taberna, P. Simon, J. F. Fauvarque and M. Chesneau, J. Power Sources, 2001, 101, 109–116 CrossRef CAS.
- R. Kötz and M. Carlen, Electrochim. Acta, 2000, 45, 2483–2498 CrossRef.
- B. A. Mei, O. Munteshari, J. Lau, B. Dunn and L. Pilon, J. Phys. Chem. C, 2018, 122, 194–206 CrossRef CAS.
- R. de Levie, Electrochim. Acta, 1963, 8, 751–780 CrossRef.
- W. Wei, Z. Chen, Y. Zhang, J. Chen, L. Wan, C. Du, M. Xie and X. Guo, J. Energy Chem., 2020, 48, 277–284 CrossRef.
- P. Navalpotro, M. Anderson, R. Marcilla and J. Palma, Electrochim. Acta, 2018, 263, 110–117 CrossRef CAS.
- B. H. Min and K. Y. Jung, RSC Adv., 2017, 7, 21314–21322 RSC.
- R. B. Macmullin and G. A. Mucclnl, AIChE J., 1956, 2, 393–403 CrossRef CAS.
- S. Krachkovskiy, M. Dontigny, S. Rochon, C. Kim, M. L. Trudeau and K. Zaghib, J. Phys. Chem. C, 2020, 124, 24624–24630 CrossRef CAS.
- C. Prehal, C. Koczwara, H. Amenitsch, V. Presser and O. Paris, Nat. Commun., 2018, 9, 4145 CrossRef CAS PubMed.
- C. Pean, B. Daffos, B. Rotenberg, P. Levitz, M. Haefele, P. L. Taberna, P. Simon and M. Salanne, J. Am. Chem. Soc., 2015, 137, 12627–12632 CrossRef CAS PubMed.
- C. Prehal, C. Koczwara, N. Jäckel, A. Schreiber, M. Burian, H. Amenitsch, M. A. Hartmann, V. Presser and O. Paris, Nat. Energy, 2017, 2, 16215 CrossRef CAS.
- L. Eliad, G. Salitra, A. Soffer and D. Aurbach, J. Phys. Chem. B, 2001, 105, 6880–6887 CrossRef CAS.
- Z. X. Luo, Y. Z. Xing, S. Liu, Y. C. Ling, A. Kleinhammes and Y. Wu, J. Phys. Chem. Lett., 2015, 6, 5022–5026 CrossRef CAS PubMed.
- A. Yamakata, E. Soeta, T. Ishiyama, M. Osawa and A. Morita, J. Am. Chem. Soc., 2013, 135, 15033–15039 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta03632h |
| This journal is © The Royal Society of Chemistry 2024 |






