 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Superionicity by design: high proton conductivity in a fluorine-free protic ionic liquid†
Hanno Maria
Schütz‡
ab,
Stefano
Nejrotti‡
 c,
Henry
Adenusi
d,
Alessandro
Mariani
c,
Henry
Adenusi
d,
Alessandro
Mariani
 *abe,
Enrico
Bodo
*abe,
Enrico
Bodo
 *f,
Matteo
Bonomo
*f,
Matteo
Bonomo
 *c,
Alessandro
Innocenti§
*c,
Alessandro
Innocenti§
 ab,
Claudia
Barolo
ab,
Claudia
Barolo
 c,
Xinpei
Gao
g and
Stefano
Passerini
c,
Xinpei
Gao
g and
Stefano
Passerini
 *ab
*ab
aHelmholtz Institute Ulm (HIU), Helmholtzstrasse 11, 89081 Ulm, Germany
bKarlsruhe Institute of Technology (KIT), P. O. Box 3640, 76021 Karlsruhe, Germany. E-mail: stefano.passerini@kit.edu
cDepartment of Chemistry, NIS Interdepartmental Centre, INSTM Reference Centre, University of Turin, Via Pietro Giuria 7, 10125 Turin, Italy. E-mail: matteo.bonomo@unito.it
dDepartment of Science and Engineering of Matter, Environment and Urban Planning, Marche Polytechnic University, Via Brecce Bianche, 60131, Ancona, Italy
eElettra Sincrotrone Trieste, 34012 Basovizza, Trieste, Italy. E-mail: alessandro.mariani@elettra.eu
fDepartment of Chemistry, Sapienza University of Rome, P. le Aldo Moro 5, 00185 Rome, Italy. E-mail: enrico.bodo@uniroma1.it
gSchool of Chemistry and Chemical Engineering, Hainan University, Haikou 570228, P. R. China
First published on 19th June 2024
Abstract
In this study, the protic ionic liquid N,N-diethyl-3-sulfopropan-1-ammonium hydrogen methanedisulfonate is synthesized and characterized with the aim of elucidating its transport properties. A unique feature of this ionic liquid are the exchangeable acidic protons present on the anion and the cation, both of which contain low proton affinity sulfonic groups. The pronounced superionicity of this liquid, highlighted in the Walden-plot (ΔW > 0.8), indicates the decoupling of the conductivity from ionic diffusion. To explicate this enhanced proton mobility, the diffusion coefficients of the protons were measured by Pulsed-Field Gradient Spin-Echo NMR experiments at different temperatures. Below 373 K the diffusion coefficients of the cationic and anionic exchangeable protons are comparable with the ones of the other protons of the respective ions, indicating a vehicular transport mechanism. However, in the temperature range 383–413 K the diffusion coefficient of one of the exchangeable protons exceeds the diffusion of both ions by an unprecedented factor between 2 and 3. This temperature-induced switch in the proton transport mechanism is the result of a mixed-ion proton-transfer chain, as also supported by computational simulations. Both experimental and theoretical findings suggest the existence of a Grotthuss(-like) proton transport mechanism at high temperature in this system.
Introduction
Protic ionic liquids (PILs) are garnering growing interest for application in the field of electrochemistry.1–3 They differ from their aprotic counterparts because of the origin of their ionic nature, arising from the exchange of a proton from a Brønsted acid to a Brønsted base. These compounds in general show a strong network of hydrogen bonds whose geometry and cohesion energy depend upon the specific molecular ions used. In specific formulations, the protons are free to participate in exchange processes either because of incomplete (i.e., non-quantitative) proton transfer from the acid to the base or because of the presence of specifically introduced proton donor groups that act as additional proton sources.4 The ease of preparation and their high ionic conductivities5 are at the base of the potential use of PILs in energy storage devices3 and in sustainable chemistry.6 In particular, some PILs have been reported to display a superionic behavior,7–9i.e., their conduction mechanism is partially decoupled from the diffusion of the ionic species, thus resulting in conductivity values larger than those of electrolytes where the charge transport is purely vehicular. This feature can be readily observed by a positive deviation (ΔW) from the ideal behavior in the Walden plot, in which molar conductivity is plotted against the reciprocal of viscosity (that is, fluidity).10–13 Superionicity in PILs relies on the mobility of the proton, which can have access to unique diffusion mechanisms. Since the commonly used acid–base dichotomy is only technically valid in diluted aqueous media, hereinafter we will refer as proton donor (PD) and proton acceptor (PA) to the commonly referred acid and base, respectively.The modelling of proton transfer processes between PD and PA in liquids can be undertaken using a variety of techniques among which ab initio static calculations on isolated proton exchanging partners,14–18 or molecular dynamics (MD) are the most used. The main drawback of MD is that, in its classical formulation, the technique presupposes a fixed bond topology, an assumption that is violated when proton transfer takes place. Despite several workarounds19–22 exist, the most common way to deal with proton transfer in MD simulations is to resort to MD variants without the limitation of the fixed topology schemes. Even if reactive force fields23,24 have often been used in this context, the majority of approaches, however, are based on the so-called ab initio MD (AIMD)25,26 where the gradient of the (DFT) electronic energy is directly used to compute the forces needed to classically propagate the nuclear motion.27 In this context, and to overcome the typical sluggishness of AIMD, we have used a semiempirical approach, already applied before,28,29 and based on density functional tight binding (DFTB).30–34 Its advantage lies in not having a fixed bonding topology, in treating electrostatics in a very accurate way (by naturally including many-body terms such as polarization) and in accounting for charge transfer phenomena among the ions.
As illustrated in a study by Ingenmey et al.,35 the presence of neutral species in N-methylimidazolium acetate can play a major role in achieving superionicity by establishing a Grotthuss(-like) proton hopping mechanism, that is not possible if the H+ is too tightly bound to the PA, and consequently not mobile enough. Since the formation reaction of a PIL is inherently an equilibrium, the ionic species and neutral precursors coexist at any given time: in other words, the degree of formation of a PIL is not necessarily quantitative.36–39 However, a high percentage of electrically neutral species could be detrimental to the thermal stability of the PIL, and cause an undesirable increase of volatility.40–42 PILs are, indeed, the ideal systems for harvesting Grotthuss(-like) proton shuttling,35 following a tailored design leading to the presence of optimal amounts of neutral precursors kickstarting the proton cascade, but not hindering the PIL's thermal stability. Pseudo-protic ionic liquids are a very good example of this aspect, showing a low ionization degree (virtually close to zero), but still being decent ionic conductors.40,43,44 A positive ΔW was attained by the group of Angell with a PIL composed of a superacid (HAlCl4) and an extremely weak base (pentafluoropyridine), in which the proton possesses very weak interactions with both species and the diffusion seems to resemble that of a “free H+” entity.7 Albeit for both the reported superionic PILs7,35 it was stressed the importance of using the ΔpKa between the Brønsted acid and base precursors as a predictor of the PIL's ionicity, it is important to acknowledge that pKa is defined only in diluted aqueous solution, where water-solvation effects are predominant. In fact, the actual ionic vs. neutral species ratio may vary from what is expected, and should be determined on a case by case basis.11,36,39 Recently, the role of water in activating a Grotthuss(-like) proton hopping was reported in triflate anion-based PILs. In this case, the cooperative charge mobility was made possible by installing a PD moiety (hydrogen sulfonate) in the cation. The obtained PIL showed at 343 K a non-vehicular proton transfer mechanism when H2O was present in a 6–7%wt content.45 However, in view of the possible application of PILs in proton exchange membranes for high-temperature polymer electrolyte fuel cells, the dependence on a significant presence of water could jeopardize the device efficiency due to water evaporation.
Additionally, it should be noted that the most stable and performing PILs found in literature are usually based on a perfluorinated acid or base (or both).46 Yet, the growing awareness of the health and environmental concerns posed by the synthesis and the disposal of poly- and perfluoroalkyl substances (PFASs) is advancing the replacement of such compounds. A recent proposal of the European Chemicals Agency (ECHA), currently under debate, may lead to a permanent and generalized ban of PFASs within the European Union;47,48 some US states as well as Japan are taking steps towards the same direction, too.49,50 The development of fluorine-free electrolytes, exhibiting the best trade-off between stability and sustainability, is a topical issue to which the scientific community has started to dedicate considerable attention.51–54
As a valuable effort in this direction, and with the aim of achieving fast proton transport through an intrinsic mechanism, we thoughtfully designed the new PIL N,N-diethyl-3-sulfopropan-1-ammonium hydrogen methanedisulfonate [DESPA][HMDS] (see Fig. 1) without any fluorine atom in the cation and the anion. In this fluorine-free system the anion bears two sulfonic moieties, and the same functional group is also present on the cation. In this respect, we envisaged that the presence of PAs with almost equivalent proton affinities in both species could facilitate the exchange mechanism, likely providing access to non-vehicular Grotthuss(-like) proton mobility,35 while maintaining a good thermal stability and low volatility.
Results and discussions
Synthesis of N,N-diethyl-3-sulfopropan-1-ammonium hydrogen methanedisulfonate [DESPA][HMDS]
Methanedisulfonic acid (H2MDS) readily forms hydrates. Depending on the synthesis route the acid contains up to two crystal-water per molecule. Due to the wide speciation of these hydrates, the mixing in perfect 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of the acid with the desired base is challenging, also considering that both the acid and our target base, i.e., 3-(diethylammonio)propane-1-sulfonate, are solid at room temperature. Nonetheless, within the limit of detection of 1H-NMR in diluted samples, the 1
1 ratio of the acid with the desired base is challenging, also considering that both the acid and our target base, i.e., 3-(diethylammonio)propane-1-sulfonate, are solid at room temperature. Nonetheless, within the limit of detection of 1H-NMR in diluted samples, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of acid and base is confirmed, and no impurities were revealed (Fig. 1).
1 ratio of acid and base is confirmed, and no impurities were revealed (Fig. 1).
The properties of [DESPA][HMDS] were investigated through NMR spectroscopy. First, the 1H NMR spectrum of the PIL in DMSO-d6 solution (Fig. 1) was acquired, which enabled the detection of the SO3H protons (two merged peaks at 11.6 ppm) and the NH one (at 9.2 ppm). The results confirmed the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between DESPA and HMDS, showing the 2
1 ratio between DESPA and HMDS, showing the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 integral ratio between the HMDS methylene protons (at 3.8 ppm) and the DESPA methyl protons (at 1.2 ppm). The spectrum in solution, albeit not reflecting the actual interactions present in the pure PIL, allows to appreciate the multiplicity of the aliphatic signals. Moreover, at a closer inspection (Fig. 1 zoom panels) it is possible to observe a series of signals that replicate those of the DESPA ion. These have been attributed to the presence of a cyclic species (depicted in the inset of Fig. 1) arising from intramolecular hydrogen bonding between the NH group and one of the oxygen atoms in the SO3H group of the cation (see Fig. S1 and corresponding discussion in ESI† for a detailed analysis of the spectrum). Then, 1D 1H NMR spectra of the neat [DESPA][HMDS] at temperatures ranging from 298 K and 413 K were also acquired, using a coaxial tube configuration (see Materials and methods section in ESI† for details). The very high viscosity of [DESPA][HMDS] prevented from obtaining any 1H spectra at 298 K.55 More defined peaks were observed at T > 328 K and especially at T > 358 K, making it possible, in the latter case, to partially deconvolve the signals of aliphatic –CH2– moieties located at around 2.6 ppm (Fig. S2†). From the comparison of these spectra, it is observed that the chemical shift of the peaks seems not to be sizeable influenced by the applied temperature (Fig. S2 and Table S1†). In all the spectra, a small peak could be detected just below 6 ppm accounting for the same closed-ring cation structure evidenced in the NMR spectrum in DMSO. However, in the NMR spectra of neat [DESPA][HMDS] it was impossible to discriminate the aliphatic protons' signals of the open and closed structures due to peak broadening and clustering of all the signal in a couple of peaks located at 2.6 ppm even at 413 K. Therefore, a 1H–15N heteronuclear multiple quantum correlation (HMQC) experiment of neat PIL was performed (see Fig. S1b†), proving that the proton at 5.9 ppm is bound to a nitrogen atom, supporting the hypothesis that the closed-ring structure is already present in the solvent-free PIL. It is worth noting that, once normalized at 2 the peaks of the methylene groups of both the anion and the cation, the sum of the integrals of the two N–H signals integrate to approximately one (considering the uncertainty due to peak broadening), thus proving that all the nitrogen atoms are protonated in [DESPA][HMDS] (see Table S1†). Following on from the above discussed data, we can fairly hypothesize a nearly complete formation of the PIL. The latter evidence shows that the ΔpKa is not a reliable metric to assess the actual formation of the PIL. In fact, in our case the difference in pKa between the donor and acceptor sites of the exchangeable proton is virtually zero being both sulfonic groups on hydrocarbons.
6 integral ratio between the HMDS methylene protons (at 3.8 ppm) and the DESPA methyl protons (at 1.2 ppm). The spectrum in solution, albeit not reflecting the actual interactions present in the pure PIL, allows to appreciate the multiplicity of the aliphatic signals. Moreover, at a closer inspection (Fig. 1 zoom panels) it is possible to observe a series of signals that replicate those of the DESPA ion. These have been attributed to the presence of a cyclic species (depicted in the inset of Fig. 1) arising from intramolecular hydrogen bonding between the NH group and one of the oxygen atoms in the SO3H group of the cation (see Fig. S1 and corresponding discussion in ESI† for a detailed analysis of the spectrum). Then, 1D 1H NMR spectra of the neat [DESPA][HMDS] at temperatures ranging from 298 K and 413 K were also acquired, using a coaxial tube configuration (see Materials and methods section in ESI† for details). The very high viscosity of [DESPA][HMDS] prevented from obtaining any 1H spectra at 298 K.55 More defined peaks were observed at T > 328 K and especially at T > 358 K, making it possible, in the latter case, to partially deconvolve the signals of aliphatic –CH2– moieties located at around 2.6 ppm (Fig. S2†). From the comparison of these spectra, it is observed that the chemical shift of the peaks seems not to be sizeable influenced by the applied temperature (Fig. S2 and Table S1†). In all the spectra, a small peak could be detected just below 6 ppm accounting for the same closed-ring cation structure evidenced in the NMR spectrum in DMSO. However, in the NMR spectra of neat [DESPA][HMDS] it was impossible to discriminate the aliphatic protons' signals of the open and closed structures due to peak broadening and clustering of all the signal in a couple of peaks located at 2.6 ppm even at 413 K. Therefore, a 1H–15N heteronuclear multiple quantum correlation (HMQC) experiment of neat PIL was performed (see Fig. S1b†), proving that the proton at 5.9 ppm is bound to a nitrogen atom, supporting the hypothesis that the closed-ring structure is already present in the solvent-free PIL. It is worth noting that, once normalized at 2 the peaks of the methylene groups of both the anion and the cation, the sum of the integrals of the two N–H signals integrate to approximately one (considering the uncertainty due to peak broadening), thus proving that all the nitrogen atoms are protonated in [DESPA][HMDS] (see Table S1†). Following on from the above discussed data, we can fairly hypothesize a nearly complete formation of the PIL. The latter evidence shows that the ΔpKa is not a reliable metric to assess the actual formation of the PIL. In fact, in our case the difference in pKa between the donor and acceptor sites of the exchangeable proton is virtually zero being both sulfonic groups on hydrocarbons.
To test the presence of unwanted ions in the final product, the sample was inspected with ICP-OES, which showed non-relevant inorganic impurities (Table S2†). From the multi-element calibration standard (see Materials and methods section in ESI†), the only ions for which an amount above 100 ppm was detected were Ca, K and Na. All of them are common ionic impurities, which are hard to avoid in the preparation of ionic liquids. Nevertheless, with these quantities there should not be a noticeable effect on the properties of the PIL.56 The main impurity is water with 4634 to 8579 ppm in the different batches due to the water-based synthesis.
The thermal stability of [DESPA][HMDS] was tested in synthetic air atmosphere, and it was found to be stable in dynamic scans at temperatures higher than 300 °C, and stable for long time at temperatures lower than 150 °C (see Fig. S3 and Table S3†). In depth discussion of the thermal characterization, including density and isobaric thermal expansivity, can be found in the ESI.†
Transport properties
Transport properties are of pivotal importance for electrolytes in electrochemical devices. We analyzed [DESPA][HMDS] in terms of viscosity, conductivity and diffusion coefficients exploiting the IonFit code (see ESI† for software details). Regarding the rheological characterization, [DESPA][HMDS] displays a Newtonian behavior for all the explored conditions. At 353 K the shear rate and shear stress are linearly correlated throughout the investigated range of 1–100 s−1 (Fig. S5a†). At 293 K the upper shear rate limit of the rheometer was 80 s−1 because of the high viscosity of the sample around 1 kPa s. Consequently, a linear shear rate sweep was not possible because of the extremely long time needed to achieve a constant shear rate. Therefore, the shear rate was increased stepwise, and each value was held for a longer period. With this measurement protocol, a 1.8% viscosity increase was observed at 293 K comparing results at 1 s−1 and 80 s−1 (Fig. S5b†), confirming that [DESPA][HMDS] is a Newtonian fluid in the whole temperature range investigated. A shear rate of 10 s−1 was selected for the further investigation of the temperature dependency of the viscosity. The temperature dependency of both the viscosity and ionic conductivity in Fig. 2a follows the Vogel–Tammann–Fulcher (VTF) behavior, defined by the well-known equation: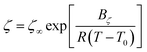 | (1) |
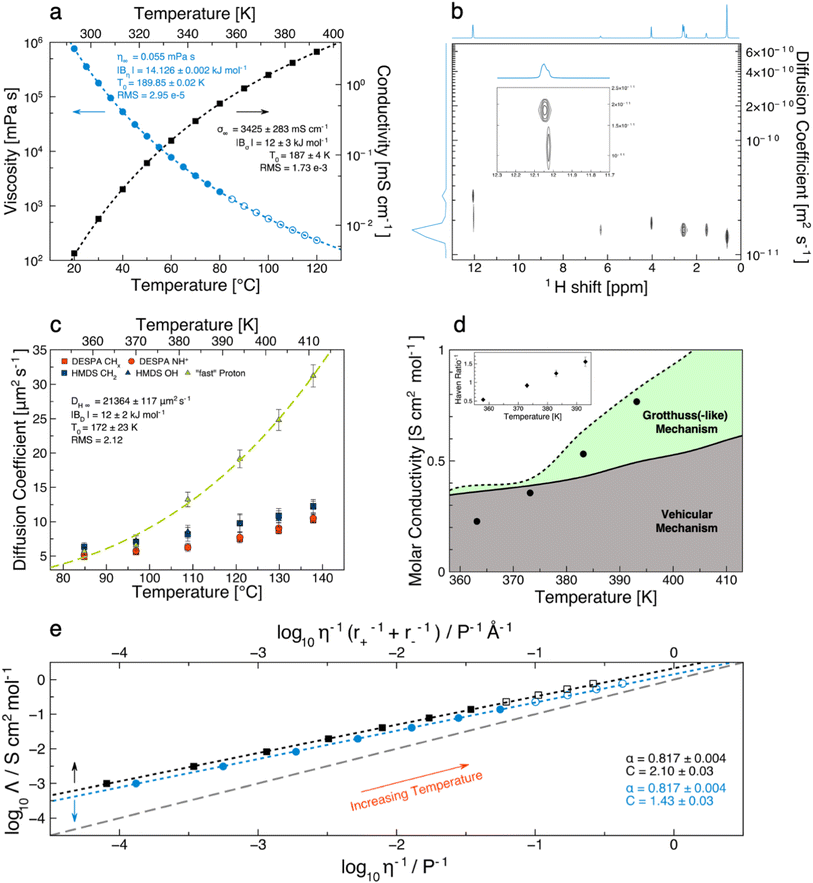 | ||
| Fig. 2 Transport properties of [DESPA][HMDS]. (a) Temperature-dependent viscosity and conductivity. The measured values are represented by filled symbols. The dashed lines are VTF fits of the data. Open symbols depict extrapolated values based on the VTF fit. (b) Bayesian representation of the PGSE-1H NMR experiment performed on pure [DESPA][HMDS] at 120 °C. The inset is a zoom on the OH region. (c) Temperature-dependent diffusion coefficients of the protons obtained from PGSE-1H NMR experiments. (d) Visualization of the proton transport mechanism of [DESPA][HMDS] as a function of temperature. The symbols represent the experimentally determined molar conductivities. The lines are the molar conductivities calculated with the Nernst–Einstein equation (eqn (6)). Values obtained by using the diffusion coefficients of the cation and the anion are depicted as a solid line, the dashed line was obtained by replacing the cation diffusion coefficients with the “fast” proton ones. The inset show the inverse Haven ratio calculated with the diffusion coefficients of the cation and the anion. (e) Walden plot (blue circles) and Walden plot with radii correction (black squares). The dashed grey diagonal reference line represents conduction by ideal vehicular mechanism. Open symbols are based on a linear extrapolation of the density and an extrapolation with the VTF equation for the viscosity. The dashed lines are arising from the data fitting with the Walden rule. | ||
A more elegant way to visualize the correlation of the viscous flow and conductivity is the Walden-plot (Fig. 2e), in which the molar conductivity is plotted against the fluidity, both in a logarithmic scale. For this kind of analysis, a reference ideal behavior line is represented by the 1 M KCl aqueous solution, which is considered fully dissociated and conducting with purely vehicular mechanism. The plot is based on the idea that, in general, it is expected for any given ionic system to obey the Walden rule:13
| Ληα = C | (2) |
MacFarlane et al. proposed a correction to consider the finite radii of the ions13 (no point mass like theoretically assumed). The Walden rule then becomes:
 | (3) |
 | (4) |
A definitive quantification of the superionicity of [DESPA][HMDS] can be achieved by determining the diffusion coefficient values of both the anion and the cation. Therefore, we performed Pulsed-Field Gradient Spin-Echo (PGSE) experiments,61–63 as this technique provides key information on the mobility of all the species in the system. Due to the unusually high viscosity of [DESPA][HMDS], it was impossible to obtain a clear and reliable dataset at temperatures below 358 K due to the inhomogeneity of the magnetic field throughout the sample.55 The diffusion coefficient values of the different species, calculated by the interpolation of the signal decay for each peak, are reported in Fig. 2c and Tables 1, S4.†
| T [K] | DESPA CHx | DESPA NH+ | HMDS CH2 | HMDS OH | “fast” proton | D ”fast”/D+ | D ”fast”/D− |
|---|---|---|---|---|---|---|---|
| 358 | 4.9 ± 0.186 | 5.2 ± 0.33 | 6.3 ± 0.6 | 5.7 ± 0.57 | 5.7 ± 0.52 | 1.16 ± 0.11 | 0.90 ± 0.12 |
| 373 | 5.6 ± 0.184 | 5.8 ± 0.45 | 7.1 ± 0.88 | 7.2 ± 0.85 | 6.6 ± 0.76 | 1.18 ± 0.14 | 0.93 ± 0.16 |
| 383 | 6.3 ± 0.229 | 6.3 ± 0.59 | 8.2 ± 1 | 8.5 ± 0.94 | 13.2 ± 1.07 | 2.10 ± 0.19 | 1.61 ± 0.24 |
| 393 | 7.5 ± 0.338 | 7.7 ± 0.8 | 9.8 ± 1.36 | 9.7 ± 1.28 | 19.1 ± 1.29 | 2.55 ± 0.21 | 1.95 ± 0.30 |
| 403 | 8.7 ± 0.379 | 9.1 ± 0.86 | 10.9 ± 1.05 | 10.4 ± 1.18 | 24.8 ± 1.52 | 2.85 ± 0.21 | 2.28 ± 0.26 |
| 413 | 10.2 ± 0.378 | 10.5 ± 0.64 | 12.3 ± 0.96 | 12.0 ± 0.96 | 31.2 ± 1.61 | 3.06 ± 0.19 | 2.54 ± 0.24 |
First, it is seen that the anion and the cation display independent mobility,64 which is also evident from the Bayesian representation of the DOSY experiment in Fig. 2b. The values of the diffusion coefficient D related to the cation are all clustered (Table S4†), and this result appears to be independent (within the experimental error) from the peak chosen for the analysis. Unfortunately, due to the relatively low intensity, it was not possible to extend the analyses to the peaks of the closed-ring population. The mobility of the anion is slightly higher compared to that of the cation at all the investigated temperature values, as expected by its lower molecular weight. This suggests that [DESPA][HMDS] follows the well-known behavior in which the D values are clearly clustered in two subsets, namely, the cation's and the anion's ones.36,64–67 On the other hand, the analysis of the OH protons signal (at ∼12 ppm) deserves a more detailed discussion as it results from the superposition of two peaks (see Fig. 1 and 2c), one centered at 12.08 ppm and the other one at 12.07 ppm (at 393 K). At 358 K and 373 K, the diffusion coefficient that can be extracted from the analyses of the two peaks are, within the experimental error, equals (see Table 1 and Fig. S6†). One should note that, at 358 K, the analysis is onerous owing to the strong overlapping of the two peaks, which are instead better resolved with increasing temperature. At T > 373 K, the peak at lower ppm still presents the same D value as the methylene protons of the anion, while for the peak at higher ppm a significantly higher D value can be extracted. Such evidence is indicating that this proton diffuses somewhat decoupled from any other ion, by a different mechanism likely due to a supramolecular structuring of [DESPA][HMDS]. Examples of ILs in which an exchangeable proton displays a mobility decoupled from that of the anion and the cation have already been reported in the literature, and a Grotthuss(-like) mechanism has been proposed to account for the 1.2–1.4 fold increase in mobility.64,68,69 It should be noted that the diffusion coefficient of the “fast” proton in [DESPA][HMDS] is 2.55 and 3.06 times larger than that of the cation at 393 K and 413 K, respectively, which can be considered as the most significant and reliable proof supporting the theorization of Grotthuss(-like) conduction mechanism in PILs. To the best of our knowledge, the temperature-dependent “on–off” behavior observed in [DESPA][HMDS] finds no precedents in the literature. To justify these findings, we hypothesized that at low temperatures (“off”-region, e.g., T < 383 K) a series of proton exchanges take place between the (protonated) sulfonic moiety of the cation and the deprotonated anion, but due to high viscosity the ions have not enough mobility to change orientation and pass the proton to a third species. In this scenario, the jumping would not affect the overall transport properties of the PIL because the “fast” proton would be trapped between the exchanging pair, thus not impacting on the formal D values of the jumping proton. Another possible proton exchange mechanism in the “off”-region is an intramolecular one, which takes place between the two sulfonic moieties of the anion, as expected by their intrinsically equal proton affinity. On the other hand, at higher temperatures (“on”-region, e.g., T > 383 K) the “fast” proton could be able to escape its immediate neighborhood thanks to the lowered viscosity enabling a more efficient re-orientation of its carriers. Following this mechanism, the jumping proton would show different D values compared to the one of the carrier species, kickstarting a chain exchange. In previous studies,45,66 a higher diffusion coefficient observed in ILs (e.g., triethylamine-based ones) was attributed to the presence of adventitious water, deriving from a non-anhydrous PIL's synthetic procedure rather than resulting from an intrinsic mechanism. In the [DESPA][HMDS] case, albeit the presence of the non-negligible amount of water of 5483 ± 189 ppm (n = 4), it could hardly be cited as the (main) reason justifying the unexpectedly high D measured for the fast proton of the cation. It is unlikely that the water plays a (significant) role at T > 373 K, not to mention that the 1H chemical shift of the fast proton indicates that it must be hopping between sulfonic moieties. Thus, we conclude that a Grotthuss mechanism mediated by water molecules, albeit possible, has not sufficient population to be noticed in the overall conductivity. On this note, it is important to highlight how substantially higher amounts of water (4 to 6 folds the amount in our PIL) have been reported to be needed to trigger less dramatic proton shuttling in similar systems.45,60 As the other transport properties, also the diffusion coefficient can be interpreted by means of the VTF model. The fitting on the “fast” proton is shown in Fig. 2c, and the activation energy of 12 kJ mol−1 is in line with what is found for the conductivity, and just below the value for viscosity (including the uncertainty). Albeit still very small, this difference clearly points at some decoupling between conductivity and viscosity.
The inverse Haven ratio H−1 is commonly used to quantify the reduced ionicity36 of electrolytes based on the Nernst–Einstein molar conductivity ΛNE and the experimental molar conductivity Λexp, and it is defined as:
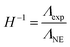 | (5) |
 | (6) |
The PIL's conductivity calculated from NMR data at 358 K is higher than the one experimentally measured but, after the trigger temperature, the experimental values become larger than the theoretical ones (considering only the ions diffusion coefficients). The results obtained for [DESPA][HMDS] are depicted in the inset of Fig. 2d and Table 2 with values of H−1 up to 1.55, confirming its superionic nature. If the diffusion coefficient of the “fast” proton is included in eqn (6) instead of the diffusion coefficient of the cation, then the inverse Haven ratio obviously changes, returning values consistently smaller than one. Nevertheless, it is unlikely that every possible exchangeable proton is decoupled from any ion, thus the values of ΛNE obtained with the diffusion coefficient of the “fast” proton should be considered as a great overestimation. To quantify the amount of “fast” protons and to obtain a fundamental understanding of the complex structural nature of such PIL, atomistic modelling was employed to render the experimental determinations intelligible.
Ab initio investigation of proton transfer barriers
The [DESPA][HMDS] system was investigated by means of two different methods, namely a “static” DFT set of calculations aimed at the determination of the energy barriers for the proton transfer, and a more realistic AIMD simulation where two ion pairs were observed.The first set of calculations was directed to establish the propensity toward proton transfer of the possible ionic pairs that can exist in the liquid. We have analyzed four possible cases: the proton exchange between two anions (A–A), two cations (C–C), a cation and an anion (C–A) and within a single anion (A-intramolecular). For each molecular pair we have calculated the energy along a concerted proton transfer (PT) path using the NEB method (see Materials and methods section in ESI†). The results obtained through two different functionals are reported in Fig. 3a. The two panels, apart from the obvious differences due to the specific geometries and energies produced by the NEB algorithm and the functionals, report the same data, i.e., the relative energy obtained along a proton transfer path between the molecular partners. The considered proton transfers are depicted schematically in Fig. 3c.
All proton exchanges, regardless of the species bearing the SO3H group, require similar energies ranging between 12 and 27 kJ mol−1 (see Fig. 3a), which is comparable to the strength of a typical hydrogen bond. It should be noted that the activation energy is calculated as the difference in energy between the maximum and the initial state. The proton exchange between anions (A–C, in green) and within the same anion (A–A, in blue) are those that have the smallest activation energies (around 13 and 17 kJ mol−1, respectively). The two different methods, r2SCAN-3c and ωB97X-D3 yielded similar results, thus providing validation of the outcomes. These simple numerical data prove that the proton exchange in these systems is a process that require only a modest energy and that a moderate temperature increase may easily trigger a variety of proton transfers among the homodimeric and heterodimeric pairs in the fluid. By assuming a unitary pre-exponential factor in the Arrhenius equation, one may obtain an estimate of the percentage of molecules having sufficient energy to overcome a kinetic barrier at a given temperature:
 | (7) |
Molecular dynamics
To provide a more realistic approach to the complexity of the bulk phase, we have increased the size of our model systems to four molecular partners. In this case, and due to the relatively large number of possible proton transfer processes that can take place, we have decided to simulate the evolution of the system using MD after an initial perturbation. To allow for a sufficiently long exploration of the dynamics, we are forced to resort to a semiempirical model of the electronic energy, namely GFN2-xTB.Our model system is composed of two anions and two cations. The initial perturbation consists in forcing a proton transfer from the SO3H of one cation onto the SO3− of one anion. This can be easily obtained by enforcing a constrain on the resulting O–H bond in the anionic structure whose distance has been fixed to 1.0 Å. The initial structure at the beginning of the dynamics is therefore made by one anion, one cation, a zwitterion (the cation that has lost the SO3H proton) and a neutral molecule (the anion that has acquired a proton). Four MDs were performed using an NVT ensemble at 383 K to elucidate the type of proton transfers that were allowed after the perturbation. The calculations differ for the initial positions of the four molecular partners. In three (see below) out of four trajectories the initial (forced) proton transfer led to additional events: (i) in trajectory 1 (schematized in Fig. 3d), the mobile proton of the neutral molecule simply migrated back to the zwitterion recreating the original (pre-perturbation) ionic pair. A second and third PT then took place, one between the two anions and another between a cation and an anion. In other words, during dynamics the initial zwitterion has transformed into a cation and another zwitterion has appeared; (ii) the second trajectory produced a more complicated pattern: a double PT between the cation and the neutral is followed by another one from the anion to the zwitterion. The zwitterion and neutral have disappeared, leaving the final cluster in a fully ionic state. This intricate exchange of protons simply ionized the initial neutral pair; (iii) trajectory 3 shows an intramolecular PT within the neutral and, at the same time, another PT from the anion to the cation. The final situation is two cations, one neutral and a di-anion.
Overall, these computations show that an initial event perturbing the expected ionic composition (which has a ∼2.5% chance of proceeding) leads to a cascade of fast PTs, taking place on a 100 ps scale, that can either shift the position of the zwitterionic molecules in space (trajectory 1), ionize the neutral pair (trajectory 2) or give rise to unexpected ionic configurations involving doubly charged anions (trajectory 3). Among the three processes illustrated above, trajectory 1 is the most interesting because it represents a way to move a proton from one cation to another using a molecular chain. The overall process along trajectory 1 is schematized in Fig. 3d. The initial configuration with a zwitterion (–SO3−), a neutral, an anion and a cation (–SO3H), after 100 ps has changed and the chain of events has effectively moved a proton from one cation to the other.
Conclusions
In summary, we have for the first time synthesized and characterized a novel and fluorine-free PIL, N,N-diethyl-3-sulfopropan-1-ammonium hydrogen methanedisulfonate [DESPA][HMDS]. With the aim of designing an IL capable of Grotthuss(-like) proton conduction, we carefully selected functional groups on the cation and the anion so that the potential energy surface would have been as flat as possible for the mobile proton. The selected approach, involving the presence of a sulfonic group on the cation and two on the anion, is clearly successful as highlighted by the experimental and theoretical results reported. [DESPA][HMDS] displays marked superionicity in the (albeit qualitative) Walden plot, with Walden reduced-ionicity values up to 1.09 (0.87 without the radii correction), the highest value ever reported for a PIL to the best of our knowledge. The PGSE-NMR findings conclusively demonstrated that above a certain temperature a “fast” mobile proton exists, which is decoupled from the diffusion of both the ions and moves 2–3 times faster than any other species in the system. Consequently, actual experimental ionic conductivities were measured to be higher than Nernst–Einstein conductivities, cementing the definition of [DESPA][HMDS] as a superionic liquid, with an unprecedented inverse Haven ratio of 1.55. The performed computational studies first showed how the activation energies for the different proton jumps were small and similar to each other, confirming the starting hypothesis of a flat potential energy surface, and second, directly displayed a proton transfer cascade reminiscent of the Grotthuss mechanism. Based on these findings, we encourage the IL community to embrace our approach and to identify alternative superior superionic liquids, overcoming the main drawback for [DESPA][HMDS] which is the extremely high viscosity at room temperature.Associated content
The IonFit code is available as open source through MIT standard license via the Github repository at the address: https://github.com/RedMageP42/IonFit. The ESI† contain the ICP-OES, the 1H–15N HMQC NMR spectrum of the neat PIL, experimental NMR spectra of the neat PIL as a function of temperature along with detailed peak positions, integrals, and FWHM, dynamic and isothermal TGA, DSC, density, isobaric thermal expansivity, along with a detailed discussion on the thermal behavior of [DESPA][HMDS], the shear rate tests results, Bayesian representation of the PGSE-NMR experiments at 85 and 120 °C, the individual diffusion coefficients of each proton in the [DESPA] cation as a function of temperature, the Materials and methods section. Moreover, a detailed description of IonFit along with several results obtained on many electrolytes. Ref. 70–99 are framed in the discussion in the ESI† file.Data availability
Most of the data supporting this article have been included as part of the ESI.† The code for the VTF fittings and Walden analysys (IonFit) can be found https://github.com/RedMageP42/IonFit. The version of the code employed for this study is version 0.7. Other data are made accessible through reasonable requests to the corresponding authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge Prof. Andrea Mele, Prof. Piercarlo Mustarelli, Dr Giovanni Battista Appetecchi, Dr Guinevere Giffin, Dr Carsten Korte, Dr Xu Liu, and Dr Xu Dong for the fundamental scientific feedback. The authors acknowledge Dr Federica Rossi for technical support in neat-state NMR measurements. The authors acknowledge the technical support by Christian Tontsch and all the staff of the NMR service of Institute of Organic Chemistry I (University Ulm) for the measurements of 1D NMR in solution. A. M. would like to thank Virgilio Ciampani and Alessandra D'Orazio for their critical role in the coding of IonFit. HIU authors acknowledge the basic funding of Helmholtz Association. H. M. S., A. M. and S. P. acknowledge the financial support of the German Federal Ministry for Economic Affairs and Energy (HiFi-PEFC, project number: 03ETB003A). S. N., M. B. and C. B. acknowledge support from the Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027” (CUP D13C22003520001). M. B. receives fundings from GENESIS project funded by the Ministero dell’Università e della Ricerca within the PRIN 2022 program. A. I. acknowledges the EU's Horizon 2020 Research and Innovation Programme under Marie Skłodowska-Curie Grant Agreement 860403 “POLYSTORAGE” for the funding.References
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206 CrossRef CAS.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379 CrossRef CAS PubMed.
- T. Stettner and A. Balducci, Energy Storage Mater., 2021, 40, 402 CrossRef.
- M. Middendorf and M. Schönhoff, J. Phys. Chem. B, 2024, 128, 2939 CrossRef CAS.
- W. Xu and C. A. Angell, Science, 2003, 302, 422 CrossRef CAS PubMed.
- J. Bailey, E. L. Byrne, P. Goodrich, P. Kavanagh and M. Swadźba-Kwaśny, Green Chem., 2024, 26, 1092 RSC.
- Y. Ansari, K. Ueno and C. A. Angell, J. Phys. Chem. B, 2021, 125, 7855 CrossRef CAS.
- J. Nowicki, M. Muszyński and J.-P. Mikkola, RSC Adv., 2016, 6, 9194 RSC.
- Z. Wojnarowska, Y. Wang, K. J. Paluch, A. P. Sokolov and M. Paluch, Phys. Chem. Chem. Phys., 2014, 16, 9123 RSC.
- M. Yoshizawa, W. Xu and C. A. Angell, J. Am. Chem. Soc., 2003, 125, 15411 CrossRef CAS PubMed.
- K. R. Harris, J. Phys. Chem. B, 2019, 123, 7014 CrossRef CAS PubMed.
- C. Schreiner, S. Zugmann, R. Hartl and H. J. Gores, J. Chem. Eng. Data, 2010, 55, 1784 CrossRef CAS.
- D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962 RSC.
- C. Wang and S. J. Paddison, Phys. Chem. Chem. Phys., 2010, 12, 970 RSC.
- F. Sepehr and S. J. Paddison, Solid State Ionics, 2017, 306, 2 CrossRef CAS.
- C. Wang, J. K. Clark II, M. Kumar and S. J. Paddison, Solid State Ionics, 2011, 199–200, 6 CrossRef CAS.
- A. Le Donne, S. Russo and E. Bodo, Chem. Phys., 2022, 552, 111365 CrossRef CAS.
- Z. Zhu, X. Luo, A. P. Sokolov and S. J. Paddison, J. Phys. Chem. A, 2020, 124, 4141 CrossRef CAS PubMed.
- F. Joerg and C. Schröder, Phys. Chem. Chem. Phys., 2022, 24, 15245 RSC.
- C. Dreßler, G. Kabbe, M. Brehm and D. Sebastiani, J. Chem. Phys., 2020, 152, 114114 CrossRef.
- F. Joerg, M. Wieder and C. Schröder, Front. Chem., 2023, 11, 1140896 CrossRef CAS PubMed.
- P. Dobrev, S. P. B. Vemulapalli, N. Nath, C. Griesinger and H. Grubmüller, J. Chem. Theory Comput., 2020, 16, 2561 CrossRef CAS.
- O. Rahaman, A. C. T. Van Duin, W. A. Goddard III and D. J. Doren, J. Phys. Chem. B, 2011, 115, 249 CrossRef CAS PubMed.
- W. Zhang and A. C. T. Van Duin, J. Phys. Chem. B, 2017, 121, 6021 CrossRef CAS PubMed.
- R. L. Hayes, S. J. Paddison and M. E. Tuckerman, J. Phys. Chem. B, 2009, 113, 16574 CrossRef CAS PubMed.
- L. Vilčiauskas, M. E. Tuckerman, G. Bester, S. J. Paddison and K.-D. Kreuer, Nat. Chem., 2012, 4, 461 CrossRef PubMed.
- E. Bodo, J. Phys. Chem. B, 2022, 126, 3 CrossRef CAS PubMed.
- H. Adenusi, A. Le Donne, F. Porcelli and E. Bodo, J. Phys. Chem. B, 2020, 124, 1955 CrossRef CAS PubMed.
- E. Bodo, M. Bonomo and A. Mariani, J. Phys. Chem. B, 2021, 125, 2781 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260 CrossRef CAS.
- Y. Yang, H. Yu, D. York, Q. Cui and M. Elstner, J. Phys. Chem. A, 2007, 111, 10861 CrossRef CAS PubMed.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931 CrossRef CAS.
- M. Gaus, X. Lu, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2014, 10, 1518 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652 CrossRef CAS PubMed.
- J. Ingenmey, S. Gehrke and B. Kirchner, ChemSusChem, 2018, 11, 1900 CrossRef CAS PubMed.
- A. Mariani, M. Bonomo, X. Gao, B. Centrella, A. Nucara, R. Buscaino, A. Barge, N. Barbero, L. Gontrani and S. Passerini, J. Mol. Liq., 2021, 324, 115069 CrossRef CAS.
- M. Hasani, S. A. Amin, J. L. Yarger, S. K. Davidowski and C. A. Angell, J. Phys. Chem. B, 2019, 123, 1815 CrossRef CAS PubMed.
- M. Shen, Y. Zhang, K. Chen, S. Che, J. Yao and H. Li, J. Phys. Chem. B, 2017, 121, 1372 CrossRef CAS PubMed.
- J. Stoimenovski, E. I. Izgorodina and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2010, 12, 10341 RSC.
- H. Doi, X. Song, B. Minofar, R. Kanzaki, T. Takamuku and Y. Umebayashi, Chem.–Eur. J., 2013, 19, 11522 CrossRef CAS PubMed.
- M. J. Earle, J. M. S. S. Esperança, M. a Gilea, J. N. Canongia Lopes, L. P. N. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831 CrossRef CAS.
- A. Idris, R. Vijayaraghavan, A. F. Patti and D. R. MacFarlane, ACS Sustain. Chem. Eng., 2014, 2, 1888 CrossRef CAS.
- M. N. Kobrak and K. G. Yager, Phys. Chem. Chem. Phys., 2018, 20, 18639 RSC.
- P. Berton, S. P. Kelley, H. Wang and R. D. Rogers, J. Mol. Liq., 2018, 269, 126 CrossRef CAS.
- J. Lin, L. Wang, T. Zinkevich, S. Indris, Y. Suo and C. Korte, Phys. Chem. Chem. Phys., 2020, 22, 1145 RSC.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190 CrossRef CAS PubMed.
- X. Lim, Nature, 2023, 620, 24 CrossRef CAS PubMed.
- N. D. Tyrrell, Org. Process Res. Dev., 2023, 27, 1422 CrossRef CAS.
- O. US EPA, Per- and Polyfluoroalkyl Substances (PFAS), can be found under https://www.epa.gov/sdwa/and-polyfluoroalkyl-substances-pfas, 2021 Search PubMed.
- PFAS, can be found under https://www.saferstates.org/toxic-chemicals/pfas/ Search PubMed.
- X. He, B. Yan, X. Zhang, Z. Liu, D. Bresser, J. Wang, R. Wang, X. Cao, Y. Su, H. Jia, C. P. Grey, H. Frielinghaus, D. G. Truhlar, M. Winter, J. Li and E. Paillard, Nat. Commun., 2018, 9, 1 CrossRef CAS PubMed.
- J. Han, M. Zarrabeitia, A. Mariani, Z. Jusys, M. Hekmatfar, H. Zhang, D. Geiger, U. Kaiser, R. J. Behm, A. Varzi and S. Passerini, Nano Energy, 2020, 77, 105176 CrossRef CAS.
- N. Karimi, M. Zarrabeitia, A. Mariani, D. Gatti, A. Varzi and S. Passerini, Adv. Energy Mater., 2021, 11, 2003521 CrossRef CAS.
- J. Han, A. Mariani, A. Varzi and S. Passerini, J. Power Sources, 2021, 485, 229329 CrossRef CAS.
- K. Damodaran, in Annu. Rep. NMR Spectrosc., Elsevier, 2016, pp. 215–244 Search PubMed.
- K. R. Seddon, A. Stark and M.-J. Torres, Pure Appl. Chem., 2000, 72, 2275 CrossRef CAS.
- S. H. Chung, S. Bajue and S. G. Greenbaum, J. Chem. Phys., 2000, 112, 8515 CrossRef CAS.
- Y. H. Zhao, M. H. Abraham and A. M. Zissimos, J. Org. Chem., 2003, 68, 7368 CrossRef CAS PubMed.
- H. Hou, H. M. Schütz, J. Giffin, K. Wippermann, X. Gao, A. Mariani, S. Passerini and C. Korte, ACS Appl. Mater. Interfaces, 2021, 13, 26649 CrossRef CAS PubMed.
- H. Hou, H. M. Schütz, J. Giffin, K. Wippermann, X. Gao, A. Mariani, S. Passerini and C. Korte, ACS Appl. Mater. Interfaces, 2021, 13, 8370 CrossRef CAS PubMed.
- A. Noda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2001, 105, 4603 CrossRef CAS.
- A. Mariani, M. Bonomo, B. Wu, B. Centrella, D. Dini, E. W. Castner and L. Gontrani, Phys. Chem. Chem. Phys., 2017, 19, 27212 RSC.
- M. Campetella, A. Mariani, C. Sadun, B. Wu, E. W. Castner and L. Gontrani, J. Chem. Phys., 2018, 148, 134507 CrossRef PubMed.
- P. Judeinstein, C. Iojoiu, J.-Y. Y. Sanchez and B. Ancian, J. Phys. Chem. B, 2008, 112, 3680 CrossRef CAS.
- S. K. Davidowski, F. Thompson, W. Huang, M. Hasani, S. A. Amin, C. A. Angell and J. L. Yarger, J. Phys. Chem. B, 2016, 120, 4279 CrossRef CAS PubMed.
- J. W. Blanchard, J.-P. Belières, T. M. Alam, J. L. Yarger and G. P. Holland, J. Phys. Chem. Lett., 2011, 2, 1077 CrossRef CAS.
- F. Philippi, D. Rauber, J. Zapp and R. Hempelmann, Phys. Chem. Chem. Phys., 2017, 19, 23015 RSC.
- A. Noda, M. A. B. H. Susan, K. Kudo, S. Mitsushima, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2003, 107, 4024 CrossRef CAS.
- S. K. Mann, S. P. Brown and D. R. MacFarlane, ChemPhysChem, 2020, 21, 1444 CrossRef CAS.
- H. J. Backer, Recl. Trav. Chim. Pays-Bas, 1929, 48, 949 CrossRef CAS.
- H. Goldwhite, M. S. Gibson and C. Harris, Tetrahedron, 1965, 21, 2743 CrossRef.
- A. Bocarsly and E. Niangar, Encyclopedia of Electrochemical Power Sources, Elsevier, 2009 Search PubMed.
- M. Martinez, Y. Molmeret, L. Cointeaux, C. Iojoiu, J. C. Leprêtre, N. El Kissi, P. Judeinstein and J. Y. Sanchez, J. Power Sources, 2010, 195, 5829 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103 CrossRef CAS PubMed.
- H. Tokuda, K. Ishii, Md. A. B. H. Susan, S. Tsuzuki, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 2833 CrossRef CAS PubMed.
- J. O. Bockris and A. K. N. Reddy, Modern Electrochemistry 1, Plenum Press, New York, 1998 Search PubMed.
- A. Mariani, R. Caminiti, F. Ramondo, G. Salvitti, F. Mocci and L. Gontrani, J. Phys. Chem. Lett., 2017, 8, 3512 CrossRef CAS PubMed.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2009, 48, 3184 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929 CrossRef PubMed.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- D. Turnbull and M. H. Cohen, J. Chem. Phys., 1961, 34, 120 CrossRef CAS.
- J. N. Canongia Lopes, J. M. S. S. Esperança, A. M. de Ferro, A. B. Pereiro, N. V. Plechkova, L. P. N. Rebelo, K. R. Seddon and I. Vázquez-Fernández, J. Phys. Chem. B, 2016, 120, 2397 CrossRef CAS PubMed.
- M. Moreno, E. Simonetti, G. B. Appetecchi, M. Carewska, M. Montanino, G.-T. Kim, N. Loeffler and S. Passerini, J. Electrochem. Soc., 2017, 164, A6026 CrossRef CAS.
- X. Liu, M. Zarrabeitia, A. Mariani, X. Gao, H. M. Schütz, S. Fang, T. Bizien, G. A. Elia and S. Passerini, Small Methods, 2021, 5, 2100168 CrossRef CAS PubMed.
- X. Liu, A. Mariani, M. Zarrabeitia, M. E. Di Pietro, X. Dong, G. A. Elia, A. Mele and S. Passerini, Energy Storage Mater., 2022, 44, 370 CrossRef.
- X. Liu, T. Diemant, A. Mariani, X. Dong, M. E. Di Pietro, A. Mele and S. Passerini, Adv. Mater., 2022, 34, 2207155 CrossRef CAS PubMed.
- X. Liu, A. Mariani, T. Diemant, M. E. D. Pietro, X. Dong, M. Kuenzel, A. Mele and S. Passerini, Adv. Energy Mater., 2022, 12, 2200862 CrossRef CAS.
- G. Horwitz, C. R. Rodríguez, P. Y. Steinberg, G. Burton and H. R. Corti, Electrochim. Acta, 2020, 359, 136915 CrossRef CAS.
- P. Porion, Y. R. Dougassa, C. Tessier, L. El Ouatani, J. Jacquemin and M. Anouti, Electrochim. Acta, 2013, 114, 95 CrossRef CAS.
- D. H. Vogel, Phys. Z., 1921, 22, 645 Search PubMed.
- G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245 CrossRef CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02880e |
| ‡ These authors gave equal contributions. |
| § Present address: Zentrum für Sonnenenergie- und Wasserstoff-Forschung Baden-Württemberg, Ulm 89081, Germany. |
| This journal is © The Royal Society of Chemistry 2024 |



![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups. (a) Results obtained with r2SCAN-3c; (a′) results obtained with ωB97X-D3, as indicated in the insets on the right (from top to bottom: A–A, C–C, A–C, and A-intra). The zero of the energy scale has been chosen by setting the lowest energy among all geometries along the path to zero. (b and b′) Boltzmann percentage of molecules having enough energy to overcome different proton transfer barriers. (b) Results obtained with r2SCAN-3c; (b′) results obtained with ωB97X-D3. For (a, a′, b and b′) panels cation–cation in red, anion–anion in blue, anion–cation in green, anion-intramolecular in brown. (c, c′, c′′ and c′′′) schematic representation of the possible proton transfers. (c) Anion-intramolecular; (c′) anion–anion; (c′′) cation–anion; (c′′′) cation–cation. (d) Scheme of the processes discovered in trajectory 1, following the initial PT.
O groups. (a) Results obtained with r2SCAN-3c; (a′) results obtained with ωB97X-D3, as indicated in the insets on the right (from top to bottom: A–A, C–C, A–C, and A-intra). The zero of the energy scale has been chosen by setting the lowest energy among all geometries along the path to zero. (b and b′) Boltzmann percentage of molecules having enough energy to overcome different proton transfer barriers. (b) Results obtained with r2SCAN-3c; (b′) results obtained with ωB97X-D3. For (a, a′, b and b′) panels cation–cation in red, anion–anion in blue, anion–cation in green, anion-intramolecular in brown. (c, c′, c′′ and c′′′) schematic representation of the possible proton transfers. (c) Anion-intramolecular; (c′) anion–anion; (c′′) cation–anion; (c′′′) cation–cation. (d) Scheme of the processes discovered in trajectory 1, following the initial PT.