Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrogen spillover drives room temperature sensing on spark plasma sintered BaTiO3 with Pt electrodes†
Jon G.
Bell
 *a,
Shangxiong
Huangfu
a,
Luca
Artiglia
*a,
Shangxiong
Huangfu
a,
Luca
Artiglia
 b,
Thomas
Graule
a and
Michael
Stuer
b,
Thomas
Graule
a and
Michael
Stuer
 a
a
aHigh Performance Ceramics Laboratory, Department of Advanced Materials and Surfaces, Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland. E-mail: Belj@zhaw.ch
bSwiss Light Source, Paul Scherrer Institute, Villigen, Switzerland
First published on 26th October 2024
Abstract
Chemiresistive gas sensing using metal oxide semiconductors has been rationalised in terms of reactions between gas phase species and the surface of the metal oxide either through oxygen vacancy creation/passivation or ionosorbed charged oxygen species; however, no convincing spectroscopic evidence has been observed for the formation of gas sensing charged oxygen surface states. We have investigated the H2 sensing characteristics of Pt-coated BaTiO3 prepared by spark plasma sintering using a combination of electrochemical impedance spectroscopy (EIS) and synchrotron-based near-ambient pressure X-ray photoelectron spectroscopy (NAP-XPS). We reveal that for undoped BaTiO3, oxygen vacancies are formed at the surface of platinum-coated BaTiO3 after reduction in hydrogen at 1000 °C and, after controlled reoxidation in air at 470 °C, are passivated by hydroxyl species detected using NAP-XPS over the temperature range 22–150 °C. EIS was used to monitor the change in electrical properties for both the reoxidation treatment at 470 °C and H2 gas sensing over the temperature range of 22–175 °C while moving through the Curie temperature of BaTiO3. NAP-XPS was used to determine the BaTiO3 surface species present as a function of H2 pressure and temperature. The results are discussed in terms of oxygen vacancy electron donor creation at the BaTiO3–Pt interface and grain boundaries, H2 dissociation on Pt and spillover onto BaTiO3, driving electronic transport in the conduction band, reaction of dissociated H2 with surface hydroxyl species, and the presence of temperature- and H2 concentration-dependent colossal dielectric permittivity and Schottky barrier height. As the H2 partial pressure increased, the grain boundary Arrhenius activation energies and pre-exponential factors followed the Meyer-Neldel rule, indicating a possible relationship between activation energy and frequency of collisions in charge trapping centres. These observations confirm the presence of surface reactions between dissociated hydrogen, oxygen vacancies, adsorbed H2O, and hydroxyl species that possibly mediate the H2 spillover process, which drives the decrease in electrical resistance at the grain boundary regions.
1 Introduction
There is an increasing demand for highly sensitive metal oxide-based gas sensors, such as SnO2, WO3, and ZnO, for flammable and toxic gas detection due to their simplicity and low production costs.1 Although these materials are understood phenomenologically, the mechanism of gas sensing remains elusive due to ambiguous results from spectroscopic studies.2 Methods for tailoring the gas sensing properties thus remain challenging due to this lack of mechanistic understanding.2,3 The two predominant models for describing chemiresistive gas sensing are: (1) the ionosorption model, involving extrinsic charged oxygen species at the grain surface; and (2) the surface conductivity model, involving intrinsic grain surface oxygen vacancies.4During processing of n-type metal oxides in oxygen containing atmospheres, it has been postulated that adsorption of oxygen occurs at grain surfaces, which, depending on the temperature, can become charged due to electron transfer from the semiconductor conduction band to adsorbed molecular oxygen, forming charged ionosorbed oxygen species (O2−, O−, O2−).2,3 If the semiconductor Fermi level is greater in energy than the adsorbed molecular oxygen lowest unoccupied molecular orbital (LUMO), electrons are transferred from the semiconductor conduction band to the LUMO of the O2 molecule, and adsorbed superoxide (O2−) is formed on the surface.5 The type of ionosorbed oxygen species generated is a function of temperature, as higher temperatures drive the dissociation of O2 to atomic Ox−.2,6 Superoxide O2− forms below 200 °C, and increasing the temperature above this drives electron transfer, forming O− and finally O2−.6 The injection of electrons from the conduction band to the molecular oxygen LUMO causes an accumulation of negative charge on the oxygen surface states and results in the formation of a positively charged depletion layer at the semiconductor surface, resulting in upward band bending and an increase in the Schottky barrier height.5 The filling of oxygen acceptors stops when the Fermi level and adsorbed O2 LUMO equalise energetically. At this point, the depletion layer width and Schottky barrier height reach a maximum value, and consequently, the capacitance and resistance of the semiconductor increase significantly. The mechanism of ionosorbed oxygen formation is shown in eqn (1)–(6) below. Here ‘ads’ represents physical or physisorption, ‘iono’ refers to ionosorption, and ‘lattice’ represents oxygen incorporated into the metal oxide crystal lattice.2
| O2 (gas) ⇌ O2 (ads) | (1) |
| O2 (ads) + e− ⇌ O2− (iono) | (2) |
| O2− (ads) + e− ⇌ O22− (iono) | (3) |
| O22− (ads) + e− ⇌ 2O− (iono) | (4) |
| O− (ads) + e− ⇌ O2− (iono) | (5) |
| O2− (ads) ⇌ O2− (lattice) | (6) |
The exposure of dielectric materials to hydrogen causes resistance and dielectric degradation, resulting in component failure.7,8 Typically, hydrogen reacts with dielectric oxides in two ways. The first operates at high temperatures where hydrogen can react with lattice oxygen to create electron-donating oxygen vacancies ( ) resulting in a decrease in electrical resistance, as shown in eqn (7).
) resulting in a decrease in electrical resistance, as shown in eqn (7).
 | (7) |
However, this reaction operates at high temperatures, as is typically employed in defect chemistry studies.9,10 Conversely, at lower temperatures, H2 can dissociate and produce two electrons, which decreases the material resistance. On metals, H2 typically dissociates homolytically, depending on the electronegativity of the metals, whereas dissociation on metal oxides generally follows heterolytic dissociation due to surface defects.11 Following this, the free protons bond with perovskite oxygen to form OH species. Water vapour can also cause component degradation by adsorbing at oxygen vacancy sites and forming OH species.12
Incorporation of a noble metal catalyst layer can facilitate oxygen dissociation and spillover onto the semiconductor surface at temperatures close to 500 °C, whereas this occurs at room temperature for H2.13 The postulated sensing mechanism for reducing gases, such as H2 and CO, occurs due to the reaction either with ionosorbed oxygen species or lattice oxygen in the vacancy model, producing H2O and CO2, respectively, which are then desorbed from the surface. Since oxygen is removed, the concentration of ionosorbed oxygen decreases for ionosorption, causing a release of electrons back to the conduction band and lowering of the grain boundary Schottky barriers, resulting in increased electronic conductivity.2,4 Additionally, the noble metal catalyst layer can also facilitate the dissociative chemisorption of molecules such as H2 and increase the sensor sensitivity towards these species.14 However, since the reaction of H2 and CO with charged oxygen species causes oxygen removal from the surface, this would result in non-reversible gas sensing at room temperature as the concentration of surface reaction sites is progressively reduced over time with increasing gas sensing switching cycles. The most convincing evidence for the operation of the ionosorption mechanism originates from electron paramagnetic resonance (EPR) studies of Chang.15 However, a lack of consensus on the assignment of the paramagnetic monotonic oxygen species, and disagreement between theory and experiment, render the findings inconclusive. Therefore, no convincing evidence for ionosorption has been presented to date.
An alternative explanation for gas sensing, opposed to the ionosorption model (IM), is the surface conductivity model (SCM) proposed by Blackman.4 The reactive species here are intrinsic positively charged lattice oxygen vacancies located at the grain surface, which form under low pO2 conditions. Blackman compares the effects of gas switching on surface band bending for both the ionosorption and surface conductivity models and uses air to CO gas switching as an example for n-type materials. Under air, for IM, charged oxygen species are present, and for SCM, no oxygen vacancies are present. This results in conduction and valence band upward bending for IM and flat band situation for SCM. The upward band bending is due to surface negative charges that are compensated by positive charges, causing the formation of a depletion layer. On exposure to CO, the extrinsic charged oxygen is removed due to CO2 formation and the CB and VC bend down with a corresponding increase in the Fermi level. Consequently, the conductivity increases. For the SCM, CO exposure causes intrinsic lattice oxygen to be removed, creating oxygen vacancies, which donate electrons to the conduction band. Oxygen vacancy creation causes the establishment of a positive surface charge and an accumulation of electrons at the interior of the grain-surface interface to compensate this positive charge, which causes the Fermi level to increase in energy, resulting in downward bending of the conduction and valence bands relative to the bulk. As the pO2 is increased, the surface oxygen vacancies are filled, and the conduction band (CB) electrons are localised, as shown in eqn (7). Therefore, the bands bend back to the flat-band situation, and the Fermi level decreases, resulting in a decrease in conductivity.4 Hence, the SCM replaces the extrinsically charged oxygen species with intrinsic lattice oxygen vacancies. In both models, the bands bend relatively down on exposure to CO, the difference being the relative starting point of the surface band energy. However, Blackman's model neglects the influence of the Madelung potential near the surface of the crystalline lattice. This would introduce intrinsic upward band bending; hence, band bending is a superimposition of the Madelung potential and the band bending introduced by surface oxygen vacancies.16 There is a growing body of experimental evidence that suggests surface intrinsic oxygen vacancies are the species responsible in gas sensing materials, such as In2O3, SnO2, ZnO, TiO2, SrTiO3, and KTaO3, rather than extrinsic grain boundary charged oxygen.17–25 The operation of either mechanism may depend on material properties, processing conditions, gas type, sensing temperature, etc. and may not be mutually exclusive but could also involve a cooperative effect. Therefore, there is still much to discover regarding the role of oxygen vacancies and ionosorbed oxygen for gas sensing metal oxides such as SnO2.2
The gas sensing properties of BaTiO3 have not been explored as widely as materials such as SnO2 and WO3, although its physicochemical properties make it an interesting candidate for gas sensing applications.26 BaTiO3 is a perovskite material that undergoes a crystallographic tetragonal to cubic phase shift that results in a ferroelectric to paraelectric transition at the material's Curie temperature (TC), which is between 100 °C and 130 °C, depending on processing conditions.27,28 The electrical properties of undoped BaTiO3 can be shifted from p-type to n-type by careful control of the oxygen partial pressure, temperature, and time during synthesis or post-synthetic modification. It is possible to produce undoped BaTiO3 with n-type semiconducting grains and insulting grain boundaries that also exhibit a positive temperature coefficient of resistivity (PTCR) effect,29,30 which is characterised by a dramatic increase in resistivity at the TC by several orders of magnitude.28 The PTCR effect in undoped and donor-doped BaTiO3 results from an increase in the back-to-back Schottky barrier height at the grain boundaries due to electron-trapping surface states. This grain boundary Schottky barrier is ferroelectrically compensated below the TC, resulting in a material with low resistance. However, as the material passes through TC, the ferroelectric phase disappears, and electrons are trapped at the grain boundaries. This causes an increase in the grain boundary depletion width and the Schottky barrier height, which in turn causes a large increase in the resistance and relative permittivity. Hence, this effect is widely exploited in dielectric, current-limiting, and self-limiting heating applications.28,31,32 Chemisorbed gases have been shown to act as electron traps and produce the PTCR effect.33,34 Therefore, the presence of ionosorbed oxygen may significantly increase the relative permittivity at the TC, as these species would act as electron-trapping surface states. Additionally, a Schottky barrier can be established at the BaTiO3–metal electrode interface, with the barrier height determined by the type of electrode material used. Brillson demonstrated that the barrier height is directly related to the heats of chemical reactivity between the metal and semiconductor for a range of metals (Pd, Pt, Au) and semiconductors (ZnO, ZnS, CdS, GaP). Small heats of reaction resulted in the largest Schottky barriers, particularly for Pt.35 Supporting this, Cann et al. observed that the enhancement of the metal–anion interaction, due to the presence of oxygen vacancies, caused a reduction in the barrier width, increasing the probability of electron tunnelling.36 Typically, the Schottky barrier height is the difference between the metal work function (Φm) and the semiconductor affinity (χ) and is approximately 1.7 eV for BaTiO3–Pt. Heidary et al. have shown that the electrode interface Schottky barrier for BaTiO3–Pt was larger than the grain boundary back-to-back Schottky barrier and can be reduced due to the presence of hydrogen atoms accumulating at the electrode, as well as diffusing along grain boundaries, which increases the probability of electron tunneling.7
Colossal relative permittivity has been observed in spark plasma sintered BaTiO3,37 but the role of adsorbed surface states has not been studied in detail. Therefore, the BaTiO3 ferroelectric to paraelectric transition could be exploited to help confirm the presence of electron trapping states by significantly increasing the relative permittivity of the material at the TC. The electrical properties of undoped, donor-doped, and acceptor-doped BaTiO3 have been studied in detail using techniques such as electrochemical impedance spectroscopy (EIS).38,39 EIS is a technique that can deconvolute the resistance (Z′) and reactance (Z′′) of bulk, grain boundary, and electrode-semiconductor interface regions, as well as surface reactions, of a specimen based on the frequency response of each electroactive component. For BaTiO3, the overall conductivity is usually dominated by the high-impedance grain boundary regions due to the formation of surface-state-induced-Schottky barriers.38 The changes in the grain boundary Schottky barrier height due to external factors, such as physically or chemically adsorbed gases, can be probed with EIS so that activation energies for charge transport can be determined. However, electrochemical determination of the species responsible is only possible using a spectroscopic method with high resolution.
Near ambient pressure X-ray photoelectron spectroscopy (NAP–XPS) is a surface characterisation technique (1–10 nm depth) that allows the chemical investigation of surface species in the presence of gases and vapours at low pressures (1–10 mbar).40,41 This is an extremely powerful technique for mechanistic catalysis studies, as key adsorbed surface species and intermediates can be identified during chemical reactions.42 The NAP-XPS surface analysis technique is routinely used for the study of surface chemical species for chemoresistive gas sensors,25,43–47 as well as other surface/bulk techniques such as electron energy loss spectroscopy (EELS) and electron paramagnetic resonance spectroscopy (EPR). Besides the brilliance and coherence, the advantage of synchrotron light over laboratory X-ray sources is that the photon energy can be tuned, thus increasing the sensitivity towards a certain element on the surface. Therefore, through a careful choice of acquisition parameters, the synchrotron-based XPS may provide high intensity and high-resolution photoemission signals in a shorter acquisition time than with a laboratory setup, which is essential during in situ measurements. This feature may allow surface states that are close in binding energy, such as hydroxyl species, adsorbed H2O, and potentially ionosorbed species (O2−/O−), which are separated within a few eVs, to be resolved.6 The presence of oxygen vacancies cannot be probed directly by XPS. However, both Francombe et al.48 and Idriss49 have shown that oxygen vacancies are passivated by hydroxyl groups and adsorbed water, and so are an indirect indication of their presence.
In this investigation, we report an impedance and near ambient pressure-X-ray photoelectron spectroscopic study (not combined in situ impedance and XPS) of the H2 sensing properties of spark plasma sintered BaTiO3 with platinum electrodes in an attempt to determine the mechanism of H2 detection. Gas sensing characteristics were formed on BaTiO3–Pt after an initial high temperature (1000 °C) reduction in H2 to form an n-type semiconductor, followed by controlled reoxidation between 460 and 470 °C. EIS was used to monitor the resistance and dielectric changes of the bulk, interface, and grain boundary regions during the reoxidation of n-type BaTiO3, as well as the electrochemical changes that occur within the material under atmospheres of Ar, N2, O2, and H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 and CO
N2 and CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2 mixtures, and as the material moves through the BaTiO3TC region. Synchrotron-based NAP-XPS was used to determine the BaTiO3 surface species present after controlled reoxidation and then upon exposure to H2 (1–4 mbar) in the temperature range 22–150 °C.
N2 mixtures, and as the material moves through the BaTiO3TC region. Synchrotron-based NAP-XPS was used to determine the BaTiO3 surface species present after controlled reoxidation and then upon exposure to H2 (1–4 mbar) in the temperature range 22–150 °C.
2 Experimental methods
2.1 Materials
BaTiO3 (99.7%) metals basis powder (Dv50 < 2 micron) was purchased from Alfa Aesar, Germany. The N2 BET surface area was 1.93 ± 0.15 m2 g−1 (ESI: Table S1 and Fig. S1†) giving a BET diameter of 0.54 ± 0.04 μm under the spherical particle assumption, which corresponds closely with the DV50 value of 0.60 ± 0.14 μm derived from laser diffraction (Fag = 1.11) (Fig. S2†). Solutions for Archimedes density measurements were prepared in nanopure water (MicroPure UV System, ThermoFisher Scientific system with resistivity equal to 18.2 MΩ cm). Gases for spark plasma sintering, controlled reduction and re-oxidation, and electrochemical impedance measurements were obtained from PanGas, Dübendorf (CH) and included: N2 (99.995%), synthetic air (N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2, (80
O2, (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20%), 2% H2 in 98% argon (99.995%), CO (99.995%), and H2 (99.995%). Platinum ink (product code 6082) for electrode contact formation was supplied by Metalor Technologies SA (CH).
20%), 2% H2 in 98% argon (99.995%), CO (99.995%), and H2 (99.995%). Platinum ink (product code 6082) for electrode contact formation was supplied by Metalor Technologies SA (CH).
2.2 Spark plasma sintering (SPS)
Spark plasma sintering of BaTiO3 powders was performed on a FCT Systeme GmbH with a Riedel Precision Cooling System and a Stange Electronik GmbH SE-607 process controller. 3 grams of BaTiO3 powder were loaded into a graphite die with a 20 mm internal bore and 20 mm upper and lower punches to generate BaTiO3 disc-shaped ceramic samples that were approximately 2 mm thick and 20 mm in diameter. A circumferential graphite sheet was placed inside the die bore, and graphite discs were placed on both the top and bottom of the powder to ensure good electrical contact between the upper and lower punches and die. The graphite die-sample assembly was placed between the SPS force rams and an initial force of 3 kN was applied (Fig. S3†). Prior to sintering in argon, two vacuum-argon flush cycles were performed to ensure air was removed from the system. The graphite die and sample assembly were initially heated to 400 °C before the uniaxial pressure was increased to 16 kN over a period of 2 minutes. Once a constant force was achieved, heating to 1200 °C commenced at 100 °C min−1 using a 12, 6, 1, 0 (ton, toff, pulse/bunch, tpause (pause between bunches)) DC pulse sequence. Samples were held at 1200 °C for 2 minutes and then the force was released back to the 3 kN baseline. Once the force was released, samples were cooled rapidly to room temperature over 5 minutes. The temperature of the sample was measured with the internal FCT system pyrometer. The samples sintered at 1200 °C and 16 kN, corresponding to 50 MPa for a 20 mm diameter die (Fig. S4a and b†), respectively, were designated with the code BTO. Following this, samples were decarbonised at 700 °C for 4 hours and then progressively polished using P1000 Buehler Carbimet silicon carbide polishing papers to remove the surface layers.2.3 Electrochemical impedance spectroscopy studies
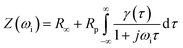 | (8) |
 | (9) |
2.4 Near ambient pressure X-ray photoelectron spectroscopy
Near ambient pressure X-ray photoelectron spectroscopy (NAP-XPS) measurements were carried out at the X07DB in situ spectroscopy beamline (Swiss Light Source, Villigen, Switzerland).42 A small, localised surface layer (100 μm) of Pt was mechanically removed from the Pt-BTO-470 sample to expose a BaTiO3 surface spot, and the sample was then mounted on the tip of an infrared heated manipulator. The manipulator was then transferred into the measurement cell, which allows precise dosing of gases and vapours under flowing conditions, using a stepper motor-controlled system.54 The X-ray beam was focused on the exposed BaTiO3 spot, and the position of the sample was adjusted to attain the highest signal from the X-ray beam using a computer-controlled stepper motor micromanipulator system. Ultrapure gases were dosed by means of mass flow controllers and pumped away with a tunable diaphragm valve connected to a root pump. This allows the dosing of relevant gas flows and precise control of the pressure during the experiments. The end-station differential pressure was monitored by means of Baratron pressure transducer measurement heads. The gas concentration and gas switching were monitored by a quadrupole mass spectrometer, which was sampled from the second differential pumping stage of the analyser. The rear of the Pt-BTO-470 sample was heated using a tunable IR laser (976 nm, max power 25 W) and the temperature was monitored with a Pt100 sensor in contact with the sample. Survey spectra and Ba 3d core levels were measured at an excitation energy of 1100 eV and the remaining core levels were measured at 850 eV. Photoemission spectra were obtained using linearly polarised light at an excitation energy of 1100 eV and 850 eV, with a pass energy of 50 eV, for C 1s, O 1s, Ti 2p, Ba 4d, Ba 3d, and Pt 4f. After the sample was aligned with the photon beam at the focal distance of the analyser, the sample surface was investigated by acquiring photoemission signals while being exposed to a specific gas at a constant temperature. Spectra were collected at 22 °C, 80 °C, 125 °C, and 150 °C. For each temperature, measurements were made initially under argon at 1 mbar, followed by increasing H2 pressures from 1 mbar to 4 mbar.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30.55 The quality of the XPS peak fitting and peak deconvolution was assessed by the chi-squared (χ2) value and the Abbe criterion (Tables S3–S8†). For spectral comparison between different pressures and temperatures, relative intensities were used and were calculated from the individual peak component areas divided by the total area of the peak envelope (i.e., OH area/O 1s envelope area). The difference spectra were calculated by dividing the experimental spectra by their areas, interpolating each spectrum to common binding energy points, and then subtracting the spectra collected in H2 from the 1 mbar argon reference spectrum collected at 22 °C.
30.55 The quality of the XPS peak fitting and peak deconvolution was assessed by the chi-squared (χ2) value and the Abbe criterion (Tables S3–S8†). For spectral comparison between different pressures and temperatures, relative intensities were used and were calculated from the individual peak component areas divided by the total area of the peak envelope (i.e., OH area/O 1s envelope area). The difference spectra were calculated by dividing the experimental spectra by their areas, interpolating each spectrum to common binding energy points, and then subtracting the spectra collected in H2 from the 1 mbar argon reference spectrum collected at 22 °C.
3 Results and discussion
3.1 Material properties
The BTO pellet exhibited a blue tint after spark plasma in argon, which is indicative of oxygen loss from the lattice and reduction of Ti4+ to Ti3+ due to charge compensation in the lattice. The sample returned to a white colour after oxidation in air at 700 °C. Scanning electron micrographs show a partially sintered, granular morphology with grain sizes of approximately 2 μm and below, as well as the presence of large macropores (Fig. S8†). The BTO pellet had a density of 95% of the theoretical value (6.02 g cm−3) calculated from Archimedes measurements, and N2 BET surface areas were 0.2 m2 g−1 due to the presence of some open porosity (Table S2†). Powder X-ray diffraction showed that the BTO was phase pure and with no preferred orientation (Fig. S9a and b†), calculated from the Lotgering factor,56 using the (100), (101), (111), (200), and (211) reflections.573.2 Controlled reduction and oxidation and initial gas sensing measurements
Spectroscopic plots of the imaginary (Z′′) and real (Z′) impedance components vs. frequency, representing reactive and resistive electrical responses, respectively, show that both Z′ and Z′′ increased with oxidation time for treatments at 460 °C and 470 °C and over the entire frequency range from 0.1 Hz to 10 MHz. For Pt-BTO-460, the spectroscopic plots (Fig. S10a and b†) show the change in Z′ and Z′′ after approximately 1800 and 4200 seconds into the oxidation procedure, and for Pt-BTO-470, the comparison is shown for oxidation at 660 and 3300 seconds (Fig. 1a and S11†). During oxidation, the low-frequency plateau maximum for Z′ vs. frequency, which approximates the total resistance, increased from 60 to 160 Ω for Pt-BTO-460 and 75 to 300 Ω for Pt-BTO-470. For BaTiO3, the Z′′ peak in the spectroscopic plot between 103 and 105 Hz is indicative of the grain boundary resistance (Rgb), with the peak height approximately equal to Rgb/2.39 The Z′′ peak increased during oxidation, resulting in an increase of Rgb from 30 to 80 Ω for Pt-BTO-460 and 40 to 150 Ω for Pt-BTO-470. When representing the data in the electric modulus formalism (M′′), which enhances peaks for the electroactive components with the smallest capacitance,38i.e., the bulk, the M′′ peak maximum in the high frequency region increased for both oxidation temperatures, indicative of an increase in the resistance of the bulk with increasing oxidation level. This is attributed to the filling of electron-donating bulk oxygen vacancies, which are formed during high temperature reduction in H2.29On first inspection, these observations are consistent with the ionosorption model, whereby incorporation of oxygen into n-type BaTiO3 results in an increase in the resistance of the grain boundary and bulk regions as electrons are withdrawn from the conduction band and are injected onto chemisorbed surface oxygen, forming charged, ionosorbed electron-trapping surface species. Fig. 1b shows the change in total resistance vs. time for Pt-BTO-470 when switching from air to 2.0% H2 and then back to air at 22 °C. A typical n-type gas sensing response is observed, as the total resistance decreased from 30 kΩ to less than 10 kΩ over the timescale of the experiment and did not reach equilibrium even after 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds. It appears that there are two exponential components describing the H2 sensing electrical profile: one fast component with a large amplitude (a 20 kΩ change over 300 s) and a second slower, exponential tail component with a smaller amplitude. However, these observations are also consistent with passivation of surface oxygen vacancies, with a varying oxygen concentration in the near surface region. The presence of two-time constants is indicative of fast generation of surface oxygen vacancies on exposure to H2, and then a second slower time constant related to the generation of oxygen vacancy donor species due to the desorption of adsorbed H2O. On switching from H2 back to air, the reverse is observed: the resistance increases rapidly and then relaxes slowly back to the original pre-switching resistance value. Fig. 1c shows the corresponding impedance spectroscopic plots for Pt-BTO-470 when switching from air to 2.0% H2. The peak in the Z′′ vs. frequency plot is attributed to the grain boundary impedance, while the major peak in the M′′ vs. frequency plot is due to the bulk impedance. There is also a small secondary M′′ peak at lower frequency that is coincident with the grain boundary Z′′ vs. frequency peak. This supports the fact that grain boundaries, which have a larger capacitance compared to the bulk, produce a smaller response in the M′′ formalism.38 On switching from air to H2, the grain boundary Z′′ peak decreased significantly and Rgb decreased from 30 kΩ to 9 kΩ and shifted to a slightly higher frequency. The high-frequency M′′ peak, representative of the bulk, decreases only slightly, indicating that the interaction of H2 is mainly with grain boundary-related surface chemistry. The procedure was repeated for the Pt-BTO-460 sample, and the trends are similar (Fig. S12a and b†). The magnitude of the response is greater for sample Pt-BTO-470 due to a higher concentration of grain boundary H2 sensing species incorporated during reoxidation at higher temperatures. In the surface conductivity model proposed by Blackman,4 the material's resistance should increase as the oxygen partial pressure is increased, which is due to the filling of oxygen vacancies. However, there was no change in impedance spectra when switching from N2 to O2 at both 22 °C and 175 °C (Fig. S13a–c†). N2 to CO switching was also performed at 22 °C to probe if a vacancy-mediated process exists. CO has been shown to adsorb on oxygen vacancies and react with lattice oxygen to produce CO2, resulting in a decrease in resistance (Fig. S14†).58 However in our study, no resistance change was observed for CO concentrations of 4% and 100%.Therefore, the change in resistance for this system when under H2 is most likely attributed to another process, such as the dissociation of H2 on Pt.7,8. However, this does not exclude oxygen vacancies as sensing species for higher temperatures and other gases, as their role has been clearly identified by several authors.4 The healing of oxygen vacancies is also expected to be an activated process,59 so below a critical temperature no significant reaction (resistance change) is observed, as has been shown for CO oxidation on SnO2(110), which proceeds via the Mars–Van Krevelen mechanism.60
000 seconds. It appears that there are two exponential components describing the H2 sensing electrical profile: one fast component with a large amplitude (a 20 kΩ change over 300 s) and a second slower, exponential tail component with a smaller amplitude. However, these observations are also consistent with passivation of surface oxygen vacancies, with a varying oxygen concentration in the near surface region. The presence of two-time constants is indicative of fast generation of surface oxygen vacancies on exposure to H2, and then a second slower time constant related to the generation of oxygen vacancy donor species due to the desorption of adsorbed H2O. On switching from H2 back to air, the reverse is observed: the resistance increases rapidly and then relaxes slowly back to the original pre-switching resistance value. Fig. 1c shows the corresponding impedance spectroscopic plots for Pt-BTO-470 when switching from air to 2.0% H2. The peak in the Z′′ vs. frequency plot is attributed to the grain boundary impedance, while the major peak in the M′′ vs. frequency plot is due to the bulk impedance. There is also a small secondary M′′ peak at lower frequency that is coincident with the grain boundary Z′′ vs. frequency peak. This supports the fact that grain boundaries, which have a larger capacitance compared to the bulk, produce a smaller response in the M′′ formalism.38 On switching from air to H2, the grain boundary Z′′ peak decreased significantly and Rgb decreased from 30 kΩ to 9 kΩ and shifted to a slightly higher frequency. The high-frequency M′′ peak, representative of the bulk, decreases only slightly, indicating that the interaction of H2 is mainly with grain boundary-related surface chemistry. The procedure was repeated for the Pt-BTO-460 sample, and the trends are similar (Fig. S12a and b†). The magnitude of the response is greater for sample Pt-BTO-470 due to a higher concentration of grain boundary H2 sensing species incorporated during reoxidation at higher temperatures. In the surface conductivity model proposed by Blackman,4 the material's resistance should increase as the oxygen partial pressure is increased, which is due to the filling of oxygen vacancies. However, there was no change in impedance spectra when switching from N2 to O2 at both 22 °C and 175 °C (Fig. S13a–c†). N2 to CO switching was also performed at 22 °C to probe if a vacancy-mediated process exists. CO has been shown to adsorb on oxygen vacancies and react with lattice oxygen to produce CO2, resulting in a decrease in resistance (Fig. S14†).58 However in our study, no resistance change was observed for CO concentrations of 4% and 100%.Therefore, the change in resistance for this system when under H2 is most likely attributed to another process, such as the dissociation of H2 on Pt.7,8. However, this does not exclude oxygen vacancies as sensing species for higher temperatures and other gases, as their role has been clearly identified by several authors.4 The healing of oxygen vacancies is also expected to be an activated process,59 so below a critical temperature no significant reaction (resistance change) is observed, as has been shown for CO oxidation on SnO2(110), which proceeds via the Mars–Van Krevelen mechanism.60
The impedance spectra were measured over the course of the Rtot recovery while in pure N2 and Fig. 1f shows the corresponding Nyquist spectra of Pt-BTO-470 initially in pure N2, before H2 exposure, and then after exposure in H2 (19%), after Rtot recovery back to 30 kΩ under pure N2. It has been reported that sensor resistance changes occur due to the reaction of H2 with O2−, O−, and O2− to produce H2O, removing oxygen from the surface.62 Additionally, for BaTiO3 and metal oxides, H2 can react with lattice oxygen and surface OH to form H2O, which then desorbs from the surface, leaving a donor oxygen vacancy.63,64 The vacancies are then healed by diffusion of oxygen from the bulk to the surface.65 Moreover, at lower temperatures, H2 can dissociate into H2 on the Pt surface and inject electrons into the conduction band of BaTiO3. These two processes could be operating in parallel, although Heidary et al.7,8 have shown proton diffusion is dominant at lower temperatures and diffuses along the grain boundary and electrode interface regions. This causes a reduction in the Schottky barrier heights for both regions. The present work shows that the resistance after H2 exposure recovers to baseline in both air and N2. Therefore, it could be that in air the vacancies are healed extrinsically, while in N2 they are healed intrinsically. In the context of the ionosorption model, the switching process should be irreversible if charged oxygen is removed from the surface, which will lead to a gradual decrease in the total resistance with increasing switching cycles, or reversible, if oxygen can be re-adsorbed at the surface and charged through electron donation from the conduction band. However, over short cycles, this does not occur. The fact that the resistance reaches baseline in N2 suggests that oxygen vacancies are being healed by diffusion from the bulk. Reversibility due to passivation of vacancies implies that the vacancy mechanism is in operation, and hence H2O should be observed on the surface as H2 reacts to form OH and H2O, while the ionosorption model would require chemisorption of oxygen at room temperature to be reversible. In addition, Heidary et al. have shown that for BaTiO3 on immediate change from H2 to inert gas that the resistance increases, and this occurs as the electron injection process has ceased.7,8 The calculated diffusion coefficients at 240 °C ranged from 2 × 10−8 cm−2 s−1 for grains to 5.3 × 10−8 and 6.3 × 10−8 cm−2 s−1for grain boundaries and electrodes, respectively. Based on these findings, the two time constants in Fig. 1e could be attributed to cessation of H2 dissociation driving electron transfer to BaTiO3 and healing of oxygen vacancies due to diffusion from oxygen from the bulk. Based on the oxygen mobility diffusion coefficient equation for BaTiO3 devised by Kessel et al.66,67 (with D = 7.15 × 10−15 cm2 s−1 and an activation energy of 0.7 eV) and the Crank solution of Fick's second law of diffusion,68 this implies an unrealistic oxygen diffusion distance of approximately 0.4 μm to heal vacancies over a 60 k second period (as shown in Fig. 1e). However, this equation is only valid for temperatures >200 °C and so it is difficult to estimate the oxygen diffusion coefficient at room temperature. Therefore, it is more likely that water vapour present in the system passivates the surface oxygen vacancies, as has been shown by Li et al.63
3.3 Synchrotron-based near ambient pressure X-ray photoelectron spectroscopy (NAP-XPS)
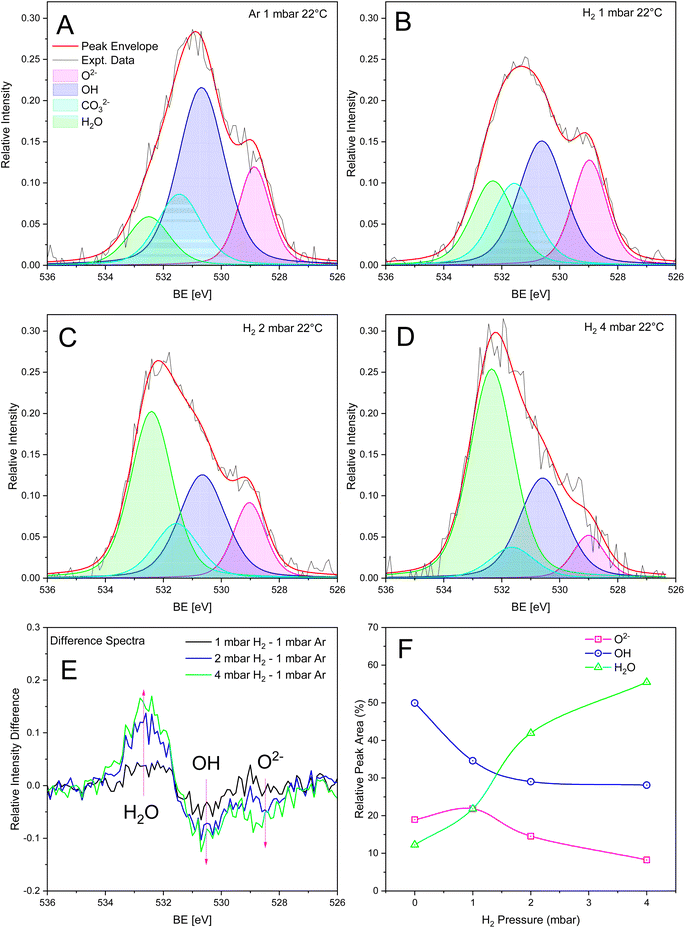
There is a scarcity of spectroscopic evidence identifying the gas sensing O− group proposed in the ionosorption model.2 Recently, the charge state of adsorbed oxygen has been identified and manipulated on TiO2 using non-contact AFM and O2−, O−, and O2− species have been identified under UHV at 77 K.69 However, the existence of the metastable O− adatom at higher temperatures remains elusive. Synchrotron-based XPS is another way to decouple these charged oxygen groups from the O 1s photoemission peak. Temperature-dependent NAP-XPS measurements were performed on Pt-BTO-470 to determine the mechanism of H2 interaction and to identify the chemical species involved in H2 detection, and thus elucidate the electrical conduction mechanism in operation during gas switching from inert to H2 gas atmospheres. A diagram showing the sample measurement location within the bulk material is shown in Fig. S15.† The XPS photon beam diameter is 300 μm and the Pt etched away, bulk spot diameter is 3 mm. A survey scan for the bulk region is shown in Fig. S16.† It is clear that no Pt peak is present in the bulk region, as we ensured that the bulk spot area could accommodate the photon beam without simultaneously measuring the BaTiO3–Pt interface region (Fig. S15†); however, there is a small peak between 300 eV that could be due to K 2p, and this could have been incorporated during the spark plasma sintering process due to system contamination. Analysis of the C 1s, O 1s, Ti 2p, Ba 4d, and Pt 4f photoemission peaks showed that only the O 1s peak changed significantly when switching from atmospheres of Ar to H2 and when increasing the H2 pressure, with minor changes occurring for the other elemental XPS spectra (Tables S3–S8 and Fig. S17–S21†).Fig. 2A–D shows the deconvolution of the O 1s photoemission spectra for Pt-BTO-470 collected at 22 °C into three distinct peaks while under an atmosphere of 1 mbar Ar and then switching to 1–4 mbar of H2. The relative intensity difference spectra shown in Fig. 2E show an increase in signal intensity at 532.5 eV, and a corresponding decrease at 531 eV when switching from 1 mbar argon and for increasing H2 pressures. According to the interpretation proposed by Dupin et al.70 for metal oxides, hydroxides, and peroxides, three major components are centered at 529 eV, 531 eV, and 532.5 eV, which correspond to lattice O2−, ionosorbed O−, and weakly bonded groups such as OH/H2O,71 respectively, with chemisorbed H2O centered at binding energies greater than 533 eV.72,73 However, considering the lack of spectroscopic evidence for O−, and the fact that the resistance recovers to baseline in N2 atmospheres (Fig. 1e), it is more likely that alternative surface reactions are occurring on the BaTiO3 surface. In addition, the Weisz limit sets a cap on the amount of negatively charged oxygen surface species that can form based on the surface electron density available.74 Hence, the formation of a O− monolayer is unlikely and therefore difficult to detect by XPS. As has been reported by both Idriss49 and Frankcombe et al.48 oxygen vacancies cannot be directly detected by XPS. Rather, vacancies promote surface reactions with H2O and H2 to form OH and adsorbed H2O species, and according to their interpretation, the peaks at 529 eV, 531 eV, and 532.5 eV are attributed to lattice oxygen (O2−), OH, and adsorbed H2O, respectively.48,49 Based on the previous arguments, this assignment fits with recent studies by Spasojevic et al.55
Additionally, both C 1s and Ba 4d photoemission spectra show that carbonate is formed on the BaTiO3 surface (Fig. S18 and S20†). Carbonate also has a component in the O 1s signal between 530 and 532 eV, depending on the charge balancing cation.75 Hence, there should be a superimposition of carbonate and OH peaks, thus explaining why the peak at 531 eV is the most intense. However, the C 1s and Ba 4d photoemission peaks show that carbonate is stable, as the relative intensities do not change progressively with increasing H2 pressure (Tables S5 and S7†), while the O 1s peak relative intensity at 531 eV decreases with increasing H2 pressure. Consequently, a carbonate peak was added to the fitting procedure to ensure the that correct relative peak areas were obtained. Therefore, the decrease in OH at 531 eV is explained by the reaction of dissociated H2 with OH and the formation of adsorbed H2O due to the H2 the spillover effect. Fig. 2F shows the change in relative peak area for adsorbed H2O, CO32−, OH, and O2− species vs. H2 pressure at 22 °C. After peak fitting and area calculation, analysis of the O 1s photoemission peaks at 22 °C and under 1 mbar argon shows that the surface is predominately covered with OH species (50% of total peak area) and H2O (20%) (see Table S3† for peak parameters). These species most likely form during the controlled oxidation or cooling process. The Probostat system is not completely gas tight, and it is possible for water vapour to condense in cold regions of the system. Therefore, any water vapour in the system can react with oxygen vacancies to produce OH groups and adsorbed H2O.48 The OH peak at 531 eV shows a decrease in the relative peak area, from 50% to 28%, and a commensurate and progressive increase in the relative peak area at 532.5 eV (H2O) from 12% to 55%, as the H2 pressure is increased from 1 mbar Ar to 4 mbar H2. This is most likely due to the reaction of dissociated H2 with OH and the interconversion of OH to adsorbed H2O. The lattice oxygen (O2−) relative peak area at 529 eV decreases from 20% to 8% as a function of H2 pressure. Therefore, H2 appears to be reacting with both surface OH and to a lesser extent O2−, as both show a reduction in relative peak area with increasing H2 pressure. The formation of adsorbed H2O due to the reaction of H2 with OH, and the subsequent desorption of H2O should result in the creation of oxygen vacancies with increasing H2 pressure. If oxygen vacancies are created, then the O lattice to cation ratio should decrease with increasing H2 pressure.76 This is indeed the case and can be seen in Fig. S17a† for O lattice to Ba and Ti ratios, supporting the proposed surface reaction mechanism mentioned above.
The O 1s photoemission peaks, and deconvoluted peaks, measured between 80 °C and 150 °C while under an atmosphere of 2 mbar of H2 are shown in Fig. S17c–g.† The spectrum under 1 mbar argon at 22 °C is shown as a reference (Fig. S17b†). When under H2 atmospheres at elevated temperatures, the same three peaks are present, with centers located at 529 eV, 531 eV, and 532.5 eV (Table S4†). Again, the difference spectra in Fig. S17f† (using the 1 mbar Ar data at 22 °C as a reference spectrum) show a clear decrease in the peak at 531 eV and an increase in the peak at 532.5 eV with increasing temperature, demonstrating that an interconversion of OH to H2O has occurred, while the O2− peak remains approximately constant, as shown in Fig. S17g.† The OH relative peak area decreases from 29% at 22 °C to 20% at 150 °C, while H2O increases from 42% to 59% (Table S4†). The reaction of H2 with OH is promoted at higher temperatures as H2 dissociation on Pt and surface diffusion are thermally activated processes and increase with temperature, producing a higher surface reaction rate. H2 switching reversibility could not be studied in the NAP-XPS experiment due to the long recovery times associated with switching from H2 back to inert atmospheres (as shown in Fig. 1e).
3.4 Electrochemical impedance spectroscopy studies
Impedance spectroscopy studies by Heidary et al.7,8 have shown that the resistances of grain boundary and electrode interface regions are reduced due to reduction of Schottky barriers driven by hydrogen diffusion in BaTiO3. At the BaTiO3 electrode interface, the barrier is determined by the degree of band bending, which is controlled mainly by the difference in the work function of the metal and electron affinity of the semiconductor, while at the grain boundary if electron trapping, or acceptor states, are present, then a depletion region can form, resulting in back-to-back Schottky barrier. Heidary et al. showed that the electrode interface region exhibited the largest resistance and resistance change. In this work, initial EIS measurements showed that during controlled oxidation at 470 °C, the impedance of the grain boundaries increased with increasing oxidation time (Fig. 1a). Under hydrogen containing atmospheres, H2 undergoes dissociative adsorption on Pt at room temperature, forming protons that can migrate from Pt to BaTiO3 due to a surface diffusion process known as the spillover mechanism.7,8 Therefore, protons could diffuse along grain boundaries and electrode interface regions and interact with oxygen vacancies, as well as drive the creation of new vacancies due to reaction with OH and desorption of H2O, as was shown in the XPS analysis. Therefore, the AC conductivity and impedance behaviour were studied as a function of H2 partial pressure to gain a deeper insight into the interaction of H2 with the different electroactive regions of BaTiO3–Pt. | (10) |
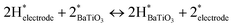 | (11) |
 | (12) |
H2 and D2 isotope exchange studies were performed in this study to elucidate the predominant charge transfer mechanism of either electron or proton conduction, as the activation barriers for proton (H+) hopping are lower compared to deuteron (D+) hopping due to the lower zero-point energies of the O–D bond compared to the O–H bond. If proton conduction is the dominant mechanism, then according to classical theory, σD+/σH+ is expected to be 0.71.78–81 If electrons are the majority carrier, then σD+/σH+ will be close to 1. Fig. 3a shows the DC conductivity (σdc/S cm−1) of Pt-BTO-470 measured at 22 °C and 130 °C vs. increasing concentration (ppm) of H2 and D2, and the results are tabulated in Table S9,† with σD+/σH+ ratios in the range 1.00–1.08 for all conditions studied. Representative Nyquist plots for impedance measurements performed at 130 °C and 290.7 × 103 ppm in atmospheres of H2 and D2 overlap over the frequency range studied (Fig. S22†). The results clearly indicate that there is no significant change in conductivity under H2 or D2, indicative of the predominance of electronic conduction across the temperature and H2 concentration ranges studied. However, H2 dissociation produces protons that can interact with grain boundary oxygen species, even though they are not the majority carriers, as shown in eqn (9). Proton diffusion in the metal oxide bulk lattice is slow at low temperatures; however, proton migration along surface oxygen species is possible.78 The mechanism of electron transport was investigated using the Jonscher interpretation of the AC frequency response of conductivity.
| σ(ω) = σdc + AωS | (13) |
Two distinct S vs. T regions can be identified for Pt-BTO-470 for both N2 and all H2 atmospheres, with an inflection point and change in mechanism occurring between 80 °C and 100 °C (Fig. S30†). Below 80 °C, the value of S increases with temperature for pure N2 and for all H2 concentrations, which is indicative of a non-overlapping small polaron tunnelling model (NSPT). Above 80 °C, the S exponent generally decreases with temperature, and this is indicative of a correlated barrier hopping (CBH) mechanism. The CBH model, proposed by Pike85 for one electron and then for two electrons by Elliot,84 explains AC conductivity in terms of electrons that hop over a potential barrier between two charged defect states, D− and D+, where the barrier height is correlated with the inter-site separation via a coulombic interaction, due to the changing overlap region of potential energy wells.84 For Pt-BTO-470, the exact nature of these sites is unknown, but the AC conductivity increase due to short-range charge mobility (and quantified by the S exponent) lies in the high frequency region (>104 rad s−1) where the bulk controls the conduction. Therefore, the NSPT mechanism could be attributed to a tunnelling process in the n-type grains.90 As the temperature and hydrogen concentration increase, more of the high frequency AC conductivity response is dominated by the grain boundary region (the peak in Z′′ moves into the AC conductivity curvature region) and is therefore controlled by charge hopping over the Schottky barrier. Hence, the charge transport is controlled by the grain boundaries via the CBH mechanism. For atmospheres of 0.4% and 1% H2, S decreases at 100 °C and then there is a second increase and inflection point at 125 °C, with S then decreasing to 0.9 as the temperature increases to 175 °C. Hence, these results demonstrate that charge transport is complex and is dependent on both temperature and H2 concentration. These observations can be described by mixed NSPT and CBH charge transport when under low H2 concentrations. However, the general trend shows a transition from the NSPT mechanism in the grains below 80–100 °C to the CBH at grain boundaries above 100 °C, which could be due to the ferroelectric–paraelectric phase transition, which drives electron trap filling and an increase in the Schottky barrier height and depletion layer width.
For our work, the conductivity should also exhibit a H2 pressure dependence, as more BaTiO3 surface sites/defects will be filled at higher H2 concentrations, increasing the concentration of electrons in the conduction band. The reaction and equilibrium equations for this model are shown in eqn (14) and (15), respectively.
 | (14) |
 | (15) |
The Mott–Schottky (MS) model assumes a uniform distribution of surface acceptor states and can be used to calculate the carrier concentration and type.101,102 A MS analysis (C−2 (F−2) vs. bias (V)) was performed for the BaTiO3–Pt electrode interface region for 0.4% and 1.0% H2, as shown in Fig. S34.† The steep positive slope is indicative of n-type conduction and the electron concentration, calculated from the slope, increased from 3.1 × 1022 to 3.8 × 1022 m−3, respectively. Due to the relatively large concentration of electrons, this could result in an increase of the electron trap emission rate, producing both an increase in capacitance and conductivity, as shown in Fig. 3e, with the effect greatly enhanced under H2 compared to N2 atmospheres. Once the traps are filled, the relative permittivity slightly decreases, and the conductivity increases at a greater rate. Therefore, the ferroelectric-paraelectric transition in BaTiO3 was successfully exploited to highlight the effect of oxygen vacancies/electron-trapping species on the material's electrical properties. However, more work is required to understand the influence of proton mobility, electron traps, and oxygen vacancies on the Schottky barrier characteristics and to decouple the complex interplay of processes.
In addition, bulk capacitances were derived from the distribution of relaxation times deconvolution of impedance spectra and the Curie–Weiss analysis demonstrates a TC of approximately 120 °C (Fig. S35†) when under N2 atmospheres. However, under H2 atmospheres, the TC appears to be shifted to a lower temperature of 80 °C based on the capacitance measurements (Fig. 3d). Ferroelectric materials are sensitive to defects and surface chemistry, and there is a delicate balance between long-range coulombic forces, which favour the ferroelectric state, and short-range repulsions, which favour the nonpolar cubic structure, with hybridisation between oxygen 2p and titanium 3d states being essential for ferroelectricity.103 Hence, the release of electrons and the interaction of protons with BaTiO3 seems to promote short-range repulsion effects, leading to destabilisation of the ferroelectric state and a shift of TC to a lower temperature. However, there were insufficient temperature points to confirm this categorically via Curie–Weiss analysis.
 .39 Another method to deconvolute EIS spectra is to use the distribution of relaxation time (DRT) approach, which assumes a linear sum of numerous parallel RC elements, each with a characteristic relaxation time.50Fig. 4a shows the fitting of the DRT model to experimental impedance data for Pt-BTO-470 measured under pure N2 and 0.4% H2 atmospheres at 22 °C and is represented in the Nyquist formalism. The DRT fits and fitting residuals presented in the spectroscopic formalism are shown in Fig. S36a and b,† which shows a residual fitting error of less than 2% over the frequency range studied. Fig. 4b shows the corresponding distribution of relaxation times obtained from the model fit in Fig. 4a. Two distinct peaks can be observed, attributable to the bulk (fast process, small τ) and grain boundary (intermediate τ) regions. A third peak may be tentatively observed at large τ, representative of slower electrode processes.
.39 Another method to deconvolute EIS spectra is to use the distribution of relaxation time (DRT) approach, which assumes a linear sum of numerous parallel RC elements, each with a characteristic relaxation time.50Fig. 4a shows the fitting of the DRT model to experimental impedance data for Pt-BTO-470 measured under pure N2 and 0.4% H2 atmospheres at 22 °C and is represented in the Nyquist formalism. The DRT fits and fitting residuals presented in the spectroscopic formalism are shown in Fig. S36a and b,† which shows a residual fitting error of less than 2% over the frequency range studied. Fig. 4b shows the corresponding distribution of relaxation times obtained from the model fit in Fig. 4a. Two distinct peaks can be observed, attributable to the bulk (fast process, small τ) and grain boundary (intermediate τ) regions. A third peak may be tentatively observed at large τ, representative of slower electrode processes.
Between 80–100 °C, the Ea increases progressively with H2 concentration from 0.4 to 0.6 eV, and above 100 °C Ea is approximately constant at 0.36 eV and shows no H2 concentration dependence. Hence, the results demonstrate that in the temperature region 80–100 °C, where the ferroelectric to paraelectric transition occurs, there is a strong dependence of Ea on the H2 concentration. For n-doped BaTiO3, the conduction band grain boundary Schottky barrier increases sharply at the Curie temperature (TC), as ferroelectric compensation of the Schottky barrier decreases significantly. In this study, this effect is enhanced by increasing the H2 concentration and hence the concentration of electrons in the system and could be due to the filling of grain boundary electron traps, depletion of oxygen vacancies, or due to the mobility of protons along grain boundaries,100 which increase the Schottky barrier height and width.
The Rgb values determined from DRT peak deconvolution were used to calculate Ea values for electronic conduction as a function of H2 concentration for the grain boundary regions. Plots of ln(1/Rgb) vs. 1/T and Ea values calculated from these plots are shown in Fig. 5a and b, respectively. The trends observed using Rgb from DRT analysis are comparable to those found from the total conductivity (σdc) data described above (from Jonscher analysis). The same three temperature dependent regions exist in the Arrhenius plots and show the same H2 concentration dependence. This is due to the grain boundary's back-to-back Schottky barriers dominating the overall conductivity under all conditions studied. For the grain boundary region, and when under N2 atmospheres, the Arrhenius plot gradient in Fig. 5a is constant across the entire temperature range studied at approximately 0.17 eV (Fig. 5b). However, under H2 atmospheres, three temperature-dependent linear regions exist for T < 80 °C, T between 80 °C and 100 °C, and T > 100 °C and are present for all H2 concentrations studied. For temperatures below 80 °C and above 100 °C, the Ea values are approximately constant with H2 concentration and are 0.24 eV and 0.5 eV, respectively. The Arrhenius gradient increases systematically in the temperature region 80–100 °C with H2 concentration, as shown in Fig. 5b, and this is coincident with the point at which the material's relative permittivity increases, which is indicative of the BaTiO3 Curie temperature, where the transition from the ferroelectric tetragonal phase to the paraelectric cubic phase occurs. Fig. 5b shows that the Ea increases monotonically from 0.5 to 0.8 eV as the H2 pressure is increased from 0–19%. The values for the grain boundary activation energies are slightly higher than the total resistance activation energies, and this is due to a stronger temperature dependence of the grain boundary region. The grain boundary Schottky barrier is also sensitive to the H2 concentration when in the Curie transition temperature range. Conversely, the bulk and electrode interface regions showed a lower sensitivity to the change in gas atmosphere (Fig. S44†). The Ea of bulk and electrode are 0.14 eV and 0.07 eV, respectively, demonstrating that the reduction process and oxygen vacancy creation reduced the Schottky barrier of the interface considerably (ideal Schottky barrier is 1.74 eV for BaTiO3–Pt). Ea increases over the H2 concentrations range of 0.4–3.0% up to 0.28 eV for the bulk and 0.2 eV for the electrode interface. For H2 concentrations >3%, the Ea for both bulk and electrode reached a plateau of 0.2 eV. This is in opposition to the findings of Heidary et al.7,8 where the electrode interface exhibited the largest barrier to charge transport for a BaTiO3–Pt electrode system; hence, highlighting the sensitivity of BaTiO3 grain boundary regions to spark plasma sintering and post-synthetic reduction and oxidation.57 In concordance with our study, Heidary observed a reduction in the barrier height from 1.1–1.2 eV (in agreement with the difference between the work function of Ni (5.01–5.10 eV) and electron affinity of BaTiO3 (3.9 eV)) to 0.2 eV for a BaTiO3–Ni electrode system under H2.8
The Meyer–Neldel rule (MNR), also known as the compensation effect, has been observed in several systems where a linear relationship between Ea and the natural logarithm of the preexponential factor (ln(A)) exists and where the pre-exponential factor (A) describes the frequency of molecular collisions within the system.104–106 This effect has been frequently observed in semiconductors and has been attributed to the vibronic intersection regions, or crossover points, of 1-dimensional harmonic oscillators describing empty and filled traps, and this controls the activation barrier for electron hopping and tunnelling.107–110 In this work, for Arrhenius plots derived from the DC component of the conductivity data (σdc), there is a general linear relationship between Ea and ln(A) for the three temperature regions identified in the Arrhenius plots (Fig. S45a†). However, the 22–80 °C and 100–175 °C regions show no systematic change with H2 concentration but do follow a general linear trend over the entire ln(A) and Ea range. There is a linear trend for the temperature region 80–100 °C, where the Ea and ln(A) values increase proportionally with H2 concentration (Fig. S45b†). The same trends are observed for the grain boundary region (Fig. 5c and S46†), where the Arrhenius pre-exponential factor, ln(A), and Ea increase linearly with H2 concentration in Curie temperature region (80–100 °C), as shown in Fig. 5c. In the region 80–100 °C, the activation barrier controlling electron transport increases with H2 concentration. For a true compensation effect, the Arrhenius plots for each H2 concentration should intersect at an isokinetic temperature where the rates become equal,105 and this has been observed for the BaTiO3 H2 system (Fig. S47†), which occurs at approximately 30 °C. Additionally, both the conductivity and capacitance increase with temperature and H2 concentration, which implies that electrons are trapped at the grain boundaries; however, the trap emission rate increases with electron concentration and temperature. In terms of classical rate theory, the pre-exponential factor (A) is representative of collisional frequency and Ea represents the activation barrier, or, in this case, the grain boundary Schottky barrier height formed due to trapped electrons at the grain boundaries. These results imply that as the H2 concentration is increased, there are more electrons in the conduction band due to dissociation and charge separation from H2. As the grain boundary Schottky barrier increases in the Curie temperature region, this causes an increase in the frequency of electronic collisions due to the deepening of conduction band trapping states. However, this interpretation is probably far too simplistic for semiconductor systems, and a more robust theory of MNR is required for semiconductors and surface charge-trapping states. The conduction process in this study is complex and involves the interplay of donor oxygen vacancies (concentration and mobility), H2 dissociation resulting in electron transfer and surface reactions, proton transport, the ferroelectric properties of BaTiO3, and the resulting influence on the grain boundary and electrode interface Schottky barrier height and width. Indeed, these processes are most likely occurring in parallel and are coupled; therefore, it is difficult to describe the sensing mechanism in detail at this stage.
4 Conclusions
Synchrotron-based near ambient pressure X-ray photoelectron spectroscopy studies have shown that OH groups were detected on the surface of platinum-coated, undoped, n-type BaTiO3, which were formed after a controlled reduction-oxidation procedure and cooling to room temperature. On switching from argon to H2, the OH species decreased and adsorbed H2O increased systematically with increasing H2 pressure, and over the temperature range 22–150 °C. Electrochemical impedance spectroscopy studies revealed that on switching from N2 to H2 between 22–175 °C, n-type gas sensing was observed, as the material's total resistance decreased by an order of magnitude at room temperature, driven by the resistance decrease of the grain boundary regions, which decreased further with increasing H2 concentration. This process was reversible under N2 and two time constants were present for both H2 sensing and recovery of the sensor. However, no resistance change was observed when switching from N2 to O2 between 22–175 °C and N2 to CO at 22 °C. Colossal relative permittivity (εr) values were obtained when under N2 and H2 atmospheres. When under H2 alone, εr increased by an order of magnitude when passing through the Curie temperature between 100–120 °C. Therefore, these results are consistent with the following:(1) Reduction of p-type BaTiO3 in H2 at high temperature introduces donor oxygen vacancies close to the conduction band that transform the material into an n-type semiconductor.
(2) During controlled oxidation and cooling, the reaction of O2 and H2O with oxygen vacancies produces a BaTiO3 surface decorated with OH and adsorbed H2O groups. This causes a resistance increase due to the healing of oxygen vacancies.
(3) On exposure to H2 containing atmospheres, H2 dissociates on platinum creating proton-electron pairs. Electrons enter the BaTiO3 conduction band and decrease the resistance. The grain boundaries show the largest resistance and resistance change on exposure to H2.
(4) Dissociated protons diffuse along the grain boundaries and electrode interface regions and react with surface OH, creating adsorbed H2O on the surface of the grains. H2O desorbs and creates additional electron-donating oxygen vacancies that increase the charge carrier concentration.
(5) These processes manifest in two time constant components indicative of fast H2 dissociation on Pt, which creates a rapid decrease in resistance, and a slow proton diffusion process along grain boundaries, which drives H2O desorption and oxygen vacancy creation, resulting in a slower increase in the resistance.
Consequently, it is possible to tune the sensing properties through modification of the oxygen vacancy concentration at the grain boundary and electrode interface regions by controlling the reduction–oxidation process. This is vitally important for gas sensing, dielectric, fuel cell, thermal and electrocatalysis, and even H2 storage applications.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest present in this work.Acknowledgements
Jon. G. Bell acknowledges funding provided by the European Research Council under the Horizon 2020 Marie Sklodowska-Curie Actions Scheme for funding of the Individual Fellowship SmartSorp project (Smart Ceramic Hollow Fibers for Energy Efficient Gas and Vapour Sorption), grant agreement no. 843988. The work was also carried out as part of the Paul Scherrer Institute Swiss Light Source research proposal No. 20220652.References
- A. Dey, Semiconductor metal oxide gas sensors: A review, Mater. Sci. Eng. B, 2018, 229, 206–217 CrossRef CAS.
- A. Gurlo, Interplay between O2 and SnO2: Oxygen Ionosorption and Spectroscopic Evidence for Adsorbed Oxygen, ChemPhysChem, 2006, 7(10), 2041–2052 CrossRef CAS PubMed.
- K. V. Sopiha, O. I. Malyi, C. Persson and P. Wu, Chemistry of Oxygen Ionosorption on SnO2 Surfaces, ACS Appl. Mater. Interfaces, 2021, 13(28), 33664–33676 CrossRef.
- C. Blackman, Do We Need “Ionosorbed” Oxygen Species? (Or, “A Surface Conductivity Model of Gas Sensitivity in Metal Oxides Based on Variable Surface Oxygen Vacancy Concentration”), ACS Sens., 2021, 6(10), 3509–3516 CrossRef PubMed.
- Z. Zhang and J. T. Yates Jr, Band Bending in Semiconductors: Chemical and Physical Consequences at Surfaces and Interfaces, Chem. Rev., 2012, 112(10), 5520–5551 CrossRef PubMed.
- E. Ciftyurek, Z. Li and K. Schierbaum, Adsorbed Oxygen Ions and Oxygen Vacancies: Their Concentration and Distribution in Metal Oxide Chemical Sensors and Influencing Role in Sensitivity and Sensing Mechanisms, Sensors, 2023, 23(1), 29 CrossRef.
- D. Sohrabi Baba Heidary and C. A. Randall, Analysis of the degradation of BaTiO3 resistivity due to hydrogen ion incorporation: Impedance spectroscopy and diffusion analysis, Acta Mater., 2015, 96, 344–351 CrossRef.
- D. S. B. Heidary, W. Qu and C. A. Randall, Electrical characterization and analysis of the degradation of electrode Schottky barriers in BaTiO3 dielectric materials due to hydrogen exposure, J. Appl. Phys., 2015, 117(12), 4104 CrossRef.
- H. I. Yoo, C. R. Song and D. K. Lee, Electronic carrier mobilities of BaTiO3, J. Eur. Ceram. Soc., 2004, 24(6), 1259–1263 CrossRef.
- S. Aggarwal, S. R. Perusse, C. W. Tipton, R. Ramesh, H. D. Drew, T. Venkatesan, D. B. Romero, V. B. Podobedov and A. Weber, Effect of hydrogen on Pb(Zr,Ti)O3-based ferroelectric capacitors, Appl. Phys. Lett., 1998, 73(14), 1973–1975 CrossRef.
- D. R. Aireddy and K. Ding, Heterolytic Dissociation of H2 in Heterogeneous Catalysis, ACS Catal., 2022, 12(8), 4707–4723 CrossRef CAS.
- K. D. Kreuer, Aspects of the formation and mobility of protonic charge carriers and the stability of perovskite-type oxides, Solid State Ionics, 1999, 125(1), 285–302 CrossRef.
- G. Hultquist, M. J. Graham, A. T. S. Wee, R. Liu, G. I. Sproule, Q. Dong and C. Anghel, Effects of O2 Dissociation on a Porous Platinum Coating in the Thermal Oxidation of GaAs, J. Electrochem. Soc., 2006, 153(2), G182 CrossRef.
- M. Yuasa, T. Nagano, N. Tachibana, T. Kida and K. Shimanoe, Catalytic Combustion-Type Hydrogen Sensor Using BaTiO3-based PTC Thermistor, J. Am. Ceram. Soc., 2013, 96(6), 1789–1794 CrossRef.
- S. C. Chang, Oxygen chemisorption on tin oxide: Correlation between electrical conductivity and EPR measurements, J. Vac. Sci. Technol., 1980, 17(1), 366–369 CrossRef.
- X. Zhang, T. Liu, L. Zhu, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, C. R. A. Catlow and A. A. Sokol, Bulk and Surface Contributions to Ionisation Potentials of Metal Oxides, Angew. Chem., Int. Ed., 2023, 62(40), e202308411 CrossRef.
- C. Y. Su, C. Pithan, D. F. Hennings and R. Waser, Proton defects in BaTiO3: New aspects regarding the re-oxidation of dielectric materials fired in reducing atmospheres, J. Eur. Ceram. Soc., 2013, 33(15–16), 3007–3013 CrossRef.
- K. H. Zhang, R. G. Egdell, F. Offi, S. Iacobucci, L. Petaccia, S. Gorovikov and P. D. King, Microscopic origin of electron accumulation in In2O3, Phys. Rev. Lett., 2013, 110(5), 056803 CrossRef.
- V. Jovic, S. Moser, A. Papadogianni, R. J. Koch, A. Rossi, C. Jozwiak, A. Bostwick, E. Rotenberg, J. V. Kennedy, O. Bierwagen and K. E. Smith, The Itinerant 2D Electron Gas of the Indium Oxide (111) Surface: Implications for Carbon- and Energy-Conversion Applications, Small, 2020, 16(12), e1903321 CrossRef PubMed.
- S. K. Vasheghani Farahani, T. D. Veal, J. J. Mudd, D. O. Scanlon, G. W. Watson, O. Bierwagen, M. E. White, J. S. Speck and C. F. McConville, Valence-band density of states and surface electron accumulation in epitaxialSnO2films, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(15), 155413 CrossRef.
- J. Dai, E. Frantzeskakis, F. Fortuna, P. Lömker, R. Yukawa, M. Thees, S. Sengupta, P. Le Fèvre, F. Bertran, J. E. Rault, K. Horiba, M. Müller, H. Kumigashira and A. F. Santander-Syro, Tunable two-dimensional electron system at the (110) surface of SnO2, Phys. Rev. B, 2020, 101(8), 085121 CrossRef.
- T. C. Rödel, J. Dai, F. Fortuna, E. Frantzeskakis, P. Le Fèvre, F. Bertran, M. Kobayashi, R. Yukawa, T. Mitsuhashi, M. Kitamura, K. Horiba, H. Kumigashira and A. F. Santander-Syro, High-density two-dimensional electron system induced by oxygen vacancies in ZnO, Phys. Rev. Mater., 2018, 2(5), 051601 CrossRef.
- A. F. Santander-Syro, O. Copie, T. Kondo, F. Fortuna, S. Pailhès, R. Weht, X. G. Qiu, F. Bertran, A. Nicolaou, A. Taleb-Ibrahimi, P. Le Fèvre, G. Herranz, M. Bibes, N. Reyren, Y. Apertet, P. Lecoeur, A. Barthélémy and M. J. Rozenberg, Two-dimensional electron gas with universal subbands at the surface of SrTiO3, Nature, 2011, 469(7329), 189–193 CrossRef PubMed.
- P. D. King, R. H. He, T. Eknapakul, P. Buaphet, S. K. Mo, Y. Kaneko, S. Harashima, Y. Hikita, M. S. Bahramy, C. Bell, Z. Hussain, Y. Tokura, Z. X. Shen, H. Y. Hwang, F. Baumberger and W. Meevasana, Subband structure of a two-dimensional electron gas formed at the polar surface of the strong spin-orbit perovskite KTaO3, Phys. Rev. Lett., 2012, 108(11), 117602 CrossRef.
- S. Kucharski, P. Ferrer, F. Venturini, G. Held, A. S. Walton, C. Byrne, J. A. Covington, S. K. Ayyala, A. M. Beale and C. Blackman, Direct in situ spectroscopic evidence of the crucial role played by surface oxygen vacancies in the O2-sensing mechanism of SnO2, Chem. Sci., 2022, 13(20), 6089–6097 RSC.
- B. Szafraniak, Ł. Fuśnik, J. Xu, F. Gao, A. Brudnik and A. Rydosz, Semiconducting Metal Oxides: SrTiO3, BaTiO3 and BaSrTiO3 in Gas-Sensing Applications: A Review, Coatings, 2021, 11(2), 185 CrossRef.
- H. D. Megaw, Crystal Structure of Barium Titanium Oxide at Different Temperatures, Experientia, 1946, 2(5), 183–184 CrossRef.
- J. G. Bell, T. Graule and M. Stuer, Barium titanate-based thermistors: Past achievements, state of the art, and future perspectives, Appl. Phys. Rev., 2021, 8(3), 1318 Search PubMed.
- L. Ben, L. Li, J. H. Harding, C. L. Freeman and D. C. Sinclair, Tuning the electrical conductivity of Rare Earth-doped BaTiO3 using Gd2O3 as an exemplar, Open Ceram., 2022, 9, 100250 CrossRef.
- H. Beltrán, E. Cordoncillo, P. Escribano, D. C. Sinclair and A. R. West, Oxygen loss, semiconductivity, and positive temperature coefficient of resistance behavior in undoped cation-stoichiometric BaTiO3 ceramics, J. Appl. Phys., 2005, 98(9), 4102 CrossRef.
- E. Andrich, Ptc Thermistors as Self-Regulating Heating Elements, Philips Tech. Rev., 1969, 30(6–7), 170 Search PubMed.
- J. G. Bell, K. Angus, C. Todd and K. M. Thomas, Functional Hollow Fiber Adsorbent Materials with a Self-Regulating Composite Outer Layer for Gas Purification with Energy Efficient Electrothermal Regeneration, Ind. Eng. Chem. Res., 2013, 52(3), 1335–1351 CrossRef.
- G. H. Jonker, Halogen Treatment of Barium Titanate Semiconductors, Mater. Res. Bull., 1967, 2(4), 401 CrossRef.
- G. H. Jonker, Some Aspects of Semiconducting Barium Titanate, Solid-State Electron., 1964, 7(12), 895–903 CrossRef.
- L. J. Brillson, Chemical reaction and charge redistribution at metal–semiconductor interfaces, J. Vac. Sci. Technol., 1978, 15(4), 1378–1383 CrossRef.
- D. P. Cann, J. P. Maria and C. A. Randall, Relationship between wetting and electrical contact properties of pure metals and alloys on semiconducting barium titanate ceramics, J. Mater. Sci., 2001, 36(20), 4969–4976 CrossRef.
- Z. Valdez-Nava, S. Guillemet-Fritsch, C. Tenailleau, T. Lebey, B. Durand and J. Y. Chane-Ching, Colossal dielectric permittivity of BaTiO3-based nanocrystalline ceramics sintered by spark plasma sintering, J. Electroceram., 2009, 22(1), 238–244 CrossRef.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2(3), 132–138 CrossRef.
- D. C. Sinclair, Characterisation of Electro-materials using ac Impedance Spectroscopy, Bol. Soc. Esp. Ceram. Vidrio, 1995, 34(2), 55–65 CAS.
- L. Trotochaud, A. R. Head, O. Karslıoğlu, L. Kyhl and H. Bluhm, Ambient pressure photoelectron spectroscopy: Practical considerations and experimental frontiers, J. Phys.: Condens. Matter, 2017, 29(5), 053002 CrossRef.
- J. Schnadt, J. Knudsen and N. Johansson, Present and new frontiers in materials research by ambient pressure x-ray photoelectron spectroscopy, J. Phys.: Condens. Matter, 2020, 32(41), 413003 CrossRef CAS.
- K. Roy, L. Artiglia and J. A. van Bokhoven, Ambient Pressure Photoelectron Spectroscopy: Opportunities in Catalysis from Solids to Liquids and Introducing Time Resolution, ChemCatChem, 2018, 10(4), 666–682 CrossRef CAS.
- M. Vorokhta, I. Khalakhan, M. Vondráček, D. Tomeček, M. Vorokhta, E. Marešová, J. Nováková, J. Vlček, P. Fitl, M. Novotný, P. Hozák, J. Lančok, M. Vrňata, I. Matolínová and V. Matolín, Investigation of gas sensing mechanism of SnO2 based chemiresistor using near ambient pressure XPS, Surf. Sci., 2018, 677, 284–290 CrossRef CAS.
- B. Junker, M. Favaro, D. E. Starr, M. Hävecker, U. Weimar and N. Barsan, NAP-XPS as a new tool for in-situ studies of SMOX gas sensors, J. Phys. D: Appl. Phys., 2022, 55(6), 064002 CrossRef CAS.
- V. Brinzari, B. K. Cho, M. Kamei and G. Korotcenkov, Photoemission surface characterization of (001) In2O3 thin film through the interactions with oxygen, water and carbon monoxide: Comparison with (111) orientation, Appl. Surf. Sci., 2015, 324, 123–133 CrossRef CAS.
- E. Ciftyürek, B. Šmíd, Z. Li, V. Matolín and K. Schierbaum, Spectroscopic Understanding of SnO2 and WO3 Metal Oxide Surfaces with Advanced Synchrotron Based; XPS-UPS and Near Ambient Pressure (NAP) XPS Surface Sensitive Techniques for Gas Sensor Applications under Operational Conditions, Sensors, 2019, 19(21), 4737 CrossRef PubMed.
- Y. Gassenbauer, R. Schafranek, A. Klein, S. Zafeiratos, M. Hävecker, A. Knop-Gericke and R. Schlögl, Surface potential changes of semiconducting oxides monitored by high-pressure photoelectron spectroscopy: Importance of electron concentration at the surface, Solid State Ionics, 2006, 177(35), 3123–3127 CrossRef CAS.
- T. J. Frankcombe and Y. Liu, Interpretation of Oxygen 1s X-ray Photoelectron Spectroscopy of ZnO, Chem. Mater., 2023, 35(14), 5468–5474 CrossRef CAS.
- H. Idriss, On the wrong assignment of the XPS O 1s signal at 531–532 eV attributed to oxygen vacancies in photo- and electro-catalysts for water splitting and other materials applications, Surf. Sci., 2021, 712, 121894 CrossRef CAS.
- B. A. Boukamp, Distribution (function) of relaxation times, successor to complex nonlinear least squares analysis of electrochemical impedance spectroscopy?, J. Phys.: Energy, 2020, 2(4), 042001 CAS.
- G. J. Brug, A. L. G. van den Eeden, M. Sluyters-Rehbach and J. H. Sluyters, The analysis of electrode impedances complicated by the presence of a constant phase element, J. Electroanal. Chem. Interfacial Electrochem., 1984, 176(1), 275–295 CrossRef CAS.
- K. Kobayashi, Y. Sakka and T. S. Suzuki, Development of an electrochemical impedance analysis program based on the expanded measurement model, J. Ceram. Soc. Jpn., 2016, 124(9), 943–949 CrossRef CAS.
- K. Kobayashi and T. S. Suzuki, Development of Impedance Analysis Software Implementing a Support Function to Find Good Initial Guess Using an Interactive Graphical User Interface, Electrochemistry, 2020, 88(1), 39–44 CrossRef CAS.
- F. Orlando, A. Waldner, T. Bartels-Rausch, M. Birrer, S. Kato, M.-T. Lee, C. Proff, T. Huthwelker, A. Kleibert, J. van Bokhoven and M. Ammann, The Environmental Photochemistry of Oxide Surfaces and the Nature of Frozen Salt Solutions: A New in Situ XPS Approach, Top. Catal., 2016, 59(5), 591–604 CrossRef CAS.
- I. Spasojevic, G. Sauthier, J. M. Caicedo, A. Verdaguer and N. Domingo, Oxidation processes at the surface of BaTiO3 thin films under environmental conditions, Appl. Surf. Sci., 2021, 565, 150288 CrossRef CAS.
- D. R. Franklin, J. P. Anderton and A. J. Pointon, Experimental evidence for a relationship between Lotgering index and ferromagnetic resonance linewidth, J. Magn. Magn. Mater., 1996, 159(1), L51–L54 CrossRef CAS.
- J. G. Bell, T. Graule and M. Stuer, Tuning of the microstructural and electrical properties of undoped BaTiO3 by spark plasma sintering, Open Ceram., 2022, 9, 100244 CrossRef CAS.
- H. Idriss, Oxygen vacancies role in thermally driven and photon driven catalytic reactions, Chem Catal., 2022, 2, 1549 CrossRef CAS.
- J. J. Brown, Z. Ke, W. Geng and A. J. Page, Oxygen Vacancy Defect Migration in Titanate Perovskite Surfaces: Effect of the A-Site Cations, J. Phys. Chem. C, 2018, 122(26), 14590–14597 CrossRef CAS.
- Z. Lu, D. Ma, L. Yang, X. Wang, G. Xu and Z. Yang, Direct CO oxidation by lattice oxygen on the SnO2 (110) surface: a DFT study, Phys. Chem. Chem. Phys., 2014, 16(24), 12488–12494 RSC.
- X. Zhou, N. Mousseau and J. Song, Is Hydrogen Diffusion along Grain Boundaries Fast or Slow? Atomistic Origin and Mechanistic Modeling, Phys. Rev. Lett., 2019, 122(21), 215501 CrossRef CAS PubMed.
- Z. Li, Z. Yao, A. A. Haidry, T. Plecenik, L. Xie, L. Sun and Q. Fatima, Resistive-type hydrogen gas sensor based on TiO2: A review, Int. J. Hydrogen Energy, 2018, 43(45), 21114–21132 CrossRef CAS.
- X. Li, B. Wang, T.-Y. Zhang and Y. Su, Water Adsorption and Dissociation on BaTiO3 Single-Crystal Surfaces, J. Phys. Chem. C, 2014, 118(29), 15910–15918 CrossRef CAS.
- O. Matz and M. Calatayud, H2 Dissociation and Oxygen Vacancy Formation on Ce2O3 Surfaces, Top. Catal., 2019, 62(12), 956–967 CrossRef CAS.
- F. Cordero, F. Trequattrini, D. A. B. Quiroga and P. S. Silva, Hopping and clustering of oxygen vacancies in BaTiO3−δ and the influence of the off-centred Ti atoms, J. Alloys Compd., 2021, 874, 159753 CrossRef CAS.
- M. Kessel, R. A. De Souza and M. Martin, Oxygen diffusion in single crystal barium titanate, Phys. Chem. Chem. Phys., 2015, 17(19), 12587–12597 RSC.
- M. Kessel, R. A. De Souza and M. Martin, Oxygen diffusion in single crystal barium titanate, Phys. Chem. Chem. Phys., 2018, 20(46), 29568 RSC.
- J. Crank, The Mathematics of Diffusion, Oxford University Press, London, 2nd edn, 1975 Search PubMed.
- Q. Zhang, Y. J. Li, H. F. Wen, Y. Adachi, M. Miyazaki, Y. Sugawara, R. Xu, Z. H. Cheng, J. Brndiar, L. Kantorovich and I. Štich, Measurement and Manipulation of the Charge State of an Adsorbed Oxygen Adatom on the Rutile TiO2(110)-1×1 Surface by nc-AFM and KPFM, J. Am. Chem. Soc., 2018, 140(46), 15668–15674 CrossRef CAS.
- J.-C. Dupin, D. Gonbeau, P. Vinatier and A. Levasseur, Systematic XPS studies of metal oxides, hydroxides and peroxides, Phys. Chem. Chem. Phys., 2000, 2(6), 1319–1324 RSC.
- S. Chakrabarti, S. Ginnaram, S. Jana, Z.-Y. Wu, K. Singh, A. Roy, P. Kumar, S. Maikap, J.-T. Qiu, H.-M. Cheng, L.-N. Tsai, Y.-L. Chang, R. Mahapatra and J.-R. Yang, Negative voltage modulated multi-level resistive switching by using a Cr/BaTiOx/TiN structure and quantum conductance through evidence of H2O2 sensing mechanism, Sci. Rep., 2017, 7(1), 4735 CrossRef.
- Z. Wang, R. Lin, Y. Huo, H. Li and L. Wang, Formation, Detection, and Function of Oxygen Vacancy in Metal Oxides for Solar Energy Conversion, Adv. Funct. Mater., 2022, 32(7), 2109503 CrossRef CAS.
- S. Yamamoto, T. Kendelewicz, J. T. Newberg, G. Ketteler, D. E. Starr, E. R. Mysak, K. J. Andersson, H. Ogasawara, H. Bluhm, M. Salmeron, G. E. Brown Jr and A. Nilsson, Water Adsorption on α-Fe2O3(0001) at near Ambient Conditions, J. Phys. Chem. C, 2010, 114(5), 2256–2266 CrossRef CAS.
- P. B. Weisz, Effects of Electronic Charge Transfer between Adsorbate and Solid on Chemisorption and Catalysis, J. Chem. Phys., 1953, 21(9), 1531–1538 CrossRef CAS.
- A. Shchukarev and D. Korolkov, XPS Study of group IA carbonates, Open Chem., 2004, 2(2), 347–362 CrossRef CAS.
- J. Wang, D. N. Mueller and E. J. Crumlin, Recommended strategies for quantifying oxygen vacancies with X-ray photoelectron spectroscopy, J. Eur. Ceram. Soc., 2024, 44(15), 116709 CrossRef CAS.
- H. Shen, H. Li, Z. Yang and C. Li, Magic of hydrogen spillover: Understanding and application, Green Energy Environ., 2022, 7(6), 1161–1198 CrossRef CAS.
- T. Matsuda, R. Ishibashi, Y. Koshizuka, H. Tsuneki and Y. Sekine, Quantitative investigation of CeO2 surface proton conduction in H2 atmosphere, Chem. Commun., 2022, 58(77), 10789–10792 RSC.
- J. Bigeleisen, The Relative Reaction Velocities of Isotopic Molecules, J. Chem. Phys., 2004, 17(8), 675–678 CrossRef.
- T. Scherban, W. K. Lee and A. S. Nowick, Bulk protonic conduction in Yb-doped SrCeO3 and BaCeO3, Solid State Ionics, 1988, 28–30, 585–588 CrossRef.
- A. S. Nowick and Y. Du, High-temperature protonic conductors with perovskite-related structures, Solid State Ionics, 1995, 77, 137–146 CrossRef CAS.
- A. K. Jonscher, The ‘universal’ dielectric response, Nature, 1977, 267(5613), 673–679 CrossRef CAS.
- D. P. Almond, A. R. West and R. J. Grant, Temperature dependence of the a.c. conductivity of Naβ-alumina, Solid State Commun., 1982, 44(8), 1277–1280 CrossRef CAS.
- S. R. Elliott, A theory of a.c. conduction in chalcogenide glasses, Phil. Mag., 1977, 36(6), 1291–1304 CrossRef CAS.
- G. E. Pike, ac Conductivity of Scandium Oxide and a New Hopping Model for Conductivity, Phys. Rev. B, 1972, 6(4), 1572–1580 CrossRef CAS.
- I. G. Austin and N. F. Mott, Polarons in crystalline and non-crystalline materials, Adv. Phys., 1969, 18(71), 41–102 CrossRef CAS.
- A. R. Long, Frequency-dependent loss in amorphous semiconductors, Adv. Phys., 1982, 31(5), 553–637 CrossRef CAS.
- M. Pollak, Temperature Dependence of ac Hopping Conductivity, Phys. Rev., 1965, 138(6A), A1822–A1826 CrossRef.
- A. Ghosh and D. Chakravorty, AC conduction in semiconducting CuO-Bi2O3-P2O5 glasses, J. Phys.: Condens. Matter, 1990, 2(24), 5365 CrossRef CAS.
- A. Radoń, D. Łukowiec, M. Kremzer, J. Mikuła and P. Włodarczyk, Electrical Conduction Mechanism and Dielectric Properties of Spherical Shaped Fe3O4 Nanoparticles Synthesized by Co-Precipitation Method, Materials, 2018, 11(5), 735 CrossRef PubMed.
- Y. Tan, J. Zhang, Y. Wu, C. Wang, V. Koval, B. Shi, H. Ye, R. McKinnon, G. Viola and H. Yan, Unfolding grain size effects in barium titanate ferroelectric ceramics, Sci. Rep., 2015, 5(1), 9953 CrossRef CAS.
- M. Iwamoto, Maxwell–Wagner Effect, in Encyclopedia of Nanotechnology, ed. Bhushan, B., Springer, Netherlands: Dordrecht, 2012, pp 1276–1285 Search PubMed.
- N. T. Taylor, F. H. Davies, S. G. Davies, C. J. Price and S. P. Hepplestone, The Fundamental Mechanism Behind Colossal Permittivity in Oxides, Adv. Mater., 2019, 31(51), 1904746 CrossRef CAS.
- M. Nolan, Charge Compensation and Ce3+ Formation in Trivalent Doping of the CeO2(110) Surface: The Key Role of Dopant Ionic Radius, J. Phys. Chem. C, 2011, 115(14), 6671–6681 CrossRef CAS.
- I. Marri and S. Ossicini, Oxygen vacancy effects on the Schottky barrier height at the Au/TiO2(110) interface: A first principle study, Solid State Commun., 2008, 147(5), 205–207 CrossRef CAS.
- C. Funck and S. Menzel, An atomistic view on the Schottky barrier lowering applied to SrTiO3/Pt contacts, AIP Adv., 2019, 9(4), 5116 Search PubMed.
- M. Hellenbrand, B. Bakhit, H. Dou, M. Xiao, M. O. Hill, Z. Sun, A. Mehonic, A. Chen, Q. Jia, H. Wang and J. L. MacManus-Driscoll, Thin film design of amorphous hafnium oxide nanocomposites enabling strong interfacial resistive switching uniformity, Sci. Adv., 2023, 9(25), eadg1946 CrossRef CAS.
- J. Zhang, H. Zhao, F. Wei, M. Yang, Z. Yang, Q. Chen and J. Chen, Resistive switching behaviour of highly epitaxial CeO2 thin film for memory application, Phys. Status Solidi RRL, 2014, 8(1), 95–99 CrossRef CAS.
- M. Hellenbrand, B. Bakhit, H. Dou, M. Xiao, M. O. Hill, Z. Sun, A. Mehonic, A. Chen, Q. Jia and H. Wang, Thin film design of amorphous hafnium oxide nanocomposites enabling strong interfacial resistive switching uniformity, Sci. Adv., 2023, 9(25), eadg1946 CrossRef CAS PubMed.
- P. Gonon and F. El Kamel, High-density capacitors based on amorphous BaTiO3 layers grown under hydrogen containing atmosphere, Appl. Phys. Lett., 2007, 90(23), 2902 CrossRef.
- K. Gelderman, L. Lee and S. W. Donne, Flat-Band Potential of a Semiconductor: Using the Mott–Schottky Equation, J. Chem. Educ., 2007, 84(4), 685 CrossRef CAS.
- A. Hankin, F. E. Bedoya-Lora, J. C. Alexander, A. Regoutz and G. H. Kelsall, Flat band potential determination: avoiding the pitfalls, J. Mater. Chem. A, 2019, 7(45), 26162–26176 RSC.
- R. E. Cohen, Origin of ferroelectricity in perovskite oxides, Nature, 1992, 358(6382), 136–138 CrossRef CAS.
- A. J. Fletcher and K. M. Thomas, Compensation Effect for the Kinetics of Adsorption/Desorption of Gases/Vapors on Microporous Carbon Materials, Langmuir, 2000, 16(15), 6253–6266 CrossRef CAS.
- R. K. Agrawal, On the compensation effect, J. Therm. Anal., 1986, 31(1), 73–86 CrossRef CAS.
- A. K. Galwey, Compensation Effect in Heterogeneous Catalysis, in Advances in Catalysis, ed. Eley, D. D., Pines, H. and Weisz, P. B., Academic Press, 1977, vol. 26, pp. 247–322 Search PubMed.
- D. Mardare, A. Yildiz, R. Apetrei, P. Rambu, D. Florea, N. G. Gheorghe, D. Macovei, C. M. Teodorescu and D. Luca, The Meyer–Neldel rule in amorphous TiO2 films with different Fe content, J. Mater. Res., 2012, 27(17), 2271–2277 CrossRef CAS.
- H. Schmidt, M. Wiebe, B. Dittes and M. Grundmann, Meyer-Neldel rule in ZnO, Appl. Phys. Lett., 2007, 91(23), 2110 CrossRef.
- R. Metselaar and G. Oversluizen, The meyer-neldel rule in semiconductors, J. Solid State Chem., 1984, 55(3), 320–326 CrossRef CAS.
- O. Engstrom, Compensation effects at electron traps in semiconductors, Monatsh. Chem., 2013, 144(1), 73–82 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02865a |
| This journal is © The Royal Society of Chemistry 2024 |