Computational discovery of stable Na-ion sulfide solid electrolytes with high conductivity at room temperature

Abstract

The search for inorganic solid electrolytes suitable for the realization of solid-state batteries with structural stability and high ion conductivity at room temperature remains a significant challenge. In this study, we employed a multi-stage density functional theory molecular dynamics (DFT-MD) sampling workflow, focusing on Na-ion sulfides with trivalent (M) and pentavalent (M′) metal ions and an expanded selection of parent structures (Ω). This led to the identification of two promising sampling spaces (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄). The predictions were validated through multi-temperature DFT-MD calculations, wherein σ_Na,300K ≳ 10⁻³ S cm⁻¹ are attained within a thermodynamic phase stability range of 9 < E_hull < 25 meV per atom (E_hull is convex hull decomposition energy): Na₄Ga_0.5P_0.5S₄, Na_3.75Ga_0.375P_0.625S₄, Na_4.25Ga_0.625P_0.375S₄, Na_3.75Si_0.75Ta_0.25S₄, Na_3.625Si_0.625Ta_0.375S₄, and Na_3.5Si_0.5Ta_0.5S₄. These compounds are highly suggested for experimental synthesis and investigation. Moreover, our brute-force and highly generalized sampling technique is expected to be applicable in uncovering other solid electrolyte classes, thus potentially contributing to the advancement of solid-state battery technology.

---

The quest to identify inorganic solid electrolytes (SEs) suited for solid-state batteries, characterized by structural stability, including experimental synthesizability and high ion conductivity at room temperature, remains a longstanding challenge. Among the various classes of solid electrolytes under investigation, Na-ion sulfides have recently gained significant attention. This increased interest can be attributed to the abundant presence of Na in the earth's crust and excellent mechanical performance while interfacing with active electrodes, such as formability, processability, and low elastic moduli.^1–4 Moreover, the discovery of the high room-temperature Na-ion conductivity σ_Na,300K = 3.2 × 10⁻² S cm⁻¹ in Na_2.88Sb_0.88W_0.12S₄ underscores the potential for further advancements in the material search in this class,⁵ with other notable series.^3,6–10

While numerous high-throughput sampling techniques have been rigorously developed for the material search of SEs,^11–14 we built our own multi-stage density functional theory molecular dynamics (DFT-MD) sampling workflow in a bid to efficiently find stable Na-ion sulfides with high σ_Na,300K as demonstrated in our previous study.¹⁵ Encompassing various ions [M and M′ denote two distinct metal ions characterized by varying valence states, denoted as ν(M) and ν(M′), respectively, and n, m, and m′ are the contents of Na-, M-, and M′-ions, respectively] while maintaining parent structures Ω (given by Na_nΩM_mS₄; n_Ω is the content of Na ions in the structure), our analysis yielded that a significant proportion of several promising candidates with σ_Na,300K > 10⁻³ S cm⁻¹ features ν(M) = 3 and ν(M′) = 5, M = Si with ν(M) = 4, and M = Ta with ν(M′) = 5.

In this study, leveraging the methodology and knowledge from our previous study,¹⁵ we aim to expand the scope of candidate parent structures Ω considering the promising combinations of (M,M′), freeing Ω from a direct association with M (Ω = Na_nΩM_ΩS₄; M_Ω is the host metal ion for Ω, not necessarily being M). This new approach will broaden the exploration scope for material space, thereby enhancing the efficiency of identifying uncharted but synthesizable materials possessing superior target properties such as σ_Na,300K. Our objective was to investigate whether (M,M′) may exhibit increased stability in different polymorphs. Initially, we thoroughly explored the material space (M,M′,Ω) while maintaining a fixed value of m = m′ = 0.5 for 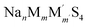: 112 cases of (M,M′,Ω) in total. This selection, driven by the maximization of mixing entropy, resulted in the attainment of the highest value of σ_Na,300K as reported in the preceding study.¹⁵ Within this framework, we identified two stable sampling spaces (Si,Ta,Na₄SiS₄) and (Ga,P,Na₄SiS₄), both showing high promise for σ_Na,300K. Subsequently, we extended our exploration by varying the values of m and m′ within (Si,Ta,Na₄SiS₄) and (Ga,P,Na₄SiS₄). This expanded approach resulted in the discovery of crystal structures with not only promising σ_Na,300K but also significantly decreased convex hull decomposition energy per atom E_hull, thereby greatly improving our ability to predict stable crystal frameworks Ω capable of accommodating M and M′.

Sampling protocol

We established a sampling protocol, illustrated in Fig. 1, and briefly outlined here, with further details provided in Discussion S1.† The sampling space (M,M′,Ω) encompasses combinations of trivalent M (Al, Ga, and In), pentavalent metal ions M′ (P, V, Nb, Sb, and Ta), as well as (M,M′) = (Si,Ta), and seven different Ω, namely Na₅AlS₄,^10,16 with which Na₅GaS₄ is isostructural,¹⁷ Na₅InS₄,¹⁸ Na_4.5Al_0.5Si_0.5S₄,¹⁰ Na₄SiS₄,^6,10,19,20 Na₄SnS₄,^7,9,21 Na₃VS₄,^8,22,23 and Na₃SbS₄.^5,24–26 Initially, we generated a substantial number of random site arrangements for supercells to represent (M,M′,Ω), resulting in a total dataset size of n_data = 5, 290, 074, 920. From these arrangements, we selected fewer than six with the lowest Ewald coulombic energies E_Ewald for each (M,M′,Ω): n_data = 469.^27–29 In the subsequent step of DFT geometry optimizations, we fully relaxed the site positions and lattice parameters for the selected arrangements. The cell structure with the lowest DFT energy E_DFT, or equivalently, the lowest E_hull, was identified to determine the most suitable Ω for (M,M′): n_data = 16. Then, we conducted a DFT-MD sampling, named the single-temperature “long-time” diagnosis, for the selected (M,M′,Ω), estimating (represented as σ_Na,300K values in this step). This was achieved by performing DFT-MD calculations with a time step of τ = 1 fs over a simulation time of τ = 250 ps at a constant temperature of T = 300 K. Two criteria were applied for selecting promising samples: E_hull < 25 meV per atom, which is comparable to the case of Li₁₀GeP₂S₁₂ (E_hull = 19 meV per atom),³⁰ and 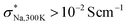. Based on these criteria, we selected two sampling spaces, namely (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄), for further analysis in the multi-temperature diagnosis.

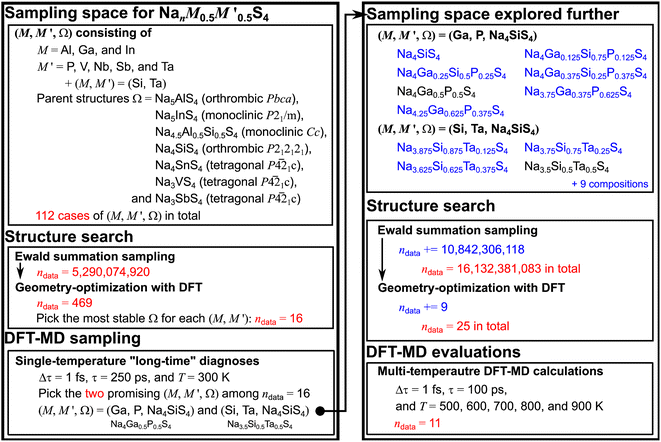Fig. 1 Sampling protocol to identify stable Na-ion sulfide solid electrolytes with high conductivity at room temperature. The protocol comprises two parts: sampling for and further sampling within two material space (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄) (For denotations, please refer to the main text. Details are provide in Discussion S1.†).

Next, we employed 11 compositions with varying m (and correspondingly, m′) for (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄) by adding 9 compositions (Na₄SiS₄, Na₄Ga_0.125Si_0.75P_0.125S₄, Na₄Ga_0.25Si_0.5P_0.25S₄, Na₄Ga_0.375Si_0.125P_0.375S₄, Na_3.75Ga_0.375P_0.625S₄, Na_4.25Ga_0.625P_0.375S₄, Na_3.875Si_0.875Ta_0.125S₄, Na_3.75Si_0.75Ta_0.25S₄, and Na_3.625Si_0.625Ta_0.375S₄) to the existing 2 compositions (Na₄Ga_0.5P_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄). The same procedure for the structure search was executed again. We generated a substantial number of random site arrangements for these supercells by adding a dataset size of n_data = 10, 842, 306, 118 for the 9 compositions. From these arrangements, we selected the lowest E_Ewald case for each composition by adding n_data = 9.^27–29 In the subsequent step of DFT geometry optimizations, we fully relaxed the site positions and lattice parameters for the selected arrangements. Then, we estimated σ_Na,300K and Na-ion activation energies E_a by performing DFT-MD simulations with τ = 1 fs and τ = 100 ps at different temperatures T = 500, 600, 700, 800, and 900 K.

Promising material spaces

The results of the geometry optimizations for and Na_3.5Si_0.5Ta_0.5S₄ are presented in Table 1. Among the various combinations of M and M′, it was observed that M = Al or Ga, Ω = Na₄SiS₄ tends to be the most stable, except for M′ = Sb, in which Ω = Na₄SnS₄ appeared to be more stable. Notably, with M = In, stability was exclusively observed in Ω = Na₄SnS₄. In terms of the calculated E_hull values, the majority of the optimized cell structures exhibited E_hull < 25 meV per atom, with a few exceptions, such as Na₄In_0.5P_0.5S₄ (E_hull = 30.8 meV per atom), Na₄In_0.5V_0.5S₄ (E_hull = 35.9 meV per atom), and Na₄In_0.5Ta_0.5S₄ (E_hull = 26.0 meV per atom). Additional cases of Ω are provided in Table S1.† Furthermore, the results from the single-temperature “long-time” diagnosis indicated that Na₄Ga_0.5P_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄ meet E_hull < 25 meV per atom and .

Table 1 Lattice constants a, b, and c, unit cell volumes V, and convex hull decomposition energies per atom E_hull for 16 compositions and Na_3.5Si_0.5Ta_0.5S₄ whose structures were relaxed by using DFT with parent structures Ω that stabilized most (giving the lowest E_hull for each composition). The two compositions satisfying E_hull < 25 meV per atom and are boldened: Na₄Ga_0.5Ta_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄. Lattice constants α, β, and γ were close to 90°. In the first row, the compositions per unit cell are presented in parentheses. In the last row, the room-temperature Na-ion conductivities are presented, which were estimated by performing the single-temperature “long-time” diagnosis with τ = 1 fs, τ = 250 ps, and T = 300 K, and “—” denotes the absence of observed Na-ion migrations)

Composition	Ω	a (Å)	b (Å)	c (Å)	V (Å^3)	E hull (meV per atom)
Na4Al0.5P0.5S4 (Na96Al12P12S96)	Na4SiS4	41.87	8.917	13.86	5174	14.6	4.10 × 10^−3
Na4Al0.5V0.5S4 (Na96Al12V12S96)	Na4SiS4	41.90	8.780	14.08	5181	16.8	3.25 × 10^−3
Na4Al0.5Nb0.5S4 (Na96Al12Nb12S96)	Na4SiS4	42.20	8.951	14.15	5346	17.2	—
Na4Al0.5Sb0.5S4 (Na96Al12Sb12S96)	Na4SnS4	15.74	15.74	13.86	3434	13.9	1.52 × 10^−3
Na4Al0.5Ta0.5S4 (Na96Al12Ta12S96)	Na4SiS4	42.23	8.954	14.14	5346	19.4	—
Na 4 Ga 0.5 P 0.5 S 4 (Na 96 Ga 12 P 12 S 96 )	Na 4 SiS 4	41.76	8.977	13.87	5201	15.8	1.03 × 10 ^−2
Na4Ga0.5V0.5S4 (Na96Ga12V12S96)	Na4SiS4	42.02	8.807	14.05	5200	17.3	3.04 × 10^−3
Na4Ga0.5Nb0.5S4 (Na96Ga12Nb12S96)	Na4SiS4	42.24	8.989	14.13	5366	17.7	1.10 × 10^−3
Na4Ga0.5Sb0.5S4 (Na96Ga12Sb12S96)	Na4SnS4	15.76	15.76	13.90	3449	15.5	3.73 × 10^−4
Na4Ga0.5Ta0.5S4 (Na96Ga12Ta12S96)	Na4SiS4	42.30	8.997	14.11	5369	19.7	2.35 × 10^−4
Na4In0.5P0.5S4(Na96In12P12S96)	Na4SnS4	15.93	15.93	13.65	3464	30.8	1.66 × 10^−3
Na4In0.5V0.5S4 (Na96In12V12S96)	Na4SnS4	15.83	15.83	13.82	3464	35.9	5.16 × 10^−5
Na4In0.5Nb0.5S4 (Na96In12Nb12S96)	Na4SnS4	15.84	15.84	13.97	3503	23.5	8.41 × 10^−3
Na4In0.5Sb0.5S4 (Na96In12Sb12S96)	Na4SnS4	15.92	15.92	13.96	3536	17.4	—
Na4In0.5Ta0.5S4 (Na96In12Ta12S96)	Na4SnS4	15.85	15.85	13.97	3507	26.0	2.44 × 10^−5
Na 3.5 Si 0.5 Ta 0.5 S 4 (Na 84 Si 12 Ta 12 S 96 )	Na 4 SiS 4	41.65	8.937	14.08	5241	24.1	3.34 × 10 ^−2

---

As illustrated in our previous study, 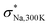is limited by the short timescale for site-to-site jumps at low T, however, it serves as a computationally efficient metric for identifying promising candidates with high σ_Na,300K.¹⁵ Besides, in our previous study, given the fixed v(M) and v(M′), we identified two key descriptors for achieving high σ_Na,300K: the average widest Na–3S solid angle max(Ω_NaSx) for NaS_x polyhedra and the average Na–S bond length d_Na–S.¹⁵ These descriptors with high values would facilitate the release of self-diffusing Na-ions from the cages of NaS_x. Notably, Na₄Ga_0.5P_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄ exhibit high values for not only but also max(Ω_NaSx) and d_Na–S (see Fig. 2), indicating their potential for excellent σ_Na,300K. Based on these observations, our focus shifted towards investigating (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄) with varying m.

Fig. 2 Average widest Na–3S solid angles max(Ω_NaSx) for polyhedra NaS_x and average Na–S bond lengths d_Na–S for 16 compositions and Na_3.5Si_0.5Ta_0.5S₄ whose structures were relaxed by using DFT with parent structures Ω that stabilized most (giving the lowest E_hull for each composition). Each composition is denoted by M and M′, and 9 (7) compositions in the high (low) region of d_Na–S have Ω = Na₄SiS₄ (Na₄SnS₄). The red dots represent the cases of Na₄Ga_0.5P_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄ with high values of both max(Ω_NaSx) and d_Na–S.

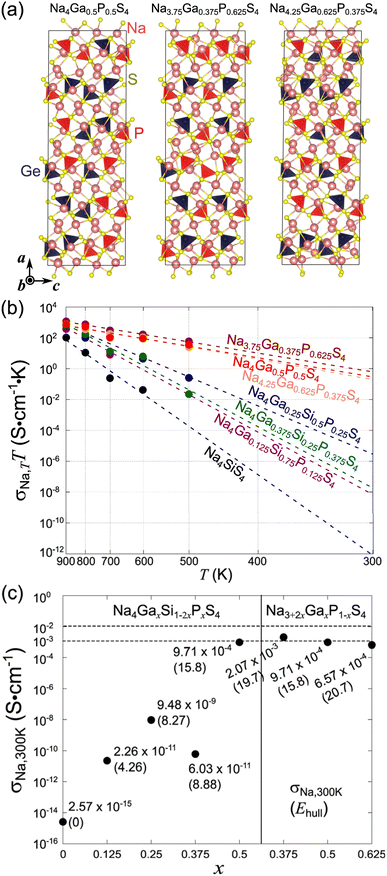
The outcomes of the geometric optimizations conducted for the 11 compositions across (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄) are presented in Table 2 as well. It is noteworthy that a decrease in the Si content (that is, the deviation from Ω) results in an increase in the value of E_hull. For all the investigated compositions, E_hull remains below 25 meV per atom, signifying their structural (meta)stability and the feasibility of their synthesis. We represent several examples of the visualized crystal structures in Fig. 3a and 4a. In addition, their bandgap energies E_g, a metric for electron-insulating properties, exhibited high values: around 3 eV for most cases.

Table 2 Lattice constants a, b, and c, unit cell volumes V, convex hull decomposition energies per atom E_hull, and bandgap energies E_g for the 11 compositions adopted in the multi-temperature diagnosis. Lattice constants α, β, and γ were close to 90°. The parent structures p were set to Na₄SiS₄ for all the cases. In the first row, the compositions per unit cell are presented in parentheses

Composition	a (Å)	b (Å)	c (Å)	V (Å^3)	E hull (meV per atom)	E g (eV)
Na4SiS4 (Na96Si24S96)	41.61	8.791	13.88	5077	0	4.03
Na4Ga0.125Si0.75P0.125S4 (Na96Ga3Si18P3S96)	41.71	8.820	13.88	5106	4.26	2.98
Na4Ga0.25Si0.5P0.25S4 (Na96Ga6Si12P6S96)	41.86	8.843	13.87	5136	8.27	3.12
Na4Ga0.375Si0.25P0.375S4 (Na96Ga9Si6P9S96)	41.60	8.912	13.88	5145	8.88	3.12
Na4Ga0.5P0.5S4 (Na96Ga12P12S96)	41.76	8.977	13.87	5201	15.8	2.44
Na3.75Ga0.375P0.625S4 (Na90Ga9P15S96)	40.81	8.953	13.93	5091	19.7	3.00
Na4.25Ga0.625P0.375S4 (Na102Ga15P9S96)	42.21	8.996	13.98	5308	20.7	2.92
Na3.875Si0.875Ta0.125S4 (Na93Si21Ta3S96)	41.66	8.782	13.95	5102	5.20	3.03
Na3.75Si0.75Ta0.25S4 (Na90Si18Ta6S96)	41.75	8.782	14.00	5134	9.26	3.02
Na3.625Si0.625Ta0.375S4 (Na87Si15Ta9S96)	41.77	8.767	14.10	5134	14.7	2.70
Na3.5Si0.5Ta0.5S4 (Na84Al12Ta12S96)	41.65	8.937	14.08	5241	24.1	2.85

---

Fig. 3 (a) Crystal structures of Na₄Ga_0.5P_0.5S₄, Na_3.75Ga_0.375P_0.625S₄, and Na_4.25Ga_0.625P_0.375S₄, (b) Arrhenius plots in the σ_Na,TT–T domain, and (c) σ_Na,300K values extrapolated in (b) for the seven samples within (M,M′,Ω) = (Ga,P,Na₄SiS₄): Na₄SiS₄, Na₄Ga_0.125Si_0.75P_0.125S₄, Na₄Ga_0.25Si_0.5P_0.25S₄, Na₄Ga_0.375Si_0.25P_0.375S₄, Na₄Ga_0.5P_0.5S₄, Na_3.75Ga_0.375P_0.625S₄, and Na_4.25Ga_0.625P_0.375S₄. In (c), convex hull decomposition energies per atom E_hull in meV per atom are also represented in parentheses.

Fig. 4 (a) Crystal structures for Na_3.75Si_0.75Ta_0.25S₄, Na_3.625Si_0.625Ta_0.375S₄, and Na_3.5Si_0.5Ta_0.5S₄, (b) Arrhenius plots in the σ_Na,TT–T domain, and (c) σ_Na,300K values extrapolated in (b) for the five samples within (M,M′,Ω) = (Si,Ta,Na₄SiS₄): Na₄SiS₄, Na_3.875Si_0.875Ta_0.125S₄, Na_3.75Si_0.75Ta_0.25S₄, Na_3.625Si_0.625Ta_0.375S₄, and Na_3.5Si_0.5Ta_0.5S₄. In (c), convex hull decomposition energies per atom E_hull in meV per atom are also represented in parentheses.

In Table S2,† we provide the values for σ_Na,T and D_Na,T obtained through multi-temperature DFT-MD calculations for (M,M′,Ω) = (Ga,P,Na₄SiS₄). Furthermore, in Fig. S1a–g,† we present mean squared displacement (MSD) curves, most of which exhibit linear responses against the sampled time intervals τ_MSD. As indicated in their insets, the trajectories at T = 500 K showed limited interconnectivity until the Si-ion content becomes zero. The interconnected trajectories, indicative of site-to-site jumps, are noticeable in Na₄Ga_0.5P_0.5S₄, Na_3.75Ga_0.375P_0.625S₄, and Na_4.25Ga_0.625P_0.375S₄. This observed trend is also reflected in the Arrhenius plot, where we estimated the interpolated E_a and the extrapolated σ_Na,300K (see Fig. 3b). For these three samples, E_a was suppressed to less than 350 meV, while σ_Na,300K either exceeded or remained around 10⁻³ S cm⁻¹. We note that a possible explanation of an order of magnitude discrepancy between and σ_Na,300K ≈ 10⁻³ S cm⁻¹ for Na₄Ga_0.5P_0.5S₄ is the insufficient timescale for site-to-site jumps considered in 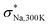. It is noteworthy that a decrease in the Na-ion content, as seen in Na_3.75Ga_0.375P_0.625S₄, resulted in a suppression of E_a and an enhancement of σ_Na,300K, likely due to the creation of the additional free space for Na-ion self-diffusions. As illustrated in Fig. 3c, achieving σ_Na,300K ≳ 10⁻³ S cm⁻¹ for (M,M′,Ω) = (Ga,P,Na₄SiS₄) would be realized at the expense of decreased phase stability (15 < E_hull < 21 meV per atom, which are relative to zero decomposition energy of the pristine structure Ω): Na₄Ga_0.5P_0.5S₄, Na_3.75Ga_0.375P_0.625S₄, and Na_4.25Ga_0.625P_0.375S₄.

In Table S2,† we also provide the values for σ_Na,T and D_Na,T obtained through multi-temperature DFT-MD calculations for (M,M′,Ω) = (Si,Ta,Na₄SiS₄). Additionally, in Fig. S2a–d,† we present linear MSD curves against τ_MSD. As indicated in their insets, even at T = 500 K, trajectories exhibited interconnectivity, even for the relatively low doping levels of the Ta-ion. Notably, the interconnected features were predominantly observed around Ta-ions, wherein Na vacancies exist. This trend is reflected in the Arrhenius plot (see Fig. 4b). For instance, in the case of Na_3.875Si_0.875Ta_0.125S₄, E_a = 413 meV and σ_Na,300K = 4.93 × 10⁻⁵ S cm⁻¹ were estimated. Furthermore, with an increase in the Ta-ion doping level (or a decrease in the Na-ion content), E_a was further suppressed, accompanied by an enhancement of σ_Na,300K. In the case of Na_3.5Si_0.5Ta_0.5S₄, E_a = 215 meV and σ_Na,300K = 1.35 × 10⁻² S cm⁻¹ were estimated. As illustrated in Fig. 4c, achieving σ_Na,300K ≳ 10⁻³ S cm⁻¹ for (M,M′,Ω) = (Si,Ta,Na₄SiS₄) would be realized at the expense of decreased phase stability (9 < E_hull < 25 meV per atom): Na_3.75Si_0.75Ta_0.25S₄, Na_3.625Si_0.625Ta_0.375S₄, and Na_3.5Si_0.5Ta_0.5S₄. The high values of σ_Na,300K ≳ 10⁻³ S cm⁻¹ for Na₄Ga_0.5P_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄ partly justify the use of m = m′ = 0.5 in the initial step of the sampling protocol. We also discuss the electrochemical stability windows for the 11 compositions in the Discussion S2.†

Descriptors for convex hull decomposition energy

We established a multivariate linear regression model to discern descriptors influencing E_hull, leveraging a dataset of given in the structure search step, encompassing various Ω = Na_nΩM_ΩS₄; the data are presented in Table S1† (n_data = 110). The proposed model comprises three descriptors:

The model exhibits a substantial R²-value (R² = 0.711) and an F-value of 87.0 with a significantly low p-value (p < 0.001), while all t-tests for the constant term and the three coefficients revealed p < 0.001. The variance inflation factors (VIF) were sufficiently small, indicating an absence of multicollinearity issues: VIF = 1.02, 1.06, and, 1.08 for the first, second, and third coefficients, respectively. Here, r(M) denotes the Shannon ionic radius for a metal ion M.^31,32 The data plot for this model is presented in Fig. 5.

Fig. 5 Data plot for the multivariate regression model against E_hull calculated by using DFT (presented in Table S1†) with a substantial R²-value (R² = 0.711). For the model, eqn (1) was adopted with n_data = 110.

The first term n − n_Ω suggests that E_hull would increase if the Na-ion sites are added (rather than omitted) during structural modifications from the pristine Ω. The second term suggests that E_hull would increase when the average valence for M and M′ deviates from that of M_Ω. The third term 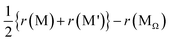suggests that E_hull would increase with a larger average ionic radius for M and M′ compared to that of M_Ω. In light of these findings, two sampling spaces, namely (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄), with high σ_Na,300K, are deemed appealing for experimental realizations. For Na₄Ga_0.5P_0.5S₄ with E_hull = 15.8 meV per atom, it is given that n − n_Ω = 0, 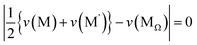, and . Similarly, for Na_3.5Si_0.5Ta_0.5S₄E_hull = 24.1 meV per atom, it is given that n − n_Ω = −0.5, , and . The numerical analyses elucidate that a combination of Ga, P, and Ta would constitute an appropriate blend for the parent structure Na₄SiS₄.

Summary and outlook

In this study, we employed the multi-stage sampling protocol¹¹ to identify promising Na-ion sulfides characterized by high σ_Na,300K within the constraints of limited choices for M and M′, but with an expanded selection of parent structures Ω to effectively pinpoint unexplored yet synthesizable materials with superior conductivity σ_Na,300K. Our approach began with the identification of Ω that stabilizes each combination of (M,M′) most. Subsequently, circumventing the tedious tasks of the exhaustive access for the sampling spaces, we efficiently predicted that (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄), characterized by wide max(Ω_NaSx) and long d_Na–S, have the potential to achieve high σ_Na,300K through the single-temperature “long-time” diagnosis.

These predictions were subsequently validated through multi-temperature DFT-MD calculations. Notably, σ_Na,300K ≳ 10⁻³ S cm⁻¹ were attainable within a range of 9 < E_hull < 25 meV per atom: Na₄Ga_0.5P_0.5S₄, Na_3.75Ga_0.375P_0.625S₄, Na_4.25Ga_0.625P_0.375S₄, Na_3.75Si_0.75Ta_0.25S₄, Na_3.625Si_0.625Ta_0.375S₄, and Na_3.5Si_0.5Ta_0.5S₄. Based on our observations, we expect that the co-doping of Ga, P, and Ta into the parent structure Na₄SiS₄, leading to the formation of compositions Na_4+g−p−tGa_gSi_{1−g−p−t}P_pTa_tS₄, would present an intriguing avenue for further investigation in future studies. The limitation of this study should be noted also; although σ_Na,300K were optimized at m = m′ = 0.5, as observed in Na₄Ga_0.5P_0.5S₄ and Na_3.5Si_0.5Ta_0.5S₄, other choices of m (m′) in the initial step of the sampling protocol are worth exploring. Future studies should assess these alternatives.

We believe that these two identified sampling spaces, characterized by both thermodynamic stability and fast Na-ion conductivity, warrant further experimental investigations. Additionally, this brute-force sampling technique has the potential to explore other classes of solid electrolytes, which could be pivotal in the ongoing advancement of solid-state battery technology.

Data availability

Data for this article, including crystal structures and molecular dynamics results for (M,M′,Ω) = (Ga,P,Na₄SiS₄) and (Si,Ta,Na₄SiS₄) are available at github at https://github.com/JerryGarcia1995/NasulfidesExt. The data supporting this article have been included as part of the ESI† as well.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported in part by MEXT as “Program for Promoting Research on the Supercomputer Fugaku” grant number JPMXP1020230325, Data Creation and Utilization Type Material Research and Development Project grant number JPMXP1122712807 and Materials Processing Science project (“Materealize”) grant number JPMXP0219207397, and by JSPS KAKENHI grant numbers JP21K14729 and JP24H02203, as well as JST through ALCA-SPRING grant number JPMJAL1301, COI-NEXT grant number JPMJPF2016, and GteX Program Japan grant number JPMJGX23S4. The calculations were performed on the supercomputers at NIMS (Numerical Materials Simulator) and the supercomputer Fugaku at the RIKEN through the HPCI System Research Project (project IDs: hp230154 and hp230205). Visualization for crystal structures was made with the VESTA software.³³ Plots were generated using gnuplot 5.4.³⁴

References

1. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Research Development on Sodium-Ion Batteries, Chem. Rev., 2014, 114(23), 11636–11682,  DOI:10.1021/cr500192f.
2. H. Pan, Y.-S. Hu and L. Chen, Room-Temperature Stationary Sodium-Ion Batteries for Large-Scale Electric Energy Storage, Energy Environ. Sci., 2013, 6(8), 2338–2360,  10.1039/c3ee40847g.
3. A. Hayashi, A. Sakuda and M. Tatsumisago, Development of Sulfide Solid Electrolytes and Interface Formation Processes for Bulk-Type All-Solid-State Li and Na Batteries, Front. Energy Res., 2016, 4, 25,  DOI:10.3389/fenrg.2016.00025.
4. F. Li, Z. Wei, A. Manthiram, Y. Feng, J. Ma and L. Mai, Sodium-Based Batteries: From Critical Materials to Battery Systems, J. Mater. Chem. A, 2019, 7(16), 9406–9431,  10.1039/c8ta11999f.
5. A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, A Sodium-Ion Sulfide Solid Electrolyte with Unprecedented Conductivity at Room Temperature, Nat. Commun., 2019, 10(1), 5266,  DOI:10.1038/s41467-019-13178-2.
6. N. Tanibata, K. Noi, A. Hayashi and M. Tatsumisago, Preparation and Characterization of Highly Sodium Ion Conducting Na₃PS₄–Na₄SiS₄ Solid Electrolytes, RSC Adv., 2014, 4(33), 17120–17123,  10.1039/c4ra00996g.
7. J. W. Heo, A. Banerjee, K. H. Park, Y. S. Jung and S. Hong, New Na-Ion Solid Electrolytes Na_4-xSn_1-xSb_xS₄ (0.02 ≤ x ≤ 0.33) for All-Solid-State Na-Ion Batteries, Adv. Energy Mater., 2018, 8(11), 1702716,  DOI:10.1002/aenm.201702716.
8. Y. He, F. Lu and X. Kuang, Enhanced Sodium Ion Conductivity in Na₃VS₄ by P-Doping, RSC Adv., 2019, 9(67), 39180–39186,  10.1039/c9ra08900d.
9. S. Xiong, Z. Liu, L. Yang, Y. Ma, W. Xu, J. Bai and H. Chen, Anion and Cation Co-Doping of Na₄SnS₄ as Sodium Superionic Conductors, Mater. Today Phys., 2020, 15, 100281–100288,  DOI:10.1016/j.mtphys.2020.100281.
10. S. Harm, A. Hatz, C. Schneider, C. A. Hoefer, C. Hoch and B. V. Lotsch, Finding the Right Blend: Interplay between Structure and Sodium Ion Conductivity in the System Na₅AlS₄-Na₄SiS₄, Front. Chem., 2020, 8, 90,  DOI:10.3389/fchem.2020.00090.
11. Z. Zhu, I.-H. Chu and S. P. Ong, Li₃Y(PS₄)₂ and Li₅PS₄Cl₂: New Lithium Superionic Conductors Predicted from Silver Thiophosphates using Efficiently Tiered Ab Initio Molecular Dynamics Simulations, Chem. Mater., 2017, 29(6), 2474–2484,  DOI:10.1021/acs.chemmater.6b04049.
12. A. D. Sendek, Q. Yang, E. D. Cubuk, K.-A. N. Duerloo, Y. Cui and E. J. Reed, Holistic Computational Structure Screening of More Than 12000 Candidates for Solid Lithium-Ion Conductor Materials, Energy Environ. Sci., 2017, 10, 306–320,  10.1039/C6EE02697D.
13. S. Muy, J. Voss, R. Schlem, R. Koerver, S. J. Sedlmaier, F. Maglia, P. Lamp, W. G. Zeier and S.-H. Yao, High-Throughput Screening of Solid-State Li-Ion Conductors Using Lattice-Dynamics Descriptors, iScience, 2019, 16, 270–282,  DOI:10.1016/j.isci.2019.05.036.
14. R. Jalem, Y. Tateyama, K. Takada and S.-H. Jang, Multiobjective Solid Electrolyte Design of Tetragonal and Cubic Inverse-Perovskites for All-Solid-State Lithium-Ion Batteries by High-Throughput Density Functional Theory Calculations and AI-Driven Methods, J. Phys. Chem. C, 2023, 127(35), 17307–17323,  DOI:10.1021/acs.jpcc.3c02801.
15. S.-H. Jang, Y. Tateyama and R. Jalem, High-Throughput Data-Driven Prediction of Stable High-Performance Na-Ion Sulfide Solid Electrolytes, Adv. Funct. Mater., 2022, 32(48), 2206036,  DOI:10.1002/adfm.202206036.
16. A. Brown and B. Tani, Powder X-Ray Diffraction Identification of Some New Phases in the Na₂S-Al₂S₃ System, Mater. Res. Bull., 1987, 22(8), 1029–1037,  DOI:10.1016/0025-5408(87)90231-5.
17. S. Balijapelly, P. Sandineni, A. Adhikary, N. Gerasimchuk, A. V. Chernatynskiy and A. Choudhury, Ternary Alkali Ion Thiogallates, A₅GaS₄ (A = Li and Na), with Isolated Tetrahedral Building Units and Their Ionic Conductivities, Dalton Trans., 2021, 50(21), 7372–7379,  10.1039/d1dt00766a.
18. B. Eisenmann and A. Hofmann, Crystal Structure of Pentasodium Tetrathioindate(III), Na5InS4, Z. Kristallogr. – Cryst. Mater., 1991, 197(1–2), 169–170,  DOI:10.1524/zkri.1991.197.1-2.169.
19. N. Tanibata, K. Noi, A. Hayashi, N. Kitamura, Y. Idemoto and M. Tatsumisago, X-Ray Crystal Structure Analysis of Sodium-Ion Conductivity in 94Na₃PS₄·6Na₄SiS₄ Glass-Ceramic Electrolytes, ChemElectroChem, 2014, 1(7), 1130–1132,  DOI:10.1002/celc.201402016.
20. N. Tanibata, A. Hayashi and M. Tatsumisago, Improvement of Rate Performance for All-Solid-State Na₁₅Sn₄/Amorphous TiS₃ Cells Using 94Na₃PS₄·6Na₄SiS₄ Glass-Ceramic Electrolytes, J. Electrochem. Soc., 2015, 162(6), A793–A795,  DOI:10.1149/2.0011506jes.
21. J.-C. Jumas, E. Philippot, F. Vermot-Gaud-Daniel, M. Ribes and M. Maurin, Etude de la tétracoordination de l’etain dans deux orthothiostannates: Na₄SnS₄ et Ba₂SnS₄ (α), J. Solid State Chem., 1975, 14(4), 319–327,  DOI:10.1016/0022-4596(75)90050-x.
22. M. V. Peskov and V. A. Blatov, Comparative Crystal-Chemical Analysis of d-Metal Sulfides, Selenides, and Tellurides and Binary Compounds, Russ. J. Inorg. Chem., 2006, 51(4), 590–598,  DOI:10.1134/s0036023606040140.
23. K. O. Klepp and G. Gabl, New Complex Sulfides of the VA-Metals: Preparation and Crystal Structure of Na₃VS₄ (With a Note on the Crystal Structure of the Low Temperature Modification of Na₃PO₄), Eur. J. Solid State Inorg. Chem., 1997, 34(10), 1143–1154.
24. H. Graf and H. Schäfer, Zur Strukturchemie der Alkalisalze der Tetrathiosäuren der Elemente der 5. Hauptgruppe, Z. Anorg. Allg. Chem., 1976, 425(1), 67–80,  DOI:10.1002/zaac.19764250109.
25. H. Wang, Y. Chen, Z. D. Hood, G. Sahu, S. P. Amaresh, J. K. Keum, K. An and C. Liang, An Air-Stable Na₃SbS₄ Superionic Conductor Prepared by a Rapid and Economic Synthetic Procedure, Angew. Chem., 2016, 55(30), 8551–8555,  DOI:10.1002/anie.201601546.
26. A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S.-T. Hong and Y. S. Jung, Na₃SbS₄: A Solution Processable Sodium Superionic Conductor for All-Solid-State Sodium-Ion Batteries, Angew. Chem., Int. Ed., 2016, 55(33), 9634–9638,  DOI:10.1002/anie.201604158.
27. P. P. Ewald, Die Berechnung Optischer und Elektrostatischer Gitterpotentiale, Ann. Phys., 1921, 369(3), 253–287,  DOI:10.1002/andp.19213690304.
28. A. Y. Toukmaji and J. A. Board, Ewald Summation Techniques in Perspective: A Survey, Comput. Phys. Commun., 1996, 95(2–3), 73–92,  DOI:10.1016/0010-4655(96)00016-1.
29. S. Jang, R. Jalem and Y. Tateyama, EwaldSolidSolution: A High-Throughput Application to Quickly Sample Stable Site Arrangements for Ionic Solid Solutions, J. Phys. Chem. A, 2023, 127(27), 5734–5744,  DOI:10.1021/acs.jpca.3c00076.
30. K. Persson, Materials Data on Li10Ge(PS6)2 (SG:1) by Materials Project. MaterialsProject, 2016,  DOI:10.17188/1284960, accessed 2024-03-21.
31. R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., 1976, A32, 751–767,  DOI:10.1107/S0567739476001551.
32. A. A. B. Baloch, S. M. Alqahtani, F. Mumtaz, A. H. Muqaibel, S. N. Rashkeev and F. H. Alharbi, Extending Shannon's Ionic Radii Database Using Machine Learning, Phys. Rev. Mater., 2021, 5(4), 043804,  DOI:10.1103/PhysRevMaterials.5.043804.
33. K. Momma and F. Izumi, VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276,  DOI:10.1107/S0021889811038970.
34. T. Williams and C. Kelley, gnuplot 5.4: an Interactive Plotting Programhttp://www.gnuplot.info/docs_5.4/Gnuplot_5_4.pdf, accessed 2023-09-29.

---

Footnote

† Electronic supplementary information (ESI) available: Details of sampling protocol, comprehensive dataset for lattice constants, unit cell volumes, and convex hull decomposition energies for (M,M′,Ω) at m = m′ = 0.5, and the results of the multi-temperature diagnosis. See DOI: https://doi.org/10.1039/d4ta02522a

---