 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy landscapes in alkali aluminum germanium phosphate glasses as probed by alkali proton substitution†
Kevin
Rein
and
Karl-Michael
Weitzel
 *
*
Chemistry Department, Philipps-Universität Marburg, 35032, Marburg, Germany. E-mail: weitzel@chemie.uni-marburg.de
First published on 13th May 2024
Abstract
The transport of native alkali ions in the energy landscape of alkali aluminum germanium phosphate (AAGP) glasses has been investigated by means of an alkali proton substitution (APS) experiment. This energy landscape is demonstrated to be dominated by the network former rather than the identity of the alkali ion. To this end AAGP glasses of composition A1.5Al0.5Ge1.5(PO4)3 with A = Li, Na, K were subjected to APS, leading to a replacement of native alkali ions by foreign protons in a region reaching several 100 nm below the surface of the sample. Quantification of the concentration depth profiles by means of secondary ion mass spectrometry (SIMS) and modelling by means of Nernst–Planck–Poisson transport theory leads to the conclusion that the width of the site energy distributions (SED) only slightly varies from 114 meV, to 122 meV and 126 meV, FWHM, for the LAGP, the NAGP and the KAGP respectively.
Introduction
In recent years one of the pivotal goals in material science has been to elucidate the relation between structure and function of solid materials. Much attention has been given to structural landscapes, implying aspects of morphology, short and long range order as well as surface topology.1,2 However, the relation between structure and function is mediated by energy landscapes.3–5 The discussion of energy landscapes is currently mostly of qualitative nature.6,7 In a perfect single crystal on one hand long range order with periodicities in the spatial domain dominate and all atoms of a chemical kind feel the same site energy and the same energy barrier around them. In a perfectly amorphous solid (here termed a glass) without any long range order a distribution of energy minima (termed sites) and of energy maxima (termed barriers) is operative.3 The fact that a distribution of sites and barriers interrelated with a distribution of activation energies is operative, is clear on conceptual, experimental and theoretical grounds. However, there doesn't appear to be a general consensus on the width of such site energy distributions (SED), not even on the form.Recently the quantification of the populated part of a site energy distribution (PSED) has been demonstrated from charge attachment induced transport experiments (CAIT) combined with secondary ion mass spectrometry (SIMS) and time dependent Nernst–Planck–Poisson analysis (NPP).8–10 Overall, there are now reports on the width of PSEDs ranging from about 100 meV to 300 meV. This appears technically relevant since the relation between effective diffusion coefficients and activation energies is typically of the form D = D0 × exp(−Eact/kBT). This implies that a variation in Eact of 0.3 eV translates at room temperature into a variation in the effective D of more than 4 orders of magnitude.
In this work we present the results of a systematic investigation of a series of glasses with common glass network but differing in the mobile alkali ion, i.e. the network modifier. The goal is to elaborate how large the influence of the network modifier is on the potential energy landscape of the material. In searching for a suitable chemical system several conditions need to be fulfilled. First, the material must be chemically stable for several alkali ions, it must be possible to prepare those materials as a glass and finally it must be possible to polish the samples to a surface roughness on the order of a few nm. Here, we chose the alkali aluminum germanium phosphate system, A1.5Al0.5Ge1.5(PO4)3 A = (Li–Cs) for which we reported DC ion conductivities and activation energies for alkali ion transport in previous work.11 These glasses can be considered to be derived from the NASICON (sodium super ion conductors) class of materials.12 The eponymous material is the Na1+xZr2SixP3−xO12 (ref. 13 and 14) whose transport properties have been pioneered by Goodenough et al.15 Today a wide range of materials with structural and electrochemical similarities are discussed as NASICONs, e.g. the Li1.5Al0.5Ge1.5(PO4)3 (LAGP).16 In the context of technically relevant ionic conductivities the LAGP is an attractive candidate in its glass-ceramics form.17–19 Glass ceramics are generated by heat treatment of amorphous glasses causing partial crystallization. This will lead to poly-crystallinity with crystalline regions separated by grain boundaries as well as possibly remaining amorphous regions.18,20,21 From the point of view of energy landscapes glass ceramics are located between single crystals and perfectly amorphous solids. According to Kirchheim the energy landscape of a crystalline material with grain boundaries may be difficult to distinguish from that of a perfect glass.22 For the sake of the uniqueness of the SED analysis aimed at in this work, we concentrate on perfectly amorphous glasses. More specifically the focus will be on lithium, sodium and potassium as network modifiers, i.e. on A1.5Al0.5Ge1.5(PO4)3 with A = Li, Na, K.
In previous work, the quantification of SED and PSED was based on the alkali CAIT approach where alkali ions M+ = Li+, Na+, K+, Rb+ or Cs+ were generated by thermionic emission and then used for ion attachment. More recently the list of attachable monovalent ions has been extended to protons and deuterons in a Plasma-CAIT experiment, where polarity selected charge carriers were extracted from a femtosecond-laser plasma.10 The possibility to replace native alkali ions by foreign protons or deuteron in fact appears to be a general phenomenon – as will be demonstrated in this work. In this context a very robust approach to alkali proton substitution (APS) has been demonstrated by Omata and coworkers.23–25 In that approach a sample is placed between two electrodes one of those being a thin platinum electrode. The entire sample is placed into hydrogen atmosphere. Here, hydrogen molecules dissociatively adsorb to the platinum electrode and eventually diffuse into this thin electrode. Then, as soon as a potential drop is applied to the two electrodes, hydrogen atoms are converted to protons, most likely at the Pt/sample interface, and subsequently these protons substitute native alkali ions in a unidirectional transport experiment very similar to the CAIT process of generating replacement zones.
Experiment
Sample preparation
Three batches of alkali–aluminum–germanium–phosphate (AAGP) glasses with the general composition A1.5Al0.5Ge1.5(PO4)3 (with A = Li–K) were synthesized via the melt-quenching method.11,26 The educts of glass synthesis, A2CO3, GeO2, (NH4)2HPO4 and Al2O3 were dried for 12 h at 120 °C in an oven. Stoichiometric amounts of the compounds were mixed with an agate mortar. An excess of 10% for the A2CO3 were used. The mixture was placed in a platinum crucible and heated from room-temperature to 450 °C. The temperature was kept stable for 2 hours to drive off CO2, H2O und NH3. Within 60 minutes, the mixture was heated to 1400 °C for A = Li and 1475 °C for A = Na and K. After 2 h the melt was quenched in a stainless steel crucible at 450 °C for A = Li and 550 °C for A = Na/K and left at this temperature for 12 h. The thermally relaxed glasses were cooled down to room-temperature with a cooling rate of 1 °C min−1. The resulting glass cylinder was cut into glass discs with a cutting machine (Struers Accutom-5). The mass per glass batch produced is 15.0 g ± 0.2 g. For each batch, 5–8 cylindrical glass discs with a diameter of 1.4 cm and thicknesses from 0.5 mm to 1.2 mm were obtained. Both sides of the glass discs were polished using a polishing machine (Struers LaboPol-5). The polishing procedure was carried out in two steps with decreasing grain size (Kemet 6-KD-C3 and 3-KD-C3). The roughness of the polished surfaces have been determined by a profilometer (Bruker DektakXT). Typical rms values range from 80 to 120 Å. Subsequently thin platinum layers with thickness of 100 nm were sputtered on both sides of the glass samples (Leica EM ACE600).The mass density of the glass samples were measured using a pycnometer (Blaubrand) with an accuracy of ±0.001 g cm−3. The amorphicity of the glass batches has been validated by X-ray diffraction (Philipps/Panalytical X'Pert Pro PW3040/60) (see Fig. S1–S3 of the ESI†).
APS method
The alkali-proton substitution (APS) approach was first described by Ishiyama et al.23,24 In this work, we use an experimentally adapted version of the original published method. A glass disc sputtered with platinum (see sample preparation) is placed between two stainless steel electrodes in an experimental setup as shown in Fig. 1. As a subtle detail we note that the steel electrode representing the anode is mounted on a three-point support while the steel electrode representing the cathode is pressed to the sample with the planar face. This ensures free access of molecular hydrogen to the front side platinum electrode.The entire setup is located in a closed chamber in a defined atmosphere of 200 mbar H2. An integrated heating unit allows the sample to be tempered to a desired temperature. On one of the two electrodes a positive DC bias up to 50 V is applied (anode). The other electrode is grounded through a transimpedance amplifier (cathode). The application of the positive DC potential to the anode results in a static electric field between anode and cathode. Mobile, positive alkali ions in the AAGP glass migrate along the electric field. Ions arriving at the cathode are neutralized by electrons. The electron current is detected by the transimpedance amplifier, A/D converted and recorded by a computer software. On the anode side, the molecular hydrogen dissociates and the resulting atomic hydrogen binds to the platinum surface. The hydrogen atoms are transported through the porous platinum layer and are most likely oxidized to H+ at the platinum glass interface due to the positive potential.23,27 The H+ ions can now enter into glass. Upon entering into the glass the H+ ions replace native alkali ions such that electro-neutrality is overall conserved. This leads to unique concentration depth profiles which can be quantified by means of time-of-flight secondary ion mass spectrometry (ToF-SIMS). The H+ formation and migration is schematically shown in Fig. 2. The experimental conditions employed ensured that at all times a sufficient number of protons can be converted at the platinum electrode and that, as a result, a sufficient number of protons are available for substitution.
 | ||
| Fig. 2 Schematic representation of the formation of H+ ions and replacement of alkali ions A+ during the APS experiment. | ||
There are two options how the APS can be used to determine characteristic sample properties, (i) the DC conductivity measurements and (ii) the formation of concentration depth profiles. The concept of measuring DC conductivity data for glasses has been described elsewhere.11 For the DC conductivity measurement, a DC bias is applied to the electrodes for a short time and the resulting current is measured. By variation of the DC bias, the conductivity of the sample at a given temperature can be determined. The measurement of the conductivity at different temperatures allows for an Arrhenius analysis. The result of this analysis is the activation energy Eact for long range ion transport.11 The DC conductivity measurements are carried out in such way that the overall charge flown is small, so that the conductivity of the sample is not influenced by the ingoing H+ ions.
By applying a constant static voltage to the electrodes over an extended period of time (tens of hours) concentration depth profiles are generated beneath the anode. They can reach up to 2000 nm deep into the sample as quantified by ToF-SIMS. The electric current transported during the experiments is monitored. It typically decreases slightly over time, when the overall conductivity of the sample is changed by the APS process.
Measurement of concentration depth profiles
The concentration depth profiles generated with the APS are measured with a time-of-flight secondary ion mass spectrometer (ToF-SIMS 5, IONTOF GmbH) equipped with an extended dynamic range (EDR) detector. The surface of the sample is analyzed by a Bi+ beam, generated by a liquid metal ion gun. The Bi+ ions have a kinetic energy of 25 keV. The high-energetic Bi+ ions impinging the surface cause a collision cascade, where neutral particles, secondary electrons and secondary ions are released. The secondary ions are drawn into the time-of-flight analyzer and separated by their mass to charge ratio. The time-of-flight of a specific ion can be translated to the mass of the ion. The analyzer is operated in the positive mode, such that only positive ions are analyzed. A sputter gun consisting of an O2+ ion beam exposes deeper layers of the surface. The O2+ ions have a kinetic energy of 2 keV. During a sputter cycle, no ions can enter the analyzer. The analyzer beam (Bi+) and the sputter beam are used alternately. For each analysis cycle, an area of 100 × 100 μm, by a total of 128 × 128 spots is analyzed. Since the samples examined are not electrically conductive, the sample is additionally charged negatively with an electron beam on the surface. This prevents the surface from being positively charged due to the emission of secondary electrons and thus reducing the ion yield. For a one-dimensional depth profile the secondary ions in each cycle are counted, Poisson corrected and integrated over the entire layer. The sputtering area is 300 μm × 300 μm. The depth of the crater formed during the profiling is subsequently analyzed by a depth profilometer (Bruker DektakXT). Assuming a constant sputter rate for the sample, the ToF-SIMS profile can be calibrated by the measured depth. The sputtered platinum electrode on the glass sample can be washed away in an ultrasonic bath without losing any information in the concentration depth profile. This work is focused on the concentration depth profiles beneath the anode.Theory
Nernst–Planck–Poisson equations
The result of an APS experiment is the macroscopic substitution of mobile native alkali ions by foreign H+ ions beneath the anode. This substitution process can be visualized by one-dimensional concentration depth profiles. The Nernst–Planck–Poisson equations, as a set of coupled differential equations, allow an analysis of the measured depth profiles. The Nernst–Planck equation in its one-dimensional form is: | (1) |
A translocation of charge carriers of any kind influences the electric potential and thus the electric field inside a material. The relation between the charge carrier distribution and the electric potential is given by the Poisson equation. The one-dimensional form of the Poisson equation is given by:
 | (2) |
The time-dependent ion motion is described by Fick's second law:
 | (3) |
The only free parameters entering eqn (1)–(3) are the diffusion coefficients Di(ni) of the mobile species. All other direct or indirect parameters, such as the temperature, the sample geometry or the electric potentials on both sides of the sample are explicitly given and constant throughout the entire experiment. Ultimately, the diffusion coefficients of the native mobile ion (in the following termed DA) and the external H+ ion (in the following termed DH), are chosen such as to minimize the rms between the theoretical concentration depth profile and the experimental one. Details on the implementation of the diffusion coefficients and its numerical variation will be given below.
Concentration dependence of diffusion coefficients
As eqn (1) implies, the diffusion coefficient is conceptually considered to be a function of the ion density of the species in a given volume.8,28 In principle, this applies to both the native and the foreign ions. Previous studies in our group showed empirically that agreement between experimental and modelled concentration depth profiles can only be reached, if the native Di is assumed to strongly vary with ni, but the foreign Di has to be kept effectively constant. Simulations with a constant native diffusion coefficient and/or a strongly varying foreign diffusion coefficient do not fit the experimental results.8–10,29 As shown in the result section, this situation also applies to the current work. Below we will provide a brief introduction to the concept of concentration dependent diffusion coefficients.During the preparation of the glass using melt-quenching, the glass framework is formed. The alkali ions now occupy the sites in the glass framework. The sites of lower energy are occupied with preference over sites of higher energy. The sites are thus filled from bottom up in the direction of increasing energy. In previous work we showed that we can model the sites available for alkali ions by a site energy distribution.8–10 The energetically highest occupied site corresponds to a Fermi level with an energy, EF, the ionic Fermi energy.8,30,31 This concept is analogous to the concept of an electronic Fermi level in metals or semiconductors, but must be distinguished from the latter. Transport of ions here takes place by hopping in the potential energy landscape involving vacancies. For long range transport a threshold, EDC, has to be overcome constituting a transport path of least energy. Setting this long range threshold to 0 eV, the activation energy Eact(nA) of an alkali ion A can be calculated from:
| Eact(nA) = EDC − EF(nA) = −EF(nA) | (4) |
Consequently, the diffusion coefficient DA(nA) of the corresponding ion can be calculated by
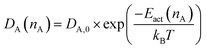 | (5) |
For modelling of the SED we choose a sin2 function. The sin2 function is similar in form to an assumed Gaussian function but mathematically easier to integrate numerically. The general form of the SED S(E) used in this work is given by:
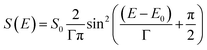 | (6) |
 | (7) |
Note, that we define S(E) to be zero outside of the two zero points of the sin2 function.
While the preparation of a glass can be visualized as an energy landscape being filled up bottom-up, the ion exchange process can be visualized as occurring energetically top-down. At the beginning of the ion exchange experiment, those native ions sitting near the Fermi level experience the lowest activation energy for long range transport and will be replaced by foreign ions first. As the ion exchange proceeds in time, the Fermi level of the native ions decreases. The corresponding native activation energy increases and the diffusion coefficient decreases according to eqn (4) and (5). Concomitantly, foreign ions fill in the energy landscape. As illustrated in the middle and the right part of Fig. 3, this can also be envisaged as taking place energetically top-down. This picture automatically implies, that the Fermi level of the foreign ion stays constant and so does its activation energy and its diffusion coefficient.
Clearly, Fig. 3 implies the evolution of an energy distribution of the population of both the native and the foreign ion. Therefore, one can envisage an experiment, where not only the diffusion coefficient of the native but also the foreign ion may exhibit a concentration dependence. Such an experiment is indeed feasibly, but it is not the current experiment. As elaborated elsewhere, in this kind of unidirectional ion exchange, the effective diffusion coefficient for the foreign ion will always appear as concentration independent as long as Dforeign ≪ Dnative,bulk.32 This is a characteristic of the experiment. Since the goal of the experiment is to quantify only the native ion SED, no problem arises from this.
Ultimately, the theoretical analysis depends on only two free parameters for the native alkali ion considered, i.e. the pre exponential factor DA,0 and the width of the SED, Γ, and a single diffusion coefficient for the foreign ion, DH, i.e. the proton.
So far, the model presented only takes into account the unrestricted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 replacement of native alkali ions by external protons. However, it is possible that certain alkali sites are not accessible to protons. In that case those alkali ions would remain in their site, i.e. would seem to be (nearly) immobile, at least on the time scale of the experiment. To include this behavior, we modified the diffusion coefficient DA(nA) as given in eqn (5). For small ion densities, nA, in the context of this work typically below 15% of the bulk ion density, the diffusion coefficient of the native ion is reduced artificially, causing ions to remain in the replacement zone. Note, that a 1
1 replacement of native alkali ions by external protons. However, it is possible that certain alkali sites are not accessible to protons. In that case those alkali ions would remain in their site, i.e. would seem to be (nearly) immobile, at least on the time scale of the experiment. To include this behavior, we modified the diffusion coefficient DA(nA) as given in eqn (5). For small ion densities, nA, in the context of this work typically below 15% of the bulk ion density, the diffusion coefficient of the native ion is reduced artificially, causing ions to remain in the replacement zone. Note, that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 exchange does not necessarily imply that the external protons occupy sites which have just been vacated by the native mobile ion. In principle the external proton may occupy a site different from the one being vacated subject to local charge balance.
1 exchange does not necessarily imply that the external protons occupy sites which have just been vacated by the native mobile ion. In principle the external proton may occupy a site different from the one being vacated subject to local charge balance.
Conductivity measurements
In recently published work, we investigated the activation energies and the conductivities of the AAGP glasses using DC conductivity studies in vacuum and in hydrogen.11 An increase in the activation energy with a simultaneous decrease in conductivity as the alkali ions increased in size was observed. The temperature-dependence of the conductivity follows the law of Arrhenius. The activation energy of the DC long-range transport Eact can be determined using the logarithmic form of the Arrhenius law: | (8) |
Results and discussion
Conductivity measurements
The DC conductivities of the AAGP (A = Li–K) glasses have been examined employing the APS technique. Here, the conductivity measurements were performed in a 200 mbar hydrogen atmosphere as a function of the temperature. The results are presented in Fig. 4 in the form of an Arrhenius plot. Clearly, the overall conductivity decreases in the order σ(LAGP) > σ(NAGP) > σ(KAGP). The order of magnitude and the sequence of conductivities observed in this work is identical to the one observed in ref. 11. The activation energies derived are Eact(Li) = 0.78 eV, Eact(Na) = 0.73 eV and Eact(K) = 0.98 eV with an uncertainty of ±0.03 eV for all three values. The activation energies of LAGP and NAGP glass are therefore indistinguishable, while the activation energy of KAGP is significantly higher. This trend is similar to data reported in the literature.33,34 Please note that the sequence of ionic conductivities shown here is characteristic for the temperature window shown. A difference in the activation energy implies the possibility that the order of the ionic conductivities reverses at some temperature. The data reported here compare well to previous results obtained by Plasma-CAIT and by a direct DC approach.11 The latter measurements employed the same experimental setup as the one used in this work. However, the DC measurements in ref. 11 were performed in high vacuum, i.e. without applying a hydrogen atmosphere. This implies subtle differences between the two DC experiments. As it turns out, the differences are small on the short time scale, on which the conductivities are measured. In ref. 11, the activation energy of LAGP was observed approx. 30 meV lower than for NAGP. Since the difference in activation energies is within the experimental inaccuracies, the data in this paper are fully compatible with those in ref. 11. Minor differences in absolute numbers for the conductivities and the activation energies observed between ref. 11 and this work originate from the fact that a different batch was used here. These differences relate to subtle differences in the preparation of the glass samples. Small variations in the preparation, for example, the cooling rate of the molten glass are known to lead to measurable changes in the glass properties.35,36 The characterization of the current batch is important, since the activation energies determines the diffusion coefficient as given by eqn (5). | ||
| Fig. 4 Arrhenius plot of the measured DC conductivities vs. 1000/T. The glasses investigated were LAGP (orange), NAGP (green) and KAGP (red). Activation energies are given in the legend. | ||
The measurement of conductivities and activation energies described above relies on a fast measurement ensuring that the sample properties are not altered by the experiment. Here, it is important to note that electrode polarization does not limit the charge transport. As demonstrated in the ESI† the current recorded during the actual APS experiment only slightly decreases over the course of several tens of hours (Fig. S4–S6†). That decrease of current versus time reflects the evolution of alkali proton substitution as will be discussed in detail in the next section.
Concentration depth profiles of the APS treated glasses
One sample of each batch of the three AAGP glasses has been treated by an APS experiment. As mentioned, the measured current time curves are shown and described in the ESI (see Fig. S4–S6†). Subsequently, the APS treated samples have been analyzed by means of ToF-SIMS. Conceptually, the protons can only enter the material through the anode. Therefore, only the anode side of the samples have been analyzed by ToF-SIMS. The raw data of the ToF-SIMS concentration depth profiles are presented as Fig. S7–S9 of the ESI.† In addition, the raw profiles shown in the ESI (Fig. S7–S9†) show that no electrochemical decomposition reactions have taken place at the electrodes. The normalization of the depth profiles is also described in the ESI.† The normalized concentration depth profiles are presented as Fig. S10–S12 of the ESI.† They are also displayed as symbols in Fig. 5, 7 and 9.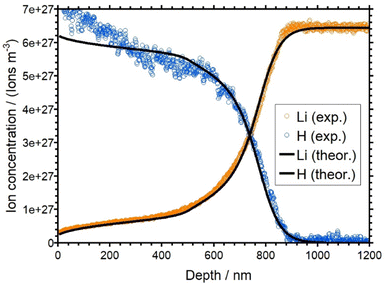 | ||
| Fig. 5 Overlay of the experimental (orange and blue) and simulated (black) concentration depth profiles for LAGP. | ||
The concentration depth profiles show a pronounced replacement of native alkali ions by protons. The replacement zones observed for the three samples differ in shape and depth. As for the current–time curves, the shape of the LAGP and NAGP profiles differs markedly from the KAGP profile.
The profiles for the LAGP and NAGP samples both show a clear depletion of the alkali ions with the concomitant formation of a plateau-like region in the first approx. 500 nm of the depth profile for LAGP and 200 nm for NAGP, where part of the native ions are not replaced on the time scale of the experiment. The level of both plateaus is at about 10 percent of the bulk ion concentration, i.e. here, 90 percent of the native alkali ions have been displaced by protons. Overall, the concentration of hydrogen is complementary to the alkali concentration as expected for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution. However, in the first 50 nm, the hydrogen concentrations is higher than expected assuming charge conservation. This is a small effect, probably due to a chemical reaction on the surface. The bulk ion density for the LAGP is reached at a depth of around 900 nm, while for the NAGP it is reached at a depth of around 400 nm. This seems plausible, since the total charge transported in the APS experiment of the LAGP sample was larger than that for the NAGP sample. For both glasses, the diffusion front is rather steep. For LAGP, the lithium and the hydrogen signals intersect at approx. 720 nm and for NAGP the sodium and the hydrogen signals intersect at 260 nm.
1 substitution. However, in the first 50 nm, the hydrogen concentrations is higher than expected assuming charge conservation. This is a small effect, probably due to a chemical reaction on the surface. The bulk ion density for the LAGP is reached at a depth of around 900 nm, while for the NAGP it is reached at a depth of around 400 nm. This seems plausible, since the total charge transported in the APS experiment of the LAGP sample was larger than that for the NAGP sample. For both glasses, the diffusion front is rather steep. For LAGP, the lithium and the hydrogen signals intersect at approx. 720 nm and for NAGP the sodium and the hydrogen signals intersect at 260 nm.
In the KAGP profile (Fig. 9), the intersection of the potassium signal and the hydrogen signal occurs close to the beginning of the profile at 0 nm depth. Thus, within the time of the experiment only 50% of the native K+ ions have been replaced at the front side of the sample. Another 50 percent of the potassium ions remain in their corresponding sites and are not displaced by the protons. For an even longer transport time the profile and as a consequence also the intersection point would be driven further into the sample. It is impossible to predict whether a plateau would evolve at such extended times. In contrast to LAGP/NAGP profiles, the KAGP profile is flat and rather deep. The bulk concentration is reached at a depth of 1800 nm. The observations described in this section will be rationalized by theoretical modelling in the next section.
Simulation of the concentration depth profiles
The concentration depth profiles of the APS treated AAGP samples from Fig. 5, 7, and 9 have been quantitatively simulated by numerically solving the Nernst–Planck–Poisson equations employing the Marburg-NPP code.37,38 The experimental and computational parameters used for the best fitting calculations are given in Table 1.| Parameter | LAGP | NAGP | KAGP |
|---|---|---|---|
| Bulk density (A+)/1027 m3 | 6.44 (±2%) (Li+) | 6.67 (±2%) (Na+) | 6.27 (±2%) (K+) |
| Temperature/°C | 90 (±0.1) | 100 (±0.1) | 190 (±0.1) |
| Time/h | 40.84 | 42.92 | 146.64 |
| E act/eV | 0.78 (±0.03) | 0.73 (±0.03) | 0.98 (±0.03) |
| D A(xA = 1)/10−18 m2 s−1 | 2.62 (±10%) | 1.20 (±10%) | 0.70 (±20%) |
| D H/10−19 m2 s−1 | 1.8 (±30%) | 0.45 (±30%) | 5.5 (±50%) |
| Γ/meV | 73 (±20) | 78 (±30) | 80 (+70/−30) |
| FWHM of SED/meV | 114.6 | 122.52 | 125.66 |
The values for DA(xA = 1) in Table 1 show the same trend as observed in the Arrhenius plots (see Fig. 4). Although the experimental temperature for the KAGP glass is significantly higher than for the other two glasses, the actual diffusion coefficient DA,0 is lower. Interestingly, this trend is not observed for the diffusion coefficient of the hydrogen. The diffusion coefficient of hydrogen in LAGP is higher than in the NAGP despite a higher temperature during the APS of NAGP. The high diffusion coefficient of hydrogen for KAGP can be due to the high temperature during the experiment. The data indicates that the diffusion coefficient of hydrogen differs for each glass system. However, a possible variation of DH with T is beyond the scope of this work. The parameters listed in Table 1 are the ones leading to the best agreement between the modelled and the experimental profiles. The comparison of these profiles will be discussed below, as well as the variation of diffusion coefficients with the molar fraction xA. Note, that the molar fraction xA is directly proportional to the ion density of the given glass. The error margins of the determined values DA,0, DH and Γ are discussed in a later section and in the ESI.†
The best match between the theoretical and the experimental concentration depth profiles of the LAGP sample is shown in Fig. 5. The simulated curves are shown in black. The simulated profiles show good agreement with the experimental data. The agreement of the simulated profiles is better for the lithium curve than for the hydrogen curve. The experimental hydrogen profile clearly shows concentration at the beginning of the profile, which is higher than the bulk density of the lithium ions. This behavior would not be in an agreement of the charge conservation and therefore is not reflected in our theoretical model. The diffusion coefficients of Li+ and H+ as a function of x, which were used for the theoretical curves, are shown in Fig. 6. While DH is set to a constant value (see Table 1), DLi shows a strong concentration dependence. The red curve shows the diffusion coefficient obtained by a SED function (see eqn (6)) with Γ set to 73 meV. According to this curve, DLi decreases from 2.62 × 10−18 m2 s−1 (xLi = 1) to approx. 1 × 10−20 m2 s−1 for very small xLi. With this behavior for small xLi, the plateau like regime of the lithium curve in the first 500 nm could not be realized. Therefore, we introduced an artificially reduction of the diffusion coefficient for xLi < 0.15. This reduction is shown as the solid line at xLi < 0.15 in Fig. 6. Effectively, this line represents an upper bound to the true diffusion coefficient. At xLi < 0.15 the analysis is not sensitive to smaller values of DLi. On the other hand, the sensitivity of the theory to the experimental data is good for xLi > 0.15.
In previous work, the SED of Li+ ions in a LAGP glass with the same composition has been determined by means of the fs-plasma CAIT technique, where native Li+ ions were replaced by foreign D+ ions. That analysis led to a value of Γ = 72 meV,3 in very good agreement with the value of Γ = 73 meV derived in this work. The activation energies of the LAGP glass batch in the work of Wiemer et al. was 0.73 eV,10 which is slightly lower than the activation energy of the LAGP glass batch in this work with 0.78 eV. These differences are within the measurement uncertainties. Therefore, the data are consistent with ref. 10. It appears important to stress that in the work of Wiemer et al.10,11 a LAGP glass of the same stoichiometry was subjected to a CAIT analysis. The experimental conditions, namely the temperature, voltage and the transport duration of the experiment were vastly different from this work. As a consequence, the absolute values of the native Li+ ion diffusion coefficient were also different. But the SED derived was basically the same as the one derived in this work. This lends strong support to the conclusion that the SED derived, in particular its width FWHM, for the native ions is indeed characteristic for the material.
Overall, it is concluded, that the width of the SED in the LAGP class derived using different techniques is representative for the LAGP glass system.
In Fig. 7 the experimental and the simulated concentration depth profiles of the APS treated NAGP sample are shown. The simulated profiles are in a good agreement with the experimental data. As for the LAGP, the experimental hydrogen curve at small values of the depth is higher than the bulk density of Na+ of the material. Again, this is considered a minor artefact of the experiment. The concentration dependence of the diffusion coefficient DNa is shown in Fig. 8 together with DH. The blue curve is derived by assuming a SED with Γ = 78 meV (see eqn (6)). DNa decreases from 1.20 × 10−18 m2 s−1 (for x = 1) to approx. 4 × 10−21 m2 s−1 for small xNa. Employing the complete diffusion coefficient derived from the SED function, the 200 nm deep plateau of the sodium ions at the beginning of the profile could not be replicated. Therefore, similar to the analysis of LAGP, we artificially decreased DNa for all values with xNa < 0.13 (solid curve in Fig. 8) to get a better match between experimental and simulated profile. As in the case of the LAGP sample, this line represents an upper bound to the true diffusion coefficient. Here, at xNa < 0.13 the analysis is not sensitive to smaller values of DNa. Overall, the sensitivity of the theory to the experimental data is good for xNa > 0.13. As in basically all our theoretical studies, the diffusion coefficient of the foreign ion, DH, is assumed constant.
 | ||
| Fig. 7 Overlay of the experimental (blue and green) and simulated (black) concentration depth profiles for NAGP. | ||
The calculated and the simulated concentration depth profiles of the KAGP sample are shown in Fig. 9. The simulated curves fit the experimental curves well. The diffusion coefficients DK as a function of the molar fraction and DH are shown in Fig. 10. DK decreases from 7.00 × 10−19 m2 s−1 (for x = 1) to approx. 1 × 10−21 m2 s−1 for small xK. Note that DH is 5.50 × 10−19 m2 s−1. Therefore, the hydrogen ions have almost the same diffusion coefficient as the potassium ions at bulk concentration. This is in contrast to the results from the LAGP and NAGP analyses. Because of the small difference of the diffusion coefficients, the potassium ions are only replaced to approx. 50 percent at the front of the sample. Furthermore, the small difference in D values leads to a rather flat diffusion front, in contrast to the steep diffusion fronts in the LAGP and NAGP profiles. Since a maximum of 50 percent of the potassium ions were displaced, no statement can be made about the course of the diffusion coefficient for xK < 0.5. In other words, the APS experiment at KAGP is only sensitive to the potassium ions sitting in the energetically upper 50 percent of the available sites.
 | ||
| Fig. 9 Overlay of the experimental (blue and red) and simulated (black) concentration depth profiles for KAGP. | ||
 | ||
| Fig. 10 Plot of the diffusion coefficients DK and DH as a function of the molar fraction xK. DH is constant. | ||
Evaluation of confidence interval for simulation parameters
The central result of this work is the sequence of parameters, DA,0, DH and Γ, adjusted in the NPP simulations, in order to obtain the best match between experimental and theoretical concentration profiles as shown in Fig. 5, 7 and 9. In the following we discuss the uncertainty of these parameters, i.e. the confidence interval within which the match between experiment and theory is still considered reasonable. This confidence interval is defined as the difference between the best fitting parameter and the one which produces the least acceptable match. To this end, for each of the three AAGP glasses, DA,0, DH and Γ were systematically varied. Ultimately the confidence intervals are included as uncertainties in Table 1, which summarized the results for the three glasses.As the concentration depth profiles of LAGP and NAGP exhibit qualitative similarity but are substantially different from the KAGP profile, the discussion is grouped accordingly.
The following clear trends emerge. The values for DA,0 are precise with an uncertainty of 10% for LAGP/NAGP and 20% for KAGP. This reflects the high sensitivity the APS experiment has towards the bulk diffusion coefficient of the alkali ions. In contrast, the sensitivity of the diffusion coefficient of the ingoing hydrogen ions is much lower, resulting in uncertainties of 30% for LAGP/NAGP and 50% for KAGP. The focus of this work is on the width of the site energy distributions as given by the Γ value in (7), respectively the corresponding FWHM. Here, the uncertainty of the Γ value is ±20 meV for the LAGP and ±30 meV for the NAGP. For the KAGP the uncertainty is concluded to be +70 meV/−30 meV. This translates into FWHM values of 114 meV, 122 meV and 126 meV, FWHM, for the LAGP, the NAGP and the KAGP respectively. Thus, the uncertainty of all the NPP parameters is largest for the KAGP. The main difference between the LAGP/NAGP on one side and the KAGP on the other is encoded in the ratio between the native diffusion coefficient in the bulk region and the (concentration independent) diffusion coefficient of the external proton. That ratio is close to 100 for LAGP and NAGP but it is less than 10 for the KAGP. The latter implies that diffusion coefficient of the H+ is larger than that of K+ for a significant fraction of the K+ population. As a consequence, a major fraction of the K+ appears immobile in this experiment. For the experimental time chosen, this fraction amounts to roughly 50% of the native K+ ions. From another point of view the ratio between initial Dnative and Dforeign determines the steepness of the diffusion front. The larger Dnative/Dforeign is, the steeper is the diffusion front. Since this ratio is smallest for the KAGP sample, its diffusion front is particularly flat.
For the illustration of the confidence intervals the concentration depth profiles obtained for the NPP calculation employing the limiting simulation parameters given in Table 1 are shown in the ESI (see Fig. S13–S21†). In general, higher values for DA,0 lead to deeper profiles with a steeper diffusion front. Lower values lead to less deep profiles and flatter profiles. For DH and Γ the trend is the opposite.
Finally, in Fig. 11 the SEDs derived in this work are illustrated in a plot of the site density as a function of E–Eact as obtained by the theoretical analysis. Here, the pivotal observation is that the SED, i.e. the energetic distribution of available sites for alkali ions, are indeed very similar for the three different glasses. This leads to the conclusion that the SED in the AAGP glass system is determined by the negatively charged glass formers. The influence of the corresponding alkali ion on the potential energy landscape seems to be rather small.
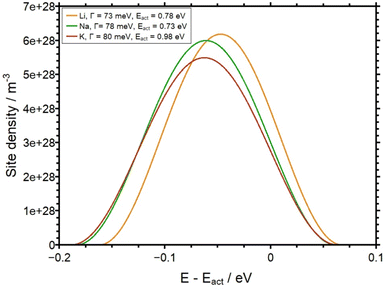 | ||
| Fig. 11 Site density as a function of E–Eact for all three AAGP glasses. The FWHM of each function is given in Table 1. | ||
Conclusion and summary
The APS is a technique for changing the structure of near-surface areas of a glass sample. In the present work we use the APS technique for the analysis of conductivities, potential energy landscapes and concentration-dependent diffusion coefficients for the first time.With the APS, H+ ions are generated on sputtered platinum electrodes using an electric field. According to the field gradient, these ions migrate into the sample and displace native, mobile alkali ions there. This results in unique concentration depth profiles. In this work we have studied self-synthesized AAGP glasses, with the general composition A1.5Al0.5Ge1.5(PO4)3 (with A = Li–K). By applying the Nernst–Planck–Poisson theory we were able to simulate the experimental depth profiles. The concentration dependence of the diffusion coefficients of the respective alkali ions could be obtained by modeling a potential-energy landscape of a defined width. The findings of the analysis show a pronounced concentration dependency for all three glass systems. The full width at half maximum (FWHM) of the site energy distribution is found to be 114 meV, 122 meV and 126 meV, FWHM, for the LAGP, the NAGP and the KAGP respectively. The observation that the width of the alkali ion site distribution function is very similar for LAGP, NAGP and KAGP implies that the glass matrix is dominated by the network former but effectively independent of the type of alkali ion in question. The FWHM of the site energy distribution determined here is significantly lower than in borate glasses (FWHM around 300 meV)9 and calcium phosphate glasses (FWHM around 200 meV).8
The accuracy of the simulated values has been specified with the help of parameter variations. The accuracy of the diffusion coefficients of the alkali ions is 10% for LAGP and NAGP and 20% for KAGP. For the respective diffusion coefficients of hydrogen, the uncertainties are 30% (LAGP/NAGP) and 50% (KAGP). The width of the potential energy landscape in our model was determined to an accuracy of ±20 meV (LAGP), ±30 meV (NAGP) and +70 meV/−30 meV (KAGP). The slightly lower accuracy of the values for KAGP, as well as the qualitatively very different depth profile for KAGP, can be rationalized by the small difference in the diffusion coefficients for K+ and H+.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are very grateful to Jan Wiemer for drawing our attention to the APS concept and for technical assistance in the early stage of this work. We also thank Martin Schäfer for continuous discussion on the general topic, in particular on the NPP model. Financial support of this work through the DFG research unit FOR5065 (Energy Landscapes and Structure in Ion conducting Solids, ELSICS) project P1 is also gratefully acknowledged.References
- T. D. B. Jacobs and L. Pastewka, Surface topography as a material parameter, MRS Bull., 2022, 47, 1205–1210, DOI:10.1557/s43577-022-00465-5.
- J. Bréger, N. Dupré, P. J. Chupas, P. L. Lee, T. Proffen, J. B. Parise and C. P. Grey, Short- and long-range order in the positive electrode material, Li(NiMn)0.5O2: a joint X-ray and neutron diffraction, pair distribution function analysis and NMR study, J. Am. Chem. Soc., 2005, 127, 7529–7537, DOI:10.1021/ja050697u.
- N. L. Allan, S. Conejeros, J. N. Hart and C. E. Mohn, Energy landscapes of perfect and defective solids: from structure prediction to ion conduction, Theor. Chem. Acc., 2021, 140, 151, DOI:10.1007/s00214-021-02834-w.
- A. R. Oganov and M. Valle, How to quantify energy landscapes of solids, J. Chem. Phys., 2009, 130, 104504, DOI:10.1063/1.3079326.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Materials design of ionic conductors for solid state batteries, Prog. Energy, 2020, 2, 022001, DOI:10.1088/2516-1083/ab73dd.
- D. Di Stefano, A. Miglio, K. Robeyns, Y. Filinchuk, M. Lechartier, A. Senyshyn, H. Ishida, S. Spannenberger, D. Prutsch, S. Lunghammer, D. Rettenwander, M. Wilkening, B. Roling, Y. Kato and G. Hautier, Superionic Diffusion through Frustrated Energy Landscape, Chem, 2019, 5, 2450–2460, DOI:10.1016/j.chempr.2019.07.001.
- B. C. Wood, J. B. Varley, K. E. Kweon, P. Shea, A. T. Hall, A. Grieder, M. Ward, V. P. Aguirre, D. Rigling, E. Lopez Ventura, C. Stancill and N. Adelstein, Paradigms of frustration in superionic solid electrolytes, Philos. Trans. R. Soc., A, 2021, 379, 20190467, DOI:10.1098/rsta.2019.0467.
- M. Schäfer and K.-M. Weitzel, Site energy distribution of ions in the potential energy landscape of amorphous solids, Mater. Today Phys., 2018, 5, 12–19, DOI:10.1016/j.mtphys.2018.05.002.
- M. Schäfer, D. Budina and K.-M. Weitzel, Site energy distribution of sodium ions in a sodium rubidium borate glass, Phys. Chem. Chem. Phys., 2019, 21, 26251–26261, 10.1039/c9cp05194e.
- J. L. Wiemer, M. Schäfer and K.-M. Weitzel, Li + Ion Site Energy Distribution in Lithium Aluminum Germanium Phosphate, J. Phys. Chem. C, 2021, 125, 4977–4985, DOI:10.1021/acs.jpcc.0c11164.
- J. L. Wiemer, K. Rein and K.-M. Weitzel, The ionic conductivity of alkali aluminum germanium phosphate glasses – comparison of Plasma CAIT with two electrode DC measurements, Z. Phys. Chem., 2022, 236, 1001–1012, DOI:10.1515/zpch-2021-3091.
- M. Hou, F. Liang, K. Chen, Y. Dai and D. Xue, Challenges and perspectives of NASICON-type solid electrolytes for all-solid-state lithium batteries, Nanotechnology, 2020, 31, 132003, DOI:10.1088/1361-6528/ab5be7.
- H.-P. Hong, Crystal structures and crystal chemistry in the system Na1+xZr2SixP3−xO12, Mater. Res. Bull., 1976, 11, 173–182, DOI:10.1016/0025-5408(76)90073-8.
- C. Li, R. Li, K. Liu, R. Si, Z. Zhang and Y.-S. Hu, NaSICON: A promising solid electrolyte for solid-state sodium batteries, Interdiscipl. Mater., 2022, 1, 396–416, DOI:10.1002/idm2.12044.
- J. B. Goodenough, H.-P. Hong and J. A. Kafalas, Fast Na+-ion transport in skeleton structures, Mater. Res. Bull., 1976, 11, 203–220, DOI:10.1016/0025-5408(76)90077-5.
- R. DeWees and H. Wang, Synthesis and Properties of NaSICON-type LATP and LAGP Solid Electrolytes, ChemSusChem, 2019, 12, 3713–3725, DOI:10.1002/cssc.201900725.
- B. Chowdari, G. V. Subba Rao and G. Lee, XPS and ionic conductivity studies on Li2O–Al2O3–(TiO2 or GeO2)–P2O5 glass–ceramics, Solid State Ionics, 2000, 136–137, 1067–1075, DOI:10.1016/S0167-2738(00)00500-2.
- Y. Cui, M. M. Mahmoud, M. Rohde, C. Ziebert and H. J. Seifert, Thermal and ionic conductivity studies of lithium aluminum germanium phosphate solid-state electrolyte, Solid State Ionics, 2016, 289, 125–132, DOI:10.1016/j.ssi.2016.03.007.
- A. Vyalikh, M. Schikora, K. P. Seipel, M. Weigler, M. Zschornak, F. Meutzner, W. Münchgesang, T. Nestler, V. Vizgalov, D. Itkis, A. F. Privalov, M. Vogel and D. C. Meyer, NMR studies of Li mobility in NASICON-type glass-ceramic ionic conductors with optimized microstructure, J. Mater. Chem. A, 2019, 7, 13968–13977, 10.1039/C8TA11686E.
- H. Bradtmüller, A. M. Nieto-Muñoz, J. F. Ortiz-Mosquera, A. C. Rodrigues and H. Eckert, Glass-to-crystal transition in the NASICON glass-ceramic system Na1+xAlxM2−x(PO4)3 (M=Ge, Ti), J. Non-Cryst. Solids, 2018, 489, 91–101, DOI:10.1016/j.jnoncrysol.2017.10.057.
- Y. Zhu, T. Wu, J. Sun and M. Kotobuki, Highly conductive lithium aluminum germanium phosphate solid electrolyte prepared by sol-gel method and hot-pressing, Solid State Ionics, 2020, 350, 115320, DOI:10.1016/j.ssi.2020.115320.
- R. Kirchheim, Solid Solutions of Hydrogen in Complex Materials, Solid State Physics, Elsevier, 2004, pp. 203–291 Search PubMed.
- T. Ishiyama, S. Suzuki, J. Nishii, T. Yamashita, H. Kawazoe and T. Omata, Electrochemical Substitution of Sodium Ions in Tungsten Phosphate Glass with Protons, J. Electrochem. Soc., 2013, 160, E143–E147, DOI:10.1149/2.093311jes.
- T. Ishiyama, J. Nishii, T. Yamashita, H. Kawazoe and T. Omata, Electrochemical substitution of sodium ions with protons in phosphate glass to fabricate pure proton conducting glass at intermediate temperatures, J. Mater. Chem. A, 2014, 2, 3940, 10.1039/C3TA14561A.
- A. Sharma, I. Suzuki, T. Ishiyama and T. Omata, Enhancing proton mobility and thermal stability in phosphate glasses with WO3: the mixed glass former effect in proton conducting glasses, Phys. Chem. Chem. Phys., 2023, 25, 18766–18774, 10.1039/d3cp01453c.
- Y. S. Zhu, L. L. Li, C. Y. Li, L. Zhou and Y. P. Wu, Na1+xAlxGe2−xP3O12 (x = 0.5) glass–ceramic as a solid ionic conductor for sodium ion, Solid State Ionics, 2016, 289, 113–117, DOI:10.1016/j.ssi.2016.02.021.
- T. Yamaguchi, T. Ishiyama, K. Sakuragi, J. Nishii, T. Yamashita, H. Kawazoe and T. Omata, Improving thermal stability and its effects on proton mobility in proton-conducting phosphate glasses prepared by the electrochemical substitution of sodium ions with protons, Solid State Ionics, 2015, 275, 62–65, DOI:10.1016/j.ssi.2015.03.003.
- A. Lupascu, Modeling ion exchange in glass with concentration-dependent diffusion coefficients and mobilities, Opt. Eng., 1996, 35, 1603, DOI:10.1117/1.600727.
- L. Rossrucker, P. V. Menezes, J. Zakel, M. Schäfer, B. Roling and K.-M. Weitzel, Bombardment Induced Potassium Ion Transport Through a Sodium Ion Conductor: Conductivities and Diffusion Profiles, Z. Phys. Chem., 2012, 226, 341–353, DOI:10.1524/zpch.2012.0215.
- P. Maass, Towards a theory for the mixed alkali effect in glasses, J. Non-Cryst. Solids, 1999, 255, 35–46, DOI:10.1016/S0022-3093(99)00422-6.
- S. D. Baranovskii and H. Cordes, On the conduction mechanism in ionic glasses, J. Chem. Phys., 1999, 111, 7546–7557, DOI:10.1063/1.480081.
- V. H. Gunawan, M. Schäfer and K.-M. Weitzel, Manifestation of Site Energy Landscapes for Ion Transport in Borate Glasses, Phys. Chem. Chem. Phys., 2024, 26, 14430, 10.1039/d4cp00262h.
- J. E. Tsuchida, F. A. Ferri, P. S. Pizani, A. C. Martins Rodrigues, S. Kundu, J. F. Schneider and E. D. Zanotto, Ionic conductivity and mixed-ion effect in mixed alkali metaphosphate glasses, Phys. Chem. Chem. Phys., 2017, 19, 6594–6600, 10.1039/C6CP07876A.
- Y. GAO and C. CRAMER, Ionic conductivity of glasses with two and three types of alkali ions, Solid State Ionics, 2005, 176, 921–927, DOI:10.1016/j.ssi.2004.11.010.
- K. Vollmayr, W. Kob and K. Binder, How do the properties of a glass depend on the cooling rate? A computer simulation study of a Lennard-Jones system, J. Chem. Phys., 1996, 105, 4714–4728, DOI:10.1063/1.472326.
- M. Yoshiyagawa, Effect of rapid quenching on the mixed alkali effect of glass, Solid State Ionics, 1987, 23, 271–274, DOI:10.1016/0167-2738(87)90005-1.
- M. Schäfer and K.-M. Weitzel, Bombardment induced ion transport. Part I: Numerical investigation of bombardment induced ion transport through glasses and membranes on the basis of the Nernst-Planck-Poisson equations, Phys. Chem. Chem. Phys., 2011, 13, 20112–20122, 10.1039/c1cp21215j.
- M. Schäfer and K.-M. Weitzel, The Marburg program suit for modelling charge carrier transport in solids, to be published.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02421d |
| This journal is © The Royal Society of Chemistry 2024 |




