Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling the origin of capacity fade in Prussian white hard carbon full cells through operando X-ray diffraction†
Ida
Nielsen
 *a,
Charles Aram
Hall
a,
Agnes-Matilda
Mattsson
*a,
Charles Aram
Hall
a,
Agnes-Matilda
Mattsson
 a,
Reza
Younesi
a,
Reza
Younesi
 a,
Alexander
Buckel
b,
Gustav
Ek
a,
Alexander
Buckel
b,
Gustav
Ek
 a and
William R.
Brant
a and
William R.
Brant
 *a
*a
aDepartment of Chemistry – Ångström Laboratory, Uppsala University, Box 538, SE-751 21 Uppsala, Sweden. E-mail: ida.nielsen@kemi.uu.se
bAltris AB, Kungsgatan 70b, SE-753 18 Uppsala, Sweden
First published on 11th June 2024
Abstract
Prussian white (PW), Na2−xFe[Fe(CN)6], is an attractive cathode material for sodium-ion batteries due to its porous framework enabling fast sodium-ion extraction and insertion, environmentally safe elements, scalable synthesis, and performance comparable to current lithium-ion technologies. However, PW suffers from large volume changes between rhombohedral and cubic phases during cycling which is suggested to be detrimental over time because of structural degradation and increased ion insertion resistance. In particular, studies on PW hard carbon full cells revealed that most of the capacity is lost from the lower potential plateau, where this phase transition occurs. It is proposed that cycling in a restricted potential range, where the phase transition is avoided, could benefit the cycle lifetime and capacity retention. Here, we show an operando X-ray diffraction study aiming at determining how the structure evolves after prolonged cycling in different restricted potential ranges and how this impacts the cycling stability and capacity fade in PW. No signs of structural degradation were observed independently of the pre-cycling conditions used. In addition, more of the rhombohedral phase and capacity were recovered in the discharged state when a more restricted potential range had been applied. Thus, it was shown that the phase transition and corresponding volume changes have little impact on the capacity fade. Instead, the main source for capacity fade was proved to be sodium inventory loss, especially during the initial cycles, in combination with, to a lesser extent, polarization. This study gives a new perspective on PW-based batteries in that neither volume changes nor phase transitions are detrimental to battery performance. These results aid the development of improved cycling protocols and battery systems comprised of PW where the lifetime of the material is prolonged.
1 Introduction
Sodium-ion batteries have become extremely important for beyond lithium-ion battery technologies due to the possibility of cheaper, more abundant elements with fewer environmental concerns. In particular, Prussian blue analogues (PBAs) are interesting electrode materials for sodium-ion batteries because of their porous framework, environmental friendliness, and performance.1,2 In addition, the simple, low-cost, and scalable synthesis makes PBAs particularly attractive for energy storage applications where large quantities of material are required. Prussian white (PW), Na2−xFe[Fe(CN)6], is a sodium-rich hexacyanoferrate with a theoretical capacity of 171 mAh g−1 and a working potential of ∼3.2 V vs. Na/Na+ (x = 0) making it competitive to the well-known lithium-ion cathode material LiFePO4.3 Besides large material quantities, another criterion for stationary energy storage is that the batteries must last for many years and many thousands of cycles.4 Even though PBAs have been shown to enable reversible sodium extraction and insertion for up to 8000 cycles, this is only possible if the capacity is limited to about half of the theoretical (∼80 mAh g−1).5 Halving the capacity corresponds to a limited amount of sodium that can be extracted and inserted within 1 ≤ x ≤ 2 in Na2−xM[Fe(CN)6]. For iron-based PBAs, this composition corresponds to a solid solution reaction of a face-centered cubic structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) where minimal volume changes occur during cycling. Going beyond a critical sodium content (x ∼ 0.8), a phase transition to a rhombohedral structure (space group R
m) where minimal volume changes occur during cycling. Going beyond a critical sodium content (x ∼ 0.8), a phase transition to a rhombohedral structure (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) )) is observed.6 The phase transition to the higher density rhombohedral structure includes a reduction in the volume by ∼17%.7 Cycling through this phase transition over time is suggested to be detrimental to the material due to structural degradation and increased resistance for sodium-ion insertion which leads to capacity fade.3 In fact, our recent work demonstrated a capacity fade of 16% on the lower voltage plateau (1.3 to 2.9 V where the phase transition takes place) after 65 cycles.8 In contrast, much less capacity fade (<1%) is observed from the upper voltage plateau (2.9 to 3.5 V) implying that the structure must be preserved. Thus, there might be a correlation between the loss of capacity from the lower voltage plateau and the phase transition in PW-based electrodes.
)) is observed.6 The phase transition to the higher density rhombohedral structure includes a reduction in the volume by ∼17%.7 Cycling through this phase transition over time is suggested to be detrimental to the material due to structural degradation and increased resistance for sodium-ion insertion which leads to capacity fade.3 In fact, our recent work demonstrated a capacity fade of 16% on the lower voltage plateau (1.3 to 2.9 V where the phase transition takes place) after 65 cycles.8 In contrast, much less capacity fade (<1%) is observed from the upper voltage plateau (2.9 to 3.5 V) implying that the structure must be preserved. Thus, there might be a correlation between the loss of capacity from the lower voltage plateau and the phase transition in PW-based electrodes.
A way of investigating the structural changes happening in a material during electrochemical cycling is to do operando X-ray diffraction (XRD). In addition, the formation of electrochemically inactive phases during cycling can also be detected if they are crystalline. For PW, it is generally accepted that the material undergoes a phase transition from an R![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) phase to an Fm
phase to an Fm![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m phase during charge which is reversible upon discharge. However, some studies have reported the existence of a tetragonal phase at the end of charge.9,10 A phase transformation from cubic to tetragonal symmetry would involve distortions activated by e.g. Jahn–Teller active elements such as manganese.11 Indeed, this is observed for iron- and manganese-based PBAs during cycling,12 however, it would be very unlikely to be experienced in the pure iron-based PBAs. Studies of the long-term cycling of PW show that the R
m phase during charge which is reversible upon discharge. However, some studies have reported the existence of a tetragonal phase at the end of charge.9,10 A phase transformation from cubic to tetragonal symmetry would involve distortions activated by e.g. Jahn–Teller active elements such as manganese.11 Indeed, this is observed for iron- and manganese-based PBAs during cycling,12 however, it would be very unlikely to be experienced in the pure iron-based PBAs. Studies of the long-term cycling of PW show that the R![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) to Fm
to Fm![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m phase transition still exists but with a wider two-phase region relative to the initial cycles.3,13 The two-phase region exists at all times during cycling except for at the end of charge where a single Fm
m phase transition still exists but with a wider two-phase region relative to the initial cycles.3,13 The two-phase region exists at all times during cycling except for at the end of charge where a single Fm![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m phase exists. Thus, the structural evolution during long-term cycling suggests that the R
m phase exists. Thus, the structural evolution during long-term cycling suggests that the R![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) phase becomes inaccessible possibly due to structural degradation.
phase becomes inaccessible possibly due to structural degradation.
Despite the extensive research on PW as a cathode material in sodium-ion batteries, only a few operando XRD studies exist for PW where even fewer of them include refinements of a model to the XRD data. For example, refining the phase fractions of the two phases present can reveal important information that can be linked to the material performance. Here, we show operando synchrotron XRD (SXRD) data of PW-based batteries pre-cycled using different potential ranges for up to 106 and 730 cycles to understand how cycling in different potential ranges impacts the cycling stability and capacity fade in PW. The potential ranges used for the pre-cycling were selected to isolate different regions where the phase transition occurs i.e. cycling only in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase region, cycling through the phase transition, and intermediates in between these endpoints (Fig. 1a). In doing so, it is possible to investigate the impact of repeated cycling through the phase transition or if completely avoiding the phase transition is more or less beneficial. The impact of cycling through the phase transition or avoiding it was quantified from the extracted phase fractions and related to the electrochemical performance to pin down the origin of capacity fade in PW-based batteries. In addition, two different electrolyte systems were investigated. Through this study and a detailed understanding of phase transitions as a function of the potential, new cycling protocols can be developed, which will prolong the lifetime of the material.
m phase region, cycling through the phase transition, and intermediates in between these endpoints (Fig. 1a). In doing so, it is possible to investigate the impact of repeated cycling through the phase transition or if completely avoiding the phase transition is more or less beneficial. The impact of cycling through the phase transition or avoiding it was quantified from the extracted phase fractions and related to the electrochemical performance to pin down the origin of capacity fade in PW-based batteries. In addition, two different electrolyte systems were investigated. Through this study and a detailed understanding of phase transitions as a function of the potential, new cycling protocols can be developed, which will prolong the lifetime of the material.
2 Methods
2.1 Electrode preparation
The sodium-ion full cells under investigation comprise commercially available Prussian white (Fennac®, Altris AB) and hard carbon (KURANODE®, Kuraray Co., Ltd). Electrode fabrication was undertaken by LiFeSiZE AB on a pilot coating line in which a water-based slurry was coated onto a 15 μm thick aluminum current collector. The slurry was composed of the active materials sodium carboxymethyl cellulose, styrene butadiene rubber, and carbon black. The acquired Prussian white (∼12 mg cm−2) and hard carbon (∼7 mg cm−2) electrode sheets were either laser cut into circular discs with a diameter of 20 and 21 mm (BOB cells), respectively, or punched into circular discs with a diameter of 13 mm (S cells). Pouch cells were assembled in an argon-containing glovebox (O2 and H2O < 1 ppm) utilizing Dreamweaver Gold™ separator (23 μm thickness, Ahlstrom-Munksjö). The S cells were injected with 100 μl of 1 M NaPF6 (Stella 99%) in ethylene carbonate and diethyl carbonate in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v (Gotion, dried over molecular sieves and filtered through a 0.2 μm polypropylene syringe filter). The BOB cells were injected with 150 μl of saturated sodium bis(oxalato)borate in triethyl phosphate (>99.8%, Merck, dried over molecular sieves and filtered through a 0.2 μm polypropylene syringe filter). Sodium bis(oxalato)borate was synthesized according to Zavalij et al.14 with oxalic acid dihydrate (>99%, Sigma), boric acid (>99.5%, Sigma), and sodium hydroxide (>98%, Alfa Aesar) in a molar ratio of 2
1 v/v (Gotion, dried over molecular sieves and filtered through a 0.2 μm polypropylene syringe filter). The BOB cells were injected with 150 μl of saturated sodium bis(oxalato)borate in triethyl phosphate (>99.8%, Merck, dried over molecular sieves and filtered through a 0.2 μm polypropylene syringe filter). Sodium bis(oxalato)borate was synthesized according to Zavalij et al.14 with oxalic acid dihydrate (>99%, Sigma), boric acid (>99.5%, Sigma), and sodium hydroxide (>98%, Alfa Aesar) in a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The synthesized white powder underwent purification through recrystallization in hot acetonitrile followed by an additional recrystallization process in trimethyl phosphate as outlined by Mogensen et al.15 The resulting electrolyte salt was vacuum dried at 100 °C for 48 hours in an argon-containing glovebox before use.
1. The synthesized white powder underwent purification through recrystallization in hot acetonitrile followed by an additional recrystallization process in trimethyl phosphate as outlined by Mogensen et al.15 The resulting electrolyte salt was vacuum dried at 100 °C for 48 hours in an argon-containing glovebox before use.
2.2 Electrochemical cycling
Galvanostatic cycling was conducted on a Neware BTS4000 cycler with a uniform formation protocol of three cycles at C/10 between 1.3 and 3.8 V. Following formation, each cell was charged and discharged using a C/3 current rate (C/5 for the BOB cells) within varying potential windows namely 3.6 V (3.5 V for the BOB cells) to 1.3, 1.7, 2.3, 2.6, 2.75 and 2.9 V, respectively (Fig. S1†). For the S cells, intermittent lower-rate cycles (C/5) were used every 10th cycle to assess whether there are significant capacity losses from kinetic effects (Fig. S2†). The current was calculated assuming 150 mAh g−1 practical capacity of the Prussian white electrode1 with an active material content of 93%. A rudimentary stack pressure was applied. Fig. 1a presents an overview of potential ranges used for the pre-cycling. In this study, the word “pre-cycling” refers to the non-formation cycles conducted before the cycling at the beamline (Fig. 1b).All cells were charged to 3.0 V before being taken off the cycling equipment and transported to the beamline. At the beamline, all cells were cycled galvanostatically using a BioLogic potentiostat in the potential window 1.3 to 3.6 V (3.5 V for the BOB cells) using a current of C/5 except for cell S8, where a current of C/10 was used (Fig. S3†). Fig. 1b presents an overview of all the cells used in this study.
2.3 Operando X-ray diffraction
In-house operando XRD was performed using a STOE Stadi P diffractometer operating in transmission mode using monochromated Cu Kα1 radiation (45 kV, 40 mA). The pouch cell was mounted on a holder in flat cell geometry.16 A multi Dectris Mythen detector was used covering a 2θ range from 0° to 55° with an angular resolution of 0.015° 2θ. The collection time for each pattern was 15 minutes, which was running continuously until stopped manually.Operando synchrotron X-ray diffraction was performed at the DanMAX beamline at MaxIV in Lund, Sweden. The pouch cells were mounted in a pouch cell holder17 optimized to hold up to six pouch cells simultaneously. No stack pressure was applied to the cells while measuring operando SXRD data (other than that imposed by the vacuum seal on the pouch cells). A Dectris Pilatus3 2 M CdTe detector was used to collect data in transmission mode with data collected every two minutes for each pouch cell. The wavelength was determined to be λ = 0.35424 Å from measurements of a LaB6 standard.
All Pawley fits and peak fitting were performed using the TOPAS Academic V6 software.18
2.4 Calculation of phase fractions
As it was not possible to do Rietveld refinements of a model to the XRD data due to the data quality and low scattering power of the PW active material relative to the aluminium from the pouch, information about phase fractions of the two phases present during cycling was obtained via intensity ratios of the 200 and 102 reflections in theFm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases, respectively.
phases, respectively.
XRD patterns of the two-phase region were calculated using the TOPAS Academic V6 software18 by fixing the sodium content to 1.2 (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and 1.8 (R
m) and 1.8 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) sodium-ions per formula unit (f.u.) for the two phases according to where the two-phase region is predicted to exist for iron- and sodium-based PBAs.6,19 The isotropic atomic displacement factors (ADPs) were set to 0.5 Å2 for all atoms. Phase fractions for the two-phase region were obtained by relating the scale factors of each phase to each other in a linear relation
) sodium-ions per formula unit (f.u.) for the two phases according to where the two-phase region is predicted to exist for iron- and sodium-based PBAs.6,19 The isotropic atomic displacement factors (ADPs) were set to 0.5 Å2 for all atoms. Phase fractions for the two-phase region were obtained by relating the scale factors of each phase to each other in a linear relation
ScaleFm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m = 1 − scaleR m = 1 − scaleR![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase to a specific value. The value of the scale factor was varied between 0.00 and 1.00 in steps of 0.01 to obtain phase fractions for the Fm
phase to a specific value. The value of the scale factor was varied between 0.00 and 1.00 in steps of 0.01 to obtain phase fractions for the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase ranging from 0 to 100%. The calculated XRD patterns were fitted using a pseudo-Voigt function where the peak position, intensity, and the Lorentzian fraction and peak width were refined. The background was fixed by straight-line segments to avoid variation in the background, which would affect the calculated intensities of the two reflections. The experimental data were fitted similarly to obtain experimental intensity ratios. Knowing the calculated intensity ratios, calculated phase fractions, and the experimental intensity ratios, the experimental phase fractions were determined using linear interpolation in Python.
m phase ranging from 0 to 100%. The calculated XRD patterns were fitted using a pseudo-Voigt function where the peak position, intensity, and the Lorentzian fraction and peak width were refined. The background was fixed by straight-line segments to avoid variation in the background, which would affect the calculated intensities of the two reflections. The experimental data were fitted similarly to obtain experimental intensity ratios. Knowing the calculated intensity ratios, calculated phase fractions, and the experimental intensity ratios, the experimental phase fractions were determined using linear interpolation in Python.
2.5 Scanning electron microscopy
The high resolution scanning electron microscopy (HR-SEM) images were obtained using a Merlin Zeiss HR-SEM instrument working with an accelerating voltage of 3 kV and a working distance of about 6.7 mm using both in-lens and high efficiency secondary electron (HE-SE) detectors. Sample preparation was performed in an argon-containing glovebox (O2 and H2O < 1 ppm), where the electrodes were extracted from the pouch cells, washed with dimethyl carbonate, and loaded onto the SEM stubs in an inert atmosphere sample transfer device (Semilab). The Semilab device was used to ensure a controlled inert sample transfer from the glovebox to the HR-SEM.3 Results
The cycling curve of PW shows two distinct plateaus at 3.0 V and 3.2 V (vs. Na/Na+) corresponding to the redox activity of the high-spin FeN and low-spin FeC sites, respectively.3 As mentioned in the introduction, PW undergoes a transition between Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases during charge and discharge (i.e. sodium extraction and insertion), which takes place during the lower voltage plateau at 3.0 V.3 On the upper voltage plateau, there is no phase transition but only a solid solution reaction. Thus, it is expected to have 100% Fm
phases during charge and discharge (i.e. sodium extraction and insertion), which takes place during the lower voltage plateau at 3.0 V.3 On the upper voltage plateau, there is no phase transition but only a solid solution reaction. Thus, it is expected to have 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase at the end of charge and 100% R
m phase at the end of charge and 100% R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase at the end of discharge. The two-phase region occurring during cycling is very narrow3 and exists only for sodium contents between 1.2 and 1.8 sodium-ions per f.u. (i.e. 0.2 ≤ x ≤ 0.8 in Na2−xFe[Fe(CN)6]).6 However, for all cells in this study (both pristine and aged cells), the two-phase region extends over a wider range (Fig. S4†) and only 100% Fm
phase at the end of discharge. The two-phase region occurring during cycling is very narrow3 and exists only for sodium contents between 1.2 and 1.8 sodium-ions per f.u. (i.e. 0.2 ≤ x ≤ 0.8 in Na2−xFe[Fe(CN)6]).6 However, for all cells in this study (both pristine and aged cells), the two-phase region extends over a wider range (Fig. S4†) and only 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is observed at the end of charge in line with previous long-term studies of PW.13 The fact that 100% R
m phase is observed at the end of charge in line with previous long-term studies of PW.13 The fact that 100% R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is never observed at the end of discharge questions the accessibility of the R
phase is never observed at the end of discharge questions the accessibility of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase during charging and discharging. Therefore, information about the amount of the Fm
phase during charging and discharging. Therefore, information about the amount of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases at different states of charge is important for understanding the structural changes and linking it to the material performance.
phases at different states of charge is important for understanding the structural changes and linking it to the material performance.
The discharge capacity from the first discharge done at the beamtime and the phase fraction at that specific point in time were extracted (Fig. 2a) and plotted in Fig. 2b for all cells. It can be seen that a narrower pre-cycling range results in more capacity recovered as well as a lower amount of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase present. All the cells follow the same trend despite differences in the electrolyte used and the number of pre-cycles done before the beamtime cycling (e.g. S4 with 75 pre-cycles relative to BOB3 with 730 pre-cycles using the same pre-cycling conditions). Noticeably, BOB7 lies outside this trend. This is due to high polarization, which the NaBOB electrolyte is well-known to cause.15 Therefore, within the potential range of 1.3 to 3.5 V applied, the PW electrode is not fully charged resulting in a low capacity (also evident in Fig. 4 below). A trend line was fitted to the data points (excluding cell BOB7) giving the equation
m phase present. All the cells follow the same trend despite differences in the electrolyte used and the number of pre-cycles done before the beamtime cycling (e.g. S4 with 75 pre-cycles relative to BOB3 with 730 pre-cycles using the same pre-cycling conditions). Noticeably, BOB7 lies outside this trend. This is due to high polarization, which the NaBOB electrolyte is well-known to cause.15 Therefore, within the potential range of 1.3 to 3.5 V applied, the PW electrode is not fully charged resulting in a low capacity (also evident in Fig. 4 below). A trend line was fitted to the data points (excluding cell BOB7) giving the equation
DChgCap = −1.32 mAh g−1 %−1 × [% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m] + 168.3 mAh g−1 m] + 168.3 mAh g−1 |
Interestingly, the intersection is close to the theoretical capacity of 171 mAh g−1 for Na2Fe[Fe(CN)6]. Thus, the proportion of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase from XRD can give indications about the capacity from the PW electrode in PW/hard carbon full cells and vice versa.
m phase from XRD can give indications about the capacity from the PW electrode in PW/hard carbon full cells and vice versa.
3.1 Phase evolution during cycling
To investigate at what full cell potential the phase transition takes place, the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction was plotted as a function of the full cell potential for all cells. The ideal behavior is shown in Fig. 3 together with the results from the pristine cell S10. The two-phase region is expected to take place during the lower plateau (Fig. 3a), where low-spin FeN is redox active. Thus, there will be an increase in the Fm
m phase fraction was plotted as a function of the full cell potential for all cells. The ideal behavior is shown in Fig. 3 together with the results from the pristine cell S10. The two-phase region is expected to take place during the lower plateau (Fig. 3a), where low-spin FeN is redox active. Thus, there will be an increase in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction until it reaches 100% at ∼2.8 V (Fig. 3b). Thereafter, the Fm
m phase fraction until it reaches 100% at ∼2.8 V (Fig. 3b). Thereafter, the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction is constant at 100%. For cell S10, which is a pristine cell with no formation or pre-cycling, the Fm
m phase fraction is constant at 100%. For cell S10, which is a pristine cell with no formation or pre-cycling, the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction is almost zero initially as expected (Fig. 3c). The deviation from zero Fm
m phase fraction is almost zero initially as expected (Fig. 3c). The deviation from zero Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction might be due to slight oxidation of the PW powder during electrode processing. The Fm
m phase fraction might be due to slight oxidation of the PW powder during electrode processing. The Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction remains at this value until ∼3.3 V, where a rapid increase is observed. The increase continues until 100% Fm
m phase fraction remains at this value until ∼3.3 V, where a rapid increase is observed. The increase continues until 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is reached at 3.42 V after which it remains at 100%. Thus, the observed evolution of the Fm
m phase is reached at 3.42 V after which it remains at 100%. Thus, the observed evolution of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction as a function of the potential does not follow the ideal behavior as shown in Fig. 3b. Instead, the phase transition occurs on the upper plateau (Fig. 3d). During discharge, the Fm
m phase fraction as a function of the potential does not follow the ideal behavior as shown in Fig. 3b. Instead, the phase transition occurs on the upper plateau (Fig. 3d). During discharge, the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction decreases over a range of potentials until it reaches 25% at 1.3 V. The fact that the potential at which the phase transition occurs is shifted to 3.3 V during charge and occurs over a range of potentials during discharge indicates polarization and inhomogeneous sodiation of the material. The second charge starts from 25% Fm
m phase fraction decreases over a range of potentials until it reaches 25% at 1.3 V. The fact that the potential at which the phase transition occurs is shifted to 3.3 V during charge and occurs over a range of potentials during discharge indicates polarization and inhomogeneous sodiation of the material. The second charge starts from 25% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction and shows similar behavior as during the first charge. This indicates that already after the first cycle, some capacity is lost since not all sodium has been inserted back into the structure of PW, which would have resulted in no Fm
m phase fraction and shows similar behavior as during the first charge. This indicates that already after the first cycle, some capacity is lost since not all sodium has been inserted back into the structure of PW, which would have resulted in no Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase present in the SXRD data in the discharged state. This is also reflected in the electrochemical performance, where the first discharge capacity is 136 mAh g−1 (∼88% of the initial charge capacity of 155 mAh g−1). This initial capacity fade is most likely due to solid electrolyte interphase (SEI) formation and/or side reactions.
m phase present in the SXRD data in the discharged state. This is also reflected in the electrochemical performance, where the first discharge capacity is 136 mAh g−1 (∼88% of the initial charge capacity of 155 mAh g−1). This initial capacity fade is most likely due to solid electrolyte interphase (SEI) formation and/or side reactions.
 | ||
Fig. 3 (a) Theoretical full cell cycling curve for a PW/hard carbon cell with the two-phase region marked with orange. Initially, PW has a rhombohedral structure which during charging converts to a cubic structure. The phase transition is reversible upon discharge. The crystal structures were generated using CrystalMaker®20 (b) the ideal evolution of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction as a function of the potential. The orange line marks the two-phase region. (c) The Fm m phase fraction as a function of the potential. The orange line marks the two-phase region. (c) The Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction as a function of the potential for cell S10 (a pristine cell). (d) The cycling curve for cell S10 with the two-phase region from (c) marked with cyan. m phase fraction as a function of the potential for cell S10 (a pristine cell). (d) The cycling curve for cell S10 with the two-phase region from (c) marked with cyan. | ||
Fig. 4 shows the calculated Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fractions plotted against the potential for the first discharge and second charge of the beamtime cycling for all cells. Similarly to cell S10, there is a rapid increase in the Fm
m phase fractions plotted against the potential for the first discharge and second charge of the beamtime cycling for all cells. Similarly to cell S10, there is a rapid increase in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction at ∼3.3 V until 100% is reached for all cells. Likewise, on discharge, the conversion occurs over a wider potential range for all cells. The cell BOB7 only reaches ∼60% Fm
m phase fraction at ∼3.3 V until 100% is reached for all cells. Likewise, on discharge, the conversion occurs over a wider potential range for all cells. The cell BOB7 only reaches ∼60% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction during the second charge, which is reflected in the low reversible capacity (Fig. S3†) illustrating the high polarization in the cell in the potential range applied. The cell S11 had undergone two formation cycles before the beamtime, thus, the two cycles at the beamtime correspond to cycles three and four relative to cell S10. The amount of the Fm
m phase fraction during the second charge, which is reflected in the low reversible capacity (Fig. S3†) illustrating the high polarization in the cell in the potential range applied. The cell S11 had undergone two formation cycles before the beamtime, thus, the two cycles at the beamtime correspond to cycles three and four relative to cell S10. The amount of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction remaining at the end of the fourth discharge is 42% suggesting a rapid decrease of the R
m phase fraction remaining at the end of the fourth discharge is 42% suggesting a rapid decrease of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase fraction during the first few cycles of the PW material, which over multiple cycles slows down (60% increase in the Fm
phase fraction during the first few cycles of the PW material, which over multiple cycles slows down (60% increase in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction going from 2nd (S10) to 4th (S11) cycle vs. 59% increase going from 4th (S11) to 111th (S7) cycle). We propose here that the capacity fade is either due to structural degradation, polarization, sodium inventory loss, particle orphaning (covering both delamination and/or particle cracking), or a combination of these.
m phase fraction going from 2nd (S10) to 4th (S11) cycle vs. 59% increase going from 4th (S11) to 111th (S7) cycle). We propose here that the capacity fade is either due to structural degradation, polarization, sodium inventory loss, particle orphaning (covering both delamination and/or particle cracking), or a combination of these.
The effect of the pre-cycling conditions is illustrated by the cells S1 to S7, which have been pre-cycled with a narrow to broad potential range, respectively, and subsequently cycled in the full potential range of 1.3 to 3.6 V at the beamtime. Cell S1 has the lowest Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction of 31% (i.e. the highest amount of the R
m phase fraction of 31% (i.e. the highest amount of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase present), while cell S7 reaches 72% Fm
phase present), while cell S7 reaches 72% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase present at the end of the first discharge. Thus, with increasing pre-cycling potential range, the amount of the Fm
m phase present at the end of the first discharge. Thus, with increasing pre-cycling potential range, the amount of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction increases in the discharged state meaning that less of the R
m phase fraction increases in the discharged state meaning that less of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is accessible since less material is sodiated during discharge. This is consistent with a lower discharge capacity for cell S7 (70 mAh g−1) compared to cell S1 (121 mAh g−1). Cells S1 to S4 have quite similar amounts of the Fm
phase is accessible since less material is sodiated during discharge. This is consistent with a lower discharge capacity for cell S7 (70 mAh g−1) compared to cell S1 (121 mAh g−1). Cells S1 to S4 have quite similar amounts of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction at the end of discharge (31% to 39%), while cells S6 and S7 have significantly higher amounts (60% and 72%, respectively) suggesting a pre-cycling range from 2.3 to 3.6 V is the best range to use for long-term cycling without losing too much capacity.
m phase fraction at the end of discharge (31% to 39%), while cells S6 and S7 have significantly higher amounts (60% and 72%, respectively) suggesting a pre-cycling range from 2.3 to 3.6 V is the best range to use for long-term cycling without losing too much capacity.
To investigate the effect of polarization, two cells (S7 and S8) were pre-cycled under similar conditions (potential range 1.3 to 3.6 V), but the current was varied at the beamtime cycling (C/5 for cell S7 and C/10 for cell S8). By reducing the current, the amount of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction at the end of discharge is reduced and more capacity is recovered (96 mAh g−1 for cell S8 vs. 70 mAh g−1 for cell S7). Thus, a lower current reduces the overpotential and generally results in a more homogeneous sodiation. This result also indicates that the structure is not necessarily degraded to a state where sodiation is not possible, but that it might be other features, such as sodium inventory loss or particle orphaning, that play a role in the loss of capacity in combination with polarization. A mechanism for the observed polarization is not attributed and this may well be due to e.g. electronic resistance increase from volume changes on either the cathode or anode side. A rudimentary estimation of the overpotential for the beamtime cycles of the S cells is presented in Fig. S5.† The relatively minor difference in the overpotential suggests that kinetic limitations are similar despite the different pre-cycling conditions, except for cell S7 which shows a slightly higher overpotential. Particle orphaning seems unlikely based on the SXRD data since it would be expected to have a distribution of particles isolated in both the Fm
m phase fraction at the end of discharge is reduced and more capacity is recovered (96 mAh g−1 for cell S8 vs. 70 mAh g−1 for cell S7). Thus, a lower current reduces the overpotential and generally results in a more homogeneous sodiation. This result also indicates that the structure is not necessarily degraded to a state where sodiation is not possible, but that it might be other features, such as sodium inventory loss or particle orphaning, that play a role in the loss of capacity in combination with polarization. A mechanism for the observed polarization is not attributed and this may well be due to e.g. electronic resistance increase from volume changes on either the cathode or anode side. A rudimentary estimation of the overpotential for the beamtime cycles of the S cells is presented in Fig. S5.† The relatively minor difference in the overpotential suggests that kinetic limitations are similar despite the different pre-cycling conditions, except for cell S7 which shows a slightly higher overpotential. Particle orphaning seems unlikely based on the SXRD data since it would be expected to have a distribution of particles isolated in both the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases meaning that there should not be 100% Fm
phases meaning that there should not be 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase at the end of charge. The jump in the Fm
m phase at the end of charge. The jump in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction from ∼90% to 100% observed for all cells is due to fitting uncertainties. When the intensity of the R
m phase fraction from ∼90% to 100% observed for all cells is due to fitting uncertainties. When the intensity of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 102 reflection becomes too low to fit, it was assumed to be non-existent resulting in the small jump in the Fm
102 reflection becomes too low to fit, it was assumed to be non-existent resulting in the small jump in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction. SEM images of some of the PW electrodes of the cells also suggest that no severe particle cracking or isolation of particles is present (Fig. S6†). However, the particles in S1 are very porous compared to the particles in cells S11 and S7. Despite the porous particles in cell S1, this cell recovered the most capacity upon discharge when cycled in the full potential range at the beamtime. It is hard to say whether it is the extended cycling in the narrow potential range (the potential range where no phase transitions take place), the subsequent cycling in the full potential range (where the phase transition takes place), or other factors, such as dissolution by the electrolyte, that have affected the porosity of the particles and why they perform better than the particles that are similar to the pristine material. It might be that the increased porosity increases the sodium-ion diffusion within the particles. In addition, there is no significant peak broadening observed for all cells (Fig. S7†) or signs of the formation of additional phases in the SXRD data (Fig. S8†). Thus, the data indicate that the capacity loss is mainly due to sodium inventory loss and some polarization. The effect of the electrolyte used does not appear to have an impact on the long-term cycling (see discussion in ESI†).
m phase fraction. SEM images of some of the PW electrodes of the cells also suggest that no severe particle cracking or isolation of particles is present (Fig. S6†). However, the particles in S1 are very porous compared to the particles in cells S11 and S7. Despite the porous particles in cell S1, this cell recovered the most capacity upon discharge when cycled in the full potential range at the beamtime. It is hard to say whether it is the extended cycling in the narrow potential range (the potential range where no phase transitions take place), the subsequent cycling in the full potential range (where the phase transition takes place), or other factors, such as dissolution by the electrolyte, that have affected the porosity of the particles and why they perform better than the particles that are similar to the pristine material. It might be that the increased porosity increases the sodium-ion diffusion within the particles. In addition, there is no significant peak broadening observed for all cells (Fig. S7†) or signs of the formation of additional phases in the SXRD data (Fig. S8†). Thus, the data indicate that the capacity loss is mainly due to sodium inventory loss and some polarization. The effect of the electrolyte used does not appear to have an impact on the long-term cycling (see discussion in ESI†).
3.2 Changes in lattice parameters
The changes in lattice parameters of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase give information about the degree of sodiation and desodiation in the material. The data were fitted with an Fm
m phase give information about the degree of sodiation and desodiation in the material. The data were fitted with an Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and an R
m and an R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase (as well as an aluminium phase and single peaks for the separator used in the pouch cells) using the Pawley method to follow the changes in the lattice parameters during cycling (Fig. S8†).
phase (as well as an aluminium phase and single peaks for the separator used in the pouch cells) using the Pawley method to follow the changes in the lattice parameters during cycling (Fig. S8†).
The refined lattice parameters for the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase as a function of the potential for the first discharge and second charge of the beamtime cycling are shown in Fig. 5. The Fm
m phase as a function of the potential for the first discharge and second charge of the beamtime cycling are shown in Fig. 5. The Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice parameter increased more rapidly at ∼3.2 V and decreased similarly upon discharge. The dashed grey line indicates at which potential the material has reached 100% Fm
m lattice parameter increased more rapidly at ∼3.2 V and decreased similarly upon discharge. The dashed grey line indicates at which potential the material has reached 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase based on the above calculated Fm
m phase based on the above calculated Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fractions. The fact that the lattice parameters and the phase fractions change simultaneously (to the left of the grey line) indicates an inhomogeneous distribution of material state of charge through the porous electrode during charging and discharging.
m phase fractions. The fact that the lattice parameters and the phase fractions change simultaneously (to the left of the grey line) indicates an inhomogeneous distribution of material state of charge through the porous electrode during charging and discharging.
 | ||
Fig. 5 Refined Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice parameters for the first discharge (the brighter color) and second charge (the darker color) of the beamtime cycling as a function of the potential. For cell S6, the second charge and discharge are shown due to lack of SXRD data during the first discharge. The arrows are present to help guide the direction of the curves. The grey dotted lines indicate at which potential 100% Fm m lattice parameters for the first discharge (the brighter color) and second charge (the darker color) of the beamtime cycling as a function of the potential. For cell S6, the second charge and discharge are shown due to lack of SXRD data during the first discharge. The arrows are present to help guide the direction of the curves. The grey dotted lines indicate at which potential 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is reached (based on Fig. 4). The shaded area between the data points represents the error bars for the refined lattice parameters. The insets show the pre-cycling ranges used for the different cells. The data for cell S11 were of too low quality to obtain reasonable refined values and are therefore omitted. m phase is reached (based on Fig. 4). The shaded area between the data points represents the error bars for the refined lattice parameters. The insets show the pre-cycling ranges used for the different cells. The data for cell S11 were of too low quality to obtain reasonable refined values and are therefore omitted. | ||
Comparing the two pristine cells, S10 and BOB7, the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice parameter is generally lower for cell BOB7 meaning that there is a larger contraction of the Fm
m lattice parameter is generally lower for cell BOB7 meaning that there is a larger contraction of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell upon sodiation. This is consistent with the lower Fm
m unit cell upon sodiation. This is consistent with the lower Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction at the end of discharge for BOB7 relative to S10 (16% vs. 25%, respectively). The higher degree of contraction is due to increased electrostatic interactions and backbonding effect when sodium is inserted into the structure and iron is reduced from Fe3+ to Fe2+. The Fm
m phase fraction at the end of discharge for BOB7 relative to S10 (16% vs. 25%, respectively). The higher degree of contraction is due to increased electrostatic interactions and backbonding effect when sodium is inserted into the structure and iron is reduced from Fe3+ to Fe2+. The Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice parameter is generally lower for the cells pre-cycled in a narrow potential range indicating a higher degree of contraction of the Fm
m lattice parameter is generally lower for the cells pre-cycled in a narrow potential range indicating a higher degree of contraction of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell consistent with the calculated Fm
m unit cell consistent with the calculated Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fractions at the end of discharge presented above i.e. the lower the amount of the Fm
m phase fractions at the end of discharge presented above i.e. the lower the amount of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase present, the higher degree of sodiation and thus more contraction of the Fm
m phase present, the higher degree of sodiation and thus more contraction of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell. Thus, a higher degree of sodiation is occurring in the cells pre-cycled in a narrow potential range. When the current is reduced (cells S7 vs. S8), there is a larger contraction of the Fm
m unit cell. Thus, a higher degree of sodiation is occurring in the cells pre-cycled in a narrow potential range. When the current is reduced (cells S7 vs. S8), there is a larger contraction of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell also in line with the calculated phase fractions. The S cells and BOB cells generally show similar Fm
m unit cell also in line with the calculated phase fractions. The S cells and BOB cells generally show similar Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice parameters despite differences in the electrolyte system used and the number of pre-cycling cycles.
m lattice parameters despite differences in the electrolyte system used and the number of pre-cycling cycles.
4 Discussion
Based on the above SXRD analysis, an evaluation of the possible degradation mechanisms that can lead to capacity fade is given. Since no additional phases are formed during cycling and no significant peak broadening is observed (Fig. S7 and S8†), it appears that the structure is preserved. In addition, when the current is reduced or a narrower pre-cycling potential range is used, it is possible to obtain more of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase during discharge (i.e. sodiation). This indicates that the structure of PW is not degraded. Therefore, the observed capacity fade during long-term cycling is thought to be mainly due to any combination of polarization, particle orphaning (covering both delamination and cracking), and/or sodium inventory loss (i.e. the sodium is inaccessible for reversible reactions due to e.g. prolonged SEI formation, SEI dissolution, and/or trapping of sodium in the hard carbon anode). Sodium inventory loss is evident in Fig. 4 since there is only a contraction along the y-axis in one direction (the Fm
phase during discharge (i.e. sodiation). This indicates that the structure of PW is not degraded. Therefore, the observed capacity fade during long-term cycling is thought to be mainly due to any combination of polarization, particle orphaning (covering both delamination and cracking), and/or sodium inventory loss (i.e. the sodium is inaccessible for reversible reactions due to e.g. prolonged SEI formation, SEI dissolution, and/or trapping of sodium in the hard carbon anode). Sodium inventory loss is evident in Fig. 4 since there is only a contraction along the y-axis in one direction (the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction always reaches 100% but never 0%). Therefore, it is more likely that the R
m phase fraction always reaches 100% but never 0%). Therefore, it is more likely that the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is inaccessible because there is not enough sodium in the system that can be inserted into the structure and thus convert all of the particles to the R
phase is inaccessible because there is not enough sodium in the system that can be inserted into the structure and thus convert all of the particles to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase. This is also illustrated in the first two cycles (cells S10 and S11), where a greater percentage of the R
phase. This is also illustrated in the first two cycles (cells S10 and S11), where a greater percentage of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase fraction is lost possibly due to the formation of SEI on the hard carbon anode and side reactions during the formation cycles. The loss of sodium inventory to SEI formation and side reactions results in less sodium available in the system to be inserted into the structure of PW leading to less of the R
phase fraction is lost possibly due to the formation of SEI on the hard carbon anode and side reactions during the formation cycles. The loss of sodium inventory to SEI formation and side reactions results in less sodium available in the system to be inserted into the structure of PW leading to less of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase present at the end of discharge. Noticeably, a previous study using X-ray absorption spectroscopy of PW electrodes at different states of charge suggested that there is a reduced use of the high-spin FeN3+/high-spin FeN2+ redox pair (corresponding to the lower voltage plateau where the phase transition takes place).3 This result hints towards sodium inventory loss since sodium-ions need to be inserted into the structure to reduce FeN3+ to FeN2+ during discharge. In addition, particle orphaning was not observed in either the SXRD data or from SEM. Thus, once the material is dehydrated prior to electrochemically cycling (which involves an increased strain in the material3,21), it stays intact even after undergoing multiple volume changes during cycling (Fig. S6†). The effect of polarization, tested by applying different currents, was found to play a role in the sodiation and desodiation process, but to a lesser extent than sodium inventory loss. Previous work on PW sodium metal half cells shows a reduction of ∼14 mAh g−1 in the capacity after 50 cycles originating from polarization in the cell when excess sodium is available.3
phase present at the end of discharge. Noticeably, a previous study using X-ray absorption spectroscopy of PW electrodes at different states of charge suggested that there is a reduced use of the high-spin FeN3+/high-spin FeN2+ redox pair (corresponding to the lower voltage plateau where the phase transition takes place).3 This result hints towards sodium inventory loss since sodium-ions need to be inserted into the structure to reduce FeN3+ to FeN2+ during discharge. In addition, particle orphaning was not observed in either the SXRD data or from SEM. Thus, once the material is dehydrated prior to electrochemically cycling (which involves an increased strain in the material3,21), it stays intact even after undergoing multiple volume changes during cycling (Fig. S6†). The effect of polarization, tested by applying different currents, was found to play a role in the sodiation and desodiation process, but to a lesser extent than sodium inventory loss. Previous work on PW sodium metal half cells shows a reduction of ∼14 mAh g−1 in the capacity after 50 cycles originating from polarization in the cell when excess sodium is available.3
To investigate the hypothesis about sodium inventory loss, an in-house operando XRD experiment was performed. A 3-electrode cell consisting of a PW working electrode, a hard carbon counter electrode, and a Na metal reference electrode (NaPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC 1
DEC 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
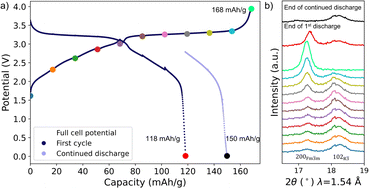
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) was assembled. The pouch cell was mounted in a holder (without any stack pressure applied) and was cycled for 2.5 hours with constant current corresponding to C/25 followed by a 2 hour rest (to obtain good XRD data when the cell is at equilibrium) for 10 cycles on charge and 7 cycles on discharge. The cycling curve is shown in Fig. 6a and S9a.† Sodium inventory loss is evident from the rapid increase of the hard carbon electrode potential upon discharge. In contrast, the PW electrode is still on the lower voltage plateau, when the full cell potential rapidly drops to 1.3 V resulting in a discharge capacity of 118 mAh g−1. The difference between the initial charge capacity of 168 mAh g−1 and the discharge capacity of 118 mAh g−1 is also affected by SEI formation and side reactions. The XRD data in Fig. 6b shows the conversion to the Fm
1 v/v) was assembled. The pouch cell was mounted in a holder (without any stack pressure applied) and was cycled for 2.5 hours with constant current corresponding to C/25 followed by a 2 hour rest (to obtain good XRD data when the cell is at equilibrium) for 10 cycles on charge and 7 cycles on discharge. The cycling curve is shown in Fig. 6a and S9a.† Sodium inventory loss is evident from the rapid increase of the hard carbon electrode potential upon discharge. In contrast, the PW electrode is still on the lower voltage plateau, when the full cell potential rapidly drops to 1.3 V resulting in a discharge capacity of 118 mAh g−1. The difference between the initial charge capacity of 168 mAh g−1 and the discharge capacity of 118 mAh g−1 is also affected by SEI formation and side reactions. The XRD data in Fig. 6b shows the conversion to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase during charge (noticeable, the pure Fm
m phase during charge (noticeable, the pure Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is not obtained until at the end of the charge similarly to the SXRD data), while there is a phase mixture of Fm
m phase is not obtained until at the end of the charge similarly to the SXRD data), while there is a phase mixture of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phases at the end of the discharge (51% Fm
phases at the end of the discharge (51% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase present). The hard carbon counter electrode was sodiated overnight using the Na metal reference electrode (Fig. S9b†) and continued discharging while collecting XRD data the day after (Fig. 6b and S9c†). An additional 32 mAh g−1 was achieved resulting in a total discharge capacity of 150 mAh g−1 and a Fm
m phase present). The hard carbon counter electrode was sodiated overnight using the Na metal reference electrode (Fig. S9b†) and continued discharging while collecting XRD data the day after (Fig. 6b and S9c†). An additional 32 mAh g−1 was achieved resulting in a total discharge capacity of 150 mAh g−1 and a Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction calculated to be 7.0%. Thus, by sodiating the hard carbon counter electrode, it was possible to obtain a higher degree of the R
m phase fraction calculated to be 7.0%. Thus, by sodiating the hard carbon counter electrode, it was possible to obtain a higher degree of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase during discharge proving that it is possible to insert sodium into the structure and that the structure is not degraded. The obtained discharge capacities and Fm
phase during discharge proving that it is possible to insert sodium into the structure and that the structure is not degraded. The obtained discharge capacities and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fractions at the end of discharge also follow the same trend as observed from the SXRD data (Fig. S10c†). The slight deviation might be due to the low data quality of the in-house XRD data giving a higher uncertainty in the calculation of the Fm
m phase fractions at the end of discharge also follow the same trend as observed from the SXRD data (Fig. S10c†). The slight deviation might be due to the low data quality of the in-house XRD data giving a higher uncertainty in the calculation of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fractions. The capacity difference between the initial charge capacity of 168 mAh g−1 and the discharge capacity of 150 mAh g−1 might be due to side reactions, inactive material, and/or polarization since the full cell potential has passed the lower plateau of the PW electrode (Fig. S9c†).
m phase fractions. The capacity difference between the initial charge capacity of 168 mAh g−1 and the discharge capacity of 150 mAh g−1 might be due to side reactions, inactive material, and/or polarization since the full cell potential has passed the lower plateau of the PW electrode (Fig. S9c†).
As the capacity fade is mainly from sodium inventory loss according to these data, strategies to reduce the capacity loss and improve the long-term cycling of PW could therefore be to sodiate the hard carbon anode before cell assembly either chemically or electrochemically, optimize the SEI formation to not consume as much sodium, or introduce additional sodium through the electrolyte such as sacrificial sodium salts. Electrochemical or chemical sodiation of hard carbon both have disadvantages such as cell reassembly, which consumes time and is more complicated, and safety issues regarding the handling of chemically sodiated hard carbon. However, the idea of having sodiated hard carbon, an optimized SEI formation process, or more sodium in the electrolyte from sacrificial sodium salts would ensure that there is more sodium in the system that can be used for insertion into the structure of PW to gain additional capacity over multiple cycles (relative to non-sodiated hard carbon, non-optimized SEI formation, or no addition of sacrificial sodium salts). These data also suggest that sodium is not stuck in the structure of PW (since 100% Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is always observed at the end of charge), but it might be elsewhere in the system e.g. in the hard carbon anode (after SEI formation). Thus, more research into the sodium storage mechanism in PW/hard carbon systems during long-term cycling is needed together with the impact of the anode on battery performance.
m phase is always observed at the end of charge), but it might be elsewhere in the system e.g. in the hard carbon anode (after SEI formation). Thus, more research into the sodium storage mechanism in PW/hard carbon systems during long-term cycling is needed together with the impact of the anode on battery performance.
When it comes to cycling conditions, the data presented indicate that the capacity retention is enhanced when cycling above 2.3 to 3.6 V. However, further studies are needed to draw further conclusions and provide a deeper understanding of the underlying mechanisms. Even though a cap on the maximum capacity is introduced when cycling in a restricted potential range, it is valuable to keep the cycling within a certain range over multiple cycles when comparing the energy density passed through the cell relative to a cell cycled in the full potential range. The presence of both phases does not seem to affect the performance. For example, cell S1 has an extended two-phase region but still performs relatively well compared to the initial capacity of a fresh cell (Fig. 2 and 4). This is also illustrated by the fact that the pre-cycling range within 2.3 to 3.6 V enhances the capacity retention the most, which is where the two-phase region occurs (Fig. 1a). Instead, it becomes a matter of having enough sodium in the system to gain the full discharge capacity of the cell (Fig. 6), which also proves that the large volume changes are not necessarily disadvantageous for cycle life. This has also been proposed previously in a theoretical study of Na2Mn[Fe(CN)6], where a maximum volume change of 27% was observed despite excellent cyclability.22 Therefore, it might not be relevant to consider if the two-phase region can be skipped by manipulating the cycling protocol since it seems to be an inevitable feature of how PW-based batteries work. Additionally, one could optimize the cycling protocols to include a higher current during the high voltage plateau and/or a lower current during the lower voltage plateau to decrease the cycling time used for long-term cycling. Furthermore, the appliance of stack pressure would increase the electronic conductivity during the cycling of the cells and this could further be improved for the operando SXRD multi pouch cell holder.
5 Conclusion
As PW suffers from capacity fade during long-term cycling, it is desired to find and understand the origin of this capacity fade. In this study, the role of phase transitions on capacity fade during long-term cycling of PW hard carbon full cells was explored using operando X-ray diffraction. Contrary to earlier hypotheses, there was no evidence of structural degradation during extended cycling. Rather, the main contributor to capacity fade during long-term cycling was found to be sodium inventory loss in combination with polarization. Thus, the long-standing argument that structural degradation due to large volume changes is the cause of capacity fade was disproved. This study sheds light on the fact that phase transitions and volume changes are not detrimental to battery performance in PW hard carbon full cells. In addition, it was found that pre-cycling between 2.3 and 3.6 V is best for long-term cycling. This work provides vital insight into the structural changes during long-term cycling of PW and the origin of capacity fade, and proposes new topics within this cell system that need to be investigated further to mitigate the loss of capacity and improve the lifetime of sodium-ion batteries comprised of PW.Author contributions
Ida Nielsen: conceptualization, methodology, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization, project administration. Charles Aram Hall: formal analysis, investigation, resources, data curation, writing – review & editing. Agnes-Matilda Mattsson: conceptualization, methodology, resources, data curation. Reza Younesi: supervision. Alexander Buckel: conceptualization, resources, data curation, writing – review & editing. Gustav Ek: formal analysis, investigation, data curation, writing – review & editing. William R. Brant: conceptualization, methodology, supervision, writing – review & editing, funding acquisition.Conflicts of interest
W. R. B. and R. Y. are co-founders of the company Altris AB, which provided the Prussian white electrodes used in this study. A. B. is employed in Altris AB.Acknowledgements
The authors gratefully acknowledge funding from Stiftelsen för Strategisk Forskning (SSF) within the Swedish National Graduate School in Neutron Scattering, SwedNess (GSn15-0008). We acknowledge MAX IV Laboratory for time on beamline DanMAX under proposal 20211101 and 20221292. Research conducted at MAX IV is supported by the Swedish Research Council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496. DanMAX is funded by the NUFI grant no. 4059-00009B. I. N. acknowledges Meghdad Hosseinzadegan for doing the SEM images used in this study. I. N. acknowledges the discussions about the calculations of the phase fractions with Nicolas P. L. Magnard and Frederik H. Gjørup.Notes and references
- L. Wang, J. Song, R. Qiao, L. A. Wray, M. A. Hossain, Y. D. Chuang, W. Yang, Y. Lu, D. Evans, J. J. Lee, S. Vail, X. Zhao, M. Nishijima, S. Kakimoto and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2548–2554 CrossRef CAS PubMed.
- A. Bauer, J. Song, S. Vail, W. Pan, J. Barker and Y. Lu, Adv. Energy Mater., 2018, 8, 1–13 Search PubMed.
- W. R. Brant, R. Mogensen, S. Colbin, D. O. Ojwang, S. Schmid, L. Häggström, T. Ericsson, A. Jaworski, A. J. Pell and R. Younesi, Chem. Mater., 2019, 31, 7203–7211 CrossRef CAS.
- J. Cho, S. Jeong and Y. Kim, Prog. Energy Combust. Sci., 2015, 48, 84–101 CrossRef.
- L. Shen, Y. Jiang, Y. Liu, J. Ma, T. Sun and N. Zhu, Chem. Eng. J., 2020, 388, 124228 CrossRef CAS.
- H. L. B. Boström and W. R. Brant, J. Mater. Chem. C, 2022, 10, 13690–13699 RSC.
- N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y.-S. Choi, S. I. R. Costa, M. Crespo Ribadeneyra, S. A. Cussen, E. J. Cussen, W. I. F. David, A. V. Desai, S. A. M. Dickson, E. I. Eweka, J. D. Forero-Saboya, C. P. Grey, J. M. Griffin, P. Gross, X. Hua, J. T. S. Irvine, P. Johansson, M. O. Jones, M. Karlsmo, E. Kendrick, E. Kim, O. V. Kolosov, Z. Li, S. F. L. Mertens, R. Mogensen, L. Monconduit, R. E. Morris, A. J. Naylor, S. Nikman, C. A. O'Keefe, D. M. C. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silván, M. T. Sougrati, L. Stievano, G. S. Stone, C. I. Thomas, M.-M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, J. Phys.: Energy, 2021, 3, 031503 CAS.
- A. Buckel, C. A. Hall, L. A. Ma, L. O. Colbin, H. Eriksson, R. Mogensen and R. Younesi, Batteries Supercaps, 2023, 202300533, 1–12 Search PubMed.
- W. Wang, Z. Hu, Z. Yan, J. Peng, M. Chen, W. Lai, Q.-f. Gu, S.-l. Chou, H.-k. Liu and S.-x. Dou, Energy Storage Mater., 2020, 30, 42–51 CrossRef.
- W. Wang, Y. Gang, Z. Hu, Z. Yan, W. Li, Y. Li, Q. F. Gu, Z. Wang, S. L. Chou, H. K. Liu and S. X. Dou, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- J. Cattermull, M. Pasta and A. L. Goodwin, Mater. Horiz., 2021, 8, 3178–3186 RSC.
- J. Song, L. Wang, Y. Lu, J. Liu, B. Guo, P. Xiao, J. J. Lee, X. Q. Yang, G. Henkelman and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2658–2664 CrossRef CAS PubMed.
- N. Y. Samoylova, I. A. Bobrikov, I. Razanau, S. V. Sumnikov, R. N. Vasin, E. A. Korneeva, O. Y. Ponomareva and U. Novikau, J. Alloys Compd., 2024, 983, 173849 CrossRef CAS.
- P. Y. Zavalij, S. Yang and M. S. Whittingham, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 753–759 CrossRef PubMed.
- R. Mogensen, S. Colbin, A. S. Menon, E. Björklund and R. Younesi, ACS Appl. Energy Mater., 2020, 3, 4974–4982 CrossRef CAS.
- O. Bergström, T. Gustafsson and J. O. Thomas, J. Appl. Crystallogr., 1998, 31, 103–105 CrossRef.
- O. Gustafsson, A. Schökel and W. R. Brant, Batteries Supercaps, 2021, 1–7 Search PubMed.
- A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- D. Boras, I. Nielsen, A. Buckel, T. Ericsson, L. Häggström, R. Younesi, T. Stabb and W. R. Brant, J. Mater. Sci., 2023, 58, 16344–16356 CrossRef CAS.
- Images and Video Generated Using CrystalMaker®: A Crystal and Molecular Structures Program for Mac and Windows, CrystalMaker Software Ltd, Oxford, England, https://www.crystalmaker.com Search PubMed.
- I. Nielsen, D. Dzodan, D. O. Ojwang, P. F. Henry, A. Ulander, G. Ek, L. Häggström, T. Ericsson, H. L. B. Boström and W. R. Brant, J. Phys.: Energy, 2022, 4, 044012 CAS.
- P. Xiao, J. Song, L. Wang, J. B. Goodenough and G. Henkelman, Chem. Mater., 2015, 27, 3763–3768 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Pre-cycling and beamtime cycling data, XRD refinement results, SEM images. See DOI: https://doi.org/10.1039/d4ta02325k |
| This journal is © The Royal Society of Chemistry 2024 |