The potential of zero charge and solvation effects on single-atom M–N–C catalysts for oxygen electrocatalysis

Abstract

Metal–nitrogen–carbon (M–N–C) catalysts are a class of emerging materials for oxygen electrocatalysis. However, a precise understanding of the predominant factors that affect their electrocatalytic activities is still preliminary, significantly hampering the rational design of high-performance M–N–C electrocatalysts. Accurate structure–activity relationship modeling necessitates considering the potential of zero charge (PZC) and solvation effects, pivotal for pH-dependent activities on a reversible hydrogen electrode scale through direct impact on reaction energetics. These factors, however, have been largely omitted in theoretical and microkinetic models due to the computational intensity of explicit solvation models. Herein, we fill in this significant knowledge gap by employing large-scale sampling via ab initio molecular dynamics and structural relaxations based on density functional theory with van der Waals corrections, on twelve distinct M–N–C configurations (M₁-pyridine-N₄ and M₁-pyrrole-N₄; M = Cr, Mn, Fe, Co, Ni, and Cu) with explicit solvation models. Interestingly, our analysis reveals that the PZCs and solvation effects, particularly hydrogen bonding adjustments to crucial reaction intermediates (HO*, O*, and HOO*), vary substantially based on the M–N–C catalysts' structures, notably the metal type and nitrogen configuration (pyridine- or pyrrole-N). Besides, both the PZCs and solvation effects of M–N–C catalysts are found to be a function of HO* binding energy; however, the PZCs follow two distinct trends on the pyridine- and pyrrole-N structures, respectively. This study shows the intricate relationship between PZC/solvation effects and M–N–Cs, and emphasizes that these effects should be considered to further improve the accuracy of microkinetic modeling.

---

Di Zhang

Dr Di Zhang is an Assistant Professor at the Advanced Institute for Materials Research (AIMR) at Tohoku University in Japan. Having completed his PhD at Shanghai Jiao Tong University in 2021, Dr. Zhang's research primarily focuses on the theoretical computation of materials and the development of artificial intelligence methods. His expertise extends to the theoretical modeling and prediction of electrochemical processes, as well as the design and development of advanced materials for hydrogen energy.

Introduction

The effective electrocatalytic generation and usage of hydrogen are the keys to meet the demand of a sustainable society.^1–3 In these processes, many key challenges remain in oxygen electrocatalysis, including the sluggish kinetics of the oxygen evolution reaction (OER) at the anode of a water elecrolyzer⁴ and the oxygen reduction reaction (ORR) at the cathode of a hydrogen fuel cell,⁵ which significantly hamper the development of large-scale techniques for hydrogen generation and usage based on green electricity. Another long-lasting challenge is the reliance on using Pt-group-metal (PGM) catalysts to drive oxygen electrocatalysis (e.g., Ir- and Ru-based catalysts for OER, and Pt-based catalysts for ORR),⁶ limiting the widespread applications of these hydrogen techniques.

The emerging metal–nitrogen–carbon (M–N–C) catalysts are a class of low-cost and promising alternatives to PGM catalysts – plenty of reports in the recent decade have provided evidence that M–N–C catalysts doped with earth-abundant metal elements (e.g., 3d metals) have versatile performance in oxygen electrocatalysis,^7,8 some of which have the performance comparable to PGM catalysts. Besides, the structure of a M–N–C catalyst can be easily tuned by either controlling the synthetic conditions in the pyrolysis of carbon substrate,^9–11 or the direct use of structurally well-defined molecular catalysts to anchor the metal active centers,^12–14 which can lead to various local M–N–C structures (e.g., M₁-pyridine-N₄ and M₁-pyrrole-N₄) that possess distinct target reaction activity and/or selectivity. Though the long-term stability issue still remains largely unaddressed (like many other PGM-based catalysts to date) under ORR and OER conditions,⁶ the above-mentioned advantages bring M–N–C catalysts to the table as competitive future candidates for oxygen electrocatalysis.

To reduce the resource- and time-consuming trial-and-error process in experimental catalyst search, much attention has been paid on the understanding of structure–performance relationships of M–N–C catalysts, in particular, M–N–C single atom catalysts (SACs).^9,15 Theoretical computations and microkinetic modeling, preliminarily based on density functional theory (DFT), are powerful methods to understand the reaction energetics over a catalyst surface and make predictions based on a “volcano/Sabatier activity model” derived for a concrete reaction system. For example, Wang and co-works⁹ performed pioneering works on understanding the ORR energetics at M–N–C SACs with various structures. Subsequently, analyses on the possible active sites of Fe–N–C SACs were performed recently, showing that Fe₁-pyrrole-N₄ could be a more active site than Fe₁-pyridine-N₄.³ However, the experimentally observed pH-dependency of ORR (at the scale of reversible hydrogen electrode, RHE) over M–N–C SACs (where a higher pH leads to a higher current density but lower four-electron selectivity) were not precisely modelled until a very recent study that Li and co-workers coupled the RHE-scale's pH effects with electric field simulations and microkinetic modeling - an interesting “acid-trap” was identified in those M–N–C SACs with moderate-binding capacity.⁷

However, though the understanding of the structure–performance relationships of M–N–C SACs has been enhanced during the past years, most studies focused on the direction correction to the catalytic reaction energetics, while dismissing other key factors, such as the potential of zero charge (PZC) and solvation effects.^16,17 In our recent benchmarking study between ORR experiments and pH-field coupled microkinetic modeling, it was found that only when we considered a more realistic value as the PZC of Fe–azaphthalocyanine catalysts in modeling, can we obtain a correct performance trend under different pH.¹⁴ In these computational models, the energies of all adsorbates must be corrected for both the standard hydrogen electrode (SHE) and reverse hydrogen electrode (RHE) potentials. The electrostatic field near to the catalyst surface is determined by U_SHE and a parallel-plate capacitor model,¹⁶i.e., E = σ/εε₀ = C_H(U_SHE − U_PZC)/εε₀, where εε₀ is the dielectric constant of water near a surface. C_H is the Helmholtz capacitance. It is evident that U_PZC can modulate the authentic electrostatic field circumventing the catalyst surface, which in turn governs the reaction energetics pursuant to the equation G_ads = G^PZC_ads + μE − (α/2)E² − neU_RHE, where E is the electric field, μ is the dipole moment, and α is polarizability. G_ads and G^PZC_ads are the corrected adsorption free energy and the adsorption free energy at the PZC, respectively. However, in most of the previous studies, the PZC terms were either calculated as the work function of the surface in an implicit solvation model (e.g., using the VASPsol package^18,19), or directly set to zero, which may lead to a dramatic discrepancy between theoretical simulations and actual experiments.

Another widely dismissed factor in ORR/OER is the solvation effect via the hydrogen bonding between water molecules and the key reaction intermediates of oxygen electrocatalysis (i.e., HO*, O*, and HOO*). Previous studies on transition metal (111) surfaces²⁰ and rutile IrO₂ (110)²¹ found that these solvation corrections could be significant because the binding strengths of HO* and HOO* can be further stabilized by ∼0.15–0.45 eV through hydrogen-bonding,¹⁷ which are also surface-sensitive.²² Note that even a difference of ∼0.1 eV in the reaction energetics can lead to a huge difference in the derived turnover frequency because it is in the exponential term of reaction kinetics (k = (k_BT/h)/exp(−G_a/k_BT), where k_B is the Boltzmann constant, T is the Kelvin temperature, and h is the Planck's constant. G_a is the activation energy for a reaction). The manner in which the PZC and solvation effects contribute to the precise modeling of single-atom catalysts is elucidated in our previous work.⁷ By explicitly accounting for the PZCs and solvation effects of M–N–C catalysts, we unveil a pH-dependent evolution in the ORR activity volcanos—from a single peak in alkaline media to a bifurcated peak in acidic media, in excellent concordance with experimental observations. This also demonstrates the approach to selectively identify exceptional ORR/OER M–N–C catalysts based on their PZCs and solvation effects. However, to the best of our knowledge, very few studies have explored such an effect over M–N–C SACs for oxygen electrocatalysis, which was in part due to the requirement of computationally expensive explicit solvation models in modeling solvation effects and PZCs.

Motivated by the current stages, herein, we performed large-scale sampling via ab initio molecular dynamics (AIMD) simulations and structural relaxations based on density functional theory (DFT) calculations with van der Waals corrections, on twelve distinct M–N–C configurations (M₁-pyridine-N₄ and M₁-pyrrole-N₄; M = Cr, Mn, Fe, Co, Ni, and Cu) with explicit solvation models. Interestingly, we found that the PZCs and solvation effects (i.e., the hydrogen-bonding corrections to the key reaction intermediates, HO*, O*, and HOO*) of these catalysts strongly depend on the structure of a M–N–C catalyst: the type of metal and the local N-configuration (e.g., pyridine- or pyrrole-N) can make a significant difference in the PZCs and solvation correction values. Besides, both the PZCs and solvation effects of M–N–C catalysts are found to be a function of HO* binding energy; however, the PZCs follow two distinct trends on the pyridine- and pyrrole-N structures, respectively. This study shows the intricate relationship between PZC/solvation effects and M–N–Cs, and emphasizes that these effects should be considered to further improve the accuracy of microkinetic modeling.

Computational and modeling methods

AIMD simulations

We performed AIMD simulations using the VASP code, adopting the revised Perdew–Burke–Ernzerhof functionals (RPBE)^23,24 exchange–correlation functional and D3 dispersion correction²⁵ for accurate metal–water interface modeling.^17,26 Our setup involved a 400 eV plane-wave cutoff and 0.1 eV Gaussian smearing, relaxing the electronic structure until forces were below 0.05 eV Å⁻¹. Simulations ran at the Γ-point with a 1 fs timestep, using a Nosé thermostat at 300 K for 10 000 steps. Interfaces were modeled with 46 water molecules for M-pyridine-N and 24 for M-pyrrole-N, ensuring at least three static water layers. In post-simulation, we selected 100 structures for geometry relaxation at a 520 eV cutoff and increased k-point density, ensuring k × a > 20 Å. These structures were analyzed to calculate PZCs and solvation effects. AIMD calculations of the initial and final state structures used in this work are available at https://github.com/tohokudizhang/Explicit_Solvation.

PZC calculations

U _PZC can be obtained by examining the reduction in work function that happens when comparing a surface in water to its counterpart in a vacuum.²⁷ Trasatti et al.²⁸ have demonstrated that U_PZC can be directly calculated from a material's work function in ion-free water (ϕ) using eqn (1):

ϕ = eU_PZC + ϕ_SHE (1)

Here, ϕ_SHE represents the absolute potential energy of the SHE. It's worth mentioning that the value of ϕ_SHE might change based on the specifics of the experimental setup, with reported values typically ranging between 4.3 and 4.8 eV. For the purposes of our study, we adopted the IUPAC (International Union of Pure and Applied Chemistry) recommended value of 4.44 eV, ensuring consistency and reliability in our findings regarding U_PZC.

Solvation effects

The starting point for calculating solvation effects was the catalyst–water structures obtained from our AIMD simulations. First, 100 of these structures were selected at regular intervals from the AIMD data. Then, adsorbates involved in the oxygen electrocatalysis like HO*, O*, and HOO* were placed on top of the metal sites. If a water molecule was already present on a metal site, it was removed before adding the adsorbate. Next, the geometry of the substrate–adsorbate structure in the solvated environment was optimized until the forces fell below 0.05 eV Å⁻¹. After this, the adsorbates were removed, and the geometry was optimized again to find the energy of the clean slab-water system. Then, the solvation effects were calculated using eqn (2)–(5):

E^solv_HO* = E^solv_slab-HO* − E^solv_slab − E_H2O + 1/2E_H2 (2)

E^solv_O* = E^solv_slab-O* − E^solv_slab − E_H2O + E_H2 (3)

E^solv_HOO* = E^solv_slab-HOO* − E^solv_slab − 2E_H2O + 3/2E_H2 (4)

E^change_ads* = E^solv_ads* − E^vacuum_ads* (5)

where E^solv_slab-ads* represents the total energy of the surface with adsorbate and water molecules. E^solv_slab denotes the total energy of a slab surface with water molecules. All these energies were obtained from DFT structural relaxations. After these calculations, E^change_ads* is considered as the solvation effect. Atomic structures used in the calculations for this work are available at https://github.com/tohokudizhang/Explicit_Solvation.

Results and discussion

PZCs

Fig. 1a shows the workflow of acquiring the PZC values on the M–N–C configurations (M₁-pyridine-N₄ and M₁-pyrrole-N₄; M = Cr, Mn, Fe, Co, Ni, and Cu). For each M–N–C structure, the procedure started with an AIMD sampling for 10 000 structures over 10 ps, followed by a selection and geometry relaxation of 100 uniformly sampled structures. Then, the PZCs were acquired as the work functions of the M–N–C configurations sampled under explicit solvation environment, which were obtained by using the absolute potential energy of standard hydrogen electrode (SHE) as reference (Fig. 1b).²²Fig. 1c shows the statistics of the PZCs across different metal centers respectively for M₁-pyrrole-N₄ (left-frame) and M₁-pyridine-N₄ (right-frame), with each value sampled from 100 fully relaxed structures. Interestingly, M₁-pyridine-N₄ and M₁-pyrrole-N₄ have quite different PZCs: M₁-pyridine-N₄ have the PZCs from −1.0 to −0.24 V/SHE across the six metal center elements, while the PZCs of M₁-pyrrole-N₄ are above zero (i.e., between 0 and 0.5 V/SHE). This opposite direction in the PZC values suggest that pyridine- and pyrrole-N may have significantly different electrocatalytic behavior. Another notable finding is that for both M₁-pyridine-N₄ and M₁-pyrrole-N₄, the PZCs generally become more positive with the evolution of the center metal element from the left- to the ride-side of the periodic table (i.e., from Cr to Cu), except that Cu₁-pyridine-N₄ has slightly more negative PZCs than Ni₁-pyridine-N₄. To the best of our knowledge, no reported results of the experimental PZC for single-atom M–N–C catalysts are available yet. Precisely controlling the metal density and obtaining an ideal graphene in M–N–C catalysts experimentally is challenging, which makes it difficult to acquire results that can be directly compared with theoretical values. Previous literature has reported the experimental PZC of pristine graphene to be −0.07 V vs. SHE.²⁹ However, vacancy sites and metal dopants are expected to alter the PZC value if present at relatively high concentrations. In our calculations, the significantly different PZC values obtained are due to the varying metal densities and carbon vacancies in the pyridine and pyrrole structures.

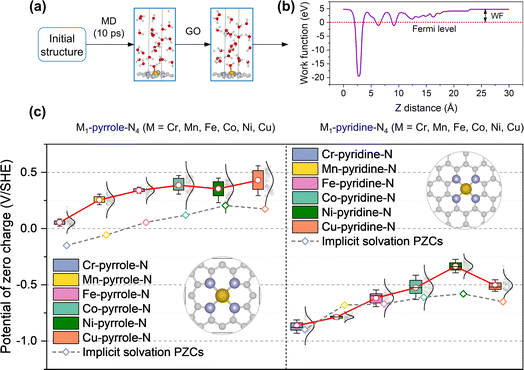Fig. 1 Determination of the potential of zero charge (PZC) in M–N–C catalysts using an explicit solvation model. (a) Illustration of the PZC calculation workflow, starting with an AIMD sampling for 10 000 structures over 10 ps, followed by a selection and geometry optimization (GO) of 100 uniformly sampled structures. (b) The work function (WF) of materials in ion-free water is utilized to calculate PZC, which is obtained by using the absolute potential energy of standard hydrogen electrode (SHE) as reference. (c) PZCs of the two typical M–N–C configurations: M-pyrrole-N₄ and M-pyridine-N₄, with insets depicting their molecular structures. Carbon, nitrogen, metal, oxygen, hydrogen atoms are gray, lavender, yellow, red, and white, respectively.

To further explore the origin of the PZC difference across different metal center elements, we defined the planes where metal atoms and hydrogen atoms have the highest occurrence probability (i.e., the highest average density) as the metal plane and the hydrogen plane, respectively, as shown in Fig. 2a. The average atomic densities of oxygen and hydrogen in water at the catalyst–water interface were summarized from both the M₁-pyrrole-N₄ (Fig. 2b) and M₁-pyridine-N₄ (Fig. 2c) structures during AIMD simulations. The vertical dashed lines indicate the highest peak positions for hydrogen (blue) and metal atoms (black) from the uppermost catalysts as references. Interestingly, these results suggest that there should be a correlation between the PZC value and the distance between metal and hydrogen atoms, as well as the average position of the highest hydrogen peak. From Fig. 2b and c, it can be observed that as the number of electrons in the 3d and 4s orbitals of the central metal atoms increases, the distance between the metal plane and the hydrogen plane also gradually increases. At the same time, the average distance between the metal plane and the hydrogen plane in M-pyrrole-N types is narrower than the average distance between the metal plane and the hydrogen plane in M-pyridine-N types. Therefore, the different distribution characteristics of water molecules on the surfaces of various catalysts are the main reason for the differences in their PZC.

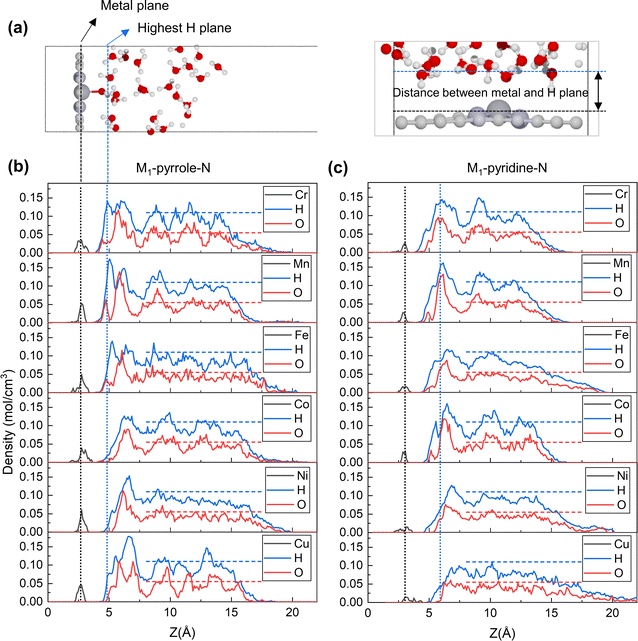Fig. 2 Average atomic densities of oxygen and hydrogen in water at the catalyst–water interface. (a) Illustration of the distance between the metal plane and the hydrogen plane (i.e., the plane where hydrogen achieves the highest density). Carbon, nitrogen, metal, oxygen, hydrogen atoms are gray, lavender, dark gray, red, and white, respectively. (b and c) The atomic densities of (b) M-pyrrole-N catalysts and (c) M-pyridine-N catalysts, with metals (M) including Cr, Mn, Fe, Co, Ni, and Cu, shown from top to bottom. The experimental atomic densities of liquid water are represented as horizontal dashed lines for comparison.²² Notably, the vertical dashed lines indicate the highest peak positions for hydrogen (blue) and metal atoms (black) from the uppermost catalysts as references. It suggests there should be a correlation between the PZC and the distance between metal and hydrogen atoms, as well as the average position of the highest hydrogen peak.

To further illustrate this, we performed correlation analyses between the metal–hydrogen distance and PZCs, as shown in Fig. 3a and b. Interestingly, the PZCs of M₁-pyrrole-N₄ (Fig. 3a) and M₁-pyridine-N₄ (Fig. 3b) structures follow two distinct correlations with the metal–hydrogen distance, as defined in Fig. 2: the PZCs of M₁-pyrrole-N₄ exhibit an increasing trend with the increase in metal–hydrogen distance. However, when the metal–hydrogen distance increases to a certain extent, the PZC appears to no longer change with the metal–hydrogen distance, indicating a weak adsorption surface.³⁰ Therefore, the overall linear fitting regression R² of M₁-pyrrole-N₄ is 0.68 (Fig. 3a); however, the PZCs of M₁-pyridine-N₄ show a high-correlation linear trend (R² = 0.95) as a function of metal–hydrogen distance (Fig. 3b). Besides, when plotting the simple HO* binding energy (calculated without solvation environment) against the metal–hydrogen distance (Fig. 3c and d), high correlation linear trends were identified for both the M₁-pyrrole-N₄ (Fig. 3c, with the slope and intercept of 1.1 and −2.3, respectively) and M₁-pyridine-N₄ (Fig. 3d, with the slope and intercept of 2.2 and −7.4, respectively). Therefore, these results suggest that the HO* binding energy can be a simple but effective descriptor that can predict the PZCs of M–N–C SACs (the correlation plot is provided in Fig. S2†), except for those weak-binding M₁-pyrrole-N₄ surfaces (i.e., Ni-pyrrole-N₄ and Cu-pyrrole-N₄). Plotting the PZCs against the HO* binding energy, we can find two different trends for M₁-pyrrole-N₄ (Fig. 3e) and M₁-pyridine-N₄ (Fig. 3f), respectively. Note that this HO* binding energy is also a proven sole descriptor for the pH-dependent microkinetic modeling of ORR on M–N–C SACs – these nice PZCs correlations with HO* binding energy suggests that the accuracy of ORR microkinetic models may be further improved by considering these PZC vs. HO*-bonding information.

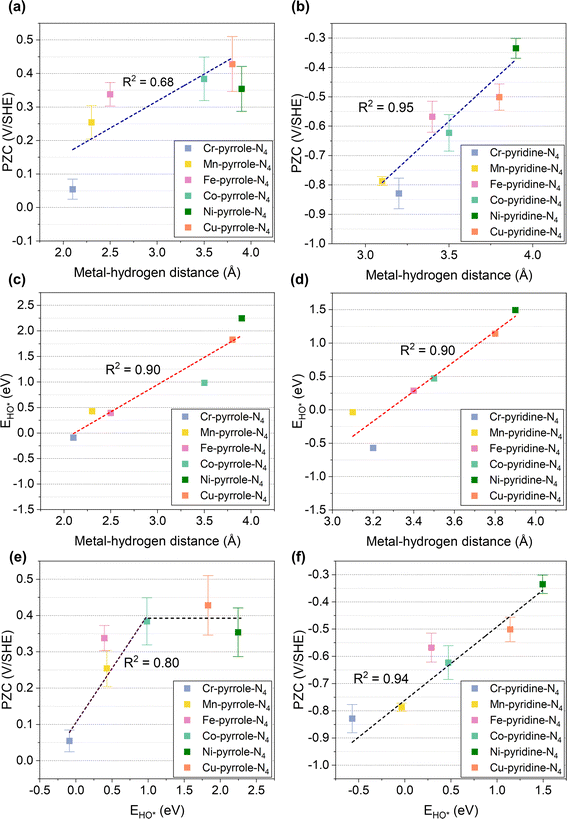Fig. 3 Linear correlations among PZC, E_HO*, and metal–hydrogen distances. (a and b) The linear correlations between PZC and metal–hydrogen distances of (a) M₁-pyrrole-N₄ and (b) M₁-pyridine-N₄ catalysts. (c and d) Linear correlations between E_HO* and metal–hydrogen distances of (c) M₁-pyrrole-N₄ and (d) M₁-pyridine-N₄ catalysts. (e and f) Correlations between PZC and E_HO* of (e) M₁-pyrrole-N₄ and (f) M₁-pyridine-N₄ catalysts. Apart from the weak-binding surfaces, such as Ni-pyrrole-N₄ and Cu-pyrrole-N₄, the PZCs of M–N–C catalysts exhibit a high-correlation linear correlation with E_HO*. For M₁-pyrrole-N₄ surfaces with weak binding properties—characterized by E_HO* values exceeding 1.0 eV—the PZC remains approximately constant regardless of E_HO* variations.

Solvation effects

Next, we analyzed the solvation effect via hydrogen-bonding between the adsorbates of oxygen electrocatalysis (HO*, O*, and HOO*) and explicit solvents. The solvation correction is primarily due to the hydrogen bonding between the ORR adsorbates and the surrounding water molecules. Each H-bond in an aqueous solvent is thought to contribute approximately 0.15 eV of energy, based on an enthalpy difference of 0.45 eV as water transitions from the gas to the liquid phase.^31,32 Ideally, this would lead to solvation energy corrections of 0.05, 0.35, and 0.40 eV for O*, HO*, and HOO*, respectively. However, the actual solvation effects are usually influenced by the charge states of the ORR adsorbates. Therefore, for each M–N–C SAC, we herein sampled 100 configurations for each adsorbate adsorption, with each of the configuration fully relaxed by DFT-D3. Therefore, we analyzed the distribution probabilities of the binding energies of HO*, O*, and HOO* at the six M₁-pyrrole-N₄ SACs (Fig. 4) and six M₁-pyridine-N₄ SAC (Fig. S1†), from which we can see that many of these are close to a normal distribution. By taking the difference between the average binding energies in explicit solvation environment and the binding energies calculated in a vacuum model (eqn (5) in the Method Section), we can acquire the solvation corrections for these binding energies at M–N–C SACs (Fig. 5a). Interestingly, it can be seen that the solvation corrections to HO*, O*, and HOO* binding energies all seem to be the function of the HO* binding energy calculated in vacuum, where a more positive HO* binding energy (i.e., a weaker HO* bonding strength) will result in a larger solvation correction (Table 1). Fig. 5b further illustrates that larger metal–adsorbate–O* bond lengths (e.g., those found at weak-binding Ni₁-pyrrole-N₄) will results in a stronger hydrogen-bonding between the solvation water molecules and the adsorbates. This further illustrates that the solvation corrections to the oxygen electrocatalysis absorbates can be directly predicted by the HO* binding energy, and that both the PZCs and solvation effects are predictable with a minimal computational cost. Meanwhile, by comparing the calculated solvation effects using implicit models with the VASPsol package (Table S2†), we found that the results obtained from implicit solvation may underestimate the solvation effects for some weaker-binding surfaces, such as Ni-pyrrole-N₄ (Fig. 5b and S2†), which is mainly because of the lack of the consideration of hydrogen-bonding effects. This further emphasizes that the solvation correction to the adsorbate binding should be considered through explicit models.

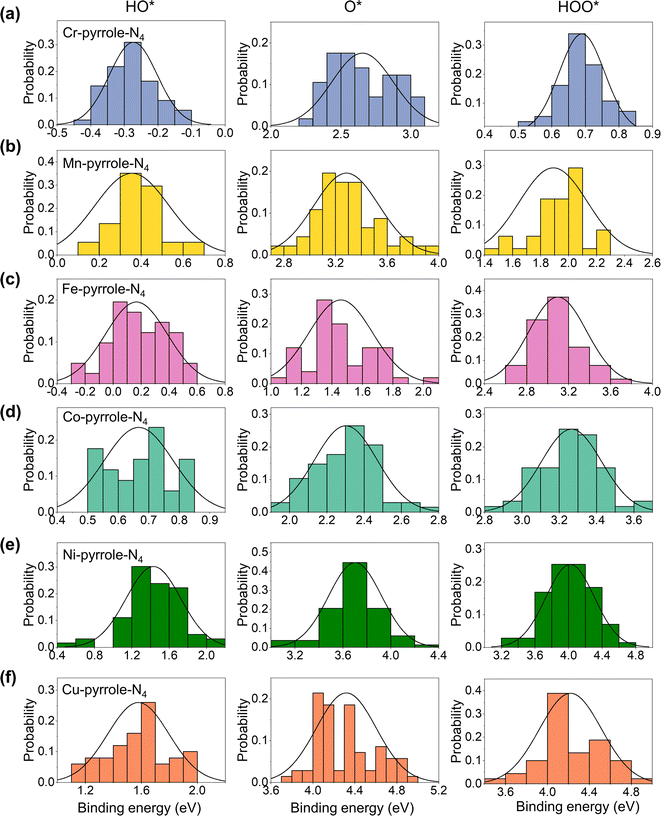Fig. 4 Solvation effects on the adsorption energy of HO*, O*, and HOO* on M–N–C catalysts. Panels (a–f) detail the adsorption energies of HO*, O*, and HOO* in a solvation environment on (a) Cr-, (b) Mn-, (c) Fe-, (d) Co-, (e) Ni-, and (f) Cu-pyrrole-N₄, respectively. Data for M₁-pyridine-N₄ catalysts are provided in Fig. S1.† The data, spread across three columns for HO*, O*, and HOO*, illustrate the adsorption energy fluctuations due to solvation, varying roughly between 0.4 and 1.6 eV around a central value, emphasizing the significant solvation influence on adsorption free energies.

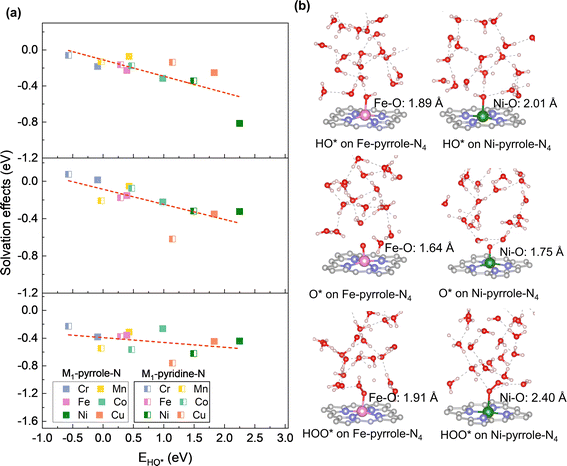Fig. 5 Analyses of solvation effects on the adsorption energies of HO*, O*, and HOO*. (a) Solvation effects as a function of E_HO* on M₁-pyrrole-N₄ and M₁-pyridine-N₄ catalysts. For catalysts with strong to moderate binding, solvation impacts are observed as follows: HO* exhibits solvation effects within 0.15 to 0.20 eV, O* within 0.10 to 0.15 eV, and HOO* within 0.33 to 0.50 eV. As E_HO* increases, the solvation effects generally become more significant. Average solvation values and further details are available in Table 1. (b) Metal–oxygen bond lengths and hydrogen bondings between adsorbates and water molecules reveal that a longer metal–oxygen bond correlates with an enhanced hydrogen bonding.

Table 1 Summary of the explicit solvation effects (E^change_ads*) on M–N–C catalysts (unit: eV)

Metal site	M1-pyrrole-N4			M1-pyridine-N4
	HO*	O*	HOO*	HO*	O*	HOO*
Cr	−0.184	0.015	−0.382	−0.061	0.075	−0.229
Mn	−0.071	−0.054	−0.313	−0.130	−0.209	−0.548
Fe	−0.227	−0.152	−0.357	−0.166	−0.177	−0.378
Co	−0.317	−0.220	−0.263	−0.176	−0.076	−0.566
Ni	−0.815	−0.323	−0.442	−0.343	−0.320	−0.624
Cu	−0.251	−0.351	−0.447	−0.138	−0.619	−0.761

---

Conclusion

In summary, we have analyzed the PZCs and solvation effects for ORR/OER adsorbates on twelve distinct M–N–C configurations (M₁-pyridine-N₄ and M₁-pyrrole-N₄; M = Cr, Mn, Fe, Co, Ni, and Cu) with explicit solvation models, by large-scale sampling via AIMD simulations and structural relaxations. We have found that the PZCs and solvation effects (i.e., the hydrogen-bonding corrections to the key reaction intermediates HO*, O*, and HOO*) of these catalysts strongly depend on the structure of a M–N–C catalyst: the type of metal and the local N-configuration (e.g., pyridine- or pyrrole-N) can make a considerable difference in the PZC and solvation correction values. Besides, both the PZCs and solvation effects of M–N–C catalysts are found to be a function of HO* binding energy; however, the PZCs follow two distinct trends on the pyridine- and pyrrole-N structures, respectively. Most importantly, this study shows that the PZCs and solvation effects should be explicitly considered for the precise design and understanding of M–N–C oxygen electrocatalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JSPS KAKENHI (No. JP23K13703), the Hirose Foundation. Di Zhang also acknowledges the support of Shanghai Jiao Tong University Outstanding Doctoral Student Development Fund and National Natural Science Foundation of China (No. 22309109). The authors acknowledge the Center for Computational Materials Science, Institute for Materials Research, Tohoku University for the use of MASAMUNE-IMR (Project No. 202312-SCKXX-0203, 202312-SCKXX-0207) and the Institute for Solid State Physics (ISSP) at the University of Tokyo for the use of their supercomputers.

References

1. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
2. X. X. Wang, M. T. Swihart and G. Wu, Nat. Catal., 2019, 2, 578–589.
3. S. Liu, C. Li, M. J. Zachman, Y. Zeng, H. Yu, B. Li, M. Wang, J. Braaten, J. Liu, H. M. Meyer, M. Lucero, A. J. Kropf, E. E. Alp, Q. Gong, Q. Shi, Z. Feng, H. Xu, G. Wang, D. J. Myers, J. Xie, D. A. Cullen, S. Litster and G. Wu, Nat. Energy, 2022, 7, 652–663.
4. N.-T. Suen, S.-F. Hung, Q. Quan, N. Zhang, Y.-J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337–365.
5. A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312.
6. M. B. Stevens, M. Anand, M. E. Kreider, E. K. Price, J. Z. Zeledón, L. Wang, J. Peng, H. Li, J. M. Gregoire, J. Hummelshøj, T. F. Jaramillo, H. Jia, J. K. Nørskov, Y. Roman-Leshkov, Y. Shao-Horn, B. D. Storey, S. K. Suram, S. B. Torrisi and J. H. Montoya, Energy Environ. Sci., 2022, 15, 3775–3794.
7. D. Zhang, Z. Wang, F. Liu, P. Yi, L. Peng, Y. Chen, L. Wei and H. Li, J. Am. Chem. Soc., 2024, 146, 3210–3219.
8. C. Liu, H. Li, F. Liu, J. Chen, Z. Yu, Z. Yuan, C. Wang, H. Zheng, G. Henkelman, L. Wei and Y. Chen, J. Am. Chem. Soc., 2020, 142, 21861–21871.
9. B. Li, E. F. Holby and G. Wang, J. Mater. Chem. A, 2022, 10, 23959–23972.
10. Y. Wang, Y.-J. Tang and K. Zhou, J. Am. Chem. Soc., 2019, 141, 14115–14119.
11. H. T. Chung, D. A. Cullen, D. Higgins, B. T. Sneed, E. F. Holby, K. L. More and P. Zelenay, Science, 2017, 357, 479–484.
12. C. Liu, Z. Yu, F. She, J. Chen, F. Liu, J. Qu, J. M. Cairney, C. Wu, K. Liu, W. Yang, H. Zheng, Y. Chen, H. Li and L. Wei, Energy Environ. Sci., 2023, 16, 446–459.
13. G. Wu, K. L. More, C. M. Johnston and P. Zelenay, Science, 2011, 332, 443–447.
14. D. Zhang, Y. Hirai, K. Nakamura, K. Ito, Y. Matsuo, K. Ishibashi, Y. Hashimoto, H. Yabu and H. Li, Chem. Sci., 2024, 15, 5123–5132.
15. X. Zhao, Z. H. Levell, S. Yu and Y. Liu, Chem. Rev., 2022, 122, 10675–10709.
16. S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2020, 124, 14581–14591.
17. H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, J. Chem. Phys., 2020, 152, 144703.
18. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101.
19. S. M. R. Islam, F. Khezeli, S. Ringe and C. Plaisance, J. Chem. Phys., 2023, 159, 234117.
20. Z.-D. He, S. Hanselman, Y.-X. Chen, M. T. M. Koper and F. Calle-Vallejo, J. Phys. Chem. Lett., 2017, 8, 2243–2246.
21. J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 11455–11463.
22. S. R. Kelly, H. H. Heenen, N. Govindarajan, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2022, 126, 5521–5528.
23. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B, 1999, 59, 7413–7421.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
26. S. Sakong, K. Forster-Tonigold and A. Groß, J. Chem. Phys., 2016, 144, 194701.
27. J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Phys. Rev. Lett., 2017, 119, 016801.
28. S. Trasatti, Electrochim. Acta, 1991, 36, 1659–1667.
29. C. H. Choi, H.-K. Lim, M. W. Chung, G. Chon, N. Ranjbar Sahraie, A. Altin, M.-T. Sougrati, L. Stievano, H. S. Oh, E. S. Park, F. Luo, P. Strasser, G. Dražić, K. J. J. Mayrhofer, H. Kim and F. Jaouen, Energy Environ. Sci., 2018, 11, 3176–3182.
30. D. Zhang, F. She, J. Chen, L. Wei and H. Li, arXiv, 2024, preprint, arXiv:2402.05405,  DOI:10.48550/arXiv.2402.05405.
31. F. Calle-Vallejo, J. I. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643.
32. A. S. Nair and B. Pathak, J. Phys. Chem. C, 2022, 126, 6171–6188.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02285h

---