Influence of misfit dislocations on ionic conductivity at oxide interfaces

Abstract

Mismatched complex oxide thin films and heterostructures have gained significant traction for use as electrolytes in intermediate temperature solid oxide fuel cells, wherein interfaces exhibit variation in ionic conductivity as compared to the bulk. Although misfit dislocations present at interfaces in these structures impact ionic conductivity, the fundamental mechanisms responsible for this effect are not well understood. To this end, a kinetic lattice Monte Carlo (KLMC) model was developed to trace oxygen vacancy diffusion at misfit dislocations in SrTiO₃/BaZrO₃ heterostructures and elucidate the atomistic mechanisms governing ionic diffusion at oxide interfaces. The KLMC model utilized oxygen vacancy migration energy barriers computed using molecular statics. While some interfaces promote oxygen vacancy diffusion, others impede their transport. Fundamental factors such as interface layer chemistry, misfit dislocation structure, and starting and ending sites of migrating ions play a crucial role in oxygen diffusivity. Molecular dynamics (MD) simulations were further performed to support qualitative trends for oxygen vacancy diffusion. Overall, the agreement between KLMC and MD is quite good, though MD tends to predict slightly higher conductivities, perhaps a reflection of nuanced structural relaxations that are not captured by KLMC. The current framework comprising KLMC modeling integrated with molecular statics offers a powerful tool to perform mechanistic studies focused on ionic transport in thin film oxide electrolytes and facilitate their rational design.

---

1. Introduction

Complex oxide heterostructures, a class of materials in which two different oxide crystals are bonded directly,^1–3 often exhibit superior and emergent properties over their individual constituents.^4–6 In mismatched oxide heterostructures, interfaces between the two oxides are critical as they are conducive to the formation of point and line defects, which significantly impact the material properties. For instance, in the case of semi-coherent oxide heterostructures, extended defects (misfit dislocations) are formed at the interface to mitigate the strain between the mismatched oxides. Fundamentally, misfit dislocations are the inevitable microstructural features present at the interfaces of semi-coherent oxide heterostructures.^7,8 Although misfit dislocations impact the material properties for applications in Solid Oxide Fuel Cells (SOFCs),^9–11 batteries,¹² nuclear materials,¹³ catalysis,¹⁴ solar cells,¹⁵ and information storage,^6,16 little is known about their fundamental role at oxide interfaces.

Due to the ever-growing miniaturization of nanotechnologies such as SOFCs and the resulting high interface-to-volume ratio, the role of interfaces has never been more critical. In SOFCs, the solid ceramic oxide electrolyte is one of the most important components as it facilitates the passage of oxide ions from the cathode to the anode. Because high ionic conductivity is imperative for the development of next-generation SOFCs, significant research efforts have been dedicated toward the design of electrolytes that facilitate faster ionic diffusion.^17–27 Since high operating temperatures result in issues related to stability and durability, widespread deployment of SOFC technology necessitates lowering their operating temperatures to the intermediate-temperature (IT-SOFC) range of 773–973 K.^28–33 One promising route toward achieving this goal is via the implementation of IT-SOFC electrolytes based on semi-coherent oxide thin films and heterostructures,^{9–11,17–25} which exhibit superior performance in the IT range.^28,30 Nonetheless, the atomistic mechanisms responsible for the observed enhancement or the impediment of ionic conduction across oxide interfaces, specifically at misfit dislocations, are not well understood. The observed ambiguity exists due to contrasting results in the literature, wherein several experiments report fast ionic transport across misfit dislocations.^{10,11,17–23} In contrast, this enrichment is not observed in other experiments.^24,25,34,35 Furthermore, computational studies report slower oxygen diffusion at homophase dislocations^36,37 and misfit dislocations.²⁶ Largely, in thin film SOFC electrolytes, the basic role of misfit dislocations and their influence on oxide ion conductivity are not well understood.

The lack of knowledge pertaining to ionic transport mechanisms at misfit dislocations in oxides can be attributed to the challenges in studying their atomic and electronic structure from both theory and experiments.³⁸ In experiments, these challenges are associated with visualizing dopants, characterizing oxygen vacancies, and resolving the nanoscale structure and chemistry of misfit dislocations. On the other hand, challenges in theory and simulations are related to system size, limiting density functional theory (DFT) based studies to coherent interfaces in order to reduce the supercell size.^8,38 As a result, studying ionic transport mechanisms at misfit dislocations is beyond the realm of DFT. A realistic alternative to DFT is the effective use of atomistic simulations based on empirical interatomic potentials, which can tackle the large system sizes often needed to simulate misfit dislocations in semi-coherent oxide heterostructures, though admittedly at the cost of loss of accuracy.³⁸

Perovskite oxide heterostructures have garnered recent interest owing to their versatility in diverse technologies. For applications as SOFC electrolytes, perovskites are often doped to tune their functionality, wherein acceptor doping (p-type) is a common practice to improve their ionic properties.³⁹ Since multifunctional oxides SrTiO₃ (STO)⁴⁰ and BaZrO₃ (BZO) have applications as SOFC electrolytes,^9,10,41 oxide heterostructures synthesized using either of them have gained prominence.^26,42,43 They also serve as suitable model systems for understanding ionic transport across oxide interfaces. Essentially, since the lattice mismatch between these perovskites falls within the range of semi-coherent interfaces,⁹ we have used the STO/BZO heterostructure^44,45 as a model thin film electrolyte to study the role of misfit dislocations and their impact on ionic transport. Although perovskites (ABO₃) exhibit compositional flexibility wherein dopants can replace either A-site, B-site, or O-site ions, we employed acceptor doping at the B-site,⁴⁶ since our work is primarily focused on ionic transport. In acceptor doping at the B-site, either Ti⁴⁺ in STO or Zr⁴⁺ in BZO could be replaced with trivalent dopants, which results in the formation of oxygen vacancies so as to maintain the defect equilibria and charge neutrality. The main benefit of acceptor doping is that the diffusion of these added carriers (vacancies) increases the overall ionic conductivity. Although acceptor doping has been extensively used to improve the properties of bulk STO⁴⁷ and bulk BZO,⁴⁸ in perovskite oxide heterostructures, especially near misfit dislocations, how dopants influence the diffusion of oxygen vacancies is not clear. This is also true for semi-coherent oxide heterostructures in general as the atomic scale interaction of oxygen vacancies with dopants and misfit dislocations is unexplored, which could lead to the contradictory results reported for ionic transport at misfit dislocations.

Due to their predictive power, lattice kinetic Monte Carlo models have been used to investigate a wide array of fundamental material processes such as surface catalysis,⁴⁹ surface diffusion,⁵⁰ atomic diffusion in alloys,⁵¹ thin film growth,⁵² ionic diffusion in fuel cell electrolytes,⁵³ ion implantation,⁵⁴ impurity diffusion,⁵⁵etc. In light of the knowledge gap in the research field of thin film ionic conductors and the predictive capabilities of kinetic Monte Carlo, we have developed a Kinetic Lattice Monte Carlo (KLMC) model to investigate the fundamental mechanisms responsible for oxygen vacancy diffusion at oxide interfaces. Recently, we developed a high-throughput framework to compute thousands of activation energy barriers for nearest neighbor migration of oxygen vacancies near the interface and at misfit dislocations in STO/BZO heterostructures.⁵⁶ The KLMC model developed in this work leverages the rates of each of these nearest neighbor migration events to study the diffusion kinetics of oxygen vacancies at STO/BZO interfaces.⁵⁶ At these interfaces, there are multiple options for how the two materials are terminated, leading to four chemically distinct interfacial structures. To study the mechanisms for vacancy diffusion and predict the trends in ionic conductivity, KLMC simulations were performed for SrO–BaO, SrO–ZrO₂, TiO₂–BaO, and TiO₂–ZrO₂ interfaces. Basic trends in ionic diffusion are qualitatively supported by molecular dynamics (MD) simulations, which, while unable to reach the same timescales of transport as KLMC simulations, also relax some of the assumptions of that model. The present approach offers fundamental insights into the role of termination chemistry and misfit dislocation structures on ionic conductivity and assists in understanding the complex interplay between trivalent dopants, oxygen vacancies, and misfit dislocations. The KLMC model further allows for comparison between interface conductivity and bulk conductivity, which has been a fundamental issue in the research field focused on ionic transport in thin film SOFC electrolytes.⁹ To the best of our knowledge, the integrated approach of combining KLMC modeling with molecular statics developed in this work has not been reported in the literature, particularly in the study of ionic diffusion in thin film oxide electrolytes.

2. Methodology

2.1 Material system

Herein, we used an STO/BZO heterostructure with a supercell comprising 21 900 atoms.^45,56 Atomic models of STO/BZO heterostructures were assembled for the cube-on-cube orientation relationship, wherein the crystallographic directions are (001)_STO‖(001)_BZO‖interface and [010]_STO‖[010]_BZO.⁵⁷ With the lattice parameters of a_STO = 3.905 Å and a_BZO = 4.197 Å, the interface is semi-coherent, and the lattice mismatch resulting from this epitaxial relationship is accommodated via the formation of misfit dislocations. The basic details of these atomic models and the resulting misfit dislocation structures are given in our recent work.^45,56 Depending on which layers meet at the interface—since STO can be terminated at charge neutral SrO or TiO₂ layers and BZO can be terminated at BaO or ZrO₂ layers—the four possible combinations of interfaces considered in this work are SrO–BaO, SrO–ZrO₂, TiO₂–BaO, and TiO₂–ZrO₂. Fig. 1(a) and (b) illustrate the interface layer atomic arrangements and the resulting misfit dislocation structures for SrO–BaO and TiO₂–ZrO₂ interfaces, respectively. Misfit dislocation structures for SrO–ZrO₂ and TiO₂–BaO interfaces are more or less similar to those observed in the SrO–BaO interface.^45,56

Fig. 1 The interface layers in STO/BZO heterostructures for (a) the SrO–BaO interface and (b) the TiO₂–ZrO₂ interface. The view is normal to the interface plane with the STO layer shown on top. Coherent stackings are shown, which are separated by misfit dislocations (black lines). Atomic colors are given below the figure panel, where oxygen ions in STO and BZO are colored differently for clarity.

2.2 Kinetic lattice Monte Carlo (KLMC)

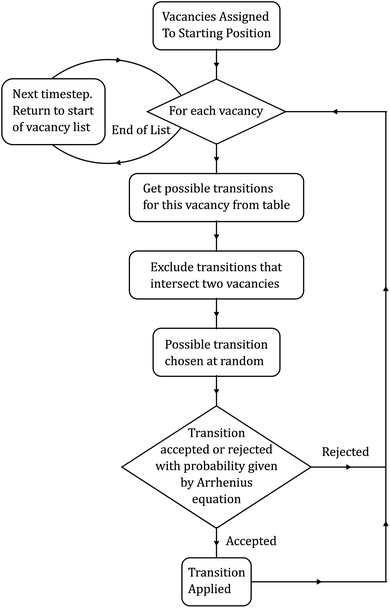
KLMC algorithms focus on using random numbers to simulate the motion of particles. KLMC simulations based on atomic-scale microscopic processes can describe the evolution of the system over time. While MD simulations explicitly track the position and momentum of all particles over time, KLMC algorithms reduce the problem to a set of coarser-grained distinct states, not concerning themselves with the finer details of how those transitions occur.⁵⁸ By dodging the finer details, KLMC algorithms are capable of simulating large structures over much larger timescales than MD. However, since KLMC does not discover how transitions occur, it is up to the developer to impose an algorithm for cataloging and choosing the said transitions.⁵⁸ Herein, the Metropolis algorithm was implemented (Fig. 2), which is a simple yet well-established method employed in a wide variety of fields due to its ability to sample the statistical distributions observed in nature.⁵⁹ Another commonly used algorithm for kinetic Monte Carlo simulations is the Bortz–Kalos–Lebowitz (BKL) algorithm.⁶⁰ However, for studying ionic conductivity in oxides, the Metropolis algorithm has been shown to offer very good agreement with experimental observations.^61,62

Fig. 2 Basic overview of the Metropolis algorithm. At each step, a random state change is chosen, which has a random probability of being accepted or rejected.

2.3 Activation energies for vacancy migration

KLMC simulations require some way of computing the probability for a state change to occur. In the KLMC model, the atomic structure of the lattice is still explicitly described and all atoms in the lattice are assumed to occupy local potential minima. The only meaningful events in these models are when an atom attempts to hop from one lattice position to another. In the current model, such hops are mediated by oxygen vacancies and the transition probabilities correspond to the so-called activation energy barriers for oxygen vacancy migration. A potential barrier E_xy then describes the barrier for a vacancy to move between separated adjacent lattice sites x and y. In our case, we only consider the transfer of oxygen vacancies as the primary type of defect responsible for ionic diffusion. Using the Boltzmann probability P,^61,62 we can convert these energy barriers into transition probabilities:where E_xy is the energy barrier between sites x and y, ν₀ is the attempt frequency or the preexponential factor often ranging between 10¹² and 10¹³ Hz,^58,61,62k_B is the Boltzmann constant, and T is the temperature. Generally, the activation energy of a defect includes two contributions – the migration energy (E_mig) and the vacancy formation energy (E_f). However, in the present case, oxygen vacancies are extrinsic and form to maintain charge balance due to the addition of aliovalent dopants, which means that vacancy concentration is directly related to the dopant fraction. Since the dopants and vacancies are associated, the number of mobile vacancies is determined by defect association energy E_ass. As a result, in aliovalently doped electrolytes, E_xy can be expressed as a sum of E_mig and E_ass, where E_mig would be the migration energy of the isolated vacancy far from the dopant. At higher temperatures, since these vacancies are essentially dissociated, the term E_xy in eqn (1) consists primarily of vacancy migration energy (E_mig).

For a material system as complex as oxide heterostructures, these barriers are too expensive to calculate on-the-fly and must be tabulated beforehand. Fortunately, this work builds on our recent work in mapping out the nearest neighbor vacancy migration energy barriers in Gd-doped STO/BZO.⁵⁶ Using molecular statics, these barriers were computed using nudged-elastic band (NEB) calculations as implemented in LAMMPS.⁶³ With this approach, we developed a framework to map out hundreds of thousands of barriers across several interface scenarios.⁵⁶ This framework essentially captures the variation of migration barriers as a function of proximity to the microstructure.⁵⁶ Complete data sets map out the entire supercell (∼130 000 barriers per supercell), which includes the interface layers as well as the bulk region. In total, 4 different configurations were studied, wherein owing to charge neutrality, 10 Gd³⁺ dopants and the consequent 5 oxygen vacancies were included. In the STO/BZO supercell (21 900 atoms), 10 dopants indicate a rather dilute doping limit. However, to examine the influence of interfaces, barriers were computed by deliberately placing the dopants at the interface layer, resulting in an interface dopant fraction of ∼1.7–1.9%, which offers a rational comparison with realistic scenarios.⁵⁶ These data offer us precisely the tabulated barriers needed for performing the KLMC simulations.

2.4 KLMC implementation

The KLMC simulator was developed and implemented as part of a Python package owing to its convenience for rapid scripting. The package contains methods for running simulations, tools for analyzing the results thereof, and even a command-line parser. However, for now we will consider only the simulator module and its implementation. The core simulator, as shown in Fig. 3, consists of several stages. First, the vacancies are randomly assigned a position in the structure. Additionally, the number of vacancies assigned should match that of the original simulated structure that the barriers came from to preserve the charge neutrality due to the presence of trivalent dopants and resulting vacancies.

Fig. 3 The complete algorithm used by the KLMC simulator.

With the initial setup done, the simulator then runs its main loop for a specified number of KLMC timesteps, which in our case is one million. At each timestep, all vacancies are offered the chance to migrate. So, for each vacancy, we retrieve all possible transitions from the tabulated data set. Additionally, any transition overlapping with an existing vacancy is discarded, as this would lead to the unphysical creation and destruction of oxygen atoms. Next, a possible transition is chosen at random and is either accepted or rejected as described previously using eqn (1). Then, we repeat this process for the remaining vacancies, thus completing a single full timestep. This approach, previously used to predict the ionic conductivity in bulk oxide electrolytes, has shown good agreement with experimental observations.^62,64 A key innovation in this work is the development of a KLMC model that can be applied to study diffusion at diverse mismatched oxide interfaces and in the vicinity of misfit dislocations, which necessitates the mapping of hundreds of thousands of migration pathways. That is, within the assumptions stated, every barrier was explicitly calculated as a function of the local microstructure, which has not been studied in the literature, especially near misfit dislocations at oxide interfaces.⁵⁶

2.5 Ionic conductivity

Ionic conductivity serves as a measure of how well charge migrates within a material. To compute this, one would typically start with the mean-squared displacement (MSD). The MSD is given by the average total squared displacement:where N is the number of vacancies, t is the time, and R_i,t is the jump distance of the ith vacancy at time t. Using the MSD, we can compute the next essential piece needed for computing ionic conductivity, which is diffusion coefficients. The diffusion coefficient, D_v, given in eqn (3) measures the ability of a vacancy to migrate over time. It is proportional to the limiting slope of the MSD.⁶²

Using D_v, we can finally compute the ionic conductivity by means of the Nernst–Einstein relationship:⁶²

where C_i is the number of ionic carriers (vacancies, in this case) per unit volume, q_e is the carrier charge, k_B is the Boltzmann constant, and T is the temperature.

2.6 Rolling window analysis

It is not unreasonable to suggest that diffusivity within the heterostructure may vary locally. For example, one interface might be more conducive to diffusion than another. Essentially, over the course of the simulation, one would expect some degree of fluctuation in the diffusion coefficient and therefore ionic conductivity. For this, we introduced a rolling window, across which we first computed the MSD. Additionally, the MSD was computed on a per-vacancy basis at this stage, rather than being treated as an ensemble average. Then, when calculating the diffusion coefficient, the maximum time, t, was simply the size of the window. Finally, the diffusion coefficients are fed into eqn (4) to obtain a time-varying conductivity. An example of this analysis is shown in Fig. 4.

Fig. 4 Time-varying ionic conductivity for a single vacancy. Data were taken from a simulation run for the TiO₂–BaO/SrO–ZrO₂ heterostructure at 3500 K. Window size was chosen to be 10 000 timesteps.

When paired with each rolling window's average position, this method allows us to track the ionic conductivity of a vacancy as it migrates throughout the structure. Additionally, we can obtain an ensemble average of a particular area of the structure by first filtering out all data outside the region of interest. Then, we average across the vacancy's conductivity history within the said region, while using the standard deviation to gauge the corresponding uncertainty. After performing this for each individual vacancy, we take a simple uncertainty-weighted average to obtain a singular number and uncertainty for the region. As compared to KLMC models developed for tracing ionic diffusion in the bulk,^53,61,62,64 an innovative aspect of the current KLMC model is the rolling window analysis. This analysis facilitates disentangling the complexity associated with tracing oxygen ion diffusion in local regions, which allows us to study the dependence of ionic conductivity on a particular interface layer chemistry and identify the differences or commonalities in the behavior of oxide interfaces in thin film electrolytes.

2.7 Molecular dynamics simulations

To provide a comparison of the metrics extracted from KLMC simulations, Molecular Dynamics (MD) simulations were conducted in analogous bulk and interfacial systems. These simulations used the atomic simulation code LAMMPS⁶³ with interactions modelled using the same potential^65,66 as used in the NEB calculations previously described.⁵⁶ The simulation box size is chosen to be approximately 5.4 × 5.4 × 5.4 nm³ containing ∼11 000 atoms, depending on the exact interface. 20 oxygen vacancies were initialized in random positions throughout the system or just at the interface, depending on the simulation setup. The introduction of oxygen vacancies induces a positive charge on the system, which is countered by adjusting the charge on all other atoms by a small percentage relative to their concentration to negate this effect; this strategy has previously been used successfully in ionic systems when measuring diffusivity.^67–70 This contrasts with what was done in the KLMC simulations, in which charge compensating dopants were introduced, but we do not expect that will significantly influence the comparisons between the two. Simulations are run until an MD time of 10 ns and throughout each run, the simulation box is held at the 0 K volume, and this decision is made to allow for a closer comparison to the KLMC simulation, where the barriers are effectively calculated at 0 K.

There are a few notable differences between the simulation setups used for MD and KLMC. Firstly, to aid in computational efficiency the MD simulation box is smaller, though importantly it retains the same dislocation patterns as in the KLMC systems. Secondly, the MD simulation boxes have the same interface on either side of the atomic system, and this allows for the targeted assessment of the oxygen diffusivity at each interface but breaks the stoichiometry of the simulation cell. Finally, no dopants have been added to the MD systems, and this is due to the strong trapping of oxygen vacancies in the vicinity of the Gd dopants (discovered during KLMC), which would impede the transport of the oxygen vacancies, not allowing for reliable transport measurements to be extracted. Regardless of these differences, we believe that MD can serve as a reliable comparison to the observable quantities measured by KLMC.

Similarly to KLMC simulations, the MSD of oxygen vacancies is measured, and the ionic conductivity is inferred through the combination of eqn (2)–(4). Further, while KLMC has an explicit description of the location of oxygen vacancies at any timestep, in MD the detection of oxygen vacancies must be done implicitly. This is achieved through Ovito's implementation of the Wigner–Seitz defect identification tool.⁷¹

3. Results

3.1 Bulk ionic conductivity

To begin, we tested our KLMC simulations on simple bulk STO and bulk BZO. Our goal with these tests was to ensure that the simulation and analysis tools were working correctly. The supercells consisted of 11 760 atoms and 10 140 atoms respectively, with both having dimensions of about 5.0 × 5.0 × 5.0 nm³. To map out a reasonably broad range, we ran simulations at temperatures ranging from 1 K to 5000 K. Additionally, ten simulations were run at each temperature to dampen the noise in any single simulation. It must be noted that the table of migration barriers used to run these simulations had somewhat higher barriers than those observed in experiments.⁷² As a result, conductivity at lower temperatures (<1000 K) would be unrealistically low, which can be circumvented by choosing higher temperatures to compensate for the lack of diffusion at lower temperatures. Though this prevents us from achieving quantitatively accurate results in the intermediate temperature (IT) range, the qualitative behavior should still be preserved. Evident from Fig. 5 is the regular increase in ionic conductivity as a function of temperature for both bulk materials. Such a trend is expected, as higher temperatures provide more energy for vacancies to overcome migration barriers. Not only that, but the higher symmetry and greater self-similarity of vacancy sites in the bulk materials (as compared to at interfaces) allow for a relatively noise-free, regular increase in conductivity, as depicted in Fig. 5.

Fig. 5 Averages of ten simulations at ten temperatures are shown for ionic conductivity in bulk STO and BZO.

Given in Table 1 are ionic conductivities for bulk STO and BZO from the current work and experimental literature. To demonstrate that the trends predicted using KLMC simulations performed at high temperatures offer accurate qualitative understanding, we have included values for ionic conductivities in bulk STO obtained using the KLMC-E model, which uses migration energy barriers in bulk STO taken from experiments and DFT calculations as input. Evidently, the data shown in Table 1 demonstrate that the KLMC model offers a reasonable comparison with the experimental values of ionic conductivity given that the energy barriers incorporated to trace oxygen vacancy diffusion are closer to experimental values. The fact that the KLMC-E model agrees well with experimental data provides confidence that the model itself reproduces experimental behavior. In this work, the goal of the KLMC model is to study the mechanisms for ionic transport and distinguish bulk vs. interfacial transport, so, while the absolute values differ from experimental values, we expect that the relative values of bulk vs. interface will still be meaningful.

Table 1 Ionic conductivities (S cm⁻¹) for bulk STO and bulk BZO predicted in the current work and reported measurements in the literature. Approximate values from the literature are included only at a single temperature (K), which in most cases is the highest temperature among the reported values. For additional data points, the reader is referred to the actual reference. In the KLMC-E model, the oxygen vacancy migration barrier of 0.60 eV in bulk STO was utilized, which was taken from experiments⁷³ and DFT calculations.⁷⁴ In the KLMC model, an oxygen vacancy migration barrier of 1.20 eV was utilized, which was obtained from molecular statics⁵⁶

Material	Ionic conductivity (S cm^−1)	Temperature (K)	Reference
STO bulk	0.50 ± 0.02 × 10^−4	2000	This work, KLMC
STO bulk	0.10 × 10^−4	2000	This work, MD
STO bulk	2.40 ± 0.5 × 10^−6	700	This work, KLMC-E
STO bulk	7.0 ± 0.8 × 10^−6	800	This work, KLMC-E
STO bulk	1.70 ± 0.1 × 10^−5	900	This work, KLMC-E
STO bulk	5.0 × 10^−2	1173	Li et al.^75
STO bulk	6.74 × 10^−4	813	Gregori et al.^76
STO bulk	8.0 × 10^−6	973	Siebenhofer et al.^72
STO bulk	1.36 × 10^−6	673	Maier et al.^39
BZO bulk	0.29 ± 0.02 × 10^−4	2000	This work, KLMC
BZO bulk	0.30 × 10^−4	2000	This work, MD
BZO bulk	2.0 × 10^−5	800	Gilardi et al.^77

---

3.2 Interface ionic conductivity

So far, results for bulk conductivity indicate that KLMC simulations are showing reasonable agreement with experimental results.⁷² With that in hand we now move on to the heterostructures. Here, we focus on the region within a few angstroms of the interfaces, allowing us to compare their varying effects. Looking at Fig. 6, we see a somewhat noisier, but otherwise consistent increase in ionic conductivity with temperature. It is worth noting that the conductivities are somewhat lower for the heterointerfaces compared to the bulk, indicating that more thermal energy is required for vacancies to traverse the landscape. One of the fundamental reasons for this behavior is that heterointerfaces introduce nonhomogeneity and asymmetry in the migration pathways of vacancies. Not only does this introduce noise into the simulation results, but the regions of significant atomic relaxation can serve to trap vacancies should they not have sufficient thermal energy to escape. This effect will be discussed later in the manuscript.

Fig. 6 Averages of ten simulations at fourteen temperatures ranging between 1000 and 5000 K. Error bars were calculated using the standard deviation between simulations.

As for comparing the different interfaces, the SrO–BaO interface shows the highest conductivity, followed by SrO–ZrO₂, TiO₂–BaO, and TiO₂–ZrO₂. This ordering is likely due to the degree of induced atomic relaxation and reconstruction at each interface, with greater relaxation creating more opportunities for the formation of vacancy-impeding traps.^45,56 For example, the SrO–BaO interface exhibited the least amount of atomic relaxation from its reconstruction, resulting in relatively fewer traps. In contrast, the TiO₂–ZrO₂ interface possessed the greatest amount of atomic relaxation, which results in numerous traps that ultimately bring down the conductivity.⁵⁶ These traps can be interpreted from the migration barriers as well since certain locations near the interface were conducive to jumping in one direction, but the reverse jump required significantly higher energies, ensuring that the vacancies would likely get trapped after reaching those locations.⁵⁶

Given in Table 2 are ionic conductivities at 2000 K for STO/BZO computed using KLMC and MD. Although there are no reports in the literature for ionic conductivity measurements on STO/BZO, a few experimental measurements for thin film electrolytes, wherein either one of the components is STO or BZO, are included in Table 2. It is imperative to note that since the experimental conductivities were measured at lower temperatures (<1000 K), the main goal here is not to offer any quantitative comparison but to discuss the qualitative behavior. Similar to the explanation for ionic conductivity in bulk STO, since the migration energy barriers in the KLMC simulations are higher than experimental values, the conductivity values at the same temperatures are expected to be lower than experimental values. In addition, fundamental factors such as experimental processing conditions, higher carrier concentration resulting from a higher dopant fraction, and having one component as an intrinsic ionic conductor (e.g., SDC and YSZ) are further responsible for the difference in ionic conductivities predicted from simulations and reported experiments. Analogous to the bulk STO behavior, we expect that the KLMC conductivities in STO/BZO will scale appropriately in accordance with lower migration barriers and fall within the range of the experimental measurements. That is, the KLMC model has adequate fidelity to offer a qualitative understanding of the fundamental mechanisms dictating the trends in ionic conductivity at oxide interfaces, which will be discussed in the subsequent sections.

Table 2 Ionic conductivities (S cm⁻¹) for the STO/BZO heterostructure predicted in the current work and reported measurements on thin film oxide electrolytes based on either BZO or STO. Approximate values from the literature are included only at a single temperature (K), which in most cases is the highest temperature among the reported values. For additional data points, the reader is referred to the actual references as well as review articles.^9,30 YSZ and SDC correspond to yttria stabilized zirconia and Sm-doped ceria, respectively

Material	Ionic conductivity (S cm^−1)	Temperature (K)	Reference
STO/BZO	0.35 ± 0.39 × 10^−4	2000	This work, KLMC
STO/BZO	0.35 × 10^−4	2000	This work, MD
BZO/Quartz	7.94 × 10^−3	1000	Park et al.^78
STO/YSZ	5.15 × 10^−6	773	Ruiz-Trejo et al.^79
STO/YSZ	3.25 × 10^−3	773	Sillassen et al.^11
STO/YSZ	1.40 × 10^−2	357	Garcia-Barriocanal et al.^10
STO/CeO2	2.40 × 10^−1	823	Shi et al.^80
SDC/STO	3.0 × 10^−2	673	Yang et al.^41

---

3.3 Mapping ionic conductivity

Recall that the rolling window method grants us the ability to track local changes in conductivity experienced by a vacancy as it traverses the structure. Using this, we can generate a map of local ionic conductivity and its variation as a function of location, which in this case was generated for the sample at 3500 K. Starting with the TiO₂–BaO/SrO–ZrO₂ heterostructure, Fig. 7(a) suggests that vacancies experience lower conductivity along the dislocation lines. This holds true for both the SrO–ZrO₂ interface across the periodic boundary and, though partially obscured, the TiO₂–BaO interface in the middle. Interestingly, the coherent terraces of TiO₂–BaO demonstrate slightly higher conductivity than the dislocation lines. It should also be noted that most of the bulk is sorely undersampled, with relatively few trajectories passing through it. This reveals that vacancies spend most of their time near the interfaces, an observation that will be further discussed in the next section. The SrO–BaO/TiO₂–ZrO₂ heterostructure, as seen in Fig. 7(b), demonstrates a very different story. Specifically, the TiO₂–ZrO₂ interface offers consistently meager conductivities in both its coherent terrace and dislocation lines, not just one or the other. Interestingly, the SrO–BaO interface in the center exhibits an extremely regular pattern as well as higher conductivities.

Fig. 7 3D plot of windowed ionic conductivity and position of every vacancy. Data were taken from aggregating all the simulations run at 3500 K. (a) TiO₂–BaO (central)/SrO–ZrO₂ (periodic). In this case, the color scale was capped at 1.3 × 10⁻⁴ S cm⁻¹ for (b) SrO–BaO (central)/TiO₂–ZrO₂ (periodic). The red lines indicate the location of misfit dislocations, wherein only one side of the periodic boundary is shown, as the other is hidden in the back of the figure but has the same structure.

To further investigate the influence of misfit dislocations on conductivity, we took cross-sections (Fig. 8) of the two interfaces in the SrO–BaO/TiO₂–ZrO₂ heterostructure at 2500 K. For the SrO–BaO interface (Fig. 8(a)), we observe an almost hour-glass shaped region of higher conductivity. The observed regularity indicates that this interface exhibits relatively low atomic relaxation, as far as conductivity is concerned. Additionally, this region coincides with the misfit dislocation lines, indicating that misfit dislocations generally improve conductivity, at least in their immediate vicinity, at this interface. In contrast, at the TiO₂–ZrO₂ interface (Fig. 8(b)), lower conductivities are encountered, with misfit dislocations having minimal impact on increasing conductivities. The horizontal streaks in Fig. 8(b) are due to the alternating pattern of favorable and unfavorable sites for oxygen vacancy migration in the ZrO₂ layer. As a result, the migration pathway out of the favorable sites takes the oxygen vacancy one layer inward from the interface. However, due to the atomic arrangement of the interface, this is not possible in the vertical direction for nearest-neighbor jumps as barium atoms are in the way, resulting in the observed pattern. This variation in conductivities between SrO–BaO and TiO₂–ZrO₂ interfaces reveals that not all misfit dislocations are conducive to faster ionic transport. In addition to the interfaces, it is likely that the vacancies could spend more time in the bulk if more trajectories are sampled in that area due to, e.g., entropic considerations (i.e., there simply being more bulk than interfacial sites for the vacancy). However, it must be noted that these conductivity plots cannot offer a complete understanding of where vacancies spend the most of their time. Since trajectories tend to obscure one another, it can only indicate that vacancies spent some of their time in a given place. In fact, as we will explore in the next section, vacancies actually spent rather little time in the bulk compared to the interface.

Fig. 8 2D cross section of windowed ionic conductivity and position of every vacancy at the (a) SrO–BaO and (b) TiO₂–ZrO₂ interfaces. Shown here is the subset of all data that traveled within 5 Å of the SrO–BaO and TiO₂–ZrO₂ interfaces, projected onto the YZ (interfacial) plane. Data taken from aggregating all simulations for this heterostructure run at 2500 K.

3.4 Mechanisms for ionic diffusion

To investigate the atomistic mechanisms for ionic diffusion, we begin by looking at how the vacancies are diffusing and where they spend most of their time. Firstly, in all cases where the temperature was high enough to allow vacancy movement, the vacancies spent the vast majority of their time near the interfaces. To illustrate this, Fig. 9 shows a histogram of the total number of timesteps that vacancies spent at a particular position. As evident from Fig. 9(a) for the TiO₂–BaO/SrO–ZrO₂ heterostructure, vacancies appear to spend a similar amount of time at the TiO₂–BaO interface as they do at the SrO–ZrO₂ interface. However, not all interfaces exhibit such a tight grip over vacancies. As shown in Fig. 9(b) for SrO–BaO/TiO₂–ZrO₂ heterostructures, vacancies did not spend a significant amount of time near the SrO–BaO interface compared to the TiO₂–ZrO₂ interface. This outcome is primarily due to the SrO–BaO interface exhibiting the least amount of atomic relaxation among the four interfaces. As a result, the odds of any traps forming at the SrO–BaO interface would have been greatly reduced, and vacancies would escape to the TiO₂–ZrO₂ interface, where they are likely to be trapped.

Fig. 9 Histogram showing the total number of timesteps all vacancies spent within a range of 48 x-bins, one for each atomic layer in the crystal in (a) TiO₂–BaO/SrO–ZrO₂ and (b) SrO–BaO/TiO₂–ZrO₂ heterostructures. These data were aggregated from all simulations run at 3500 K. The system is periodic, so the left end of the plot wraps around to the right end.

Rather importantly, the disproportionate amount of time spent at the interface demonstrates that the vacancies are, indeed, getting trapped. From here, we can easily determine where in the interface they are being trapped. To this end, Fig. 10(a) displays the total number of timesteps all vacancies spent at various sites in the SrO–BaO/TiO₂–ZrO₂ heterostructure. Immediately, we can observe that vacancies spend the majority of their time on or near the misfit dislocation lines. Conversely, relatively little time is spent in the bulk and coherent terrace alike. Meanwhile, as shown in Fig. 10(b), the TiO₂–BaO/SrO–ZrO₂ heterostructure exhibits radically different behavior. Here, the situation appears to be reversed as vacancies tend to spend the majority of their time on the coherent terrace, with slightly less time spent on the dislocations. Such an effect appears to be strongly driven by the interfacial chemistry, which was also a key driving factor in influencing the oxygen vacancy migration barriers.⁵⁶ Through further analysis, we found that these sites where the vacancies spend the majority of their time on the coherent terraces perfectly lined up with locations next to the zirconium or titanium atoms on the opposite side of the interface. Since these cations are part of an electrostatically favorable interface region, oxygen vacancies avoid hopping to the site opposite to these cations and prefer spending time at sites where there are no cations or anions across the interface.⁵⁶ The observed trend in ionic diffusion reveals a fundamental influence of the atomic layer chemistry across both sides of the interface and its ultimate impact on ionic conductivity.

Fig. 10 The total number of timesteps during which various sites were visited by all vacancies in (a) SrO–BaO/TiO₂–ZrO₂ and (b) TiO₂–BaO/SrO–ZrO₂ heterostructures. These data were aggregated from all simulations run at 3500 K. In (a), the TiO₂–ZrO₂ interface is across the periodic boundary, while the SrO–BaO interface is in the center. In (b), the SrO–ZrO₂ interface is across the periodic boundary, while the TiO₂–BaO interface is in the center. The opposite (periodic) sides in (a) show a similar pattern. The pattern visible in (b) shows up on both the opposite (periodic) side and the center.

3.5 Oxygen vacancy traps

As mentioned sporadically, a major impediment to vacancy migration is when vacancies become trapped at a particular site. Trapping occurs when a vacancy falls into a deep local energy minimum, where higher thermal energy is required to escape. In our simulations, we found vacancy trapping to be a common occurrence. Fig. S1† shows the proportion of time spent by all vacancies in the top one thousand most frequently visited sites. Here, we see that only a handful of atoms account for the vast majority of time spent by vacancies. Indeed, in the case of TiO₂–BaO/SrO–ZrO₂ at 3500 K (Fig. S1a†), we found that a mere five sites out of 13 140 account for a quarter of the time spent by the vacancies. A similar story unfolds in the SrO–BaO/TiO₂–ZrO₂ heterostructure (Fig. S1b†), wherein only four atoms account for a quarter of the time spent by vacancies. Furthermore, three of those four sites lie on the TiO₂–ZrO₂ interface, demonstrating its ability to trap vacancies. This behavior is consistent with the landscape for migration energy barriers,⁵⁶ since lower activation energies are uncovered when oxygen vacancies migrate toward certain locations, but higher energies when they hop away, revealing that vacancies would eventually get trapped and impact the ionic transport.

3.6 Comparison to molecular dynamics simulations

As with KLMC, MD simulations were first conducted in bulk STO and BZO. Fig. 11 shows the diffusivity of oxygen vacancies in a range of temperatures using eqn (2) and (3), as well as the ionic conductivity using eqn (4). The MD simulations agree well with the KLMC model showing 0 S cm⁻¹ ionic conductivity at temperatures <1500 K and an exponentially increasing conductivity with temperatures >1500 K. Further, at the highest temperature shown in both methodologies, MD predicts ∼5 × 10⁻⁴ S cm⁻¹ for BZO and ∼3 × 10⁻⁴ S cm⁻¹ for STO, remarkably similar to the values from KLMC of ∼4 × 10⁻⁴ S cm⁻¹ and ∼3 × 10⁻⁴ S cm⁻¹. Some small discrepancies between the methodologies do exist at temperatures between these extremes, which is likely due to the larger amount of sampling done during the KLMC procedure compared to the single trajectory generated through MD. Overall this indicates that the KLMC procedure is capturing the necessary features of the MD and recovering comparable trajectories.

Fig. 11 (a) Diffusivity and (b) ionic conductivity of oxygen vacancies against inverse temperature in bulk STO and BZO averaged over 10 ns of MD. The dashed line in (b) is generated from the exponential fit in (a).

Diffusivity and ionic conductivity results at the interfaces of interest are shown in Fig. 12. Overall, they show strong agreement with KLMC results particularly at SrO–BaO, SrO–ZrO₂ and TiO₂–BaO interfaces, although, generally, MD finds slightly higher conductivities. This is likely due to atomic rearrangements at the interface caused by the high temperature, which are captured in the oxygen MSD, rather than the actual motion of the oxygen vacancies. This effect would not be captured in the KLMC model as it explicitly only tracks the motion of the pre-determined vacancies. Further, the TiO₂–ZrO₂ interface shows significantly higher ionic conductivity than suggested by KLMC, specifically at higher temperatures. However, no MD data are generated at >2800 K, so this may be a result of an unreliable extrapolated fit due to the high effective energy barrier for the migration of oxygen vacancies at this interface of ∼1.5 eV (extracted from the diffusivity plot) and the resulting lack of MD sampling in the lower temperature range. In MD simulations, the operational temperature range is limited at low temperature by the lack of transport within the timescale of our simulations, while, at high temperature, the structure of the interfaces begins to change, an effect we are not interested in this work. This problem is not present in KLMC, as can be seen in Fig. 9(b), which shows high sampling at this interface and presumably a more reliable result highlighting the need for these discrete-time based methods which are, in some sense, indifferent to the height of the energy barrier.

Fig. 12 (a) Diffusivity and (b) ionic conductivity of oxygen vacancies against inverse temperature at the interfaces of interest averaged over 10 ns of MD. The dashed line in (b) is generated from the exponential fit in (a).

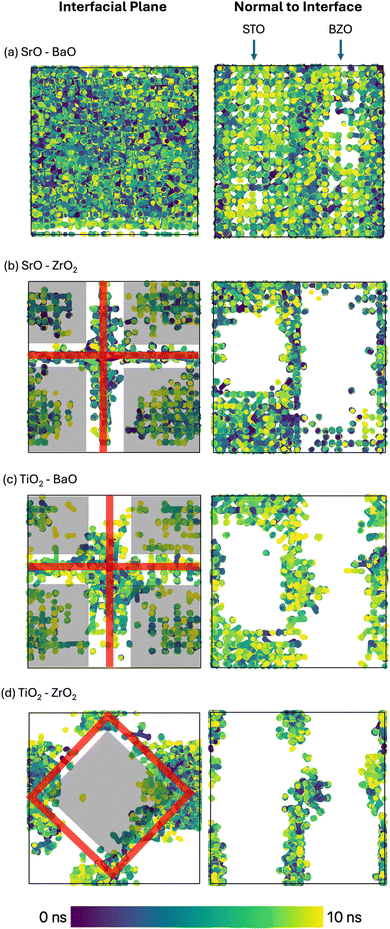
During MD, the locations of oxygen vacancies were captured and are presented in Fig. 13. Interestingly, in the atomic system containing SrO–BaO interfaces (Fig. 13(a)) there are significant signals of oxygen vacancies in the bulk-like regions, away from the interface. This indicates that the vacancies are not strongly bound to the interface and perhaps can migrate between interfaces, which will contribute to the high diffusivity seen in Fig. 12. Additionally, the vacancies seem to favor the STO side of the interface, indicating a lower formation energy on this side of the interface. In contrast to this, oxygen vacancies appear strongly bound to the TiO₂–ZrO₂ interfaces (Fig. 13(d)), where no oxygen vacancies were detected in the bulk-like regions. In systems containing SrO–ZrO₂ (Fig. 13(b)) and TiO₂–BaO (Fig. 13(c)), there is some low trace of oxygen vacancies in the bulk-like regions, which seem to favor the STO bulk over the BZO bulk, indicating some transport through these bulk regions. Additionally, the vacancies are concentrated within varying widths of the interfacial plane from tight profiles such as in SrO–ZrO₂ (Fig. 13(b)) or more distributed profiles as in TiO₂–BaO (Fig. 13(b)), highlighting the complex influence that the chemistry/structure of the interface has on the defect dynamics.

Fig. 13 Normalized histogram of the location of oxygen vacancies averaged over the 10 ns MD runs at 2600 K for (a) SrO–BaO (b) SrO–ZrO₂ (c) TiO₂–BaO and (d) TiO₂–ZrO₂ interfaces. The dashed lines indicate the approximate positions of the interfaces.

As we have seen, both methodologies find that ionic conductivity at SrO–BaO is predicted to be significantly higher than that at all other interfaces over the full range of temperatures investigated. Interestingly, analyzing the MD trajectories at this interface as shown in Fig. 14(a), we see no detectable influence of the dislocation patterns on the migration pathways of oxygen vacancies, and the vacancies seemingly exhibit a random walk at the interface and into the bulk. This is seemingly in stark contrast to the analogous image from KLMC (Fig. 8(a)). However, the analysis of the KLMC trajectories only reveals motion along the dislocations as a consequence of the ability to quantify the local ionic conductivity. This is only possible due to the explicit treatment of the location of the vacancies, which is not possible in MD. This presents yet another advantage of the KLMC algorithm as it enhances the ability to conduct in-depth analysis of this type.

Fig. 14 Trajectory of oxygen atoms in the MD simulation at 2600 K colored by the time of the trajectory for (a) SrO–BaO (b) SrO–ZrO₂ (c) TiO₂–BaO and (d) TiO₂–ZrO₂ interfaces. Orange lines represent the approximate position of the interfacial dislocations and pink regions indicate the approximate position of the coherent terraces between the dislocations.

In contrast, we recover sharp outlines of the dislocation pattern and coherent terraces in SrO–ZrO₂, shown in Fig. 14(b). Firstly, we see that the dislocations provide pathways for oxygen migration within the interface. Presumably, oxygen vacancies are attracted to these dislocation lines and use them as fast pathways along the interface. Additionally, we can see that the coherent terraces provide pathways for oxygen vacancy migration through the STO bulk-like region between interfaces. Since the oxygen vacancy behavior in Fig. 13(b) shows similar activity on either side of the STO region, we infer that there is not necessarily a net translation of atoms to either interface, but rather a churning mechanism where oxygen continuously cycles between interfaces. We also see much fewer trajectories through the BZO bulk-like region, consistent with Fig. 13(b). This effect is seen to a lesser degree in TiO₂–BaO (Fig. 13(c)), where dislocation lines can be recovered less clearly, implying a lower binding energy of the oxygen vacancy to the dislocation lines and migration into the bulk-like STO is also seen within coherent terraces.

Finally, in TiO₂–ZrO₂, we can partially recover the dislocation lines, though there is significant oxygen vacancy activity extending around the intersection point of the dislocation lines rather than along them, and this could indicate that these regions are traps for oxygen vacancies, which may be the reason for the low diffusivity at this interface. Further, we can see that in this case, coherent terraces do not provide pathways for migration into bulk-like STO/BZO; indeed, the vacancies are strongly bound to the interface, which is likely a result of the strong binding to the dislocation intersections, which would contribute to the lower diffusivity at this interface and is consistent with Fig. 13(d).

4. Discussion

Diffusion mechanisms in bulk oxides are essentially governed by the diffusion of point defects, namely interstitials and vacancies.⁸¹ In bulk perovskites⁸² and SOFC electrolytes in general,⁸³ oxygen vacancy diffusion is the primary mechanism for ionic transport. While mechanisms for oxygen vacancy diffusion in bulk oxides are widely accepted,^30,82,83 the same cannot be argued for vacancy diffusion at oxide interfaces.⁹ The complexity associated with studying vacancy diffusion mechanisms at oxide interfaces is obvious from the results herein as careful consideration of several basic factors is necessitated. Foremost is the inclusion of misfit dislocations in mismatched semi-coherent oxide interfaces. Next is the interface layer chemistry, which also dictates the misfit dislocation structure. As revealed here, these fundamental factors not only influence the thermodynamics of oxygen vacancy formation and migration⁵⁶ and the formation of dopant-defect clusters,⁴⁵ but also impact the kinetics of oxide ion diffusion.

Fig. 6 clearly shows the variation in ionic conductivities as a function of interface layer chemistry, an effect that is unlikely to be observed in bulk oxides as, again, sites are much more alike in the bulk than at the interface, wherein the chemical environment surrounding the starting and ending location of the oxygen vacancy is more or less homogeneous, barring in the vicinity of dopants. The influence of interface layer chemistry and the resulting misfit dislocation structure on ionic conductivity could be some of the basic factors accountable for reported polarizing results in ionic conductivity measurements^{10,11,17–25,34,35} and computational studies.^26,36,37 In general, these experiments do not report the precise termination layer chemistry or the prevailing misfit dislocation structure at oxide interfaces. In addition, it is probable that there are mixed terminations at oxide interfaces.⁸⁴ As a result, it is conceivable that for a given thin film oxide electrolyte, measurements performed in different experiments or perhaps even in the same experiment are characteristic of different interface layer chemistries and the resulting misfit dislocation structures, which could potentially lead to discrepancies in the reported values of ionic conductivities.

Despite the fact that interfaces offer favorable locations for oxygen vacancy formation in STO/BZO heterostructures,^45,56 certain interfaces generate traps for oxygen vacancies in coherent terraces as well as at misfit dislocations, which decreases the ionic conductivity. These results convey that neighborhoods encouraging vacancy formation might not necessarily lead to favorable migration pathways. That is, depending on the precise defect location and chemistry across the interface, some of these vacancies could sit in a deep potential minimum that requires very high thermal energies to escape, which will ultimately influence conductivity. Nonetheless, trapping of oxygen vacancies owing to structural and chemical environments as observed at oxide interfaces is not plausible in the bulk, which is one of the reasons for the disparities in ionic conductivities at the interfaces versus the bulk. In bulk oxide electrolytes, vacancy–dopant association, vacancy–vacancy repulsion, and vacancy clustering are potential mechanisms impeding ionic conductivity^62,81 and leading to an observed maximum in ionic conductivity as a function of dopant concentration.^82,85 Because KLMC simulations were performed at high temperatures and low dopant fractions, vacancy–dopant association, an effect dominant at low temperatures, was not witnessed. Analogous to the bulk, it is likely that an average interface dopant fraction yields a maximum in conductivity in thin film oxide electrolytes. However, to exclusively focus on the role of interfaces, we only considered a few distinct dopant arrangements with low dopant concentrations at the interface layer. Consequently, the results herein cannot predict the ideal dopant concentration at oxide interfaces that lead to a peak in conductivity. It is worth noting that scanning every possible dopant arrangement and concentration enters the realm of the impossible in large oxide heterostructures and is beyond the scope of the current work.

In general, the results reveal that ionic conductivity at STO/BZO interfaces (Fig. 6) is somewhat lower than the bulk conductivity in STO and BZO (Fig. 5). While these trends reveal that misfit dislocations at oxide interfaces strongly influence ionic diffusion, appraisals pertaining to bulk versus interface conductivity should be avoided for now as further work is necessitated to offer a comprehensive picture. For instance, KLMC simulations were performed at low dopant concentrations. At higher dopant fractions and ensuing higher vacancy fractions, mechanisms such as vacancy ordering,⁸⁶ vacancy–vacancy repulsion,⁶² and vacancy–dopant association^87,88 could come into play. In thin film nano-oxides,⁸⁹ owing to the high interface to volume ratio, several interfaces, including a mixture of different termination layers, could contribute toward total ionic conductivity. The formation of interface space charge regions^89,90 and their impact on ionic diffusion in the vicinity of misfit dislocations demand attention.^9,30 How these various effects or a combination of them would play out will be addressed in future work via targeted KLMC models and additional migration barrier calculations for higher dopant and vacancy concentrations.

Finally, we have demonstrated the significance of scrutinizing the basic role of misfit dislocations in influencing ionic diffusion in thin film electrolytes. Similar to STO/BZO, interfaces in semi-coherent oxide heterostructures are likely to exhibit chemically frustrated neighborhoods at misfit dislocations separated by electrostatically stable coherent terraces,^42,44,45 which would impact ionic transport. As a result, fundamental insights pertinent to the impact of the atomic scale structure of misfit dislocations and interface chemical composition on ionic conductivity are germane to a broader class of semi-coherent oxide heterostructures.^8,38 As shown here for the SrO–BaO interface in STO/BZO, certain interfaces in oxide heterostructures are likely to yield better conductivities. Since advanced synthesis and atomic layer deposition techniques allow for better control of interface layer chemistry, designing next-generation thin film oxide electrolytes with desired interfaces and the resulting misfit dislocation structure might offer a rational approach to improving the performance of IT-SOFCs.

5. Conclusions

We developed a KLMC model to study ionic diffusion in oxide heterostructures. The model was initially tested for bulk samples, which demonstrated the anticipated increase in ionic conductivity with rising temperature. Mismatched oxide interfaces in STO/BZO heterostructures yielded a similar trend of increasing conductivity as a function of temperature. As opposed to the bulk, asymmetry at the interface, the atomic scale structure of misfit dislocations, and interfacial chemical composition play a crucial role in vacancy diffusion as varying conductivities were uncovered amongst the four possible interfaces. The SrO–BaO interface yielded the highest conductivity due to the least amount of atomic relaxation, whereas the TiO₂–ZrO₂ interface was the least conducive to ionic transport owing to the significant atomic relaxation. In between are the SrO–ZrO₂ and TiO₂–BaO interfaces, which are less conducive to ionic conductivity, and in some cases tend to impede conductivity with their misfit dislocation lines frequently trapping vacancies. In several instances, oxygen vacancies were caught within traps, wherein the interface structure, especially the presence of misfit dislocations, plays a critical role. Even in cases where the thermal energy was sufficient to overcome the traps, oxygen vacancies nevertheless spent the majority of their time in the vicinity of the interfaces, often but not always near the misfit dislocations. These results shed light on the fundamental factors responsible for variation in ionic conductivity at oxide interfaces as compared to the grain interior. Crucially, it demonstrates that even within a given oxide heterostructure, disparate interfaces are likely to exhibit different conductivities owing to the interface structure, particularly that of misfit dislocations. This behavior could potentially elucidate the reported inconsistencies in ionic conductivities from experimental results for thin film oxide electrolytes.

Data availability

The majority of the data generated and analyzed in this work are included in this published article and associated ESI.† Additional data and scripts that support the findings of this work are available from the corresponding author upon reasonable request. The KLMC code developed in this work will be released on the corresponding author's website after project completion and following National Science Foundation (NSF) guidelines for public access to data.

Author contributions

P. P. D. conceptualized the KLMC study and supervised W. E., who developed the KLMC code and performed the KLMC simulations. W. E. and P. P. D. wrote the initial draft of the manuscript. B. P. U. conceptualized the MD study and supervised P. H., who performed the MD simulations. P. H. and B. P. U. wrote the MD section of the manuscript. The interpretation of the results was conducted by all authors. All authors discussed and provided input on writing the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the NSF CAREER Award grant number DMR-2042311 in the Division of Materials Research. The authors acknowledge Research Computing at the Rochester Institute of Technology for providing computational resources and support that have contributed to the research results reported in this publication. This work used the Expanse Cluster at the San Diego Supercomputer Center through allocation PHY180045 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported through NSF grants 2138259, 2138286, 2138307, 2137603, and 2138296. This research also used resources of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Work at LANL was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division under award LANLE4BU. The Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001).

References

1. P. Zubko, S. Gariglio, M. Gabay, P. Ghosez and J.-M. Triscone, Annu. Rev. Condens. Matter Phys., 2011, 2, 141.
2. J. A. Sulpizio, S. Ilani, P. Irvin and J. Levy, Annu. Rev. Mater. Res., 2014, 44, 117.
3. N. Pryds and V. Esposito, J. Electroceram., 2017, 38, 1.
4. P. Yu, Y.-H. Chu and R. Ramesh, Mater. Today, 2012, 15, 320.
5. Z. Huang, Ariando, X. R. Wang, A. Rusydi, J. Chen, H. Yang and T. Venkatesan, Adv. Mater., 2018, 30, 1802439.
6. H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa and Y. Tokura, Nat. Mater., 2012, 11, 103.
7. S. Pennycook, H. Zhou, M. Chisholm, A. Borisevich, M. Varela, J. Gazquez, T. Pennycook and J. Narayan, Acta Mater., 2013, 61, 2725.
8. B. P. Uberuaga, P. P. Dholabhai, G. Pilania and A. Chen, APL Mater., 2019, 7, 100904.
9. E. Fabbri, D. Pergolesi and E. Traversa, Sci. Technol. Adv. Mater., 2010, 11, 054503.
10. J. Garcia-Barriocanal, A. Rivera-Calzada, M. Varela, Z. Sefrioui, E. Iborra, C. Leon, S. J. Pennycook and J. Santamaria, Science, 2008, 321, 676.
11. M. Sillassen, P. Eklund, N. Pryds, E. Johnson, U. Helmersson and J. Bøttiger, Adv. Funct. Mater., 2010, 20, 2071.
12. F. Zhang, H. Cao, D. Yue, J. Zhang and M. Qu, Inorg. Chem., 2012, 51, 9544.
13. I. J. Beyerlein, M. J. Demkowicz, A. Misra and B. P. Uberuaga, Prog. Mater. Sci., 2015, 74, 125.
14. H. Jeen, W. S. Choi, M. D. Biegalski, C. M. Folkman, I.-C. Tung, D. D. Fong, J. W. Freeland, D. Shin, H. Ohta, M. F. Chisholm and H. N. Lee, Nat. Mater., 2013, 12, 1057.
15. E. Assmann, P. Blaha, R. Laskowski, K. Held, S. Okamoto and G. Sangiovanni, Phys. Rev. Lett., 2013, 110, 078701.
16. M. Salluzzo, S. Gariglio, D. Stornaiuolo, V. Sessi, S. Rusponi, C. Piamonteze, G. M. De Luca, M. Minola, D. Marre, A. Gadaleta, H. Brune, F. Nolting, N. B. Brookes and G. Ghiringhelli, Phys. Rev. Lett., 2013, 111, 087204.
17. N. Schichtel, C. Korte, D. Hesse and J. Janek, Phys. Chem. Chem. Phys., 2009, 11, 3043.
18. A. Peters, C. Korte, D. Hesse, N. Zakharov and J. Janek, Solid State Ionics, 2007, 178, 67.
19. V. Sadykov, V. Usoltsev, N. Yeremeev, N. Mezentseva, V. Pelipenko, T. Krieger, V. Belyaev, E. Sadovskaya, V. Muzykantov, Y. Fedorova, A. Lukashevich, A. Ishchenko, A. Salanov, Y. Okhlupin, N. Uvarov, O. Smorygo, A. Arzhannikov, M. Korobeynikov and M. Thumm, J. Eur. Ceram. Soc., 2013, 33, 2241.
20. S. Lee, W. Zhang, F. Khatkhatay, H. Wang, Q. Jia and J. L. MacManus-Driscoll, Nano Lett., 2015, 15, 7362.
21. I. Kosacki, C. M. Rouleau, P. F. Becher, J. Bentley and D. H. Lowndes, Solid State Ionics, 2005, 176, 1319.
22. D. Pergolesi, M. Fronzi, E. Fabbri, A. Tebano and E. Traversa, Mater. Renew. Sustain. Energy, 2012, 2, 6.
23. Y. Saito, J. Cheng, K. Crabb, H. Huang, R. Pornprasertsuk, P. C. Su and F. Prinz, ECS Trans., 2008, 11, 3.
24. X. Guo, Science, 2009, 324, 465.
25. G. F. Harrington, A. Cavallaro, D. W. McComb, S. J. Skinner and J. A. Kilner, Phys. Chem. Chem. Phys., 2017, 19, 14319.
26. P. P. Dholabhai, E. Martinez, N. T. Brown and B. P. Uberuaga, Phys. Chem. Chem. Phys., 2017, 19, 23122.
27. S. C. Singhal and K. Kendall, High-temperature Solid Oxide Fuel Cells: Fundamentals, Design and Applications, Elsevier, Oxford, 2003.
28. A. Jaiswal, A. Pesaran, S. Omar and E. D. Wachsman, ECS Trans., 2017, 78, 361.
29. E. D. Wachsman and K. T. Lee, Science, 2011, 334, 935.
30. J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 11(1)–11(29).
31. D. J. L. Brett, A. Atkinson, N. P. Brandon and S. J. Skinner, Chem. Soc. Rev., 2008, 37, 1568–1578.
32. A. Lashtabeg and S. J. Skinner, J. Mater. Chem., 2006, 16, 3161–3170.
33. S. J. Skinner, S. Cook and J. A. Kilner, Materials for Next Generation SOFCs, in Solid Oxide Fuels Cells: Facts and Figures, ed. J. Irvine, and P. Connor, Green Energy and Technology. Springer, London, 2013, pp. 181–201.
34. B. Li, J. Zhang, T. Kaspar, V. Shutthanandan, R. C. Ewing and J. Lian, Phys. Chem. Chem. Phys., 2013, 15, 1296.
35. X. Guo, E. Vasco, S. Mi, K. Szot, E. Wachsman and R. Waser, Acta Mater., 2005, 53, 5161.
36. L. Sun, D. Marrocchelli and B. Yildiz, Nat. Commun., 2015, 6, 6294.
37. V. Metlenko, A. H. H. Ramadan, F. Gunkel, H. Du, H. Schraknepper, S. Hoffmann-Eifert, R. Dittmann, R. Waser and R. A. De Souza, Nanoscale, 2014, 6, 12864.
38. P. P. Dholabhai and B. P. Uberuaga, Adv. Theory Simul., 2019, 2, 1900078.
39. R. A. Maier and C. A. Randall, J. Am. Ceram. Soc., 2016, 99, 3350.
40. Y. Pai, A. Tylan-Tyler, P. Irvin and J. Levy, Rep. Prog. Phys., 2018, 81, 036503.
41. S. M. Yang, S. Lee, J. Jian, W. Zhang, P. Lu, Q. Jia, H. Wang, T. W. Noh, S. V. Kalinin and J. L. MacManus-Driscoll, Nat. Commun., 2015, 6, 8588.
42. P. P. Dholabhai, G. Pilania, J. A. Aguiar, A. Misra and B. P. Uberuaga, Nat. Commun., 2014, 5, 5043.
43. P. P. Dholabhai, J. A. Aguiar, A. Misra and B. P. Uberuaga, J. Chem. Phys., 2014, 140, 194701.
44. G. Pilania, P. P. Dholabhai and B. P. Uberuaga, Matter, 2020, 2, 1324–1337.
45. C. Marzano and P. P. Dholabhai, J. Phys. Chem. C, 2023, 127, 15988–15999.
46. W. Luo, W. Duan, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 214109.
47. P. C. Bowes, J. N. Baker and D. L. Irving, J. Am. Ceram. Soc., 2020, 103, 1156–11733.
48. C. Y. R. Vera, H. Ding, D. Peterson, W. T. Gibbons, M. Zhou and D. Ding, J. Phys.: Energy, 2021, 3, 032019.
49. M. Hoffmann, S. Matera and K. Reuter, Comput. Phys. Commun., 2014, 185, 2138.
50. X. He, F. Cheng and Z. X. Chen, Sci. Rep., 2016, 6, 33128.
51. D. R. Alfonso and D. N. Tafen, J. Phys. Chem. C, 2015, 119, 11809.
52. Z. Wong, Y. Li and J. B. Adams, Surf. Sci., 2000, 450, 51.
53. P. Hein, B. O. H. Grope, J. Koettgen, S. Grieshammer and M. Martin, Mater. Chem. Phys., 2021, 257, 123767.
54. M. Strobel, K. H. Heinig and W. Möller, Nucl. Instrum. Meth. B, 1999, 148, 104.
55. M. M. Bunea and S. T. Dunham, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R2397(R).
56. W. Ebmeyer and P. P. Dholabhai, Mater. Adv., 2024, 5, 315–328.
57. P. R. Choudhury and S. B. Krupanidhi, J. Appl. Phys., 2008, 104, 114105.
58. A. F. Voter, Introduction to the Kinetic Monte Carlo Method, in Radiation Effects in Solids, ed. K. E. Sickafus, E. A. Kotomin, and B. P. Uberuaga, Springer Netherlands, Dordrecht, 2007, pp. 1–23.
59. J. E. Gubernatis, Marshall Rosenbluth and the Metropolis algorithm, Phys. Plasmas, 2005, 12, 057303.
60. A. B. Bortz, M. H. Kalos and J. L. Lebowitz, J. Comp. Physiol., 1975, 17, 10.
61. S. Grieshammer, B. O. H. Grope, J. Koettgen and M. Martin, Phys. Chem. Chem. Phys., 2014, 16, 9974.
62. P. P. Dholabhai, S. Anwar, J. B. Adams, P. Crozier and R. Sharma, J. Solid State Chem., 2011, 184, 811.
63. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
64. P. P. Dholabhai and J. B. Adams, J. Mater. Sci., 2012, 47, 7530.
65. G. Busker, A. Chroneos, R. W. Grimes and I. Chen, J. Am. Ceram. Soc., 1999, 82, 1553.
66. M. O. Zacate, L. Minervini, D. J. Bradfield, R. W. Grimes and K. E. Sickafus, Solid State Ionics, 2000, 128, 243.
67. T. Heisig, J. Kler, H. Du, C. Baeumer, F. Hensling, M. Glöβ, M. Moors, A. Locatelli, T. Onur Menteş, F. Genuzio, J. Mayer, R. A. De Souza and R. Dittmann, Adv. Funct. Mater., 2020, 30, 2004118.
68. H. Zhang, A. H. Ramadan and R. A. De Souza, J. Mater. Chem. A, 2018, 6, 9116.
69. H. Zhang and R. A. De Souza, J. Mater. Chem. A, 2019, 7, 25274.
70. P. Hatton and B. P. Uberuaga, J. Mater. Chem. A, 2023, 11, 3471.
71. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
72. M. Siebenhofer, F. Baiutti, J. de Dios Sirvent, T. M. Huber, A. Viernstein, S. Smetaczek, C. Herzig, M. O. Liedke, M. Butterling, A. Wagner, E. Hirschmann, A. Limbeck, A. Tarancon, J. Fleig and M. Kubicek, J. Eur. Ceram. Soc., 2022, 42, 1510.
73. R. A. De Souza, V. Metlenko, D. Park and T. E. Weirich, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174109.
74. M. Lontsi-Fomena, A. Villesuzanne, J.-P. Doumerc, C. Frayret and M. Pouchard, Comput. Mater. Sci., 2008, 44, 53.
75. R. Li, C. Zhang, J. Liu, J. Zhou and L. Xu, Mater. Res. Express, 2019, 6, 102006.
76. G. Gregori, P. Lupetin and J. Maier, ECS Trans., 2012, 45, 19.
77. E. Gilardi, E. Fabbri, L. Bi, J. L. M. Rupp, T. Lippert, D. Pergolesi and E. Traversa, J. Phys. Chem. C, 2017, 121, 9739.
78. J. S. Park, Y. Kim, J. An, J. H. Shim, T. M. Gür and F. B. Prinz, Thin Solid Films, 2013, 539, 166.
79. E. Ruiz-Trejo, K. Thyden, N. Bonanos and M. B. Mogensen, Solid State Ionics, 2016, 288, 82.
80. Q. Shi, J. Chen, Y. Xing, B. Zhu and Y. Wu, J. Electrochem. Soc., 2020, 167, 054504.
81. J. A. Van Orman and K. L. Crispin, Rev. Mineral. Geochem., 2010, 72, 757.
82. T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, J. Solid State Chem., 1988, 73, 179.
83. J. B. Goodenough, Annu. Rev. Mater. Res., 2003, 33, 91.
84. J. A. Aguiar, P. P. Dholabhai, Z. Bi, Q. Jia, E. G. Fu, Y. Wang, T. Aoki, J. Zhu, A. Misra and B. P. Uberuaga, Adv. Mater. Interfaces, 2014, 1, 1300142.
85. J. Koettgen, S. Grieshammer, P. Hein, B. O. H. Grope, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2018, 20, 14291.
86. D. R. Ou, T. Mori, F. Ye, J. Zou J, G. Auchterlonie and J. Drennan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024108.
87. S. Grieshammer, M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2016, 18, 3804.
88. R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2003, 5, 2297.
89. H. T. Tuller, Solid State Ionics, 2000, 131, 143.
90. J. Maier, Prog. Solid State Chem., 1995, 23, 171.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02034k

---