Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Doping implications of Li solid state electrolyte Li7La3Zr2O12†
Kristoffer
Eggestad
 ,
Sverre M.
Selbach
,
Sverre M.
Selbach
 and
Benjamin A. D.
Williamson
and
Benjamin A. D.
Williamson
 *
*
Department of Materials Science and Engineering, NTNU Norwegian University of Science and Technology, Trondheim 7491, Norway. E-mail: benjamin.williamson@ntnu.no
First published on 29th May 2024
Abstract
Solid-state electrolytes, like Li7La3Zr2O12 (LLZO), can enable safer, more energy dense and longer lasting batteries. We investigate the effect of doping in LLZO with Al, Ga, Nb, Ta, and Y by hybrid density functional theory calculations and a full defect model. The site preferences of Al, Ga, Nb, and Ta result in donor defects that favour more Li vacancies and thus a more disordered Li substructure. This also implies stabilisation of the more ionic conducting cubic phase at the expense of the tetragonal, as seen experimentally. Furthermore, our calculations indicate that the effect of the dopants on the sintering process is even more important than the ability to induce more ionic charge carriers. Finally, differences in Li vacancy formation energies suggest a new possible explanation for the two orders of magnitude increase in ionic conductivity upon stabilising the cubic phase.
1 Introduction
Li-ion batteries are present in almost all portable electronic devices and play a crucial role in modern society. There is, however, a rising demand for safer batteries with both higher energy density and longer lifetime. One possibility is to replace the current liquid electrolyte with a solid-state electrolyte (SSE). In this way, one can theoretically increase the energy density with the use of Li metal anodes1 by physically hindering Li dendrite formation and growth.2 Additionally, the use of SSEs will result in safer batteries due to the removal of the highly flammable liquid electrolyte, thus facilitating a wider range of operating temperatures.3 However, the implementation of SSEs has proven challenging as current materials suffering from low ionic conductivities,4,5 poor air and water stability,6,7 poor electrolyte–electrode interfaces,8 as well as dendrite growth across grains and cracks, in spite of the solid electrolyte.9,10 Good contact between the electrolyte and the electrodes is necessary to realise a well-functioning battery with long-term cyclability. Chemical expansion as well as different thermal expansion coefficients make good electrode–electrolyte interfaces very challenging to prepare and to maintain throughout operation.8In 2003 a group of materials with the garnet structure were suggested as potential SSEs.11 Early studies on garnet materials displayed high stability alongside Li-ion conductivities of about 10−6 S cm−1. To date, arguably the most well studied garnet SSE is Li7La3Zr2O12 (LLZO) displaying relatively high Li-ion conductivities of ∼10−6 − 10−3 S cm−1 depending on doping, synthesis technique and environment, and the structural phase of LLZO.12–17 At room temperature (RT), the structure is stable in its tetragonal form (space group: I41/acd), whilst at higher temperatures it undergoes a phase transition into the disordered cubic phase (space group: Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d) which possesses ionic conductivities around two orders of magnitude higher than the tetragonal phase.12,18
d) which possesses ionic conductivities around two orders of magnitude higher than the tetragonal phase.12,18
The wide electrochemical stability window of LLZO allows it to benignly contact with Li metal anodes.12,19,20 However, a very thin layer of tetragonal-like LLZO structure has been observed at the interface between cubic LLZO and Li metal19,21 potentially resulting in a bottleneck to the Li-ion conductivity at the electrolyte–anode interface. Such a phenomenon means that it is important to understand Li transport and defects within both tetragonal LLZO as well as cubic LLZO.
In the first reported synthesis Murugan et al. made use of a conventional solid-state method with LiOH, La2O3, and ZrO2 with a sintering temperature of 1230 °C.12 Unfortunately, such a high sintering temperature results in substantial Li loss22 and can furthermore lead to destabilisation of the LLZO structure and formation of the competing pyrochlore: La2Zr2O7.23 Undoped materials prepared by sol–gel synthesis has been shown to have approximately 3 times higher conductivity than solid-state prepared, most likely due to more homogenous and dense samples. However, LLZO prepared by the sol–gel method show lower thermal stability, due to larger grain size.24 A further alternative is to use pulsed laser deposition (PLD) allowing for precise control of composition and stoichiometry, and can be used to prepare thin films of LLZO.25,26
One of the challenges concerning LLZO is the relatively poor ionic conductivity at grain boundaries,27 the reasons for which are debated.28,29 In general, grain boundaries in oxide electrolytes are known to reduce the overall ionic conductivity,12,29 although the opposite30 can also be true for some materials. As a result, the sintering process of the electrolyte is important for reducing the grain boundary to bulk ratio. Grain boundaries in LLZO have also shown a susceptibility to Li dendrite formation and propagation. Additionally, good electrode–electrolyte contact is difficult to achieve, and easily forms cracks, leading to poor ionic conductivities as well as dendrite growth.10
The main difference between the cubic and the tetragonal LLZO structure is the Li substructure. In the tetragonal structure there are three fully occupied Li Wyckoff sites; Li8a, Li16f, Li32g, a tetrahedral, an octahedral and a distorted octahedral site, respectively.31 In the cubic structure there are only two different Wyckoff sites; Li24d, Li96h, a tetrahedral and a distorted octahedral site.31 Both sites are partially occupied32 and thus the Li substructure in the cubic structure is often described as disordered. Furthermore, a third Wyckoff site, Li48g, is also often mentioned, but is an average position of a pair of Li96h sites.33 The tetragonal and the cubic structure are visualised together with their Li Wyckoff sites in Fig. 1 and ESI S1,† respectively.
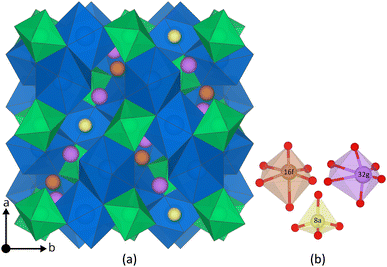 | ||
| Fig. 1 (a) The tetragonal LLZO structure. La and Zr polyhedra are coloured in blue and green, respectively, O is omitted for clarity, and Li Wyckoff sites (16f = orange, 32g = purple, and 8a = yellow) are displayed in more detail in (b). The figure is made using the visualisation software VESTA.72 | ||
Stabilising the cubic structure at RT is often achieved through aliovalent doping motivated by increasing the disorder on the Li substructure. Bernstein et al.31 postulate that there is a critical amount of VLi which results in an increased configurational entropy on the Li substructure, thus disfavouring an ordering of the Li sites and stabilising the cubic structure. The large increase in ionic conductivity is often attributed to the slightly shorter distances between the Li sites in the cubic structure and to the partial occupancy of these sites.31 Several different dopants have been shown experimentally to enhance Li-ion conductivity in LLZO, however the mechanism of the resulting enhancement in conductivity is not well understood. Additionally, reported ionic conductivities are typically not easily comparable between studies due to differences in experimental setups.
The Li24d site preference of Al in LLZO is well documented34–36 and is also reported for Ga.37,38 However, NMR studies found both Al and Ga ions to be equally distributed over the 24d and 96h sites.39 NMR spectroscopy studies also indicate that Al substitutes both Zr and La sites at high doping concentrations.40 Experiments with co-doping with both Al and Ga have been shown to stabilise the cubic phase and increase the ionic conductivity39,41,42 with Ga often reported to give higher ionic conductivities,43,44 however the reason for this is not well understood. In garnet materials, other phases with relatively low melting temperatures, such as LiAlO2, Li5AlO4, and LiGaO2, are often reported in the grain boundaries and are believed to aid grain growth and densification during sintering.45,46
Nb and Ta have also been shown to stabilise the cubic LLZO structure,47,48 both preferring Zr sites,49 thus acting as donor dopants and increasing the 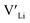 concentration.
concentration.
Y is commonly used as a sintering aid in LLZO50 helping with densification, which in turn results in higher ionic conductivities.15,51 Gai et al.52 have shown that co-doping with Nb and Y gives good ionic conductivity and improved air stability. The effect of Y-doping on the stabilisation of the cubic phase has not been explicitly studied despite Y-doped cubic LLZO having been reported.15 The site preference of Y and the resulting defects are also not clear, with YZr and YLa sites being reported in the literature.15,51 Out of the common dopants, Y is the only dopant, which is predicted by Liu et al.53 to result in a thermodynamically stable structure against Li metal anodes.
Here we use hybrid density functional theory (DFT) to investigate the role of Al, Ga, Nb, Ta, and Y doping in tetragonal LLZO. We calculate and compare defect formation energies, and investigate binding energies between dopants and charge carriers. Furthermore, we use calculated defect formation energies to predict changes in 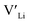 concentrations resulting from the addition of the different dopants.
concentrations resulting from the addition of the different dopants.
2 Computational methods
Density functional theory (DFT) calculations have been performed with the VASP54–56 code to investigate the effect of Al, Ga, Nb, Ta and Y doping on the defect chemistry of tetragonal LLZO. Handling partial occupancies with DFT is computationally demanding as a large number of possible configurations needs to be evaluated and as such, no calculations were performed on the cubic LLZO structure. Additionally, the cubic structure is not the ground state structure and thus relaxing different configurations of the cubic structure can result in the cells transforming into the tetragonal structure as symmetry constraints must be turned off. The PBEsol57 (Perdew–Burke–Ernzerhof revised for solids) functional was used for the initial screening of dominant intrinsic defects to reduce computational cost which were then treated with the Heyd–Scuseria–Ernzerhof screened hybrid functional (HSE), with mixing parameter α = 0.25 and screening parameter ω = 0.11 bohr−1 (HSE06).58 Hybrid functionals have consistently been shown to offer a greater agreement with experiment, particularly with respect to defect chemistry.59–61 All defects cells (96-atom unit cell) and their respective charge states were subjected to a geometry relaxation, keeping the cell parameters fixed, using a plane wave cutoff energy of 600 eV and a Monhorst-Pack k-point of 2 × 2 × 2. The geometry was optimised until the forces on the ions were below 0.01 eV Å−1. Li (1s2, 2s1), La (4s2, 4p6, 5s2, 5d1), Zr (3s2, 3p6, 4s2, 4d2), O (2s2, 2p4), Al (3s2, 3p1), Ga (3s2, 3d10, 4p1), Nb (3s2, 3p6, 4s2, 4d3), Ta (4p6, 5s2, 5d3), Y (3s2, 3p6, 4s2, 4d1) were treated as valence electrons, and the interactions between valence electrons and cores were described by the projector-augmented wave method (PAW).62 Inequivalent interstitial sites were determined using a Voronoi tessellation approach as implemented within the pymatgen package.632.1 Thermodynamic transition levels
Defect formation energies were calculated using.64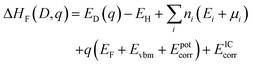 | (1) |
2.2 Chemical potential limits
The thermodynamic stability region at the athermal limit of tetragonal LLZO was found by calculating possible competing phases. All structures were first geometrically optimised using the PBEsol functional to the same convergence criterion as bulk LLZO. Individual k-points and formation enthalpies for each phase are provided in ESI Tables S3–S8.† Thereafter, the Chemical Potential Limits Analysis Program (CPLAP)67 was used to determine the thermodynamic stability region and thus the constrained chemical potential limits for LLZO. The phases that make up the boundaries of the stability region were then subjected to a geometry optimisation using HSE06 and new enthalpies of formation were calculated the details or which are given in ESI Table S9.†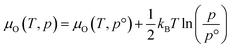 | (2) |
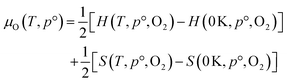 | (3) |
2.3 Equilibrium defect concentrations
The equilibrium defect concentration for a defect D with charge q is given by: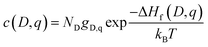 | (4) |
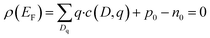 | (5) |
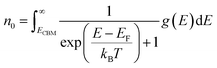 | (6) |
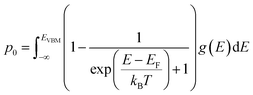 | (7) |
SC-FERMI by Buckeridge71 was used to calculate the self consistent Fermi level within this work. Defect concentrations and Fermi levels are determined for a range of temperatures from the sintering temperature of 1200 °C to RT.
3 Results and discussion
The DFT optimised tetragonal LLZO structure with its three Li Wyckoff sites: 8a, 16f, and 32g are displayed in Fig. 1.The calculated lattice parameters, displayed in ESI Table S1† are in excellent agreement with reported experimental XRD data (within ∼0.6%).73,74 The calculated band gap of 5.92 eV is also in good agreement with experiments showing an optical band gap of ∼6 eV.75 Other DFT simulations using HSE06 show a similar band gap to our results76 and hybrid functionals such as HSE06 are known to accurately reproduce the electronic structure of semiconductors and insulators.61 The PBEsol bandgap is calculated to be ∼4 eV in line with PBEsol's typical underestimation of the bandgap due to the well known self-interaction error.77,78
3.1 Intrinsic defects
The thermodynamic transition levels for the dominant intrinsic defects (a) and dopant species (b–f) calculated using the HSE06 functional at chemical potentials representative of the sintering temperature in air at 1200 °C are given in Fig. 2. Based on the study by Squires et al.76 and an initial screening using PBEsol (transition levels given in ESI Fig. S4†), it can be seen that the formation energies of the Li Frenkel defect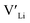 and
and 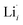 , eqn (8), are >1 eV lower than all other intrinsic defects at the Fermi level (EF), with the exception of
, eqn (8), are >1 eV lower than all other intrinsic defects at the Fermi level (EF), with the exception of 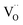 and
and 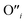 at very O poor or rich conditions respectively. As both Li and O defects dominate the defect chemistry in LLZO these were calculated using HSE06 in order to determine the effects of extrinsic doping. Our initial screening and calculations performed by Squires et al.76 show a very small difference in formation energy (<0.05 eV) between tetrahedrally and octahedrally coordinated
at very O poor or rich conditions respectively. As both Li and O defects dominate the defect chemistry in LLZO these were calculated using HSE06 in order to determine the effects of extrinsic doping. Our initial screening and calculations performed by Squires et al.76 show a very small difference in formation energy (<0.05 eV) between tetrahedrally and octahedrally coordinated 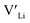 . In spite of these results, our calculations using HSE06 result in notably larger differences in the formation energies of these defects.
. In spite of these results, our calculations using HSE06 result in notably larger differences in the formation energies of these defects. 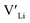 (32g) and
(32g) and 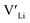 (8a) possess very similar formation energies of ∼0.47 and ∼0.55 eV, respectively. However, the formation energy of
(8a) possess very similar formation energies of ∼0.47 and ∼0.55 eV, respectively. However, the formation energy of 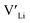 (16f) is ∼0.76 eV, which is 0.29 eV higher than the formation energy of
(16f) is ∼0.76 eV, which is 0.29 eV higher than the formation energy of 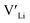 (32g) thus we expect a strong ordering of the
(32g) thus we expect a strong ordering of the 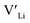 defects at the sintering temperature. It can be proposed that this will result in larger migration barriers to and from the 16f sites than between the 8a and 32g sites. If one were to assume an increase in the migration barrier of ∼0.2 eV, (similar to ΔHf[
defects at the sintering temperature. It can be proposed that this will result in larger migration barriers to and from the 16f sites than between the 8a and 32g sites. If one were to assume an increase in the migration barrier of ∼0.2 eV, (similar to ΔHf[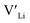 (16g)] − ΔHf[
(16g)] − ΔHf[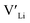 (8a)]) a reduced jump probability at RT from Boltzmann distribution of almost four orders of magnitude would be expected resulting in a drastically reduced ionic conductivity. More likely, however, Li ions will instead favour an alternative path without the 16f sites (8a ↔ 32g ↔ 32g ↔ 8a) and slightly longer jumps, thus also likely slightly larger migration barriers. This path is displayed in ESI Fig. S3.†
(8a)]) a reduced jump probability at RT from Boltzmann distribution of almost four orders of magnitude would be expected resulting in a drastically reduced ionic conductivity. More likely, however, Li ions will instead favour an alternative path without the 16f sites (8a ↔ 32g ↔ 32g ↔ 8a) and slightly longer jumps, thus also likely slightly larger migration barriers. This path is displayed in ESI Fig. S3.†
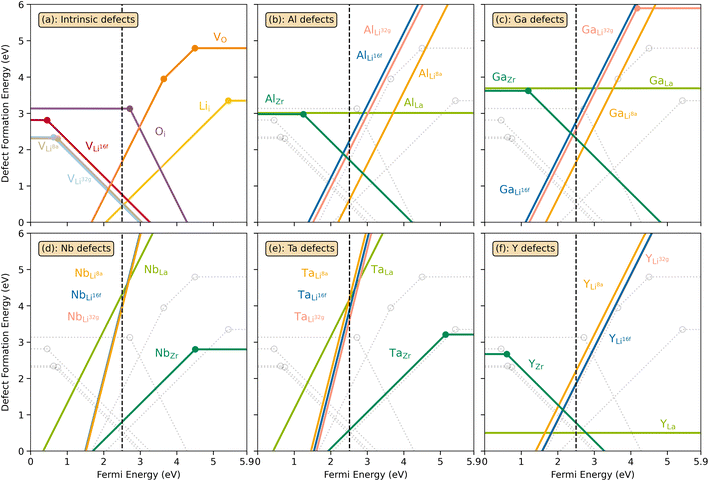 | ||
| Fig. 2 Transition level diagrams for the formation energies of intrinsic defects (a) and selected dopants: Al (b), Ga (c), Nb (d), Ta (e) and Y (f). In each panel, the Fermi energy ranges from the valence band maximum (VBM) at 0 eV to the conduction band minimum (CBM) at ∼5.9 eV. The chemical potentials, used for the calculated formation energies, were chosen to resemble sintering in air at 1200 °C and are displayed in ESI Fig. S2.† The black dashed vertical lines display the self-consistent Fermi level. Intrinsic defects are also displayed together with dopants as grey, transparent lines for clarity. Transition level diagrams for oxygen poor and oxygen rich environments are displayed in ESI Fig. S5 and S6.† | ||
In the cubic LLZO structure, however, there are only two different Li sites: 24d and 96h which are similar in symmetry to the 8a and 32g sites in the tetragonal structure, respectively. Both the 8a and 24d sites are tetrahedrally coordinated, while the 32g and 96h sites are octahedrally coordinated. Furthermore, the 16f sites are slightly less distorted than the 32g and the 96h sites thus it is reasonable to argue that the 16f sites disappear when the cubic structure is formed and thus the removal of the 16f sites could explain the large difference in ionic conductivity between the tetragonal and cubic LLZO structure.
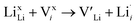 | (8) |
3.2 Extrinsic defects
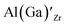 defects have the second lowest formation energies of ∼1.72 eV (∼2.31 eV) followed by
defects have the second lowest formation energies of ∼1.72 eV (∼2.31 eV) followed by 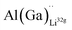 and
and 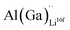 and lastly Al(Ga)xLa with formation energies of ∼1.99 eV (∼2.56 eV), ∼2.25 eV (∼2.77 eV), and ∼3.01 eV (∼3.69 eV) respectively. As both Al and Ga prefer Li sites, these dopants will be charge compensated mainly by the formation of
and lastly Al(Ga)xLa with formation energies of ∼1.99 eV (∼2.56 eV), ∼2.25 eV (∼2.77 eV), and ∼3.01 eV (∼3.69 eV) respectively. As both Al and Ga prefer Li sites, these dopants will be charge compensated mainly by the formation of 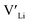 , see eqn (9). All Ga defects have formation energies 0.5–1 eV higher than the corresponding Al defects at the EF, indicating much lower solubility than Al.
, see eqn (9). All Ga defects have formation energies 0.5–1 eV higher than the corresponding Al defects at the EF, indicating much lower solubility than Al.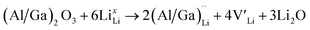 | (9) |
Considering the ionic radii of 4 and 6 coordinated Al (0.39 Å, 0.535 Å) and Ga (0.47 Å, 0.62 Å) ions, a preference for the smallest sites, Li8a/24d (0.59 Å), is expected. However, despite what is reported on the site preference of Al and Ga ions in cubic LLZO,34–38 the low formation energy for 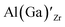 is likely due to the small charge difference between the Al(Ga) and Zr ions. Considering the similarity between the Zr sites in the tetragonal and the cubic structure, we do not expect the formation energies of dopants at Zr sites to be notably different in the cubic structure. However, the same argument cannot be made for the Li sites, and therefore, the formation energies of dopants at Li sites in the cubic structure could be slightly different to what is presented in Fig. 2. There exists a high degree of ambiguity on the site preference of Al and Ga in cubic LLZO in the reported literature;34–40 our results suggest a preference for the Li24d sites, but do not discount the possibility of Al or Ga being located on Zr or Li96h sites.
is likely due to the small charge difference between the Al(Ga) and Zr ions. Considering the similarity between the Zr sites in the tetragonal and the cubic structure, we do not expect the formation energies of dopants at Zr sites to be notably different in the cubic structure. However, the same argument cannot be made for the Li sites, and therefore, the formation energies of dopants at Li sites in the cubic structure could be slightly different to what is presented in Fig. 2. There exists a high degree of ambiguity on the site preference of Al and Ga in cubic LLZO in the reported literature;34–40 our results suggest a preference for the Li24d sites, but do not discount the possibility of Al or Ga being located on Zr or Li96h sites.
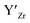 at EF.
at EF. 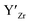 enhances
enhances 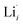 concentration as charge compensation, eqn (10).
concentration as charge compensation, eqn (10).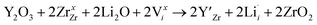 | (10) |
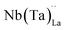 possess formation energies ∼3.5 eV higher than
possess formation energies ∼3.5 eV higher than 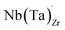 at EF. The formation energy for
at EF. The formation energy for 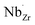 is about 0.2 eV higher than
is about 0.2 eV higher than 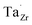 implying a higher solubility of Ta than Nb in LLZO. Similar to Al and Ga, Nb and Ta will be charge compensated by the formation of additional
implying a higher solubility of Ta than Nb in LLZO. Similar to Al and Ga, Nb and Ta will be charge compensated by the formation of additional 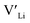 , eqn (11).
, eqn (11).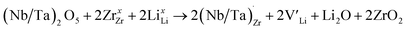 | (11) |
3.3 Electronic conductivity
Electrical conductivity (σe) in LLZO which has been linked to dendrite formation and growth;79,80 thus a low σe is essential for longterm cyclability.81 The electronic conductivity of tetragonal LLZO has also been investigated by first principles calculations by Squires et al.82 wherein it is suggested that the bulk electronic conductivity of the structure is too low for governing dendrite growth and attributes the dendrite growth to surface and defect contributions. Our calculations show that in doped LLZO, EF is trapped mid gap (∼2.5 eV above the VBM) and each transition level of the aliovalent dopants occurs far from the band edges (tabulated in ESI Table S10†) thus no increase in conductivity is expected. Additionally, donor defects, such as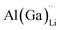 and
and 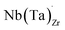 , are compensated for by
, are compensated for by 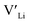 , while acceptor defects, such as
, while acceptor defects, such as 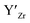 , are compensated by
, are compensated by 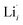 .
.
3.4 Defect concentrations
Li ions are highly mobile in LLZO even at very low temperatures, which is obviously also a prerequisite for its application as a solid-state electrolyte.36 Two implications of this mobility is that, firstly, after sintering, all Li Frenkel pairs that emerge at elevated temperatures will relax back to the equilibrium RT concentration upon cooling. Secondly, when LLZO as an electrolyte layer is in electrical contact with a Li reservoir, like e.g. a Li metal anode, the Li concentration in LLZO will adjust according to the concentration of aliovalent dopants in the structure, regardless of possible Li loss during high-temperature synthesis and processing. In contrast with highly mobile Li, cation dopants are expected to be highly immobile due to their higher formal charge, low polarizability and general refractoryness of LLZO as a host crystal. Hence, the concentration of dopants is expected to freeze-in at elevated specific temperatures, causing non-equilibrium defect concentrations at lower temperatures. This situation has been described as broken ergodicity by Grande et al.83 and the freezing-in of point defect populations is well-known in solid state ionics.84In the following we discuss the experimentally important distinction between synthesis methods were the final cation stoichiometry (with the exception of Li) of the sample is constrained to the nominal stoichiometry of the precursor materials, and the situation where the final sample of interest can freely exchange dopants with the surroundings. Examples of the former situation are solid-state and sol–gel synthesis where all reactants contribute to the final sample material, thus maintaining the nominal stoichiometry. The latter situation applies to e.g. thin film deposition methods like pulsed lased deposition (PLD) or sputtering where there is not necessarily stochiometric transfer from target to film, and where there can be substantial segregation to the film edges, which are usually not investigated. Single crystal growth from melt and hydrothermal crystallization are also methods where the nominal composition of the reactants are not necessarily reflected by the true composition of the final material.
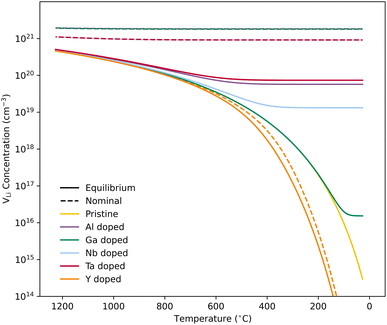
We first discuss the situation with constrained dopant stoichiometry. Typical nominal dopant concentrations in LLZO are 0.25 dopant per formula unit.15,43,44,47,48 Assuming that all dopants are incorporated into the LLZO structure, this results in expected 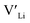 concentrations of ∼0.5 and ∼0.25 per formula unit for Al/Ga and Nb/Ta, respectively, dashed lines in Fig. 3. This is typically what is assumed as the response to the addition of dopants when making LLZO by solid-state and sol–gel syntheses. However, as indicated by the differences in the defect formation energies, some dopants are less energetically favoured than others, and thus may result in the formation of secondary phases or segregation towards grain boundaries or surfaces. Strain fields associated with grain boundaries are known to often reduce defect formation energies,85 and lead to defects accumulation at or close to grain boundaries. Secondary phases at grain boundaries may be difficult to detect, but may still strongly affect the sintering properties, density and electrical properties of polycrystals.
concentrations of ∼0.5 and ∼0.25 per formula unit for Al/Ga and Nb/Ta, respectively, dashed lines in Fig. 3. This is typically what is assumed as the response to the addition of dopants when making LLZO by solid-state and sol–gel syntheses. However, as indicated by the differences in the defect formation energies, some dopants are less energetically favoured than others, and thus may result in the formation of secondary phases or segregation towards grain boundaries or surfaces. Strain fields associated with grain boundaries are known to often reduce defect formation energies,85 and lead to defects accumulation at or close to grain boundaries. Secondary phases at grain boundaries may be difficult to detect, but may still strongly affect the sintering properties, density and electrical properties of polycrystals.
Equilibrium dopant concentrations, Table 1, and resulting 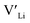 concentrations, solid lines in Fig. 3, have been calculated to better address the solubility of the different dopants as well as dopant concentrations from open system synthesis methods. These concentrations have been estimated from athermal defect formation energies at the dilute limit with the assumption of equilibrium, meaning that elements can freely be added to or removed from the system. Except for Y, typical dopant concentrations are >10 times higher than the equilibrium concentrations calculated herein. In for example solid state synthesis, only volatile elements such as Li can disappear from the system, and thus lower equilibrium concentrations than nominal concentrations imply that there is a driving force for the formation of secondary phases.
concentrations, solid lines in Fig. 3, have been calculated to better address the solubility of the different dopants as well as dopant concentrations from open system synthesis methods. These concentrations have been estimated from athermal defect formation energies at the dilute limit with the assumption of equilibrium, meaning that elements can freely be added to or removed from the system. Except for Y, typical dopant concentrations are >10 times higher than the equilibrium concentrations calculated herein. In for example solid state synthesis, only volatile elements such as Li can disappear from the system, and thus lower equilibrium concentrations than nominal concentrations imply that there is a driving force for the formation of secondary phases.
| Dopant | Nominal (p.f.u.) | Equilibrium (p.f.u.) |
|---|---|---|
| Al | 0.25 | 7.8 × 10−3 |
| Ga | 0.25 | 2.1 × 10−6 |
| Nb | 0.25 | 3.6 × 10−3 |
| Ta | 0.25 | 2.0 × 10−2 |
| Y | 0.25 | 5.9 × 10−1 |
As equilibrium concentrations give an indication of the solubility of a specific dopant, out predicted value for Ga is several orders of magnitude lower than the other dopants, and doping with Ga is known to result in the formation of secondary phases.46 Moreover, it has been reported by Schwab et al.86 that 0.20 Ga per formula unit exceed the solubility limit of Ga in LLZO, and in their study, the amount of the secondary phases formed could not be detected by XRD. Furthermore, if we assume that all Ga added in this experiment result in the formation of LiGaO2, the resulting volume fraction is ∼3%, relatively close to the detection limit of regular XRDs. Therefore, the formation of relatively small amounts of secondary phases can easily be missed.
Fig. 3 shows how the 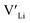 concentration changes as a function of cooling temperature for the pristine structure and different doping regimes, where the dopant concentrations are frozen-in at the sintering temperature. The dashed lines describe [
concentration changes as a function of cooling temperature for the pristine structure and different doping regimes, where the dopant concentrations are frozen-in at the sintering temperature. The dashed lines describe [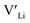 ] resulting from a nominal dopant concentration of 0.25 per formula unit and the assumption that all added dopants will be incorporated into the structure. The solid lines show [
] resulting from a nominal dopant concentration of 0.25 per formula unit and the assumption that all added dopants will be incorporated into the structure. The solid lines show [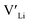 ] resulting from equilibrium dopant concentrations. Regardless of the synthesis technique, dopants incorporated into the structure require charge compensation and will stabilise additional defects. Therefore, a dopant's “success” is highly dependent on both the quantity of dopant incorporated into the structure during sintering as well as the temperature at which its defects freezes-in. At what temperature the different dopants freezes-in is highly complex and has not been investigated in our work.
] resulting from equilibrium dopant concentrations. Regardless of the synthesis technique, dopants incorporated into the structure require charge compensation and will stabilise additional defects. Therefore, a dopant's “success” is highly dependent on both the quantity of dopant incorporated into the structure during sintering as well as the temperature at which its defects freezes-in. At what temperature the different dopants freezes-in is highly complex and has not been investigated in our work.
From our analysis, it is clear that all dopants, with the exception of Y, result in a drastic increase in the 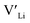 concentration at RT. Ta-doping results in the largest estimated equilibrium [
concentration at RT. Ta-doping results in the largest estimated equilibrium [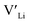 ] at RT of 7.4 × 1019 cm−3 corresponding to ∼0.02 defects per formula unit. The [
] at RT of 7.4 × 1019 cm−3 corresponding to ∼0.02 defects per formula unit. The [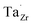 ] frozen in at the sintering temperature is also 7.4 × 1019 thus it can be assumed that this is solely responsible for the increased [
] frozen in at the sintering temperature is also 7.4 × 1019 thus it can be assumed that this is solely responsible for the increased [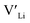 ]. Low formation energies of YxLa and
]. Low formation energies of YxLa and 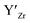 result in a higher equilibrium concentration than the nominal dopant concentration and hence the nominal dopant concentration showing less destabilisation of
result in a higher equilibrium concentration than the nominal dopant concentration and hence the nominal dopant concentration showing less destabilisation of 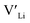 .
.
Furthermore, it is often assumed that the added dopants only will reside on the lowest energy sites. This, however, is not true and is especially important to keep in mind when investigating dopants that result in defects with relatively high and similar formation energies at the Fermi level such as Ga:LLZO. There will be a Boltzmann distribution over all available lattice sites, and for Ga, this means that the dopants will mainly be located at Li and Zr sites, but also at La sites. This type of non-convergent disordering of cations has for instance been studied in spinels,87,88 complex oxide LaSr2−xCaxCu2GaO7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 89 and more recently in tetragonal tungsten bronzes.90
89 and more recently in tetragonal tungsten bronzes.90
3.5 Binding energies
Binding energies between dopants and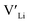 give an indication of whether or not a dopant acts as a trapping point. Substantial binding energies could in turn result in reduced Li-ion mobility, and thus a reduced ionic conductivity. The binding energies displayed in Table 2 were calculated by subtracting the energy of a cell with a defect pair, where the defect related to a dopant is located close to (∼3 Å) a
give an indication of whether or not a dopant acts as a trapping point. Substantial binding energies could in turn result in reduced Li-ion mobility, and thus a reduced ionic conductivity. The binding energies displayed in Table 2 were calculated by subtracting the energy of a cell with a defect pair, where the defect related to a dopant is located close to (∼3 Å) a 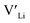 , from the energy of a cell, where they are located far away (∼6 Å) from each other. Neutral cells (q = 0) were used for all calculations. The shortest distance between two Li8a sites is ∼6 Å, and therefore there are no calculated binding energies for Al(Ga)Li8a with
, from the energy of a cell, where they are located far away (∼6 Å) from each other. Neutral cells (q = 0) were used for all calculations. The shortest distance between two Li8a sites is ∼6 Å, and therefore there are no calculated binding energies for Al(Ga)Li8a with 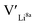 . This is also true for the Li16f sites. The Y defects show the largest binding energies, closely followed by Ga. Both Nb and Ta show very small binding energies, indicating only weak trapping. A couple of the defect pairs show negative binding energies which means that the
. This is also true for the Li16f sites. The Y defects show the largest binding energies, closely followed by Ga. Both Nb and Ta show very small binding energies, indicating only weak trapping. A couple of the defect pairs show negative binding energies which means that the 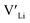 is repelled by the dopant. At RT kBT ∼ 0.025 eV, and thus defect pairs with binding energies lower than 0.025 eV will not be noticeably affected by this barrier. However, small binding energies can contribute to a slight increase in migration barriers.
is repelled by the dopant. At RT kBT ∼ 0.025 eV, and thus defect pairs with binding energies lower than 0.025 eV will not be noticeably affected by this barrier. However, small binding energies can contribute to a slight increase in migration barriers.
| VLi8a | VLi16f | VLi32g | |
|---|---|---|---|
| AlLi8a | — | — | 0.060 |
| GaLi8a | — | — | 0.183 |
| NbZr | 0.013 | 0.016 | −0.006 |
| TaZr | 0.003 | 0.013 | −0.016 |
| YZr | 0.144 | 0.221 | 0.063 |
| YLa | 0.213 | −0.033 | −0.088 |
Neither Nb nor Ta are located on the Li substructure, and thus do not give strong 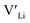 trapping, and have very low formation energies. However, both Al and Ga are reported with similar ionic conductivities despite being located on the Li substructure, and showing relatively high binding energies. Doping with Al, Ga, Nb or Ta increases disorder within the structure, in particular on the Li substructure, and therefore helps stabilise the cubic phase. We can therefore conclude that the stabilisation of the cubic structure is the main contribution to the high ionic conductivity and that the differences in the
trapping, and have very low formation energies. However, both Al and Ga are reported with similar ionic conductivities despite being located on the Li substructure, and showing relatively high binding energies. Doping with Al, Ga, Nb or Ta increases disorder within the structure, in particular on the Li substructure, and therefore helps stabilise the cubic phase. We can therefore conclude that the stabilisation of the cubic structure is the main contribution to the high ionic conductivity and that the differences in the 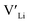 concentrations are less important. Such a conclusion is in good agreement with the work carried out by Allen et al.91 wherein they showed that codoping Ta-stabilised cubic LLZO with Al and Ga resulted in a reduction in the ionic conductivity from the monodoped Ta:LLZO (cubic phase), furthermore indicating that Al and Ga doping into the Li substructure disrupts Li-ion mobility. In addition, significant binding energies between Al/Ga and
concentrations are less important. Such a conclusion is in good agreement with the work carried out by Allen et al.91 wherein they showed that codoping Ta-stabilised cubic LLZO with Al and Ga resulted in a reduction in the ionic conductivity from the monodoped Ta:LLZO (cubic phase), furthermore indicating that Al and Ga doping into the Li substructure disrupts Li-ion mobility. In addition, significant binding energies between Al/Ga and 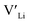 suggest increased migration barriers, which supports the deactivation of Li-ion diffusion around Al and Ga ions observed in molecular dynamics simulations performed by García Daza et al.92 Moreover, NMR studies by Posch et al.93 also suggest enlarged migration barriers around Al ions. It is also important to note that not only migration energy barriers, as emphasized here, are important to the ionic conductivity, but also Arrhenius prefactors, as found in NMR studies of LLZO doped with Mo and Ta.94,95
suggest increased migration barriers, which supports the deactivation of Li-ion diffusion around Al and Ga ions observed in molecular dynamics simulations performed by García Daza et al.92 Moreover, NMR studies by Posch et al.93 also suggest enlarged migration barriers around Al ions. It is also important to note that not only migration energy barriers, as emphasized here, are important to the ionic conductivity, but also Arrhenius prefactors, as found in NMR studies of LLZO doped with Mo and Ta.94,95
3.6 Solid solubility, grain boundaries and sintering
Ga-doped LLZO is commonly reported with a higher ionic conductivities than the Al-doped variations. Our results, showing lower formation energies for Al defects, indicate that Al should be easier to incorporate into the structure, thus stabilising more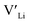 and increasing the number of charge carriers. However, this enhanced incorporation of Al in the structure will, in addition to increase the
and increasing the number of charge carriers. However, this enhanced incorporation of Al in the structure will, in addition to increase the 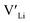 concentration, result in more disruption of the Li diffusion paths than Ga. Furthermore, Al and Ga are known to segregate towards the grain boundaries forming competing phases with relatively low melting temperatures which beneficially act as sintering aids.45,46 In so, Al and Ga crucially affect the poor grain boundary conductivity in polycrystalline LLZO. Based on Ga substitutional defects being less energetically favourable than Al defects in the structure, and thus Ga is expected to show a lower solid solubility, we expect this effect to be greater in Ga doped structures. The effect of Al and Ga acting as a sintering aid is likely a part of the explanation for why the reported ionic conductivities of both Al and Ga doped LLZO are similar to the Nb and Ta doped structures.
concentration, result in more disruption of the Li diffusion paths than Ga. Furthermore, Al and Ga are known to segregate towards the grain boundaries forming competing phases with relatively low melting temperatures which beneficially act as sintering aids.45,46 In so, Al and Ga crucially affect the poor grain boundary conductivity in polycrystalline LLZO. Based on Ga substitutional defects being less energetically favourable than Al defects in the structure, and thus Ga is expected to show a lower solid solubility, we expect this effect to be greater in Ga doped structures. The effect of Al and Ga acting as a sintering aid is likely a part of the explanation for why the reported ionic conductivities of both Al and Ga doped LLZO are similar to the Nb and Ta doped structures.
4 Conclusion
In summary, our calculations performed on the tetragonal LLZO polymorph are in agreement with published experimental work on the cubic polymorph. This implies that our results on the tetragonal phase are good indications of what to expect of the cubic. We suggest the disappearance of the Li16f sites as a possible explanation for the large difference in ionic conductivity between the tetragonal and cubic polymorphs. Doping with Y does not result in an increased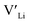 concentration. Doping with Al, Ga, Nb, or Ta will increase the
concentration. Doping with Al, Ga, Nb, or Ta will increase the 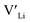 concentration and increase disorder on the Li substructure, thus stabilising the cubic LLZO structure. Al and Ga are located on tetrahedrally coordinated Li sites and will as a result block Li paths and disrupt Li ion mobility. Doping LLZO with Ga has been shown experimentally to give the best ionic conductivities, but our calculations show that doping with Ga will result in some trapping and less stabilisation of
concentration and increase disorder on the Li substructure, thus stabilising the cubic LLZO structure. Al and Ga are located on tetrahedrally coordinated Li sites and will as a result block Li paths and disrupt Li ion mobility. Doping LLZO with Ga has been shown experimentally to give the best ionic conductivities, but our calculations show that doping with Ga will result in some trapping and less stabilisation of 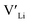 than the other donor defects. Therefore, we suggest that the effect of dopants on the sintering process is the most important property of the dopant after the ability to stabilise the cubic LLZO structure.
than the other donor defects. Therefore, we suggest that the effect of dopants on the sintering process is the most important property of the dopant after the ability to stabilise the cubic LLZO structure.
Author contributions
KE performed all the calculations and analysis related to this work with supervision from BADW. SMS contributed to the reviewing, editing and supervision of the work. All authors contributed to the review and editing of the final manuscript and have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts of interest in this work.Acknowledgements
Computational resources were provided by UNINETT Sigma2 through Project NN9264K. Support for this project was provided from the Research Council of Norway (Project Numbers 287890, 302506, 301954).Notes and references
- Y. Shen, Y. Zhang, S. Han, J. Wang, Z. Peng and L. Chen, Joule, 2018, 2, 1674–1689 CrossRef CAS.
- K. B. Hatzell, X. C. Chen, C. L. Cobb, N. P. Dasgupta, M. B. Dixit, L. E. Marbella, M. T. McDowell, P. P. Mukherjee, A. Verma, V. Viswanathan, A. S. Westover and W. G. Zeier, ACS Energy Lett., 2020, 5, 922–934 CrossRef CAS.
- D. Aurbach, Y. Talyosef, B. Markovsky, E. Markevich, E. Zinigrad, L. Asraf, J. S. Gnanaraj and H.-J. Kim, Electrochim. Acta, 2004, 50, 247–254 CrossRef CAS.
- J. G. Kim, B. Son, S. Mukherjee, N. Schuppert, A. Bates, O. Kwon, M. J. Choi, H. Y. Chung and S. Park, J. Power Sources, 2015, 282, 299–322 CrossRef CAS.
- M.-J. Uddin and S.-J. Cho, Sustainable Energy Fuels, 2018, 2, 1458–1462 RSC.
- G. Sahu, Z. Lin, J. Li, Z. Liu, N. Dudney and C. Liang, Energy Environ. Sci., 2014, 7, 1053–1058 RSC.
- Q. Zhao, S. Stalin, C.-Z. Zhao and L. A. Archer, Nat. Rev. Mater., 2020, 5, 229–252 CrossRef CAS.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- C. Monroe and J. Newman, J. Electrochem. Soc., 2005, 152, A396 CrossRef CAS.
- C. Zhang, Q. Hu, Y. Shen and W. Liu, Adv. Energy Sustainability Res., 2022, 3, 2100203 CrossRef.
- V. Thangadurai, H. Kaack and W. J. F. Weppner, J. Am. Ceram. Soc., 2003, 86, 437–440 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- C. Li, Y. Liu, J. He and K. S. Brinkman, J. Alloys Compd., 2017, 695, 3744–3752 CrossRef CAS.
- D. Rettenwander, G. Redhammer, F. Preishuber-Pflügl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. M. Doeff, M. Wilkening, J. Fleig and G. Amthauer, Chem. Mater., 2016, 28, 2384–2392 CrossRef CAS PubMed.
- C. Deviannapoorani, L. S. Shankar, S. Ramakumar and R. Murugan, Ionics, 2016, 22, 1281–1289 CrossRef CAS.
- Y. Li, J.-T. Han, C.-A. Wang, H. Xie and J. B. Goodenough, J. Mater. Chem., 2012, 22, 15357–15361 RSC.
- S. Ohta, T. Kobayashi and T. Asaoka, J. Power Sources, 2011, 196, 3342–3345 CrossRef CAS.
- J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, J. Solid State Chem., 2009, 182, 2046–2052 CrossRef CAS.
- C. Ma, Y. Cheng, K. Yin, J. Luo, A. Sharafi, J. Sakamoto, J. Li, K. L. More, N. J. Dudney and M. Chi, Nano Lett., 2016, 16, 7030–7036 CrossRef CAS PubMed.
- A. Sharafi, H. M. Meyer, J. Nanda, J. Wolfenstine and J. Sakamoto, J. Power Sources, 2016, 302, 135–139 CrossRef CAS.
- D. Rettenwander, R. Wagner, A. Reyer, M. Bonta, L. Cheng, M. M. Doeff, A. Limbeck, M. Wilkening and G. Amthauer, J. Phys. Chem. C, 2018, 122, 3780–3785 CrossRef CAS PubMed.
- Y. Shimonishi, A. Toda, T. Zhang, A. Hirano, N. Imanishi, O. Yamamoto and Y. Takeda, Solid State Ionics, 2011, 183, 48–53 CrossRef CAS.
- E. Rangasamy, J. Wolfenstine and J. Sakamoto, Solid State Ionics, 2012, 206, 28–32 CrossRef CAS.
- J. Košir, S. Mousavihashemi, B. P. Wilson, E.-L. Rautama and T. Kallio, Solid State Ionics, 2022, 380, 115943 CrossRef.
- M. Saccoccio, J. Yu, Z. Lu, S. C. Kwok, J. Wang, K. K. Yeung, M. M. Yuen and F. Ciucci, J. Power Sources, 2017, 365, 43–52 CrossRef CAS.
- J. Tan and A. Tiwari, ECS Solid State Lett., 2012, 1, Q57–Q60 CrossRef CAS.
- S. Yu and D. J. Siegel, Chem. Mater., 2017, 29, 9639–9647 CrossRef CAS.
- T. W. Heo, A. Grieder, B. Wang, M. Wood, T. Hsu, S. A. Akhade, L. F. Wan, L.-Q. Chen, N. Adelstein and B. C. Wood, npj Comput. Mater., 2021, 7, 214 CrossRef CAS.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef CAS PubMed.
- K. Kawahara, R. Ishikawa, K. Nakayama, T. Higashi, T. Kimura, Y. H. Ikuhara, N. Shibata and Y. Ikuhara, J. Power Sources, 2019, 441, 227187 CrossRef CAS.
- N. Bernstein, M. D. Johannes and K. Hoang, Phys. Rev. Lett., 2012, 109, 205702 CrossRef CAS PubMed.
- H. Xie, J. A. Alonso, Y. Li, M. T. Fernández-Díaz and J. B. Goodenough, Chem. Mater., 2011, 23, 3587–3589 CrossRef CAS.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef CAS.
- D. Rettenwander, P. Blaha, R. Laskowski, K. Schwarz, P. Bottke, M. Wilkening, C. A. Geiger and G. Amthauer, Chem. Mater., 2014, 26, 2617–2623 CrossRef CAS PubMed.
- B. Karasulu, S. P. Emge, M. F. Groh, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2020, 142, 3132–3148 CrossRef CAS PubMed.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392 RSC.
- M. A. Howard, O. Clemens, E. Kendrick, K. S. Knight, D. C. Apperley, P. A. Anderson and P. R. Slater, Dalton Trans., 2012, 41, 12048–12053 RSC.
- C. Bernuy-Lopez, W. Manalastas, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS.
- D. Rettenwander, J. Langer, W. Schmidt, C. Arrer, K. J. Harris, V. Terskikh, G. R. Goward, M. Wilkening and G. Amthauer, Chem. Mater., 2015, 27, 3135–3142 CrossRef CAS.
- A. Düvel, A. Kuhn, L. Robben, M. Wilkening and P. Heitjans, J. Phys. Chem. C, 2012, 116, 15192–15202 CrossRef.
- Z. Hu, H. Liu, H. Ruan, R. Hu, Y. Su and L. Zhang, Ceram. Int., 2016, 42, 12156–12160 CrossRef CAS.
- Y. Jin and P. J. McGinn, J. Power Sources, 2011, 196, 8683–8687 CrossRef CAS.
- J. Sastre, A. Priebe, M. Döbeli, J. Michler, A. N. Tiwari and Y. E. Romanyuk, Adv. Mater. Interfaces, 2020, 7, 2000425 CrossRef CAS.
- R. Wagner, G. J. Redhammer, D. Rettenwander, A. Senyshyn, W. Schmidt, M. Wilkening and G. Amthauer, Chem. Mater., 2016, 28, 1861–1871 CrossRef CAS PubMed.
- S. Lobe, A. Bauer, D. Sebold, N. Wettengl, D. Fattakhova-Rohlfing and S. Uhlenbruck, Open Ceram., 2022, 10, 100268 CrossRef CAS.
- H. El Shinawi and J. Janek, J. Power Sources, 2013, 225, 13–19 CrossRef CAS.
- K. Ishiguro, Y. Nakata, M. Matsui, I. Uechi, Y. Takeda, O. Yamamoto and N. Imanishi, J. Electrochem. Soc., 2013, 160, A1690–A1693 CrossRef CAS.
- X. Zhang, T.-S. Oh and J. W. Fergus, J. Electrochem. Soc., 2019, 166, A3753–A3759 CrossRef CAS.
- L. J. Miara, W. D. Richards, Y. E. Wang and G. Ceder, Chem. Mater., 2015, 27, 4040–4047 CrossRef CAS.
- L. Dhivya and R. Murugan, ACS Appl. Mater. Interfaces, 2014, 6, 17606–17615 CrossRef CAS PubMed.
- M. Kotobuki and M. Koishi, J. Alloys Compd., 2020, 826, 154213 CrossRef CAS.
- J. Gai, E. Zhao, F. Ma, D. Sun, X. Ma, Y. Jin, Q. Wu and Y. Cui, J. Eur. Ceram. Soc., 2018, 38, 1673–1678 CrossRef CAS.
- B. Liu, J. Yang, H. Yang, C. Ye, Y. Mao, J. Wang, S. Shi, J. Yang and W. Zhang, J. Mater. Chem. A, 2019, 7, 19961–19969 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- B. A. D. Williamson, J. Buckeridge, N. P. Chadwick, S. Sathasivam, C. J. Carmalt, I. P. Parkin and D. O. Scanlon, Chem. Mater., 2019, 31, 2577–2589 CrossRef CAS PubMed.
- P. Deák, B. Aradi, T. Frauenheim, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153203 CrossRef.
- B. A. D. Williamson, G. J. Limburn, G. W. Watson, G. Hyett and D. O. Scanlon, Matter, 2020, 3, 759–781 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Shen nwinner, J. Riebesell and J. Zeng, materialsproject/pymatgen-analysis-defects: v2023.02.07, 2023 Search PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- S. T. Murphy and N. D. M. Hine, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094111 CrossRef.
- J. Buckeridge, D. Scanlon, A. Walsh and C. Catlow, Comput. Phys. Commun., 2014, 185, 330–338 CrossRef CAS.
- M. Kotobuki, K. Kanamura, Y. Sato, K. Yamamoto and T. Yoshida, J. Power Sources, 2012, 199, 346–349 CrossRef CAS.
- M. W. Chase Jr, NIST-JANAF Thermochemical Tables, American Chemical Society, American Institute of Physics for the National Institute of Standards and Technology, Washington, DC, New York, 4th edn, 1998 Search PubMed.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- J. Buckeridge, Comput. Phys. Commun., 2019, 244, 329–342 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- K. Kataoka and J. Akimoto, Solid State Ionics, 2020, 349, 115312 CrossRef CAS.
- T. Kimura, Y. Yamada, K. Yamamoto, T. Matsuda, H. Nomura and T. Hirayama, J. Am. Ceram. Soc., 2017, 100, 1313–1319 CrossRef CAS.
- K. Ajith, P. Christopher Selvin, K. Abhilash, P. Sivaraj, B. Nalini and G. Soundarya, Mater. Today: Proc., 2022, 50, 2836–2839 CAS.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, Chem. Mater., 2020, 32, 1876–1886 CrossRef CAS.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187–196 CrossRef CAS.
- F. Aguesse, W. Manalastas, L. Buannic, J. M. Lopez del Amo, G. Singh, A. Llordés and J. Kilner, ACS Appl. Mater. Interfaces, 2017, 9, 3808–3816 CrossRef CAS PubMed.
- Y. Song, L. Yang, W. Zhao, Z. Wang, Y. Zhao, Z. Wang, Q. Zhao, H. Liu and F. Pan, Adv. Energy Mater., 2019, 9, 1900671 CrossRef.
- A. G. Squires, D. W. Davies, S. Kim, D. O. Scanlon, A. Walsh and B. J. Morgan, Phys. Rev. Mater., 2022, 6, 085401 CrossRef CAS.
- T. Grande, J. R. Tolchard and S. M. Selbach, Chem. Mater., 2012, 24, 338–345 CrossRef CAS.
- J. Maier, Phys. Chem. Chem. Phys., 2003, 5, 2164–2173 RSC.
- U. Aschauer, R. Pfenninger, S. M. Selbach, T. Grande and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054111 CrossRef.
- C. Schwab, G. Häuschen, M. Mann, C. Roitzheim, O. Guillon, D. Fattakhova-Rohlfing and M. Finsterbusch, J. Mater. Chem. A, 2023, 11, 5670–5680 RSC.
- A. Navrotsky and O. Kleppa, J. Inorg. Nucl. Chem., 1967, 29, 2701–2714 CrossRef CAS.
- H. S. C. O'Neill and A. Navrotsky, Am. Mineral., 1983, 68, 181–194 Search PubMed.
- K. Greenwood, D. Ko, D. Vander Griend, G. Sarjeant, J. Milgram, E. Garrity, D. DeLoach, K. Poeppetmeier, P. Salvador and T. Mason, Inorg. Chem., 2000, 39, 3386–3391 CrossRef CAS.
- G. H. Olsen, S. M. Selbach and T. Grande, Phys. Chem. Chem. Phys., 2015, 17, 30343–30351 RSC.
- J. Allen, J. Wolfenstine, E. Rangasamy and J. Sakamoto, J. Power Sources, 2012, 206, 315–319 CrossRef CAS.
- F. A. García Daza, M. R. Bonilla, A. Llordés, J. Carrasco and E. Akhmatskaya, ACS Appl. Mater. Interfaces, 2019, 11, 753–765 CrossRef.
- P. Posch, S. Lunghammer, S. Berendts, S. Ganschow, G. J. Redhammer, A. Wilkening, M. Lerch, B. Gadermaier, D. Rettenwander and H. M. R. Wilkening, Energy Storage Mater., 2020, 24, 220–228 CrossRef.
- P. Bottke, D. Rettenwander, W. Schmidt, G. Amthauer and M. Wilkening, Chem. Mater., 2015, 27, 6571–6582 CrossRef CAS.
- B. Stanje, D. Rettenwander, S. Breuer, M. Uitz, S. Berendts, M. Lerch, R. Uecker, G. Redhammer, I. Hanzu and M. Wilkening, Ann. Phys., 2017, 529, 1700140 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta01487a |
| This journal is © The Royal Society of Chemistry 2024 |