BaCuTP₂ (T = Al, Ga, In): a semiconducting black sheep in the ThCr₂Si₂ intermetallic family

Abstract

The ThCr₂Si₂ structure type has been well explored for decades with diverse magnetic, superconducting, and heavy-fermion behavior. For transition metal-containing ThCr₂Si₂-type compounds, a metallic band structure and properties are typical. In this work, a rare example of semiconducting BaCuTP₂ (T = Al, Ga, In) materials is reported. BaCuTP₂ materials retain the tetragonal I4/mmm ThCr₂Si₂-type crystal structure with a large c/a ratio of ∼3.3, where Cu and T metals jointly occupy the Cr-site. Edge-sharing (Cu/T)P₄ tetrahedra form [CuTP₂]²⁻ layers stacked along the crystallographic [001] direction, with the Ba²⁺ cations located in the interlayer spaces. Solid state NMR revealed partial short-range ordering in the Cu/T sublattice. The composition of the produced phases is electron balanced, Ba²⁺Cu¹⁺T³⁺(P³⁻)₂. High values of Seebeck coefficients were experimentally observed due to the high valley degeneracy in the band structure. Heat capacity and structural studies show that Ba exhibits anisotropic ‘rattling-like’ behavior along the [001] direction in Ga- and In-containing compounds. A combination of Ba rattling, short range Cu/T ordering, and a recently discovered coupling between acoustic and optical phonons for ThCr₂Si₂-type phosphides, resulted in ultralow thermal conductivity (<0.50 W m⁻¹ K⁻¹) for the title compounds.

---

Introduction

One of the most common structural types of ternary intermetallics is the ThCr₂Si₂-type family, which was first reported in 1965 by Ban and Sikirica.^1,2 The general formula of this structure type is often expressed as AM₂X₂ (A = alkali, alkaline-earth, rare-earth, or an early transition metal; M = transition metal or a main group element; X = main group element or late transition metal). ThCr₂Si₂-type compounds mostly crystallize in the tetragonal I4/mmm space group. The [M₂X₂]-layers are stacked along the crystallographic [001] direction with the A-site cations located in the interlayer spaces. The unique structural features of these materials give rise to a variety of properties such as superconductivity,^3–6 magnetism,^7–9 and, recently, thermoelectricity.^10–12 Selective preferences for elements to occupy either the M-site or the X-site have been noticed. For example, Al prefers the M-site in materials such as CeGa₂Al₂, CeBe_1.2Al_2.8, CeCuAl₃, and CaZn₂Al₂.^2,13,14 It has been further reported that the M-site preference of Al decreases with the increase in the size of the A-site cation.¹⁵ The site-preferences also depend on the electronegativity difference of the elements in the M and X sites. More electronegative transition metals seem to prefer the X-site.² For certain combinations of the main group and late transition metal of the same period (viz. Cu and Ga), establishing site preferences using X-ray diffraction is challenging due to similarities of X-ray scattering factors.^16,17 Most of the materials from the ThCr₂Si₂ family are metallic in nature with a partially filled transition metal d-band.¹⁸ The formation of vacancies at the M-site is common for compounds of late transition metals, such as ACu_1.7–1.9Pn₂ (A = Ca, Sr, Eu; Pn = P, As)^19,20 and RENi_1.7–1.9P₂ (RE = La, Ce, Pr).^21,22

There are two subclasses within the ThCr₂Si₂ structure type, differing by the absence or presence of covalent interlayer X–X interactions. The first type is classified as the “normal” ThCr₂Si₂ type structures (sometimes as a BaZn₂P₂ type structure), while the second type is classified as the “collapsed” ThCr₂Si₂-type structures.¹⁸ Materials with a c/a ratio of the unit cell parameters higher than ∼3.2 can be considered as the “normal” type, and they only account for about 10% of all reported ThCr₂Si₂ type materials.² On the other hand, “collapsed” structures tend to form with materials consisting of late transition metals with high valence electron counts.

A vast majority of the transition metal pnictides with a ThCr₂Si₂ structure exhibit metallic properties. For transition metals with a partially filled d-shell, the features of the electronic structure are elegantly summarized by Hoffmann and Zheng.^2,18 A closed-shell d¹⁰ electronic configuration can be achieved by late transition metals, like Cu⁺, which tend to form collapsed ThCr₂Si₂ structures with close to covalent P–P or As–As interlayer distances. To realize semiconducting properties, an opening of the bandgap in the electronic band structure is required. Moreover, the compound should be charge-balanced to position the Fermi level on the top of the valence band. Collapsed alkali metal ThCr₂Si₂-type compounds are not charge balanced, such as Li⁺(Cu⁺)₂(P²⁻)₂, while collapsed A²⁺(Cu⁺)₂(Pn²⁻)₂ should be electron balanced. Yet, the opening of the bandgap is not guaranteed and the non-zero density of states at the Fermi level is expected for the hypothetical alkaline-earth copper pnictides, ACu₂Pn₂. The experimental observations of 10–15% vacancies in the Cu sites, such as in BaCu_1.88As₂ and CaCu_1.75P₂, indicate system relaxation aiming at the reduction of the number of states at the Fermi level in a metallic system. Replacing Cu with Zn, 3d orbitals of which are more localized and located way below the Fermi level, allow semiconducting properties to be achieved in electron-balanced “normal” ThCr₂Si₂-type structures, Ba²⁺(Zn²⁺)₂(Pn³⁻)₂.²³

ThCr₂Si₂-type pnictides have been studied as thermoelectrics.¹⁰ Since many of these materials show metallic behavior, carrier doping is required to reduce their carrier concentrations to an optimum level. For example, BaZn₂As₂ is metallic in nature and has been doped with K to enhance the thermoelectric figure of merit. Low lattice thermal conductivity in these materials was attributed to the randomness and lattice instability arising from doping.^11,12 Recently, density functional theory (DFT) calculations revealed that the origin of the low lattice thermal conductivity of ThCr₂Si₂-type materials lies in the coupling of acoustic and low lying polar optical phonons, as well as the anisotropic chemical bonding.^24,25 The anisotropic displacement behavior of alkaline-earth or rare-earth cations in ThCr₂Si₂-type pnictides can be compared to the ‘rattling’ nature of the guest atoms in clathrate materials, which can lead to significant phonon dispersion, resulting in ultra-low thermal conductivities.^26–28 Given such characteristics, we focused on synthesis of charge balanced semiconducting ThCr₂Si₂-type pnictides.

In this work, we have explored a set of new ThCr₂Si₂-type phosphides with the general formula BaCuTP₂ (T = Al, Ga, In). The M-site is jointly occupied by Cu and one of the triel elements. BaCuAlP₂, BaCuGaP₂, and BaCuInP₂ crystallize in the ThCr₂Si₂-type structure, with a tetragonal I4/mmm space group, in the rare ‘normal’ structure type with an elongated c-axis. Anisotropic displacement or ‘rattling-like’ behavior of the interlayer Ba atoms along the [001] direction was confirmed with detailed structural analysis and heat capacity measurements. Solid state ³¹P NMR studies suggested the presence of local ordering involving Cu/T distribution and/or Ba displacement. Electron balanced composition of Ba²⁺Cu⁺T³⁺(P³⁻)₂ gives rise to a semiconducting behavior with valley degeneracy, which results in high values of Seebeck coefficient and ultralow thermal conductivity.

Results and discussion

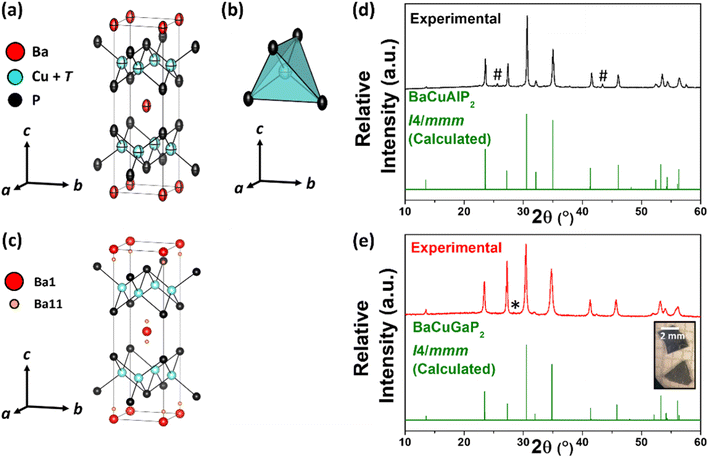
Three new ThCr₂Si₂-type phosphides were synthesized: BaCuAlP₂, BaCuGaP₂, and BaCuInP₂. The synthesis conditions were different for each material, owing to their varying thermal stabilities at elevated temperatures and the existence of competing phases. Samples of BaCuAlP₂ were synthesized from elements utilizing a high temperature solid state reaction at 1373 K, followed by slow cooling and long isothermal annealing at 1173 K (Fig. 1d). BaCuGaP₂ on the other hand could not be synthesized in high yield from elements due to the formation of the competing stable binary phase, GaP. Such an occurrence has been reported before while working with other quaternary Ba–Cu–Ga–P phases.¹⁷ To mitigate this problem, a BaGa₄ precursor was used as a Ga-source instead of elemental Ga (Fig. S1†). High purity BaCuGaP₂ sample was synthesized following the BaGa₄ precursor synthetic route by annealing the reaction mixture at 1123 K (Fig. 1e). Fine plate-like crystals of BaCuGaP₂ were resulted from this reaction (Fig. 1e inset). A wide range of temperatures and two types of reactants, either with elements or from BaIn₄ precursors, were attempted to produce BaCuInP₂. Either way, substantial amounts of admixtures were present all the time in the resulting product (Fig. S2†). However, the BaCuInP₂ sample contained large plate-like single crystals that were handpicked using an optical microscope, for characterization.

Fig. 1 (a) General crystal structure of BaCuTP₂ (T = Al, Ga, In) depicting the unit cell and the individual atoms in an ellipsoid form; (b) tetrahedral (Cu/T)P₄ units; (c) crystal structure of BaCuGaP₂ depicting split Ba sites, where Ba1 is at the center and the origin of the unit cell and Ba11 is displaced along [001] to two symmetry equivalent sites; (d) calculated (green) and experimental (black) PXRD patterns of BaCuAlP₂, and peaks of AlP impurity are denoted with #; (e) calculated (green) and experimental (red) PXRD patterns of BaCuGaP₂, a peak of the GaP impurity is denoted with *; (inset) microscopic image of selected BaCuGaP₂ crystals.

Single crystal X-ray diffraction (SCXRD) studies were carried out on selected crystals from all three samples. All three phases crystallize in the ThCr₂Si₂-type tetragonal I4/mmm space group (Fig. 1a–c). The M-site is jointly occupied by Cu and corresponding triel elements (T = Al, Ga, or In). The refined compositions from SCXRD characterization were BaCu_1.00(1)Al_1.00(1)P₂, BaCu_1.3(2)Ga_0.7(2)P₂, and BaCu_1.13(2)In_0.87(2)P₂. Due to similar X-ray scattering factors of Cu and Ga, the precision of the site occupancy determination is low.¹⁷ The Cu : T ratio for BaCuAlP₂ and BaCuGaP₂ was close to 1 : 1 within 3 standard deviations, while the BaCuInP₂ single crystal was found to be Cu-rich. The occurrence of the Cu : T ratio being closer to 1 : 1 with Ba(+2), Cu(+1), T(+3), and 2 P(−3) resulted in electron-balanced compositions. The crystallographic parameters and the details of all structures are provided in Table 1. The crystal structures are composed of [CuTP₂]²⁻ layers sandwiched with layers of Ba²⁺ ions (Fig. 1a and c). The atomic displacement parameter (ADP) ellipsoid of the Ba atom in BaCuAlP₂ was elongated along the [001] direction (Tables S1 and S2†). In the structures of BaCuGaP₂ and BaCuInP₂, the Ba site refined better as split into Ba1/Ba11 sites (Fig. 1c and Tables S3–S6†), with the split Ba11 site having occupancies of 5% (Ga) and 9% (In). This splitting could be due to an increase in the unit cell volume of the Ga- and In-containing compounds as compared to the Al counterpart (Table 1), resulting in an increased anisotropy for Ba along the [001] crystallographic direction. To quantify the ADP elongation, we performed the refinement of all three structures with a single non-split Ba site. The ADP ratio (U₃₃/U₁₁) of the Ba atom increases from 1.6 (BaCuAlP₂) to 2.3 (BaCuGaP₂) and 2.1 (BaCuInP₂). This increase indicates an anisotropic rattling of Ba in Ga- and In-containing compounds.

Table 1 Composition, crystal data, and structure refinement parameters for BaCuTP₂

Nominal composition	BaCuAlP2	BaCuGaP2	BaCuInP2
SCXRD composition	BaCu1.00(1)Al1.00(1)P2	BaCu1.3(2)Ga0.7(2)P2	BaCu1.14(2)In0.86(2)P2
CSD-numbers	2285843	2285844	2285845
Temperature (K)	100(2)		173(2)
Radiation (Å)	Mo-Kα, 0.71073
Crystal system	Tetragonal
Space group	I4/mmm (no. 139)
a (Å)	3.9357(5)	3.9572(8)	4.0773(4)
c (Å)	13.114(2)	13.057(3)	13.451(2)
Volume (Å^3)	203.13(6)	204.5(1)	223.61(5)
Z	2
Data/parameters	169/9	147/10	161/10
Density (g cm^−3)	4.738	5.368	5.498
μ (mm^−1)	15.23	21.77	19.03
R int	0.034	0.037	0.094
G-o-F	1.199	1.174	1.304
R 1 [I > 2σ(I)]	0.022	0.026	0.031
wR2 [I > 2σ(I)]	0.031	0.052	0.073
R 1 [all data]	0.027	0.031	0.033
wR2 [all data]	0.032	0.054	0.075
Max diff. peak/hole [e Å^−3]	1.10 and −1.29	1.69 and −1.26	2.63 and −1.32

---

(Cu/T)P₄ tetrahedra share edges to form the anionic layers (Fig. 1b). The interlayer P–P distance in all cases was ∼3.6 Å, much longer than a covalent P–P single bond length (2.20 Å),²⁹ confirming that all structures are a “normal” ThCr₂Si₂ type instead of a “collapsed” one. The c/a ratios of around 3.3 are in the range for the “normal” ThCr₂Si₂ type structure. Powder X-ray diffraction (PXRD) experiments confirmed that the samples are mainly BaCuAlP₂ and BaCuGaP₂ phases with tiny impurities of either AlP or GaP (Fig. 1d and e). For BaCuInP₂ samples, PXRD indicated the presence of several impurity phases such as Ba–P, Cu–In and Cu–P binaries, and unreacted in (Fig. S2†).

Energy dispersive X-ray spectroscopy (EDS) studies were carried out to further confirm the compositions of these new phases (Fig. S3†). Average compositions were found to be Ba_0.97(3)Cu_1.13(6)Al_0.87(6)P_1.79(6) and Ba_1.01(6)Cu_1.05(2)Ga_0.95(2)P_1.73(9), which agrees with the refined SCXRD compositions (Table 1). Underestimation of lighter elements is a common phenomenon in EDS analysis, leading to the underestimation of Al and P contents.³⁰ Since BaCuInP₂ could not be synthesized in a pure phase, the single crystal that was used for SCXRD was selected for EDS analysis. The composition of the selected single crystal was Ba_0.88(4)Cu_1.18(3)In_0.82(3)P_1.71(5) (Fig. S3e and f†), where the Cu : In ratio was close to the Cu : In ratio determined from SCXRD refinement (Table 1). The slight underestimation of Ba could be due to the slanted surface of the single crystal with respect to the incident X-ray during the analysis, which is a common occurrence in EDS analysis of non-flat samples.³⁰

Powdered BaCuAlP₂ and BaCuGaP₂ samples were studied with solid-state NMR spectroscopy (ssNMR), which is a robust technique to probe the local environment of a nucleus of interest. When paired with SCXRD, ssNMR provides a complimentary technique to verify the SCXRD model and overcome certain SCXRD limitations.^31–36 Here, ³¹P ssNMR spectroscopy was performed to probe possible local ordering, which is not detected by the long-range probing techniques, such as X-ray diffraction. According to the X-ray crystallography model, P has only one unique site in the I4/mmm crystal structures of BaCuAlP₂ and BaCuGaP₂, yet the ³¹P ssNMR spectra of both compounds show two inhomogeneously broadened asymmetrical peaks with peak maxima at −206 ppm and −258 ppm for BaCuAlP₂ and at −214 ppm and −264 ppm for BaCuGaP₂ (Fig. 2a and b). Both ³¹P NMR spectra exhibit similar isotropic chemical shifts and the frequency difference between the two peaks is approximately 50 ppm for both compounds. The origin of the signal broadening is further discussed below. The main difference in the 1D NMR spectra of the two compounds is the intensity ratio, as the lower frequency NMR signal in BaCuAlP₂ is more intense than the higher frequency one (Fig. 2a), while the intensity ratio was reversed for BaCuGaP₂ (Fig. 2b).

Fig. 2 ³¹P spin echo ssNMR spectra of (a) BaCuAlP₂ and (b) BaCuGaP₂. (c–f) ³¹P(X) J-resolved ssNMR spectra recorded (red) with or (blue) without X saturation pulses with X being (c and d) ⁶³Cu, (e) ²⁷Al, and (f) ⁷¹Ga, respectively. The difference spectrum (Δ) was obtained by subtracting the NMR spectrum obtained without X saturation pulses from that obtained with the X saturation pulse. (g) ³¹P refocused INADEQUATE 2D NMR spectra of BaCuAlP₂ and BaCuGaP₂. All NMR spectra were recorded with a 25 kHz magic angle spinning (MAS) frequency. # indicates an unknown phosphorus impurity.

The refined SCXRD structures assume an equal probability of Cu/Al or Cu/Ga atoms being found in each metal atom position and show that each P atom is bonded to 4 metal atoms. The most obvious explanation for why two types of ³¹P NMR signals are observed is that the ³¹P chemical shift will change depending upon the type and number of each metal atom bonded to P. For example, a structure with maximum short-range disorder would have five possible combinations of the four metal atoms bonded to the P atoms (PCu₄, PCu₃T, PCu₂T₂, PCuT₃, and PT₄ motifs), and hence there could possibly be up to five distinct ³¹P NMR signals. To investigate Cu/T short range ordering, heteronuclear NMR experiments were performed to probe the connectivity between P and the NMR-active metal isotopes ⁶³Cu, ²⁷Al, and ⁷¹Ga, which are moderate gyromagnetic ratio half-integer quadrupolar nuclei that possess a high natural isotopic abundance of 60%, 100%, and 50%, respectively. We performed ³¹P(X) perfect echo (PE) J-resolved experiments to probe for metal-phosphorus covalent bonds. A PE sequence was required to refocus the homonuclear J_PP coupling while allowing the evolution of the J_PX coupling (Fig. S4†).^37,38 The application of CT selective π-pulses to ⁶³Cu, ²⁷Al, or ⁷¹Ga during the PE sequence results in evolution of ³¹P-X scalar couplings, creation of heteronuclear anti-phase magnetization, and a reduction in the intensity of the observable ³¹P NMR signal (dephasing). Note that the duration of the perfect echo sequence was optimized to give maximal dephasing for each metal nucleus. Fig. 2 shows ³¹P NMR spectra obtained without (“off”) and with the π-pulses (“on”) applied to the metal nucleus. The difference spectrum obtained by subtraction is also shown. For BaCuAlP₂, the ³¹P(⁶³Cu) PE J-resolved experiment shows that application of a ⁶³Cu saturation pulse results in dephasing of both ³¹P NMR signals confirming that both arise from P atoms covalently bonded to Cu (Fig. 2c). However, the higher frequency peak shows enhanced intensity in the difference spectrum, suggesting that the higher frequency signal arises from P atoms that form bonds to a larger number of Cu atoms on average (e.g., PCu₃Al). This observation implies that the lower frequency ³¹P NMR signals arise from P atoms that have a larger average number of Al atoms in their first coordination sphere. Consistent with this hypothesis, the ³¹P(²⁷Al) PE J-resolved experiments show enhanced dephasing for the lower frequency ³¹P NMR signals.

The ³¹P(⁶³Cu) PE J-resolved experiment on BaCuGaP₂ shows a slight excess of dephasing for the higher frequency ³¹P NMR signal (Fig. 2d). The ³¹P(⁷¹Ga) PE J-resolved experiment shows that the lower frequency ³¹P NMR signal exhibits slightly higher dephasing (based on the peak intensity ratios in the difference spectrum). Therefore, the higher frequency ³¹P NMR signal is assigned to P atoms that tend to be bonded to Cu atoms, while the lower frequency ³¹P NMR signals should originate from P atoms that tend to be bonded to Ga. However, given the subtle differences in dephasing for both peaks, it is clear that P atoms bonded to both Cu and Ga can contribute to both the high and low frequency ³¹P NMR signals.

We performed homonuclear ³¹P refocused incredible natural abundance double resonance transfer (INADEQUATE) experiments to understand the connectivity of the P atoms (Fig. 2g).³⁹ In the refocused INADEQUATE experiment, double quantum (DQ) NMR signals are generated by evolution of 2-bond (P–M–P) ³¹P homonuclear J-couplings. Optimization of the echo delays in the refocused INADEQUATE experiments suggests that the ³¹P J-couplings are approximately 120 Hz. The position of the NMR signal in the indirect DQ dimension indicates the sum of the single-quantum (SQ) chemical shift of the two J-coupled spins. To aid in interpreting the INADEQUATE NMR spectra, we have plotted them such that the width of the indirect dimension is twice the width of the direct dimension (in units of ppm). Therefore, any signals falling on the diagonal correspond to auto-correlations that arise when ³¹P spins with approximately the same chemical shift are J-coupled. Any signals in the 2D NMR spectrum that are off the diagonal line arise from ³¹P spin pairs that have distinct chemical shifts. We note that the INADEQUATE 2D NMR spectra show elongated correlation where the intensity is distributed along the diagonal direction. For example, the SQ peak separation is constant between the off-diagonal peaks in the spectrum of BaCuGaP₂ and is approximately 56 ppm. The skewing of the correlation peaks is characteristic of anisotropic bulk magnetic susceptibility (ABMS) signal broadening.^40,41 We plan to perform additional NMR experiments, such as diluting the samples in an isotropic diamagnetic medium, to confirm that susceptibility effects are the primary origin of the inhomogeneous broadening.

We first analyze the INADEQUATE spectrum of BaCuGaP₂. Considering the results of the ³¹P{X} J-resolved experiments, the auto-correlation centered at −250 ppm SQ chemical shift should arise from pairs of P atoms that are predominantly bridging gallium atoms, e.g., (CuGa₂)P–Ga–P(Ga₂Cu). The auto-correlation centered at −204 ppm SQ then arises from pairs of P atoms primarily bonded to Cu atoms such as (GaCu₂)P–Cu–P(Cu₂Ga). There are also intense off-diagonal correlations centered at SQ chemical shifts of −204 ppm and −260 ppm. These correlations should arise from pairs of P atoms where one P atom is predominantly bonded to Ga, while the other is predominantly bonded to Cu, i.e., GaCu₂P–Cu–PGa₃. The INADEQUATE spectrum of BaCuAlP₂ shows a similar pattern of correlations to that seen for BaCuGaP₂. The lower frequency ³¹P NMR signal shows auto-correlations. Recall that the ³¹P{²⁷Al} J-resolved experiments indicate that lower frequency ³¹P NMR signals primarily correspond to P atoms bonded to Al. Therefore, the presence of this auto-correlation suggests that P coordinated by Al atoms may be clustered, e.g., the presence of (CuAl₂)P–Al–P(Al₂Cu). The higher frequency ³¹P NMR signals were assigned to P atoms bonded to Cu and these mainly show off-diagonal correlations. This observation suggests the presence of connections between Cu and Al bonded P atoms, e.g., (Cu₂Al)P–Cu–P(Al₃). In summary, ssNMR studies reveal that complex short-range ordering may be present in the structures of reported compounds with partial but incomplete clustering of tetrel and Cu atoms in the square-planar layers.

Differential scanning calorimetry (DSC) was used to determine the thermal stability. BaCuAlP₂ was thermally stable upon heating to 1373 K. However, a tiny exothermic peak was noticed around 1055 K upon cooling (Fig. S6c†). PXRD carried out on the sample after cooling showed minor occurrence of AlP and Ba₈Cu₁₆P₃₀ clathrate impurities in the sample (Fig. S6d and Table S8†). The latter one is expected to crystallize around 1055 K.⁴² BaCuGaP₂ exhibits peaks upon heating and cooling with an onset temperature of 1336 K and 1353 K, respectively (Fig. S6b†), with two additional low intensity exothermic peaks at lower temperatures. The formation of GaP and Ba₈Cu₁₆P₃₀ clathrate admixtures was identified by PXRD (Table S8†) in the sample after DSC. The thermal behavior of BaCuInP₂ was not clear from DSC studies as multiple low intensity peaks were obtained between 1050 K and 1100 K (Fig. S6a†), which could be due to the main BaCuInP₂ phase, or the several other impurity phases present (Table S8†).

Transport properties were measured on sintered pellets of polycrystalline BaCuAlP₂ and BaCuGaP₂ (95% and 93% dense, respectively) in a temperature range of 10–823 K (Fig. 2). PXRD on the sintered pellets revealed no substantial changes in the samples after sintering (Fig. S8†). 4-Probe resistivity measurement on the polycrystalline samples of those materials revealed semiconducting behavior, as opposed to most ThCr₂Si₂-type materials that are reported to be metallic.² At 673 K, BaCuAlP₂ and BaCuGaP₂ exhibit resistivity values of 2093 mΩ cm and 110 mΩ cm, respectively (Fig. 3b and inset). The semiconducting behaviors can be explained by the charge balanced nature and gapped electronic structure. Resistivity was run on a selected crystal of BaCuInP₂ in the temperature range of 2–300 K, which revealed a semiconducting behavior as well, reaching a value of 79 mΩ cm at 300 K (Fig. 3b). Some examples of similar charge-balanced ThCr₂Si₂-type semiconductors include BaZn₂P₂ and BaZn₂As₂ with comparable resistivity values.^23,44 In turn, the resistivities of RECuZnP₂ (RE = Pr, Nd, Er) increase with temperature and lie in the range of 1–10 mΩ cm.²⁵

Fig. 3 Transport properties of BaCuAlP₂ and BaCuGaP₂ in the temperature range of 10–850 K; (a) total thermal conductivity; (b) electrical resistivity (including the electrical resistivity of the BaCuInP₂ crystal in the temperature range of 2 to 300 K), and electrical resistivity of BaCuAlP₂ (inset); (c) Seebeck coefficient; (d) figure of merit (zT). The discontinuity at 300 K is due to two different setups used for high- and low-temperature measurements.

The Seebeck coefficient indicated p-type behavior for both BaCuAlP₂ and BaCuGaP₂, signifying holes as the majority carriers. Both materials showed overall high values of the Seebeck coefficient throughout the temperature range, reaching peak values of 317 μV K⁻¹ at 798 K for BaCuAlP₂ and 235 μV K⁻¹ at 648 K for BaCuGaP₂ (Fig. 3c). The high Seebeck coefficient and high resistivity signify a relatively low hole concentration or low hole mobility or both.²⁶ For comparison, high Seebeck coefficients of ∼200 μV K⁻¹ at similarly high temperatures have been reported for other ThCr₂Si₂-type materials, such as BaMn₂Sb₂, BaZn₂P₂, and BaMnZn_0.9Cu_0.1P₂.^23,44–46 Another notable example is BaZn₂As₂, which reaches ∼300 μV K⁻¹ around the same temperature range.¹¹ Due to high resistivity, relatively low values of the thermoelectric figures of merit (zT) were obtained for polycrystalline BaCuAlP₂ and BaCuGaP₂ (Fig. 3d). Undoped BaZn₂As₂ shows similarly low zT and only proper hole doping demonstrated an increase in the overall power factor, resulting in a peak zT of 0.67 for Ba_0.98K_0.02Zn₂As₂ at 900 K, an improvement of more than 335% compared to the undoped one. Such an example leaves the room open for hole-doping as a promising step forward to improve the thermoelectric performance of the reported materials in the future.^11,12,47

Goldschmidt-Sharp band gaps (E_g) of 0.51 eV and 0.18 eV were calculated using the peak Seebeck coefficient values for BaCuAlP₂ and BaCuGaP₂, respectively.⁴⁸ However, the logarithmic plots of electrical conductivity against the inverse temperature revealed activation energies of 0.07, 0.05, and 0.10 eV for BaCuAlP₂, BaCuGaP₂, and BaCuInP₂, respectively (Fig. S9† and Table 2). The experimental solid-state optical absorption measurement revealed possible direct transitions of 0.36 and 0.91 eV for BaCuAlP₂ (Fig. S7†), which is close to the corresponding Goldschmidt-Sharp band gap of 0.51 eV and the calculated band gap of 0.36 eV (vide infra) (Fig. 5a). For comparison, β-BaZn₂As₂ has a narrow experimental bandgap of 0.23 eV.⁴³

Table 2 Comparison of different values of the band gap (eV) of BaCuAlP₂, BaCuGaP₂ and BaCuInP₂ derived from different experimental and theoretical methods

	Goldschmidt-Sharp band gap (eV)	LMTO band gap (eV)	Band gap derived from resistivity (eV)
BaCuAlP2	0.51	0.36	0.07
BaCuGaP2	0.18	0	0.05
BaCuInP2	—	0.44	0.10

---

The thermal conductivity of both the studied pellets showed sharp characteristic peaks at ∼50 K, typical for crystalline materials.²⁶ Ultra-low thermal conductivity values of 0.38 W m⁻¹ K⁻¹ at 823 K for BaCuAlP₂ and 0.59 W m⁻¹ K⁻¹ at 673 K for BaCuGaP₂ were observed (Fig. 3a). Low thermal conductivity in ThCr₂Si₂ type phosphides was shown to originate from the coupling of the acoustic and the low-lying optical phonon modes, such as in the case of RECuZnP₂ (RE = Pr, Nd, Er).^24,25 Besides this phenomenon, the complex short-range ordering detected by NMR, as well as the anisotropic chemical bonding may play an important role in reducing the thermal conductivity of BaCuAlP₂. For BaCuGaP₂, displacement or an enhanced anisotropic rattling of Ba cations may additionally contribute to the reduction of the lattice thermal conductivity (Tables S3–S6†).

Heat capacity (C_p) measurements were carried out on BaCuGaP₂ and BaCuInP₂ crystals in the temperature range of 2–300 K (Fig. 4). An image of the BaCuGaP₂ crystal on the heat capacity puck is shown in the Fig. 4a inset. The plot of C_p/T³vs. T revealed Boson peaks for BaCuGaP₂ and BaCuInP₂ at 18.2 K and 14.2 K, respectively (Fig. 4b), establishing the possible anisotropic displacement behavior of the Ba atoms in the interlayer spaces. This phenomenon has been suggested as the reason behind the origin of low thermal conductivity for similar layered materials.^24,25 Ba atom displacement can be compared to the rattling nature of the guest cations in inorganic clathrates and fullerenes.^49,50 The position of the peak was proposed to be inversely proportional to free space available to the cation.^51–53 The Boson peak positions are considered to be at ∼20% of the Einstein temperature (θ_E), and the values of θ_E were calculated to be 91 K and 71 K for BaCuGaP₂ and BaCuInP₂, respectively.⁵⁴ BaCuTP₂ can be considered as having elongated polyhedral cages around Ba (Fig. 4e) with a cage volume of 102.2 ų for BaCuGaP₂. Such a cage volume is comparable to that of the pentagonal dodecahedron cages present in clathrate-I materials.²⁶ The average distance between Ba and framework atoms in clathrate cages is typically between 3.3 and 3.6 Å. In the structure of BaCuGaP₂, the distance from Ba to the nearest P atom (Ba–P₁) is 3.35 Å (Fig. 4f). The Ba–Cu/T distance is 3.81 Å, which is slightly longer than that of their clathrate counterparts, where it is ∼3.60 Å for BaCu₂P₄ and ∼3.20–3.70 Å for Ba₈Cu₁₆P₃₀.²⁶ The observed anisotropic displacement of Ba atoms along [001] agrees well with such an elongated polyhedral description.

Fig. 4 (a) Temperature-dependent specific heat capacity (C_p) at constant pressure (inset: heat capacity set-up of the BaCuGaP₂ crystal); (b) heat capacity data represented as C_p/T³vs. T; (c) low temperature heat capacity data represented as C_p/T vs. T²; (d) table showing the physical parameters derived from the heat capacity data for (red) BaCuGaP₂ and (blue) BaCuInP₂ crystals; (e) a clathrate-like view of the BaCuGaP₂ crystal structure depicting Ba ion encapsulated inside an elongated polyhedron with the Ba-framework distances tabulated in (f).

C _p/T vs. T² plots (Fig. 4c) revealed Sommerfeld coefficient (γ) values of 2.95 mJ mol⁻¹ K⁻² and 1.20 mJ mol⁻¹ K⁻² for BaCuGaP₂ and BaCuInP₂, respectively (Fig. 4d). The higher value for BaCuGaP₂ points to a higher density of states near the Fermi level (E_f) for BaCuGaP₂ in comparison to BaCuInP₂. Most of the metallic ThCr₂Si₂-type pnictides have higher values of the Sommerfeld coefficient, 6–37 mJ mol⁻¹ K⁻², with the notable exceptions of small gap semiconductors BaMn₂Bi₂ and BaMn₂As₂, where the values of γ are close to zero. Debye temperatures (θ_D) for BaCuGaP₂ and BaCuInP₂ were 193 K and 139 K respectively. The value of Debye temperature is usually proportional to the lattice rigidity and the average speed of sound in the materials. Overall, a softer lattice can also lead to ultra-low thermal conductivities.^55,56 Heat capacity behavior has been explored for various ThCr₂Si₂-type pnictides. Most arsenides such as CaFe₂As₂, BaFe₂As₂, BaMn₂As₂, and BaNi₂As₂ have overall higher Debye temperatures, 200–300 K, suggesting stiffer lattices compared to the materials reported here. Even though the thermal conductivity of most of the metallic ThCr₂Si₂-type pnictides has not been well explored, we hypothesize that the ultra-low thermal conductivities for BaCuAlP₂ and BaCuGaP₂ are partially due to the less structural rigidity compared to other materials from this family.^57–59

The BaNi₂P₄ twisted clathrate has a split Ba site, where the Ba rattling gives rise to a Boson peak, with θ_E being 124 K, which is higher than those of BaCuGaP₂ and BaCuInP₂.⁴⁹ BaNi₂P₄ has a θ_D of 205 K, signifying a stiffer lattice than BaCuGaP₂ and BaCuInP₂. On the other hand, a clathrate-like material, Ba₂Zn₅As₆, has different cages encapsulating Ba atoms, one of which being a hendecahedron cage with a cage volume of 116 ų, close to that of BaCuGaP₂ and La_1.6Ba_6.4Cu₁₆P₃₀.^60,61 Ba₂Zn₅As₆ has a θ_E of 80 K and a θ_D of 109 K, comparable to those of BaCuGaP₂ and BaCuInP₂. The softer lattice in Ba₂Zn₅As₆ gives rise to low thermal conductivity. Overall, these results agree with the semiconducting nature and high Seebeck coefficients of BaCuTP₂ materials with overall lower Sommerfeld coefficients and a lower density of states near the Fermi level compared to their metallic counterparts.

Density functional theory (DFT) calculations were carried out with the linear muffin-tin orbital (LMTO) method using an ordered hypothetical I4̄m2 structural model (Fig. S10†) of BaCuTP₂ (T = Al, Ga, In). Similar ordered models have been used for DFT calculations on disordered ThCr₂Si₂-type structures.⁶² The band structures of BaCuAlP₂ and BaCuInP₂ revealed almost direct band gaps, with the valence band maxima at Γ- and Z-points and the conduction band minimum at the Z-point (Fig. 5a and e). Band gaps were calculated to be 0.36 eV and 0.44 eV for BaCuAlP₂ and BaCuInP₂, respectively. This was a slight underestimation in comparison to the corresponding Goldschmidt-Sharp and the experimental band gaps (Table 2), but such underestimation of band gaps is characteristic of DFT calculations. BaCuGaP₂ appeared to not have a band gap according to the calculations (Fig. 5c), which is an underestimation from the corresponding narrow Goldschmidt-Sharp band gap of 0.18 eV (Table 2). The presence of a higher density of states (DOS) around the Fermi level for BaCuGaP₂ (Fig. 5c) compared to BaCuInP₂ agrees with its higher Sommerfeld coefficient (γ) (Fig. 4d). The presence of high valley degeneracy (N_v) at the top of the valence bands (Fig. 5a, c and e) explains the observed high Seebeck coefficients (Fig. 3c) of BaCuAlP₂ and BaCuGaP₂. Similar high Seebeck coefficient values can be expected for BaCuInP₂. P and Cu have the highest contributions towards the states on the top of the valence band (VBM), with minor contributions from the triel and Ba. In turn, Ba has a major contribution to the states at the bottom of the conduction band (CBM). A similar band structure was reported for β-BaZn₂P₂, which has a small (∼0.03 eV) indirect band gap along Γ → Z points, with P states dominating the VBM and Ba states dominating the CBM.²³ On the other hand, β-BaZn₂As₂ has a direct band gap of 0.23 eV along the Γ-point, with As states dominating the VBM and Ba states predominantly contributing to the CBM.⁴³

Fig. 5 (Left) Band structures and (right) total and partial density-of-states (DOS) of hypothetical ordered I4̄m2 models of (a and b) BaCuAlP₂; (c and d) BaCuGaP₂; (e and f) BaCuInP₂. All energies are plotted with respect of the Fermi energy (E_F), depicted by the dotted straight line in each plot.

In a nutshell, the formation of semiconducting ThCr₂Si₂-type phases is uncommon. Hofmann and Zheng¹⁸ showed that the properties of the ThCr₂Si₂-type structures depend on the filling of the transition metal d-band. The substitution on the transition metal site was extensively used to modify the electronic, magnetic, and superconducting properties of ThCr₂Si₂-type compounds.^63–66 Full replacement of the transition metal with a main group element resulted in the formation of compounds with different crystal structures, such as BaGe₂P₂ or EuIn₂P₂. This can be rationalized in the necessity to maintain a +2 formal oxidation state for the main group M element to stabilize the ThCr₂Si₂-type structure, with the sole example being BaZn₂Pn₂. In our approach, we combined a T³⁺ main group element and Cu¹⁺ late transition metal. This realizes semiconducting materials by opening a bandgap. We hypothesize that even higher formal charge main group elements, such as Si⁴⁺ or Ge⁴⁺, can be accommodated in ThCr₂Si₂-type structures upon proper balancing with Cu¹⁺. Further studies on such semiconductors are currently underway.

In conclusion, new ThCr₂Si₂-type phosphides were synthesized with the general formula BaCuTP₂ (T = Al, Ga, In). The mixing of a transition metal (Cu) and a main group triel element (Al, Ga, and In) at the M-site resulted in the formation of charge balanced semiconductors. The crystal structures retained the tetragonal I4/mmm structure of the ThCr₂Si₂ materials. Solid state ³¹P NMR studies revealed the presence of partial short-range ordering in the Cu-T metal sublattice. Transport property measurements revealed high Seebeck coefficients owing to the high valley degeneracy shown by DFT calculations. Ultra-low thermal conductivities were observed, contributed by phonon scattering from their soft lattices due to the intense ‘anisotropic rattling’ of the Ba atom in the interlayer spaces, and the coupling of the acoustic and optical phonon modes. The combination of the semiconducting electronic structure, ultra-low thermal conductivity, and high Seebeck coefficient is a rare example among the few thousand reported ThCr₂Si₂-type materials thus far, most of which are metallic in nature. This paves the way for further modification of these materials such as hole-doping, band engineering, and isovalent doping, to increase the carrier concentration and eventually the overall thermoelectric performance.

Data availability

The data supporting the findings in this research paper are available from the corresponding author upon reasonable request.

Author contributions

The manuscript was written through contributions of all authors.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under award number DE-SC0023509. The PPMS instrument used for property measurements was supported by the Ames National Laboratory, U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division. Solid-state NMR work was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The Ames National Laboratory is operated for the U.S. DOE by Iowa State University under contract #DE-AC02-07CH11358. The authors are thankful to Professor Julia V. Zaikina (Iowa State University) for access to the Spark Plasma Sintering (SPS) and Diffuse Reflectance UV-vis Spectrometer, and Dr Warren Straszheim for help with the EDS/SEM data collection at MARL, Iowa State University.

References

1. Z. Ban and M. Sikirica, The crystal structure of ternary silicides ThM₂Si₂(M = Cr, Mn, Fe, Co, Ni and Cu), Acta Crystallogr., 1965, 18(4), 594–599,  DOI:10.1107/S0365110X6500141X.
2. M. Shatruk, ThCr₂Si₂ structure type: the “perovskite” of intermetallics, J. Solid State Chem., 2019, 272, 198–209,  DOI:10.1016/j.jssc.2019.02.012.
3. P. C. Canfield and S. L. Bud’ko, FeAs-based superconductivity: a case study of the effects of transition metal doping on BaFe₂As₂, Annu. Rev. Condens. Matter Phys., 2010, 1(1), 27–50,  DOI:10.1146/annurev-conmatphys-070909-104041.
4. K.-H. Müller and V. N. Narozhnyi, Interaction of superconductivity and magnetism in borocarbide superconductors, Rep. Prog. Phys., 2001, 64(8), 943–1008,  DOI:10.1088/0034-4885/64/8/202.
5. A. K. Ganguli and J. Prakash, Iron-based superconductors with extended FeX₄ (X = As and Se) tetrahedra, Eur. J. Inorg. Chem., 2011, 2011(26), 3868–3876,  DOI:10.1002/ejic.201100371.
6. A. L. Ivanovskii, New ternary ThCr₂Si₂-type iron–selenide superconducting materials: synthesis, properties and simulations, Physica C, 2011, 471(13), 409–427,  DOI:10.1016/j.physc.2011.04.009.
7. A. Szytula and J. Leciejewicz, Magnetic Properties of Ternary Intermetallic Compounds of the RT₂X₂ Type: Handbook on the Physics and Chemistry of Rare Earths, Elsevier, Amsterdam, 1989, pp. 133–211.
8. G. Huan, M. Greenblatt and M. Croft, New ternary transition metal chalcogenides AM₂X₂ (A=K,Rb,Cs; M=Co; A=K, M=Ni; X=S, Se): magnetically ordered Metals with the ThCr₂Si₂-type structure, Eur. J. Solid State Inorg. Chem., 1989, 26(2), 193–220.
9. X. Tan, Z. P. Tener and M. Shatruk, Correlating itinerant magnetism in RCo₂Pn₂ pnictides (R = La, Ce, Pr, Nd, Eu, Ca; Pn = P, As) to their crystal and electronic structures, Acc. Chem. Res., 2018, 51(2), 230–239,  DOI:10.1021/acs.accounts.7b00533.
10. W. Peng, S. Chanakian and A. Zevalkink, Crystal chemistry and thermoelectric transport of layered AM₂X₂ compounds, Inorg. Chem. Front., 2018, 5(8), 1744–1759,  10.1039/C7QI00813A.
11. H. Kunioka, K. Kihou, D. Kato, H. Usui, T. Iida, H. Nishiate, K. Kuroki, A. Yamamoto and C.-H. Lee, Thermoelectric properties of (Ba,K)Zn₂As₂ crystallized in the ThCr₂Si₂-type structure, Inorg. Chem., 2020, 59(9), 5828–5834,  DOI:10.1021/acs.inorgchem.9b02680.
12. K. Kihou, H. Nishiate, A. Yamamoto and C.-H. Lee, Thermoelectric properties of as-based zintl compounds Ba_1–xK_xZn₂As₂, Inorg. Chem., 2017, 56(6), 3709–3712,  DOI:10.1021/acs.inorgchem.7b00232.
13. G. Cordier, E. Czech and H. Schäfer, CaZn₂Al₂, the first example of an “inverse” ThCr₂Si₂-structure, Z. Naturforsch. B, 1984, 39(12), 1629–1632,  DOI:10.1515/znb-1984-1201.
14. O. Zarechnyuk, P. Kripyakevich and E. Gladyshevskiy, Ternary intermetallic compounds with a BaAl₄ type superstructure, Kristallografiya, 1964, 9, 835–838.
15. U. Häussermann, S. Amerioun, L. Eriksson, C.-S. Lee and G. J. Miller, The s–p bonded representatives of the prominent BaAl₄ structure type: a case study on structural stability of polar intermetallic network structures, J. Am. Chem. Soc., 2002, 124(16), 4371–4383,  DOI:10.1021/ja012392v.
16. Yu. N. Grin, M. Ellner, K. Hiebl and P. Rogl, New ytterbium compounds with the BaAl₄ type of structure: crystal chemistry and magnetic properties of Yb(Cu,Ag,Au,Pd,Pt)_xGa_4−x, J. Alloys Compd., 1993, 196(1), 207–212,  DOI:10.1016/0925-8388(93)90597-G.
17. A. Sarkar, G. Viswanathan, P. Yox, S. Harycki, F. T. Cerasoli, J. Wang, F. A. Perras, A. Gundlach-Graham, D. Donadio and K. Kovnir, Evolution of structure and transport properties of the Ba₈Cu₁₆P₃₀ clathrate-I framework with the introduction of Ga, Appl. Phys. Lett., 2022, 120(19), 191901,  DOI:10.1063/5.0093646.
18. R. Hoffmann and C. Zheng, Making and breaking bonds in the solid state: the ThCr₂Si₂ structure, J. Phys. Chem., 1985, 89, 4175–4181.
19. J. Dünner, A. Mewis, M. Roepke and G. Michels, New ternary copper pnictides with modified BaAl₄ structures, Z. Anorg. Allg. Chem., 1995, 621(9), 1523–1530,  DOI:10.1002/zaac.19956210915.
20. I. Pilchowski and A. Mewis, Ternary BaAl₄ variants. representation and structure of CaCu₂As₂, Ca₂Cu₆P₅, and Ba₂Cu₃P₄, Z. Anorg. Allg. Chem., 1990, 581(1), 173–182,  DOI:10.1002/zaac.19905810121.
21. S. Bobev, S. Xia, E. D. Bauer, F. Ronning, J. D. Thompson and J. L. Sarrao, Nickel deficiency in RENi_2–xP₂ (RE = La, Ce, Pr). Combined crystallographic and physical property studies, J. Solid State Chem., 2009, 182(6), 1473–1480,  DOI:10.1016/j.jssc.2009.03.014.
22. W. K. Hofmann and W. Jeitschko, Structural investigations of ternary lanthanoid and uranium nickel phosphides, J. Solid State Chem., 1984, 51(2), 152–158,  DOI:10.1016/0022-4596(84)90328-1.
23. A. Balvanz, S. Baranets, M. O. Ogunbunmi and S. Bobev, Two polymorphs of BaZn₂P₂: crystal structures, phase transition, and transport properties, Inorg. Chem., 2021, 60(18), 14426–14435,  DOI:10.1021/acs.inorgchem.1c02209.
24. K. Guo, T. Weng, Y. Jiang, Y. Zhu, H. Li, S. Yuan, J. Yang, J. Zhang, J. Luo, Y. Grin and J.-T. Zhao, Unveiling the origins of low lattice thermal conductivity in 122-phase zintl compounds, Mater. Today Phys., 2021, 21, 100480,  DOI:10.1016/j.mtphys.2021.100480.
25. J.-H. Pöhls, S. Chanakian, J. Park, A. M. Ganose, A. Dunn, N. Friesen, A. Bhattacharya, B. Hogan, S. Bux, A. Jain, A. Mar and A. Zevalkink, Experimental validation of high thermoelectric performance in RECuZnP₂ predicted by high-throughput DFT calculations, Mater. Horiz., 2021, 8(1), 209–215,  10.1039/D0MH01112F.
26. J.-A. Dolyniuk, B. Owens-Baird, J. Wang, J. V. Zaikina and K. Kovnir, Clathrate thermoelectrics, Mater. Sci. Eng. R Rep., 2016, 108, 1–46,  DOI:10.1016/j.mser.2016.08.001.
27. B. Owens-Baird, S. Heinrich and K. Kovnir, Thermoelectric materials, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd, 2017, pp. 1–35,  DOI:10.1002/9781119951438.eibc2497.
28. P. Yox, G. Viswanathan, A. Sarkar, J. Wang and K. Kovnir, Thermoelectric materials, in Comprehensive Inorganic Chemistry III, ed. J. Reedijk and K. R. Poeppelmeier, Elsevier, Oxford, 3rd edn, 2023, pp. 45–79,  DOI:10.1016/B978-0-12-823144-9.00109-6.
29. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Covalent radii revisited, Dalton Trans., 2008,(21), 2832–2838,  10.1039/B801115J.
30. D. C. Bell and A. J. Garratt-Reed, Energy dispersive X-ray analysis in the electron microscope, Garland Science, 2003.
31. R. Tycko, G. Dabbagh, S. R. Kurtz and J. P. Goral, Quantitative study of atomic ordering in Ga_0.5In_0.5P thin films by ³¹P nuclear magnetic resonance, Phys. Rev. B, 1992, 45(23), 13452–13457,  DOI:10.1103/PhysRevB.45.13452.
32. J. Xu, S. Jiang and Y. Du, Unravelling the mystery of solid solutions: a case study of ⁸⁹Y solid-state NMR spectroscopy, ChemPhysChem, 2020, 21(9), 825–836,  DOI:10.1002/cphc.202000148.
33. P. Yox, A. P. Porter, R. W. Dorn, V. Kyveryga, A. J. Rossini and K. Kovnir, Semiconducting silicon–phosphorus frameworks for caging exotic polycations, Chem. Commun., 2022, 58(55), 7622–7625,  10.1039/D2CC02304K.
34. L. Corti, D. Iuga, J. B. Claridge, M. J. Rosseinsky and F. Blanc, Disorder and oxide ion diffusion mechanism in La_1.54Sr_0.46Ga₃O_7.27 melilite from nuclear magnetic resonance, J. Am. Chem. Soc., 2023, 145(40), 21817–21831,  DOI:10.1021/jacs.3c04821.
35. D. Sarkar, A. Bhattacharya, J. Meyer, A. M. Kirchberger, V. Mishra, T. Nilges and V. K. Michaelis, Unraveling sodium-ion dynamics in honeycomb-layered Na₂Mg_xZn_2−xTeO₆ solid electrolytes with solid-state NMR, J. Am. Chem. Soc., 2023, 145(36), 19727–19745,  DOI:10.1021/jacs.3c04928.
36. I. D. Seymour, D. S. Middlemiss, D. M. Halat, N. M. Trease, A. J. Pell and C. P. Grey, Characterizing oxygen local environments in paramagnetic battery materials via¹⁷O NMR and DFT calculations, J. Am. Chem. Soc., 2016, 138(30), 9405–9408,  DOI:10.1021/jacs.6b05747.
37. T. Parella, Towards perfect NMR: spin-echo versus perfect-echo building blocks, Magn. Reson. Chem., 2019, 57(1), 13–29,  DOI:10.1002/mrc.4776.
38. K. Takegoshi, K. Ogura and K. Hikichi, A perfect spin echo in a weakly homonuclear J-coupled two spin-12 system, J. Magn. Reson., 1989, 84(3), 611–615,  DOI:10.1016/0022-2364(89)90127-3.
39. A. Lesage, C. Auger, S. Caldarelli and L. Emsley, Determination of through-bond carbon−carbon connectivities in solid-state NMR Using the INADEQUATE experiment, J. Am. Chem. Soc., 1997, 119(33), 7867–7868,  DOI:10.1021/ja971089k.
40. G. Kervern, G. Pintacuda, Y. Zhang, E. Oldfield, C. Roukoss, E. Kuntz, E. Herdtweck, J.-M. Basset, S. Cadars, A. Lesage, C. Copéret and L. Emsley, Solid-state NMR of a paramagnetic DIAD-Fe^II catalyst: sensitivity, resolution enhancement, and structure-based assignments, J. Am. Chem. Soc., 2006, 128(41), 13545–13552,  DOI:10.1021/ja063510n.
41. D. Sakellariou, S. P. Brown, A. Lesage, S. Hediger, M. Bardet, C. A. Meriles, A. Pines and L. Emsley, High-resolution NMR correlation spectra of disordered solids, J. Am. Chem. Soc., 2003, 125(14), 4376–4380,  DOI:10.1021/ja0292389.
42. J. Wang, J. Voyles, S. Grzybowski and K. Kovnir, Synthesis, structure, and transport properties of Ba₈Cu_16−xAu_xP₃₀ clathrate solid solution, J. Appl. Phys., 2020, 127(5), 055104,  DOI:10.1063/1.5134080.
43. Z. Xiao, H. Hiramatsu, S. Ueda, Y. Toda, F.-Y. Ran, J. Guo, H. Lei, S. Matsuishi, H. Hosono and T. Kamiya, Narrow bandgap in β-BaZn₂As₂ and its chemical origins, J. Am. Chem. Soc., 2014, 136(42), 14959–14965,  DOI:10.1021/ja507890u.
44. V. Ponnambalam, S. Lindsey, W. Xie, D. Thompson, F. Drymiotis and T. M. Tritt, High seebeck coefficient AMXP₂ (A = Ca and Yb; M, X = Zn, Cu and Mn) Zintl phosphides as high-temperature thermoelectric materials, J. Phys. D: Appl. Phys., 2011, 44(15), 155406,  DOI:10.1088/0022-3727/44/15/155406.
45. V. Ponnambalam and D. T. Morelli, Thermoelectric properties of light-element-containing Zintl compounds CaZn_2−xCu_xP₂ and CaMnZn_1−xCu_xP₂ (x = 0.0–0.2), J. Electron. Mater., 2014, 43(6), 1875–1880,  DOI:10.1007/s11664-013-2895-2.
46. H. F. Wang, K. F. Cai, H. Li, L. Wang and C. W. Zhou, Synthesis and thermoelectric properties of BaMn₂Sb₂ single crystals, J. Alloys Compd., 2009, 477(1–2), 519–522,  DOI:10.1016/j.jallcom.2008.10.080.
47. H. Kunioka, K. Kihou, H. Nishiate, A. Yamamoto, H. Usui, K. Kuroki and C. H. Lee, Thermoelectric properties of (Ba,K)Cd₂As₂ crystallized in the CaAl₂Si₂-type structure, Dalton Trans., 2018, 47(45), 16205–16210,  10.1039/C8DT02955E.
48. Z. M. Gibbs, H.-S. Kim, H. Wang and G. J. Snyder, Band gap estimation from temperature dependent seebeck measurement—deviations from the 2e|S|_maxT_max relation, Appl. Phys. Lett., 2015, 106(2), 022112,  DOI:10.1063/1.4905922.
49. J. Wang, J.-A. Dolyniuk, E. H. Krenkel, J. L. Niedziela, M. A. Tanatar, E. I. Timmons, T. Lanigan-Atkins, H. Zhou, Y. Cheng, A. J. Ramirez-Cuesta, D. L. Schlagel, U. S. Kaluarachchi, L.-L. Wang, S. L. Bud’ko, P. C. Canfield, R. Prozorov, O. Delaire and K. Kovnir, Clathrate BaNi₂P₄: an interplay of heat and charge transport due to strong host–guest interactions, Chem. Mater., 2020, 32(18), 7932–7940,  DOI:10.1021/acs.chemmater.0c02758.
50. G. P. Johari, Librational heat capacity of fullerenes in the einstein model, J. Chem. Phys., 2003, 119(22), 11912–11916,  DOI:10.1063/1.1624052.
51. K. Suekuni, M. A. Avila, K. Umeo and T. Takabatake, Cage-size control of guest vibration and thermal conductivity in Sr₈Ga₁₆Si_30−xGe_x, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(19), 195210,  DOI:10.1103/PhysRevB.75.195210.
52. J. Xu, S. Heguri, Y. Tanabe, G. Mu, J. Wu and K. Tanigaki, Heat capacity studies on rattling vibrations in Ba-TM-Ge Type-I clathrates, J. Phys. Chem. Solids, 2012, 73(12), 1521–1523,  DOI:10.1016/j.jpcs.2011.11.044.
53. K. Suekuni, S. Yamamoto, M. A. Avila and T. Takabatake, Universal relation between guest free space and lattice thermal conductivity reduction by anharmonic rattling in type-I clathrates, J. Phys. Soc. Jpn., 2008, 77(Suppl.A), 61–66,  DOI:10.1143/JPSJS.77SA.61.
54. K. Kovnir, U. Stockert, S. Budnyk, Y. Prots, M. Baitinger, S. Paschen, A. V. Shevelkov and Y. Grin, Introducing a magnetic guest to a tetrel-free clathrate: synthesis, structure, and properties of Eu_xBa_8–xCu₁₆P₃₀ (0 ≤ x ≤ 1.5), Inorg. Chem., 2011, 50(20), 10387–10396,  DOI:10.1021/ic201474h.
55. Y. Xiao, C. Chang, Y. Pei, D. Wu, K. Peng, X. Zhou, S. Gong, J. He, Y. Zhang, Z. Zeng and L.-D. Zhao, Origin of low thermal conductivity in SnSe, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94(12), 125203,  DOI:10.1103/PhysRevB.94.125203.
56. K. A. Denault, J. Brgoch, S. D. Kloss, M. W. Gaultois, J. Siewenie, K. Page and R. Seshadri, Average and local structure, debye temperature, and structural rigidity in some oxide compounds related to phosphor hosts, ACS Appl. Mater. Interfaces, 2015, 7(13), 7264–7272,  DOI:10.1021/acsami.5b00445.
57. Y. Singh, A. Ellern and D. C. Johnston, Magnetic, Transport, and thermal properties of single crystals of the layered arsenide BaMn₂As₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(9), 094519,  DOI:10.1103/PhysRevB.79.094519.
58. F. Ronning, N. Kurita, E. D. Bauer, B. L. Scott, T. Park, T. Klimczuk, R. Movshovich and J. D. Thompson, The first order phase transition and superconductivity in BaNi₂As₂ single crystals, J. Condens. Matter Phys., 2008, 20(34), 342203,  DOI:10.1088/0953-8984/20/34/342203.
59. F. Ronning, T. Klimczuk, E. D. Bauer, H. Volz and J. D. Thompson, Synthesis and properties of CaFe₂As₂ single crystals, J. Condens. Matter Phys., 2008, 20(32), 322201,  DOI:10.1088/0953-8984/20/32/322201.
60. J. Wang, Y. He, N. E. Mordvinova, O. I. Lebedev and K. Kovnir, The smaller the better: hosting trivalent rare-earth guests in Cu–P clathrate cages, Chem, 2018, 4(6), 1465–1475,  DOI:10.1016/j.chempr.2018.04.001.
61. P. Yox, F. Cerasoli, A. Sarkar, V. Kyveryga, G. Viswanathan, D. Donadio and K. Kovnir, New trick for an old dog: from prediction to properties of “hidden clathrates” Ba₂Zn₅As₆ and Ba₂Zn₅Sb₆, J. Am. Chem. Soc., 2023, 145(8), 4638–4646,  DOI:10.1021/jacs.2c12435.
62. J. A. McLeod, A. Buling, R. J. Green, T. D. Boyko, N. A. Skorikov, E. Z. Kurmaev, M. Neumann, L. D. Finkelstein, N. Ni, A. Thaler, S. L. Bud’ko, P. C. Canfield and A. Moewes, Effect of 3d doping on the electronic structure of BaFe₂As₂, J. Phys.: Condens. Matter, 2012, 24(21), 215501,  DOI:10.1088/0953-8984/24/21/215501.
63. A. S. Sefat, R. Jin, M. A. McGuire, B. C. Sales, D. J. Singh and D. Mandrus, Superconductivity at 22 K in Co-doped BaFe₂As₂ crystals, Phys. Rev. Lett., 2008, 101(11), 117004,  DOI:10.1103/PhysRevLett.101.117004.
64. K. Kovnir, V. O. Garlea, C. M. Thompson, H. D. Zhou, W. M. Reiff, A. Ozarowski and M. Shatruk, Spin-glass behavior in LaFe_xCo_2–xP₂ solid solutions: interplay between magnetic properties and crystal and electronic structures, Inorg. Chem., 2011, 50(20), 10274–10283,  DOI:10.1021/ic201328y.
65. J. V. Zaikina, M. Y. Kwong, B. Baccam and S. M. Kauzlarich, Superconductor-in-an-hour: spark plasma synthesis of Co- and Ni-Doped BaFe₂As₂, Chem. Mater., 2018, 30(24), 8883–8890,  DOI:10.1021/acs.chemmater.8b04039.
66. N. Ni, M. E. Tillman, J.-Q. Yan, A. Kracher, S. T. Hannahs, S. L. Bud’ko and P. C. Canfield, Effects of Co substitution on thermodynamic and transport properties and anisotropic Hc₂ in Ba(Fe_1−xCo_x)₂As₂ single crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(21), 214515,  DOI:10.1103/PhysRevB.78.214515.

---

Footnote

† Electronic supplementary information (ESI) available: The synthetic details and characterization, alongside figures and tables associated with characterization techniques: powder X-ray diffraction, single crystal X-ray diffraction, energy dispersive X-ray (EDS) spectroscopy, nuclear magnetic resonance, differential scanning calorimetry, heat capacity, and transport property measurements. CCDC 2285843–2285845. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ta01063a

---