Configuration-entropy effects on BiFeO₃–BaTiO₃ relaxor ferroelectric ceramics for high-density energy storage

Abstract

High energy-storage capability and electric breakdown strength are critical elements in next-generation pulse-power dielectric capacitors. In this report, perovskite (Bi_0.7Ba_0.3)_1−xNa_x(Fe_0.7Ti_0.3)_1−xTa_xO₃ relaxor ferroelectric ceramics (x = 0–0.3) were tailored in terms of configuration entropy from a medium entropy of 1.21R to a high entropy of 2.07R to improve energy storage. The integration of paraelectric NaTaO₃ into BiFeO₃–BaTiO₃ results in breaking of the long-range order and formation of multiple lattice distortions toward relaxor ferroelectric characteristics. Excellent recoverable energy densities of 9.6 J cm⁻³ and 10.3 J cm⁻³ with efficiencies of 77% and 68% at 350 kV cm⁻¹ and 550 kV cm⁻¹ (at 10 Hz) were achieved for x = 0.15 and 0.20, respectively. Wide operating frequency (1–100 Hz) and temperature (25 °C–150 °C) stabilities were confirmed at 300 kV cm⁻¹. Grain boundaries and nanoclusters play critical roles as electric barriers to suppress charge mobility and increase electric breakdown strength. This study presents a promising scheme to utilize high-configuration entropy BiFeO₃–BaTiO₃-based ceramics for high energy-density electrostatic capacitors.

---

1. Introduction

Compared to other general energy-storage technologies (such as solid oxide fuel cells, electrochemical capacitors, and flywheels), dielectric (or electrostatic) capacitors have the advantages of high-voltage applications and high fatigue resistance for long-term use. They offer promising technological applications, such as electric vehicles and computation memory devices. The dielectric material is sandwiched between two electrodes wherein electric dipoles are aligned with an external electric (E) field with the formation of surface-bound charges. Consequently, the electrical energy can be stored through polarization reorientation induced by the E field upon the charging process. This mechanism permits dielectric capacitors to have a quick charging–discharging response superior to those of other energy-storage devices. Therefore, dielectric capacitors have been utilized in various electronics, such as medical and research devices.¹

The energy-storing capability (ESC) of a dielectric capacitor is characterized by high power density, but relatively low recoverable energy density (W_rec). Thus, the development of dielectric capacitors has prompted great interest in enhancing W_rec. W_rec is defined as where E, P, P_max, and P_r are the E field, polarization, maximum polarization at maximum E field, and residual polarization after discharging (at zero E field), respectively.² Thus, a larger P_max and a smaller P_r (or larger ΔP = P_max − P_r) can result in a higher W_rec. A large P_max can be achieved by applying a higher E field, which has prompted researchers to explore strategies for enhancing the electric breakdown strength (E_b). E_b is the E-field threshold that the material can accommodate before it breaks. Another essential indicator in energy storage is the efficiency determined by the relation, η = W_rec/(W_rec + W_loss), where W_tot and W_loss are total energy density stored during charging and the dissipated energy remaining in the material after discharging, respectively.²

Bismuth ferrite (BiFeO₃, abbreviated as BF) is a perovskite ferroelectric (FE) system with a large spontaneous polarization (P_s ∼ 90–100 μC cm⁻²) as proposed by first-principles calculation,³ and P_s ∼ 90–150 μC cm⁻² in the BF thin film.^4,5 Similar to Pb²⁺, Bi³⁺ in BF with the electron configuration of a 6s² lone pair makes BF a potential substitute for lead-based materials in energy-storage applications.⁶ However, a pure BF ceramic suffers from current leakage and low breakdown strength due to Bi volatilization and Fe³⁺ to Fe²⁺ valence hybridization.^7,8 The drawbacks of utilizing BF for energy storage have been overcome by rare-earth doping and/or designing binary materials such as BiFeO₃–BaTiO₃ (BF–BT).^7,9–15 The BF–BT binary system exhibits a temperature-dependent morphotropic phase boundary (MPB) that permits composition-driven structural transition resulting in improved energy storage properties.¹ The substantial polarization of P_max > 40 μC cm⁻², moderate remanent polarizations (P_r), and moderate E_b were reported at the MPB in Nd-doped BF–BT ceramics.¹⁶ The addition of 3 mol% Nb₂O₅ in 0.65BF–0.35BT reduced P_r from ∼40 μC cm⁻² to 5.33 μC cm⁻².¹⁷ These results are due to disruption of the long-range order and simultaneous induction of a relaxor ferroelectric (RFE) phase characterized by nanoscale domains and polar nanoregions (PNRs).¹⁸ Several studies have shown that (1 − x)BF − xBT undergoes a composition-driven structural transition from rhombohedral R3c at x = 0–0.25 to pseudo-cubic at x = 0.33–0.94.^19–21 Although BF-BT- and BT-based ceramics have made some progress in energy storage, they still have relatively lower energy storage than lead-based systems.^22–27

Since the local compositional inhomogeneity is linked to the disorder and random E field in the REFs, the design of REFs has been approached by modulating the configuration entropy (S_config) to improve energy-storage performance.^18–21S_config in oxide systems is defined as where x_i and x_j describe the mole percentage of various elements in cation and anion sites.²⁸R is the universal gas constant. S_config is divided into three levels: low entropy (S_config < 1R), medium entropy (1R ≤ S_config < 1.5R), and high entropy (S_config ≥ 1.5R).²⁸ A high-S_config scheme has been employed in many studies because it can stabilize a single-phase structure²⁹ and multiphase mixtures³⁰ and enhance E_b.²⁸

The energy-storage performance of dielectric materials mostly depends on the breakdown strength, which is influenced by dielectric characteristic, electronic bandgap, and grain size. Paraelectric NaTaO₃ (NT) appears to be a good candidate for adding into BF-BT to increase S_config due to its incipient FE nature with a glass-like or relaxor-like phase.^2,31 A high W_rec = 6.3 J cm⁻³ and a high η ≥ 86% were achieved in NT-doped BF-based ceramics with an E_b ∼ 425 kV cm⁻¹ and ΔP = P_max − P_r ∼ 38.5 μC cm⁻².² An enhanced bandgap was attributed to a high W_rec = 6.5 J cm⁻³ and a high η = 94% accompanied by temperature stability in a Ta-doped sodium niobate-based relaxor ceramic, (Na_0.8Bi_0.1)(Nb_0.9−xTa_xTi_0.1)O₃, with a high E_b = 450 kV cm⁻¹.³² NT-doped (Bi_0.5Na_0.5)TiO₃ exhibited a large P_max with low P_r owing to the coexistence of R3c nanodomains and P4bm PNRs.³³ These results demonstrated that NT promotes RFE behavior, causing lower P_r and higher η.

A schematic diagram of the design in this study is shown in Fig. 1 for improving energy-storage properties by tailoring S_config. In this study, paraelectric NT was added into 0.7BiFeO₃–0.3BaTiO₃ to produce (Bi_0.7Ba_0.3)_1−xNa_x(Fe_0.7Ti_0.3)_1−xTa_xO₃ ceramics with x = 0–0.30, yielding high S_config values from 1.21R to 2.07R and E_b from 175 kV cm⁻¹ to 550 kV cm⁻¹.

Fig. 1 Schematic diagram of the design for tailoring superior energy-storage properties.

2. Experimental procedure

The solid–state reaction method was used to prepare (Bi_0.7Ba_0.3)_1−xNa_x(Fe_0.7Ti_0.3)_1−xTa_xO₃ (abbreviated as BBNFTT-x) bulk ceramics with x = 0, 0.05, 0.10, 0.15, 0.20, and 0.30. The calculated S_config values are 1.21R, 1.55R, 1.74R, 1.88R, 1.97R, and 2.07R for x = 0, 0.05, 0.10, 0.15, 0.20, and 0.30, respectively. The calculation process for the value of S_config is illustrated in Fig. S1 (Electronic Supplementary Information, hereafter denoted ESI†). Bi₂O₃, Fe₂O₃, BaCO₃, and TiO₂ raw powders were mixed according to the stoichiometric ratio of the desired composition to obtain (Bi_0.7Ba_0.3) (Fe_0.7Ti_0.3) O₃ (abbreviated as BBFT) powders. At the same time, Na₂CO₃ and Ta₂O₅ raw powders were mixed to form NaTaO₃ (NT) powders. All raw powders were of analytical grade (>99 wt% purity). The ball milling process of the BBFT and NT powders lasted 24 h with 10 mm-diameter ZrO₂ balls and alcohol as mixing agent. BBFT and the NT powders then underwent a drying process before the first calcination process (at 800 °C for 3 h) to initiate reactions in the BBFT and NT powders, respectively. The next step was to prepare calcined powders for high-energy ball milling (HEBM) using 1.5 mm-diameter ZrO₂ balls and water. For the first HEBM, the BBFT and NT powders were ball milled for 12 h and 24 h, respectively. Different ball milling times were employed due to the difference particle sizes of the powders. After the first HEBM, the BBFT and NT powders were dried, sieved, and further mixed stoichiometrically to form BBNFTT-x powders. Extra 0.05 mol% Bi₂O₃ and 0.1 wt% MnO₂ powders were added to execute the second HEBM for 12 h. The use of additional Bi₂O₃ and MnO₂ (as a sintering aid) was to compensate for Bi volatilization and to enhance electrical resistivity, respectively.¹⁸ The combined powders underwent drying, a second calcination at 800 °C for 3 h, and final HEBM for 12 h. Finally, the dried powders were sieved and pressed before sintering at 980 °C for 2 h in an oxygen furnace.

A scanning electron microscope (SEM, JEOLJSM-7610F plus) was used to image cross-section grain morphologies. A Bruker X-ray diffractometer (D8 ADVANCE ECO) was employed to investigate lattice structures assisted by Rietveld refinement analyses using HighScore Plus software version 3.0.5. A HORIBA LabRAM HR Evolution system was used with a 532 nm laser to acquire Raman scattering spectra. Using a Workstation 2000 (Radiant Technologies Precision LC II), polarization vs. E field (P–E) hysteresis loops were acquired at frequencies of 1 Hz and 10 Hz. For the P–E loop experiment, to construct the structure of a parallel-plate capacitor, samples were carefully polished to 0.05 mm thickness, which is much smaller than the electrode's diameter of 1 mm, as shown in Fig. S2 (ESI).† Au electrodes were deposited using the dc sputtering method. The nanoscale morphology and electron diffraction were investigated with a JEOL transmission electron microscope (JEM-2100 LaB₆) with 200 kV-acceleration capability. A phase impedance analyzer (Wayne-Kerr PMA6420A) was used to assess dielectric properties. The electrical potential distribution on the gain matrix was probed by employing a Kelvin probe force microscope (KPFM, Bruker Multimode 8).

3. Results and discussion

To inspect whether sintering parameters used are suitable, the SEM cross-section morphologies of as-sintered BBNFTT-x are presented in Fig. 2a–f, including grain size distributions. The cross-section morphologies prove they are dense ceramic matrices with decreasing average grain size from 3.5 μm at x = 0 to 1.2 μm at x = 0.20. The decreasing average grain size may be due to the sluggish diffusion effect attributed to the increasing S_config.³⁴ The sluggish diffusion results from various nanoscale barriers formed by the mixture of different elements. However, the larger average grain size (2.5 μm) at x = 0.30 was perhaps associated with structural transitions due to the larger amount of NT integration, as revealed by XRD refinement analyses. The integration of aliovalent cations in the high-configuration entropy range can cause local vacancies, which can favor ionic diffusion for grain growth. E_b is expected to have an inverse relationship with the grain size of ceramics (E_b ∝ G^−1/2).³⁵ Thus, the decreasing average grain size from x = 0 to x = 0.20 is beneficial for achieving high E_b.

Fig. 2 Thermally etched fractured cross-section SEM micrographs of BBNFTT-x (x = 0–0.30). Insets are the distributions of grain sizes.

To identify the structural evolution, XRD spectra from 20 to 80 at 2θ degrees are presented in Fig. 3a, showing perovskite structures. The elaborations of (110), (111), and (200) diffraction peaks in Fig. 3b show a shift toward higher 2θ degrees from x = 0 to x = 0.30. This phenomenon indicates an A-site replacement of Bi³⁺ (∼1.4 Å) and Ba³⁺ (∼1.6 Å) in the lattice with smaller cations Na⁺ (<1.4 Å) causing a reduction in lattice d spacing. It is noticeable that the peaks are narrow (without splitting) suggesting an overall pseudo-cubic structure.³⁶ In particular, extra peaks appeared at ∼29°, ∼34.5°, ∼49°, and ∼58° in NT-contained specimens, as observed in Fig. 3a and were identified as a cubic Fd3̄m Na₂Ta₂O₆-like structure by the refinements in Fig. S3 (ESI).† The refinement analyses suggest multiple phases and lattice distortions due to the integration of aliovalent cations, namely, Na⁺ into the A-site and Ta⁵⁺ into the B-site. The lattice distortions, due to the increasing configuration entropy, restrain the formation of secondary phases³⁷ while stabilizing co-existing multiphases.^28,34 Rietveld refinement analyses were carried out to quantify the percentages of various symmetries, as displayed in Fig. 3c. The Rietveld refinement reveals the coexistence of nonpolar cubic Pm3̄m, FE rhombohedral R3c, and nonpolar orthorhombic Pnma symmetries at x = 0. The variation in phase percentages, as presented in Fig. S4 (ESI),† shows a rapid decline in R3c symmetry accompanied by an increase in orthorhombic Pnma symmetry with integration of an increasing amount of NT, while cubic Fd3̄m symmetry exhibits rapid growth from x = 0.20 to x = 0.30.

Fig. 3 (a) XRD patterns of BBNFTT-x. (b) Enlargements of (110), (111), and (200) peaks. (c) Rietveld refinements. I_obs and I_calc are experimental data and calculated curves. R_exp, R_wp, and χ² are expected R value, weighted-profile, and goodness-of-fit, respectively. The reference ICSD numbers are 15299 (for R3c space group), 27973 and 1533883 (for Pm3̄m), 1001030 (for Fd3̄m), 1520943 (for Pbam), and 1532213 (for Pnma).

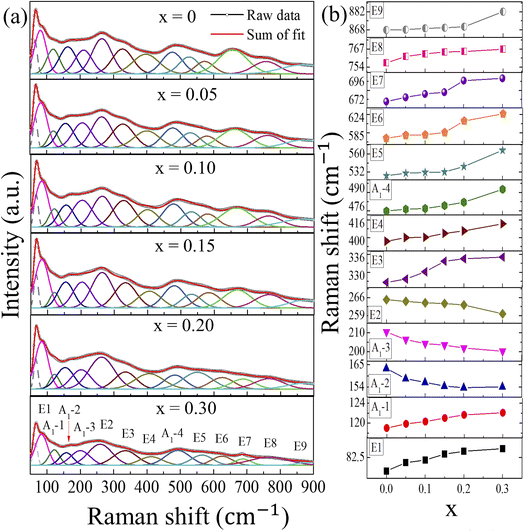
To investigate the local structural alteration, Raman spectra were acquired, as displayed in Fig. 4a, showing broad profiles with wavenumbers ranging from 50 cm⁻¹ to 900 cm⁻¹. The 13 Raman-active modes of pure BF in the rhombohedral R3c space group are indicated in Fig. 4a. The solid curves in Fig. 4a show the fitted peaks of the Raman spectra using Peakfit software. The frequency trends of Raman modes with respect to NT content are plotted in Fig. 4b to clearly visualize gradual shifts. The broad Raman-active modes indicate that the aliovalent integration of the cations (Bi³⁺, Ba²⁺, and Na⁺) in the A site and (Fe³⁺, Ti⁴⁺, and Ta⁵⁺) in the B site has increased the configuration entropy to favor cubic symmetry.³⁸ Typically, three zones that correspond to various cationic interactions may be distinguished in the Raman spectra of a perovskite ABO₃ structure. Wavenumbers < ∼150 cm⁻¹ were assigned to the A-site cationic vibrations (E1 and A₁-1) and slower lattice motion. Wavenumbers between ∼150 cm⁻¹ and 300 cm⁻¹ assigned to A₁-2, A₁-3, and E2 are related to B-site cationic vibrations (B–O bonds), and wavenumbers > ∼300 cm⁻¹ assigned to E3, E4, A₁-4, E5, E6, E7, E8, and E9 are related to the bending/stretching modes of the BO₆ octahedron.^39,40 E1 and A₁-1 modes show an upward trend, indicating that the lighter Na⁺ cations have successfully replaced Bi³⁺ cations in the A site of the unit cell. The downward trend in the A₁-2, A₁-3, and E2 modes signifies the B-site occupancy of the Ta⁵⁺ cations, which are heavier than Fe³⁺ and Ti⁴⁺ cations. An upward trend was obtained in the E3, E4, A₁-4, E5, E6, E7, E8, and E9 modes, implying an increase in interatomic bonding strength.

Fig. 4 (a) Raman scattering spectra with fitted curves of BBNFTT-x. (b) Frequency evolution of various Raman modes. The dashed curve at ∼64–65 cm⁻¹ is an artifact due to the cut-off of Rayleigh scattering.

The polarization vs. E field (P–E) hysteresis loops were assessed using various applied E fields at 1 Hz, as shown in Fig. 5a, to ascertain the influence of integration of NT on the ESC. As NT (x) increases, the P–E hysteresis loop evolves from a typical FE loop characterized by high P_max and P_r at x = 0 to one with an RFE nature at x = 0.05, 0.15, then towards an almost linear loop at x = 0.20 and 0.30. Noticeably, E_b significantly rises from 175 kV cm⁻¹ at x = 0 to 550 kV cm⁻¹ at x = 0.20 and drops to 425 kV cm⁻¹ at x = 0.30. The grain size is a crucial factor affecting the dielectric breakdown strength.⁴¹ The evolution of E_b is consistent with the trend in average grain sizes in Fig. 2. The larger E_b at x = 0.3, which has a larger average grain size (compared to x = 0.1 and 0.15), may result from a collective effect. E_b can be affected by intrinsic or extrinsic factors. E_b is intrinsically affected by local defect structures (such as dipolar defects and vacancies),⁴² secondary phase, band gap, space charge, and nanostructures (such as nanodomains and nanoclusters). E_b can be also changed by extrinsic factors, including grain size, sample thickness, and porosity. Moreover, declining R3c symmetry occurring with rising nonpolar Pnma and Fd3̄m symmetries, as shown in Fig. S4 (ESI),† is accountable for the reduced P_max and P_r as NT increases. The trends in W_rec (J cm⁻³) and η (%) vs. E field in Fig. 5b show that W_rec increases from 2.5 J cm⁻³ to 8.7 J cm⁻³, and η increases from 25% to 66% at x = 0 to x = 0.20 at E_b (or maximum E field). However, W_rec and η at E_b drop to 4.6 J cm⁻³ and 57%, respectively, at x = 0.30, which is attributed to the development of a nonpolar characteristic by a high configuration entropy.³⁰ Additionally, ΔP (= P_max − P_r) and E_c were plotted as functions of E field from 100 kV cm⁻¹ up to E_b, as shown in Fig. 5c, which shows an increasing trend in ΔP for x ≤ 0.15 and later a decline for x ≥ 0.20 due to the decreasing P_max. This confirms a diminishing FE R3c structure accompanied by increasing nonpolar Pnma and Fd3̄m symmetries as NT increases, as evidenced in Fig. S4 (ESI).† In addition, P–E loops of BBNFTT-x (x = 0.15 and 0.20) were measured at 10 Hz under various E fields, as shown in Fig. 5d, with curves of W_rec, η, ΔP, and E_cvs. applied E field in Fig. 5e and f, respectively. Recoverable energy densities of 9.6 J cm⁻³ and 10.3 J cm⁻³ with efficiencies of 77% and 68% under E fields of 350 kV cm⁻¹ and 550 kV cm⁻¹ were achieved at x = 0.15 and 0.20, respectively.

Fig. 5 (a) P–E loops of BBNFTT-x at 1 Hz and curves of (b) W_rec and η and (c) ΔP (=P_max − P_r) and E_cvs. applied E field. (d) P–E loops of BBNFTT-x (x = 0.15 and 0.20) at 10 Hz and curves of (e) W_rec and η and (f) ΔP and E_cvs. applied E field.

The evolution trends in P_max and P_r at E_b based on Fig. 5a are plotted in Fig. S5 (ESI).† The P_max ∼ 110.6 μC cm⁻² and P_r ∼ 71.6 μC cm⁻² are initially high at x = 0, as a result of the FE character. The significant reductions in P_max (∼32.6 μC cm⁻²) and P_r (∼7.2 μC cm⁻²) at x = 0.30 indicate that the integration of NT into BF–BT is favorable for disrupting the long-range FE order toward an RFE characteristic.⁴³ The enhanced relaxor characteristic with increasing NT content confirms that a high S_config, can contribute to disruption of the long-range FE order, facilitating PNR formation.²⁹ The collapse of long-range polar order is responsible for the reduction in P_max and P_r. Fig. S5b (ESI)† summarizes E_b, W_rec (at E_b), and η (at E_b) with increasing NT content. The energy storage parameters of BF- and BF–BT-based ceramics reported by other researches together with this work are presented in Table S1 (ESI),† ^{14,15,44–51} which demonstrate that the results from this work are superior to reported parameters of E_b and W_rec. The energy-storage parameters are also higher than those in BNT-BT-based ceramics.⁵² To assess the ESC per unit E field, recoverable energy-storage intensities (ρ) were calculated based on Fig. 5b, c, e and f using the relation ρ = W_rec/ΔE (ref. 53) and are presented in Table S2 (ESI).† ΔE is E_b − E_s, and E_s is the initial E field. The calculated maximum ρ of 27.4 × 10⁻³ J kV⁻¹·cm⁻² at 10 Hz was attained at x = 0.15 and is larger than those reported in BT-, BF-, NN-, KNN- or BNT-based ceramics.⁵³ Furthermore, a high W_rec of 10.5 J cm⁻³ and η of 87% were achieved in 0.62BiFeO₃–0.3BaTiO₃–0.08Nd(Zn_0.5Zr_0.5)O₃ multilayer ceramic (7-active layer) at an E field of 700 kV cm⁻¹.⁴⁵ An ultrahigh W_rec of 18.5 J cm⁻³ with an E_b of 995 kV cm⁻¹ was also reported in the relaxor–antiferroelectric 0.90NaNbO₃–0.10BiFeO₃ ceramic.⁵⁴

Fig. 6a–d exhibit frequency- and temperature-dependent P–E loops for BBNFTT-0.2, showing good operating frequency (1–100 Hz) and thermal (25 °C–150 °C at 1 Hz and 10 Hz) stabilities under 300 kV cm⁻¹. The results indicate excellent operating frequency and thermal stabilities. To confirm the reliability of experimental E_b fields, Weibull distributions have been plotted in Fig. 6e for BBNFTT-x (x = 0.1, 0.15, 0.20, and 0.30) based on relations, X_i = ln(E_i) and where i, E_i, and n are the ordinal of the sample, the E_b of the ith sample, and the total number of samples, respectively.² The fitted Weibull moduli (β) are close to 20, suggesting the high reliability of experimental E_b values. In addition, cycling P–E loops (3 × 10³ cycles) under 300 kV cm⁻¹ at 10 Hz for BBNFTT-0.2 in Fig. 6f demonstrate that P_max and P_r vary insignificantly with continuously increasing cycle number. The curves of W_rec and η vs. cycle number shown in Fig. 6g reveal reliable fatigue resistance with insignificant changes in W_rec or η.

Fig. 6 Frequency- and temperature-dependent (a and b) P–E loops and (c and d) evolution of W_rec and η for BBNFTT-0.2. (e) Weibull distributions of E_b values for BBNFTT-x (x = 0.1–0.3). (f and g) Cycle-number-variant P–E loops at 10 Hz and evolution of W_rec and η for BBNFTT-0.2.

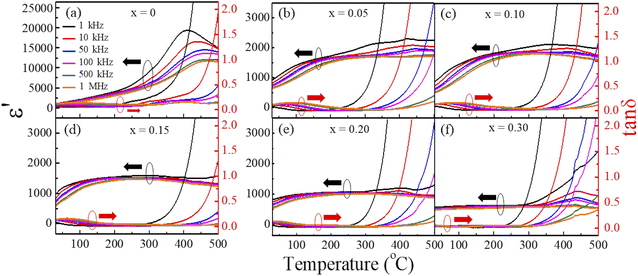
To further verify the RFE characteristic and thermal stability induced by the integration of NT, the temperature-dependent dielectric permittivity (ε_r) and loss (tan δ) were collected at varying frequencies of 1 kHz–1 MHz, as presented in Fig. 7a–f. The dielectric permittivity maxima become broad with declining ε_r, as NT increases from x = 0 to x = 0.30, which is characterized by a dispersed frequency shifted towards a lower temperature. The dielectric behavior suggests that the integration of an increasing amount of NT induces RFE characteristic evolving towards a linear-like dielectric.^2,43 The broad dielectric maximum can be associated with the nanoscale relaxor nature, originating from compositional disorder due to high configuration entropy. The increase in the loss (tan δ) at higher temperatures (>300 °C) possibly originates from the ionic conductivity.^55–57 The flattening and compression of the ε_r curve with rising temperature imply that energy-storage properties are thermally stable. Enhancement in E_b is made possible by the decline in ε_r as NT increases, because of the transformation of FE domains into nanodomains and/or PNRs and nanoclusters attributed to the enhanced relaxor characteristic induced by integration of an increasing amount of NT.³⁸ The temperature coefficients of capacitance (TCC) were used to evaluate the thermal stabilities at 25 °C–125 °C, as shown in Fig. S6 (ESI).† TCC was determined using the equation where C₂₅ is the capacitance at 25 °C, and C_T is the capacitance at temperature T. Ceramics with x = 0.20 and x = 0.30 remain thermally stable with TCC < 25%, reflecting an improved temperature stability via integration of NT.^28,56

Fig. 7 (a–f) Dielectric permittivity and tanδ of BBNFTT-x for various frequencies upon heating.

Nanoscale TEM images and selected area electron diffraction (SAED) patterns were examined in BBNFTT-0.1 and BBNFTT-0.2, as shown in Fig. 8. The typical granular microstructures of nanoclusters and dark/light-contrast structures in the grain matrix can be identified in Fig. 8a. A contrast in bright-field (BF) TEM images usually results from various intensities of diffraction. A non-uniform distribution of elemental composition inside a grain can yield dark/light contrasts in the BF TEM images. A magnified image of the nanoclusters from light-contrast region “b” in the pink box in Fig. 8a is displayed in Fig. 8b. The spot pattern of the cubic Pm3̄m space group shown in the inset of Fig. 8b from the [100]_c-zoned SAED suggests that the nanoclusters are segregated in the grain with the same crystalline orientation. The morphologies of the nanoclusters are different from nanograins, which are typically identified by ring patterns.⁵⁸ The high-resolution TEM image of the nanoclusters with stripes in Fig. 8c from the dark-contrast region “c” in Fig. 8a shows a parallel-striped superlattice perpendicular to the [001] direction. The inset of Fig. 8c shows a corresponding [100]_c-zoned SAED pattern with superlattice spots, suggesting a multi-symmetry structure of cubic Pm3̄m and orthorhombic Pnma space groups. The SAEDs along the [110]_c-zone axis in Fig. 8d and e indicate the coexistence of R3c, Pm3̄m, and Pnma symmetries accompanied by 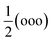and superlattice diffractions in regions “d” (light-contrast) and “e” (dark-contrast) in Fig. 8a. The antiphase oxygen octahedral tilt along the [111]_c direction, designated as the a⁻a⁻a⁻ tilt system is the origin of the superlattice reflection marked by green circles, indicating FE R3c symmetry.^55,57 Here, subscript “c” refers to the pseudo-cubic notation, while “o” stands for an odd Miller index. The octahedral tilt twin disorder in the [001]_c direction gives rise to the superlattice diffraction pattern, which reflects Pnma symmetry with the a⁻a⁻c⁺ mixed tilt system.^59–61 According to first-principles calculation, the antiferroelectric Pnma structure is accompanied by the presence of two sublattices with opposite polarizations.⁶² The superlattice ordering of cation polarization arrangements in the orthorhombic Pnma structure is connected to the stripes seen in Fig. 8d. Fig. S5a–c (ESI)† show EDX spectra, revealing that the light-contrast and dark-contrast regions from “d” and “e” areas in Fig. 8a are Ba/Ti-rich and Fe-rich, respectively. High-configuration entropy ceramics typically consist of disordered multi-cation sublattices originating from fluctuations in composition and charge.⁶³

Fig. 8 (a–c) TEM images and (d and e) SAED patterns of BBNFTT-0.1. The insets in (b) and (c) are corresponding SAED patterns. (f and g) TEM images and (h and i) SAED patterns of BBNFTT-0.2.

The TEM images and SAED patterns for BBNFTT-0.2 were also probed, as displayed in Fig. 8f–i, revealing smaller grains, dark-contrast precipitates along the grain boundary (GB), and nanoclusters. The overall sizes of the nanoclusters are smaller than those in BBNFTT-0.1, indicating more interfaces of nanoclusters, as shown in Fig. 8g. Cubic Pm3̄m, Fd3̄m, and orthorhombic Pnma space groups are revealed from [110]_c and [111]_c-zone-viewed SAEDs in Fig. 8h and i from “h” and “i” regions in Fig. 8f. Fig. 8h presents the SAED pattern from the smaller grain with dark contrast. The streak-like diffraction pattern indicated by yellow arrows in Fig. 8h could result from incommensurate structures along the [001]_c direction in the Pnma symmetry, possibly due to disordered multi-cation sublattices resulting from fluctuations in composition and charge.⁶³Fig. 8i shows the [111]_c-zone-viewed SAED from the GB region in Fig. 8f, indicating a cubic Fd3̄m phase. The cubic structure precipitated along GBs may increase electric insulation to enhance E_b. The EDX spectra of BBNFTT-0.2 are displayed in Fig. S7d–f (ESI),† reflecting a stoichiometric distribution in the grain interior, an Fe/Ta-rich GB, and an Fe/Bi-rich triple junction.

To assess the electric characteristics of GBs, potential mapping images from BBNFTT-0.0 and BBNFTT-0.2 were acquired across the GBs in a 15 μm × 15 μm area, as shown in Fig. 9a and b. The electrical potential gradient (or change per unit distance) is steeper at the GBs than in the grain interior. According to the relation E = −dV/dx (potential difference per unit distance), this result suggests that the GB has higher local E fields, which can act as barriers to suppress the charge transport and thus enhance E_b. A recent study shows that interfacial polarization (between GBs and grains) plays a significant role in local E-field redistribution and affects energy-storage performance.⁶⁴ Interfacial polarization (also known as Maxwell–Wagner polarization) results from space charges in inhomogeneous systems and causes non-uniform E fields along the GBs. The potential peaks suggest accumulation of positive charges at the GBs and are consistent with EDX mapping, as shown Fig. S7e and f (ESI).†

Fig. 9 (a and b) Surface potential mapping images and potential variations across grain boundaries (GBs) in BBNFTT-0.0 and BBNFTT-0.2. (c and d) Nanocluster structures in BBNFTT-0 and BBNFTT-0.2 gain matrices. (e) Enlargement of the squared region in (d).

From the perspective of nanoscale structures, randomly distributed compositions with increasing S_config can give rise to the formation of a local random field, nanodomains, and nanoclusters.^65,66 As demonstrated in Fig. 9c and d, the sizes of the nanoclusters in BBNFTT-0.2 are considerably smaller than those in BBNFTT-0. Fig. 9e shows the high-resolution TEM image of the nanoclusters in BBNFTT-0.2. The small nanocluster size in BBNFTT-0.2 indicates a higher-density nanocluster boundary that will cause local lattice distortion and elastic strain. Nanoscale segregations (such as nanoclusters) can result in a scattering effect of charge carriers to decrease the probability of electric breakdown and improve E_b.⁶⁷ Thus, the superb E_b and relaxor nature can be linked to the reduced sizes of grains and nanoclusters as the amount of NT integrated increases.

4. Conclusions

We have revealed a design of adding NaTaO₃ into (Bi_0.7Ba_0.3)(Fe_0.7Ti_0.3)O₃ to increase the configuration entropy to break the long-range polar order with multiple lattice distortions. High energy-storage performances of W_rec ∼ 9.6 J cm⁻³ with η ∼ 77% at 350 kV cm⁻¹ and W_rec ∼ 10.3 J cm⁻³ with η ∼ 68% at 550 kV cm⁻¹ were achieved at x = 0.15 and x = 0.20, respectively. The improved storage capability can be mainly attributed to reduced grain and nanocluster sizes. The higher E fields at grain boundaries become charge-transport barriers raising the electrical resistivity of the gain matrix.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research is supported by the National Science and Technology Council of Taiwan under Project Nos. 112-2221-E-030-002-MY2, 110-2221-E-146-001-MY2, 112-2221-E-146-001, and 112-2221-E-131-016.

References

1. B. Deka and K.-H. Cho, BiFeO₃-based relaxor ferroelectrics for energy storage: progress and prospects, Materials, 2021, 14, 7188,  DOI:10.3390/ma14237188.
2. H. Guo, F. Zeng, W. Xiao, S. Jiang, Y. Chen, B. Wang, G. Fan, W. Lu and Z. Tu, Realizing high energy density in BiFeO₃-based ceramics capacitors via bandgap engineering and polarization optimization, Chem. Eng. J., 2023, 461, 142071,  DOI:10.1016/j.cej.2023.142071.
3. J. B. Neaton, C. Ederer, U. V. Waghmare, N. A. Spaldin and K. M. Rabe, First-principles study of spontaneous polarization in multiferroic BiFeO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 14113,  DOI:10.1103/PhysRevB.71.014113.
4. A. J. Hatt, N. A. Spaldin and C. Ederer, Strain-induced isosymmetric phase transition in BiFeO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 54109,  DOI:10.1103/PhysRevB.81.054109.
5. R. J. Zeches, M. D. Rossell, J. X. Zhang, A. J. Hatt, Q. He, C.-H. Yang, A. Kumar, C. H. Wang, A. Melville, C. Adamo, G. Sheng, Y.-H. Chu, J. F. Ihlefeld, R. Erni, C. Ederer, V. Gopalan, L. Q. Chen, D. G. Schlom, N. A. Spaldin, L. W. Martin and R. Ramesh, A strain-driven morphotropic phase boundary in BiFeO₃, Science, 2009, 326, 977–980,  DOI:10.1126/science.1177046.
6. F. Kang, L. Zhang, W. Yang, R. Kang, R. Xue, L. He, Q. Sun, T. Zhang, Z. Wang, J. Wang and K. Zeng, Achieving ultrahigh energy storage performance in BiFeO₃-BaTiO₃ based lead free relaxors via a composition optimization strategy, J. Eur. Ceram. Soc., 2022, 42, 6958–6967,  DOI:10.1016/j.jeurceramsoc.2022.08.021.
7. L. Wang, R. Liang, Z. Zhou, M. Li, M. Gu, P. Wang and X. Dong, Electrical conduction mechanisms and effect of atmosphere annealing on the electrical properties of BiFeO₃-BaTiO₃ ceramics, J. Eur. Ceram. Soc., 2019, 39, 4727–4734,  DOI:10.1016/j.jeurceramsoc.2019.07.054.
8. C.-S. Tu, P.-Y. Chen, Y.-S. Jou, C.-S. Chen, R. R. Chien, V. H. Schmidt and S.-C. Haw, Polarization-modulated photovoltaic conversion in polycrystalline bismuth ferrite, Acta Mater., 2019, 176, 1–10,  DOI:10.1016/j.actamat.2019.06.046.
9. F. Shang, J. Wei, Y. Deng, G. Tang, J. Xu, D. Zhou, H. Xu and G. Chen, A novel route to produce BaTiO₃ glass-ceramics with nanosized cubic BaTiO₃ phase precipitating for high energy-storage applications, J. Eur. Ceram. Soc., 2023, 43, 3307–3317,  DOI:10.1016/j.jeurceramsoc.2023.02.026.
10. Z. Chen, X. Bu, B. Ruan, J. Du, P. Zheng, L. Li, F. Wen, W. Bai, W. Wu, L. Zheng and Y. Zhang, Simultaneously achieving high energy storage density and efficiency under low electric field in BiFeO₃-based lead-free relaxor ferroelectric ceramics, J. Eur. Ceram. Soc., 2020, 40, 5450–5457,  DOI:10.1016/j.jeurceramsoc.2020.06.073.
11. L. Zhang, G. Li, X. Gong, J. Tang and Y. Lu, Enhanced dielectric, ferroelectric, and ferromagnetic properties of 0.7Bi_1−xTm_xFeO₃–0.3BaTiO₃ ceramics by Tm-induced structural modification, Ceram. Int., 2022, 48, 17760–17767,  DOI:10.1016/j.ceramint.2022.03.046.
12. R. Montecillo, C.-S. Chen, Y.-T. Lee, P.-Y. Chen and C.-S. Tu, Optimized electric-energy storage in BiFeO₃–BaTiO₃ ceramics via tailoring microstructure and nanocluster, J. Eur. Ceram. Soc., 2023, 43, 1941–1951,  DOI:10.1016/j.jeurceramsoc.2022.12.064.
13. R. Montecillo, J.-C. Lin, C.-S. Chen, P.-Y. Chen and C.-S. Tu, Tailoring energy storage in Nb₂O₅-added 0.7BiFeO₃–0.3BaTiO₃ ceramics via A-site Gd³⁺ substitution, J. Alloys Compd., 2023, 963, 171144,  DOI:10.1016/j.jallcom.2023.171144.
14. R. Montecillo, C.-S. Chen, K.-C. Feng, R. R. Chien, S.-C. Haw, P.-Y. Chen and C.-S. Tu, Achieving superb electric energy storage in relaxor ferroelectric BiFeO₃-BaTiO₃-NaNbO₃ ceramics via O₂ atmosphere, J. Eur. Ceram. Soc., 2023, 43, 7446–7454,  DOI:10.1016/j.jeurceramsoc.2023.07.081.
15. K. Meng, W. Li, X.-G. Tang, Q.-X. Liu and Y.-P. Jiang, A review of a good binary ferroelectric ceramic: BaTiO₃–BiFeO₃, ACS Appl. Electron. Mater., 2022, 4, 2109–2145,  DOI:10.1021/acsaelm.1c00109.
16. Q. Zheng, L. Luo, K. H. Lam, N. Jiang, Y. Guo and D. Lin, Enhanced ferroelectricity, piezoelectricity, and ferromagnetism in Nd-modified BiFeO₃-BaTiO₃ lead-free ceramics, J. Appl. Phys., 2014, 116, 184101,  DOI:10.1063/1.4901198.
17. T. Wang, Y. Tian, L. Shu, Q. Hu and X. Wei, Microstructure and ferroelectric properties of Nb₂O₅-modified BiFeO₃-BaTiO₃ lead-free ceramics for energy storage, Mater. Lett., 2014, 137, 79–81,  DOI:10.1016/j.matlet.2014.08.133.
18. D. Wang, A. Khesro, S. Murakami, A. Feteira, Q. Zhao and I. M. Reaney, Temperature dependent, large electromechanical strain in Nd-doped BiFeO₃-BaTiO₃ lead-free ceramics, J. Eur. Ceram. Soc., 2017, 37, 1857–1860,  DOI:10.1016/j.jeurceramsoc.2016.10.027.
19. J. Wu, Z. Fan, D. Xiao, J. Zhu and J. Wang, Multiferroic bismuth ferrite-based materials for multifunctional applications: ceramic bulks, thin films and nanostructures, Prog. Mater. Sci., 2016, 84, 335–402,  DOI:10.1016/j.pmatsci.2016.09.001.
20. S. O. Leontsev and R. E. Eitel, Dielectric and piezoelectric properties in Mn-modified (1−x)BiFeO₃–xBaTiO₃ Ceramics, J. Am. Ceram. Soc., 2009, 92, 2957–2961,  DOI:10.1111/j.1551-2916.2009.03313.x.
21. S. Cheng, B.-P. Zhang, L. Zhao and K.-K. Wang, Enhanced insulating and piezoelectric properties of 0.7BiFeO₃–0.3BaTiO₃ lead-free ceramics by optimizing calcination temperature: analysis of Bi³⁺ volatilization and phase structures, J. Mater. Chem. C, 2018, 6, 3982–3989,  10.1039/C8TC00329G.
22. J. Sigman, G. L. Brennecka, P. G. Clem and B. A. Tuttle, Fabrication of perovskite-based high-value integrated capacitors by chemical solution deposition, J. Am. Ceram. Soc., 2008, 91, 1851–1857,  DOI:10.1111/j.1551-2916.2008.02390.x.
23. L. Yang, X. Kong, F. Li, H. Hao, Z. Cheng, H. Liu, J.-F. Li and S. Zhang, Perovskite lead-free dielectrics for energy storage applications, Prog. Mater. Sci., 2019, 102, 72–108,  DOI:10.1016/j.pmatsci.2018.12.005.
24. M. D. Nguyen, E. P. Houwman, M. Dekkers, C. T. Q. Nguyen, H. N. Vu and G. Rijnders, Research update: enhanced energy storage density and energy efficiency of epitaxial Pb_0.9La_0.1(Zr_0.52Ti_0.48)O₃ relaxor-ferroelectric thin-films deposited on silicon by pulsed laser deposition, APL Mater., 2016, 4, 080701,  DOI:10.1063/1.4961636.
25. R. Montecillo, C. Y. Chen, R. F. G. Sinajon, Y.-T. Lee, R. R. Chien, K.-C. Feng, P.-Y. Chen, C.-S. Chen and C.-S. Tu, Optimizing energy storage under low electric field in A-site dysprosium modified BiFeO₃-BaTiO₃ ceramics, J. Alloys Compd., 2024, 983, 173918,  DOI:10.1016/j.jallcom.2024.173918.
26. W.-B. Li, D. Zhou, W.-F. Liu, J.-Z. Su, F. Hussain, D.-W. Wang, G. Wang, Z.-L. Lu and Q.-P. Wang, High-temperature BaTiO₃-based ternary dielectric multilayers for energy storage applications with high efficiency, Chem. Eng. J., 2021, 414, 128760,  DOI:10.1016/j.cej.2021.128760.
27. W.-B. Li, D. Zhou, R. Xu, D.-W. Wang, J.-Z. Su, L.-X. Pang, W.-F. Liu and G.-H. Chen, BaTiO₃-based multilayers with outstanding energy storage performance for high temperature capacitor applications, ACS Appl. Energy Mater., 2019, 2, 5499–5506,  DOI:10.1021/acsaem.9b00664.
28. B. Yang, Q. Zhang, H. Huang, H. Pan, W. Zhu, F. Meng, S. Lan, Y. Liu, B. Wei, Y. Liu, L. Yang, L. Gu, L.-Q. Chen, C.-W. Nan and Y.-H. Lin, Engineering relaxors by entropy for high energy storage performance, Nat. Energy, 2023, 8, 956–964,  DOI:10.1038/s41560-023-01300-0.
29. X. Tang, H. Zhang, F. Li, D. Wang, Y. Huang and H. Ke, High energy storage density under low electric fields in BiFeO₃-based ceramics with max configurational entropy, J. Eur. Ceram. Soc., 2023, 43, 6875–6882,  DOI:10.1016/j.jeurceramsoc.2023.07.047.
30. A. Sarkar, R. Djenadic, D. Wang, C. Hein, R. Kautenburger, O. Clemens and H. Hahn, Rare earth and transition metal based entropy stabilised perovskite type oxides, J. Eur. Ceram. Soc., 2018, 38, 2318–2327,  DOI:10.1016/j.jeurceramsoc.2017.12.058.
31. A. Tkach, A. Almeida, J. A. Moreira, J. de la Cruz, Y. Romaguera-Barcelay and P. M. Vilarinho, Low-temperature dielectric response of NaTaO₃ ceramics and films, Appl. Phys. Lett., 2012, 100, 192909,  DOI:10.1063/1.4714527.
32. L. Yang, X. Kong, Q. Li, Y. Lin, S. Zhang and C. Nan, excellent energy storage properties achieved in sodium niobate-based relaxor ceramics through doping tantalum, ACS Appl. Mater. Interfaces, 2022, 14, 32218–32226,  DOI:10.1021/acsami.2c05205.
33. X. Zhou, H. Qi, Z. Yan, G. Xue, H. Luo and D. Zhang, Superior thermal stability of high energy density and power density in domain-engineered Bi_0.5Na_0.5TiO₃–NaTaO₃ relaxor ferroelectrics, ACS Appl. Mater. Interfaces, 2019, 11, 43107–43115,  DOI:10.1021/acsami.9b13215.
34. F. Wang, X. Zhang, X. Yan, Y. Lu, M. Nastasi, Y. Chen and B. Cui, The effect of submicron grain size on thermal stability and mechanical properties of high-entropy carbide ceramics, J. Am. Ceram. Soc., 2020, 103, 4463–4472,  DOI:10.1111/jace.17103.
35. T. Tunkasiri and G. Rujijanagul, Dielectric strength of fine grained barium titanate ceramics, J. Mater. Sci. Lett., 1996, 15, 1767–1769,  DOI:10.1007/BF00275336.
36. T. Cui, J. Zhang, J. Guo, X. Li, S. Guo, Y. Huan, J. Wang, S.-T. Zhang and Y. Wang, Outstanding comprehensive energy storage performance in lead-free BiFeO₃-based relaxor ferroelectric ceramics by multiple optimization design, Acta Mater., 2022, 240, 118286,  DOI:10.1016/j.actamat.2022.118286.
37. H. Xiang, Y. Xing, F. Dai, H. Wang, L. Su, L. Miao, G. Zhang, Y. Wang, X. Qi, L. Yao, H. Wang, B. Zhao, J. Li and Y. Zhou, High-entropy ceramics: present status, challenges, and a look forward, J. Adv. Ceram., 2021, 10, 385–441,  DOI:10.1007/s40145-021-0477-y.
38. L.-F. Zhu, A. Song, B.-P. Zhang, X.-Q. Gao, Z.-H. Shan, G.-L. Zhao, J. Yuan, D. Deng, H. Shu and J.-F. Li, Boosting energy storage performance of BiFeO₃-based multilayer capacitors via enhancing ionic bonding and relaxor behavior, J. Mater. Chem. A, 2022, 10, 7382–7390,  10.1039/D1TA10971E.
39. C. Li, T. Zheng and J. Wu, Competitive mechanism of temperature-dependent electrical properties in BiFeO₃-BaTiO₃ ferroelectrics controlled by domain evolution, Acta Mater., 2021, 206, 116601,  DOI:10.1016/j.actamat.2020.116601.
40. A. Taibi, S. Chaguetmi, P. E. Sánchez-Jiménez, A. Perejón, J. E. García, H. Satha and L. A. Pérez-Maqueda, Pure perovskite BiFeO₃–BaTiO₃ ceramics prepared by reaction flash sintering of Bi₂O₃–Fe₂O₃–BaTiO₃ mixed powders, Ceram. Int., 2021, 47, 26947–26954,  DOI:10.1016/j.ceramint.2021.06.108.
41. Z. Song, H. Liu, S. Zhang, Z. Wang, Y. Shi, H. Hao, M. Cao, Z. Yao and Z. Yu, Effect of grain size on the energy storage properties of (Ba_0.4Sr_0.6)TiO₃ paraelectric ceramics, J. Eur. Ceram. Soc., 2014, 34, 1209–1217,  DOI:10.1016/j.jeurceramsoc.2013.11.039.
42. X. Yang, W. Li, Y. Zhang, Q. Yulong, Y. Yang and W. Fei, High energy storage density achieved in Bi³⁺-Li⁺ co-doped SrTi_0.99Mn_0.01O₃ thin film via ionic pair doping-engineering, J. Eur. Ceram. Soc., 2019, 40, 707–711,  DOI:10.1016/j.jeurceramsoc.2019.11.002.
43. Z.-N. Guan, Y. Yan, J. Ma, T. Pan, X. Li, S. Guo, J. Zhang, J. Wang and Y. Wang, Significantly enhanced energy storage performance of lead-free BiFeO₃-based ceramics via synergic optimization strategy, ACS Appl. Mater. Interfaces, 2022, 14, 44539–44549,  DOI:10.1021/acsami.2c11599.
44. P. Zhao, Z. Cai, L. Wu, C. Zhu, L. Li and X. Wang, Perspectives and challenges for lead-free energy-storage multilayer ceramic capacitors, J. Adv. Ceram., 2021, 10, 1153–1193,  DOI:10.1007/s40145-021-0516-8.
45. G. Wang, J. Li, X. Zhang, Z. Fan, F. Yang, A. Feteira, D. Zhou, D. C. Sinclair, T. Ma, X. Tan, D. Wang and I. M. Reaney, Ultrahigh energy storage density lead-free multilayers by controlled electrical homogeneity, Energy Environ. Sci., 2019, 12, 582–588,  10.1039/C8EE03287D.
46. Z. Yang, H. Du, L. Jin and D. Poelman, High-performance lead-free bulk ceramics for electrical energy storage applications: design strategies and challenges, J. Mater. Chem. A, 2021, 9, 18026–18085,  10.1039/D1TA04504K.
47. M. Wang, Y. Lin, M. Chen, M. Zhang, Q. Yuan and H. Yang, High energy storage efficiency and excellent recoverable energy storage density realized in 0.65Bi_0.5Na_0.5TiO₃–0.35BaTiO₃–SrZr_0.5Ti_0.5O₃ ceramics, J. Mater. Chem. C, 2023, 11, 6407–6416,  10.1039/D3TC00220A.
48. W. Zhu, Z.-Y. Shen, W. Deng, K. Li, W. Luo, F. Song, X. Zeng, Z. Wang and Y. Li, A review: (Bi,Na)TiO₃ (BNT)-based energy storage ceramics, J. Mater., 2024, 10, 86–123,  DOI:10.1016/j.jmat.2023.05.002.
49. G. Luo, A. Li, Y. Zhang, G. Zhang, Y. Sun, R. Tu and Q. Shen, Improvement of energy storage properties of NaNbO₃-based ceramics through the cooperation of relaxation and oxygen vacancy defects, Ceram. Int., 2023, 49, 801–807,  DOI:10.1016/j.ceramint.2022.09.053.
50. P. Nong, D. Zeng, Y. Pan, Q. Dong, M. Xu, X. Wang, J. Wang, H. Zhou, X. Li and X. Chen, Simultaneous enhancement of energy storage performance and thermal stability of NaNbO₃-based ceramics via multi-scale modulation, J. Mater., 2024 DOI:10.1016/j.jmat.2023.09.004.
51. M. Xu, D. Zeng, X. Wang, P. Nong, Y. Pan, Q. Dong, J. Wang, H. Zhou and X. Chen, Optimizing the energy storage performance of NaNbO₃ ceramics by rare-earth-based composite perovskite Sm(Mg_0.5Zr_0.5)O₃ modification, Microstructures, 2023, 3, 2023034,  DOI:10.20517/microstructures.2023.19.
52. C.-S. Chen, Z.-Q. Lin, R. Montecillo, J.-Y. Liao, P.-Y. Chen and C.-S. Tu, Improved energy storage in antiferroelectric AgNbO₃-modulated 0.925Bi_0.5Na_0.5TiO3 – 0.075BaTiO₃ relaxor ferroelectric ceramics, Ceram. Int., 2022, 48, 35452–35460,  DOI:10.1016/j.ceramint.2022.08.148.
53. X. Tang, Z. Hu, V. Koval, B. Yang, G. C. Smith and H. Yan, Energy storage properties of samarium-doped bismuth sodium titanate-based lead-free ceramics, Chem. Eng. J., 2023, 473, 145363,  DOI:10.1016/j.cej.2023.145363.
54. J. Jiang, X. Meng, L. Li, S. Guo, M. Huang, J. Zhang, J. Wang, X. Hao, H. Zhu and S.-T. Zhang, Ultrahigh energy storage density in lead-free relaxor antiferroelectric ceramics via domain engineering, Energy Storage Mater., 2021, 43, 383–390,  DOI:10.1016/j.ensm.2021.09.018.
55. C. S. Tu, I. G. Siny and V. H. Schmidt, Sequence of dielectric anomalies and high-temperature relaxation behavior in Na_1/2Bi_1/2TiO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 11550–11559,  DOI:10.1103/PhysRevB.49.11550.
56. Y. Ning, Y. Pu, C. Wu, S. Zhou, L. Zhang, J. Zhang, X. Zhang and Y. Shang, Enhanced capacitive energy storage and dielectric temperature stability of A-site disordered high-entropy perovskite oxides, J. Mater. Sci. Technol., 2023, 145, 66–73,  DOI:10.1016/j.jmst.2022.10.053.
57. J. König, B. Jančar and D. Suvorov, New Na_0.5Bi_0.5TiO₃–NaTaO₃-based perovskite ceramics, J. Am. Ceram. Soc., 2007, 90, 3621–3627,  DOI:10.1111/j.1551-2916.2007.01960.x.
58. Z. Huang, J. Deng, H. Wang, Y. Zhang, J. Duan, Z. Tang, Z. Cao, J. Qi, D. He and T. Lu, Fast low-temperature densification of translucent bulk nanograin Gd₂Zr₂O₇ ceramics with average grain size below 10 nm, J. Alloys Compd., 2020, 830, 154617,  DOI:10.1016/j.jallcom.2020.154617.
59. S. Karimi, I. M. Reaney, Y. Han, J. Pokorny and I. Sterianou, Crystal chemistry and domain structure of rare-earth doped BiFeO₃ ceramics, J. Mater. Sci., 2009, 44, 5102–5112,  DOI:10.1007/s10853-009-3545-1.
60. C.-S. Chen, C.-S. Tu, P.-Y. Chen, W. S. Chang, Y. U. Idzerda, Y. Ting, J.-M. Lee and C. W. Yu, Micro-to-nano domain structure and orbital hybridization in rare-earth-doped BiFeO₃ across morphotropic phase boundary, J. Am. Ceram. Soc., 2018, 101, 883–896,  DOI:10.1111/jace.15226.
61. M. Marezio, J. P. Remeika and P. D. Dernier, The crystal chemistry of the rare earth orthoferrites, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 2008–2022,  DOI:10.1107/S0567740870005319.
62. M. Graf, M. Sepliarsky, S. Tinte and M. Stachiotti, Phase transitions and antiferroelectrivity in BiFeO₃ from atomic level simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184108,  DOI:10.1103/PhysRevB.90.184108.
63. C. Toher, C. Oses, M. Esters, D. Hicks, G. N. Kotsonis, C. M. Rost, D. W. Brenner, J.-P. Maria and S. Curtarolo, High-entropy ceramics: propelling applications through disorder, MRS Bull., 2022, 47, 194–202,  DOI:10.1557/s43577-022-00281-x.
64. W. Cao, R. Lin, X. Hou, L. Li, F. Li, D. Bo, B. Ge, D. Song, J. Zhang, Z. Cheng and C. Wang, Interfacial polarization restriction for ultrahigh energy-storage density in lead-free ceramics, Adv. Funct. Mater., 2023, 33, 2301027,  DOI:10.1002/adfm.202301027.
65. L. Chen, H. Yu, J. Wu, S. Deng, H. Liu, L. Zhu, H. Qi and J. Chen, Large energy capacitive high-entropy lead-free ferroelectrics, Nano-Micro Lett., 2023, 15, 65,  DOI:10.1007/s40820-023-01036-2.
66. R. H. Mi, B. H. Chen, X. L. Zhu and X. M. Chen, Dielectric and ferroelectric characteristics of Ba(Ti_0.25Zr_0.25Hf_0.25Sn_0.25)O₃ high-entropy ceramics, J. Mater., 2023, 9, 634–641,  DOI:10.1016/j.jmat.2023.01.005.
67. J. Qi, M. Zhang, Y. Chen, Z. Luo, P. Zhao, H. Su, J. Wang, H. Wang, L. Yang, H. Pan, S. Lan, Z.-H. Shen, D. Yi and Y.-H. Lin, High-entropy assisted BaTiO₃-based ceramic capacitors for energy storage, Cell Rep. Phys. Sci., 2022, 3, 101110,  DOI:10.1016/j.xcrp.2022.101110.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta00921e

---