Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate description of ion migration in solid-state ion conductors from machine-learning molecular dynamics†
Takeru
Miyagawa
,
Namita
Krishnan
,
Manuel
Grumet
,
Christian Reverón
Baecker
,
Waldemar
Kaiser
 * and
David A.
Egger
* and
David A.
Egger
 *
*
Department of Physics, TUM School of Natural Sciences, Technical University of Munich, 85748 Garching, Germany. E-mail: waldemar.kaiser@tum.de; david.egger@tum.de
First published on 9th April 2024
Abstract
Solid-state ion conductors (SSICs) have emerged as a promising material class for electrochemical storage devices and novel compounds of this kind are continuously being discovered. High-throughout approaches that enable a rapid screening among the plethora of candidate SSIC compounds have been essential in this quest. While first-principles methods are routinely exploited in this context to provide atomic-level details on ion migration mechanisms, dynamic calculations of this type are computationally expensive and limit us in the time- and length-scales accessible during the simulations. Here, we explore the potential of recently developed machine-learning force fields for predicting different ion migration mechanisms in SSICs. Specifically, we systematically investigate three classes of SSICs that all exhibit complex ion dynamics including vibrational anharmonicities: AgI, a strongly disordered Ag+-conductor; Na3SbS4, a Na+ vacancy conductor; and Li10GeP2S12, which features concerted Li+ migration. Through systematic comparison with ab initio molecular dynamics data, we demonstrate that machine-learning molecular dynamics provides very accurate predictions of the structural and vibrational properties including the complex anharmonic dynamics in these SSICs. The ab initio accuracy of machine-learning molecular dynamics simulations at relatively low computational cost opens a promising path toward the rapid design of novel SSICs.
1. Introduction
Solid-state ion conductors (SSICs) are essential components of electrochemical energy storage devices such as all-solid-state batteries.1–7 Compared to their liquid counterparts, SSICs offer improved safety and high energy density.8–10 Recent advances have increased the ionic conductivities to values comparable to the ones of liquid electrolytes, making them a feasible alternative for future battery technologies.11,12 The synergy among theoretical and experimental materials studies has led to a continuous improvement of our understanding of ion-conduction phenomena, thereby generating a plethora of novel material candidates for usage of SSICs in battery devices.Deriving structure–property relations between SSIC compositions and their ionic conductivities is key when establishing design rules for screening potential SSIC candidates in experimental and theoretical high-throughput approaches.13–17 Probing the ion dynamics within the solid host lattice experimentally can be achieved via impedance spectroscopy18,19 and scattering techniques, e.g. Raman20,21 or inelastic neutron scattering.22,23 The former technique provides important insights on the frequency range at which different ionic species migrate as well as on their densities. The latter ones complement this in important ways by providing the overall vibrational spectrum of the material, including the features associated with mobile cations and the host lattice. The interpretation of such spectra, however, is not always straightforward and often relies on suitable reference materials. Consequently, experimental efforts alone can fall short in providing a complete microscopic picture of the ion conduction mechanism.
Therefore, atomistic simulations are essential in complementing experimental investigations as they offer valuable insights into microscopic details of the conduction mechanism of mobile cations through the complex host lattice. Furthermore, they allow the virtual investigation of novel material candidates and structural phases to guide the experimental design of SSICs in a synergistic approach. Ab initio molecular dynamics (AIMD) simulations have been widely used to study the ion dynamics and particularly the coupling between mobile ions and the host lattice in SSICs,24–29 unraveling a variety of interesting phenomena that drive the conduction of mobile cations. Such computational studies have suggested various mechanisms, including the ‘paddle-wheel effect’ that is coupling cation translational and polyanion rotational motions to impact cation conduction.30–34 Furthermore, various SSICs were found to exhibit anharmonic host lattice dynamics, which involve the mobile ions being driven into strongly anharmonic regions of the potential energy surface.26,35–37 Moreover, the collective motion of cations through the soft lattice, in the form of concerted migration, was found to substantially alter the local potential barriers experienced by cations for a variety of lithium and sodium ion conductors.38–41
Despite being a powerful and useful tool to elucidate the dynamical properties of SSICs, it is well-known that AIMD simulations suffer from a tremendous computational cost associated with the need to perform density functional theory (DFT) calculations at each time step. This limits accessible simulation times to the picosecond range and further restricts us to a small number of material systems and properties at small length scales. The prospect of machine-learning molecular dynamics (MLMD) is to overcome these shortcomings via much faster but equally accurate calculations of dynamical properties of materials.42,43 More rapid computational schemes will not only accelerate the in silico design of novel SSICs but in fact enable us to conduct more realistic calculations, e.g., regarding doped supercells. We anticipate that this will bring computational studies closer to laboratory realities and enhance their synergy with experimental synthesis and characterization.44,45
Throughout an AIMD simulation, an enormous set of ab initio forces and energies is collected for atoms that typically move within a relatively narrow phase space around their equilibrium positions. This scenario appears to be ideal for machine-learning force fields (MLFFs), i.e., predicting the potential energy surface around individual atoms via supervised machine-learning (ML) techniques. Various MLMD methods have therefore been developed to mitigate the intrinsic limitations of AIMD.46–52 Among them, on-the-fly active learning methods can update the MLFF by training with additional DFT calculations when facing structures of low certainty that have not been sufficiently sampled during the training steps.52–57
The enormous recent progress in the area of MLMD has already had an impact in the SSIC community, e.g., several recent studies employed MLMD to investigate ion diffusion properties and the role of the host lattice.58–64 The common target of several studies is to investigate ion diffusion phenomena on large timescales and to exceed the structural complexity beyond classical bulk systems. Notable examples include MLFFs derived from a self-learning and adaptive database approach, which predicted anisotropic motion of Li ions in Li10GeP2S12 (LGPS).58 Xu et al. employed moment tensor potentials for Li conductors and identified spontaneous polyanion rotation over the timescale of μs, which were however found to hamper Li-ion migration.62 Ref. 63 showed activation of PS4 flipping events to drive structural transitions to the highly conductive Li3PS4 phase at high temperatures, ruling out paddle-wheel effects in Li-ion conduction via a two-level ML scheme and ns-long MLMD simulations. Staacke et al. developed a Gaussian approximation potential to tackle ion diffusion within a lithium thiophosphate glass.60 These studies exemplify the extent by which structural complexity and/or simulation times of AIMD can be exceeded when using MLMD methods, which is important for obtaining mechanistic insights for SSICs.
Despite these incredible recent efforts, the question of whether and to what extent MLMD simulations can capture the physical mechanism behind ion transport within the strongly anharmonic potential energy surfaces of SSICs remains unaddressed. In particular, when high-throughput screening techniques shall be able to discern materials showing different ion-transport mechanisms, the question of whether MLFFs are accurate across the variety of ion-transport phenomena known to occur in SSICs is very pertinent. Here, an applicability of MLMD can deliver improved microscopic understandings of structure–property relations and the ion-migration mechanism, which will impact the design of novel material candidates. However, such prospects demand an accurate MLMD characterization of both the cation and the host lattice dynamics in SSICs.
In this work, we systematically investigate the dynamical properties of three characteristic SSICs candidates representing different transport mechanisms: AgI, a strongly disordered SSIC showing liquid-like Ag-conduction; Li10GeP2S12, showing concerted Li+ migration; and Na3SbS4, a Na+ vacancy conductor. These materials represent a variety of challenges for MLFFs including anharmonicities, highly dynamical potential energy surfaces as well as point defects. MLMD simulations were performed and compared with AIMD reference results in terms of the structural and vibrational properties of the SSIC host lattice as well as the diffusion mechanism of the mobile cations. We observe an accurate prediction of the vibrational density of states and diffusion coefficients for all systems. Moreover, even anharmonic distributions in the tilting angles within the host lattice are precisely captured. Most significantly, we demonstrate that MLMD can accurately predict the conduction mechanism of the different systems even in the presence of such extreme lattice anharmonicities. Overall, our findings demonstrate the high suitability of MLMD simulations for broad investigations of SSICs.
2. Computational methods
Ab initio molecular dynamics (AIMD) and machine-learning molecular dynamics (MLMD) simulations were carried out with the Vienna Ab initio Simulation Package (VASP).65,66 The projector augmented wave method67,68 and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional were used for AIMD simulations.69 The Brillouin zone was sampled at the Γ-point only. A canonical (NVT) ensemble was applied in each simulation.In this work, we train MLFFs ‘on-the-fly’ using the ML method implemented in VASP.52,56,70 After convergence of the force field, MLMD simulations are performed using the generated MLFFs to investigate their suitability for the prediction of the atomic dynamics in SSICs. The descriptors of the utilized ML method are based on a non-linear mixing of two- and three-body atomic functions describing the radial and angular distributions, respectively, within the local environment. The implemented method is a kernel-based ML model that uses a Bayesian linear regression to train on the DFT-calculated energy, forces, and stress tensors. The MLMD then makes use of a weighted sum of Kernel similarity measures, with weights obtained from the Bayesian linear regression model, to yield the prediction of forces. A summary of the ML method is given in the ESI;† for further details, we refer the reader to the original literature.52,56,70 System-specific parameters for all investigated SSICs (see Fig. 1) used in the AIMD and MLMD simulations are summarized in the ESI.†
We analyze the AIMD and MLFF data in two ways: first, we report the accuracy of the derived MLFFs using the Bayesian estimated error of the force (BEEF), as implemented in VASP,52,56,70 which gives us insights into the expected force accuracies and allows to check for convergence of the MLFFs. Additionally, forces from MLFFs are explicitly compared with DFT single-point calculations for randomly selected snapshots along the AIMD trajectories in order to quantify deviations with the root mean square error (RMSE). Hereby, we assess the quality of the MLFFs to describe the forces acting on each element separately.
Second, we calculate a variety of dynamic structural observables that are relevant for SSICs and ion conduction, starting with the atomic pair correlation function, g(r), which quantifies the short- and long-range correlation between two atomic species A and B defined as
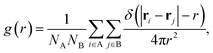 | (1) |
The vibrational density of states (VDOS) quantifies the number of modes per unit frequency range and is relevant for ion conduction because, e.g., the zero-frequency component is related to the diffusion constant, D,71 and a presence of low-frequency vibrational modes was discussed to imply higher ion conductivity.72,73 The VDOS of an atomic species i is computed as the Fourier transform of the velocity autocorrelation:
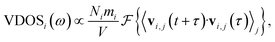 | (2) |
The band center of a given atomic species i, ωavg,i, is calculated as the average VDOS of species i, indicated as a subscript, given as
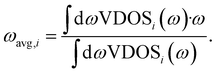 | (3) |
For AgI, previous work identified that significant angular fluctuations of AgI4 units are involved in anharmonic contributions to the structural dynamics that impact ion conductivity.26 LGPS and W-doped Na3SbS4 host lattices are also composed of tetrahedral units AS4 (A = Ge, P, Sb, W), whose internal dynamics may impact the motion of mobile cations. Therefore, we calculate tetrahedral angles in AgI4 (AS4) units representing I–I–I (S–S–S) bond angles, θi, via
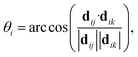 | (4) |
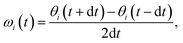 | (5) |
Focusing on the mobile ionic species and diffusion properties, we obtain the mean-squared displacement (MSD) according to
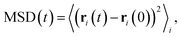 | (6) |
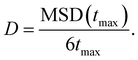 | (7) |
Finally, we calculate the van Hove correlation74 and exploit it to quantify spatiotemporal correlations between cation dynamics. Specifically, the distinctive part, Gd, describes the radial distribution of cations (indexed with j) with respect to a reference cation of the same type (indexed with i) as a function of a time interval Δt:
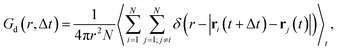 | (8) |
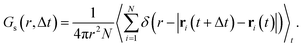 | (9) |
The relatively low computational costs of MLMD calculations, reported in Table S1, ESI,† allowed us to conduct five independent runs for each system in order to quantify statistical deviations of selected observables.
3. Results
3.1 Silver iodide (AgI)
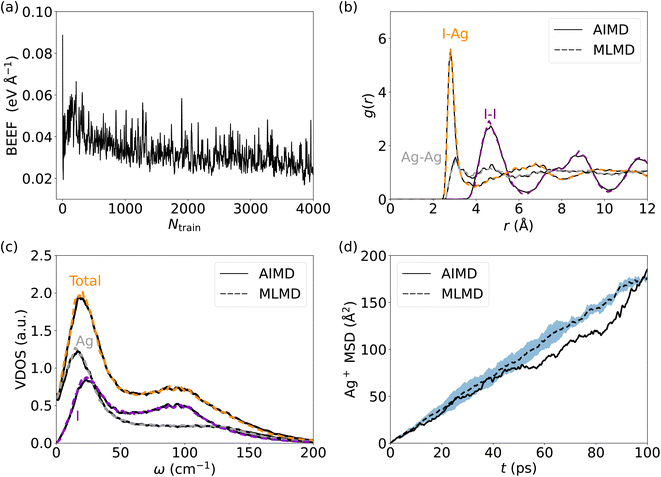
We start our analysis with silver iodide in its α-phase, AgI, which is a prototype solid-state superionic conductor: at temperatures above 420 K, AgI forms a superionic cubic phase with excellent Ag+ conduction. I− ions form a body-centered cubic (bcc) lattice with a large number of interstices (6 octahedral, 12 tetrahedral, and 24 trigonal), allowing a facile motion of Ag+ ions.31,75 The multitude of available Ag+ sites and their strong diffusivity induce a static and dynamic disorder, and the harmonic phonon approximation is breaking down in AgI with important ramification for its ion conductivity.26,27,76 All of these render AgI an ideal, challenging system to understand the accuracy and limitations of MLFF to predict the properties and elucidate the conduction mechanisms of SSICs.We first investigate the MLFF accuracy via the Bayesian error estimate of forces (BEEF) during the training period (Fig. 2a), showing well-converged force predictions to ≤0.05 eV Å−1. The actual root mean squared errors (RMSE) of the forces in the MLFF, referred to explicit DFT force calculations, are 45.5 meV Å−1 and 40.2 meV Å−1 for I and Ag atoms, respectively, see Fig. S1, ESI.† Next, we consider the AIMD-computed (see Methods section for computational details) atomic pair correlation function, g(r), which shows a distinct I–Ag peak at 2.8 Å and a significant broadening at larger distances, see Fig. 2b. I− ions exhibit long-range order, while the Ag–Ag g(r) shows a liquid-like behavior with a value of ∼1 across the whole range. Remarkably, MLMD simulations reproduce the AIMD-calculated g(r) of both the iodide host lattice and the disordered Ag+ ions. In view of the very different dynamic characteristics of the mobile Ag cation and I host lattice, this finding is important and encouraging. We further investigate the VDOS (see Fig. 2c and Methods section for computational details) and find two broad peaks around 25 and 100 cm−1. Contributions from Ag+ and I− ions dominate the former, while the latter is dominated by I− modes, in good agreement with previous reports.26,77 We further obtain non-zero values at 0 cm−1 due to slow Ag+ vibrational modes, which is in line with the high ion conductivity of AgI. Our MLMD simulations show an excellent agreement over the whole frequency range from 0 to 200 cm−1, suggesting that MLFFs can accurately capture and reproduce not only structural but also vibrational properties even in the highly complex potential energy surface of AgI.
We now focus on the Ag+ ion conduction mechanism and investigate the MSD of Ag+ ions, see Fig. 2d and Methods section for computational details. We observe a close to linear relationship for MSD(t) in both AIMD and MLMD simulations. Notably, the linear increase of MSD with time is known from Brownian motion,78 which together with g(r) ∼ 1 suggests random dynamics of Ag+ ions in a liquid-like environment. D+Ag values extracted from the MSD from AIMD and MLMD simulations are 2.61 × 10−5 cm2 s−1 and 2.99 × 10−5 cm2 s−1, respectively, which are in reasonable agreement and in line with previous experimental and theoretical studies.79,80
Because anharmonic relaxational dynamics of the iodide host-lattice were discussed as a driving force for Ag+ conduction,26 it is important to examine whether MLFFs can capture such dynamic effects. First, in both AIMD and MLMD we observe large deviations of I–I–I bond angles, θ, from the expected value of 70.5° to below 45° and above 100°, see Fig. 3a. As shown by Brenner et al.,26 these distortions remain present for long timescales, as also seen in the slow relaxational components of the θ angles we compute (see Fig. 3a). Interestingly, AIMD and MLMD simulations show a comparable extent of deviations from the expected value. A statistical analysis of the angle probability density, ρ(θ), taken from 48 different tetrahedral angles in the supercell along the trajectory, shows that values between 30° and 110° occur in the simulations (see Fig. 3b). ρ(θ) as computed in AIMD shows a more skewed form, while the counterpart from MLMD is slightly more pronounced at 70.5°. The tail at small values of θ is captured well by MLMD but a more pronounced disagreement is observed for larger values of θ. The standard deviation among several MLMD runs is found to be small, which indicates a high degree of reproducibility of these simulations for capturing such distinct local distortions.
 | ||
| Fig. 3 (a) Representative time evolution of I–I–I bond angle, θ, for selected AgI4 tetrahedra (see Fig. S2, ESI,† for schematic representation). Thick (thin) lines in panel (a) represent the Fourier filtered (unfiltered) values of θ using a cutoff frequency of 5 cm−1. (b) Probability density, ρ(θ), as obtained from 48 tetrahedra within the AgI supercell. (c) Probability densities of the angular velocity, ρ(ω), calculated from the time evolution of θ. For ρ(θ) and ρ(ω), data averaged from 5 independent MLMD runs are shown and the light-blue area indicates the standard deviation. | ||
To further examine the θ distributions, we compute the angular velocity, ω, see eqn (5). Because of the highly dynamic nature of AgI, the restoring force acting on iodide ions are anticipated to be rather small, i.e. small ω values may be predicted. This is in line with the results shown in Fig. 3a, where deviations in θ from the expected value occur for long timescales of ∼20 ps. Indeed, we find small values of ω between −0.2° fs−1 and 0.2° fs−1 (see Fig. 3c), confirming the weak restoring forces. MLMD simulations accurately capture the AIMD probability density of angular velocities, ρ(ω), over the entire range suggesting an accurate prediction of the dynamical changes in the iodide host lattice (see Fig. 3c).
A potential reason for the deviations in the θ distribution of MLMD compared to AIMD may be rooted in the limited phase space that is being sampled during MLFF training. To investigate this hypothesis, we retrained the MLFF at an increased temperature of 800 K and performed another MLMD simulation at 500 K using the alternative MLFF. In this way, the system explores a larger part of phase space during MLFF training, expanding into strongly anharmonic regions due to the increased thermal fluctuations. This is a known strategy to reduce the risk of excessive extrapolation during MLMD simulations.42,81 However, the deviation in ρ(θ) is found to be similar even when training is conducted at higher temperatures (Fig. S3, ESI†). Consequently, we may assign the remaining deviations to the choice of two- and three-body descriptors in the MLFFs, for which more complex ones may be required to capture all aspects of ρ(θ) with a high accuracy.
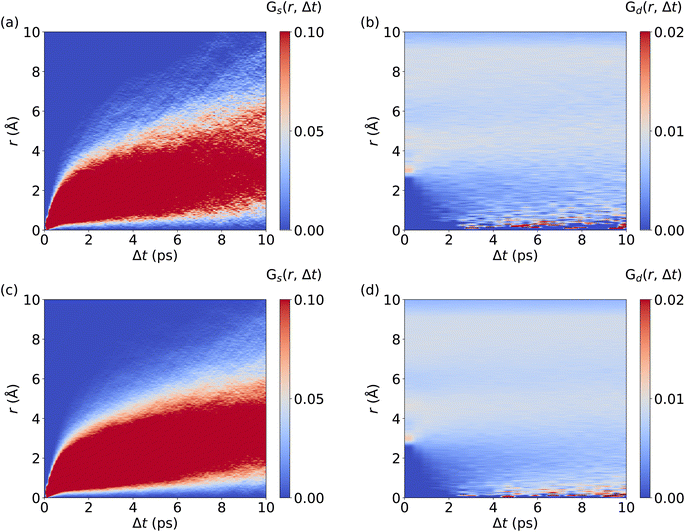
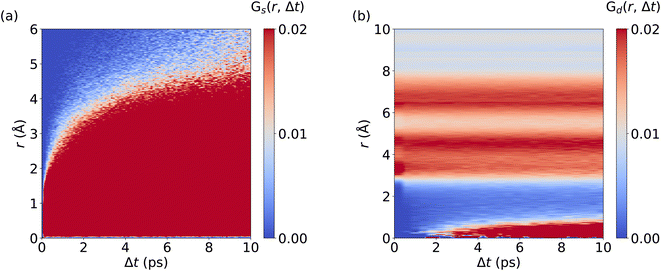
We now investigate the van Hove correlation function of Ag+ ions, considering the self part, Gs and the distinctive part, Gd, see Fig. 4 and Methods section for the computational details. In line with the monotonous increase of the MSD (cf.Fig. 2d), an increasing width in the Gs values with time is observed. Interestingly, Gs values at r = 0 Å quickly drop to zero as Δt is increased. This implies that Ag+ ions barely return to their previous location, which is a further aspect confirming the randomness in the Ag+ ion dynamics. Furthermore, after fast broadening of the strongly correlated Gs domain within Δt ≤ 0.5 ps, its center increases continuously with time. The diffusive character of Ag+ dynamics is visible as a rapid and continuous increase of Gs values that reflect traveled distances of Ag+ ions, contributing to the remarkable ion conductivity of AgI. At the same time, no significant Gd peaks are observed. Rather, the Gd data confirm the fully homogeneous distribution of cations over space and time without significant temporal correlations between different Ag+ ions. Importantly, MLMD simulations accurately capture the shape and intensities of Gs and Gd as obtained in AIMD. Overall, our results suggest that MLMD is able to capture the structural, vibrational, diffusive, and angular properties of AgI even with the intricate potential energy surface this material experiences at higher temperatures.
Finally, we investigate size transferability and apply the generated MLFF from the 128 atom supercell to predict the structural and dynamical properties of a 1024 atom supercell of AgI. We find an excellent match in the g(r), VDOS, and Ag+ MSD, see Fig. S4.† Notably, we observe that the Ag+ MSD gets more linear, which is caused by the larger amount of Ag+ ions that can move within the larger supercell. The findings suggest a transferability of MLFFs to larger systems sizes for cases where the crystal structure remains unchanged.
3.2 Li10GeP2S12 (LGPS)
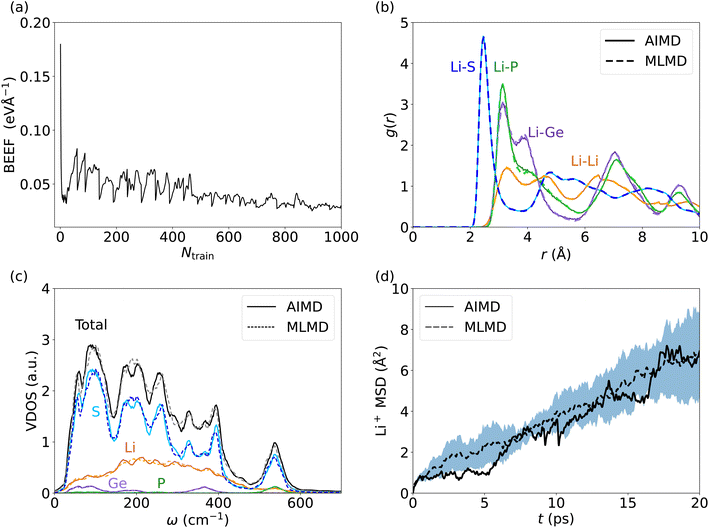
Lithium-based SSICs emerged as a promising alternative to replace their liquid counterparts without changing the full battery stack because of their excellent ion conductivities.82 Among them, Li10GeP2S12 (LGPS) was discovered as one of the first Li-based SSICs with an ion conductivity comparable to those of liquid electrolytes.15,39,58,83–92 Many studies have investigated the underlying mechanism that drives Li+ migration through the solid host lattice,89,93–95 and AIMD studies suggested a concerted migration of Li+ ions to be at play.39,96 Specifically, the coupled motion of multiple Li+ ions can lower migration energy barriers significantly compared to a scenario where ions migrate individually. This mechanism of coupled Li+ motion is similar to the situation in liquid electrolytes97,98 and likely is accompanied by anharmonic dynamical changes in the local potential energy surface of the material. It is critically important to assess whether MLFFs can capture such concerted dynamic phenomena, despite being based on local two- and three-body descriptors and a limited size of the AIMD snapshots available for MLFF training. Consequently, we investigate the accuracy of MLMD simulations to capture the concerted motion of Li+ ions as well as the interactions with the host lattice in the prototypical LGPS material.As above, we analyze the accuracy of the trained MLFF first via the force errors during the training period (Fig. 2a) and observe fast convergence of the BEEF to values below 0.05 eV Å−1 (see Fig. 5a). For the individual chemical species, we observe RMSE values of MLFF with respect to DFT force values of 27.7 meV Å−1 for Li, 75.7 meV Å−1 for Ge, 85.0 meV Å−1 for P, and 45.4 meV Å−1 for S (see Fig. S5, ESI†). The calculated g(r) show a first-order peak around 2.5 Å for Li–S and broadened higher-order peaks (see Fig. 5b). The g(r) data for Li–P and Li–Ge both show a peak at 3.5 Å and exhibit an overall structure that is consistent with the expected long-range order of the host lattice. By contrast, a suppressed long-range order is found for Li–Li with g(r) ≈ 1 across the whole range. MLMD simulations accurately capture the features of g(r) for Li with most elements, in particular for Li–Li and Li–S. However, we do observe small differences in the Li–P and Li–Ge g(r) peak intensities, whereas their peak positions are accurately captured. Specifically, their second g(r) peaks are not precisely reproduced by MLMD. These deviations are in line with the slightly enhanced RMSE values for Ge and P atoms, which is likely caused by the small amount of Ge and P atoms in the supercell, i.e. 8 and 16 atoms, respectively, and consequently the low number of local reference configurations for each type, as mentioned in the computational details. It is noted that MLMD further captures the g(r) within the polyanions of the host lattice (see Fig. S6, ESI†).
We now investigate the VDOS of LGPS (see Fig. 5c) and obtain good agreement between AIMD and MLMD simulations for the entire frequency range. All element-wise contributions, particularly the ones of Li+ ions, are closely mirrored in MLMD. Li vibrations appear throughout the whole frequency range up to 650 cm−1, being strongly coupled to S vibrations in particular in the region between 200 cm−1 to 400 cm−1, whereas contributions by Ge and P are found mostly for higher-frequency modes at 550 cm−1. There are some deviations between AIMD and MLMD visible in the high-frequency range of the polyanion data, which are likely not very relevant because ion migration is driven by lower-frequency modes. Furthermore, we observe a finite VDOS value at zero frequency, pointing to the Li+ migration. MLMD simulations, averaged across 5 runs, show a continuous increase in the MSD (Fig. 5d). In contrast to our findings for AgI, we notice that the variation in the Li+ MSD is substantial, which suggests an increased stochastic nature of the ion-migration mechanism. The MSD from the single AIMD run follows the MLMD one to a good extent. D+Li values of 5.33 × 10−6 cm2 s−1 and 4.50 × 10−6 cm2 s−1 from AIMD and MLMD simulations, respectively, were extracted, which are in line with previous computational studies99 and quasi-elastic neutron scattering measurements.100 We assign the observed deviations to the increased stochastic character of Li migration in LGPS. Thus, large simulation times – exceeding feasible AIMD timescales – are required to predict reliable MSD values.
We now analyze the migration mechanism of Li+ ions. Here, we calculate the self and distinctive part of the van Hove correlation function for Li+ ions in LGPS from AIMD and MLMD trajectories. MLMD results of Gd(r, Δt) show a substantial correlation at 0 Å starting at ∼1 ps. This means that a Li+ ion follows a migrating one within timescales of around 1 ps, supporting the concerted motion of Li+ ions (see Fig. 6 and S7, ESI†). Strong correlations exist around 4 Å and 6.5 Å, confirming that the long-range order of Li+ ions remains unaffected even though Li+ ions migrate, in line with previous results.39Gs(r, Δt) shows a continuous increase in correlation during the simulations, showing that the Li+ ions are migrating, which is consistent with the MSD (see Fig. 5d). In contrast to AgI, we observe a substantial correlation at r = 0 Å for all Δt values. This underpins that a substantial amount of Li+ ions remain located near their equilibrium positions, while all Ag+ ions contribute to the overall conduction in AgI. Notably, the MLMD shows a fair agreement for Gs(r, Δt) and Gd(r, Δt) with the AIMD reference (see Fig. S7, ESI†). Deviations in the overall values and intensities are caused by the limited available timescales from AIMD simulations. Importantly, we can still confirm that MLMD captures the concerted migration mechanism in LGPS.
 | ||
| Fig. 6 Spatiotemporal correlations of Li+ ion migration in LGPS: Panels (a) and (b) visualize Gs(r, Δt) and Gd(r, Δt), respectively. MLMD data were averaged across 5 independent trajectories. | ||
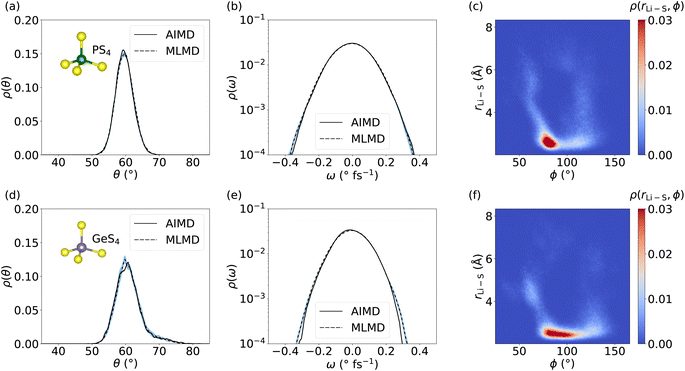
We now focus on the dynamics of the PS4 and GeS4 tetrahedra in the LGPS host lattice because distortions in the polyanion backbone are likely to play a crucial role in facilitating cation diffusion.101 Moreover, it is interesting to investigate the aforementioned consequences of the increased RMSE of the MLFF for Ge and P, as well as the deviations seen in g(r), for the dynamical properties of the host lattice. We compute the distribution of θ angles within the PS4 and GeS4 tetrahedra and compare the AIMD and MLMD probability densities, ρ(θ), see Fig. 7. The agreement between AIMD and MLMD is overall good. We generally find small variations in the θ angles suggesting relatively rigid tetrahedra. PS4 tetrahedra show fluctuations that are largely harmonic in the range between 50° and 70°. Interestingly, the angles in GeS4 tetrahedra exhibit a distribution that is significantly more asymmetric with an extended tail toward large values. This suggests the presence of substantial anharmonicities in the rotational dynamics of GeS4 tetrahedra. The angular velocity distribution, ρ(ω), further underlines the accuracy of the MLMD simulations in capturing not only the angular distribution but also their dynamical changes (Fig. 7). The higher RMSE values of the forces from MLFFs for P and Ge atoms (see Fig. S5, ESI†) may explain the remaining deviations present in the angular distributions. In contrast, the RMSE of Li forces is considerably lower, in line with our finding that Li+ migration is captured well.
Having assessed the dynamical properties of mobile cations and host lattice separately, we now investigate the interaction between PS4 and GeS4 polyanions and adjacent Li+ ions. An accurate description from MLMD is relevant for capturing pertinent dynamic coupling phenomena, such as paddle-wheel effects, which potentially drive Li+ ion migration.30,34,62 We compute the 2D probability distribution, ρ(rLi–S, ϕ), which measures occurrences of Li–S distances, rLi–S, as a function of P–S–Li bond angles, ϕ, see also Fig. S8, ESI,† for a graphical representation. The highest correlation between PS4 tetrahedra and Li ions is found in a small range of 80° ≤ ϕ ≤ 95° at small Li–S distances of ≤3 Å (see Fig. 7 and S9, ESI†). Two less intense branches are found leaving this highly correlated region. The first one reaches higher ϕ angles of up to 130° with Li–S distances spread over the whole considered range. The second, less-intense branch simultaneously goes to smaller ϕ angles and larger Li–S distances. The correlation of Li–S distances with GeS4 tetrahedra exhibits a squeezed form with small changes in the distances, showing ϕ angles of 75° to 110°. This suggests a larger rotational degree of freedom of Li ions around GeS4 than around PS4 tetrahedra, which we may assign to the larger mass and less negative charge of the [GeS4]2− polyanions. Interestingly, Li–S distances increase only when ϕ ≤ 70° or ϕ ≥ 120°, representing a potential indicator for the design of host lattice structures to enable Li ion migration. Direct comparison with AIMD results (see Fig. S9, ESI†) shows an excellent match in the probability distributions with MLMD data, supporting the accurate prediction of interactions between mobile cations and the host lattice. These results underline that MLMD captures and reproduces the structural and vibrational properties, as well as the concerted nature of Li ion migration in LGPS.
3.3 Sodium thioantimonate (Na3SbS4)
Na-based SSICs gained significant attention as a potential replacement for their Li-based counterparts. Sodium thiophosphates, Na3PS4,102,103 and sodium thioantimoniates, Na3SbS4,104–106 have been the focus of many studies in this context because of their integrability into all-solid-state sodium batteries and due to their high ion conductivities.107,108 Moreover, a variety of interesting findings have been reported on the atomic dynamics in these materials. This includes vibrational anharmonicity,28,36 a rich polymorphism,24,109 and coupled dynamics of anions and cations that have been discussed in the context of paddle-wheel effects.24,32 A peculiarity of current Na-based SSICs is their tunable ion conductivity by introducing Na vacancies via aliovalent doping. Several studies suggested that Na+ diffusion in pristine materials remains absent even at temperatures as high as 900 K and only becomes viable upon introduction of defects.110,111 Such can be achieved through a variety of different dopants, including halides112–114 and tungsten,106,115,116 which commonly substitute a pnictogen or chalcogen, respectively, and leave Na+ vacancies behind to counterbalance the change in oxidation state. Na+ ions may then diffuse via vacancy migration with DFT-computed migration barriers as low as 0.1 eV, resulting in ion conductivities in the mS cm−1 range.117AIMD has been instrumental in demonstrating the migration of Na+ vacancies within the network of [PnCh4]3− (Pn = {P, Sb}; Ch = {S, Se}) polyanions.24,28,111,114 Specifically, the anharmonic character of the host-lattice vibrations and local symmetry breaking, which cannot be captured by harmonic phonon calculations alone, have motivated the use of finite-temperature MD simulations.36,72,109,118 However, computational costs associated with doped scenarios of, e.g., Na3PnCh4 SSICs, are very high. First, large supercells are needed to mimic small doping concentrations at the Pn site. Second, Na+ migration occurs by hopping across vacancies, which are rare events despite modest ion conductivities and low migration barriers found in these materials. Consequently, long simulation times are needed to sample sufficiently many hopping events and describe the coupling between host lattice and migrating Na+ ions.
MLMD trained via AIMD data may well constitute a promising way to overcome these computational challenges, potentially allowing for the study of extended length and time scales, which we investigate here for the scenario of aliovalent doping. Specifically, we focus on tungsten-doped Na3−xSb1−xWxS4, which was shown to attain excellent ion conductivities.115,116 The mechanism involves W substituting a Sb site, forming [WS4]2− polyanions that exhibit different charges than the original [SbS4]3− ones, and a variation in the chemical environment of S atoms. As a consequence, Na vacancies, V−Na, are introduced which may diffuse within the crystal. The local variation in chemical bonds and charge as well as changes in the potential energy surface due to V−Na migration, can be expected to result in challenges for the training procedure of MLFFs.
We start by considering the accuracy of MLMD simulations for pristine Na3SbS4 at T = 300 K. The MLFF quickly converges within 1000 steps, showing maximum force errors of below 0.02 eV Å−1 after 200 steps already (see Fig. S10, ESI†). This results in precise predictions of g(r) among all elements in the anion host lattice and the Na+ ions (see Fig. S11, ESI†). The VDOS shows the expected polyanion vibrations at larger frequencies of 350 cm−1 to 400 cm−1, and broad contributions in the range of ≤200 cm−1 caused in particular by Na and S vibrations (see Fig. S12, ESI†). The latter suggests the presence of anion–cation coupling, in line with previous studies.28,36,109 Notably, the MLMD data capture mode frequencies across the entire frequency range of vibrations, but moderate differences in their intensities remain present. We further observe that Na+ ions merely oscillate around their lowest-energy positions, while migration throughout the pristine lattice remains absent in our AIMD and MLMD simulations (see Fig. S13–S15, ESI†), as previously reported.110
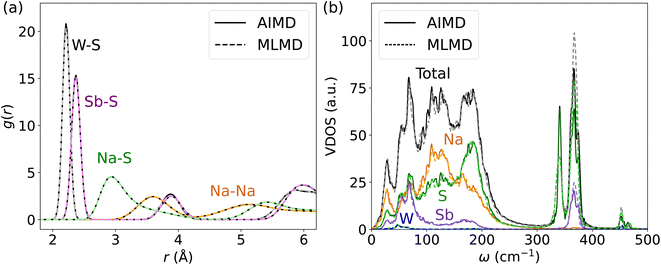
Next, we investigate the accuracy of MLFFs for the tungsten-doped Na2.94Sb0.94W0.06S4. A new set of force fields is trained starting from the MLFF of the pristine Na3SbS4. The BEEF values during the training procedure largely remain below 0.02 eV Å−1 after around 1000 steps (see Fig. S16, ESI†). As expected, the error of the MLFF is higher than the one for the pristine system due to increased variations in the local coordination of S atoms in the W-substituted polyanions. Explicit calculation of errors from MLFF to DFT forces were 14.0 meV Å−1, 41.4 meV Å−1, 24.3 meV Å−1 and 52.3 meV Å−1 for Na, Sb, S, and W, respectively (see Fig. S17, ESI†). Comparing these results to the above findings, these forces are in the range of what we found for AgI and below the ones reported for Ge and P in LGPS. Consequently, the MLMD simulations accurately describe g(r) within the [SbS4]3− polyanions as well as between Na+ and S2− ions when compared to AIMD data (see Fig. 8a). We observe only minor deviations in the W–S g(r), where MLMD results show slightly lower peak intensities than the AIMD ones (see also Fig. S18, ESI†). The W–S g(r) exhibits a pronounced peak at 2.21 Å, confirming that bond lengths are shortened compared to Sb–S of 2.36 Å in the pristine case because of the more positive W6+ ions. g(r) for Na–Na remains largely unaffected by doping and still shows a first-order peak at 3.61 Å with broadened long-range distributions.
An important question is whether MLMD simulations accurately describe the vibrational properties of W-doped Na2.94Sb0.94W0.06S4. Indeed, we observe good agreement between MLMD and AIMD data for the overall shape of the VDOS and individual element-wise contributions in the region ≤300 cm−1 (see Fig. 8b) despite substantial changes in the local chemical environments. However, the intensity of higher-energy sulfide modes shows larger deviations despite their frequencies being captured well, as explicitly shown in ΔVDOS plots (Fig. S19, ESI†). While an accurate representation of low-frequency modes is more important for describing SSICs, reducing such deviations for the high-frequency vibrational regime could be achieved with improved MLFFs. We also investigate the Na band center, given by the average vibrational frequencies of the projected Na VDOS (see Eq. (3)), because it was recently identified as a good indicator for changes in the overall lattice stiffness.72 Here, AIMD and MLMD simulations give Na band center values of ωavg,Na = 127.5 cm−1 and 126.5 cm−1, respectively, showing excellent agreement. By contrast, the pristine Na3SbS4 exhibits a larger value of 129.7 cm−1 (129.1 cm−1) from MLMD (AIMD) simulations, which shows that a small softening of the lattice occurs upon introducing W dopants and that this correlates with the higher Na+ conductivity.
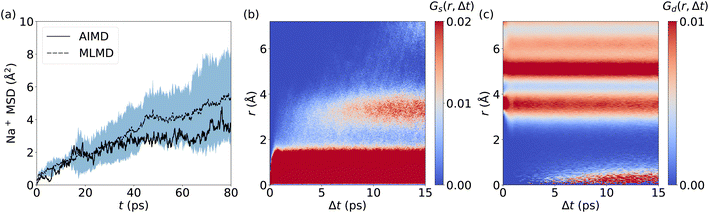
The prediction of Na+ diffusion coefficients from AIMD simulations is greatly complicated by random Na+ hopping processes. Consequently, long simulations and/or large cell sizes are required to obtain reliable MSD values, which again underlines the need for reliable MLMD. Our analysis of the Na+ MSD from MLMD simulations highlights these complications by showing a wide spread of MSD values over time (Fig. 9a), from which we obtain DNa+ = (1.13 ± 0.69) × 10−6 cm2 s−1. The MSD computed from the single AIMD trajectory lies within the standard deviation of MLMD values. Van Hove correlations for Na2.94Sb0.94W0.06S4 exhibit a behavior that significantly deviates from AgI and LGPS: Gs develops an additional region of strong correlations after 7 ps at approximately 3.5 Å, corresponding to the distance between neighboring Na+ sites and confirming the migration of Na+ ions (see Fig. 9b and S20, ESI†). Notably, the region between the two strongly correlated Gs features is only weakly populated, which points to the migration of Na+ ions via thermally activated hopping. Concerted migration can be ruled out from Gd (see Fig. 9c), showing only a slowly increasing component after 6 ps.
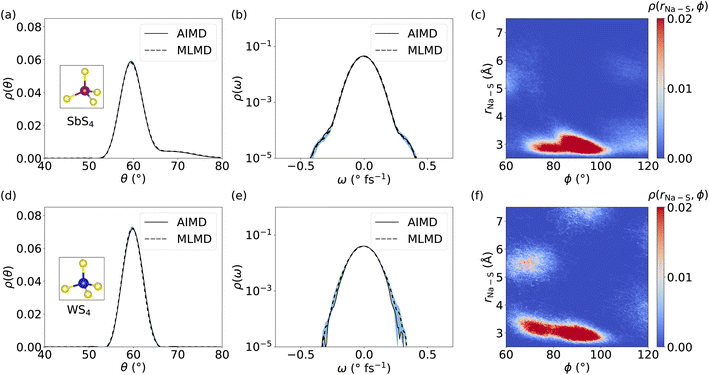
Because several studies suggested that coupling between cations and host lattice is a key factor in facilitating cation diffusion,24,32 we investigate the dynamics of SbS4 and WS4 tetrahedra in the host lattice of Na2.94Sb0.94W0.06S4. Distributions of θ angles within SbS4 and WS4 tetrahedra are obtained in order to compare the AIMD and MLMD probability densities, ρ(θ), see Fig. 10a and d, respectively. The overall agreement between AIMD and MLMD is again satisfactory. The overall small dynamic changes of θ indicate that the tetrahedra form relatively rigid structures. Notably, θ of SbS4 tetrahedra exhibit an asymmetric distribution with an extended tail toward larger angle values whereas θ of WS4 tetrahedra exhibit an essentially symmetric characteristic. This indicates the existence of anharmonicity in the rotational motions of SbS4 tetrahedra. This is also visible in the angular distribution, ρ(ω), of SbS4 tetrahedra, which shows small deviations around −0.5 and 0.5 ° fs−1 from the otherwise harmonic behavior. Notably, ρ(ω) of WS4 tetrahedra shows a more harmonic distribution. The overall small deviations between AIMD and MLMD are found to be more pronounced for WS4, which likely is a result of the small sampling size of WS4.
We now focus on correlations between SbS4 and WS4 tetrahedra and neighboring Na+ ions. We obtain the 2D probability density ρ(rNa–S, ϕ), by defining the distance, rNa–S, between neighboring Na+ ions and S atoms, and the dihedral angle ϕ, see Fig. 10 for MLMD and Fig. S21, ESI,† for AIMD results. The largest correlation between SbS4 tetrahedra and Na ions exists in a small range of 80° ≤ ϕ ≤ 100° with rNa–S remaining below ≤4 Å. Minor intensities are found in two regions: one in a range of 100° ≤ ϕ ≤ 120° and rNa–S of ≤4 Å, and the other in 60° ≤ ϕ ≤ 80° and 5 Å ≤ rNa–S ≤ 6 Å. The noticeable intensities at lower rNa–S values showing a broadened ϕ distribution between 80° and 120° indicate that Na+ ions experience a significant degree of rotational freedom around SbS4 tetrahedra. In regard to WS4 tetrahedra, the intensity in the range 60° ≤ ϕ ≤ 80° and 5 Å ≤ rNa–S ≤ 6 Å is found to be more pronounced than in case of SbS4 ones. This observation suggests a facilitated ion migration when Na+ cations are passing by WS4 tetrahedra, which can be explained by W–S bond lengths being shorter than the Sb–S ones and the fact that WS4 tetrahedra occupy less space. Consequently, Na+ ions are given more space to migrate in the proximity of the W-dopant. The absence of correlated branches as we found in case of LGPS (see Fig. 7) can be rationalized by the nature of Na+ migration as visible in the Gs for Na2.94Sb0.94W0.06S4 (see Fig. 9): Na+ cations spend comparably little time in-between equilibrium sites, which is characteristic of a thermally-activated cation hopping, whereas Li+ ions in LGPS spend more time in-between their equilibrium sites. Altogether, these findings show that the host lattice dynamics of Na2.94Sb0.94W0.06S4 are correlated with cation diffusion and suggest that ion conduction can be tuned through adjusting the dynamics of the host lattice.
4. Discussion
Our systematic analysis found that MLMD simulations are accurate for calculating the vibrational properties of mobile cations and the host lattice. Anharmonic properties are predicted well, and the interactions between mobile cations and the polyanionic backbone are precisely captured for all investigated systems. These results are especially intriguing as various ion-conduction mechanisms were investigated: liquid-like behavior of Ag+ ions in AgI, concerted migration of Li+ in LGPS, and thermally activated VNa− vacancy hopping in Na3SbS4. To the best of our knowledge, a systematic investigation of MLFF accuracy covering such diverse ion migration phenomena in SSICs has not been reported yet. The majority of existing studies rely on the accuracy of MLFFs in comparison to DFT reference calculations. However, recent reports highlight that benchmarking the accuracy of forces alone does not necessarily align with an accurate prediction of relevant material properties.119 Here, both structural and vibrational properties of mobile cations and host lattice are found to be captured well, providing confidence that the utilized MLFFs are highly suitable for a broad range of SSICs.We emphasize that such accurate predictions from the exploited MLMD model were not necessarily expected. The locality of descriptors, which only include atoms that are located within a certain cutoff radius, is often discussed as one downside for larger systems next to advantages such as simplicity and transferability.42,120 Such concerns have led to the development of novel MLFF methods that correct for nonlocal effects including long-range electrostatic interactions.121–124 In the case of SSICs, the short-range nature of interactions and the large dynamical distortions exhibited by the ions likely aid the kernel-based ML procedure. A dominance of short-range interactions can lead to long-range phenomena being less relevant effectively, which can rationalize our accurate MLMD simulation results. Correlated ion phenomena at short ranges still remain well represented as we have demonstrated in the case study of concerted migration of Li+ ions in LGPS.
Finally, we would like to provide a compact perspective on the relevance of our findings for future development of materials and the role MLMD simulations may play in this regard. Fast and reliable MLMD simulations with ab initio accuracy can open novel possibilities when guiding experimental materials design and characterization. Raman spectroscopy, for example, represents one of the most widely used, non-destructive techniques for providing vibrational fingerprints of a solid-state material. Even though promising approaches towards high-throughput Raman calculations and characterization have been made recently,125–129 first-principles calculations of Raman spectra remain essential for the interpretation of experimental measurements and prediction of vibrational properties in novel material systems. Commonly used Raman calculations based on the harmonic approximation are, however, not sufficient to capture the entire vibrational dynamics of materials that are as anharmonic as the investigated SSICs here. These inherent limitations can be overcome through molecular dynamics simulations that account for the entirety of vibrational anharmonicity in such materials,130–132 which in the past found only limited attention due to the tremendous computational costs associated with AIMD. The excellent accuracy of the presented MLMD results for the variety of vibrational properties in the investigated SSICs may render calculations of finite-temperature Raman spectra viable and inspire novel data-driven approaches, combining ML-models for Raman activities133–139 with MLMD to launch a flourishing synergy between experiments and computation.
Moreover, we envision that computationally efficient and precise MLMD simulations may enrich the physical information that is contained in datasets for a tailored design of novel materials.140–142 Here, the majority of existing approaches for data-driven screening of suitable material candidates mainly relies on properties that are derived in the ground state.14,143–146 Incorporating vibrational properties as well as information about the ion-conduction characteristics predicted from MLMD simulations may improve the selectivity of existing screening approaches and potentially deepen our understanding of the structure–property relations of SSICs.
5. Conclusion
In summary, we have provided a systematic investigation of the accuracy of MLMD simulations to predict the dynamical properties associated with ion conduction across various phenomena in a broad range of SSICs. Results from MLMD were compared to AIMD reference data using several measures that include the actual force errors, structural and dynamical properties of mobile cations as well as of the host lattice, and correlations among the motion of cations and rotational degrees of freedom in the polyanion backbone. Our results demonstrate that precise predictions of dynamical properties of SSICs exhibiting different transport mechanisms that involve liquid-like cation motion in AgI, concerted cation migration in LGPS, and thermally-activated vacancy hopping in W-doped Na3SbS4. Through our MLMD simulations, we could further provide a detailed analysis of the anharmonic character of host lattice vibrations, which take a significant role in enabling a facile migration of mobile cations. Our findings are very encouraging and may further enhance trust in MLMD simulation results and their suitability for a broad range of SSICs with different physical effects governing ion migration and structural variability. We believe that the increasing availability of MLMD methods can enhance synergies among experiments, computations, and material design efforts. An exciting avenue along this quest revolves around the development of novel data-driven screening techniques for SSICs, which will be aided by finite-temperature materials predictions through MLMD simulations at relatively low computational cost. Finally, the computationally efficient yet accurate calculations enabled by MLMD are likely to leverage precise investigations of dynamic phenomena in SSICs, including the complicated coupling between mobile-ion and host-lattice dynamics.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Funding provided by the Alexander von Humboldt–Foundation in the framework of the Sofja Kovalevskaja Award, endowed by the German Federal Ministry of Education and Research, by the Deutsche Forschungsgemeinschaft via Germany's Excellence Strategy – EXC 2089/1-390776260, and by the TUM-Oerlikon Advanced Manufacturing Institute, are gratefully acknowledged. The authors further acknowledge the Gauss Centre for Supercomputing e.V. for funding this project by providing computing time through the John von Neumann Institute for Computing on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre.References
- M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, A review of conduction phenomena in Li-ion batteries, J. Power Sources, 2010, 195, 7904 CrossRef CAS.
- E. Quartarone and P. Mustarelli, Electrolytes for solid-state lithium rechargeable batteries: recent advances and perspectives, Chem. Soc. Rev., 2011, 40, 2525 RSC.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Li–O2 and Li–S batteries with high energy storage, Nat. Mater., 2012, 11, 19 CrossRef CAS PubMed.
- W. Zhou, Y. Li, S. Xin and J. B. Goodenough, Rechargeable sodium all-solid-state battery, ACS Cent. Sci., 2017, 3, 52 CrossRef CAS PubMed.
- T. Ye, L. Li and Y. Zhang, Recent progress in solid electrolytes for energy storage devices, Adv. Funct. Mater., 2020, 30, 2000077 CrossRef CAS.
- M. Balaish, J. C. Gonzalez-Rosillo, K. J. Kim, Y. Zhu, Z. D. Hood and J. L. Rupp, Processing thin but robust electrolytes for solid-state batteries, Nat. Energy, 2021, 6, 227 CrossRef CAS.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. M. Rupp, Solid-state Li–metal batteries: Challenges and horizons of oxide and sulfide solid electrolytes and their interfaces, Adv. Energy Mater., 2021, 11, 2002689 CrossRef CAS.
- B. V. Lotsch and J. Maier, Relevance of solid electrolytes for lithium-based batteries: A realistic view, J. Electroceram., 2017, 38, 128 CrossRef.
- T. Placke, R. Kloepsch, S. Dühnen and M. Winter, Lithium ion, lithium metal, and alternative rechargeable battery technologies: the odyssey for high energy density, J. Solid State Electrochem., 2017, 21, 1939 CrossRef CAS.
- Y. Guo, S. Wu, Y.-B. He, F. Kang, L. Chen, H. Li and Q.-H. Yang, Solid-state lithium batteries: Safety and prospects, eScience, 2022, 2, 138 CrossRef.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier and M. Armand, et al., New horizons for inorganic solid state ion conductors, Energy Environ. Sci., 2018, 11, 1945 RSC.
- R. Usiskin, Y. Lu, J. Popovic, M. Law, P. Balaya, Y.-S. Hu and J. Maier, Fundamentals, status and promise of sodium-based batteries, Nat. Rev. Mater., 2021, 6, 1020 CrossRef CAS.
- H. Rickert, Solid ionic conductors: Principles and applications, Angew. Chem., Int. Ed., 1978, 17, 37 CrossRef.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Design principles for solid-state lithium superionic conductors, Nat. Mater., 2015, 14, 1026 CrossRef CAS PubMed.
- Y. Kato, S. Hori and R. Kanno, Li10GeP2S12-type superionic conductors: Synthesis, structure, and ionic transportation, Adv. Energy Mater., 2020, 10, 2002153 CrossRef CAS.
- R. Kim, L. J. Miara, J.-H. Kim, J.-S. Kim, D. Im and Y. Wang, Computational design and experimental synthesis of air-stable solid-state ionic conductors with high conductivity, Chem. Mater., 2021, 33, 6909 CrossRef CAS.
- H. Yang and N. Wu, Ionic conductivity and ion transport mechanisms of solid-state lithium-ion battery electrolytes: A review, Energy Sci. Eng., 2022, 10, 1643 CrossRef CAS.
- J. R. Macdonald, Impedance spectroscopy and its use in analyzing the steady-state ac response of solid and liquid electrolytes, J. Electroanal. Chem. Interfacial Electrochem., 1987, 223, 25 CrossRef CAS.
- P. Vadhva, J. Hu, M. J. Johnson, R. Stocker, M. Braglia, D. J. Brett and A. J. Rettie, Electrochemical impedance spectroscopy for all-solid-state batteries: Theory, methods and future outlook, ChemElectroChem, 2021, 8, 1930 CrossRef CAS.
- T. Geisel, A liquid-like picture for the interpretation of Raman scattering in superionic conductors, Solid State Commun., 1977, 24, 155 CrossRef CAS.
- J. Langer, D. Jimenez de Aberasturi, J. Aizpurua, R. A. Alvarez-Puebla, B. Auguié, J. J. Baumberg, G. C. Bazan, S. E. Bell, A. Boisen and A. G. Brolo, et al., Present and future of surface-enhanced Raman scattering, ACS Nano, 2019, 14, 28 CrossRef PubMed.
- C. G. Shull, Early development of neutron scattering, Rev. Mod. Phys., 1995, 67, 753 CrossRef CAS.
- B. S. Hudson, Vibrational spectroscopy using inelastic neutron scattering: Overview and outlook, Vib. Spectrosc., 2006, 42, 25 CrossRef CAS.
- T. Famprikis, J. A. Dawson, F. Fauth, O. Clemens, E. Suard, B. Fleutot, M. Courty, J.-N. Chotard, M. S. Islam and C. Masquelier, A new superionic plastic polymorph of the Na+ conductor Na3PS4, ACS Mater. Lett., 2019, 1, 641 CrossRef CAS.
- A. K. Sagotra, D. Chu and C. Cazorla, Influence of lattice dynamics on lithium-ion conductivity: A first-principles study, Phys. Rev. Mater., 2019, 3, 035405 CrossRef CAS.
- T. M. Brenner, C. Gehrmann, R. Korobko, T. Livneh, D. A. Egger and O. Yaffe, Anharmonic host-lattice dynamics enable fast ion conduction in superionic AgI, Phys. Rev. Mater., 2020, 4, 115402 CrossRef CAS.
- J. Ding, J. L. Niedziela, D. Bansal, J. Wang, X. He, A. F. May, G. Ehlers, D. L. Abernathy, A. Said, A. Alatas, Y. Ren, G. Arya and O. Delaire, Anharmonic lattice dynamics and superionic transition in AgCrSe2, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 3930 CrossRef CAS.
- M. K. Gupta, J. Ding, N. C. Osti, D. L. Abernathy, W. Arnold, H. Wang, Z. Hood and O. Delaire, Fast na diffusion and anharmonic phonon dynamics in superionic Na3PS4, Energy Environ. Sci., 2021, 14, 6554 RSC.
- G. Krenzer, C.-E. Kim, K. Tolborg, B. J. Morgan and A. Walsh, Anharmonic lattice dynamics of superionic lithium nitride, J. Mater. Chem. A, 2022, 10, 2295 RSC.
- M. Jansen, Volume effect or paddle-wheel mechanism—fast alkali-metal ionic conduction in solids with rotationally disordered complex anions, Angew. Chem., Int. Ed., 1991, 30, 1547 CrossRef.
- S. Hull, Superionics: crystal structures and conduction processes, Rep. Prog. Phys., 2004, 67, 1233 CrossRef CAS.
- Z. Zhang, P.-N. Roy, H. Li, M. Avdeev and L. F. Nazar, Coupled cation–anion dynamics enhances cation mobility in room-temperature superionic solid-state electrolytes, J. Am. Chem. Soc., 2019, 141, 19360 CrossRef CAS PubMed.
- Z. Xu and Y. Xia, Progress, challenges and perspectives of computational studies on glassy superionic conductors for solid-state batteries, J. Mater. Chem. A, 2022, 10, 11854 RSC.
- Z. Zhang and L. F. Nazar, Exploiting the paddle-wheel mechanism for the design of fast ion conductors, Nat. Rev. Mater., 2022, 7, 389 CrossRef.
- Z. Zhang, H. Li, K. Kaup, L. Zhou, P.-N. Roy and L. F. Nazar, Targeting superionic conductivity by turning on anion rotation at room temperature in fast ion conductors, Matter, 2020, 2, 1667 CrossRef.
- T. M. Brenner, M. Grumet, P. Till, M. Asher, W. G. Zeier, D. A. Egger and O. Yaffe, Anharmonic lattice dynamics in sodium ion conductors, J. Phys. Chem. Lett., 2022, 13, 5938 CrossRef CAS PubMed.
- Q. Ren, M. K. Gupta, M. Jin, J. Ding, J. Wu, Z. Chen, S. Lin, O. Fabelo, J. A. Rodríguez-Velamazán and M. Kofu, et al., Extreme phonon anharmonicity underpins superionic diffusion and ultralow thermal conductivity in argyrodite Ag8SnSe6, Nat. Mater., 2023, 22, 999–1006 CrossRef CAS PubMed.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Concerted migration mechanism in the Li ion dynamics of garnet-type Li7La3Zr2O12, Chem. Mater., 2013, 25, 425 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 15893 CrossRef CAS.
- J. Peng, Y. Liu, Y. Pan, J. Wu, Y. Su, Y. Guo, X. Wu, C. Wu and Y. Xie, Fast lithium ion conductivity in layered (Li–Ag)CrS2, J. Am. Chem. Soc., 2020, 142, 18645 CrossRef CAS PubMed.
- Z. Zou, N. Ma, A. Wang, Y. Ran, T. Song, Y. Jiao, J. Liu, H. Zhou, W. Shi and B. He, et al., Relationships between Na+ distribution, concerted migration, and diffusion properties in rhombohedral NASICON, Adv. Energy Mater., 2020, 10, 2001486 CrossRef CAS.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine learning force fields, Chem. Rev., 2021, 121, 10142 CrossRef CAS PubMed.
- N. Fedik, R. Zubatyuk, M. Kulichenko, N. Lubbers, J. S. Smith, B. Nebgen, R. Messerly, Y. W. Li, A. I. Boldyrev and K. Barros, et al., Extending machine learning beyond interatomic potentials for predicting molecular properties, Nat. Rev. Chem, 2022, 6, 653 CrossRef CAS PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547 CrossRef CAS PubMed.
- L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Data-driven materials science: Status, challenges, and perspectives, Adv. Sci., 2019, 6, 1900808 CrossRef PubMed.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, Neural network potential-energy surfaces in chemistry: a tool for large-scale simulations, Phys. Chem. Chem. Phys., 2011, 13, 17930 RSC.
- W. J. Szlachta, A. P. Bartók and G. Csányi, Accuracy and transferability of Gaussian approximation potential models for tungsten, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 104108 CrossRef.
- Z. Li, J. R. Kermode and A. De Vita, Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces, Phys. Rev. Lett., 2015, 114, 096405 CrossRef PubMed.
- H. Wang, L. Zhang, J. Han and E. Weinan, Deepmd-kit: A deep learning package for many-body potential energy representation and molecular dynamics, Comput. Phys. Commun., 2018, 228, 178 CrossRef CAS.
- L. Zhang, D.-Y. Lin, H. Wang, R. Car and E. Weinan, Active learning of uniformly accurate interatomic potentials for materials simulation, Phys. Rev. Mater., 2019, 3, 023804 CrossRef CAS.
- R. Jinnouchi, F. Karsai and G. Kresse, On-the-fly machine learning force field generation: Application to melting points, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- Z. Li, J. R. Kermode and A. De Vita, Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces, Phys. Rev. Lett., 2015, 114, 096405 CrossRef PubMed.
- T. K. Patra, V. Meenakshisundaram, J.-H. Hung and D. S. Simmons, Neural-network-biased genetic algorithms for materials design: Evolutionary algorithms that learn, ACS Comb. Sci., 2017, 19, 96 CrossRef CAS PubMed.
- T. L. Jacobsen, M. S. Jørgensen and B. Hammer, On-the-fly machine learning of atomic potential in density functional theory structure optimization, Phys. Rev. Lett., 2018, 120, 026102 CrossRef CAS PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phase transitions of hybrid perovskites simulated by machine-learning force fields trained on the fly with bayesian inference, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-fly active learning of interpretable bayesian force fields for atomistic rare events, npj Comput. Mater., 2020, 6, 20 CrossRef.
- K. Miwa and R. Asahi, Molecular dynamics simulations of lithium superionic conductor Li10GeP2S12 using a machine learning potential, Solid State Ionics, 2021, 361, 115567 CrossRef CAS.
- J. Huang, L. Zhang, H. Wang, J. Zhao and J. Cheng, et al., Deep potential generation scheme and simulation protocol for the Li10GeP2S12-type superionic conductors, J. Chem. Phys., 2021, 154, 094703 CrossRef CAS.
- C. G. Staacke, T. Huss, J. T. Margraf, K. Reuter and C. Scheurer, Tackling structural complexity in Li2S-P2S5 solid-state electrolytes using machine learning potentials, Nanomaterials, 2022, 12, 2950 CrossRef CAS PubMed.
- G. Winter and R. Gómez-Bombarelli, Simulations with machine learning potentials identify the ion conduction mechanism mediating non-arrhenius behavior in lgps, J. Phys.: Energy, 2023, 5, 024004 Search PubMed.
- Z. Xu, H. Duan, Z. Dou, M. Zheng, Y. Lin, Y. Xia, H. Zhao and Y. Xia, Machine learning molecular dynamics simulation identifying weakly negative effect of polyanion rotation on li-ion migration, npj Comput. Mater., 2023, 9, 105 CrossRef CAS.
- L. Gigli, D. Tisi, F. Grasselli and M. Ceriotti, Mechanism of charge transport in lithium thiophosphate, Chem. Mater., 2024, 36, 1482 CrossRef CAS PubMed.
- D. Tisi, F. Grasselli, L. Gigli, and M. Ceriotti, Thermal Transport of Li3ps_4 Solid Electrolytes with Ab Initio Accuracy, arXiv, 2024, preprint arXiv:2401.12936 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. Hafner, Ab-initio simulations of materials using vasp: Density-functional theory and beyond, J. Comput. Chem., 2008, 29, 2044 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, Descriptors representing two-and three-body atomic distributions and their effects on the accuracy of machine-learned inter-atomic potentials, J. Chem. Phys., 2020, 152, 234102 CrossRef CAS PubMed.
- A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems, Oxford University Press, 2006 Search PubMed.
- T. Krauskopf, S. Muy, S. P. Culver, S. Ohno, O. Delaire, Y. Shao-Horn and W. G. Zeier, Comparing the descriptors for investigating the influence of lattice dynamics on ionic transport using the superionic conductor Na3PS4−xSex, J. Am. Chem. Soc., 2018, 140, 14464 CrossRef CAS PubMed.
- T. Bernges, R. Hanus, B. Wankmiller, K. Imasato, S. Lin, M. Ghidiu, M. Gerlitz, M. Peterlechner, S. Graham and G. Hautier, et al., Considering the role of ion transport in diffuson-dominated thermal conductivity, Adv. Energy Mater., 2022, 12, 2200717 CrossRef CAS.
- L. Van Hove, Correlations in space and time and born approximation scattering in systems of interacting particles, Phys. Rev., 1954, 95, 249 CrossRef CAS.
- R. C. Hanson, T. A. Fjeldly and H. D. Hochheimer, Raman scattering from five phases of silver iodide, Phys. Status Solidi B, 1975, 70, 567 CrossRef CAS.
- J. L. Niedziela, D. Bansal, A. F. May, J. Ding, T. Lanigan-Atkins, G. Ehlers, D. L. Abernathy, A. Said and O. Delaire, Selective breakdown of phonon quasiparticles across superionic transition in cucrse2, Nat. Phys., 2019, 15, 73 Search PubMed.
- K. O'Sullivan, G. Chiarotti and P. A. Madden, Silver-ion disorder in α-AgI: A computer simulation study, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13536 CrossRef PubMed.
- G. E. Uhlenbeck and L. S. Ornstein, On the theory of the brownian motion, Phys. Rev., 1930, 36, 823 CrossRef CAS.
- A. Kvist and R. Tärneberg, Self-diffusion of silver ions in the cubic high temperature modification of silver iodide, Z. Naturforsch. A, 1970, 25, 257 CAS.
- W. Schommers, Correlations in the motion of particles in α-AgI: A molecular-dynamics study, Phys. Rev. Lett., 1977, 38, 1536 CrossRef CAS.
- L. Ranalli, C. Verdi, L. Monacelli, G. Kresse, M. Calandra and C. Franchini, Temperature-dependent anharmonic phonons in quantum paraelectric ktao3 by first principles and machine-learned force fields, Adv. Quantum Technol., 2023, 6, 2200131 CrossRef CAS.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. Rupp, Solid-state li–metal batteries: challenges and horizons of oxide and sulfide solid electrolytes and their interfaces, Adv. Energy Mater., 2021, 11, 2002689 CrossRef CAS.
- H.-P. Hong, Crystal structure and ionic conductivity of Li14Zn(GeO) and other new Li+ superionic conductors, Mater. Res. Bull., 1978, 13, 117 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, A lithium superionic conductor, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed.
- S. Adams and R. Prasada Rao, Structural requirements for fast lithium ion migration in Li10GeP2S12, J. Mater. Chem., 2012, 22, 7687 RSC.
- A. Kuhn, J. Köhler and B. V. Lotsch, Single-crystal x-ray structure analysis of the superionic conductor Li10GeP2S12, Phys. Chem. Chem. Phys., 2013, 15, 11620 RSC.
- A. Kuhn, V. Duppel and B. V. Lotsch, Tetragonal Li10GeP2S12 and Li7GePS8 – exploring the Li ion dynamics in LGPS Li electrolytes, Energy Environ. Sci., 2013, 6, 3548 RSC.
- O. Kwon, M. Hirayama, K. Suzuki, Y. Kato, T. Saito, M. Yonemura, T. Kamiyama and R. Kanno, Synthesis, structure, and conduction mechanism of the lithium superionic conductor Li10+δGe1+δP2−δS12, J. Mater. Chem. A, 2015, 3, 438 RSC.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-power all-solid-state batteries using sulfide superionic conductors, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- Y. Sun, K. Suzuki, K. Hara, S. Hori, T. aki Yano, M. Hara, M. Hirayama and R. Kanno, Oxygen substitution effects in Li10GeP2S12 solid electrolyte, J. Power Sources, 2016, 324, 798 CrossRef CAS.
- R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Synthesis of a new lithium ionic conductor, thio-LISICON–lithium germanium sulfide system, Solid State Ionics, 2000, 130, 97 CrossRef CAS.
- L. Ye, W. Fitzhugh, E. Gil-González, Y. Wang, Y. Su, H. Su, T. Qiao, L. Ma, H. Zhou, E. Hu and X. Li, Toward higher voltage solid-state batteries by metastability and kinetic stability design, Adv. Energy Mater., 2020, 10, 2001569 CrossRef CAS.
- R. Kanno and M. Murayama, Lithium ionic conductor thio-LISICON: The Li2S-GeS2-P2S5 system, J. Electrochem. Soc., 2001, 148, A742 CrossRef CAS.
- S. Nachimuthu, H.-J. Cheng, H.-J. Lai, Y.-H. Cheng, R.-T. Kuo, W. Zeier, B. Hwang and J.-C. Jiang, First-principles study on selenium-doped Li10GeP2S12 solid electrolyte: Effects of doping on moisture stability and li-ion transport properties, Mater. Today Chem., 2022, 26, 101223 CrossRef CAS.
- X. Wang, K. He, S. Li, J. Zhang and Y. Lu, Realizing high-performance all-solid-state batteries with sulfide solid electrolyte and silicon anode: A review, Nano Res., 2022, 16, 1 Search PubMed.
- M. Xu, J. Ding and E. Ma, One-dimensional stringlike cooperative migration of lithium ions in an ultrafast ionic conductor, Appl. Phys. Lett., 2012, 101, 031901 CrossRef.
- C. Donati, J. F. Douglas, W. Kob, S. J. Plimpton, P. H. Poole and S. C. Glotzer, Stringlike cooperative motion in a supercooled liquid, Phys. Rev. Lett., 1998, 80, 2338 CrossRef CAS.
- A. S. Keys, L. O. Hedges, J. P. Garrahan, S. C. Glotzer and D. Chandler, Excitations are localized and relaxation is hierarchical in glass-forming liquids, Phys. Rev. X, 2011, 1, 021013 Search PubMed.
- Y. Mo, S. Ong and G. Ceder, First principles study of the Li10GeP2S12 lithium super ionic conductor material, Chem. Mater., 2011, 24, 15–17 CrossRef.
- S. Hori, R. Kanno, O. Kwon, Y. Kato, T. Yamada, M. Matsuura, M. Yonemura, T. Kamiyama, K. Shibata and Y. Kawakita, Revealing the ion dynamics in li10gep2s12 by quasi-elastic neutron scattering measurements, J. Phys. Chem. C, 2022, 126, 9518 CrossRef CAS.
- K. Jun, Y. Sun, Y. Xiao, Y. Zeng, R. Kim, H. Kim, L. J. Miara, D. Im, Y. Wang and G. Ceder, Lithium superionic conductors with corner-sharing frameworks, Nat. Mater., 2022, 21, 924 CrossRef CAS PubMed.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- N. J. De Klerk and M. Wagemaker, Diffusion mechanism of the sodium-ion solid electrolyte Na3PS4 and potential improvements of halogen doping, Chem. Mater., 2016, 28, 3122 CrossRef CAS.
- H. Wang, Y. Chen, Z. D. Hood, G. Sahu, A. S. Pandian, J. K. Keum, K. An and C. Liang, An air-stable Na3SbS4 superionic conductor prepared by a rapid and economic synthetic procedure, Angew. Chem., Int. Ed., 2016, 55, 8551 CrossRef CAS PubMed.
- L. Zhang, D. Zhang, K. Yang, X. Yan, L. Wang, J. Mi, B. Xu and Y. Li, Vacancy-contained tetragonal Na3SbS4 superionic conductor, Adv. Sci., 2016, 3, 1600089 CrossRef PubMed.
- A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, A sodium-ion sulfide solid electrolyte with unprecedented conductivity at room temperature, Nat. Commun., 2019, 10, 5266 CrossRef CAS PubMed.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S.-T. Hong and Y. S. Jung, Na3SbS4: a solution processable sodium superionic conductor for all-solid-state sodium-ion batteries, Angew. Chem., Int. Ed., 2016, 55, 9634 CrossRef CAS PubMed.
- D. Zhang, X. Cao, D. Xu, N. Wang, C. Yu, W. Hu, X. Yan, J. Mi, B. Wen and L. Wang, et al., Synthesis of cubic Na3SbS4 solid electrolyte with enhanced ion transport for all-solid-state sodium-ion batteries, Electrochim. Acta, 2018, 259, 100 CrossRef CAS.
- T. Famprikis, H. Bouyanfif, P. Canepa, M. Zbiri, J. A. Dawson, E. Suard, F. Fauth, H. Y. Playford, D. Dambournet and O. J. Borkiewicz, et al., Insights into the rich polymorphism of the Na+ ion conductor Na3PS4 from the perspective of variable-temperature diffraction and spectroscopy, Chem. Mater., 2021, 33, 5652 CrossRef CAS PubMed.
- S.-H. Bo, Y. Wang, J. C. Kim, W. D. Richards and G. Ceder, Computational and experimental investigations of na-ion conduction in cubic na3pse4, Chem. Mater., 2016, 28, 252 CrossRef CAS.
- C. K. Moon, H.-J. Lee, K. H. Park, H. Kwak, J. W. Heo, K. Choi, H. Yang, M.-S. Kim, S.-T. Hong and J. H. Lee, et al., Vacancy-driven Na+ superionic conduction in new Ca-doped Na3PS4 for all-solid-state na-ion batteries, ACS Energy Lett., 2018, 3, 2504 CrossRef CAS.
- I.-H. Chu, C. S. Kompella, H. Nguyen, Z. Zhu, S. Hy, Z. Deng, Y. S. Meng and S. P. Ong, Room-temperature all-solid-state rechargeable sodium-ion batteries with a cl-doped Na3PS4 superionic conductor, Sci. Rep., 2016, 6, 33733 CrossRef CAS PubMed.
- X. Feng, P.-H. Chien, Z. Zhu, I.-H. Chu, P. Wang, M. Immediato-Scuotto, H. Arabzadeh, S. P. Ong and Y.-Y. Hu, Studies of functional defects for fast na-ion conduction in Na3−yPS4−xClx with a combined experimental and computational approach, Adv. Funct. Mater., 2019, 29, 1807951 CrossRef.
- R. Jalem, B. Gao, H.-K. Tian and Y. Tateyama, Theoretical study on stability and ion transport property with halide doping of Na3SbS4 electrolyte for all-solid-state batteries, J. Mater. Chem. A, 2022, 10, 2235 RSC.
- T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, Defect-mediated conductivity enhancements in Na3−xPn1−xWxS4 (Pn=P, Sb) using aliovalent substitutions, ACS Energy Lett., 2019, 5, 146 CrossRef.
- X. Feng, H. Fang, P. Liu, N. Wu, E. C. Self, L. Yin, P. Wang, X. Li, P. Jena and J. Nanda, et al., Heavily tungsten-doped sodium thioantimonate solid-state electrolytes with exceptionally low activation energy for ionic diffusion, Angew. Chem., Int. Ed., 2021, 60, 26158 CrossRef CAS PubMed.
- L. E. Rush Jr, Z. D. Hood and N. Holzwarth, Unraveling the electrolyte properties of Na3SbS4 through computation and experiment, Phys. Rev. Mater., 2017, 1, 075405 CrossRef.
- T. Krauskopf, S. P. Culver and W. G. Zeier, Local tetragonal structure of the cubic superionic conductor Na3PS4, Inorg. Chem., 2018, 57, 4739 CrossRef CAS PubMed.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. S. Jaakkola, Forces are not enough: Benchmark and critical evaluation for machine learning force fields with molecular simulations, Trans. Mach. Learn. Res, 2023, https://openreview.net/forum?id=A8pqQipwkt Search PubMed.
- W. Pronobis, A. Tkatchenko and K.-R. Müller, Many-body descriptors for predicting molecular properties with machine learning: Analysis of pairwise and three-body interactions in molecules, J. Chem. Theory Comput., 2018, 14, 2991 CrossRef CAS PubMed.
- A. Grisafi and M. Ceriotti, Incorporating long-range physics in atomic-scale machine learning, J. Chem. Phys., 2019, 151, 204105 CrossRef PubMed.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer, Nat. Commun., 2021, 12, 398 CrossRef CAS PubMed.
- O. T. Unke, S. Chmiela, M. Gastegger, K. T. Schütt, H. E. Sauceda and K.-R. Müller, Spookynet: Learning force fields with electronic degrees of freedom and nonlocal effects, Nat. Commun., 2021, 12, 7273 CrossRef CAS PubMed.
- A. Kabylda, V. Vassilev-Galindo, S. Chmiela, I. Poltavsky and A. Tkatchenko, Efficient interatomic descriptors for accurate machine learning force fields of extended molecules, Nat. Commun., 2023, 14, 3562 CrossRef CAS PubMed.
- A. Cui, K. Jiang, M. Jiang, L. Shang, L. Zhu, Z. Hu, G. Xu and J. Chu, et al., Decoding phases of matter by machine-learning Raman spectroscopy, Phys. Rev. Appl., 2019, 12, 054049 CrossRef CAS.
- Q. Liang, S. Dwaraknath and K. A. Persson, High-throughput computation and evaluation of Raman spectra, Sci. Data, 2019, 6, 135 CrossRef PubMed.
- N. Sheremetyeva, M. Lamparski, C. Daniels, B. Van Troeye and V. Meunier, Machine-learning models for Raman spectra analysis of twisted bilayer graphene, Carbon, 2020, 169, 455 CrossRef CAS.
- M. Bagheri and H.-P. Komsa, High-throughput computation of Raman spectra from first principles, Sci. Data, 2023, 10, 80 CrossRef CAS PubMed.
- Y. Qi, D. Hu, Y. Jiang, Z. Wu, M. Zheng, E. X. Chen, Y. Liang, M. A. Sadi, K. Zhang and Y. P. Chen, Recent progresses in machine learning assisted Raman spectroscopy, Adv. Opt. Mater., 2023, 2203104 CrossRef CAS.
- A. Putrino and M. Parrinello, Anharmonic Raman spectra in high-pressure ice from ab initio simulations, Phys. Rev. Lett., 2002, 88, 176401 CrossRef PubMed.
- M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Computing vibrational spectra from ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2013, 15, 6608 RSC.
- E. Ditler and S. Luber, Vibrational spectroscopy by means of first-principles molecular dynamics simulations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1605 CAS.
- N. Raimbault, A. Grisafi, M. Ceriotti and M. Rossi, Using Gaussian process regression to simulate the vibrational Raman spectra of molecular crystals, New J. Phys., 2019, 21, 105001 CrossRef CAS.
- G. M. Sommers, M. F. C. Andrade, L. Zhang, H. Wang and R. Car, Raman spectrum and polarizability of liquid water from deep neural networks, Phys. Chem. Chem. Phys., 2020, 22, 10592 RSC.
- H. Shang and H. Wang, Anharmonic Raman spectra simulation of crystals from deep neural networks, AIP Adv., 2021, 11, 035105 CrossRef CAS.
- R. Han, R. Ketkaew and S. Luber, A Concise Review on Recent Developments of Machine Learning for the Prediction of Vibrational Spectra, J. Phys. Chem. A, 2022, 126(6), 801–812 CrossRef CAS PubMed.
- E. Berger and H.-P. Komsa, Polarizability Models for Simulations of Finite Temperature Raman Spectra from Machine Learning Molecular Dynamics, arXiv, 2023, preprint, arXiv:2310.13310 Search PubMed.
- M. Grumet, C. von Scarpatetti, T. Bučko, and D. A. Egger, Delta machine learning for predicting dielectric properties and Raman spectra, arXiv, 2023, Preprint, arXiv:2307.10578 Search PubMed.
- A. M. Lewis, P. Lazzaroni and M. Rossi, Predicting the electronic density response of condensed-phase systems to electric field perturbations, J. Chem. Phys., 2023, 159, 014103 CrossRef CAS PubMed.
- A. M. Nolan, Y. Zhu, X. He, Q. Bai and Y. Mo, Computation-accelerated design of materials and interfaces for all-solid-state lithium-ion batteries, Joule, 2018, 2, 2016 CrossRef CAS.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Materials design of ionic conductors for solid state batteries, Prog. Energy, 2020, 2, 022001 CrossRef.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 624, 80 CrossRef CAS PubMed.
- K. Fujimura, A. Seko, Y. Koyama, A. Kuwabara, I. Kishida, K. Shitara, C. A. Fisher, H. Moriwake and I. Tanaka, Accelerated materials design of lithium superionic conductors based on first-principles calculations and machine learning algorithms, Adv. Energy Mater., 2013, 3, 980 CrossRef CAS.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Machine learning-assisted discovery of solid li-ion conducting materials, Chem. Mater., 2018, 31, 342 CrossRef.
- S. Muy, J. Voss, R. Schlem, R. Koerver, S. J. Sedlmaier, F. Maglia, P. Lamp, W. G. Zeier and Y. Shao-Horn, High-throughput screening of solid-state Li-ion conductors using lattice-dynamics descriptors, Iscience, 2019, 16, 270 CrossRef CAS PubMed.
- L. Kahle, A. Marcolongo and N. Marzari, High-throughput computational screening for solid-state Li-ion conductors, Energy Environ. Sci., 2020, 13, 928 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of the MLFF theory; detailed numerical parameters and settings for AIMD and MLMD simulations; additional figures on the analysis of force error, as well as of structural and dynamical SSIC properties. See DOI: https://doi.org/10.1039/d4ta00452c |
| This journal is © The Royal Society of Chemistry 2024 |