Open Access Article
Open Access ArticleSurface termination dependent carbon dioxide reduction reaction on Ti3C2 MXene†
Ling
Meng
 ab,
Li-Kai
Yan
ab,
Li-Kai
Yan
 *b,
Francesc
Viñes
*b,
Francesc
Viñes
 *a and
Francesc
Illas
*a and
Francesc
Illas
 a
a
aDepartament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, c/ Martí i Franquès 1-11, 08028, Barcelona, Spain. E-mail: francesc.vines@ub.edu
bInstitute of Functional Material Chemistry, Key Laboratory of Polyoxometalate Science of Ministry of Education, Faculty of Chemistry, Northeast Normal University, Changchun 130024, P. R. China. E-mail: yanlk924@nenu.edu.cn
First published on 15th February 2024
Abstract
The use of two-dimensional (2D) MXene materials as highly efficient electrocatalysts for the carbon dioxide reduction reaction (CO2RR) has gained considerable attention in the last few years. However, current computational studies on the CO2RR are primarily focused on MXene materials with different types of metals or displaying fully –O or –OH terminated surfaces, which fail to account for the fact that as-synthesized MXenes possess mixtures of –O, –OH, –F, and/or –H surface groups. Here, a comprehensive density functional theory (DFT) study is carried out on the stability and impact of different surface terminations and moiety distributions on CO2RR performance done on the prototype Ti3C2 MXene, analyzing the possible electrocatalytic synthesis of a series of CO2RR products, from CO to H2CO, HCOOH, CH3OH, and CH4 under favorable low pH and potential, U, reaction conditions, while considering the competitive H2 evolution reaction (HER). From ca. 450 distinct surface terminations, four F-free models are selected as dominant in Pourbaix surface stability diagrams under low pH and U conditions, namely –OH, –OH2/3O1/3, –OH1/2O1/2, and –OH1/3O2/3, and one F-containing model, –F1/3OH1/3O1/3. Results highlight the participation of surface –OH groups as H-donors, and the benefits of simultaneous hydrogenation from proton reduction and –OH H transfer. In addition, the presence of both –OH and –O groups is beneficial, reducing limiting potential, UL, costs, as experimentally observed. On the –F1/3OH1/3O1/3 model, the presence of –F is per se non-detrimental, moving the limiting step to an early stage and reducing the UL. The overall results underscore the competitiveness of MXenes in the CO2RR with respect to a Cu electrocatalyst reference, and the tunability possibilities to maximize the selectivity towards either the CO2RR or the HER.
1. Introduction
With the steadily growing use of fossil fuels, carbon dioxide (CO2) emissions have increased to a worrying exceedingly high level. One of the major issues facing nowadays society is climate change and the ultra-high energy prices, recently highlighted by the impressive European energy crisis in the winter of 2022.1 Thus, the exploitation of new energy sources is crucial to avoid such energy constrains, where one very appealing way is to use carbon dioxide (CO2) emissions as a C1 chemical source, turning CO2 economy into a waste-to-product model, and, by that, contributing to a carbon-neutral cycle.2 For this, carbon reduction technologies are key, one of which is the use of electrocatalytic CO2 reduction reaction (CO2RR) to convert it into other useful chemicals and fuels. Most of these processes imply hydrogenation reactions, and the full technology can be thought as green when powered by renewable energy sources, such as solar and wind power, and when the used hydrogen (H2) is produced in the same way.3–6So far, despite receiving widespread attention from both theoretical and experimental research communities,7–9 the CO2RR is yet not widely implemented on an industrial scale due to multiple reasons, main ones being its cost and the low reaction activity reached by present catalysts, implying that novel and/or costly materials are needed, often accompanied by slow reaction kinetics, which altogether increases the process price and efficiency.10,11 In addition to the aforementioned factors, achieving high levels of selectivity, stability, and durability is still a critical challenge in the field of the CO2RR.12 Over the last few years, extensive research endeavours have been focused on countless catalysts, including both non-precious metal13,14 and non-metal catalysts.15,16 Among them, Cu-based heterogeneous catalysts have attracted much attention due to their ability to convert CO2 to abundant multi-carbon products, such as hydrocarbons and alcohols, while being accessible in cost.17,18 However, using these catalysts, the formation of methane (CH4), the main component of biogas, still starts at potentials ranging from −0.9 V to −1.1 V vs. the reversible hydrogen electrode (RHE).19,20 In addition, their low reaction kinetics has been found to be influenced by limitations arising from linear scaling relations between reaction intermediate binding energies, translated in a restricted stability of adsorbed carbon monoxide (CO), i.e. CO*, and similar reaction intermediates such as CHO*, which eventually leads to a reduced activity.21,22 Thus, the quest for new cost-effective CO2RR catalysts with less negative potentials is still open.
In this context, MXenes, few-layered transition metal carbides and/or nitrides, have arisen as an attractive family of materials for the CO2RR, given their superior conductivity and hydrophilicity, making them very promising catalysts for this purpose.23 MXenes are two-dimensional (2D) materials with Mn+1XnTx general chemical formula, where M denotes an early transition metal, X generally represents C and/or N, Tx denotes the surface functional group, intrinsic to the MXene synthesis procedure, and n normally ranges from 1 to 3,24–26 although MXenes with n = 4 have been already reported.27 MXenes are normally gained by selective etching from precursor MAX phases, where A, normally a p-element like Al or Si, is removed using a hydrofluoric acid (HF) solution,28 although in situ HF can be used admixing lithium fluoride (LiF) with hydrochloric acid (HCl).29 With these methods, a mixture of –O, –H, –OH, and –F of terminations is gained.30,31 Still, the type and quantity of such terminations are highly sensitive to synthesis conditions such as etching time, temperature, or HF concentration.32,33 For instance, high concentrations of HF lead to a larger number of –F terminations, while when lower HF concentrations are used more –O species are found.31,34 On top of that, successful F-free synthesis protocols have been reported,35 even cleaning protocols36 or new synthetic routes37 to acquire Tx-free MXenes and even tune the Tx with many other terminations. In short, all this casuistry can be used to design MXenes to suit specific applications, playing with composition, size, and surface termination.38
Focusing back on the CO2RR, recently Li et al.39 computationally screened bare M3C2 (groups IV, V, and VI) MXenes for the CO2RR by density functional theory (DFT) means, predicting Cr3C2 and Mo3C2 as most promising candidates, with limiting potentials of −1.05 and −1.31 V to form CH4. Handoko et al.40 and Chen et al.41 accounted for surface termination exploring –O and –OH moieties, respectively, finding that O-terminated MXenes can enhance the stability of reaction intermediates by coordinating hydrogen atoms, while OH-terminated MXenes display a high reactivity owing to the already presence of hydrogen atoms. As a result, the catalysts exhibited a lower overpotential and challenged the traditional scaling relationships, while simultaneously establishing new ones. Recently, Handoko et al.42 also experimentally reported that the CO2RR activity of Ti2CTx is related to the proportion of surface –F and –O moieties, in the sense that a higher amount of –F leads to a lower activity and selectivity. Note that C2 coupling is also a current research focus, although the use of pure MXene is still a challenge, and most of the recent approaches dealt with defect engineering or heterostructures,43,44 a common strategy to boost the CO2RR to C2,45 like using Cu or Fe transition metal single atoms on Ti3C2Tx or Mo2C, respectively,46,47 or dioxygen vacancies on Mo2TiC2O2.48 The focus here is on non-modified MXenes, and, therefore, on C1 products. Despite the numerous DFT investigations on bare or fully terminated MXenes, there is still a lack of analysis under realistic conditions, hindering the correlation between theoretical simulations and experimental results. Therefore, further comprehensive studies are required to finally elucidate and comprehend CO2RR performance on MXenes.
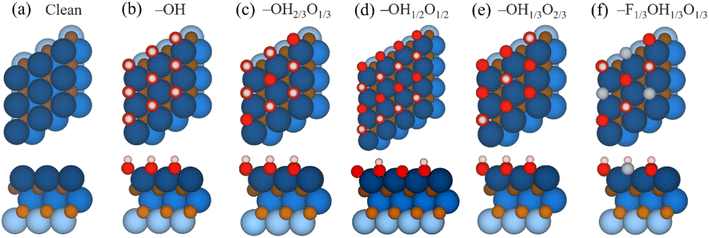
This is tackled here taking the paradigmatic Ti3C2 MXene as a case study. This material, first synthesized in 2011,49 is considered a MXene prototype, being the target of extensive research and development, and currently the most well-studied and mature MXene material.50 Here we systematically analyze, by first-principles based calculations, the CO2RR performance on Ti3C2 MXene with four different but realistic terminations in specific ranges of pH and potential, U, based on a surface stability assessment using computational Pourbaix diagrams51,52 created by considering about 450 different surface terminations with different combinations of surface species.53 By using these suited models, we gain valuable and detailed insights into the CO2RR process under realistic working conditions, highlighting (i) the CO2 activation capacity of the selected models considering the working temperature, T, and CO2 partial pressure, pCO2, (ii) that the presence of –F species is unavoidable under acidic conditions when the MXene is extracted using fluorinated solvents, (iii) that, contrary to previous studies,41,54,55 the fully –OH or –O terminated MXene models are challenged at less negative potentials, while MXene with mixed terminations would be more realistic CO2RR electrocatalytic models under such conditions, with (iv) a new CO2RR mechanism involving these termination groups in the hydrogenation steps, while (v) the presence of –F groups is found to be inherently not only non-detrimental, but to positively contribute when the surface coverage is limited, so that finally (vi) Ti3C2 with a stable ternary mixture containing –O and –OH groups with a small amount of –F exhibits one of the lowest bias-demanding CO2RR, even if fully –OH terminated is, a priori, more selective, all in all showing that (vii) MXenes are, in general, improved electrocatalysts with respect to the usual Cu-electrocatalyst reference.
2. Theoretical aspects
2.1. Computational details
All the presented periodic DFT calculations were carried out using the Vienna ab initio simulation package (VASP).56 The generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional57 was used, accurately suited in the description of MXenes energetics.58–60 Additionally, Grimme's D3 approach was included to account for dispersive force interactions.61 The core electron density and its impact on the valence electron density were described using the projector augmented wave (PAW) method developed by Blöchl,62 as implemented by Kresse and Joubert.63 Besides, the valence electron density was expanded on a plane wave basis set with a cutoff kinetic energy of 415 eV, high enough to acquire total energies converged below the chemical accuracy of 1 kcal mol−1, ca. 0.04 eV,64 the same order of accuracy obtained when performing test calculations using an implicit solvent model65 and thus found to be not required in the oncoming discussion.Different supercell models were used in the construction of Pourbaix diagrams, in particular, p(2×2) and p(3×3) supercells of Ti3C2, where a full monolayer (ML) coverage is defined as having one surface moiety per each surface metal atom. The p(2×2) supercell was used to evaluate the pristine, fully –O, –OH, –H, and –F covered Ti3C2, as well as mixed cases with ½ ML vs. ½ ML, ¼ vs. ¾ of a ML binary coverage, and ¼, ¼, and ½ of a ML ternary situation, while the p(3×3) supercell was employed to investigate binary situations with ⅓ vs. ⅔ coverage, as well as ternary situations with an equal coverage of each component. For reaction mechanism evaluation, p(3×3) or p(4×4) supercells were used. A 20 Å vacuum was added to the slab models to ensure their appropriate isolation, while the Brillouin zone was sampled using an optimal 5×5×1 k-point Γ-centered Monkhorst–Pack grid,66 achieving as well the aforementioned chemical accuracy.
During the structural optimization, a convergence criterion of 10−5 eV was used for the electronic self-consistent field steps, while atomic positions were relaxed until forces acting on atoms were below 0.01 eV Å−1. Unless stated otherwise, all calculations were carried out spin polarized. The vibrational frequencies of the reaction surface species minima were determined by constructing and diagonalizing the Hessian matrix using finite differences of 0.03 Å in length to evaluate the analytical gradients,67,68 yet only atomic displacements on the adsorbed species and terminations were considered, while substrate atoms were held fixed, i.e. a decoupling of surface species with the material phonons was assumed.
2.2. Surface Pourbaix diagrams
The purpose of constructing a Pourbaix diagram in this study is to identify the most thermodynamically stable surface termination of the Ti3C2 MXene under the realistic working conditions of pH and U during the CO2RR. Details can be found in previous work,53 but still let us briefly explain the procedure here. Initially, a systematic sampling approach was employed to explore various high-symmetry adsorption sites for each studied termination, as illustrated in Fig. S1 of the ESI,† revealing that the HTi site was consistently the most favorable site for adsorption of any of the Tx surface terminations. This information was used to optimize and gain the free-energy of different surface terminations, either with single moieties, or with ratios in mixed situations, all as a function of the applied electrode potential, U, and pH, using to this end the computational hydrogen electrode (CHE) approach.69 Note that diverse distributions of functional groups were accounted for, encompassing both highly regular and irregular arrangements. To account for the number of electrons (e−), protons (H+) and fluorine ions (F−) involved during the adsorption processes, the stoichiometric coefficients ν(e−), ν(H+), and ν(F−) were considered when constructing the reaction formation free energy equations required for the Pourbaix diagrams,70 as;ΔG(pH, U) = ΔG(0, 0) − υ(H+)kBT × ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × pH − υ(e−)eU − υ(F−)eUF, 10 × pH − υ(e−)eU − υ(F−)eUF, | (1) |
Ideally, for the CO2RR, one would pursue situations with a minimal negative potential, and with low pH, in order to prompt the reaction kinetics. Thus, taking into account the potential working conditions of T = 298.15 K, pH2 = 1 bar, pH < 4, and an improved applied potential U range of −0.75 V < U < 0 V, as commonly used in the CO2RR towards CH4 using MXene-based electrocatalysts,39–42,74 the most suitable and realistic Ti3C2Tx models were F-free OH2/3O1/3, OH1/2O1/2, OH1/3O2/3, and fully OH-terminated, as well as the F-containing F1/3OH1/3O1/3, as illustrated in Fig. S2 of the ESI.† Already at this stage, one should notice how mixed situations are more the rule than the exception, and that fully OH-terminated models would be realistic only at low potentials, while O-terminated models would not be accurate situations for the CO2RR. However, one must advert that most of the previous literature on MXenes focused on bare or fully O-terminated MXenes,75,76 with only a limited number of studies considering –OH termination, and only Chen et al.41 regarded the involvement of H atoms from the –OH termination in the CO2RR.
2.3. CO2RR mechanism
In general, the first step of CO2 reduction is its adsorption from the gas phase, CO2(g), on a catalyst free surface site (*);| CO2(g) + * → CO2*. | (2) |
After this sine qua non step, the rest of the reaction mechanism would imply proton-coupled electron transfer (PCET) steps, where protons, H+, and electrons, e−, are sequentially added. The full reduction of adsorbed CO2 to adsorbed CH4* and water (H2O*) requires eight PCET electrochemical steps,77 as:
| CO2* + 8H+ + 8e− + * → CH4* + 2H2O*, | (3) |
| CH4* + 2H2O* → 2* + CH4(g) + 2H2O(l). | (4) |
For convenience, most of the earlier studies assumed that, for any precursor adsorbed species, A*, its reduction is done in a single elementary reaction, where one H+ and one electron e− are directly involved in producing AH*, as:
| A* + H+ + e- → AH*. | (5) |
However, we here contemplated as well the possible involvement of termination –OH groups as a hydrogen source. Thus, for instance, in the presence of –OH surface moieties, the A* could be hydrogenated from the –OH group, as:
| A* + –OH → AH* + –O, | (6) |
| –O + H+ + e- → –OH. | (7) |
Notice as well that, thus, –O terminations could be reducing sites for medium H+, which would act as a reservoir. According to this, one could elaborate an alternative path, where H+ is reduced on a –O site, as in eqn (7), and in a later step, the as-formed –OH could be involved in the chemical hydrogenation of A* species, as in eqn (6). These different ordering pathways have been contemplated here, to gain a more complete understanding and involvement of surface terminations in the course of the CO2RR and the followed mechanism.53
2.4. Thermodynamic approach
To outline the reaction mechanisms, a thermodynamic approach, as extendedly used in previous studies, has been used.78,79 It implies that only the difference in Gibbs free energies between the different reaction intermediate states are relevant, and so used in determining the necessary limiting potential, UL, for the reaction to take place. This succinctly implies that any PCET step features a latest transition state when endergonic, and an earliest transition state when exergonic, although a proportionality could be expected when the system under study follows the Brønsted–Evans–Polanyi (BEP) relationships.80,81 Notice, still, that approaches are available to account for the transition states in the course of the reaction,82,83 yet here, for comparative purposes with earlier studies,84–86 they have not been accounted for.The first step in outlining the reaction free energy profiles is to estimate the total adsorption energies of the intermediate species, ΔEiads, so that
| ΔEiads = Ei/sub − (Esub + Ei). | (8) |
When addressing the reaction ΔG calculations, one has to keep in mind that, by using the above-mentioned CHE reference,69 under the standard equilibrium conditions of pH = 0, U = 0 V, a temperature T of 298.15 K, and a partial pressure of H2, pH2, of 1 bar, the chemical potential of a pair of H+ and e− can be related to that of H2 at 0 V vs. the SHE, so that
| H(aq)+ + e− → ½ H2(g); ΔG° = 0 eV, | (9) |
| ΔG = ΔE + ΔEZPE − TΔS, | (10) |
| ΔE = EAH* − EA* − ½ EH2. | (11) |
Similarly, the ΔEZPE term can be gained as:
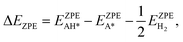 | (12) |
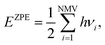 | (13) |
| ΔS = SAH∗ − SA∗ − ½SH2. | (14) |
The entropy of gas phase molecules has been obtained from the National Institute of Standards and Technology (NIST) webbook,87 while for the adsorbed moieties, only the vibrational entropy (Svib) is considered due to the ground state character and the hindrance of translations and rotations upon adsorption.88 Thus, for adsorbed species, one has:
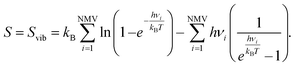 | (15) |
Given the reaction Gibbs free energy profiles, one can assess the reaction limiting potential, UL, defined as the minimum potential required for a specific electrochemical reaction to occur spontaneously under given reaction conditions. In the case of the CO2RR, UL would be the potential at which each elementary electrochemical hydrogenation step becomes exergonic, indicating the minimum energy input required for the reaction to proceed. The descriptor ΔGmax, a free-energy model extracting the largest free-energy difference between intermediate states of an elementary step at a given target electrode potential, is used to quantify limiting potential for the CO2RR, as
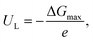 | (16) |
2.5. Adsorption/desorption rates
Apart from the previous thermodynamic approach, it is worth keeping in mind that CO2 adsorption must occur under the reaction conditions, while ideally a product such as CH4 should desorb easily. This can be tackled here by profiling kinetic phase diagrams as used in the past.89,90 In this approach, the molecule adsorption rate is compared to its desorption rate at different T and molecular partial pressures, finding turning points where adsorption and desorption rates are equal, i.e. equilibrium points. For the adsorption rate, rads, one can use non-activated collision theory,91 such as: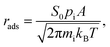 | (17) |
To estimate the desorption rates, rdes, transition state theory (TST)94 is used assuming that the desorbed transition state (TS) is a late two-dimensional (2D) TS. In this case, the energy barrier is given by the desorption energy, ΔEdes, which is simply the negative of the adsorption energy, ΔEdes, here without ZPE, as this term is already accounted for in the vibrational partition function, see below. Thus, rdes is defined as:
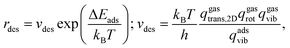 | (18) |
The vdes prefactor is obtained from various partition functions, q, including qgastrans,2D, qgasrot, and qgasvib, which refer to the 2D translational, the rotational, and the vibrational partition functions, respectively, defined as
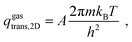 | (19) |
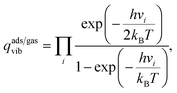 | (20) |
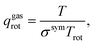 | (21) |
3. Results and discussion
3.1. MXene models, CO2 activation, and CH4 physisorption
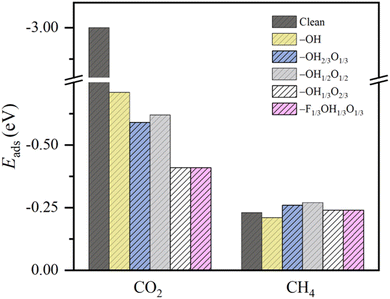
The CO2RR species have been optimized on the five considered surface-terminated Ti3C2Tx models as depicted in Fig. 1, in turn derived from Pourbaix diagrams shown in Fig. S2 of the ESI.† Notice that according to their density of states (DOS) and projected DOS (PDOS), all models exhibit a metallic character, and generally with a large number of states at the Fermi energy, see Fig. S3 of the ESI,† which is a prerequisite for electrocatalysis, cf. ref. 47. One of the first aspects to tackle is whether CO2 is attached and activated on such terminations. According to Le Sabatier principle,98 CO2 should moderately adsorb, enough to remain not strongly bound to prevent catalyst poisoning, yet not weakly enough to enable sufficient opportunities for its chemical bond breaking.99 On the other hand, a product such as CH4 should also moderately adsorb, enough to permit its release, and, more importantly, not too strongly, to avoid the self-poisoning of the electrocatalyst by the methane product.In order to investigate the interaction between CO2 and the chosen surface-terminated Ti3C2Tx models, various adsorption sites were examined in a systematic fashion, taking into account the interaction with respect to different surface moieties (cf. Fig. S4a of the ESI†) and CO2 orientations (cf. Fig. S4b of the ESI†), including vertical orientations, but also planar situations with different molecular orientations. This systematic procedure, here exemplified on CO2, has been carried out for the rest of the reaction species and intermediates, with energy minima structures duly characterized by frequency analysis. The adsorptive configurations are shown in Fig. 2, and comparative adsorption energies in Fig. 3. As can be seen, generally CO2 keeps its linear geometry on any explored surface termination, except for the full –OH termination, where the molecule has an Eads of −0.71 eV, gets bent by 135.9°, negatively charged by 0.80 e, and with a mean bond elongation of C–O bonds by 1.25 Å, in full accordance with CO2 being activated.100,101 Clearly, the presence of surface –O groups is detrimental to activating CO2, and only on fully –OH terminated MXene, the negatively charged CO2, with charge mostly present on its O atoms, is stabilized with the slightly positively charged H atoms of surface –OH groups, see Fig. 2, with Bader charges of −0.73e, and it is also observed with the –OH group H charge depletion shown in the charge density difference (CDD) plots, see Fig. S5 of the ESI.†,53
 | ||
| Fig. 2 Top views of optimal CO2 adsorption sites on the Ti3C2 MXene model (0001) surface with (a) a clean surface, (b) full –OH, (c) –OH2/3O1/3, (d) –OH1/2O1/2, (e) –OH1/3O2/3, and (f) –F1/3OH1/3O1/3 terminations. Colour coding as in Fig. 1, with CO2 C and O atoms shown as orange and pink spheres, respectively. | ||
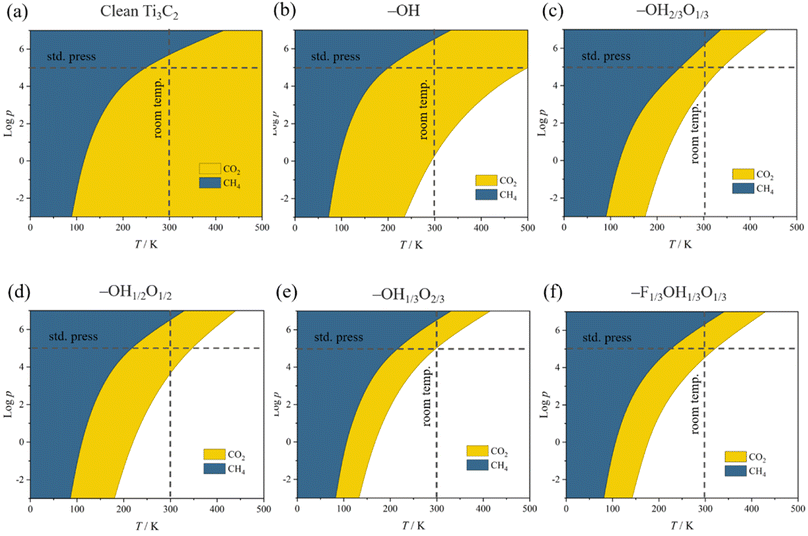
This behavior contrasts with, e.g. CH4 adsorption energies, see Fig. 3, where methane is physisorbed in any surface model, with Eads ranging −0.21 to −0.27 eV. Here, actually, the presence of –O groups is slightly beneficial, allegedly forming H bonds with those of CH4. Curiously, the stronger affinity towards CO2 compared to CH4 is in line with previous reports on pristine, surface termination free MXenes, as reported in the literature,102 where such values were used to estimate CO2 and CH4 adsorption and desorption rates in the context of biogas upgrading. Note that the adsorption energies for both CO2 and CH4 are coincidental on –OH1/3O2/3 and –F1/3OH1/3O1/3 models, since they belong to very similar local environments. Analogously, we estimated such adsorption/desorption rates as explained above, see Fig. S6 of the ESI,† in order to generate the so-called kinetic phase diagrams, present in Fig. 4.
Briefly, there, depending on the working conditions of temperature, T, and gases pressure, p, one can estimate the preference of the surfaces in adsorbing (or desorbing) such species. From them, it is evident that, e.g., working at 300 K and 1 bar pressure, all surface models are favourable for attaching the CO2 reactant, a premise of the reaction that is met. Moreover, the release of the eventual CH4 product would be favoured in any explored model even in an atmosphere of 1 bar of CH4, according to the kinetic phase diagrams of Fig. 4, a sought-after feature of a working electrocatalyst which underlies that no CH4 self-poisoning is envisaged on such MXene models. From all the surface-terminated studied models, the fully –OH terminated model exhibits the strongest CO2 adsorption and CH4 desorption capabilities, while, as the surface concentration of –OH moiety decreases, these differences gradually diminish. Furthermore, when –F is present, as in –F1/3OH1/3O1/3, similar kinetic phase diagrams are gained compared to –OH2/3O1/3, implying, to some extent, a similar role of both –OH and –F groups, with similar charges of ca. −1 e, and comparable electric fields.
3.2. CO2RR electrocatalysis mechanisms
After having established the suited surface-terminated MXene models for CO2RR conditions, and the CO2 and CH4 adsorptive/desorptive conditions, the electrocatalytic performance is put under the inspection light, depicting the Gibbs free energy landscapes under standard working conditions, T = 298.15 K, pH2 = 1 bar, pH = 0, and U = 0 V, to extract from them the limiting potential, UL, as the main indicator of the electrocatalytic performance, yet the H-vacancy energetic cost, EHvac, is also used here to discuss the ease of Tx trapping H adatoms from surface –OH groups, defined as| EHvac = ETx-H + ½EH2 − ETx, | (22) |
Let us begin the analysis with the highly active –OH surface termination, as observed with the high affinity towards CO2, see Fig. 4. This affinity prompts the formation of stable HCO2* during the CO2 adsorption involving a H atom from a surface –OH group, being more stable by 2.22 eV, see Fig. 5, and energetically preferred over the direct electrochemical hydrogenation of CO2 over an otherwise untouched –OH surface termination. It is mandatory here to note that the H transfer from the –OH group is spontaneous, and not artificial, neither in the –OH surface termination nor in the other models, as several attempts were made to prevent it. Thus, it is apparent that the resulting moiety is quite stable, and that drives the H transfer from neighboring –OH due to their proximity. Once HCO2* is formed in a chemical step, the attention is driven towards the first PCET electrochemical step, finding that hydrogenation at the C atom is most favorable, H2CO hydrogenation at the O atom implies at least a ΔG of 1.89 eV, yet stabilizing the system by only 0.04 eV. This step spontaneously draws two more surface H atoms from two vicinal –OH groups, forming a H2C(OH)2 compound, i.e. methanediol or methylene glycol. In the second PCET, the involvement of one –OH in the methylene glycol synthesis is then reverted so that hydrogenation of the as-formed surface –O group back to –OH proceeds with a ΔG of 0.73 eV.
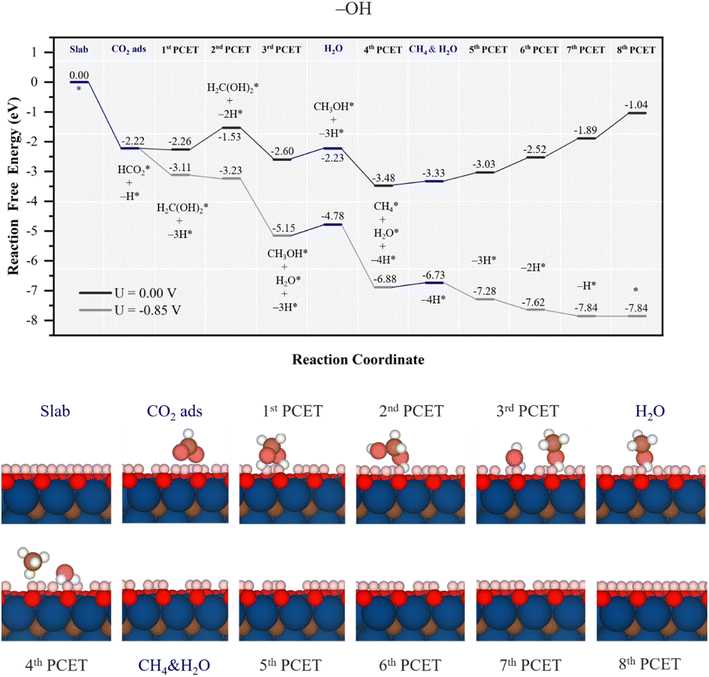 | ||
| Fig. 5 Gibbs free energy, ΔG, diagram of the CO2RR on fully –OH terminated Ti3C2 MXene, under standard working conditions. Blue lines represent chemical steps of as-generated H2O or CH4 desorption, or CO2 adsorption, while black and grey lines represent the electrochemical proton-coupled electron transfer (PCET) steps under zero and applied U = UL calculated potential of −0.85 V vs. SHE, respectively. The nH* symbols refer to how many H atoms have been transferred from surface –OH groups at the reaction stage. Bottom panels show side views of atomic structures of different reaction stages. Colour coding as in Fig. 2. | ||
Still, the regenerated –OH is able to again participate in the course of the reaction, along with the third PCET, forming methanol and water, i.e.
| H2C(OH)2* + H+ + e− + –OH → H3COH* + H2O* + –O, | (23) |
| H3COH* + H+ + e− + –OH → CH4* + H2O* + –O, | (24) |
Notice here how energetically influential is the cooperative and simultaneous hydrogenation from solution protons and surface –OH groups, quite reducing the methylene glycol, methanol, and methane formation steps. This mechanism occurs thanks to the low EHvac of the –OH surface termination, with a value of −0.56 eV, see Table 1, implying that such surface H atoms are relatively easy to capture and thus to participate in the reaction, and underscores the exceptionally high participation of the H atoms from the –OH groups, to the point that molecular synthesis is not the potential determining step (PDS), but the electrocatalyst surface regeneration, with a ΔGmax of 0.85 eV. The corresponding theoretical limiting potential UL is −0.85 V vs. RHE, as depicted in Fig. 5, in which each electrochemical step is exergonic, while the chemical steps demand, at most, 0.37 eV for water release, feasible under working conditions. In addition, the UL falls well within the stability region of the –OH model on the Pourbaix diagram in Fig. S2 of the ESI† at low pH, consistently implying the stability and recovery of the –OH terminated Ti3C2 electrocatalyst.
| Model | PCET | PDS | E Hvac | U L |
|---|---|---|---|---|
| –OH | 8th | –H* → * | −0.56 | −0.85 |
| –OH2/3O1/3 | 7th | CH3OH* + * → CH3OH* + H* | 0.12 | −0.84 |
| –OH1/2O1/2 | 6th | CH3OH* + –H* → CH3OH* + * | 0.26 | −0.70 |
| –OH1/3O2/3 | 1st | CO2* → HCOOH* + –H* | 0.73 | −0.37 |
| –F1/3OH1/3O1/3 | 2nd | HCOOH* + –H* → HCOOH* + * | 0.31 | −0.51 |
Furthermore, the selectivity of the catalyst is also, a priori, remarkable. As can be seen in alternative reaction paths shown in Fig. S7 of the ESI,† the two-electron synthesis of formic acid, HCOOH(l), is quite hindered by the formation of HCOOH* from HCO2*, requiring 1.88 eV, while four-electron synthesis of formaldehyde, CH2O*, from methylene glycol is disfavoured by 0.88 eV. Apart from these possible products, CO formation is avoided given the high stability of HCO2* and the downhill formation of methylene glycol thanks to the participation of surface –OH groups transferring H atoms. Similarly, methanol synthesis is also quite hindered by the quite downhill formation of methane and water, see Fig. 5 and S7 of the ESI.† Thus, apart from the competitive hydrogen evolution reaction (HER), with an estimated UL of −0.48 V using the very same computational scheme,53 the synthesis of CH4 competes with that of CH2O in a similar fashion on fully –OH terminated Ti3C2 MXene, and only formic acid would be obtained at a very low potential of −1.88 V.
When –OH groups are partially replaced by –O, as in the –OH2/3O1/3 model, a different scenario unfolds, as illustrated in Fig. 6. In contrast to the full –OH coverage case, the reduced availability of surface H atoms, in line with a positive value of EHvac of 0.12 eV, see Table 1, hampers the CO2 molecule ability to capture surface H atoms before the electrochemical steps start, and so diminishes the involvement of surface H atoms in the oncoming PCET steps. Thus, CO2 adsorption is mild, of −0.16 eV, and the initial formation of HCO2* occurs by a PCET, with a ΔG of −0.35 eV, whereas the possible step related to surface H atom leading to adsorbed formic acid, HCOOH*, is disadvantageous by 0.21 eV, see Fig. S8 of the ESI.† From HCO2*, the formation of methylene glycol is fostered by a PCET step coupled with two surface H transfers, being an uphill process of 0.71 eV, see Fig. 6, but still more favorable than formic acid formation by a second PCET, with a ΔG of 0.92 eV, see Fig. S8 of the ESI.† However, in the subsequent step, *HCO2 captures a total of two surface H atoms, which play a crucial role in the second PCET to form methylene glycol. Here, the third PCET is similar to that occurring on the fully –OH covered model, with regeneration of a surface –OH group after methylene glycol formation, here downhill by 0.3 eV, while following regeneration is uphill by 0.24 eV.
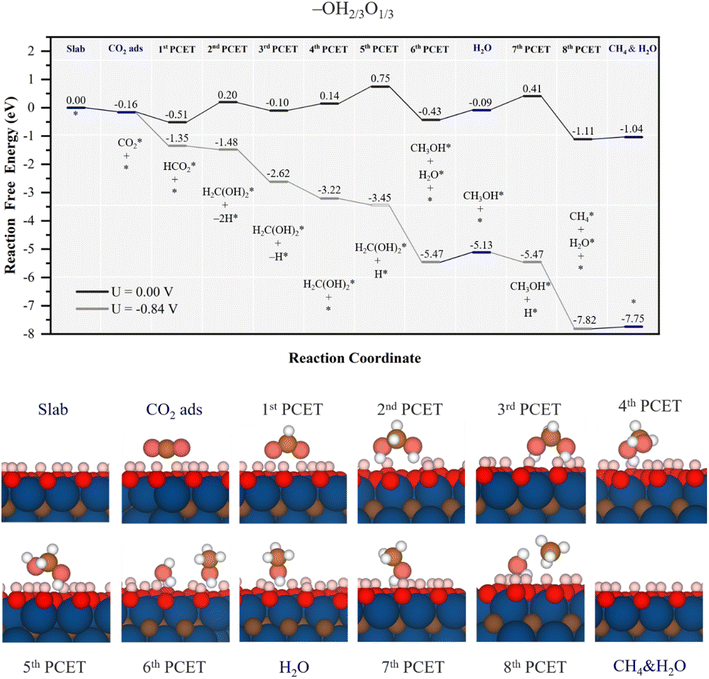 | ||
| Fig. 6 Gibbs free energy, ΔG, diagram of the CO2RR on the –OH2/3O1/3 Ti3C2 MXene model, under standard working conditions and at a U = UL calculated potential of −0.84 V vs. SHE. Colour code as in Fig. 6. The nH* symbols refer to how many H atoms have been reduced over surface –O groups at the given reaction stage. Bottom panels show side views of atomic structures of different reaction stages. Colour coding as in Fig. 2. | ||
However, from the 5th PCET on, there is a notable shift of –O termination activity, with a higher propensity for proton reduction. Thus, this reduction has a ΔG of 0.61 eV, and preferred by 0.12 eV over the proton-reduction induced methylene glycol decomposition into formaldehyde and water, see Fig. S8 of the ESI,† as:
| H2C(OH)2* → H2CO* + H2O*, | (25) |
When further increasing the –O/–OH ratio as in the –OH1/2O1/2 model, again some similitudes with respect to the profile on the –OH2/3O1/3 model are kept, see Fig. 6 and 7, also in line with a similar degree of H transfer, with an EHvac of 0.26 eV, see Table 1, similar to the value of 0.12 eV for the –OH2/3O1/3 model. Again, the reaction starts with CO2 physisorption with an Eads of −0.06 eV only, but now, given the extra room to accommodate formic acid, the 1st PCET is coupled with an –OH group H transfer leading to HCOOH*, which is exergonic by −0.3 eV, see Fig. 7. However, this formic acid is strongly adsorbed by 1.08 eV, see Fig. S9 of the ESI,† thus preventing its release. Consequently, the reaction advances through a 2nd PCET forming formate with a ΔG of −0.17 eV, i.e. transferring one H back to the substrate, thus reducing a nearby –O group, underscoring that formate stability is quite related to the presence of nearby –O groups.
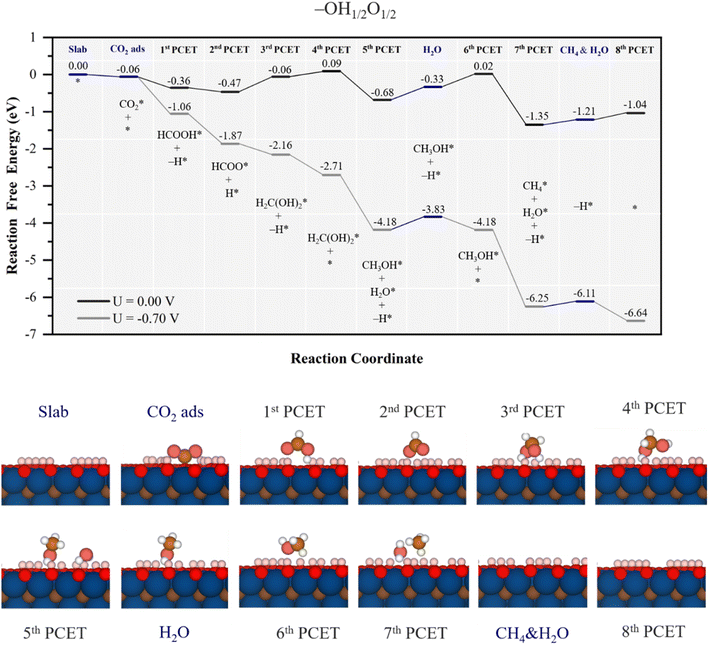 | ||
| Fig. 7 Gibbs free energy, ΔG, diagram of the CO2RR on the –OH1/2O1/2 Ti3C2 MXene model, under standard working conditions and at a U = UL calculated potential of −0.70 V vs. SHE. Colour code and notation as in Fig. 6 and 7. Bottom panels show side views of atomic structures of different reaction stages. Colour coding as in Fig. 2. | ||
After formate is synthesized, a 3rd PCET involves again H transfer from two nearby –OH groups and one proton reduction, to again lead to the adsorbed methylene glycol moiety, with an energy cost of 0.41 eV, followed once more by on surface –O group reduction, costly only by 0.15 eV. Similarly to the model with –OH2/3O1/3 surface terminations, the rest of the reaction follows a similar pathway; the methylene glycol decomposition, as induced by a proton reduction coupled to a surface –OH hydrogen transfer results in CH3OH* and H2O* in a quite exergonic electrochemical step with a ΔG of −0.77 eV, much more preferred than, e.g. decomposition towards formaldehyde, endergonic by 0.46 eV. After water desorption, methanol competes in between desorbing, ΔG of 0.63 eV, or refreshing the nearby lost –OH group, ΔG = 0.35 eV, as shown in Fig. S9 of the ESI.† From this point on, again, methanol decomposition into CH4* and H2O*, implying the joint hydrogenation from a reduced proton and one H from an –OH group, results in an exergonic step with ΔG = −1.37 eV, see Fig. 7, followed by product release and surface regeneration with a ΔG of 0.31 eV. Altogether, the PDS is the electrochemical step leading to adsorbed methanol, ready for its reaction towards CH4, with a UL of −0.7 V vs. SHE. This potential would lead also to full –OH termination under strongly acidic conditions, see Fig. S2 of the ESI.†
In any case, the CO2RR mechanism is essentially kept, with a role of –O surface groups as reducing sites for protons, and later –OH groups as being H-donors, with the steps of formation and decomposition of methylene glycol and methanol, yet here with an initial formation and stabilization of formic acid triggered by the increase of surface –O groups. As per the selectivity, no path to CO is found, while formic acid release is prevented by the high desorption energy of 1.08 eV. Here, the formaldehyde path implies going through methylene glycol, whose conversion towards methanol is very exergonic by −0.77 eV, and the same applies to methanol decomposition to CH4. Thus, a high selectivity towards CH4 would be forecasted, although still the model would compete with the HER, with a UL of −0.23 V,53 H2(g) being the main expected product.
When even increasing the surface –O content, such as in the –OH1/3O2/3 model, the reaction path mimics to some extent that of the –OH1/2O1/2 model, as shown in Fig. 8 and S10 of the ESI.† Starting from a mild physisorption of CO2, the first PCET already combines proton reduction with H transfer from –OH, forming HCOOH*, with a ΔG value of 0.37 eV. From this point on, the 2nd and 3rd PCETs are essentially isoenergetic proton reductions on surface –O moieties, with the possibility of desorbing HCOOH, requiring 0.4 eV energy, and no more involvement of –OH groups, which may be related to the increase of EHvac up to 0.73 eV, making the H transfer from vicinal –OH groups more difficult. In the 4th PCET, the methylene glycol formation path is essentially isoenergetic by 0.03 eV, while CO formation induced by nearby –O proton reduction upon is uphill by 0.36 eV. After this point, the reaction is downhill, first by a –O proton reduction, followed later by methylene glycol decomposition into methanol, with a ΔG of −0.5 eV.
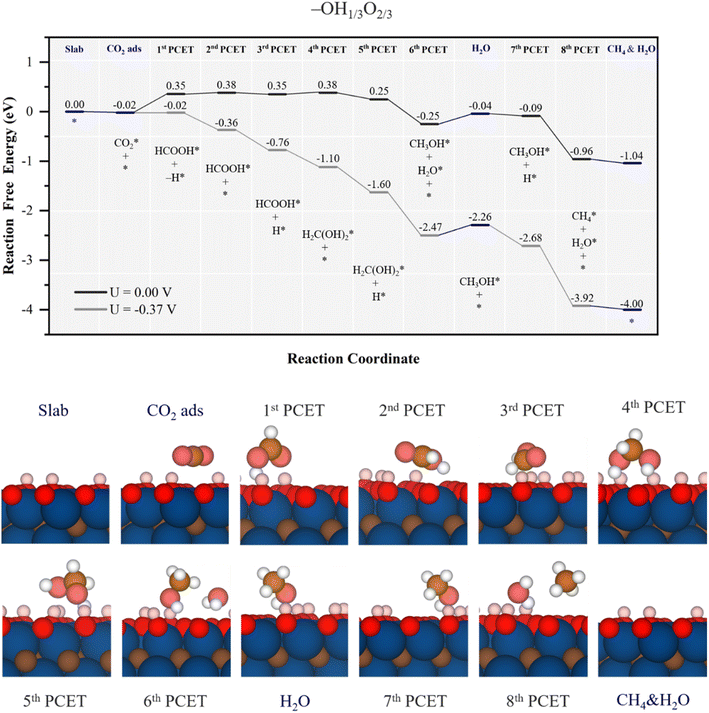 | ||
| Fig. 8 Gibbs free energy, ΔG, diagram of the CO2RR on the –OH1/3O2/3 Ti3C2 MXene model, under standard working conditions and at a U = UL calculated potential of −0.37 V vs. SHE. Colour code and notation as in Fig. 6 and 7. Bottom panels show side views of atomic structures of different reaction stages. Colour coding as in Fig. 2. | ||
Also similar to the case of the –OH1/2O1/2 model, the formed H2O in methanol synthesis can easily desorb, requiring 0.21 eV, see Fig. 8, while methanol desorption is more costly as it requires 0.51 eV, see Fig. S10 of the ESI.† Actually, the minimum energy path implies proton reduction nearby on an –O site, from which the proton reduction can again be coupled with –OH H transfer, turning the electrochemical step being quite exergonic by −0.87 eV, see Fig. 8. In general terms, the reaction profile is closer to the ΔG = 0 eV than the other inspected models so far, and with less ups and downs in energy, which translates into reduced limiting potential. In fact, the full process can be made exergonic with a limiting potential of −0.37 V vs. SHE, corresponding to the initial formic acid formation in the first PCET, at variance with previous models, where the PDS is found at a late stage. Still, the UL is too large for this surface stability, see the Pourbaix diagram in Fig. S2 of the ESI,† and the model would be valid for less acid conditions. Still, as low as the UL of −0.37 V may seem, as per the selectivity, the –OH1/3O2/3 model has a very low UL for the HER, of solely −0.01 V,53 and so, the selectivity towards CH4(g) would be low, and other reaction products, such as HCOOH, CH3OH, and CO, would be possible with a UL of −0.37 V, even if their detachment from the surface would be energetically more costly than further reacting towards CH4, implying a lower content of them.
From the above analysis, one could draw a general trend: namely, the UL decreases as the –OH proportion decreases. However, no minimum would be expected at a full –O termination. Firstly, according to a previous study conducted by Handoko et al.,40 a larger UL of 0.52 V vs. RHE was found for Ti2CO2, while Morales et al.104 pointed out a similar activity between Ti3C2 and Ti2C MXenes. Moreover, according to the Pourbaix diagrams in Fig. S2 of the ESI,† even at zero potential, a full –O termination would require a pH larger than 7, and, as aforementioned, alkaline media is not the best case scenario for the CO2RR electrocatalytic activity.
At this point, one may wonder what would be the effect of –F surface groups on CO2RR performance, particularly relevant at low pH and U, see Fig. S2 of the ESI.† This is analysed on the –F1/3OH1/3O1/3 model shown in Fig. 9. Actually, if one would assume –F surface groups being mere spectators, the –OH/–O ratio would be comparable to that of the –OH1/2O1/2 model, and so a similar performance would be expected, at least in UL, even if the production rates per electrocatalyst gram would decrease as a third of the surface sites are blocked by –F groups. Mechanistically, as the EHvac value of 0.31 eV is similar to the value of 0.26 eV for the –OH1/2O1/2 model, see Table 1, one would envisage a similar involvement of –OH/–O groups in the hydrogenation sequence. By inspecting the actual Gibbs free energy profile in Fig. 9, one observes a small physisorption of CO2 with an Eads of 0.04 eV, followed by the 1st PCET and nearby –OH H transfer to form HCOOH*, with a ΔG = −0.13 eV, actually reminiscent of that found for the –OH1/2O1/2 model. However, on –F1/3OH1/3O1/3 the second PCET does not lead to formate, but rather to a regeneration of the consumed –OH, here costly by 0.51 eV, again similar to that corresponding to the –OH1/2O1/2 model, with ΔG = 0.5 eV, see Fig. 7, and competing with methylene glycol formation, 0.08 eV more costly, see Fig. S11 of the ESI.†
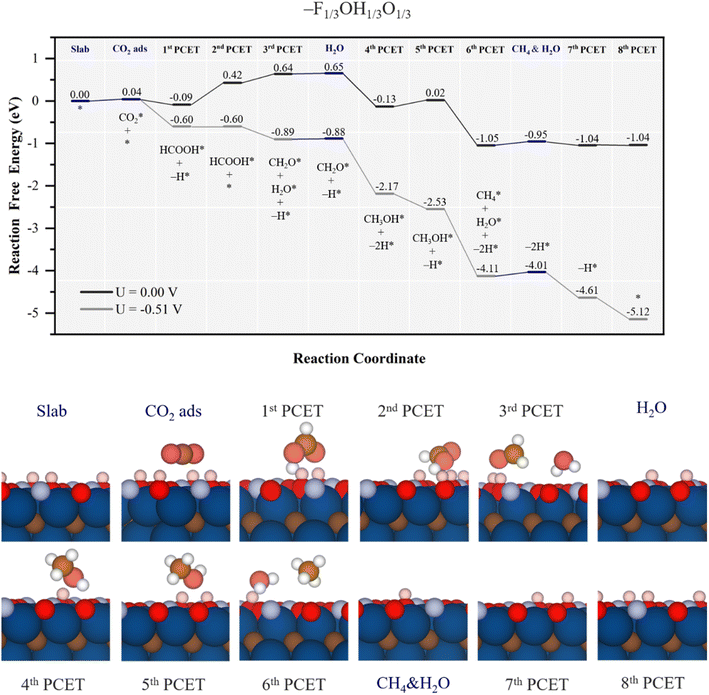 | ||
| Fig. 9 Gibbs free energy, ΔG, diagram of the CO2RR on the –F1/3OH1/3O1/3 Ti3C2 MXene model, under standard working conditions and at a U = UL calculated potential of −0.51 V vs. SHE. Colour code and notation as in Fig. 6 and 7. Bottom panels show side views of atomic structures of different reaction stages. Colour coding as in Fig. 2. | ||
Actually, the absence of the formate intermediate has consequences on the oncoming steps since, at variance with the mechanism for the –OH1/2O1/2 model, methylene glycol intermediate formation is not preferred, but the hydrogenation of formic acid coupled with a surface –OH H transfer leads to formaldehyde and water formation, as:
| HCOOH* + H+ + e− + –OH → CH2O* + H2O* + –O, | (26) |
Thus, the PDS corresponds to an early step of –OH regeneration right after formic acid formation, with UL = −0.51 V, different from the –OH regeneration right after methanol formation on the –OH1/2O1/2 model, with UL = −0.70 V. Actually, the easier reduction cost on –O groups vicinal to CH3OH* is the reason behind the change in the reaction profile, lowering the cost of the equivalent PDS on the –OH1/2O1/2 model, and leaving the PDS to formic acid formation, essentially unaltered by the presence of –F groups. Thus, on the –F1/3OH1/3O1/3 model, the UL is −0.51 V, close to its stability region according to Pourbaix diagrams, see Fig. S2 of the ESI.† As per the selectivity, formic acid is likely formed under the same UL, although CH2O(g) and CH3OH(l) desorption compete with quite exergonic further reaction steps, moving towards more generation of methane. No channel to CO formation is found, as well. However, as happened with the –OH2/3O1/3 model, the main competition is with the HER, with a UL of solely −0.01 V.53
Table 1 summarizes results for the five studied models indicating which PCET is the PDS and to which electrochemical step does it correspond to, including EHvac and UL values as well. As encompassed in Table 1, but also visible in the captured trends in Fig. 10, the EHvac linearly varies with respect to the –OH/–O ratio, with similar values for the –OH1/2O1/2 and –F1/3OH1/3O1/3 models. As EHvac increases with the presence of more surface –O groups, the UL decreases, see Fig. 10, to the point that two regions can be differentiated: one where –OH is the main surface termination site, with quite low UL values, and the other with the participation of –O groups in reducing protons, and later transferring such H atoms, with even smaller UL values. The higher involvement of –O surface moieties generally eases the latest PCET steps and moves PDS to an earlier stage of the reaction. Last but not least, the presence of –F groups is not per se detrimental, and in fact leads to a deviation of the trend, reducing UL costs. Besides, the reaction profiles question the conventional mechanism of the sole H+ reduction upon the reacting molecule, and unfolds (i) the sequences of Volmer steps on nearby –O surface groups, followed by H transfer to the reacting molecule from such as-formed –OH, (ii) the H transfer from already existing –OH groups, followed by proton reduction on the as-generated –O moieties, and (iii) the simultaneous hydrogenation of a moiety, coupling H+ reduction electrochemical step with H chemical transfers from surface –OH groups. Indeed, it can be claimed that the simultaneous existence of –OH and –O groups offers a versatility of reactive paths that ultimately expresses in a reduction of the reaction bias cost.
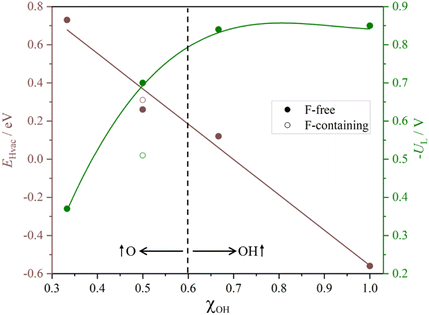 | ||
| Fig. 10 Plots of H-vacancy energies, EHvac, given in eV, and minus the limiting potential, UL, given in V, as a function of –OH group partition coefficients (χOH) with respect to –O groups. | ||
3.3. CO2RR electrocatalysis performance
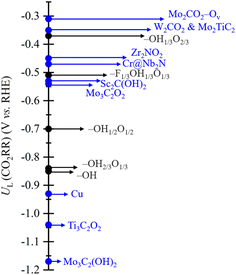
We now focus on the CO2RR performance of the scrutinized models keeping in mind that an optimal catalyst would feature the smallest possible UL and that the closer the UL to zero, the higher the activity and faster the CO2RR kinetics. The present results are already fully consistent with previous studies,39 in that a higher proportion of –O termination leads to a quite small UL resulting in a higher CO2RR activity, see Table 1. However, keeping in mind the electrocatalyst surface stability predicted in the Pourbaix diagram of Fig. S2 of the ESI,† even if certain models feature reduced UL values, e.g. −0.37 V for –OH1/3O2/3 or −0.51 V for –F1/3OH1/3O1/3, their range of stability implies that at low pH the surface would eventually transform into the full –OH model, or when working at higher pH would imply sluggish reaction conditions, yet to be partially compensated by a larger potential applicability. In addition, the fact that models with larger –F content do not appear in the Pourbaix diagrams helps explaining previous experimental findings,105 particularly in that such models would make the reaction infeasible. However, low contents such as is –F1/3OH1/3O1/3 are non-detrimental per se, as such moieties can help in moving the PDS to an earlier stage, with a concomitant UL reduction and, hence, operating costs. This opens the door to a control of the electrocatalyst performance by the degree of –F appearing at the surface, a point missed under F-free synthesis methodologies.73Another key point of interest is the comparison of the here reported CO2RR activity with that of other MXenes reported in the literature, such as fully OH-terminated Mo3C2(OH)2,39 and Sc2C(OH)2,41 O-terminated Mo3C2O2,39 Zr2NO2,69 Ti3C2O2,106 and W2CO2,40 pristine surface MXene Mo2TiC2,68 Mo2CO2-Ov model containing surface oxygen vacancies,107 and Cr@Nb2NO2,108 a case with a Cr single atom on a fully –O terminated Nb2N MXene. No pure –F termination is here compared to, as shown to consistently deliver high UL for the CO2RR and HER on MXenes,42,53 plus is not a reachable stable situation according to Pourbaix diagrams in Fig. S2 of the ESI.† For a more comprehensive comparison, Cu metal is also considered as it has been reported to be a highly efficient CO2RR catalyst.41,109Fig. 11 clearly shows that, even if accounting from deviations from different computational approaches between present models and results in the literature, in general terms, MXene-based electrocatalysts feature lower UL compared to the Cu reference of −0.93 V, underscoring the potential of such a family of materials for CO2 conversion purposes. Still, one has to be critical with the display of values. For instance, some of the systems with the lowest UL are Mo2CO2-Ov and W2CO2, with values of −0.31 and −0.35 V, respectively, while to a lower extent, other O-terminated MXenes have relatively low UL values, like −0.45 V for Zr2NO2, −1.04 V for Ti3C2O2,106 or the value of −0.47 V for Cr@Nb2NO2. However, from the Pourbaix diagram in Fig. S2 of the ESI,† and others reported in the literature, the full O-termination is only stable at positive UL values, and so, such surface termination gets unrealistic under CO2RR conditions. Actually, under these conditions, more realistic values are −1.17 and −0.53 V reported for Mo3C2(OH)2 and Sc2(OH)2, respectively, the latter representing a clear improvement with respect to the Cu reference by around 0.4 V. It is with respect to these fully OH-terminated models where we find that O-rich –OH1/3O2/3 and F-containing –F1/3OH1/3O1/3 models have an UL improvement by at least 0.16 and 0.02 V compared with Sc2(OH)2, underscoring that the slight presence of –F moieties and a balance between –OH and –O groups represent tuning points towards decreasing UL costs.
In order to understand the differences with prior calculations, one has to note that they are regularly focused on pure –O termination. Thus, the main discrepancy is attributed to the commented involvement of –F and –OH groups, and to the strong hydrophilicity of –O groups. Based on EHvac, the strength of this H bond seems to be related to the distribution of –OH groups, which, eventually, endows the MXene surface with a new source of H atoms, making the reaction easier, a feature absent in previous studies with only –O groups. Besides, –F and –OH terminations have the same charge close to −1e, but as in the CDD plot in Fig. S5 of the SI,† the electron density on –F termination is more localized, leading to a stronger effective charge, and so, a priori more repulsion, features that may affect the MXene activity at different stages of the reaction.
Last but not least, it is worth addressing the competition between the CO2RR, here examined with respect to methane formation, and the HER, a crucial concurrent reaction in aqueous solutions.53,110 Even if a rigorous study of the selectivity requires addressing the kinetic barriers,41,111 the UL difference among both types of reactions can be used as a sound thermodynamic metric.112 This is graphically shown in Fig. 12 as a parity plot, gaining HER values from an equivalent previous study.53 Note that, different from previous studies focusing only on –O terminations,113,114 we considered here the involvement of H atoms of the –OH groups, and, in the case of the HER, different reaction mechanisms have been evaluated, beyond the spreadly used, yet limitedly justified, assumption of the reaction being controlled by the first PCET;108,115 see more details in the literature.53 Notice that, even if none of the proposed surface terminations is more selective towards the CO2RR than towards the HER, a general trend can be captured; the smaller the UL needed, the less the selectivity towards the CO2RR is. Actually, the CO2RR selectivity seems to be improved when increasing the –OH/–O ratio, with a maximum for the fully –OH terminated model. Still, even if such models are per se selective towards the HER, or very selective, in the cases of the –OH1/3O2/3 and –F1/3OH1/3O1/3 models, strategies are available to inhibit the HER, such as limiting H+ transfer rates,116–118 employing non-water proton donors,119,120 limiting electron transfer rates,121,122 or regulating the magnetic moment of the active site.123
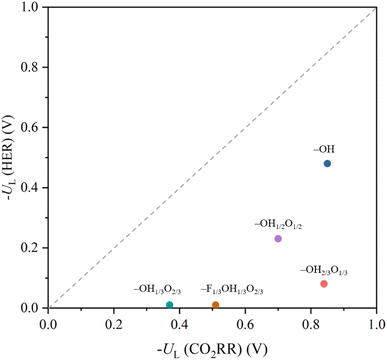 | ||
| Fig. 12 Comparison of −UL for the CO2RR vs. −UL for the HER on the explored terminated Ti3C2Tx models. Values for the HER are taken from the literature.53 | ||
4. Conclusions
Here we have profoundly analyzed the possible use of Ti3C2 MXene based materials as electrocatalysts for the CO2RR, examining the surface composition under working conditions via Pourbaix diagrams and systematically studying the reaction mechanisms considering the involvement of different surface termination species, and aspects such as limiting potential towards methane production, selectivity, and competition with respect to H2(g) production. Based on the surface stability dictated by the calculated Pourbaix diagrams, several surface models are investigated that may have potential interest towards the CO2RR, namely full –OH, as well as –OH2/3O1/3, –OH1/2O1/2, and –OH1/3O2/3 models, and the F-containing –F1/3OH1/3O1/3 model. Apart from their stability under working conditions, kinetic phase diagrams show that these models meet the requirement of CO2 capture and activation, and the CH4 product release.The calculated reaction Gibbs free energy profiles reveal that, in general, for F-free models the reaction mechanism involves formic acid and methylene glycol formation, which decomposes into methanol and water. In subsequent steps, methanol decomposes into methane and water as well. However, on the F-containing –F1/3OH1/3O1/3 model, the reaction involves the initial formation of formic acid, and its decomposition into formaldehyde, which later hydrogenates up to methanol. The present profiles help in understanding the experimental observations, in the sense that, the larger the –O content, the smaller the UL,42 mostly arising from the dual role of –O and –OH groups, acting as H acceptors and donors, respectively, which make the hydrogenation steps more flexible, allowing for reduction of UL costs, and also add the possibility of reaction species to be simultaneously hydrogenated from H+ reduction and surface –OH group H transfers, the latest fostered by a relatively low energetic cost of deprotonation. Note that the role of the –OH groups is reminiscent of the Mars-van Krevelen mechanism on oxide surfaces where the lattice O directly participates in the reaction with the left O vacancy healed by O2 from the gas phase at a subsequent step.
Generally speaking, the presently studied Ti3C2Tx surface MXene models, together with results from the literature, underscore the effectiveness of such materials for the CO2RR when compared to the reference Cu electrocatalyst, with significantly improved UL values by up to ca. 0.6 V. However, they still face aspects to be improved; on one hand, the required UL in many of the models with binary and ternary terminations underscores the eventual gradual conversion into a fully –OH terminated model, which has a larger value of UL of −0.85 V, yet lower by almost 0.1 V than the equivalent value for the Cu reference. On the other hand, the selectivity of the CO2RR on the studied models with respect to the HER is far from optimal, yet the fully –OH terminated model is the most competitive one, and so significant degrees of the CO2RR are to be expected when using it for this purpose. In any case, on such surface terminated Ti3C2Tx MXenes, an optimal HER performance is to be expected at low UL values, while a significant improvement in the CO2RR is to be expected when reducing the UL up to the requirements of the fully –OH terminated model. Given the vast family of possible MXene materials, and the surface tunability, the present study sheds light on the effective selection and tuning of MXenes for high performance and selective CO2RR electrocatalysis.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge financial support from the Spanish Ministerio de Ciencia e Innovación through grants MCIN/AEI/10.13039/501100011033 PID2021-126076NB-I00 and TED2021-129506B–C22, funded partially by FEDER Una manera de hacer Europa, the unit of excellence María de Maeztu CEX2021-001202 M granted to the IQTCUB, the COST Action CA18234, and the Generalitat de Catalunya 2021SGR00079 grant. F. V. acknowledges the ICREA Academia Award 2023 Ref. Ac2216561. L. M. thanks the China Scholarship Council (CSC) for financing her PhD (CSC202108390032). A significant part of the computational resources has been provided by the Red Española de Supercomputación (RES) QHS-2022-1-0004 and QHS-2021-3-0012. L. M. acknowledges the HPC-Europa3 (HPC17OOIBY) project supported by the EC Research Innovation Action under the H2020 Programme.References
- International Energy Agency: CO2 Emissions In 2022; Typeset in France by IEA - March 2023, https://www.iea.org/ Search PubMed.
- European Central Bank: Looking Through Higher Energy Prices? Monetary Policy and The Preen Transition, https://www.ecb.europa.eu/home/html/index.en.html Search PubMed.
- S. Posada-Pérez, F. Viñes, P. J. Ramirez, A. B. Vidal, J. A. Rodriguez and F. Illas, Phys. Chem. Chem. Phys., 2014, 16, 14912–14921 RSC.
- X. Liu, C. Kunkel, P. Ramírez de la Piscina, N. Homs, F. Viñes and F. Illas, ACS Catal., 2017, 7, 4323–4335 CrossRef CAS.
- J. A. Rodriguez, J. Evans, L. Feria, A. B. Vidal, P. Liu, K. Nakamura and F. Illas, J. Catal., 2013, 307, 162–169 CrossRef CAS.
- G. Pacchioni, J. M. Ricart and F. Illas, J. Am. Chem. Soc., 1994, 116, 10152–10158 CrossRef CAS.
- S. Posada-Pérez, P. J. Ramírez, J. Evans, F. Viñes, P. Liu, F. Illas and J. A. Rodriguez, J. Am. Chem. Soc., 2016, 138, 8269–8278 CrossRef PubMed.
- S. Yang, M. Jiang, W. Zhang, Y. Hu, J. Liang, Y. Wang, Z. Tie and Z. Jin, Adv. Funct. Mater., 2023, 33, 2301984 CrossRef CAS.
- C. Sun, Y. Hou, N. Lüdi, H. Hu, M. de Jesús Gálvez-Vázquez, M. Liechti, Y. Kong, M. Liu, R. Erni, A. V. Rudnev and P. Broekmann, J. Catal., 2022, 407, 198–205 CrossRef CAS.
- M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382–386 CrossRef CAS PubMed.
- M. J. Cheng, E. L. Clark, H. H. Pham, A. T. Bell and M. Head-Gordon, ACS Catal., 2016, 6, 7769–7777 CrossRef CAS.
- K. P. Kuhl, T. Hatsukade, E. R. Cave, D. N. Abram, J. Kibsgaard and T. F. Jaramillo, J. Am. Chem. Soc., 2014, 136, 14107–14113 CrossRef CAS PubMed.
- Y. Chen, J. Zhang, L. Yang, X. Wang, Q. Wu and Z. Hu, Electrochem. Energy Rev., 2022, 5, 11 CrossRef CAS.
- J. J. Wang, X. P. Li, B. F. Cui, Z. Zhang, X. F. Hu, J. Ding, Y. D. Deng, X. P. Han and W. B. Hu, Rare Met., 2021, 40, 3019–3037 CrossRef CAS.
- H. Hu, J. Z. Ou, X. Xu, Y. Lin, Y. Zhang, H. Zhao, D. Chen, M. He, Y. Huang and L. Deng, J. Chem. Eng., 2021, 425, 130587 CrossRef CAS.
- S. Zhou, W. Pei, Y. Zhao, X. Yang, N. Liu and J. Zhao, Npj Comput. mater., 2021, 7, 186 CrossRef CAS.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5, 7050–7059 RSC.
- D. Ren, Y. Deng, A. D. Handoko, C. S. Chen, S. Malkhandi and B. S. Yeo, ACS Catal., 2015, 5, 2814–2821 CrossRef CAS.
- Y. Hori, A. Murata and R. Takahashi, J. Chem. Soc., Faraday Trans., 1989, 85, 2309–2326 RSC.
- Y. Huang, A. D. Handoko, P. Hirunsit and B. S. Yeo, ACS Catal., 2017, 7, 1749–1756 CrossRef CAS.
- H. Shin, Y. Ha and H. Kim, J. Phys. Chem., 2016, 7, 4124–4129 CAS.
- X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Nat. Commun., 2017, 8, 15438 CrossRef CAS PubMed.
- Á. Morales-García, F. Calle-Vallejo and F. Illas, ACS Catal., 2020, 10, 13487–13503 CrossRef.
- M. Naguib, J. Halim, J. Lu, K. M. Cook, L. Hultman, Y. Gogotsi and M. W. Barsoum, J. Am. Chem. Soc., 2013, 135, 15966–15969 CrossRef CAS PubMed.
- M. Naguib, V. Presser, N. Lane, D. Tallman, Y. Gogotsi, J. Lu, L. Hultman and M. W. Barsoum, RSC Adv., 2011, 1, 1493–1499 RSC.
- M. Ahmaruzzaman, RSC Adv., 2022, 12, 34766–34789 RSC.
- G. Deysher, C. E. Shuck, K. Hantanasirisakul, N. C. Frey, A. C. Foucher, K. Maleski, A. Sarycheva, V. B. Shenoy, E. A. Stach, B. Anasori and Y. Gogotsi, ACS Nano, 2020, 14, 204–217 CrossRef CAS PubMed.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- M. Ghidiu, M. R. Lukatskaya, M.-Q. Zhao, Y. Gogotsi and M. W. Barsoum, Nature, 2014, 516, 78–81 CrossRef CAS PubMed.
- X. Q. Tan, W. Mo, X. Lin, J. Y. Loh, A. R. Mohamed and W. J. Ong, Nanoscale, 2023, 15, 6536–6562 RSC.
- M. A. Hope, A. C. Forse, K. J. Griffith, M. R. Lukatskaya, M. Ghidiu, Y. Gogotsi and C. P. Grey, Phys. Chem. Chem. Phys., 2016, 18, 5099–5102 RSC.
- B. C. Wyatt, A. Rosenkranz and B. Anasori, Adv. Mater., 2021, 33, 2007973 CrossRef CAS PubMed.
- M. Benchakar, L. Loupias, C. Garnero, T. Bilyk, C. Morais, C. Canaff, N. Guignard, S. Morisset, H. Pazniak, S. Hurand, P. Chartier, J. Pacaud, V. Mauchamp, M. W. Barsoum, A. Habrioux and S. Célérier, Appl. Surf. Sci., 2020, 530, 147209 CrossRef CAS.
- J. Sun, B. Liu, Q. Zhao, C. H. Kirk and J. Wang, Adv. Mater., 2023, 35, 2306072 CrossRef CAS PubMed.
- S. Y. Pang, Y. T. Wong, S. Yuan, Y. Liu, M. K. Tsang, Z. Yang, H. Huang, W. T. Wong and J. Hao, J. Am. Chem. Soc., 2019, 141, 9610–9616 CrossRef CAS PubMed.
- R. Meshkian, H. Lind, J. Halim, A. El Ghazaly, J. Thörnberg, Q. Tao, M. Dahlqvist, J. Palisaitis, P. O. Å. Persson and J. Rosen, ACS Appl. Nano Mater., 2019, 2, 6209–6219 CrossRef CAS.
- V. Kamysbayev, A. S. Filatov, H. Hu, X. Rui, F. Lagunas, D. Wang, R. F. Klie and D. V. Talapin, Science, 2020, 369, 979–983 CrossRef CAS PubMed.
- D. Ontiveros, F. Viñes and C. Sousa, J. Mater. Chem. A, 2023, 11, 13754–13764 RSC.
- N. Li, X. Chen, W. J. Ong, D. R. MacFarlane, X. Zhao, A. K. Cheetham and C. Sun, ACS Nano, 2017, 11, 10825–10833 CrossRef CAS PubMed.
- A. D. Handoko, K. H. Khoo, T. L. Tan, H. Jin and Z. W. Seh, J. Mater. chem. A, 2018, 6, 21885–21890 RSC.
- H. Chen, A. D. Handoko, J. Xiao, X. Feng, Y. Fan, T. Wang, D. Legut, Z. W. Seh and Q. Zhang, ACS Appl. Mater. Interfaces, 2019, 11, 36571–36579 CrossRef CAS PubMed.
- A. D. Handoko, H. Chen, Y. Lum, Q. Zhang, B. Anasori and Z. W. Seh, iScience, 2020, 23, 101181 CrossRef CAS PubMed.
- C. Y. J. Lim, A. D. Handoko and Z. W. Seh, Diamond Relat. Mater., 2022, 130, 109461 CrossRef CAS.
- G. T. M. Kadja, M. M. Ilm, N. J. Azhar, A. Febrianti, J. J. M. Siregar, N. Nurdini, U. Pratomo and M. I. Khalil, FlatChem, 2023, 38, 100481 CrossRef CAS.
- X. Li, Y. Chen, X. Zhan, Y. Xu, L. Hao, L. Xu, X. Li, M. Umer, X. Tan, B. Han, A. W. Robertson and Z. Sun, Innov. Mater., 2023, 1, 100014 CrossRef.
- H. Bao, Y. Qiu, X. Peng, J.-a. Wang, Y. Mi, S. Zhao, X. Liu, Y. Liu, R. Cao, L. Zhuo, J. Ren, J. Sun, J. Luo and X. Sun, Nat. Commun., 2021, 12, 238 CrossRef CAS PubMed.
- Y. Zhang and Z. Cao, J. Phys. Chem. C, 2021, 125, 13331–13342 CrossRef CAS.
- X. Qian, L. Li, Y. Li, Z. Liu, Z. Tian, C. Zhan and L. Chen, Phys. Chem. Chem. Phys., 2021, 23, 12431–12438 RSC.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- M. Tahir, A. Ali Khan, S. Tasleem, R. Mansoor and W. K. Fan, Energy Fuels, 2021, 35, 10374–10404 CrossRef CAS.
- M. Pourbaix, Atlas of Electrochemical Equilibria in Aqueous Solutions, National Association of Corrosion Engineers (NACE), Houston, Texas, USA, 1974 Search PubMed.
- M. López, K. S Exner, F. Viñes and F. Illas, Adv. Theory Simul., 2023, 6, 2200217 CrossRef.
- L. Meng, L. K. Yan, F. Viñes and F. Illas, J. Mater. Chem. A, 2023, 11, 6886–6900 RSC.
- Y. Cheng, X. Xu, Y. Li, Y. Zhang and Y. Song, Comput. Mater. Sci., 2022, 202, 110971 CrossRef CAS.
- X. Qian, L. Li, Y. Li, Z. Liu, Z. Tian, C. Zhan and L. Chen, Phys. Chem. Chem. Phys., 2021, 23, 12431–12438 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. D. Gouveia, Á. Morales-García, F. Viñes, J. R. B. Gomes and F. Illas, ACS Nano, 2022, 16, 12541–12552 CrossRef CAS PubMed.
- V. Parey, B. M. Abraham, S. H. Mir and J. K. Singh, ACS Appl. Mater. Interfaces, 2021, 13, 35585–35594 CrossRef CAS PubMed.
- G. Gao, A. P. O'Mullane and A. Du, ACS Catal., 2017, 7, 494–500 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- R. Morales-Salvador, J. D. Gouveia, Á. Morales-García, F. Viñes, J. R. B. Gomes and F. Illas, ACS Catal., 2021, 11, 11248–11255 CrossRef CAS.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- M. López, Á. Morales-García, F. Viñes and F. Illas, ACS Catal., 2021, 11, 12850–12857 CrossRef.
- J. D. Gouveia, Á. Morales-García, F. Viñes, F. Illas and J. R. B. Gomes, Appl. Catal., B, 2020, 260, 118191 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- H. A. Hansen, I. C. Man, F. Studt, F. Abild-Pedersen, T. Bligaard and J. Rossmeisl, Phys. Chem. Chem. Phys., 2010, 12, 283–290 RSC.
- W. Yuan, L. Cheng, Y. An, H. Wu, N. Yao, X. Fan and X. Guo, ACS Sustain. Chem. Eng., 2018, 6, 8976–8982 CrossRef CAS.
- N. A. Adibah, S. N. A. Zaine and M. F. A. Shukur, Mater. Sci. Forum, 2021, 1023, 15–20 Search PubMed.
- T. Li, L. Yao, Q. Liu, J. Gu, R. Luo, J. Li, X. Yan, W. Wang, P. Liu, B. Chen, W. Zhang, W. Abbas, R. Naz and D. Zhang, Angew. Chem., Int. Ed., 2018, 57, 6115–6119 CrossRef CAS PubMed.
- Z. Guo, Y. Li, B. Sa, Y. Fang, J. Lin, Y. Huang, C. Tang, J. Zhou, N. Miao and Z. Sun, Appl. Surf. Sci., 2020, 521, 146436 CrossRef CAS.
- Y. Li, Y. Chen, Z. Guo, C. Tang, B. Sa, N. Miao, J. Zhou and Z. Sun, J. Chem. Eng., 2022, 429, 132171 CrossRef CAS.
- V. Parey, B. M. Abraham, M. V. Jyothirmai and J. K. Singh, Catal. Sci. Technol., 2022, 12, 2223–2231 RSC.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- I. Fishtik and R. Datta, Chem. Eng. Sci., 2000, 55, 4029–4043 CrossRef CAS.
- Y. Xiao and W. Zhang, Nanoscale, 2020, 12, 7660–7673 RSC.
- J. N. Brønsted, Chem. Rev., 1928, 5, 231–338 CrossRef.
- K. Niu, L. Chi, J. Rosen and J. Björk, J. Phys. Chem. Lett., 2022, 13, 2800–2807 CrossRef CAS PubMed.
- K. S. Exner and H. Over, Acc. Chem. Res., 2017, 50, 1240–1247 CrossRef CAS PubMed.
- M. López, K. S. Exner, F. Viñes and F. Illas, J. Catal., 2023, 421, 252–263 CrossRef.
- H. Chen, A. D. Handoko, T. Wang, J. Qu, J. Xiao, X. Liu, D. Legut, Z. Wei Seh and Q. Zhang, ChemSusChem, 2020, 13, 5690–5698 CrossRef CAS PubMed.
- N. Li, X. Wang, X. Lu, P. Zhang and W. J. Ong, Chem.–An Euro. J., 2021, 27, 17900–17909 CrossRef CAS PubMed.
- S. Baskaran and J. Jung, Appl. Surf. Sci., 2022, 592, 153339 CrossRef CAS.
- NIST Standard Reference Database SRD Number 69, DOI:10.18434/T4D303.
- Q. Li, Y. Ouyang, S. Lu, X. Bai, Y. Zhang, L. Shi, C. Ling and J. Wang, Chem. Commun., 2020, 56, 9937–9949 RSC.
- Á. Morales-García, A. Fernández-Fernández, F. Viñes and F. Illas, J. Mater. Chem. A, 2018, 6, 3381–3385 RSC.
- R. Morales-Salvador, Á. Morales-García, F. Viñes and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 17117–17124 RSC.
- Collision Theory, Chemistry LibreTexts, Libretexts, 2017 Search PubMed.
- S. Pogodin and N. López, ACS Catal., 2014, 4, 2328–2332 CrossRef CAS PubMed.
- R. Bisson, M. Sacchi, T. T. Dang, B. Yoder, P. Maroni and R. D. Beck, J. Phys. Chem. A, 2007, 111, 12679–12683 CrossRef CAS PubMed.
- C. Kunkel, F. Viñes and F. Illas, Energy Environ. Sci., 2016, 9, 141–144 RSC.
- T. Shimanouchi, Tables of Molecular Vibrational Frequencies Consolidated Volume I, National Bureau of Standards, 1972, pp. 1–160 Search PubMed.
- P. W. Atkins and J. De Paula, Atkins' Physical Chemistry. Oxford University Press, 8th edn, 2006 Search PubMed.
- A. V. Leont’eva, A. Y. Zakharov and A. Y. Prokhorov, arXiv, 2017, preprint, arXiv:1708.08077, DOI:10.48550/arXiv.1708.08077.
- H. Ooka, J. Huang and K. S. Exner, Front. Energy Res., 2021, 9, 654460 CrossRef.
- J. R. Pankhurst, P. Iyengar, A. Loiudice, M. Mensi and R. Buonsanti, Chem. Sci., 2020, 11, 9296–9302 RSC.
- A. Mazheika, Y. G. Wang, R. Valero, F. Viñes, F. Illas, L. M. Ghiringhelli, S. V. Levchenko and M. Scheffler, Nat. Commun., 2022, 13, 419 CrossRef CAS PubMed.
- M. López, L. Broderick, J. J. Carey, F. Viñes, M. Nolan and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 22179–22186 RSC.
- H. Prats, H. McAloone, F. Viñes and F. Illas, J. Mater. Chem. A, 2020, 8, 12296–12300 RSC.
- J. D. Wiensch, J. John, J. M. Velazquez, D. A. Torelli, A. P. Pieterick, M. T. McDowell, K. Sun, X. Zhao, B. S. Brunschwig and N. S. Lewis, ACS Energy Lett., 2017, 2, 2234–2238 CrossRef CAS.
- Á. Morales-García, M. Mayans-Llorach, F. Viñes and F. Illas, Phys. Chem. Chem. Phys., 2019, 21, 23136–23142 RSC.
- A. D. Handoko, K. D. Fredrickson, B. Anasori, K. W. Convey, L. R. Johnson, Y. Gogotsi, A. Vojvodic and Z. W. Seh, ACS Appl. Energy Mater., 2018, 1, 173–180 CrossRef CAS.
- N. H. Attanayake, H. R. Banjade, A. C. Thenuwara, B. Anasori, Q. Yan and D. R. Strongin, Chem. Commun., 2021, 57, 1675–1678 RSC.
- S. Cao, Y. Hu, C. Yang, J. Li, H. Chen, S. Wei, S. Liu, Z. Wang, D. Sun and X. Lu, J. CO2 Util., 2022, 62, 102074 CrossRef CAS.
- S. Lu, Y. Zhang, F. Lou and Z. Yu, J. CO2 Util., 2022, 62, 102069 CrossRef CAS.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315 RSC.
- Z. W. Seh, K. D. Fredrickson, B. Anasori, J. Kibsgaard, A. L. Strickler, M. R. Lukatskaya, Y. Gogotsi, T. F. Jaramillo and A. Vojvodic, ACS Energy Lett., 2016, 1, 589–594 CrossRef CAS.
- C. Shi, H. A. Hansen, A. C. Lausche and J. K. Nørskov, Phys. Chem. Chem. Phys., 2014, 16, 4720–4727 RSC.
- X. Hong, K. Chan, C. Tsai and J. K. Nørskov, ACS Catal., 2016, 6, 4428–4437 CrossRef CAS.
- Y. W. Cheng, J. H. Dai, Y. M. Zhang and Y. Song, J. Mater. Chem. A, 2018, 6, 20956–20965 RSC.
- Y. W. Cheng, J.-H. Dai, Y. M. Zhang and Y. Song, J. Phys. Chem. C, 2018, 122, 28113–28122 CrossRef CAS.
- S. Lu, H. L. Huynh, F. Lou, M. Guo and Z. Yu, J. CO2 Util., 2021, 51, 101645 CrossRef CAS.
- B. L. Sheets and G. G. Botte, ChemComm, 2018, 54, 4250–4253 RSC.
- M. A. Ortuño, O. Hollóczki, B. Kirchner and N. López, J. Phys. Chem. Lett., 2019, 10, 513–517 CrossRef PubMed.
- J. M. McEnaney, A. R. Singh, J. A. Schwalbe, J. Kibsgaard, J. C. Lin, M. Cargnello, T. F. Jaramillo and J. K. Nørskov, Energy Environ. Sci., 2017, 10, 1621–1630 RSC.
- S. Malkhandi, B. Yang, A. K. Manohar, G. K. S. Prakash and S. R. Narayanan, J. Am. Chem. Soc., 2013, 135, 347–353 CrossRef CAS PubMed.
- A. K. Manohar, S. Malkhandi, B. Yang, C. Yang, G. K. Surya Prakash and S. R. Narayanan, J. Electrochem. Soc., 2012, 159, A1209 CrossRef CAS.
- K. A. Brown, D. F. Harris, M. B. Wilker, A. Rasmussen, N. Khadka, H. Hamby, S. Keable, G. Dukovic, J. W. Peters, L. C. Seefeldt and P. W. King, Science, 2016, 352, 448–450 CrossRef CAS PubMed.
- D. Zhu, L. Zhang, R. E. Ruther and R. J. Hamers, Nat. Mater., 2013, 12, 836–841 CrossRef CAS PubMed.
- X. Guo and S. Huang, Electrochim. Acta, 2018, 284, 392–399 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta00320a |
| This journal is © The Royal Society of Chemistry 2024 |