Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of the lithium plating triggering criterion in graphite electrodes†
Jiani
Li
a,
Lubing
Wang
b and
Jun
Xu
 *cd
*cd
aDepartment of Mechanical Engineering and Engineering Science, The University of North Carolina at Charlotte, Charlotte, NC 28223, USA
bKey Laboratory Impact & Safety Engineering, Ministry of Education, Ningbo University, Ningbo, Zhejiang 315211, China
cDepartment of Mechanical Engineering, University of Delaware, Newark, DE 19716, USA. E-mail: junxu@udel.edu; Fax: +1-302-831-0121; Tel: +1-302-831-0121
dEnergy Sustainability and Mechanics Laboratory (ESMLab), University of Delaware, Newark, DE 19716, USA
First published on 16th April 2024
Abstract
Lithium plating is considered an undesirable side reaction because it can induce capacity fading and pose safety concerns in Li-ion batteries. The timely detection of lithium plating onset is crucial for both mechanistic investigations and ensuring the safe and durable operation of batteries. In this study, discharging tests were conducted by varying the set capacity in graphite/Li cells to induce lithium plating on the graphite electrode. Based on a comprehensive analysis of the voltage curves and the morphological characterization of disassembled cells, the inflection point on the differential voltage curve during the discharging process was identified as the precise onset time of lithium plating. Electrochemical models were developed to further elucidate the mechanisms governing the onset of lithium plating. Compared with the model based on the potential criterion, the model employing the concentration criterion demonstrated enhanced precision in predicting lithium plating, particularly under high C rates. Based on the model with the concentration criterion, the discharging protocol was optimized parametrically to achieve high discharging efficiency and restrain lithium plating. This nuanced understanding contributes to determining the onset of lithium plating more accurately, thereby facilitating a more robust battery design and durable yet fast charging protocols.
1. Introduction
Lithium-ion batteries (LIBs) have gained widespread recognition in consumer electronics1,2 and electric transportation3,4 owing to their outstanding attributes such as high energy density,5 high power density,6 prolonged lifecycle, and cost-effectiveness. During typical charging conditions, lithium ions intercalate into the layered structure of graphite in a series of stages, culminating in the formation of LiC6 upon complete lithiation.7 However, under specific conditions such as high charging rates (C rates),8–10 overcharging,11–13 and low temperatures,14,15 lithium ions can undergo direct reduction to form metallic lithium on the graphite surface, a phenomenon known as “lithium plating”. This unwanted side reaction may result in increased internal resistance, capacity fading,16,17 Li dendrite formation,18,19 and internal short circuits. Detecting the onset of lithium plating is imperative to determine the health and safety status of a running cell.Various experimental methods have been employed to comprehensively understand lithium plating and detect its occurrence, including electrochemical techniques and physical characterization methods.20 Leveraging the reaction of the plated Li metal with the electrolyte and the different electrochemical properties of the plated Li metal and intercalated carbon (LixC6),21 various electrochemical methods have been explored to detect lithium plating on graphite electrodes, such as the measurement of coulombic efficiency,13 discharging/rest voltage curves8,22–24 and the potential of graphite electrodes in cells in 2-electrode25 and 3-electrode26 setups. While these methods are nondestructive and convenient for engineering applications, they can only partially confirm the presence of plated lithium and do not detect the precise onset of lithium plating in situ.20 Physical characterization methods such as optical microscopy,10,27 scanning electron microscopy (SEM),28 transmission electron microscopy (TEM),29 nuclear magnetic resonance spectroscopy (NMR),30 and in situ neutron diffraction,17 offer direct detection of plated lithium metal but their widespread application is hindered by expensive equipment and implementation challenges. Consequently, there is a need for an economical, convenient, nondestructive, and accurate in situ method for detecting the onset of lithium plating.
Understanding the mechanism of lithium plating is imperative to determining its onset. Conventionally, it is considered that lithium plating becomes thermodynamically possible when the over-potential of the lithium plating reaction reaches a value smaller than 0 V vs. Li/Li+ (ηpla < 0 V).3,31,32 Elevated polarization resulting from high C rates25 and low temperatures33 contributes to the reduction in graphite potential, thereby promoting the occurrence of lithium plating. However, although the potential criterion (ηpla < 0 V) is considered a necessary condition for lithium plating, it is insufficient, as demonstrated by several experiments.26,34–37 Uhlmann et al.,35 for instance, subjected graphite/Li cells to charging pulses at varying C rates after reaching a certain state of charge (SOC). Their results indicated that during charging pulses at 5C and 10C, lithium plating did not occur until the graphite potential fell significantly below 0 V. Gao et al.,37 by utilizing in situ optical microscopy coupled with electrochemical measurements, observed that a single graphite particle could withstand a negative potential of −115 mV before any plated Li metal was observed during discharging at 0.6C. The above experiments were conducted on cells with a 2-electrode setup, which may affect the measurement accuracy of graphite potential due to polarization on the counter electrode. Based on this, Wandt et al.26 performed forced lithium plating on cells with a 3-electrode setup. By employing operando electron paramagnetic resonance (EPR) spectroscopy, they observed that the onset of lithium plating happened at a negative graphite potential measured with a reference electrode setup. Besides, the electrolyte concentration gradient between the graphite electrode and reference electrode was less significant due to the low C rate of 0.1C, guaranteeing the measurement accuracy of graphite potential. It has been demonstrated that the potential criterion (ηpla < 0 V) alone is inadequate to determine lithium plating onset. Factors other than potential, such as concentration, may play vital roles in triggering lithium plating. Using in situ optical microscopy, some researchers37–39 found that the lithium plating occurred exclusively on the fully lithiated parts of the graphite electrode, while the onset voltage was much below 0 V versus Li/Li+.37,38 Such observations illustrate that Li concentration in graphite is a more accurate indicator of lithium plating than graphite potential, and this has been rationalized by analyzing the energetics and kinetics of the lithium intercalation and lithium plating.37 During the charging process, lithium intercalation is always more favored energetically and kinetically than lithium plating even when the potential criterion for lithium plating is satisfied (ηpla < 0 V). The tipping point occurs when the graphite surface is saturated with intercalated Li ions (cs,surf ≥ cs,max). At this point, lithium intercalation is energetically equally favorable but kinetically less favorable than lithium plating due to the lack of sites for Li ions to intercalate and the drop in nucleation barrier for lithium plating. As a result, the intercalation reaction is restrained, and the applied current is redirected to lithium plating. Numerical models have been developed to predict the onset of lithium plating. While most researchers have traditionally adopted graphite potential as the primary indicator13,32,40–42 that signifies lithium plating occurrence when the graphite potential falls below 0 V vs. Li/Li+, it is emphasized that the potential criterion (ηpla < 0 V) is not universally applicable under all conditions, as mentioned previously. Therefore, the Li concentration in graphite has emerged as an equally critical parameter in modeling and predicting lithium plating onset.
In this study, our primary objective is the precise detection of the onset of lithium plating on graphite by exploring the underlying mechanisms through the synergistic integration of experiments and electrochemical modeling. To achieve this, discharging tests were conducted on graphite/Li cells by setting different capacities and intentionally inducing lithium plating on the graphite electrode. The onset of lithium plating was discerned by analyzing the indirect differential voltage curves and direct morphological characterization of the disassembled cells. Subsequently, an electrochemical model was formulated to provide a comprehensive understanding of the mechanism governing the onset of lithium plating. In addition, various models incorporating different lithium plating criteria, such as the potential criterion (ηpla < 0 V) and the concentration criterion (cs,surf ≥ cs,max), were developed and systematically compared across different C rates. The modified criterion in our proposed model serves as a nuanced improvement, allowing for a more accurate depiction of the onset of lithium plating. Building upon the insights obtained from our models, we propose two optimal discharging protocols designed to enhance efficiency while mitigating the occurrence of lithium plating.
2. Experimental details
The electrochemical performance of the graphite electrode during overdischarge was assessed using CR2032 coin cells on an electrochemical workstation (Metrohm Autolab). The experimental cells were meticulously assembled in a glove box under an argon atmosphere using graphite as the working electrode and a Li plate as the counter electrode. The nominal capacity of the cells (Qn = 2.03 mA h) was calculated from the material loading on the graphite electrode (ESI†). Before the formal tests, the experimental cells underwent a pre-cycling process at 0.1C, involving three consecutive from 0.005 V to 2 V. The charging capacity observed during the third cycle was the rated capacity. Subsequently, only cells exhibiting rated capacity in the 1.81–1.92 mA h range were selected for the subsequent formal tests. This stringent selection criterion was followed to ensure consistency and reliability of electrochemical performance evaluation during the overdischarge process of the graphite electrode.In the formal experiments, the selected cells with similar rate capacities were discharged at 0.5C to different extents by setting different discharging capacities from 1 to 5 mA h. Subsequently, without any relaxation period, the cells were promptly charged at 0.5C until they reached a cut-off voltage of 2 V. Differential analyses7,8,22 were then applied to the discharging and charging curves mentioned above by employing an indirect detection method to assess the occurrence of lithium plating during the discharging process. Furthermore, the morphology of the disassembled cells was characterized to detect lithium plating directly. Specifically, the cells were initially discharged at 0.5C to different extents and immediately disassembled within the confines of a glove box to prevent stripping of the plated Li metal and the potential reaction between Li metal and the air. Additionally, overdischarge tests of the cells were conducted at 0.1C and 0.2C to validate the numerical model. The equilibrium potential of the graphite electrode (Fig. S1(a)†) used in the model was derived from the discharging test conducted at 0.01C. This comprehensive experimental approach, encompassing indirect and direct detection methods and numerical model validation, contributes to a robust understanding of lithium plating dynamics on the graphite electrode.
3. Numerical model
The electrochemical model applied in this work was developed based on the pseudo-two-dimensional (P2D) model,14,43,44 which consists of a one-dimensional representation of the cell and a second dimension representing the spherical active material particles. The basic equations in the model consist of charge conservation equations that describe potential distribution in the solid and liquid phases, mass conservation equations to describe the Li concentration distribution in the solid and liquid phases, and electrochemical kinetic equations that describe the reaction rates of lithium intercalation and lithium plating. In most cases,12,13,16,31,32 the potential of graphite is commonly used as the indicator of lithium plating. Lithium plating starts when the graphite potential drops below 0 V vs. Li/Li+. However, according to the assumption of solid diffusion limitation in graphite,37,45 lithium plating is triggered when the inserted Li ions saturate the graphite surface due to slow solid diffusion compared with intercalation. Accordingly, the criterion of Li concentration needs to be considered in some cases. In this work, a model with the concentration criterion is established to predict the onset of lithium plating and analyze the underlying mechanism.3.1. Charge conservation equations
In the battery, the solid-phase potential distribution is governed by Ohm's law:43,46| ∇ × (σeffs∇φs) = jtotal | (1) |
 | (2) |
 | (3) |
The governing equation of the liquid phase potential distribution and the corresponding boundary conditions at the current collector/graphite interface and graphite/separator interface are as follows:
 | (4) |
 | (5) |
 | (6) |
3.2. Mass conservation equations
The distribution of Li concentration inside the solid active material particles follows Fick's law47 (eqn (7)). cs denotes the Li concentration in the solid phase, Ds represents the solid phase diffusion coefficient (Fig. S2†), and r is the radius of the particle. The boundary condition at the particle center (r = 0) (eqn (8)) indicates that no Li source exists at the center of the particle. At the particle surface (r = Rs), the Li flux is determined by the local current density of lithium intercalation (jint). Here as represents the specific surface area of the particle.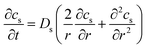 | (7) |
 | (8) |
 | (9) |
Li+ distribution in the liquid phase is directed by the Nernst–Plank equation (eqn (10)).48 The related boundary condition at the current collector/graphite interface is expressed as eqn (11).
 | (10) |
 | (11) |
 | (12) |
 | (13) |
3.3. Electrochemical kinetic equations
During the overdischarging process of the graphite/Li cell, lithium intercalation is the main electrochemical reaction at the surface of the graphite particles, while lithium plating is regarded as a side reaction that takes place when the required criterion is satisfied. Accordingly, the total volumetric current density jtotal is the sum of the current densities of lithium plating jpla and lithium intercalation jint.| jtotal = jpla + jint | (14) |
As mentioned above, jtotal is used in the charge conservation eqn (1) and (4) and the mass conservation eqn (10) as the reaction source. However, only jint is applied as the reaction source in eqn (9) since lithium present inside the particle comes entirely from lithium intercalation at the particle surface, irrelevant to lithium plating.
The volumetric current density of lithium plating jpla is expressed by the Butler–Volmer equation presented as eqn (15). Unlike the widely used models, which adopt the overpotential of lithium plating as the indicator of lithium plating (ηpla < 0 V),12,13,16,31,32 the Li concentration criterion is applied in the current model. Specifically, the expression of the exchange current density of lithium plating i0,pla (eqn (16)) indicates that lithium plating is induced when the Li concentration at the particle surface cs,surf exceeds the maximum value cs,max.
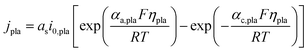 | (15) |
| i0,pla = Fkplacl(cs,surf ≥ cs,max) | (16) |
 | (17) |
α c,pla and αa,pla are the charge transfer coefficients of the cathode and anode, respectively. kpla represents the reaction rate constant for lithium plating. ηpla is the overpotential of lithium plating, and Eeq,pla is the equilibrium potential of lithium plating, which equals 0 V vs. Li/Li+. Rfilm represents the resistance of the surface film.
The volumetric current density of lithium intercalation jint is also expressed by the Butler–Volmer equation.31
 | (18) |
 | (19) |
| Δcs = min{max[(cs,max − cs,surf),cs1],cs2 − cs,surf} | (20) |
η int is the overpotential of lithium intercalation, which is calculated as
 | (21) |
The general expression of Δcs in a traditional P2D model is Δcs = cs,max − cs,surf,13,32 which will lead to non-convergence in models with the concentration criterion (ESI†). To avoid computational conflict and simulate the transition from lithium intercalation to lithium plating during the discharging progress, Δcs was modified as the function of cs,surf (eqn (20)), as depicted in Fig. S2.†cs1 and cs2 are the parameters that define Δcs and are adjusted by the calibration of the experimental and simulated voltages. Besides, kint is the reaction rate constant, and cl,ref represents the reference Li+ concentration in the liquid phase. αc,int and αa,int are the charge transfer coefficients of the cathode and anode, respectively. Eeq,int is the equilibrium potential of lithium intercalation on graphite (Fig. S1(a)†).
Based on mass conservation, the thickness of the plated Li metal layer δpla can be expressed as:
 | (22) |
 | (23) |
Besides, the pores in the graphite electrode are occupied by plated Li metal. As a result, the porosity of graphite can be written as:
| εl = εl,0 − asδpla | (24) |
The model was established and presented in COMSOL Multiphysics. The electrochemical parameters applied in the model are listed in Table S2.†
4. Results and discussion
4.1. Detection of the onset of lithium plating via experiments
To induce lithium plating on the graphite electrode and detect the onset of lithium plating, overdischarge tests were conducted on graphite/Li cells with 1.0 M LiPF6/EC + PC + EDC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as the electrolyte. Four cells denoted as A1–A4 were discharged at 0.5C to different extents by setting different discharging capacities (A1: 4.53 mA h, A2: 2.14 mA h, A3: 1.70 mA h, and A4: 1.38 mA h), and then immediately charged at 0.5C to 2 V with no relaxation. The U–Q and dU/dQ–Q curves of the discharging process (Fig. 1(a)) show the reliable repeatability of cell performance. The curves obtained during the subsequent charging process (Fig. 1(b)) were further analyzed to help determine the onset of Lithium plating. Lithium stripping plateaus were observed in the starting stage of the U–Q curves of cells A1 and A2. These stripping plateaus are attributed to the preferential stripping of plated Li metal due to its lower standard potential than lithium intercalated inside graphite.21 Besides, the peaks in the dU/dQ–Q curves of cells A1 and A2 correspond with the transition from lithium stripping to lithium deintercalation, which indicates that the capacity at the dU/dQ peak can be regarded as the amount of reversible Li metal. The lithium stripping plateau and peak indicate that lithium stripping occurs during the initial charging process in cells A1 and A2. Furthermore, they demonstrate that lithium plating occurs during the overdischarging process in A1 and A2. Cells A3 and A4 had no obvious Li stripping plateau or peak during the charging process (Fig. 1(b)). There are two possible explanations for this phenomenon: (i) lithium stripping does not occur during charging; (ii) lithium stripping occurs, but the amount of plated Li metal is too small to be detected. As a result, it is challenging to determine if lithium plating occurred in cells A3 and A4 during the discharging process.
1) as the electrolyte. Four cells denoted as A1–A4 were discharged at 0.5C to different extents by setting different discharging capacities (A1: 4.53 mA h, A2: 2.14 mA h, A3: 1.70 mA h, and A4: 1.38 mA h), and then immediately charged at 0.5C to 2 V with no relaxation. The U–Q and dU/dQ–Q curves of the discharging process (Fig. 1(a)) show the reliable repeatability of cell performance. The curves obtained during the subsequent charging process (Fig. 1(b)) were further analyzed to help determine the onset of Lithium plating. Lithium stripping plateaus were observed in the starting stage of the U–Q curves of cells A1 and A2. These stripping plateaus are attributed to the preferential stripping of plated Li metal due to its lower standard potential than lithium intercalated inside graphite.21 Besides, the peaks in the dU/dQ–Q curves of cells A1 and A2 correspond with the transition from lithium stripping to lithium deintercalation, which indicates that the capacity at the dU/dQ peak can be regarded as the amount of reversible Li metal. The lithium stripping plateau and peak indicate that lithium stripping occurs during the initial charging process in cells A1 and A2. Furthermore, they demonstrate that lithium plating occurs during the overdischarging process in A1 and A2. Cells A3 and A4 had no obvious Li stripping plateau or peak during the charging process (Fig. 1(b)). There are two possible explanations for this phenomenon: (i) lithium stripping does not occur during charging; (ii) lithium stripping occurs, but the amount of plated Li metal is too small to be detected. As a result, it is challenging to determine if lithium plating occurred in cells A3 and A4 during the discharging process.
 | ||
| Fig. 1 The U–Q and dU/dQ–Q curves cells A1 to A4 during (a) discharging tests to different capacities and (b) charging tests. | ||
The results confirm that lithium plating occurs in cells A1 and A2 during the discharging process. Based on this, three possible locations for lithium plating onset defined as P0, P1, and P2 were identified according to the characteristics of the U–Q and dU/dQ–Q curves obtained during discharging (Fig. 1(a)). P0 was defined at U = 0 V since most researchers12,13,31,32 believe that lithium plating occurs when the graphite voltage drops below 0 V (based on potential criterion). P1 was defined at the valley of dU/dQ–Q. In comparison with the normal discharge test at 0.01C (Fig. S1(b)†), the dU/dQ–Q curve of the overdischarge test at 0.5C (Fig. 1(a)) presented an additional valley at around 1.63 mA h, which may result from the occurrence of lithium plating. Further, P2 was defined at dU/dQ = 0, representing the onset of the final plateau stage of the U–Q curve. Generally, the plateaus of the U–Q curve represent the coexisting phase regions since the chemical potential of Li in coexisting phases is equal.49 Accordingly, the plateau after P2 represents the coexisting phase region of LiC6 and Li metal.
To further determine the onset of lithium plating, the morphologies of the disassembled cells with varying discharging capacities were systematically characterized (Fig. 2). Cells B1 and B2 were discharged to capacities exceeding P2 (Fig. 2(a)) and promptly disassembled within the glove box. Evident silver Li metal deposits were observed on the graphite surface of both B1 and B2 (Fig. 2(b)). Cell B3, which was discharged to a capacity surpassing P1 but lower than P2 (Fig. 2(a)), exhibited a modest amount of Li metal on its graphite surface (Fig. 2(b)). In contrast, cell B4, which was discharged to a capacity below P1, displayed no discernible plated Li metal on the disassembled graphite electrode. Consequently, it can be inferred that the onset of lithium plating happens at a capacity value between those of B3 and B4, close to or precisely at P1. This characterization allows for the precise identification of the lithium plating onset point in the specific discharge capacity range defined by cells B3 and B4. Besides, the graphite voltage range between B3 and B4 (−0.076 to −0.021 V) indicates that lithium plating occurs at a negative graphite voltage, which is not explained by the traditional potential criterion (ηpla < 0 V).3,31,32 As described in some reports,37,50,51 Li concentration in graphite is considered as the indicator of lithium plating instead of graphite voltage. In this case, lithium plating may be induced since Li concentration on the graphite particle surface reaches the saturation level.
 | ||
| Fig. 2 (a) Curves of cells B1–B4 discharged at 0.5C to different capacities. (b) Morphology of the graphite electrodes disassembled from cells B1–B4. | ||
4.2. Detection of the onset of lithium plating via simulations
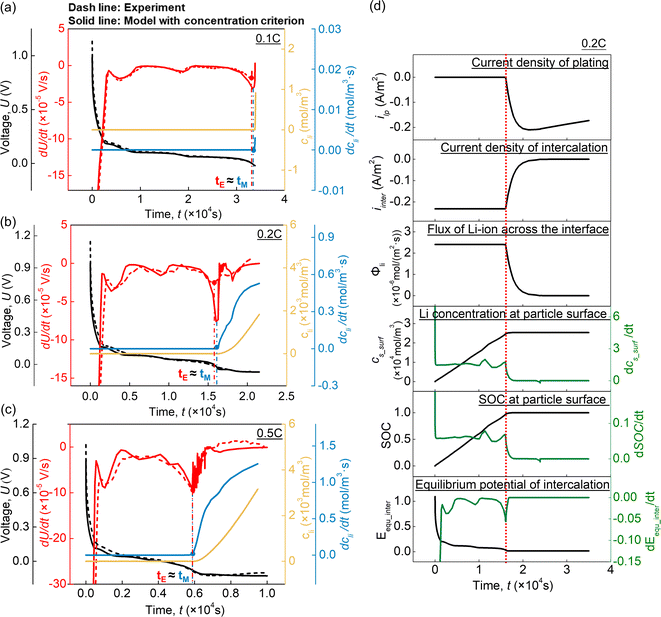
The above experiments provide a relatively narrow range for lithium plating onset, yet the precise location of lithium plating onset and the underlying mechanism were confirmed and interpreted by simulation. Considering that the potential criterion (ηpla < 0 V) is not suitable to elucidate the occurrence of lithium plating in this case, a model was established using the concentration criterion for lithium plating (cs,surf ≥ cs,max). Fig. 3(a–c) show the model predictions, in which the dashed lines denote the experimental results, while the simulated results are shown by solid lines. The simulated U–t and dU/dt–t curves of the overdischarging cases at 0.1C, 0.2C, and 0.5C fitted the experimental results well, validating the accuracy of the model. Besides, according to the rate of plated Li metal concentration variation dcli/dt, the turning point of the simulated dcli/dt curve can be determined as the onset of lithium plating and is denoted as tM. When lithium plating occurs at tM, valley points appear on the simulated dU/dt–t curves in all cases, indicating that this valley point P1 arises due to the occurrence of lithium plating. Based on this, the valley points on the experimental dU/dt–t curves can be determined as the experimental onset points of lithium plating tE. Therefore, this model with the concentration criterion can precisely predict the actual lithium plating onset point (tE ≈ tM) at various C rates.Further analysis was conducted to interpret the relationship between lithium plating occurrence and the valley point on the dU/dt–t curve (Fig. 3(d)). When lithium plating occurs, the current density of plating ipla starts to increase from 0, while the current density of intercalation iint starts to decrease. As a result, the flux of Li ions across the particle surface Φli, which is determined by iint, starts to decrease. With the decrement of Φli, the Li concentration and SOC at the particle surface keep increasing, but the corresponding variation rates (dcs_surf/dt, dSOC/dt) begin to decrease. Since the equilibrium potential of intercalation Eequ_int is the function of SOC, the decrease in dSOC/dt leads to a decrease in dEequ_int/dt, which finally causes the valley on the dU/dt–t curve.
As described above, the model with the concentration criterion can predict the onset of lithium plating precisely. To further demonstrate the superiority of the concentration criterion in lithium plating onset prediction, the simulated results obtained using the models based on the concentration criterion (cs,surf ≥ cs,max) and the potential criterion (ηpla < 0 V) were compared. The governing equations and results of the model based on the potential criterion (ηpla < 0 V) (Fig. S3†) are given in detail as ESI.† In order to quantify the accuracy of the model in lithium plating onset prediction, the prediction error of the lithium plating onset time ε is defined as the ratio of the interval between the time of simulated and experimental lithium plating onset (|tM − tE|) to the experimental lithium plating onset time (tE). As shown in Fig. 4(a), for the model with the potential criterion, the error in predicted lithium plating onset ε generally increased from 1.21% to 8.34% as the C rate varied from 0.1C to 0.5C. In comparison, ε of the model involving the concentration criterion increased initially from 0.84% to 2.27% as the C rate was changed from 0.1C to 0.2C but remained at this level while the C rate was increased from 0.2C to 0.5C. These results demonstrate that the concentration criterion is more suitable to predict the actual lithium plating onset time under a high C rate than the potential criterion. The adoption of the concentration criterion can keep the lithium plating onset prediction error at a relatively low level for all C rates, indicating that experimental lithium plating is more likely to be induced by the saturated Li concentration on the graphite particle surface rather than the negative overpotential of lithium plating.
Furthermore, the evolution of the minimum overpotential of lithium plating ηpla_min in the graphite electrode at different C rates and the maximum surface concentration of Li ions cs,surf_max among these graphite electrodes were extracted and analyzed, as shown in Fig. 4(b)ηpla_min continued to decrease as time increased, and the potential criterion was triggered when ηpla_min reached 0 V (red circle). cs,surf_max continued to increase with time, and the concentration criterion was triggered when cs,surf_max reached cs_max (blue circle). It was observed that the potential criterion was triggered earlier than the concentration criterion in all cases. As the C rate increased, the difference between the triggering times of the potential criterion and the concentration criterion became larger since cs,surf_max at the potential criterion triggering time (red circle) decreased. As a result, the lithium plating onset time predicted by the model with the potential criterion was earlier than the actual lithium plating onset at a high C rate of 0.5C (Fig. S3(c)†).
4.3. Optimal discharging protocol
By applying the concentration criterion for lithium plating, the model can precisely predict the lithium plating onset under various C rates. Based on this, the discharging protocol was optimized to restrain lithium plating and enhance the discharging efficiency. First, two typical protocols CC(0.5C)_CV and CC(0.5C)_CC(0.4C) are proposed (Fig. 5(a) and (b)). In CC(0.5C)_CV, the cell is discharged at a constant current of 0.5C (grey part) until the concentration criterion of lithium plating is triggered (cs,surf = cs,max); then the cell is discharged at a constant voltage to a certain SOC (green part). The simulated result of the current density of lithium plating ipla shows that lithium plating occurs at the starting point of the CV process since cs,surf continues to increase and remains larger than cs,max during the CV process. The traditional CC_CV protocol cannot restrain lithium plating. In CC(0.5C)_CC(0.4C), as shown in Fig. 5(b), the cell is discharged at 0.5C (grey part) until cs,surf = cs,max; then it is discharged at 0.4C to a certain SOC (green part). During the CC(0.4C) process, cs,surf first decreases from cs,max and then increases to exceed cs,max. As a result, the onset of lithium plating is postponed in CC(0.5C)_CC(0.4C) compared with CC(0.5C)_CV.Furthermore, different C rates denoted as nC (n = 0.1, 0.2, 0.3, and 0.4) were adopted for the second CC process, and the effects of C rate (nC) were analyzed, as presented in Fig. 5(c–f). As the C rate decreased from 0.4C to 0.1C, the voltage recovery at the starting point of the CC(nC) process increased from 0.02 V to 0.11 V. Besides, while the C rate decreased from 0.4C to 0.2C, the onset of lithium plating was postponed from t1 (6027 s) to t3 (7340 s) (Fig. 5(d)) since that the triggering time of the concentration criterion cs,surf ≥ cs,max is postponed from t1 (6027 s) to t3 (7340 s) (Fig. 5(e)). It should be noted that lithium plating would not occur in the CC(0.5C)_CC(0.1C) case since the concentration criterion is not triggered during the whole discharging process. Although the decrease in the C rate in the second CC process contributes to the delay in lithium plating, the discharging efficiency also becomes poorer since it takes more discharging time to reach the set discharging SOC. Besides, when lithium plating occurs respectively at t1 (6027 s), t2 (6400 s) and t3 (7340 s) for n = 0.4, 0.3 and 0.2 (Fig. 5(d)), valley points appear on the dU/dt–t curves (Fig. 5(c)). The specific valley points on dU/dt–t curves can be recognized as the indicator of concentration saturation at the graphite particle surface and lithium plating occurrence. Accordingly, the lithium plating onset point can be detected in situ by monitoring the dU/dt–t data, which is simple and suitable for engineering applications.
As mentioned above, lithium plating is not induced when the cell is discharged according to CC(0.5C)_CC(0.1C). Based on this protocol and the model involving the concentration criterion, four multi-CC discharging protocols (Table 1, modes 1–4) are proposed by inserting CC steps between CC(0.5C) and CC(0.1C). The ΔC rate is defined as the difference in C rates between the adjacent CC steps. The multi-CC discharging protocols are based on the concentration criteria of lithium plating. Specifically, the transition between two adjacent CC steps is induced when the concentration criterion is triggered (cs,surf = cs,max). No lithium plating occurs in these four modes (Fig. 6(b)) since cs,surf remains lower than or equal to cs,max during the whole discharging process (Fig. 6(c)). Besides, as the ΔC rate decreases from 0.4C (mode 1) to 0.05C (mode 4), the discharging time to reach the set discharging SOC becomes shorter (Fig. 6(d)). This indicates that decreasing the ΔC rate in the multi-CC protocol can enhance the discharging efficiency of the cell with no lithium plating.
| Name | C-rate of each CC step | ΔC rate |
|---|---|---|
| Mode 1 | 0.5C_0.1C | 0.4C |
| Mode 2 | 0.5C_0.3C_0.1C | 0.2C |
| Mode 3 | 0.5C_0.4C_0.3C_0.2C_0.1C | 0.1C |
| Mode 4 | 0.5C_0.45C_0.4C_0.35C_0.3C_0.25C_0.2C_0.15C_0.1C | 0.05C |
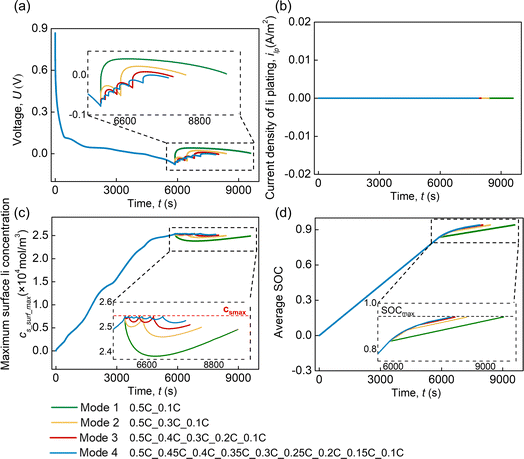 | ||
| Fig. 6 (a) Voltage and (b) current density of lithium plating, (c) the maximum surface Li concentration, and (d) average SOC in the multi-CC discharging protocols with different ΔC rates. | ||
5. Conclusions
Detecting the initiation of lithium plating on graphite electrodes holds paramount importance in ensuring the safety of batteries. In this study, we conducted a comprehensive experimental investigation to precisely determine the onset of lithium plating on graphite. Additionally, we developed electrochemical models by employing different lithium plating criteria, specifically the potential and concentration criteria, to elucidate the mechanisms governing the initiation of lithium plating. Using the modified model, a parametric study was undertaken to derive an optimized discharging protocol that not only exhibits high discharging efficiency but also mitigates the occurrence of lithium plating. The key findings and conclusions drawn from this research can be summarized as follows:(1) We introduced and validated a novel method for the in situ detection of the onset of lithium plating based on the distinctive characteristics of the dU/dt–t curve. The valley point, denoted as P1, in the dU/dt–t curve of the discharging process was established as a precise indicator of the initiation of lithium plating.
(2) Electrochemical models incorporating distinct lithium plating criteria were formulated and examined. Comparative analysis revealed that the model incorporating a concentration criterion demonstrated superior suitability in predicting the onset of lithium plating, particularly under elevated C rates, in contrast to the model that relied on a potential criterion.
(3) In the context of multi-CC (constant current) protocols, our investigation determined that the reduction in ΔC rate between adjacent CC steps contributes to an enhanced discharging efficiency, while concurrently mitigating the occurrence of lithium plating. This finding underscores the significance of protocol design in achieving optimal battery performance with minimal risk of lithium plating.
These findings contribute to advancing the understanding of lithium plating phenomena and offer practical implications for the design and operation of lithium-ion batteries to enhance both safety and efficiency.
Data availability
The datasets used in this study are available from the corresponding author upon request.Conflicts of interest
The authors declare no competing interests for this work.Acknowledgements
L. W. appreciates the financial support from the National Science Foundation of China (12102212, 11872099).References
- J. Zhang, Y. Wang, B. Jiang, H. He, S. Huang, C. Wang, Y. Zhang, X. Han, D. Guo, G. He and M. Ouyang, Nat. Commun., 2023, 14, 5940 CrossRef CAS PubMed.
- S. Li, J. Niu, Y. C. Zhao, K. P. So, C. Wang, C. A. Wang and J. Li, Nat. Commun., 2023, 14, 5664 CrossRef CAS PubMed.
- T. Waldmann, B.-I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2018, 384, 107–124 CrossRef CAS.
- B. Liu, X. Duan, C. Yuan, L. Wang, J. Li, D. P. Finegan, B. Feng and J. Xu, J. Mater. Chem. A, 2021, 9, 7102–7113 RSC.
- X. Gao, W. Lu and J. Xu, Nano Energy, 2021, 81, 105591 CrossRef CAS.
- W. Wu, X. Xiao and X. Huang, Electrochim. Acta, 2012, 83, 227–240 CrossRef CAS.
- S. Weng, S. Wu, Z. Liu, G. Yang, X. Liu, X. Zhang, C. Zhang, Q. Liu, Y. Huang and Y. Li, Carbon Energy, 2023, 5, 10 CrossRef.
- Y. Chen, L. Torres-Castro, K.-H. Chen, D. Penley, J. Lamb, M. Karulkar and N. P. Dasgupta, J. Power Sources, 2022, 539, 231601 CrossRef CAS.
- K. S. N. Vikrant and S. Allu, J. Electrochem. Soc., 2021, 168, 020536 CrossRef CAS.
- Y. Chen, K.-H. Chen, A. J. Sanchez, E. Kazyak, V. Goel, Y. Gorlin, J. Christensen, K. Thornton and N. P. Dasgupta, J. Mater. Chem. A, 2021, 9, 23522–23536 RSC.
- D. Ren, X. Feng, L. Lu, X. He and M. Ouyang, Appl. Energy, 2019, 250, 323–332 CrossRef CAS.
- W. Mei, L. Zhang, J. Sun and Q. Wang, Energy Storage Mater., 2020, 32, 91–104 CrossRef.
- W. Mei, L. Jiang, C. Liang, J. Sun and Q. Wang, Energy Storage Mater., 2021, 41, 209–221 CrossRef.
- T. Sun, T. Shen, Y. Zheng, D. Ren, W. Zhu, J. Li, Y. Wang, K. Kuang, X. Rui, S. Wang, L. Wang, X. Han, L. Lu and M. Ouyang, Electrochim. Acta, 2022, 425, 140701 CrossRef CAS.
- M. Storch, J. P. Fath, J. Sieg, D. Vrankovic, C. Krupp, B. Spier and R. Riedel, J. Energy Storage, 2021, 41, 102887 CrossRef.
- X.-G. Yang, Y. Leng, G. Zhang, S. Ge and C.-Y. Wang, J. Power Sources, 2017, 360, 28–40 CrossRef CAS.
- N. Paul, J. Wandt, S. Seidlmayer, S. Schebesta, M. J. Mühlbauer, O. Dolotko, H. A. Gasteiger and R. Gilles, J. Power Sources, 2017, 345, 85–96 CrossRef CAS.
- C. Yuan, X. Gao, Y. Jia, W. Zhang, Q. Wu and J. Xu, Nano Energy, 2021, 86, 106057 CrossRef CAS.
- X. Yang, X. Gao, C. Zhao, Q. Sun, Y. Zhao, K. Adair, J. Luo, X. Lin, J. Liang, H. Huang, L. Zhang, S. Lu, R. Li and X. Sun, Energy Storage Mater., 2020, 27, 198–204 CrossRef.
- P. P. Paul, E. J. McShane, A. M. Colclasure, N. Balsara, D. E. Brown, C. Cao, B.-R. Chen, P. R. Chinnam, Y. Cui, E. J. Dufek, D. P. Finegan, S. Gillard, W. Huang, Z. M. Konz, R. Kostecki, F. Liu, S. Lubner, R. Prasher, M. B. Preefer, J. Qian, M.-T. F. Rodrigues, M. Schnabel, S.-B. Son, V. Srinivasan, H.-G. Steinrück, T. R. Tanim, M. F. Toney, W. Tong, F. Usseglio-Viretta, J. Wan, M. Yusuf, B. D. McCloskey and J. Nelson Weker, Adv. Energy Mater., 2021, 11, 2100372 CrossRef CAS.
- Q. Liu, C. Du, B. Shen, P. Zuo, X. Cheng, Y. Ma, G. Yin and Y. Gao, RSC Adv., 2016, 6, 88683 RSC.
- M. Koseoglou, E. Tsioumas, D. Ferentinou, I. Panagiotidis, N. Jabbour, D. Papagiannis and C. Mademlis, J. Energy Storage, 2022, 54, 105345 CrossRef.
- A. Adam, E. Knobbe, J. Wandt and A. Kwade, J. Power Sources, 2021, 495, 229794 CrossRef CAS.
- X.-G. Yang, S. Ge, T. Liu, Y. Leng and C.-Y. Wang, J. Power Sources, 2018, 395, 251–261 CrossRef CAS.
- M.-T. F. Rodrigues, K. Kalaga, S. E. Trask, D. W. Dees, I. A. Shkrob and D. P. Abraham, J. Electrochem. Soc., 2019, 166, A996–A1003 CrossRef CAS.
- J. Wandt, P. Jakes, J. Granwehr, R.-A. Eichel and H. A. Gasteiger, Mater. Today, 2018, 21, 231–240 CrossRef CAS.
- C. Fear, T. Adhikary, R. Carter, A. N. Mistry, C. T. Love and P. P. Mukherjee, ACS Appl. Mater. Interfaces, 2020, 12, 30438–30448 CrossRef CAS PubMed.
- S. P. Rangarajan, Y. Barsukov and P. P. Mukherjee, J. Mater. Chem. A, 2019, 7, 20683–20695 RSC.
- H. Park, Y. Jeon, W. J. Chung, Y. Bae, J. Kim, H. Baek and J. Park, ACS Energy Lett., 2023, 8, 715–721 CrossRef CAS.
- H. Ge, T. Aoki, N. Ikeda, S. Suga, T. Isobe, Z. Li, Y. Tabuchi and J. Zhang, J. Electrochem. Soc., 2017, 164, A1050–A1060 CrossRef CAS.
- P. Arora, M. Doyle and R. E. White, J. Electrochem. Soc., 1999, 146, 3543–3553 CrossRef CAS.
- C. von Lüders, J. Keil, M. Webersberger and A. Jossen, J. Power Sources, 2019, 414, 41–47 CrossRef.
- M. Angeles Cabañero, J. Altmann, L. Gold, N. Boaretto, J. Müller, S. Hein, J. Zausch, J. Kallo and A. Latz, Energy, 2019, 171, 1217–1228 CrossRef.
- I. A. Shkrob, M.-T. F. Rodrigues, D. W. Dees and D. P. Abraham, J. Electrochem. Soc., 2019, 166, A3305–A3313 CrossRef CAS.
- C. Uhlmann, J. Illig, M. Ender, R. Schuster and E. Ivers-Tiffée, J. Power Sources, 2015, 279, 428–438 CrossRef CAS.
- M. W. Verbrugge and B. J. Koch, J. Electroanal. Chem., 1997, 436, 1–7 CrossRef CAS.
- T. Gao, Y. Han, D. Fraggedakis, S. Das and M. Z. Bazant, Joule, 2021, 5, 393–414 CrossRef CAS.
- X. Lu, M. Lagnoni, A. Bertei, S. Das, R. E. Owen, Q. Li, K. O'Regan, A. Wade, D. P. Finegan, E. Kendrick, M. Z. Bazant, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2023, 14, 5127 CrossRef CAS PubMed.
- Z. Guo, J. Zhu, J. Feng and S. Du, RSC Adv., 2015, 5, 69514–69521 RSC.
- X. Zhao, Y. Yin, Y. Hu and S.-Y. Choe, J. Power Sources, 2019, 418, 61–73 CrossRef CAS.
- J. Li, B. Liu, S. Li, D. Hu, L. Wang and J. Xu, J. Power Sources, 2022, 521, 230936 CrossRef CAS.
- X. Duan, B. Li, J. Li, X. Gao, L. Wang and J. Xu, Adv. Energy Mater., 2023, 13, 2203767 CrossRef CAS.
- M. Doyle, J. Electrochem. Soc., 1993, 140, 1526 CrossRef CAS.
- S. Santhanagopalan, Q. Guo, P. Ramadass and R. E. White, J. Power Sources, 2006, 156, 620–628 CrossRef CAS.
- N. Legrand, B. Knosp, P. Desprez, F. Lapicque and S. Raël, J. Power Sources, 2014, 245, 208–216 CrossRef CAS.
- A. Samba, N. Omar, H. Gualous, O. Capron, P. Van den Bossche and J. Van Mierlo, Electrochim. Acta, 2014, 147, 319–329 CrossRef CAS.
- D. Ren, K. Smith, D. Guo, X. Han, X. Feng, L. Lu, M. Ouyang and J. Li, J. Electrochem. Soc., 2018, 165, A2167–A2178 CrossRef CAS.
- B. Liu, Y. Jia, C. Yuan, L. Wang, X. Gao, S. Yin and J. Xu, Energy Storage Mater., 2020, 24, 85–112 CrossRef.
- J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9170–9177 CrossRef CAS PubMed.
- D. Fraggedakis, N. Nadkarni, T. Gao, T. Zhou, Y. Zhang, Y. Han, R. M. Stephens, Y. Shao-Horn and M. Z. Bazant, Energy Environ. Sci., 2020, 13, 2142–2152 RSC.
- R. B. Smith, E. Khoo and M. Z. Bazant, J. Phys. Chem. C, 2017, 121, 12505–12523 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta00244j |
| This journal is © The Royal Society of Chemistry 2024 |