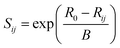Unveiling the local structure of doubly doped CeO₂: a synchrotron X-ray pair distribution function study

Abstract

Rare earth-doped ceria systems form one of the most thoroughly studied materials classes to be employed as solid electrolytes in solid oxide cells. In order to unveil the structural details ruling the ionic conductivity properties, the (Ce_1−xRE_x)O_2−x/2 series with RE = (Nd_0.63Dy_0.37), (Nd_0.74Tm_0.26), and (Sm_0.67Gd_0.33), and x ranging between 0.05 and 0.60, has been synthesized and characterized by means of synchrotron X-ray powder diffraction and pair distribution function analyses. By coupling the mentioned techniques, the whole spectrum of structural order and disorder characterizing these compounds at different length scales was revealed and discussed in detail. With reference to the average scale, for x ≥ 0.40 or 0.50, depending on the system, the Fm3̄m crystal structure of the CeO₂-based solid solution is accompanied by defect aggregates with the Ia3̄ structure growing within the ceria matrix. The local structure (r < 10 Å), in contrast, even at the lowest doping degree can be described as a disordered fluctuation between the average structures characterizing the Fm3̄m and Ia3̄ phases, which explains the reduction in ionic conductivity observed even within the stability range of the CeO₂-based solid solution.

---

Introduction

The oxygen diffusion coefficient is many orders of magnitude greater in materials possessing extended defects; this feature is obtained in CeO₂-based oxides by a partial substitution of Ce⁴⁺ with di- and tri-valent metallic ions. Such systems, characterized by an open atomic arrangement, are able to convey oxygen ions through their structure, taking advantage of the oxygen vacancies created by the partial replacement of Ce⁴⁺ by ions with a lower valence.¹ Among all the possible dopants, trivalent rare earth ions (RE) have attracted a lot of attention, since they allow (Ce_1−xRE_x)O_2−x/2 systems to be obtained, which are characterized by a high ionic conductivity between 673 and 973 K, namely ranging between 0.01 and 0.1 S cm⁻¹ at temperatures close to 873 K,^2,3 with the highest values occurring when RE ≡ Gd, Sm.

RE-doped ceria systems are studied to be used as electrolytes in solid oxide fuel and electrolysis cells working at intermediate temperature (IT-SOFCs and IT-SOECs, respectively), to replace the common Y₂O₃-stabilized ZrO₂ system,⁴ which requires higher working temperatures to properly conduct oxygen ions. Another advantage associated with (Ce_1−xRE_x)O_2−x/2 systems is their compatibility with the highly performing perovskite-based air electrodes, such as (La_1−xSr_x)(Co_1−yFe_y)O_3−δ,⁵ which is a mixed ionic–electronic conductor considered as a state-of-the-art material. As electrodes need both ionic and electronic conductivity, doped ceria can also be mixed with the cited perovskites, obtaining air electrodes with enhanced ionic conductivity: these composites can be synthesized through different techniques, such as co-electrospinning⁶ or infiltration.⁷

However, factors ruling ionic conductivity in doped ceria are quite complex. In general, a high ionic conductivity is observed as long as, despite doping, the fluorite-like cubic structure (named F, belonging to the Fm3̄m space group) of pure ceria is retained. This situation is observed up to a certain compositional threshold, called x_max; for x > x_max, different scenarios appear, mainly depending on the RE nature. When Ce⁴⁺ and RE³⁺ are close in size, the so-called hybrid phase (H) is observed: it can be described as an intimate intergrowth between the F and the C phases, where C indicates the typical cubic structure of the smallest RE₂O₃, belonging to the Ia3̄ space group.^8,9 Conversely, the occurrence of a biphasic F + C field is observed for x > x_max, when the size mismatch between Ce⁴⁺ and RE³⁺ is larger (such as in the case of Lu-doped ceria).¹⁰

Interestingly, both the C and the H phase are characterized by a much lower ionic conductivity than F. In H the presence of C nanodomains growing within the F matrix was detected even at a very low dopant amount (x < x_max) by means of different methods, such as Raman spectroscopy,^9,10 high pressure X-ray diffraction,¹¹ or local techniques, like transmission electron microscopy (TEM)¹² and pair distribution function analysis (PDF).¹³ In particular, the PDF technique has been extensively used to explore the local structure of doped ceria in many singly doped systems,^14–21 providing interesting details on the onset of the structural deformation leading to the occurrence of the C phase, to be coupled with the information deriving from the analysis at the average scale.

Based on atomistic simulations, several different configurations have been invoked to describe the possible arrangements of the C defect aggregates and their effect on ionic conductivity.^22–25 Among these, the ones characterized by the highest binding energies, thus the most effective in blocking the vacancy movement, are those involving the vacancy in the nearest neighbour (NN) position with respect to either one or two RE ions, giving rise to neutral trimers and positively charged dimers, respectively. When the vacancy is located in the next nearest neighbour (NNN) position, the blocking effect is weaker. Taking into account just the defects with the vacancy in the NN position, due to their relevance in reducing the ionic conductivity, it can be inferred that the stability of trimers and dimers is strongly dependent on temperature due to their different configurational entropies. Since C clusters exert a blocking effect on the movement of oxygen vacancies, their occurrence explains why the maximum ionic conductivity is not observed at x_max, the doping amount that should correspond to the maximum concentration of oxygen vacancies in F, but at significantly lower x values.

In the last few years, attention towards co-doped ceria, namely systems in which two or more doping ions are simultaneously used, has considerably grown due to the generally improved ionic conductivity properties with respect to singly-doped systems. Within this framework, La/Sm-,²⁶ Ca/Sm-,²⁷ Sm/Nd-,²⁸ Nd/Gd-,²⁹ La/Dy-,³⁰ Gd/Sm/La-,³¹ and Sm/Pr/Nd-³² doped ceria, and many other systems were investigated. Nonetheless, the effectiveness of co-doping was questioned by molecular dynamics simulations; in fact, the increased ionic conductivity was described as an average of the conductivities of singly doped materials.³³

In this work, the structural deformations taking place at the local scale in three doubly doped ceria systems are studied through PDF. The couples of RE ions (RE ≡ Nd/Tm, Nd/Dy and Gd/Sm) were selected relying on the results of studies previously performed by the research group:^34–37 the Nd/Tm and the Nd/Dy proportions were selected so as to reproduce the ionic size of Sm³⁺ with coordination number 8 (1.079 Å),³⁸ namely one of the most effective dopants for ceria; the Gd/Sm system was chosen as it contained a mixture of the best doping ions in terms of ionic conductivity, namely Gd³⁺ and Sm³⁺.

To the authors' knowledge, the present work is the first attempt to unravel the complex scenario characterizing the short-range structural properties in co-doped ceria by PDF analysis. In particular, it is found that Ce⁴⁺ and RE³⁺ ions tend to retain their respective structural environment in the inspected (Ce_1−xRE_x)O_2−x/2 compounds, thus producing a fluctuation between the local structures observed in CeO₂ and RE₂O₃ compounds.

Experimental

Three different series of samples with nominal composition (Ce_1−xRE_x)O_2−x/2 were prepared and labelled as follows:

ND series: with RE = (Nd_0.63Dy_0.37) and x = 0.05, 0.10, 0.15, 0.20, 0.30, 0.40, 0.50, 0.60;

NT series: with RE = (Nd_0.74Tm_0.26) and x = 0.05, 0.10, 0.15, 0.20, 0.30, 0.40, 0.50, 0.60;

SG series: with RE = (Sm_0.67Gd_0.33) and x = 0.10, 0.20, 0.30, 0.40, 0.50, 0.60.

In general, the most investigated compositions of doped ceria are characterized by x < 0.30, as the maximum ionic conductivity is generally observed for 0.10 ≤ x ≤ 0.20, depending on the doping ion. However, since this study aims to clarify the complex structural changes occurring in the chosen systems with increasing the dopant amount, considering a wider compositional range can be helpful.

Samples belonging to the Ce_1−x(Nd_0.74Tm_0.26)_xO_2−x/2, the Ce_1−x(Nd_0.63Dy_0.37)_xO_2−x/2, and the Ce_1−x(Gd_0.67Sm_0.33)_xO_2−x/2 systems were synthesized through a well-established co-precipitation method, which provides highly homogeneous polycrystalline samples.^10,39 For each composition, stoichiometric amounts of metallic Ce (Johnson Matthey ALPHA, 99.99% wt) and the desired trivalent rare earth oxides (Gd₂O₃ and Nd₂O₃ by Alfa Aesar, 99.99 wt%; Tm₂O₃ by Mateck, 99.99%; Sm₂O₃ and Dy₂O₃ by Sigma-Aldrich, 99.9%) were separately dissolved in HCl (13% v/v). This way, three different rare earth ion solutions were prepared for each composition, and subsequently mixed; then, a further solution of oxalic acid was added to each solution of mixed ions, inducing the precipitation of the corresponding mixed oxalate. Oxalate powders were then filtered, rinsed with milli-Q water to reach pH = 7, and dried at 363 K in an oven in air for one day. Oxalates were thermally treated at 1373 K in air for four days, to obtain the corresponding mixed oxides via the calcination process; the high temperature is justified by the need for a high crystallinity degree of samples.

Synchrotron X-ray elastic scattering data were collected at room temperature at the ID22 beamline of the European Synchrotron Radiation Facility (ESRF-Grenoble, France)⁴⁰ using a wavelength λ = 0.3543 Å.⁴¹ X-ray powder diffraction (XRPD) data collected in the 1.2–8.7 Å⁻¹Q-range were used for structural refinements. These refinements were carried out according to the Rietveld method⁴² using the FullProf program;⁴³ in particular, a file describing the instrumental resolution function (obtained by using LaB₆ as a standard) and a Thompson–Cox–Hastings pseudo-Voigt convoluted with axial divergence asymmetry function were used during calculations. In the structural model the cationic site occupations were fixed to the nominal compositions. In the final cycle, the following parameters were refined: the scale factor; the zero point of the detector; the background; the unit cell parameters; the atomic site coordinates not constrained by symmetry; the isotropic displacement parameters. Parameters defining line profiles provide information on the size of diffracting domains and on structural deformation (microstrain); to this end, also the anisotropic strain and the Lorentzian isotropic size parameters were included in the refinement.

In order to gain information on the local structure, pair distribution function (PDF) analysis⁴⁴ was carried out. Reduction of the total scattering data was achieved using PDFgetX3 software⁴⁵ with Q_max = 30.7 Å, a range sufficient for an accurate analysis.⁴⁶ In this way, the following functions were obtained: the I(Q) function (the background-corrected diffraction intensities), the total-scattering structure function S(Q) (with intensities normalized by average scattering factors and corrected by a polynomial fit), and the G(r) (the reduced PDF).⁴⁷ Full-profile fitting of the G(r) function was carried out using the PDFgui software.⁴⁸ Data from an empty borosilicate capillary were collected to subtract the container scattering; moreover, LaB₆ was analyzed under the same experimental conditions to describe the experimental resolution effects. In the structural model the cationic site occupations were fixed to the nominal compositions. In the last cycle of the fitting, the following parameters were refined: the scale factor; the unit-cell parameters; the atomic positions not constrained by symmetry; the anisotropic atomic displacement parameters; the dynamic correlation factor. Moreover, the parameters describing the experimental resolution effects (Q_damp and Q_broad) were fixed to the values refined LaB₆. PDF data fitting was carried out by adopting different length scales, to unveil the evolution of the structural properties as a function of distance.

The bond valence sum method (BVS) was applied to evaluate the structural stability and identify the possible ionic conduction paths in the crystal structure. The BVS method empirically correlates the ionic valence S and the bond length R separating the ionic species i and j as follows:⁴⁹

where R₀ and B are parameters defined for each specific i–j bond. In particular, the sum of the bond valences around a specific ion should correspond to the atomic valence.

Results and discussion

Long-range structural description

CeO₂ crystallizes in the cubic system belonging to the Fm3̄m space group type, adopting a CaF₂-type structure. Ce atoms are surrounded by 8 O atoms at the vertices of a cube, whereas O atoms coordinate with 4 Ce atoms at the vertices of a regular tetrahedron. The crystal structure can be thus described as a network constituted of edge-sharing tetrahedra centred by Ce atoms. When two Ce atoms lying along a body-diagonal are removed, the interstitial derivative structure characterizing RE₂O₃ compounds (crystallizing in the cubic Ia3̄ space group; RE = Gd–Lu) is obtained (Fig. 1). These two structures are related by a complex group – subgroup relationship:
where t and k indicate the transformation type (t: translationsgleich; k: klassengleich) and the adjacent number the transformation index. According to this transformation chain, the RE atoms at the 4a site in the Fm3̄m space group split into the 8a and 24d sites in the Ia3̄ space group, whereas O atoms at the 8c site should split into 48e and 16c sites. Nevertheless, the 16c site is not occupied in the RE₂O₃ structure, thus accounting for O vacancies.

Fig. 1 Comparison between the crystal structures of CeO₂ and Dy₂O₃.

A thorough analysis of the long-range order occurring in RE-doped ceria was already performed by synchrotron XRPD analysis and described in several previous publications,^8–10 even with particular regard to the three systems treated in this work.^34–36 Indeed, the XRPD analysis and Rietveld refinement performed for the present study confirm previous investigations; details of the results are reported in the ESI Section.† Therefore, hereinafter the main structural findings will only be recalled, and just the previously unaddressed details will be added, to pave the way for the description of the local structural features, which are the focus of this work.

A single Fm3̄m phase is observed in XRPD data at a low substitution degree; the Ia3̄ phase starts growing finely interlaced with the CeO₂-based matrix from x = 0.40 in the GS series,³⁶ and from x = 0.50 in the NT³⁵ and ND³⁴ series. Regarding the behaviour of lattice parameters, similarly to what occurs in singly-doped ceria,⁸ even in doubly-doped systems the unit cell size almost linearly increases with x within the stability range of the F-based structure (as illustrated in Fig. S3 in the ESI Section†); however, as the substitution degree further increases, reaching the composition where superstructure peaks appear, the slope of the curves decreases. This behaviour can be related to the progressive oxygen depletion taking place with the Ce⁴⁺ substitution by RE³⁺ ions, a phenomenon that has been extensively discussed in prior studies.⁹

The isotropic displacement parameters (B_iso) at the oxygen and RE crystallographic sites as a function of the average RE ionic radius 〈RE〉 are shown in Fig. 2; the correspondence between 〈RE〉 and composition can be found in Table S1 of the ESI.† An increase in both crystallographic positions with substitution is evident, as a consequence of the growing disorder at the cationic site, which produces a fluctuation of the RE–O bond lengths, namely a static structural disorder at the local scale. The inset shows the tensor isosurfaces at selected compositions for the ND series (chosen as representative), so depicting the evolution of the microstrain-like broadening of the diffraction lines. In this case, microstrain-like broadening originates from the fluctuation of interplanar distances produced by the corresponding compositional fluctuations, thus representing a measure of the local scale disordering. It is evident that the shape of the tensor isosurfaces develops into a spherical shape with increasing the substitution degree, thus indicating a progressive isotropic disordering at the atomic scale, as expected for the homogeneous distribution of RE elements within the structure.

Fig. 2 Evolution of the isotropic displacement parameters (B_iso) at both oxygen and RE structural sites vs. the average RE ionic radius in all the sample series; the inset shows tensor isosurfaces depicting the evolution of the microstrain-like broadening of diffraction lines.

The analysis of the diffraction line broadening allows the average diffraction domain size and shape to be evaluated. Fig. 3 highlights that chemical substitution significantly reduces the domain size, whereas diffraction domains are characterized by a quite regular polyhedral shape (Fig. 3, inset, depicts the average particle shape as evaluated after the refinement of the anisotropic size parameters).

Fig. 3 Evolution of the diffraction domain size as a function of 〈RE〉 (only single-phase sample data are reported); the inset depicts the average diffracting domain shape.

Structural stability can be evaluated by applying the BVS method^49,50 and using the interatomic distances deriving from the refined structural data obtained via the Rietveld method. In the absence of structural strains determining the stretching or compression of bonds, the difference between the calculated BVS and the expected valence (Δv) is generally <0.1 vu (vu: valence unit); larger values of Δv are thus indicative of strained bonds that progressively destabilize the crystal structure.⁵¹ According to data reported in Fig. 4, for CeO₂ the result of the BVS calculation agrees well with the expected value, while Δv measured at the RE-site progressively increases with the chemical substitution. In particular, structural strain becomes significant at x = 0.30, and it exceeds 0.2 vu for x ≥ 0.40. Such a Δv should in principle lead to an instability of the crystal structure, which is indeed confirmed by the occurrence of superstructure peaks in the diffraction pattern, releasing the stress accumulated by the structure as a consequence of the introduction of foreign atoms. The Δv value obtained from the BVS calculation derives from the underlying idea of the occurrence of a single CeO₂-based phase having the nominal composition of the oxide. This scenario definitely does not correspond to the real one, on account of the Ia3̄ phase demixing. In more detail, these very high values of Δv suggest an unequal distribution of cations between the F and the C phase, with a higher Ce content in the former, and a higher RE content in the latter. This evidence means that Ce preferentially dissolves into the Fm3̄m structure, whereas the remaining RE ions concentrate in the Ia3̄ phase, which confirms the crystallochemistry evidence. This outcome is also in good agreement with the atomistic simulations, predicting that with decreasing the RE³⁺ radius, the binding energy of defect aggregates increases;²³ according to this result, smaller RE ions are expected to enter mainly defect aggregates, while the CeO₂-based solid solution is enriched in Ce⁴⁺ with respect to the nominal overall composition of the oxide.

Fig. 4 Dependence of Δv at the 〈RE〉 site on composition x in (Ce_1−xRE_x)O_2−x/2.

Possible ionic conduction paths can be calculated and visualized by applying the BVS method; Fig. 5 shows the bond valence isosurface of O²⁻ in CeO₂ calculated using the BondStr program included in the FullProf suite;⁴³ the isosurface identifies areas with a low energy barrier and therefore represents the most likely pathway for ion transport. It is evident that oxygen diffusion takes place by a vacancy-assisted mechanism involving the unoccupied 24e Wyckoff site (with coordinates x,0,0; x = 0.5 for the interstitial site sketched out in Fig. 5), which represents an unoccupied octahedral position in the Ce sub-structure. Such a mechanism is consistent with molecular dynamics simulations and molecular static calculations revealing an ionic diffusion mechanism by vacancy hopping along the 〈100〉 direction.⁵² Remarkably, neutron PDF analysis revealed the occurrence of extended Frenkel defects, with O atoms located in the interstitial site, although displaced from the centre of the octahedron along 〈100〉;⁵³ such a structural feature is in good agreement with the possible ionic conduction paths outlined by BVS.

Fig. 5 Bond valence isosurface of O²⁻ in CeO₂; interstitial sites (grey spheres) are located at the 24e Wyckoff site (with x = 0.5).

Pair distribution function analysis

XRPD analysis provides a periodic structural model; nonetheless, deviations from perfect periodicity occur at the local scale even in crystalline materials, producing significant effects on their properties. Such deviations characterizing the local structure of a material can be unveiled by PDF.

Chemical substitution induces a progressive increase in the structural disorder. Such an effect can be appreciated by inspecting the total scattering structure function data, S(Q), at high Q-values; this kind of structural disorder produces an increase of the scattered background (where broad oscillations are progressively enhanced by substitution) and a damping of diffraction peak intensities (see Fig. 6, where a representative selection of data pertaining to the ND system is reported). In particular, broad oscillations at higher Q-values can be roughly ascribed to dynamical short-ranged correlations involving the tetrahedral network, whereas the damping of the diffraction peak intensities can be ascribed to static disorder. The damping observed for the G(r) functions in the high r-range (see Fig. S4 in the ESI Section†) evidences the progressive reduction of the structural coherence with chemical substitution in good agreement with the results obtained by the diffraction line broadening analysis.

Fig. 6 Superposition of S(Q) data at high Q-values for selected samples pertaining to the ND series.

Fig. 7 shows the G(r) functions collected for the whole ND, NT and GS series in the low r-region; peaks pertaining to RE–O (∼2.3 Å; ∼4.5 Å; ∼5.9 Å) and RE–RE (∼3.8 Å; ∼4.2 Å; ∼5.5 Å) bond pairs can be observed. In particular, the intensity of the RE–RE peak at ∼4.2 Å increases with x, whereas both peaks at ∼4.5 Å and ∼5.9 Å (pertaining to RE–O bond pairs) progressively decrease in intensity.

Fig. 7 Evolution of the G(r) function as a function of substitution in the r-range 1.5–6.5 Å for the three different sample series.

Generally speaking, the peak width is determined by the distribution spread of the interatomic distances between a given pair of atoms (thus depending on the static or dynamic disorder of the atoms involved in the pair); for this purpose, the fitting of peaks was carried out using pseudo-Voigt functions after background subtraction.

Fig. 8, upper panel, shows the dependence of the full width at half maximum (FWHM) of the peak at ∼2.3 Å sampling the nearest RE–O bond pair for the three whole series. Two different regimes can be clearly recognized.

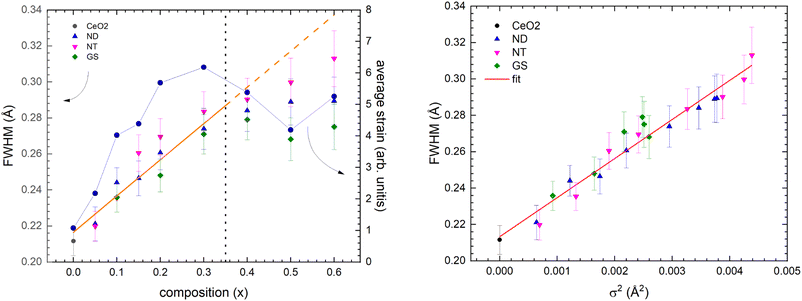Fig. 8 Evolution of the FWHM of the peak at ∼2.3 Å (pertaining to the nearest RE–O bond pair) as a function of composition (left panel) and of cationic size variance σ² (right panel).

(1) For 0 ≤ x ≤ 0.30 the broadening of the PDF peak roughly follows a linear trend with x, thus indicating a progressive increase of the distribution spread of the interatomic RE–O distances.

(2) For x > 0.30 the broadening of the PDF peak negatively deviates from the linear trend, as highlighted by the dashed line in Fig. 8, left panel, and in some cases, it tends to saturate.

Both regimes can be related to the evolution of the average structural strain on composition, also reported in the figure. In fact, even this parameter, measured using the corresponding XRPD data, quite homogeneously increases for x ≤ 0.30, approaching an almost constant value at higher x. This behaviour can be explained at the microscopic scale as follows: for a small amount of substituting ions, the CeO₂ structure can accommodate the strain fields around each solute RE without a relevant increase of the local disorder, and the local deformation induced by the dissolved atoms can be absorbed by local distortions. As the amount of static disordering produced by chemical substitution at the RE site increases, the distribution of RE–O bond lengths increases as well. The strain fields around each solute RE atom start to overlap, but the CeO₂-type structure can still accommodate the global strain. With further increasing the substitution degree, the global amount of structural strain produced by the overlapping strain fields destabilizes the CeO₂-type structure. As a result, the C-phase demixes and two different phases coexist even if strictly interlaced, as evidenced by XRPD data (see Fig. S1 in the ESI Section†). Then the broadening of the PDF peak width tends to saturate due to phase coexistence: in fact, the RE–O bond distances tend to be fixed inside each co-existing crystallographic phase and fluctuations cannot further increase.

As a general remark, the disorder due to the random distribution of different RE cations at the same crystallographic site, namely due to the mismatch of individual RE cation radii, can be parametrized by the size variance σ²(r_RE) = 〈r_RE²〉 − 〈r_RE〉² (〈r_RE〉: mean RE cation radius).⁵⁴ By plotting FWHM vs. σ²(r_RE), a linear relationship is observed, clearly evidencing the direct dependence of the RE–O bond length distribution on the cationic site disordering (Fig. 8, right panel).

Fig. 9 shows the experimental G(r) functions for samples belonging to the ND series (selected as representative) with 0 ≤ x ≤ 0.30, namely the ones only formed of the F phase; the cited functions are thus fitted in the 1.5 < r < 30 Å range by using an Fm3̄m structural model. It is evident that the fitting of the peak at ∼3.8 Å, corresponding to the nearest RE–RE bond pair, progressively worsens with substitution. Remarkably, the RE–O peak at ∼2.3 Å is not well fitted, independently on composition, also for pure CeO₂; these data demonstrate that a significant deviation from the ideal structure occurs at the very local scale (r < 9–10 Å), while the Fm3̄m structural model accounts well for the experimental G(r) functions of the whole sample series for larger distances (r > 10 Å). Interestingly, the model fails in fitting the peak at ∼4.2 Å. This peak is predicted by the Ia3̄ structural model characterizing C domains, and it originates from RE–RE bond pairs; these data thus suggest that at the local scale significant deviations from the average Fm3̄m structural model can take place even at a very low substitution degree, and confirm the outcome deriving from other techniques, such as high pressure X-ray diffraction.¹¹ Moreover, this result suggests that the decrease in ionic conductivity taking place within the stability range of the ceria-based solid solution is caused by the occurrence of the non-conducting Ia3̄-based defect aggregates even at a very low doping degree.

Fig. 9 Experimental G(r) functions obtained for the ND-sample series fitted with an Fm3̄m single-phase structural model in the range 1.5 < r < 30 Å (distance is shown on a logarithmic scale in order to highlight data at shorter r values).

Unfortunately, X-ray PDF data are dominated by the RE contribution, and the reduced X-ray scattering length of O prevents the testing of a structural model characterized by a significant content of Frenkel defects, as reported for previous neutron PDF studies.⁵³

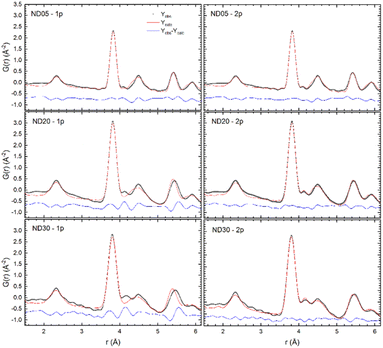
Nevertheless, to gain information on the structural properties at the local scale, a 2-phase model was also applied, made up of the Fm3̄m + Ia3̄ structures. It is noteworthy that such a model is not intended for describing a real phase separation within the inspected samples (at least for samples with x ≤ 0.30); rather, it is used to model the fluctuation of the local structural properties produced by chemical substitution and the consequent progressive increase of the O-vacancy amount. Predictably, a significant improvement is gained, and the experimental G(r) functions are well fitted in the 1.5 < r < 6.15 Å range.

In Fig. 10 a comparison is reported between selected experimental G(r) functions fitted in the 1.5 < r < 6.15 Å range by using a single phase Fm3̄m (1p) and a 2-phase Fm3̄m + Ia3̄ (2p) structural model, respectively. In general, the 2-phase structural model provides a better fitting of experimental data, as also indicated by the lower R_wp values (Fig. 11, upper panel). Nonetheless, it is imperative to determine if the larger number of refinable parameters characterizing the 2-phase model leads to a significant improvement of the fit, i.e. if this improvement is really determined by a better description of the physical system, or if it is simply a consequence of overparameterization. To this end, a significance test was carried out on the crystallographic R_w factor.⁵⁵ As a result, the 2-phase structural model can be rejected for samples with x = 0 and 0.05; conversely, the probability of error is less than 5% for samples with 0.10 ≤ x ≤ 0.60. It can be thus concluded that the peak at ∼4.2 Å is a termination ripple (not originating from structural features) of the G(r) function for x = 0.00 and 0.05; in contrast, its occurrence originates from the structural properties for samples with x ≥ 0.10, and thus it represents a real RE–RE interatomic distance. Similar arguments hold for both NT and GS series, whose results, shown in Fig. 11, are in good agreement with previous studies of RE-substituted CeO₂ where a biphasic model was used to provide the best description of the local structure.¹⁴

Fig. 10 Experimental G(r) functions obtained for the ND series fitted with a single (Fm3̄m; panels on the left) and a double-phase (Fm3̄m + Ia3̄; panels on the right) structural model in the range 1.5 < r < 6.15 Å.

Fig. 11 Upper panel: comparison of the R_w values as a function of composition as obtained after fitting the G(r) functions in the range 1.5 < r < 6.15 Å by using a single and the 2-phase structural model. Lower panel: relative amounts (mass%) of the two phases provided by the 2-phase structural model fitting.

Fig. 11, lower panel, reports the compositional dependence of the relative amounts (mass%) of the Fm3̄m and Ia3̄ phases, as provided by the 2-phase structural model. Remarkably, this model, adopted for describing the local structure (r ≤ 6 Å), actually indicates a fluctuation between the local structure observed in CeO₂ and RE₂O₃ compounds, rather than representing a true phase separation between them (at least for samples with x ≤ 0.30). In fact, the exsolution of an Ia3̄ phase within an Fm3̄m matrix would notably affect the size of the structurally coherent domains; conversely, the domain size does not significantly change in the 0.10 ≤ x ≤ 0.40 compositional range (see Fig. 3 and S4 in the ESI Section†), indicating that within the same structurally coherent domain the local structure fluctuates between the ones of the Fm3̄m and the Ia3̄ phase. The information gained is thus that cations tend to retain the same local environment as in the corresponding pure oxides.

It is noteworthy that RE–O bond lengths calculated by Rietveld refinement, and G(r) functions fitting up to 30 Å, nicely superpose, as they clearly increase with increasing x. Conversely, the same bond lengths exhibit an opposite behaviour when obtained by fitting the G(r) functions up to 6.15 Å (Fig. 12); a similar behaviour also characterizes the nearest neighbour RE–RE pairs. These findings are in good agreement with previous local structural studies carried out by PDF and EXAFS on similar RE-substituted CeO₂ samples.^15,56,57 The observed decoupling between bond distances calculated at the average and local scale can be explained by considering that the amount of O vacancies in the structure increases with substitution.

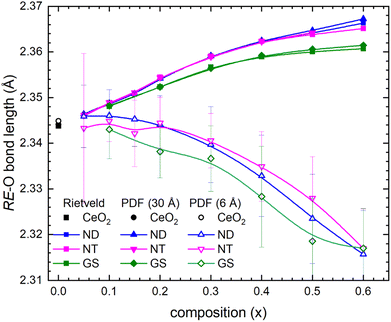Fig. 12 RE–O bond lengths plotted as a function of composition as obtained by Rietveld refinement and PDF fittings up to distance ranges 6.15 and 30 Å.

Fig. 13 depicts the structural environment around an O vacancy (represented by the yellow sphere). White spheres represent the structural positions occupied by O and RE atoms in the Fm3̄m structure, whereas the coloured hemi-spheres represent the direction of the shift due to uncorrelated static or dynamic displacements producing local scale atomic disordering. When a vacancy is formed, the positive charges of the nearest neighbour RE atoms are no longer separated by a bridging O atom; as the intervening negative charge is removed, these ions are displaced in opposite directions on account of Coulombic repulsion. This phenomenon has two main consequences in terms of (1) RE displacement and (2) O displacement. (1) The RE atoms displaced by coulombic repulsion move close to the other RE atoms, thus decreasing the average RE–RE bond distance at the local scale. (2) Around the vacancy, nearest neighbor RE atoms experience an excess of positive charge (resulting from the missing O) that must be compensated for by decreasing the interatomic distances between RE and still bonded O atoms. Moreover, this mechanism of charge compensation is expected to affect also next nearest neighbor RE atoms. Indeed, next nearest neighbor RE atoms gain a fractional positive charge as O atoms displace to nearest neighbor RE atoms; this in turn is compensated for by other O atoms, thus explaining the global decrease of the RE–O bond lengths measured at the local scale. This situation, coupled with the disordered distribution of both charges and ionic sizes in the RE sub-structure, gives rise to a dynamic disordering. As can be qualitatively evaluated from the background oscillations at high Q-values of the total scattering structure function S(Q) (Fig. 6), dynamic disorder increases with substitution, as expected, because it is triggered by vacancies at the O sub-structure. To conclude, it is useful to make a comparison between the structural and microstructural properties observed for our doubly substituted CeO₂ samples with those reported in the literature for singly substituted samples.

Fig. 13 Representation of possible local structure configurations around a vacancy in substituted CeO₂; coloured hemi-spheres represent atomic uncorrelated displacement from the average position (white spheres) in the long-range structure.

Regarding Gd-doped ceria, namely one of the most studied doped ceria systems, a large number of papers report the compositional extent of the F phase; an overview of these results can be found in ref. 1. Despite the small discrepancies among different studies,^15,58 the boundary can be located between x = 0.20 and 0.30. Sm-doped ceria is also a subject of many investigations, and the F phase is reported to extend up to x ∼0.30. In general, the extent of the F phase seems to be mainly ruled by the Ce⁴⁺/RE³⁺ size similarity. By comparing singly and doubly doped ceria systems with the same average doping ion size, an enlargement of the stability extent of the F phase has been observed, associated with an increased cell parameter of the doubly doped systems with respect to the corresponding singly doped one. This is for instance the case of Ce_1−x(Nd_0.63Dy_0.37)_xO_2−x/2 (ref. 34) and Ce_1−x(Nd_0.74Tm_0.26)_xO_2−x/2,³⁵ both having the same average ionic radius of the doping mixture as Sm³⁺, and showing a larger F stability extent than Sm-doped ceria. Similarly, (Gd,Sm) doped ceria exhibits an analogous behaviour with respect both to Gd- and Sm-doped ceria.³⁶ This evidence, widely discussed in (ref. 34–36), has to be ascribed to the preferential entrance of the larger doping ion into the F lattice.

Nevertheless, the presence of Ia3̄ nanodomains has been demonstrated even at the lowest doping ion content by high pressure X-ray diffraction for several singly and doubly doped ceria systems.¹¹ The results of the present and other^13,15,20 PDF studies performed on doped ceria systems are in good agreement with the outcome of the last-mentioned work, thus pointing at the existence of aggregates even at very low x values, where they cannot be revealed by X-ray diffraction in terms of superstructure peaks due to their tiny amount and/or their nanometric size. Anyway, despite the presence of Ia3̄ domains even at very low x values, it can be inferred that the average Fm3̄m structure prevails in the whole inspected compositional range: in the GS series, for example, only ∼30 wt% of the Ia3̄ polymorph is found as a secondary phase for x = 0.60. These results suggest that double substitution is effective in stabilizing the Fm3̄m structure.

The general conclusion that can be drawn from this and all the PDF studies performed on doped ceria, irrespective of single or multiple doping, is that Ce⁴⁺ and RE³⁺ have a strong tendency to be surrounded by the crystallographic environment typical of CeO₂ and RE₂O₃, respectively. The local structure (<10 Å) of Gd-substituted samples, for instance, is properly represented as an extended defect cluster, rather than a phase separate state, where Ce and Gd atoms tend to retain the environments as in pure CeO₂ and Gd₂O₃, respectively.^15,16 These results are in good agreement with our findings in double substituted samples, where the structural fluctuations at the short range scale are modelled by applying a 2-phase structural model for fitting the G(r) functions (Fig. 10).

The enlargement of the F phase compositional extent observed in doubly doped ceria with respect to singly doped ceria exerts an effect on ionic conductivity. This issue has been thoroughly studied in previous works of this^35,36 and other^59,60 research groups, and the most remarkable outcome is that multiply doped systems exhibit a lowering of the activation energy to ionic conductivity with respect to singly doped ones, at least at temperatures higher than ∼750 K,^35,36 as well as an increase of ionic conductivity;^59,60 in addition, also an effect of partial suppression of Ia3̄ clusters was observed.⁶¹ In this respect, the investigation of the properties of doubly doped ceria systems is a highly promising topic in the search for effective electrolytes to be used in solid oxide cells.

Conclusions

The structural properties of three double RE-substituted ceria systems (Ce_1−xRE_xO_2−x/2, RE ≡ Nd/Tm, Nd/Dy, Gd/Sm) have been investigated from the macro down to the nano scale by means of synchrotron X-ray powder diffraction and pair distribution function analysis. Samples of all series are constituted of a single Fm3̄m phase up to x = 0.30, whereas an Ia3̄ phase grows finely interlaced with the former at higher x values. The coherent diffracting domain size decreases with substitution up to x = 0.10, whereas static disorder and vacancy concentration in the oxygen sub-structure increase. In particular, the local scale structure (r < 10 Å) can be described as a disordered fluctuation between the average structures characterizing the Fm3̄m and Ia3̄ phases; due to the non-conducting nature of the Ia3̄ phase, this evidence can be deemed as the reason behind the drop in ionic conductivity commonly observed in doped ceria systems even within the stability range of the CeO₂-solid solution. The static disorder is triggered by the local concentration of RE substituents, mainly affected by the amount and distribution of neighbouring oxygen vacancies. Moreover, also dynamic structural disorder is present, determined by uncorrelated atomic displacement (mainly affecting the O sub-structure) providing notable deviation in the bond-length distribution.

Author contributions

Conceptualization: C. A., M. C., M. P.; formal analysis: A. M., S. M.; funding acquisition: M. P.; investigation: S. M., M. P.; methodology: A. M., S. M.; resources: C. A., M. P.; visualization: A. M.; writing – original draft: A. M.; writing – review and editing: A. M., S. M., C. A., M. C., M. P.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out with the support of the European Synchrotron Radiation Facility (proposal HC-4993; https://doi.org/10.15151/ESRF-ES-891426152); authors acknowledge Ola G. Grendal for his assistance during data collection at the ID22 beamline. This work received financial support from the San Paolo Project ‘COELUS – Production of renewable fuel by CO-ELectrolysis and reUSe of carbon dioxide’ (ID ROL 32604).

References

1. C. Artini, RE-doped ceria systems and their performance as solid electrolytes: a puzzling tangle of structural issues at the average and local scale, Inorg. Chem., 2018, 57, 13047–13062.
2. M. Mogensen, N. M. Sammes and G. A. Tompsett, Physical, chemical and electrochemical properties of pure and doped ceria, Solid State Ionics, 2000, 129, 63–94.
3. H. Inaba and H. Tagawa, Ceria-based solid electrolytes, Solid State Ionics, 1996, 83, 1–16.
4. M. Mogensen, Physical, chemical and electrochemical properties of pure and doped ceria, Solid State Ionics, 2000, 129, 63–94.
5. S. P. Jiang, Development of lanthanum strontium cobalt ferrite perovskite electrodes of solid oxide fuel cells – a review, Int. J. Hydrog. Energy, 2019, 44, 7448–7493.
6. C. Sanna, W. Zhang, P. Costamagna and P. Holtappels, Synthesis and electrochemical characterization of La_0.6Sr_0.4Co_0.2Fe_0.8O_3–δ/Ce_0.9Gd_0.1O_1.95 co-electrospun nanofiber cathodes for intermediate-temperature solid oxide fuel cells, Int. J. Hydrog. Energy, 2021, 46, 13818–13831.
7. L. Spiridigliozzi, E. Di Bartolomeo, G. Dell'Agli and F. Zurlo, GDC-based infiltrated electrodes for solid oxide electrolyzer cells (SOECs), Appl. Sci., 2020, 10, 3882.
8. C. Artini, G. A. Costa, M. Pani, A. Lausi and J. Plaisier, Structural characterization of the CeO₂/Gd₂O₃ mixed system by synchrotron X-ray diffraction, J. Solid State Chem., 2012, 190, 24–28.
9. C. Artini, M. Pani, M. M. Carnasciali, M. T. Buscaglia, J. Plaisier and G. A. Costa, Structural features of Sm-and Gd-doped ceria studied by synchrotron X-ray diffraction and μ-Raman spectroscopy, Inorg. Chem., 2015, 54, 4126–4137.
10. C. Artini, M. Pani, M. M. Carnasciali, J. Plaisier and G. A. Costa, Lu-, Sm- and Gd-doped ceria: a comparative approach to their structural properties, Inorg. Chem., 2016, 55, 10567–10579.
11. C. Artini, S. Massardo, M. M. Carnasciali, B. Joseph and M. Pani, Evaluation of the defect clusters content in singly- and doubly-doped ceria through in situ high pressure X-ray diffraction, Inorg. Chem., 2021, 60, 7306–7314.
12. F. Ye, T. Mori, D. R. Ou, J. Zou and J. Drennan, A structure model of nano-sized domain in Gd-doped ceria, Solid State Ionics, 2009, 180, 1414–1420.
13. M. Coduri, P. Masala, M. Allieta, I. Peral, M. Brunelli, C. A. Biffi and M. Scavini, Phase transformations in the CeO₂–Sm₂O₃ system: a multiscale powder diffraction investigation, Inorg. Chem., 2018, 57, 879–891.
14. M. Coduri, M. Brunelli, M. Scavini, M. Allieta, P. Masala, L. Capogna, H. E. Fischer and C. Ferrero, Rare Earth doped ceria: a combined X-ray and neutron pair distribution function study, Z. Kristallogr., 2012, 227, 272–279.
15. M. Scavini, M. Coduri, M. Allieta, M. Brunelli and C. Ferrero, Probing complex disorder in Ce_1−xGd_xO_2−x/2 using the pair distribution function analysis, Chem. Mater., 2012, 24, 1338–1345.
16. M. Coduri, M. Scavini, M. Allieta, M. Brunelli and C. Ferrero, Defect structure of Y-doped ceria on different length scales, Chem. Mater., 2013, 25, 4278–4289.
17. M. Coduri, M. Scavini, M. Pani, M. M. Carnasciali, H. Klein and C. Artini, From nano to microcrystals: effect of different synthetic pathways on defects architecture in heavily Gd-doped ceria, Phys. Chem. Chem. Phys., 2017, 19, 11612–11630.
18. S. Checchia, M. Scavini, M. Allieta, M. Brunelli, C. Ferrero and M. Coduri, Size and spatial correlation of defective domains in yttrium-doped CeO₂, Powder Diffr., 2015, 30, S119–S126.
19. M. Coduri, P. Masala, M. Allieta, I. Peral, M. Brunelli, C. A. Biffi and M. Scavini, Phase transformations in the CeO₂–Sm₂O₃ system: a multiscale powder diffraction investigation, Inorg. Chem., 2018, 57, 879–891.
20. M. Scavini, M. Coduri, M. Allieta, P. Masala, S. Cappelli, C. Oliva, M. Brunelli, F. Orsini and C. Ferrero, Percolating hierarchical defect structures drive phase transformation in Ce_1−xGd_xO_2−x/2: a total scattering study, IUCrJ, 2015, 2, 511–522.
21. M. Scavini, M. Coduri, M. Brunelli and M. P. Masala, In situ pair distribution function study on lanthanum doped ceria, Phys. Chem. Chem. Phys., 2013, 15, 8495–8505.
22. L. Minervini, M. O. Zacate and R. W. Grimes, Defect cluster formation in M₂O₃-doped CeO₂, Solid State Ionics, 1999, 116, 339–349.
23. Z. P. Li, T. Mori, J. Zou and J. Drennan, Defects clustering and ordering in di- and trivalently doped ceria, Mater. Res. Bull., 2013, 48, 807–812.
24. R. Schmitt, A. Nenning, O. Kraynis, R. Korobko, A. I. Frenkel, I. Lubomirsky, S. M. Haile and J. L. M. Rupp, A review of defect structure and chemistry in ceria and its solid solutions, Chem. Soc. Rev., 2020, 49, 554–592.
25. S. Grieshammer, B. O. H. Grope, J. Koettgen and M. Martin, A combined DFT + U and Monte Carlo study on rare earth doped ceria, Phys. Chem. Chem. Phys., 2014, 16, 9974–9986.
26. X. Sha, Z. Lü, X. Huang, J. Miao, Z. Ding, X. Xin and W. Su, Study on La and Y co-doped ceria-based electrolyte materials, J. Alloys Compd., 2007, 428, 59–64.
27. R. Raza, X. Wang, Y. Ma and B. Zhu, Study on calcium and samarium co-doped ceria based nanocomposite electrolytes, J. Power Sources, 2010, 195, 6491–6495.
28. S. Omar, E. Wachsman and J. Nino, Higher conductivity Sm³⁺ and Nd³⁺ co-doped ceria-based electrolyte materials, Solid State Ionics, 2008, 178, 1890–1897.
29. A. Arabaci, T. G. Altınçekiç and M. A. F. Der Öksüzömer, Preparation and properties of ceramic electrolytes in the Nd and Gd Co-doped ceria systems prepared by polyol method, J. Alloys Compd., 2019, 792, 1141–1149.
30. K. Venkataramana, C. Madhuri, C. Madhusudan, Y. Suresh Reddy, G. Bhikshamaiah and C. Vishnuvardhan Reddy, Investigation on La³⁺ and Dy³⁺ co-doped ceria ceramics with an optimized average atomic number of dopants for electrolytes in IT-SOFCs, Ceram. Int., 2018, 44, 6300–6310.
31. K. Venkataramana, C. Madhuri, C. Madhusudan, Y. Suresh Reddy and C. Vishnuvardhan Reddy, Investigation on micro-structural, structural, electrical and thermal properties of La³⁺, Sm³⁺ & Gd³⁺ triple-doped ceria as solid-electrolyte for intermediate temperature-solid oxide fuel cell applications, J. Appl. Phys., 2019, 126, 144901.
32. Y. Liu, L. Fan, Y. Cai, W. Zhang, B. Wang and B. Zhu, Superionic conductivity of Sm³⁺, Pr³⁺, and Nd³⁺ triple-doped ceria through bulk and surface two-step doping approach, ACS Appl. Mater. Interfaces, 2017, 9, 23614–23623.
33. M. Burbano, S. Nadin, D. Marrocchelli, M. Salannec and G. W. Watson, Ceria co-doping: synergistic or average effect?, Phys. Chem. Chem. Phys., 2014, 16, 8320.
34. C. Artini, L. Gigli, M. M. Carnasciali and M. Pani, Effect of the (Nd,Dy)-double doping on the structural properties of ceria, Inorganics, 2019, 7, 94.
35. C. Artini, S. Presto, M. Viviani, S. Massardo, M. M. Carnasciali, L. Gigli and M. Pani, The role of defects association in structural and transport properties of the Ce_1−x(Nd_0.74Tm_0.26)_xO_2−x/2 system, J. Energy Chem., 2021, 60, 494–502.
36. C. Artini, M. Viviani, S. Presto, S. Massardo, M. M. Carnasciali and M. Pani, Correlations between structure, microstructure and ionic conductivity in (Gd,Sm)-doped ceria, Phys. Chem. Chem. Phys., 2022, 24, 23622–23633.
37. S. Massardo, M. Pani, S. Presto, M. Viviani and C. Artini, Defect chemistry of (Nd,Tm)- and (Nd,Dy)-doped ceria as revealed by Raman and electrochemical impedance spectroscopy, Solid State Ionics, 2023, 403, 116403.
38. R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Cryst. A, 1976, 32, 751–767.
39. A. Ubaldini, C. Artini, G. A. Costa, M. M. Carnasciali and R. Masini, Synthesis and thermal decomposition of mixed Gd – Nd oxalates, J. Therm. Anal. Calorim., 2008, 91, 797–803.
40. A. Fitch, C. Dejoie, E. Covacci, G. Confalonieri, O. Grendal, L. Claustre, P. Guillou, J. Kieffer, W. de Nolf, S. Petitdemange, M. Ruat and Y. Watier, ID22 – the high-resolution powder-diffraction beamline at ESRF, J. Synchrotron Radiat., 2023, 30, 1003–1012.
41. S. Massardo, Exploring the Local Structure of Complex Doped Ceria Systems by PDF Analyses [Data Set], European Synchrotron Radiation Facility, 2025,  DOI:10.15151/ESRF-ES-891426152.
42. R. A. Young, in The Rietveld Method, ed. R. A. Young, Oxford University Press, Oxford, 1993, vol. 5, pp. 1–38.
43. J. Rodriguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55–69.
44. Local Structure from Diffraction, ed. S. J. L. Billinge and M. F. Thorpe, Springer, New York, 1998.
45. P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, PDFgetX3: a rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions, J. Appl. Crystallogr., 2013, 46, 560–566.
46. B. H. Toby and T. Egami, Accuracy of pair distribution function analysis applied to crystalline and non-crystalline materials, Acta Cryst. A, 1992, 48, 336–346.
47. T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Pergamon Materials Series, Elsevier, Amsterdam, 2003.
48. C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals, J. Phys.: Condens. Matter, 2007, 19, 335219.
49. I. D. Brown, The Chemical Bond in Inorganic Chemistry: the Bond Valence Model, IUCr Monographs on Crystallography, Oxford University Press, Oxford, 2002, vol. 12.
50. I. D. Brown and D. Altermatt, Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database, Acta Crystallogr. B, 1985, 41, 244–247.
51. I. D. Brown, Chemical and steric constraints in inorganic solids, Acta Crystallogr. B, 1992, 48, 553–572.
52. F. Yuan, Y. Zhang and W. J. Weber, Vacancy–vacancy interaction induced oxygen diffusivity enhancement in undoped nonstoichiometric ceria, J. Phys. Chem. C, 2015, 119, 13153–13159.
53. E. Mamontov and T. Egami, Structural defects in a nano-scale powder of CeO₂ studied by pulsed neutron diffraction, J. Phys. Chem. Solids, 2000, 61, 1345–1356.
54. J. P. Attfield, ‘A’ cation control of perovskite properties, Cryst. Eng., 2002, 5, 427–438.
55. W. C. Hamilton, Significance tests on the crystallographic R factor, Acta Crystallogr., 1965, 18, 502–510.
56. T. Ohashi, S. Yamazaki, T. Tokunaga, Y. Arita, T. Matsui, T. Harami and K. Kobayashi, EXAFS study of Ce_1−xGd_xO_2−x/2, Solid State Ionics, 1998, 113–115, 559–564.
57. H. Deguchi, H. Yoshida, T. Inagaki and M. Horiuchi, EXAFS study of doped ceria using multiple data set fit, Solid State Ionics, 2005, 176, 1817–1825.
58. V. Grover and A. K. Tyagi, Phase relations, lattice thermal expansion in CeO₂–Gd₂O₃ system, and stabilization of cubic gadolinia, Mater. Res. Bull., 2004, 39, 859–866.
59. M. Gupta, S. Shirbhate, P. Ojha and S. Acharya, Processing and conductivity behavior of La, Sm, Fe singly and doubly doped ceria: as electrolytes for IT-SOFCs, Solid State Ionics, 2018, 320, 199–209.
60. A. V. Coles-Aldridge and R. T. Baker, Ionic conductivity in multiply substituted ceria-based electrolytes, Solid State Ionics, 2018, 316, 9–19.
61. H. Yamamura, E. Katoh, M. Ichikawa, K. Kakinuma, T. Mori and H. Haneda, Multiple doping effect on the electrical conductivity in the (Ce_1−x−yLa_xM_y)O_2−δ (M = Ca, Sr) system, Electrochem, 2000, 68, 455–459.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details on the results of Rietveld refinements and of the pair distribution function analysis (PDF). See DOI: https://doi.org/10.1039/d3ta07027a

---