Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Navigating the unknown with AI: multiobjective Bayesian optimization of non-noble acidic OER catalysts†
Ken J.
Jenewein
 *ab,
Luca
Torresi
*ab,
Luca
Torresi
 c,
Navid
Haghmoradi
c,
Navid
Haghmoradi
 d,
Attila
Kormányos
d,
Attila
Kormányos
 ae,
Pascal
Friederich
ae,
Pascal
Friederich
 cd and
Serhiy
Cherevko
cd and
Serhiy
Cherevko
 *a
*a
aHelmholtz-Institute Erlangen-Nürnberg for Renewable Energy (IEK-11), Forschungszentrum Jülich, Cauerstrasse 1, 91058 Erlangen, Germany. E-mail: k.jenewein@fz-juelich.de; s.cherevko@fz-juelich.de
bDepartment of Chemical and Biological Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg, Egerlandstrasse 3, 91058 Erlangen, Germany
cInstitute of Theoretical Informatics, Karlsruhe Institute of Technology, Engler-Bunte-Ring 8, 76131 Karlsruhe, Germany
dInstitute of Nanotechnology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
eDepartment of Physical Chemistry and Materials Science, Interdisciplinary Excellence Centre, University of Szeged, Aradi Square 1, Szeged, H-6720 Hungary
First published on 13th December 2023
Abstract
Experimental catalyst optimization is plagued by slow and laborious efforts. Finding innovative materials is key to advancing research areas for sustainable energy conversion, such as electrocatalysis. Artificial intelligence (AI)-guided optimization bears great potential to autonomously learn from data and plan new experiments, identifying a global optimum significantly faster than traditional design of experiment approaches. Furthermore, it is vital to incorporate essential electrocatalyst features such as activity and stability into the optimization campaign to screen for a truly high-performing material. In this study, a multiobjective Bayesian optimization (MOBO) was used in conjunction with an experimental high-throughput (HT) pipeline to refine the composition of a non-noble Co–Mn–Sb–Sn–Ti oxide toward its activity and stability for the oxygen evolution reaction (OER) in acid. The viability of the MOBO algorithm was verified on a gathered data set, and an acceleration of 17x was achieved in subsequent experimental screening compared to a hypothetical grid search scenario. During the ML-driven assessment, Mn-rich compositions were critical to designing high-performing OER catalysts, while Ti incorporation into MnOx triggered an improved activity after short accelerated stress tests. To examine this finding further, an operando mass spectrometry technique was used to probe the evolution of activity, metal dissolution, and surface area over 3 h of operation. This work demonstrates the importance of respecting the multiobjective nature in electrocatalyst performance during HT campaigns. AI-based decision-making helps to bridge the gap between fast HT screening (limited property extraction) and slow fundamental research (rich property extraction) by avoiding less informative experiments.
Introduction
The task of optimization is prevalent in any scientific discipline. Material optimization and discovery, in particular, have propelled technological advancements, creating a materially different generation compared to previous ones. The current climate crisis poses a severe threat to the well-being of humanity, where innovation in energy materials is needed to tackle a monumental challenge of this scale. Establishing a renewable energy landscape is of utmost importance to secure a sustainable energy supply while maintaining current living standards in the near future. Electricity from wind and solar is intermittent, necessitating its storage into energy-dense molecules such as hydrogen to cover energy demands at any time, even during downtimes of renewable electricity production.Polymer electrolyte membrane water electrolysis (PEMWE) will be a cornerstone in the future energy transition, generating green hydrogen to end the reliance on current fossil-based energy carriers.1,2 Here, the oxygen evolution reaction (OER) is profoundly more sluggish than the hydrogen evolution reaction (HER). Given that anodic and cathodic reactions proceed simultaneously, the slower reaction ultimately determines the total device efficiency, making the improvement of OER kinetics a main target of many research endeavors in the water-splitting community. Electrocatalysts build the heart of electrochemical devices and act as reaction promoters. So far, IrOx has become the state-of-the-art OER catalyst for PEMWEs. Despite decades of research, no marketable alternative consisting of cheap earth-abundant elements has emerged to replace this scarce and expensive noble metal catalyst, necessitating impactful materials innovation. Catalysts in commercial PEMWE applications must not only be active but also durable over an extended time. The particular challenge lies in overcoming the inherent instability of non-noble metals at lower pHs, which is the operating environment of PEMWEs.
Transition metal oxides represent a popular class to explore, as oxides are inherently more stable compared to alternatives based on, e.g., phosphides, sulfides, or nitrides. Besides, many materials transform into their oxide form when subjected to OER conditions due to the highly oxidative environment.3
Recently, some promising demonstrations have proved the viability of Co- and Mn-based oxides. For instance, Mondschein et al. showed that Co3O4 can perform the OER over several days in strongly acidic electrolytes, albeit at low current densities, using a three-electrode cell.4 In terms of practical applicability, γ-MnO2 was used to operate a PEM setup for 400 h at 10 mA cm−2.5 When 100 mA cm−2 was applied, the system shut down after 8 h, which was attributed to extensive Mn leaching and calls for the need to stabilize the noble metal-free OER catalyst further.
One strategy to achieve higher stabilization is the expansion to multinary compositions.6,7 This method forms thermodynamically more stable alloys or bonds by adding elements that can alter electronic structures and act as stabilizing additives.8 The incorporation of Mn into the spinel lattice of Co3O4 can extend the catalyst lifetime by two orders of magnitude without compromising any activity during acidic OER. This effect was attributed to the formation of a stable Mn–O bond, suppressing dissolution.9 Chong et al. even demonstrated a La- and Mn-doped cobalt spinel OER catalyst that was able to operate at current densities of 200 mA cm−2 within a PEM setup for 100 h.10 In fact, recent literature has shown that targeted alloying/doping of cobalt or manganese oxides with stabilizing elements such as Sb, Ti, or Sn can profoundly impact the overall catalyst stability, for instance through stabilization of a specific oxidation state or strengthening of the metal–oxygen bond.11–13
So far, studies on multimetallic transition metal catalysts for acidic OER have primarily focused on binary oxide systems. A plethora of unexplored mixed metal systems still exists that need to be screened for their viability as non-noble alternatives to IrOx. Constructing multinary systems represents a combinatorial problem, scaling exponentially with a new parameter (e.g., elements) added to the mix. Traditional material optimization is laborious and slow, partly due to the commonly utilized one-parameter-at-a-time approach, requiring many experiments to screen a grid of parameter combinations. Such grid search becomes time-intensive and thus infeasible when subjected to large search space. High-throughput (HT) methods have contributed greatly to this challenge, where individual laboratory tasks can be automated (e.g., synthesis, measurement, and data analysis) to accelerate the testing of thousands of samples.14 Automation in HT methods not only expedites the workflow but introduces less human bias and error into the optimization campaign. Such approaches have already proven useful in screening non-noble multinary oxides toward acidic OER.15,16
The effectiveness of HT experiments in uncovering promising electrocatalysts lies in the proper definition of the main objective, i.e., which property to optimize. While many HT campaigns focus solely on the catalyst activity, screening the stability is crucial to adequately identify high-performing catalysts.17,18 However, the evaluation becomes more time and resource-intensive with each additional property being assessed.19 Combining thorough testing of each sample with a grid-search-based strategy for vast search spaces prolongs the total measurement time, losing the essence of HT screening. Additionally, not all experiments are equally useful. Spending time-intensive measurements on unpromising candidates during grid search can be a waste of resources.
As an alternative, iterative approaches are more favorable, where a small subset across the entire parameter space is explored in the first iteration. The obtained information serves as prior knowledge, informing which regions in the parameter space to investigate next and which ones to neglect in order to optimize the objective. In a way, this heuristic approach has been performed by human scientists for many centuries. However, with the recent emergence of predictive machine learning (ML) algorithms, such experimental planning can be performed autonomously without human intervention, excluding human bias from research.20 ML techniques have catapulted the scientific community into a new paradigm, whereas the implementation for energy material research and especially electrocatalysis has just started.21–23 A ML algorithm is often discussed in conjunction with big data, with massive amounts of data providing the basis for training ML models. However, some ML approaches are specifically geared toward dealing with data-poor optimization campaigns, which are often prevalent in experimental materials science, let alone electrocatalysis.24 One active learning approach is Bayesian optimization (BO), an adaptive sampling strategy relying on an iterative optimization process to find the global optimum in a predefined parameter space.25 The BO algorithm consists of the following steps: (i) initialization, in which some observations are collected, building the starting point for the optimization process. (ii) Machine learning, in which a surrogate model (typically a Gaussian process (GP)) is fitted on the given observations. (iii) Optimization policy, in which an acquisition function decides which parameter combinations are most informative to reach the global optimum. (iv) Experimental evaluation of the newly suggested candidates and starting over at (ii).
The feasibility of BO for materials science has been demonstrated for photovoltaics,26,27 thin-films,28 photocatalysts,29 and organic compounds,30 where it builds the heart of fully autonomous self-driving laboratories (SDL).31 SDLs are still very rarely applied to electrocatalytic applications. So far, only Black et al. have demonstrated a use-case in which they optimized a non-noble metal composition for acidic OER using an SDL.32
Besides SDLs, BO can be implemented into workflows without any robotic orchestration, such as computational studies to identify new electrocatalysts.33–36 BO has also been used to guide traditional laboratory workflows with manual involvement in either the synthesis or characterization to refine catalysts for electrochemical reactions. Yamauchi et al. demonstrated the viability of BO for effectively screening the Pt–Pd–Au composition space for methanol oxidation.37 It was concluded that only 1% of the entire search space was screened to find the optimum. In another report, Arenz et al. used BO to explore a multidimensional high-entropy alloy composition space comprised of Pt–Ru–Pd–Rh–Au for H2/CO electrooxidation.38 Zelenay et al. implemented adaptive learning into an automated synthesis workflow for electrocatalyst development, which guided the optimization of a Fe–N–C catalyst for the oxygen reduction reaction.39
While these studies mostly focused on singly optimizing the catalyst activity, high-performing electrocatalysts must combine high activity and stability, as mentioned earlier, representing a multiobjective optimization task. Therefore, multiobjective BO (MOBO) is crucial, in which both objectives (activity and stability) are simultaneously optimized.19 In electrocatalysis, activity and stability tend to be inversely correlated, i.e., a catalyst with exceptionally high activity commonly shows poor stability and vice versa.40 Thus, MOBO aims to identify catalysts that possess the best compromise between these two properties. Our previous report demonstrated an HT workflow that allows rapid synthesis and testing of electrocatalysts for their OER activity and stability using single-task automation.41,42 However, the underlying optimization strategy always relied on a grid search without any feedback loop driven by ML.
In this work, MOBO was implemented into a previously established HT platform to adaptively screen a Co–Mn–Sb–Sn–Ti oxide space to simultaneously maximize the activity and stability toward acidic OER. To test the viability of ML-driven experiments for the present optimization task, a data set was curated from a grid search of the Co–Mn–Sb–Sn–Ti oxide space. Based on this data set, a simulated MOBO was performed to evaluate whether the algorithm can identify the global optimum faster than a random sampler. After this validation, the algorithm was applied to suggest new compositions to be synthesized and screened in the laboratory to iteratively narrow down the optimal compositions. This strategy is illustrated in Fig. 1. Once interesting compositions were identified, more detailed and time-consuming testing was carried out on selected candidates to study the observed behavior in greater depth, for example, by using operando mass spectrometry to probe the degradation behavior.
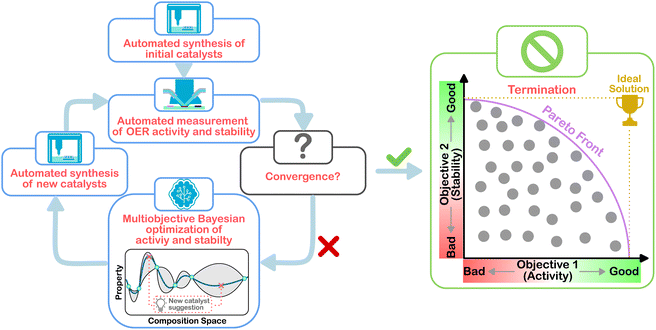 | ||
| Fig. 1 Schematic workflow of the multiobjective Bayesian optimization for the experimental OER catalyst composition optimization. | ||
Results and discussion
Simulated optimization of composition through MOBO
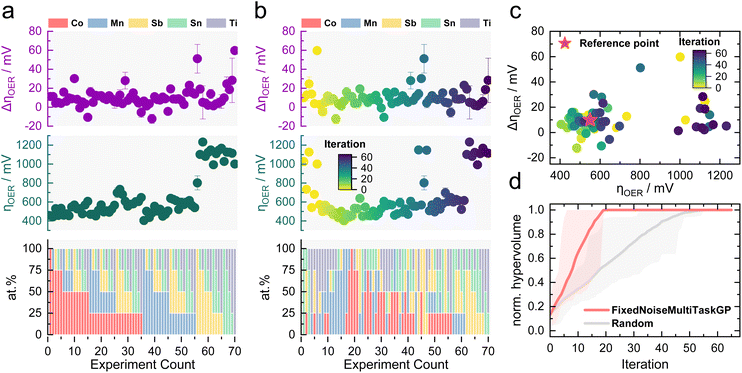
An initial proof of concept needs to validate the viability of MOBO for the OER activity–stability optimization of Co–Mn–Sb–Sn–Ti oxides. To avoid resynthesis and testing in each new iteration, a complete data set was constructed first using in-house HT capabilities. This step was taken as no open-source data sets exist that resemble this multiobjective optimization task with 5 elements as features and activity and stability as properties. A grid search approach was chosen, where 70 samples (25 at% difference between each composition) were synthesized using the pipetting robot with subsequent annealing. The samples were then assessed for their activity and stability for acidic OER in 0.1 M HNO3 using the automated scanning flow cell (SFC) developed in an earlier study.41,42 The testing protocol applied to each sample is shown in Fig. S1.† The activity was assessed through the OER overpotential (ηOER) reached during the first 1 mA cm−2 hold, whereas the stability is determined from the ηOER change (ΔηOER) after the accelerated stress test (AST). The protocol was designed around 1 mA cm−2 as higher current densities would cause more oxygen bubbles due to the OER, causing blockage of the current path within the SFC, impeding HT measurements. Bubbles can also block active sites on the catalyst, causing lower activity without any relation to the intrinsic properties of the material.43 Characterizing stability via ΔηOER is a classical and relatively facile approach in electrocatalysis, which was the main reason for its adoption for the MOBO-driven screening. This method provides a comprehensive view of the performance deterioration over time. For deeper insights into material degradation, a more involved operando technique based on mass spectrometry was used in subsequent investigations within this study, offering a detailed understanding of the catalyst dissolution during electrochemical testing.To ensure an accurate interpretation of the composition-performance results during this study, the discrepancy between the nominal and actual composition must be assessed. However, determining the actual composition of the samples on the FTO substrate with energy-dispersive X-ray (EDX) or X-ray fluorescence (XRF) is challenging as Sn signals will be overshadowed by the Sn in the substrate and Sb signals overlap with those of Sn. Instead, the composition of the drop-casted solutions was evaluated using an inductively coupled plasma mass spectrometer (ICP-MS) as a proxy measurement. The final film composition should closely resemble the ink composition, as no metal evaporation is expected during the annealing step. Table S1† shows that the ink composition for four random mixtures is in close proximity to the nominal targeted composition, confirming the accuracy of the pipetting sequence.
It is important to note that features such as morphology, phases, or surface facets undoubtedly influence the electrocatalytic performance.44,45 However, such features often come as a result of compositional tuning and can turn out to be secondary information for material discovery campaigns. Such information becomes indispensable when focusing on revealing a detailed structure–property relation to, e.g., derive new descriptors. Implementing X-ray diffraction (XRD) or X-ray photoelectron spectroscopy (XPS) into SDLs to extract such supportive information adds more engineering complexity. Hence, recording the electrocatalytic performance as a function of the composition remains a popular route for automated HT workflows in electrocatalysis and represents an intuitive research question in materials science. Nevertheless, it is worth noting that recent studies have successfully incorporated crystal structure information into active learning campaigns to boost the discovery of perovskite oxides for the OER.46
Fig. 2a depicts the obtained ηOER and ΔηOER for each composition. The data set can be found in Table S2 in the ESI.† It is noticeable that the lack of Co or Mn manifests in a massive activity drop indicated by the increase in ηOER around experiment count 55. This result aligns with expectations, as Sb, Sn, and Ti oxides are known to be poor OER catalysts.2 An obvious trend in the stability results was not observed. Surprisingly, some ΔηOER values are negative, indicating that the catalyst became more active after the AST. Overpotentials typically increase as a result of deactivation.47 A so-called activation step, as encountered for noble metals48,49 or MEAs,50,51 was not observed in the majority of the tested samples. A follow-up investigation on this irregular phenomenon will be present towards the end of this study. For now, it seems that most samples exhibit a ΔηOER around 0–20 mV.
The data shown in Fig. 2a were used to simulate a MOBO process without running additional experiments to evaluate if the algorithm can quickly identify the most active and stable compositions within the data set. q-Noisy expected hypervolume improvement (qNEHVI) was chosen as the acquisition function to identify the Pareto front as it can weigh trade-offs among multiple objectives. Additionally, it does not require a prior selection of a known trade-off between the objectives.52 A fixed noise multitask GP surrogate model was used as an ML model, which allows for the inclusion of experimental noise determined during the HT screening into the model. Experimental noise can arise from slight variations during the synthesis or measuring conditions that are typically reflected by error bars. Nevertheless, the overall repeatability of the experiments is adequate, as shown by the small error bar for most of the samples shown in Fig. 2a.
The algorithm was initialized with five random entries. Based on the results in Fig. 2a, a ηOER of 550 mV and a ΔηOER of 10 mV were determined as suitable reference points for the optimization, presenting values that are both desirable and realistically achievable. This choice also guarantees that the MOBO algorithm does not spend resources on exploring candidates that are not active or stable at all during the subsequent MOBO-guided experiments. After initialization, the MOBO algorithm picked one new candidate from the remaining data set per iteration, rearranging the data as shown in Fig. 2b. By constructing a Pareto plot by mapping the activity over stability, it becomes clear that the algorithm rapidly selected points within the optimal quarter (left bottom corner) during the first 20 iterations. Once no better compositions are left within the data set, the points scatter to less active and stable regions.
To evaluate the speed of optimization, the fixed noise multitask GP model was benchmarked against a random sampler that does not learn from previous iterations. For this comparison, the normalized hypervolume is plotted over each sampling iteration. The hypervolume is the area that spans between the Pareto optimal points and the reference point. When dealing with random sampling, multiple repetitions are required to probe the statistical significance. If the random sampler happens to sample the best compositions at the beginning, and this repetition is compared, it would insinuate MOBO to be inferior. Fig. 2d shows the comparison of the fixed noise multitask GP surrogate model against a random sampler after 500 repetitions. The adaptive sampling strategy indeed outperforms an uninformed sampler and finds the optimum already after 20 iterations. The fixed noise multitask GP model was also compared to a multitask GP model that does not consider noise. The performance is just marginally worse (see Fig. S2†). Different initialization conditions were also probed to assess the robustness of the MOBO algorithm. Even when the optimization campaign was initialized with two random samples, i.e., less information about the system at the beginning, the adaptive sampler still beat a random sampler similar to what is shown in Fig. S2† (see Fig. S3†). As heteroscedasticity (different variance in each data point) is an important and more realistic consideration during ML-guided HT screening, the fixed noise multitask GP was chosen as the surrogate model for the subsequent MOBO-driven experimental optimization of the Co–Mn–Sb–Sn–Ti oxide space.
Experimental optimization of composition through MOBO
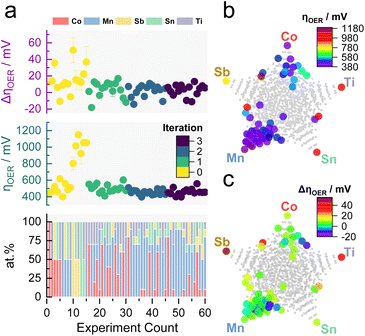
The previous results showed the validity of MOBO to optimize the OER catalyst activity and stability simultaneously in a 5-dimensional space and laid the groundwork for the subsequent ML-driven experiments. The algorithm now suggests new compositions that a scientist would synthesize and screen in the laboratory, realizing a human-in-the-loop ML-driven catalyst optimization. The campaign began with screening 15 homogeneously distributed samples over the entire quinary search space (each composition differing by 50 at%, see Table S3†). As a rule of thumb, BO campaigns should be initialized with around 2 × (n + 1) samples, where n is the dimensionality of the optimization campaign (5 in this case).52 The samples were screened using the same protocol shown in Fig. S1.† The observations serve as prior, whereupon the MOBO algorithm suggests 15 new candidates from a total composition space of 1001 candidates (each composition differing by 10 at%) that will be synthesized and screened. This loop is continued until a convergence is reached (see Fig. 1).Fig. 3a shows a summary of the recorded composition-dependent ηOER and ΔηOER for each MOBO iteration. The data set can be found in Table S4 in the ESI.† After initialization, subsequent suggestions all focus on compositions yielding an ηOER below 550 mV and ΔηOER below 15 mV. Multidimensional scaling (MDS) of the quinary parameter space in Fig. 3b (for activity) and Fig. 3c (for stability) indicates that Mn seems to play an important role in achieving the global optimum. The gray points in the MDS plots represent the total search space. Fig. S4† illustrates how, after initialization, the MOBO algorithm quickly focuses on sampling Mn-rich compositions.
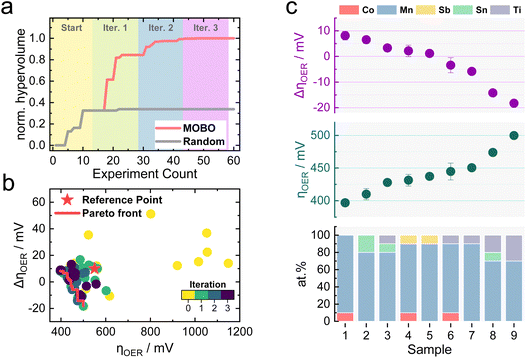
Similar to the previously simulated proof-of-concept, the MOBO algorithm improved the hypervolume significantly faster than random sampling (see Fig. 4a). A summary of the random sampling can be found in Fig. S5† and its corresponding data set in Table S5.† The hypervolume increases sharply during the first iteration and plateaus during the third iteration, suggesting that most non-dominated compositions are found during the first two optimization cycles. This rapid optimization is anticipated to be partly due to the broad information on the composition space encoded within the initial 15 samples, demonstrating the importance of initialization strategies for MOBO campaigns. From Table S6,† one can observe that all suggested sampling points for a potential 4th MOBO iteration are very similar, implying that the algorithm is already trying to exploit a particular region. This observation, combined with the marginal improvement of the hypervolume between the 2nd and 3rd iteration, served as criteria to terminate the MOBO-driven experiments. Fig. 4b shows how almost every sampled candidate is better than the predefined reference point. Compared to the grid search performed earlier, the MOBO was able to significantly improve the hypervolume and explore more non-dominated compositions that reside on the Pareto front, as indicated by Fig. S6.†
Inspecting the Pareto compositions in Fig. 4c more closely reveals that Mn90Co10Ox achieves the highest activity while suffering from an ΔηOER of around 10 mV after the AST. It is important to note that this result is highly dependent on the testing protocol chosen and should not necessarily mean that Mn90Co10Ox is the universally highest active sample. Rather than finding the one and only optimal catalyst, it is equally intriguing to discover certain trends that MOBO was able to unravel. For instance, incorporating Ti into the catalyst triggers an activity improvement after the AST, shown by the negative ΔηOER. The more Ti is incorporated, the more pronounced this effect, but at a sacrifice of activity. This trend prevailed throughout the sampled compositions, which is evident from the analysis of the 2nd, 3rd, and 4th best Pareto front shown in Fig. S7.† To clarify, the 2nd best Pareto front is obtained when all points from the 1st Pareto front are deleted. The 3rd is obtained by deleting the 1st and 2nd, and so on. More elaborate follow-up investigations are needed to understand this behavior, which will be highlighted in the upcoming sections.
Literature reports have demonstrated the beneficial role of Sb incorporation into mixed Mn oxides to improve electrocatalytic stability during acidic OER.11,53,54 Slight improvements in the stability of Mn-oxides through the addition of Sb could also be observed in this study, indicated by a lowered ΔηOER for a Mn90Sb10Ox sample compared to bare MnOx in Fig. S8.† To compare the performance of the mixed metal oxides against a state-of-the-art catalyst, a IrOx sample was synthesized with the same procedure used for the non-noble samples (see Fig. S8†). As expected, IrOx outperforms the Pareto compositions in terms of activity by 180 mV due to its superior OER kinetics. The ΔηOER after the AST is near 0, demonstrating good stability.
Overall, it seems that binary and ternary compositions are more frequently sampled during the MOBO campaign (see Fig. S9†). Fig. S9b† illustrates once more how little samples were needed (6% of total space) to arrive at an optimum. Quinary compositions were not explored at all. Fig. S10† depicts the predicted ηOER and ΔηOER values for the unexplored compositions after training the fixed noise multitask GP model on the observations made during the MOBO campaign. Here, quinary catalysts are predicted to have no potential to come close to the Pareto front, as the maximum incorporable amount of Mn would be 60% while higher Mn contents are necessary to construct highly active and stable catalysts, which would improve the hypervolume. However, making predictions into new composition spaces without being trained on them is not straightforward and requires more sophisticated transfer learning approaches.55
Extended OER testing of selected compositions
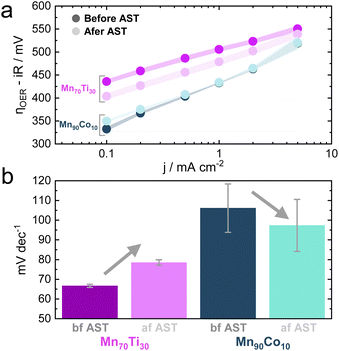
As outlined earlier, the addition of Ti into MnOx triggers an improvement in activity after ASTs, a recurring behavior observed across the entire optimization campaign. To investigate this particular behavior in more detail, the Mn70Ti30Ox composition, which showed this phenomenon the strongest within the Pareto compositions, was subjected to more extensive electrochemical testing (see Fig. S11†). The objective was to conduct a Tafel analysis before and after the same AST that was applied during the MOBO-guided screening. The Tafel analysis was performed by recording the ηOER at chronopotentiometric (CP) holds of 0.1, 0.2, 0.5, 1, 2, and 5 mA cm−2.56 A Mn90Co10Ox sample was also subjected to this testing to probe the behavior of a candidate at the opposite spectrum on the Pareto front (see Fig. 5a).As observed before, the overall activity is lower than that of a Mn90Co10Ox sample. The ηOER of both mixed metal oxides becomes similar as the current density approaches 5 mA cm—2, reasoned by the fact that Mn is the main constituent performing the OER and both being Mn-rich.
The AST once more causes the ηOER to decrease for the Mn70Ti30Ox composition. However, the Tafel slope increased (see Fig. 5b). This outcome suggests that OER kinetics worsened after the AST, implying that the improvement in OER activity might stem from extrinsic factors, e.g., an increase in the surface area. Surface roughening due to dissolution is one option that could cause an increase in the electrochemically active surface area, exposing more active sites to catalysis.57 On the other hand, the kinetics improved slightly for the Mn90Co10Ox sample. Pinning down the exact mechanism is complicated and requires more elaborate in situ testing. However, attention was devoted to the increase in activity for Ti-incorporated MnOx samples due to its irregular behavior compared to all other samples.
Hence, as a final follow-up, the Mn70Ti30Ox sample was subjected to even more rigorous testing using in situ ICP-MS.58 The coupling of a mass spectrometer to the SFC allows for studying the real-time Mn and Ti dissolution during electrochemical operations with high sensitivities. This approach will help understand catalyst stability from the perspective of active site leaching, a key degradation pathway for electrocatalysis.59
Operando dissolution study of the Mn70Ti30Ox catalyst
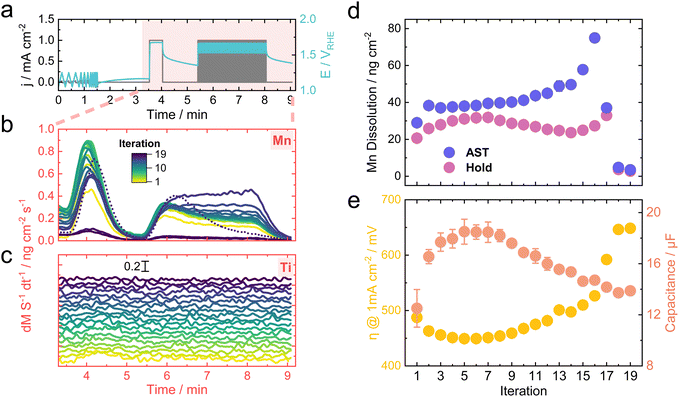
The protocol used for the follow-up measurement is shown in Fig. 6a. The objective was to record the activity, dissolution behavior, and change in surface area over a prolonged time span. The protocol was applied in a loop up to 19 times, starting with three cyclic voltammograms (CVs) between 1.1 and 1.3 VRHE. Scan rates of 25, 50, 100, and 200 mV s−1 were chosen to extract the capacitance from the capacitive current, which was treated as a proxy metric for the electrochemical surface area.60 A final hold at 1 mA cm−2 and 80 AST cycles between 0 and 1 mA cm−2 conclude the protocol.Fig. 6b and c show the dissolution traces for Mn and Ti, respectively, for each iteration of the protocol. The traces were overlaid for Mn, which helps visualize the change in their shape over time. Interestingly, the initial Mn dissolution during the AST shows a transient behavior. However, the transience gradually disappears toward the end, where the dissolution rate remains constant throughout the AST until a complete deactivation is reached, which in this case occurred around iteration 17. A tentative hypothesis includes the increasing upper potential limit for the ASTs towards the end, which would destabilize Mn more due to its transition to a soluble MnO4− phase based on the Pourbaix diagram.61 Similar OER-triggered MnO2 dissolution was reported in alkaline media, where the main driver for destabilization was attributed to the MnO2/MnO4− redox transition.62 It is worth noting that the highest Mn dissolution was actually recorded when changing the potentiostat from galvanostatic (CP hold) to potentiostatic (CV) between each iteration, which resulted in a sharp potential drop from around 1.4–1.5 VRHE to 1.1 VRHE (see Fig. S12†). This pronounced Mn leaching could result from the redox transition from MnO2 to an aqueous Mn2+ phase, which would thermodynamically occur at these potentials.5,61 Based on this argumentation, it is logical that the Mn dissolution observed when initiating the CP hold at 1 mA cm−2 is comparatively less, as the reverse redox transition is triggered, going from Mn2+ to the solid MnO2 phase.
Due to the lower signal-to-noise ratio for Ti, a stacked representation was chosen. A slight peak is present during the hold for the first two to four iterations, after which no clear dissolution signal is recognizable. This behavior could imply that Ti stabilizes over time or dissolves at rates lower than the detection limit of the ICP-MS. Nevertheless, TiO2 is thermodynamically much more stable in acidic media compared to Mn and should be resistive to dissolution up until 2.1 V at pH 0.61 Hence, most of the Ti dissolution could be originating from a cooperative dissolution mechanism, in which predominant Mn leaching rips off Ti atoms from the surface. Similar behavior was observed for Fe–Ni oxide systems during neutral OER.41
Fig. 6d shows the total dissolved amount of Mn calculated as the integral of the dissolution rates for the hold and AST. Calculating the integral for the Ti signals was more challenging due to the noisy signal, which impeded the baselining. Superimposing the Mn dissolution with the activity (as η at 1 mA cm—2) and electrochemical surface area proxy (as capacitance) shown in Fig. 6e implies some intriguing trends. Initially, the η decreases with a concomitant increase in the surface area. Preferential leaching of unalloyed Mn species could trigger such behavior, which is reasoned by the increase in Mn dissolution during the hold until the 7th iteration. The initial leaching could cause an increase in surface roughness that would lead to more active sites exposed for catalytic processes.
Interestingly, the peak of the Mn dissolution during the holds around iteration 7 coincides with the peak in the activity and surface area, implying that a transformation of the surface comes to a halt at this point. After the initial surface composition change, more stable MnxTiyOz alloys reside at the interface to the electrolyte. Subsequently, the Mn dissolution decreases between iterations 7 and 14, which could be attributed to the stabilizing effect of Ti toward Mn, as demonstrated in previous reports.12,63 It would be expected that the dissolved amount of Mn during the ASTs shows the same trend. Instead, it keeps increasing as the iteration progresses, ascribed to the harsher conditions applied during ASTs with longer exposure to fluctuating potentials. Past iteration 14, the sample deactivates fully, shown by the sudden drop in activity accompanied by a final rise in Mn dissolution caused by the high potentials before ceasing to near zero. This Mn dissolution increasing toward the end supports the hypothesis that the drop in Mn leaching during iterations 7 and 14 comes from the Ti-stabilized Mn rather than solely from a simple depletion of the sample.
Conclusions
Material optimization is needed to tackle highly relevant challenges of the 21st century. Electrocatalysis is not exempt from this urgency. Mixed metal oxides are a promising material class to be studied as an earth-abundant alternative for OER catalysis in PEMWEs. Screening the vast composition space efficiently is key to accelerating material optimization, where a brute-force approach (e.g., grid search) might be highly resource-intensive when subjected to millions of test samples. The typical countermeasure in HT studies is to reduce the testing time per candidate, compromising the amount of information extractable during the measurement. OER stability, in particular, requires extended testing to accurately probe destabilization. Electrocatalytic performance is highly impacted by the choice of the electrochemical protocol due to the dynamic electrode|electrolyte interface. In other words, the chosen protocol will decide the final outcome of an optimization campaign and its translatability toward real applications.In an effort to implement these concepts into HT electrocatalysis research, we have relied on ML-driven decision-making based on multiobjective Bayesian optimization to simultaneously optimize the activity and stability within a Co–Mn–Sb–Sn–Ti oxide space for acidic OER using an in-house HT platform. The electrochemical testing took around 5 minutes per sample and is already longer than what would be encountered in common HT literature (usually a few seconds per sample) but was required to test stability. Adaptive sampling helped to bridge the gap between fast HT screening (limited property extraction) and slow fundamental research (rich property extraction) to identify the Pareto front in just 15 h of pure measurement time. Testing each possible triplicated composition (3003 samples) would have required 250 h, representing an acceleration of around 17x.
The MOBO-assisted HT campaign revealed that Ti incorporation into a MnOx host triggers an activity improvement after ASTs. Follow-up studies using an operando ICP-MS technique were employed to promote the understanding of underlying processes during extended OER testing. It was concluded that initial Mn dissolution coming from unalloyed Mn induces surface roughness to increase the electrochemically active surface area. The remaining MnxTiyOz displays better electrochemical stability before complete deactivation. While Mn leaching was dominant, Ti mostly remained stable.
None of the noble metal-free alternatives outperformed a self-synthesized IrOx reference, which will remain a great challenge in the realm of PEMWEs. Nonetheless, we demonstrated the viability of MOBO guidance as a tool to experimentally optimize OER catalysts regarding two essential properties, namely activity and stability. Such tools can help to recognize interesting trends in a large parameter space significantly faster, where more fundamental approaches can further study certain aspects to foster scientific knowledge. The scanning flow cell setup allows for the coverage of the entire pipeline, going from fast high-level screening (5 min per sample) to slow but fundamental understanding (3 h per sample).
Experimental methods
Materials
Co(NO3)2·6H2O (99.99%), Mn(NO3)2·4H2O (97%), SnCl4·5H2O (98%), Ti-butoxide (97%), H2Cl6Ir·xH2O (99.9%), glycerol (≥99.5%), isopropanol (≥99.5%), dichlorodimethylsilane (≥99.5%), hexane (≥99%), and 5 × 5 cm glass slides with an FTO coating (TEC 15) were purchased from Sigma-Aldrich. The Sb precursor was a 10 mg mL−1 stock solution in tartaric acid/HNO3 (Specpure) and was purchased from Alfa Aesar. Concentrated HNO3 (65%) from VWR was used to prepare diluted electrolyte solutions.All chemicals were used as received without any further purification.
Sample preparation
The sample preparation using an automated pipetting robot is described in detail elsewhere.41 In short, 12 mM inks of Co, Mn, Sb, and Sn were prepared in a 2 mL solution containing 70% v/v 1% HNO3 and 30% v/v glycerol. A 12 mM Ti ink was prepared similarly, except using 2 M instead of 1% HNO3 to retain the Ti in the solution. A 12 mM ink corresponds to 7 mg of Co(NO3)2·6H2O, 6 mg of Mn(NO3)2·4H2O, 0.292 mL of a 10 mg mL−1 Sb stock solution in tartaric acid/HNO3, 8 mg of SnCl4·5H2O, and 8 μL of Ti-butoxide. An IrOx benchmark was prepared as well, for which 10 mg of H2IrCl6·xH2O was used to achieve a 12 mM ink. The FTO substrate was first cleaned by ultrasonicating 5 min each in a 2% Hellmanex III solution, water, and IPA. The FTO was then air-dried and subjected to a silanization step by immersing the substrate in a 6% v/v dichlorodimethylsilane solution in hexane for 5 min. This step was used to render the FTO surface hydrophobic, which helped locally contain the deposited droplet on the substrate.64 The FTO was subsequently rinsed with hexane to remove the residual silane solution and dried in air before final use.The drop-casting volume for the mixed inks was 0.3 μL. Subsequent annealing in air first at 300 °C for 10 min using a heating rate of 1 °C min−1 and then at 500 °C for 4 h using a heating rate of 2.5 °C min−1 using a box furnace (KLC 10/14, Thermconcept) converts the mixed transition metals into their oxide form.
Physical characterization
Electrochemical testing
The development of automated SFC measurements is described in detail elsewhere.41,42 In short, a laser microscope (VK-X250, Keyence) was used in conjunction with an image detection algorithm to extract spot coordinates and geometric surface areas. The coordinates were used for the xy translation of the SFC during HT measurements. The geometric surface area was used to normalize obtained currents.Electrochemical measurements were controlled with a Gamry REF 600 potentiostat. The reference electrode was a double-junction Ag/AgCl electrode in 3 M KCl (Metrohm). The counter electrode was a glassy carbon rod (SIGRADUR G, HTW). Samples were typically contacted with copper tape at the FTO substrate. Measured potentials, EAg/AgCl, were all corrected to the reversible hydrogen electrode (RHE) scale. The electrolyte was constantly purged with 30 mL min−1 of Ar. The electrolyte flow was regulated using a peristaltic pump (Reglo ICC, Ismatec) set to 15 RPM.
The protocol utilized for the initial grid search and MOBO-guided experiments is shown in Fig. S1.† Each composition was subjected to a galvanostatic protocol starting with a 20 s hold at 1 mA cm−2, where the activity of the sample is extracted as OER overpotential (ηOER). After performing a short accelerated stress test (AST) of 120 cycles between 0 and 1 mA cm−2 with a 1 s hold each, the activity is assessed again at 1 mA cm−2. The change in ηOER (ΔηOER) before and after the AST serves as a proxy metric for stability.
The total protocol used for follow-up measurements on Mn70Ti30Ox and Mn90Co10Ox samples is shown in Fig. S11.† The activity is assessed through multiple 30 second chronopotentiometric (CP) steps at 0.1, 0.2, 0.5, 1, 2, 5 mA cm−2 to allow a Tafel analysis. As higher currents are reached during this protocol, the potential was iR corrected using the resistance measured through electrochemical impedance spectroscopy (EIS) between 100 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz at open circuit potential. The CP holds are followed by the same AST outlined earlier (120 cycles between 0 and 1 mA cm−2 for 1 s each) before concluding with another Tafel analysis with the same current steps.
000 Hz at open circuit potential. The CP holds are followed by the same AST outlined earlier (120 cycles between 0 and 1 mA cm−2 for 1 s each) before concluding with another Tafel analysis with the same current steps.
Finally, another electrochemical protocol is designed to study the operando dissolution behavior of Mn70Ti30Ox. The objective was to record the activity, dissolution behavior, and change in surface area over a prolonged time span, for which the protocol was applied in a loop up to 19 times. Each iteration starts with three cyclic voltammograms (CVs) between 1.1 and 1.3 VRHE. Scan rates of 25, 50, 100, and 200 mV s−1 were chosen to extract the capacitance from the capacitive current, which serves as a proxy for the electrochemical surface area.60 The obtained capacitance is purposely not converted to an area value as the specific capacitance for this system is unknown. However, as the change throughout the operation is more relevant, reporting the capacitance alone is thought to be sufficient. Afterward, a 30second hold at 1 mA cm−2 and 80 AST cycles between 0 and 1 mA cm−2 are performed to roughly mimic testing conditions applied previously.
Inductively coupled plasma mass spectrometry
An inductively coupled plasma mass spectrometer (ICP-MS, Nexion 350X, PerkinElmer) was used in two ways during this study. First, it was used to determine the elemental composition of the drop-casting ink. Later, it was used to record the operando dissolution of selected compositions identified during the MOBO-guided experiments. For the latter, the ICP-MS was connected through Tygon tubings (Proliquid) with the outlet of the SFC. The ICP-MS was always calibrated before measurements by a four-point calibration (0, 1, 10, and 50 μg L−1) using Merck Certipur ICP standards. 59Co, 55Mn, 121Sb, 120Sn, and 47Ti were used as analytes. 48Ti, which would be the more abundant isotope of Ti, was deliberately not chosen as it had higher background counts, increasing the detection limit. The calibration matrix was 0.1 M HNO3 to mimic the supporting electrolyte for subsequent operando measurements. Internal standards were prepared in 1–2% HNO3 at 5 μg L−1, where 74Ge was the internal standard for Co and Mn, 138Ba for Sb, 103Rh for Sn, and 45Sc for Ti. Internal standards were used to ensure a stable and reliable system performance. A Y-connector was used to simultaneously ingest the analyte and internal standard during measurements.Computational methods
Multidimensional scaling
Multidimensional scaling (MDS) is another dimensionality reduction tool that can help to visualize high-dimensional data in 2D. This technique can be employed when the property of interest is the similarity/dissimilarity of compositions, which can be readily visualized by the distance of a compositional data point from all others. MDS is performed using the scikit-learn65 package in Python, employing two dimensions to represent the dissimilarities.Multiobjective Bayesian optimization
BoTorch,66 an open-source framework built on PyTorch67 was used to implement the multiobjective Bayesian optimization in Python. A fixed noise multitask GP was used as the surrogate model to fit the observed data points. This model also permits feeding in experimentally determined noise around each data point (error bar). As a comparison, a multitask GP model without noise input was also tested during initial benchmarking using a data set. A q-noisy expected hypervolume improvement (qNEHVI) acquisition function was used as a decision-making policy with a reference point of 550 mV and 10 mV for activity (ηOER) and stability (ΔηOER), respectively. The reference point represents a compromise between being realistically attainable and not too far from the desired optimum. The qNEHVI acquisition function allows batched optimization in which multiple candidates can be suggested per iteration, which is needed to couple MOBO guidance with the developed HT pipeline most efficiently.All features (i.e., compositions) were normalized to 1. The ηOER, ΔηOER, and reference point had to be negated to depict a problem where higher values are more desired. This conversion is necessary, as the algorithm can only deal with maximization problems. Additionally, all values except the features were standardized using the StandardScaler from scikit-learn, which removes the mean and scales the data to unit variance.
During the initial benchmarking of MOBO using a data set, 5 randomly sampled compositions depict the starting condition. Then, one new composition is sampled from the data set during each iteration with the objective to improve the hypervolume. The optimization finishes when all candidates within the data set have been sampled. To gain statistical significance, 500 repetitions of such optimization runs have been performed. The seed for the random initialization went from 0 to 499. The fixed noise multitask GP and multitask GP models were compared against a random sampler with a random see concomitantly going from 0 to 499. The final performance was evaluated by calculating the average normalized hypervolume per iteration within an upper percentile of 75% and a lower percentile of 25%.
During MOBO-driven experiments, the acquisition function value is calculated for a constrained parameter space. The sum of all elements must be 1 (i.e., 100%), and each element must be within 0 and 1 (i.e., between 0 and 100%). The acquisition function then suggests 15 new candidates where each element is outputted with a value within the continuous 5-dimensional space (output value has many decimal places). Such elemental fractions are unfeasible to be synthesized using the pipetting robot. Thus, the most similar composition within the total search space of 1001 compositions (each differing in 10 at%) is chosen based on the smallest Euclidean distance to the suggested candidate. Every evaluated candidate is eliminated from the total search space to avoid re-sampling.
Data and code availability
Obtained data sets and Python codes used throughout this study are available at the following link. https://github.com/kjenewein/Multiobjective-Bayesian-Optimization.Author contributions
K. J. J. designed and performed all experiments, computational methods, data evaluation, and visualization. K. J. J., P. F., and S. C. conceptualized the study. K. J. J. wrote the original draft. All authors participated in scientific discussions. All authors reviewed and edited the manuscript. P. F. and S. C. supervised the work.Conflicts of interest
The authors declare no competing interests.Acknowledgements
We would like to acknowledge the Helmholtz Information & Data Science Academy (HIDA) for providing financial support within the HIDA Trainee Network program. Additionally, the authors thank the Bavarian Ministry of Economic Affairs, Regional Development and Energy for partially funding this research. P. F. and N. H. acknowledge support by the Federal Ministry of Education and Research (BMBF) under Grant No. 01DM21001B (German-Canadian Materials Acceleration Center). P. F. and L. T. acknowledges support by BMBF under Grant No. 01DM21002A (FLAIM). We would like to thank Jonas Möller for developing the custom-made LabVIEW software employed for the automated electrochemical measurements. We would also like to acknowledge Christian Göllner for his help during operando ICP-MS measurements.Notes and references
- F. Dawood, M. Anda and G. M. Shafiullah, Int. J. Hydrogen Energy, 2020, 45, 3847–3869 CrossRef CAS.
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schafer, Chem. Soc. Rev., 2022, 51, 4583–4762 RSC.
- K. Kawashima, R. A. Marquez, L. A. Smith, R. R. Vaidyula, O. A. Carrasco-Jaim, Z. Wang, Y. J. Son, C. L. Cao and C. B. Mullins, Chem. Rev., 2023, 123, 12795–13208 CrossRef CAS PubMed.
- J. S. Mondschein, J. F. Callejas, C. G. Read, J. Y. C. Chen, C. F. Holder, C. K. Badding and R. E. Schaak, Chem. Mater., 2017, 29, 950–957 CrossRef CAS.
- A. Li, H. Ooka, N. Bonnet, T. Hayashi, Y. Sun, Q. Jiang, C. Li, H. Han and R. Nakamura, Angew Chem. Int. Ed., 2019, 58, 5054–5058 CrossRef CAS.
- B. Wang, Y. Yao, X. Yu, C. Wang, C. Wu and Z. Zou, J. Mater. Chem. A, 2021, 9, 19410–19438 RSC.
- L. Xiao, Z. Wang and J. Guan, Chem. Sci., 2023, 14, 12850–12868 RSC.
- S. Cherevko, Curr. Opin. Electrochem., 2023, 38, 101213 CrossRef CAS.
- A. Li, S. Kong, C. Guo, H. Ooka, K. Adachi, D. Hashizume, Q. Jiang, H. Han, J. Xiao and R. Nakamura, Nat. Catal., 2022, 5, 109–118 CrossRef CAS.
- L. Chong, G. Gao, J. Wen, H. Li, H. Xu, Z. Green, J. D. Sugar, A. J. Kropf, W. Xu, X. M. Lin, H. Xu, L. W. Wang and D. J. Liu, Science, 2023, 380, 609–616 CrossRef CAS PubMed.
- L. Zhou, A. Shinde, J. H. Montoya, A. Singh, S. Gul, J. Yano, Y. Ye, E. J. Crumlin, M. H. Richter, J. K. Cooper, H. S. Stein, J. A. Haber, K. A. Persson and J. M. Gregoire, ACS Catal., 2018, 8, 10938–10948 CrossRef CAS.
- R. Frydendal, E. A. Paoli, I. Chorkendorff, J. Rossmeisl and I. E. L. Stephens, Adv. Energy Mater., 2015, 5, 1500991 CrossRef.
- Z. Wang, Y.-R. Zheng, I. Chorkendorff and J. K. Nørskov, ACS Energy Lett., 2020, 5, 2905–2908 CrossRef CAS.
- H. S. Stein and J. M. Gregoire, Chem. Sci., 2019, 10, 9640–9649 RSC.
- H. S. Stein, D. Guevarra, A. Shinde, R. J. R. Jones, J. M. Gregoire and J. A. Haber, Mater. Horiz., 2019, 6, 1251–1258 RSC.
- A. Shinde, R. J. R. Jones, D. Guevarra, S. Mitrovic, N. Becerra-Stasiewicz, J. A. Haber, J. Jin and J. M. Gregoire, Electrocatalysis, 2014, 6, 229–236 CrossRef.
- A. J. Martín, S. Mitchell, C. Mondelli, S. Jaydev and J. Pérez-Ramírez, Nat. Catal., 2022, 5, 854–866 CrossRef.
- E. Kolle-Görgen, G. Fortunato and M. Ledendecker, Chem. Mater., 2022, 34, 10223–10236 CrossRef.
- A. Kormányos, K. J. Jenewein and S. Cherevko, Trends Chem., 2022, 4, 475–478 CrossRef.
- E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi, I. Foster, C. P. Gomes, J. M. Gregoire, A. Mehta, J. Montoya, E. Olivetti, C. Park, E. Rotenberg, S. K. Saikin, S. Smullin, V. Stanev and B. Maruyama, Matter, 2021, 4, 2702–2726 CrossRef.
- Z. Wang, Z. Sun, H. Yin, X. Liu, J. Wang, H. Zhao, C. H. Pang, T. Wu, S. Li, Z. Yin and X. F. Yu, Adv. Mater., 2022, 34, e2104113 CrossRef PubMed.
- Z. Yao, Y. Lum, A. Johnston, L. M. Mejia-Mendoza, X. Zhou, Y. Wen, A. Aspuru-Guzik, E. H. Sargent and Z. W. Seh, Nat. Rev. Mater., 2023, 8, 202–215 CrossRef PubMed.
- S. Zhu, K. Jiang, B. Chen and S. Zheng, J. Mater. Chem. A, 2023, 11, 3849–3870 RSC.
- B. Boyce, R. Dingreville, S. Desai, E. Walker, T. Shilt, K. L. Bassett, R. R. Wixom, A. P. Stebner, R. Arroyave, J. Hattrick-Simpers and J. A. Warren, Matter, 2023, 6, 1320–1323 CrossRef CAS.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175 Search PubMed.
- B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, F. Hase, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. E. Yunker, M. B. Rooney, J. R. Deeth, V. Lai, G. J. Ng, H. Situ, R. H. Zhang, M. S. Elliott, T. H. Haley, D. J. Dvorak, A. Aspuru-Guzik, J. E. Hein and C. P. Berlinguette, Sci. Adv., 2020, 6, eaaz8867 CrossRef CAS PubMed.
- J. Wagner, C. G. Berger, X. Du, T. Stubhan, J. A. Hauch and C. J. Brabec, J. Mater. Sci., 2021, 56, 16422–16446 CrossRef CAS.
- B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney, N. Taherimakhsousi, D. J. Dvorak, H. N. Chiu, C. E. B. Waizenegger, K. Ocean, M. Mokhtari and C. P. Berlinguette, Nat. Commun., 2022, 13, 995 CrossRef CAS PubMed.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- S. Steiner, J. Wolf, S. Glatzel, A. Andreou, J. M. Granda, G. Keenan, T. Hinkley, G. Aragon-Camarasa, P. J. Kitson, D. Angelone and L. Cronin, Science, 2019, 363 Search PubMed.
- M. Abolhasani and E. Kumacheva, Nat. Synth., 2023, 2, 483–492 CrossRef.
- E. Fatehi, M. Thadani, G. Birsan and R. W. Black, arXiv, 2023, preprint, DOI:10.48550/arXiv.2305.12541.
- R. A. Flores, C. Paolucci, K. T. Winther, A. Jain, J. A. G. Torres, M. Aykol, J. Montoya, J. K. Nørskov, M. Bajdich and T. Bligaard, Chem. Mater., 2020, 32, 5854–5863 CrossRef CAS.
- B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber, M. Aykol, S. K. Suram and J. M. Gregoire, Chem. Sci., 2020, 11, 2696–2706 RSC.
- M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C. T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C. S. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S. C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Nature, 2020, 581, 178–183 CrossRef CAS PubMed.
- J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Loffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig and J. Rossmeisl, Angew Chem. Int. Ed., 2021, 60, 24144–24152 CrossRef CAS PubMed.
- A. S. Nugraha, G. Lambard, J. Na, M. S. A. Hossain, T. Asahi, W. Chaikittisilp and Y. Yamauchi, J. Mater. Chem. A, 2020, 8, 13532–13540 RSC.
- V. A. Mints, J. K. Pedersen, A. Bagger, J. Quinson, A. S. Anker, K. M. Ø. Jensen, J. Rossmeisl and M. Arenz, ACS Catal., 2022, 12, 11263–11271 CrossRef CAS.
- W. J. M. Kort-Kamp, M. Ferrandon, X. Wang, J. H. Park, R. K. Malla, T. Ahmed, E. F. Holby, D. J. Myers and P. Zelenay, J. Power Sources, 2023, 559 Search PubMed.
- N. Danilovic, R. Subbaraman, K. C. Chang, S. H. Chang, Y. J. Kang, J. Snyder, A. P. Paulikas, D. Strmcnik, Y. T. Kim, D. Myers, V. R. Stamenkovic and N. M. Markovic, J. Phys. Chem. Lett., 2014, 5, 2474–2478 CrossRef CAS PubMed.
- K. J. Jenewein, G. D. Akkoc, A. Kormányos and S. Cherevko, Chem Catal., 2022, 2, 2778–2794 CrossRef CAS.
- K. J. Jenewein, S. Thienhaus, A. Kormanyos, A. Ludwig and S. Cherevko, Chem. Sci., 2022, 13, 13774–13781 RSC.
- C. Wei, R. R. Rao, J. Peng, B. Huang, I. E. L. Stephens, M. Risch, Z. J. Xu and Y. Shao-Horn, Adv. Mater., 2019, 31, e1806296 CrossRef PubMed.
- J. Linnemann, K. Kanokkanchana and K. Tschulik, ACS Catal., 2021, 11, 5318–5346 CrossRef CAS.
- A. R. Akbashev, Curr. Opin. Electrochem., 2022, 35, 101095 CrossRef CAS.
- J. Moon, W. Beker, M. Siek, J. Kim, H. S. Lee, T. Hyeon and B. A. Grzybowski, Nat. Mater., 2023 DOI:10.1038/s41563-023-01707-w.
- M. Risch, Curr. Opin. Electrochem., 2023, 38, 101247 CrossRef CAS.
- J. C. Meier, C. Galeano, I. Katsounaros, J. Witte, H. J. Bongard, A. A. Topalov, C. Baldizzone, S. Mezzavilla, F. Schuth and K. J. J. Mayrhofer, Beilstein J. Nanotechnol., 2014, 5, 44–67 CrossRef PubMed.
- R. Chattot, C. Roiron, K. Kumar, V. Martin, C. A. Campos Roldan, M. Mirolo, I. Martens, L. Castanheira, A. Viola, R. Bacabe, S. Cavaliere, P.-Y. Blanchard, L. Dubau, F. Maillard and J. Drnec, ACS Catal., 2022, 12, 15675–15685 CrossRef CAS.
- E. Kuhnert, V. Hacker, M. Bodner and P. Subramanian, Int. J. Energy Res., 2023, 2023, 1–23 CrossRef.
- P. Pei, X. Fu, Z. Zhu, P. Ren and D. Chen, Int. J. Hydrogen Energy, 2022, 47, 24897–24915 CrossRef CAS.
- S. Daulton, M. Balandat and E. Bakshy, arXiv, 2021, preprint, DOI:10.48550/arXiv.2105.08195.
- S. Luke, M. Chatti, D. Simondson, K. N. Dinh, B. V. Kerr, T. D. Nguyen, G. Yilmaz, B. Johannessen, D. R. MacFarlane, A. Yella, R. K. Hocking and A. N. Simonov, EES Catal., 2023, 1, 730–741 RSC.
- I. A. Moreno-Hernandez, C. A. MacFarland, C. G. Read, K. M. Papadantonakis, B. S. Brunschwig and N. S. Lewis, Energy Environ. Sci., 2017, 10, 2103–2108 RSC.
- S. Kong, D. Guevarra, C. P. Gomes and J. M. Gregoire, Appl. Phys. Rev., 2021, 8, 021409 CAS.
- S. Anantharaj, S. Noda, M. Driess and P. W. Menezes, ACS Energy Lett., 2021, 1607–1611, DOI:10.1021/acsenergylett.1c00608.
- C. Spori, J. T. H. Kwan, A. Bonakdarpour, D. P. Wilkinson and P. Strasser, Angew Chem. Int. Ed., 2017, 56, 5994–6021 CrossRef PubMed.
- O. Kasian, S. Geiger, K. J. J. Mayrhofer and S. Cherevko, Chem. Rec., 2019, 19, 2130–2142 CrossRef CAS PubMed.
- S. Cherevko, Curr. Opin. Electrochem., 2018, 8, 118–125 CrossRef CAS.
- C. C. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- M. Pourbaix, Atlas of Electrochemical Equlibria in Aqueous Solutions, NACE International, 1974 Search PubMed.
- F. D. Speck, P. G. Santori, F. Jaouen and S. Cherevko, J. Phys. Chem. C, 2019, 123, 25267–25277 CrossRef CAS.
- J. Peng, L. Giordano, T. C. Davenport and Y. Shao-Horn, Chem. Mater., 2022, 34, 7774–7787 CrossRef CAS.
- S. P. Berglund, H. C. Lee, P. D. Nunez, A. J. Bard and C. B. Mullins, Phys. Chem. Chem. Phys., 2013, 15, 4554–4565 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, Adv. Neural Inf. Process. Syst., 33, 2020, DOI:10.48550/arXiv.1910.06403.
- A. G. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Adv. Neural Inf. Process. Syst., 2019, 32, 8026–8037 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06651g |
| This journal is © The Royal Society of Chemistry 2024 |