Effect of Pb 6s² lone pair on the potential flattening of fluoride-ion conduction in perovskite-type fluoride

Abstract

Materials containing ns² lone pairs exhibit superior fluoride-ion conductivity, acting as promising candidates for solid electrolytes in all-solid-state fluoride-ion batteries. However, the effect of lone pairs on fluoride-ion conduction remains unclear, especially for 6s² in Pb²⁺. This study investigated the relationships between the ionic conductivity, crystal structure, and electronic structure of CsPb_0.9K_0.1F_2.9. Cubic CsPb_0.9K_0.1F_2.9 exhibited a low activation energy of 7.9 kJ mol⁻¹, resulting in high conductivity at 223 K (1.0 × 10⁻³ S cm⁻¹, bulk conductivity). ¹⁹F nuclear magnetic resonance spectroscopy confirmed facile local migration of the fluoride ions with a low activation barrier of 3.8 kJ mol⁻¹. Theoretical calculations revealed that the fluoride ions migrated with a low migration energy via an exchange reaction between the Pb 6s lone pairs and fluoride ions. The localised lone pair in the PbF₅ polyhedron stabilised the saddle-point structure and mitigated the migration barrier. These findings are beneficial for material design, providing superionic conductivity with a low migration barrier for fluoride ions as well as other anions, such as oxide and chloride.

---

Introduction

Materials containing cations with ns² (n = 5, 6) lone pair electrons, such as Pb²⁺, Sn²⁺, and Bi³⁺, exhibit excellent macroscopic properties. Ferroelectric oxides of PbTiO₃ display superior dielectric properties, and perovskite-type Na_0.5Bi_0.5TiO₃ and layered fluorite-type PbSnF₄ exhibit high anion conductivities.^1–3 These cations with lone pairs possess high electronic polarisability.⁴ The larger the polarisation of the lattice ions in the same structure, the lower the activation barrier for ionic conduction of the carrier ion.⁵ Several superior anion conductors have been found in polarisable cation systems with ns² valence electron configuration.^1,6–11 Particularly, the demand for the fluoride-ion conductors as solid electrolytes for use in all-solid-state fluoride-ion batteries (ASSFIBs) has increased.¹² ASSFIBs exhibit high energy density, making them suitable candidates for post-lithium-ion batteries.¹³ Fluoride-ion conductors exhibiting high conductivity in a wide temperature range are essential to achieve ASSFIBs with high power densities and wide operating temperature ranges. Various crystal structures are known for fluoride-ion conductors, such as fluorite-type MSnF₄ (M = Pb, Ba)^14,15 and Pb_1−xM_xF_2±δ (M = K, Zr),^16,17 perovskite-type APbF₃ (A = Cs, Rb),^9,18 and ASn₂F₅-type compounds (A = Na–Cs, Tl, and NH₄).¹⁹ Ternary tin fluorides with open space in their structures, such as PbSnF₄ and ASn₂F₅, exhibit high fluoride-ion conductivities above 10⁻⁴ S cm⁻¹. The strong stereochemical activity of the Sn 5s² lone pair leads to its localisation, resulting in an asymmetric local structure.²⁰ Therefore, fluorides containing Sn²⁺ possess open spaces in their structures. The effect of the Sn²⁺ lone pair on the fluoride-ion conductivity has been investigated in MSnF₄ (M = Pb, Ba),²¹ wherein the lone pair of Sn²⁺ pushes the F away from the tetrahedral towards octahedral sites, forming the Frenkel defect pair F_i and V_F, which are interstitial F and F vacancies, respectively. In the layered fluorite-type PbSnF₄, the cations stack in the [Pb–Pb–Sn–Sn] manner along the c-axis in the tetragonal lattice. G. Dénès et al. systematically investigated the coordination environment and charge density of Sn²⁺ using neutron diffraction and ¹¹⁹Sn Mössbauer spectroscopy.^23,24 According to their research, the stereoactive lone pair of Sn is oriented to the [Sn–Sn] interlayer along the c-axis in tetragonal PbSnF₄. The fluoride ions disappear in the [Sn–Sn] interlayer; however, they occupy the interstitial sites in the [Pb–Sn] interlayer. This arrangement enables concerted fluoride-ion migration involving interstitial sites with a low activation energy.²² In contrast, the role of the Pb 6s² lone pair in fluoride-ion conduction remains unclear.

The stereochemical activity of 6s² in Pb²⁺ is relatively low compared to that of 5s² in Sn²⁺.²⁰ Consequently, no defect structure is present in the lead fluoride system, and the effect of the 6s² lone pair on the conductivity is overlooked. Cubic perovskite-type CsPbF₃, in which Cs⁺ and Pb²⁺ occupy A- and B-sites, respectively, exhibit high ionic conductivity on the order of 10⁻⁵ S cm⁻¹ at room temperature.⁹ Recently, exceptionally high ionic conductivity of the order 10⁻³ S cm⁻¹ was reported for CsPb_0.9K_0.1F_2.9.²⁵ The F vacancy introduced via the substitution of K⁺ at the host Pb²⁺ site triggered fast fluoride-ion conduction. However, the detailed conduction mechanism in addition to the effect of the lone pair remains unclear. This study investigated the ionic conductivities and crystal structures of CsPbF₃ and CsPb_0.9K_0.1F_2.9 in detail using impedance spectroscopy and neutron diffraction measurements. Additionally, the F dynamics was studied using nuclear magnetic resonance (NMR) spectroscopy. Furthermore, the effect of the lone pair of Pb²⁺ ions on the high fluoride-ion conductivity was elucidated using first-principles calculations. This study provides new insights into the mechanism through which migration energies are mitigated in Pb-perovskite systems.

Experimental

Synthesis

CsPbF₃ and CsPb_0.9K_0.1F_2.9 were prepared via mechanochemical synthesis. The starting materials, CsF, PbF₂, and KF, were weighed in an Ar-filled glove box and subjected to mechanochemical milling (zirconia pot with a volume of 45 mL and 18 balls of diameter 10 mm) in an Ar atmosphere for 12 h at 600 rpm using a planetary ball mill (Fritsch, P-7). The obtained sample was enclosed in an airtight Cu capsule under an Ar atmosphere and then annealed at 473 K for 12 h.

Characterisation

The ionic conductivities were determined using alternating current (AC) impedance spectroscopy. The sample was compressed to a diameter of 10.0 mm, thickness of approximately 1 mm, and relative density of over 90% under a pressure of 340 MPa. The Pt sheets were used as current collectors. The AC impedance measurements were performed using a frequency response analyser (Keysight E4990A) at an applied voltage of 10 mV and a frequency range of 100 MHz–20 Hz in the 423–173 K temperature range. The activation energy (E_a) was obtained using the Arrhenius equation, σ = A₀/T exp(–E_a/kT), where A₀, k, and T are pre-exponential factor, Boltzmann constant, and absolute temperature, respectively.

Synchrotron X-ray diffraction data were collected at the BL02B2 beamline within the SPring-8 facility.²⁶ Diffraction data were collected in the 2–75° 2θ range using a Debye–Scherrer diffraction camera. Neutron powder diffraction (NPD) data were acquired using a time-of-flight neutron powder diffractometer (BL09 SPICA) at the J-PARC facility.²⁷ The crystal structures were refined via Rietveld analysis using the computer programs Z-Rietveld and RIETAN-FP.^28,29 The nuclear scattering length density distribution was analysed through the maximum entropy method (MEM) using the Z-MEM code.³⁰ The NMR measurements were performed using a JEOL ECA600 NMR spectrometer at 14 T with the triply tuned magic-angle spinning (MAS) probe (Agilent Technologies Inc.) with a 1.6 mm rotor. The resonance frequencies for ¹⁹F and ²⁰⁷Pb were 564 and 126 MHz, respectively. The ¹⁹F chemical shifts were calibrated in ppm relative to CCl₃F, employing the ¹⁹F chemical shift for C₆F₆ (−163 ppm (ref. 31)) as an external reference. The ²⁰⁷Pb chemical shifts were calibrated in ppm relative to a saturated aqueous solution of Pb(NO₃)₂. The temperature-calibration experiment was conducted using ²⁰⁷Pb NMR of Pb(NO₃)₂.³² The NMR spectra of ¹⁹F and ²⁰⁷Pb were observed using a single pulse with the Hahn echo under MAS at 35 kHz. Application of ¹⁹F decoupling showed no appreciable narrowing effects on the ²⁰⁷Pb spectra (not shown). The two-dimensional (2D) exchange NMR experiment was performed with the conventional three-pulse sequence.³³ The spin–lattice relaxation time (T₁) was obtained using the saturation-recovery method under MAS. The ²⁰⁷Pb T₁ was also measured at 4.7 T by utilizing an OPENCORE spectrometer.³⁴

Calculation

First-principles density functional theory calculations were performed using the projector-augmented wave method³⁵ and the PBEsol functional³⁶ as implemented in the Vienna Ab initio Simulation Package code.^37,38 Firstly, geometrical optimisation of the unit cell of CsMF₃ (M = Pb, Sr) was conducted. The energy cutoff was set to 520 eV for structural optimisation. The Cs 5s5p6s, Pb 6s6p, Sr 4s4p5s, and F 2s2p orbitals were treated as valence states. The total energies and forces converged to less than 1 × 10⁻⁵ eV, and the force criterion was 0.01 eV Å⁻¹. Nudged elastic band (NEB) calculation, the most convenient method for finding the saddle point and path that requires the least energy, was performed for the F⁻ vacant supercell with an energy cutoff at 400 eV. Five intermediate points were considered in the NEB calculations. A 2 × 2 × 2 supercell with a gamma-centred 2 × 2 × 2 k-mesh was used. The F⁻ vacancy was charge-compensated by removing eight electrons from the valence electrons in the supercell. The densities of states (DOSs) for the initial, intermediate, and endpoint structures in the NEB calculations were determined using the hybrid exchange–correlation functional (HSE06).^39–41 The partial electron density was analysed for states between −10 eV and the Fermi level. The crystal structures and electron densities were visualised using visualisation for electronic and structural analysis.⁴²

Results and discussion

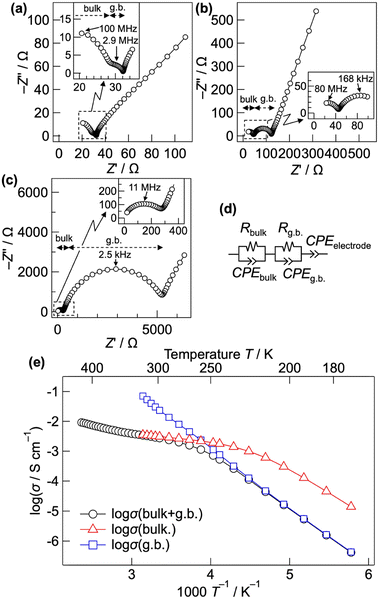
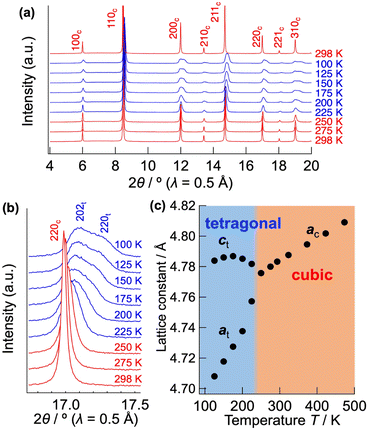
Fig. 1(a)–(c) show the Nyquist plots of CsPb_0.9K_0.1F_2.9 at 298, 248, and 203 K, respectively. Two semicircles with capacitances of 3 × 10⁻¹¹ and 1 × 10⁻⁸ F, corresponding to the bulk and grain-boundary resistances, respectively, are observed in the high frequency region. The bulk and grain boundary resistances were calculated by fitting the Nyquist plots to the equivalent circuit, as shown in Fig. 1(d). The total ionic conductivity was obtained by taking the sum of the bulk and grain boundary resistances. Above 323 K, the total conductivity was calculated solely from the bulk resistance owing to the difficult separation of the grain boundary resistance. Fig. 1(e) shows the Arrhenius plot of the ionic conductivity of CsPb_0.9K_0.1F_2.9. Table S1† summarises the conductivities and activation energies of the bulk, grain boundary, and total conductivities. The total conductivity is 2.7 × 10⁻³ S cm⁻¹ at 298 K, which is comparable to the previously reported value of 1.2 × 10⁻³ S cm⁻¹.²⁵ A low activation energy of 10.89(4) kJ mol⁻¹ for the total conductivity is observed in the 298–348 K range, similar to those of the superionic conductors α-Ag₃SI (13–19 kJ mol⁻¹)^43,44 and PbSnF₄ (10 kJ mol⁻¹).¹ At temperatures below 258 K, the activation energy increases to 37.62(17) kJ mol⁻¹, considerably decreasing the total conductivity. The increased activation energy can be explained by the change of the dominant component of the resistance from the bulk to the grain-boundary resistance, as shown in Fig. 1(b) and (c). The bulk conductivity is 3.1 × 10⁻³ S cm⁻¹ at 298 K, with an exceptionally low activation energy of 7.92(9) kJ mol⁻¹. Owing to this low activation energy, high ionic conductivity is maintained even at temperatures lower than room temperature, with a bulk conductivity of 1.0 × 10⁻³ at 223 K. At temperatures below 233 K, the activation energy of the bulk conductivity spontaneously increases to 31.8(5) kJ mol⁻¹. This increase is attributed to the displacive phase transition from a cubic to a tetragonal system, as discussed later. In contrast, the grain boundary conductivity consistently follows the Arrhenius-law in the wide temperature range of 173–318 K, yielding an activation energy of 40.0(2) kJ mol⁻¹. For comparison, the ionic conductivity of CsPbF₃ was evaluated, as shown in Fig. S1.† The total conductivity is 2.1 × 10⁻⁴ S cm⁻¹ at 298 K, which is one order of magnitude lower than that of CsPb_0.9K_0.1F_2.9. The activation energy is 7.1(2) kJ mol⁻¹ for the bulk conductivity in the 193–233 K temperature range. The low activation energies of CsPbF₃ and CsPb_0.9K_0.1F_2.9 reflect an intrinsically low migration barrier for the fluoride-ion conduction in CsPbF₃, whereas the enhanced conductivity of CsPb_0.9K_0.1F_2.9 is attributable to the increased carrier concentration, i.e. F vacancies.

Fig. 1 Nyquist plot of CsPb_0.9K_0.1F_2.9 at (a) 298 K, (b) 248 K, and (c) 203 K. The dashed horizontal arrows represent the bulk and grain boundary resistances. Expansions of the high frequency regions are shown in the insets. (d) Equivalent circuit for fitting the observed data points. (e) Arrhenius plot of the ionic conductivities of CsPb_0.9K_0.1F_2.9. The bulk, grain boundary (g.b.), and total conductivities are shown as red triangles, blue squares, and black circles, respectively.

Fig. 2(a) shows the low temperature XRD patterns of CsPb_0.9K_0.1F_2.9. With decreasing temperature, the symmetry changes at 225 K, represented by splitting of the hh0 reflection into two (Fig. 2(b)). Fig. 2(c) depicts the temperature dependence of the lattice parameters. Cubic CsPb_0.9K_0.1F_2.9 exhibits monotonic thermal expansion in the 250–450 K temperature range. Conversely, it undergoes a phase transition to the tetragonal phase associated with a contraction of the a-axis and an expansion of the c-axis from 225 to 175 K. Fig. S2(a)† presents the Rietveld refinement results for tetragonal CsPb_0.9K_0.1F_2.9 at 200 K. In tetragonal CsPb_0.9K_0.1F_2.9 with a space group of P4mm, the B-site Pb²⁺ is marginally displaced from the PbF₆ octahedral centre (z(Pb²⁺) ≈ 0.47), elongating the c-axis (a ≈ 4.71 Å, c ≈ 4.78 Å, Fig. S2(b) and Table S2†). Off-centred Pb²⁺ has been previously observed in other perovskite halides⁴⁵ owing to the localised 6s² lone pair of Pb²⁺. Additionally, the P4mm space group is consistent with that of ferroelectric PbTiO₃. In contrast, the bare CsPbF₃ undergoes a phase transition from a cubic to a rhombohedral structure at 185 K, featuring PbF₆ octahedra tilting.⁹ This phase transition is supported by a sudden decrease in the ionic conductivity from 188 to 183 K for CsPbF₃ (Fig. S1†). However, such a transition is absent in CsPb_0.9K_0.1F_2.9. The different low temperature forms, tetragonal CsPb_0.9K_0.1F_2.9 and rhombohedral CsPbF₃, can be attributed to fluoride ion vacancies. Given the presence of open space in the structure, the Pb lone pair preferentially localises to fill this open space.⁴⁶ The fluoride-ion vacancy in CsPb_0.9K_0.1F_2.9 can induce the stereochemical activity of Pb 6s, stabilising the tetragonal form by orienting the lone pair along its c-axis while displacing Pb²⁺ along the opposite direction. The tetragonal form possesses two crystallographically non-equivalent F sites, resulting in an anisotropic energy landscape for fluoride-ion conduction. In contrast, within the cubic structure of CsPb_0.9K_0.1F_2.9, the lone pair of Pb is expected to be randomly oriented, providing an isotropic conduction pathway. This displacive phase transition from a cubic to a tetragonal system in CsPb_0.9K_0.1F_2.9 is responsible for the spontaneous change in the activation energy of the bulk conductivity below 233 K (Fig. 1(e)).

Fig. 2 (a) Low temperature XRD patterns of CsPb_0.9K_0.1F_2.9, recorded between 298 K and 100 K. (b) Expansion of the 220 reflection. The diffraction patterns exhibiting cubic and tetragonal phases are displayed as red and blue lines, respectively. Mirror indices are given for each Bragg reflection, representing the cubic and tetragonal crystal systems as c and t, respectively. (c) Temperature dependence of the lattice parameters of CsPb_0.9K_0.1F_2.9.

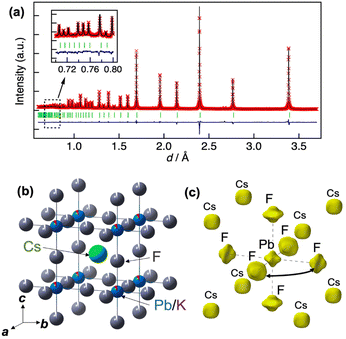
Fig. 3(a) shows the Rietveld analysis results for the neutron powder diffraction data for cubic CsPb_0.9K_0.1F_2.9 (see Table 1 for the structural parameters). The presence of 9% K at the Pb site and approximately 3% vacancies at the F site ensure charge compensation of the F vacancies for K substitution at the Pb site. The atomic displacement parameter (ADP) of F is large, U_eq = 0.0835(2) Ų. Additionally, the ADP of F exhibits remarkable anisotropy, with U₂₂ = 0.0990(3) and U₁₁ = 0.0525(4) Ų. The large U₂₂ value for F corresponds to a substantial displacement perpendicular to the Pb–F bond. The large U₂₂ value is confirmed for un-doped CsPbF₃ (see Fig. S3†), which features an intrinsically flat energy landscape for F towards neighbouring sites in CsPbF₃. Fig. 3(c) presents the nuclear density distribution obtained using MEM. MEM analysis reproduces the wide distribution of F perpendicular to the Pb–F bond direction. No other nuclear densities corresponding to interstitial F are observed. The nuclear density for the Pb site shows a non-spherical shape spreading towards neighbour F sites, whereas Pb exhibits a spherical shape in the density map of CsPbF₃ (Fig. S3(c)†). The non-spherical shape of the Pb site in CsPb_0.9K_0.1F_2.9 could be attributed to the static disorder of Pb owing to the K⁺-substitution, which was detected in the NMR study discussed later. In addition to the presence of vacancies at the F site, the broad distribution of F towards adjacent sites suggests that fluoride ions diffuse via single hopping between adjacent F sites along the edges of the PbF₆ octahedron.

Fig. 3 (a) Rietveld refinement result for neutron diffraction data of CsPb_0.9K_0.1F_2.9 at 298 K. The red crosses, black line, blue line, and green marks represent the observed intensities, calculated intensities, difference curve, and positions of the Bragg reflections of cubic-CsPb_0.9K_0.1F_2.9, respectively. (b) Refined structure of CsPb_0.9K_0.1F_2.9. The green, blue, purple, and grey balls represent Cs, Pb, K, and F atoms, respectively. (c) Three-dimensional isosurface of nuclear scattering length density of CsPb_0.9K_0.1F_2.9 obtained using MEM analysis. The yellow isosurfaces correspond to the positive nuclear scattering length density at 5 fm Å⁻³.

Table 1 Rietveld refinement results from the neutron diffraction data of CsPb_0.9K_0.1F_2.9 (CsPb_0.91K_0.09F_2.91) at 298 K^a

Atom	Site	g	x	y	z	U eq/Å^2	U 11/Å^2	U 22/Å^2	U 33/Å^2
a Unit cell: cubic Pm3̄m (221); a = b = c = 4.788192(6) Å, Rwp = 3.51%, Re = 2.19%, Rp = 3.11%, RB = 4.21%, RF = 6.28%, goodness of fit S = Rwp/Re = 1.60.
Cs	1b	1	0.5	0.5	0.5	0.03932(15)	0.03932(15)	=U11(Cs)	=U11(Cs)
Pb	1a	0.910(2)	0	0	0	0.019105(10)	0.019105(10)	=U11(Pb)	=U11(Pb)
K	1a	=1 − g(Pb)	0	0	0	=Ueq(Pb)	=U11(Pb)	=U11(Pb)	=U11(Pb)
F	3d	0.9701(7)	0.5	0	0	0.0835(2)	0.0525(4)	0.0990(3)	=U22(F)

---

To explore the origin of the low activation energy for fluoride-ion conduction in CsPbF₃, NEB calculations were performed. Fig. 4 shows the migration barrier of fluoride ions between adjacent F sites through vacancy-mediated hopping in cubic CsPbF₃ obtained using NEB calculations. The estimated migration barrier is 8 kJ mol⁻¹, which is close to the experimental value, E_a = 7.1(2) kJ mol⁻¹. For comparison, the migration barrier of fluoride ions for CsSrF₃ was calculated, in which Sr²⁺ at the B site has a similar ionic radius (r_Sr²⁺ = 1.18 Å and r_Pb²⁺ = 1.19 Å)⁴⁷ and lacks ns² electrons within the valence electron configuration (Fig. S4†). CsSrF₃ exhibits a relatively high migration barrier of 35 kJ mol⁻¹, highlighting the effect of ns² electrons in the B-site cations, which facilitate reduction of the migration barrier.

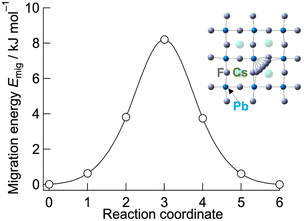Fig. 4 Migration energy of fluoride ions in cubic CsPbF₃. The migrating fluoride ions corresponding to the reaction coordinate are depicted in the inset.

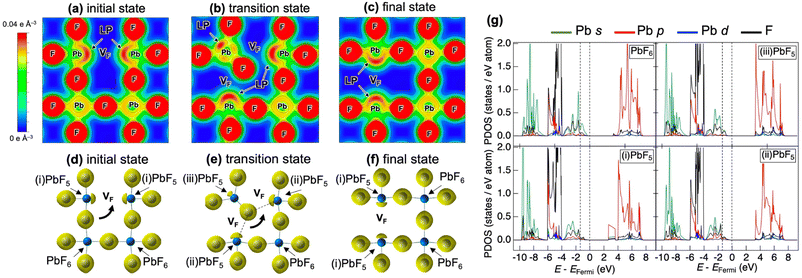
Fig. 5 shows the partial density of states (PDOS) for CsPbF₃, including one F⁻ vacancy corresponding to the initial state of the NEB calculation. The valence band comprises three regions. The first region near the Fermi level primarily comprises the F 2p orbital with the hybridisation of the Pb 6s orbital. The other F 2p orbitals are located below −4 eV, partly hybridising the Cs 5p and Pb 6p orbitals in the second region. The third region around −8 eV encompasses contributions from Pb 6s and Cs 5p orbitals, in addition to a small amount of F. The partial electron densities were analysed for states between −10 eV and the Fermi level to gain deeper insight into the role of the lone pair in the conduction mechanism. Fig. 6(a)––(f) present the cross-sectional contour and isosurface plots, respectively, of the partial electron density during fluoride-ion migration in CsPbF₃. The stereochemical activity of Pb 6s depends on its coordination environment. In the initial structure, the electron density of Pb in the PbF₅ square pyramid adjacent to the F vacancy is asymmetric and localised in the direction of the F vacancy (V_F). In contrast, the electron density of Pb in the PbF₆ octahedral region, which is not adjacent to the F vacancy, is symmetrical and delocalised. Walsh reported similar selectivity for the stereochemical activity of Pb 6s electrons, where Pb 6s in the PbO₆ octahedra of rock salt-type PbO was delocalised.⁴⁶ Conversely, Pb 6s in the distorted PbO₈ hexahedra is asymmetrically localised towards open space in litharge-type PbO. Similarly, Pb 6s becomes stereochemically active when five F atoms coordinate with Pb in F-defective CsPbF₃, localising the 6s lone pair towards open space at F-vacant sites. During the transition state, one fluoride ion in the PbF₆ octahedron cleaves the Pb–F bond and passes through a bottleneck comprising 1 × Pb and 2 × Cs. The former delocalised Pb electron density in the PbF₆ octahedra localises towards the new V_F created by the cleavage of the Pb–F bond. Furthermore, the electron density of Pb in the PbF₅ trigonal bipyramid labelled as (iii) in Fig. 6(e) is marginally localised in the opposite direction to the travelling F. In the endpoint structure, the travelling F is associated with the PbF₅ square pyramid to form a PbF₆ octahedron, delocalising the Pb electron density. These results confirm that fluoride ions are carried by the exchange reaction between the fluoride ions and the Pb 6s lone pair localised in the V_F. Fig. 6(g) shows the site-projected PDOS of the PbF₆ octahedra and three PbF₅ polyhedra: (i) and (ii) square pyramids and (iii) a trigonal bipyramid. The region near the Fermi level of PbF₆ is occupied by Pb 6s and F 2p electrons. In contrast, in the PbF₅ polyhedron, the DOS of Pb shifts to the lower-energy side (as indicated by the dashed line), stabilising the Pb 6s state and PbF₅ geometry. One V_F and two PbF₅ geometries exist in the initial structure, but two V_F and three PbF₅ geometries are present in the transition structure. The three stable PbF₅ polyhedral geometries in the transition state stabilise the structure and reduce the migration barrier of fluoride ions.

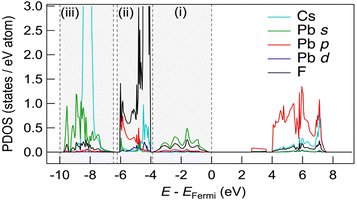Fig. 5 PDOS of the supercell of CsPbF₃ with an F-defective structure. Three valence band regions are surrounded by dashed vertical lines.

Fig. 6 (a–c) Contour plots of the cross-section of the (100) plane and (d–f) isosurface plots of partial electron density from −10 eV to the Fermi level of CsPbF₃. (a and d) Initial, (b and e) transition, and (c and f) final states of the fluoride-ion migration via adjacent F-vacancy in the NEB calculation. The contour plots are drawn from 0 to 0.04 e Å⁻³ with a 0.005 e Å⁻³ interval. The three-dimensional isosurfaces of 0.035 e Å⁻³ are depicted in yellow. (g) Site-projected PDOS of Pb and F in PbF₆ and three PbF₅ polyhedrons. The valence band region near the Fermi level is represented by the dashed vertical line.

Further, high resolution ¹⁹F/²⁰⁷Pb NMR spectroscopy was used to explore the F dynamics correlated with Pb in CsPb_0.9K_0.1F_2.9. Fig. 7 compares the ¹⁹F and ²⁰⁷Pb MAS NMR spectra of CsPbF₃ and CsPb_0.9K_0.1F_2.9. The narrower ¹⁹F line shape for CsPb_0.9K_0.1F_2.9 indicates efficient motional narrowing, which is consistent with its better ionic conductivity. The ²⁰⁷Pb spectrum of CsPbF₃ is a simple Lorentzian reflecting better local symmetry in the unit cell than that of the CsPb_0.9K_0.1F_2.9, which exhibits substantial broadening. The broad line shape does not depend on temperature up to 100 °C (not shown). To explore the nature of this broadening, a 2D exchange spectrum at 80 °C with a mixing time of 50 ms was obtained (Fig. 8), in which only the narrow diagonal signal exists. This finding indicates that the broad linewidth in the 1D spectrum is a sum of an individual sharp signal with its isotropic chemical shift distributed over 1000–1800 ppm, approximately. Further, the absence of off-diagonal signals indicates that exchange among these broadly distributed ²⁰⁷Pb signals is less evident in 50 ms at 80 °C. The linewidth of each ²⁰⁷Pb spin isochromat is separately observed via the Hahn-echo sequence to be 470 Hz (T₂ ∼ 0.68(3) ms), which is consistent with the narrow diagonal signal in Fig. 8. The broad distribution of the isotropic chemical shift of ²⁰⁷Pb in CsPb_0.9K_0.1F_2.9 is attributed to the variation of the local structure of the Pb atom owing to 10% K⁺ substitution on the Pb site. The distortion of the Pb site is observed as non-spherical nuclear density obtained using the MEM analysis (Fig. 3(c)). The ²⁰⁷Pb chemical shift is sensitive to its local structure, leading to the wide chemical shift range from −6000 to 6000 ppm.⁴⁸

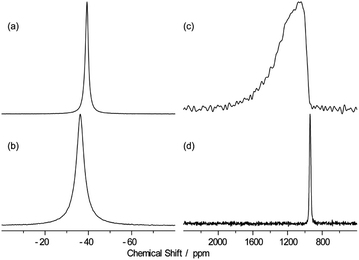Fig. 7 ¹⁹F (a and b) and ²⁰⁷Pb (c and d) MAS spectra of CsPbF₃ (b and d) and CsPb_0.9K_0.1F_2.9 (a and c) with the MAS frequency of 25 kHz at 40 °C.

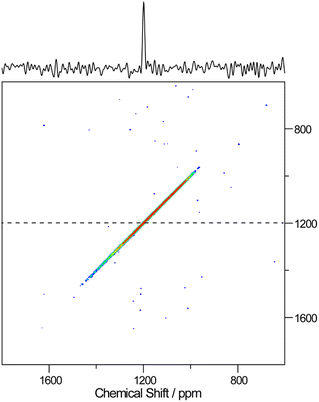Fig. 8 ²⁰⁷Pb–²⁰⁷Pb 2D-exchange spectrum of CsPb_0.9K_0.1F_2.9 obtained at 80 °C with a mixing time of 50 ms. The cross-section spectrum at 1200 ppm is represented by the dashed line at the top.

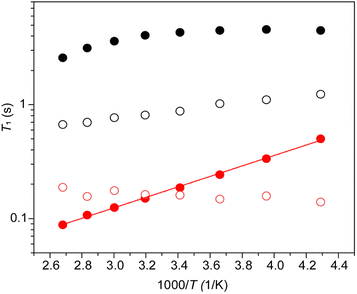
The absence of exchange among the different Pb sites in CsPb_0.9K_0.1F_2.9 as confirmed by the 2D-exchange NMR experiment establishes that the broad distribution of the chemical shift of ²⁰⁷Pb is due to the variation of the configuration between Pb and immobile K rather than mobile F (or F vacancy). The dynamics of Pb and F by T₁ were examined further. At first, the anisotropy of ²⁰⁷Pb-T₁ for the broadly distributed peaks of CsPb_0.9K_0.1F_2.9 was ignored and ²⁰⁷Pb-T₁ was obtained from the recovery curve for the whole signal. Fig. 9 shows the temperature dependence of T₁ of ¹⁹F and ²⁰⁷Pb in CsPbF₃ and CsPb_0.9K_0.1F_2.9. The ¹⁹F-T₁ of CsPbF₃ shows that fluoride-ion motion is too slow to affect T₁ below 20 °C. The 10% K⁺ substitution reduces the ¹⁹F-T₁ of CsPb_0.9K_0.1F_2.9 by more than one order of magnitude, indicating better fluoride-ion mobility in CsPb_0.9K_0.1F_2.9. The slope of log(T₁) vs. 1/T gives an activation energy of 3.8(1) kJ mol⁻¹, which is much smaller than the value of 7.92(9) kJ mol⁻¹ obtained from the temperature dependence of the bulk ionic conductivity in the similar temperature range. It appears that the motion governing ¹⁹F T₁ is local with smaller activation energies. The T₁ of immobile ²⁰⁷Pb is smaller than that of mobile ¹⁹F for CsPbF₃ and ²⁰⁷Pb-T₁ ∼ ¹⁹F-T₁ for CsPb_0.9K_0.1F_2.9. Short T₁ has been reported for ¹¹⁹Sn spin in PbSnF₄,⁴⁹ in which the 5s² lone pair of Sn²⁺ is stereochemically active and the fluctuating chemical-shielding anisotropy (CSA) invokes the relaxation. To confirm that the ²⁰⁷Pb-T₁ is governed by the fluctuation of CSA, the ²⁰⁷Pb-T₁ of CsPb_0.9K_0.1F_2.9 was observed at 4.7 T. The observed ²⁰⁷Pb-T₁ at 40 °C is 0.43 s, which is longer than that observed at 14 T (0.16 s). The ratio 0.43/0.16 is close to the ratio of the strength of the static field (14/4.7), confirming the relaxation mechanism being the fluctuation of CSA. The CSA relaxation is consistent with the exchange model among the fluoride ions and the F vacancies, as illustrated in Fig. 6(d)–(f). It should be mentioned here that a simple F–F mutual exchange around a ²⁰⁷Pb spin does not affect the CSA of the ²⁰⁷Pb spin and the fluctuation of CSA is only caused by the migration of F vacancies.⁴⁹ The temperature dependence of the ²⁰⁷Pb-T₁ of CsPb_0.9K_0.1F_2.9 is limited (Fig. 9), which could be ascribed to a broad distribution of the correlation time of CSA fluctuation.

Fig. 9 Temperature dependence of the ¹⁹F (●) and ²⁰⁷Pb (○) spin–lattice relaxation times (T₁) for CsPbF₃ (black) and CsPb_0.9K_0.1F_2.9 (red). The straight line through the ¹⁹F T₁ data points for CsPb_0.9K_0.1F_2.9 is T₁ ∝ exp(E_a/kT) with E_a = 3.8 kJ mol⁻¹.

Further, the anisotropy of ²⁰⁷Pb-T₁ of CsPb_0.9K_0.1F_2.9 was investigated. The broad ²⁰⁷Pb signal at 40 °C was separated into two components: 800–1200 ppm and 1200–1700 ppm. The obtained ²⁰⁷Pb-T₁ values were 0.174(8) s for the former and 0.057(6) s for the latter. As the shorter T₁ value indicates a larger CSA, in this case, the observed high frequency ²⁰⁷Pb shift for CsPb_0.9K_0.1F_2.9 compared to that of the CsPbF₃ peak correlates with the size of CSA. This shift of ²⁰⁷Pb towards the high frequency region represents a diverse configuration against the 10% K substitution at the Pb sites because the 2D exchange spectrum shows no exchange between the different ²⁰⁷Pb sites (Fig. 8). The large CSA for the high frequency side of ²⁰⁷Pb suggests that the migration of F vacancies is considerably pronounced around Pb, yielding a more distorted local structure near K in CsPb_0.9K_0.1F_2.9.

Conclusion

Cubic CsPb_0.9K_0.1F_2.9 exhibits an exceptionally low activation energy of 7.9 kJ mol⁻¹ for fluoride-ion conductivity. A combination of structural analysis using NPD data and NEB calculations elucidated the conduction mechanism as single F hopping via neighbouring vacancies. ¹⁹F and ²⁰⁷Pb NMR studies indicated facile migration of the fluoride ions involving F vacancies. The electron density analysis suggested that the fluoride ions migrated via an exchange reaction between the Pb 6s lone pairs and fluoride ions. Furthermore, the origin of the mitigated migration barrier was revealed: the localised lone pair in the PbF₅ polyhedron stabilised the saddle-point structure. The low migration energy enabled the retention of high conductivity at 223 K (1.0 × 10⁻³ S cm⁻¹ for bulk conductivity). These findings provide valuable insights into material design for achieving superior ionic conductivity with a low migration barrier for fluoride as well as other anions, such as oxide and chloride.

Author contributions

R. K. designed and directed the project. K. M. and T. S. conducted neutron powder diffraction measurement. M. M. conducted NMR measurement. N. M. conducted first-principles calculations, synchrotron X-ray diffraction, and impedance measurements. N. M. wrote the manuscript in consultation with M. M., K. S., K. S., and R. K. All authors discussed the results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was conducted using grants from two projects (JPNP16001 and JPNP21006) commissioned by the New Energy and Industrial Technology Development Organization (NEDO). The synchrotron XRD experiments were performed as approved by the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2020A1645). Neutron diffraction studies were conducted as part of a project approved by the Neutron Scattering Program Advisory Committee of the Institute of Materials Structure Science and KEK (Proposal No. 2019S10). The computational sources of the TSUBAME3.0 supercomputer at the Tokyo Institute of Technology were used. The authors thank Mr Sugihara at the Design and Manufacturing Division, Open Facility Centre, Tokyo Institute of Technology, for manufacturing the sample holder.

References

1. R. Kanno, S. Nakamura, S. Kawamura and Y. Kawamoto, Solid State Ionics, 1992, 51, 53–59.
2. M. Li, M. J. Pietrowski, R. A. De Souza, H. R. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35.
3. R. E. Cohen, Nature, 1992, 358, 136–138.
4. R. D. Shannon and R. X. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235111–235128.
5. M. A. Kraft, S. P. Culver, M. Calderon, F. Bocher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918.
6. M. W. Shafer, G. V. Chandrashekhar and R. A. Figat, Solid State Ionics, 1981, 5, 633–636.
7. F. Abraham, J. C. Boivin, G. Mairesse and G. Nowogrocki, Solid State Ionics, 1990, 40–1, 934–937.
8. P. Shuk, H. D. Wiemhofer, U. Guth, W. Gopel and M. Greenblatt, Solid State Ionics, 1996, 89, 179–196.
9. P. Berastegui, S. Hull and S. G. Eriksson, J. Phys.: Condens.Matter, 2001, 13, 5077–5088.
10. M. Uno, M. Onitsuka, Y. Ito and S. Yoshikado, Solid State Ionics, 2005, 176, 2493–2498.
11. L. N. Patro and K. Hariharan, Solid State Ionics, 2013, 239, 41–49.
12. M. A. Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059–17062.
13. F. Gschwind, G. Rodriguez-Garcia, D. J. S. Sandbeck, A. Gross, M. Weil, M. Fichtner and N. Hormann, J. Fluorine Chem., 2016, 182, 76–90.
14. K. Mori, A. Mineshige, T. Emoto, M. Sugiura, T. Saito, K. Namba, T. Otomo, T. Abe and T. Fukunaga, J. Phys. Chem. C, 2021, 125, 12568–12577.
15. M. Murakami, F. Fujisaki and Y. Morita, Solid State Ionics, 2020, 355, 115398.
16. S. Hull and P. Berastegui, J. Phys.: Condens.Matter, 1999, 11, 5257–5272.
17. V. Y. Kavun, A. B. Slobodyuk, E. A. Tararako, E. Y. Mikhteeva, V. K. Goncharuk, N. F. Uvarov and V. I. Sergienko, Inorg. Mater., 2005, 41, 1228–1235.
18. Y. Yamane, K. Yamada and K. Inoue, Solid State Ionics, 2008, 179, 605–610.
19. G. Denes, T. Birchall, M. Sayer and M. F. Bell, Solid State Ionics, 1984, 13, 213–219.
20. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463.
21. S. F. Matar and J. Galy, Solid State Sci., 2016, 52, 29–36.
22. F. Fujisaki, K. Mori, M. Yonemura, Y. Ishikawa, T. Kamiyama, T. Otomo, E. Matsubara and T. Fukunaga, J. Solid State Chem., 2017, 253, 287–293.
23. T. Birchall, G. Dénès, K. Ruebenbauer and J. Pannetier, Hyperfine Interact., 1986, 29, 1331–1334.
24. G. Dénès, M. C. Madamba, H. Merazig, A. Muntasar and Z. Zhu, AIP Conf. Proc., 2016, 1781, 020006.
25. J. Z. Wang, J. P. Hao, C. M. Duan, X. C. Wang, K. Wang and C. Ma, Small, 2022, 18, 2104508.
26. S. Kawaguchi, M. Takemoto, K. Osaka, E. Nishibori, C. Moriyoshi, Y. Kubota, Y. Kuroiwa and K. Sugimoto, Rev. Sci. Instrum., 2017, 88, 085111.
27. M. Yonemura, K. Mori, T. Kamiyama, T. Fukunaga, S. Torii, M. Nagao, Y. Ishikawa, Y. Onodera, D. S. Adipranoto, H. Arai, Y. Uchimoto and Z. Ogumi, J. Phys.: Conf. Ser., 2014, 502, 012053.
28. R. Oishi, M. Yonemura, Y. Nishimaki, S. Torii, A. Hoshikawa, T. Ishigaki, T. Morishima, K. Mori and T. Kamiyama, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 600, 94–96.
29. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15–20.
30. Y. Ishikawa, J. R. Zhang, R. Kiyanagi, M. Yonemura, T. Matsukawa, A. Hoshikawa, T. Ishigaki, S. Torii, R. Oishi-Tomiyasu and T. Kamiyama, Phys. B, 2018, 551, 472–475.
31. W. S. Brey and M. L. Brey, in Encyclopedia of Nuclear Magnetic Resonance, John Wiley and Sons, Inc., Chichester, 1996, vol. 3, pp. 2063–2071.
32. A. Bielecki and D. P. Brum, J. Magn. Reson., Ser. A, 1995, 116, 215–220.
33. J. Jeener, B. H. Meier, P. Bachmann and R. P. Ernst, J. Chem. Phys., 1979, 71, 4546–4563.
34. K. Takeda, J. Magn. Reson., 2008, 192, 218–229.
35. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
36. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. L. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
37. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
38. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
39. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
40. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219901–219906.
41. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Angyan, J. Chem. Phys., 2006, 125, 249901–249902.
42. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
43. M. Gombotz, I. Hanghofer, S. Eisbacher-Lubensky and H. M. R. Wilkening, Solid State Sci., 2021, 118, 106680.
44. A. Kojima, K. Tozaki, T. Ogawa, T. Takizawa and T. Kanashiro, J. Phys. Soc. Jpn., 1988, 57, 176–187.
45. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
46. A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422–1428.
47. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767.
48. C. Brevard and P. Granger, Handbook of High Resolution Multinuclear NMR, Wiley, New York, 1981.
49. M. Murakami, Y. Morita and M. Mizuno, J. Phys. Chem. C, 2017, 121, 2627–2634.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06367d

---