Crystalline phase transition in as-synthesized pure silica zeolite RTH containing tetra-alkyl phosphonium as organic structure directing agent

Abstract

The choice of structure directing agents (SDAs) in zeolite synthesis significantly impacts the arrangement of active sites, thereby influencing the stabilization of reaction intermediates with profound implications for catalytic applications. Therefore, understanding the distribution of SDAs along with the substitution of heteroatoms for silicon in zeolites is imperative for tailoring optimized materials for specific applications. This study is centered on the synthesis of all-silica RTH type zeolites in the presence of fluoride, utilizing triisopropyl(methyl)phosphonium as the organic SDA (OSDA). Zeolites produced under varying conditions of time and temperature exhibit differences in their X-ray diffractograms, indicating the presence of two distinct crystalline phases. The ¹⁹F NMR spectra confirm the presence of fluoride within the small rth cage and exhibit two distinct signals depending on the sample. The ²⁹Si NMR spectra reveal the existence of penta-coordinated F-SiO₄ species, resulting in sixteen non-equivalent Si sites. Through ab initio DFT methods, the stabilization energy and ²⁹Si chemical shielding of several models featuring F-SiO₄ situated at all crystallographic sites were computed. Comparison with experimental results enabled the identification of the framework position where the five-coordinate silicon is located, which differs between the two crystalline phases of the as-synthesized RTH zeolites. Consequently, the placement of fluoride in either of these two sites within the RTH zeolite can be controlled during the synthesis. It is expected that this methodology can be extended to manipulate the position of trivalent atoms (e.g., Al³⁺ or B³⁺), which can affect the catalytic properties of the RTH zeolite.

---

1. Introduction

Zeolites are crystalline microporous materials primarily composed of silica (SiO₄ tetrahedra) interconnected by oxygen atoms, resulting in three-dimensional networks with molecular-sized channels and cavities. Over the years, substantial efforts have been invested in developing diverse zeolite structures,^1–8 leading to 255 distinct framework configurations recognized by the International Zeolite Association.⁹ These materials can incorporate various atoms, yielding a range of chemical compositions. Most commonly, Al³⁺ partially replaces Si⁴⁺ generating negative charges that can be compensated by H⁺ forming Brønsted acid sites crucial in most zeolite catalytic applications. Additionally, metal cations can be incorporated to balance the charges, acting as active sites for redox or basic reactions in catalysis. The diverse chemical compositions and physicochemical properties combined with the numerous framework topologies has prompted the commercial utilization of zeolites in petrochemical, chemical, adsorption and separation processes.^10–12

Many zeolites are synthesized hydrothermally from gels containing organic cations as structure directing agents (OSDA⁺) in the presence of OH⁻ or F⁻ as mineralizing agents.^7,13,14 Tetra-alkyl ammonium cations are the most commonly employed OSDAs, occupying the zeolite void volume to guide crystallization towards specific topologies.^1–8 Due to their crucial role in zeolite synthesis, extensive research has focused on developing new OSDAs, particularly those aimed at creating structures with larger pore openings to allow processing bulkier molecules.^15–17 This research has recently expanded to the synthesis of small-pore zeolites, driven by their growing applications as catalysts for environmental reactions and in adsorption/separation processes.^18,19 In recent years, a new class of OSDAs based on tetra-alkyl phosphonium and phosphazenes cations has attracted significant interest. Notably, phosphonium-based cations offer superior thermal stability compared to ammonium-based counterparts, enabling higher synthesis temperatures and opening new avenues in zeolite synthesis.²⁰ Indeed, the utilization of this new family of phosphorus-containing OSDAs has led to the synthesis of known zeolites with new compositions^21–26 and novel structures.^27–36 The synthesis of zeolites in fluoride medium has proven highly effective in producing high- or all-silica large crystals free of connectivity defects. This method has facilitated the obtention of novel zeolites and of known materials that cannot be prepared through other means.^{13,14,18,37,38} All silica-based zeolites possess a neutral network, and the positive charges of the OSDA⁺ cations, enclosed in the larger cavities or channels of the structure, are counterbalanced by the F⁻ anions occupying the smallest cages. Specifically, F⁻ exhibits a notable preference for occupying the double four-membered rings (d4r) in zeolites containing these units in their structure.

Solid-state magic-angle spinning (ssMAS) ¹⁹F NMR spectroscopy is highly sensitive to the local environment, with the ¹⁹F chemical shift (δ¹⁹F) being dependent on the geometry and chemical composition of the cages where F⁻ resides, thus serving as a probe of the local zeolite structure.^39–44 In zeolites where d4r are absent, fluoride is incorporated within other small cages forming a bond with a Si atom, resulting in penta-coordinated silicon [SiO₄F]⁻ in a distorted trigonal bipyramidal environment that occupy preferably the corners of four membered rings (4R).⁴¹ The five coordinated [SiO₄F]⁻ species are recognized by the presence of a doublet at δ²⁹Si ≈ −148 ppm with scalar (J) couplings J_F–Si ≈ 165 Hz in the ²⁹Si MAS NMR spectra.^45–49 Due to tendency of fluoride to occupy specific positions, it is acknowledged as a structure-directing agent, promoting the crystallization of zeolites containing 4R and especially those with d4r units.

Determining the precise positioning of F⁻ within the cages and of OSDA⁺ in the cavities or channels of all-silica zeolites has been addressed through X-ray diffraction of single crystals or highly crystalline powdered zeolite samples employing synchrotron radiation.^50,51 Nevertheless, identifying their exact location remains challenging. Typically, the fluoride anion incorporated into a small cage of the zeolite will bind only one of the Si sites and only a portion of the cages capable of hosting fluoride anions are occupied, resulting in long-range structural disorder.^52–54 In some instances, fluoride anions can move within the cage among equivalent Si sites, which changes continuously its coordination between four and five in the scale of time of the NMR measurement giving a very large ill-resolved signal at a δ²⁹Si intermediate between SiO₄ and [SiO₄F]⁻.^47,55 This dynamic disorder is evidenced by the observation of the characteristic doublet of [SiO₄F]⁻ species in the ²⁹Si ss-NMR spectra recorded at a low enough temperature to immobilize fluoride at one Si position.⁴⁶ The occurrence of disorder in fluoride distribution make it difficult to precisely resolve the structure of all-silica zeolites through XRD.⁴⁸ Moreover, the stabilization energies of the [SiO₄F]⁻ located in all possible sites calculated by theoretical DFT are very similar, making it difficult to assign the fluoride position.⁵⁶ The presence of dynamic and static disorder in F⁻-containing pure silica zeolites depend on the framework topology but also on the OSDA⁺ used in their syntheses. For instance, dynamic disorder is present in silicalite-1 synthesized using the typical tetrapropylammonium (TPA⁺), whereas static disorder becomes predominant when the more asymmetric tributyl(methyl)ammonium (TBMA⁺) is used as OSDA.^49,57 This is attributed to the shorter F⁻-TBMA⁺ distance and the stronger electrostatic interactions with the organic cation containing the short methyl group, which immobilizes fluoride ions at room temperature inhibiting dynamic disorder.

Substituting framework Si⁴⁺ by Al³⁺ introduces negative charges in the zeolite that are balanced by the OSDA⁺ cations. Subsequent calcination removes the OSDA⁺ leaving behind Brønsted acid sites maintaining the charge neutrality. The position of these acid sites associated with Al³⁺ significantly influences the catalytic performance of zeolites in acid reactions.⁵⁸ Additionally, the formation of Al³⁺ pairs facilitate the incorporation of divalent transition metal ions with redox properties, impacting catalytic behaviour in reactions like de-NOx.⁵⁹ Therefore, precise placement and distribution of Al³⁺ within the framework are crucial for the catalytic application of zeolites. This aspect has been extensively investigated emphasizing the influence of synthesis conditions and the choice of OSDA.⁶⁰ Recent research has begun considering the nature of the mineralizing agent (F⁻ or OH⁻) as an alternative method for directing the Al³⁺ siting in ZSM-5.⁶¹ Varying the Si/Al ratio alters the Al³⁺ siting when the synthesis is conducted in a fluoride medium, whereas it remains unchanged in an OH⁻ medium across a wide range of Si/Al ratios. This is attributed to the specific crystallographic locations of F⁻, as observed in pure silica zeolites, compared to the distribution of siloxy groups spread across different crystallographic sites in OH⁻ medium. These findings highlight the importance of considering the spatial distribution of all negative charges within the zeolite framework for a comprehensive understanding and control of aluminum siting, and consequently, its ultimate applications as catalysts.

In this work, we focus on the study of RTH-type zeolites, which exhibit a two-dimensional eight-membered ring small-pore structure. Al- or B-containing RTH zeolites have demonstrated to be promising catalysts for the methanol-to-olefin (MTO) reaction, with their catalytic performance being closely linked to the distribution and density of acid sites.^62–64 More specifically we provide a detailed structural characterization of pure silica RTH-type zeolites synthesized via the fluoride route, employing triisopropyl(methyl)phosphonium cation as OSDA varying synthesis conditions. We have identified two distinct highly crystalline phases associated with the bonding of fluoride anions to Si at two different crystallographic sites in the as-synthesized materials. The phase obtained after longer synthesis times exhibits a greater long-range order compared to the polymorph obtained at shorter crystallization times. Through a combination of XRD, ss-NMR, and theoretical calculations, we have successfully determined the fluoride distribution in these two RTH phases. This knowledge is crucial for understanding the crystallization process and charge distribution in zeolites, and may pave the way for future investigations into the distribution of Al³⁺ within the RTH-type structure, with potentially significant implications for their applications.

2. Materials and methods

2.1. Synthesis of triisopropyl(methyl)phosphonium hydroxide

In a typical synthesis, a solution of 25.5 g (179.8 mmol, 99 wt%, Aldrich) of iodomethane in 50 ml of anhydrous acetonitrile (99 wt%, Alfa-Aesar) was added dropwise under stirring to a solution of 17.6 g (119.9 mmol, 98 wt%, ABCR) of triisopropylphosphine in 200 ml of anhydrous acetonitrile (99 wt%, Alfa-Aesar) under nitrogen atmosphere at 0 °C (warning: alkylphosphines must be handled with extreme caution in fume hood and under inert atmosphere. They are highly toxic and flammable). The mixture was stirred at room temperature for three days. The resulting solution was rotary evaporated until a white precipitate appeared and then, diethyl ether was added to completely precipitate the desired product. The precipitate was recovered by filtration, washed with a mixture of acetonitrile and diethyl ether and dried under vacuum. The product triisopropyl(methyl)phosphonium (P-OSDA⁺) iodide was obtained as a white powder with a yield over 98%. Then, the product was dissolved in Milli-Q water and exchanged to the hydroxide form using an anionic exchange Amberlite IRN-78 resin in batch overnight, resulting in a 0.22 M solution of the P-OSDA⁺ hydroxide. The schematic synthesis and the characterization results of the P-OSDA⁺ are discussed in the ESI.†

2.2. Synthesis of the zeolitic materials

In a typical synthesis of all-silica zeolites, a certain amount of tetraethyl orthosilicate (99% TEOS, Aldrich) was added over the desired quantity of a solution of P-OSDA⁺ in its hydroxide form and stirred until the complete hydrolysis of TEOS and the evaporation of the necessary amount of water and ethanol. Then, the appropriate amount of a solution of HF in water (Aldrich, 48% v/v) was added in order to obtain a synthesis gel with the following molar composition:

1.0 SiO₂: 0.4 P-OSDA(OH): 10H₂O: 0.4 HF

The resulting gel was transferred to Teflon lined stainless-steel autoclaves and heated at 175 °C at its autogenous pressure under tumbling (60 rpm) for times ranging from 3 days to 30 days. The solid was recovered by filtration, washed exhaustively with distilled water and dried at 100 °C overnight to obtain the as-made all-silica RTH zeolite. The resulting samples, labelled as RTH-x where x denotes the crystallization time (in days), have the chemical composition shown in Table 1.

Table 1 Chemical composition of the pure silica RTH zeolites

Sample	P-OSDA^+^a (mmol g^−1)	P-OSDA^+/u.c.	% wt F^b	F/u.c.	F/P-OSDA^+^c
a Determined by ICP analysis. b Determined by ^19F NMR analysis. c Expressed as molar ratio.
RTH-3	0.82	1.9	1.77	2.1	1.14
RTH-9	0.81	1.9	1.54	1.9	1.00
RTH-13	0.84	1.9	1.68	1.9	1.05
RTH-19	0.81	2.0	1.66	2.1	1.08
RTH-30	0.82	2.0	1.57	2.0	1.01

---

The organic content was determined by inductively couple plasma (ICP) using a Varian 710-ES equipment and the fluoride content by MAS NMR as described below. All zeolites hold about two P-OSDA⁺ cations and two fluoride anions per unit cell resulting in a F⁻/P-OSDA⁺ ≈ 1 molar ratios. The Field Emission Scanning Electron Microscopy (FESEM) images, displayed in Fig. S1† for samples RTH-9 and RTH-30, show that the size and morphology of the crystals are quite similar in the samples obtained at different synthesis times.

2.3. Powder X-ray diffraction measurements

Routine powder X-ray diffraction patterns (PXRD) were obtained at room temperature (25 °C) using a PANalytical CUBIX diffractometer with Cu K_α radiation and a Panalytical X'Celerator detector. Variable divergence slits were used to obtain a higher detail of the patterns at high angles for qualitative analysis. High resolution PXRD (HRPXRD) data of the RTH-9 sample were collected using a PANalytical X'Pert PRO diffractometer equipped with a hybrid monochromator (Cu K_α1 radiation) and an X'Celerator detector. Prior to the measurements, the sample was placed in a sealed glass capillary. The HRPXRD data of the sample RTH-30 were collected at beamline MSPD of the Spanish Synchrotron ALBA, using a wavelength of 0.619805 Å and a MAD detector. Finally, the PXRD patterns of the RTH samples at different temperatures were collected using an Anton-Paar XRK-900 reaction chamber attached to a Malvern-Panalytical Empyrean diffractometer with a PIXcel detector. The measurements were performed using Cu K_α radiation.

2.4. Solid state nuclear magnetic resonance

A Bruker Avance III HD 400 MHz WB spectrometer was employed to record the solid-state Nuclear Magnetic Resonance (ss-NMR) spectra spinning the sample at the magic angle (MAS). ¹H MAS NMR spectra were acquired in a 2.5 mm probe at 25 kHz using a π/2 pulse length of 3.6 μs and 10 s recycle delay. ¹⁹F measurements, ν₀(¹⁹F) = 376.5 MHz, were carried out in a 3.2 mm probe, at MAS rates in the range 3–20 kHz, with a ¹⁹F π/2 pulse length of 4.8 μs and 60 s as recycle delays. The quantification of the fluoride in the solid samples was done by comparing the corresponding ¹⁹F NMR spectra with that of a sample of known fluorine content. ²⁹Si MAS-NMR spectra, ν₀(²⁹Si) = 79.5 MHz, were recorded in a 7 mm probe spinning the sample at 5 kHz, using a ²⁹Si pulse length of 4.0 μs corresponding to 60° flip angle, and 180 s as a recycle delay. ¹⁹F–²⁹Si cross polarization (CP) MAS NMR spectra were done at ν₀(¹⁹F) = 376.5 MHz and ν₀(²⁹Si) = 79.5 MHz using a 7 mm probe spinning the sample at 5 kHz, using a pulse length 5 μs, 400 μs as contact time and 100 s as recycle delay. The ¹H–¹⁹F double-resonance and ¹H–¹H double-quantum single-quantum (DQ-SQ) MAS NMR experiments were recorded on an 850 MHz WB Bruker NMR spectrometer equipped with a NEO console. The experiments were run on a 1.3 mm ¹H–¹⁹F–X–Y quadruple-resonance MAS NMR probe at spinning rate 60 kHz. The dipolar-based Heteronuclear Multiple Quantum (D-HMQC) ¹⁹F–¹H (HMQC varying rec time) NMR spectra were recorded using the R4₁² recoupling scheme.^65,66 Recoupling time was set to 1.7 ms. ¹⁹F and ¹H π/2 pulse length at 25 W is 3.2 μs. Recycle delay was set to 2.3 s. 56 t₁ slices with 32 transients each were recorded. The ¹H–¹H DQ-SQ NMR experiment was recorded with the BABA scheme,⁶⁷ using 200 μs recoupling time. 130 t₁ slices with 16 transients each were recorded. Phase sensitive 2D NMR spectra were obtained by applying the State procedure.⁶⁸ The ¹³C, ³¹P, ¹H, ¹⁹F and ²⁹Si NMR spectra were referenced to adamantane, phosphoric acid, water, CFCl₃, and TMS, respectively. NMR spectra were fitted using the freely available DmFit software⁶⁹ and SOLA package from Bruker Top spin 3.6.1.

2.5. Computational details

Periodic calculations were carried out with the VASP code.⁷⁰ Energy minimizations were performed with the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE).^71–74 In all calculations, the projected augmented wave (PAW)⁷⁵ pseudopotentials were used to describe the interaction of the valence electrons with the nuclei and core electrons. An energy cutoff of 600 eV was used to expand the plane wave basis set. For zeolites and molecules, the Brillouin zone was sampled at the gamma point but for fluorinated compounds convergence of the energy with respect to the k-points was checked. At least Monkhorst–Pack grids of 8 × 8 × 1 k-points were needed. The structures were considered converged when the forces acting on atoms were lower than 0.01 eV Å⁻¹. Dispersion energies were evaluated using the D3 Grimme's method^76–78 with the Becke–Johnson damping.⁷⁹ The NMR absolute shielding tensors were computed with the GIPAW approach implemented in VASP. The same energy cut-off as in the optimizations was used but with a tighter convergence criterion of 10⁻¹⁰ eV for the electronic energy. The underestimation of band gaps calculated with GGA functionals leads to a slope that deviates from unity when predicting the chemical shift of alkaline fluorides using linear regression models as shown by Laskowski et al.^80,81 The modified Becke–Johnson exchange potential (TB-mBJ)⁸² gives a better relation between experimental chemical shifts (δ_iso) and absolute isotropic shieldings (σ_iso). Here, we used a similar dataset of fluorinated compounds to predict the chemical shift from the absolute isotropic shieldings and therefore all NMR calculations were performed with TB-mBJ on the optimized structures. The dataset of 18 known fluorinated compounds to obtain the regression between δ_iso and σ_iso is shown in Fig. S2 and Table S1.†

3. Results and discussion

3.1. Structural characterization of the RTH zeolites

Fig. 1a shows the PXRD patterns of the P-RTH samples synthesized at 175 °C using the P-OSDA⁺ cation and varying times between 3 (sample RTH-3) and 30 days (RTH-30). All diffractograms are typical of highly crystalline pure silica RTH zeolite without the presence of amorphous or any other impurity, even for the samples obtained at very short synthesis times (RTH-3). However, inspection of Fig. 1a reveals some differences in the position and relative intensities of particular diffraction peaks, pointing out that small modifications arise in the zeolite crystals as a function of the crystallization time. This is illustrated in Fig. 1b for the region 2θ = 17–21°, where it can be observed the disappearance of the peak at 17.9° at 13 days and the strong diminution of the intensity of the diffraction at 19° at 30 days of synthesis time.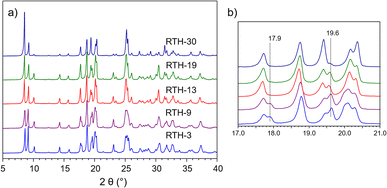

Fig. 1 (a) PXRD patterns of the pure silica RTH zeolites and (b) detail of the PXRD patterns at the 17–21° (2θ) region.

All samples possess a F⁻/P-OSDA⁺ ≈ 1 molar ratio (see Table 1) indicating that the P-OSDA⁺ cations are compensated by F⁻ and thus, that the samples must be free of [SiO⁻⋯(HOSi)_x] connectivity defects.^83,84 The ³¹P and ¹H–¹³C CP MAS NMR spectra of all RTH samples are similar and show the peaks characteristic of the P-OSDA⁺ (see Fig. S3† for further details), proving the integrity of the cations within the zeolite and suggesting that their position within the cavities should be roughly the same. However, substantial differences are observed in the ²⁹Si and ¹⁹F MAS NMR spectra.

The ²⁹Si ss-NMR spectra of the RTH zeolites, shown in Fig. 2a, are significantly different for the samples synthesized at short (RTH-3 and RTH-9) and long (RTH-19 and RTH-30) crystallization times. The spectra of the RTH-3 and RTH-9 zeolites show a doublet at δ²⁹Si ≈ −146.0 ppm due to the scalar J_SiF = 160 Hz coupling with the fluoride ¹⁹F (I = 1/2) typical of penta-coordinated [F–²⁹Si(OSi)₄]⁻ silicon species.^46,48 The simulation of the spectrum of the RTH-9 zeolite (Fig. S4†) proves the presence of other fifteen signals of ²⁹Si(OSi)₄ in the region between δ²⁹Si = −100 ppm and δ²⁹Si = −120 ppm. The ²⁹Si MAS NMR spectra of the RTH-19 and RTH-30 samples, obtained at long synthesis times, also consist of 16 signals with equal intensity, fifteen ²⁹Si(OSi)₄ and a doublet due to [F–²⁹Si(OSi)4]⁻ species (δ ²⁹Si ≈ −145.0 ppm, J_SiF = 170 Hz), but with δ²⁹Si and J_SiF values different to those of sample RTH-9. The spectra of the samples obtained at short times are characterized by the presence of a low field signal at δ²⁹Si = −103.7 ppm attributed to a T crystallographic site with a small T–O–T angle.⁸⁵ This signal is absent in the spectra of the zeolites synthesized at long times, which otherwise display a much better resolution indicating higher long-range structural order. The ²⁹Si NMR spectra of the RTH-9 and RTH-30 zeolites, chosen as representative of the two types of samples, and their simulation using individual components are compared in Fig. S4.†

Fig. 2 (a) ²⁹Si MAS NMR spectra of the RTH zeolites (b) comparison of the ²⁹Si (up) and the ¹⁹F–²⁹Si CP (with 0.4 ms of contact time) (bottom) MAS NMR spectra of the RTH-9 and RTH-30 zeolites.

The ²⁹Si MAS NMR spectra as well as the XRD patterns of all RTH samples are nearly identical after calcination disappearing the differences observed for the as-synthesized materials. The unit cell of the RTH-type structure, without organic molecules inside the pore system, contains 32 T atoms (Si₃₂O₆₄) distributed in four crystallographic sites each of them with a multiplicity of eight, and thus, four peaks of equal intensity are expected in the ²⁹Si NMR spectra. Accordingly, the ²⁹Si NMR spectra of the thermally treated (under hydrogen and subsequent calcination) materials consist of three signals with areas 1 : 2 : 1 due to the proximity of the δ²⁹Si of two of the four Si sites, the contribution of which can be distinguished in the spectrum of the RTH-30 sample (Fig. S5†). Thus, it is concluded that regardless the crystallization time, all samples consist on pure siliceous RTH zeolite. However, according to the ²⁹Si NMR spectra the number of T sites increases from four in the calcined to sixteen in the as-synthesized materials (Fig. 2). As reported previously for the STF-type zeolite,⁴⁸ this reduction of the crystal symmetry is originated by the bonding of fluoride to Si. Assuming that the occurrence of [F–Si(OSi)₄]⁻ species does not change the size of the unit cell still formed by 32 SiO₄, the RTH zeolites must contain at least 16 crystallographic sites with multiplicity of two.

Fig. 2b compares the ²⁹Si and the ¹⁹F–²⁹Si CP MAS NMR spectra of the RTH-9 and RTH-30 zeolites representative of the RTH structures at short and long crystallization times, respectively. As expected, the ¹⁹F–²⁹Si CP MAS NMR spectra show a sharp increase of the signal assigned to [F–²⁹Si(OSi)₄]⁻ and to lesser extent, of other resonances that differ for the two samples, indicating that the Si close to F⁻ are at different sites. It must be noted the enhancement of the signal at δ²⁹Si = −103.7 ppm in the CP MAS NMR spectrum of the RTH-9 indicating the proximity to fluoride of this silicon site.

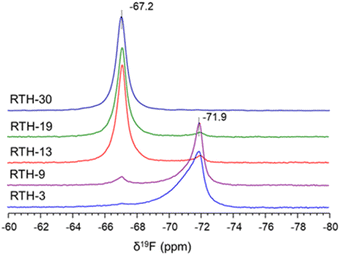
The ¹⁹F ss-NMR spectra, shown in Fig. 3, are also different for the RTH zeolites obtained at different synthesis time. The spectrum of the RTH-3 sample contains a main signal at δ¹⁹F = −71.9 ppm and another very weak at δ¹⁹F = −67.2 ppm. This latter resonance is slightly more intense for the RTH-9 zeolite, becomes dominant for the RTH-13 and RTH-19 and is the only one in the spectrum of the RTH-30. Analysis of the ¹⁹F NMR spectra recorded at low spinning rates (Fig. S6†) confirms the effective bonding of F⁻ to SiO₄ at room temperature, according to the observation of [F–²⁹Si(OSi)₄]⁻ sites in the ²⁹Si ss-NMR spectra. In the RTH structure, F⁻ anions must be placed within the rth cages formed by four 4R and four 5R (i.e. [4⁴.5⁴] following the notation recommended by the International Zeolite Association – IZA). The fact that both the ¹⁹F and the ²⁹Si NMR signals of penta-coordinated silicon are different for the samples obtained at short (δ¹⁹F = −71.9 ppm) and long (δ¹⁹F = −67.2 ppm) times, indicate that the [F–Si(OSi)₄]⁻ species must be placed at different positions of the rth cage.

Fig. 3 ¹⁹F MAS NMR spectra of the RTH zeolites.

Therefore, the bonding of F⁻ anions to Si at different positions of the rth cage at short and long time of synthesis gives rise to two unlike structures that are denoted as RTH-A and RTH-B, respectively. From now on, the study is focussed on RTH-9 and RTH-30 zeolites as representative of the RTH-A and RTH-B phases, respectively.

Information on the spatial proximity of the P-OSDA⁺ cations and the F⁻ anions in the RTH-9 and RTH-30 zeolites is gained by recording bidimensional (2D) ¹H–¹⁹F dipolar based heteronuclear multiple-quantum coherence (D-HMQC) MAS NMR spectra at high magnetic field (850 MHz) and very fast spinning rate (60 kHz) shown in Fig. 4. Examination of the full projection of the ¹H signals in the F2 (horizontal) dimension of the spectra of the RTH-9 and RTH-30 zeolites show peaks at δ¹H = 2.7 ppm attributed to the methylene P–CH(–CH₃)₂ and at δ¹H = 1.7 ppm assigned to the –CH₃ groups of the P-OSDA⁺ cation. The spectrum of the RTH-9 sample shows a shoulder at δ¹H 1.9 ppm, the origin of which was investigated by recording the 2D ¹H double quantum-single quantum (DQ-SQ) spectrum, displayed in the inset of Fig. 4a. It shows a cross correlation peak at (1.7 ppm, 4.8 ppm) from the signals at δ¹H = 1.7 ppm and at δ¹H = 2.7 ppm but not with the resonance at δ¹H = 1.9 ppm. Then, the signal at δ¹H = 1.7 ppm is assigned to the terminal methyl group of the isopropyl chain as they are close to the –CH group (≡P–CH(CH₃)₂) and the signal at δ¹H ≈ 1.9 ppm is attributed to the methyl directly linked to phosphorus (≡P–CH₃). The fact that the two methyl groups are not distinguishable in the F2 ¹H projection of the ¹H–¹⁹F HMQC spectrum of the RTH-30 zeolite (see Fig. 4b), suggests that the orientation of the P-OSDA⁺ cation is slightly different than in the RTH-9 sample, as supported by the differences observed in the ¹³C NMR spectra (Fig. S3†).

Fig. 4 ¹H–¹⁹F 2D D-HMQC MAS-NMR spectra of the samples: (a) RTH-9 and (b) RTH-30 (recoupling time of 1.7 ms). The inset in (a) is the 2D DQ-SQ ¹H MAS-NMR spectrum of the RTH-9 sample.

The 2D ¹⁹F–¹H D-HMQC NMR spectrum of the RTH-30 sample shows two correlation signals at (1.7, −67) ppm and (2.7, −67) ppm of the unique ¹⁹F resonance at δ¹⁹F = −67.2 ppm with the –CH– (δ¹H = 2.7 ppm) and the terminal –CH₃ groups (δ¹H = 1.7 ppm) of the isopropyl chain of the P-OSDA⁺ cation. These two cross peaks are also present in the 2D ¹⁹F–¹H D-HMQC NMR spectrum of the RTH-9 sample coming from the weak ¹⁹F resonance at δ¹⁹F = −67.2 (Fig. 4a), besides two more cross peaks at (2.7, −72) and (1.7, −72) ppm of the –CH- and –CH₃ groups of the isopropyl chain with the intense ¹⁹F signals (δ¹⁹F = −72 ppm). Interestingly, the spectrum of the RTH-9 sample shows a fifth correlation at (1.9, −72) ppm, again confirming the assignment of the signal at δ¹H = 1.9 ppm to the ≡P–CH₃ group of the P-OSDA⁺ in zeolite and proves that the local interaction of the cations with the inorganic network are slightly different in the two samples.

Summarizing, the results obtained by ss-NMR spectroscopy for the RTH zeolites indicate that the RTH-A and RTH-B present sharp differences in the Si crystallographic sites and the local environment of F⁻ and subtle differences on the orientation of the P-OSDA⁺ cations. The two phases can be easily distinguished by ¹⁹F NMR, as the RTH-A phase gives a signal at δ¹⁹F ≈ −72 ppm and the RTH-B phase at δ¹⁹F ≈ −67 ppm.^39,47,48,53 Moreover, the ²⁹Si NMR spectra of the RTH-A phase presents a characteristic low field signal at δ²⁹Si ≈ −104 ppm absent in the RTH-B phase.

The influence of other parameters such as the temperature of synthesis were also investigated by ss-NMR. The spectra of all samples synthesized at lower temperature (150 °C) with P-OSDA⁺ show the contribution of signals corresponding to phases RTH-A and RTH-B, as illustrated in the ¹⁹F NMR spectrum of Fig. S7.† Therefore, the use of high temperature and long crystallization times in the zeolite synthesis favors the formation of the RTH-B phase, which is more stable thermodynamically than the RTH-A.

3.2. Structure resolution of the pure silica RTH-A and RTH-B phases

3.2.1. Redefinition of the RTH unit cell by DFT calculations. According to the IZA database⁹ the structure of the calcined pure silica RTH is monoclinic and the unit cell contains four inequivalent T sites, namely T1, T2, T3 and T4, each of them with multiplicity 8. The increase in the number of non-equivalent crystallographic T sites up to 16 in the as-made material observed by NMR is the result of a decrease in the symmetry, related to the bonding of the fluoride to a Si site. This causes that the T-sites equivalent by symmetry in the calcined material become non-equivalent in the as-made zeolite, in a similar way to that reported for the STF type structure.⁴⁸

In order to understand the changes of symmetry of the as-synthesized zeolite, we built a model starting from the RTH topology, with two P-OSDA⁺ cations and two F⁻ anions per unit cell. The HRPXRD data of the RTH-9 and RTH-30 samples were used to localize the P-OSDA⁺ cations, starting the calculations using the known monoclinic structure of calcined RTH.⁹ The position of the phosphorus atoms, with higher electron density than the other atoms of the P-OSDA⁺, was determined by calculating difference Fourier map using the programs FullProf and GFourier. After that, the approximated locations of the C atoms connected to P have been easily obtained. The remaining C atoms were positioned close to the previous ones, imposing geometrical restraints to C–C bond distances and P–C–C tetrahedral angles (Tables S2 and S3†). Unfortunately, it was not possible to accurately find the position of the F⁻ anions. The two P-OSDA⁺ cations in the unit cell occupy similar positions in the large cavities in the RTH structure in the RTH-9 (phase RTH-A) and RTH-30 (phase RTH-B) samples. Subsequently, the resulting structure including the P-OSDA⁺ was used as a starting point for modelling the structural changes by means of theoretical calculations.

Thus, theoretical calculations were envisaged for locating the two compensating F⁻ anions within the RTH structure containing two P-OSDA⁺ cations in the unit cell. The possible models of the as-synthesized RTH unit cell were developed by positioning the P and the C atoms of the two P-OSDA⁺ cations from the refinement of the PXRD patterns, completing the valence of the C atoms with H. The observation of a unique ¹⁹F NMR resonance in each of the two phases indicates a unique local environment and then the two F⁻ atoms included in the unit cell were bonded to two equivalent Si crystallographic sites. This approach gives rise to a total of 112 combinations, 28 for each of the T1–T4 sites in the calcined material (see Fig. S8 and S9† for a full description of the procedure). However, the calculated NMR absolute shielding of the two F⁻ in the unit cell is equal for only 16 models, which correspond to four combinations for each T1–T4 sites (Fig. S9, Tables S4–S7,† see also crystallographic information files (.cif) supplied as ESI† for atomic coordinates and the structures with Deposition Numbers CSD 2297811-2297850). Interestingly, in these 16 models, the 32 Si atoms of the unit cell can be grouped in 16 pairs with 16 calculated ²⁹Si σ_iso which agree with the 16 signals observed in the ²⁹Si NMR spectra. This is not true for the rest of the 96 models. These 16 configurations are among the most stable because the distance between both fluoride anions is maximized (Fig. S10†) and are consistent with the experimental evidence observed by solid state NMR.

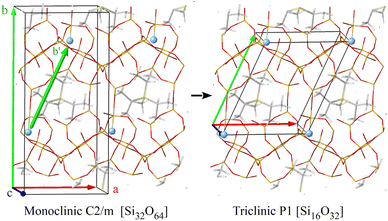
A close inspection of these 16 models reveals that the fluoride distribution is not compatible with any monoclinic space group and, consequently, the unit cell was redefined. To that end, we found three cell vectors such that all fluoride atoms are related by translations (Fig. S10†). Thus, the new unit cell vectors can be defined choosing one F⁻ and connecting it to the three nearest F⁻ in the three (x, y, z) directions of space (Fig. 5). This operation resulted in a triclinic unit cell with the following parameters, optimized with PBE: a = 9.753 Å, b = 11.471 Å, c = 9.729 Å, α = 86.32°, β = 95.78°, γ = 115.84°. The new triclinic unit cell contains 16 T atoms, in 16 crystallographic T sites (T1 to T16 with multiplicity 1), one F⁻ anion and one P-OSDA⁺ cation.

Fig. 5 Redefinition of the RTH unit cell. The vector, b′, connecting the F pairs related by (x + 1/2,_y + 1/2,_z) symmetry operation will now define the new b vector. Si, O, P, C, H, F are depicted in orange, red, yellow, grey, light grey, blue respectively. Unit cell vectors a, b and c are depicted in red, green and blue respectively.

The feasibility of the redefined RTH structure using the triclinic cells calculated theoretically was checked by using them used as starting point for further refinements of the cell parameters using the PXRD data with the new symmetry. The data calculated were in good agreement with the experimental PXRD. The refined unit cell parameters for the RTH-9 sample (phase RTH-A) with the new triclinic cell are a = 9.7265(5) Å, b = 11.3864(6) Å, c = 9.8017(5) Å, α = 87.853(3)°, β = 96.205(3)°, γ = 114.988(3)°, V = 978.12(8) ų, and for the RTH-30 sample (phase RTH-B) a = 9.7516(4) Å, b = 11.5072(3) Å, c = 9.6825(2) Å, α = 87.327(2)°, β = 96.330(2)°, γ = 115.102(2)°, V = 977.90(5) ų.

3.2.2. Location of fluoride anions in the pure silica RTH-type zeolite. The low electron density of fluoride makes unfeasible the location of this anion by the analysis of the PXRD data, and then, DFT calculations were used. The lattice parameters and atomic coordinates taken from the refinement in the triclinic system of the PXRD patterns of the RTH-9 and RTH-30 samples were used as initial guess for a new round of DFT optimizations. The new triclinic unit cell (Si₁₆O₃₂) has 16 crystallographic sites (1–16) each with a multiplicity of 1, instead of the 4 T-sites (T1-T4) with multiplicities of 4 in the monoclinic cell of the calcined material.

Fig. 6 depicts the correspondence among the T1–T4 crystallographic positions of the monoclinic system with the 1–16 sites of the triclinic unit cell. The structure models were created by bonding a fluoride anion to each of the 16 positions of the triclinic unit cells. In the case of 9–12 (T3) and 13–16 (T4) sites, which are forming the 4-membered rings joining two rth cages, the fluoride anion may point to the center of any of the two cages (I and II in Fig. 6). As a result, there are 24 possible arrangements for the fluoride anions in the 16 T crystallographic positions that are labeled according to the index of the Si atom to which the F is bonded, that is, from 1 to 16, and the duplicates of 9–16 sites of the two-joined rth cages are labelled I and II depending on which cage the fluoride is pointing to (Fig. 6). Table 2 summarizes the Si–F bond length, the P–F distance, the optimized volume of the unit cell, the predicted δ_iso¹⁹F and the relative energy with respect to the most stable (position 6) for each of the 24 models. The calculated chemical shielding ²⁹Si σ_iso of the 24 structures in the triclinic system are listed in Tables S8–S10.†

Fig. 6 Illustration of the two possible orientations of the fluoride anion bonded to the Si at the position 14 (a T4 site in the monoclinic unit cell). The fluoride anion can be oriented towards the center of cage I or II. The same applies to positions 9, 10, 11, 12, 13 and 15. Cages are joined by 4-membered rings (4MR) made up of sites 9–12 (T3 in the monoclinic unit cell) and 13–16 (T4 in the monoclinic unit cell). For visual aid of the cage B the periodic image of the positions 10, 11, 13 and 15 are also represented.

Table 2 Si–F bond lengths, P–F distance, unit cell volume, predicted isotropic chemical shift (δ_iso) of ¹⁹F, and relative energy with respect to position 6. The δ_iso¹⁹F were calculated using regression equation shown in Fig. S2 and taking as predictor variable the absolute isotropic shielding calculated with TB-mBJ

Triclinic model	Monoclinic site	Si–F bond (Å)	P–F distance (Å)	Unit cell volume (Å^3)	Predicted δiso (ppm)	E rel (kJ mol^−1)
1	T1	1.816	7.00	980.4	−56.1	15.9
2	T1	1.784	7.30	985.2	−62.8	7.5
3	T1	1.820	6.74	985.0	−62.1	16.3
4	T1	1.820	7.02	980.7	−56.6	18.4
5	T2	1.785	6.94	973.2	−66.3	2.5
6	T2	1.788	6.74	979.3	−65.9	0.0
7	T2	1.784	7.25	974.3	−66.4	1.7
8	T2	1.791	7.29	977.5	−65.0	2.9
9-I	T3	1.800	6.88	981.0	−58.1	10.0
9-II	T3	1.764	6.58	970.0	−75.7	18.8
10-I	T3	1.770	6.68	973.4	−73.0	22.2
10-II	T3	1.809	6.71	984.8	−49.5	17.6
11-I	T3	1.810	7.13	989.4	−50.6	16.3
11-II	T3	1.765	6.73	972.2	−72.7	20.9
12-I	T3	1.767	6.66	971.0	−73.4	20.9
12-II	T3	1.807	7.04	982.7	−58.7	12.5
13-I	T4	1.770	6.79	972.1	−71.9	18.0
13-II	T4	1.796	6.85	975.4	−58.5	8.4
14-I	T4	1.794	6.79	976.0	−58.5	1.7
14-II	T4	1.780	6.91	968.0	−70.8	16.3
15-I	T4	1.798	7.03	976.2	−57.8	9.2
15-II	T4	1.766	6.35	970.0	−71.8	15.1
16-I	T4	1.773	6.52	967.8	−70.4	21.8
16-II	T4	1.798	6.96	976.2	−59.0	4.6

---

The plot of Fig. 7 shows that as the Si–F bond lengths enlarges from 1.77 Å to 1.82 Å, the predicted NMR δ_iso¹⁹F shifts from −73 ppm to −48 ppm with a good correlation R² ∼ 0.8. The data in Table 2 points out that shorter P–F distances are generally accompanied by smaller unit cell volumes and more negative δ_iso¹⁹F. These observations agree with the experimental results since the unit cell volume of the RTH-9 sample (975.8 ų) with a ¹⁹F NMR signal at δ¹⁹F = −71.2 ppm is smaller than that of the RTH-30 sample (980 ų, δ¹⁹F = −67.2 ppm). It is worth noting that the lesser unit cell volumes are predicted for the structures where the fluoride is bonded to silicon atoms at the four-member rings, that is, at the 9–12 (T3 in the monoclinic cell) and 13–16 (T4 in the monoclinic cell) sites.

Fig. 7 Correlation of the ¹⁹F NMR chemical shift with Si–F bond length of the theoretical models of the RTH zeolite built in this work.

Interestingly, the observation of Table 2 indicates that the predicted δ_iso¹⁹F values depend on the crystallographic T1–T4 sites of the former monoclinic structure where fluoride is bonded. The general trends observed are: (i) T1 (1–4 in the triclinic) has δ_iso¹⁹F between −56 ppm and −62 ppm; (ii) T2 (5–8 in the triclinic) shows a very narrow distribution of chemical shifts centered at δ_iso¹⁹F ≈ −66 ppm; (iii) T3 (9–12 in the triclinic) displays values at δiso¹⁹F ≈ −50 ppm, δiso¹⁹F ≈ −58 ppm or δiso¹⁹F ≈ −73 ppm and finally, (iv) T4 (13–16 in the triclinic) has calculated values of δ¹⁹F = −58 ppm or −71 ppm.

The criteria to choose the models that better depict the real structures are a compromise of the higher relative stability and the best correlation between calculated and experimental ¹⁹F and ²⁹Si NMR chemical shifts. The most stable structure corresponds to model 6 in Table 2, with a calculated δ_iso¹⁹F = − 65.9 ppm that agrees very well with the signal at δ¹⁹F = − 67.2 ppm of the RTH-30 sample (phase RTH-B). The model 6 is represented in Fig. 8, besides the plots showing the good correlation existing between theoretical σ_iso²⁹Si (Table S8,† column in italics) and the experimental δ²⁹Si of the RTH-30 sample. Although there are only small differences among the relative energies and δ¹⁹F_iso of models 5–8 (T2 in the monoclinic cell), model 6 (Table 2, Fig. 8) with the fluoride bonding a Si at the position 6 (T2 in the former monoclinic cell), is the one that shows the best correlation between calculated and experimental ²⁹Si chemical shifts (Fig. S11†). As expected, longer time and higher temperature of synthesis would lead to the most thermodynamically stable phase and then the model 6 can be unambiguously assigned to the RTH-B phase.

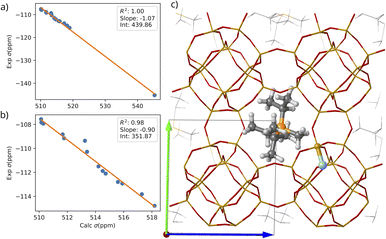Fig. 8 Correlation between the calculated σ_iso²⁹Si and the experimental δ²⁹Si of sample RTH-30 for the 16 Si atoms (a) and leaving out the Si atom bonded to fluoride (b). (c) Optimized structure with the fluoride anion sitting on position 6 (T2 in the monoclinic). Only one P-OSDA⁺ and the nearest fluoride are represented with balls. Si, O, P, C, H, F are depicted in orange, red, yellow, gray, light gray, blue respectively. The calculated ²⁹Si σ_iso are included in Table S6.†

The ¹⁹F NMR signal of the RTH-9 sample (phase RTH-A) appears at δ¹⁹F = −71.8 ppm, which fits well with the value predicted for the models 9-II, 10-II 11-II and 12-I (F⁻ bonded to T3 sites in the monoclinic cell) and 13-I, 14-II, 15-II and 16-I (F⁻ bonded to T4 sites in the monoclinic cell), as shown in Table 2. However, from them, the calculated σ_iso²⁹Si values of model 16-I shows the best correlation with the experimental δ²⁹Si of sample RTH-9 (Fig. S12 and S13† and 9). Accordingly, the model 16-I represented in Fig. 9, less stable than the model 6 (RTH-B phase), can be ascribed to the RTH-A phase obtained at shorter crystallization times or lower temperature. Nevertheless, it must be noted that also σ_iso²⁹Si of model 12-I shows a good correlation with the experimental δ²⁹Si and the differences in the relative energy of all structures are small. The unit cell parameters of models 6 and 16-I are compared with those of samples RTH-9 and RTH-30 in Table S11.†

Fig. 9 Correlation between the calculated ²⁹Si σ_iso and the experimental δ²⁹Si of sample RTH-9 for the 16 Si atoms (a) and leaving out the Si atom bonded to fluoride (b). (c) Optimized structure with the fluoride anion sitting on position 16-I (T4 site). Only one P-OSDA⁺ and the nearest fluoride are represented with balls. Si, O, P, C, H, F are depicted in orange, red, yellow, gray, light gray, blue respectively. The calculated ²⁹Si σ_iso are included in Table S8.†

3.3. Thermal behavior of RTH-A and RTH-B phases

The results reported here indicate that the RTH-A and RTH-B phases are obtained at short and long synthesis times at 175 °C, respectively. The DFT calculations suggests that the energetic difference between them is relatively small and thus, we thought about the possibility that phase transitions could occur just by simple heating–cooling cycling. To check this possibility, a calorimetric study was carried out on the RTH-9 and RTH-30 samples. The plots of the heat flow vs. temperature upon heating (Fig. S14a†) show intense endothermic signals at 95 °C with a heat of 3.1 J g⁻¹ for the RTH-9 sample and at 134 °C and 5.0 J g⁻¹ for the RTH-30 sample. These signals must be associated to a phase transition since there are no mass changes in the temperature range used. Upon subsequent cooling down, the calorimetry plots show exothermic signals at 79 °C and 3.1 J g⁻¹ for the RTH-9 and at 96 °C and 5.1 J g⁻¹ for the RTH-30 samples. Thus, the phase transitions observed on both RTH materials during heating were reversible, although shifted to lower temperatures during cooling (Fig. S14b†). However, the coincidence of the heat values (endothermic during heating exothermic during cooling) strongly support that the systems are mostly reverting back to the original phases during cooling down. The calorimetry study on the RTH samples clearly shows that there is a completely reversible phase transition which occurs at higher temperature and with higher heat for the RTH-30 sample, supporting the higher thermodynamic stability of the RTH-B phase. The results indicate that the two phases do not transform each other (if this occurs, two signals would appear in the calorimetric plots), but that they transform directly into a third unknown phase upon heating, which may be the same or not for the two samples. Unfortunately, calorimetry does not provide any further information about the structural changes occurring during these phase transformations.

To gain more insight on the phase transformations observed by calorimetry, the ss-NMR spectra and the PXRD patterns of the RTH-9 (RTH-A phase) and the RTH-30 (RTH-B phase) samples were recorded at variable temperature between 25 °C and 150 °C. The ¹H–²⁹Si CP MAS NMR spectra were measured to shorten the acquisition time by exploiting the proximity of all framework Si atoms to the ¹H from the P-OSDA⁺ within the zeolite cavities. The ¹⁹F MAS NMR spectra were recorded at low spinning rates to observe the spinning side bands (SSB) pattern from the chemical shift anisotropy (CSA) to monitor possible changes in the symmetry environment of fluoride atoms.

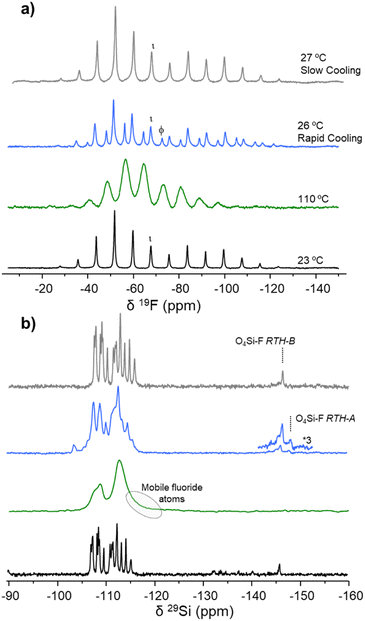
Fig. 10 shows the ²⁹Si and ¹⁹F ss-NMR spectra of the RTH-9 sample recorded at variable temperature. The NMR spectra recorded at 23 °C (room temperature) have already been depicted above. The ¹⁹F NMR spectrum is dominated by the signal at δ_iso¹⁹F ≈ −72 ppm, typical of the RTH-A phase, with a very weak contribution at δ_iso¹⁹F ≈ −67 ppm of the RTH-B phase, both axially symmetric (Fig. 10a). The ²⁹Si NMR spectrum displays a low field peak at δ_iso²⁹Si ≈ −104 ppm characteristic of the RTH-A phase with the doublet at δ_iso²⁹Si ≈ −148 ppm due to the penta-coordinated silicon as described before. When the temperature of the RTH-9 sample is increased to 80 °C, the ¹⁹F NMR spectrum (Fig. 10a) shows an SSB pattern with broad signals attributed to mobile fluoride jumping between various Si crystallographic positions, as previously reported for silicalite-1.⁴⁷ Accordingly, the corresponding ²⁹Si NMR spectrum consists of two broad bands. The spectrum shows a tail at high field, and the disappearance of the doublet of F–²⁹Si(OSi)₄ and of the low field signal at δ_iso²⁹Si ≈ −104 ppm. After fast cooling down the sample to ∼25 °C, the original ¹⁹F and ²⁹Si NMR spectra are recovered with slightly higher relative intensity of the RTH-B phase and wider peaks, indicating higher heterogeneity of sites and then less short-range order. Similar spectra were recorded in a second cycle, by heating again up to 80 °C and then slowly cooling (in steps of 5 °C) down to 30 °C. The ¹⁹F NMR spectrum shows narrower peaks, indicating a higher homogeneity and slightly more ordered material than after fast cooling.

Fig. 10 (A) ¹⁹F MAS NMR spectra (2 kHz) and (B) ²⁹Si CP-MAS NMR spectra of the RTH-9 sample recorded at the temperature indicated in the spectra. The δ_iso¹⁹F peaks corresponding to phase RTH-A is indicated by (ϕ) and to phase RTH-B by (ι). The rest of the peaks in the spectra are spinning sidebands. Rapid cooling (for about thirty minutes) was done by switching the heating off on the sample at the higher temperature. During slow cooling down (for about ninety minutes) the sample at the higher temperature was decreased by steps of 10 °C. (Same color of spectra indicates same temperature of measurement).

A similar ss-NMR experiment was carried out on the RTH-30 zeolite exhibiting the RTH-B phase and the main results are summarized in Fig. 11. At room temperature, the ¹⁹F NMR spectrum shows the signal at δ_iso¹⁹F ≈ −67 ppm and the highly resolved ²⁹Si NMR spectrum, representative of the RTH-B phase, which do not experience relevant changes up to 110 °C. At this recording temperature, the ¹⁹F and ²⁹Si NMR spectra are similar to those of the RTH-9 sample at 80 °C (Fig. 10), indicative of dynamic disorder because of the fluoride mobility. After rapidly cooling down the RTH-30 sample from 100 °C to 26 °C, the ¹⁹F NMR spectrum shows the overlapping of the SSB patterns of the signal at δ_iso¹⁹F ≈ −67 ppm from the RTH-B phase with a weaker but significant contribution of the signal at δ_iso¹⁹F ≈ −72 ppm indicating the development of the RTH-A phase. The presence of phase RTH-A is confirmed by the appearance of the signal at δ_iso²⁹Si ≈ −104 ppm in the ²⁹Si NMR spectrum. However, when the RTH-30 sample is heated again up to 110 °C and then slowly (in steps of 5 °C) cooled down to 25 °C, the original ¹⁹F and ²⁹Si NMR spectra corresponding to the RTH-B phase are fully recovered, this process being completely reversible.

Fig. 11 (a) ¹⁹F MAS NMR spectra (2 kHz) and (b) ²⁹Si CP-MAS NMR spectra of the RTH-30 sample recorded at the temperature indicated in the spectra. The δ_iso¹⁹F peaks corresponding to phase RTH-A is indicated by (ϕ) and to phase RTH-B by (ι). The rest of the peaks in the spectra are spinning sidebands. Rapid cooling (for about thirty minutes) was done by switching the heating off on the sample at the higher temperature. During slow cooling down (for about ninety minutes) the sample at the higher temperature was decreased by steps of 10 °C. (Same color of spectra indicates same temperature of measurement).

Thus, the ss-NMR spectra recorded at variable temperature indicate that the fluoride anions detach from the silicon position 16-I in the RTH-A phase at 80 °C and from the site 6 in the RTH-B phase at 110 °C. The process is fully reversible when slowly cooling down, although a fraction of RTH-A phase appears when the RTH-30 sample (RTH-B phase) is rapidly cooled down to 25 °C. The results obtained by ss-NMR strongly suggest that the phase developed at high temperature with the fluoride anions detached from the SiO₄ tetrahedra, is the same independently of the location of fluoride anions in the original RTH sample. To fully confirm these changes of phases, the in situ XRD study of the thermal evolution of RTH samples were carried out.

Fig. 12 top shows the peaks in the 2θ = 8.0–9.5° region of the PXRD patterns of the RTH-30 zeolite (mainly RTH-B phase), registered at increasing temperatures under dry nitrogen. The diffractogram recorded at room temperature presents two distinctive peaks at 2θ = 8.46° and 9.16°, which slightly shift toward lower angles upon heating up to 100 °C, indicating a subtle expansion of the unit cell. At around 125 °C an abrupt change of the unit cell parameters occurs with a contraction of a and b and an expansion of c till a = 9.7376(3) Å, b = 11.4669(3) Å, c = 9.7640(2) Å, α = 87.4456(15)°, β = 96.063(2)° and γ = 115.0690(18)° indicating the formation of a new phase, denoted as RTH-C, that remains constant up to at least 150 °C. After rapid cooling down the material to room temperature, the RTH-B phase reappears accompanied by the RTH-A phase (a = 9.7265(5) Å, b = 11.3864(6) Å, c = 9.8017(5) Å, α = 87.853(3) °, β = 96.205(3)° and γ = 114.988(3)°). Then, this sample was submitted to a second heating cycle (Fig. 12, top right). At 100 °C, the RTH-C phase appears and the RTH-A disappears while the RTH-B persists. When the temperature is increased to 150 °C, as in the previous heating cycle only the RTH-C phase is observed. During subsequent slow cooling down, the RTH-B emerges at 75 °C and the RTH-A at 50 °C while the RTH-C phase vanishes. At room temperature, there is a mixture of the two phases with a fraction of RTH-B higher than in the previous cycle. These results are completely reversible by heating and cooling down again, with the relative amounts of the two phases being observed to depend on the speed of the cooling process (Fig. 12, bottom).

Fig. 12 PXRD patterns of RTH-30 at different temperatures. (Top left) first heating cycle; from bottom to top, 25, 50, 75, 100, 125, 150 and 25 °C (after fast cooling). (Top right) second heating cycle, with the same temperatures but with a slow cooling ramp. (Bottom left) PXRD patterns of the sample at room temperature; from bottom to top: starting sample, after one cycle and fast cooling; and after two cycles and slow cooling. (Bottom right) PXRD patterns of RTH-9 at room temperature; from bottom to top: starting sample, after one cycle and fast cooling; and after two cycles and slow cooling.

When a similar PXRD experiment is carried out with the RTH-9 sample, the pure RTH-A, the formation of the RTH-B phase is precluded, so that, only RTH-A and RTH-C phase are present at low and high temperature, respectively.

Comparison of the PXRD data and the ss-NMR results suggests that the so called RTH-C phase formed by heating either the RTH-A or the RTH-B phase corresponds to the RTH zeolite in which fluoride anions are highly mobile. In this situation, fluoride is changing the bonding among different Si sites very rapidly with negligible contribution of the penta-coordinated silicon in the ²⁹Si NMR spectra. Calorimetry, ss-NMR and PXRD show that the temperature required for the practical detachment of fluoride from silicon and the formation of the RTH-C phase is higher for the RTH-B phase. Interestingly, the original RTH-A or RTH-B structures are mainly recovered by cooling down to room temperature the RTH-9 and RTH-30 samples exhibiting the RTH-C phase at 80 °C or above, Although phase RTH-B can be mixed with some amount of RTH-A depending on the specific cooling conditions, the results reported here indicate that the samples have memory effect on the precise location of fluoride.

4. Conclusions

In the as-synthesized RTH zeolite, fluoride atoms bind to framework silicon decreasing the crystal symmetry from monoclinic in the calcined material to triclinic. This change leads to an increase in the number of non-equivalent crystallographic sites, rising from four (with a multiplicity of eight, unit cell Si₃₂O₆₄) in the calcined state to sixteen (with a multiplicity of one, unit cell Si₁₆O₃₂) in the as-synthesized zeolite, indicating a higher degree of structural complexity. The findings presented in this study highlight the appearance of two distinct phases during the crystallization process of the RTH zeolite. The synthesis at 175 °C predominantly yields the RTH-A phase at short times and exclusively produces the thermodynamically more stable RTH-B phase at longer periods. Comparison of the two triclinic phases reveals a slightly smaller unit cell volume for the RTH-A phase (974.4 ų) compared to the RTH-B phase (980.69 ų).

Employing ss-NMR techniques in the study of this system yields valuable insights into the location of fluoride. The ¹⁹F and ²⁹Si NMR spectra of the RTH-9 (RTH-A phase) and RTH-30 (RTH-B phase) samples exhibit differences, signifying considerable changes in the local environments of fluoride and silicon over crystallization time. The ²⁹Si NMR spectra of both samples recorded at room temperature feature a doublet at high field of five-coordinate silicon, indicating the absence of dynamic disorder. However, differences in δ ²⁹Si and J_F–Si confirm dissimilar F–²⁹Si(SiO₄)₄ environments in the RTH-9 and RTH-30 samples. These results strongly suggest that the development of the two phases arises from fluoride bonding to distinct Si crystallographic sites, together with variations in the orientation of the P-OSDA⁺ cations within the zeolite cavities, as supported by the ¹H and ¹³C NMR results. The ²⁹Si NMR signals of the RTH-30 sample (RTH-B phase) are remarkably narrow, resulting in a highly resolved spectrum that demonstrates long-range order in the distribution of fluoride atoms within the structure. Conversely, the broader ²⁹Si NMR signals observed in the RTH-9 sample (RTH-A phase) indicate some degree of long-range static disorder in fluoride allocation within the crystals. Thus, in the RTH-type zeolite synthesized with the P-OSDA⁺, there exist two distinct, potential sites for fluoride allocation that do not experience dynamic disorder at room temperature. To our knowledge, this observation has not been reported in any other zeolitic system.

The higher electron density of phosphorus compared to nitrogen has proven advantageous in localizing the P atom of the P-OSDA⁺ inside the zeolite cavities by means of PXRD. This information is crucial for modelling the distribution of fluoride among all possible Si sites. A comprehensive comparison of parameters such as NMR δ ²⁹Si, unit cell volume, and relative energy calculated by DFT for the 24 models consistent with the experimental results has led to the identification of the RTH-A and RTH-B phases. The thermodynamically stable RTH-B phase is associated with the most stable model (Model 6), where fluoride is bound to a Si at site 6 in the triclinic system (T2 site in the monoclinic system), situated in a 4R non-shared with another rth cage. Experimental results regarding the RTH-A phase are more closely related with model 16-I. Nevertheless, the small differences in relative energies with other structural models do not allow complete exclusion of any of them based solely on this criterion. This observation, coupled with the broadness of the ²⁹Si NMR signals, suggests that fluoride may not occupy a singular position, leading to a greater static disorder than observed in the RTH-B phase. According to the general trend obtained by DFT, the most stable RTH-B structure possesses a larger unit cell volume (979.3 ų determined by XRD), slightly higher δ¹⁹F, and a slightly longer F–Si bond distance (1.79 Å) compared to the RTH-A phase (F–Si bond distance 1.77 Å, unit cell volume calculated by XRD 967.8 ų).

The energy difference between the RTH-A and RTH-B structures measured by calorimetry and between models 6 and 16-I obtained by theoretical calculations (see Table 2) is relatively small, explaining that both can coexist depending on the specific synthesis conditions. The formation of the RTH-A phase in the initial stages the zeolite crystallization may be linked to the relative orientation of P-OSDA⁺ cations and F⁻ anions, leading to coordination at one specific Si site. Shifting the position of F⁻ to a more stable location, and likely the reorientation of P-OSDA⁺ cations, requires overcoming an activation energy necessitating longer heating times during synthesis. The XRD data and NMR spectra of the samples synthesised at 150 °C, are consistent with the coexistence of phases A and B. However, it is not possible to ascertain whether this corresponds to a mixture of crystals of different phases, an intergrowth of phases A and B in the same crystals, or if F⁻ is randomly bonding to Si in the two sites (6 and 16-I).

Calorimetric and PXRD measurements reveal that both the RTH-A and RTH-B phases transform into a new one designated here as RTH-C at around 80 °C and 110 °C, respectively. The appearance of the RTH-C phase correlates with the disappearance of the doublet of the five-coordinate silicon species and modifications of the ¹⁹F signals in the NMR spectra. These results prove that in the RTH-C phase fluoride is highly mobile within the rth cage, practically detached from the silicon atoms. This explains that this phase is only observed at high temperature and that phases A and B are recovered by subsequent cooling. Nevertheless, our result indicate that a mixture of phases can be obtained upon heating-cooling the sample depending on the starting phase and the experimental conditions. This prove that there may be a transformation of one phase into another without the need of re-dissolving crystals, occurring in the solid state. Therefore, both thermodynamic and kinetic aspects must be taken into account for understanding the zeolite crystallization mechanism. The mechanism behind this phase transformation, accompanied by a significant change in the fluoride mobility, can be studied with ab initio molecular dynamics. Future work will aim at a detailed description of such dynamic behavior.

The results presented here provide evidence that the position of fluoride in the zeolite framework can be directed to different positions during the crystallization process. This concept can be extended to the crystallization of zeolites where negative charges are associated not with fluoride anions, but with substituting trivalent heteroatoms like aluminium or boron, ultimately influencing the catalytic behaviour of Al and B-containing zeolitic catalysts.

Author contributions

Conceptualization: T. B. and F. R. investigation: J. M.-O., R. M., J. S., M. H.-R., J.-A. V.-M., J. L. J., C. M.-C. and V. S.-K. supervision: M. B., T. B. and F. R. writing – original draft: J. M.-O. R. M., J. L. J., C. M.-C., M. B. writing – review and editing: J. M.-O., R. M., T. B., F. R. all authors revised the manuscript. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support by the Spanish Ministry of Science and Innovation by MCIN/AEI/10.13039/501100011033 and “ERDF A way of making Europe” (Projects: CEX2021-001230-S, PID2022-136934OB-I00, PID2020-112590GB-C21) is deeply acknowledged. The authors also thank the Spanish Ministry of Science and Innovation by MCIN/AEI/10.13039/501100011033 and “European Union Next Generation EU/PRTR” (Projects: TED2021-130191B-C41 and TED2021-130739B-I00), Generalitat Valenciana (Project: Prometeo 2021/077) and “Advanced Materials Programme” of Generalitat Valenciana “European Union Next Generation EU/PRTR” (project: MFA/2022/047). Financial support from the IR INFRANALYTICS FR2054 for conducting the research is gratefully acknowledged. J.M-O acknowledges the financial support from the European Union – NextGeneration EU through the Universitat Politècnica de València, Ministerio de Universidades, Plan de Recuperación, Transformación y Resiliencia for the Margarita Salas grant. The authors thankfully acknowledge the Red Española de Supercomputación (RES) and Servei d’Informàtica de la Universitat de València (SIUV) for computational resources and technical support. The authors acknowledge the Microscopy Service of the Universitat Politècnica de València for its assistance in microscopy characterization and beamline MSPD at synchrotron ALBA for beamtime allocation.

Notes and references

1. S. I. Zones and M. E. Davis, Zeolite materials: recent discoveries and future prospects, Curr. Opin. Solid State Mater. Sci., 1996, 1(1), 107–117.
2. M. E. Davis, Zeolites from a Materials Chemistry Perspective, Chem. Mater., 2014, 26(1), 239–245.
3. C. S. Cundy and P. A. Cox, The hydrothermal synthesis of zeolites: Precursors, intermediates and reaction mechanism, Microporous Mesoporous Mater., 2005, 82(1), 1–78.
4. L. Gómez-Hortigüela and M. A. Camblor, Introduction to the Zeolite Structure-Directing Phenomenon by Organic Species: General Aspects, Struct. Bonding, 2018, 176, 1–42.
5. M. Moliner, F. Rey and A. Corma, Towards the Rational Design of Efficient Organic Structure-Directing Agents for Zeolite Synthesis, Angew. Chem., Int. Ed., 2013, 52(52), 13880–13889.
6. J. Li, A. Corma and J. Yu, Synthesis of new zeolite structures, Chem. Soc. Rev., 2015, 44(20), 7112–7127.
7. A. W. Burton, S. I. Zones and S. Elomari, The chemistry of phase selectivity in the synthesis of high-silica zeolites, Curr. Opin. Colloid Interface Sci., 2005, 10(5), 211–219.
8. R. F. Lobo, S. I. Zones and M. E. Davis, Structure-direction in zeolite synthesis, J. Inclusion Phenom. Mol. Recognit. Chem., 1995, 21(1), 47–78.
9. C. Baerlocher and L. B. McCusker, Database of Zeolite Structures, http://www.iza-structure.org/databases/, (visited 15/11/2023).
10. B. Yilmaz and U. Müller, Catalytic Applications of Zeolites in Chemical Industry, Top. Catal., 2009, 52(6), 888–895.
11. B. Yilmaz, N. Trukhan and U. MÜLler, Industrial Outlook on Zeolites and Metal Organic Frameworks, Chin. J. Catal., 2012, 33(1), 3–10.
12. J. E. Naber, K. P. de Jong, W. H. J. Stork, H. P. C. E. Kuipers and M. F. M. Post, Industrial applications of zeolite catalysis, in Studies in Surface Science and Catalysis, ed. Weitkamp, J., Karge, H. G., Pfeifer, H. and Hölderich, W., Elsevier, 1994, vol. 84, pp. 2197–2219.
13. S. I. Zones, S.-J. Hwang, S. Elomari, I. Ogino, M. E. Davis and A. W. Burton, The fluoride-based route to all-silica molecular sieves, a strategy for synthesis of new materials based upon close-packing of guest–host products, C. R. Chim., 2005, 8(3), 267–282.
14. M. A. Camblor, L. A. Villaescusa and M. J. Díaz-Cabañas, Synthesis of all-silica and high-silica molecular sieves in fluoride media, Top. Catal., 1999, 9(1), 59–76.
15. J. Jiang, J. Yu and A. Corma, Extra-Large-Pore Zeolites: Bridging the Gap between Micro and Mesoporous Structures, Angew. Chem., Int. Ed., 2010, 49(18), 3120–3145.
16. D. E. Akporiaye, Towards a Rational Synthesis of Large-Pore Zeolite-Type Materials?, Angew. Chem., Int. Ed., 1998, 37(18), 2456–2457.
17. M. E. Davis, The Quest For Extra-Large Pore, Crystalline Molecular Sieves, Chem.–Eur. J., 1997, 3(11), 1745–1750.
18. M. Moliner, C. Martínez and A. Corma, Synthesis Strategies for Preparing Useful Small Pore Zeolites and Zeotypes for Gas Separations and Catalysis, Chem. Mater., 2014, 26(1), 246–258.
19. E. Pérez-Botella, S. Valencia and F. Rey, Zeolites in Adsorption Processes: State of the Art and Future Prospects, Chem. Rev., 2022, 122(24), 17647–17695.
20. F. Rey and J. Simancas, Beyond Nitrogen OSDAs, in Insights into the Chemistry of Organic Structure-Directing Agents in the Synthesis of Zeolitic Materials, ed. Gómez-Hortigüela, L., Springer International Publishing, Cham, Struct. Bonding 2018, vol. 175, pp. 103–138.
21. C. Pochen and N. J. Woodbury, Crystalline zeolite ZSM-11, US Pat., 3709979A, 1973.
22. J. B. Nagy, Z. Gabelica and E. G. Derouane, Position and configuration of the guest organic molecules within the framework of the ZSM-5 and ZSM-11 zeolites, Zeolites, 1983, 3(1), 43–49.
23. H. P. Rieck and H. J. Kalz, ‘Process for the Manufacture of Zeolites’, US Pat. 4528172A, 1985.
24. A. Tuel and Y. Ben Taârit, Synthesis, characterization, and catalytic properties of titanium silicates prepared using ions, Zeolites, 1993, 13(5), 357–364.
25. A. Tuel and Y. B. Taarit, Synthesis and characterization of titanium silicalite TS-1 prepared using phosphonium ions, Zeolites, 1994, 14(4), 272–281.
26. S. Sáez-Ferre, C. W. Lopes, J. Simancas, A. Vidal-Moya, T. Blasco, G. Agostini, G. Mínguez Espallargas, J. L. Jordá, F. Rey and P. Oña-Burgos, Use of Alkylarsonium Directing Agents for the Synthesis and Study of Zeolites, Chem.–Eur. J., 2019, 25(71), 16390–16396.
27. D. L. Dorset, K. G. Strohmaier, C. E. Kliewer, A. Corma, M. J. Díaz-Cabañas, F. Rey and C. J. Gilmore, Crystal Structure of ITQ-26, a 3D Framework with Extra-Large Pores, Chem. Mater., 2008, 20(16), 5325–5331.
28. D. L. Dorset, G. J. Kennedy, K. G. Strohmaier, M. J. Diaz-Cabañas, F. Rey and A. Corma, P-Derived Organic Cations as Structure-Directing Agents: Synthesis of a High-Silica Zeolite (ITQ-27) with a Two-Dimensional 12-Ring Channel System, J. Am. Chem. Soc., 2006, 128(27), 8862–8867.
29. A. Corma, M. J. Diaz-Cabanas, J. L. Jorda, F. Rey, G. Sastre and K. G. Strohmaier, A Zeolitic Structure (ITQ-34) with Connected 9- and 10-Ring Channels Obtained with Phosphonium Cations as Structure Directing Agents, J. Am. Chem. Soc., 2008, 130(49), 16482–16483.
30. R. Simancas, D. Dari, N. Velamazán, M. T. Navarro, A. Cantín, J. L. Jordá, G. Sastre, A. Corma and F. Rey, Modular Organic Structure-Directing Agents for the Synthesis of Zeolites, Science, 2010, 330(6008), 1219.
31. R. Simancas, J. L. Jordá, F. Rey, A. Corma, A. Cantín, I. Peral and C. Popescu, A New Microporous Zeolitic Silicoborate (ITQ-52) with Interconnected Small and Medium Pores, J. Am. Chem. Soc., 2014, 136(9), 3342–3345.
32. R. Simancas, T. Nishitoba, S. Park, J. N. Kondo, F. Rey, H. Gies and T. Yokoi, Versatile phosphorus-structure-directing agent for direct preparation of novel metallosilicate zeolites with IFW-topology, Microporous Mesoporous Mater., 2021, 317, 111005.
33. Y. Yun, M. Hernández, W. Wan, X. Zou, J. L. Jordá, A. Cantín, F. Rey and A. Corma, The first zeolite with a tri-directional extra-large 14-ring pore system derived using a phosphonium-based organic molecule, Chem. Commun., 2015, 51(36), 7602–7605.
34. J. Simancas, R. Simancas, P. J. Bereciartua, J. L. Jorda, F. Rey, A. Corma, S. Nicolopoulos, P. Pratim Das, M. Gemmi and E. Mugnaioli, Ultrafast Electron Diffraction Tomography for Structure Determination of the New Zeolite ITQ-58, J. Am. Chem. Soc., 2016, 138(32), 10116–10119.
35. Q.-F. Lin, Z. R. Gao, C. Lin, S. Zhang, J. Chen, Z. Li, X. Liu, W. Fan, J. Li, X. Chen, M. A. Camblor and F.-J. Chen, A stable aluminosilicate zeolite with intersecting three-dimensional extra-large pores, Science, 2021, 374(6575), 1605–1608.
36. J. Li, Z. R. Gao, Q.-F. Lin, C. Liu, F. Gao, C. Lin, S. Zhang, H. Deng, A. Mayoral, W. Fan, S. Luo, X. Chen, H. He, M. A. Camblor, F.-J. Chen and J. Yu, A 3D extra-large-pore zeolite enabled by 1D-to-3D topotactic condensation of a chain silicate, Science, 2023, 379(6629), 283–287.
37. P. Caullet, J.-L. Paillaud, A. Simon-Masseron, M. Soulard and J. Patarin, The fluoride route: a strategy to crystalline porous materials, C. R. Chim., 2005, 8(3), 245–266.
38. S. Leon and G. Sastre, Zeolite Phase Selectivity Using the Same Organic Structure-Directing Agent in Fluoride and Hydroxide Media, J. Phys. Chem. C, 2022, 126(4), 2078–2087.
39. C. A. Fyfe, A. R. Lewis, J. M. Chézeau and H. Grondey, 19F/29Si Distance Determinations in Fluoride-Containing Octadecasil from Solid-State NMR Measurements, J. Am. Chem. Soc., 1997, 119(50), 12210–12222.
40. T. Blasco, A. Corma, M. J. Díaz-Cabañas, F. Rey, J. A. Vidal-Moya and C. M. Zicovich-Wilson, Preferential Location of Ge in the Double Four-Membered Ring Units of ITQ-7 Zeolite, J. Phys. Chem. B, 2002, 106(10), 2634–2642.
41. L. Mafra, J. A. Vidal-Moya and T. Blasco, Chapter Four – Structural Characterization of Zeolites by Advanced Solid State NMR Spectroscopic Methods, in Annual Reports on NMR Spectroscopy, ed. Webb, G. A., Academic Press: 2012, vol. 77, pp. 259–351.
42. J. A. Vidal-Moya, T. Blasco, F. Rey, A. Corma and M. Puche, Distribution of Fluorine and Germanium in a New Zeolite Structure ITQ-13 Studied by 19F Nuclear Magnetic Resonance, Chem. Mater., 2003, 15(21), 3961–3963.
43. P. Lu, L. Gómez-Hortigüela and M. A. Camblor, Synthesis of Pure Silica MWW Zeolite in Fluoride Medium by Using an Imidazolium-Based Long Dication, Chem.–Eur. J., 2019, 25(6), 1561–1572.
44. A. Pulido, G. Sastre and A. Corma, Computational Study of 19F NMR Spectra of Double Four Ring-Containing Si/Ge-Zeolites, ChemPhysChem, 2006, 7(5), 1092–1099.
45. H. Koller, A. Wölker, H. Eckert, C. Panz and P. Behrens, Five-Coordinate Silicon in Zeolites: Probing SiO4/2F− Sites in Nonasil and ZSM-5 with 29Si Solid-State NMR Spectroscopy, Angew. Chem., Int. Ed. Engl., 1997, 36(24), 2823–2825.
46. H. Koller, A. Wölker, L. A. Villaescusa, M. J. Díaz-Cabañas, S. Valencia and M. A. Camblor, Five-Coordinate Silicon in High-Silica Zeolites, J. Am. Chem. Soc., 1999, 121(14), 3368–3376.
47. C. A. Fyfe, D. H. Brouwer, A. R. Lewis and J.-M. Chézeau, Location of the Fluoride Ion in Tetrapropylammonium Fluoride Silicalite-1 Determined by 1H/19F/29Si Triple Resonance CP, REDOR, and TEDOR NMR Experiments, J. Am. Chem. Soc., 2001, 123(28), 6882–6891.
48. C. A. Fyfe, D. H. Brouwer, A. R. Lewis, L. A. Villaescusa and R. E. Morris, Combined Solid State NMR and X-ray Diffraction Investigation of the Local Structure of the Five-Coordinate Silicon in Fluoride-Containing As-Synthesized STF Zeolite, J. Am. Chem. Soc., 2002, 124(26), 7770–7778.
49. S. L. Brace, P. Wormald and R. J. Darton, The effect of structure directing agents on the ordering of fluoride ions in pure silica MFI zeolites, Phys. Chem. Chem. Phys., 2015, 17(18), 11950–11953.
50. D. S. Wragg, R. E. Morris and A. W. Burton, Pure Silica Zeolite-type Frameworks: A Structural Analysis, Chem. Mater., 2008, 20(4), 1561–1570.
51. M. Arranz, J. Pérez-Pariente, P. A. Wright, A. M. Z. Slawin, T. Blasco, L. Gómez-Hortigüela and F. Corà, Cooperative Structure-Directing Effect of Fluorine-Containing Organic Molecules and Fluoride Anions in the Synthesis of Zeolites, Chem. Mater., 2005, 17(17), 4374–4385.
52. G. Fu, E. Dib, Q. Lang, H. Zhao, S. Wang, R. Ding, X. Yang and V. Valtchev, Acidic medium synthesis of zeolites – an avenue to control the structure-directing power of organic templates, Dalton Trans., 2022, 51(30), 11499–11506.
53. L. A. Villaescusa, P. S. Wheatley, I. Bull, P. Lightfoot and R. E. Morris, The Location and Ordering of Fluoride Ions in Pure Silica Zeolites with Framework Types IFR and STF; Implications for the Mechanism of Zeolite Synthesis in Fluoride Media, J. Am. Chem. Soc., 2001, 123(36), 8797–8805.
54. M. A. Camblor, M.-J. Díaz-Cabañas, J. Perez-Pariente, S. J. Teat, W. Clegg, I. J. Shannon, P. Lightfoot, P. A. Wright and R. E. Morris, SSZ-23: An Odd Zeolite with Pore Openings of Seven and Nine Tetrahedral Atoms, Angew. Chem., Int. Ed., 1998, 37(15), 2122–2126.
55. M. Fabbiani, S. Al-Nahari, L. Piveteau, E. Dib, V. Veremeienko, A. Gaje, D. G. Dumitrescu, P. Gaveau, T. Mineva, D. Massiot, A. van der Lee, J. Haines and B. Alonso, Host–Guest Silicalite-1 Zeolites: Correlated Disorder and Phase Transition Inhibition by a Small Guest Modification, Chem. Mater., 2022, 34(1), 366–387.
56. M. Fischer, Fluoride Anions in All-Silica Zeolites: Studying Preferred Fluoride Sites and Dynamic Disorder with Density Functional Theory Calculations, J. Phys. Chem. C, 2021, 125(16), 8825–8839.
57. M. Fischer, Influence of Organic Structure-Directing Agents on Fluoride Dynamics in As-Synthesized Silicalite-1, J. Phys. Chem. C, 2020, 124(10), 5690–5701.
58. J. Dědeček, E. Tabor and S. Sklenak, Tuning the Aluminum Distribution in Zeolites to Increase their Performance in Acid-Catalyzed Reactions, ChemSusChem, 2019, 12(3), 556–576.
59. S. H. Krishna, A. Goswami, Y. Wang, C. B. Jones, D. P. Dean, J. T. Miller, W. F. Schneider and R. Gounder, Influence of framework Al density in chabazite zeolites on copper ion mobility and reactivity during NOx selective catalytic reduction with NH3, Nat. Catal., 2023, 6(3), 276–285.
60. C. Martínez and A. Corma, Inorganic molecular sieves: Preparation, modification and industrial application in catalytic processes, Coord. Chem. Rev., 2011, 255(13), 1558–1580.
61. S. Al-Nahari, E. Dib, C. Cammarano, E. Saint-Germes, D. Massiot, V. Sarou-Kanian and B. Alonso, Impact of Mineralizing Agents on Aluminum Distribution and Acidity of ZSM-5 Zeolites, Angew. Chem., Int. Ed., 2023, 62(7), e202217992.
62. T. Yokoi, M. Yoshioka, H. Imai and T. Tatsumi, Diversification of RTH-Type Zeolite and Its Catalytic Application, Angew. Chem., Int. Ed., 2009, 48(52), 9884–9887.
63. Ch. Li, C. Paris, J. Martínez-Triguero, M. Boronat, M. Moliner and A. Corma, Synthesis of reaction-adapted zeolites as methanol-to-olefins catalysts with mimics of reaction intermediates as organic structure-directing agents, Nat. Catal., 2018, 1, 547–554.
64. L. Zhang, S. Wang, D. Shi, Z. Qin, P. Wang, G. Wang, J. Li, M. Dong, W. Fan and J. Wang, Methanol to olefins over H-RUB-13 zeolite: regulation of framework aluminum siting and acid density and their relationship to the catalytic performance, Catal. Sci. Technol., 2020, 10, 1835–1847.
65. J. Trebosc, B. Hu, J. P. Amoureux and Z. Gan, Through-space R3-HETCOR experiments between spin-1/2 and half-integer quadrupolar nuclei in solid-state NMR, J. Magn. Reson., 2007, 186(2), 220–227.
66. Z. Gan, 13C/14N heteronuclear multiple-quantum correlation with rotary resonance and REDOR dipolar recoupling, J. Magn. Reson., 2007, 184(1), 39–43.
67. M. Feike, D. E. Demco, R. Graf, J. Gottwald, S. Hafner and H. W. Spiess, Broadband Multiple-Quantum NMR Spectroscopy, J. Magn. Reson., Ser. A, 1996, 122(2), 214–221.
68. D. J. States, R. A. Haberkorn and D. J. Ruben, A two-dimensional nuclear overhauser experiment with pure absorption phase in four quadrants, J. Magn. Reson., 1982, 48(2), 286–292.
69. D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Modelling one- and two-dimensional solid-state NMR spectra, Magn. Reson. Chem., 2002, 40(1), 70–76.
70. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186.
71. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244–13249.
72. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671–6687.
73. J. P. Perdew, S. Kurth and M. Seidl, Exploring The Adiabatic Connection Between Weak- And Strong-Interaction Limits In Density Functional Theory, Int. J. Mod. Phys. B, 2001, 15(10n11), 1672–1683.
74. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
75. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
76. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799.
77. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
78. L. Goerigk and S. Grimme, A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions, Phys. Chem. Chem. Phys., 2011, 13(14), 6670–6688.
79. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465.
80. R. Laskowski, P. Blaha and F. Tran, Assessment of DFT functionals with NMR chemical shifts, Phys. Rev. B, 2013, 87, 195130.
81. R. Laskowski and P. Blaha, Origin of NMR shielding in fluorides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245117.
82. F. Tran and P. Blaha, Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential, Phys. Rev. Lett., 2009, 102(22), 22641.
83. A. Palčić, S. Moldovan, H. El Siblani, A. Vicente and V. Valtchev, Defect Sites in Zeolites: Origin and Healing, Adv. Sci., 2022, 9(4), 2104414.
84. H. Koller, R. F. Lobo, S. L. Burkett and M. E. Davis, SiO-···HOSi Hydrogen Bonds in As-Synthesized High-Silica Zeolites, J. Phys. Chem., 1995, 99(33), 12588–12596.
85. D. M. Dawson, R. F. Moran and S. E. Ashbrook, An NMR Crystallographic Investigation of the Relationships between the Crystal Structure and 29Si Isotropic Chemical Shift in Silica Zeolites, J. Phys. Chem. C, 2017, 121(28), 15198–15210.

---

Footnotes

† Electronic supplementary information (ESI) available: Details on the preparation of triisopropyl(methyl)phosphonium, additional ss-NMR spectra of the RTH-type zeolites; description of the procedure to build the structural models, the calculated ²⁹Si NMR chemical shielding and the comparison with the experimental chemical shifts; comparison of the unit cell parameters. See DOI: https://doi.org/10.1039/d3ta06071c

‡ Joaquín Martinez-Ortigosa and Reisel Millán contributed equally to this work.

§ Present address of Joaquín Martínez-Ortigosa: Laboratorio de Nanotecnología Molecular, Departamento de Química Inorgánica, Universidad de Alicante, Alicante, Spain.

¶ Present address of Jorge Simancas Coloma: Instituto de Materiales Avanzados, Universitat Jaume I, Castelló de la Plana, Castellón, Spain.

---