Open Access Article
Open Access ArticleAn active learning approach to model solid-electrolyte interphase formation in Li-ion batteries†
Mohammad
Soleymanibrojeni
 ,
Celso Ricardo
Caldeira Rego
,
Celso Ricardo
Caldeira Rego
 ,
Meysam
Esmaeilpour
,
Meysam
Esmaeilpour
 and
Wolfgang
Wenzel
and
Wolfgang
Wenzel
 *
*
Institute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: wolfgang.wenzel@kit.edu
First published on 19th December 2023
Abstract
Li-ion batteries store electrical energy by electrochemically reducing Li ions from a liquid electrolyte in a graphitic electrode. During these reactions, electrolytic species in contact with the electrode particles form a solid-electrolyte interphase (SEI), a layer between the electrode and electrolyte. This interphase allows the exchange of Li ions between the electrode and electrolyte while blocking electron transfer, affecting the performance and life of the battery. A network of reactions in a small region determines the final structure of this interphase. This complex problem has been studied using different multi-scale computational approaches. However, it is challenging to obtain a comprehensive characterization of these models in connection with the effects of model parameters on the output, due to the computational costs. In this work, we propose an active learning workflow coupled with a kinetic Monte Carlo (kMC) model for formation of a SEI as a function of reaction barriers including electrochemical, diffusion, and aggregation reactions. This workflow begins by receiving an initial database from a design-of-experiment approach to train an initial Gaussian process classification model. By iterative training of this model in the proposed workflow, we gradually extended the model's validity over a larger subset of reaction barriers. In this workflow, we took advantage of statistical tools to reduce the uncertainty of the model. The trained model is used to study the features of the reaction barriers in the formation of a SEI, which allows us to obtain a new and unique perspective on the reactions that control the formation of a SEI.
1 Introduction
Li-ion batteries are electrochemical devices that store electrical energy during charging and release that energy during discharge. Such a battery has three main components: the anode, cathode, and electrolyte. The anode is the host of Li in the charged state, while the cathode is the host in the discharged state. The electrodes comprise active electrode particles, graphite for the anode, metal oxide for the cathode, binders, and current collectors. The electrolyte is the carrier of Li ions between the anode and cathode.1 Most commercial Li-ion batteries are based on liquid electrolytes due to their high ionic conductivity and ability to wet the active electrode particles. Liquid electrolytes enhance the kinetics of Li-ion exchange in the bulk and at the interface, making higher charging rates possible. At the same time, parasitic reactions that deviate from the desired Li-ion exchange mechanism lead to capacity loss and a reduction in battery life. In previous studies, it has been suggested that the formation of a SEI can have a deterministic role in controlling these unwanted reactions.2–4 During the charging half-cycle, the reduced voltage at the anode causes the electrolyte to decompose into species that aggregate and cover the surface of the electrode. As a result, a SEI layer is formed on the surface of the graphitic electrode particles. This interphase is electronically insulating while being permeable to Li ions. A considerable amount of active Li and electrolyte components are consumed during the formation of the SEI. On the other hand, this interphase protects the electrode since it blocks electron conduction from the electrode to the electrolytic species.5 Previous fundamental studies proposed networks of reactions for the formation of a SEI layer.6–9 These networks suggest that the electrolytic compounds are reduced at the electrode surface and then return to the electrolyte, where they can participate in different pathways such as reactions with solvated Li, secondary reduction, and dimerization of organic compounds.10 The formation of a SEI is a local and rapid process, and reaction rates can affect the final configuration of the SEI. The reactions such as the diffusion of species and those of aggregation or dimerization of the products play a crucial role in the SEI formation mechanism. Kinetic Monte Carlo (kMC) is a technique that enables modeling the formation of inorganic and organic SEIs based on predefined reaction networks.11,12 In the kMC model, electrochemical reactions, diffusion, and species aggregation are modeled as individual reactions with independent rates. The kMC model requires reaction barriers, where a low barrier results in a higher rate or priority for a reaction, and a higher barrier results in a lower rate or priority.13 The reaction products of the SEI formation mechanism can be mainly categorized into inorganic compounds such as Li2CO3, and organic compounds such as solvated Li+ with ring-opened ethylene carbonate (Li+·oEC) and lithium ethylene dicarbonate (Li2EDC) based products.14 Four possible outcomes can be considered based on a given SEI reaction network. These include an empty output, where no SEI species are produced or left in the simulation box, production of intermediate products (Li+·oEC, Li2EDC, and dimerized Li2EDC) without obtaining final SEI products, production of a mostly inorganic SEI, and production of a mostly organic SEI. In addition to the complexities related to the modeling of the formation of a SEI, there exists the issue of handling the large amount of data related to the models with multiple parameters. These large datasets can be seen in two aspects: exploring the model input parameters, and processing the model outputs. In this regard, machine learning techniques can be utilized. The active learning frameworks have been applied in various studies such as reaction networks,15 finding free energies in chemical compounds,16 and in Li-ion batteries to develop inter-atomic force fields.17 In this work, we developed an active learning workflow. We use a kMC model developed in our work group,18 which offers a unique way to model the formation of a SEI, based on the fundamental electrochemical, aggregation, and diffusion reactions. The kMC models generically belong to a group of coarse-grained models based on reaction barriers of a reaction network.11 The model therefore is rooted in the most basic description of that system, where each parameter (reaction barrier) is essential for determining the model output. In our previous work18 we investigated a mesoscale model for the formation of the SEI in liquid electrolyte batteries. We used a kMC protocol based on a series of chemical reactions identified in the literature as the primary mechanism for the formation of the inorganic and organic components of the SEI. The reaction barrier values and their ranges were determined through a dual approach involving first principles calculations and the available data from the literature, as explained in detail in the ESI† of the publication of our kMC program.18 After some approximations, such as the discretization of space, the selection of dimensionality of the model, and the handling of diffusion versus reaction events, to name a few crucial parameters, the model is computationally feasible. Consequently, rates derived from electronic structure calculations for individual reactions cannot be directly transferred into the kMC model. The reactions of the model are summarized in Table 1. In this study, we examined a subset of the chemical reaction barrier space spanned by the relevant reactions we have considered. Using a design-of-experiments strategy, we were able to generate an initial dataset of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories for different combinations of reaction rates, of which more than half resulted in the growth of some appreciable volume fraction of inorganic and organic SEIs. Given that it is difficult to transfer the rates from first-principles calculations directly and considering that these calculations also require additional approximations, for instance, regarding the homogeneity of the environment for a specific reaction, we aim to investigate which of these reactions is the most important one in observing a particular outcome. We used this initial trajectory to create an initial training dataset for training a Gaussian process classification model. The model learns the relation between reaction barriers and the output of the kMC model. The active learning workflow is implemented to identify uncertainty regions within the reaction barrier space. This approach significantly reduces the effort compared with an exploration of parameter space where each set of barriers is independently sampled. This is accomplished by testing the model with a new sample dataset at the end of each training cycle, and determining the uncertainty of the model about these sampled points. New calculations with the kMC model are performed in these regions and these model outputs were added to the training dataset in the next cycle. By adding new results to the previous dataset, we trained a new model with updated certainty and uncertainty until we reached a representative model with a reliable understanding of the relationship between the reaction barriers and the output of the kMC model. The representative model enabled us to determine which model parameters have more deterministic effects on formation of a SEI. Moreover, this information allows us to use the kMC model in the framework of the multiscale modeling approach, which requires embedding of the lower scale model in the larger scale models, taking into account different considerations such as finding the regions of validity, calibration, and scale matching of the parameters of the two models.19,20 In the following Section 2, we present our methodology including preprocessing of data, training of the model, and performing the active learning cycles, followed by results and discussion in Section 3, which includes the discussions on the model error in active learning cycles. We conclude with the discussion on the effects of reaction barriers on the formation of a SEI based on the kMC model.
000 trajectories for different combinations of reaction rates, of which more than half resulted in the growth of some appreciable volume fraction of inorganic and organic SEIs. Given that it is difficult to transfer the rates from first-principles calculations directly and considering that these calculations also require additional approximations, for instance, regarding the homogeneity of the environment for a specific reaction, we aim to investigate which of these reactions is the most important one in observing a particular outcome. We used this initial trajectory to create an initial training dataset for training a Gaussian process classification model. The model learns the relation between reaction barriers and the output of the kMC model. The active learning workflow is implemented to identify uncertainty regions within the reaction barrier space. This approach significantly reduces the effort compared with an exploration of parameter space where each set of barriers is independently sampled. This is accomplished by testing the model with a new sample dataset at the end of each training cycle, and determining the uncertainty of the model about these sampled points. New calculations with the kMC model are performed in these regions and these model outputs were added to the training dataset in the next cycle. By adding new results to the previous dataset, we trained a new model with updated certainty and uncertainty until we reached a representative model with a reliable understanding of the relationship between the reaction barriers and the output of the kMC model. The representative model enabled us to determine which model parameters have more deterministic effects on formation of a SEI. Moreover, this information allows us to use the kMC model in the framework of the multiscale modeling approach, which requires embedding of the lower scale model in the larger scale models, taking into account different considerations such as finding the regions of validity, calibration, and scale matching of the parameters of the two models.19,20 In the following Section 2, we present our methodology including preprocessing of data, training of the model, and performing the active learning cycles, followed by results and discussion in Section 3, which includes the discussions on the model error in active learning cycles. We conclude with the discussion on the effects of reaction barriers on the formation of a SEI based on the kMC model.
| No. | Reactants/event | Product(s) | Barrier range [eV] | Rep. color |
|---|---|---|---|---|
| 1 | Electrode surface + Li+/EC− | Li+·oEC− | 0.28–0.50 | Green |
| 2 | Electrode surface + Li+·oEC− + Li+ | Li2CO3 + C2H4 ↑ | 0.27–0.47 | Red |
| 3 | Li2CO3 surface + Li+/EC− | Li+·oEC− | 0.31–0.55 | Green |
| 4 | Li+·oEC− + Li+·oEC− | Li2EDC | 0.30–0.53 | Orange |
| 5 | Li2EDC + Li2EDC | (Li2EDC)2 | 0.55–0.97 | Blue |
| 6 | (Li2EDC)2 + Li2EDC | Organic SEI | 0.47–0.83 | Magenta |
| 7 | Li2CO3 surface + Li+·oEC− + Li+ | Li2CO3 | 0.49–0.88 | Red |
| 8 | Li2EDC + organic SEI | Organic SEI | 0.46–0.81 | Magenta |
| 9 | (Li2EDC)2 + organic SEI | Organic SEI | 0.46–0.81 | Magenta |
| 10 | (Li2EDC)2 + (Li2EDC)2 | Organic SEI | 0.46–0.81 | Magenta |
| 11 | Organic SEI + organic SEI | Organic SEI | 0.46–0.82 | Magenta |
| 12 | Diffusion of (Li2EDC)2 | — | 0.40–0.70 | — |
| 13 | Diffusion of Li2EDC | — | 0.35–0.61 | — |
| 14 | Diffusion of C2H4OCOOLi | — | 0.35–0.62 | — |
| 15 | Diffusion of an organic SEI | — | 0.38–0.68 | — |
| 16 | Li+·oEC− going out of the box | — | 0.01 | — |
| 17 | (Li2EDC)2 going out of the box | — | 0.01 | — |
| 18 | Organic SEI going out of the box | — | 0.01 | — |
| 19 | Li2EDC going out of the box | — | 0.01 | — |
2 Theoretical approach and computational details
2.1 Descriptor and dimensionality reduction
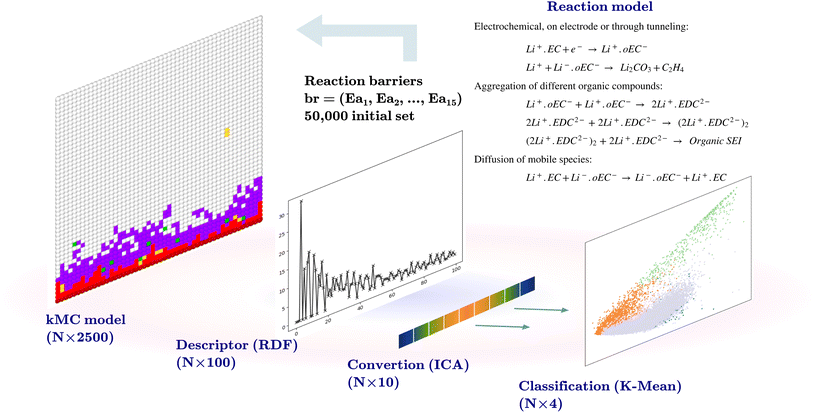
The initial dataset comprises the output of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 two-dimensional kMC calculations of size 50 × 50 nm2, with the position and the type of species, such that the coordinates of each pixel represent 1 nm2. Each kMC simulation receives 15 reaction barriers as its parameters, as shown in Table 1, and returns an output with the species type and their coordinates. A descriptor transforms the model output. The descriptor used for this purpose bins the radial distances from the center of the electrode at coordinate (0, 25) to a radius of 25 nm at 0.25 nm steps (100 indices) and counts the SEI species (Li+·oEC−, Li2CO3, and Li2EDC, and dimerizations of Li2EDC) at each bin and normalizes this number. An independent component analysis (ICA)21 is performed on this set of 100-dimensional vectors to reduce the dimensionality to 10. The ICA is performed using the FastICA algorithm.22 The ICA deals with the process of decomposing an observed variable Xn into a matrix product of As, where An×m is the unknown mixing matrix and sm is the independent component of a non-Gaussian distribution with a reduced dimension to m. The output of this section is a dataset of size (50
000 two-dimensional kMC calculations of size 50 × 50 nm2, with the position and the type of species, such that the coordinates of each pixel represent 1 nm2. Each kMC simulation receives 15 reaction barriers as its parameters, as shown in Table 1, and returns an output with the species type and their coordinates. A descriptor transforms the model output. The descriptor used for this purpose bins the radial distances from the center of the electrode at coordinate (0, 25) to a radius of 25 nm at 0.25 nm steps (100 indices) and counts the SEI species (Li+·oEC−, Li2CO3, and Li2EDC, and dimerizations of Li2EDC) at each bin and normalizes this number. An independent component analysis (ICA)21 is performed on this set of 100-dimensional vectors to reduce the dimensionality to 10. The ICA is performed using the FastICA algorithm.22 The ICA deals with the process of decomposing an observed variable Xn into a matrix product of As, where An×m is the unknown mixing matrix and sm is the independent component of a non-Gaussian distribution with a reduced dimension to m. The output of this section is a dataset of size (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × 10) and a trained FastICA model for the transformation of the kMC outputs in the following steps.
000 × 10) and a trained FastICA model for the transformation of the kMC outputs in the following steps.
2.2 Classification and labeling of data
K-Mean clustering21 is performed on the output of ICA. Four K-mean clusters consisting of class empty, class unfinished, class organic SEI, and class inorganic SEI were identified. In class empty, the reactions yield only a layer of an inorganic SEI. In class unfinished, reduced intermediate species are formed, without the formation of an organic or inorganic SEI. Class inorganic reactions mostly yield an inorganic SEI. Class organic represents the model output, which is mostly an organic SEI. At this step, the membership of each data point is determined using a closeness Euclidean distance metric, such that eqn (1) is minimized by adjusting the position of the centroids of the C classes, μ, relative to the N transformed data points obtained in Section 2.1,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , and assigning each data point i to a cluster k using the indicator function
, and assigning each data point i to a cluster k using the indicator function 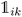 .
.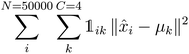 | (1) |
The clustering starts with a 1000 initial random guess for the location of centroids, and the final result is the lowest squared sum of the distances of the points from their assigned cluster. The output of this step is a set of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 labeled data, cluster centroids, and a K-mean model for labeling the future kMC outputs.
000 labeled data, cluster centroids, and a K-mean model for labeling the future kMC outputs.
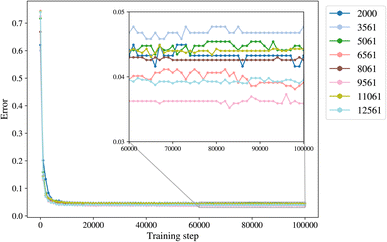
2.3 Input data trimming and training sets
The trimming aims to determine the size of the smallest dataset that we can use for training a model with the lowest error. The trimming of the initial dataset was performed based on the cut-off distance of a data point of each label from its cluster centroid so that in each class there is a maximum number of 500 to 4000 points, with increments of 500. The trimmed datasets are of size 2000, 3561, 5061, 6561, 8061, 9561, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061, and 12
061, and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561. The class empty is the smallest class with 561 members, and it is not trimmed for datasets larger than 2000.
561. The class empty is the smallest class with 561 members, and it is not trimmed for datasets larger than 2000.
2.4 Multi-class Gaussian process classification model and variational inference
We trained a Gaussian process classification model23 to classify the aforementioned four classes: inorganic SEI, organic SEI, unfinished, and empty. In this 4-class classification problem, there is a vector of latent parameters f associated with each class such that f = [f1, f2, f3, f4]⊤. A Dirichlet sample can present an observation of each class label (ESI eqn (1) and (2)†). The classification with the Gaussian process model at the test point x* finds a class label (distribution) given a training dataset (X: reaction barrier dataset, and ỹ: class labels), which is done first by finding the distribution of the latent parameters at the test set, as shown in eqn (2).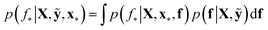 | (2) |
The term p(f|X,ỹ) is defined as inference over f. There are approximate methods to handle the determination of posteriors that are analytically intractable or expensive due to the involvement of non-Gaussian likelihoods or the inversion of large matrices. Variational inference is a method of approximate Bayesian inference. In this method, the inducing random variable u and inducing points Z, u = f(Z) are introduced, and the inference over f is approximated by using a distribution q(u).24 The distribution of the inducing points is optimized during the training of the model so that the approximate posterior, q(u), becomes close to the true posterior, p(f|X,ỹ). This closeness is determined by using Kullback–Leibler divergence.25 In the optimization of this divergence, the evidence p(ỹ|X) finds a lower bound. The prediction using approximate variational inference is defined according to eqn (3), and the actual class label obtained from 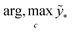 .26
.26
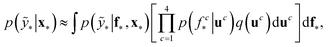 | (3) |
The probability of the observation of the corresponding distribution of classes is defined in eqn (4).
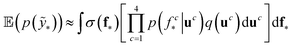 | (4) |
In this work, we used the VariationsStrategy class from the gpytorch package for creating and training the model and an anisotropic radial basis function kernel with a diagonal length scale matrix of Λ, eqn (5), which finds the relationships between the 15 input features (reaction barriers), x and x′, for each of the four classes, a total of 60 length scales.
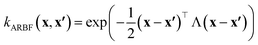 | (5) |
The DirichletClassificationLikelihood with heteroscedastic noise and α∈ = 10−2, loss function by the VariationalELBO class from gpytorch, and the Adam optimizer of the pytorch package with a learning rate of 10−3 were used. At each cycle, the dataset was divided into 30% test and 70% training sets. The inducing points were equally distributed (by class) and randomly selected from 5% of the training set. The location of the inducing points is also optimized. The optimization was carried out in 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. The output of this section is a trained model based on the training dataset and inducing points corresponding to the 5% of that training dataset.
000 steps. The output of this section is a trained model based on the training dataset and inducing points corresponding to the 5% of that training dataset.
2.5 Noise and error handling
The sources of noise and error in this study can be categorized into two main parts: (i) the noise from the kMC program and (ii) the noise from the classification. The kMC program can be seen as a function that maps a vector of reaction barriers to a model output of size 2500, where each pixel has a value representing one of the reaction species. The model output can vary by repeating the same kMC program with the same reaction barriers. Therefore, for every input there is a mean and a variance of observed outputs, e.g., the amount of inorganic or organic SEI. Based on the model results, the largest variance is realized when the reaction barriers create competitive reactions, especially in the cases where a certain amount of inorganic SEI has been produced, and then the competitive conversion of Li+·oEC− into Li2CO3 or Li2EDC determines the final reaction yield. In this special case, two class labels can be valid for one set of reaction barriers. The goal of using a dimensionality reduction and classification schema is that instead of finding a relationship between the reaction barriers and the amount of inorganic and organic SEI, we find its relationship to a class of the produced SEI so that the noises and variance of the model outputs are smoothed out. The labeling error of the kMC outputs also needs attention. The labeling is determined based on the distance of the transformed model output from the closest class centroid. If the transformed kMC output falls in a region where it is close to multiple centroids, we could receive a falsely labeled input. To address this issue, we only accept a labeled output that is meaningfully close to a centroid by requiring the difference of the distance to the second closest centroid (B), and the mean of all distances (CM) should be smaller than 1.2 times the distance to the nearest centroid (A), eqn (6).| ∣B-CM∣ < 1.2 A | (6) |
2.6 Sampling of the parameter space
We used principal component analysis21 with a polynomial kernel of degree d = 15 and 15 components to store the positional information about the points from the parameter space. The kernel principal component analysis (PCA) is trained to perform the inverse transformation. The polynomial kernel of this PCA is according to eqn (7).| kpca(X,X) = (γXX⊤ + C0)d | (7) |
2.7 Selection of informative data points
The new samples and their distance relationship with the trimmed dataset are used to make predictions using the trained model. The model calculates the probability of membership in each class. In cases where the model cannot determine the membership of a data point, it assigns a 25% chance for each class. The prediction score is evaluated by calculating the squared sum of the class membership probabilities. The lowest certainty (Pc = 0.25) corresponds to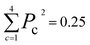 , and the maximum is 1. To consider a prediction uncertain, we have set a threshold of 0.40 for this measure. The higher the threshold, the more data must be sent for direct query with kMC. The output of this section is an uncertain dataset of variable size to be queried directly with the kMC program.
, and the maximum is 1. To consider a prediction uncertain, we have set a threshold of 0.40 for this measure. The higher the threshold, the more data must be sent for direct query with kMC. The output of this section is an uncertain dataset of variable size to be queried directly with the kMC program.
2.8 Query with the kMC program
The samples from the uncertain dataset (based on our defined threshold) are sent for direct query with the kMC program for 1800 seconds. At each cycle 50 direct queries were performed. This number controls the amount of new data points added to the training data set at each cycle. The output of the kMC model for each data point is transformed, as shown in Section 2.1, and then it is converted using the ICA model. Finally, the K-mean model labels the data point. The output of this section is a labeled dataset.2.9 Detecting the outliers
After query with kMC as shown in Section 2.8 the outliers of the datasets are detected. Sampling the 15-dimensional reaction barrier space does not mean every combination of barriers can lead to a realistic SEI reaction model. This is decided by the time the kMC algorithm returns based on the input reaction barrier set. This means a set of reaction barriers that leads to a very short or long kMC time is assigned as an outlier reaction barrier set. For this purpose, we set 1 microsecond as the lower limit and 2 seconds as the upper limit. This labeled dataset is added to the previous dataset to train a new model. This step, along with the steps mentioned in Sections 2.1, 2.2, and 2.5 constitutes our unsupervised labeling framework.2.10 Active learning workflow
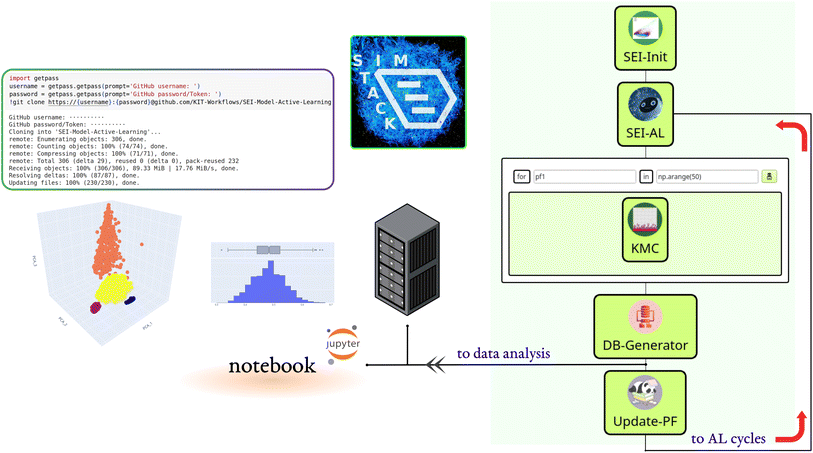
We built the active learning workflow within SimStack. This robust workflow framework ensures simulation protocol automation, reproducibility, and transferability.28,29 It also simplifies the creation of custom-tailored simulation protocols using various computer simulation approaches. As shown in Fig. 1, this workflow is made up of five Workflow Active Nodes (WaNos) SEI-Init, SEI-AL, KMC, DB-Generator and Update-PF,30 which automate the execution of the tasks.The SEI-Init WaNo reads a Pickle-file containing a collection of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kMC outputs after applying the descriptor (2.1), and a Json-file of their relevant reaction barriers. After the data processing step described in Sections 2.1, 2.2, and 2.3, the Tdata.json file is sent to the SEI-AL Wano. In the SEI-AL WaNo, the active learning cycle, including training the model, sampling the reaction barrier space, and selecting the informative data points, as described in Sections 2.4, 2.6, and 2.7 is performed. This WaNo generates the models and the data (PF.json) and is also responsible for creating a list of data points for a direct query with the kMC program in the KMC WaNo, 2.8.
000 kMC outputs after applying the descriptor (2.1), and a Json-file of their relevant reaction barriers. After the data processing step described in Sections 2.1, 2.2, and 2.3, the Tdata.json file is sent to the SEI-AL Wano. In the SEI-AL WaNo, the active learning cycle, including training the model, sampling the reaction barrier space, and selecting the informative data points, as described in Sections 2.4, 2.6, and 2.7 is performed. This WaNo generates the models and the data (PF.json) and is also responsible for creating a list of data points for a direct query with the kMC program in the KMC WaNo, 2.8.
The DB-Generator collects all the processed data from the previous WaNos into a single YAML file. It also triggers the Update-PF to update the dataset after omitting the outliers as described in Sections 2.5 and 2.9, for the next active learning cycle. This framework allows monitoring multiple batches of calculations for independent parameters during different active learning cycles. Additionally, a database is generated after each active learning cycle, which we store in a designated GitHub repository.
A Colab notebook is used for analyzing, visualizing, and processing the database. All the workflow nodes, notebooks, dependencies, and documentation are available on the following repository: https://github.com/KIT-Workflows/SEI-Model-Active-Learning.
3 Results and discussion
3.1 Preparation of the datasets
In this step, we discuss the preparation of a dataset for training an initial Gaussian process classification model. The initial model determines the progression of the active learning workflow, and its training depends on the initial training dataset. The 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kMC model output is classified into the four classes. In the classification problems, it is necessary to classify the dataset into classes with independent and distinguishable features. This requires an efficient description-conversion-classification schema. This schema effectively maps a continuous model output space into a discrete class label space. The number of classes was determined based on our expectations of the present classification problem and its distinguishable features. The classes inorganic SEI and organic SEI are the output classes for SEI products. In the class unfinished, intermediate products are mainly formed, but in the class empty, the reactions end without producing any SEI components. It is important to study the unfinished class because it helps identify the reactions that control the decomposition of the electrolyte species, or the loss of active lithium, without forming a SEI. The class empty carries information about the possibility of not producing any SEI even though the system has an active electrode and excess reactants. In the training of the model on the initial dataset, we aimed to find the smallest dataset size with the lowest error to improve the computational efficiency of the workflow. The initial dataset not only plays a role in the training of the model, but it also determines the sampling of the space, as shown in Section 2.6. We created smaller datasets, as explained in Section 2.3, called trimmed datasets, and evaluated the error of the model trained with them. The error of the classification model is the ratio of misclassified test points to the size of the test set. In the classification problem, it is not only important to be able to predict the correct class given the input parameters, but also to avoid misclassification in other class labels. This makes the expression and handling of errors in classification problems different from regression problems.
000 kMC model output is classified into the four classes. In the classification problems, it is necessary to classify the dataset into classes with independent and distinguishable features. This requires an efficient description-conversion-classification schema. This schema effectively maps a continuous model output space into a discrete class label space. The number of classes was determined based on our expectations of the present classification problem and its distinguishable features. The classes inorganic SEI and organic SEI are the output classes for SEI products. In the class unfinished, intermediate products are mainly formed, but in the class empty, the reactions end without producing any SEI components. It is important to study the unfinished class because it helps identify the reactions that control the decomposition of the electrolyte species, or the loss of active lithium, without forming a SEI. The class empty carries information about the possibility of not producing any SEI even though the system has an active electrode and excess reactants. In the training of the model on the initial dataset, we aimed to find the smallest dataset size with the lowest error to improve the computational efficiency of the workflow. The initial dataset not only plays a role in the training of the model, but it also determines the sampling of the space, as shown in Section 2.6. We created smaller datasets, as explained in Section 2.3, called trimmed datasets, and evaluated the error of the model trained with them. The error of the classification model is the ratio of misclassified test points to the size of the test set. In the classification problem, it is not only important to be able to predict the correct class given the input parameters, but also to avoid misclassification in other class labels. This makes the expression and handling of errors in classification problems different from regression problems.
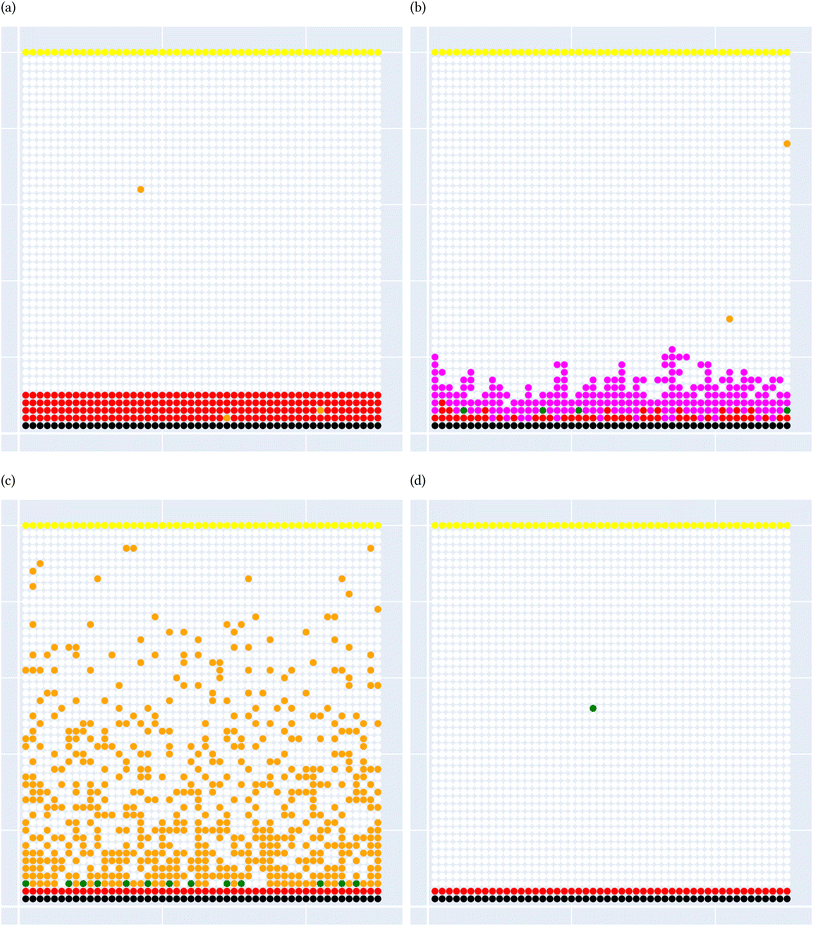
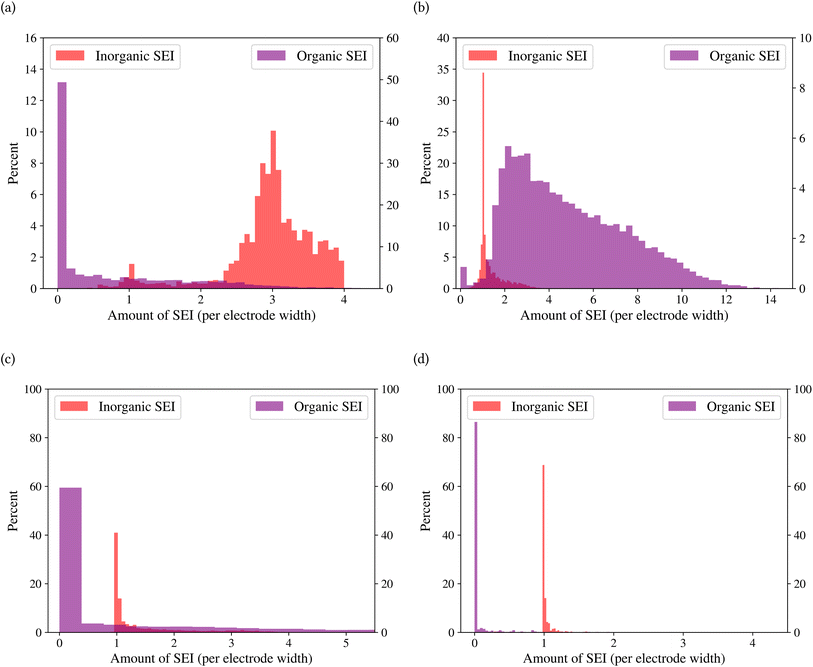
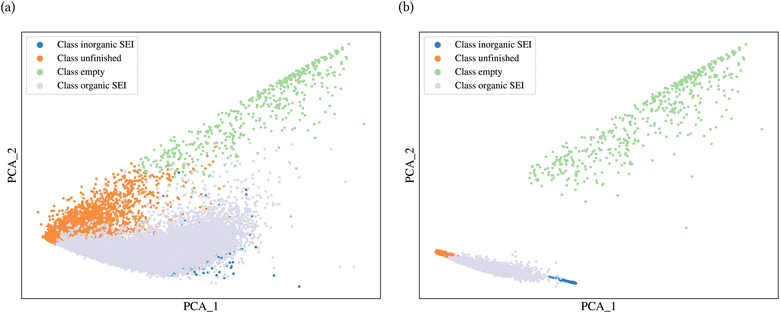
A general representation of the four classes is given in Fig. 2. The procedure for labeling the kMC outputs is presented in Fig. 3 (also ESI Fig. S1–S3†). A more detailed view of the features of classes is provided by presenting the amount of organic and inorganic SEI produced in each class. Fig. 4 shows the corresponding main component of the SEI in the inorganic and organic classes. In Fig. 4a, an inorganic SEI is produced with a maximum of 4 layers (per electrode width of 50 nm), and this maximum corresponds to the length of electron tunneling that was set in our model to be 4 nm. In this class, a minimal amount of organic SEI is produced. In Fig. 4b, the trend is reversed. We see a minimal amount of inorganic SEI (typically one layer) that is the product of the rapid reduction of Li+·EC on the electrode surface. The plot shows a wide range of the amount of produced organic SEI, up to a maximum of 14 layers and most frequently between 2 and 4 layers (per electrode width of 50 nm). Fig. 4c and d show negligible amounts of either organic or inorganic SEI in their classes. The analysis of the error of the model trained with the trimmed datasets in Fig. 6 shows that the lowest error was for the dataset of size 9561. The range of error was between 0.03 and 0.05. We can see that increasing the dataset size did not necessarily lower the error of the model. The dataset with a size of 9561 is selected as the initial training dataset. Fig. 5b illustratively shows the trimmed dataset and its corresponding SEI classes. The results show that our labeled dataset worked well to train an initial classification model by using the provided description-conversion-classification schema and the method to find the smallest efficient trimmed dataset. The workflow continues with a much more efficient dataset and a lower computational cost for training the model at each cycle.
3.2 Active learning cycles
The trimmed dataset and the initial classification model discussed in the previous section are based on reaction barriers that were labeled and assigned to their corresponding classes of kMC model output in a supervised manner. As the next step, we will improve this model using the active learning workflow in order to have a representative model that is accurate over a larger subset of reaction barrier space.In contrast to the creation of the initial dataset through a design-of-experiment approach, the present active learning approach uses the uncertainty of the model to dynamically choose the next set of training data points to expand the domain of validity of the model. The benefit of this approach is the curation of a training dataset in a fast and efficient way. The strategy of selection of new points, estimation of uncertainty, decision of the size of new data points and the computational cost of labeling, and monitoring the classification error after each cycle are essential in order to successfully train a model through an active learning workflow. The selection of the most informative data points in active learning reduces the need for labeling large amounts of data, making the training process more efficient. Additionally, by including various representative data points the model can generalize better to unseen data. The probability that a test point belongs to one of the four classes is used as a metric to measure the uncertainty of the classification model, as shown in Section 2.7. We determined the class labels of the uncertain test points through a direct query with the kMC program, followed by a description, conversion, and classification of the kMC outputs. The uncertainty of the model about a test point is determined based on a predefined threshold. This threshold also controls the computational costs of direct query and labeling, as well as the growth of the dataset and the computational cost of training the model in the next cycle. The uncertain test points and their determined class labels are added to the dataset for training the model in the next cycle. In each cycle, we analyzed the classification error of the trained model, described as the ratio of misclassified test points to the size of the test dataset, and the confusion matrix, which shows the misclassifications for each class and the instances in which other classes were confused with a given class. Thus, a set of workflow hyperparameters controls the training of a model through active learning. The workflow design in this work guarantees the reproducibility of the results and facilitates control over these hyperparameters.
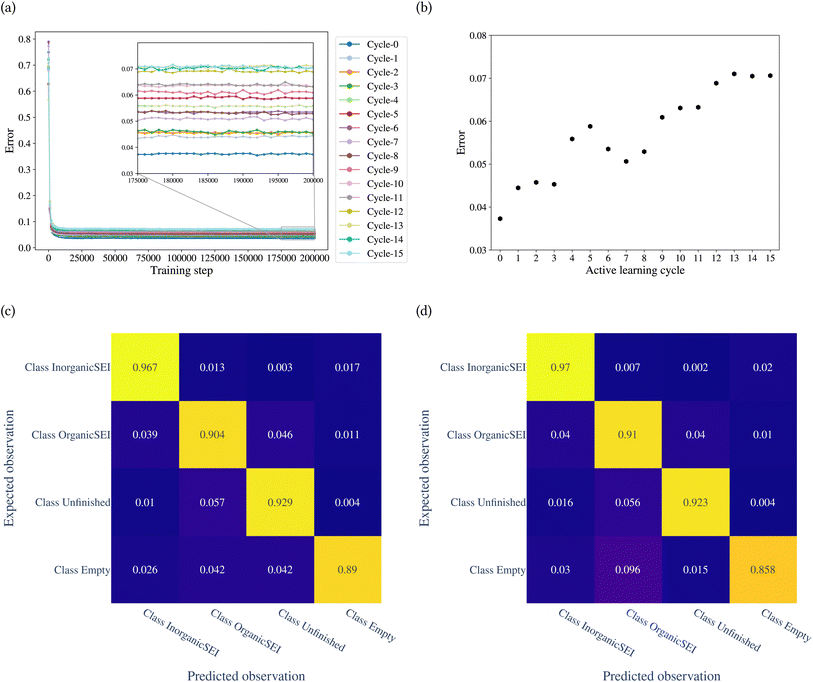
The model was trained through 15 cycles of active learning. The error of the model with the training step is shown in Fig. 7a. Fig. 7b shows the classification error of the model for each cycle. The figure shows that up to the 8th cycle, there are fluctuations in the error, and after that, the changes in error are reduced. Fig. 7c and d show the confusion matrices after the 14th and 15th cycles. The confusion matrices can be analyzed for each row and each column. A row in the confusion matrix shows the misclassification of the given class. A column, on the other hand, shows the misclassifications of other classes as the corresponding class of the column. For example, in Fig. 7d, the row related to class empty shows that of the total test points belonging to class empty, 0.03 of them were classified as class inorganic SEI, 0.096 as class organic SEI, and 0.015 as class unfinished. The column related to class empty shows that 0.02 of test points of class inorganic SEI, 0.01 of class organic SEI, and 0.004 of class unfinished were classified as class empty.
The overall error at the 14th cycle is 0.070. In the 15th cycle, we see an overall error of 0.071, but with different details. In Fig. 7d, the result shows an increase in confusion between class empty and class organic SEI compared to the 14th cycle. But this confusion is not symmetric, which means there is no confusion between class organic SEI and class empty. In fact, the confusion with class empty is overall minimal. This means it is not likely that the regions of reaction barrier space corresponding to the classes inorganic SEI, organic SEI, or unfinished will be confused with class empty.
We used the confusion matrix at the 15th cycle to calculate the probability of actually observing the organic SEI class using the trained model, using eqn (8). This equation includes the confusion and errors from other classes and determines the reliability of a prediction for the class organic SEI.
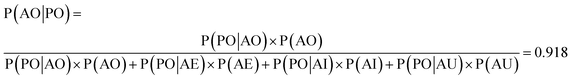 | (8) |
In this equation, AO and PO are the actual class organic SEI and predicted class organic SEI, respectively, and similarly, AE, AI, and AU, are actual class empty, inorganic SEI and unfinished, respectively (ESI eqn (3)†). This means that when the model predicts a data point in the test set as belonging to class organic SEI, the probability of it actually belonging to class organic SEI is 0.918. Similar analyses for other classes are as follows: P(AI|PI) = 0.940, P(AU|PU) = 0.952, and P(AE|PE) = 0.842. These are a comprehensive measure of the accuracy of the model in the prediction of a given class in connection with the probability of observing that class, and confusion of the model about features of classes. The results express that the probability of actual occurrence of class unfinished is greater than that of class inorganic SEI, followed by that of class organic SEI. It is also less likely to observe class empty. In this regard, it should be noted that the class empty corresponds to a condition where the kMC model produces no reaction products despite the electrolyte being in direct contact with the active electrolyte material. This particular condition explains the smaller size of class empty.
One reason for the higher chance of misclassification for class organic SEI compared to class inorganic SEI is due to the broadness of features in this class, as shown in Fig. 4b. This class has an overlap with the features of other classes, which makes other classes an extreme example of class organic SEI.
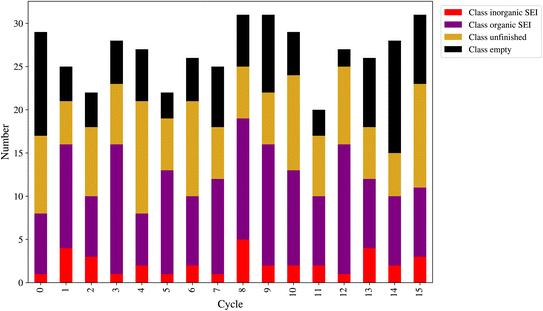
At the end of each cycle, 50 direct queries with the kMC program were performed. After performing the outlier detection method, as shown in Section 2.9, the final number of new entries to the dataset can be lower than 50. This number is a workflow hyperparameter that controls the computational cost of labeling the new model outputs and training the next model. Fig. 8 shows the number of new entries added to the dataset from each class at the end of each active learning cycle. The lowest number belonged to the class inorganic SEI, and the class empty came in second. The total number of points added to the dataset was as follows: for class inorganic SEI 36, class empty 100, class unfinished 127, and class organic SEI 164. The model inquired about more data points to capture the general features of class organic SEI. On the other hand, the model needed comparatively fewer additional data points about class inorganic SEI and class empty.
In this active learning workflow, a total of 427 new data points were added to the dataset, the training of the model after each cycle converged, and the error of the model evolved and reached a certain level after 15 cycles without significantly increasing the dataset size. The addition of new data points to the dataset during each cycle allowed the model to continuously improve its performance. The convergence of the training after each cycle indicates that the model was able to effectively learn from the newly added data. This shows the hyperparameters of the workflow and the description-conversion-classification schema explained in the previous section integrated well in the active learning cycles.
3.3 Evolution of the model with active learning cycles
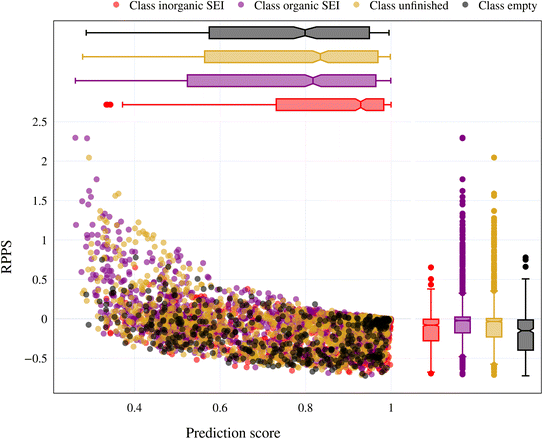
In the previous section, we discussed the training of the model through 15 active learning cycles. In this section, we discuss in more detail the behavior of the model within each cycle and the methods we used for this purpose.The behavior of the model after each training cycle was studied using the prediction score, as described in Section 2.7. A sample dataset was created as described in Section 2.6, and each sample point received a prediction score from the trained model at the end of each cycle. Then, for each of the four classes, we obtained a distribution of prediction scores that has an upper quartile, median, and lower quartile. These quartiles allow us to study the performance of the model for each class after each cycle. In addition, we can examine the prediction score of the model for the higher, median, and lower ranges separately through active learning cycles. By analyzing the distribution of prediction scores, we can identify any patterns or trends in the behavior of the model after each cycle. This information allows us to assess the consistency and stability of the model during the active learning cycles, enabling us to make informed decisions regarding necessary adjustments in the performance of the workflow and the number of active learning cycles. In addition, each test point had a relative change in its prediction score with each cycle. We used the relative prediction probability score (RPPS), eqn (9), to discuss this change for the sample dataset. The RPPS provides a quantitative measure of the change in the prediction score for each sample point using the trained model at any cycle, compared to the initial trained model. For each of the four classes, we obtained a distribution of RPPS that has an upper quartile, median, and lower quartile. This information is used to study the relative change in the prediction score for different classes with different prediction scores.
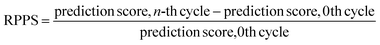 | (9) |
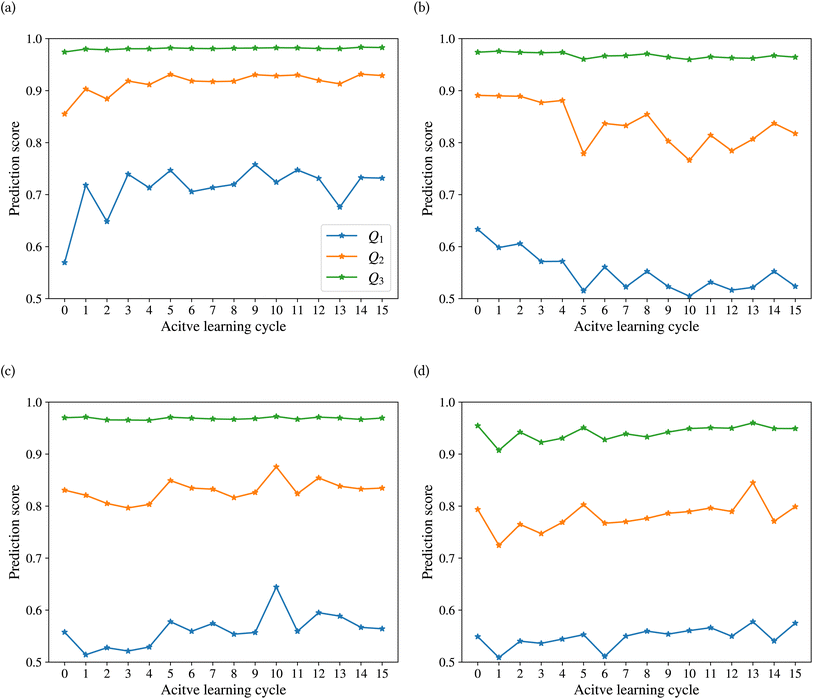
Fig. 9 shows the range of prediction scores between 0.25 and 1. The figure shows a reduction in the prediction score at the end of the 15th cycle compared to the initial prediction score for the sample points with high prediction scores. At the same time, the trend is an increase in prediction score for the samples that initially had a low score, which was defined by our framework hyperparameter of 0.4, as described in Section 2.7. The first quartile of RPPS for classes inorganic SEI, organic SEI, unfinished, and empty is −0.27, −0.20, −0.21, and −0.36, respectively. The sample points that received high prediction scores using the initial model maintained their high scores after active learning cycles. For example, a 0.2 reduction in the prediction score in the range of 0.8 to 0.9 is still in the range of 0.64 to 0.72. The result shows that for the sample points with prediction scores very close to 1, the prediction score does not change after 15 cycles, and RPPS is zero. Through the progression of the active learning cycles, the model readjusts its understanding of the features compared to its initial comprehension. Considering the kernel of the Gaussian process model, eqn (5), the similarity of the features is captured via two metrics: one is their Euclidean distance, and the other is the kernel length scale. An additional learned noise is also added to the model during the training. With the addition of more informative points to the model, the kernel length scale for each feature of each class is adjusted so that all the points within a class are close together (ESI Fig. S4†). Within this optimization of the model hyperparameters, an optimal point is reached where all previous and newly added data points share a maximum likelihood of membership in a class, and this comes with a possible reduction in prediction scores for some data points that initially had a high prediction score. In Fig. 9, the horizontal axis shows the prediction score in the 15th cycle for different classes. The quartiles of the sample dataset having different prediction scores, which are shown as dented color bars on the top, are used for providing more details in the next figure.
Fig. 10 shows the changes in the first (Q1), second (Q2), and third (Q3) quartiles of the prediction scores for the sample dataset vs. the active learning cycles. The Q3 for all classes is consistently high, except for class empty, which shows an increasing trend after the first cycle. The Q2 of the prediction score of the test set for the classes inorganic SEI, unfinished, and empty also shows an increasing trend. The results show a stable value of this quartile of the prediction score of around 0.8 for all classes, except class inorganic SEI, which has reached above 0.9 to 0.93. In contrast to other classes, we see that after the 4th cycle, the Q2 of the class organic SEI reduces from 0.88 to below 0.85 and finally to 0.82, which is closer to that of the classes unfinished and empty. As shown in Fig. 10b and d, the last two cycles show opposite trends. The results show that where the Q2 for class empty increases, it decreases for class organic SEI. This behavior was also visible in the confusion matrix in Fig. 7c and d. The results show that the model's status at the 15th cycle is more representative than at the 14th cycle. The Q1 of the prediction score of the classes also shows similar trends to their own Q2. Except for class inorganic, which reached above 0.7, other classes stabilized between 0.5 and 0.6.
The effectiveness of this active learning workflow in training the classification model is described using a confusion matrix for the different classes at the last cycle, the difference in the number of new entries added to the dataset from each class, and the details of the prediction score using the trained model at each cycle. These results show that the model had different training performances for each class. For classes inorganic SEI and empty, the training through active learning cycles showed a distinct improvement in prediction scores. This can be due to the easier detection of features in these classes compared to the more complex classes of organic SEI and unfinished. The confusion matrix of class unfinished showed minimal confusion with other classes. On the other hand, the model added more new entries about class unfinished compared to class inorganic SEI and class empty. The model added the most new entries related to class organic SEI. The progression of the prediction scores during the active learning cycles shows that with the addition of more entries related to class organic SEI, the prediction scores changed and reached a level of stability. This result also demonstrates the effectiveness of the presented sampling procedure in identifying the most informative data points from the reaction barrier space to improve the ability of the model to find the features of this class. This active learning workflow ensures that the training dataset is representative, resulting in a more accurate training and generalized model.
3.4 Generation of the parameter space with the model
In the previous sections, we discussed training a representative classification model through active learning cycles. This section will discuss the reaction barrier space for each of the four classes with the trained classification model. The reaction barrier space of each class has 15 features related to the 15 chemical reactions in Table 1. These features play a crucial role in understanding the dynamics of chemical reactions and can help us understand the reaction conditions for desired outcomes.We created a sample test, as described in Section 2.6. The model classifies the test set. The minimum prediction score threshold of 0.6 was also set to exclude less certain predictions. We obtained a distribution of reaction barriers for each of the 15 reactions in each of the four classes. These distributions provide valuable insights into the behavior of the features across different classes, allowing us to identify patterns and draw conclusions. We measured the upper quartile, median, and lower quartile from each distribution. Quartiles are used to understand a distribution's spread and the presence of outliers. They are particularly useful for the characterization of a distribution that is skewed or has extreme values. We defined a parameter Δ as eqn (10),
Δi = Q3,i − Q1,i,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i∈{1, 2, …, 15} i∈{1, 2, …, 15} | (10) |
which is the interquartile range between the third and the first quartile of the generated parameters for each SEI class. We used this metric as a measure of the expansion of the parameter distribution for each SEI class. The location of the second quartile, or median, is also used as the representative value of the feature for each class. In this case, the reaction barrier with the unit of eV, which determines the rate of the reaction, is the median, and the observed spread of this reaction barrier is Δ2, with the unit of [eV]2. The collection of results is given in Tables 2 and 3 (also ESI Fig. S5–S7†). These tables provide a comprehensive overview of the reaction barriers and their spread for each reaction and each class. The data presented allows a clear comparison between the reactions of each class. It also helps with understanding the factors that contribute to the observation of each class. We discuss the table once for each class and once for the reactions. The results for each class can be interpreted using Δ2 [eV]2 and Q2 [eV]. In these tables, the reactions are divided into three categories: electrochemical (1–4), aggregation (5–11), and diffusion (12–15), in order of their appearance on the table. The electrochemical reactions are divided into two categories: those that happen directly in contact with the electrode and those that happen through electron tunneling. It should be noted that the reactions in this table have been rearranged compared to Table 1 for more contextual clarity. The output of the model is more sensitive to the parameters with a lower Δ2, compared to the parameters with a higher Δ2. The median is used for comparing the reaction barriers between different classes. We also used the median to test these generated parameters to see if they would lead to the correct outputs. For class inorganic SEI, Table 2 shows a small value for Δ2 for the 4th reaction, which controls the electron tunneling from the electrode. The second lowest Δ2 is for the 6th reaction, which controls the aggregation of Li2EDC species. For other reactions, Δ2 is in the same order, and the largest values belong to the 14th and 15th reactions that control diffusion of the aggregated organic SEI.
| Reaction | Class inorganic SEI | Class organic SEI | ||
|---|---|---|---|---|
| Δ 2 | Q 2 [eV] | Δ 2 | Q 2 [eV] | |
| (1) Electrode: Li+/EC− → Li+·oEC− | 2.66 × 10−2 | 0.349 | 2.96 × 10−2 | 0.347 |
| (2) Electrode: Li+·oEC− + Li+ → Li2CO3 + C2H4 | 2.53 × 10−2 | 0.344 | 1.96 × 10−2 | 0.292 |
| (3) Tunneling: Li+/EC− → Li+·oEC− | 2.69 × 10−2 | 0.371 | 2.66 × 10−2 | 0.374 |
| (4) Tunneling: Li+·oEC− + Li+ → Li2CO3 + C2H4 | 6.40 × 10−5 | 0.484 | 2.13 × 10−2 | 0.628 |
| (5) Li+·oEC− + Li+·oEC− → Li2EDC | 2.66 × 10−2 | 0.380 | 2.59 × 10−2 | 0.364 |
| (6) Li2EDC + Li2EDC → (Li2EDC)2 | 1.74 × 10−2 | 0.801 | 1.35 × 10−2 | 0.636 |
| (7) (Li2EDC)2 + Li2EDC → organic·SEI | 2.34 × 10−2 | 0.592 | 2.50 × 10−2 | 0.554 |
| (8) (Li2EDC)2 + (Li2EDC)2 → organic·SEI | 2.99 × 10−2 | 0.562 | 2.76 × 10−2 | 0.547 |
| (9) Organic·SEI + Li2EDC → organic·SEI | 2.62 × 10−2 | 0.557 | 2.31 × 10−2 | 0.544 |
| (10) Organic·SEI + (Li2EDC)2 → organic·SEI | 2.59 × 10−2 | 0.556 | 2.22 × 10−2 | 0.558 |
| (11) Organic·SEI + organic·SEI → organic·SEI | 2.76 × 10−2 | 0.555 | 2.40 × 10−2 | 0.557 |
| (12) Li+·oEC− + Li+/EC− → Li+/EC− + Li+·oEC− | 2.79 × 10−2 | 0.452 | 2.64 × 10−2 | 0.407 |
| (13) Li2EDC + Li+/EC− → Li+/EC− + Li2EDC | 2.10 × 10−2 | 0.471 | 9.60 × 10−3 | 0.476 |
| (14) (Li2EDC)2 + Li+/EC− → Li+/EC− + (Li2EDC)2 | 3.17 × 10−2 | 0.469 | 3.31 × 10−2 | 0.480 |
| (15) Organic·SEI + Li+/EC− → Li+/EC− + organic·SEI | 3.24 × 10−2 | 0.465 | 2.92 × 10−2 | 0.468 |
| Reaction | Class unfinished | Class empty | ||
|---|---|---|---|---|
| Δ 2 | Q 2 [eV] | Δ 2 | Q 2 [eV] | |
| (1) Electrode: Li+/EC− → Li+·oEC− | 2.96 × 10−2 | 0.350 | 2.19 × 10−2 | 0.362 |
| (2) Electrode: Li+·oEC− + Li+ → Li2CO3 + C2H4 | 1.23 × 10−2 | 0.286 | 3.72 × 10−3 | 0.456 |
| (3) Tunneling: Li+/EC− → Li+·oEC− | 2.66 × 10−2 | 0.372 | 2.16 × 10−2 | 0.376 |
| (4) Tunneling: Li+·oEC− + Li+ → Li2CO3 + C2H4 | 1.56 × 10−2 | 0.646 | 1.23 × 10−2 | 0.679 |
| (5) Li+·oEC− + Li+·oEC− → Li2EDC | 2.76 × 10−2 | 0.365 | 2.31 × 10−2 | 0.371 |
| (6) Li2EDC + Li2EDC → (Li2EDC)2 | 2.22 × 10−2 | 0.813 | 3.76 × 10−2 | 0.705 |
| (7) (Li2EDC)2 + Li2EDC → organic·SEI | 3.20 × 10−2 | 0.592 | 2.79 × 10−2 | 0.587 |
| (8) (Li2EDC)2 + (Li2EDC)2 → organic·SEI | 2.72 × 10−2 | 0.557 | 2.56 × 10−2 | 0.568 |
| (9) Organic·SEI + Li2EDC → organic·SEI | 2.79 × 10−2 | 0.574 | 2.10 × 10−2 | 0.523 |
| (10) Organic·SEI + (Li2EDC)2 → organic·SEI | 2.76 × 10−2 | 0.555 | 2.19 × 10−2 | 0.570 |
| (11) Organic·SEI + organic·SEI → organic·SEI | 2.40 × 10−2 | 0.560 | 2.56 × 10−2 | 0.570 |
| (12) Li+·oEC− + Li+/EC− → Li+/EC− + Li+·oEC− | 2.69 × 10−2 | 0.411 | 2.76 × 10−2 | 0.413 |
| (13) Li2EDC + Li+/EC− → Li+/EC− + Li2EDC | 7.92 × 10−3 | 0.371 | 4.36 × 10−3 | 0.341 |
| (14) (Li2EDC)2 + Li+/EC− → Li+/EC− + (Li2EDC)2 | 3.03 × 10−2 | 0.472 | 3.20 × 10−2 | 0.476 |
| (15) Organic·SEI + Li+/EC− → Li+/EC− + organic·SEI | 3.13 × 10−2 | 0.458 | 3.88 × 10−2 | 0.463 |
For class organic SEI, as shown in Table 2, the lowest Δ2 belongs to the 13th reaction, which controls the diffusion of Li2EDC, followed by the 6th reaction which controls the aggregation of Li2EDC species, followed by the 2nd and 4th reactions, which control the electrochemical reduction of Li+·oEC− on the surface of the electrode and through electron tunneling, respectively.
For class unfinished in Table 3, the lowest Δ2 belongs to the 13th reaction, which controls the diffusion of Li2EDC, followed by the 2nd and 4th reactions, which control the electrochemical reduction of Li+·oEC− on the surface of the electrode and through electron tunneling, respectively.
For class empty, as shown in Table 3, the lowest Δ2 belongs to the 2nd reaction which controls the electrochemical reduction of Li+·oEC− on the surface of the electrode, followed by the 13th reaction which controls the diffusion of Li2EDC, followed by the 4th reaction which controls the electrochemical reduction of Li+·oEC− through electron tunneling.
The results show a repeating pattern of the lowest Δ2 for the 2nd, 4th, 6th, and 13th reactions. Tables 2 and 3 show the median (Q2) of the reaction barriers for each class. For class inorganic, the reduction of Li+·oEC− through electron tunneling should happen with a barrier of 0.484 eV and the aggregation of Li2EDC species should happen with a barrier of 0.801 eV. This high barrier for aggregation of Li2EDC species also appears for class unfinished and empty, but it is lower for class organic SEI, with a value of 0.636 eV. This difference indicates that aggregation of Li2EDC species is more important for the formation of an organic SEI than other aggregation reactions. For class organic SEI, the results show that the diffusion of Li2EDC happens with a higher barrier compared to class unfinished and class empty. This barrier is 0.476 eV while for class unfinished and empty, it is 0.371 and 0.341 eV, respectively. These results indicate that faster diffusion and slower aggregation of Li2EDC lead to the delay or even prevention of the formation of an organic SEI.
These results can be summarized in the following order:
• For an inorganic SEI, Li+·oEC− should be reduced to Li2CO3 with the reaction barrier a lot lower than the reaction for its aggregation into Li2EDC, as they are competing reactions.
• For an organic SEI, slower diffusion of Li2EDC and faster aggregation of Li2EDC into (Li2EDC)2 are essential to obtain an organic SEI.
• Slow reduction of Li+·oEC−, along with sluggish aggregation of Li2EDC into (Li2EDC)2, combined with fast diffusion of Li2EDC, cause delay in the formation of a SEI.
• Slow formation of Li+·oEC− and fast diffusion of their aggregate Li2EDC, lead to absence of either an organic or inorganic SEI.
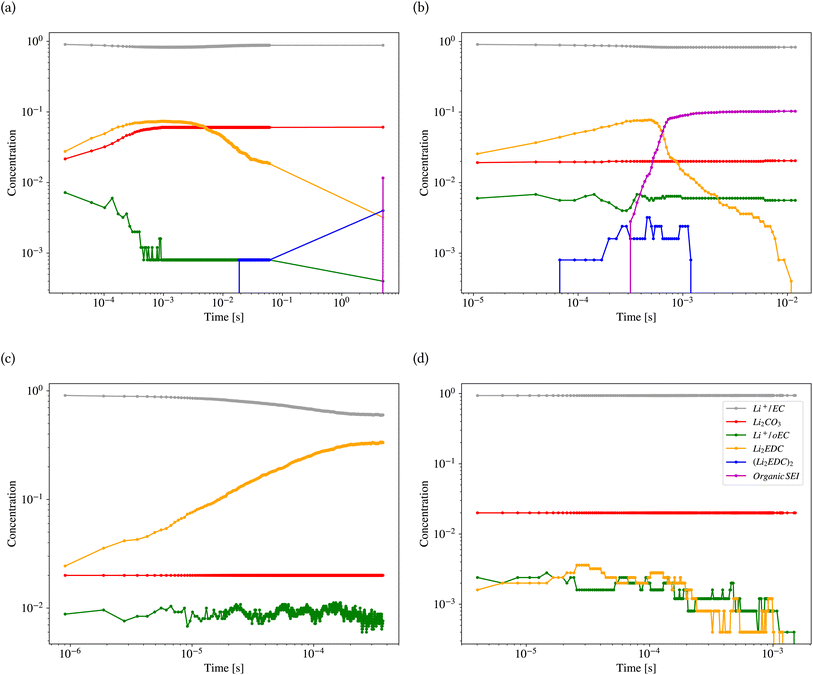
Fig. 11 shows the results of kMC calculations based on the parameters generated by the model in Tables 2 and 3 for the different classes (also ESI Fig. S8†). Each calculation was carried out for 1800 s. Fig. 11a shows the concentration (the number of pixels occupied by the species divided by the system size) of different reactants and products of the kMC model for the inorganic SEI sample. The plot shows that the concentration of Li2EDC product reaches a maximum of 7.0 × 10−2 after 3.0 × 10−4 s and with the same trend, the inorganic SEI, Li2CO3 is produced. Fig. 11b shows that the starting time for formation of (Li2EDC)2 is around 7.0 × 10−5 s. After 6.06 × 10−4 s the concentration of Li2EDC reaches its maximum of 7.0 × 10−2, which subsequently causes the organic SEI to reach its maximum concentration.
Fig. 11c shows that Li2EDC is continuously produced with an increase in its concentration, while the production of Li+·oEC− shows a steady and stable trend with a concentration of around 1.0 × 10−2, without formation of any further organic or inorganic SEI. Fig. 11d shows that both Li2EDC and Li+·oEC− were produced at a limited concentration of maximum 4.0 × 10−3 followed by a downfall trend to zero, without production of any inorganic or organic SEI. The event of diffusion out of the box occurred for inorganic SEI 137, organic SEI 8, unfinished 584, and empty 29 times (ESI Fig. S9†). Delay in the formation of a SEI causes the reduced species to diffuse out of the simulation box without the formation of SEI products, which means exhaustion of Li resources. This result shows that the model learned the features of the parameter space corresponding to each class of SEI.
4 Conclusion
The anodes in Li-ion batteries are a dynamic environment of different reactions. The reactions in the formation of a SEI are controlled by the effects of interfaces, geometrical confinements, and the presence of a wide range of chemical species. These reactions are affected at any location of an electrode, given the local composition of species and other aspects of electrode design. These conditions can change the rate at which any of the reactions occur. In this study, we have shown that certain reactions have a more deterministic role in SEI formation. This helped us understand the response of the reaction network in a model electrode–electrolyte configuration, which can be considered an element of the larger-scale electrode. The final SEI structure of the electrode is the collection of all SEI formations in each element. This framework can help us find an efficient way for multiscale modeling by finding the determining parameters at the mesoscale. In this study, the model trained through active learning cycles enabled us to understand the features of each class of possible SEI outcomes. This was accomplished through a workflow with different hyperparameters that can be adjusted for desired applications, such as active learning of certain categories of reactions, in such a way that only the parameters related to those reactions are sampled from the parameter space.Author contributions
MS: conceptualization, methodology, software (active learning), review & editing, CR: software (Simstack), review & editing, ME: data curation, software (kMC program), and WW: project administration, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement No. 957189. The project is part of BATTERY 2030+, the large-scale European research initiative for inventing the sustainable batteries of the future, and the German Federal Ministry of Education and Research (BMBF) for financial support of the project Innovation-Platform MaterialDigital (https://www.materialdigital.de) through project funding FKZ number: 13XP5094A.References
- A. M. Colclasure and R. J. Kee, Thermodynamically consistent modeling of elementary electrochemistry in lithium-ion batteries, Electrochim. Acta, 2010, 55(28), 8960–8973 CrossRef CAS.
- M. He, R. Guo, G. M. Hobold, H. Gao and B. M. Gallant, The intrinsic behavior of lithium fluoride in solid electrolyte interphases on lithium, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(1), 73–79 CrossRef CAS PubMed.
- M. R. Busche, M. Weiss, T. Leichtweiss, C. Fiedler, T. Drossel, M. Geiss, A. Kronenberger, D. A. Weber and J. Janek, The formation of the solid/liquid electrolyte interphase (slei) on nasicon-type glass ceramics and lipon, Adv. Mater. Interfaces, 2020, 7(19), 2000380 CrossRef CAS.
- A. C. Kozen, C.-Fu Lin, J. P. Alexander, M. A. Schroeder, X. Han, L. Hu, S.-B. Lee, G. W. Rubloff and M. Noked, Next-generation lithium metal anode engineering via atomic layer deposition, ACS Nano, 2015, 9(6), 5884–5892 CrossRef CAS PubMed.
- S. K. Heiskanen, J. Kim and B. L. Lucht, Generation and evolution of the solid electrolyte interphase of lithium-ion batteries, Joule, 2019, 3(10), 2322–2333 CrossRef CAS.
- S. M. Blau, H. D. Patel, E. W. C. Spotte-Smith, X. Xie, S. Dwaraknath and K. A. Persson, A chemically consistent graph architecture for massive reaction networks applied to solid-electrolyte interphase formation, Chem. Sci., 2021, 12(13), 4931–4939 RSC.
- G. M. Hobold, A. Khurram and B. M. Gallant, Operando gas monitoring of solid electrolyte interphase reactions on lithium, Chem. Mater., 2020, 32(6), 2341–2352 CrossRef CAS.
- B. S. Parimalam, A. D. MacIntosh, R. Kadam and B. L. Lucht, Decomposition reactions of anode solid electrolyte interphase (sei) components with lipf6, J. Phys. Chem. C, 2017, 121(41), 22733–22738 CrossRef CAS.
- N. Dubouis, P. Lemaire, B. Mirvaux, E. Salager, M. Deschamps and A. Grimaud, The role of the hydrogen evolution reaction in the solid–electrolyte interphase formation mechanism for “water-in-salt” electrolytes, Energy Environ. Sci., 2018, 11(12), 3491–3499 RSC.
- K. Ushirogata, K. Sodeyama, Z. Futera, Y. Tateyama and Y. Okuno, Near-shore aggregation mechanism of electrolyte decomposition products to explain solid electrolyte interphase formation, J. Electrochem. Soc., 2015, 162(14), A2670 CrossRef CAS.
- M. A. Katsoulakis, A. J. Majda and D. G. Vlachos, Coarse-grained stochastic processes for microscopic lattice systems, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(3), 782–787 CrossRef CAS PubMed.
- A. B. Bortz, M. H. Kalos and J. L. Lebowitz, A new algorithm for monte carlo simulation of ising spin systems, J. Comput. Phys., 1975, 17(1), 10–18 CrossRef.
- D. T. Gillespie, A rigorous derivation of the chemical master equation, Phys. A, 1992, 188(1–3), 404–425 CrossRef CAS.
- S. S. Zhang, K. Xu and T. R. Jow, Eis study on the formation of solid electrolyte interface in li-ion battery, Electrochim. Acta, 2006, 51(8–9), 1636–1640 CrossRef CAS.
- M. Cohen, T. Goculdas and D. G. Vlachos, Active learning of chemical reaction networks via probabilistic graphical models and boolean reaction circuits, React. Chem. Eng., 2023, 8, 824–837 RSC.
- K. D. Konze, P. H. Bos, M. K. Dahlgren, L. Karl, I. Tubert-Brohman, A. Bortolato, B. Robbason, R. Abel and S. Bhat, Reaction-based enumeration, active learning, and free energy calculations to rapidly explore synthetically tractable chemical space and optimize potency of cyclin-dependent kinase 2 inhibitors, J. Chem. Inf. Model., 2019, 59(9), 3782–3793 CrossRef CAS PubMed.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-fly active learning of interpretable bayesian force fields for atomistic rare events, npj Comput. Mater., 2020, 6(1), 20 CrossRef.
- M. Esmaeilpour, S. Jana, H. Li, M. Soleymanibrojeni and W. Wenzel, A solution-mediated pathway for the growth of the solid electrolyte interphase in lithium-ion batteries, Adv. Energy Mater., 2023, 2203966 CrossRef CAS.
- H. Lee Woodcock, B. T. Miller, M. Hodoscek, A. Okur, J. D. Larkin, J. W. Ponder and B. R. Brooks, Mscale: a general utility for multiscale modeling, J. Chem. Theory Comput., 2011, 7(4), 1208–1219 CrossRef PubMed.
- L. Visscher, P. Bolhuis and F. Matthias Bickelhaupt, Multiscale modelling, Phys. Chem. Chem. Phys., 2011, 13(22), 10399–10400 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, T. Bertrand, O. Grisel, M. Blondel, P. Peter, R. Weiss, D. Vincent, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-learn: machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- A. Hyvärinen and E. Oja, Independent component analysis: algorithms and applications, Neural Networks, 2000, 13(4), 411–430 CrossRef PubMed.
- C. E. Rasmussen and C. Williams, Gaussian Processes for Machine Learning, Springer, 2006, vol. 1 Search PubMed.
- H. James, A. Matthews and Z. Ghahramani, Scalable variational Gaussian process classification, in Artificial Intelligence and Statistics, PMLR, 2015, pp. 351–360 Search PubMed.
- F. Leibfried, D. Vincent, S. T. John and N. Durrande, A tutorial on sparse Gaussian processes and variational inference, arXiv, 2022, Preprint, arXiv:2012.13962v14, DOI:10.48550/arXiv.2012.13962.
- C. Villacampa-Calvo, B. Zaldívar, E. C. Garrido-Merchán and D. Hernández-Lobato, Multi-class gaussian process classification with noisy inputs, J. Mach. Learn. Res., 2021, 22(1), 1696–1747 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Warren, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. Jarrod Millman, N. Mayorov, R. Andrew, J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, F. Yu, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- C. R. C. Rêgo, J. Schaarschmidt, T. Schlöder, M. Penaloza-Amion, S. Bag, T. Neumann, T. Strunk and W. Wenzel, SimStack: an intuitive workflow framework, Front. Mater., 2022, 9, 877597 CrossRef.
- J. Schaarschmidt, J. Yuan, T. Strunk, I. Kondov, S. P. Huber, P. Giovanni, L. Kahle, F. T. Bölle, I. E. Castelli, T. Vegge, F. Hanke, T. Hickel, J. Neugebauer, R. Celso, C. Rêgo and W. Wenzel, Workflow engineering in materials design within the battery 2030+ project, Adv. Energy Mater., 2022, 12(17), 2102638 CrossRef CAS.
- M. Soleymanibrojeni and C. R. Caldeira Rêgo, Sei-Model-Active-Learning, https://github.com/KIT-Workflows/SEI-Model-Active-Learning Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06054c |
| This journal is © The Royal Society of Chemistry 2024 |