Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of crystal structure on the lattice thermal conductivity of the IV–VI chalcogenides†
Sophie K.
Guillemot
 ab,
Ady
Suwardi
ab,
Ady
Suwardi
 b,
Nikolas
Kaltsoyannis
b,
Nikolas
Kaltsoyannis
 a and
Jonathan M.
Skelton
a and
Jonathan M.
Skelton
 *a
*a
aDepartment of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: jonathan.skelton@manchester.ac.uk
bInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 1 Fusionopolis Way, #20-10 Connexis North Tower, Singapore 138632, Singapore
First published on 14th December 2023
Abstract
We present a detailed comparative study of the lattice thermal conductivity κlatt of ten reported phases of the IV–VI chalcogenides GeSe, GeTe, SnSe and SnTe, calculated within the single-mode relaxation-time approximation based on third-order interatomic force constants. Differences in κlatt are attributed quantitatively to the phonon group velocities and lifetimes, and differences in the lifetimes are further attributed to the averaged three-phonon interaction strengths and the “phase space” of allowed energy- and momentum-conserving scattering pathways. Our analysis reveals a complex dependence of the κlatt on the crystal structure: structures that constrain the tetrel atoms to locally-symmetric environments show strong phonon anharmonicity and short lifetimes, but in simple structures such as the rocksalt phase these are counterbalanced by large group velocities and a smaller phase space. We find that these competing effects are optimised for orthorhombic Cmcm SnSe, resulting in the lowest predicted κlatt across the ten systems examined. Our findings provide new insight into the interplay between crystal structure and lattice thermal conductivity, and allow us to propose some new guidelines for how to optimise the thermal transport of the IV–VI chalcogenides through crystal engineering.
1 Introduction
In 2015, 196 countries pledged to work together to combat climate change. The Paris Agreements, initiated in 2016, sought to limit the increase in global temperature by the end of this century to 1.5 °C above pre-industrial levels.1 To meet this goal requires significant changes to how we generate and consume energy: by 2030, 30% of global energy must come from renewable sources, and the efficiency with which energy is used must improve by 32.5%.2,3 A 2017 report by the International Energy Agency identified key areas of improvement for each of the major signatories to the Paris Agreements, and outlined a “Bridge Scenario” in which improved energy efficiency could account for a 48% reduction in global emissions by 2030.4 The building, industry and housing sectors alone have the potential to contribute ca. 20.7% of this reduction.4While intensive research has led to rapid improvements in primary energy-generation technologies such as photovoltaics and supporting technologies such as batteries and grid-level storage, technologies aimed at enhancing energy efficiency have received less attention. Given that an estimated 60% of the energy used globally is wasted as heat,5,6 a strong contender in this area are thermoelectric generators (TEGs) to recover waste heat as electrical energy. (The dual function of thermoelectric cooling also has a number of important contemporary applications.7) TEGs are solid-state devices with no moving parts, allowing for maintenance-free operation, and have proven reliability in the aerospace industry.8 They have also been proposed for, among other things, powering wireless sensors, recovering waste heat from household chimneys, and improving the efficiency of combustion engines.5,9
The performance of a thermoelectric material is often measured through the dimensionless figure of merit ZT:10
 | (1) |
The IV–VI chalcogenides show a good balance of favourable electrical transport properties and low κlatt, and as such are among the most widely-studied TEs for mid- to high-temperature applications.13–15 The lead chalcogenides PbS, PbSe and PbTe have been widely studied, and nanostructured PbTe, with a maximum ZTmax of 2.2 at 915 K, is a current industry-standard high-temperature TE.16,17 The high thermoelectric performance of PbTe arises from a low κlatt due to strong phonon anharmonicity and favourable electronic transport due to “band convergence” at elevated temperature.18,19 Both phenomena are thought to be linked to the high-symmetry cubic rocksalt (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure adopted by these materials, although the extent of the phonon anharmonicity is disputed.20–23 However, the toxicity of Pb and the low abundance of Te prevent widespread deployment of PbTe-based TEGs.24
m) structure adopted by these materials, although the extent of the phonon anharmonicity is disputed.20–23 However, the toxicity of Pb and the low abundance of Te prevent widespread deployment of PbTe-based TEGs.24
Given the high performance of PbTe, SnTe and GeTe have been explored as alternatives. These systems both adopt a rhombohedral (R3m) structure, related to the rocksalt structure by a cation off-centering along the [111] direction, below ≈100 and 700 K respectively.25,26 GeTe shows large intrinsic cation vacancy concentrations, resulting in high carrier concentrations and good electrical conductivity.15 Co-doping with Group V elements such as Sb, In and Bi, and also alloying with PbTe, has been shown to enhance the electrical properties of GeTe to yield ZT > 2.15,26–28 (We note however that alloying with Pb raises the same issues as the Pb chalcogenides.) Cu- and Mn-doped SnTe also show good thermoelectric performance, with a reported ZTmax = 1.6 at 925 K.29 However, a working TEG requires both p- and n-type materials to form a complete device,17 but to date n-type chalcogenides remain scarce, with one of few examples being (GeTe)1−x(AgBiSe2)x with x > 20%.30,31
The rarity of Te has also motivated research into the Group IV sulphides and selenides. In particular, SnSe has become one of the benchmark chalcogenide TEs following reports of an unprecedented bulk ZT of 2.6 (ref. 32) and a potential ZT > 3 in polycrystalline samples.28 Unlike the Pb chalcogenides and the tellurides, SnSe adopts an orthorhombic Pnma structure at low temperature and transforms to a higher-symmetry orthorhombic Cmcm phase on heating. As for PbTe, the record thermoelectric performance of Cmcm SnSe32 has been attributed to a combination of strong phonon anharmonicity, leading to low κlatt,33,34 and a multi-valley band structure that results in favourable electronic transport.35 The layered structure of SnSe also results in anisotropic transport, such that along the out-of-plane direction the thermal conductivity approaches the amorphous limit while facile electronic transport is retained.14,28 This effect is somewhat diminished in polycrystalline samples, but is offset by improved mechanical properties.14 Due to its chemical similarity to SnSe and the isostructural low-temperature Pnma phase, GeSe has also seen renewed interest, but the predicted ZTmax ≈ 2.5 has not yet been realised in experiments.13 This is attributed to the difficulty of forming Ge vacancies leading to a low intrinsic charge-carrier concentration of n ≈ 1016 cm−3, and the detrimental effect on the power factor is difficult to counteract with single-atom doping due to the low solubility of typical dopants such as Ag and Na in GeSe.13 GeTe and SnTe are both also reported to undergo a pressure-induced transition to the Pnma phase,28,36,37 and therefore analogous telluride phases may be synthetically accessible.
Given that the high thermoelectric performance of the chalcogenides is due in part to low κlatt attributed to intrinsic phonon anharmonicity, it is of interest to understand the impact of the different crystal structure types adopted across the series on the structural dynamics and thermal transport. First-principles modelling using techniques such as the single-mode relaxation-time approximation (SM-RTA) allows for accurate prediction of the lattice thermal conductivity while providing microscopic detail at the level of individual phonon modes,38,39 and these calculations have for example played an important role in understanding the low κlatt of SnSe.33,34 We recently developed a set of techniques for analysing SM-RTA calculations that can be used to attribute differences in κlatt quantitatively to differences in the phonon group velocities and lifetimes, and to quantify the contribution of the strength of the anharmonic phonon interactions to the latter.40–42 These were recently applied to a family of silicon allotropes and highlighted the important role of structural complexity in determining the κlatt.42
In this work, we apply these techniques to investigate the impact of the crystal structure on the lattice thermal conductivity of the Group IV–VI chalcogenides GeSe, GeTe, SnSe and SnTe. We find that the link between the κlatt and different structure types results from a balance of low phonon group velocities, favoured by large primitive cells, and strong phonon anharmonicity and short lifetimes, favoured by structures where the tetrel atoms are constrained to locally symmetric environments. We also find that the shape of the phonon spectra, which determines the so-called “scattering phase space” (the number of allowed energy- and momentum-conserving scattering pathways), also has a prominent influence on the phonon lifetimes. These effects are optimally balanced in the high-temperature Cmcm structure of SnSe, which has the lowest κlatt across the ten structures we examine. Our results demonstrate that the crystal structure has a far larger impact on the κlatt than the atomic masses, and the microscopic insight from this analysis provides clear guidelines for optimising the heat transport in the IV–VI chalcogenides through crystal-structure engineering.
2 Methods
Periodic density-functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP) code.43 Initial structures were obtained from the Materials Project Database44 or taken from previous work.33 The PBEsol generalised-gradient approximation (GGA) functional was used to describe electron exchange and correlation.45 A Hubbard U correction of Ueff = 4 eV was applied to the Sn d electrons using the method of Dudarev et al.46 The valence Kohn–Sham orbitals were modelled using plane-wave basis sets with kinetic-energy cutoffs of 400–500 eV (Table 1). The electronic Brillouin zones were integrated using the Γ-centered Monkhorst–Pack k-point meshes shown in Table 1. Both parameters were chosen by explicit testing to converge the total energies to <1 meV atom−1 and the external pressure to <1 kbar (0.1 GPa). Projector augmented-wave (PAW) pseudopotentials47,48 were used to model the ion cores, with valence configurations of: Se – 4s24p4; Te – 5s25p4; Ge – 3d104s24p2; and Sn – 4d105s25p2. Each of the structures were fully optimised to tolerances of 10−8 eV and 10−2 eV Å−1 on the electronic total energy and atomic forces respectively. The PAW projections were performed in real space, and the precision of the charge density grids was set automatically to avoid aliasing errors.| # atoms | Cutoff [eV] | k -points | 2nd-order FCs Φ(2) | 3rd-order FCs Φ(3) | κ latt q -points | |||
|---|---|---|---|---|---|---|---|---|
| Supercell (# atoms) | k -points | Supercell (# atoms) | k -points | |||||
| GeSe (Pnma) | 8 (8) | 500 | 3 × 9 × 7 | 2 × 4 × 4 (256) | 2 × 3 × 2 | 1 × 3 × 3 (72) | 3 × 3 × 3 | 10 × 10 × 10 |
GeSe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
2 (8) | 500 | 5 × 5 × 5 | 3 × 3 × 3 (216) | 2 × 2 × 2 | 2 × 2 × 2 (64) | 3 × 3 × 3 | 15 × 15 × 15 |
| SnSe (Pnma) | 8 (8) | 450 | 3 × 9 × 8 | 2 × 4 × 4 (256) | 2 × 3 × 2 | 1 × 3 × 3 (72) | 3 × 3 × 3 | 9 × 9 × 9 |
| SnSe (Cmcm) | 4 (8) | 450 | 8 × 3 × 9 | 4 × 2 × 4 (256) | 2 × 2 × 3 | 3 × 1 × 3 (72) | 3 × 3 × 3 | 12 × 12 × 12 |
| GeTe (Pnma) | 8 (8) | 500 | 3 × 9 × 8 | 2 × 4 × 4 (256) | 2 × 3 × 2 | 1 × 3 × 3 (72) | 3 × 3 × 3 | 10 × 10 × 10 |
| GeTe (R3m) | 2 (6) | 500 | 8 × 8 × 2 | 6 × 6 × 2 (432) | 2 × 2 × 2 | 3 × 3 × 1 (54) | 3 × 3 × 2 | 12 × 12 × 12 |
GeTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
2 (8) | 500 | 5 × 5 × 5 | 3 × 3 × 3 (216) | 2 × 2 × 2 | 2 × 2 × 2 (64) | 3 × 3 × 3 | 15 × 15 × 15 |
| SnTe (Pnma) | 8 (8) | 400 | 3 × 10 × 9 | 2 × 4 × 4 (256) | 2 × 3 × 3 | 1 × 3 × 3 (72) | 3 × 3 × 3 | 9 × 9 × 9 |
| SnTe (R3m) | 2 (6) | 450 | 12 × 12 × 4 | 6 × 6 × 2 (432) | 2 × 2 × 2 | 3 × 3 × 1 (54) | 3 × 3 × 2 | 11 × 11 × 11 |
SnTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
8 (8) | 400 | 6 × 6 × 6 | 3 × 3 × 3 (216) | 2 × 2 × 2 | 2 × 2 × 2 (64) | 3 × 3 × 3 | 10 × 10 × 10 |
Lattice-dynamics and thermal-conductivity calculations were set up and post-processed using the Phonopy and Phono3py codes.39,49 The second and third-order force constants Φ(2)/Φ(3) were determined using the supercell finite-difference approach with the supercell expansions and reduced k-point sampling listed in Table 1 and displacement step sizes of 10−2 and 3 × 10−2 Å respectively. Phonon density of states (DoS) and atom-projected DoS (PDoS) curves g(ν) were computed by interpolating frequencies onto uniform Γ-centered grids with 24 × 24 × 24 (DoS) and 16 × 16 × 16 subdivisions (PDoS) with a Gaussian smearing of width σ = 0.032 THz. Phonon dispersion curves νj(q) were computed by interpolating the frequencies along strings of q-points passing through the high-symmetry wavevectors of the respective Brillouin zones. Where required, transformation matrices were applied to convert the structures and force constants in the conventional cells to the primitive cells for the dispersion calculations. The lattice thermal conductivities were computed using the single-mode relaxation-time approximation (SM-RTA) from modal properties calculated on the Γ-centered q-point grids listed in Table 1. We also calculated the κlatt from the full solution of the linearised phonon Boltzmann transport equation (LBTE). The calculated κlatt from the SM-RTA were analysed using the procedures outlined in our previous work.40–42
3 Results and discussion
3.1 Chalcogenide phases and optimised structures
We examine ten Group IV–VI chalcogenide systems spanning four compositions, viz. GeSe, GeTe, SnSe and SnTe, and four structure types, viz. the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, rhombohedral R3m and orthorhombic Pnma and Cmcm structures.
m, rhombohedral R3m and orthorhombic Pnma and Cmcm structures.
Representative images of the four structure types are shown in Fig. 1. GeSe adopts the disordered orthorhombic Pnma structure at low temperature but undergoes a transition to the highly-symmetric Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (rocksalt) structure at T ≈ 920 K.50,51 GeTe adopts the rhombohedral R3m phase below 690 K and transitions to the Fm
m (rocksalt) structure at T ≈ 920 K.50,51 GeTe adopts the rhombohedral R3m phase below 690 K and transitions to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase above this temperature.27 The Pnma phase of GeTe is also reported to be accessible under applied pressures in the range of 15–37 GPa.37,52 SnTe behaves similarly to GeTe but the transition from the rhombohedral to the cubic phase occurs below 100 K.28 A bulk orthorhombic phase is also reported to be accessible under pressure, and has been observed as nanoscale defects in cubic SnTe under ambient conditions.28 Finally, SnSe adopts the Pnma phase at low temperature but undergoes a phase transition to the higher-symmetry orthorhombic Cmcm phase around 750 K,53,54 the latter of which has been shown to display strong phonon anharmonicity thought to contribute to its exceptional thermoelectric performance.34,55
m phase above this temperature.27 The Pnma phase of GeTe is also reported to be accessible under applied pressures in the range of 15–37 GPa.37,52 SnTe behaves similarly to GeTe but the transition from the rhombohedral to the cubic phase occurs below 100 K.28 A bulk orthorhombic phase is also reported to be accessible under pressure, and has been observed as nanoscale defects in cubic SnTe under ambient conditions.28 Finally, SnSe adopts the Pnma phase at low temperature but undergoes a phase transition to the higher-symmetry orthorhombic Cmcm phase around 750 K,53,54 the latter of which has been shown to display strong phonon anharmonicity thought to contribute to its exceptional thermoelectric performance.34,55
 | ||
Fig. 1 Representative structures showing the four chalcogenide phases examined in this work: (a) Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe; (b) R3m GeTe; (c) Cmcm SnSe; and (d) Pnma GeSe. All four structures are shown in the conventional unit cells. The tetrel atoms are shown in grey and the Te and Se atoms are shown in gold and green, respectively. These images were generated using the VESTA software.56 m SnTe; (b) R3m GeTe; (c) Cmcm SnSe; and (d) Pnma GeSe. All four structures are shown in the conventional unit cells. The tetrel atoms are shown in grey and the Te and Se atoms are shown in gold and green, respectively. These images were generated using the VESTA software.56 | ||
The optimised lattice parameters of each of the ten structures are shown in Table 2. The parameters of all the low-temperature phases are within 5% of literature values.27,36,50,51,53,54,57–59 Larger errors are obtained for the high-temperature phases, with the calculations predicting an 11% reduction in the cell volume of Cmcm SnSe. This is expected given that standard DFT optimisations yield the athermal equilibrium structures, and we therefore attribute the larger % differences for the high-temperature structures to a larger degree of thermal expansion in the measurements.60
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and mass difference Δm
and mass difference Δm
| a [Å] | b [Å] | c [Å] | V [Å3] | m [amu] | ||
|---|---|---|---|---|---|---|
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
|
Δm | |||||
| GeSe (Pnma) | 10.79 (−0.4) | 3.85 (+0.4) | 4.44 (−1.4) | 180.6 (−1.1) | 75.8 | 6.34 |
GeSe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
5.54 (−3.4) | 5.54 (−3.4) | 5.54 (−3.4) | 169.9 (−9.7) | ||
| SnSe (Pnma) | 11.35 (−1.3) | 4.12 (−0.7) | 4.34 (−2.5) | 203.0 (−4.4) | 98.8 | 39.74 |
| SnSe (Cmcm) | 4.15 (−3.4) | 11.35 (−3.1) | 4.12 (−4.5) | 194.3 (−10.6) | ||
| GeTe (Pnma) | 11.52 (−2.1) | 4.17 (+0.4) | 4.45 (+2.1) | 213.7 (+0.4) | 100.1 | 54.97 |
| GeTe (R3m) | 4.15 (−0.6) | 4.15 (−0.6) | 10.41 (−2.6) | 155.1 (−4.0) | ||
GeTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
5.87 (−2.5) | 5.87 (−2.5) | 5.87 (−2.5) | 202.3 (−7.3) | ||
| SnTe (Pnma) | 11.86 (+2.3) | 4.34 (−0.7) | 4.51 (+0.7) | 232.3 (+2.4) | 123.2 | 8.89 |
SnTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
6.25 (−1.0) | 6.25 (−1.0) | 6.25 (−1.0) | 244.4 (−3.5) | ||
| SnTe (R3m) | 4.38 | 4.38 | 10.84 | 180.1 | ||
3.2 Harmonic phonon spectra
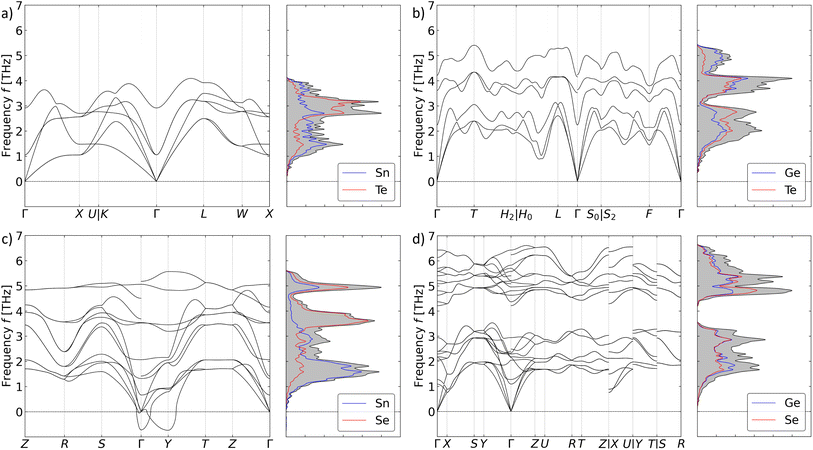
Representative phonon spectra of the four structure types are shown in Fig. 2 arranged by decreasing symmetry from Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → R3m → Cmcm → Pnma. Phonon dispersion and DoS curves for all ten systems are provided in Section 1 of the ESI.†
m → R3m → Cmcm → Pnma. Phonon dispersion and DoS curves for all ten systems are provided in Section 1 of the ESI.†
The number of atoms na in the primitive cells increases with decreasing symmetry (c.f.Table 1), which results in the number of bands at each wavevector q increasing from 3na = 6 in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m systems to 3na = 24 in the Pnma structures. Comparison of the phonon spectra of the Fm
m systems to 3na = 24 in the Pnma structures. Comparison of the phonon spectra of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R3m structures in Fig. 2a and b, which both have six branches in the dispersion, shows that the symmetry lowering due to the rhombohedral distortion leads to lower degeneracy among the phonon bands. Similarly, the spectra of the orthorhombic Cmcm and Pnma structures in Fig. 2c and d show more fine structure due to having 12 and 24 branches in the dispersion, respectively.
m and R3m structures in Fig. 2a and b, which both have six branches in the dispersion, shows that the symmetry lowering due to the rhombohedral distortion leads to lower degeneracy among the phonon bands. Similarly, the spectra of the orthorhombic Cmcm and Pnma structures in Fig. 2c and d show more fine structure due to having 12 and 24 branches in the dispersion, respectively.
In Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe and Cmcm SnSe, the PDoS curves show that the lower and upper-frequency bands are dominated by the tetrel and chalcogen atoms, respectively (Fig. 2a and c). On the other hand, this is not the case for R3m GeTe and Pnma GeSe, for which both atoms make similar contributions across the full frequency spectrum (Fig. 2b and d). Considering the mass differences in Table 2, this behaviour cannot be put down to the difference in atomic masses of the tetrel and chalcogen, and instead indicates a difference in the bonding in the Ge and Sn systems. Indeed, the relative contributions of the tetrel and chalcogen atoms to the phonon spectra appear to depend on both the composition and the crystal symmetry. All three Fm
m SnTe and Cmcm SnSe, the PDoS curves show that the lower and upper-frequency bands are dominated by the tetrel and chalcogen atoms, respectively (Fig. 2a and c). On the other hand, this is not the case for R3m GeTe and Pnma GeSe, for which both atoms make similar contributions across the full frequency spectrum (Fig. 2b and d). Considering the mass differences in Table 2, this behaviour cannot be put down to the difference in atomic masses of the tetrel and chalcogen, and instead indicates a difference in the bonding in the Ge and Sn systems. Indeed, the relative contributions of the tetrel and chalcogen atoms to the phonon spectra appear to depend on both the composition and the crystal symmetry. All three Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures show some level of split contributions, which are most prominent in GeSe. R3m GeTe shows roughly equal contributions from both elements across the frequency spectrum, whereas the spectrum of R3m SnTe shows unequal contributions that are particularly prominent in a feature between ∼2.5–3.5 THz. With the exception of SnSe, the Pnma phases also show roughly equal contributions from the tetrel and chalcogen atoms across the full phonon spectrum, whereas tin selenide shows larger contributions from Sn at low frequencies and larger contributions from Se at higher frequencies. This is also evident in the phonon spectrum of Cmcm SnSe. The lower coordination number and more directional bonding in the orthorhombic Pnma and Cmcm phases may indicate a higher degree of covalent character compared to the higher-symmetry Fm
m structures show some level of split contributions, which are most prominent in GeSe. R3m GeTe shows roughly equal contributions from both elements across the frequency spectrum, whereas the spectrum of R3m SnTe shows unequal contributions that are particularly prominent in a feature between ∼2.5–3.5 THz. With the exception of SnSe, the Pnma phases also show roughly equal contributions from the tetrel and chalcogen atoms across the full phonon spectrum, whereas tin selenide shows larger contributions from Sn at low frequencies and larger contributions from Se at higher frequencies. This is also evident in the phonon spectrum of Cmcm SnSe. The lower coordination number and more directional bonding in the orthorhombic Pnma and Cmcm phases may indicate a higher degree of covalent character compared to the higher-symmetry Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R3m phases, which could partially explain differences in the atomic contributions to the phonon spectra. However, to confirm this, or otherwise, would require a more detailed analysis of the chemical bonding, and the different contributions of the tetrel and chalcogen atoms to the lower- and higher-frequency parts of the spectra of the two orthorhombic phases of SnSe suggests there are some deeper subtleties.
m and R3m phases, which could partially explain differences in the atomic contributions to the phonon spectra. However, to confirm this, or otherwise, would require a more detailed analysis of the chemical bonding, and the different contributions of the tetrel and chalcogen atoms to the lower- and higher-frequency parts of the spectra of the two orthorhombic phases of SnSe suggests there are some deeper subtleties.
The dispersion of Pnma GeSe also displays a prominent “band gap” from ∼3.5–4 THz (Fig. 2d). This appears to be a feature of the Pnma structure, and is most prominent in GeSe and GeTe but also evident in SnSe and SnTe. In the case of SnSe, the gap marks the point where the relative contributions of the tetrel and chalcogen atoms reverse. The spectrum of R3m GeTe also shows a notable reduction in the DoS at mid frequencies, but this is not seen in the spectrum of R3m SnTe, suggesting that the nature of the tetrel atom plays a role in the gap in this structure type. The absence/lower density of modes in the gap range implies that there is no/little contribution to the lattice thermal conductivity at these frequencies, a point to which we return below.
The range of the frequency spectra closely track the average masses. The phonon frequencies in Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe, which has the largest average mass of the four systems for which phonon spectra are shown in Fig. 2, range up to ∼4 THz, whereas the frequencies in Pnma GeSe, which has the smallest average mass, range up to ∼7 THz. The frequencies in Cmcm SnSe and R3m GeTe, which have similar average masses, both range up to around 6 THz, i.e. intermediate between the limits set by SnTe and GeSe. This pattern is observed across all ten systems, regardless of structure type. The “compression” of the phonon spectrum with increasing average mass would be expected to increase the density of allowed phonon scattering pathways at a given frequency, i.e. the scattering phase space, which we again investigate further below.
m SnTe, which has the largest average mass of the four systems for which phonon spectra are shown in Fig. 2, range up to ∼4 THz, whereas the frequencies in Pnma GeSe, which has the smallest average mass, range up to ∼7 THz. The frequencies in Cmcm SnSe and R3m GeTe, which have similar average masses, both range up to around 6 THz, i.e. intermediate between the limits set by SnTe and GeSe. This pattern is observed across all ten systems, regardless of structure type. The “compression” of the phonon spectrum with increasing average mass would be expected to increase the density of allowed phonon scattering pathways at a given frequency, i.e. the scattering phase space, which we again investigate further below.
Finally, the spectrum of Cmcm SnSe in Fig. 2c shows two imaginary phonon modes at the q = Γ and Y wavevectors. These modes are linked to the soft-mode phase transition to the Pnma phase.34 Mapping the instability as a function of the distortion amplitudes QΓ and QY (Fig. 3) shows that the Cmcm phase is a local maximum on the two-dimensional potential-energy surface (PES) spanned by the principal imaginary modes, connecting two minima located along q = Y. These minima correspond to two equivalent distortions of the Cmcm structure to the lower-symmetry Pnma phase, and the Cmcm phase is therefore a “hilltop” on the structural PES connecting Pnma minima. The minima are relatively shallow with respect to the hilltop at (QΓ = 0, QY = 0), and at temperatures above the phase transition the two minima can interconvert sufficiently quickly that experimental techniques that probe the long-range structure (e.g. X-ray diffraction) will effectively “see” the Cmcm phase as an average structure.61 On the other hand, Pnma SnSe, and indeed all four of the Pnma structures examined here, are dynamically stable and do not have imaginary harmonic modes in the dispersion. The soft-mode transition in Cmcm SnSe, and its impact on the structure and lattice dynamics, has been the subject of a number of previous studies.33,34,60,62
We also note that the spectrum of GeSe has a triply-degenerate imaginary optic mode at the q = Γ wavevector, which becomes doubly-degenerate when a non-analytical correction is applied, and this likely indicates a distortion to the R3m phase. However, we did not pursue this further.
3.3 Lattice thermal conductivity
Within the single-mode relaxation time approximation (SM-RTA) the macroscopic κlatt, hereafter κ, is determined as a sum over microscopic contributions κλ from individual phonon modes λ = qj according to: | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
Fig. 4 compares the calculated κ of the ten systems as a function of temperature, and values at T = 300 K are summarised in Table 3. For ease of comparison we discuss here the isotropic scalar average κiso defined as:
 | (7) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase, whereas for the R3m phase κxx = κyy ≠ κzz and for the orthorhombic Pnma and Cmcm phases κxx ≠ κyy ≠ κzz. For each compound, we show the separate temperature dependencies of the κxx, κyy and κzz in Section 2 of the ESI† and the values at 300 K are included in Table 3.
m phase, whereas for the R3m phase κxx = κyy ≠ κzz and for the orthorhombic Pnma and Cmcm phases κxx ≠ κyy ≠ κzz. For each compound, we show the separate temperature dependencies of the κxx, κyy and κzz in Section 2 of the ESI† and the values at 300 K are included in Table 3.
 | ||
| Fig. 4 Calculated scalar-average lattice thermal conductivity κiso (eqn (7)) as a function of temperature for the ten systems examined in this work. | ||
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 defined in eqn (13) from 0 to the maximum frequencies fmax in the phonon spectra, and the averaged phonon–phonon interaction strength
2 defined in eqn (13) from 0 to the maximum frequencies fmax in the phonon spectra, and the averaged phonon–phonon interaction strength ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) and number of scattering channels Ñ2 defined in eqn (12)–(17)
and number of scattering channels Ñ2 defined in eqn (12)–(17)
| κ [W m−1 K−1] | (κ/τCRTA)iso [W m−1 K−1 ps−1] | τ CRTA [ps] |
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) × (3na)2 [eV2] × (3na)2 [eV2] |
Ñ 2/(3na)2 [THz−1] | |||||
|---|---|---|---|---|---|---|---|---|---|
| κ xx | κ yy | κ zz | κ iso | ||||||
| SnSe (Cmcm) | 0.39 | 0.79 | 1.18 | 0.96 | 1.09 | 0.88 | 1.36 | 1.46 × 10−7 | 4.74 × 10−3 |
| SnTe (Pnma) | 0.63 | 1.41 | 1.23 | 1.09 | 0.27 | 3.98 | 6.22 | 9.02 × 10−9 | 1.70 × 10−2 |
| GeTe (Pnma) | 0.45 | 2.09 | 1.43 | 1.32 | 0.34 | 3.91 | 5.39 | 1.35 × 10−8 | 1.15 × 10−2 |
| SnSe (Pnma) | 0.91 | 1.83 | 1.34 | 1.36 | 0.35 | 3.89 | 5.22 | 1.20 × 10−8 | 1.31 × 10−2 |
GeSe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
1.57 | — | — | 1.57 | 3.29 | 0.48 | 0.28 | 2.24 × 10−6 | 5.69 × 10−4 |
GeTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
1.67 | — | — | 1.67 | 2.99 | 0.56 | 0.33 | 1.31 × 10−6 | 8.35 × 10−4 |
| GeSe (Pnma) | 1.05 | 3.93 | 2.09 | 2.36 | 0.39 | 6.03 | 4.39 | 1.36 × 10−8 | 7.44 × 10−3 |
| SnTe (R3m) | 4.27 | — | 3.99 | 4.18 | 0.69 | 6.07 | 0.63 | 5.20 × 10−8 | 1.93 × 10−3 |
| GeTe (R3m) | 4.71 | — | 3.67 | 4.36 | 0.87 | 5.01 | 0.53 | 8.97 × 10−8 | 1.36 × 10−3 |
SnTe (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
5.01 | — | — | 5.01 | 1.07 | 4.67 | 0.37 | 1.09 × 10−7 | 1.20 × 10−3 |
The 300 K κiso = 1.36 W m−1 K−1 calculated for Pnma SnSe is comparable to our previous calculations of 1.28 and 1.58 W m−1 K−1, and to the higher range of the experimental measurements of 0.7–1.4 and 0.5–0.9 W m−1 K−1 along the in-plane and layering directions.32,33,41 We attribute the differences to previous calculations primarily to the different supercell used for the force-constant calculations compared to ref. 33 and to the omission of a dispersion correction compared to ref. 41. Our previous calculations on Cmcm SnSe yielded a κiso of 0.33 W m−1 K−1 at 800 K, and we obtain a similar 0.36 W m−1 K−1 here. Two separate reports give the κiso of Pnma GeSe to be 2.63 and 1.77 W m−1 K−1 at 300 K,13,63 and our calculated value of 2.35 W m−1 K−1 falls within this range. Our calculated room-temperature κiso = 4.36 W m−1 K−1 for R3m GeTe is around 30% higher than the experimentally-measured ∼3.4 W m−1 K−1.64 The thermal conductivity of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m GeTe has been measured as ∼1.5 W m−1 K−1 and predicted to be 0.75–1.25 at 700 K,27,65 the latter of which compares well to the value of 0.72 W m−1 K−1 from our calculations. The room-temperature κiso of Fm
m GeTe has been measured as ∼1.5 W m−1 K−1 and predicted to be 0.75–1.25 at 700 K,27,65 the latter of which compares well to the value of 0.72 W m−1 K−1 from our calculations. The room-temperature κiso of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe has been measured between ∼2–4.5 W m−1 K−1 at 300 K,25,66,67 and our predicted value of 5.01 W m−1 K−1 is compatible with the upper limit. We note that the variation among the four samples reported in ref. 66 highlights the sensitivity of the measured thermal conductivity to the sample preparation.
m SnTe has been measured between ∼2–4.5 W m−1 K−1 at 300 K,25,66,67 and our predicted value of 5.01 W m−1 K−1 is compatible with the upper limit. We note that the variation among the four samples reported in ref. 66 highlights the sensitivity of the measured thermal conductivity to the sample preparation.
Barring two exceptions, the materials can be grouped by structure type. Cmcm SnSe has the lowest κiso, followed by Pnma SnTe, GeTe and SnSe, then Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m GeSe and GeTe, and finally R3m SnTe and GeTe. Cmcm SnSe is therefore predicted to have the smallest κiso across all ten systems, which is consistent with its exceptional thermoelectric performance.55,68,69 The two exceptions to the trend are Pnma GeSe, which falls between the two lighter Fm
m GeSe and GeTe, and finally R3m SnTe and GeTe. Cmcm SnSe is therefore predicted to have the smallest κiso across all ten systems, which is consistent with its exceptional thermoelectric performance.55,68,69 The two exceptions to the trend are Pnma GeSe, which falls between the two lighter Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m systems and the R3m systems, and Fm
m systems and the R3m systems, and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe. Among the four Pnma systems, the ordering in the 300 K thermal conductivity of SnTe < SnSe ≃ GeSe < GeSe largely follows the average masses in Table 2. We therefore do not consider the κiso of GeSe to be an outlier. The same holds for the two R3m phases, i.e. the κiso of SnTe is lower than that of GeTe, but with just two data points we cannot really consider this a trend. On the other hand, while Fm
m SnTe. Among the four Pnma systems, the ordering in the 300 K thermal conductivity of SnTe < SnSe ≃ GeSe < GeSe largely follows the average masses in Table 2. We therefore do not consider the κiso of GeSe to be an outlier. The same holds for the two R3m phases, i.e. the κiso of SnTe is lower than that of GeTe, but with just two data points we cannot really consider this a trend. On the other hand, while Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m GeSe has a lower κiso than GeTe, as expected, SnTe, with the largest average mass, has a much larger predicted κiso, and therefore does represent an outlier here.
m GeSe has a lower κiso than GeTe, as expected, SnTe, with the largest average mass, has a much larger predicted κiso, and therefore does represent an outlier here.
It is also of interest to investigate how modes with different frequencies contribute to the κ. This can be determined from a cumulative sum of the κλ in eqn (2) as a function of frequency at a reference temperature T:
 | (8) |
Fig. 5 shows the cumulative κiso at T = 300 K for the four representative systems in Fig. 2, viz. Pnma GeSe, R3m GeTe, Cmcm SnSe and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe. For Pnma GeSe, which has a bandgap in its dispersion (c.f.Fig. 2d), around 85% of the thermal conductivity is due to transport through the 50% of the modes below the gap. There is also a clear flattening of the cumulative κiso over the gap region, as the absence of modes means there is no thermal transport over this frequency range. The cumulative κiso of R3m GeTe shows similar behaviour, with a notable reduction in the rate of accumulation around ca. 3 THz coinciding with the dip in the DoS (c.f.Fig. 2b) and a ∼75–80% contribution from the modes below this frequency. While Cmcm SnSe does not have a phonon bandgap, if we take the midpoint of the spectrum to be ∼3 THz, around 85% of the κiso is from transport through modes with frequencies below this cutoff, which is consistent with the Pnma and R3m systems. On the other hand, for the heaviest compound, Fm
m SnTe. For Pnma GeSe, which has a bandgap in its dispersion (c.f.Fig. 2d), around 85% of the thermal conductivity is due to transport through the 50% of the modes below the gap. There is also a clear flattening of the cumulative κiso over the gap region, as the absence of modes means there is no thermal transport over this frequency range. The cumulative κiso of R3m GeTe shows similar behaviour, with a notable reduction in the rate of accumulation around ca. 3 THz coinciding with the dip in the DoS (c.f.Fig. 2b) and a ∼75–80% contribution from the modes below this frequency. While Cmcm SnSe does not have a phonon bandgap, if we take the midpoint of the spectrum to be ∼3 THz, around 85% of the κiso is from transport through modes with frequencies below this cutoff, which is consistent with the Pnma and R3m systems. On the other hand, for the heaviest compound, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe, for which the phonon spectrum extends to around 4 THz, around 95% of the thermal conductivity is through modes below ∼3 THz. Across all four compounds, therefore, the low-frequency phonon modes with fλ < 2.5–3 THz contribute > 75% of κiso. This can be understood based on the fact that the lower-frequency modes tend to have wider dispersions than the higher-frequency modes, resulting in larger group velocities, and are also more heavily populated, i.e. have larger occupation numbers nλ at a given temperature (c.f.Fig. 2, eqn (4) and (5)).
m SnTe, for which the phonon spectrum extends to around 4 THz, around 95% of the thermal conductivity is through modes below ∼3 THz. Across all four compounds, therefore, the low-frequency phonon modes with fλ < 2.5–3 THz contribute > 75% of κiso. This can be understood based on the fact that the lower-frequency modes tend to have wider dispersions than the higher-frequency modes, resulting in larger group velocities, and are also more heavily populated, i.e. have larger occupation numbers nλ at a given temperature (c.f.Fig. 2, eqn (4) and (5)).
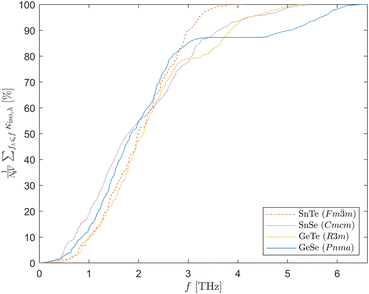 | ||
Fig. 5 Cumulative κiso as a function of frequency at T = 300 K for Pnma GeSe, R3m GeTe, Cmcm SnSe and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe. m SnTe. | ||
3.4 Group velocity versus lifetimes
We have previously shown that differences in lattice thermal conductivity can be attributed quantitatively to differences in the phonon group velocities and lifetimes using a constant relaxation-time approximation (CRTA) analysis.40–42 In this model, we choose a (scalar) temperature-dependent average lifetime τCRTA such that the κ can be written approximately as: | (9) |
The (κ/τCRTA)iso as a function of temperature are shown for the ten compounds in Fig. 6a, and the values at 300 K are provided in Table 3. As found in our previous work on the silicon clathrates,42 we see a strong dependence on the number of atoms na in the primitive cell and the crystal symmetry. The four Pnma phases, which have the largest na = 8, have the lowest values, the two R3m phases have intermediate values (na = 2, lower symmetry), and the three Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases have the largest values (na = 2, higher symmetry). The large unit cell of the Pnma structure therefore lends itself to lower phonon group velocities, as does the symmetry breaking in the R3m structure compared to the Fm
m phases have the largest values (na = 2, higher symmetry). The large unit cell of the Pnma structure therefore lends itself to lower phonon group velocities, as does the symmetry breaking in the R3m structure compared to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. Cmcm SnSe is an outlier here, as despite its relatively large primitive cell (na = 4) and low orthorhombic symmetry it has a larger (κ/τCRTA)iso than R3m GeTe and SnTe and Fm
m phase. Cmcm SnSe is an outlier here, as despite its relatively large primitive cell (na = 4) and low orthorhombic symmetry it has a larger (κ/τCRTA)iso than R3m GeTe and SnTe and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe. We attribute this to the imaginary modes leading to a sharp dispersion and large νλ in some of the phonon branches (c.f.Fig. 2c and eqn (5)). In reality, above the Pnma → Cmcm transition temperature we would expect the imaginary modes to be “renormalised” to real frequencies.33,62 The experiments in ref. 34 noted a substantial phonon softening in SnSe with temperature, leading to a reduction in the νλ on the order of 20%, which would not be captured by the fixed-volume structures used in our calculations. It is therefore not clear whether this phenomenon is a feature of materials with soft-mode phase transitions. Finally, for a given crystal structure we observe a clear dependence of the (κ/τCRTA)iso on the average mass, such that the values fall in the order of SnTe < SnSe ≃ GeTe < GeSe, SnTe < GeTe, and SnTe ≪ GeTe < GeSe for the Pnma, R3m and Fm
m SnTe. We attribute this to the imaginary modes leading to a sharp dispersion and large νλ in some of the phonon branches (c.f.Fig. 2c and eqn (5)). In reality, above the Pnma → Cmcm transition temperature we would expect the imaginary modes to be “renormalised” to real frequencies.33,62 The experiments in ref. 34 noted a substantial phonon softening in SnSe with temperature, leading to a reduction in the νλ on the order of 20%, which would not be captured by the fixed-volume structures used in our calculations. It is therefore not clear whether this phenomenon is a feature of materials with soft-mode phase transitions. Finally, for a given crystal structure we observe a clear dependence of the (κ/τCRTA)iso on the average mass, such that the values fall in the order of SnTe < SnSe ≃ GeTe < GeSe, SnTe < GeTe, and SnTe ≪ GeTe < GeSe for the Pnma, R3m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases.
m phases.
 | ||
| Fig. 6 Constant relaxation-time approximation (CRTA) analysis of the lattice thermal conductivity of the ten chalcogenides examined in this work (eqn (9)): (a) calculated averaged harmonic sum (κ/τCRTA)iso and (b) calculated average lifetimes τCRTA as a function of temperature. | ||
On the other hand, the τCRTA values do not exhibit any obvious trends (Fig. 6b and Table 3). Three of the four Pnma crystal structures, SnSe, GeTe, and SnTe, have very similar averaged phonon lifetimes between 3.89–3.98 ps at 300 K, whereas the τCRTA of the lighter Pnma GeSe is approximately ∼50% longer at 6.03 ps. Among the three Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures, both GeSe and GeTe display very short averaged lifetimes of around 0.5 ps, whereas SnTe has a much longer τCRTA of 4.67 ps that exceeds those of three of the four Pnma systems. The two R3m crystal structures both exhibit consistently longer τCRTA than other phases with the same chemical composition. Lastly, the τCRTA of Cmcm SnSe is approximately ∼25% that of the Pnma phase at 300 K. This shorter τCRTA plays a crucial role in compensating for the roughly threefold increase in the (κ/τCRTA)iso term, resulting in an overall lower κiso compared to the lower-symmetry Pnma phase. The variation in the τCRTA values across the ten systems is thus somewhat intricate, necessitating a more detailed analysis of the underlying physical mechanisms, which is the subject of the following section.
m structures, both GeSe and GeTe display very short averaged lifetimes of around 0.5 ps, whereas SnTe has a much longer τCRTA of 4.67 ps that exceeds those of three of the four Pnma systems. The two R3m crystal structures both exhibit consistently longer τCRTA than other phases with the same chemical composition. Lastly, the τCRTA of Cmcm SnSe is approximately ∼25% that of the Pnma phase at 300 K. This shorter τCRTA plays a crucial role in compensating for the roughly threefold increase in the (κ/τCRTA)iso term, resulting in an overall lower κiso compared to the lower-symmetry Pnma phase. The variation in the τCRTA values across the ten systems is thus somewhat intricate, necessitating a more detailed analysis of the underlying physical mechanisms, which is the subject of the following section.
3.5 Anharmonicity versus conservation of energy
In the SM-RTA model employed in this work the phonon lifetimes τλ are calculated as the inverse of the linewidths Γλ. The Γλ are determined as twice the imaginary part of the phonon self-energy from a sum of contributions from three-phonon scattering processes according to:39 | (10) |
Following ref. 39, we define an approximate linewidth ![[capital Gamma, Greek, tilde]](https://www.rsc.org/images/entities/char_e1eb.gif) λ as:
λ as:
 | (11) |
 | (12) |
| N2(q,ω,T) = N(1)2(q,ω,T) + N(2)2(q,ω,T) | (13) |
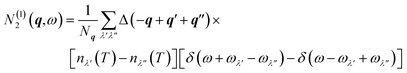 | (14) |
 | (15) |
For comparison between systems, it is useful to average the N2 over q to obtain functions of frequency only, i.e.:
 | (16) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 need to be scaled by a factor of 1/(3na)2, which is folded into the definition of the Pλ in eqn (12).
2 need to be scaled by a factor of 1/(3na)2, which is folded into the definition of the Pλ in eqn (12).
The calculated ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2(1) and
2(1) and ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2(2) of Cmcm SnSe at 300 K are shown in Fig. 7, and equivalent plots for all ten systems are provided in Section 4 of the ESI.† In general, collisions are dominant at low frequencies up to around 2 THz, above which phonons have sufficient energy to access decay pathways, and these become competitive with collisions from ∼2–3 THz and dominate at higher frequencies. The total number of scattering pathways also generally increases considerably at frequencies approaching the maximum frequency fmax in the phonon spectrum. With reference to the cumulative κiso in Fig. 5, which indicate that the majority of the thermal transport occurs through modes with fλ < 3 THz, this analysis shows that the averaged lifetimes are limited mainly by collision processes, and, assuming similar interaction strengths, that transport through the higher-energy modes may be limited by a larger scattering phase space.
2(2) of Cmcm SnSe at 300 K are shown in Fig. 7, and equivalent plots for all ten systems are provided in Section 4 of the ESI.† In general, collisions are dominant at low frequencies up to around 2 THz, above which phonons have sufficient energy to access decay pathways, and these become competitive with collisions from ∼2–3 THz and dominate at higher frequencies. The total number of scattering pathways also generally increases considerably at frequencies approaching the maximum frequency fmax in the phonon spectrum. With reference to the cumulative κiso in Fig. 5, which indicate that the majority of the thermal transport occurs through modes with fλ < 3 THz, this analysis shows that the averaged lifetimes are limited mainly by collision processes, and, assuming similar interaction strengths, that transport through the higher-energy modes may be limited by a larger scattering phase space.
 | ||
Fig. 7 Averaged two-phonon weighted joint density of states (w-JDoS) ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2(f) (eqn (16)) for Cmcm SnSe. The separate contributions from collision ( 2(f) (eqn (16)) for Cmcm SnSe. The separate contributions from collision (![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) (1)2) and decay processes ( (1)2) and decay processes (![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) (2)2) are shown in blue and red, respectively, as a stacked-area plot. (2)2) are shown in blue and red, respectively, as a stacked-area plot. | ||
A comparison of the normalised ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 of the ten systems (Fig. 8a) reveals some notable trends. After normalisation the scattering phase space depends strongly on na, such that at most frequencies the
2 of the ten systems (Fig. 8a) reveals some notable trends. After normalisation the scattering phase space depends strongly on na, such that at most frequencies the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 are highest for the Pnma phases (na = 8), intermediate for Cmcm SnSe (na = 4), and lowest and comparable for the R3m and Fm
2 are highest for the Pnma phases (na = 8), intermediate for Cmcm SnSe (na = 4), and lowest and comparable for the R3m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases (na = 2). This can be attributed to the more complex phonon spectra enabling more scattering pathways (c.f.Fig. 2). Also, the fine structure in the phonon DoS curves is partially reflected in the
m phases (na = 2). This can be attributed to the more complex phonon spectra enabling more scattering pathways (c.f.Fig. 2). Also, the fine structure in the phonon DoS curves is partially reflected in the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2, with those of the Pnma phases showing a mid-frequency reduction reminiscent of the phonon bandgaps in the DoS. However, whereas the phonon bandgap in Pnma GeSe occurs at ∼3.5–3 THz, the minimum in the
2, with those of the Pnma phases showing a mid-frequency reduction reminiscent of the phonon bandgaps in the DoS. However, whereas the phonon bandgap in Pnma GeSe occurs at ∼3.5–3 THz, the minimum in the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 occurs around 6 THz, and the absence of modes in the bandgap therefore affects the scattering (largely decay processes) of the high-frequency optic modes. However, the reduction in the DoS of R3m GeTe at intermediate frequencies in Fig. 2b does not appear to be reflected in the
2 occurs around 6 THz, and the absence of modes in the bandgap therefore affects the scattering (largely decay processes) of the high-frequency optic modes. However, the reduction in the DoS of R3m GeTe at intermediate frequencies in Fig. 2b does not appear to be reflected in the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2, at least not as clearly as in the corresponding Pnma phase. Finally, the spread of the
2, at least not as clearly as in the corresponding Pnma phase. Finally, the spread of the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 depends on the spread of the frequency spectra. Among the four Pnma phases, the
2 depends on the spread of the frequency spectra. Among the four Pnma phases, the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 of SnTe is notably “compressed” compared to that of GeTe, with larger features at lower frequencies, while SnSe and GeTe have similar
2 of SnTe is notably “compressed” compared to that of GeTe, with larger features at lower frequencies, while SnSe and GeTe have similar ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2. A crude comparison of the size of the phase space obtained by integrating the
2. A crude comparison of the size of the phase space obtained by integrating the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 from zero to the maximum frequency fmax in the phonon spectra confirms that a narrower frequency spectrum generally results in a larger scattering phase space (Table 3).
2 from zero to the maximum frequency fmax in the phonon spectra confirms that a narrower frequency spectrum generally results in a larger scattering phase space (Table 3).
 | ||
Fig. 8 Analysis of the phonon lifetimes of the ten systems examined in this work. (a) Averaged two-phonon weighted joint density of states (w-JDoS) functions ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2(f), defined in eqn (16), for the ten materials examined in this study. The functions have been normalised by 1/(3na)2 to be comparable between the phases with different na. (b) Comparison of the averaged lifetimes τCRTA and inverse three-phonon interaction strengths 2(f), defined in eqn (16), for the ten materials examined in this study. The functions have been normalised by 1/(3na)2 to be comparable between the phases with different na. (b) Comparison of the averaged lifetimes τCRTA and inverse three-phonon interaction strengths ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) for the ten materials examined in this work at T = 300 K. The trendline shows the correlation for the three Fm for the ten materials examined in this work at T = 300 K. The trendline shows the correlation for the three Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m systems (R2 ≈ 1). m systems (R2 ≈ 1). | ||
For a more quantitative analysis, we replace the |Φ−λλ′λ′′|2 in eqn (10) with a constant value ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) representing a weighted average of the Pλ defined in eqn (12). With this substitution, the κ is inversely proportional to
representing a weighted average of the Pλ defined in eqn (12). With this substitution, the κ is inversely proportional to ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) and a suitable value to reproduce the κ at a given temperature can be determined from a linear fit.40–42 In the same way as the τCRTA are a weighted-average lifetime, the
and a suitable value to reproduce the κ at a given temperature can be determined from a linear fit.40–42 In the same way as the τCRTA are a weighted-average lifetime, the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) are a weighted average of the Φ−λλ′λ′′/Pλ. We note that, like the N2/
are a weighted average of the Φ−λλ′λ′′/Pλ. We note that, like the N2/![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2, the
2, the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) scale with the size of the primitive cell and need to be multiplied by (3na)2 to compare between systems. The values of
scale with the size of the primitive cell and need to be multiplied by (3na)2 to compare between systems. The values of ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) computed at T = 300 K are presented alongside the κ in Table 3. We also show the linear fits performed to determine these parameters, together with a comparison of the
computed at T = 300 K are presented alongside the κ in Table 3. We also show the linear fits performed to determine these parameters, together with a comparison of the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) to the frequency spectra of the Pλ, in Section 5 of the ESI.†
to the frequency spectra of the Pλ, in Section 5 of the ESI.†
Finally, we can combine the averaged lifetimes τCRTA with the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) using eqn (11) to determine a weighted average number of scattering pathways Ñ2 as:
using eqn (11) to determine a weighted average number of scattering pathways Ñ2 as:
 | (17) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 to assess the impact of differences in the size of the scattering phase space on the phonon linewidths/lifetimes.
2 to assess the impact of differences in the size of the scattering phase space on the phonon linewidths/lifetimes.
This analysis allows us to discuss the τCRTA in terms of the strength of the interactions between phonons – anharmonicity in this model – and the size of the scattering phase space enabled by the shape of the phonon spectrum. Systems with a short τCRTA may show strong phonon–phonon interactions (large ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ) and/or a large phase space (large Ñ2). Conversely, systems with long averaged lifetimes could show weak anharmonicity (small
) and/or a large phase space (large Ñ2). Conversely, systems with long averaged lifetimes could show weak anharmonicity (small ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ) and/or a small phase space (small Ñ2).
) and/or a small phase space (small Ñ2).
The normalised ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) in Table 3 span two orders of magnitude and show a clear variation with structure type. The four Pnma phases have the smallest values, while Fm
in Table 3 span two orders of magnitude and show a clear variation with structure type. The four Pnma phases have the smallest values, while Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m GeTe and GeSe have the largest. Fm
m GeTe and GeSe have the largest. Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe appears to be an outlier with an order of magnitude smaller
m SnTe appears to be an outlier with an order of magnitude smaller ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) than the other two Fm
than the other two Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures, which accounts for the longer τCRTA highlighted in the preceding discussion. R3m GeTe and SnTe, and Cmcm SnSe, all have intermediate values.
m structures, which accounts for the longer τCRTA highlighted in the preceding discussion. R3m GeTe and SnTe, and Cmcm SnSe, all have intermediate values.
The inverse of the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) are plotted against the averaged lifetimes τCRTA at 300 K in Fig. 8b. If the differences in the τCRTA are mainly determined by differences in the interaction strengths, we would expect a good linear correlation.42 The three Fm
are plotted against the averaged lifetimes τCRTA at 300 K in Fig. 8b. If the differences in the τCRTA are mainly determined by differences in the interaction strengths, we would expect a good linear correlation.42 The three Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m do show a very good linear correlation (R2 ≈ 1), which suggests anharmonicity predominantly accounts for the differences in the lifetimes. While it appears that this correlation could be extended to the two R3m phases and Cmcm SnSe, the correlation was found not to be statistically significant when tested. On the other hand, the four Pnma phases form a discrete cluster that clearly does not fall on the trendline set by the other six systems. Compared to the other structures, the lifetimes are considerably shorter than would be expected given the weaker
m do show a very good linear correlation (R2 ≈ 1), which suggests anharmonicity predominantly accounts for the differences in the lifetimes. While it appears that this correlation could be extended to the two R3m phases and Cmcm SnSe, the correlation was found not to be statistically significant when tested. On the other hand, the four Pnma phases form a discrete cluster that clearly does not fall on the trendline set by the other six systems. Compared to the other structures, the lifetimes are considerably shorter than would be expected given the weaker ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) , indicating that the lifetimes of the Pnma phases are strongly influenced by the size of the scattering phase space.
, indicating that the lifetimes of the Pnma phases are strongly influenced by the size of the scattering phase space.
The Ñ2 vary over approximately an order of magnitude – i.e. they show an order of magnitude less variation than the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) – and generally in the opposite direction, being largest for the four Pnma phases and smallest for the three Fm
– and generally in the opposite direction, being largest for the four Pnma phases and smallest for the three Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases. Noting again that the majority of the heat transport occurs through the low-frequency modes (c.f.Fig. 5), the Ñ2 (and also the τCRTA and
m phases. Noting again that the majority of the heat transport occurs through the low-frequency modes (c.f.Fig. 5), the Ñ2 (and also the τCRTA and ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ) will be weighted towards these modes, and the trends among compounds with the same structures reflect the impact of the range of the frequency spectra on the
) will be weighted towards these modes, and the trends among compounds with the same structures reflect the impact of the range of the frequency spectra on the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 (c.f.Fig. 8a).
2 (c.f.Fig. 8a).
Overall, the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) span two orders of magnitude and are largest for the more symmetric structures, whereas the Ñ2 span one order of magnitude and are largest for the less symmetric structures. Together, these two competing factors account for the roughly one order of magnitude variation in the τCRTA. The long τCRTA of Fm
span two orders of magnitude and are largest for the more symmetric structures, whereas the Ñ2 span one order of magnitude and are largest for the less symmetric structures. Together, these two competing factors account for the roughly one order of magnitude variation in the τCRTA. The long τCRTA of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m SnTe and the two R3m phases highlighted in the previous section can, based on the analysis here, be attributed to a combination of relatively low
m SnTe and the two R3m phases highlighted in the previous section can, based on the analysis here, be attributed to a combination of relatively low ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) and Ñ2, indicative of weak anharmonicity and a small scattering phase space, respectively. Similarly, as noted above, the analysis shows that the weak anharmonicity (low
and Ñ2, indicative of weak anharmonicity and a small scattering phase space, respectively. Similarly, as noted above, the analysis shows that the weak anharmonicity (low ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) ) of the Pnma phases is compensated by a large number of scattering pathways (large Ñ2) due to the large primitive cells and relatively complex phonon spectra, and this is why these four systems do not follow the trend in Fig. 8b. Finally, the ∼80% shorter averaged lifetime of Cmcm SnSe compared to the related Pnma phase is a favourable balance of an order of magnitude higher
) of the Pnma phases is compensated by a large number of scattering pathways (large Ñ2) due to the large primitive cells and relatively complex phonon spectra, and this is why these four systems do not follow the trend in Fig. 8b. Finally, the ∼80% shorter averaged lifetime of Cmcm SnSe compared to the related Pnma phase is a favourable balance of an order of magnitude higher ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) but a 50% smaller Ñ2.
but a 50% smaller Ñ2.
3.6 Discussion
Our analysis shows that the link between the κ and structure type of the group IV–VI chalcogenides can be explained through two opposing trends.The first trend is that the complexity of the structure, in particular the number of atoms na in the primitive cell, determines the phonon group velocities. To explain this, we consider the “toy model” of a 1D diatomic chain comprising a unit cell of length a with two independent atoms of mass m and two bond force constants k and g (Fig. 9). In this model, the group velocity of the acoustic modes is given analytically by:
 | (18) |
For completeness, we also consider the effect of increasing the average bond strength by 25% and increasing the mass by 50%. In the first case, at small Δ the va is larger, as expected, but around Δ ∼ 0.45 the group velocity falls below that of the first model with k = g = 1. This shows that large bonding inhomogeneity can potentially offset stronger (average) bonding to produce overall lower group velocities. In the second case, the νa are simply scaled down by  , which shows how increasing the (average) mass also reduces the group velocities.
, which shows how increasing the (average) mass also reduces the group velocities.
An important qualitative conclusion is that large average mass and/or weak chemical bonding, which are often taken to be indicators of low lattice thermal conductivity, are secondary to the complexity of the structure. On this point we note that, with the exception of the two R3m structures, the chalcogenide phases with larger na are also in lower-symmetry space groups, so we cannot easily decouple these in our definition of “structural complexity”. However, our previous work on the Si clathrates42 strongly suggests that the na rather than the crystal (spacegroup) symmetry is likely to be the key descriptor. Another interesting observation from our analysis is the imaginary modes in Cmcm SnSe producing a steep dispersion and larger νλ compared to the Pnma phase. The impact of anharmonic renormalisation and potential phonon softening at elevated temperature34 on this behaviour requires further investigation.
The second trend is that the crystal symmetry has a strong bearing on the phonon lifetimes through opposing effects on the anharmonic three-phonon interaction strengths and the size of the scattering phase space.
We propose a structural basis for the differences in interaction strengths based on the revised lone-pair model of Walsh et al.70 In the IV–VI monochalcogenides, the tetrel atoms adopt the +2 oxidation state with a valence ns2 lone pair of electrons. The lone pair is not chemically inert and interacts with the anion p orbitals to form bonding and antibonding states. When this interaction is strong, and the antibonding states have substantial cation s character, the antibonding states can mix with the vacant cation p states through on-site hybridisation, resulting in further stabilisation. The interaction is forbidden by symmetry in a centrosymmetric environment, and therefore drives the tetrel atoms toward distorted, low-coordinate geometries in which an “active” lone pair effectively occupies a coordination site and is often projected into a structural void such as the interlayer space in the Pnma and Cmcm structures (c.f.Fig. 1). When the tetrel atoms are constrained to a symmetric environment, the lone pair is “strained”, which can provide a driving force for anharmonic lattice dynamics. In the extreme, this manifests as imaginary harmonic modes, for example in Cmcm SnSe, as shown in the present work (c.f.Fig. 2c and 3), but also in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Cmcm phases of SnS60 and the Fm
m and Cmcm phases of SnS60 and the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase of GeSe. Competing with this, however, is the potential energetic destabilisation associated with the lower coordination number, and if the interaction between the cation s and anion p states is weak the stabilisation from an active lone pair does not outweigh the reduction in coordination number and a symmetric structure is energetically preferred. In the PbX series, PbO adopts the distorted litharge structure with an active lone pair, whereas the lead chalcogenides PbS, PbSe and PbTe adopt the centrosymmetric rocksalt structure without an active lone pair.70 Similarly, the strong anion/cation interaction in SnS results in an energetic preference for the Pnma structure and the Fm
m phase of GeSe. Competing with this, however, is the potential energetic destabilisation associated with the lower coordination number, and if the interaction between the cation s and anion p states is weak the stabilisation from an active lone pair does not outweigh the reduction in coordination number and a symmetric structure is energetically preferred. In the PbX series, PbO adopts the distorted litharge structure with an active lone pair, whereas the lead chalcogenides PbS, PbSe and PbTe adopt the centrosymmetric rocksalt structure without an active lone pair.70 Similarly, the strong anion/cation interaction in SnS results in an energetic preference for the Pnma structure and the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure being dynamically unstable, whereas the weaker interaction in SnSe results in the rocksalt phase being both dynamically stable and much closer to the convex hull.60
m structure being dynamically unstable, whereas the weaker interaction in SnSe results in the rocksalt phase being both dynamically stable and much closer to the convex hull.60
In the SM-RTA model used in these calculations, strong three-phonon interactions arise from a large response of the system to atomic displacements at third order. It has been demonstrated that the electron-phonon coupling due to the lone-pair activity in Cmcm SnSe contributes directly to large third-order force constants and strong phonon–phonon interactions.34 Similarly, although the Pb chalcogenides are stable in the rocksalt phase, indicating, in principle, weaker electron-phonon coupling, PbTe has been characterised as an “incipient ferroelectric”,71 which could also be driven by lone pair activity and which has been linked to strong scattering and suppressed heat transport through the longitudinal acoustic (LA) modes.18 Similarly, while in principle the interaction between Ge and S/Se might be expected to be too weak to drive a structural distortion, both materials readily form in the Pnma structure, and the presence of active lone pairs has been confirmed both experimentally and theoretically.72 In our view, these observations provide evidence that lone pair activity could support strong three-phonon interactions across all of the IV–VI chalcogenides, even in systems where the electron-phonon coupling is not strong enough to manifest in the second-order force constants as imaginary harmonic modes.
This mechanism explains the strong link between the crystal symmetry and the phonon interaction strengths. In the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure the tetrel atoms are forced by symmetry to adopt a centrosymmetric environment, resulting in a “strained” lone pair and strong three-phonon interactions reflected in large
m structure the tetrel atoms are forced by symmetry to adopt a centrosymmetric environment, resulting in a “strained” lone pair and strong three-phonon interactions reflected in large ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) . In the Pnma structure, on the other hand, the tetrel atoms can adopt a distorted local geometry with active lone pairs projecting into the interlayer space, leading to weak three-phonon interactions and low
. In the Pnma structure, on the other hand, the tetrel atoms can adopt a distorted local geometry with active lone pairs projecting into the interlayer space, leading to weak three-phonon interactions and low ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) . In the R3m structure, the tetrel atoms are in a less symmetric environment than in the Fm
. In the R3m structure, the tetrel atoms are in a less symmetric environment than in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase, allowing for some relaxation of the strain, but not as much as in the Pnma phase. Similarly, in the Cmcm structure the tetrel atoms are forced to adopt a more symmetric environment than in the Pnma phase, which leads to larger three-phonon interactions. Both of these systems therefore have
m phase, allowing for some relaxation of the strain, but not as much as in the Pnma phase. Similarly, in the Cmcm structure the tetrel atoms are forced to adopt a more symmetric environment than in the Pnma phase, which leads to larger three-phonon interactions. Both of these systems therefore have ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) intermediate between the bounds set by the (fully) symmetric Fm
intermediate between the bounds set by the (fully) symmetric Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and (fully) distorted Pnma phases. Finally, the strength of the electronic interactions is determined by the energy match between the cation s and anion p states, and this can potentially explain the variation in anharmonicity among different compounds in the same structure type, although to explore this further would require a detailed analysis of the atomic energy levels and the chemical bonding in the different chalcogenide systems.70
m and (fully) distorted Pnma phases. Finally, the strength of the electronic interactions is determined by the energy match between the cation s and anion p states, and this can potentially explain the variation in anharmonicity among different compounds in the same structure type, although to explore this further would require a detailed analysis of the atomic energy levels and the chemical bonding in the different chalcogenide systems.70
Finally, our analysis of the averaged lifetimes shows that the three-phonon interaction strengths and anharmonicity, as defined by the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) , are not the only important factor, and that the reduced anharmonicity of the lower-symmetry crystal structures is partially offset by the more complex phonon spectra facilitating a larger scattering phase space. Our analysis suggests that this plays a particularly important role in determining the low κ of the Pnma structures.
, are not the only important factor, and that the reduced anharmonicity of the lower-symmetry crystal structures is partially offset by the more complex phonon spectra facilitating a larger scattering phase space. Our analysis suggests that this plays a particularly important role in determining the low κ of the Pnma structures.
Table 4 summarises qualitatively the factors that determine the κ across the four chalcogenide phases examined in this work. Given that low group velocities are favoured by inhomogeneous bonding typical of large unit cells and low-symmetry structures, whereas strong anharmonicity is favoured by symmetric tetrel environments typical of high-symmetry structures, the κ is in principle a balance of two competing trends. However, some chalcogenide structure types appear to “decouple” these factors. The Cmcm phase is a low-symmetry structure, but the tetrel atoms are confined to locally-symmetric environments, resulting in an optimal trade-off between relatively low group velocities and strong anharmonicity. The recently-discovered π-cubic structure, reported as a synthetically-accessible phase of SnS and SnSe,73,74 has a high-symmetry cubic P213 spacegroup but a complex structure with na = 64 atoms in the primitive cell that allows the tetrel atoms to adopt distorted local geometries similar to the Pnma phase. Based on our findings we would anticipate ultra-low group velocities compensating for weak anharmonicity, representing perhaps the other “extreme” to the Cmcm phase. Exploring crystal-engineering routes to obtain the IV–VI chalcogenides in different crystal phases is therefore likely to be a fruitful avenue for optimising the lattice thermal conductivity for thermoelectric applications.
| Bonding | Tetrel environment | Group velocities | Lifetimes | Interaction strengths | Phase space | |
|---|---|---|---|---|---|---|
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Homogeneous | Most constrained | Large | Shortest | Strongest | Small |
| R3m | <Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Intermediate | Medium | Longest | Weak | Small |
| Cmcm | <R3m | Intermediate | Medium | Short | Strong | Medium |
| Pnma | Least homogeneous | Least constrained | Small | Long | Weakest | Large |
Another potential avenue would be to try to optimise the κ of the rocksalt systems by reducing the group velocities while retaining the strong intrinsic anharmonicity. Experimental studies have demonstrated that solid solutions of Pnma SnS and SnSe can display lower κ than both endpoints,75–78 and our recent modelling suggests this is primarily due to a reduction in the νλ,41 so alloying may be a facile route to achieving this. Another possibility is the “discordant doping” approach demonstrated by Xie et al.79 where a carefully-selected dopant is incorporated into the lattice at a few at% to deliberately induce structural distortion and chemical bond strain. Based on the analysis presented here, we would expect this to also lead to a reduction in the group velocities, and to thus be a viable strategy to lower the κ of rocksalt-structured chalcogenides.
More generally, the links between the group velocities and the size of the scattering phase space, and the structural complexity, are likely to be “universal”, with the caveat that stronger bonding and/or lighter elements will result in a larger range of phonon frequencies, and, consequently, larger group velocities and potentially a smaller scattering phase space. On the other hand, the link between the phonon interaction strengths and the local coordination environment of the tetrel atoms will be specific to compounds including species that can show stereochemically active lone pairs, such as IV(II) and V(III) ions. We would therefore expect this to generalize to Group IV oxides and perhaps to Group V sesquioxides and sesquichalcogenides, but it is unlikely to be universal. It is noteworthy, however, that strain induced by local symmetry has also been proposed as a factor in the low lattice thermal conductivity of CuFe1−xGexS2,80 AgInSe2 (ref. 81) and Cu1−xAgxGaTe2, suggesting there may be a more general principle.82
Finally, we also discuss the key approximations in our methodology. First of all, we determine the κ within the SM-RTA, as opposed to solving the linearised phonon Boltzmann transport equation (LBTE). To test the impact of this, we calculated the κ of the ten materials by solving the LBTE and compared the results to the RTA calculations (see Section 6 of the ESI†). The LBTE solution results in a significant increase in the predicted room-temperature κ of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m systems, of 75 and 80% for GeSe and GeTe, respectively, and 28% for SnTe. The LBTE also has a smaller but significant impact on the two R3m phases and Cmcm SnSe, increasing the κ by 11/12 and 22%, respectively. The impact on the Pnma phases is smallest, increasing the κ by between 0.3% for Pnma SnSe and 7% for Pnma SnTe. Interestingly, the size of the difference appears to correlate well with the
m systems, of 75 and 80% for GeSe and GeTe, respectively, and 28% for SnTe. The LBTE also has a smaller but significant impact on the two R3m phases and Cmcm SnSe, increasing the κ by 11/12 and 22%, respectively. The impact on the Pnma phases is smallest, increasing the κ by between 0.3% for Pnma SnSe and 7% for Pnma SnTe. Interestingly, the size of the difference appears to correlate well with the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) , such that compounds with stronger phonon–phonon interactions in this definition show a larger increase in κ from solving the LBTE over using the simpler RTA method. Given that solving the LBTE entails diagonalising collision matrices, which depend on the interaction strengths, this is perhaps not surprising.
, such that compounds with stronger phonon–phonon interactions in this definition show a larger increase in κ from solving the LBTE over using the simpler RTA method. Given that solving the LBTE entails diagonalising collision matrices, which depend on the interaction strengths, this is perhaps not surprising.
Secondly, the method uses the νλ and Cλ calculated within the harmonic approximation, and linewidths and lifetimes are determined from perturbative anharmonicity at third order, both using force constants calculated for the (athermal) equilibrium lattice volume. In reality, we would expect some temperature renormalisation of the phonon spectrum, as discussed above for Cmcm SnSe, and we might also expect a contribution to the phonon linewidths from higher-order (e.g. 4th-order) scattering processes. A variety of techniques exist for modelling the temperature renormalisation of the phonon spectrum, including the decoupled anharmonic mode approximation (DAMA)83 and temperature-dependent effective potential (TDEP) methods84 and the stochastic self-consistent harmonic approximation (SSCHA).85 We previously found that using a simple approach, similar to the DAMA method, to renormalise the soft modes in Cmcm SnSe had a minimal impact on the calculated κ,33 whereas the more sophisticated SSCHA approach, including non-perturbative anharmonicity at third order, indicated a much larger impact.62 A recent study also highlighted a significant impact of fourth-order anharmonicity on the κ of Cmcm SnSe.86 Furthermore, the study in ref. 34 found evidence for strong temperature renormalisation in Pnma SnSe, which does not have imaginary harmonic modes.
Accounting for temperature renormalisation of the harmonic phonon spectrum and/or higher-order phonon interactions would, however, significantly increase the cost of the calculations, to the point where a comparative study of a large number of materials, as in the present work, would be impractical. On this point, a recent study on BaXYF (X = Cu, Ag, Y = Se, Te) found that the SM-RTA model may benefit from a favourable cancellation of errors, such that more sophisticated calculations need to include both effects to obtain accurate results.87 We note that this may explain why our predicted κ are generally a good match to experimental measurements despite the approximations inherent to the method.
Finally, it has been proposed that the quasiparticle description of phonons breaks down, and full-spectrum renormalisation approaches are required, when the anharmonicity is sufficiently strong that the lifetimes fall below the so-called Ioffe–Regel limit in time of 1/(2πfλ).88 We therefore compared the spectra of τλ for each of the ten systems at our chosen analysis temperature of 300 K to this limit, and found that, in all cases, the lifetimes were above it, indicating that the quasiparticle description should be reasonable (see Section 7 of the ESI†). However, we observe a similar trend to comparing the RTA and LBTE κ, whereby the spectra of τλ for the systems with larger averaged interaction strengths are closer to the Ioffe–Regel limit. This suggests that, despite the approximations inherent in calculating them, the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) are a reasonable qualitative descriptor of anharmonicity.
are a reasonable qualitative descriptor of anharmonicity.
An important point is that more sophisticated theoretical treatments would complicate the data analysis and make extracting chemical insight much more challenging. The key question, then, is whether the RTA calculations are sufficiently accurate to capture the qualitative links between crystal structure and thermal conductivity. The fact that our analysis is consistent with previous theories for the low κ of various IV–VI chalcogenides suggests this most likely is the case. We therefore believe the present study should serve as a useful baseline against which to establish the impact of more intricate physics and chemistry on the thermal conductivity of these materials.
4 Conclusions
In summary, we have performed a detailed microscopic analysis of the lattice thermal conductivity of ten Group IV–VI chalcogenides within the single-mode relaxation-time approximation. Using the constant relaxation-time model, we find that the phonon group velocities are strongly related to the homogeneity in the chemical bonding, captured by the size and symmetry of the primitive unit cell, with a secondary dependence on the atomic masses of the constituent elements. The phonon lifetimes depend more intricately on the structure type and composition through a balance of the intrinsic anharmonicity, maximised in structures that force the tetrel atoms to adopt symmetric local environments, and the size of the scattering phase space, maximised by low-symmetry structures with complex phonon spectra. These effects are best balanced in the high-temperature Cmcm phase of SnSe, which shows the lowest κlatt of the ten systems examined, accounting for its ultra-low thermal conductivity and exceptional thermoelectric performance.Our analysis provides some clear guidance for optimising the thermal transport in the Group IV–VI chalcogenides. If low κlatt is desired, as for thermoelectric applications, a structure with a large and/or low-symmetry unit cell in which the tetrel atoms are constrained to a locally-symmetric environment should be sought. While seemingly contradictory, these requirements appear to be met in the Cmcm phase, which is accessible to some of the chalcogenides at high temperature and/or under pressure.60 Alternatively, it might be possible to use alloying or doping to stabilise the chalcogenide in a rocksalt or R3m phase while reducing the group velocities. If, on the other hand, high κlatt is required, as might be the case e.g. for power electronics, a relatively simple structure in which the tetrel atom can adopt a low-coordinate geometry with an active lone pair should be sought. We note also that while we have focused on (tetrel) selenides and tellurides in this work, it is likely that the same considerations would apply to the analogous Group VI oxides, and possibly more generally e.g. to Group V sesquichalcogenides (and sesquioxides).
This study also suggests a number of avenues for future computational studies. Firstly, analysis of the π-cubic phases of e.g. SnS and SnSe would confirm, or otherwise, that: (1) the size of the primitive cell, rather than the crystal symmetry, is the key predictor of low group velocities; and (2) that the local environment of the tetrel atoms, rather than the “global” crystal symmetry, is the key predictor of anharmonicity. Secondly, extension of this study to GeS and SnS, and to the Pb chalcogenides PbS, PbSe and PbTe, would provide a more complete picture of the role of the chalcogen and tetrel in defining the κlatt, and would also complement previous studies with new insight into the anharmonicity in the Pb chalcogenides. We aim to address both points in the near future.
Data availability
Raw data from this study, including optimised structures and input and output files from the phonon and lattice-thermal conductivity calculations, will be made available to download free of charge in an online repository at https://doi.org/10.17632/tkzvj899bx.Author contributions
Conceptualisation: JMS; data curation: SKG; formal analysis: JMS and SKG; funding acquisition: JMS, AS and NK; investigation: SKG and JMS; methodology: SKG and JMS; project administration: JMS and AS; supervision: JMS and AS; writing – original draft: SKG; writing – review and editing: all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge helpful discussions with Dr L. Whalley, Dr J. Buckeridge and Dr A. A. Sokol. SKG is supported by the A*STAR PhD programme. JMS is supported by a UK Research and Innovation (UKRI) Future Leaders Fellowship (MR/T043121/1) and previously held a University of Manchester (UoM) Presidential Fellowship. AS acknowledges funding from the A*STAR Career Development Fund (CDF; C210112022). The majority of these calculations were performed on the UK national ARCHER 2 high-performance computing facility via JMS's membership of the UK Materials Chemistry Consortium (MCC), which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC; EP/R029431 and EP/X035859). A subset of the calculations and analysis were performed on the UoM Computational Shared Facility, which is maintained by UoM Research IT.Notes and references
- Clean Energy for all Europeans Package, European Commission Rreport, 2019 Search PubMed.
- Amending Directive on Energy Efficiency, European Commission Report 2018/844/EU, 2018 Search PubMed.
- Energy Performance of Buildings Directive, European Commission Report EU 2018/844, 2018 Search PubMed.
- IEA, Meeting Climate Change Goals through Energy Efficiency, 2017 Search PubMed.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- A. Firth, B. Zhang and A. Yang, Appl. Energy, 2019, 235, 1314–1334 CrossRef.
- C. Cazorla, Novel Mechanocaloric Materials for Solid-State Cooling Applications, 2019 Search PubMed.
- G. Bennett, J. Lombardo, R. Hemler, G. Silverman, C. Whitmore, W. Amos, E. Johnson, A. Schock, R. Zocher, T. Keenan, J. Hagan and R. Englehart, in Mission of Daring: the General-Purpose Heat Source Radioisotope Thermoelectric Generator, American Institute of Aeronautics and Astronautics, 2006 Search PubMed.
- H. Jaber, M. Khaled, T. Lemenand, R. Murr, J. Faraj and M. Ramadan, Energy, 2019, 170, 1036–1050 CrossRef.
- G. Tan, L.-D. Zhao and M. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew Chem. Int. Ed. Engl., 2016, 55, 6826–6841 CrossRef CAS PubMed.
- Z. Li, C. Xiao and Y. Xie, Applied Physics Reviews, 2022, 9, 011303 CrossRef CAS.
- T. Lyu, X. Li, Q. Yang, J. Cheng, Y. Zhang, C. Zhang, F. Liu, J. Li, W. Ao, H. Xie and L. Hu, Chem. Eng. J., 2022, 442, 136332 CrossRef.
- K. Manibalan, M. Y. Ho, Y. C. Du, H. W. Chen and H. J. Wu, Materials, 2023, 16, 509 CrossRef CAS PubMed.
- X. Y. Tan, J.-F. Dong, N. Jia, H.-X. Zhang, R. Ji, A. Suwardi, Z.-L. Li, Q. Zhu, J.-W. Xu and Q.-Y. Yan, Rare Met., 2022, 3027–3034 CrossRef CAS.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- C. Guo, D. Wang, X. Zhang and L.-D. Zhao, Chem. Mater., 2022, 34, 3423–3429 CrossRef CAS.
- O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M.-H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden and B. C. Sales, Nat. Mater., 2011, 10, 614–619 CrossRef CAS PubMed.
- Z. M. Gibbs, H. Kim, H. Wang, R. L. White, F. Drymiotis, M. Kaviany and G. Jeffrey Snyder, Appl. Phys. Lett., 2013, 103, 262109 CrossRef.
- E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis and S. J. L. Billinge, Science, 2010, 330, 1660–1663 CrossRef PubMed.
- S. Kastbjerg, N. Bindzus, M. Søndergaard, S. Johnsen, N. Lock, M. Christensen, M. Takata, M. A. Spackman and B. Brummerstedt Iversen, Adv. Funct. Mater., 2013, 23, 5477–5483 CrossRef CAS.
- T. Keiber, F. Bridges and B. C. Sales, Phys. Rev. Lett., 2013, 111, 095504 CrossRef CAS PubMed.
- K. S. Knight, J. Phys.: Condens. Matter, 2014, 26, 385403 CrossRef CAS PubMed.
- A. Feltrin and A. Freundlich, Renewable Energy, 2008, 33, 180–185 CrossRef CAS.
- R. Moshwan, L. Yang, J. Zou and Z. Chen, Adv. Funct. Mater., 2017, 27, 1703278 CrossRef.
- J. Cao, S. W. Chien, X. Y. Tan, C. K. I. Tan, Q. Zhu, J. Wu, X. Wang, Y. Zhao, L. Yang, Q. Yan, H. Liu, J. Xu and A. Suwardi, ChemNanoMat, 2021, 7, 476–482 CrossRef CAS.
- S. Perumal, M. Samanta, T. Ghosh, U. S. Shenoy, A. K. Bohra, S. Bhattacharya, A. Singh, U. V. Waghmare and K. Biswas, Joule, 2019, 3, 2565–2580 CrossRef CAS.
- H. Zhang, S. D. Cheng, L. Lu and S. B. Mi, Nanoscale, 2021, 13, 15205–15209 RSC.
- J. Li, Y. Pan, C. Wu, F. Sun and T. Wei, Sci. China: Technol. Sci., 2017, 60, 1347–1364 CrossRef.
- M. Samanta, T. Ghosh, R. Arora, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2019, 141, 19505–19512 CrossRef CAS PubMed.
- Z. Liu, N. Sato, Q. Guo, W. Gao and T. Mori, NPG Asia Mater., 2020, 12, 66 CrossRef CAS.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- J. M. Skelton, L. A. Burton, S. C. Parker, A. Walsh, C.-E. Kim, A. Soon, J. Buckeridge, A. A. Sokol, C. R. A. Catlow, A. Togo and I. Tanaka, Phys. Rev. Lett., 2016, 117, 075502 CrossRef PubMed.
- C. W. Li, J. Hong, A. F. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063–1069 Search PubMed.
- S. Li, L. Yin, Y. Liu, X. Wang, C. Chen and Q. Zhang, J. Mater. Sci. Technol., 2023, 143, 234–241 CrossRef CAS.
- J. A. Kafalas and A. N. Mariano, Science, 1964, 143, 952 CrossRef CAS PubMed.
- H. Yu and Y. Chen, J. Phys. Chem. C, 2018, 122, 15673–15677 CrossRef CAS.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- J. Tang and J. M. Skelton, J. Phys.: Condens. Matter, 2021, 164002 CrossRef CAS PubMed.
- J. M. Skelton, J. Mater. Chem. C, 2021, 9, 11772–11787 RSC.
- B. Wei, J. M. Flitcroft and J. M. Skelton, Structural Dynamics, Phonon Spectra and Thermal Transport in the Silicon Clathrates, 2022 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- H. Wiedemeier and P. A. Siemers, Z. Anorg. Allg. Chem., 1975, 411, 90–96 CrossRef.
- P. A. E. Murgatroyd, M. J. Smiles, C. N. Savory, T. P. Shalvey, J. E. N. Swallow, N. Fleck, C. M. Robertson, F. Jäckel, J. Alaria, J. D. Major, D. O. Scanlon and T. D. Veal, Chem. Mater., 2020, 32, 3245–3253 CrossRef CAS PubMed.
- M. G. Herrmann, R. P. Stoffel, M. Kupers, M. Ait Haddouch, A. Eich, K. Glazyrin, A. Grzechnik, R. Dronskowski and K. Friese, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 246–256 CrossRef CAS PubMed.
- P. Wu, Y. Ishikawa, M. Hagihala, S. Lee, K. Peng, G. Wang, S. Torii and T. Kamiyama, Phys. B, 2018, 551, 64–68 CrossRef CAS.
- M. Sist, J. Zhang and B. Brummerstedt Iversen, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 310–316 CrossRef CAS PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- L. Shelimova, N. K. Abrikosov and V. Zhdanova, Zh. Neorg. Khim., 1965, 10, 1200–1205 CAS.
- S. Karbanov, V. Zlomanov and A. Novoselova, Dokl. Akad. Nauk SSSR, 1968, 182, 862–863 Search PubMed.
- P. Bauer Pereira, I. Sergueev, S. Gorsse, J. Dadda, E. Müller and R. P. Hermann, Phys. Status Solidi B, 2013, 250, 1300–1307 CrossRef CAS.
- I. Pallikara and J. M. Skelton, Phys. Chem. Chem. Phys., 2021, 23, 19219–19236 RSC.
- M. T. Dove, Am. Mineral., 1997, 82, 213–244 CAS.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. Lett., 2019, 122, 075901 CrossRef CAS PubMed.
- K. Yuan, Z. Sun, X. Zhang and D. Tang, Sci. Rep., 2019, 9, 9490 CrossRef CAS PubMed.
- Z. Zheng, X. Su, R. Deng, C. Stoumpos, H. Xie, W. Liu, Y. Yan, S. Hao, C. Uher, C. Wolverton, M. G. Kanatzidis and X. Tang, J. Am. Chem. Soc., 2018, 140, 2673–2686 CrossRef CAS PubMed.
- M. Ghim, Y.-J. Choi and S.-H. Jhi, Phys. Rev. B, 2023, 107, 184301 CrossRef CAS.
- D. H. Damon, J. Appl. Phys., 2004, 37, 3181–3190 CrossRef.
- S. K. Kihoi, U. S. Shenoy, J. N. Kahiu, H. Kim, D. K. Bhat and H. S. Lee, ACS Sustain. Chem. Eng., 2022, 10, 1367–1372 CrossRef CAS.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144 CrossRef CAS PubMed.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen, J. Y. Lee, O. Cojocaru-Mirédin, H. Chang, J. Im, S.-P. Cho, M. Wuttig, V. P. Dravid, M. G. Kanatzidis and I. Chung, Nat. Mater., 2021, 20, 1378–1384 CrossRef CAS PubMed.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- R. T. Bate, D. L. Carter and J. S. Wrobel, Phys. Rev. Lett., 1970, 25, 159–162 CrossRef CAS.
- M. J. Smiles, J. M. Skelton, H. Shiel, L. A. H. Jones, J. E. N. Swallow, H. J. Edwards, P. A. E. Murgatroyd, T. J. Featherstone, P. K. Thakur, T.-L. Lee, V. R. Dhanak and T. D. Veal, J. Mater. Chem. A, 2021, 9, 22440–22452 RSC.
- R. E. Abutbul, A. R. Garcia-Angelmo, Z. Burshtein, M. T. S. Nair, P. K. Nair and Y. Golan, CrystEngComm, 2016, 18, 5188–5194 RSC.
- R. E. Abutbul, E. Segev, S. Samuha, L. Zeiri, V. Ezersky, G. Makov and Y. Golan, CrystEngComm, 2016, 18, 1918–1923 RSC.
- Y.-M. Han, J. Zhao, M. Zhou, X.-X. Jiang, H.-Q. Leng and L.-F. Li, J. Mater. Chem. A, 2015, 3, 4555–4559 RSC.
- C.-C. Lin, R. Lydia, J. H. Yun, H. S. Lee and J. S. Rhyee, Chem. Mater., 2017, 29, 5344–5352 CrossRef CAS.
- Asfandiyar, T.-R. Wei, Z. Li, F.-H. Sun, Y. Pan, C.-F. Wu, M. U. Farooq, H. Tang, F. Li, B. Li and J.-F. Li, Sci. Rep., 2017, 7, 43262 CrossRef CAS PubMed.
- W. He, D. Wang, H. Wu, Y. Xiao, Y. Zhang, D. He, Y. Feng, Y.-J. Hao, J.-F. Dong, R. Chetty, L. Hao, D. Chen, J. Qin, Q. Yang, X. Li, J.-M. Song, Y. Zhu, W. Xu, C. Niu, X. Li, G. Wang, C. Liu, M. Ohta, S. J. Pennycook, J. He, J.-F. Li and L.-D. Zhao, Science, 2019, 365, 1418–1424 CrossRef CAS PubMed.
- H. Xie, X. Su, S. Hao, C. Zhang, Z. Zhang, W. Liu, Y. Yan, C. Wolverton, X. Tang and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 18900–18909 CrossRef CAS PubMed.
- S. Tippireddy, F. Azough, Vikram, A. Bhui, P. Chater, D. Kepaptsoglou, Q. Ramasse, R. Freer, R. Grau-Crespo, K. Biswas, P. Vaqueiro and A. V. Powell, J. Mater. Chem. A, 2022, 10, 23874–23885 RSC.
- Y. Zhu, B. Wei, J. Liu, N. Z. Koocher, Y. Li, L. Hu, W. He, G. Deng, W. Xu, X. Wang, J. M. Rondinelli, L.-D. Zhao, G. J. Snyder and J. Hong, Mater. Today Phys., 2021, 19, 100428 CrossRef CAS.
- H. Xie, Z. Li, Y. Liu, Y. Zhang, C. Uher, V. P. Dravid, C. Wolverton and M. G. Kanatzidis, J. Am. Chem. Soc., 2023, 145, 3211–3220 CrossRef CAS PubMed.
- D. J. Adams and D. Passerone, J. Phys.: Condens. Matter, 2016, 28, 305401 CrossRef PubMed.
- O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104111 CrossRef.
- L. Monacelli, R. Bianco, M. Cherubini, M. Calandra, I. Errea and F. Mauri, J. Phys.: Condens. Matter, 2021, 33, 363001 CrossRef CAS PubMed.
- J. Sun, C. Zhang, Z. Yang, Y. Shen, M. Hu and Q. Wang, ACS Appl. Mater. Interfaces, 2022, 14, 11493–11499 CrossRef CAS PubMed.
- T. Yue, Y. Zhao, J. Ni, S. Meng and Z. Dai, Phys. Rev. B, 2023, 107, 024301 CrossRef CAS.
- M. Simoncelli, N. Marzari and F. Mauri, Phys. Rev. X, 2022, 12, 041011 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Phonon dispersion and density of states curves of the ten systems examined in this work; anisotropy in the calculated lattice thermal conductivity; comparison of the averaged phonon lifetimes at 300 K to the frequency spectra of the lifetimes; phonon-scattering phase spaces including contributions from collision and decay processes; determination of the averaged three-phonon interaction strengths and comparison to the frequency spectra of the modal interaction strengths; comparison of thermal-conductivity calculations using the single-mode relaxation-time approximation and by direct solution of the linearised phonon Boltzmann transport equation; and comparison of the frequency spectra of the phonon lifetimes at 300 K to the Ioffe–Regel limit in time. See DOI: https://doi.org/10.1039/d3ta05885a |
| This journal is © The Royal Society of Chemistry 2024 |