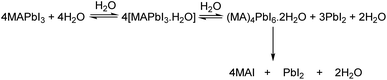Temperature and pressure induced structural transitions of lead iodide perovskites
Pratap
Vishnoi
 * and
C. N. R.
Rao
* and
C. N. R.
Rao
 *
*
New Chemistry Unit, International Centre for Materials Science, School of Advanced Materials, Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR), Jakkur, Bangalore, 560064, India. E-mail: pvishnoi@jncasr.ac.in; cnrrao@jncasr.ac.in
First published on 3rd November 2023
Abstract
During the past fourteen years, conventional lead iodide perovskites, APbI3 [A = Cs+, methylammonium (CH3NH3+) and formamidinium (NH2CHNH2+)], have emerged as the forerunner materials for optoelectronic applications, including photovoltaics. However, their photoactive phases suffer from structural instabilities – including phase transitions under extrinsic factors such as heat, light, pressure etc. They even show chemical instability in water, oxygen and humid air. Consequently, their optical and electronic properties show marked changes under device working conditions, which is one of the major obstacles in long-term use. At the same time, phase transition offers plenty of opportunities for modulating structures to physical properties. Hence, there is a need for a comprehensive understanding of the structural instabilities and phase transitions of APbI3 perovskites. This perspective focuses on three conventional lead iodide perovskites, CsPbI3, MAPbI3 and FAPbI3, which are among the most widely studied materials in this family. We critically review the experimentally known structures as a function of temperature or pressure. We describe crystal structures of these three perovskites as well as highlight the reason for their instabilities, mechanism of structural transitions, and fundamental insights into their optoelectronic properties. In addition to temperature- and pressure-driven structural changes, we highlight structural changes due to chemical instability towards water and oxygen. We focus mainly on the structures reported based on X-ray, synchrotron, and neutron diffraction data. We conclude the perspective by discussing current challenges in these exciting materials, possible future opportunities to improve them and our thoughts on new directions.
1. Introduction
For several decades, conventional oxide perovskites have been intensely explored as phase transition materials by condensed matter physics and solid-state chemistry communities. Some common examples of oxides include ferroelectric titanate materials and high-temperature cuprate superconductors.1,2 On the other hand, lead halide perovskites, with the general chemical formula of APbI3, have come to the fore very recently, opening an entirely new avenue of phase transition materials. They are composed of a three-dimensional [PbI3]− framework of corner-sharing [PbI6]4− octahedra and mono-cation, known as A-cation, in the interstices (Fig. 1a). The A-cation is typically a large inorganic cation, such as Cs+ or an organic cation, such as methylammonium (CH3NH3+) and formamidinium (NH2CHNH2+). APbI3 perovskites with these three A-cations and their mixed cation variants are among the most widely studied compounds of the lead halide perovskite family. Their semiconducting behaviour combined with narrow, tuneable and direct bandgaps (Fig. 1b) gives rise to exceptional optoelectronic properties.3,4 They exhibit high absorption coefficients, broad-spectrum light absorption, low exciton binding energies, high charge-carrier mobilities, long carrier diffusion lengths and defect tolerance.5,6 The widespread success of APbI3 perovskites is also due to their ability to be solution-processed into thin films. These are all beneficial for high efficiency of solar cells and other optoelectronic devices.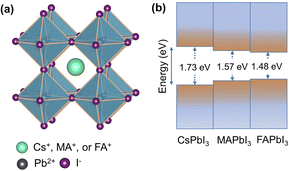 | ||
Fig. 1 (a) Crystal structure of an archetypical APbI3 perovskite in the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. (b) Schematic presentation of optical bandgaps. m symmetry. (b) Schematic presentation of optical bandgaps. | ||
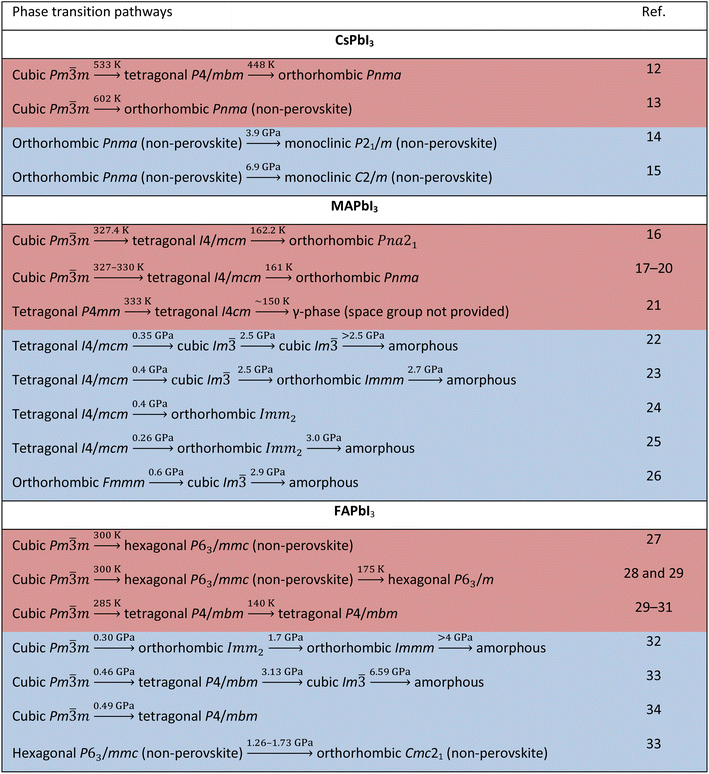
Another fascinating feature of lead iodide perovskites is that they offer substantial opportunities for modulating their structures and physical properties through phase transitions.7 The ideal perovskite adopts a cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure typically at high temperature with no structural distortion. Low symmetry phases are obtained from this structure by changing temperature or pressure. The A-cation tumbling dynamics and the [PbI6]4− octahedral tilting are the primary reasons for phase transitions. The phase transition is intriguing, yet a flipside exists: their phase transition temperatures range across room temperature, causing marked changes in the physical properties under device working conditions, which is one of the major obstacles to their use.8–10 Additionally, some of them form photoinactive non-perovskites under ambient conditions.11 Thus, understanding crystal structures of the different phases is crucial because all the physical properties are dependent on the structure in addition to chemical composition. Table 1 lists the structural transition pathways of CsPbI3, MAPbI3 and FAPbI3 found under heat and pressure. Tables 2 and 3 list the structural parameters of the temperature and pressure induced phases, respectively. Clearly, there are diverse views about the transition pathways as well as crystallographic symmetries and there is a need for having a deeper understanding of their structures.
m structure typically at high temperature with no structural distortion. Low symmetry phases are obtained from this structure by changing temperature or pressure. The A-cation tumbling dynamics and the [PbI6]4− octahedral tilting are the primary reasons for phase transitions. The phase transition is intriguing, yet a flipside exists: their phase transition temperatures range across room temperature, causing marked changes in the physical properties under device working conditions, which is one of the major obstacles to their use.8–10 Additionally, some of them form photoinactive non-perovskites under ambient conditions.11 Thus, understanding crystal structures of the different phases is crucial because all the physical properties are dependent on the structure in addition to chemical composition. Table 1 lists the structural transition pathways of CsPbI3, MAPbI3 and FAPbI3 found under heat and pressure. Tables 2 and 3 list the structural parameters of the temperature and pressure induced phases, respectively. Clearly, there are diverse views about the transition pathways as well as crystallographic symmetries and there is a need for having a deeper understanding of their structures.
| Compound | Space group | Unit cell constants | Atomic coordinates | ||||
|---|---|---|---|---|---|---|---|
| Atom | x | y | z | Occ. | |||
| CsPbI3 | Cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 221)12 (α-phase) m (no. 221)12 (α-phase) |
a = b = c = 6.29658(2) Å, α = β = γ = 90° (T = 646.6 K) | Cs | 0.5 | 0.5 | 0.5 | 1 |
| Pb | 0.0 | 0.0 | 0.0 | 1 | |||
| I | 0.5 | 0.0 | 0.0 | 1 | |||
| Tetragonal P4/mbm (no. 127)12 (β-phase) | a = b = 8.82690(3) Å and c = 6.29902(3) Å, α = β = γ = 90° (T = 511.7 K) | Cs | −0.5 | 0.0 | 0.5 | 1 | |
| Pb | 0.0 | 0.0 | 0.0 | 1 | |||
| I1 | 0.0 | 0.0 | 0.5 | 1 | |||
| I2 | −0.212 | 0.288 | 0.0 | 1 | |||
| Orthorhombic Pbnm (no. 62)12 (γ-phase) | a = 8.61979(6) Å, b = 8.85176(6) Å and c = 12.50128(7) Å; α = β = γ = 90° (T = 324.6 K) | Cs | −0.0165 | 0.4451 | 0.25 | 1 | |
| Pb | 0.0 | 0.0 | 0.5 | 1 | |||
| I1 | 0.1973 | 0.2993 | 0.5306 | 1 | |||
| I2 | −0.0631 | −0.0017 | 0.75 | 1 | |||
| Orthorhombic Pbnm (no. 62)58 (δ-phase, non-perovskite) | a = 10.4581(3) Å, b = 4.80171(13) Å and c = 17.7761(5) Å; α = β = γ = 90° (T = 298 K) | Cs | 0.4156 | 0.25 | 0.82924 | 1 | |
| Pb | 0.16049 | 0.25 | 0.06185 | 1 | |||
| I1 | 0.2997 | 0.25 | 0.2127 | 1 | |||
| I2 | 0.3355 | 0.75 | 0.9979 | 1 | |||
| I3 | 0.0331 | 0.25 | 0.88541 | 1 | |||
| MAPbI3 | Cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 221)19 (α-phase) m (no. 221)19 (α-phase) |
a = b = c = 6.31728(27) Å; α = β = γ = 90° (T = 352 K) | Pb | 0.0 | 0.0 | 0.0 | 1 |
| I | 0.5 | 0.0 | 0.0 | 1 | |||
| Tetragonal P4mm (no. 99)21 (α-phase) | a = b = 6.3115(2) Å and c = 6.3161(2) Å; α = β = γ = 90° (T = 400(2) K) | Pb | 0.5 | 0.5 | 0.50813 | 1 | |
| I1 | 0.5 | 0.0 | 0.5122 | 1 | |||
| I2 | 0.5 | 0.5 | −0.0006 | 1 | |||
| Tetragonal I4/mcm (no. 140)19 (β-phase) | a = b = 8.80625(28) Å and c = 8.80625 Å; α = β = γ = 90° (T = 180 K) | Pb | 0.5 | 0.5 | 0.5 | 1 | |
| I1 | 0.5 | 0.5 | 0.75 | 1 | |||
| I2 | 0.20122 | 0.29878 | 0.5 | 1 | |||
| Tetragonal I4cm (no. 108)59 (β-phase) | a = b = 8.8438(3) Å and c = 12.6215(5) Å; α = β = γ = 90° (T = 293 K) | Pb | 0.0 | 0.0 | 0.00012 | 1 | |
| I1 | 0.0 | 0.0 | 0.25 | 1 | |||
| I2 | 0.2135 | 0.7135 | 0.0007 | 1 | |||
| Tetragonal I422 (no. 97)60 (β-phase) | a = b = 8.88375(18) Å and c = 12.7010(3) Å; α = β = γ = 90° (T = 293 K) | Pb | 1.0 | 1.0 | 0.7498 | 1 | |
| I1_1 | 1.0 | 1.0 | 0.5 | 1 | |||
| I1_2 | 1.0 | 1.0 | 1.0 | 1 | |||
| I2 | 0.28604 | 0.78604 | 0.75 | 1 | |||
| Orthorhombic Fmmm (no. 69)26 | a = 12.4984(7) Å, b = 12.5181(7) Å and c = 12.6012(8) Å; α = β = γ = 90° (T = 296(2) K) | Pb | 0.25 | 0.25 | 0.5 | 1 | |
| I1 | 0.2241 | 0.5 | 0.5 | 1 | |||
| I2A | 0.5 | 0.2981 | 0.5 | 0.75 | |||
| I2B | 0.5 | 0.267 | 0.462 | 0.125 | |||
| I3A | 0.25 | 0.25 | 0.25 | 0.75 | |||
| I3B | 0.294 | 0.25 | 0.25 | 0.125 | |||
| Orthorhombic Pnma (no. 62)17 (γ-phase) | a = 8.8362(11) Å, b = 12.5804(15) Å and c = 8.5551(10) Å; α = β = γ = 90° (T = 100 K) | Pb | 0.5 | 0.0 | 0.0 | 1 | |
| I1 | 0.485720 | 0.25 | −0.05291 | 1 | |||
| I2 | 0.1902 | 0.01719 | 0.18615 | 1 | |||
| FAPbI3 | Trigonal P3m1 (no. 156)21 (α-phase) | a = 8.9817(13) Å, b = 8.9817(13) Å and c = 11.006(2) Å; α = β = 90° and γ = 120° (T = 293(2) K) | Pb1 | 0.666667 | 0.333333 | 0.837860 | 1 |
| Pb2 | 0.0 | 0.0 | 0.50454 | 1 | |||
| Pb3 | 0.666667 | 0.333333 | 0.17092 | 1 | |||
| I1 | 0.1662 | 0.8338 | 0.33757 | 1 | |||
| I2 | 0.83303 | 0.16697 | 0.67107 | 1 | |||
| I3 | 0.49956 | 0.50044 | 0.00447 | 1 | |||
Cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 221)61 (α-phase) m (no. 221)61 (α-phase) |
a = b = c = 6.3620(8) Å; α = β = γ = 90° (T = 298 K) | Pb | 0.0 | 0.0 | 0.0 | 1 | |
| I | 0.5 | 0.0 | 0.0 | 1 | |||
| Tetragonal P4/mbm (no. 127)30 (β-phase) | a = b = 8.922756(12) Å and c = 6.326256(14) Å; α = β = γ = 90° (T = 200 K) | Pb | 0.0 | 0.0 | 0.0 | 1 | |
| I1 | 0.0 | 0.0 | 0.5 | 1 | |||
| I2 | 0.230 | 0.730 | 0.0 | 1 | |||
| Hexagonal P63mc (no. 186)21 (δ-phase, non-perovskite) | a = b = 8.6603(14) Å and c = 7.9022(6) Å; α = β = 90° and γ = 120° (T = 293(2) K) | Pb | 0.0 | 0.0 | 0.006 | 1 | |
| I | 0.83117 | 0.16883 | 0.251 | 1 | |||
| Hexagonal P63/mmc (no. 194)31 (δ-phase, non-perovskite) | a = b = 8.5891(5) Å and c = 7.853(7) Å; α = β = 90° and γ = 120° (T = 298 K) | Pb | 0.0 | 0.0 | 0.0 | 1 | |
| I | 0.82957 | 0.17043 | 0.25 | 1 | |||
| Compound | Space group & unit cell constants |
|---|---|
| CsPbI3 | Monoclinic P21/m (no. 11) (P = 3.9 GPa)14a = 9.832(2) Å, b = 4.543(1) Å and c = 16.919(2) Å; α = γ = 90° and β = 90.34(3)° |
| MAPbI3 | Monoclinic C2/m (no. 12) (P = 40 GPa)15a = 15.3402(3) Å, b = 3.52911(2) Å and c = 18.1236(5) Å; α = γ = 90° and β = 132.892(2)° |
Cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 204) (P = 0.45(2) GPa)22a = b = c = 12.4067(5) Å; α = β = γ = 90° (no. 204) (P = 0.45(2) GPa)22a = b = c = 12.4067(5) Å; α = β = γ = 90° |
|
| Orthorhombic Immm (no. 71) (P = 3.21 GPa)23a = 12.1360(4) Å, b = 12.1022(2) Å and c = 11.8177(5) Å; α = β = γ = 90° | |
| FAPbI3 | Orthorhombic Imm2 (no. 44) (P = 0.40 GPa)23a = 12.408(3) Å, b = 12.419(3) Å and c = 12.25(5) Å; α = β = γ = 90° |
| Orthorhombic Imm2 (no. 44) (P = 0.34 GPa)32a = 12.4950 Å, b = 12.4900 Å and c = 12.5428 Å; α = β = γ = 90° | |
| Orthorhombic Immm (no. 71) (P = 0.67 GPa)32a = 12.2264 Å, b = 12.4900 Å and c = 12.3583 Å; α = β = γ = 90° | |
| Tetragonal P4/mbm (no. 127) (P = 0.49 GPa)34a = b = 8.9148(6) Å and c = 6.3138(7) Å; α = β = γ = 90° | |
Cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (no. 204) (P = 3.13 GPa)33a = b = c = 12.0654(6) Å; α = β = γ = 90° (no. 204) (P = 3.13 GPa)33a = b = c = 12.0654(6) Å; α = β = γ = 90° |
|
| Orthorhombic Cmc21 (no. 36) (P = 1.73 GPa)33 (non-perovskite) a = 14.0957(8) Å, b = 10.2072(4) Å and c = 13.9906(2) Å; α = β = γ = 90° |
In this perspective, we critically examine the structures of various phases of CsPbI3, MAPbI3, and FAPbI3 perovskites, reported in the crystallographic database. Our aim is to understand structures and underlying optoelectronic properties. Our perspective is expected to raise the current understanding level of structures at the atomic level and provide some new strategies to further design and synthesize stable halide perovskites.
2. Thermodynamics of solid-to-solid phase transitions
A solid-to-solid phase transition of a material is a transition between its different crystalline forms (also known as phases or polymorphs), each of which possesses uniform structure and composition throughout and separates from the other form by the phase boundary.35 Thermodynamically, phase transition is the transformation of a thermodynamic system from one phase into another in response to a change in one or more thermodynamic variables (such as temperature or pressure) which is distinguishable by a change in one or more thermodynamic quantities or order parameters (such as entropy, enthalpy, heat capacity etc.).36 Temperature and pressure can be precisely controlled to study changes in the free energy and the order parameters of a phase. Entropy (S) and volume (V) are first order parameters, i.e. first derivatives of the Gibbs free energy as defined using equations: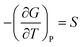 | (1) |
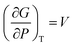 | (2) |
Heat capacity, volume thermal expansivity, compressibility and magnetic susceptibility are some of the second order parameters, i.e. second derivatives of the Gibbs free energy as defined using equations:
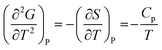 | (3) |
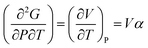 | (4) |
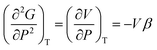 | (5) |
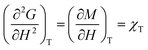 | (6) |
According to Ehrenfest,37 a phase transition is defined as an nth order transition, if at-least one of the nth order derivatives of the Gibbs free energy, such as entropy (S), volume (V), enthalpy (H), heat capacity (Cp) etc., exhibits discontinuity at the transition point. Thus, in the first order phase transition, at-least one of the first derivatives exhibits a discontinuity. Additionally, the specific heat capacity (Cp) shows extremely sharp and symmetrical shape of the peak at the transition point in a first order transition.38,39 According to modern thermodynamics, a first order phase transition includes latent heat (or change in enthalpy) (ΔH = TΔS), making the first order transition materials promising heat storage systems.40 When first order derivatives change continuously but at-least one of the second-order derivatives (such as Cp) shows discontinuity, the phase transition is defined to be a second order. Higher order transitions are also possible but are perhaps not very useful as the difference between the thermodynamic quantities becomes smaller.
3. A brief history of the lead iodide perovskite renaissance
The discovery of halide perovskite dates to 1893 when Wells synthesized CsPbX3 (X = Cl, Br, or I).41 The X-ray structures were first reported in 1957 by Møller.42 At room temperature, the chloride and the bromide were shown to exhibit 3-dimensional structures, while the iodide had a 1-dimensional chain structure.43 Furthermore, at higher temperatures, all these perovskites were reported to show phase transitions to intensively coloured phases, which was also the first report on the structural transition of lead halide perovskites. In 1978, Weber reported hybrid lead halide perovskites MAPbX3 (MA = methylammonium; X = Cl, Br or I), which were suggested to adopt cubic symmetry.44 Since then research on lead halide perovskites progressed almost steadily, focusing largely on understanding the nature of structural phase transitions45,46 and electronic properties.47,48 The breakthrough happened in 2009 when Kojima et al.,4 fabricated dye-sensitized solar cells (DSSCs) by using MAPbBr3 and MAPbI3 as photosensitizers. This development quickly captured the wide attention of the PV community. As a consequence, APbI3 perovskites have become one of the fastest growing PV materials with the solar to power conversion efficiency (PCE) for single-junction solar cells reaching 25% (certified 25.5%),49–52 surpassing the organic photovoltaics by a large margin and rivalling silicon solar cells. The field is still thriving, and many more developments are anticipated in the near future.4. Origin of structural transitions in lead iodide perovskites
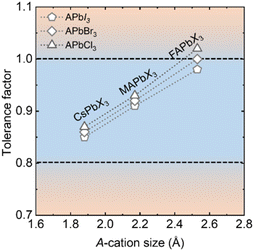
The highest symmetry cubic structure of APbI3 perovskites consists of a [PbI3]− framework of corner-sharing [PbI6]4− octahedra with all Pb–I–Pb bond angles of 180°, similar to the ReO3 structure.53 Between the octahedra, large A-cation occupies the 12-coordinated interstices and serves as a structural template for stabilization of the perovskite structure. Due to flexibility of the [PbI3]− sub-lattice and dynamic nature of the A-cation, the cubic perovskite tends to form octahedrally tilted lower-symmetry phases to achieve structural and thermodynamic stability. Without exception, more than one structure is reported for each of the APbI3 perovskites, depending on temperature, pressure and even the preparation method. To be consistent with the nomenclature of different phases mentioned in the literature, in this article we designate the highest symmetry phase as the α-phase, the phases after first and second transitions as the β-phase and γ-phase, respectively, and the non-perovskite phase as the δ-phase.The structural stability of perovskites can be empirically pre-screened using the tolerance factor (t),54 and the octahedral factor (μ),55 calculated from the ionic radii of the constituent ions using the expressions: t = (rA + rX)/√2(rX + rB) and μ = rB/rX (here, rA, rB, and rX are the radii of the A-site cation, B-site metal ion and X-site halide, respectively). The octahedral factor assesses formability of the [PbI3]− framework which essentially needs octahedral coordination around the B-site metal ion. Its geometric limit is between 0.414 and 0.732. For lead iodide perovskites, the octahedral factor is 0.541 (rPb = 1.19 Å; rI = 2.2 Å) which is well within the perovskite range. The tolerance factor assesses the fitting of the A-cation within the A-site interstices. For a perovskite structure, the value of the tolerance factor should be in the 0.8–1.0 range. At a tolerance factor of 1.0, a perfect fit of the A-cation, thereby an un-tilted cubic structure is expected. A tolerance factor of 0.8 < t < 1.0 indicates that the A-cation is undersized and to strengthen the ionic interaction with the A-cation, the octahedra show tilting with Pb–I–Pb angles less than 180°. The tilting often leads to symmetry lowering from cubic to tetragonal to orthorhombic systems.56 With the tolerance factor below 0.80, structures, such as ilmenite-type (FeTiO3),57 are expected to be stable, while structures with face-sharing octahedra are expected to form with a tolerance factor above 1.0.62 In the case of hybrid perovskites, the hydrogen bonding and the order-disorder dynamics of the A-cation also play an important role in addition to the tolerance factor. Thus, the phase transition of the hybrid systems is more complex compared to that of all-inorganic analogues.
The A-site cavity of APbI3 perovskites is large and, to our knowledge, only three mono-cations, Cs+ (1.88 Å) MA+ (2.17 Å) and FA+ (2.53 Å) are of appropriate size. Some reports ascribe the phase instability of CsPbI3 to its tolerance factor being less than 0.9.63 The increase in A-cation size in the Cs+ < MA+ < FA+ order adjusts the tolerance factor close to 1.0 (Fig. 2), thereby structurally stabilizing the highest symmetry phase at lower temperature. Furthermore, a decrease in the halide radius adjusts the tolerance factor closer to 1.0 and halide mixing is, therefore, a powerful strategy for making stable perovskite structures.64
5. Temperature induced phase transition
5.1. Cesium lead triiodide (CsPbI3)
CsPbI3 in the black perovskite phase exhibits a narrow bandgap of 1.7 eV and can effectively absorb visible light when applied as an absorber layer in perovskite-solar cells. However, the black phase is structurally stable only at high temperature and undergoes two types of phase transitions upon decreasing the temperature (Fig. 3a): (i) perovskite to perovskite transition – the α-phase (cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to the β-phase (tetragonal P4/mbm) to the γ-phase (orthorhombic Pnma) and (ii) perovskite to non-perovskite transition – the α-phase to the δ-phase or ‘yellow phase’ (orthorhombic Pnma). Each of the perovskite phases (α-, β- or γ-) is composed of a 3-dimensional [PbI3]− framework, with Cs+ ions in the A-site voids. The perovskite phases differ from each other in the magnitude and the direction of octahedral tilts. The α-phase is the un-tilted form with a Glazer's tilt notation of a0a0a0. The β-phase shows one in-phase tilt (Glazer's tilt notation a0a0c+), while the γ-phase shows one in-phase and one out-of-phase tilt (Glazer's tilt notation a−b+a−). These three (pseudo-)cubic phases are collectively called the “black” phase as they typically exhibit similar optical properties. They are metastable at room temperature and transform into the thermodynamically more stable δ-phase through the first-order transition. The δ-phase shows a NH4CdCl3-type structure, comprising 1-dimensional double chains of edge-sharing [PbI6]4− octahedra and the Cs+ cation in the interchain space.
m) to the β-phase (tetragonal P4/mbm) to the γ-phase (orthorhombic Pnma) and (ii) perovskite to non-perovskite transition – the α-phase to the δ-phase or ‘yellow phase’ (orthorhombic Pnma). Each of the perovskite phases (α-, β- or γ-) is composed of a 3-dimensional [PbI3]− framework, with Cs+ ions in the A-site voids. The perovskite phases differ from each other in the magnitude and the direction of octahedral tilts. The α-phase is the un-tilted form with a Glazer's tilt notation of a0a0a0. The β-phase shows one in-phase tilt (Glazer's tilt notation a0a0c+), while the γ-phase shows one in-phase and one out-of-phase tilt (Glazer's tilt notation a−b+a−). These three (pseudo-)cubic phases are collectively called the “black” phase as they typically exhibit similar optical properties. They are metastable at room temperature and transform into the thermodynamically more stable δ-phase through the first-order transition. The δ-phase shows a NH4CdCl3-type structure, comprising 1-dimensional double chains of edge-sharing [PbI6]4− octahedra and the Cs+ cation in the interchain space.
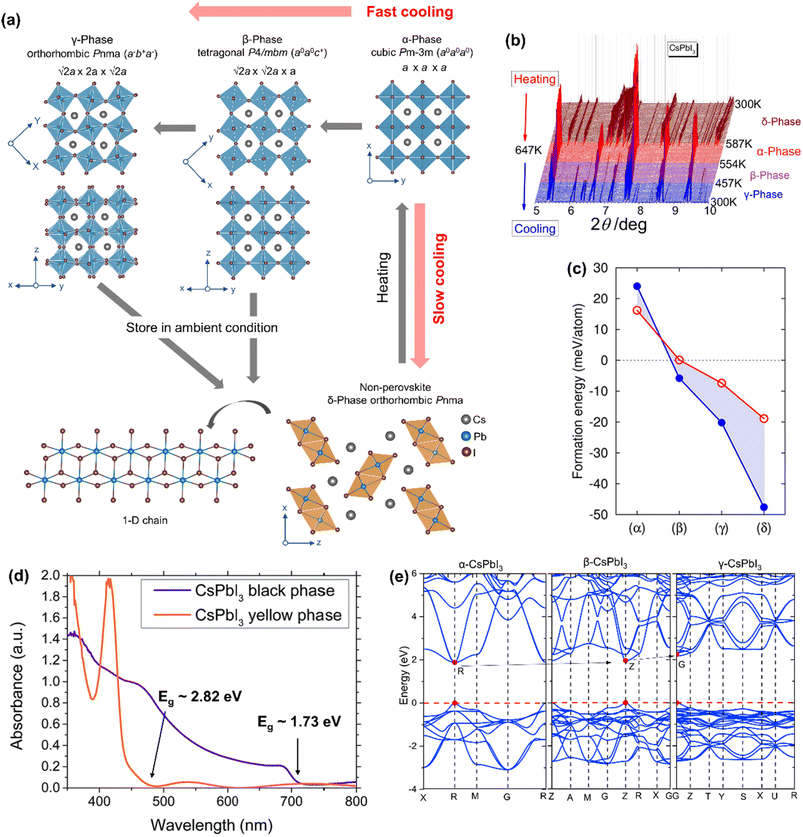 | ||
| Fig. 3 (a) Temperature-driven phases of CsPbI3. (b) Temperature-dependent PXRD patterns, showing that the transition pathways are different for heating and cooling steps. Reproduced with permission from ref. 12 copyright 2018 American Chemical Society. (c) Calculated formation energies (Ef) for CsPbI3 polymorphs with respect to the precursor's energies. The red circles and the blue dots correspond to DFT/PBE and DFT/LDA calculations, respectively. Reproduced with permission from ref. 65 copyright 2018 American Chemical Society. (d) Optical absorption spectra of the black and the yellow phases of CsPbI3. Adapted with permission from ref. 66 copyright the Royal Society of Chemistry 2015. (e) Calculated band structures for the black phases of CsPbI3 along the high-symmetry points in the Brillouin zone by using the GGA-PBE function. Reproduced with permission from ref. 67 copyright 2020 Elsevier B.V. | ||
Møller in 1958,43 diffracted yellow crystals of CsPbI3 at room temperature on a Geiger–Muller X-ray diffractometer and proposed an orthorhombic chain structure with the Pnma space group (a = 4.795 Å, b = 10.45 Å, and c = 17.76 Å). A color change from yellow to black was reported on heating to 578–581 K. The black phase was reported to have a monoclinically distorted 3D structure (a = b = 6.15 Å and c = 6.23 Å; β = 88.15°). Later studies by Trots et al.58 have shown that CsPbI3 changes from orthorhombic Pnma [a = 10.4581(3) Å, b = 4.80171(13) Å, and c = 17.7761(5) Å] to cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m [a = 6.28940(19) Å] symmetry upon heating at 634 K, but there was no information on the cooling step. Marronnier et al.,12 studied the phase transition of CsPbI3 by using high-resolution in situ synchrotron X-ray diffraction. They synthesized δ-CsPbI3 at room temperature and converted it to α-CsPbI3 [cubic Pm
m [a = 6.28940(19) Å] symmetry upon heating at 634 K, but there was no information on the cooling step. Marronnier et al.,12 studied the phase transition of CsPbI3 by using high-resolution in situ synchrotron X-ray diffraction. They synthesized δ-CsPbI3 at room temperature and converted it to α-CsPbI3 [cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; a = 6.29658(2) Å] by heating at around 600 K. On further heating, the α-CsPbI3 phase remained structurally unchanged before melting at 753 K.58 The powder XRD patterns (Fig. 3b) show that δ-CsPbI3 changes to α-CsPbI3 in one step, but upon cooling, α-CsPbI3 slowly returns to δ-CsPbI3 form through the β-phase [tetragonal P4/mbm; a = 8.82690(3) Å, b = 8.82690(3) Å, and c = 6.29902(3) Å] at 533 K and the γ-phase [orthorhombic Pbnm; a = 8.61979(6) Å, b= 8.85176(6) Å, and c = 12.50128(7) Å] at 448 K. The γ-phase transforms into the δ-phase within ∼48 h on further cooling to room temperature,12 or on exposure to humid air.68 The room temperature formation energy of α-CsPbI3 is much larger (∼14.1 kJ mol−1) than that for the δ-phase as confirmed by calorimetric measurements.13 Therefore, the α-phase (even if it is successfully synthesized at ambient temperature) is difficult to store under ambient conditions. Sutton et al.65 calculated the formation energies of the CsPbI3 polymorphs and found that the δ-phase has the largest formation enthalpy (Fig. 3c). The authors have further reported that rapid cooling leads to the γ-phase, while slow cooling (or on storing samples under ambient conditions, even in a vacuum) leads to the formation of the δ-phase. This indicates that the former compound is a kinetic product, while the latter compound is a thermodynamic product.68 Although the perovskite phase of CsPbI3 is metastable at room temperature, it has a small energy barrier before transitioning to the δ-phase and can therefore be realized at room temperature.69–72 By using the energy barrier, Steele et al.73 kinetically trapped the black phase CsPbI3 at room temperature through rapid cooling its strain induced thin film. Straus et al.68 showed that bulk γ-CsPbI3 crystals can be obtained at room temperature by rapid quenching the reaction in an ice–water bath and stored for up to 39 days under dry conditions in an evacuated ampule but exposure to humid air leads to the formation of the δ-phase within a few minutes. Their single-crystal X-ray diffraction and X-ray pair distribution function (PDF) studies suggested that γ-CsPbI3 crystals remain structurally unchanged in the 100–295 K range.74 However, the Cs cation was found disordered at two sites.74 Furthermore, water molecules lower the transition energy barrier and accelerate the conversion to the δ-phase.71 Also pure γ-CsPbI3 is reported to show PCE above 18% and retain 95% of the initial efficiency after 30 days.75 Ke et al.69 carried out in situ synchrotron XRD and Raman scattering measurements to show that γ-CsPbI3 can be synthesized and preserved at room temperature by heating and cooling under pressure. The authors first compressed δ-CsPbI3 to pressures of 0.1–0.6 GPa at room temperature followed by heating up to 130 °C and cooling back to room temperature at a cooling rate of 25–35 °C h−1. Eperon et al.66 trapped α-CsPbI3 at room temperature by carrying out device fabrication in an inert atmosphere, which showed 10% higher PCE compared with the other perovskite polymorphs.
m; a = 6.29658(2) Å] by heating at around 600 K. On further heating, the α-CsPbI3 phase remained structurally unchanged before melting at 753 K.58 The powder XRD patterns (Fig. 3b) show that δ-CsPbI3 changes to α-CsPbI3 in one step, but upon cooling, α-CsPbI3 slowly returns to δ-CsPbI3 form through the β-phase [tetragonal P4/mbm; a = 8.82690(3) Å, b = 8.82690(3) Å, and c = 6.29902(3) Å] at 533 K and the γ-phase [orthorhombic Pbnm; a = 8.61979(6) Å, b= 8.85176(6) Å, and c = 12.50128(7) Å] at 448 K. The γ-phase transforms into the δ-phase within ∼48 h on further cooling to room temperature,12 or on exposure to humid air.68 The room temperature formation energy of α-CsPbI3 is much larger (∼14.1 kJ mol−1) than that for the δ-phase as confirmed by calorimetric measurements.13 Therefore, the α-phase (even if it is successfully synthesized at ambient temperature) is difficult to store under ambient conditions. Sutton et al.65 calculated the formation energies of the CsPbI3 polymorphs and found that the δ-phase has the largest formation enthalpy (Fig. 3c). The authors have further reported that rapid cooling leads to the γ-phase, while slow cooling (or on storing samples under ambient conditions, even in a vacuum) leads to the formation of the δ-phase. This indicates that the former compound is a kinetic product, while the latter compound is a thermodynamic product.68 Although the perovskite phase of CsPbI3 is metastable at room temperature, it has a small energy barrier before transitioning to the δ-phase and can therefore be realized at room temperature.69–72 By using the energy barrier, Steele et al.73 kinetically trapped the black phase CsPbI3 at room temperature through rapid cooling its strain induced thin film. Straus et al.68 showed that bulk γ-CsPbI3 crystals can be obtained at room temperature by rapid quenching the reaction in an ice–water bath and stored for up to 39 days under dry conditions in an evacuated ampule but exposure to humid air leads to the formation of the δ-phase within a few minutes. Their single-crystal X-ray diffraction and X-ray pair distribution function (PDF) studies suggested that γ-CsPbI3 crystals remain structurally unchanged in the 100–295 K range.74 However, the Cs cation was found disordered at two sites.74 Furthermore, water molecules lower the transition energy barrier and accelerate the conversion to the δ-phase.71 Also pure γ-CsPbI3 is reported to show PCE above 18% and retain 95% of the initial efficiency after 30 days.75 Ke et al.69 carried out in situ synchrotron XRD and Raman scattering measurements to show that γ-CsPbI3 can be synthesized and preserved at room temperature by heating and cooling under pressure. The authors first compressed δ-CsPbI3 to pressures of 0.1–0.6 GPa at room temperature followed by heating up to 130 °C and cooling back to room temperature at a cooling rate of 25–35 °C h−1. Eperon et al.66 trapped α-CsPbI3 at room temperature by carrying out device fabrication in an inert atmosphere, which showed 10% higher PCE compared with the other perovskite polymorphs.
Due to reduced structural dimensionality, the optoelectronic properties of δ-CsPbI3 differ completely from those of the α-, β- or γ-phases (collectively called the black phase). The optical absorption spectra (Fig. 3d) show that the black CsPbI3 can absorb below ∼715 nm (∼1.73 eV), while the yellow CsPbI3 can only absorb below ∼440 nm (∼2.82 eV).66 This essentially indicates that the yellow phase is photoinactive from a solar cell point of view. Within the black phases, the bandgap marginally increases from α-CsPbI3 (Eg = 1.63 eV),68 β-CsPbI3 (Eg = 1.68 eV),76 and γ-CsPbI3 (Eg = 1.72 eV)68 depending on the degree of PbI6 octahedral tilting compared with the highest symmetry α-CsPbI3. Furthermore, the bandgaps of these phases remain direct (Fig. 3e).67
5.2. Methylammonium lead triiodide (MAPbI3)
Just like CsPbI3, MAPbI3 also exhibits symmetry lowering phase transitions upon decreasing temperature (Fig. 4a): the α-phase (cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to the β-phase (tetragonal I4/mbm) to the γ-phase (orthorhombic Pnma) in which the MA+ cation is fully disordered, partially disorder and fully ordered, respectively. The α- to β-phase transition is a consequence of one out-of-phase octahedral tilt (Glazer's tilt notation a0a0c−), which is opposite in direction compared to the corresponding transition of CsPbI3. All Pb–I–Pb bond angles in the α-phase are necessarily 180°. Owing to C3V symmetry, the MA+ cation is expected to be orientationally disordered in cubic symmetry, with its C–N bond axis oriented along any of the three 〈100〉 directions.18,77 Different studies have pointed out that the I⋯H hydrogen bonds play an important role in the MA+ dynamics, thereby in the phase transition of MAPbI3.78,79 Therefore, the order-disorder dynamics of the MA+ cation has been widely studied using a range of techniques such as solid-state NMR spectroscopy,10,80 dielectric spectroscopy,81 and quasi-elastic neutron scattering measurements.82–84 The β- to γ-phase transition is a consequence of two simultaneous in-phase and out-of-phase tilts (Glazer's tilt notation a−b+a−) with respect to the α-phase. During the phase transition, although the symmetry of [PbI6]4− octahedra reduces from a perfect octahedral, it remains centrosymmetric with the Pb2+ metal ion at the centre of the octahedra. This indicates that the 6s2 lone pair electrons of the Pb2+ ion are stereochemically hidden which has been the subject of intense discussion, particularly in connection with the ferroelectric phase transition.20,56,85
m) to the β-phase (tetragonal I4/mbm) to the γ-phase (orthorhombic Pnma) in which the MA+ cation is fully disordered, partially disorder and fully ordered, respectively. The α- to β-phase transition is a consequence of one out-of-phase octahedral tilt (Glazer's tilt notation a0a0c−), which is opposite in direction compared to the corresponding transition of CsPbI3. All Pb–I–Pb bond angles in the α-phase are necessarily 180°. Owing to C3V symmetry, the MA+ cation is expected to be orientationally disordered in cubic symmetry, with its C–N bond axis oriented along any of the three 〈100〉 directions.18,77 Different studies have pointed out that the I⋯H hydrogen bonds play an important role in the MA+ dynamics, thereby in the phase transition of MAPbI3.78,79 Therefore, the order-disorder dynamics of the MA+ cation has been widely studied using a range of techniques such as solid-state NMR spectroscopy,10,80 dielectric spectroscopy,81 and quasi-elastic neutron scattering measurements.82–84 The β- to γ-phase transition is a consequence of two simultaneous in-phase and out-of-phase tilts (Glazer's tilt notation a−b+a−) with respect to the α-phase. During the phase transition, although the symmetry of [PbI6]4− octahedra reduces from a perfect octahedral, it remains centrosymmetric with the Pb2+ metal ion at the centre of the octahedra. This indicates that the 6s2 lone pair electrons of the Pb2+ ion are stereochemically hidden which has been the subject of intense discussion, particularly in connection with the ferroelectric phase transition.20,56,85
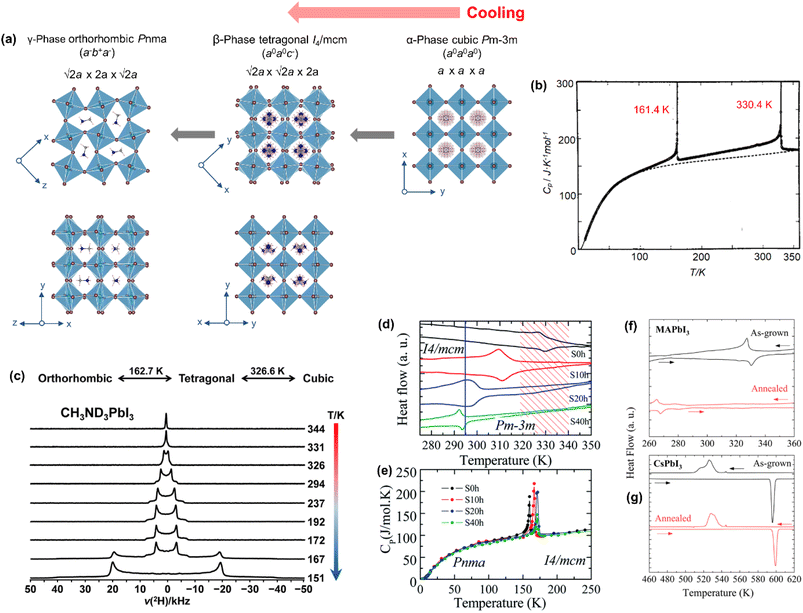 | ||
| Fig. 4 (a) Temperature-driven phases of MAPbI3. (b) Molar heat capacity at constant pressure, showing two phase transitions. Reproduced with permission from ref. 87 copyright 1990 Pergamon Press plc. (c) Variable temperature 2H NMR spectra of CH3ND3PbI3, acquired at 11.75 T. Reproduced with permission from ref. 88 copyright 2018 American Chemical Society. (d) DSC plots with the vertical line (blue) showing the room temperature and the hachured region (red) showing the solar cell working temperature range. (e) Temperature dependent molar heat capacity of MAPbI3 pellets annealed at 523 K for different times. Adapted with permission from ref. 91 copyright the Royal Society of Chemistry 2021. (f and g) DSC plots of as-grown and thermally annealed polycrystalline samples of MAPbI3 and CsPbI3, respectively. Reproduced with permission from ref. 92 copyright 2023 American Chemical Society. | ||
Weber in 1978 modelled the ambient temperature and pressure phase of MAPbI3 in the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (a = 6.27 Å) by using powder X-ray diffraction.44 Its temperature driven phase transition was studied by Poglitsch and Weber in 1987 using X-ray diffraction data.16 They found that it crystallizes in the α-phase [cubic Pm
m space group (a = 6.27 Å) by using powder X-ray diffraction.44 Its temperature driven phase transition was studied by Poglitsch and Weber in 1987 using X-ray diffraction data.16 They found that it crystallizes in the α-phase [cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; a = 6.3285(5) Å] above 327.4 K, in the β-phase [tetragonal I4/mcm; a = b = 8.855(6) Å and c = 12.659 (8) Å] in the 327.4–162.2 K temperature range and in the γ-phase [orthorhombic Pna21; a = 8.861 (2) Å, b = 8.581 (2) Å and c = 12.620 (3) Å] below 162.2 K.16 Later, the γ-phase was reassigned as the orthorhombic Pnma space group due to the absence of (or weak) ferroelectric behaviour.86 The orthorhombic Pnma structure was further confirmed by Baikie et al.17 from the single crystal X-ray diffraction data. No further phase transition was observed down to a temperature of 10 K.18 These two phase transitions were subsequently supported by calorimetric (Fig. 4b)87 and NMR spectroscopic studies (Fig. 4c).88 The β- to γ-phase transition follows first-order thermodynamics based on heat capacity measurements,87,89 as well as time-of-flight neutron and synchrotron diffraction studies.18 The α- to β-phase transition is close to second order as the volume change is continuous.77,90 However, a thermal hysteresis observed during the heating step suggests that the nature of the transition could be of first-order.90,91 Furthermore, the whole phase transition process was found to be reversible during cooling and heating cycles.18
m; a = 6.3285(5) Å] above 327.4 K, in the β-phase [tetragonal I4/mcm; a = b = 8.855(6) Å and c = 12.659 (8) Å] in the 327.4–162.2 K temperature range and in the γ-phase [orthorhombic Pna21; a = 8.861 (2) Å, b = 8.581 (2) Å and c = 12.620 (3) Å] below 162.2 K.16 Later, the γ-phase was reassigned as the orthorhombic Pnma space group due to the absence of (or weak) ferroelectric behaviour.86 The orthorhombic Pnma structure was further confirmed by Baikie et al.17 from the single crystal X-ray diffraction data. No further phase transition was observed down to a temperature of 10 K.18 These two phase transitions were subsequently supported by calorimetric (Fig. 4b)87 and NMR spectroscopic studies (Fig. 4c).88 The β- to γ-phase transition follows first-order thermodynamics based on heat capacity measurements,87,89 as well as time-of-flight neutron and synchrotron diffraction studies.18 The α- to β-phase transition is close to second order as the volume change is continuous.77,90 However, a thermal hysteresis observed during the heating step suggests that the nature of the transition could be of first-order.90,91 Furthermore, the whole phase transition process was found to be reversible during cooling and heating cycles.18
The α- → β-phase transition of MAPbI3 falls within the typical device working temperature range (∼327 K), which often leads to adverse changes in the photophysical properties, affecting functioning of the whole device. Thus, stabilizing α-MAPbI3 at room temperature by either suppressing the transition or by shifting the transition to a lower temperature has been an active research direction. Bonadio et al.91 showed that 40 h long thermal annealing of a MAPbI3 film at 523 K lowers the α- → β-phase transition temperature by 36 K, stabilizing the α-phase at room temperature. The DSC data (Fig. 4d) and the heat capacity data (Fig. 4e) clearly show the lowering of the transition temperature as a function of annealing time. In their recent thermal annealing of the polycrystalline MAPbI3 sample,92 the α-phase has been stabilized even at below room temperature by a shift of 62 K in the transition temperature (Fig. 4f). Furthermore, it was observed that thermal annealing has no influence on the transition temperature for the CsPbI3 sample (Fig. 4g), indicating that the ordered–disordered orientation of MA+ has a substantial role in the phase transition.92
Most of the studies suggest that the tetragonal I4/mcm space group is the commonly accepted structure of MAPbI3 at room temperature. This is a non-polar space group, thereby excluding the possibility of ferroelectric behaviour. However, MAPbI3 has been hotly debated as a promising ferroelectric material, for which the structure needs to be polar.59,93–95 Indeed, there have been many reports, suggesting polar space groups for the room temperature β-phase: tetragonal I4cm [a = b = 8.8438(3) Å and c = 12.6215(5) Å],21,59,96,97I422 [a = b = 8.88374(18) Å and c = 12.7010(3) Å].60,98 These polar groups exhibit group/subgroup relationships with the non-polar I4/mcm space group.59 In these groups, the [PbI6]4− octahedra exhibit second order Jahn–Teller distortion [Pb–I(1) distance = 3.125 Å × 2; Pb–I(2) distance = 3.161 Å × 4].21 The orientation of the MA+ cation in the [PbI3]− sublattice is believed to be responsible for the polarization.93 Despite many structural studies, the symmetry assignment of MAPbI3 to a polar or non-polar space group is still debated, and so is its ferroic behaviour.20,59,93,99,100 The challenges that crystallographers encounter are often attributed to the disordered nature of the MA+ cation and the extremely complicated hydrogen bonding pattern.101,102 Crystal twinning further makes the process challenging.26,103
Symmetry lowering of the [PbI3]− framework (or the deviation of the Pb–I–Pb bond angle from linear 180°) influences the electronic structure and the optical bandgap which eventually influences the optoelectronic properties. First-principles calculations have suggested that the valence band maximum (VBM) of MAPbI3 is mainly composed of Pb 6s–I 5p* antibonding MOs, while the conduction band minimum (CMB) is mainly composed of Pb 6p–I 5p MOs with less antibonding character and more nonbonding character.79,104 Any deviation in the Pb–I–Pb bond angle from 180° reduces the Pb–I orbital overlap and stabilizes the VBM, lowering its energy, whilst due to nonbonding character the effect of lattice distortions is less on the CBM. This leads to an increase in the energy gap between the VBM and CBM.
We note that unlike δ-CsPbI3 (vide supra) and δ-FAPbI3 (vide infra), non-perovskite phases of MAPbI3 are not experimentally reported but some theoretical calculations have predicted them as stable polymorphs.105–107 Although not strictly a phase transition, there have been reports on the solvent driven reconstructive transition of MAPbI3. Huang et al.108 reported the 1D δ-phase to 3D α-phase transition, driven by ethylamine (CH3NH2) intercalation. In the δ-phase, the CH3NH2 molecules form weak hydrogen bonds with the MA+ cations to form CH3NH2⋯CH3NH3+ dimers in the space between face-sharing [PbI3]− chains. The increased ionic radius of the dimeric cation (4.45 Å), compared to the MA+ cation (2.17 Å), exceeds the tolerance factor beyond 1.0, which helps stabilizing the 1D structure. The yellow δ-phase (CH3NH2⋯CH3NH3+)PbI3 irreversibly changes to the black (CH3NH3+)PbI3 on exposure to air for few minutes. In the presence of solvents with hydrogen bonding capability (such as water, dimethyl sulfoxide, dimethylformamide etc.), MAPbI3 can form needle-shaped yellow 1D chain compounds MAPbI3·S (here, S = solvent molecule).109 They spontaneously convert to the black perovskite phase on removal of solvent. The transitions due to water are discussed separately in Section 7.
5.3. Formamidinium lead triiodide (FAPbI3)
FAPbI3 exhibits four temperature driven structures: the α-phase (cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at high temperature, the β-phase and the γ-phase at low temperature (both crystallize in the tetragonal P4/mbm space group) and a yellow δ-phase (hexagonal P63mc) at room temperature (Fig. 5a). The α-phase has an un-tilted structure (Glazer's notation a0a0a0) with all Pb–I–Pb angles of 180° and a fully disordered FA+ cation at the A-site. The β-phase and the γ-phase exhibit one in-phase octahedral tilt (Glazer's notation a0a0c+). The δ-phase has a one-dimensional chain structure of face-sharing [PbI6]− octahedra along the (001) direction and the ordered FA+ cation located in the interchain space.110 Note that the structure of δ-FAPbI3 is strikingly different than that of the δ-CsPbI3 phase. As shown in Fig. 5b the bandgap of δ-FAPbI3 (Eg = 2.17 eV) is wider compared to that of α-FAPbI3 (Eg = 1.53 eV),111,112 making it unsuitable for most of the optoelectronic properties, including solar cells. The α-FAPbI3 film usually contains a δ-phase impurity, which reduces light absorption and retards device efficiency.113 It is worthwhile to note that α-FAPbI3 is more attractive than α-MAPbI3 and α-CsPbI3 because its bandgap is closer to the theoretically optimal bandgap (1.4 eV) required for solar cells.
m) at high temperature, the β-phase and the γ-phase at low temperature (both crystallize in the tetragonal P4/mbm space group) and a yellow δ-phase (hexagonal P63mc) at room temperature (Fig. 5a). The α-phase has an un-tilted structure (Glazer's notation a0a0a0) with all Pb–I–Pb angles of 180° and a fully disordered FA+ cation at the A-site. The β-phase and the γ-phase exhibit one in-phase octahedral tilt (Glazer's notation a0a0c+). The δ-phase has a one-dimensional chain structure of face-sharing [PbI6]− octahedra along the (001) direction and the ordered FA+ cation located in the interchain space.110 Note that the structure of δ-FAPbI3 is strikingly different than that of the δ-CsPbI3 phase. As shown in Fig. 5b the bandgap of δ-FAPbI3 (Eg = 2.17 eV) is wider compared to that of α-FAPbI3 (Eg = 1.53 eV),111,112 making it unsuitable for most of the optoelectronic properties, including solar cells. The α-FAPbI3 film usually contains a δ-phase impurity, which reduces light absorption and retards device efficiency.113 It is worthwhile to note that α-FAPbI3 is more attractive than α-MAPbI3 and α-CsPbI3 because its bandgap is closer to the theoretically optimal bandgap (1.4 eV) required for solar cells.
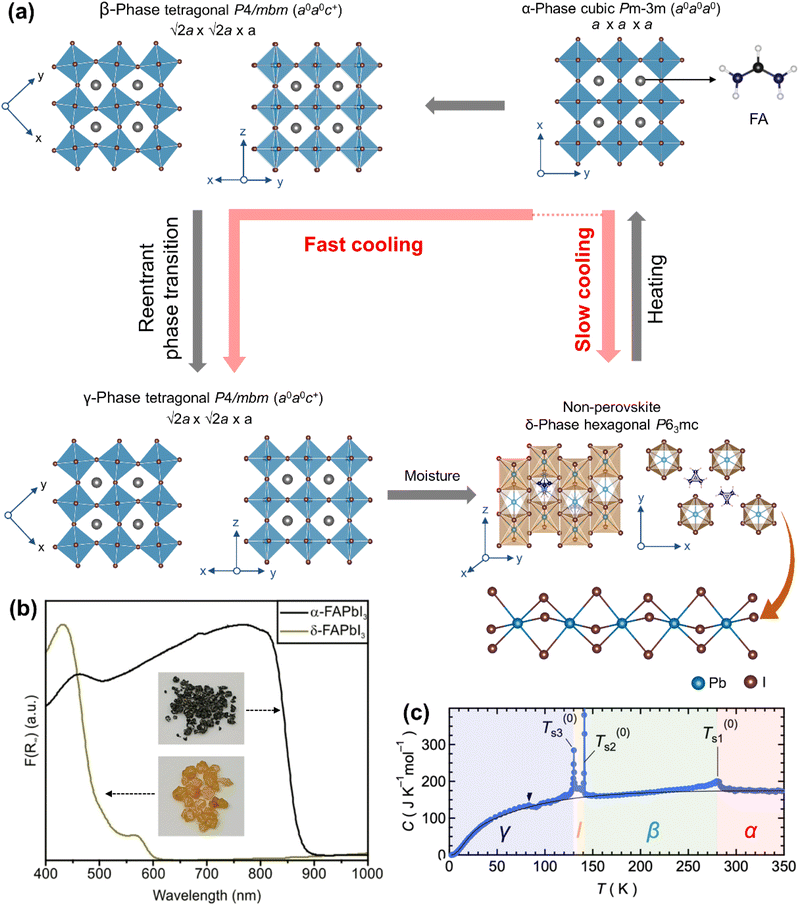 | ||
| Fig. 5 (a) Temperature-driven phases of FAPbI3. (b) Diffuse reflectance spectra of α-FAPbI3 and δ-FAPbI3 with the inset showing photographs of their single crystals. Adapted from ref. 111 copyright 2021 the authors under CC-BY-NC-ND 4.0. (c) Temperature dependent heat capacity of FAPbI3 at constant pressure. Reproduced with permission from ref. 119. Copyright 2019 American Chemical Society. | ||
Clearly, the symmetries of α-FAPbI3 and δ-FAPbI3 are not corelated by a simple group/subgroup relation, meaning that the δ- ↔ α-phase transition is a complex process of structural reconstruction. The density functional theory (DFT) calculations have suggested that the formation enthalpy (ΔH) of δ-FAPbI3 is ∼70 meV per formula unit lower than that of α-FAPbI3.28 This means that the Gibbs free energy (ΔG = ΔH − TΔS) of α-FAPbI3 is higher. The difference between the free energies of the two phases is largely attributed to the isotropic rotation of the FA+ cation. At temperature higher than the δ- → α-phase transition temperature, the increased entropy of the disordered FA+ cation lowers the free energy of the system, thereby stabilizing α-FAPbI3. At low temperature, the FA+ cation adopts preferred orientation with lower entropy and high Gibbs free energy, favouring the δ-phase. With mixed A-cation variants, such as MA1−xFAxPbI3,114,115 and FA1−xCsxPbI3,116 the α- → δ-phase transition can be inhibited, wherein the tolerance factor and the entropic factor are in favour of α-FAPbI3.
There have been several reports on the structural studies of the α-FAPbI3 → δ-FAPbI3 transition. Stoumpos et al.21 isolated both α-FAPbI3 and δ-FAPbI3 phases at room temperature from solution synthesis. They modelled the former phase in the trigonal P3m1 space group [a = b = 8.9817(13) Å and c = 11.006(2) Å, measured at 293 K] with a 3-fold disordered FA+ cation at the A-site and the latter phase in the hexagonal P63mc space group [a = b = 8.6603(14) Å and c = 7.9022(6) Å, measured at 293 K]. The authors observed that α-FAPbI3 forms at above 333 K and transforms slowly into δ-FAPbI3. Weller et al.61 revisited the X-ray structure of the high temperature phase and modelled it in the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group [a = 6.3620(8) Å] which is isostructural to α-CsPbI3 [a = 6.1769(3) Å] and α-MAPbI3 [a = 6.315(3) Å]. They used neutron powder diffraction which is a more sensitive tool compared to X-ray diffraction for locating light atoms of the FA+ cation. The FA+ cation was found to be orientationally disordered within the [PbI3]− framework of α-FAPbI3 and fully ordered between the [PbI3]− chains of δ-FAPbI3. The variable temperature X-ray diffraction studies have found that δ-FAPbI3 undergoes a sharp first-order transition to α-FAPbI3 above 350 K, which is reversible on cooling but at a lower temperature of 290 K.28 This large thermal hysteresis has been further supported by the first-principles calculations which suggest that there is a kinetic energy barrier (∼0.84 eV) between these two phases.28,110 By making use of the barrier, α-FAPbI3 has been trapped by thermal quenching at 8.2 K,28 which changes to δ-FAPbI3 on exposure to humid air. Furthermore, applied pressure is found to accelerate the α-FAPbI3 to δ-FAPbI3 transition by reducing the kinetic energy barrier.33 Reports have also suggested that water vapor can trigger the α-FAPbI3 to δ-FAPbI3 transition.117 Keshavarz et al.118 reported that δ-FAPbI3 also undergoes phase transitions at 173 K and 54 K which show negative thermal expansion (NTE) with a large NTE coefficient (α) of −1.3 × 10−4 K−1 and −2.5 × 10−4 K−1, respectively.
m space group [a = 6.3620(8) Å] which is isostructural to α-CsPbI3 [a = 6.1769(3) Å] and α-MAPbI3 [a = 6.315(3) Å]. They used neutron powder diffraction which is a more sensitive tool compared to X-ray diffraction for locating light atoms of the FA+ cation. The FA+ cation was found to be orientationally disordered within the [PbI3]− framework of α-FAPbI3 and fully ordered between the [PbI3]− chains of δ-FAPbI3. The variable temperature X-ray diffraction studies have found that δ-FAPbI3 undergoes a sharp first-order transition to α-FAPbI3 above 350 K, which is reversible on cooling but at a lower temperature of 290 K.28 This large thermal hysteresis has been further supported by the first-principles calculations which suggest that there is a kinetic energy barrier (∼0.84 eV) between these two phases.28,110 By making use of the barrier, α-FAPbI3 has been trapped by thermal quenching at 8.2 K,28 which changes to δ-FAPbI3 on exposure to humid air. Furthermore, applied pressure is found to accelerate the α-FAPbI3 to δ-FAPbI3 transition by reducing the kinetic energy barrier.33 Reports have also suggested that water vapor can trigger the α-FAPbI3 to δ-FAPbI3 transition.117 Keshavarz et al.118 reported that δ-FAPbI3 also undergoes phase transitions at 173 K and 54 K which show negative thermal expansion (NTE) with a large NTE coefficient (α) of −1.3 × 10−4 K−1 and −2.5 × 10−4 K−1, respectively.
Compared to the α- → δ-FAPbI3 transition, there have been fewer studies on the α-FAPbI3 → β-FAPbI3 → γ-FAPbI3 phase transition. Fabini et al.30 reported that α-FAPbI3 (cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; a = 6.35788 Å, measured at 299 K) undergoes a second-order transition to the β-phase [tetragonal P4/mbm; a = b = 8.9227(1) Å and c = 6.3263(1) Å, measured at 200 K] below 285 K, followed by a first-order re-entrant transition to the γ-phase [tetragonal P4/mbm; a = b = 8.8752(3) Å and c = 6.2792(4) Å, measured at 100 K] below 140 K. In this study, the atomic positions of the FA+ cation were not found in the diffraction due to its dynamic disorder and limited sensitivity of the X-ray diffractometer. It was modelled as a single pseudo-atom with an equivalent scattering factor. For this experiment, δ-FAPbI3 was synthesized at room temperature, and packed and sealed in a Kapton capillary, and converted to α-FAPbI3 by in situ heating up to 490 K during the X-ray data acquisition. Although the phase transition is continuous, there were discontinuous changes observed in the dielectric and the optical properties. Subsequent heat capacity measurements (Fig. 5c) on FAPbI3 single crystals have suggested that there exists another phase, named I-phase,119 between β-FAPbI3 and γ-FAPbI3 in the temperature range of 141.2–130.2 K, but no further characterization of the I-phase was reported.
m; a = 6.35788 Å, measured at 299 K) undergoes a second-order transition to the β-phase [tetragonal P4/mbm; a = b = 8.9227(1) Å and c = 6.3263(1) Å, measured at 200 K] below 285 K, followed by a first-order re-entrant transition to the γ-phase [tetragonal P4/mbm; a = b = 8.8752(3) Å and c = 6.2792(4) Å, measured at 100 K] below 140 K. In this study, the atomic positions of the FA+ cation were not found in the diffraction due to its dynamic disorder and limited sensitivity of the X-ray diffractometer. It was modelled as a single pseudo-atom with an equivalent scattering factor. For this experiment, δ-FAPbI3 was synthesized at room temperature, and packed and sealed in a Kapton capillary, and converted to α-FAPbI3 by in situ heating up to 490 K during the X-ray data acquisition. Although the phase transition is continuous, there were discontinuous changes observed in the dielectric and the optical properties. Subsequent heat capacity measurements (Fig. 5c) on FAPbI3 single crystals have suggested that there exists another phase, named I-phase,119 between β-FAPbI3 and γ-FAPbI3 in the temperature range of 141.2–130.2 K, but no further characterization of the I-phase was reported.
6. Pressure induced phase transition
6.1. Cesium lead triiodide (CsPbI3)
Pressure has emerged as an effective way of tuning structures and revealing novel properties of various materials.120–122 In the recent past, tremendous research efforts have been devoted to pressure driven behaviour of lead iodide perovskites. To our knowledge, the studies on CsPbI3 are less prolific, compared to those on MAPbI3 and FAPbI3 perovskites. Ke et al.69 showed that metastable γ-CsPbI3 can be stored at room temperature by heating yellow δ-CsPbI3 followed by rapid quenching under an applied pressure in the 0.1 GPa to 0.6 GPa range. Yuan et al.14 reported reversible transformation of the orthorhombic δ-CsPbI3 to the monoclinic P21/m structure [a = 9.832(2) Å, b = 4.543(1) Å, and c = 16.919(2) Å; β = 90.34(3)°, measured at ambient temperature and 3.9 GPa pressure]. The Raman scattering studies, carried out up to ∼15 GPa pressure, have suggested that the transition is reversible on decompression. Liang et al.15 reported that the room temperature δ-CsPbI3 shows a first-order transition to the monoclinic C2/m structure [a = 15.423(2) Å, b = 3.511(3) Å, c = 18.461(1) Å, and β = 132.829(2)°] at 6.9 GPa, with complete conversion to the monoclinic phase at 18 GPa. The C2/m phase exhibits highly distorted [PbI6]4− octahedra with the shortest Pb–I bond length among the known phases of CsPbI3. The shortening of Pb–I bond length under pressure gives rise to strong hybridization of Pb 6s–I 5p* orbitals, which pushes up the energy of the VBM and decreases the bandgap energy.24 The bandgap redshifts from 2.5 to 1.2 eV as pressure reaches 15 GPa. At high pressure, the bandgap closes and the insulator to metal transition occurs at 39.3 GPa.156.2. Methylammonium lead triiodide (MAPbI3)
Upon compression, Ou et al.123 observed discontinuous changes in the electric transport properties of MAPbI3 nanorods. They found a mixed tetragonal and orthorhombic phase in the pressure range of 0.5–0.7 GPa and amorphous phase above 11.5 GPa from in situ synchrotron powder X-ray diffraction data, but lattice parameters and structural transition pathways were not reported as a function of applied pressure. A more comprehensive study has been carried out by Szafrański et al.22 from in situ single-crystal X-ray diffraction. The room temperature phase is fully consistent with the tetragonal I4/mcm symmetry which is stable up to 0.35 GPa. At higher pressure, it transforms into a ReO3-type cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase [a = 12.4076(8) Å, measured at 293 K and 0.45(2) GPa] (Fig. 6a). A complete transformation into the Im
phase [a = 12.4076(8) Å, measured at 293 K and 0.45(2) GPa] (Fig. 6a). A complete transformation into the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase has been observed when the pressure is above 0.40 GPa.23 The Im
phase has been observed when the pressure is above 0.40 GPa.23 The Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) unit cell is a bilayer 2 × 2 × 2 supercell of the high temperature α-phase.23 The octahedra show three equal component tilts along all three axes (Glazer's tilt notation: a+a+a+), generating two inequivalent A-sites. The space group assignment is consistent with the assignments in ref. 26 and 23 but is inconsistent with the orthorhombic symmetry reported in ref. 123. On increasing pressure, an isostructural phase transition occurs above 2.5 GPa, with discontinuous changes in the unit cell constants [a = 11.7936(13) Å, measured at 293 K and 2.71(2) GPa]. The authors measured the absorption spectra of MAPbI3 as a function of applied pressure (Fig. 6b). The bandgap reduces upto 0.35 GPa followed by an abrupt widening and then is almost unchanged up to 2.5 GPa (Fig. 6c). Above 3.5 GPa, the bandgap abruptly widens again, and the crystal turns black to transparent red. The bandgap variation was ascribed to the pressure-induced Pb–I bond contraction and hindered Pb–I–Pb angle bending in the compressed perovskite framework. By using a confocal μ-spectroscope, Liu et al.124 measured the absorption and the emission spectra of single-crystal MAPbI3 up to a pressure of 20.43 GPa. The bandgap first decreases from ambient pressure to 0.23 GPa due to contraction of the Pb–I bonds in the tetragonal I4/mcm phase. At 0.46 GPa, the bandgap suddenly increases due to the tetragonal to cubic phase transition and then increases slightly up to 2.72 GPa. After the isostructural phase transition at above 3.02 to 3.57 GPa, the bandgap further increases. This trend in the electronic structure change is broadly consistent with other reports.22
unit cell is a bilayer 2 × 2 × 2 supercell of the high temperature α-phase.23 The octahedra show three equal component tilts along all three axes (Glazer's tilt notation: a+a+a+), generating two inequivalent A-sites. The space group assignment is consistent with the assignments in ref. 26 and 23 but is inconsistent with the orthorhombic symmetry reported in ref. 123. On increasing pressure, an isostructural phase transition occurs above 2.5 GPa, with discontinuous changes in the unit cell constants [a = 11.7936(13) Å, measured at 293 K and 2.71(2) GPa]. The authors measured the absorption spectra of MAPbI3 as a function of applied pressure (Fig. 6b). The bandgap reduces upto 0.35 GPa followed by an abrupt widening and then is almost unchanged up to 2.5 GPa (Fig. 6c). Above 3.5 GPa, the bandgap abruptly widens again, and the crystal turns black to transparent red. The bandgap variation was ascribed to the pressure-induced Pb–I bond contraction and hindered Pb–I–Pb angle bending in the compressed perovskite framework. By using a confocal μ-spectroscope, Liu et al.124 measured the absorption and the emission spectra of single-crystal MAPbI3 up to a pressure of 20.43 GPa. The bandgap first decreases from ambient pressure to 0.23 GPa due to contraction of the Pb–I bonds in the tetragonal I4/mcm phase. At 0.46 GPa, the bandgap suddenly increases due to the tetragonal to cubic phase transition and then increases slightly up to 2.72 GPa. After the isostructural phase transition at above 3.02 to 3.57 GPa, the bandgap further increases. This trend in the electronic structure change is broadly consistent with other reports.22
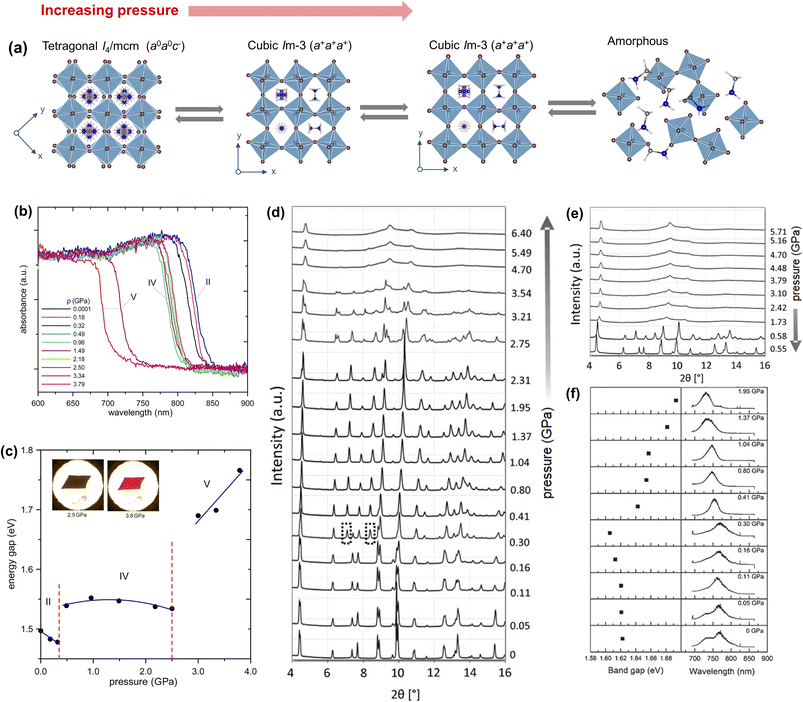 | ||
| Fig. 6 (a) Schematic illustration of pressure-induced phases of MAPbI3. (b) Absorption spectra of MAPbI3 as a function of pressure and (c) optical bandgaps versus pressure estimated from the spectra in (b), with the insets showing change in the colour of the crystal with pressure. Reproduced with permission from ref. 22 copyright 2016 American Chemical Society. (d) Synchrotron powder XRD patterns collected at room temperature under compression with diamond anvil cells (DACs) and (e) XRD patterns under decompression. (f) Room temperature photoluminescence spectra (right panel) and estimated bandgaps (left panel) as a function of pressure. Reproduced with permission from ref. 23 copyright 2016 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
By using in situ synchrotron X-ray diffraction data, Jiang et al.23 showed that the room temperature tetragonal I4/mcm phase changes to cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) [a = 12.4076(8) Å, measured at 0.41 GPa and room temperature] in the pressure range of 0.40–2.7 GPa, followed by a lower symmetry orthorhombic Immm phase [a = 12.0137(3) Å; b = 12.1984(8) Å; c = 11.9623(3) Å, measured at 2.75 GPa and room temperature] above 2.7 GPa. The authors found that the crystals gradually turn amorphous at a pressure above 4.0 GPa, reaching complete amorphization at 4.7 GPa and no further changes were noticed in the powder diffraction pattern up to 6.4 GPa (Fig. 6d).23 The unit cell lengths of the Immm phase are marginally different than that of the Im
[a = 12.4076(8) Å, measured at 0.41 GPa and room temperature] in the pressure range of 0.40–2.7 GPa, followed by a lower symmetry orthorhombic Immm phase [a = 12.0137(3) Å; b = 12.1984(8) Å; c = 11.9623(3) Å, measured at 2.75 GPa and room temperature] above 2.7 GPa. The authors found that the crystals gradually turn amorphous at a pressure above 4.0 GPa, reaching complete amorphization at 4.7 GPa and no further changes were noticed in the powder diffraction pattern up to 6.4 GPa (Fig. 6d).23 The unit cell lengths of the Immm phase are marginally different than that of the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase. During decompression, the structural changes are reversible as shown in the PXRD patterns (Fig. 6e). The sample remains partially amorphous until above 0.58 GPa and the Im
phase. During decompression, the structural changes are reversible as shown in the PXRD patterns (Fig. 6e). The sample remains partially amorphous until above 0.58 GPa and the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and I4/mcm phases were restored at 0.58 GPa and 0.55 GPa, respectively. The in situ photoluminescence spectra (Fig. 6f) suggest narrowing of the bandgap with increasing pressure up to ≈0.3 GPa, followed by bandgap widening up to 2.7 GPa. Beyond 2.7 GPa, the PL band weakens and slowly vanishes. A high pressure study on the MAPbI3 single-crystal by Jaffe et al.125 has suggested that the bandgap widening happens up to 60 GPa, followed by a semiconductor to metal transition due to high distortion in the structure. The structure as well as the bandgap are reversible between ambient pressure and 66 GPa.125 The bandgap widening is attributed to pressure induced lattice strain in the perovskite framework, triggered by disordering of the MA+ ion in the squeezed A-site cavity.
and I4/mcm phases were restored at 0.58 GPa and 0.55 GPa, respectively. The in situ photoluminescence spectra (Fig. 6f) suggest narrowing of the bandgap with increasing pressure up to ≈0.3 GPa, followed by bandgap widening up to 2.7 GPa. Beyond 2.7 GPa, the PL band weakens and slowly vanishes. A high pressure study on the MAPbI3 single-crystal by Jaffe et al.125 has suggested that the bandgap widening happens up to 60 GPa, followed by a semiconductor to metal transition due to high distortion in the structure. The structure as well as the bandgap are reversible between ambient pressure and 66 GPa.125 The bandgap widening is attributed to pressure induced lattice strain in the perovskite framework, triggered by disordering of the MA+ ion in the squeezed A-site cavity.
Despite substantial work on pressure-driven structural phenomena of MAPbI3, there are considerable inconsistencies in the structures and the structural transition sequence. Kong et al.24 carried out a high pressure single crystal X-ray diffraction study and suggested that the ambient pressure I4/mcm phase changes to an orthorhombic Imm2 space group [a = 12.408(3) Å; b = 12.419(3) Å; c = 12.25(5) Å] upon increasing pressure to 0.4 GPa.24 Capitani et al.25 also reported the Imm2 phase but at a lower pressure of 0.26 GPa which remains unchanged up to amorphization in the 2.3–3.0 GPa pressure range. They observed that the bandgap of MAPbI3 steadily reduces up to 0.32 GPa before phase change, which is consistent with the other studies.22,124 The bandgap decreases due to compression of Pb–I bonds, leading to enhanced overlap between Pb 6s and I 5p orbitals. This pushes up the VBM, while the CBM, being mostly nonbonding, is insensitive to bond length or pressure. This effect reverses when the tetragonal phase changes to the orthorhombic Imm2 or cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) in which the Pb–I–Pb bond angle deviates from 180°. The deviation in the angle reduces overlap between Pb 6s and I 5p orbitals, which narrows down the width of the VBM and increases the energy gap between the VBM and CBM. Jaffe et al.26 even modelled the ambient pressure phase in an orthorhombic Fmmm space group [a = 12.326 Å; b = 12.346 Å; c = 12.897 Å; α = 88.828°; β = 90.199°; γ = 89.895°] by using high pressure synchrotron single crystal and powder X-ray diffraction. This contradicts reports about the tetragonal I4/mcm space group reported at ambient pressure and temperature. Upon compression up to 0.6 GPa, the Fmmm structure changes to a cubic Im
in which the Pb–I–Pb bond angle deviates from 180°. The deviation in the angle reduces overlap between Pb 6s and I 5p orbitals, which narrows down the width of the VBM and increases the energy gap between the VBM and CBM. Jaffe et al.26 even modelled the ambient pressure phase in an orthorhombic Fmmm space group [a = 12.326 Å; b = 12.346 Å; c = 12.897 Å; α = 88.828°; β = 90.199°; γ = 89.895°] by using high pressure synchrotron single crystal and powder X-ray diffraction. This contradicts reports about the tetragonal I4/mcm space group reported at ambient pressure and temperature. Upon compression up to 0.6 GPa, the Fmmm structure changes to a cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) structure which is consistent with other high pressure studies.22,23 Though the material undergoes amorphization at above ca. 2.7 GPa, some degree of crystallinity is retained up to ca. 50 GPa.26 Furthermore, the amorphous and the crystalline phases co-exist at all pressures above 4.0 GPa.125,126 Upon decompression, the original orthorhombic phase was recovered with a small hysteresis.
structure which is consistent with other high pressure studies.22,23 Though the material undergoes amorphization at above ca. 2.7 GPa, some degree of crystallinity is retained up to ca. 50 GPa.26 Furthermore, the amorphous and the crystalline phases co-exist at all pressures above 4.0 GPa.125,126 Upon decompression, the original orthorhombic phase was recovered with a small hysteresis.
6.3. Formamidinium lead triiodide (FAPbI3)
Under compression, the response of the FA+ cation is very different than that of the MA+ cation due to differences in their symmetries and H-bonding patterns. Liu et al.127 studied optoelectronic properties of α-FAPbI3 under pressure up to 2.1 GPa. The authors reported shrinking of the bandgap from 1.489 eV to 1.337 eV, but they did not report any structural phase transition up to a pressure of 7.0 GPa. This finding is in sharp contrast to another study based on in situ synchrotron X-ray diffraction by Wang et al.32 who identified two new low symmetry phases of FAPbI3 under applied pressure: an orthorhombic Imm2 phase [reduced cell parameters, a = 6.2475 Å, b = 6.2450 Å, and c = 6.2714 Å] at 0.3 GPa and an orthorhombic Immm phase [reduced cell parameters of a = 6.1132 Å, b = 6.0920 Å, and c = 6.1792 Å] at 1.7 GPa. The compound becomes amorphous at a pressure above 4.0 GPa. Sun et al.34 carried out high pressure single crystal X-ray diffraction study under an applied pressure of up to 0.74 GPa and suggested that cubic α-FAPbI3 changes to the tetragonal P4/mbm phase at 0.49 GPa. Importantly, they could locate the orientation of the FA+ cation in the tetragonal lattice with its N–N axis in the ab-plane. By using high pressure powder XRD, Jiang et al.33 observed two phase transitions of α-FAPbI3 (Fig. 7a–c): cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m [a = 6.3651(1) Å, measured at ambient temperature and pressure] to tetragonal P4/mbm [a = b = 8.8388(8) Å, c = 6.2732(2) Å, measured at ambient temperature and 0.46 GPa pressure] at 0.46 GPa, followed by cubic Im
m [a = 6.3651(1) Å, measured at ambient temperature and pressure] to tetragonal P4/mbm [a = b = 8.8388(8) Å, c = 6.2732(2) Å, measured at ambient temperature and 0.46 GPa pressure] at 0.46 GPa, followed by cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase [a = 12.0654(6) Å, measured at ambient temperature and 3.13 GPa pressure] at 3.13 GPa. These results contrast with those of an earlier study,32 suggesting Pm
phase [a = 12.0654(6) Å, measured at ambient temperature and 3.13 GPa pressure] at 3.13 GPa. These results contrast with those of an earlier study,32 suggesting Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → Imm2 → Immm → partially amorphous. Upon decompression, the crystalline phase was completely restored (Fig. 7d), showing reversibility of the transition process. The authors also studied that δ-FAPbI3 shows a pressure-induced reversible transition from hexagonal P63mc to an orthorhombic Cmc21 phase between 1.26 and 1.73 GPa pressure. Note that the transition pressures for FAPbI3 are slightly higher than those of MAPbI3 (Table 1), indicating that the former compound is structurally more stable. This arises from better packing of the FA+ cation in the A-site cavity as indicated by the tolerance factor as well as its enhanced H-bonding capability.128
m → Imm2 → Immm → partially amorphous. Upon decompression, the crystalline phase was completely restored (Fig. 7d), showing reversibility of the transition process. The authors also studied that δ-FAPbI3 shows a pressure-induced reversible transition from hexagonal P63mc to an orthorhombic Cmc21 phase between 1.26 and 1.73 GPa pressure. Note that the transition pressures for FAPbI3 are slightly higher than those of MAPbI3 (Table 1), indicating that the former compound is structurally more stable. This arises from better packing of the FA+ cation in the A-site cavity as indicated by the tolerance factor as well as its enhanced H-bonding capability.128
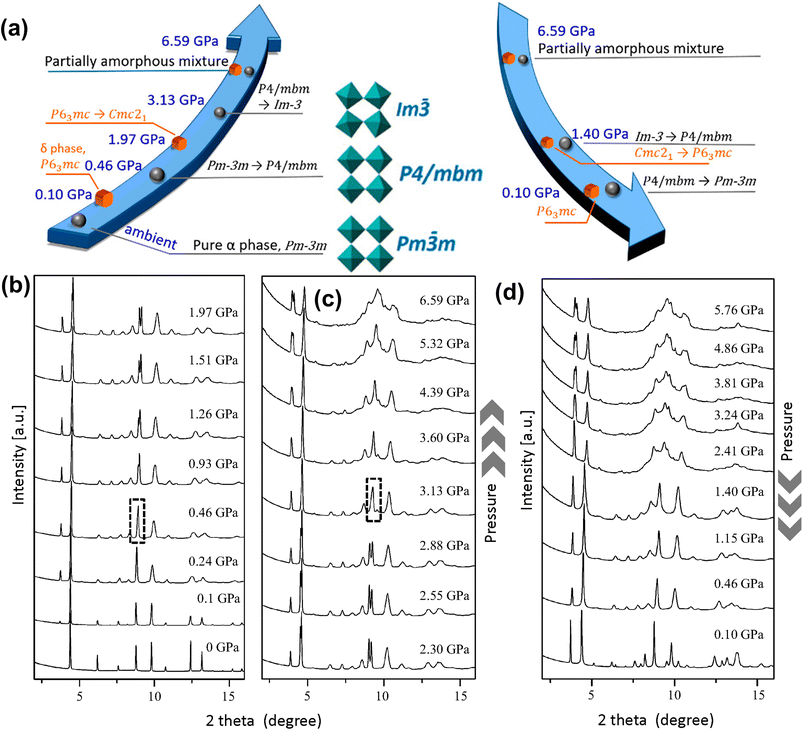 | ||
| Fig. 7 (a) Schematic illustration of pressure-induced phases of α-FAPbI3. (b and c) Powder XRD patterns of α-FAPbI3 under applied pressure. (d) Powder XRD patterns measured during decompression. Reproduced with permission from ref. 33 copyright 2018 American Chemical Society. | ||
7. Decomposition under humid conditions
Irrespective of the phase, lead iodide perovskites decompose into constituents or transform into low dimensional structures in moist air which is detrimental to their applications. Many studies have shown that water present in humid air reacts with perovskites and accelerates their decomposition.129–133 A general belief is that decomposition by humidity occurs within a condensed liquid phase on the grain/crystal surface. The studies are more prolific in the case of MAPbI3 and various pathways of decomposition have been proposed in different studies.133–135 In this section we shall focus on those studies which report the structural aspect. From single crystal X-ray diffraction data, Leguy et al.136 showed that MAPbI3 forms two hydrated phases upon exposure to water vapour at room temperature MAPbI3·H2O (pale yellow and needle-shaped crystals) and MA4PbI6·2H2O (Fig. 8). With liquid water, decomposition into PbI2 and MAI takes place. The monohydrate, structurally reported first by Hao et al.109 consists of 1-D [PbI3]− chains separated by zig-zag chains of hydrogen bonded MA+ cations and water molecules. The [PbI3]− chain adopts a “double chain” structure and is reminiscent of δ-CsPbI3. It crystallizes in the monoclinic P21/m space group [a = 4.5760(2) Å, b = 25.4930(17) Å, and c = 12.2186(6) Å; β = 96.065(4) °]. The dihydrate has a 0-D structure with isolated [PbI6]4− octahedra separated by a hydrogen bonded [(MA⋯H2O⋯MA)2]4+ dimeric cation.137 It crystallizes in the monoclinic P21/n space group [a = 10.3937(3) Å, b = b 11.3055(2) Å, and c = 10.5519(2) Å; β = 91.2981(13)°].138 Although monohydrates and dihydrates co-exist on prolonged exposure to humid air, they essentially form via a two-step sequential process as shown in Scheme 1.136 The second step leads to irreversible formation of PbI2 with the loss of MAI and H2O. The monohydrate is an intermediate which either changes back to black MAPbI3 by losing the crystalline water upon exposure to dry nitrogen/applying vacuum or further allows water infiltration to form MA4PbI6·2H2O. Computational studies have shown that PbI2 is thermodynamically more stable than MAPbI3 but it has an activation energy barrier which is lowered upon interaction with water molecules.139 On exposure to low humidity, the perovskite phase of MAPbI3 remains stable for several weeks and shows only a slight decrease in the device performance but on long exposure to high humidity or liquid water leads to irreversible decomposition of MAPI3 into MAI and PbI2 species, which then dissolve in excess water. Unlike MAPbI3, FAPbI3 is found to be more stable under ambient conditions. At low relative humidity (<50%), the δ-phase shows no signs of decomposition, but on dipping in liquid water it decomposes into yellow PbI2 and other constituents.140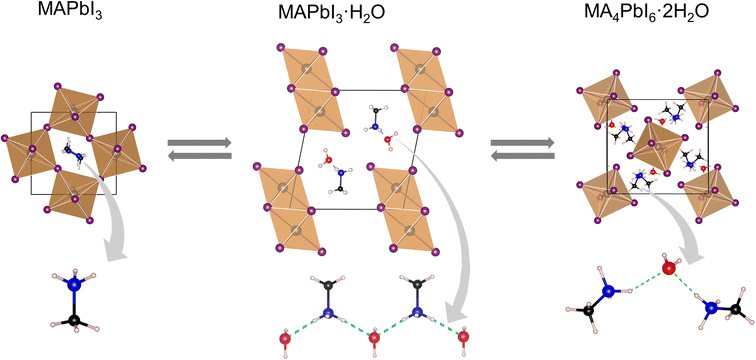 | ||
| Fig. 8 X-ray structures of MAPbI3 and its hydrated products, with the hydrogen bonded (green dashed bonds) MA+ cation and water molecules. | ||
MAPbI3 can also decompose into PbI2 and other constituents on exposure to oxygen and light.141 The decomposition is induced by oxygen insertion at the iodide vacancies followed by the formation of superoxide (O2−) species in the presence of light. The photogenerated superoxide can deprotonate the methylammonium cation (CH3NH3+) of photo-excited MAPbI3 and decompose it into PbI2, water, methylamine and iodine.
8. Concluding remarks
Lead halide perovskites have come to the fore very recently and have opened an entirely new avenue of phase transition materials. In this article, we have reviewed temperature and pressure induced structures of three conventional lead iodide perovskites, CsPbI3, MAPbI3 and FAPbI3. They show transitions to higher symmetry on heating and lower symmetry on compressing. There are diverse views about the number of phases, the phase transition pathways and important physical properties including electronic and ferroelectric. Tables 1–3 list several of such intricacies in the lattice symmetries. The complexity is more in the hybrid systems primarily due to dynamic disorder in the molecular lattice of organic amine cations. Such local disorders are challenging to find through Bragg scattering. Thus, phase transitions in these perovskites deserve continued studies. X-ray diffraction needs to be employed in combination with other highly sensitive techniques such as neutron scattering, pair distribution function (PDF), time-resolved spectroscopies (such as NMR, infrared and Raman), and high-resolution electron microscope imaging to fully unravel structures.In addition to revisiting the phase transition pathways and the phase structures, there are plenty of new directions waiting to be explored. Firstly, it is reasonable to ask whether we already know all polymorphs of these perovskites that are possible? To answer this, investigations in a wider range of temperature and pressure need to be carried out. Furthermore, studies need to be carried out to explore simultaneous effects of temperature and pressure. Under combined P–T effect, new structures with novel phenomena can be expected. Computation tools can help in this aspect by predicting unknown phases. Secondly, the phase transitions often show large entropy change at transition temperatures, thus leading to a large caloric effect which might make them potential candidates for heat storage. Study of the caloric effect presents an important avenue for future studies. Thirdly, we note that the conventional iodide perovskites that have been reported until now are all monometallic, meaning that they contain only one type of metal ion at the B-site (such as Pb2+ or Sn2+). Incorporation of other metal ions offers a new direction for chemical tunability in addition to structures. A very recent report on the iodide double perovskite Cs2NaLnI6 (Ln = Ce, Nd, Gd, Tb, Dy)142 family is one such example, presenting an opportunity to develop non-toxic (or less toxic) alternatives to lead iodide perovskites for magnetic and optoelectronic applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
PV acknowledges the Science & Engineering Research Board (SERB) of the Govt. of India for a Ramanujan Fellowship (Award No. RJF/2020/000106).References
- C. N. R. Rao, Annu. Rev. Phys. Chem., 1989, 40, 291–326 CrossRef CAS.
- C. N. R. Rao and A. K. Ganguli, Chem. Soc. Rev., 1995, 24, 1–7 RSC.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS.
- C. C. Stoumpos and M. G. Kanatzidis, Acc. Chem. Res., 2015, 48, 2791–2802 CrossRef CAS.
- J. Even, M. Carignano and C. Katan, Nanoscale, 2016, 8, 6222–6236 RSC.
- D. H. Fabini, T. A. Siaw, C. C. Stoumpos, G. Laurita, D. Olds, K. Page, J. G. Hu, M. G. Kanatzidis, S. Han and R. Seshadri, J. Am. Chem. Soc., 2017, 139, 16875–16884 CrossRef CAS PubMed.
- E. M. Mozur and J. R. Neilson, Annu. Rev. Mater. Res., 2021, 51, 269–291 CrossRef CAS.
- A. Mishra, M. A. Hope, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2023, 145, 978–990 CrossRef CAS PubMed.
- Y. An, J. Hidalgo, C. A. R. Perini, A.-F. Castro-Méndez, J. N. Vagott, K. Bairley, S. Wang, X. Li and J.-P. Correa-Baena, ACS Energy Lett., 2021, 6, 1942–1969 CrossRef CAS.
- A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J.-M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis and J. Even, ACS Nano, 2018, 12, 3477–3486 CrossRef CAS PubMed.
- B. Wang, N. Novendra and A. Navrotsky, J. Am. Chem. Soc., 2019, 141, 14501–14504 CrossRef CAS.
- G. Yuan, S. Qin, X. Wu, H. Ding and A. Lu, Phase Transitions, 2018, 91, 38–47 CrossRef CAS.
- Y. Liang, X. Huang, Y. Huang, X. Wang, F. Li, Y. Wang, F. Tian, B. Liu, Z. X. Shen and T. Cui, Adv. Sci., 2019, 6, 1900399 CrossRef PubMed.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641 RSC.
- P. S. Whitfield, N. Herron, W. E. Guise, K. Page, Y. Q. Cheng, I. Milas and M. K. Crawford, Sci. Rep., 2016, 6, 35685 CrossRef CAS PubMed.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- G. Sharada, P. Mahale, B. P. Kore, S. Mukherjee, M. S. Pavan, C. De, S. Ghara, A. Sundaresan, A. Pandey, T. N. G. Row and D. D. Sarma, J. Phys. Chem. Lett., 2016, 7, 2412–2419 CrossRef.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2016, 7, 3458–3466 CrossRef.
- S. Jiang, Y. Fang, R. Li, H. Xiao, J. Crowley, C. Wang, T. J. White, W. A. Goddard III, Z. Wang, T. Baikie and J. Fang, Angew. Chem., Int. Ed., 2016, 55, 6540–6544 CrossRef CAS PubMed.
- L. Kong, G. Liu, J. Gong, Q. Hu, R. D. Schaller, P. Dera, D. Zhang, Z. Liu, W. Yang, K. Zhu, Y. Tang, C. Wang, S.-H. Wei, T. Xu and H. Mao, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8910–8915 CrossRef CAS.
- F. Capitani, C. Marini, S. Caramazza, P. Postorino, G. Garbarino, M. Hanfland, A. Pisanu, P. Quadrelli and L. Malavasi, J. Appl. Phys., 2016, 119, 185901 CrossRef.
- A. Jaffe, Y. Lin, C. M. Beavers, J. Voss, W. L. Mao and H. I. Karunadasa, ACS Cent. Sci., 2016, 2, 201–209 CrossRef CAS PubMed.
- Q. Han, S.-H. Bae, P. Sun, Y.-T. Hsieh, Y. M. Yang, Y. S. Rim, H. Zhao, Q. Chen, W. Shi, G. Li and Y. Yang, Adv. Mater., 2016, 28, 2253–2258 CrossRef CAS.
- T. Chen, B. J. Foley, C. Park, C. M. Brown, L. W. Harriger, J. Lee, J. Ruff, M. Yoon, J. J. Choi and S.-H. Lee, Sci. Adv., 2022, 2, e1601650 CrossRef.
- T. Chen, W.-L. Chen, B. J. Foley, J. Lee, J. P. C. Ruff, J. Y. P. Ko, C. M. Brown, L. W. Harriger, D. Zhang, C. Park, M. Yoon, Y.-M. Chang, J. J. Choi and S.-H. Lee, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7519–7524 CrossRef CAS.
- D. H. Fabini, C. C. Stoumpos, G. Laurita, A. Kaltzoglou, A. G. Kontos, P. Falaras, M. G. Kanatzidis and R. Seshadri, Angew. Chem., Int. Ed., 2016, 55, 15392–15396 CrossRef CAS PubMed.
- O. J. Weber, D. Ghosh, S. Gaines, P. F. Henry, A. B. Walker, M. S. Islam and M. T. Weller, Chem. Mater., 2018, 30, 3768–3778 CrossRef CAS.
- P. Wang, J. Guan, D. T. K. Galeschuk, Y. Yao, C. F. He, S. Jiang, S. Zhang, Y. Liu, M. Jin, C. Jin and Y. Song, J. Phys. Chem. Lett., 2017, 8, 2119–2125 CrossRef CAS PubMed.
- S. Jiang, Y. Luan, J. I. Jang, T. Baikie, X. Huang, R. Li, F. O. Saouma, Z. Wang, T. J. White and J. Fang, J. Am. Chem. Soc., 2018, 140, 13952–13957 CrossRef CAS PubMed.
- S. Sun, Z. Deng, Y. Wu, F. Wei, F. H. Isikgor, F. Brivio, M. W. Gaultois, J. Ouyang, P. D. Bristowe, A. K. Cheetham and G. Kieslich, Chem. Commun., 2017, 53, 7537–7540 RSC.
- C. N. R. Rao, Acc. Chem. Res., 1984, 17, 83–89 CrossRef CAS.
- C. N. R. Rao and K. J. Rao, Phase Transitions in Solids: An Approach to the Study of the Chemistry and Physics of Solids, McGraw-Hill, New York, 1978 Search PubMed.
- P. Ehrenfest, Proc. R. Acad. Sci. Amsterdam, 1933, 36, 153–157 CAS.
- M. Stavinoha, J. A. Cooley, S. G. Minasian, T. M. McQueen, S. M. Kauzlarich, C.-L. Huang and E. Morosan, Phys. Rev. B, 2018, 97, 195146 CrossRef CAS.
- F. Guillou, A. K. Pathak, D. Paudyal, Y. Mudryk, F. Wilhelm, A. Rogalev and V. K. Pecharsky, Nat. Commun., 2018, 9, 2925 CrossRef CAS PubMed.
- W. Aftab, A. Usman, J. Shi, K. Yuan, M. Qin and R. Zou, Energy Environ. Sci., 2021, 14, 4268–4291 RSC.
- H. L. Wells, Z. Anorg. Allg. Chem., 1893, 3, 195–210 CrossRef.
- C. K. Møller, Nature, 1957, 180, 981–982 CrossRef.
- C. K. Møller, Nature, 1958, 182, 1436 CrossRef.
- D. Weber, Z. Naturforsch., B: Chem. Sci., 1978, 33, 1443–1445 CrossRef.
- A. Maalej, Y. Abid, A. Kallel, A. Daoud, A. Lautié and F. Romain, Solid State Commun., 1997, 103, 279–284 CrossRef CAS.
- R. J. Worhatch, H. Kim, I. P. Swainson, A. L. Yonkeu and S. J. L. Billinge, Chem. Mater., 2008, 20, 1272–1277 CrossRef CAS.
- I. B. Koutselas, L. Ducasse and G. C. Papavassiliou, J. Phys.: Condens.Matter, 1996, 8, 1217–1227 CrossRef CAS.
- K. Yamada, H. Kawaguchi, T. Matsui, T. Okuda and S. Ichiba, Bull. Chem. Soc. Jpn., 1990, 63, 2521–2525 CrossRef CAS.
- K. V Saurav and P. Vishnoi, in Energy Materials, World Scientific, 2022, pp. 141–174 Search PubMed.
- H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. Il Seok, Nature, 2021, 598, 444–450 CrossRef CAS.
- J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381–385 CrossRef CAS PubMed.
- J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918 CrossRef CAS PubMed.
- D. V. S. Muthu, P. Teredesai, S. Saha, Suchitra, U. V. Waghmare, A. K. Sood and C. N. R. Rao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224308 CrossRef.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- L. Pauling, J. Am. Chem. Soc., 1927, 49, 765–790 CrossRef CAS.
- Y. Fu, S. Jin and X.-Y. Zhu, Nat. Rev. Chem, 2021, 5, 838–852 CrossRef CAS.
- S. Bera, A. Saha, S. Mondal, A. Biswas, S. Mallick, R. Chatterjee and S. Roy, Mater. Adv., 2022, 3, 5234–5247 RSC.
- D. M. Trots and S. V Myagkota, J. Phys. Chem. Solids, 2008, 69, 2520–2526 CrossRef CAS.
- J. Breternitz, F. Lehmann, S. A. Barnett, H. Nowell and S. Schorr, Angew. Chem., Int. Ed., 2020, 59, 424–428 CrossRef CAS PubMed.
- A. Arakcheeva, D. Chernyshov, M. Spina, L. Forró and E. Horváth, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 716–722 CrossRef CAS.
- M. T. Weller, O. J. Weber, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2015, 6, 3209–3212 CrossRef CAS.
- P. Vishnoi, R. Seshadri and A. K. Cheetham, J. Phys. Chem. C, 2021, 125, 11756–11764 CrossRef CAS.
- X. Ding, M. Cai, X. Liu, Y. Ding, X. Liu, Y. Wu, T. Hayat, A. Alsaedi and S. Dai, ACS Appl. Mater. Interfaces, 2019, 11, 37720–37725 CrossRef CAS PubMed.
- J. Hieulle, X. Wang, C. Stecker, D.-Y. Son, L. Qiu, R. Ohmann, L. K. Ono, A. Mugarza, Y. Yan and Y. Qi, J. Am. Chem. Soc., 2019, 141, 3515–3523 CrossRef CAS PubMed.
- R. J. Sutton, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, F. Giustino and H. J. Snaith, ACS Energy Lett., 2018, 3, 1787–1794 CrossRef CAS.
- G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3, 19688–19695 RSC.
- M. A. Fadla, B. Bentria, T. Dahame and A. Benghia, Phys. B, 2020, 585, 412118 CrossRef CAS.
- D. B. Straus, S. Guo and R. J. Cava, J. Am. Chem. Soc., 2019, 141, 11435–11439 CrossRef CAS PubMed.
- F. Ke, C. Wang, C. Jia, N. R. Wolf, J. Yan, S. Niu, T. P. Devereaux, H. I. Karunadasa, W. L. Mao and Y. Lin, Nat. Commun., 2021, 12, 461 CrossRef CAS PubMed.
- X. Kong, K. Shayan, S. Hua, S. Strauf and S. S. Lee, ACS Appl. Energy Mater., 2019, 2, 2948–2955 CrossRef CAS.
- J. A. Steele, V. Prakasam, H. Huang, E. Solano, D. Chernyshov, J. Hofkens and M. B. J. Roeffaers, J. Am. Chem. Soc., 2021, 143, 10500–10508 CrossRef CAS PubMed.
- Z.-G. Li, M. Zacharias, Y. Zhang, F. Wei, Y. Qin, Y.-Q. Yang, L.-C. An, F.-F. Gao, W. Li, J. Even and X.-H. Bu, ACS Energy Lett., 2023, 8, 3016–3024 CrossRef CAS.
- J. A. Steele, H. Jin, I. Dovgaliuk, R. F. Berger, T. Braeckevelt, H. Yuan, C. Martin, E. Solano, K. Lejaeghere, S. M. J. Rogge, C. Notebaert, W. Vandezande, K. P. F. Janssen, B. Goderis, E. Debroye, Y.-K. Wang, Y. Dong, D. Ma, M. Saidaminov, H. Tan, Z. Lu, V. Dyadkin, D. Chernyshov, V. Van Speybroeck, E. H. Sargent, J. Hofkens and M. B. J. Roeffaers, Science, 2019, 365, 679–684 CrossRef CAS.
- D. B. Straus, S. Guo, A. M. M. Abeykoon and R. J. Cava, Adv. Mater., 2020, 32, 2001069 CrossRef CAS PubMed.
- L. Duan, H. Zhang, M. Liu, M. Grätzel and J. Luo, ACS Energy Lett., 2022, 7, 2911–2918 CrossRef CAS.
- W. Yong, D. M. Ibrahim, L. K. Ono, Z. Taiyang, K. Miao, L. Yawen, Z. Lijun, W. Xingtao, Y. Yingguo, G. Xingyu, Q. Yabing, G. Michael and Z. Yixin, Science, 2019, 365, 591–595 CrossRef PubMed.
- Y. Kawamura, H. Mashiyama and K. Hasebe, J. Phys. Soc. Jpn., 2002, 71, 1694–1697 CrossRef CAS.
- K. P. Ong, T. W. Goh, Q. Xu and A. Huan, J. Phys. Chem. Lett., 2015, 6, 681–685 CrossRef CAS PubMed.
- J.-H. Lee, N. C. Bristowe, J. H. Lee, S.-H. Lee, P. D. Bristowe, A. K. Cheetham and H. M. Jang, Chem. Mater., 2016, 28, 4259–4266 CrossRef CAS.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Péchy, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10055–10061 CrossRef CAS.
- I. Anusca, S. Balčiūnas, P. Gemeiner, Š. Svirskas, M. Sanlialp, G. Lackner, C. Fettkenhauer, J. Belovickis, V. Samulionis, M. Ivanov, B. Dkhil, J. Banys, V. V Shvartsman and D. C. Lupascu, Adv. Energy Mater., 2017, 7, 1700600 CrossRef.
- A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kockelmann, C. Law, X. Li, F. Foglia, A. Walsh, B. C. O'Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, Nat. Commun., 2015, 6, 7124 CrossRef.
- T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi and S.-H. Lee, Phys. Chem. Chem. Phys., 2015, 17, 31278–31286 RSC.
- B. Li, Y. Kawakita, Y. Liu, M. Wang, M. Matsuura, K. Shibata, S. Ohira-Kawamura, T. Yamada, S. Lin, K. Nakajima and S. F. Liu, Nat. Commun., 2017, 8, 16086 CrossRef CAS.
- A. Gómez, Q. Wang, A. R. Goñi, M. Campoy-Quiles and A. Abate, Energy Environ. Sci., 2019, 12, 2537–2547 RSC.
- I. P. Swainson, R. P. Hammond, C. Soullière, O. Knop and W. Massa, J. Solid State Chem., 2003, 176, 97–104 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395 CrossRef CAS.
- G. M. Bernard, R. E. Wasylishen, C. I. Ratcliffe, V. Terskikh, Q. Wu, J. M. Buriak and T. Hauger, J. Phys. Chem. A, 2018, 122, 1560–1573 CrossRef CAS PubMed.
- N. Onoda-Yamamuro, O. Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1992, 53, 277–281 CrossRef CAS.
- G. Sombrio, Z. Zhang, A. Bonadio, L. S. de Oliveira, T. B. de Queiroz, F. F. Ferreira, A. Janotti and J. A. Souza, J. Phys. Chem. C, 2020, 124, 10793–10803 CrossRef CAS.
- A. Bonadio, C. A. Escanhoela, F. P. Sabino, G. Sombrio, V. G. de Paula, F. F. Ferreira, A. Janotti, G. M. Dalpian and J. A. Souza, J. Mater. Chem. A, 2021, 9, 1089–1099 RSC.
- A. Bonadio, F. P. Sabino, A. L. M. Freitas, M. R. Felez, G. M. Dalpian and J. A. Souza, Inorg. Chem., 2023, 62, 7533–7544 CrossRef CAS PubMed.
- H. Röhm, T. Leonhard, M. J. Hoffmann and A. Colsmann, Energy Environ. Sci., 2017, 10, 950–955 RSC.
- X.-K. Wei, N. Domingo, Y. Sun, N. Balke, R. E. Dunin-Borkowski and J. Mayer, Adv. Energy Mater., 2022, 12, 2201199 CrossRef CAS.
- L. M. Garten, D. T. Moore, S. U. Nanayakkara, S. Dwaraknath, P. Schulz, J. Wands, A. Rockett, B. Newell, K. A. Persson, S. Trolier-McKinstry and D. S. Ginley, Sci. Adv., 2023, 5, eaas9311 CrossRef.
- Y. Dang, Y. Liu, Y. Sun, D. Yuan, X. Liu, W. Lu, G. Liu, H. Xia and X. Tao, CrystEngComm, 2015, 17, 665–670 RSC.
- Y. Rakita, O. Bar-Elli, E. Meirzadeh, H. Kaslasi, Y. Peleg, G. Hodes, I. Lubomirsky, D. Oron, D. Ehre and D. Cahen, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5504–E5512 CrossRef CAS PubMed.
- A. Glushkova, K. Mantulnikovs, G. Giriat, K. Semeniuk, L. Forró, E. Horváth and A. Arakcheeva, Sol. RRL, 2019, 3, 1900044 CrossRef.
- M. Manzi, G. Pica, M. De Bastiani, S. Kundu, G. Grancini and M. I. Saidaminov, J. Phys. Chem. Lett., 2023, 14, 3535–3552 CrossRef CAS PubMed.
- F. Ambrosio, F. De Angelis and A. R. Goñi, J. Phys. Chem. Lett., 2022, 13, 7731–7740 CrossRef CAS PubMed.
- Y. Ren, I. W. H. Oswald, X. Wang, G. T. McCandless and J. Y. Chan, Cryst. Growth Des., 2016, 16, 2945–2951 CrossRef CAS.
- J.-H. Lee, N. C. Bristowe, P. D. Bristowe and A. K. Cheetham, Chem. Commun., 2015, 51, 6434–6437 RSC.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2017, 8, 2496–2506 CrossRef PubMed.
- R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H.-G. Boyen, M. F. Toney and M. D. McGehee, J. Am. Chem. Soc., 2017, 139, 11117–11124 CrossRef CAS PubMed.
- A. S. Thind, X. Huang, J. Sun and R. Mishra, Chem. Mater., 2017, 29, 6003–6011 CrossRef CAS.
- J. A. Finkler and S. Goedecker, Mater. Adv., 2023, 4, 184–194 RSC.
- J. A. Flores-Livas, D. Tomerini, M. Amsler, A. Boziki, U. Rothlisberger and S. Goedecker, Phys. Rev. Mater., 2018, 2, 85201 CrossRef CAS.
- X. Huang, R. Chen, G. Deng, F. Han, P. Ruan, F. Cheng, J. Yin, B. Wu and N. Zheng, J. Am. Chem. Soc., 2020, 142, 6149–6157 CrossRef CAS PubMed.
- F. Hao, C. C. Stoumpos, Z. Liu, R. P. H. Chang and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 16411–16419 CrossRef CAS PubMed.
- M. Lai, T. Lei, Y. Zhang, J. Jin, J. A. Steele and P. Yang, MRS Bull., 2021, 46, 310–316 CrossRef CAS.
- M. Aebli, N. Porenta, N. Aregger and M. V Kovalenko, Chem. Mater., 2021, 33, 6965–6973 CrossRef CAS.
- X. Chen, Y. Xia, Z. Zheng, X. Xiao, C. Ling, M. Xia, Y. Hu, A. Mei, R. Cheacharoen, Y. Rong and H. Han, Chem. Mater., 2022, 34, 728–735 CrossRef CAS.
- S. Li, J. Xia, Z. Wen, H. Gu, J. Guo, C. Liang, H. Pan, X. Wang and S. Chen, Adv. Sci., 2023, 10, 2300056 CrossRef CAS PubMed.
- O. J. Weber, B. Charles and M. T. Weller, J. Mater. Chem. A, 2016, 4, 15375–15382 RSC.
- B. Charles, J. Dillon, O. J. Weber, M. S. Islam and M. T. Weller, J. Mater. Chem. A, 2017, 5, 22495–22499 RSC.
- Z. Li, M. Yang, J.-S. Park, S.-H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS.
- P. Raval, R. M. Kennard, E. S. Vasileiadou, C. J. Dahlman, I. Spanopoulos, M. L. Chabinyc, M. Kanatzidis and G. N. Manjunatha Reddy, ACS Energy Lett., 2022, 7, 1534–1543 CrossRef CAS.
- M. Keshavarz, M. Ottesen, S. Wiedmann, M. Wharmby, R. Küchler, H. Yuan, E. Debroye, J. A. Steele, J. Martens, N. E. Hussey, M. Bremholm, M. B. J. Roeffaers and J. Hofkens, Adv. Mater., 2019, 31, 1900521 CrossRef PubMed.
- S. Kawachi, M. Atsumi, N. Saito, N. Ohashi, Y. Murakami and J. Yamaura, J. Phys. Chem. Lett., 2019, 10, 6967–6972 CrossRef CAS PubMed.
- C. Zhu, X. Niu, Y. Fu, N. Li, C. Hu, Y. Chen, X. He, G. Na, P. Liu, H. Zai, Y. Ge, Y. Lu, X. Ke, Y. Bai, S. Yang, P. Chen, Y. Li, M. Sui, L. Zhang, H. Zhou and Q. Chen, Nat. Commun., 2019, 10, 815 CrossRef CAS PubMed.
- D. Ghosh, A. Aziz, J. A. Dawson, A. B. Walker and M. S. Islam, Chem. Mater., 2019, 31, 4063–4071 CrossRef CAS PubMed.
- P. V Teredesai, A. K. Sood, D. V. S. Muthu, R. Sen, A. Govindaraj and C. N. R. Rao, Chem. Phys. Lett., 2000, 319, 296–302 CrossRef.
- T. Ou, J. Yan, C. Xiao, W. Shen, C. Liu, X. Liu, Y. Han, Y. Ma and C. Gao, Nanoscale, 2016, 8, 11426–11431 RSC.
- C. Liu, Z. Li, L. Yang, X. Yao, H. Li, X. Liu, Y. Zhao, P. Zhu, T. Cui, C. Sun and Y. Bao, J. Phys. Chem. C, 2019, 123, 30221–30227 CrossRef CAS.
- A. Jaffe, Y. Lin, W. L. Mao and H. I. Karunadasa, J. Am. Chem. Soc., 2017, 139, 4330–4333 CrossRef CAS PubMed.
- A. Arakcheeva, V. Svitlyk, E. Polini, L. Henry, D. Chernyshov, A. Sienkiewicz, G. Giriat, A. Glushkova, M. Kollar, B. Náfrádi, L. Forro and E. Horváth, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 361–370 CrossRef CAS PubMed.
- G. Liu, L. Kong, J. Gong, W. Yang, H. Mao, Q. Hu, Z. Liu, R. D. Schaller, D. Zhang and T. Xu, Adv. Funct. Mater., 2017, 27, 361–370 Search PubMed.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. Grätzel and F. De Angelis, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS PubMed.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- G. E. Eperon, S. N. Habisreutinger, T. Leijtens, B. J. Bruijnaers, J. J. van Franeker, D. W. deQuilettes, S. Pathak, R. J. Sutton, G. Grancini, D. S. Ginger, R. A. J. Janssen, A. Petrozza and H. J. Snaith, ACS Nano, 2015, 9, 9380–9393 CrossRef CAS PubMed.
- C. Müller, T. Glaser, M. Plogmeyer, M. Sendner, S. Döring, A. A. Bakulin, C. Brzuska, R. Scheer, M. S. Pshenichnikov, W. Kowalsky, A. Pucci and R. Lovrinčić, Chem. Mater., 2015, 27, 7835–7841 CrossRef.
- J. Yang, B. D. Siempelkamp, D. Liu and T. L. Kelly, ACS Nano, 2015, 9, 1955–1963 CrossRef CAS PubMed.
- T. D. Siegler, W. A. Dunlap-Shohl, Y. Meng, Y. Yang, W. F. Kau, P. P. Sunkari, C. E. Tsai, Z. J. Armstrong, Y.-C. Chen, D. A. C. Beck, M. Meilă and H. W. Hillhouse, J. Am. Chem. Soc., 2022, 144, 5552–5561 CrossRef CAS PubMed.
- A. Kakekhani, R. N. Katti and A. M. Rappe, APL Mater., 2019, 7, 41112 CrossRef.
- P. Toloueinia, H. Khassaf, A. S. Amin, Z. M. Tobin, S. P. Alpay and S. L. Suib, ACS Appl. Energy Mater., 2020, 3, 8240–8248 CrossRef CAS.
- A. M. A. Leguy, Y. Hu, M. Campoy-Quiles, M. I. Alonso, O. J. Weber, P. Azarhoosh, M. van Schilfgaarde, M. T. Weller, T. Bein, J. Nelson, P. Docampo and P. R. F. Barnes, Chem. Mater., 2015, 27, 3397–3407 CrossRef CAS.
- B. R. Vincent, K. N. Robertson, T. S. Cameron and O. Knop, Can. J. Chem., 1987, 65, 1042–1046 CrossRef CAS.
- A. Wakamiya, M. Endo, T. Sasamori, N. Tokitoh, Y. Ogomi, S. Hayase and Y. Murata, Chem. Lett., 2014, 43, 711–713 CrossRef CAS.
- E. Smecca, Y. Numata, I. Deretzis, G. Pellegrino, S. Boninelli, T. Miyasaka, A. La Magna and A. Alberti, Phys. Chem. Chem. Phys., 2016, 18, 13413–13422 RSC.
- J. S. Yun, J. Kim, T. Young, R. J. Patterson, D. Kim, J. Seidel, S. Lim, M. A. Green, S. Huang and A. Ho-Baillie, Adv. Funct. Mater., 2018, 28, 1705363 CrossRef.
- N. Aristidou, C. Eames, I. Sanchez-Molina, X. Bu, J. Kosco, M. S. Islam and S. A. Haque, Nat. Commun., 2017, 8, 15218 CrossRef PubMed.
- G. Kent, E. Morgan, K. R. Albanese, A. Kallistova, A. Brumberg, L. Kautzsch, G. Wu, P. Vishnoi, R. Seshadri and A. K. Cheetham, Angew. Chem., Int. Ed., 2023, e202306000 CAS.
| This journal is © The Royal Society of Chemistry 2024 |