Orientational order/disorder and network flexibility in deuterated methylammonium lead iodide perovskite by neutron total scattering

Abstract

The phase transitions and orientational order of the methylammonium molecular ion in a deuterated sample of [CH₃NH₃]PbI₃ have been studied using neutron total scattering and Reverse Monte Carlo methods. From analysis of the C–N bond orientational distribution functions, obtained both by forming histograms and by analysis using orthonormal spherical functions, we showed that the molecular ions were found to have an almost completely uniform distribution of orientations in the high-temperature cubic phase. The C–N bonds then show progressively increasing order on cooling within the intermediate phase, and complete order in the low-temperature phase. Analysis of the network of connected PbI₆ octahedra has shown that the rigidity of the PbI₆ octahedra is similar to that in the related cubic perovskite CsPbI₃, and is intermediate between the oxide perovskite SrTiO₃ and the more flexible ScF₃. Both the fluctuations of the I–Pb–I right angle and the orientations of the PbI₆ show normal variation with temperature across the range of temperatures of all three phases. The Pb–I bond has been found to be highly anharmonic, comparable to the same bond in CsPbI₃. We find no evidence for static ferroelectric distortions at any temperature, but dynamic fluctuations in the local dipole moment are found to be larger than in some other materials.

---

1 Introduction

Methylammonium lead iodide ([CH₃NH₃]PbI₃; denoted here as MAPbI₃) is the parent of the large and rapidly growing family of halide perovskite photovoltaics. This family combines a high power conversion efficiency with easy and cheap solution processing and good defect tolerance, and thus shows tremendous potential for solar cells among many other optoelectronic devices.^1–5

The atomic structure of MAPbI₃ is analogous to that of the inorganic perovskites, such as CsPbI₃.⁶ The crystal structure consists of a network of corner-linked PbI₆ octahedra as in CsPbI₃, but with the methylammonium (MA) cations rather than Cs⁺ cations in the interstices with 12-fold coordination to the iodine anions.^7–10 MAPbI₃ has been shown to undergo two phase transitions, with the highest-temperature phase having the same cubic symmetry as the high-temperature phase of CsPbI₃, but with orientational disorder of the MA cations, and with the intermediate-temperature phase also having some degree of orientational disorder.^8–11

In this paper we use neutron total scattering measurements coupled with analysis using the Reverse Monte Carlo (RMC) method¹² to study the atomic structure of MAPbI₃ in its ordered, partially ordered and disordered phases. We address two issues: the changes in the orientational order/disorder of the MA cations on heating from low to high temperature, and the behaviour of the inorganic PbI₃ network. Both of these issues are where total scattering with RMC can provide information that is harder to obtain using diffraction methods with standard crystal structure analysis, which usually need to identify specific sites for the positions of the disordered atoms prior to refinement.^8–10 Detailed analysis of the Bragg diffraction data from this study was recently published.¹¹

The total scattering method yields the pair distribution function (PDF),^13,14 which is similar to a histogram of instantaneous interatomic distances, and as such it contains information about fluctuations of the local structure. The RMC method is used to generate supercell configurations of atoms – effectively instantaneous images – that are simultaneously consistent with the long-range order revealed by the information contained in the Bragg scattering and with the fluctuations of the local structure revealed by the PDF. The configurations can therefore give information about the distributions of orientations of molecules and molecular ions in ordered, partially ordered and disordered phases,^15–21 and about fluctuations within inorganic crystal networks.^6,22,23 We believe that the total scattering method coupled with RMC analysis gives a unique view of disordered crystalline materials.^12,14

In the next section we give the crystallographic background necessary to understand the scientific problem being tackled in this paper. We review the current information about the phase transitions and what is currently known about the atomic structures of the three phases of MAPbI₃ from previous diffraction studies. In Section 3 we describe the methods used in this study. Results are given in two sections. Section 4 presents an analysis of the distribution of the orientations of the MA cations in the three phases of MAPbI₃. In Section 5 we analyse the flexibility and fluctuations of the inorganic network of corner-linked PbI₆ octahedra. Finally the results are discussed with conclusions in Section 6. Some details are given in the ESI.† Analysis of the Bragg diffraction data giving information about the variation of the crystal structure of the inorganic network of MAPbI₃ through the phase transitions has been given in a preceding publication.¹¹

2 Crystallographic background

At high temperatures MAPbI₃ adopts the aristotype cubic perovskite structure,⁷ space group Pm3̄m, with corner-linked PbI₆ octahedra, and with the MA cations lying within the large cages bounded by 12 iodine anions.²⁵ The symmetry of this structure implies that the MA cations are orientationally disordered, the molecular symmetry 3m being lower than that of the site, m3̄m.

On cooling MAPbI₃ undergoes two phase transitions, involving rotational distortions of the network of linked PbI₆ octahedra and progressive ordering of the orientations of the MA molecular cations.^8–11 The crystal structures of all three phases are shown in Fig. 1, where the coordinates are taken from the refinement of Weller et al.⁸ and as refined as a function of temperature in our previous report.¹¹

Fig. 1 Schematic representation of (a) orthorhombic Pnma phase (vertical axis [010], structure at 10 K), (b) tetragonal I4/mcm (vertical axis [001], structure at 200 K), and (c) cubic Pm3̄m phase (structure at 380 K) represented as a supercell of the cubic aristotype with 45° rotation of the a–b axes. The crystallographic parameters for these structure diagrams were taken from our earlier work,¹¹ which was based on the atomic coordinates first obtained by Weller et al.⁸ The disordered MA ions are represented by placing atoms with partial occupancies in sites that were refined, but the sites do not have actual significance. For clarity of comparison between different phases, the cubic phase is shown as a . supercell, and the origin of the orthorhombic phase has been shifted by a/2. Images were produced using CrystalMaker®.²⁴

The first phase transition on cooling from high temperature is at 327 K. The new phase has a body-centred tetragonal structure of space group I4/mcm.^8–10 The network of PbI₆ octahedra shows rotations about the tetragonal [001] axis, described as a⁰a⁰c⁻ using the Glazer notation.^26,27 This means that there are no rotations about the [100] and [010] axes, but rotations about the [001], and with alternate (001) layers having opposite rotations leading to a doubling of the c repeat distance. This pattern of orientations is identical to that in the famous example of SrTiO₃. The phase transition at 327 K is nearly continuous. The variation of the octahedral rotations with temperature is close to that of a classical tricritical phase transition,^9,11 where the rotation angle varies as (T_c − T)^1/4, but in fact the phase transition is weakly discontinuous with thermal hysteresis, and can described by a Landau free energy function appropriate for a first-order phase transition (that is, with a negative coefficient for the term in the fourth power of the rotation angle, even though the nearly-continuous nature of the phase transition means that the value of this coefficient is small).¹¹ The small discontinuity observed in the previous diffraction studies is consistent with a small latent heat observed through calorimetry.²⁸

The second phase transition occurs at 165 K. In the phase below this temperature MAPbI₃ has an orthorhombic crystal structure, space group Pnma, with ordered orientations of the MA cations.^8,9,11 The rotations of the PbI₆ octahedra in this phase are described as a⁻b⁺a⁻ in Glazer notation.^26,27 In this case there are rotations about the new [010] axis in which alternate layers have the same rotation, and with equal rotations about the [100] and [001] axes with alternate layers having opposite rotations. This pattern of rotations is identical to that seen in the mineral perovskite, CaTiO₃. The orthorhombic and tetragonal phases do not have a direct group-theoretical symmetry relationship, and thus the phase transition between these two phases at 165 K is necessarily discontinuous.¹¹ There appears to be only a weak variation of the symmetry-breaking distortions and coupled lattice strains in this phase with temperature.¹¹

Before the recent neutron powder diffraction studies^8,9,11 there had been suggestions of different symmetries for the lower-temperature phases, including the possibility of ferroelectric phases.^29,30 These are not consistent with the diffraction data, and other recent work has indicated that none of the bulk phases are ferroelectric.³¹

Although the octahedral tilts in MAPbI₃, their variation with temperature, and their relationship to spontaneous lattice strains have been characterised,¹¹ the orientations of the MA cations are completely undetermined. Previous work on the orientations has tended to be concerned with the dynamics, using techniques such as NMR,³² inelastic and quasielastic neutron scattering,^33–35 and ultrasound absorption.³⁶ These are indirect probes of structure, and whilst their data indicate the existence of orientational disorder in the tetragonal and cubic phases – and indeed see a gradual change in the orientational behaviour on changing temperature across the tetragonal–cubic phase transition – they give divergent opinions on the extent to which the MA cations are freely rotating or executing rotational jumps between a set of well-defined orientations. This is exactly the sort of question that total scattering methods analysed by the RMC method can tackle and provide useful, and unique, new insights.^15–21

3 Methods

3.1 Sample synthesis

Synthesis of deuterated samples of MAPbI₃ for this work has been described in detail in our recent paper,¹¹ and readers are referred there for details. Diffraction data show that the sample has no observable impurity phases. The diffraction data for the low-temperature ordered phase show some evidence for incomplete deuteration. Refined site occupancies on the D/H sites in the ordered phase suggested that the rehydrogenation was on the N–H bonds, and were used to establish the degree of deuteration.¹¹ This degree of deuteration was used in all subsequent analysis described in this paper, including in the processing of the total scattering data as discussed next.

3.2 Neutron total scattering measurements, data processing, and the RMC simulations

Neutron total scattering experiments were performed on the POLARIS diffractometer at the ISIS spallation neutron source.³⁷ The sample temperature was controlled by a closed-cycle refrigerator (CCR) capable of heating above room temperature. Measurements of total scattering for RMC analysis were performed at temperatures of 10, 100, 155, 170, 293, 300, 320, 335, 350, 375, and 400 K. Data correction measurements were taken, at room temperature, of the empty instrument, empty CCR, and empty can within the CCR, together with a calibration measurement from a vanadium rod.

The GUDRUN package was used to obtain the corrected scattering functions and PDFs from the raw data.³⁸ Fundamental equations for total scattering and the transformation to the pair distribution function D(r)^13,14,39 are provided in Section S1 of the ESI.†

We remark that the corrections for inelasticity are least satisfactory for light elements such as deuterium – which in the case of MAPbI₃ means half the atoms – and we encountered some difficulties in achieving a good match between the scattering functions measured by different banks of detectors. Our approach to deal with this problem was to use a combination of the top-hat function⁴⁰ and fitting the sample packing efficiency. This approach will also effectively sweep up errors in the levels of the self-scattering function and incoherent scattering caused by errors in our knowledge of the exact H/D ratio.

Experience has shown that the effects of errors in the processing of total scattering data have the largest impact on the lowest-r peaks in the PDF. It is probably because of errors associated with the inelasticity corrections that the consistency of results we will report in this paper is not quite as high as was achieved in our other recent RMC studies, such as of CsPbI₃ (ref. 6) and ScF₃.²³

Rietveld refinements were performed using the GSAS package⁴¹ with the EXPGUI interface.⁴² The detailed analysis of these results was published recently,¹¹ including data for many intermediate temperatures. The point to note here is that the refined crystal structures from this work were used to generate starting configurations for the RMC using the RMCcreate/data2config tool,⁴³ adapted to allow for the molecular ions to be oriented in any chosen state. For the ordered orthorhombic Pnma phase we used the refined crystal structures as the starting points at each temperature. For the disordered phases (tetragonal 4/mcm and cubic Pm3̄m) we used the refined values of lattice parameters and coordinates of the PbI₆ network, and placed MA cations at their nominal positions. The MA orientations were then disordered by various types of random rotations after the creation of the supercell, from simple single rotations to completely random disorder. It was found that the final results in the RMC were not affected by the exact choice of starting point, perhaps because (anticipating the results described below) the final states in the RMC are highly disordered. The initial configurations were prepared to contain 6 × 4 × 6, 6 × 6 × 4 and 8 × 8 × 8 supercells of the conventional unit cells of the orthorhombic, tetragonal and cubic phases respectively, with an approximate configuration edge length of 50 Å.

Reverse Monte Carlo simulations were performed using the RMCprofile package (v6.7).⁴⁴ Details are given in Section S2 of the ESI.† Data included were the scattering function i(Q), the PDF D(r) – equations are defined in several papers^14,39 and are reproduced and explained in the ESI† – and the Bragg profile extracted by GSAS. Further information, together with the best fits to the data (Fig. S1), are shown in the ESI.†

4 Orientational ordering of the methylammonium molecular cations

4.1 Visual analysis of atomic configurations

Representative configurations from the RMC simulations are shown in Fig. 2a–c. The images for the two lower-symmetry phases show the large rotations of the PbI₆ octahedra, with alternate layers having opposite rotations in the I4/mcm phase and the same rotations in the Pnma phase. The Pmna phase also has smaller rotations of opposite sense about the other two axes, as can be seen from the upper vertices of the octahedra. On the other hand, the Pm3̄m phase has the octahedra perfectly aligned on average, but the effects of thermal motion are clear, both in terms of rotations and shear distortions of the octahedra.

Fig. 2 Panels (a–c) show projections of the atomic configurations of the three phases from the RMC simulations at a single temperature each, showing the correlations between rotations of octahedra and orientational disorder of the MA molecular ions. (d) Slice of one configuration of the cubic phase in the plane parallel to (001) at height z = 1/2 of the cubic unit cell, with all atoms of the simulation translated into a single unit cell, where black and blue spheres stand for C and N atoms respectively, pink and silver spheres represent H and D atoms respectively, and purple spheres represent iodine atoms. Panels (e–g) show the corresponding atomic density of the C, N and D/H atoms respectively in the cubic phase. The visualisations in panels (a–d) were constructed using CrystalMaker®.²⁴

Fig. 2 also shows the onset of orientational disorder of the MA molecular ions on transforming from the Pmna phase to the I4/mcm phase and then to the cubic Pm3̄m phase. The disorder in the cubic phase is visualised in panels (d–g) of Fig. 2. Fig. 2d shows the atoms of several configurations collapsed into one unit cell by applying the appropriate lattice translations, representing a slice of atoms parallel to the (001) plane at height z = 1/2 of the cubic unit cell, containing iodine atoms and the MA ions. The disorder is clear, with a central distribution of C and N atoms surrounded by the hydrogen (mostly deuterium) atoms. Unfortunately, although such plots have a large visual impact, they can be misleading since we see only the outer atoms of a cluster. Thus the same plane was also analysed by calculating the atomic density, which is shown in panels (e–g) of Fig. 2 for each of the three types of atom in the MA molecular ion. It is seen that there is an inner shell of C/N atoms surrounded by an outer shell of the D/H atoms.

4.2 Orientational disorder in the high-temperature cubic phase of (CD₃ND₃)PbI₃

Here we analyse the orientational order of the MA molecular ions quantitatively by focussing on the orientations of the C–N bonds; the orientational distribution that includes the C–D and N–D/H bonds is much more disordered and less informative.

The C–N distribution function for the cubic phase has been extracted from 30 independent RMC configurations for each temperature, with all configurations containing 512 MA cations. The orientational distribution function P(Ω), where Ω represents the pair of polar angles θ, ϕ with θ as the zenith angle and ϕ as the azimuthal angle, is defined such that the number of bonds lying within the angular range θ ± dθ/2 and ϕ ± dϕ/2 is equal to (N/4π)P(Ω) sin θ dθ dϕ, where N is the total number of bonds. For completely random disorder P(Ω) = 1/4π ≃ 0.08. The results for the highest temperature, 400 K, are shown in Fig. 3 for three arcs of orientations, namely for the (11̄0) plane (θ = 45°), which includes the [001], [111] and [110] directions, for the (010) plane (θ = 90°) which includes the [001], [101] and [100] directions, and for the (001) plane (ϕ = 90°) which includes the [100], [110] and [010] directions (of course, the second and third are identical, but they probe the statistical distributions in different ways given the definition of the axis system for the polar coordinates). Results for other temperatures are given in the ESI (Fig. S2–S4†). The distribution functions are close to the random value in all cases, with departures from the random value being inconsistent and due to the effects of statistical noise.

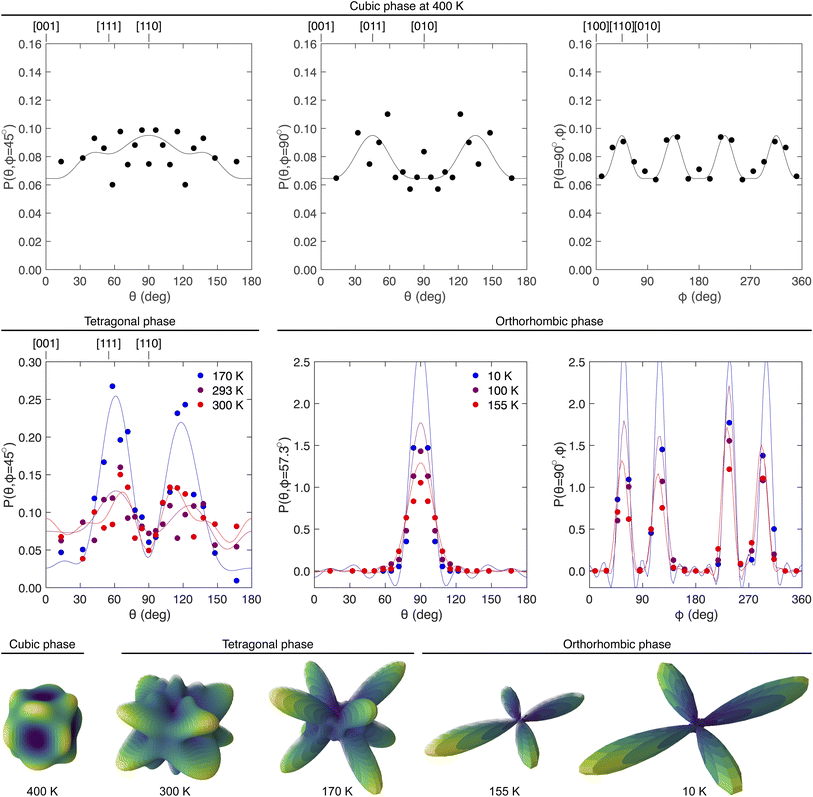Fig. 3 The orientational distribution functions P(Ω) of C–N bonds in the three phases of MAPbI₃. The top row shows the ODFs for the cubic phase at 400 K. Left to right are, respectively, P(θ, ϕ) for orientations in the (11̄0) plane with ϕ = 45°, in the (01̄0) plane with ϕ = 90°, and in the (001) plane with with θ = 90°. The middle row left shows P(Ω) with Ω oriented in the (11̄0) plane for the tetragonal phase at temperatures 170 K, 293 K and 300 K. The middle row, centre and right, show P(Ω) for the orthorhombic phase at 10 K, 100 K and 155 K. Lattice vectors, where given at the top of a diagram, correspond to specific values of Ω. The filled circles in each case represent P(Ω) obtained directly from the atomic configurations, and the continuous lines show the corresponding functions calculated using the derived harmonics as described in the text (eqn (1) and (2) for the cubic phase; eqn (3)–(5) for the other phases). For a completely uniform distribution in each case, P(Ω) = 1/4π ≃ 0.08. The bottom row shows the three-dimensional representation of the C–N orientational distribution functions for each data set.

To assist in the analysis we represent the orientational distribution function P(Ω) as an expansion of symmetry-adapted spherical variables. For molecules lying on sites of cubic symmetry m3̄m, it is convenient to expand P(Ω) in terms of Kubic harmonics:^45,46

The functions are defined in the ESI,† and here we only need K₀ = 1 and even values of 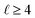. Whereas in the analysis of crystallographic data the coefficients might be fitted to data for the structure factors of Bragg reflections,⁴⁶ the orthonormality of the functions means that we can obtain the values of directly from the distribution of atoms in the RMC configurations rather than by fitting, making use of the relationshipwhere the averages are over all molecules in a set of configurations. This approach has been used recently to analyse the RMC configurations of the cubic phases of KCN,¹⁸ BaCO₃,¹⁹ methane²⁰ and SF₆.²¹

In Fig. 3 the data for P(Ω) extracted directly from the configurations are compared with the form of P(Ω) calculated by eqn (1) and (2), obtained from the configurations generated from data at a temperature of 400 K. Corresponding results for three other temperatures are given in the ESI (Fig. S2–S4†), together with the calculated values of for all temperatures (Table S1†). It is clear from these results – particularly when compared with corresponding data for other systems, such as SF₆ and CBr₄ (ref. 46) – that the distribution is never significantly different from random. There appears to be a slight overall preference towards alignment of the C–N bond away from the 〈001〉 and 〈111〉 directions, and a preference towards directions in the (011) planes at an angle of around 30° to the nearest major axis. Similar results were anticipated in a neutron diffraction experiment with a single crystal with refinements of site occupancies.¹⁰ However, the effects are small, albeit with some degree of consistency between the different temperatures, but clearly susceptible to statistical noise in the data, and the preference for alignment of the C–N bonds along the 〈110〉 directions in P(Ω) is at most only about 25% different from the random value of 1/4π.

An image of the full three-dimensional P(Ω) function from eqn (1) and (2) obtained from analysis of the data at 400 K is shown as an inset in Fig. 3, with the corresponding images for other temperatures being shown in the ESI (Fig. S2–S4†). The functions are roughly spherical in shape with some small ripples, consistent with the data shown in Fig. 3. Visual differences between the orientational distribution functions for different temperatures are purely due to statistical noise.

The key finding from this analysis is that the orientations of the MA cations are close to being randomly oriented, with just some weak preferences for preferred orientations. This is different to the behaviour identified for some other orientationally disordered crystals, where molecules or molecular ions execute jumps between a small set of well-defined orientations, but similar to that seen in some other systems. Our recent RMC study of orientational disorder in deuterated adamantane¹⁵ shows that the RMC method is quite capable of obtaining well-defined orientations if they exist. Thus we conclude that in the cubic phase of MAPbI₃, the MA molecular cations have a nearly random orientational disorder. The distribution is more random than in some other systems as noted (including SF₆ and CBr₄ (ref. 46)), but not very different from the orientational disorder of cyanide molecular anions in KCN.¹⁸

4.3 Partial orientational order and disorder in the intermediate-temperature phase of [CD₃ND₃]PbI₃

The site symmetry of the MA cation in the tetragonal phase is 4̄2m, which is again higher that the symmetry of the MA molecular ion (3m), which means that some degree of orientational disorder must be present in this phase. Previously attempts have been made to fit the orientations of the MA cations to Bragg diffraction data via the use of atomic sites with partial occupancy and allowing large thermal displacement parameters.^8,9 However, two different models, allowing or not allowing head-to-tail disorder, were reported, both apparently with the satisfactory agreement between the observed and calculated diffraction patterns.

For molecules lying on sites of lower than the full cubic symmetry, the equivalent of eqn (1) will make use of appropriate combinations of the real spherical harmonics,¹⁸ defined for m > 0 as

We can then expand the bond orientational distribution function as

where the allowed values of [small script l] and m, and whether we have the terms c and s, can be determined by symmetry.⁴⁷ As in eqn (2) we can obtain the coefficients directly from the atomic configurations.⁴⁸

Fig. 3 shows the histograms of orientations of the C–N bonds for all directions in the tetragonal (11̄0) plane for temperatures 170 K, 293 K and 300 K, together with the corresponding functions P(Ω) calculated using eqn (5) (values of the coefficients are tabulated in the ESI, Table S3†). Fig. 3 also shows the three-dimensional P(Ω) functions at 170 K and 293 K. The clear features are peaks within the (11̄0) planes at an angle of around ±30° to the (001) plane. These directions are closest to the eight directions [±1, 0, ±1] and [0, ±1, ±1] in the cubic phase, and may reflect the weak peaks in the calculated P(Ω) functions close to the set of [110] directions in the high-temperature cubic phase discussed above. The high degree of disorder in our room-temperature data confirms the finding from the single-crystal study of Ren et al.¹⁰ Unfortunately these authors did not record data below room temperature, so they were unable to see the onset of order seen in our work.

The most striking feature of the results shown in Fig. 3 is that the distribution P(Ω) sharpens considerably on cooling from 300 K to 170 K. The crystallography shows a gradual increase of the rotations of the PbI₆ octahedra on cooling below the cubic–tetragonal phase transition,¹¹ and this appears to be reflected in a gradual sharpening of the C–N bond orientation distribution function.‡ That is, the nature of the orientational disorder changes on cooling from a near-uniform distribution of orientations of the MA molecular ions towards disorder involving a defined set of specific orientations.

4.4 Orientational order in the low-temperature phase of [CD₃ND₃]PbI₃

The symmetry of the site occupied by the MA ions in the low-temperature orthorhombic phase is m, much lower than in the other two phases, and lower than the symmetry of the molecule. This lower symmetry allows for complete orientational order of the MA cations.

The C–N bonds lie within the (010) planes, as can be seen in Fig. 1, at an angle of around 57° to the [100] direction. Fig. 3 shows the orientational distribution of the C–N bonds for three temperatures in this phase, together with the three-dimensional representation for the lowest and highest temperatures. In these plots [010] is taken as the zenith direction that defines the angle θ. The histograms and calculated P(Ω) from eqn (5) are shown for two arcs, namely one for ϕ = 57.3° with varying θ, and one for θ = 90° with varying ϕ (that is, within the (010) plane). These two arcs both pass through the peaks of P(Ω).

It can be observed that for each temperature in this phase there is a high degree of orientational order. We showed above that on cooling across the range of temperatures in the intermediate tetragonal phase there is a growth in some degree of orientational order that accompanies the gradual increase in the size of the network distortion as characterised by the rotations of the PbI₆ octahedra and accompanying lattice strains.¹¹ On the other hand, our results here show that the orientational order is complete for all temperatures within the orthorhombic phase, which is consistent with the lack of significant changes in PbI₆ octahedral orientations and lattice strains across the full range of temperatures. The only effect of temperature seen in Fig. 3 is simply due to thermal motion rather than changes in orientational ordering.

4.5 Comment on the thermodynamics

Onada-Yamamuro et al. have reported extensive measurements of the thermodynamics of MAPbI₃ and other MA-halides.²⁸ For MAPbI₃ they report entropy changes of ΔS = 9.7 J K⁻¹ mol⁻¹ = R ln 3.2 and 19.0 J K⁻¹ mol⁻¹ = R ln 9.8 for the cubic–tetragonal and tetragonal–orthorhombic phase transitions respectively. They interpreted these results in terms of changes in the numbers of specific molecular orientations of the MA molecular ions in each phase (see their Fig. 14). Essentially their interpretation (with a slight change in their sequences in their figure) would be that in the cubic phase the MA molecular ions have 12 possible orientations of the C–N bond with 2 orientations around this axis, changing to 8 orientations of the C–N bonds in the tetragonal phase, giving an entropy change of ΔS = R ln 3. The transition to the orthorhombic phase would involve complete ordering, and hence an entropy change of ΔS = R ln 8. We can make three points to take the discussion further.

The first point is that the thermodynamic data of Onoda-Yamamuro et al.²⁸ show a gradual change in entropy over the temperature range of the tetragonal phase, with a sharp change at the lower-temperature phase transition and with little change over the temperature range of the orthorhombic phase. This is fully consistent with our observation of a high degree of disorder in the cubic phase, a high degree of order across the temperature range of the orthorhombic phase, but with a continuous change in the degree of orientational order in the intermediate-temperature phase. The observation of a gradual change in the ordering of the MA orientations in the tetragonal phase matches the observed behaviour of the rotations of the PbI₆ octahedra in this phase, with a nearly-continuous phase transition which is closely approximated by a tricritical phase transition in which the rotation angle closely follows the temperature dependence (T_c − T)^1/4. However, there is a small discontinuity at the phase transition, seen in the diffraction data,¹¹ consistent with the small latent heat seen in the thermodynamic data.²⁸

The second point is that the change in entropy associated with the change in order from the tetragonal to orthorhombic phase is significantly higher – nearly by a factor of 2 – than that associated with the change in order from the cubic to tetragonal phase. This ratio is not very different from the ratio ln 8/ln 3, which is consistent with the change on orientations seen in our study.

The third point is that the changes in entropy seen by Onoda-Yamamuro et al.²⁸ are larger than the simple R ln 3 and R ln 8 predicted by the simple model of ordering. If we accept that the entropy should be modelled as configurational, then two factors account for this difference. One is that in the cubic phase the preference for alignment of the C–N bonds along the cubic 〈110〉 directions is only weak, with a much broader range of orientations (as shown in our Fig. 3. The second is that there is a much greater degree of disorder of the rotations about the C–N bond than assumed by Onoda-Yamamuro et al.²⁸ However, treating the entropy as purely configurational, without allowing for a vibrational contribution, is equivalent to assuming that the potential energy minima associated with each orientation of the MA ion have identical shapes. In practice, this is unlikely to be true, so that vibrational contributions must also be included for an accurate assessment of the entropy change.⁴⁹ For instance, we recently showed that the entropy change in ammonium sulfate, despite being very close to 3R ln 2, is best interpreted in vibrational terms rather than twofold configurational disorder of the three molecular units.⁵⁰

5 Flexibility and fluctuations of the lead iodide octahedral network

5.1 Rigidity of the PbI₆ octahdedra

Since the two phase transitions in MAPbI₃ involve rotations of the PbI₆ octahedra, it has been suggested that the coupling between the orientations and motions of the PbI₆ octahedra and of the MA ions may have an impact on the optical properties.⁵¹ It is therefore interesting to analyse the flexibility of the PbI₆ octahedra and of the network of connected octahedra.

We start by using the approach encapsulated within the GASP method.^52–54 In brief, the GASP method analyses the positions of polyhedron-vertex atoms in a single configuration in terms of their displacements from either an ideal set of positions or else from the positions in a second configuration. It decomposes these displacements into motions associated with polyhedral rotations, whole-body translations, bond-bending distortions, and bond-stretching distortions, using a least-squares matching algorithm. More details have been documented elsewhere,^52–54 and a number of examples of analysis of RMC configurations using the GASP method have been reported previously in both tetrahedral networks,^53,55 perovskite networks of octahedra,^6,23,56 and mixed networks.⁵⁷ Our recent paper on ScF₃ (ref. 23) gives further details and an example of this approach for a related system.

The results of the GASP analysis for MAPbI₃ are shown in Fig. 4, where we show how the instantaneous displacements of the iodine atoms within the PbI₆ octahedra can be decomposed, on average, into Pb–I bond stretching, bending of the I–Pb–I bonds, and whole-body rotations of the PbI₆ octahedra. Results are given across the full range of temperatures in this study. For the cubic phase, we find on average that around half of the atomic motions associated with the PbI₆ octahedra are associated with bending of the I–Pb–I right angle bonds, around a quarter with octahedral rotation, and around a quarter with Pb–I stretching. The trend is similar for the higher-temperature data in the intermediate tetragonal phase, although the results for 170 K are not as consistent with the overall trend as are the other temperatures. On cooling into the lower-temperature phases the bending motion remains dominant, but the rotations become more important than the bond stretching.

Fig. 4 The breakdown of three motions inherent to the PbI₆ coordination octahedra obtained from the GASP analysis.^52–54 namely bending of the right-angle I–Pb–I connections, whole-body rotations of the PbI₆ octahedra, and stretching of the Pb–I bonds.

It is interesting to compare the behaviour in the high-temperature cubic phase of MAPbI₃ with corresponding results for other cubic perovskites obtained from analysis of RMC configurations. Fig. 5 shows results for SrTiO₃,⁵⁶ CsPbI₃,⁶ and ScF₃ (ref. 23) together with our results presented here for MAPbI₃. The interesting feature is the size of the bond bending component compared to the whole-body rotation. The first key point is that the results are quite similar to those of CsPbI₃,⁶ which is not surprising. The second key point is that CsPbI₃ and MAPbI₃ are intermediate between those of SrTiO₃ (ref. 56) and ScF₃.²³ Generally we might expect the oxide octahedra to be stiffer than the halide octahedra in terms of bond bending, as is clearly seen in Fig. 5. It is interesting that the fluoride octahedra show the greater degree of bond bending than the iodide octahedra, a point that we will discuss further as we now analyse the distributions of atomic motions in more detail.

Fig. 5 Comparison of the GASP^52–54 results for a selection of cubic perovskite phases, namely SrTiO₃,⁵⁶ CsPbI₃,⁶ MAPbI₃, and ScF₃.²³

The GASP analysis gives the absolute motion in addition to the relative motions shown in Fig. 4, and in 6 we show the distributions of the absolute PbI₆ rotations from their average orientations (summing the rotations about the three axes in quadrature). Note that in these distributions the value of zero angle represents the average orientation, which differs in each phase and differs with temperature¹¹) throughout the range of temperatures. Fig. 6 specifically shows the fluctuations in the orientations away from the mean orientations, not the distribution of exact orientations.

Fig. 6 Angle distribution functions (normalised histograms) of the PbI₆ whole-body rotations from the GASP analysis of the RMC configurations of MAPbI₃ for the full range of temperatures, with separate plots given for each of the three phases as indicated in the legend.

Unsurprisingly the distributions of rotational angles becomes broader on heating, with a commensurate shift of the maximum in the distribution to higher angle on heating. At very low temperature (10 K) the distribution of rotation angles has a maximum below 2°. Strikingly the distribution of angles increases quickly on heating to 155 K in the low-temperature disordered phase. In the two disordered phases (the intermediate-temperature tetragonal phase, and the high-temperature cubic phase) the distribution of octahedral rotations broadens rather more gradually with temperature than as is seen in the low-temperature ordered phase. This presumably reflects the role of the orientational disorder of the MA ions.

It is interesting to compare the results in Fig. 6 for the high-temperature cubic phase with those obtained for some other systems. From Fig. 6 we see that at 400 K the maximum in the distribution, which will be close to the mean value, is around 5°. On the other hand, corresponding results for both CsPbI₃ (ref. 6) and ScF₃ (ref. 23) are around 10° at the same temperature. Data presented for SrTiO₃ are in different form, showing the distributions for the individual axes and for positive and negative angles rather than as absolute magnitudes, but we can see that the distributions at the maximum temperature of 300 K are of order 2° only. Presumably the larger size and shape of the MA cation as compared to the Cs cation acts to limit the rotations of the PbI₆ octahedra in MAPbI₃.

We now consider the distribution of I–Pb–I angles within the PbI₆ octahedra. Fig. 7 (top row) shows the full distribution of all I–Pb–I angles, from both the right angle and linear connectivities. Whilst a simple normalised one-dimensional histogram is useful for the right angles, giving a peak very close to 90°, the one-dimensional histogram cannot give a peak at 180° because this is a maximum value, and since the solid angle around this angle becomes vanishingly small for angles close to 180°, the histogram necessarily has a value close to zero for an angle close to 180°. We therefore also show in Fig. 7 (bottom row) the same distributions for the near-linear I–Pb–I angles scaled by the sine of the angles. In all cases these show that the three-dimensional distribution function is peaked at 180°.

Fig. 7 (Top row) The one-dimensional angle distribution functions (normalised histograms) of the octahedral I–Pb–I angles in MAPbI₃ for the full range of temperatures, with separate plots given for each of the three phases as in Fig. 6. (Bottom row) The same distribution functions scaled by the sine of the octahedral I–Pb–I angles for the nominally linear angles, showing that the full three-dimensional angular distribution functions for these angles have their peaks at 180°.

It is clear from Fig. 7 that both distributions of bond angles broaden on heating, and for the linear bond this means that the maximum in the distribution function appears to shift away from 180°. It is interesting to compare the variance of the angle distributed around 90° shown in Fig. 7 with the variance of the whole-octahedral rotations give in Fig. 6, and this comparison is shown in Fig. 8. It can be seen that the variance of the bending motions is slightly more than twice as large as the whole-octahedral rotations. This is a larger difference than in ScF₃,²³ where these two variances were more-or-less of equal value. It is possible that this difference arises from the fact that MAPbI₃ has the large MA ion within the perovskite A site, whereas this site is empty in ScF₃.

Fig. 8 Angular fluctuations in MAPbI₃ across the range of temperatures. Filled circles represent the square of the PbI₆ octahedral rotations, and open circles represent the variance of the bending of the I–Pb–I right angle in the PbI₆ octahedra. The curves are fitted to the data as guides to the eye, using the form x = x₀ + (x′/θ) cot h(θ/T), where we set θ = 50 K and fit the values of x₀ and x′ to the data.

Recently Liang et al.⁵⁸ reported a molecular dynamics simulation of MAPbI₃ using a machine-learning force field. They performed analyses of octahedral rotations. Their rotation angles appear to be larger than those reported in Fig. 8, but it is not clear from their work whether they have decoupled the effects of octahedral bond bending in the way that we have. Therefore at this point we do not consider it to be straightforward to compare the two sets of results.

5.2 Flexibility of the linear Pb–I–Pb linkage

The distributions of the near-linear inter-octahedra Pb–I–Pb angles are shown as normalised histograms in Fig. 9 for the various temperatures corresponding to each of the three phases. As for the near-linear I–Pb–I bonds shown in Fig. 7, in the cubic phase the one-dimensional histograms fall to zero at an angle of 180°, whereas the distribution functions scaled by the sine of the angle show peaks at 180° for the angles in the cubic phase and for two angles in the tetragonal phase, as expected in the full three-dimensional distribution function.

Fig. 9 (Top row) The angle distribution functions (normalised histograms) of the linear inter-octahedral Pb–I–Pb angles in MAPbI₃ for the full range of temperatures, with separate plots given for each of the three phases as in Fig. 6. (Bottom row) The same distribution functions scaled by the sine of the octahedral Pb–I–Pb angles, showing that the full three-dimensional angular distribution functions for these angles in the cubic phase, and for two angles in the tetragonal phase, have their peaks at 180°.

In the cubic phase, the distribution functions are centred on an angle θ of around 15° from exact linearity, with a tail extending to higher angle. This is slightly larger than twice the octahedral rotation angle, consistent with a significant contribution from bond-bending motions as well as arising from rotations of two Pb–I angles. This is consistent with the corresponding findings in both CsPbI₃ (ref. 6) and ScF₃.²³

Carignano et al.⁵⁹ have reported ab initio molecular dynamics simulations of MAPbI₃ nominally in the cubic phase. They studied this angle, at a higher temperature, in terms of the transverse displacement of the iodine atom from the centre of the Pb–Pb vector. Their distribution of displacements peaks at a value around 0.6 Å, which corresponds roughly to a peak in the angular distribution function of around 158°. This is slightly larger than obtained in our RMC configurations, as shown in Fig. 9. Whilst the higher temperature may be a factor in explaining this difference, we also believe that the small size of the configuration in the molecular dynamics simulation (4 × 4 × 4 unit cells) will be important.§

In the tetragonal phase, one of the Pb–I–Pb linkages has an equilibrium value less that 180° due to rotations of the PbI₆ octahedra around the [001] axis (Fig. 1b). The equilibrium value from the crystallographic data reported previously¹¹ has a range from close to zero at the nearly-continuous phase transition from the cubic phase to a value of θ = 157° at 170 K. In Fig. 9 we see that at a temperature of 170 K there is one peak centred on θ = 155° consistent with the crystallographic data. There is a second peak at around θ = 174°, which represents the thermally-induced fluctuations from the linear arrangement along the [001] directions. The amplitude of this fluctuation is reduced from that seen in the cubic phase. On the other hand for the other two data sets, at temperatures of 293 K and 300 K, which are closer to the temperature for the cubic–tetragonal phase transitions, the crystallographic data¹¹ give a Pb–I–Pb bond angle of θ = 163°, which is closer to linear than for 170 K. The maxima in distribution functions f(θ) are again consistent with this mean value, but the distribution is broader due to increased thermal motion, probably due in part both to the increased temperature and the greater proximity to the cubic phase. It is noticeable that the maxima in the distributions of the angle for linkages parallel to [001], which are not centred on θ = 180° because of the solid-angle argument, are actually broader and with a maximum at a higher angle than the corresponding distribution for 170 K. This again reflects the increased thermally-induced disorder.

Finally the crystallography of the orthorhombic phase¹¹ shows that there are two Pb–I–Pb angles of around 151° and 162°. The distribution function for a temperature of 10 K shown in Fig. 9 is consistent with the crystallography, with the maxima in the distribution corresponding to the angles from the crystallographic analysis. On heating it is clear that the distributions broaden considerably. The crystallography shows that the average values of both angles do not change significantly on heating,¹¹ and this is consistent with the shapes of the distributions at higher temperatures, even though the broadening means that the two peaks overlap and blur the maxima.

5.3 Anharmonicity in the Pb–I bonds

Our recent RMC study of CsPbI₃ found that there is considerable anharmonicity of the Pb–I bond.⁶ This was identified through a significant asymmetry in the distribution of nearest-neighbour Pb–I distances. Here we show that there is a similar anharmonicity in the Pb–I bond in MAPbI₃.

Fig. 10 shows the distribution of nearest-neighbour Pb–I distances in MAPbI₃ at different temperatures in the cubic phase. There is a very similar asymmetry to the distributions as found in CsPbI₃.⁶ Initially we might expect the distribution of Pb–I distances for the first neighbour to be symmetrical, since the two types of atoms lie in lines with equal spacing. Expansion of one Pb–I bond along the line should lead to an equal contraction of a neighbouring bond. Thus it is most likely that the asymmetry arises from transverse rather than longitudinal motions.

Fig. 10 (Top) Pb–I bond distance distribution function in the cubic phase of MAPbI₃ from the RMC configurations (points), fitted with a probability distribution described by a Morse potential as discussed in the text (lines). (Bottom) Fitted Morse potentials (solid lines) and the corresponding harmonic potentials (broken lines) for CsPbI₃ (ref. 6) (black) and MAPbI₃ (red).

As in our work on CsPbI₃ we have characterised this asymmetry by fitting the distribution of Pb–I distances by a function of the form P(r) ∝ exp(−ϕ(r)/k_BT), where ϕ(r) is an effective potential energy function, which we have assumed can be described by a conventional Morse potential to give the asymmetry in the distribution function:

Here r₀ represents the point of minimum energy and therefore represents the low-temperature equilibrium bond length; k is the effective harmonic force constant at the point of minimum energy; and α is defined such that the minimum of the energy is equal to E₀ = −k/2α².¶ We fitted a single set of values of r₀, k and α to the data for all temperatures of MAPbI₃ in the cubic phase, obtaining values r₀ = 3.16 Å, k = 1.21 meV Å⁻², and α = 1.72 Å⁻¹. The fitting is shown in Fig. 10.||

These results are quite similar to those found for CsPbI₃.⁶ In Fig. 10 we show the calculated form of ϕ(r) for both MAPbI₃ and CsPbI₃, and compare with a harmonic function defined as ϕ_harm(r) = E₀ + (k/2)(r − r₀)². Although the cases of MAPbI₃ and CsPbI₃ have different values of E₀, as seen by the vertical offsets of the functions ϕ(r), the way ϕ(r) departs from ϕ_harm(r) for both r < r₀ (positive departure) and r > r₀ (negative departure) is similar in both cases.

For the lower temperatures, where the octahedra are rotated on average, the first peak in the Pb–I distributions became more symmetric. The bond anharmonicity is a particular feature of the high-symmetry cubic phase.⁶¹

5.4 Ferroelectric fluctuations

There have been occasional reports of ferroelectricity in MAPbI₃, although the consensus is now against this view. Certainly the existence of bulk ferroelectricity is not compatible with the accepted crystallography over the full range of temperatures.^8,9,11

We have investigated whether the RMC configurations support the existence of ferroelectric fluctuations by calculating the instantaneous dipole moment associated with each PbI₆ octahedron (calculated associating a unit of charge of ±e/2 either end of the Pb–I bond, and summing over the 6 bonds from each lead atom). Presumably any ferroelectricity will arise, at least in part, from fluctuations of the positions of the lead atoms away from the centres of the octahedra.

The mean value of the dipole moment is effectively zero to within noise. The mean-square dipole moment, representing the fluctuations, is shown as a function of temperature in Fig. 11. This shows a linear increase with temperature, suggesting that the fluctuations in the octahedral dipole moments are thermally excited. For comparison, we note that this value of the variance of the fluctuation of the dipole moment in MAPbI₃ is an order of magnitude larger than the dipolar fluctuation of the OCu₄ squares in CuO.^62,63 This suggests a degree of flexibility of the PbI₆ octahedra, as indicated by the other results in this study.

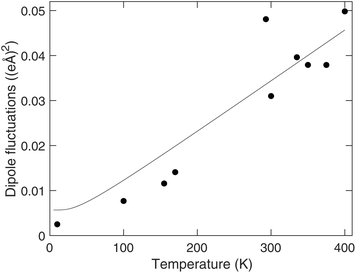Fig. 11 Variation of the mean-square dipole moments of the PbI₆ octahedra in MAPbI₃ with temperature. The curved line, given as a guide to the eye, was obtained as in Fig. 8.

6 Discussion and conclusions

In this paper we have reported an extensive analysis of the results of an RMC study of MAPbI₃ using neutron total scattering data and deuterated samples. The focus has concerned changes in structure and local structure fluctuations associated with the two phase transitions involving both octahedral rotations and ordering of the orientations of the MA ions.

Orientational disorder of molecules within crystals is very difficult to study using normal diffraction methods, particularly if the distribution of molecular orientations cannot be simply described by a small number of possible orientations. This is where total scattering and the RMC method play a unique role in structural studies. We have shown that in the cubic phase there is almost a completely random distribution of orientations of the MA ions. We have also characterised the orientational disorder in the intermediate tetragonal phase, showing a significant departure from random disorder on cooling, with clear preferred directions for the C–N vector in the MA ions. In the ordered low-temperature phase the MA ions show a high degree of orientational order, with increased librational amplitude on heating from low temperature. These results are fully consistent with, but significantly extending, prior knowledge from crystallographic studies.^8,9,11

We have also explored the flexibility of the backbone network of connected PbI₆ octahedra, comparing with some other recent studies. We have shown by comparison with other systems that the PbI₆ octahedra move as rigid units but also have a high degree of flexibility regarding flexing of the I–Pb–I bonds. The same flexibility leads to a marked anisotropy of the distribution of Pb–I neighbour distances and of thermally-induced dipolar fluctuations of the PbI₆ octahedra.

Data availability

The original neutron scattering data are available from the ISIS repository, with https://doi.org/10.5286/ISIS.E.RB1720436. The atomic configurations generated by the RMC method are available from the corresponding author on request.

Author contributions

Jiaxun Liu: investigation, formal analysis, software, validation, writing (original draft), writing (review & editing), visualisation. Juan Du: investigation, writing (review & editing). Anthony E. Phillips: investigation, formal analysis, software, supervision, validation, writing (review & editing). Peter B. Wyatt: investigation, writing (review & editing). David A. Keen: investigation, formal analysis, writing (review & editing). Martin T. Dove: funding acquisition, investigation, formal analysis, methodology, validation, supervision, software, writing (original draft), writing (review & editing), visualisation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to ISIS for provision of neutron beam time (experiment proposal RB1720436). The raw data are archived according to the data availability statement above. JL and JD are grateful to the China Scholarship Council and Queen Mary University of London for financial support. Funding was provided by the National Natural Science Foundation of China (project number 12174274, MTD). This research utilised Queen Mary's Apocrita HPC facility (http://doi.org/10.5281/zenodo.438045), supported by QMUL Research-IT and funded by EPSRC grants EP/K000128/1 and EP/K000233/1 (MTD).

References

1. C. S. Ponseca, T. J. Savenije, M. Abdellah, K. Zheng, A. Yartsev, T. Pascher, T. Harlang, P. Chabera, T. Pullerits, A. Stepanov, J.-P. Wolf and V. Sundström, Organometal Halide Perovskite Solar Cell Materials Rationalized: Ultrafast Charge Generation, High and Microsecond-Long Balanced Mobilities, and Slow Recombination, J. Am. Chem. Soc., 2014, 136, 5189–5192,  DOI:10.1021/ja412583t.
2. X. Zhu, The Perovskite Fever and Beyond, Acc. Chem. Res., 2016, 49, 355–356,  DOI:10.1021/acs.accounts.6b00067.
3. D. A. Egger, A. M. Rappe and L. Kronik, Hybrid Organic–Inorganic Perovskites on the Move, Acc. Chem. Res., 2016, 49, 573–581,  DOI:10.1021/acs.accounts.5b00540.
4. J. M. Frost and A. Walsh, What Is Moving in Hybrid Halide Perovskite Solar Cells?, Acc. Chem. Res., 2016, 49, 528–535,  DOI:10.1021/acs.accounts.5b00431.
5. A. K. Jena, A. Kulkarni and T. Miyasaka, Halide Perovskite Photovoltaics: Background, Status, and Future Prospects, Chem. Rev., 2019, 119, 3036–3103,  DOI:10.1021/acs.chemrev.8b00539.
6. J. Liu, A. E. Phillips, D. A. Keen and M. T. Dove, Thermal Disorder and Bond Anharmonicity in Cesium Lead Iodide Studied by Neutron Total Scattering and the Reverse Monte Carlo Method, J. Phys. Chem. C, 2019, 123, 14934–14940,  DOI:10.1021/acs.jpcc.9b02936.
7. W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Chemically diverse and multifunctional hybrid organic–inorganic perovskites, Nat. Rev. Mater., 2017, 2, 16099,  DOI:10.1038/natrevmats.2016.99.
8. M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Complete structure and cation orientation in the perovskite photovoltaic methylammonium lead iodide between 100 and 352 K, Chem. Commun., 2015, 51, 4180–4183,  10.1039/C4CC09944C.
9. P. S. Whitfield, N. Herron, W. E. Guise, K. Page, Y. Q. Cheng, I. Milas and M. K. Crawford, Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide, Sci. Rep., 2016, 6, 35685,  DOI:10.1038/srep35685.
10. Y. Ren, I. W. H. Oswald, X. Wang, G. T. McCandless and J. Y. Chan, Orientation of Organic Cations in Hybrid Inorganic–Organic Perovskite CH₃NH₃PbI₃ from Subatomic Resolution Single Crystal Neutron Diffraction Structural Studies, Cryst. Growth Des., 2016, 16, 2945–2951,  DOI:10.1021/acs.cgd.6b00297.
11. J. Liu, J. Du, A. E. Phillips, P. B. Wyatt, D. A. Keen and M. T. Dove, Neutron powder diffraction study of the phase transitions in deuterated methylammonium lead iodide, J. Phys.: Condens. Matter, 2022, 34, 145401,  DOI:10.1088/1361-648x/ac4aa9.
12. D. A. Keen, M. G. Tucker and M. T. Dove, Reverse Monte Carlo modelling of crystalline disorder, J. Phys.: Condens. Matter, 2005, 17, S15–S22,  DOI:10.1088/0953-8984/17/5/002.
13. D. A. Keen, Total scattering and the pair distribution function in crystallography, Crystallogr. Rev., 2020, 26, 141–199,  DOI:10.1080/0889311x.2020.1797708.
14. M. T. Dove and G. Li, Review: Pair distribution functions from neutron total scattering for the study of local structure in disordered materials, Nucl. Anal., 2022, 1, 100037,  DOI:10.1016/j.nucana.2022.100037.
15. E. O. Beake, M. G. Tucker, M. T. Dove and A. E. Phillips, Orientational Disorder in Adamantane and Adamantanecarboxylic Acid, ChemPhysChem, 2017, 18, 459–464,  DOI:10.1002/cphc.201601219.
16. H. D. Duncan, E. O. R. Beake, H. Y. Playford, M. T. Dove and A. E. Phillips, Local structure of a switchable dielectric Prussian blue analogue, CrystEngComm, 2017, 19, 7316–7321,  10.1039/c7ce01883e.
17. H. D. Duncan, M. T. Dove, D. A. Keen and A. E. Phillips, Local structure of the metal-organic perovskite dimethylammonium manganese(II) formate, Dalton Trans., 2016, 45, 4380–4391,  10.1039/c5dt03687a.
18. G. Cai, A. E. Phillips, D. A. Keen, M. G. Tucker and M. T. Dove, Neutron scattering study of the orientational disorder in potassium cyanide, J. Phys. Commun., 2020, 4, 023001,  DOI:10.1088/2399-6528/ab7318.
19. G. Cai, A. E. Phillips, M. G. Tucker and M. T. Dove, Neutron scattering study of the orientational disorder and phase transitions in barium carbonate, J. Phys.: Condens. Matter, 2020, 32, 374014,  DOI:10.1088/1361-648X/ab8cde.
20. Y. Qin, S. Zhang, S. Zhang, M. G. Tucker, D. A. Keen, G. Cai, A. E. Phillips and M. T. Dove, Orientational order and phase transitions in deuterated methane: a neutron total scattering and reverse Monte Carlo study, J. Phys.: Condens. Matter, 2021, 34, 015401,  DOI:10.1088/1361-648x/ac2db8.
21. S. Zhang, Y. Qin, S. Zhang, M. Gao, M. G. Tucker, D. A. Keen, G. Cai, A. E. Phillips and M. T. Dove, Orientational disorder in sulfur hexafluoride: a neutron total scattering and reverse Monte Carlo study, J. Phys.: Condens. Matter, 2022, 34, 295401,  DOI:10.1088/1361-648x/ac6b74.
22. J. Du, A. E. Phillips, D. C. Arnold, D. A. Keen, M. G. Tucker and M. T. Dove, Structural study of bismuth ferrite BiFeO₃ by neutron total scattering and the reverse Monte Carlo method, Phys. Rev. B, 2019, 100, 104111,  DOI:10.1103/PhysRevB.100.104111.
23. M. T. Dove, J. Du, Z. Wei, D. A. Keen, M. G. Tucker and A. E. Phillips, Quantitative understanding of negative thermal expansion in scandium trifluoride from neutron total scattering measurements, Phys. Rev. B, 2020, 102, 094105,  DOI:10.1103/PhysRevB.102.094105.
24. D. C. Palmer, Visualization and analysis of crystal structures using CrystalMaker software, Z Kristallogr. Cryst. Mater., 2015, 230, 559–572,  DOI:10.1515/zkri-2015-1869.
25. D. Weber, CH₃NH₃PbX₃, a Pb(II)-system with cubic perovskite structure, Z Naturforsh B, 2015, 33, 1443–1445,  DOI:10.1515/znb-1978-1214.
26. A. M. Glazer, The classification of tilted octahedra in perovskites, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 1–12,  DOI:10.1107/S0567740872007976.
27. A. M. Glazer, Simple ways of determining perovskite structures, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 756–762,  DOI:10.1107/S0567739475001635.
28. N. Onoda-Yamamuro, T. Matsuo and H. Suga, Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II), J. Phys. Chem. Solids, 1990, 51, 1383–1395,  DOI:10.1016/0022-3697(90)90021-7.
29. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties, Inorg. Chem., 2013, 52, 9019–9038,  DOI:10.1021/ic401215x.
30. Y. Kutes, L. Ye, Y. Zhou, S. Pang, B. D. Huey and N. P. Padture, Direct Observation of Ferroelectric Domains in Solution-Processed CH₃NH₃PbI₃ Perovskite Thin Films, J. Phys. Chem. Lett., 2014, 5, 3335–3339,  DOI:10.1021/jz501697b.
31. J. Beilsten-Edmands, G. E. Eperon, R. D. Johnson, H. J. Snaith and P. G. Radaelli, Non-ferroelectric nature of the conductance hysteresis in CH₃NH₃PbI₃ perovskite-based photovoltaic devices, Appl. Phys. Lett., 2015, 106, 173502,  DOI:10.1063/1.4919109.
32. G. M. Bernard, R. E. Wasylishen, C. I. Ratcliffe, V. Terskikh, Q. Wu, J. M. Buriak and T. Hauger, Methylammonium Cation Dynamics in Methylammonium Lead Halide Perovskites: A Solid-State NMR Perspective, J. Phys. Chem. A, 2018, 122, 1560–1573,  DOI:10.1021/acs.jpca.7b11558.
33. A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kockelmann, C. Law, X. Li, F. Foglia, A. Walsh, B. C. O’Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, The dynamics of methylammonium ions in hybrid organic–inorganic perovskite solar cells, Nat. Commun., 2015, 6, 7124,  DOI:10.1038/ncomms8124.
34. J. Li and P. Rinke, Atomic structure of metal-halide perovskites from first principles: The chicken-and-egg paradox of the organic-inorganic interaction, Phys. Rev. B, 2016, 94, 045201,  DOI:10.1103/PhysRevB.94.045201.
35. T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi and S.-H. Lee, Rotational dynamics of organic cations in the CH₃NH₃PbI₃ perovskite, Phys. Chem. Chem. Phys., 2015, 17, 31278–31286,  10.1039/C5CP05348J.
36. J. R. Harwell, J. L. Payne, M. T. Sajjad, F. J. L. Heutz, D. M. Dawson, P. S. Whitfield, J. T. S. Irvine, I. D. W. Samuel and M. A. Carpenter, Role of lattice distortion and A site cation in the phase transitions of methylammonium lead halide perovskites, Phys. Rev. Mater., 2018, 065404,  DOI:10.1103/PhysRevMaterials.2.065404.
37. R. I. Smith, S. Hull, M. G. Tucker, H. Y. Playford, D. J. McPhail, S. P. Waller and S. T. Norberg, The upgraded Polaris powder diffractometer at the ISIS neutron source, Rev. Sci. Instrum., 2019, 90, 115101,  DOI:10.1063/1.5099568.
38. A. K. Soper, GudrunN and GudrunX : Programs for Correcting Raw Neutron and X-Ray Diffraction Data to Differential Scattering Cross Section, Rutherford Appleton Laboratory Technical Report RAL-TR-2011-013, 2011.
39. D. A. Keen, A comparison of various commonly used correlation functions for describing total scattering, J. Appl. Crystallogr., 2001, 34, 172–177,  DOI:10.1107/S0021889800019993.
40. A. K. Soper and E. R. Barney, Extracting the pair distribution function from white-beam X-ray total scattering data, J. Appl. Crystallogr., 2011, 44, 1–13,  DOI:10.1107/s0021889811021455.
41. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Technical Report LAUR 86-748, 2004.
42. B. H. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210–213,  DOI:10.1107/S0021889801002242.
43. M. T. Dove and G. Rigg, RMCgui: a new interface for the workflow associated with running Reverse Monte Carlo simulations, J. Phys.: Condens. Matter, 2013, 25, 454222,  DOI:10.1088/0953-8984/25/45/454222.
44. M. G. Tucker, D. A. Keen, M. T. Dove, A. L. Goodwin and Q. Hui, RMCProfile: reverse Monte Carlo for polycrystalline materials, J. Phys.: Condens. Matter, 2007, 19, 335218,  DOI:10.1088/0953-8984/19/33/335218.
45. W. R. Fehlner and S. H. Vosko, A product representation for cubic harmonics and special directions for the determination of the Fermi surface and related properties, Can. J. Phys., 1976, 54, 2159–2169,  DOI:10.1139/p76-256.
46. G. Dolling, B. M. Powell and V. F. Sears, Neutron diffraction study of the plastic phases of polycrystalline SF₆ and CBr₄, Mol. Phys., 1979, 37, 1859–1883,  DOI:10.1080/00268977900101381.
47. C. Bradley and A. Cracknell, The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups, Oxford University Press, Oxford, 2009.
48. A. E. Phillips, spharmonic, https://github.com/AEPhillipsGroup/spharmonic, 2023, accessed: 2023-06-14.
49. A. E. Phillips and H. C. Walker, On (not) deriving the entropy of barocaloric phase transitions from crystallography and neutron spectroscopy, J. Phys:. Energy, 2023, 6, 011001,  DOI:10.1088/2515-7655/ad0d00.
50. S. Yuan, B. E. Meijer, G. Cai, R. J. C. Dixey, F. Demmel, M. T. Dove, J. Liu, H. Y. Playford, H. C. Walker and A. E. Phillips, Origin of the Large Entropy Change in the Molecular Caloric and Ferroelectric Ammonium Sulfate, Adv. Funct. Mater., 2022, 32, 2207717,  DOI:10.1002/adfm.202207717.
51. A. Mehdizadeh, S. F. Akhtarianfar and S. Shojaei, Role of Methylammonium Rotation in Hybrid Halide MAPbX₃ (X = I, Br, and Cl) Perovskites by a Density Functional Theory Approach: Optical and Electronic Properties, J. Phys. Chem. C, 2019, 123, 6725–6734,  DOI:10.1021/acs.jpcc.8b11422.
52. S. A. Wells, M. T. Dove and M. G. Tucker, Finding best-fit polyhedral rotations with geometric algebra, J. Phys.: Condens. Matter, 2002, 14, 4567–4584,  DOI:10.1088/0953-8984/14/17/327.
53. S. A. Wells, M. T. Dove, M. G. Tucker and K. Trachenko, Real-space rigid-unit-mode analysis of dynamic disorder in quartz, cristobalite and amorphous silica, J. Phys.: Condens. Matter, 2002, 14, 4645–4657,  DOI:10.1088/0953-8984/14/18/302.
54. S. Wells, M. Dove and M. Tucker, Reverse Monte Carlo with geometric analysis − RMC+GA, J. Appl. Crystallogr., 2004, 37, 536–544,  DOI:10.1107/S0021889804008957.
55. A. M. Walker, L. A. Sullivan, K. Trachenko, R. P. Bruin, T. O. H. White, M. T. Dove, R. P. Tyer, I. T. Todorov and S. A. Wells, The origin of the compressibility anomaly in amorphous silica: a molecular dynamics study, J. Phys.: Condens. Matter, 2007, 19, 275210,  DOI:10.1088/0953-8984/19/27/275210.
56. Q. Hui, M. G. Tucker, M. T. Dove, S. A. Wells and D. A. Keen, Total scattering and reverse Monte Carlo study of the 105 K displacive phase transition in strontium titanate, J. Phys.: Condens. Matter, 2005, 17, S111–S124,  DOI:10.1088/0953-8984/17/5/012.
57. M. G. Tucker, A. L. Goodwin, M. T. Dove, D. A. Keen, S. A. Wells and J. S. O. Evans, Negative Thermal Expansion in ZrW₂O₈: Mechanisms, Rigid Unit Modes, and Neutron Total Scattering, Phys. Rev. Lett., 2005, 95, 255501,  DOI:10.1103/PhysRevLett.95.255501.
58. X. Liang, J. Klarbring, W. J. Baldwin, Z. Li, G. Csányi and A. Walsh, Structural Dynamics Descriptors for Metal Halide Perovskites, J. Phys. Chem. C, 2023, 127, 19141–19151,  DOI:10.1021/acs.jpcc.3c03377.
59. M. A. Carignano, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, Critical Fluctuations and Anharmonicity in Lead Iodide Perovskites from Molecular Dynamics Supercell Simulations, J. Phys. Chem. C, 2017, 121, 20729–20738,  DOI:10.1021/acs.jpcc.7b08220.
60. M. T. Dove, Flexibility of network materials and the Rigid Unit Mode model: a personal perspective, Philos. Trans. R. Soc., A, 2019, 377, 20180222,  DOI:10.1098/rsta.2018.0222.
61. Z.-G. Li, M. Zacharias, Y. Zhang, F. Wei, Y. Qin, Y.-Q. Yang, L.-C. An, F.-F. Gao, W. Li, J. Even and X.-H. Bu, Origin of Phase Transitions in Inorganic Lead Halide Perovskites: Interplay between Harmonic and Anharmonic Vibrations, ACS Energy Lett., 2023, 8, 3016–3024,  DOI:10.1021/acsenergylett.3c00881.
62. J. Du, Reverse Monte Carlo Studies of Inorganic Functional Materials Based on Neutron Scattering, PhD Dissertation, Queen Mary, University of London, 2018.
63. J. Du, A. E. Phillips, J. Liu, D. A. Keen, M. G. Tucker and M. T. Dove, In preparation.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta04586b

‡ It is to be regretted that we do not have data for more temperatures within the tetragonal phase, but this is the hazard of experiments at central-site facilities: you never quite know what measurements you need to perform in the limited time available for the experiment until after you have done the analysis.

§ A small configuration gives only a coarse sampling of wave vectors in reciprocal space, giving a larger relative weighting to the line of Rigid Unit Modes (RUMs) along the edges of the Brillouin zone – 12/64 wave vectors, whereas the weighting of a line to volume in an extended sample is close to zero – which means there is an exaggerated weighting to the amplitude of the RUMs; these are the phonons that primarily give rise to octahedral tilting.⁶⁰

¶ In many representations eqn (6) has prefactor D, where D = −E₀.

|| We need to stress that this is an effective potential, and it is not reasonable to treat the parameter D as a bond dissociation energy. It is also not reasonable to treat the force constant k as representing a pure bond-stretching force constant.

---