Incorporation of Fe³⁺ into MnO₂ birnessite for enhanced energy storage: impact on the structure and the charge storage mechanisms

Abstract

Birnessite δ-MnO₂, with its low cost, high theoretical capacity, and stable cycling performance in aqueous electrolytes, holds promise as an electrode material for high-power and cost-effective electrochemical energy storage devices. To address its poor electronic conductivity, we incorporated environmentally friendly iron into birnessite and conducted a comprehensive study on its influence on crystal structure, electrochemical reaction mechanisms, and energy storage performance. In this study, a series of birnessite samples with varying iron content (δ-Mn_1−xFe_xO₂ with 0 ≤ x ≤ 0.20) were synthesized using solid-state reactions, resulting in well-crystallized particles with micrometric platelet morphology. Through X-ray absorption and Mössbauer spectroscopies, we clearly demonstrated that Fe replaces Mn in the metal oxide layer, while X-ray diffraction revealed that iron content significantly affects interlayer site symmetry and the resulting polytype. The sample with the lowest iron content (δ-Mn_0.96Fe_0.04O₂) exhibits a monoclinic birnessite structure with an octahedral interlayer site (O-type phase), while increasing iron content leads to hexagonal symmetry with prismatic interlayer sites (P-type phase). Electrochemical investigations indicated that these prismatic sites facilitate the diffusion of partially hydrated alkaline ions and exhibit superior rate capabilities compared to the O-type phase. Furthermore, operando XAS revealed that Fe is electrochemically inactive and that the charge storage in birnessite-type phases in a 0.5 M K₂SO₄ electrolyte primarily relies on the redox reaction of Mn. Finally, we determined that P-type δ-Mn_0.87Fe_0.13O₂ achieved the best compromise between enhancing electrical conductivity and maintaining a maximum content of electrochemically active Mn cations.

---

Introduction

Similarly to EDL materials such as porous carbons, pseudocapacitive materials operating in aqueous electrolytes offer the advantages of fast charging and high safety during their charge and discharge cycles, which are two crucial characteristics desired for electrochemical energy storage devices.^1,2 Among the most promising pseudocapacitive materials, the birnessite δ-MnO₂ stands out due to its abundance, low cost, high theoretical capacity and stable cycling performance in aqueous electrolyte.^3–10 Moreover, its reaction mechanisms upon cycling in aqueous electrolytes (1 M K₂SO₄), subject of debate, was recently elucidated by Augustyn et al.¹¹ They demonstrated that birnessite 2D structure, with a large interlayer spacing resulting from the presence of nanoconfined structural water molecules, enables extremely fast and efficient intercalation of partially hydrated alkaline ions, leading to capacitive like electrochemical signature.

Nonetheless, the practical application of δ-MnO₂ phases is strongly hindered by their low electronic conductivity that negatively impacts the capacity at high rates.^12–15 To address this issue, various strategies have been explored in the literature. One of the most common approaches involves synthetizing hybrid compounds by combining MnO₂ with electronically conductive carbon material such as carbon nanotube,^16–18 carbon fiber,^19,20 graphene^21,22 or conductive polymer.^23,24 Another interesting approach to boost the electronic conductivity is the elaboration of composites-nanocomposites MnO₂/conductive metal²⁵ or MnO₂/transition metal oxides.^26,27 Although these approaches improve overall conductivity, the intrinsic electronic conductivity of the birnessite phase remains unchanged and the performance of composite electrode materials heavily relies on achieving a homogeneous distribution between the electronic conductive phase and MnO₂.²⁷ To overcome this issue, it is possible to incorporate heteroatom into birnessite to change its electronic structure and reduce its electronic band gap.^28–31 For instance, Liu et al. have demonstrated through first principle calculations that a partial substitution of Mn^3+/4+ by Fe³⁺ in the metal oxide layer reduces the electronic band gap from 1.03 eV to 0.62 eV (for 33 mol% of substitution) and enhances the specific capacity when compared to δ-MnO₂ at equivalent charging/discharging rates.³² However, some aspects related to Fe incorporation into δ-MnO₂ (Fe–MnO₂) still require clarification. The commonly used low-temperature synthesis, aiming at achieving nano-structuration, results in birnessite phases with poor crystallinity, limiting detailed structural investigations of the localization of Fe and its impact on the interlayer site (prismatic or octahedral). Furthermore, the reaction mechanisms in Fe–MnO₂ during cycling remain unknown due to the potential redox activity of both Fe and Mn elements.^32,33

Therefore, the objectives of this work are to investigate the impact of incorporating environmentally friendly iron into birnessite phases on the crystal structure, electrochemical reaction mechanisms, and performance. Well-crystallized birnessite-type phases with varying iron content were synthesized and a detailed study on the structure and iron local environment for each phase was performed using complementary techniques, including X-ray diffraction, Mössbauer, X-ray absorption and Raman spectroscopy. Operando X-ray absorption spectroscopy experiments were performed at both Mn and Fe edges to reveal the nature of the redox mechanisms upon cycling in neutral electrolyte. Finally, the rate capability, long-term stability and materials resistivity were correlated with the amount of iron and the nature of the alkaline site in the interlayer spacing.

Experimental part

Synthesis

The birnessite phase δ-MnO₂ was obtained through the thermal decomposition of potassium permanganate.³⁴ To achieve this, 1 g of KMnO₄ (Sigma Aldrich) was grounded in a mortar and then placed into an alumina boat. The powder was heated at 800 °C for 5 hours, with heating and cooling ramp rates of 5 °C min⁻¹. The resulting dark powder was washed multiple times with deionized water to remove the two impurity phases K₂MnO₄ and K₃MnO₄ which are soluble in water (forming a blue/green and then purple solution). The final sample was air-dried for two days at 50 °C and named δ-MnO₂. For the iron birnessite samples, 1 g of KMnO₄ was thoroughly mixed with Fe(NO₃)₃·9H₂O (Sigma Aldrich) in a mortar to achieve the molar ratio Mn_1−xFe_x of x = 0.04, 0.09, 0.13 and 0.20. The subsequent steps of the synthesis were the same as for δ-MnO₂. The iron birnessites were designated as δ-Mn_1−xFe_xO₂ where x corresponds to the amount of iron in the structure.

Powder X-ray diffraction

A Philips Panalytical X'Pert Pro diffractometer was used to record the XRD patterns with a copper source (K_α radiation: λ_Kα1 = 0.1540 nm and λ_Kα2 = 0.1544 nm). X-ray diffractograms were recorded for about 3 hours in the 10°–80° (2θ) angular range, with a 0.02° (2θ) step size and a 2.022° (2θ) active width in the detector.

Structural powder data analysis was performed using either a profile matching mode or the Rietveld refinement method, using the single crystal structure model within the JANA2006 crystallographic system.³⁵ The background was fitted with a Chebyshev polynomial function, and the peak shapes were described using a Pseudo-Voigt function. To achieve a stable crystal chemical model, certain parameters, such as Fe/Mn (since distinguishing Fe and Mn by XRD is challenging due to their close X-ray scattering form factors), were constrained during the final stages of the refinement process to align with other experimental methods utilized in this study (see Tables S2–S4† for further details).

Inductively coupled plasma – optical emission spectroscopy (ICP-OES)

The quantities of Mn, Fe and K elements were evaluated in our materials by chemical analyses using a Varian 720ES ICP-OES spectrometer. The samples were prepared by dissolving ∼10 mg of powder into a 37% solution of HCl. The solutions were heated until the total dissolution of powders. To obtain a concentration of the target element between 1 and 200 mg L⁻¹, the solutions were diluted through the addition of deionized water. The solution is then introduced in a nebulization chamber along with an argon flow to create an aerosol. Five measurements were realized for each sample for accuracy.

CHNS analysis

1.5 mg was weighted in a tin foil and burned at 920 °C under oxygen excess to quantify the % of hydrogen in the sample. The combustion products (H₂O) were detected and quantified by a Thermo Flash EA 111E Series apparatus. To control the accuracy two measurements are conducted.

Scanning electron microscopy

The scanning electron microscopy (SEM) images were taken using a TESCAN Vega microscope with a tungsten source at 15 kV accelerating voltage. The EDX analysis was carried out on a SEM Tescan Vega microscope (TESCAN, Czech Republic) equipped with the energy-dispersive spectrometer X-Act (Oxford Instruments, UK) and this revealed a homogeneous distribution of Fe within the samples.

⁵⁷Fe Mössbauer spectroscopy

⁵⁷Fe Mössbauer experiments were performed at room temperature (293 K) in transmission geometry with a constant acceleration Halder-type spectrometer equipped with a 1.85 GBq ⁵⁷Co radioactive source (embedded in a Rh matrix), which was maintained at 293 K. The velocity scale (in mm s⁻¹) was calibrated regarding the Mössbauer spectrum of a pure α-Fe⁰ thin foil. In order to avoid any saturation effects, the mass of sample powder was adjusted to prepare thin absorbers with about 5 mg cm⁻² of iron. The Mössbauer hyperfine parameters and the relative areas of each component were refined using the WinNormos software (Wissenschaftliche Elektronik GmbH).

X-ray absorption spectroscopy

Synchrotron XAS measurements were performed at manganese and iron K-edges in transmission mode at the ROCK beamline of the SOLEIL synchrotron (France). Reference samples available for Mn (MnO, Mn₃O₄, Mn₂O₃ and MnO₂) and Fe (Fe₂O₃ and Ferrihydrite) were measured to assign the oxidation states of Mn and Fe, respectively. The operando XAS spectra at Mn and Fe K-edges were recorded on the same electrode made of δ-Mn_0.80Fe_0.20O₂, carbon black (Alfa Aesar, 99.9+%), and polytetrafluoroethylene (PTFE, Sigma-Aldrich, 99.9%) as a binder, with a weight ratio of 80/15/5 and the mass loading of 2–4 mg cm⁻². The Si(111) channel-cut monochromator with an oscillation frequency of 2 Hz was used to select the incident energy, and the angle and oscillation range were optimized to cover the whole energy range from Mn to Fe K-edge. We have used a pellet made of a mixture of MnO₂ and Fe₂O₃ and placed between I1 and I2 to ensure the energy calibration versus a Mn and Fe foils. The quick-XAS spectra were averaged over 25 seconds to obtain a reasonable signal to noise ratio at both edges. We have used the in situ 3-electrodes electrochemical cell designed by IMN (Nantes) and described in Fig. S1.† (ref. 36) Electrochemical cycling was performed in 0.5 M K₂SO₄ electrolyte at 2 mV s⁻¹ and in the potential range −0.2 to 1 V vs. Ag/AgCl. The XAS analysis was performed using the Demeter software package.³⁷ For the extended X-ray absorption fine structure (EXAFS) analysis, Fourier transforms of the k2-weighted EXAFS oscillations for Mn and Fe K-edges were carried out in the k-ranges of 2.7 and 11.2 Å⁻¹ using a sine window. The partial radial distribution is not corrected by the phase shifts.

Electrode preparation

To evaluate the electrochemical performance of each sample, the birnessite was mixed with carbon black and polytetrafluoroethylene (PTFE) in a weight ratio of 80/15/5 for active material/carbon black/PTFE. The resulting mixture was then used to prepare the working electrode, which was pressed at 5 bars onto a stainless-steel substrate for one minute. The mass loading of each electrode was approximately 10 mg cm⁻². Measurements were performed in a 0.5 M K₂SO₄ solution using a 3-electrode configuration in a beaker cell at 25 °C. The reference electrode used was Ag/AgCl, while a platinum wire served as the counter electrode. Specific capacities were obtained from galvanostatic charge/discharge measurements by calculating the number of exchanged electron during the discharge. The ohmic drop observed at high current densities was not corrected for capacity calculation, only the discharge time was taken into account. Electrochemical impedance spectroscopy (EIS) measurements were conducted using electrodes that were pressed onto stainless steel current collectors, which were gold-coated via sputtering. This gold coating was applied to suppress or minimize the contact impedance between the current collector and the active material. The EIS measurements of the composites were performed at open circuit potentials in 0.5 M K₂SO₄. A perturbation of 5 mV was used for the measurements, and the frequency range was set from 10 kHz down to 10 mHz.

Results and discussion

General structural characterization

The high-temperature syntheses employed in this study allowed for the production of a series of well-crystallized compounds, which is crucial for investigating the influence of chemical composition (specifically iron vs. manganese content) on the crystal structure of the electrode materials. The powder XRD patterns (PXRD) of the obtained 5 materials are presented in Fig. 1a, revealing that the thermal treatment of KMnO₄ at 800 °C, with or without the presence of iron nitrate, consistently resulted in the formation of the birnessite-type phases, regardless of the Fe content in the precursors mixture.

Fig. 1 (a) Powder XRD patterns of the δ-Mn_1−xFe_xO₂ samples with 0% (black), 4% (red), 7% (blue), 13% (green), and 20% (purple) of Fe synthesized at 800 °C. The asterisks and small black triangles on (b) show the secondary phases – P2 and O′3 polytypes, respectively. See text for details.

The crystal structure of δ-MnO₂ (birnessite) is built up from weakly bound brucite-like slabs made of edge-shared MnO₆ octahedra oriented parallel to the ab plane and separated by alkaline cations and a single layer of water. For all the compounds, the intense (00l) reflection corresponding to a d-spacing of approximatively 7.1 Å (2θ ≈ 12.5°) is consistent with a single intralayer of water molecules characteristic of birnessite phase. The charge deficiency within the MnO₂ slabs resulting from the presence of vacancies and/or transition metals (Mn and Fe) in oxidation states lower than 4+ is compensated by K⁺ cations in the interlayer space, as KMnO₄ was utilized as the precursor.

ICP-OES studies were conducted to determine the elemental content of Fe, Mn and K in the prepared samples. The obtained weight percent (wt%) ratios, as summarized in Table S1,† provide justification for synthesizing manganese-based oxide materials with varying iron contents (x = 0, 0.04, 0.09, 0.13, and 0.20). Accordingly, each sample is referred to as δ-Mn_1−xFe_xO₂ and their chemical formulae are reported Table S1.†

A thorough analysis of the PXRD patterns (Fig. 1b) reveals that the different Fe content has the ability to modify the crystal structure of δ-Mn_1−xFe_xO₂. It leads to the crystallization of birnessite polytypes with distinct layer stackings of MnO₂ slabs, leading to significantly different X-ray diffraction patterns. This diversity of all possible polytypes was comprehensively and systematically described by Drits et al. (See ESI Part S1†).³⁸

The iron-free synthesized material, δ-Mn_1−xFe_xO₂ (x = 0), exhibits a hexagonal layer symmetry with a two-layer periodicity, and crystallizing in the hexagonal space group P6₃/mmc. As a starting model for Rietveld refinement, we used the birnessite structure reported in the work of Gaillot et al.³⁹ This material was also obtained through a thermal decomposition of KMnO₄ at 800 °C. Its structural feature involves the presence of interlayer Mn³⁺ cations positioned above or below vacancies in octahedral Mn⁴⁺O₂ slabs (Fig. 2a). The refined unit cell parameters and the results of the Rietveld refinement for our synthesized material are given in Table S2 and Fig. S2,† respectively. In its crystal structure, oxygen sites are stacked in a … = AB = BA = AB = … stacking manner along the c-axis, while potassium cations ions are accommodated at ‘prismatic’ sites between MnO₂ slabs. This material can be classified as a P2 (or 2H₁ in a mineralogical notation) polytype. A visible broadening and asymmetry of observed XRD peaks (Fig. 1, black) also indicate a turbostratic stacking, which suggests a slight random rotation of successive slabs along the c axis. This behavior is typical for water-containing layered compounds, where H₂O molecules acts as a ‘glue’ that holds parallel sheets together, allowing adjacent sheets to potentially shift and orient relative to one another.

Fig. 2 Crystal structures of δ-Mn_1−xFe_xO₂, x = 0 (a), 0.04 (b), and 0.09 (c).

The incorporation of x = 0.04 Fe into the structure of δ-MnO₂ results in significant structural changes. Fe³⁺ and Mn³⁺ cations migrate to the slabs and occupy the vacancies, leaving only potassium and water in the interlayer spacing. Appearance of M³⁺-centered octahedra of larger dimensions (Fe³⁺ ≈ Mn³⁺ > Mn⁴⁺) and the Jahn–Teller distortion typical for Mn³⁺, both decrease the symmetry of the Mn_0.96Fe_0.04O₂ slabs to orthogonal and the whole crystal structure is now described in the monoclinic space group C2/m. Isotypical Fe-free birnessite phase was used as starting model for the Rietveld refinement of δ-Mn_0.96Fe_0.04O₂.⁴⁰ The ratio of Mn³⁺ and Mn⁴⁺ species in the metal oxide layer can be deduced from the structural data by balancing the charge of the structural formula to the neutral value. Interestingly, the structure refinement results show a higher content of Mn³⁺ in our Fe-bearing sample (Mn³⁺/Mn⁴⁺ = 0.42) compared to the reported monoclinic birnessite (Mn³⁺/Mn⁴⁺ = 0.30). (Fig. S3 and Table S3†). This finding aligns well with the chemical analyses, which revealed a slightly higher amount of K⁺ for δ-Mn_0.96Fe_0.04O₂ to compensate the charge compared to the reported Fe-free δ-MnO₂. The analysis of oxygen stacking shows the …–AB–CA–BC–AB–… oxygen packing sequence with an octahedrally coordinated K site (Fig. 2b). As a result, the δ-Mn_0.96Fe_0.04O₂ slabs repeat in a period of three, and the structure belongs to O′3 (or 1M₂) polytype, where a prime superscript symbolizes the monoclinic distortion of the unit cell.

A careful analysis of the PXRD (Fig. 1b, red) reveals the presence of additional small peaks that cannot be indexed by the O′3 polytype alone. In order to identify their origin, a series of simulations of idealized birnessite varieties was performed using the FAULTS program.⁴¹ The comparison between the experimental data and the simulated patterns allowed us to distinguish and identify two distinct polytypes, as illustrated in Fig. S4.† The second observed phase can be described by another birnessite polytype, which crystallizes in the orthorhombic Ccmm space group. The birnessite structure from the work of Gaillot et al. was used as a starting model for the simulation.⁴² This particular crystalline structure is characterized by a simple … = AB = BA = … oxygen packing, with transition metal slabs mirrored to each other and K atoms occupying prismatic sites. It belongs to the P2 (or 2O₁) polytype. Once again, the presence of distorted Mn³⁺O₆ octahedra results in the orthogonal symmetry of the slabs for this composition. Due to minor amount of the polytype in the synthesized sample, it was not possible to perform a Rietveld refinement for the orthorhombic phase.

For all other compounds with higher iron content, a different transformation of the crystal structure occurs, resulting in the growth of another birnessite polytype. The crystal structure of these phases can be refined in the rhombohedral space group R3̄m (Fig. 2c). The results of the Rietveld refinement for the compound containing x = 0.09 of Fe are presented in Fig. S5 and Table S4.† The increased presence of regular Fe³⁺O₆ octahedra in slabs leads to the restoration of hexagonal symmetry. The crystal structure corresponds to the P3 (or 3R₁) polytype, which is equivalent to an … = AB = BC = CA = AB = … oxygen stacking sequence with a prismatic environment for potassium cations.

With an iron content of x = 0.20, additional small peaks can be observed on the PXRD pattern (Fig. 1, purple), which may likely belong to the monoclinic birnessite variety (O′3 polytype) previously identified for δ-Mn_1−xFe_xO₂, x = 0.04. A joint contribution of two phases with e.g. x = 0.04 and 0.20 of Fe cannot be excluded for this material. It should be noted that the presence of second phases has also been also reported by Ogata et al. for δ-MnO₂ with high content of substituted Ni (≥15%), Co (≥50%), and Al (≥25%).⁴³

To summarize this part, the incorporation of a small amount of Fe (δ-Mn_0.96Fe_0.04O₂) results in a main birnessite-type phase crystallizing with a monoclinic space group and an octahedral interlayered site, called O-type phase (Table 1). On the other hand, a higher iron content induces a phase with hexagonal symmetry of MnO₂ slabs and interlayer potassium prismatic sites, called P-type phases. This change of symmetry is also confirmed by Raman spectroscopy, as detailed in Fig. S6.†

Table 1 Crystallographic data for synthesized materials δ-Mn_1−xFe_xO₂. Rietveld data for x = 0, 0.04 and 0.09 compositions. Profile matching for the others

x	Sp. gr.	a, Å	b, Å β, °	c, Å	Vol. (A^3)	O stacking (polytype)
a Due to its minor content, we were unable to refine the unit cell parameters of the second phase.
0.00	P63/mmc	2.8582(7)	2.8582(7)	14.246(3)	100.79(4)	P2 (2H1)
0.04	C2/m	5.1459(15)	2.8499(8)	7.11713(9)	103.34(5)	O′3 (1M2)
			100.717(10)
0.09	R3̄m	2.8815(7)	2.8815(7)	21.354(5)	153.55(6)	P3 (3R1)
0.13	R3̄m	2.8871(3)	2.8871(3)	21.330(2)	153.98(3)	P3 (3R1)
0.20	R3̄m	2.8786(13)	2.8786(13)	20.965(9)	150.45(11)	P3 (3R1)
	C2/m^a					O′3 (1M2)

---

Scanning electron microscopy (SEM) analyses of the samples (Fig. 3) reveal that the morphology of iron free sample δ-MnO₂ and the x = 0.04 compounds (Fig. 3a and b) are characterized by a three-dimensional network of interconnected platelets, exhibiting large cavities of a few microns in size. The platelet in both compounds have similar sizes, with widths ranging from 1 to 5 μm and thickness between 300 and 600 nm. For samples with higher Fe content (Fig. 3c–e), a slight decrease in the platelets size is observed, and the objects appear more randomly dispersed. The platelet width decreases and appears to be centered around 1 μm. It is likely that the presence of iron during the synthesis process induces defects that inhibit particle growth. As the Fe content increases, the primary particle size becomes smaller (Fig. 3). Similar effects have been reported in the literature following the addition of iron.^32,44–47 Nevertheless, the particle size in this series of material remains significantly larger than the typical range of 5 to 100 nm observed for birnessites obtained through “chimie douce” methods.^27,48 Finally, EDX mappings performed on the series of samples confirmed the homogeneous distribution of Fe throughout the entire sample, as illustrated Fig. 3f for the δ-Mn_0.8Fe_0.2O₂ sample.

Fig. 3 SEM images of (a) δ-MnO₂, (b) δ-Mn_0.96Fe_0.04O₂, (c) δ-Mn_0.91Fe_0.09O₂, (d) δ-Mn_0.87Fe_0.13O₂, (e) δ-Mn_0.80Fe_0.20O₂ and (f) mapping of Fe element in δ-Mn_0.80Fe_0.20O₂ sample.

Investigation of Fe local environment

⁵⁷Fe Mössbauer spectroscopy was performed to get additional structural information, particularly regarding the local environment of Fe. The spectra for all samples are displayed in Fig. 4, while the refined parameters including the isomer shift (δ), quadrupole splitting (Δ), full width at half maximum (Γ), and relative area of each signal are reported in Table 2.

Fig. 4 ⁵⁷Fe Mössbauer spectra at room temperature (25 °C) of δ-Mn_1−xFe_xO₂, (a) x = 0.04, (b) x = 0.09, (c) x = 0.13 and (d) x = 0.20.

Table 2 Room temperature ⁵⁷Fe Mössbauer hyperfine parameters values (isomer shift δ, quadrupole splitting Δ, line width Γ and the relative area) of δ-Mn_1−xFe_xO₂, (a) x = 0.04, (b) x = 0.09, (c) x = 0.13 and (d) x = 0.20

Sample	Site	δ (mm s^−1)	Δ (mm s^−1)	Γ (mm s^−1)	Area (%)
δ-Mn0.96Fe0.04O2	QD1	0.35(1)	0.89(1)	0.29(1)	85(3)
	QD2	0.36(1)	1.44(3)	0.25(2)	15(3)
δ-Mn0.91Fe0.09O2	QD1	0.34(1)	0.89(1)	0.25(1)	100
δ-Mn0.87Fe0.13O2	QD1	0.34(1)	0.90(1)	0.26(1)	100
δ-Mn0.80Fe0.20O2	QD1	0.35(1)	0.89(1)	0.29(1)	100

---

For the material with the lowest iron content (δ-Mn_0.96Fe_0.04O₂), the Mössbauer spectrum can be described as the sum of two quadrupole doublets labeled QD1 and QD2 (shown in blue and in orange on the Fig. 4), with relative areas of 85% and 15%, respectively. Both signals exhibit similar isomeric shift values (0.35–0.36 mm s⁻¹) which are characteristic of six-fold coordinated high-spin Fe³⁺.⁴⁹ The significant difference in quadrupole splitting value between the two doublets (0.89 mm s⁻¹ for QD1 and 1.44 mm s⁻¹ for QD2) indicates two distinct Fe local environments. The larger Δ value for the QD2 doublet suggests a higher distortion of the Fe³⁺ site, while QD1 is associated with a more regular Fe³⁺ environment. The large QD2 quadrupole splitting value may also reflects some heterogeneity in the distribution of the first cationic neighbors of iron ions (Fe³⁺, Mn³⁺, Mn⁴⁺), which could be linked to the mixed O′3/P2 birnessite structure revealed by X-ray diffraction. Similar observations were reported in the work of Liu et al.⁵⁰ with the presence of two quadrupole doublets for Fe-doped birnessites. For birnessites with higher iron content (x ≥ 0.09), their Mössbauer spectrum can be fitted with a single component. The quadrupole doublet is then characterized by an isomeric shift at 0.34–0.35 mm s⁻¹ and a quadrupole splitting of 0.89–0.90 mm s⁻¹ similar to the QD1 hyperfine parameters observed for δ-Mn_0.96Fe_0.04O₂, and is also attributed to high spin Fe³⁺ in an octahedral site. The presence of a single doublet, compared to x = 0.04, shows a more homogeneous distribution of iron in the MnO₂ layer. Therefore, for all iron compounds within δ-Mn_1−xFe_xO₂ series, Mössbauer spectroscopy revealed the only presence of Fe³⁺ ions in octahedral sites.

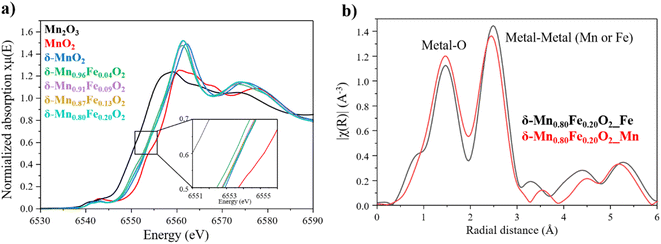
To further characterize the δ-Mn_1−xFe_xO₂ phases, X-ray absorption spectroscopy experiment were conducted at both Mn and Fe K-edge to obtain information about their valence state and local environment. The Mn K-edge XANES spectra of the birnessite series are represented on Fig. 5a and confirm a mean oxidation state of manganese between +3 and +4, which is expected for a birnessite phase. In the literature, the average manganese oxidation state in a birnessite can vary depending on the precursor used for the synthesis and the synthesis method, and typically varies between 3.5 and 3.7.⁵¹ In our series, the average oxidation state of Mn is identical for all the P-type phases (x = 0, 0.09, 0.13, 0.20) with a value of 3.67 (Fig. S7†). On the other hand, it slightly lowers for the O-type phase x = 0.04 and a Mn average oxidation state of 3.61 could be determined (Fig. S7†). This higher amount of Mn³⁺, resulting in a more pronounced Jahn–Teller effect, aligns with the monoclinic structure previously described for δ-Mn_0.96Fe_0.04O₂. Besides, the Fe K-edge XANES spectra validate the trivalent state of iron deduced from Mössbauer spectroscopy.

Fig. 5 (a) Mn K-edge XANES spectra for all the series. Mn₂O₃ and MnO₂ were used as reference to get the energy edge for Mn³⁺ and Mn⁴⁺ respectively. (b) FT-EXAFS spectra of δ-Mn_0.80Fe_0.20O₂ of the first iron (black) and manganese (red) neighbors.

Besides, Fourier transform of the EXAFS oscillations represents the radial distances from both Fe and Mn absorbing atoms in δ-Mn_0.80Fe_0.20O₂ (Fig. 5b). The first peak at ∼1.5 Å corresponds to the first coordination sphere of the transition metal (iron or manganese), specifically the metal–oxygen distance. The second peak at 2.5 Å represents the contribution of two different distances, the metal–metal and metal–oxygen distances. As shown in the Fig. 5b, the peaks at 1.5 and 2.5 Å obtained at both Mn and Fe K-edge overlap, indicating that iron is located within MnO₂ layer and has substituted manganese, which aligns perfectly with the X-ray structural determination.

Electrochemical properties

The impact of iron on the electrochemical properties was evaluated in 0.5 M K₂SO₄ by cyclic voltammetry, galvanostatic charge/discharge and electrochemical impedance spectroscopy.

At first glance, all Fe-based materials exhibit a similar electrochemical profile compared to δ-MnO_2. Their cyclic voltammogram (CV) is characterized by a rectangular shape typical of pseudocapacitive materials, along with a distinct and reversible redox peak. Notably, this latter appears to be more prominent for Fe-birnessites (Fig. 6a). The presence of this well-defined redox peak in our study is supposed to be related to the highly crystalline micrometric platelet morphology of the particles.²⁷ Indeed, Invernizzi et al. have observed a well-defined reversible redox peak only for highly crystalline birnessite when comparing the CV profiles of different birnessites.²⁷ In our series, the incorporation of iron into the manganese oxide layer, whatever the Fe content, seems to be beneficial to electrode material as it increases its specific capacity (Fig. 6a and b). It should be noticed that, in the work reported by Liu et al.,³² the electrochemical profiles of birnessites synthesized by a different soft chemistry route did not exhibit significant redox peaks whatever the iron content. This discrepancy may be related to the lower crystallinity and order of the latter materials.

Fig. 6 (a) Cyclic voltammetry of the synthetized birnessites at 5 mV s⁻¹ in 0.5 M K₂SO₄, (b) Discharge capacity retention at various current densities, (c) Nyquist plots obtained from EIS measurements at open circuit potential. (d) Capacity evolution of the series of birnessite materials upon long term cycling in 0.5 M K₂SO₄ at 3 A g⁻¹.

With further galvanostatic charge/discharge measurements, we determined that the P-type Fe-birnessite phases perform much better than δ-MnO₂ at high current densities, particularly δ-Mn_0.87Fe_0.13O₂, which delivers a capacity of approximatively 30 mA h g⁻¹ at 10 A g⁻¹versus only 3 mA h g⁻¹ for δ-MnO₂ (Fig. 6b and S8†). On the other hand, although the capacity at low rate of δ-Mn_0.96Fe_0.04O₂ (O-type phase) is higher than that of δ-MnO₂, it decreases to a similar value when the current density reaches 10 A g⁻¹. This clearly suggests that the site symmetry of the K⁺ ion strongly influences the rate capability, and similarly to layer oxide electrode material in Li-ion or Na-ion batteries, the prismatic interlayer site allows for faster diffusion of hydrated alkaline in birnessite interlayer spacing and should be favored for supercapacitor applications.⁵² Indeed, the face sharing prismatic sites provides a direct and facile ionic diffusion pathway from one P-site to another whereas the diffusion within the network of edge sharing octahedral sites implies to migrate through adjacent tetrahedral sites, which is less favorable (Fig. 7b).⁵³ This difference in conductivity is also supported by the experimental lower polarization between the redox peaks for δ-Mn_0.91Fe_0.09O₂, δ-Mn_0.87Fe_0.13O₂ and δ-Mn_0.80Fe_0.20O₂ (Fig. 6a and 7) compared to δ-Mn_0.96Fe_0.04O₂. Although δ-MnO₂ also exhibits a prismatic interlayer site, the presence on Mn in the interlayer spacing conjugated to the absence of Fe in the MO₂ layer may both hinder the alkaline diffusion and limits the electronic conductivity respectively, which therefore limits the energy storage performance.

Fig. 7 (a) Comparison of the potential difference between the maximum of oxidation and reduction peaks extracted from the CV performed at 5 mV s⁻¹ in 0.5 M K₂SO₄. (b) The direct alkaline diffusion path through face sharing prismatic site in P-type frameworks and indirect alkaline diffusion path with the intermediate tetrahedron site in O-type frameworks.

These results were further confirmed by EIS measurements that were performed at an open circuit and are displayed in the Nyquist plot of Fig. 6c. At high frequencies, the curves exhibit a semi-circle, indicative of a charge transfer mechanism, while at lower frequencies, the ionic diffusion within the sample can be estimated. From the Nyquist plots, it is evident that the incorporation of iron has a positive effect on the electrochemical properties. Regardless of the Fe content, the charge transfer resistance is reduced and mass transport is enhanced compared to δ-MnO₂. However, once again, the P-type Fe–MnO₂ demonstrates lower resistivity and better kinetics compared to the O-type phase, therefore confirming the previous findings.

The capacity retention under prolonged cycling was evaluated by galvanostatic charge discharge in 0.5 M K₂SO₄ at 3 A g⁻¹ (−0.2/1.0 V vs. Ag/AgCl) as shown in Fig. 6d. Upon 5000 cycles, the specific capacity of the P-type phases δ-MnO_2, remains rather stable. It slightly decreases for δ-Mn_0.87Fe_0.13O₂ and δ-Mn_0.91Fe_0.09O₂, (from 39 and 35 mA h g⁻¹ to 34.4 and 29 mA h g⁻¹ respectively), whereas it remains stable at 27 and 29.5 mA h g⁻¹ for δ-MnO₂ and δ-Mn_0.80Fe_0.20O₂ respectively. On the other hand, the specific capacity of δ-Mn_0.96Fe_0.04O₂ quickly drops of around 30% during the first thousand cycles, before reaching an evolution comparable to that observed for δ-Mn_0.91Fe_0.09O₂ and δ-Mn_0.87Fe_0.13O₂. (Fig. S9†). Finally, the obtained performances are very similar to those obtained in the literature by Liu et al.³² with a capacity of 30.5 mA h g⁻¹ after 6000 cycles at 5 A g⁻¹ in 1 M Na₂SO₄ (−0.1–0.9 V vs. SCE), comparable to this work with 34.4 mA h g⁻¹ for δ-Mn_0.87Fe_0.13O₂ with a similar mass loading (10 mg cm⁻²).³² This shows that Fe-birnessite micrometric particles performed as well as nanoparticles and comforts the charge storage driven by intercalation process versus capacitive one.

Finally, it was shown by Liu et al. through first principle calculations that the incorporation of Fe³⁺ into birnessite allows to lower the electronic band gap which enhances the conductivity of the material.³² This was confirmed by the electrical conductivity measurements carried out by the four-probe-method and shown as ESI (Fig. S10).† However, it remains unclear whether Fe is electrochemically active, or not, upon charge storage. To answer this question, we conducted operando X-ray absorption spectroscopy experiments on δ-Mn_0.80Fe_0.20O₂ (Fig. 7) to monitor the redox activity of the transition elements upon cycling.

The XAS spectra were acquired at both Mn and Fe K-edges during cycling in 0.5 M K₂SO₄ and at specific potentials indicated on the cyclic voltammetry curve (Fig. 8a). Firstly, it is observed that the energy position of the Fe K-edge XANES spectra remains unchanged during both charge and discharge, indicating that Fe remains in its trivalent state and is not electrochemically active (Fig. 8b). On the other hand, the reversible energy shift of ∼0.5 eV was observed in the Mn K-edge XANES spectra, clearly indicating continuous oxidation of Mn during charge and reduction during discharge (Fig. 8c). Using the energy calibration curve (Fig. S7†), the average oxidation state of Mn was determined to vary from 3.62 up to 3.74, reflecting the reversible exchange of 0.12 e⁻ during cycling between −0.2 and 1 V (vs. Ag/AgCl) at 2 mV s⁻¹. This finding is in perfect agreement with the capacity obtained from the CV curve (24.5 mA h g⁻¹) and highlights the fact that the charge storage primarily relies on the redox reaction of Mn.

Fig. 8 (a) Cyclic voltammetry at 2 mV s⁻¹ in 0.5 M K₂SO₄, (b) Fe K-edge XAS spectra at different potential (refer on the cyclic voltammetry), (c) Mn K-edge XAS spectra at different potentials and (d) change in shift energy as a function of the potential for δ-Mn_0.80Fe_0.20O₂.

Furthermore, Fig. 8d clearly shows a linear shift of the Mn K-edge with the potential, during charge and discharge, confirming the occurrence of redox reaction across the entire potential range and not solely limited to the redox peaks identified in the CV curves.

Conclusion

A comprehensive study was conducted to understand the impact of incorporating environmentally friendly iron into birnessite phases on the crystal structure, electrochemical reaction mechanisms, and performance. A series of birnessite samples with varying iron content (δ-Mn_1−xFe_xO₂ with 0 ≤ x ≤ 0.20) were synthesized by solid-state reaction, leading to well-crystallized particles with micrometric platelet morphology. We clearly demonstrated by X-ray absorption and Mössbauer spectroscopies that Fe substitutes Mn within the metal oxide layer and, by X-ray diffraction, that its content strongly impacts the interlayer site symmetry and the obtained polytype. For the sample with the lowest iron content (δ-Mn_0.96Fe_0.04O₂), a monoclinic birnessite with an octahedral interlayer site was obtained, while increasing iron content led to hexagonal symmetry of the metal oxide layer with prismatic interlayer sites. The electrochemical investigations suggest that these prismatic sites favor the diffusion of partially hydrated alkaline ions and therefore, P-type phases present better rate capabilities than the O-type one. In addition, Operando XAS have revealed that Fe did not exhibit electrochemical activity and that the charge storage of birnessite-type phases in 0.5 M K₂SO₄ electrolyte principally relies on the redox reaction of Mn. Finally, we determined that P-type δ-Mn_0.87Fe_0.13O₂ presented the best compromise between enhancing the electrical conductivity and keeping a maximum content of electrochemically active Mn cations.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors would like to thank AID as well as Bordeaux INP for financial support (PhD funding and research fees). The authors thank also Région Nouvelle Aquitaine and the French National Research Agency (STORE-EX Labex Project ANR-10-LABX-76-01) for financial support and fruitful discussions. This work was supported by a public grant overseen by the French National Research Agency (ANR) as part of the “Investissements d’Avenir” program (Reference: ANR-EQPX45). Many thanks to Catherine Denage, Emmanuel Petit, Eric Lebraud and Jérôme Kalisky for their help in the characterization of the samples for ICP, MEB, XRD and for technical support. The authors also thank Olivier Crosnier and Camille Douart from Institut des Matériaux Jean Rouxel de Nantes for sharing the Operando Cell.

References

1. T. Nguyen and M. F. de Montemor, Advanced Science, 2019, 1801797.
2. V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597.
3. S. Zhu, W. Huo, X. Liu and Y. Zhang, Nanoscale Adv., 2020, 2, 37–54.
4. Z.-H. Huang, Y. Song, D.-Y. Feng, Z. Sun, X. Sun and X.-X. Liu, ACS Nano, 2018, 12, 3557–3567.
5. M. Toupin, T. Brousse and D. Bélanger, Chem. Mater., 2004, 16, 3184–3190.
6. L. Niu, L. Yan, Z. Lu, Y. Gong, T. Chen, C. Li, X. Liu and S. Xu, J. Energy Chem., 2021, 56, 245–258.
7. Q.-Z. Zhang, D. Zhang, Z.-C. Miao, X.-L. Zhang and S.-L. Chou, Small, 2018, 14, 1702883.
8. S. Saeed, J. Fortunato, K. Ganeshan, A. C. T. Duin and V. Augustyn, ChemElectroChem, 2021, 8, 4371–4379.
9. W.-Y. Tsai, S. B. Pillai, K. Ganeshan, S. Saeed, Y. Gao, A. C. T. Van Duin, V. Augustyn and N. Balke, ACS Appl. Mater. Interfaces, 2023, 15, 26120–26127.
10. A. Lemoine, R. Invernizzi, G. Salvato Vallverdu, J. Olchowka, L. Guerlou-Demourgues, I. Baraille and D. Flahaut, ACS Appl. Energy Mater., 2022, 5, 12359–12372.
11. S. Boyd, K. Ganeshan, W.-Y. Tsai, T. Wu, S. Saeed, D. Jiang, N. Balke, A. C. T. van Duin and V. Augustyn, Nat. Mater., 2021, 20, 1689–1694.
12. C. Julien and A. Mauger, Nanomaterials, 2017, 7, 396.
13. M. Huang, F. Li, F. Dong, Y. X. Zhang and L. L. Zhang, J. Mater. Chem. A, 2015, 3, 21380–21423.
14. T. Brousse, P.-L. Taberna, O. Crosnier, R. Dugas, P. Guillemet, Y. Scudeller, Y. Zhou, F. Favier, D. Bélanger and P. Simon, J. Power Sources, 2007, 173, 633–641.
15. A. Boisset, L. Athouël, J. Jacquemin, P. Porion, T. Brousse and M. Anouti, J. Phys. Chem. C, 2013, 117, 7408–7422.
16. L. Li, Z. A. Hu, N. An, Y. Y. Yang, Z. M. Li and H. Y. Wu, J. Phys. Chem. C, 2014, 118, 22865–22872.
17. J.-W. Wang, Y. Chen and B.-Z. Chen, J. Alloys Compd., 2016, 688, 184–197.
18. E. Raymundo-Piñero, V. Khomenko, E. Frackowiak and F. Béguin, J. Electrochem. Soc., 2004, 152, A229.
19. Y. Luo, J. Jiang, W. Zhou, H. Yang, J. Luo, X. Qi, H. Zhang, D. Y. W. Yu, C. M. Li and T. Yu, J. Mater. Chem., 2012, 22, 8634.
20. Z. Lei, J. Zhang and X. S. Zhao, J. Mater. Chem., 2012, 22, 153–160.
21. M. Kim, Y. Hwang and J. Kim, J. Mater. Sci., 2013, 48, 7652–7663.
22. S. Chen, J. Zhu, X. Wu, Q. Han and X. Wang, ACS Nano, 2010, 4, 2822–2830.
23. G. A. Snook, P. Kao and A. S. Best, J. Power Sources, 2011, 196, 1–12.
24. M. P. Clark, W. Qu and D. G. Ivey, J. Appl. Electrochem., 2017, 47, 39–49.
25. J. Kang, A. Hirata, L. Kang, X. Zhang, Y. Hou, L. Chen, C. Li, T. Fujita, K. Akagi and M. Chen, Angew. Chem., Int. Ed., 2013, 52, 1664–1667.
26. C. Tang, D. Giaume, F. Weill, N. Penin, M.-A. Dourges, H. Saadaoui and L. Guerlou-Demourgues, ACS Appl. Energy Mater., 2019, 2, 7832–7842.
27. R. Invernizzi, A. Lemoine, L. Madec, F. Weill, M.-A. Dourges, C. Tang, D. Giaume, I. Baraille, P. L. Taberna, D. Flahaut, J. Olchowka and L. Guerlou-Demourgues, Nanoscale Adv., 2022, 4, 5089–5101.
28. S. Zhao, T. Liu, M. S. Javed, W. Zeng, S. Hussain, Y. Zhang and X. Peng, Electrochim. Acta, 2016, 191, 716–723.
29. J. Chen, Y. Liu, G. Wang, J. Guo and X. Wang, ACS Sustainable Chem. Eng., 2017, 5, 1594–1600.
30. Z. Hu, X. Xiao, C. Chen, T. Li, L. Huang, C. Zhang, J. Su, L. Miao, J. Jiang, Y. Zhang and J. Zhou, Nano Energy, 2015, 11, 226–234.
31. G. G. Yadav, J. W. Gallaway, D. E. Turney, M. Nyce, J. Huang, X. Wei and S. Banerjee, Nat. Commun., 2017, 8, 14424.
32. H. Liu, W. Gu, B. Luo, P. Fan, L. Liao, E. Tian, Y. Niu, J. Fu, Z. Wang, Y. Wu, G. Lv and L. Mei, Electrochim. Acta, 2018, 291, 31–40.
33. Q. Gao, J. Wang, B. Ke, J. Wang and Y. Li, Ceram. Int., 2018, 44, 18770–18775.
34. S. H. Kim, S. J. Kim and S. M. Oh, Chem. Mater., 1999, 11, 557–563.
35. V. Petříček, M. Dušek and L. Palatinus, Z. fur Krist. - Cryst. Mater., 2014, 229, 345–352.
36. N. Goubard-Bretesché, O. Crosnier, C. Douard, A. Iadecola, R. Retoux, C. Payen, M. Doublet, K. Kisu, E. Iwama, K. Naoi, F. Favier and T. Brousse, Small, 2020, 16, 2002855.
37. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
38. V. A. Drits, B. Lanson and A.-C. Gaillot, Am. Mineral., 2007, 92, 771–788.
39. A.-C. Gaillot, D. Flot, V. A. Drits, A. Manceau, M. Burghammer and B. Lanson, Chem. Mater., 2003, 15, 4666–4678.
40. A.-C. Gaillot, B. Lanson and V. A. Drits, Chem. Mater., 2005, 17, 2959–2975.
41. M. Casas-Cabanas, M. Reynaud, J. Rikarte, P. Horbach and J. Rodríguez-Carvajal, J. Appl. Crystallogr., 2016, 49, 2259–2269.
42. A.-C. Gaillot, V. A. Drits, A. Manceau and B. Lanson, Microporous Mesoporous Mater., 2007, 98, 267–282.
43. A. Ogata, S. Komaba, R. Baddour-Hadjean, J.-P. Pereira-Ramos and N. Kumagai, Electrochim. Acta, 2008, 53, 3084–3093.
44. H. Lu, W. Zhang, L. Tao, F. Liu and J. Zhang, Chemosphere, 2019, 226, 834–840.
45. H. Yin, F. Liu, X. Feng, T. Hu, L. Zheng, G. Qiu, L. K. Koopal and W. Tan, Geochim. Cosmochim. Acta, 2013, 117, 1–15.
46. W. Gu, G. Lv, L. Liao, C. Yang, H. Liu, I. Nebendahl and Z. Li, J. Hazard. Mater., 2017, 338, 428–436.
47. R. M. McKenzie, Mineral. mag., 1971, 38, 493–502.
48. R. Chen, P. Zavalij and M. S. Whittingham, Chem. Mater., 1996, 8, 1275–1280.
49. F. Menil, J. Phys. Chem. Solids, 1985, 46, 763–789.
50. H. Liu, L. Liao, G. Tippelt, W. Lottermoser and G. Amthauer, Phys. Chem. Miner., 2020, 47, 42.
51. V. A. Drits, E. Silvester, A. I. Gorshov and A. Manceau, Am. Mineral., 1997, 82, 946–961.
52. S. Guo, J. Yi, Y. Sun and H. Zhou, Energy Environ. Sci., 2016, 9, 2978–3006.
53. N. Yabuuchi and S. Komaba, Sci. Technol. Adv. Mater., 2014, 15, 043501.

---

Footnote

† Electronic supplementary information (ESI) available: Description of birnessite polymorphs, image of the operando cell, Rietveld refinements, Raman spectra of the δ-Mn_1−xFe_xO₂ series, calibration curve of Mn K-edge versus oxidation state, galvanostatic charges/discharges curves at different current densities, Table with suggested chemical composition and tables with refined lattice parameters. See DOI: https://doi.org/10.1039/d3ta04544g

---